Урок 39. задачи на встречное движение — Математика — 4 класс
Математика, 4 класс
Урок №39. Задачи на встречное движение
Перечень вопросов, рассматриваемых в теме:
— какие бывают направления движения?
— что такое скорость сближения?
— как узнать скорость сближения?
Глоссарий по теме:
Скорость сближения – расстояние, на которое сближаются движущиеся предметы в единицу времени.
Встречное движение – движение навстречу друг другу.
Основная и дополнительная литература по теме урока:
1. Моро М.И.,Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.6-8.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54.
Теоретический материал для самостоятельного изучения
Рассмотрим новый вид задач, задачи на встречное движение.
Найдите расстояние между городами. Это задача на встречное движение, потому что в ней речь идёт о двух транспортных средствах, которые движутся навстречу друг другу. При этом расстояние между ними сокращается.
После встречи автобус и автомобиль движутся в противоположных направлениях, удаляются друг от друга. Это уже другой вид движения и другой тип задач. Таким образом, существует встречное движение (навстречу друг другу) и движение в противоположных направлениях.
Сделаем чертёж к нашей задаче. На чертеже отрезком обозначают расстояние между городами. Его нужно найти. Записываем под отрезком вопросительный знак. Автобус и автомобиль движутся навстречу друг другу. Покажем это на чертеже стрелками.
В условии задачи даны скорости движения машин. Запишем их на чертеже. Место встречи машин отмечено флажком. Обрати внимание, что автомобиль двигался быстрее автобуса. Он проехал большее расстояние, чем автобус. Поэтому флажок на чертеже располагается ближе к тому месту, откуда выехал автобус. Время в пути автобуса и автомобиля одинаковое, 3 часа. Поэтому отрезки, обозначающие расстояние, пройденное до встречи каждым транспортным средством, поделим на три равные части. Каждая такая часть будет означать расстояние, пройденное за один час. Заметьте, части слева и справа от флажка получились разными, т.к. разными были скорости движения. Каждая часть слева от флажка обозначает 60 км в час. А каждая часть справа от флажка обозначает 90 км, которые проезжает за один час автомобиль.
Обрати внимание, что автомобиль двигался быстрее автобуса. Он проехал большее расстояние, чем автобус. Поэтому флажок на чертеже располагается ближе к тому месту, откуда выехал автобус. Время в пути автобуса и автомобиля одинаковое, 3 часа. Поэтому отрезки, обозначающие расстояние, пройденное до встречи каждым транспортным средством, поделим на три равные части. Каждая такая часть будет означать расстояние, пройденное за один час. Заметьте, части слева и справа от флажка получились разными, т.к. разными были скорости движения. Каждая часть слева от флажка обозначает 60 км в час. А каждая часть справа от флажка обозначает 90 км, которые проезжает за один час автомобиль.
Теперь приступим к решению задачи. Общее расстояние между городами складывается из расстояния, которое проехал автобус и расстояния, которое проехал автомобиль до их встречи. Каждое из этих расстояний находится умножением скорости на время. После этого полученные величины надо сложить. Мы ответили на вопрос задачи.
1) 60 ∙ 3 = 180 (км) – расстояние, которое проехал автобус.
2) 90 ∙ 3 = 270 (км) — расстояние, которое проехал автомобиль.
3) 180 + 270 = 450 (км) – расстояние между городами.
Ответ: расстояние между городами 450 км.
Эту задачу можно решить другим способом. Автобус и автомобиль начали движение одновременно. После первого часа пути автобус проехал 60 км, а автомобиль 90 км. Значит, за один час они сблизились на 150 км. По другому можно сказать, что скорость сближения машин равна 150 км в час. За следующий час пути автобус и автомобиль сблизились ещё на 150 км. За третий час они сблизились ещё на 150 км. И так, до встречи машины сближались три раза по 150 км, т.к. были в пути 3 часа. Значит, чтобы узнать расстояние между ними в самом начале пути, надо 150 умножить на 3. То есть, скорость сближения умножить на время движения до встречи.
1) 60 + 90 = 150 (км/ч) – скорость сближения.
2) 150 ∙ 3 = 450 (км)
Ответ: расстояние между городами 450 км.
Это второй способ решения задачи.
Расстояние, на которое сближаются движущиеся предметы в единицу времени, называют скоростью сближения.
Задания тренировочного модуля:
1. Вставьте в таблицу пропущенные данные.
Два лыжника вышли одновременно навстречу друг другу из двух посёлков и встретились через 3 часа. Первый лыжник шёл со скоростью 12 км/ч, второй – 14 км/ч. Найдите расстояние между посёлками.
Скорость | Время | Расстояние | |
Первый лыжник | ? | ||
Второй лыжник | ? |
Правильный ответ:
Скорость | Время | Расстояние | |
Первый лыжник | 12 км/ч | 3 ч | ? |
Второй лыжник | 14 км/ч | 3 ч | ? |
2. Распределите решения задач по группам. Перенесите их в соответствующие столбики.
Перенесите их в соответствующие столбики.
Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, второй – 14 км/ч. Через сколько часов лыжники встретились? | Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник? |
Варианты ответа:
(78 – 12 ∙ 3) : 3
78 : (12 + 14)
Правильный вариант:
Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, второй – 14 км/ч. Через сколько часов лыжники встретились? | Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. |
78 : (12 + 14) | (78 – 12· 3) : 3 |
3. Расположите величины по возрастанию.
От порта к бухте отправился катер. В то же время навстречу ему от бухты поплыла вёсельная лодка. Через 20 минут они одновременно проплыли мимо одного и того же пляжа.
Варианты ответа: Скорость катера; Скорость сближения катера и лодки; Скорость лодки.
Правильный вариант: Скорость лодки; Скорость катера; Скорость сближения катера и лодки.
Урок 35. задачи на движение — Математика — 5 класс
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние.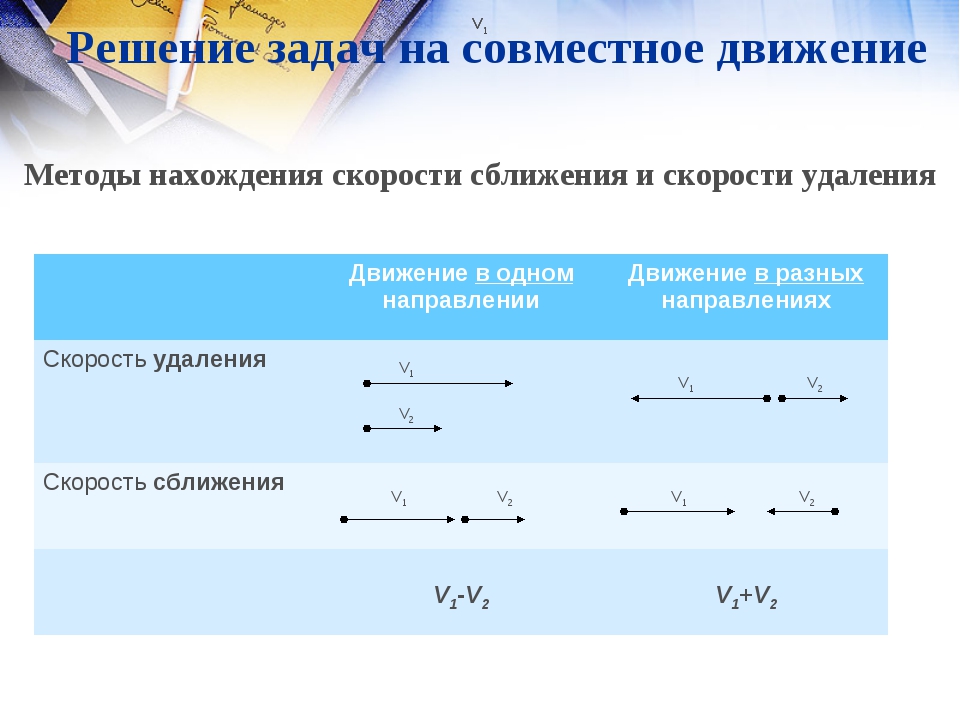
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние.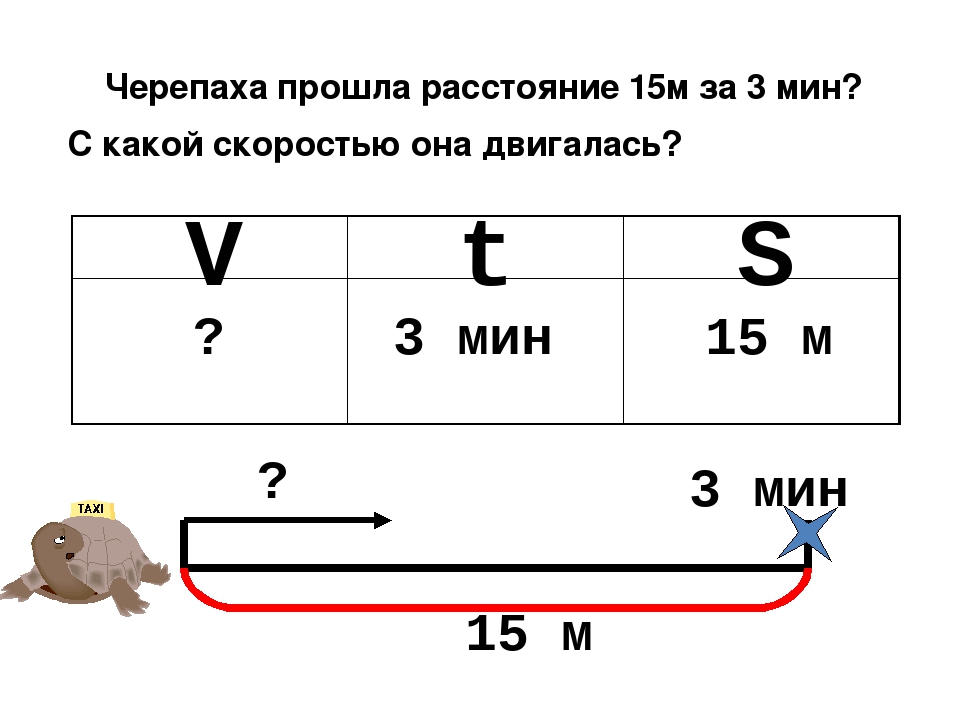 Время движения обозначается маленькой латинской буквой t.
Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
S | v | t | |
1. | 135 км | 9 км/ч | ____ ч |
2. | ____ м | 12 м/с | 4 с |
3. | 132 м | ____ м/мин | 11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
S | v | t | |
1. | 135 км | 9 км/ч | 15 часов |
2. | 48 м | 12 м/с | 4 с |
3. | 132 м | 12 м/мин | 11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе.
 Для этого:
Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
Задачи на движение в одном направлении: примеры и решение
Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч).
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
3) 160 : 20 = 8 (ч).
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч).
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
2) 5 : 1 = 5 (ч).
Ответ: Через 5 часов второй пешеход догонит первого.
Задача на скорость удаления
Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.
Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.
Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
80 — 40 = 40 (км/ч).
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
40 · 3 = 120 (км).
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
200 : 40 = 5 (ч).
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке: примеры и решение
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:
30 — 2 = 28 (км/ч) — скорость движения катера против течения.
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
112 : 28 = 4 (ч).
Решение задачи по действиям можно записать так:
1) 30 — 2 = 28 (км/ч) — скорость движения катера против течения,
2) 112 : 28 = 4 (ч).
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Рассмотрите два варианта:
1) лодка движется по течению реки;
2) лодка движется против течения реки.
Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:
27 + 3 = 30 (км/ч).
Значит расстояние между пунктами лодка преодолеет за:
120 : 30 = 4 (ч).
Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:
27 — 3 = 24 (км/ч).
Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:
120 : 24 = 5 (ч).
Решение задачи по действиям для движения по течению реки можно записать так:
1) 27 + 3 = 30 (км/ч) — скорость лодки,
2) 120 : 30 = 4 (ч).
Для движения против течения реки решение задачи по действиям можно записать так:
1) 27 — 3 = 24 (км/ч) — скорость лодки,
2) 120 : 24 = 5 (ч).
Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.
Как найти Время, Скорость и Расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой S.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: S = V * T |
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости Чтобы найти скорость, нужно разделить путь на время: V = S/T |
Показатели скорости чаще всего выражаются в м/сек; км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Единицами времени могут быть секунды, минуты, часы.
Формула времени Чтобы найти время, нужно разделить расстояние на скорость: T = S/V |
Эта формула пригодится, если нужно узнать за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 15 минут
s = v × t = 50 × 15 = 750
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.
Ответ: первый школьник добежал быстрее.
Если известна скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.
Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.
Задачи на движение 4 класс
Управление образования АДМИНИСТРАЦИИ Шатурского муниципального района
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ЛИЦЕЙ ГОРОДА ШАТУРЫ»
ШАТУРСКОГО МУНИЦИПАЛЬНОГО РАЙОНА
МОСКОВСКОЙ ОБЛАСТИ
Тема: Решение задач на движение
(в рамках Единого методического дня)
4 класс
Фураева Евгения Вячеславовна,
учитель начальных классов
г. Шатура, 2016
Тема | Решение задач на движение |
Цель | Учить решать задачи на движение |
Задачи | Образовательные: Сравнивать различные виды движения : вдогонку, навстречу друг другу, в противоположных направлениях, с отставанием. Отработать правила нахождения скорости сближения, удаления; зависимость между физическими величинами S, t и v (словесные формулировки) Воспитывать навыки работы в паре, группе. Воспитывать уважение к предмету, умение видеть математические задачи в окружающем мире. Развивать умение искать различные способы решения задач и выделять рациональные способы решения; развивать пространственное воображение обучающихся, образное мышление; |
Планируемые результаты | Учащиеся научатся решать задачи на движение, читать схематические чертежи к задачам, совершенствовать вычислительные навыки, работать в парах и группах, выполнять задания творческого и поискового характера. |
Тип урока | Систематизация и обобщение знаний |
Методы обучения | исследовательский частично-поисковый диалогический |
Методы преподавания | побуждающий словесный наглядный |
Оборудование | · опорные схемы; формулы. · распечатки тренажёра, теста. · компьютер, · мультимедийный проектор, экран, · презентация |
- Оргмомент. Слайд1.
— Много лет тому назад один античный мудрец сказал: «Не для школы, а для жизни мы учимся».
— В чём же заключалась его мудрость?
— А для чего вы учитесь?
— Для чего вы учите математику?
— Очень ли важен урок математики?
— Запишите число. Классная работа . Слайд2.
- Постановка учебной задачи.
— Чем мы будем заниматься на уроке, вы узнаете, если правильно отгадаете ребусы(скорость, время, расстояние)
— И ещё одна загадка.
Первое – предлог, второе – летний дом, а целое порой решается с трудом.
(За-дача)
— Определите тему и цель урока.
— Тема: Решение задач на движение. Слайд3
— Цель: научиться решать задачи на движение, совершенствовать вычислительные навыки.
-А девизом урока мы возьмём слова известного венгерского математика:
«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их» Д.Пойа Слайд 4
— План работы на уроке перед вами, познакомьтесь с ним.
- Актуализация знаний. Слайд 5 — 8
— Что такое движение? (перемещение в пространстве) Какие величины характеризуют движение?
Какие величины не используются в задачах на движение? (тонны, центнеры, м2, кг)
— По каким признакам можно разделить данные величины на группы?
( скорость, время, расстояние)
Дополните таблицу.
Слайд 9-10
– Вспомните, какие могут возникнуть ситуации в задачах на одновременное движение?
Ситуация 1. Два объекта начинают движение одновременно навстречу друг другу.
Ситуация 2. Два объекта начинают движение в противоположных направлениях.
Ситуация 3. Два объекта начинают одновременно движение в одном направлении.
- Устный счёт.
А пока, чтоб работать быстро и ловко,
Нам нужна ума тренировка!
— На участке дороги длиной 210км стоит знак ограничения скорости до 60 км/ч. Нарушил ли правила водитель, если это расстояние он преодолел за 3 часа? (Нарушил, т.к. скорость равнялась 70 км/ч) Почему?
— От Шатуры до Москвы 136 км. С какой скоростью едет водитель автомобиля, если его время в пути 2 часа?
— Расстояние от Шатуры до Рошаля 28км. За какое время доедет велосипедист, двигаясь со скоростью 14 км/ч? А за какое время пройдёт лыжник это расстояние, двигаясь со скоростью 7 км /ч?
На сколько км скорость велосипедиста больше? Во сколько раз скорость лыжника меньше?
— Легковая машина за 6 часов прошла 480 км, а грузовая за 4 часа прошла 160 км. Во сколько раз скорость легковой машины больше скорости грузовой машины?
— Какими рейсами нужно выехать на электричке, чтобы приехать в Москву не позднее 22 часов, если выехать из Шатуры после 18 часов? Выпиши в тетрадь номер рейса.
Расписание движения электропоездов Шатура- Москва Слайд 11
Номер рейса
| Время отправления из Шатуры
| Время прибытия в Москву |
11 | 17 ч 45 мин | 20 ч 00 мин |
12 | 18 ч 10 мин | 20 ч 25 мин |
13 | 19 ч 05 мин | 21 ч 30 мин |
14 | 20 ч 00 мин | 22 ч 15 мин |
15 | 20 ч 15 мин | 22 ч 35 мин |
- Блиц – турнир. Работа в парах.
Перед вами карточка из 9 квадратов, если вы согласны с утверждением ставите , если не согласны — .
- Скорость – это быстрая езда.
- Скорость – это расстояние, пройденное за единицу времени.
- Чтобы найти скорость, нужно расстояние умножить на время.
- Чтобы найти скорость, нужно расстояние разделить на время.
- При встречном движении расстояние между движущимися объектами уменьшается.
- Чтобы найти расстояние, нужно скорость умножить на время.
- При движении в противоположных направлениях расстояние между движущимися объектами уменьшается.
- Чтобы найти время нужно расстояние разделить на скорость.
- При движении в противоположных направлениях скорость сближения равна сумме скоростей.
Слайд 12
1 — | 4 | 7 — |
2 | 5 | 8 |
3 — | 6 | 9 |
|
|
|
- Физминутка для глаз.
- Закрепление знаний о связи скорости, времени и расстояния.
Работа с учебником на стр. 26, №82
-Прочитайте задачу.
-О какой тройке величин идёт речь? Что известно в задаче?
-Прочитайте вопрос задачи.
-Можем ли мы ответить на него сразу?
-Что нужно знать, чтобы ответить на вопрос задачи?
— С чего мы начнём решать задачу?
-Что узнаем потом?
-Что нужно сделать, чтобы ответить на главный вопрос задачи?
— Решите самостоятельно задачу.
1 способ:
1)85 60 = 145 (км/ч)
2)145 ∙ 3 = 435(км)
3) 846 — 435 = 411(км)
2 способ:
1)85 ∙ 3 = 255(км)
2)60 ∙ 3 = 180(км)
3)255 180 =435(км)
4) 846 — 435 = 411 (км)
Проверка (у доски)
- Работа в группах. Составление задач по схематическим чертежам.
— Можно ли самостоятельно составить задачу на движение? Как? Что для этого надо сделать?
( выбрать объекты движения, направление движения, место отправления, задать значение измерения величин, определить, что будет искомым)
— Подумайте, ребята, нужны ли нам умения решать задачи на движение?
— Зачем они нам необходимы? (чтобы не опаздывать на встречи, уметь спланировать время выхода, рассчитать скорость движения, чтобы не было аварий, и т.д.)
— Что общего и в чём различия этих задач?
ОБЩЕЕ: есть объекты движения, есть величины: скорость, время, расстояние
РАЗЛИЧИЯ: направление движения объектов, место отправления значения величин и единицы их измерения.
— Вспомните правила работы в группе.
— Теперь каждая группа получит схематический чертёж к задаче и карточки с частями задачи(условие, вопрос, решение и ответ). Вы должны будете соотнести со схемой, которая досталась вашей группе, части задачи: условие, вопрос, решение, ответ. А потом один из группы нам расскажет свой план рассуждения. Кто это будет, должна решить каждая группа.
1 группа
Из двух городов Шатуры и Клина, расстояние между которыми 240км одновременно навстречу друг другу выехали грузовик и велосипедист. Через сколько часов они встретятся, если скорость грузовика 60 км/ч, а скорость велосипедиста 20км/ч?
2 группа
Из посёлка Туголесский Бор одновременно в противоположном направлении друг от друга выехали два мотоциклиста. Один ехал со скоростью 62 км/ч, другой- 73 км/ч. Какое расстояние будет между ними через 2 часа?
3 группа
Из села Шарапово одновременно выехали велосипедист и мотоциклист в одном направлении. Велосипедист ехал со скоростью 15 км/ч, а скорость мотоциклиста 66 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
4 группа
Автомобиль, скорость которого 95 км/ч, догоняет автобус, движущийся по трассе Рязань-Шатура со скоростью 60 км/ч. Сейчас между ними расстояние 105 км. Через сколько времени автомобиль догонит автобус?
5 группа
От Шатуры и Егорьевска, расстояние между которыми 50 км, одновременно в разных направлениях отправились два мотоциклиста. Скорость одного 40км/ч, другого 52км/ч. Какое расстояние будет между ними через 3 часа?
9.Защита проектов решения задач.
- Рефлексия учебной деятельности. Слайд 13-14
— Итак, подведём итог урока.
— Какая тема была и какую цель ставили?
— Сколько типов задач на движение выделили?
— Какой из них для вас показался наиболее сложным?
— Оцените свою работу на уроке.
— На какую ступеньку на «лестнице успеха» вы себя бы поставили?
- Домашняя работа: подготовка к проекту: «Математика вокруг нас. Составляем сборник математических задач», стр. 40-41, учебник.
Приложение1.
План работы
- Оргмомент
- Тема и цель урока
- Устный счёт
- Блиц – турнир(работа в парах)
- Работа по учебнику
- Работа в группе
- Итог урока. Оцени себя
План работы
- Оргмомент
- Тема и цель урока
- Устный счёт
- Блиц – турнир(работа в парах)
- Работа по учебнику
- Работа в группе
- Итог урока. Оцени себя
План работы
- Оргмомент
- Тема и цель урока
- Устный счёт
- Блиц – турнир(работа в парах)
- Работа по учебнику
- Работа в группе
- Итог урока. Оцени себя
План работы
- Оргмомент
- Тема и цель урока
- Устный счёт
- Блиц – турнир(работа в парах)
- Работа по учебнику
- Работа в группе
- Итог урока.
Приложение 2.
Блиц – турнир (работа в парах)
Если вы согласны с утверждением, то ставьте , если не согласны,
то ставьте —
- Скорость – это быстрая езда.
- Скорость – это расстояние, пройденное за единицу времени.
- Чтобы найти скорость, нужно расстояние умножить на время.
- Чтобы найти скорость, нужно расстояние разделить на время.
- При встречном движении расстояние между движущимися объектами уменьшается.
- Чтобы найти расстояние, нужно скорость умножить на время.
- При движении в противоположных направлениях расстояние между движущимися объектами уменьшается.
- Чтобы найти время нужно расстояние разделить на скорость.
- При движении в противоположных направлениях скорость удаления равна сумме скоростей.
1
| 4
| 7 |
2
| 5
| 8 |
3
| 6
| 9 |
Приложение 3.
Дифференцированные карточки 4 класс
Задача 82, стр.26
1 способ:
1) … … = … (км/ч) – скорость сближения
2) … ∙ .. = …(км) – прошли два поезда
3) … — … = …(км)
2 способ:
1) 85 ∙ 3 = 255(км) – прошёл первый поезд
2) … ∙ … = …(км)
3) … … = …(км)
4) … — … = … (км)
Дифференцированные карточки 4 класс
Задача 82, стр.26
1 способ:
1) … … = … (км/ч) – скорость сближения
2) … ∙ .. = …(км) – прошли два поезда
3) … — … = …(км)
2 способ:
1) 85 ∙ 3 = 255(км) – прошёл первый поезд
2) … ∙ … = …(км)
3) … … = …(км)
4) … — … = … (км)
Дифференцированные карточки 4 класс
Задача 82, стр.26
1 способ:
1) … … = … (км/ч) – скорость сближения
2) … ∙ .. = …(км) – прошли два поезда
3) … — … = …(км)
2 способ:
1) 85 ∙ 3 = 255(км) – прошёл первый поезд
2) … ∙ … = …(км)
3) … … = …(км)
4) … — … = … (км)
Приложение 4.
Из двух городов Шатуры и Клина, расстояние между которыми 240км одновременно навстречу друг другу выехали грузовик и велосипедист.
Через сколько часов они встретятся, если скорость грузовика 60 км/ч, а скорость велосипедиста 20км/ч?
Решение:
1)60 20=80(км/ч) – скорость сближения
2)240:80=3(ч)
Ответ: через 3 часа встретится грузовик и велосипедист.
Из посёлка Туголесский Бор одновременно в противоположном направлении друг от друга выехали два мотоциклиста. Один ехал со скоростью 62 км/ч, другой- 73 км/ч.
Какое расстояние будет между двумя мотоциклистами через 2 часа?
Решение:
1)62 73=135(км/ч) – скорость удаления
2)135×2=270(км)
II способ
1)62× 2=124(км) – расстояние первого мотоциклиста
2)73×2=146(км) – расстояние второго мотоциклиста
3)124 146=270(км)
Ответ: 270 км будет между мотоциклистами через 2 часа
Из села Шарапово одновременно выехали велосипедист и мотоциклист в одном направлении. Велосипедист ехал со скоростью 15 км/ч, а скорость мотоциклиста 66 км/ч.
Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение:
1)66-15=51(км/ч) – разность скоростей
2)51×2=102(км)
II способ
1)15 × 2 = 30(км) – расстояние велосипедиста.
2)66 × 2 = 132(км) – расстояние мотоциклиста
3)132 — 30 = 102(км)
Ответ: 102 км будет между велосипедистом и мотоциклистом через 2 часа
Автомобиль, скорость которого 95 км/ч, догоняет автобус, движущийся по трассе Рязань-Шатура со скоростью 60 км/ч. Сейчас между ними расстояние 105 км.
Через сколько часов автомобиль догонит автобус?
Решение:
1)95-60=35(км/ч) – разность скоростей
2)105:35=3(ч)
Ответ: через 3 часа автомобиль догонит автобус.
От Шатуры и Егорьевска, расстояние между которыми 50 км, одновременно в разных направлениях отправились два мотоциклиста. Скорость одного 40км/ч, другого 52км/ч.
Какое расстояние будет между мотоциклистами через 3 часа?
Решение:
1)40 52=92(км/ч) – скорость удаления
2)92×3=276(км)- расстояние, пройденное за 3 часа
3)276 50=326(км)
II способ
1)40 × 3 = 120(км) – расстояние первого мотоциклиста
2)52 × 3 = 156(км) – расстояние второго мотоциклиста
3)120 156= 276(км) – расстояние, пройденное за 3 часа
4)276 50 =326(км)
Ответ: 326 км будет между мотоциклистами через 3 часа.
Самоанализ урока в 4-м классе:
Тема урока: «Решение задач на движение»
Урок проведён в соответствии с программой, согласно календарно-тематического планирования.
Цель урока: Образовательные:
Сравнивать различные виды движения : вдогонку, навстречу друг другу, в противоположных направлениях, с отставанием.
Отработать правила нахождения скорости сближения, удаления;
зависимость между физическими величинами S, t и v (словесные формулировки)
Воспитательные:
Воспитывать навыки работы в паре, группе.
Воспитывать уважение к предмету, умение видеть математические задачи в окружающем мире.
Развивающие:
Развивать умение искать различные способы решения задач и выделять рациональные способы решения;
развивать пространственное воображение обучающихся, образное мышление;
Тип урока: систематизация и обобщение знаний.
Считаю, что организация деятельности учащихся была адекватна поставленным задачам.
Этапы урока:
I.Организационный момент.
- Постановка учебной задачи.
- Актуализация знаний.
- Сообщение темы, цели урока.
- Устный счёт (решение задач на движение).
5.Блиц-турнир.(работа в парах)
- Физминутка.
II.Закрепление умения решать задачи на движение.
- Работа по учебнику. Самостоятельная работа.
- Работа в группах. Чтение схематического чертежа, моделирование задачи.
III. Подведение итогов урока, рефлексия, выставление оценок.
На уроке были применены следующие принципы обучения:
- Принцип научности заключался в том, что учащиеся для ответов использовали учебный материал, излагали материал, не упрощая лексики.
- Принцип доступности заключался в том, что всё, что прозвучало на уроке было изложено вполне понятно, на доступном детям языке
- Прослеживалась, межпредметная связь, в частности связь с уроками окружающего мира, краеведения, правил дорожного движения,
Для предупреждения утомляемости учащихся использовались физминутки, смена видов деятельности.
В процессе учебной деятельности были использованы словесные, наглядные, практические методы обучения в сочетании с индивидуальной, коллективной и фронтальной формой обучения.
Для самостоятельной работы слабым учащимся были предложен ы карточки с алгоритмом решения задачи, т. е. был осуществлён дифференцированный подход.
Применение информационно-компьютерных технологий, способствовали воспитанию интереса к занятиям математикой
На подведении итога урока использован элемент самопознания, где дети сами оценили свои способности.
Урок прошёл по намеченному плану, поставленные цели и задачи реализованы.
Автор:
Фураева Е. В.
Задачи на движение по реке
Тема: Задачи на движение по реке.
Цели:
- обобщить и систематизировать знания по теме «Задачи на движение по реке»;
- проверить знание теоретического материала, умение решать задачи арифметическим способом;
- развивать кругозор, мышление, внимание, культуру математической речи;
- прививать интерес к математике.
Методы обучения: частично-поисковый (эвристический), системные обобщения, самопроверка, взаимопроверка.
Формы организации урока: фронтальная, индивидуальная.
Оборудование: презентация к уроку, листы учета знаний.
ХОД УРОКА
I. Организационный момент
Сообщить учащимся цели урока. Настроить ребят на активную работу.
II. Проверка домашнего задания
№ 391(а).
Собственная скорость теплохода 27км/ч, скорость течения реки 3 км/ч. Сколько времени затратит теплоход на путь по течению реки между двумя причалами, если расстояние между ними 120 км?
Решение:
1) Vпо теч.= Vсоб.+ Vтеч. = 27 + 3 = 30 (км/ч).
2) tпо теч.= S : Vпо теч.= 120 : 30 = 4 (ч.)
Ответ: 4 часа.
№ 392.
Катер, имеющий собственную скорость 15 км/ч, проплыл 2 часа по течению реки и 3часа против течения. Какое расстояние проплыл катер за все время, если скорость течения реки 2 км/ч?
Решение:
1) Vпо теч.= Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
2) Vпр. теч.= Vсоб. – Vтеч.= 15 – 2 = 13 (км/ч.)
3) Sпо теч.= Vпо теч. · tпо теч. = 17 · 2 = 34 (км)
4) Sпр теч.= Vпр. теч.· t пр. теч.=13 · 3 = 39 (км)
5) S=Sпо теч.+ Sпр. теч. = 34 + 39 = 73 (км)
Ответ: 73 км
III. Актуализация знаний
(Фронтальная работа)
Вопросы: (устно или с использованием проектора.)
1. Что такое собственная скорость катера? Ответ: скорость катера в стоячей воде (озере, пруду).
2. Что такое скорость течения? Ответ: на какое расстояние относит река предмет за единицу времени.
3. Как определяется скорость катера по течению реки? Ответ: как сумма скорости собственной и течения.
4. Как определяется скорость катера против течения? Ответ: как разность скорости собственной и течения.
5. Как определяется скорость движения плота по реке? Ответ: как скорость течения реки.
Подведем итог:
Vпо течению – сумма V течения и V собственной.
V против течения – разность Vсобственной и Vтечения.
Значит, зная Vпо течению и Vпротив течения, можно найти Vтечения и Vсобственной.
Вспомним задачу на нахождение двух чисел по их сумме и разности.
1) (V по теч. – V пр. теч.) : 2 = Vтеч.
2) Vпо теч. – Vтеч. = Vсоб.
IV. Решение задач
№ 1.
Из четырех скоростей (Vсоб.,Vпо теч.,Vпр. теч.,Vтеч. ) две заданы и изображены отрезком. Вычислите две другие скорости и изобразите их отрезками:
№ 2. Заполним таблицу.
Vсоб, км/ч | V теч, км/ч | Vпо теч, км/ч | Vпр. теч, км/ч |
15 | 3 | ? | ? |
16 | ? | 18 | ? |
13 | ? | ? | 10 |
? | 2 | 11 | ? |
? | 3 | ? | 15 |
? | ? | 28 | 24 |
№ 3
Решим задачу № 393 (а).
Расстояние между двумя причалами 24 км. Сколько времени потратит моторная лодка на путь от одного причала до другого и обратно, если собственная скорость моторной лодки 10 км/ч, а скорость течения 2 км/ч?
Решение:
1) Vпо теч.= Vтеч.+ Vсоб.= 2 + 10 = 12 (км/ч)
2) Vпр. теч. = Vсоб. – Vтеч.= 10 – 2 = 8 (км/ч)
3) tпо теч.= S : Vпо теч.= 24 : 12 = 2 (ч)
4) tпр. теч.= S : Vпр. теч.= 24 : 8 = 3 (ч)
5) t = tпо теч. + tпр. теч.= 2 + 3 = 5 (ч)
Ответ: 5 часов.
V. Самостоятельная работа
I вариант | II вариант | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Скорость моторной лодки в стоячей воде 15км/ч, а скорость течения реки 3 км/ч. Сколько времени потратит моторная лодка на путь от одной пристани до другой и обратно, если расстояние между пристанями 36 км? 2)
| 1) Скорость моторной лодки в стоячей воде 10 км/ч, а скорость течения реки 2 км/ч. Сколько времени потратит моторная лодка на движение от одной пристани до другой и обратно, если расстояние между пристанями 24 км? 2)
|
VI. Подведение итогов урока
Заполнить карточку самоанализа.
Объявление оценок за урок.
Скорость обработки — когнитивные навыки
Что такое скорость обработки?
Скорость обработки — один из основных элементов когнитивного процесса, поэтому он является одним из наиболее важных навыков в обучении, академической успеваемости, интеллектуальном развитии, рассуждении и опыте.
Скорость обработки — это когнитивная способность, которую можно определить как время, необходимое человеку для выполнения умственной задачи . Это связано с скоростью, с которой человек может понимать и реагировать на информацию, которую он получает , будь то визуальная (буквы и цифры), слуховая (язык) или движение.Другими словами, скорость обработки — это время между получением стимула и ответом на него.
Медленная или низкая скорость обработки не связана с интеллектом, что означает, что одно не обязательно предсказывает другое. Низкая скорость обработки означает, что некоторые определенные задачи будут более сложными, чем другие, например чтение, выполнение математических расчетов, прослушивание и создание заметок или поддержание разговоров. Это также может мешать исполнительным функциям, поскольку человеку с низкой скоростью обработки данных будет сложнее планировать, ставить цели, принимать решения, начинать задачи, уделять внимание и т. Д.
Скорость обработки подразумевает большую способность легко выполнять простые или ранее изученные задачи. Это относится к способности автоматически обрабатывать информацию, то есть обрабатывать информацию быстро и без осознания. Чем выше скорость обработки, тем эффективнее вы можете думать и учиться. .
Скорость обработки — это время, которое проходит с момента получения информации до того момента, когда вы ее поймете и не начнете отвечать.
Примеры скорости когнитивной обработки
Скорость обработки может использоваться в упражнениях при распознавании простых визуальных образов, задачах визуального исследования, выполнении тестов, требующих принятия простых решений, выполнении основных математических вычислений, манипулировании числами или выполнении задачи рассуждения под давлением.
Вот некоторые примеры, которые могут быть идентифицированы с низкой скоростью обработки: Вам нужен час, чтобы выполнить задание, которое другим занимает всего 30 минут? Вам сложно следовать инструкциям или планировать конкретное мероприятие, особенно когда у вас нет времени на его выполнение? Вы плохо сдаетесь на экзаменах, даже зная материал?
Нарушения и патологии, связанные с низкой скоростью обработки данных
Низкая скорость обработки данных структурно не является проблемой обучения или внимания и не связана с интеллектом, хотя она влияет на каждую стадию обучения .Когда мы говорим о медленной скорости обработки данных, мы должны иметь в виду, что это может способствовать некоторым нарушениям обучения, таким как СДВГ, дислексия, дискалькулия или нарушение обработки слуховой информации.
Это может повлиять на такие задачи, как планирование целей, решение проблем и настойчивость в достижении личных целей.
Скорость обработки также связана с расстройствами аутистического спектра, и другие патологии, такие как деменция или шизофрения, также могут вызывать медленную скорость обработки.
Как определить дефицит скорости когнитивной обработки?
CogniFit может точно измерить общий когнитивный уровень пользователя с помощью нашей специализированной батареи когнитивных оценок (CAB), которая состоит из серии когнитивных тестов , предназначенных для оценки скорости обработки данных .
Чтобы оценить скорость обработки, мы используем тест для измерения скорости обработки , который основан на классическом тесте Коннерса (CPT) и тесте прямых и косвенных цифр из шкалы памяти Вешлера (WMS) .
Тест скорости обработки был разработан для автоматической оценки скорости обработки. Предполагается, что чем выше скорость обработки, тем эффективнее они будут изучать новую информацию. Этот процесс состоит из получения информации, ее понимания и генерации ответа.Если результаты недостаточны в этой области, то это существенно повлияет на способность принимать решения, исполнительные функции и выполнение инструкций .
Помимо скорости обработки, эти задачи также выполняют исчерпывающий анализ других когнитивных способностей, которые тесно связаны со скоростью обработки, таких как рабочая память и кратковременная зрительная память.
Можно ли улучшить скорость когнитивной обработки?
Определенно. Как и с любой другой когнитивной способностью, можно тренировать, обучать и улучшать скорость обработки данных, и CogniFit может вам в этом помочь.. Основа повышения скорости обработки — разработка метакогнитивных стратегий.
Ключ к повышению скорости обработки основан на создании более прочных связей в мозгу, что позволяет сигналам быстрее перемещаться друг к другу. Хотя большинство этих типов связей создается в детстве, с некоторой практикой и обучением вы можете поддерживать и даже улучшать скорость обработки информации в своем мозгу.
Благодаря пластичности мозга мозг может изменять свою структуру и функции.Пластичность мозга позволяет нам создавать новые мозговые связи и увеличивать количество нейронных цепей, улучшая функциональность.
Если нейробиология и изучение пластичности мозга что-то нам показали, так это то, что чем больше нейронных цепей мы используем, тем сильнее они станут , что применимо к скорости обработки.
CogniFit поможет вам выполнить полную нейрокогнитивную оценку, в ходе которой мы оценим вашу скорость обработки и на основе ваших результатов предоставим вам полный набор персонализированных когнитивных упражнений для повышения скорости вашей когнитивной обработки.
Когнитивная нейропсихологическая оценка и Программа стимуляции от CogniFit была разработана командой неврологов и когнитивных психологов, изучающих процессы синаптической пластичности и нейрогенеза. Вам нужно всего 15 минут в день 2-3 раза в неделю, чтобы стимулировать свои познавательные способности и когнитивные процессы .
Эта программа доступна в Интернете. Различные интерактивные упражнения представлены в виде забавных игр для мозга, которые вы можете практиковать на своем компьютере или планшете. После каждой тренировки CogniFit будет предоставлять вам подробный график с вашими успехами.
Доказано, что онлайн-упражнения CogniFit помогают в создании новых синапсов и нейронных цепей, которые позволяют реорганизовать и восстановить функции наиболее разрушенных когнитивных областей.
игр и действий, повышающих скорость обработки данных
Скорость обработки описывает, насколько эффективно ребенок может выполнять познавательную задачу. Он учитывает скорость, с которой ребенок воспринимает информацию, обрабатывает ее, а затем действует в соответствии с ней. Ребенок может испытывать трудности с одним или несколькими из этих аспектов обработки, и, поскольку разные дети обладают разными способностями в разных областях, существуют разные профили скорости обработки.Например, ребенок с низкой скоростью обработки письменных заданий может медленно видеть, что ему нужно скопировать, определять, как это делать, или медленно переносит эту информацию на бумагу.
Скорость обработки также влияет на способность быстро и автоматически выполнять познавательные задачи, особенно когда ребенок вынужден сохранять концентрацию, внимание и концентрацию. Скорость обработки информации тесно связана с успеваемостью в чтении и математике и может зависеть от нарушений управляющих функций.Недостаточная скорость обработки рутинной информации затрудняет понимание новой информации и требует много времени. Дети с низкой скоростью обработки информации часто испытывают трудности с выполнением работы, ведением заметок и эффективностью чтения и письма.
Домашние и школьные ситуации, требующие скорости обработки
- Выполнение работ в сжатые сроки.
- Понимание, мышление, реакция, движение, принятие решений и быстрое поведение (ответы на вопросы в классе, занятия спортом).
- Эффективное и эффективное выполнение заданий, работы и письма.
- Основные арифметические операции.
- Чтение.
Хотя исследования по повышению скорости обработки все еще немногочисленны, есть много многообещающих способов добиться скромных результатов. Большинство стратегий, которые были продемонстрированы для повышения скорости обработки, включают повторение и практику, так что определенные действия и воспоминания становятся автоматическими. Такой подход требует настойчивости и готовности к практике.С нашей точки зрения в LearningWorks for Kids, лучший способ заставить детей оставаться внимательными и заинтересованными — это использовать игры и технологии. Вот наши рекомендации по играм и занятиям, которые улучшают скорость обработки.
Игры и действия, которые могут повысить скорость обработкиDance Central Spotlight , Guitar Hero и Rock Band — Эти игры требуют от детей мысленно записывать то, что они видят на экране телевизора, обрабатывать эту информацию , и переводят это в свои собственные движения.Это требует физической координации и навыков быстрой обработки для быстрой реакции.
Такая игра, как Dance Central Spotlight, требует быстрой реакции и физической координации.
Boggle и Uno — Настольная и онлайн-версии этих игр стимулируют ум и отлично подходят для повышения скорости обработки информации в ограниченное время. Uno доступна в виде игры «Играть сейчас» прямо здесь, на нашем веб-сайте.
Big Brain Academy — Это игра Nintendo, которая включает в себя ряд логических головоломок, требующих внимания и концентрации.
Присоединитесь к спортивной команде или научитесь играть на музыкальном инструменте. — Эти занятия дают вашему ребенку возможность тренировать быструю зрительно-моторную координацию.
Кроссворды, Судоку , Кубик Рубика, шахматы, головоломки — Базовые упражнения на запоминание и логические головоломки позволят вашему ребенку остро реагировать и быстро обрабатывать информацию.Word Dynamo предлагает кроссворды и другие словесные игры для школьников и игроков студенческого возраста. Или попробуйте сыграть в онлайн-игру, например, Social Chess , против вашего ребенка — это хороший способ дать ему немного соревнования в менее напряженной обстановке.
Игры для тренировки мозга — Существует множество веб-сайтов, на которых дети могут участвовать в играх, предназначенных для повышения скорости обработки данных. У нас есть много игр, в которые можно играть прямо сейчас на нашем веб-сайте. Другие веб-сайты, предлагающие такие игры для тренировки мозга, включают: BrainConnection.com, Luminosity.com, HappyNeuron.com, MindHabits.com, FunBrain.com и WikiHow.com
границ | Тенденции развития визуальной обработки букв и предметов с помощью задач по скорости именования
Введение
Чтение — важнейший навык для общей траектории развития ребенка (Norton and Wolf, 2012). Чтобы лучше понять развитие этого сложного навыка, важно изучить типичное развитие когнитивной, визуальной и артикуляционной обработки, лежащей в основе чтения.Эти ключевые процессы компонентов можно изучить с помощью тестов скорости именования (NS), скорости и точности, с которыми люди могут называть знакомые буквенно-цифровые стимулы, такие как буквы или цифры, или не буквенно-цифровые стимулы, такие как предметы или цвета, представленные в виде визуальный массив (Wolf and Bowers, 1999). Эта простая парадигма является ценным инструментом для изучения многих из многочисленных когнитивных, артикуляционных и глазодвигательных процессов, задействованных при чтении, а также эффективности лежащих в основе механизмов синхронизации, которые их связывают (см. Wolf et al., 2000; Каттинг и Денкла, 2001; Al Dahhan et al., 2016, в печати). В ходе разработки было обнаружено, что NS является сильным предиктором способности к чтению (Kirby et al., 2003; Arnell et al., 2009), причем предсказательная сила буквенно-цифровых NS выше, чем у не буквенно-цифровых NS (Wolf et al., al., 1986; Cronin, Carver, 1998; Compton, 2003; Bowey et al., 2005; Araújo et al., 2015). Хотя большинство исследований NS сосредоточено на буквенно-цифровых NS, особенно на буквенных NS, неалфавитно-цифровые NS-задачи остаются полезным инструментом для маленьких детей, которые еще не освоили буквы и цифры (Kirby et al., 2003; Lervåg and Hulme, 2009).
Два ключевых когнитивных процесса, общих для чтения и NS, — это фонологическая обработка и орфографическая обработка. Однако существуют разногласия относительно того, какой из этих процессов вносит больший вклад в NS, формируя основную часть когнитивной обработки, которая лежит в основе NS. В то время как одна теория предполагает, что NS отражает автоматичность фонологической обработки (Torgesen et al., 1994, 1997), вторая предполагает, что NS вместо этого указывает на автоматичность распознавания визуальных символов и орфографической обработки (Bowers and Wolf, 1993; Бауэрс, 1995).Чтобы проверить эти две гипотезы, можно манипулировать стимулами NS-задач для увеличения их фонологического и / или орфографического сходства (Compton, 2003). Если выполнение NS зависит в первую очередь от фонологической обработки, увеличение фонологической сложности задачи NS за счет выбора стимулов, названия которых рифмуются друг с другом, должно ухудшить выполнение задачи. Однако, если NS полагается в первую очередь на орфографическую обработку, увеличение сложности орфографии за счет выбора визуально похожих друг на друга стимулов должно ухудшить производительность.Основываясь на этих предположениях, буквенные задачи NS ранее использовались для определения орфографической обработки как основного когнитивного процесса, лежащего в основе выполнения задач NS как у взрослых, так и у маленьких детей (Al Dahhan et al., 2014, 2017).
В дополнение к измерению скорости и точности наименования, понимание конкретных артикуляционных и глазодвигательных механизмов, лежащих в основе NS, может быть получено путем изучения артикуляции участников и движений глаз (Hyona and Olson, 1995; Rayner, 1997; Georgiou et al., 2006, 2008; Кирби и др., 2010). Время называния можно разделить на время артикуляции, время, затрачиваемое на произнесение названий стимулов, и время паузы, время между двумя последовательными артикуляциями (Hulme et al., 1999; Neuhaus et al., 2001; Georgiou et al., 2006, 2008) . Движения глаз можно анализировать для измерения продолжительности фиксации на стимулах, количества передних и обратных саккад, называемых регрессиями (Rayner, 1997). Отрицательная корреляция была обнаружена между эффективностью NS, относящейся к количеству элементов, правильно названных в секунду, и этими различными артикуляционными компонентами и показателями движения глаз (Al Dahhan et al., 2017), указывая на то, что более короткое время паузы и артикуляции, более короткие фиксации и меньшее количество саккад и регрессии являются маркерами улучшения выполнения задачи. Из этих конструкций время паузы и продолжительность фиксации были особенно важны для прогнозирования эффективности NS (Al Dahhan et al., 2017).
Эффективность выполнения заданий NS также может быть изучена путем анализа диапазона глаз-голоса участников (EVS), который описывает, насколько глаза опережают голос во время устного чтения (Buswell, 1922), тем самым обеспечивая понимание координации между движениями глаз. и сочленения.EVS можно рассчитать как в пространственной, так и во временной области. Пространственный EVS относится к количеству элементов между фиксированным в данный момент элементом и артикулируемым в данный момент элементом (Buswell, 1922). Предполагается, что пространственный EVS связан с обновлением фонологического цикла хранилища рабочей памяти, поскольку визуальный ввод, который был переведен в фонологический код, сохраняется в рабочей памяти до тех пор, пока его нельзя сформулировать (Baddeley and Hitch, 1974; Laubrock). и Kliegl, 2015). Было показано, что пространственный EVS дольше справляется с задачами NS для типичных читателей по сравнению с читателями с дислексией (Pan et al., 2013), поскольку последняя группа может бороться с преобразованием графемы в фонемы, что замедляет обновление буфера рабочей памяти.
Напротив, темпоральный EVS , также называемый латентностью именования, относится к времени между первой фиксацией на предмете и началом артикуляции этого предмета (Inhoff et al., 2011). Temporal EVS обеспечивает меру эффективности всех этапов когнитивной обработки и артикуляционного планирования, необходимых для идентификации и подготовки к артикуляции названия стимула (Jones et al., 2013). Соответственно, у читателей с дислексией было обнаружено более длительное время EVS, чем у типичных читателей (Jones et al., 2013), что указывает на то, что общая эффективность когнитивной и артикуляционной обработки информации снижается у читателей с дислексией. Таким образом, изучение тенденций развития как пространственного, так и временного EVS может дать ключевое представление о том, как процессы, необходимые для обновления буфера рабочей памяти и общей скорости когнитивной и артикуляционной обработки, соответственно, во время чтения развиваются на протяжении всей жизни.
В этом исследовании мы описываем типичную траекторию развития буквенно-цифровых и не буквенно-цифровых НС от детства до ранней взрослой жизни с точки зрения эффективности НС, связанных параметров артикуляции и движения глаз, а также координации между ними, измеряемых EVS как в пространственном измерении. и временные домены. Для этого мы выполняем задачи NS с письмами и объектами, содержащие стимулы с разной степенью фонологического и визуального сходства, с типично развивающимися учениками 2, 4, 7/8 классов и студентами бакалавриата.Мы предполагаем, что участники старшего возраста будут лучше выполнять задачи NS, чем младшие читатели, характеризующиеся более высокой эффективностью NS, сопровождаемой меньшим временем паузы и артикуляции, продолжительностью фиксации, количеством саккад и регрессии, а также временным EVS и более высоким пространственным EVS. В связи с преобладающей ролью орфографической обработки во время выполнения букв NS-задач мы предполагаем, что повышенное визуальное сходство ухудшит выполнение NS-задач в разных группах, с меньшим влиянием повышенного фонологического сходства у читателей старшего возраста, сопровождающего переход от фонетической фонетической обработки, зависящей от чтение — чтение с распознаванием слов, зависящее от орфографической обработки (Ehri and McCormick, 1998).Кроме того, мы прогнозируем, что выполнение задач NS с буквами будет более эффективным, чем с задачами NS с объектами из-за большей подверженности участников письмам и использования автоматического распознавания букв для чтения в повседневной жизни, а также незначительного вклада, связанного с меньшим размером набора и однозначные названия букв по сравнению с предметами. Выявление тенденций развития этих NS-конструкций даст представление о том, как ключевые когнитивные, глазодвигательные и артикуляционные процессы, необходимые для чтения, развиваются в ходе типичного развития.
Материалы и методы
Участники
В этом исследовании участвовали четыре группы здоровых участников без основных неврологических заболеваний: учащиеся 2-х классов ( n = 13, 6 мужчин, возраст 7,2–8,1 года, возраст M = 7,7 лет, возраст SD = 0,3 года ), Ученики 4-х классов ( n = 14, 7 мальчиков, возраст 9,3–10,2 года, возраст M = 9,7 лет, возраст SD = 0,3 года), ученики 7/8 классов ( n = 21, 8 мужчин, 12 лет.2–14,0 лет, возраст M = 13,4 года, возраст SD = 0,6 года) и студенты ( n = 20, 10 мужчин, возраст 20,8–22,5 года, возраст M = 21,3 года, возраст SD = 0,3 года). Эти возрастные группы были отобраны для выборки выполнения задачи NS у младших читателей, все еще проходящих обучение чтению и грамотности в начальных, младших и средних классах начальной школы, и для сравнения успеваемости этих развивающихся читателей с более старшей группой квалифицированных читателей, стремящихся к продвинутому уровню. образование.Участники были набраны из Королевского университета и большого Кингстона, Онтарио. Информированное согласие было предоставлено участниками в возрасте 18 лет и старше, а также законными опекунами участников моложе 18 лет до тестирования.
Показатели скорости именования
Были выполнены четырехбуквенные NS-задачи с двумя попытками на каждую, включая исходную буквенную NS-задачу, разработанную Denckla и Rudel (1976), и три варианта Compton (2003), предназначенные для увеличения фонологического и / или визуального сходства букв используется в задаче (рис. 1А).В задаче управления буквами (LC) использовалась матрица букв a, d, o, p и s . В фонологически подобной задаче (PS) o было заменено на v ; в задаче «Визуально подобный» (VS) o заменено на q ; а в задаче визуально и фонологически похожей (VPS) o было заменено на b . Были выполнены две задачи NS для объектов с двумя попытками на задачу (рис. 1B), включая контрольную задачу (OC), разработанную Denckla и Rudel (1976) на основе линейных рисунков собаки, шляпы, стула, кошки и star и один вариант этой задачи, предназначенный для увеличения фонологического сходства (OPS; стул заменен на bat ).В каждой задаче NS 50 букв / объектов были представлены одновременно с 10 повторениями пяти букв / объектов, расположенных полуслучайно в пять рядов по 10 букв / объектов в каждом. Участников проинструктировали как можно быстрее и точнее вслух назвать все буквы / предметы слева направо и сверху вниз, при этом записывались их артикуляции и движения глаз. Баллы были усреднены между двумя испытаниями для каждой задачи по каждому показателю для расчета единой оценки.
Рисунок 1 .Именование скорости (NS) стимулов. (А) Письмо NS заданий. Задача управления буквами (LC) была разработана Denckla и Rudel (1976), в то время как задачи фонологически похожие (PS), визуально похожие (VS) и визуально и фонологически похожие (VPS) были разработаны Комптоном (2003). (Б) Задачи объекта НС. Задача управления (OC) была разработана Denckla и Rudel (1976). Пунктирными прямоугольниками обозначены области, в которых стимулы стали похожи друг на друга.
Перед началом выполнения заданий было проведено два практических испытания как для буквенных задач NS, так и для объектных задач NS.В первом практическом испытании для задания буквы NS участникам было предложено назвать восемь букв, которые будут использоваться, чтобы убедиться, что они знакомы с этими буквами, а во втором практическом испытании им было предложено задание NS на практическую букву из четырех строк. по пять букв каждая, чтобы обеспечить понимание инструкций по заданию. Сопоставимые практические испытания также проводились для задач NS объекта, требуя от участников сначала назвать шесть объектов, которые будут использоваться, а затем выполнить задачу NS объекта практики, состоящую из двух строк по пять объектов в каждой.
Визуальный дисплей, отслеживание взгляда и записи артикуляции
Положение глаз регистрировали с помощью системы отслеживания взгляда без головы Eyelink 1000 (SR Research Ltd., Миссиссауга, Онтарио, Канада). Участники поместили головы на регулируемую подставку для подбородка / подголовник, а микрофон (Audio Technica, Токио, Япония; M-Audio, Камберленд, Род-Айленд, США) поместили возле рта участников для записи словесных ответов. Использовалась карта совместимости с ASIO с буфером задержки 10 мс. Эта настройка позволяла синхронизировать аудиозапись и отслеживание взгляда с точностью до миллисекунды.17-дюймовый ЖК-монитор (разрешение 1280 × 1024), оснащенный инфракрасной камерой для отслеживания взгляда, был расположен в 60 см от правого глаза участников. Несмотря на то, что просмотр на дисплее велся в бинокль, все записи и калибровки производились в монокуляр для правого глаза. Положение правого зрачка было оцифровано как по вертикальной, так и по горизонтальной осям с частотой дискретизации 500 Гц. Положение глаз сначала было откалибровано с использованием девяти произвольно представленных целевых местоположений на экране: восьми периферийных и одного центрального.Затем этот процесс был повторен для подтверждения калибровки. Во время 9-точечной калибровки использовалось значение отсечки 1,0 ° для средней ошибки и 1,5 ° для максимальной ошибки. У всех участников средняя ошибка 0,5 °.
Каждое испытание NS начиналось с демонстрации центральной белой точки фиксации, чтобы сориентировать каждого участника в общем месте и проверить отклонение калибровки, гарантируя, что средняя ошибка остается <2 °. Затем точка фиксации исчезла и появился массив NS. И в задачах письма и объекта NS было 2.Расстояние обзора 98 ° между каждым элементом и расстояние обзора 1,85 ° между каждым рядом. Буквы в заданиях на букву NS были напечатаны белым шрифтом Angsana New размером 60 на черном фоне. Объекты в заданиях «Объект NS» были представлены в цвете на черном фоне с размерами 2,30 ° на 2,02 °. После того, как последний элемент в испытании был назван, массив исчез и был заменен точкой фиксации перед представлением массива для следующего испытания. Экспериментатор вручную продвигал испытания, и никаких отзывов об их эффективности не поступало.
Анализ данных
Движения глаз и артикуляции были проанализированы с использованием комбинации встроенных инструментов обнаружения саккад от SR Research и специального программного обеспечения MATLAB, чтобы отмечать артикуляции и вычислять более сложные измерения.
Извлечение данных из аудиофайлов было выполнено с использованием пересмотренного протокола, основанного на ранее опубликованном методе (Georgiou et al., 2006), разработанном для удаления фонового шума и нормализации громкости аудиозаписей между участниками (также см. Al Dahhan и другие., 2017, 2020). В деталях, для каждого волнового файла (частота дискретизации 44,1 кГц) аудиозаписи мы выполнили простой алгоритм нормализации для извлечения абсолютной амплитуды. Сначала, взяв абсолютное значение формы волны, мы удалили все очень громкие всплески, используя порог на 7 стандартных отклонений выше средней амплитуды, а затем нормализовали до максимальной амплитуды. Затем мы использовали прямоугольный прямоугольный фильтр из 200 точек выборки, чтобы удалить высокочастотный шум. Эмпирическим путем мы обнаружили, что это дает чистую форму волны, но оставались некоторые громкие всплески, поэтому мы повторили удаление всплеска с порогом на 4 стандартных отклонения выше среднего.После повторной нормализации была получена чистая волновая форма амплитуды артикуляции. Чтобы отметить начало и смещение суставов, мы применили простой пороговый фильтр с 15% нормализованной амплитуды. Амплитуда должна была оставаться выше этого порога, чтобы 2000 точек выборки считались артикуляцией, чтобы избежать ложного обнаружения коротких паразитных шумов. Звуковые файлы были разделены на паузы и артикуляции на основе этого автоматизированного метода. Этот автоматический порог также согласовывался с нашей эмпирической сегментацией при прослушивании каждой артикуляции.
Также потребовалась некоторая ручная сегментация артикуляций, и для этого процесса использовался специальный программный интерфейс в MATLAB. Этот интерфейс отображал артикуляции, соответствующие саккады над буквами и время начала / смещения артикуляции. Это позволило сделать дополнительные ручные аннотации. Во-первых, некоторые участники невнятно произносили артикуляции или вообще не делали паузы между артикуляциями. Мы вручную разбиваем эти артикуляции, где амплитуда должна упасть до минимума (но все еще выше порога) между этими непрерывными высказываниями.Между этими артикуляциями время паузы будет равно 0. Во-вторых, мы вручную удалили ложные артикуляции, такие как несвязанный разговор, кашель или другие высказывания. В-третьих, очень редко мы манипулируем конечными точками артикуляции, если какой-либо другой шум мешает правильному обнаружению с помощью автоматизированного метода. В целом мы обнаружили, что в большинстве случаев требовалось небольшое ручное вмешательство, и все усилия были предприняты, чтобы полагаться на объективную автоматическую маркировку.
Далее, артикуляции были вручную оценены, чтобы вычислить оценку ошибок на основе ответов участников, соответствующую количеству ошибок именования, сделанных за испытание.Затем была рассчитана эффективность NS путем деления количества правильно названных элементов в испытании на общее время, потраченное на присвоение имен предметам в этом испытании. Время паузы для каждого испытания рассчитывалось как среднее время паузы между двумя правильно идентифицированными предметами, а время артикуляции рассчитывалось как среднее время артикуляции для правильно идентифицированных предметов. Эти параметры рассчитывались после удаления пауз и артикуляций, связанных с ошибками задания. В частности, из данных были удалены неправильные артикуляции и их пограничные паузы.Если участники исправляли себя после ошибки наименования, неправильная артикуляция и граничные паузы удалялись. Если участники пропускали элемент, время паузы между артикуляциями двух соседних элементов, а также артикуляция элемента, следующего за пропущенным элементом, удалялись.
Движения глаз были проанализированы на предмет продолжительности фиксации, показателей саккад и количества регрессий. Движение глаз считалось саккадой на основе встроенного алгоритма обнаружения саккады программного обеспечения SR Research.В частности, саккада была отмечена, когда она достигла пороговой скорости 30 ° / с или порогового ускорения 8000 ° / с 2 . Мы использовали эти начальные и конечные точки во всех последующих анализах. Амплитуда рассчитывалась как евклидово расстояние в градусах угла обзора между этими конечными точками. Фиксации рассчитывались как интервалы времени между саккадами, а продолжительность фиксации рассчитывалась для каждого испытания путем усреднения продолжительности всех фиксаций, сделанных в испытании. Регрессии определялись как направленные влево саккады с амплитудой <10 ° и в пределах горизонтального угла зрения 30 °, чтобы исключить движения глаз влево от конца одной строки массива к началу следующей строки.Мы обнаружили, что этот метод был наиболее разборчивым, так как считывание редко представляло собой чистую горизонтальную трассу вдоль каждой линии, и требовался некоторый допуск на негоризонтальную регрессию.
Мы также проанализировали координацию между фиксацией и артикуляцией каждого стимула. Мы измерили интервал между глазом и голосом (EVS), разницу между фиксацией и артикуляцией стимула. Рассчитывались как пространственные, так и временные EVS, за исключением крайнего левого и крайнего правого стимулов в каждой строке. Пространственный EVS был определен как количество букв или объектов, которые голос находился за глазом при первой фиксации стимула, и выражалось в виде действительного числа (рис. 2).Это вычислялось путем вычитания артикулируемого стимула из позиции глаза при первой фиксации, а затем преобразования в количество букв как долю расстояния между буквами (т. Е. Если участник читал ABC и находился между артикулирующими A и B, когда они зафиксированы на C, пространственное EVS будет 1,5). Temporal EVS был определен как промежуток времени между первой фиксацией стимула и началом артикуляции этого стимула. Этот расчет был более сложным, поскольку считывание не всегда было четким горизонтальным следом вдоль букв, как упоминалось ранее.Поэтому мы определили фиксацию стимула как ближайшее евклидово расстояние между центром стимула (буквы или объекта) и средним положением фиксации. Мы ограничили поиск консервативными 3,5 секундами предыдущей артикуляции, чтобы избежать ложных фиксаций от более ранних или более поздних движений.
Рисунок 2 . Образец артикуляции (красная кривая) и положения глаз (зеленая кривая), собранный у участника 4-го класса, выполняющего задание скорости именования букв. Пространственный размах глаз-голос (EVS) был рассчитан для буквы s путем определения положения артикуляции (на букве o) в начале первой фиксации на букве s (вертикальная синяя стрелка).Временная EVS была рассчитана для буквы o путем определения временной задержки от первой фиксации на букве o до начала артикуляции буквы o (горизонтальная фиолетовая стрелка). См. Текст для получения дополнительных сведений.
Два метода были использованы для исследования как пространственного, так и временного EVS: (a) EVS, специфичный для области интереса (ROI), который был рассчитан путем усреднения значений EVS всех правильно сформулированных стимулов в пределах определенных ROI (см. Пунктирные рамки на рисунке 1) в каждом испытании и (б) EVS за пределами ROI, который был рассчитан для каждого испытания путем усреднения значений EVS для всех правильно сформулированных стимулов за пределами ROI.Эти области интереса представляют собой наиболее сложные разделы каждого варианта задачи, содержащие 3–4 соседних вхождения трех букв или объектов, которые являются наиболее фонологически и / или визуально похожими. Поэтому были включены конструкции EVS, специфичные для ROI, чтобы обеспечить измерение, которое могло бы быть более чувствительным к манипуляциям со стимулами по сравнению с EVS, вычисляемым вне ROI. Движение глаз, связанное с пропущенными элементами или элементами с неправильными названиями, было удалено вручную.
Результаты
Во-первых, мы изучили, как производительность задачи NS изменилась в ходе разработки с точки зрения традиционных мер производительности задачи NS, включая эффективность NS, артикуляционные компоненты и меры движения глаз, и исследовали влияние манипуляций со стимулами на каждую из этих конструкций в траектория развития.Затем мы исследовали, как артикуляционные компоненты и соответствующие меры движения глаз координировались в процессе развития, изучая тенденции развития EVS. Наконец, мы исследовали взаимосвязь между этими поведенческими показателями и определили, какие поведенческие показатели лучше всего предсказывают эффективность NS в процессе разработки.
Тенденции в традиционных показателях выполнения задач NS
На рисунке 3 показано влияние манипуляций со стимулами на выполнение задачи в процессе разработки с точки зрения эффективности NS (рисунок 3A), времени артикуляции (рисунок 3B), времени паузы (рисунок 3C), продолжительности фиксации (рисунок 3D), количества саккад (рисунок 3E). ) и количество регрессий (рис. 3F).Серия групп x все задачи NS, смешанный дисперсионный анализ, по одному для каждой конструкции, показала значимые групповые эффекты (все p s <0,05), значимые эффекты задачи (все p s <0,001) и значимые группы. по взаимодействиям задач (все p <0,001) для всех показателей. Групповые эффекты были исследованы с помощью скорректированных по Бонферрони тестов t с использованием усредненных баллов z по шести задачам NS. Что касается эффективности NS и времени артикуляции, были существенные различия между каждой парой соседних возрастных групп, с более высокой эффективностью NS и более коротким временем артикуляции для старших групп (Рисунки 3A, B; все p s <0.05). Время паузы, количество саккад и количество регрессий были значительно ниже для учащихся 7/8 классов, чем для учащихся 4-х классов, и для студентов бакалавриата, чем для учащихся 7/8 классов (рисунки 3C, E, F; все p ‘ s <0,05) без существенной разницы между учениками 2 и 4 классов. Кроме того, продолжительность фиксации была значительно ниже для учащихся 4-х классов, чем для учащихся 2-х классов, и для студентов бакалавриата, чем для учащихся 7/8 классов (рис. 3D, все p <0.05), с плато в этом спаде развития между 4 и 7/8 классами.
Рисунок 3 . Влияние версии задачи на эффективность NS, компоненты NS и движения глаз в процессе разработки. (A) Оценка эффективности по задачам NS. (B) Среднее время артикуляции за испытание. (C) Среднее время паузы за испытание. (D) Средняя продолжительность фиксации. (E) Саккад, кол. (F) Количество регрессий. Данные для задач с буквой NS обозначены кружками и сплошными линиями, а данные для задач NS для объектов обозначены треугольниками и пунктирными линиями.LC, контрольное задание на письмо; PS, фонологически похожая задача; VS, визуально похожая задача; VPS, визуально и фонологически похожая задача; OC, задача управления объектом; ОПС, фонологически похожая задача. Показаны стандартные ошибки.
Что касается эффекта задачи, мы сначала исследовали разницу в производительности при выполнении буквенных и объектных задач NS. По всем параметрам производительность по каждой из версий задач NS с буквами и объектами достоверно коррелировала ( r = 0,68–0,98, все p s <0.01). На основе этих значимых корреляций составные баллы для каждой из задач NS с буквами и объекта были вычислены для каждой из конструкций путем усреднения исходных баллов для задач NS с четырьмя буквами и исходных баллов двух задач NS с объектами. Используя эти составные баллы, тесты парных выборок t показали, что существует значительная разница между буквенными и объектными задачами NS по всем параметрам с повышенной эффективностью [Рисунок 3A; т (67) = 15,4, р <0.001, r = 0,92, d z = 1,9], более короткие сочленения [Рисунок 3B; t (67) = −17,4, p <0,001, r = 0,84, d z = −2,1] и паузы [Рисунок 3C; t (67) = -14,4, p <0,001, r = 0,92, d z = -1,7], более короткие фиксации [Рисунок 3D; t (63) = −14,8, p <0.001, r = 0,81, d z = -1,9] и меньшее количество саккад [Рисунок 3E; t (63) = −15,5, p <0,001, r = 0,90, d z = −1,9] и регрессии [Рисунок 3F; t (63) = −10,4, p <0,001, r = 0,89, d z = −1,3] в задачах письма NS. Эти факторы обычно указывают на более высокую производительность задачи.
При рассмотрении фонологически и визуально схожих манипуляций для задач с буквой NS тесты с парными выборками t показали, что объединенные визуально и фонологически похожие манипуляции с задачами (т. в снижении эффективности NS (Рисунок 3A), более длительном времени артикуляции (Рисунок 3B), времени паузы (Рисунок 3C) и продолжительности фиксации (Рисунок 3D), а также увеличенном количестве саккад (Рисунок 3E) и регрессий (Рисунок 3F) по сравнению с контрольная задача (т.д., условие LC; все p <0,001). Фонологически похожая манипуляция (т.е. состояние PS) и визуально похожая манипуляция (т.е. состояние VS) оказали значительное влияние на каждый из этих показателей выполнения задачи по сравнению с условием LC (все p ‘s <0,01) . Манипуляция VS оказала больший эффект, чем манипуляция PS по всем параметрам, со статистически значимыми различиями между двумя условиями (все p ‘s <0.05). Примечательно, что манипуляции с VS оказали больший эффект, чем манипуляции с VPS, на время артикуляции, поскольку время артикуляции было значительно больше в состоянии VS по сравнению с состоянием VPS (рис. 3B). Для задач NS объекта парные образцы t -тесты показали, что существует значительная разница между двумя задачами по эффективности NS (рис. 3A), времени артикуляции (рис. 3B), времени паузы (рис. 3C) и количеству саккад. (Рисунок 3E), в котором участники были в целом менее эффективны и делали более короткие артикуляции, более длинные паузы и больше саккад в задаче OPS, чем в задаче OC (все p <0.05).
Затем мы исследовали значительную группу по взаимодействию задач, чтобы определить, как эффекты композиции задачи и манипуляции со стимулами различались в процессе разработки. Во-первых, чтобы определить вклад различных траекторий развития буквенных и объектных NS-задач в группу посредством взаимодействия задач, мы повторили дисперсионный анализ, используя средние буквенные и объектные составные баллы. Значимые взаимодействия между группой и задачей остались для эффективности, времени паузы, подсчета саккад и количества регрессий (все p <0.05). Визуальный осмотр тенденций развития этих конструкций показывает, что эти значительные взаимодействия можно отнести к большей разнице между эффективностью выполнения буквенных и объектных задач NS в более старых группах (рис. 3A), но большей разнице между временем паузы, количеством саккад и подсчет регрессии для буквенных и объектных задач NS в младших группах (рисунки 3C, E, F). Эти паттерны предполагают большее повышение эффективности в развитии для задач с буквой NS и большее снижение времени паузы, количества саккад и регрессии для задач NS с объектом.
Затем, чтобы определить вклад фонологически и визуально схожих манипуляций в значимую группу посредством взаимодействия задач, мы повторили дисперсионный анализ отдельно для четырехбуквенных задач NS и двух задач NS объекта. Значимые групповые взаимодействия оставались для всех конструкций на буквенных задачах NS (все p <0,01), но для задач NS объекта значимое взаимодействие было только для времени паузы [ F (3, 64 ) = 3.37, p <0,05, ηp2 = 0,14]. Эти результаты указывают на развивающиеся эффекты фонологического и визуального сходства в ходе развития. В целом эффект этих манипуляций был меньше для старших групп, с особым снижением эффекта фонологически подобной манипуляции в конструкциях для букв NS и специфическим снижением эффекта фонологически подобной манипуляции на время паузы для объекта. Задачи NS. Кроме того, хотя фонологически похожая манипуляция над буквой NS (т.е., состояние PS) оказало значительное влияние на эффективность и количество саккад во всех четырех группах, оно имело защитный эффект в группе студентов, повышая эффективность [Рисунок 3A; t (19) = 2,13, p <0,05, r = 0,95, d z = 0,48] и уменьшение количества саккад [Рисунок 3E; t (19) = −3,30, p <0,01, r = 0,88, d z = −0.74] относительно задачи управления (то есть условия LC). Эти факторы обычно связаны с улучшением производительности задачи.
Глаз-голос
После подтверждения тенденций развития, которые мы предположили для традиционных мер выполнения задач NS, мы затем исследовали координацию между артикуляциями и движениями глаз, необходимыми для NS, путем измерения пространственного и временного EVS (см. Рисунок 2 и методы). На рисунке 4 показано влияние манипуляций со стимулами на пространственный EVS только для конкретных областей интереса, проиллюстрированных пунктирными прямоугольниками на рисунке 1 (рисунок 4A), пространственное EVS, усредненное по стимулам за пределами областей интереса (рисунок 4B), временное EVS для областей интереса (рисунок 4C). ), и временные EVS, усредненные по стимулам за пределами областей интереса (рис. 4D).
Рисунок 4 . Влияние версии задачи на интервал между глазами (EVS) в процессе разработки. (A) Пространственная EVS в интересующих регионах. (B) Пространственная EVS за пределами интересующих регионов. (C) Временные EVS в интересующих регионах. (D) Временные EVS за пределами интересующих регионов. Данные для задач с буквой NS обозначены кружками и сплошными линиями, а данные для задач NS для объектов обозначены треугольниками и пунктирными линиями.LC, контрольное задание на письмо; PS, фонологически похожая задача; VS, визуально похожая задача; VPS, визуально и фонологически похожая задача; OC, задача управления объектом; ОПС, фонологически похожая задача. Показаны стандартные ошибки.
Серия смешанных дисперсионных анализов группы x NS, по одному для каждой конструкции EVS, показала значимые групповые эффекты для обоих временных показателей EVS (все p <0,001), но ни одного пространственного измерения EVS (все p s > 0,05), значимые эффекты задачи для всех показателей (все p s <0.001), а также значимое групповое взаимодействие задач для пространственного EVS и временного EVS за пределами области интереса (все p <0,05). Что касается группового эффекта для временных конструкций EVS, то тесты Bonferroni post-hoc с использованием усредненных баллов z для четырехбуквенных задач NS и двух задач объектных NS показали, что учащиеся 7/8 классов имели значительно более короткие результаты. временные EVS, чем у учеников 4-х классов и студентов бакалавриата, имели значительно более короткие временные EVS, чем у учеников 7/8 классов (у всех p <0.05) для обеих временных конструкций EVS.
Что касается эффектов задачи для четырех конструкций EVS, мы сначала исследовали разницу в производительности во время буквенных и объектных задач NS. Для всех конструкций EVS производительность по каждой из версий задач NS с буквами и объектами достоверно коррелировала ( r = 0,46–0,92, все p s <0,001). На основе этих значимых корреляций были вычислены составные баллы для задач NS с буквами и объектами для каждой из конструкций путем усреднения исходных баллов для задач NS с четырьмя буквами и исходных баллов для двух задач NS с объектами.Используя эти составные баллы, тесты для парных выборок t показали, что существует значительная разница между буквенными и объектными задачами NS по всем параметрам, причем оба пространственных EVS находятся внутри более длинных [Рис. 4A; t (65) = 5,16, p <0,001, r = 0,51, d z = 0,64] и вне [Рисунок 4B; t (65) = 5,22, p <0,001, r = 0,66, d z = 0.64] ROI и более короткие временные EVS как внутри [Рисунок 4C; t (63) = -7,35, p <0,001, r = 0,83, d z = -0,92] и вне [Рисунок 4D; t (63) = −7,91, r = 0,87, d z = −0,99] рентабельности инвестиций в задачах письма NS.
При рассмотрении вариантов задания для букв NS тесты парных выборок t- показали, что ни одна из различных манипуляций не вызвала статистически значимых изменений в любой пространственной конструкции EVS (рисунки 4A, B; все p ‘s> 0.05), но этот временной EVS как внутри, так и за пределами ROI (рисунки 4C, D) был значительно выше для задач VS и VPS по сравнению с задачей LC (все p <0,05). Однако для задач объекта NS наблюдалась значительная разница в пространственных EVS за пределами областей интереса [Рисунок 4B; t (66) = 5,31, p <0,001, r = 0,75, d z = 0,65], где участники имели значительно более длительные EVS на задаче OPS по сравнению с OC задача.
Затем мы исследовали значительную группу по взаимодействию задач, чтобы определить, как эффекты композиции задачи и манипуляции со стимулами различались в процессе разработки. Во-первых, чтобы определить вклад различных траекторий развития буквенных и объектных NS-задач в группу посредством взаимодействия задач, мы повторили дисперсионный анализ, используя средние буквенные и объектные составные баллы. Значимые взаимодействия оставались как для пространственного, так и для временного EVS за пределами областей интереса (все p <0.05). Эти взаимодействия могут отражать разницу в пространственной конструкции EVS между буквенными и объектными задачами NS, которые становятся более выраженными в старших возрастных группах (рис. 4B), в то время как последнее взаимодействие может отражать большее снижение развития временной конструкции EVS для задач объектной NS, как по сравнению с буквенными задачами NS (рис. 4D). При повторении анализа дисперсии отдельно для четырехбуквенных задач NS и двух задач объектных NS значимая группа по взаимодействию задач осталась только для временных EVS за пределами ROI для буквенных задач NS [рис. 4D; Факс (9, 186) = 2.67, p <0,01, ηp2 = 0,11], что, возможно, связано со снижением эффекта манипуляций VS и VPS с возрастом (рис. 4D).
Взаимосвязь поведенческих мер
Затем мы исследовали взаимосвязь между различными поведенческими показателями, используя усредненные баллы z для буквенных и объектных задач NS (таблица 1). Для задач с буквой NS эффективность NS была положительно коррелирована с обоими пространственными конструкциями EVS и отрицательно коррелирована со всеми другими мерами корреляций нулевого порядка (все p s <0.05). Корреляции для всех показателей, кроме пространственного и временного EVS в пределах ROI ( p ‘s> 0,05), оставались значимыми при выполнении частичных корреляций с удаленным эффектом возраста (все p ‘ s <0,05).
Таблица 1 . Корреляции между NS-мерами.
Для задач NS объекта эффективность NS отрицательно коррелировала со всеми показателями (все p <0,05), за исключением продолжительности фиксации и обеих пространственных конструкций EVS (все p s> 0.05) как для корреляций нулевого порядка, так и для частичных корреляций с удаленным эффектом возраста (Таблица 1). Корреляции между буквенными мерами NS были сильнее, чем корреляции между мерами NS объекта. Кроме того, как для буквенных, так и для объектных задач NS корреляции между эффективностью NS и двумя пространственными конструкциями EVS были более слабыми и часто не статистически значимыми по сравнению с наблюдаемыми между другими поведенческими показателями.
Прогнозирование эффективности скорости именования при разработке
Чтобы определить, какой компонент NS и переменная движения глаз лучше всего предсказали эффективность NS для букв и объектов и как эти отношения менялись в процессе разработки, пошаговый регрессионный анализ проводился отдельно для каждой группы (таблица 2).Отдельные модели были запущены для (a) компонентов NS (время артикуляции и время паузы), (b) переменных движения глаз (продолжительность фиксации, количество саккад, количество регрессий) и (c) пространственного и временного EVS. В каждом анализе предикторы добавлялись, если p <0,05, и отбрасывались, если p > 0,10. Для компонентов NS время паузы в значительной степени предсказывало эффективность NS для букв и объектов в каждой возрастной группе, а влияние времени артикуляции возрастало с 4 класса и далее. В то время как время паузы становилось относительно менее важным с увеличением возраста в предсказании буквы NS, оно оставалось более сильным предсказателем для всех возрастов для объекта NS.
Таблица 2 . Пошаговый регрессионный анализ прогнозирования эффективности НП.
Что касается измерения движений глаз, подсчета саккад и продолжительности фиксации, то в значительной степени предсказывалась эффективность NS буквы и объекта для всех групп, кроме 4-го класса, при этом подсчет саккад играет большую роль. В 4-м классе подсчет регрессии был единственным значимым предиктором эффективности как буквы, так и объекта. Этот результат может быть связан с небольшими вариациями корреляций или ограниченным размером выборки этой группы.Для проверки паттерна, обнаруженного в других группах, количество саккад и продолжительность фиксации использовались в качестве предикторов в каждом анализе 4-й степени. Подобно результатам пошагового регрессионного анализа, как количество саккад, так и продолжительность фиксации достоверно предсказывали эффективность NS буквы и объекта ( R 2 = 0,79, p <0,001 для эффективности буквы NS и R 2 = 0.90, p <0.001 для эффективности NS объекта), при этом большее значение имеет счетчик саккад (β = 0.85, p <0,001 против β = 0,41, p <0,05 для букв и β = 1,37, p <0,001 против β = 1,07, p <0,001 для объектов соответственно).
Для конструкций EVS не было четких тенденций, с помощью которых конструкции предсказывали эффективность буквенного NS. У учеников 4-х классов временные EVS за пределами ROI значительно предсказывали эффективность буквенных NS, в то время как у студентов бакалавриата пространственные EVS вне ROI и временные EVS в пределах ROI значительно предсказывали эффективность NS, причем первые играли большую роль.Не было обнаружено значимых предикторов эффективности буквы NS для учащихся 2-х классов или учащихся 7/8 классов. Интересно, что временная EVS в пределах ROI значительно предсказывала эффективность NS как у учащихся 2-х классов, так и у учащихся 7/8 классов, расходясь с результатами, наблюдаемыми для эффективности букв NS. Ни один из EVS не конструирует достоверно предсказанную эффективность NS объекта у учеников 4 класса или студентов бакалавриата.
Обсуждение
Целью этого исследования было выяснить тенденции развития производительности при выполнении заданий NS.Во всех возрастных группах, оцениваемых здесь, участники старшего возраста лучше справлялись с заданиями NS, характеризуясь более высокой эффективностью NS и более жестким временным EVS, более коротким временем паузы и артикуляции, меньшей продолжительностью фиксации и меньшим количеством саккад и регрессий. В разных группах участники были более эффективны в решении буквенных NS-задач, чем объектных NS-задач. Как визуальное, так и фонологическое сходство повлияли на выполнение задач NS, указывая на то, что как орфографическая обработка, так и, в меньшей степени, фонологическая обработка участвуют в исполнении NS, с меньшим эффектом фонологического сходства в старших группах.Наконец, множественный регрессионный анализ выявил важные вклады времени паузы, времени артикуляции, продолжительности фиксации и количества саккад в прогнозирование эффективности NS с заметным снижением предсказательной силы времени паузы для эффективности буквы NS, сопровождаемого увеличением прогнозируемой сила артикуляции времени в старших группах.
Тенденции в поведении разных возрастов в поведении NS
Мы обнаружили устойчивые различия между группами по всем поведенческим показателям; старшие группы были более эффективными, имели более короткую продолжительность фиксации, время артикуляции и время пауз и делали меньше саккад и регрессий, чем более молодые группы.Эти результаты повторяют предыдущие поведенческие исследования с использованием этих задач (например, Al Dahhan et al., 2014, 2017, 2020, в печати). NS был охарактеризован как микрокосм чтения, включающий те же когнитивные процессы, которые лежат в основе чтения, и требующий их автоматического выполнения (Wolf and Bowers, 1999; Al Dahhan et al., 2020, в печати). Таким образом, было обнаружено, что NS является сильным предиктором способности к чтению (Kirby et al., 2003; Arnell et al., 2009; Al Dahhan et al., 2017). Таким образом, интуитивно понятно, что по мере того, как успеваемость в чтении улучшается по мере развития, одновременно увеличивается и эффективность NS, что, вероятно, связано с повышением эффективности когнитивной обработки, лежащей в основе чтения (рисунок 3A; Gordon et al., 2020). Более короткая продолжительность фиксации, время артикуляции и время паузы указывают на то, что кодирование и обработка буквенно-цифровых и не буквенно-цифровых стимулов становится более автоматической в процессе разработки, что предполагает более сильную орфографическую обработку и приводит к общему повышению эффективности задачи (Rayner, 1997; Neuhaus et al., 2001; Bowers and Newby-Clark, 2002; Georgiou et al., 2008; Kirby et al., 2010; Araújo et al., 2011; Al Dahhan et al., 2017, 2020, в печати). Следует отметить, что количество саккад, сделанных во время выполнения заданий NS в этом исследовании, даже в студенческой группе, часто превышало минимальное количество, необходимое для последовательного перемещения взгляда от одного предмета к другому.Это может быть связано с тем, что участники изо всех сил пытались эффективно контролировать движения глаз во время быстрого выполнения задачи, или, наоборот, потому, что они сканировали матрицу элементов во время выполнения задачи из-за неспособности полностью посвятить свои ресурсы внимания эффективному выполнению задачи. Таким образом, снижение количества саккад, наблюдаемое в возрастных группах (рис. 3E), может отражать улучшения в любой из этих глазодвигательных областей или сфер внимания. Среди измеренных переменных движения глаз подсчет саккад был самым сильным предиктором эффективности NS в процессе развития, указывая на то, что глазодвигательный контроль и внимание, вероятно, очень важны для выполнения задачи.Регрессия к ранее названным стимулам может отражать трудности с обработкой зрительных стимулов, представляющих недостаточное получение информации от первоначальной фиксации, или, альтернативно, может быть результатом глазодвигательных ошибок, требующих коррекции гиперметрических саккад (Rayner et al., 2006). Таким образом, снижение количества регрессий в процессе развития, указанное нашими выводами (рис. 3F), может отражать улучшение когнитивной эффективности или глазодвигательного контроля, что согласуется с наблюдаемым снижением продолжительности фиксации и количества саккад.Было показано, что неспособность автоматизировать эти базовые когнитивные процессы как на поведенческом, так и на мозговом уровнях лежит в основе нарушений чтения, обнаруживаемых у читателей с дислексией (например, Al Dahhan et al., 2014, 2017, в печати).
Квалифицированные устные читатели могут начать визуальную проверку и подготовку ответов на предстоящие задания, заканчивая артикуляцию предыдущего пункта. Пространственная EVS отражает степень, в которой глаз может опережать голос при такой подготовке, и предлагается связать со способностью читателей обновлять фонологический цикл своей рабочей памяти с помощью идентифицированных названий предстоящих объектов (Baddeley and Hitch , 1974; Laubrock, Kliegl, 2015).В настоящем исследовании мы не обнаружили значительного влияния группы на пространственный EVS, что указывает на то, что, несмотря на предположительно более высокую способность к чтению, у старших читателей не было более высокого пространственного EVS, чем у младших. Это говорит о том, что пространственный EVS существенно не меняется в ходе типичного развития. В отличие от наших результатов, ранее было показано, что читатели с диагнозом дислексия имеют более короткий пространственный EVS, чем обычно развивающиеся читатели (Pan et al., 2013).В совокупности с нашими выводами это предполагает, что нарушение способности обновлять фонологическую петлю рабочей памяти не является универсальным явлением для всех людей, которые борются с чтением, таких как молодые и неопытные, но типичные читатели, которые участвовали в нашем исследовании, но могут вместо этого быть неотъемлемой характеристикой людей с нарушениями чтения, такими как дислексия.
Напротив, мы обнаружили значительное влияние группы на временный EVS, предполагая снижение темпорального EVS в развитии, которое начинается в 4 классе.Временная EVS, или задержка наименования, отражает время, необходимое для завершения всех этапов когнитивной и артикуляционной обработки, необходимой для идентификации предмета и подготовки артикуляции его имени (Jones et al., 2013). Таким образом, наши результаты показывают, что в ходе типичной разработки читатели становятся более эффективными при завершении этапов обработки, необходимых для NS и чтения, в соответствии с улучшениями в эффективности NS и времени паузы, которые также наблюдались.
Сравнение буквенно-цифровых и не буквенно-цифровых номеров NS
Буквенно-цифровые характеристики NS были более эффективны, чем показатели NS объектов, не являющихся буквенно-цифровыми (Рисунок 3A), и были связаны с более короткими артикуляциями (Рисунок 3B) и паузами (Рисунок 3C), более короткими фиксациями (Рисунок 3D), меньшим количеством саккад (Рисунок 3E) и регрессии (рисунок 3F), более длинные пространственные EVS (рисунки 4A, B) и более короткие временные EVS (рисунки 4C, D), которые являются индикаторами улучшенного выполнения задачи NS.Более эффективное выполнение задач NS с буквами может отражать большее ежедневное воздействие и зависимость участников от букв для чтения, а также более высокую визуальную сложность, больший размер набора и потенциально неоднозначные названия стимулов в задачах NS объекта, что может замедлить когнитивная обработка и снижение производительности при выполнении этих задач. Кроме того, более короткое время артикуляции, наблюдаемое для буквенных NS-задач, вероятно, связано с меньшим количеством фонем в именах букв по сравнению с именами объектов.Следует отметить, что более длительное время артикуляции для объектов может уменьшить количество времени, доступного для пауз в задачах NS объекта; как таковые, мы можем фактически недооценивать сравнительно большее время паузы для задач объекта NS и, соответственно, более медленную когнитивную обработку, лежащую в основе объекта NS. Кроме того, наши результаты показывают, что буква NS становится все более эффективной, чем объект NS в процессе разработки (рис. 3A). Это согласуется с предыдущими выводами о том, что, хотя учащиеся детских садов не обнаруживают различий в буквенно-цифровых и не буквенно-цифровых NS, буквенно-цифровые NS становятся более эффективными, чем не буквенно-цифровые NS к 1-му классу и продолжают развиваться более быстрыми темпами после этого момента (Wolf et al., 1986). Эти поведенческие результаты дополнительно подтверждаются результатами нейровизуализации увеличения активации в левополушарной сети чтения для буквенных NS-задач, чем для объектных NS-задач, что предполагает, что сеть чтения специфична для буквенных стимулов (Al Dahhan et al., 2020, в печати) и объясняет, почему буквенно-цифровые НС являются лучшим предиктором чтения, чем не буквенно-цифровые стимулы (Kirby et al., 2010).
Влияние состава стимулов на выполнение задания
Увеличение фонологического и визуального сходства стимулов ухудшало выполнение задачи NS по отношению ко всем конструкциям, кроме пространственного EVS, что согласуется с предлагаемым вкладом фонологической обработки (Torgesen et al., 1994, 1997) и орфографической обработки (Bowers and Wolf, 1993; Bowers, 1995) для отношения чтения NS. Однако производительность была ухудшена в большей степени из-за визуального сходства, что позволяет предположить, что орфографическая обработка формирует основную часть когнитивной обработки, необходимой для NS, как было установлено ранее (Compton, 2003; Al Dahhan et al., 2017, 2020, в печати). Кроме того, отсутствие эффекта повышенного фонологического и / или визуального сходства на пространственный EVS предполагает, что типичные читатели могли поддерживать постоянное расстояние между глазом и голосом и могли постоянно обновлять свою фонологическую петлю рабочей памяти, несмотря на локальные нарушения повышенной сложности задания.
Влияние фонологических и визуальных манипуляций на выполнение задачи буквы NS было ниже в старших группах, что позволяет предположить, что повышенная эффективность когнитивной обработки, лежащей в основе чтения, может позволить опытным читателям более эффективно преодолевать фонологические и орфографические проблемы. Эффект фонологического сходства заметно снизился в ходе разработки, при этом фонологически похожая манипуляция с задачей буквы NS фактически повысила эффективность (рис. 3A) и уменьшила количество саккад (рис. 3E) у студентов бакалавриата в соответствии с переход от фонетического чтения, зависящего от фонологической обработки, к чтению с распознаванием слов, зависящему от орфографической обработки, в процессе развития (Ehri and McCormick, 1998).
Примечательно, что в то время как увеличение визуального сходства увеличивало время артикуляции, возможно, отражая остаточную когнитивную обработку после начала артикуляции, которая мешает артикуляционным процессам, увеличенное фонологическое сходство уменьшало время артикуляции в сочетании с увеличенным визуальным сходством или с предметными стимулами (Рисунок 3B). Это может отражать усиление артикуляции фонологически похожих слов, повышение эффективности выполнения речевых моторных команд и смягчение пагубных последствий увеличения визуального сходства и не буквенно-цифровых стимулов.
Ограничения
Результаты нашего исследования следует интерпретировать в контексте нескольких ограничений. Хотя наши результаты свидетельствуют о тенденциях развития в поведении НС, мы признаем, что эти тенденции развития являются спекулятивными из-за перекрестного характера этого исследования и должны быть подтверждены лонгитюдными исследованиями, отслеживающими типичных читателей от детства до взрослой жизни. Поскольку размеры нашей выборки для групп 2-го и 4-го классов были относительно меньше, чем у старших групп, ограниченная статистическая мощность могла замаскировать потенциально значимые эффекты манипуляций с заданиями в этих более молодых группах.Таким образом, несущественные эффекты групповых и несущественные post-hoc межгрупповые контрасты для определенных показателей могут не быть истинными нулевыми эффектами и могут быть просто результатом низкой статистической мощности. Это может быть особенно верно для более шумных показателей, таких как EVS, которые могут потребовать высокой статистической мощности для обнаружения значительных различий между группами. Кроме того, в ходе этого исследования не собирались показатели способности к чтению, потому что нас интересовала исключительно траектория развития этих заданий NS.В будущих исследованиях следует изучить степень, в которой траектория поведения при выполнении этих задач связана с показателями способности к чтению. Кроме того, эти меньшие группы молодых читателей могут не быть действительно репрезентативными для основных групп населения, что ограничивает обобщаемость наших результатов. Кроме того, хотя оно предоставляет корреляционные данные о когнитивных процессах, лежащих в основе NS, это исследование не может установить причинно-следственные связи из-за его перекрестного характера и не включает показатели чтения.В будущих лонгитюдных исследованиях можно будет оценить эти лежащие в основе когнитивные навыки и переменные движения глаз у молодых участников с помощью не буквенно-цифровых задач до начала обучения чтению, чтобы определить прогностическую способность этих навыков при освоении чтения.
Выводы
Это исследование выявило ключевые тенденции развития в производительности NS, связанные артикуляционные компоненты и измерения движений глаз, эффекты буквенно-цифровых и не буквенно-цифровых стимулов, а также вклад фонологической и орфографической обработки в работу NS у здоровых людей.Эти данные дают представление о том, как когнитивные, артикуляционные и глазодвигательные процессы, необходимые для NS и чтения, а также механизмы, которые синхронизируют и координируют их, развиваются в ходе развития. Кроме того, это исследование позволяет по-новому взглянуть на координацию движений глаз и артикуляции путем изучения EVS, показывая, что временный EVS, показатель общей эффективности обработки, уменьшается по сравнению с типичным развитием, в то время как пространственный EVS, который отражает эффективность обновлений фонологической обработки. буфер памяти, при типичной разработке существенно не меняется.Эту типичную траекторию развития можно сравнить с нетипичными траекториями развития, собранными для различных клинических групп населения, испытывающих трудности с чтением. Наблюдение за тем, какие задачи NS, артикуляционные компоненты и меры движения глаз, в отношении которых эти клинические группы выполняют иначе, чем обычные читатели, проливают свет на точную природу когнитивной дисфункции, которая лежит в основе трудностей чтения, испытываемых этими людьми. Это будет способствовать разработке целевых диагностических инструментов для раннего выявления и более эффективных образовательных мероприятий для улучшения навыков грамотности и улучшения жизненных результатов людей с нарушениями чтения.
Заявление о доступности данных
Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без излишних оговорок.
Заявление об этике
Исследования с участием людей были рассмотрены и одобрены Советом по общей этике исследований Королевского университета. Письменное информированное согласие на участие в этом исследовании было предоставлено законным опекуном / ближайшими родственниками участников.
Авторские взносы
NA, JK, DB и DM разработали исследования.KE провела исследование. NA и KE проанализировали данные. NA, KE, JK и DM написали статью. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Эта работа была поддержана рабочим грантом Канадского института исследований в области здравоохранения: MOP-FDN-148418. DM был поддержан программой Canada Research Chair Program.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Список литературы
Аль Дахан, Н. З., Георгиу, Г. К., Хунг, Р., Муньос, Д. П., Паррила, Р., и Кирби, Дж. Р. (2014). Движение глаз студентов университета с трудностями чтения и без них во время задания на скорость именования Ann. Дислексия 64, 137–150. DOI: 10.1007 / s11881-013-0090-z
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Аль Дахан, Н. З., Кирби, Дж. Р., Брайен, Д. К., Гупта, Р., Харрисон, А., и Муньос, Д. П. (в печати). Понимание биологической основы дислексии на уровне нервных систем. Мозг Коммуна . fcaa173. DOI: 10.1093 / braincomms / fcaa173
CrossRef Полный текст | Google Scholar
Аль Дахан, Н. З., Кирби, Дж. Р., Брайен, Д. К., и Муньос, Д. П. (2017). Движения глаз и артикуляция во время задания на скорость называния букв: дети с дислексией и без нее. J. Learn. Disabil. 50, 275–285. DOI: 10.1177 / 0022219415618502
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Аль Дахан, Н. З., Кирби, Дж. Р., Чен, Ю., Брайен, Д. К., и Муньос, Д. П. (2020). Изучение нейронных и когнитивных процессов, лежащих в основе чтения, с помощью заданий на скорость именования. Eur. Дж. Neurosci . 51, 2277–2298. DOI: 10.1111 / ejn.14673
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Аль Дахан, Н. З., Кирби, Дж. Р., и Муньос, Д. П. (2016). Понимание чтения и трудностей чтения с помощью заданий на скорость: устранение разрыва между нейробиологией, познанием и образованием. AERA Open 2, 1–15.DOI: 10.1177 / 2332858416675346
CrossRef Полный текст | Google Scholar
Араужо, С., Инасио, Ф., Франсиско, А., Файска, Л., Петерссон, К. М., и Рейс, А. (2011). Компонентные процессы, обеспечивающие быстрое автоматическое наименование при дислексии и недислексических читателях. Дислексия 17, 242–255. DOI: 10.1002 / dys.433
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Араужо, С., Рейс, А., Петерссон, К. М., и Файска, Л. (2015). Быстрая автоматизация присвоения имен и чтения: метаанализ. J. Educ. Psychol. 107, 868–883. DOI: 10.1037 / edu0000006
CrossRef Полный текст | Google Scholar
Арнелл, К.М., Жоанисс, М.Ф., Кляйн, Р.М., Буссери, М.А., и Таннок, Р. (2009). Разложение взаимосвязи между быстрым автоматическим присвоением имен (RAN) и способностью к чтению. банка. J. Exp. Psychol. 63, 173–184. DOI: 10.1037 / a0015721
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Баддели, А. Д., и Хитч, Г. (1974).Рабочая память. Psychol. Учить. Мотив. 8, 47–89. DOI: 10.1016 / S0079-7421 (08) 60452-1
CrossRef Полный текст | Google Scholar
Бауэрс, П. Г. (1995). Уникальный вклад скорости именования символов отслеживания в нарушение чтения с течением времени. Читать. Запись 7, 186–216. DOI: 10.1007 / BF01027185
CrossRef Полный текст | Google Scholar
Бауэрс, П. Г., и Ньюби-Кларк, Э. (2002). Роль скорости именования в модели приобретения навыков чтения. Читать. Пишу. 15, 109–126. DOI: 10.1023 / A: 1013820421199
CrossRef Полный текст | Google Scholar
Бауэрс, П. Г., и Вольф, М. (1993). Теоретические связи между скоростью наименования, точными механизмами синхронизации и навыками орфографии при дислексии. Читать. Напишите . 5, 69–85. DOI: 10.1007 / BF01026919
CrossRef Полный текст | Google Scholar
Боуи, Дж. А., Макгиган, М., Рушена, А. (2005). О связи между скоростью последовательного именования букв и цифр и навыком чтения слов: к учету развития. J. Res. Прочтите 28, 400–422. DOI: 10.1111 / j.1467-9817.2005.00278.x
CrossRef Полный текст | Google Scholar
Басуэлл, Г. Т. (1922). Фундаментальные навыки чтения: исследование их развития . Чикаго, Иллинойс: Чикагский университет.
Google Scholar
Комптон, Д. Л. (2003). Влияние состава заданий на успеваемость букв РАН у первоклассников. J. Специальное образование. 37, 81–94. DOI: 10.1177 / 0022466
70020301CrossRef Полный текст | Google Scholar
Кронин, В.и Карвер П. (1998). Фонологическая чувствительность, быстрое наименование и начало чтения. Заявл. Психолингвист 19, 447–461. DOI: 10.1017 / S0142716400010262
CrossRef Полный текст | Google Scholar
Каттинг, Л. Э., и Денкла, М. Б. (2001). Взаимосвязь быстрого последовательного именования и чтения слов у нормально развивающихся читателей: исследовательская модель. Читать. Напишите . 14, 673–705. DOI: 10.1023 / A: 1012047622541
CrossRef Полный текст | Google Scholar
Денкла, М.Б. и Рудель Р. Г. (1976). Быстрое «автоматическое» наименование (R.A.N.): дислексия в отличие от других нарушений обучаемости. Neuropsychologia 14, 471–479. DOI: 10.1016 / 0028-3932 (76) -0
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Эри, Л. К., и Маккормик, С. (1998). Фазы изучения слов: значение для обучения с задержкой чтения и инвалидами. Читать. Пишу. Q. 14, 135–163. DOI: 10.1080 / 1057356980140202
CrossRef Полный текст | Google Scholar
Георгиу, Г.К., Паррила Р. и Кирби Дж. Р. (2006). Компоненты быстрой скорости именования и раннего чтения. Sci. Stud. Читать. 10, 199–220. DOI: 10.1207 / s1532799xssr1002_4
CrossRef Полный текст | Google Scholar
Георгиу Г. К., Паррила Р., Кирби Дж. Р. и Стефенсон К. (2008). Компоненты быстрого именования и их взаимосвязь с фонологической осведомленностью, знанием орфографии, скоростью обработки и различными результатами чтения. Sci. Stud. Читать. 12, 325–350.DOI: 10.1080 / 10888430802378518
CrossRef Полный текст | Google Scholar
Гордон П. К., Ислам А. Т. и Райт Х. Х. (2020). Быстрое автоматизированное именование (RAN): влияние старения на предсказатель навыков чтения. Aging Neuropsychol. Cogn. 1–13. DOI: 10.1080 / 13825585.2020.1806987
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Халм, К., Ньютон, П., Коуэн, Н., Стюарт, Г., и Браун, Г. (1999). Подумайте, прежде чем говорить: паузы, поиск в памяти и обработка трассировки реинтеграции в словесной памяти. J. Exp. Psychol. 25, 447–463. DOI: 10.1037 / 0278-7393.25.2.447
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хиона, Дж., И Олсон, Р. К. (1995). Паттерны фиксации взгляда среди читающих с дислексией и нормальных: влияние длины и частоты мира. J. Exp. Psychol. 21, 1430–1440. DOI: 10.1037 / 0278-7393.21.6.1430
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Инхофф А. В., Соломон М., Радах Р. и Сеймур Б.А. (2011). Временная динамика размаха глаз и голоса и контроль движений глаз при устном чтении. J. Cogn. Psychol. 23, 543–558. DOI: 10.1080 / 20445911.2011.546782
CrossRef Полный текст | Google Scholar
Джонс, М. У., Эшби, Дж., Браниган, Х. П. (2013). Дислексия и беглость: парафовеальные и фовеальные влияния на быстрое автоматическое наименование. J. Exp. Psychol. 39, 554–567. DOI: 10.1037 / a0029710
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кирби, Дж.Р., Георгиу, Г. К., Мартинуссен, Р., и Паррила, Р. (2010). Скорость именования и чтение: от предсказания к инструкции. Читать. Res. Q. 45, 341–362. DOI: 10.1598 / RRQ.45.3.4
CrossRef Полный текст | Google Scholar
Кирби, Дж. Р., Паррила, Р., и Пфайфер, С. (2003). Называя скорость и фонологическую осведомленность предикторами развития чтения. J. Educ. Психол . 95, 453–464. DOI: 10.1037 / 0022-0663.95.3.453
CrossRef Полный текст | Google Scholar
Лервог, А., и Халм, К. (2009). Быстрое автоматизированное именование (RAN) задействует механизм, который накладывает ограничения на развитие беглости чтения в раннем возрасте. Psychol. Sci. 20, 1040–1048. DOI: 10.1111 / j.1467-9280.2009.02405.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Нойхаус, Г., Форман, Б. Р., Фрэнсис, Д. Дж., И Карлсон, К. Д. (2001). Меры обработки информации при быстром автоматизированном присвоении имен (RAN) и их отношение к чтению. J. Exp. Детская Психология .78, 359–373. DOI: 10.1006 / jecp.2000.2576
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Нортон, Э. С., Вольф, М. (2012). Быстрое автоматизированное наименование (RAN) и беглость чтения: значение для понимания и лечения нарушений чтения. Annu Rev Psychol. 63, 427–452. DOI: 10.1146 / annurev-psycho-120710-100431
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Пан, Дж., Ян, М., Лауброк, Дж., Шу, Х. и Клигл, Р.(2013). Интервал между глазом и голосом при быстром автоматическом наборе цифр и игральных костей у нормальных китайских детей и детей с дислексией. Dev. Sci. 16, 967–979. DOI: 10.1111 / desc.12075
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Райнер К., Чейс К. Х., Слэттери Т. Дж. И Эшби Дж. (2006). Движение глаз как отражение обработки понимания при чтении. Sci. Stud. Читать. 10, 241–244. DOI: 10.1207 / s1532799xssr1003_3
CrossRef Полный текст | Google Scholar
Торгесен, Дж.К., Вагнер Р. К. и Рашотт К. А. (1994). Лонгитюдные исследования фонологической обработки и чтения. J. Learn. Disabil . 27, 276–286. DOI: 10.1177 / 002221949402700503
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Торгесен, Дж. К., Вагнер, Р. К., Рашотт, К. А., Берджесс, С., и Хехт, С. (1997). Вклад фонологической осведомленности и способности быстрого автоматического называния имен в росте навыков чтения слов у детей второго-пятого классов. Sci. Stud. Читать. 1, 161–185. DOI: 10.1207 / s1532799xssr0102_4
CrossRef Полный текст | Google Scholar
Вольф, М., Балли, Х., и Моррис, Р. (1986). Автоматичность, поисковые процессы и чтение: продольное исследование для средних и слабых читателей. Child Dev. 57, 988–1000. DOI: 10.2307 / 1130373
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Вольф, М., и Бауэрс, П. Г. (1999). Гипотеза двойного дефицита дислексии развития. J. Educ. Psychol. 91, 415–438. DOI: 10.1037 / 0022-0663.91.3.415
CrossRef Полный текст | Google Scholar
Вольф, М., Бауэрс, П. Г. и Биддл, К. (2000). Процессы скорости именования, время и чтение: концептуальный обзор. J. Learn. Disabil. 33, 387–407. DOI: 10.1177 / 002221940003300409
CrossRef Полный текст | Google Scholar
Скорость обработки: почему низкая скорость обработки делает простые задачи пугающими для детей
В этой статье содержится полезная информация о низкой скорости обработки данных в классе и дома.Партнерские ссылки включены для вашего удобства. Комплексные стратегии обучения (ILS) — это учебный и академический центр. Напоминаем, что ILS не является поставщиком медицинских услуг, и ни один из наших материалов или услуг не обеспечивает диагностику или лечение определенного состояния или учебной проблемы, которую вы можете увидеть у своего ребенка или учащегося. Если вы ищете диагноз или лечение для своего ребенка или ученика, обратитесь к квалифицированному специалисту, который проведет оценку состояния ребенка.
Макс, 7-летний мальчик, часто испытывает проблемы с выполнением самых простых повседневных задач.У него проблемы с вниманием в школе, и он регулярно отвлекается от того, чем должен заниматься. Например, утром Максу нужно 3-4 раза напоминать о необходимости чистить зубы. Когда он наконец сдается и выполняет это задание, он забыл, что еще ему нужно сделать, чтобы подготовиться к школе. Его одежда разложена в комнате, но он отвлекается на какие-то игрушки в шкафу и начинает играть. Его родители должны внимательно следить за ним, и они постоянно разбрасывают напоминания и указания, чтобы выполнить самые простые работы.
Эта история не уникальна. Возможно, вы слышали это в различных формах, много раз со своими учениками или даже со своими детьми. Родители рассказывают, что, хотя их ребенок, кажется, понимает предметы в школе, им требуется больше времени, чем их сверстникам, чтобы выполнить школьные задания. Одна мать говорит, что постоянно говорила дочери, чтобы она «набирала темп». Хотя многие из этих детей кажутся немотивированными или даже ленивыми, на самом деле они борются с той познавательной функцией, которая называется , скорость обработки данных .
Иногда у детей наблюдается дефицит скорости обработки данных, что может поставить их в невыгодное положение в классе. Родители, учителя и другие наставники в жизни ребенка могут заметить определенные черты, которые способствуют их низкой скорости обработки информации. Некоторые из характеристик включают следующее:
- Требуется дополнительное время для принятия решений
- Часто бывает перегружен задачей
- Проблемы с выполнением домашнего задания
- С трудом заканчивает домашнее задание
- Выполнение домашнего задания требует много времени
- Ненавидит изменения в процедурах
- Регулярно недооценивает время, необходимое для выполнения задачи
- С трудом пытается пробовать новые продукты
- Не хватает концентрации при чтении и заметках
- Пытается избежать многоступенчатых математических задач
- С трудом осознает, как их поведение влияет на других
В классе ребенок со слабой скоростью обработки может делать следующее:
- Забывает приносить из дома материалы для школьных заданий
- Не заканчивает тесты в отведенные сроки
- С трудом делает заметки, пока учитель читает лекцию
- Не выполняет классные задания в школе (часто приносит домашние задания, чтобы закончить)
- С трудом решает в уме
- На большие школьные проекты наперед не планирует
При низкой скорости обработки
Низкая скорость обработки не имеет никакого отношения к тому, насколько умен ваш ребенок.Однако слабая обработка влияет на то, как быстро ваш ребенок может выполнить задание и как он использует информацию. Тот факт, что ваш ребенок не может выполнить задание или отрывок для чтения так же быстро, как сидящая рядом Сьюзи, не означает, что он не может выполнять те же задания. Это обычная проблема, о которой часто забывают, но она может повлиять на ребенка, семью и образовательный круг разными способами.
В статье «Умные дети, которые не успевают» , написанной Эллен Браатен и Брайаном Уиллоуби, они выделяют следующее:
«Наше исследование показало, что скорость обработки данных является очень большой проблемой в домашних условиях.В целом, мы обнаружили, что чем ниже скорость обработки, тем больше проблем возникает с выполнением рутинной работы и повседневной жизнью. Когда дети с низкой скоростью обработки информации говорят о семейных отношениях, они, как правило, сообщают о более негативных отношениях со своими родителями на статистически более высоком уровне, чем их сверстники ».
Итак, что мы можем сделать, чтобы помочь нашим детям преодолеть трудности с обработкой данных и повысить их скорость? Есть один совет, который неоднократно помогал нескольким детям, поскольку мы работаем с ними ежедневно.Первое, что следует помнить, это то, что детям со слабой или недостаточной скоростью обработки обычно требуется больше времени, чтобы понять, что им было сказано устно. Все мы слышали поговорку: «Действия говорят громче, чем слова . «Помня эту фразу, давайте сделаем еще один шаг вперед, добавив наглядные пособия, которые помогут вашему ребенку.
Визуальное расписание
Вместо того, чтобы устно объяснять, что вам нужно делать от вашего ребенка, попробуйте включить визуальные эффекты и действия в его распорядок дня. ( Умные дети, которые не успевают) Например, используйте график с картинками для всех шагов и задач, необходимых ежедневно.Повесьте расписание везде, где вашему ребенку будет полезно видеть (ванная, спальня, кухня, офис и т. Д.).
Используйте часы
Часы — ваш друг и еще один визуальный инструмент, о котором нельзя забывать. Часы могут повысить осведомленность вашего ребенка о времени и помочь ему практиковать важную исполнительную функцию управления временем.
Краткие и простые указания
Вам, конечно же, нужно будет устно направлять задания своему ребенку и часто с ним разговаривать.Ключ к этому — короткие, простые шаги и постепенное увеличение сложности ваших направлений. Измените свой список шагов, чтобы дать ребенку время обдумать то, что ему нужно сделать, и спланировать действия. Попросите ребенка наблюдать за тем, как вы организуете следующий день. Затем спросите их, что они видели, что вы делаете, и посоветуйте им делать то же самое в течение дня.
Эксперименты с памятью
Эта игра веселая и увлекательная для детей, и ее можно повторять несколько раз.Используйте поднос или противень для печенья и поместите на поднос несколько забавных, разноцветных предметов (например, лего, ложки, фигурки, рождественские украшения, карандаши, игрушечные машинки, канцелярские кнопки, свистульки, бусинки и т. Д.). Попросите ребенка смотреть на предметы на подносе в течение 60 секунд и запомнить как можно больше. По прошествии 60 секунд накройте поднос и попросите ребенка написать или устно рассказать вам все предметы, которые он помнит на подносе. По мере того, как они осваивают эту деятельность, сократите время, необходимое им для запоминания объектов (может быть, 45 секунд вместо 60).Это позволяет вашему ребенку развивать более высокую скорость обработки и заставляет его запоминать и обрабатывать, какие предметы находятся на подносе, прежде чем их время истечет.
Развитие навыков обработки данных дома
Способность вашего ребенка учиться лучше в школе зависит от организации и развития у него навыков обработки информации дома. Это требует времени и практики. Помните, что не все это можно сделать в школе, поэтому важно продолжать развивать эти навыки дома.
В качестве обзора ниже приводится разбивка некоторых из вышеперечисленных шагов вместе с другими советами и приемами, которые можно попробовать дома для повышения скорости обработки:
- Используйте наглядные пособия при обучении ребенка новой концепции или помогая ему понять ее.
- Обращайтесь к часам постоянно. Продолжайте увеличивать осведомленность вашего ребенка о времени.
- Используйте график с картинками для своего распорядка дня. Разместите его в нескольких местах дома и используйте !
- Будьте примером и покажите своему ребенку, что вы делаете, чтобы организовать свой день и распорядиться своим временем.
- Разбивайте большие задачи на несколько этапов. Попросите ребенка сделать первый шаг и вернуться к вам, чтобы вы могли дать ему следующий шаг. Развивайте каждый шаг, чтобы они могли делать два шага за раз.
- Старайтесь, чтобы занятия, приемы пищи и задачи выполнялись каждый день в одно и то же время. Последовательность помогает детям, которые пытаются не отставать от обработки огромного количества информации, поступающей в их мозг.
Сопутствующие товары
Integrated Learning Strategies — это центр в штате Юта, который помогает обычным детям и детям с трудностями в учебе добиваться успехов в учебе. Наши услуги предоставляют детям нетрадиционные программы обучения в округах Дэвис, Кейсвилле, Лейтоне, Сиракузах, Фармингтоне и Сентервилле.Области, в которые можно найти интегрированные стратегии обучения, включают: репетиторов по чтению в Кейсвилле, репетиторов по математике в Кейсвилле, репетиторов Common Core в Кейсвилле, репетиторов в Юте, Юта Программы репетиторства
Неуловимый компромисс: скорость и точность в задачах визуального различения
AUDLEY, R.J., & MERCER, A. Соотношение между временем принятия решения и относительной частотой отклика в сине-зеленом различении. Британский журнал математической и статистической психологии, 1968, 21, 183–192.
Google Scholar
ОДЛИ Р. Дж. И Пайк А. Р. Некоторые альтернативные стохастические модели выбора. Британский журнал математической и статистической психологии, 1965, 18, 207–225.
Google Scholar
БИРДСОЛЛ, Т. Г., & Робертс, Р. А. Теория обнаруживаемости сигнала: теория отложенных решений. Журнал Акустического общества Америки, 1965, 37, 1064–1074.
Артикул Google Scholar
БИРРЕН, Дж. Э. и БОТВИНИК, Дж. Скорость реакции как функция сложности восприятия и возраста. Журнал геронтологии, 1955, 10, 433–436.
PubMed Google Scholar
БОТВИНИК, Дж., БРИНЛИ, Дж. Ф., & Роббин, Дж. С. Взаимодействие трудностей восприятия и времени воздействия стимула на возрастные различия в скорости и точности реакции.Геронтология, 1958, 2, 1–10.
Артикул PubMed Google Scholar
EDWARDS, W. Затраты и выплаты указаны в инструкциях. Психологическое обозрение, 1961, 68, 275–284.
Артикул PubMed Google Scholar
Эдвардс, У. Оптимальные стратегии поиска информации: модели для статистики, времени реакции выбора и обработки информации человеком. Журнал математической психологии, 1965, 2, 312–329.
Артикул Google Scholar
ЭГЕТ Х. и СМИТ Э. О природе ошибок в задаче реакции выбора. Психономическая наука, 1967, 8, 345–346.
Google Scholar
FESTINGER, L. Исследования по принятию решения: I. Время принятия решения, относительная частота суждений и субъективная уверенность в связи с различием физических стимулов. Журнал экспериментальной психологии, 1943а, 32, 291–306.
Артикул Google Scholar
FESTINGER, L. Исследования по решению: II. Эмпирический тест количественной теории принятия решений. Журнал экспериментальной психологии, 1943b, 32, 411–423.
Артикул Google Scholar
FITTS, P. M. Когнитивные аспекты обработки информации: III. Установите скорость в сравнении с точностью. Журнал экспериментальной психологии, 1966, 77, 849–857.
Артикул Google Scholar
ГРИН, Д. М., и СВЕТС, Дж. А. Теория обнаружения сигналов и психофизика . Нью-Йорк: Wiley, 1966.
. Google Scholar
Хейл, Д. Дж. Компромисс скорости и ошибки в задаче последовательной реакции с тремя вариантами ответа. Журнал экспериментальной психологии, 1969, 81, 428–435.
Артикул Google Scholar
ХЕКЕР, М.Х., СТИВЕНС, К. Н. и УИЛЬЯМС, К. Э. Измерение времени реакции в тестах на разборчивость речи. Журнал Акустического общества Америки, 1966, 39, 1188–1189.
Артикул PubMed Google Scholar
ХЕНМОН, В.А.С. Время восприятия как мера различий в ощущениях. Архивы философской психологии и научного метода, 1906, № 8.
ХЕНМОН, В.А.С. Отношение времени суждения к его точности.Психологическое обозрение, 1911, 18, 186–201.
Артикул Google Scholar
HICK, W. E. О скорости получения информации. Ежеквартальный журнал экспериментальной психологии, 1952, 4, 11–26.
Артикул Google Scholar
ДЖОНСОН, Д. М. Уверенность и скорость в суждении по двум категориям. Архив психологии, 1939, № 241.
КАХНЕМАН, Д., & NORMAN, J. Соотношение времени и интенсивности в визуальном восприятии как функция задачи наблюдателя. Журнал экспериментальной психологии, 1964, 68, 215–220.
Артикул PubMed Google Scholar
KAHNEMAN, D., NORMAN, J., & KUBOVY, M. Критическая продолжительность разрешения формы: определяется в центре или на периферии? Журнал экспериментальной психологии, 1967, 73, 323–327.
Артикул PubMed Google Scholar
KELLOGG, W.Н. Время осуждения в психометрических суждениях. Американский журнал психологии, 1931, 43, 65–86.
Артикул Google Scholar
ЛаБЕРЖ, Д. Теория простого поведения. Психометрика, 1962, 27, 375–396.
Артикул Google Scholar
ЛЭМИНГ, Д. Р. Дж. Информационная теория времени выбора-реакции . Нью-Йорк: Academic Press.1968.
Google Scholar
ЛЕММОН, В. В. Связь времени реакции с показателями интеллекта, памяти и обучения. Archives of Psychology, 1927, No. 94.
MORGAN, B. B., JR., & ALLUISI, E. A. Влияние различимости и нерелевантной информации на абсолютные суждения. Восприятие и психофизика, 1967, 2, 54–58.
Google Scholar
НИКЕРСОН, Р.С. «То же» — «разное» время отклика: модель и предварительный тест. В W. G. Koster (Ed.), Attention and performance II : Acta Psvchologica, 1969, 30, 257–275.
ОЛЛМАН, Р. Т. Быстрые догадки в выборе времени реакции. Психономическая наука, 1966, 6, 155–156.
Google Scholar
ОЛЛМАН, Р. Т., и БИЛЛИНГТОН, М. Дж. Модель крайнего срока для простого времени реакции. Журнал когнитивной психологии, 1972.в прессе.
PACHELLA, R.C. & FISHER, D. F. Влияние деградации стимула и сходства на компромисс между скоростью и точностью в абсолютных суждениях. Журнал экспериментальной психологии, 1969, 81, 7–9.
Артикул PubMed Google Scholar
PEW, R. W. Быстродействующая рабочая характеристика. В W. G. Koster (Ed.), Внимание и исполнение II . Acta Psvcholoatca, 1969, 30, 16–26.
ПИКЕТТ, Р. М. Восприятие визуальной текстуры. Журнал экспериментальной психологии, 1964, 68, 13–20.
Артикул PubMed Google Scholar
ПИКЕТТ, Р. М. Задержка ответа в ситуации восприятия паттерна. В А. Ф. Сандерсе (ред.), Внимание и производительность . Acta Psvehotogica, 1967, 27, 160–169.
Пайк, А.Р. Латентность и относительная частота ответа при психофизической дискриминации.Британский журнал математической и статистической психологии, 1968, 21, 161–182.
Google Scholar
RABBITT, P. M. A. Ошибки и исправление ошибок в задачах выбора-ответа. Журнал экспериментальной психологии, 1966, 71, 264–272.
Артикул PubMed Google Scholar
RAPOPORT, A., & BURKHEIMER, G. J. Модели для отложенного принятия решений. Journal of Mathematical Psychology, 1971, 8, 508–538,
Статья Google Scholar
SCHOUTEN, J.Ф., БЕККЕР, Дж. А. М. Время реакции и точность. В А. Ф. Сандерс (Ред.), Внимание и производительность. Acta Psvchologtca, 1967, 27, 143–153.
СМИТ, Э. Э. Выбор времени реакции: Анализ основных теоретических положений. Психологический бюллетень, 1968, 69, 77–110.
Артикул PubMed Google Scholar
STONE, M. Модели для выбора времени реакции. Психометрика, 1960, 25, 251–260.
Артикул Google Scholar
SWANSON, J.М., & БРИГГС, Г. Э. Обработка информации как функция скорости и точности. Журнал экспериментальной психологии, 1969, 81, 223–229.
Артикул Google Scholar
SWENSSON, R.G., & EDWARDS, W. Стратегии реагирования в задаче реакции с двумя вариантами ответа с постоянными затратами времени. Журнал экспериментальной психологии, 1971, 88, 67–81.
Артикул Google Scholar
SWETS, J.A., & BIRDSALL, T. G. Отложенное решение в обнаружении человеческого сигнала: предварительный эксперимент. Восприятие и психофизика, 1967, 2, 15–28.
Артикул Google Scholar
ТЕЙЛОР, М. М., ЛИНДСЕЙ. П. Х., и ФОРБЕС, С. М. Количественная оценка обработки общей мощности при слуховой и зрительной дискриминации. В А. Ф. Сандерсе (ред.), Внимание и производительность . Acta Psvchotoatca, 1967, 27, 223–229.
THURMOND, J.B., & ALLUISI, E. A. Время выбора как функция несходства и различимости стимулов. Канадский журнал психологии, 1963, 17, 326–337.
Артикул PubMed Google Scholar
ВИКЕРС, Д. Доказательства аккумуляторной модели психофизической дискриминации. Эргономика, 1970, 13, 37–58.
Артикул PubMed Google Scholar
УИВЕР, Х.R. Исследование различительного последовательного действия: Ручная реакция на цвет. Журнал экспериментальной психологии. 1942, 31, 177–201.
Артикул Google Scholar
ВЕЛФОРД А. Т. Основы мастерства. Лондон: Метуэн, 1968.
Google Scholar
YELLOTT, J. I., JR. Поправка на угадывание времени реакции выбора. Психономическая наука, 1967, 8, 321–322.
Google Scholar
ЙЕЛЛОТТ, Дж.И., младший. Поправка на угадывание и компромисс между скоростью и точностью во времени реакции выбора. Журнал математической психологии, 1971, 8, 159–199.
Артикул Google Scholar
Диссоциация и зависимости между скоростью и точностью: доказательства двухкомпонентной теории разделенного внимания в простых задачах
Реферат
Предыдущая работа наглядно продемонстрировала «затраты» на разделение внимания как в однозадачной обработке мультистимулов, так и в производительности из нескольких простых задач; , однако, отношения между ними не выяснены.В этой статье постулируются две различные причины: (1) визуальные процессы, которые начинаются без задержек и продолжаются одновременно, но демонстрируют затяжные взаимные помехи, зависящие от сложности, и (2) дискретная организация очереди на этапе выбора ответа. Первый обладает свойствами, подобными ресурсам, а второй — свойствами узких мест. Любой из них или оба могут привести к снижению производительности, наблюдаемой в любой конкретной ситуации, учитывая различные предыдущие результаты. Чтобы проверить эту теорию, было исследовано влияние асинхронности начала стимула (SOA) на точность и скорость выполнения заданий с двойным выбором.Первые два эксперимента включали выбор ответа на тон в качестве первой задачи, а вторая задача, требующая сложных перцептивных решений (идентификация цифр или поиск сочетания) с замаскированными дисплеями и нескоростных вторых ответов. Уменьшение SOA оказало незначительное влияние на точность второй задачи, а производительность в этих двух задачах была практически независимой. Однако, когда требовались ускоренные ручные (Опыт 3) или голосовые (Опыт 4) ответы на одну и ту же вторую задачу, наблюдались драматические помехи с сильной положительной зависимостью между временем реакции (RT) для двух задач.Когда обе задачи включали сложные визуальные дисплеи, сокращение SOA приводило к резкому вмешательству, но отсутствовало зависимости между производительностью, независимо от того, была ли первая задача связана с ускоренным (Опыт 5) или медленным (Опыт 6) ответом. Результаты отвергают чистые счета с поздним выбором и общие модели распределения мощности и поддерживают теорию двух компонентов. Они также предполагают, что стандартное использование термина «внимание», предполагающего один ресурс или механизм, вводит в заблуждение.
Рекомендуемые статьиЦитирующие статьи (0)
Полный текстАвторские права © 1989 Издано Elsevier Inc.
Рекомендуемые статьи
Ссылки на статьи
Оценка процедур остаточного сокращения для высокоскоростных задач
Основные моменты
- •
Общее остаточное сокращение более чем на 90% по сравнению с исходными значениями.
- •
Полученные остатки показали низкую вариабельность среди разных субъектов.
- •
Координаты различались еще больше после начала восходящей фазы теста.
- •
Изменяющиеся координаты были связаны с изменением позы тел с более высокой инерцией.
Аннотация
Предпосылки
Ошибки эксперимента и моделирования могут привести к динамически несовместимым результатам при выполнении обратного динамического анализа движения человека. Добавление недорогих остаточных приводов таза может решить такую проблему. Однако в некоторых задачах эти остатки могут оставаться довольно большими, и необходимо применять стратегии, основанные на движении или изменении силы.
Исследовательский вопрос
Можно ли с динамической несогласованностью справиться с помощью оптимального алгоритма управления, который изменяет измеренную кинематику на подготовительной фазе теста с тройным прыжком на одной ступени, задачи относительно высокоскоростной и требовательной к крутящему моменту, так что остатки сохраняются в пределах низкого диапазона?
Методы
Предложенный алгоритм оптимального управления был разработан как задача слежения, в которой использовалась неявная форма динамики. Уравнения движения были введены как ограничения траектории, а также остаточные силы и моменты, действующие на таз.Для этого для решения задачи оптимизации использовались GPOPS-II и IPOPT. Кроме того, на каждой итерации вызывается OpenSim API для решения уравнений движения посредством обратного динамического анализа.
Результаты
Результаты показали значительное сокращение всех шести компонентов остаточных приводов в течение всей задачи. Более того, результирующее движение после оптимизации показало очень похожую эволюцию, чем опорное движение до восходящей фазы задачи. После начала фазы подъема некоторые координаты представляли более значительные расхождения по сравнению с эталонными, например наклон таза и разгибание поясницы.
Значение
Результаты показывают, что предложенный алгоритм может справиться с динамической несогласованностью в высокоскоростных задачах, получая низкие остаточные силы и моменты при сохранении аналогичной кинематики. Следовательно, он может дополнять другие алгоритмы оптимального управления, моделирующие новые движения, полагаясь на динамически согласованные данные.
 С какой скоростью шёл второй лыжник?
С какой скоростью шёл второй лыжник?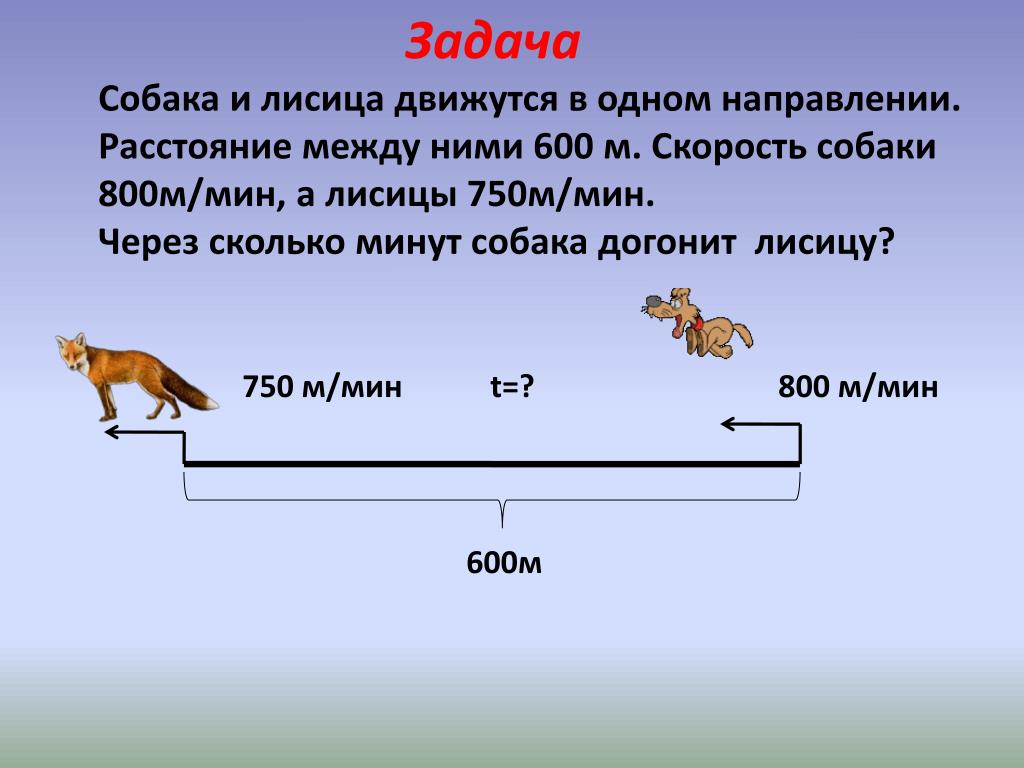 Для этого:
Для этого: