Задачи на треугольник — ПЛАНИМЕТРИЯ В ТЕЗИСАХ И РЕШЕНИЯХ — МАТЕМАТИКА В 9 КЛАССЕ — Каталог статей
При решении вычислительных задач на треугольник нужно знать следующие формулы (рис. 125):
Рис. 125.
где a, b, с – стороны треугольника;
?, ?, ? – противолежащие им углы;
r и R – радиусы вписанной и описанной окружностей;
ha, ma, la – высота, медиана и биссектриса, проведённые к стороне а;
S – площадь треугольника;
– полупериметр треугольника.
Иногда применяют формулу
а также формулу расстояния между центрами описанной и вписанной окружностей:
Примеры решения задач
1. Определите вид треугольника (остроугольный, тупоугольный или прямоугольный) со сторонами 8, 6 и 11 см (рис. 126).
Рис. 126.
Решение. Обозначим больший угол треугольника через ?. Очевидно, что он лежит напротив стороны в 11 см, так как в треугольнике больший угол лежит против большей стороны. По теореме косинусов 112= 82+ 62– 2?8?6?cos ?;
cos ? = -7/32 < 0, значит, угол ? – тупой.
Можно было рассуждать и по-другому. Если бы угол ? был равен 90°, то большая сторона по теореме Пифагора равнялась бы
Удлинение стороны на 1 см автоматически увеличивает и лежащий напротив угол – он становится тупым.
Ответ: тупоугольный.
2. Основание треугольника равно 6 см, один из углов при основании равен 105°, другой – 45°. Найдите длину стороны, лежащей против угла в 45° (рис. 127).
Рис. 127.
Решение. Пусть в треугольнике ABC будут АС = 6 см, ?А = 45°, ?С = 105°. Обозначим длину стороны ВС через х. Её нам и нужно найти. Воспользуемся теоремой синусов по которой:
Учитывая, что сумма углов в треугольнике равна 180°, получим:?В = 180° – ?A – ?C = 180°– 45°– 105° = 30°.
Итого
Ответ:
3. Найдите площадь треугольника со сторонами 2, ?5 и 3 (рис. 128).
Рис. 128.
Решение. Можно воспользоваться формулой Герона:
В нашем случае:
Полупериметр:
Проще решить задачу можно было бы так. По теореме косинусов:
Так как площадь треугольника равна половине произведения двух сторон на синус угла между ними, то:
Ответ: ?5.
4. В треугольнике ABC, где ?ACB = 120°, проведена медиана СМ. Найдите ее длину, если АС = 6, ВС = 4 (рис. 129).
Рис. 129.
Решение. Воспользуемся формулой длины медианы
У нас а = ВС = 4, b = АС = 6. Осталось найти с = АВ. Применим к треугольнику АСВ теорему косинусов: с2= АВ2= АС2+ ВС2– 2AC ? BC ? cos(?АСВ) = 62+ 42– 2 ? 6 ? 4 ? cos 120° = 36 + 16–48?(-1/2) = 76.
Ответ: ?7.
5. Найдите длины сторон АВ и АС остроугольного треугольника ABC, если ВС = 8, а длины высот, опущенных на стороны АС и ВС, равны 6, 4 и 4 соответственно (рис. 130).
Рис. 130.
Решение. Единственный угол треугольника, который остался «нетронутым», угол С.
Из прямоугольного треугольника ВМС следует:
тогда
Из ?АКС:
А теперь по теореме косинусов, применённой к треугольнику ABC, получаем:
Ответ: AB = ?41; AC = 5.
6. В треугольнике, один из углов которого равен разности двух других, длина меньшей стороны равна 1, а сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найти длину большей стороны треугольника (рис. 131).
Рис. 131.
Решение: Обозначим через ? наименьший угол в треугольнике и через ? наибольший угол. Тогда третий угол равен ? – ? – ?. По условию задачи ? – ? = ? – ? – ? (больший угол не может равняться разности двух других углов). Отсюда следует, что 2? = ?; ? = ?/2. Значит, треугольник прямоугольный. Катет ВС, лежащий против меньшего угла ?, равен по условию 1, значит, второй катет АВ равен ctg?, а гипотенуза АС равна 1/sin ?. Поэтому сумма площадей квадратов, построенных на гипотенузе и большем катете, равна:
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, и её радиус равен:
а площадь равна:
Пользуясь условием задачи, имеем уравнение:
откуда
Длина большей стороны треугольника равна
Ответ:
7. Длины сторон а, b, с треугольника равны 2, 3 и 4. Найти расстояние между центрами описанной и вписанной окружностей. (2)
Решение. Для решения задачи даже чертеж не нужен. Последовательно находим: полупериметр
Расстояние между центрами окружностей:
Ответ:
8. В треугольнике ABC величина угла ВАС равна ?/3, длина высоты, опущенной из вершины С на сторону АВ, равна ?3 см, а радиус окружности, описанной около треугольника ABC, равен 5 см. Найти длины сторон треугольника ABC (рис. 132).
Рис. 132.
Решение: Пусть CD – высота треугольника ABC, опущенная из вершины С. Возможны три случая. Основание D высоты CD попадает:
1) на отрезок АВ;
2) на продолжение отрезка АВ за точку В;
3) в точку В.
По условию радиус R окружности, описанной около треугольника ABC, равен 5 см. Следовательно, во всех трех случаях:
Теперь ясно, что точка D не совпадает с точкой В, так как ВС ? CD. Применяя теорему Пифагора к треугольникам ACD и BCD, находим, что
Отсюда следует, что точка D лежит между точками А и В, но тогда АВ = AD + BD (1 + 6?2) см.
Ответ: АВ = (6?2 + 1) см, ВС = 5?3 см, АС = 2 см.
9. В треугольниках ABC и A1B1C1 длина стороны АВ равна длине стороны А1В1, длина стороны АС равна длине стороны А1С1, величина угла ВАС равна 60° и величина угла В1А1С1 равна 120°. Известно, что отношение длины В1С1 к длине ВС равно ?n (где n – целое число). Найти отношение длины АВ к длине АС. При каких значениях n задача имеет хотя бы одно решение (рис. 133)?
Рис. 133.
Решение: Пусть ABC и A1B1C1 – данные в условии задачи треугольники. Применяя теорему косинусов к треугольникам ABC и А1В1С1, имеем:
Т. к. по условию задачи В1С1 :ВС = ?n, то
Поскольку А1В1 = АВ и А1С1 = АС, то, разделив числитель и знаменатель дроби в левой части равенства (1) на АС2и обозначив АВ: АС через х, получим равенство:
откуда ясно, что искомое отношение длины АВ к длине АС есть корень уравнения
х2(n – 1) – х(n + 1) + n – 1 = 0.
Т. к. В1С1 > ВС, то n > 1. Следовательно, уравнение является квадратным. Его дискриминант равен (n + 1)2– 4(n – 1)2= – 3n2+ 10n – 3.
Уравнение (2) будет иметь решения, если – 3n2+ 10n – 3 ? 0, т. е. при -1/3 ? n ? 3. Т. к. n – натуральное число, большее 1, то уравнение (2) имеет решения при n = 2 и n = 3. При n = 3 уравнение (2) имеет корень х = 1; при n = 2 уравнение имеет корни
Ответ: отношение длины АВ к длине АС равно
при n = 2; равно 1 при n = 3; при остальных n решений нет.
Задачи для самостоятельного решения
10. В треугольнике ABC высота AD на 4 см меньше стороны ВС. Сторона АС равна 5 см. Найдите периметр треугольника ABC, если его площадь равна 16 см2.
11. Докажите, что для любого треугольника выполняется равенство:
где ha, hb и hc – высоты треугольника, а r – радиус вписанной окружности.
12. Основание треугольника равно ?2. Найдите длину отрезка прямой, параллельной основанию и делящей площадь треугольника пополам.
13. Найдите площадь треугольника по стороне а и прилежащим к ней углам ? и ?.
14. В треугольнике ABC длина высоты BD равна 6 см, длина медианы СЕ равна 5 см, расстояние от точки пересечения отрезков BD и СЕ до стороны АС равно 1 см. Найти длину стороны АВ.
15. В треугольнике ABC высота BD равна
11,2, а высота АЕ равна 12. Точка Е лежит на стороне ВС, и BE: ЕС = 5:9.
Найти длину стороны АС.
16. В треугольнике ABC длина стороны АС равна 3, ?ВАС = ?/6 и радиус описанной окружности равен 2. Доказать, что площадь треугольника ABC меньше 3.
17. В треугольнике ABC медианы,
проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина
стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ.
Урок 36. Решение задач на применение признаков подобия Δ
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования
.
Урок 36. Решение задач на применение
признаков подобия треугольников
Основные дидактические цели урока: сформировать у учащихся навыки применения признаков подобия треугольников при решении задач; совершенствовать навыки доказательств теорем.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся
- Проверка домашнего задания. (Учитель проверяет решение задач № 559, 560 (б). Два ученика заранее готовят решение на доске.)
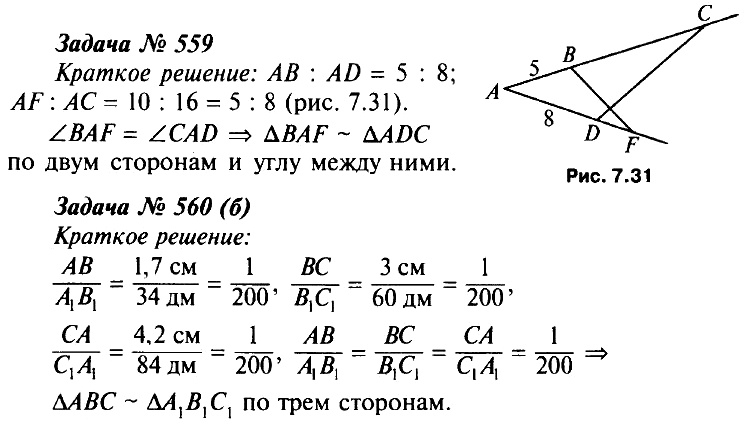
- Теоретический опрос. (Два ученика готовят доказательства теорем у доски.)
- Сформулируйте признаки подобия треугольников.
- Докажите теоремы, выражающие второй и третий признаки подобия треугольников.
- Работа по индивидуальным карточкам
I уровень сложности
Подобны ли треугольники АВС и А1В1С1, если известно, что:
- АВ = 10 см; ВС = 5 см; АС = 7 см; А1В1 = 15 см; В1С1 = 7,5 см; A1С1 = 9,5 см?
- ∠A = 37°, ∠B = 48°, ∠C1 = 95°, ∠B1 = 48°?
- АВ = 10 см, ВС = 8 см, А1В1 = 5 см, А1С1 = 3 см, ∠C = ∠C1 = 90°?
II уровень сложности
- Прямая, параллельная стороне MN треугольника MNK, пересекает стороны КМ и KN в точках Е и F соответственно, КЕ = 6 см, KN = 10 см, KF = 9 см, KN = 15 см. Найдите отношения. a) EF: MN, б) PKMN : РКЕF, в) SKEF : SKMN.
- Точка Е — середина стороны AD параллелограмма ABCD. В каком отношении прямая BE делит диагональ АС параллелограмма? Найдите отношение площади треугольника АВЕ и четырехугольника BCDE.
III уровень сложности
- Основания трапеции равны 9 и 6 см, а высота равна 10 см. Найдите разность расстояний от точки пересечения диагоналей трапеции до ее оснований.
- Докажите признак подобия прямоугольных треугольников по гипотенузе и катету.
- Решение задач по готовым чертежам.
- 1) Рис. 7.32. Найти: ∠C1, В1С1.
- 2) Рис. 7.33. Найти: ∠C, ∠C1
- 3) Рис. 7.34. Найти: ВМ.
- 4) Рис. 7.35. Найти: ВС.
- 5) Рис. 7.36. Найти: ∠DCA.
- 6) Рис. 7.37. Найти АВ, NC.

Ответы к задачам по готовым чертежам:
- 1) ∠C1 = 71°, В1С1 = 15 см.
- 2) ∠C = ∠C1 = 60°.
- 3) ВМ = 6 см.
- 4) BC = 20/3.
- 5) ∠DCA = 90°.
- 6) АВ = 8, NC= 8.
(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены пять-шесть задачи;
- оценка «4» — правильно решены четыре задачи;
- оценка «3» — правильно решены две-три задачи;
- оценка «2» — не ставится.
(Учащиеся, справившиеся со всеми задачами, решают дополнительные задачи.)
Дополнительные задачи
- Диагональ АС трапеции ABCD (АВ||CD) делит ее на два подобных треугольника. Найдите площадь трапеции ABCD, если АВ = 25 см, ВС = 20 см, АС = 15 см.
Ответ: SABCD = 204 см2.
- Угол В треугольника AВС в два раза больше угла А. Биссектриса угла В делит сторону АС на части AD = 6 см и CD = 3 см. Найдите стороны треугольника АВС.
Ответ: АС = 9 см, АВ = 6√3 см, ВС = 3√3 см.
III. Самостоятельная работа
I уровень сложности
Вариант 1
- Рис. 7.38. Доказать: ΔАВС ~ ΔА1В1С1
- Продолжения боковых сторон трапеции ABCD пересекаются в точке О. Найдите ВО и отношение площадей треугольников ВОС и AOD, AD = 5 см, ВС = 2 см, АО = 25 см.
Вариант 2
- Рис. 7.39. Доказать: ΔАВС ~ ΔА1B1С1.
- АВ и CD пересекаются в точке О, АО = 12 см, ВО = 4 см, СО = 30 см, DO = 10 см. Найдите угол САО, если ∠DBO = 61°. Найдите отношение площадей треугольников АОС и BOD.

II уровень сложности
Вариант 1.
- Рис. 7.40. Доказать: ΔАВС ~ ΔА1В1С1
- Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС соответственно в точках М и Н. Найдите АС и отношение площадей треугольников АВС и ВМН, если МВ = 14 см, АВ = 16 см, МН = 28 см.
Вариант 2
- Рис. 7.41. Доказать: ΔМВН ~ ΔСВA.
- В треугольнике АВС АВ = 15 м, АС = 20 м, ВС = 32 м. На стороне АВ отложен отрезок AD = 9 м, а на стороне АС — отрезок АЕ = 12 м. Найдите DE и отношение площадей треугольников АВС и ADE.
III уровень сложности
Вариант 1
- Дано: ∠1 = ∠2, AD = 4, АС = 9 (рис. 7.42). Найти: АВ, SABD : SABC.
- Диагонали четырехугольника ABCD пересекаются в точке О, АО • ВО = СО • DO. Докажите, что площади треугольников ACD и ABD равны.
Вариант 2
- Дано: ВС ⊥ АС, МН ⊥ ВС, 2МС = ВС, МН = 0,5АС (рис. 7.43). Доказать: АВ||СН. Найти. SАВС : SMCH.
- В трапеции ABCD AD и ВС — основания, О — точка пересечения диагоналей, АО : ОС = 3 : 2. Найдите отношение площадей треугольников АВС и ACD.

(Ответы на самостоятельную работу смотрите в уроке 37)
IV. Рефлексия учебной деятельности
- Сформулируйте признаки подобия треугольников.
- В каком случае подобны равносторонние, равнобедренные, прямоугольные треугольники?
Домашнее задание. Решить задачи № 562, 563, 604, 605.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников.
Вернуться к Списку уроков Тематического планирования.
Конспект «ЗАДАЧИ на Признаки равенства треугольников»
«ЗАДАЧИ на Признаки равенства треугольников»
1-й признак. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2-й признак. Если сторона и прилегающие к ней углы одного треугольника соответственно равны стороне и прилегающим к ней углам другого треугольника, то такие треугольники равны.
3-й признак. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
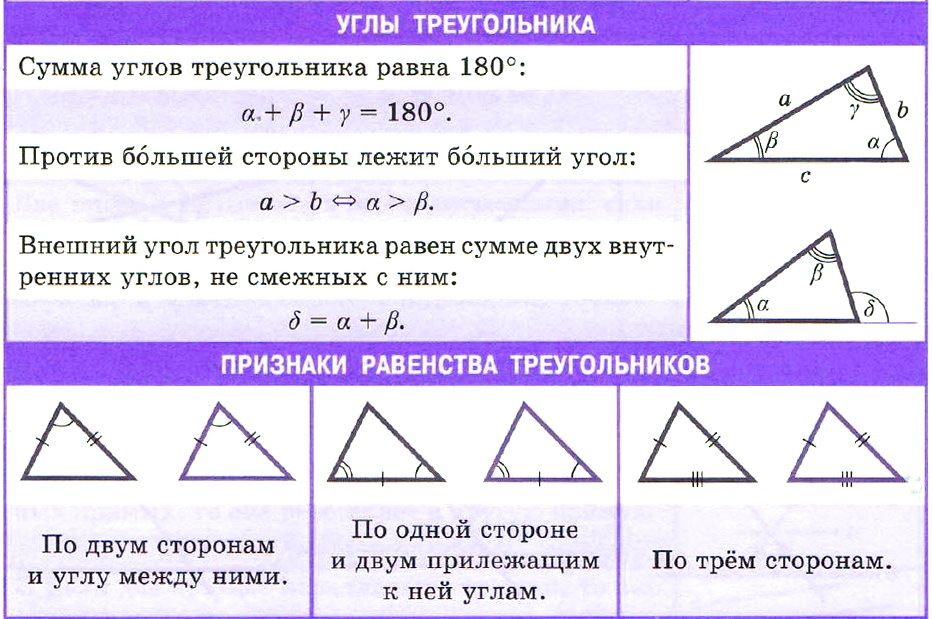
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Дано: ΔABC, Δ A1B1C1, AC=A1C1, AB=A1B1, ∠A=∠A1, AC=10см, АВ=АС+5см, ВС=АС-3см. Найти периметр Δ A1B1C1

Задача № 2. Дано: окружность (O, r), ML, NK — диаметр окружности (O, r). Доказать: ΔOMN = ΔOKL.

Задача № 3. Дано: AD ∩ BC = 0, AO = DO, ∠BAO = ∠CDO, ∠ACO = 55°, ∠ABO = 30°. Найти: ∠ACD.
Задача № 4. Дано: ΔABK, ΔACM, BK ∩ MC = D, AM = AK, DM = DK. Доказать: 1) BD = CD, 2) AB = AC.

Это конспект по теме «ЗАДАЧИ на Признаки равенства треугольников». Выберите дальнейшие действия:
Конспект «ЗАДАЧИ по теме Прямоугольные треугольники»
ЗАДАЧИ по теме Прямоугольные треугольники
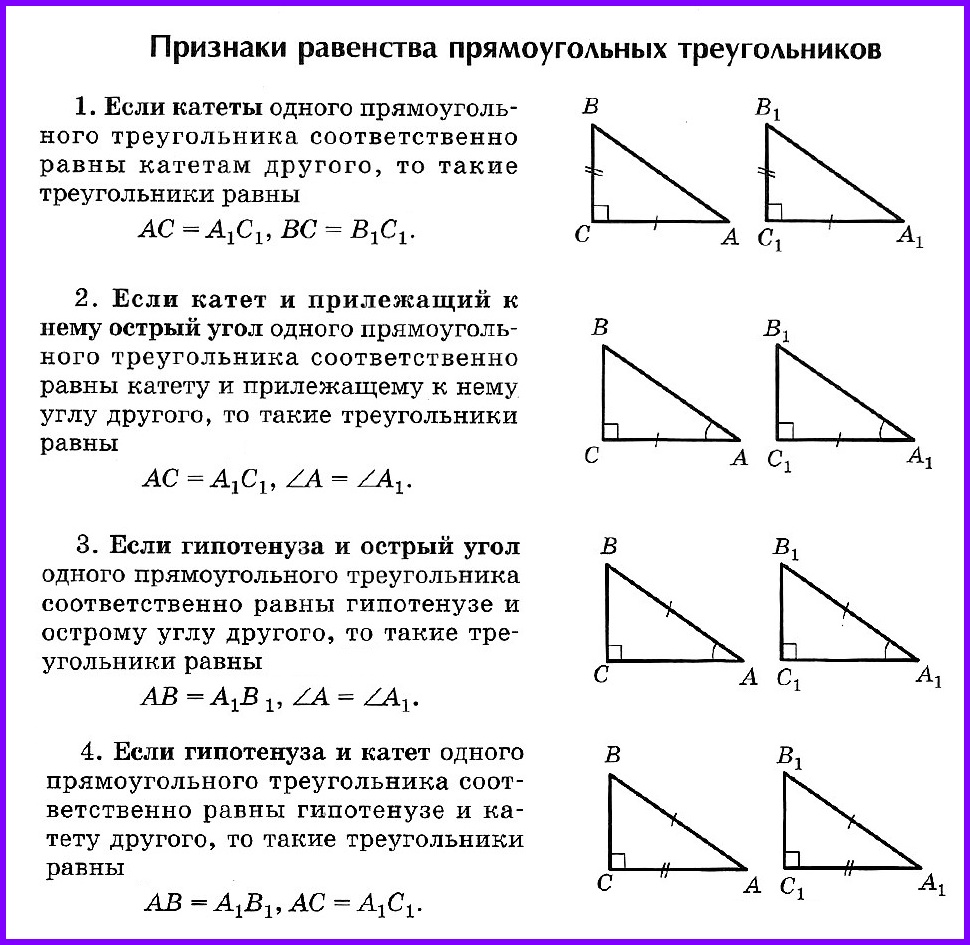
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны если:
• два катета одного треугольника равны двум катетам другого;
• катет и острый угол одного треугольника равны катету и острому углу другого треугольника;
• гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника;
• гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника.
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
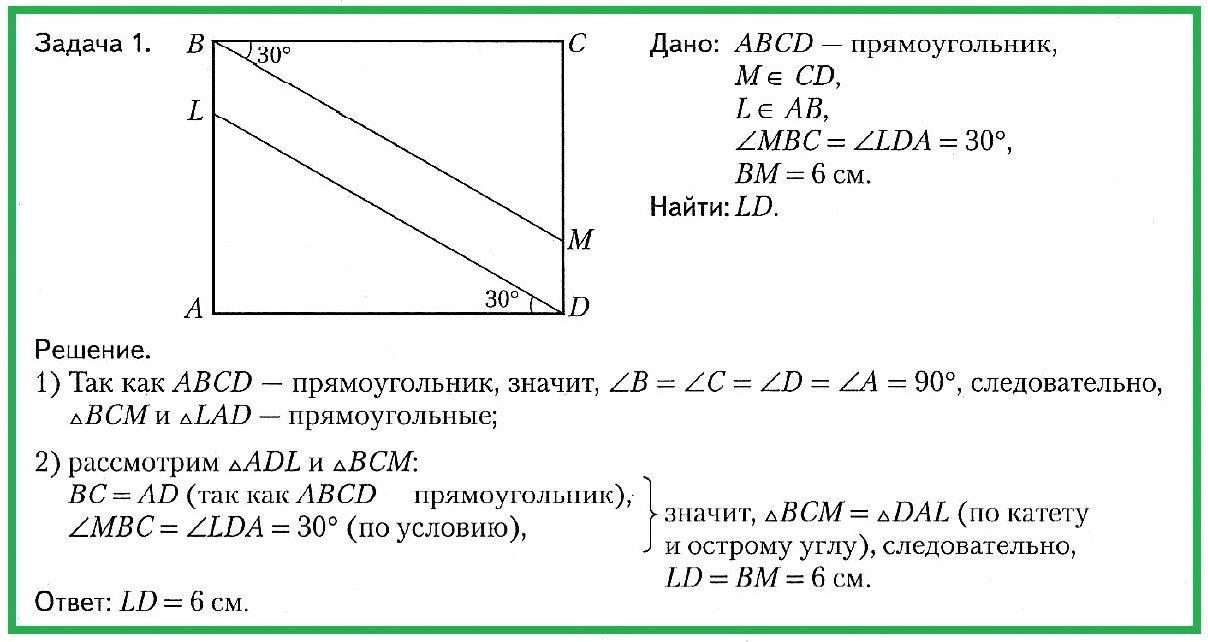
Задача № 1. Дано: ABCD — прямоугольник, M ∈ CD, L ∈ AB, ∠MBC = ∠LDA = 30°, BM = 6 см. Найти: LD.
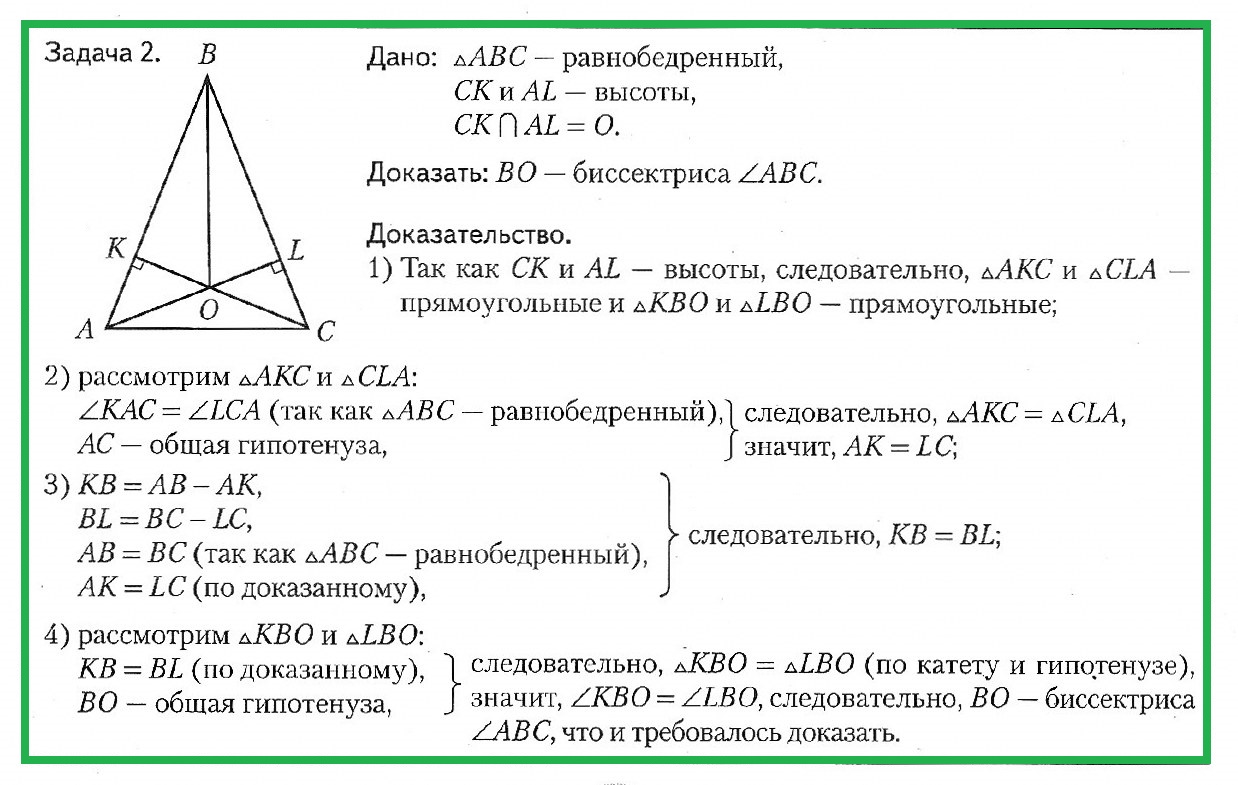
Задача № 2. Дано: ΔABC — равнобедренный, CK и AL — высоты, CK ∩ AL = 0. Доказать: BO — биссектриса ΔABC.
Задача № 3. Дано: ΔABC — прямоугольный, ∠C = 90, CO — медиана. Доказать: CO = 1/2 AB.

Это конспект по теме «ЗАДАЧИ по теме Прямоугольные треугольники». Выберите дальнейшие действия:
задач треугольника | Проблемы с геометрическим треугольником и решения
Q1. Длина основания треугольника на 4 см меньше его высоты. Площадь треугольника 96 см 2 . Длина основанияA. 24 см
Б. 12 см
C. 20 см
Д. 16 см
E. 36 см
Ответ и объяснение
Sol: опция B
Пояснение A = 96 см 2 .
B — H = 4.
Кроме того, 1/2 B.H = 96
∴ H (H — 4) = 192
⇒ H = 16 и B = 12 см
A. 15 м 2
B. 6 & redic; 6 м 2
К. 21 м 2
D. 7 & redic; 6 м 2
E. 32 м 2
Ответ и объяснение
Sol: опция BПояснение: Три стороны треугольника равны 5 м, 6 м и 7 м.∴s = (5 + 6 + 7) / 2 = 9м.
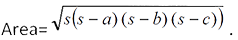 Подставляя значения, получаем площадь =
Подставляя значения, получаем площадь = 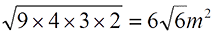 Q3. Периметр равнобедренного треугольника — 100 см. Если основание 36 см, найдите длину равных сторон.
Q3. Периметр равнобедренного треугольника — 100 см. Если основание 36 см, найдите длину равных сторон.A. 18 см
Б. 64 см
C. 32 см
Д. 36 см
E. 24 см
Ответ и объяснение
Sol: Опция C
Пояснение: Пусть длина равной стороны = x.
∴ x + x + 36 = 100
⇒ 2x = 64 ⇒ x = 32 см.
A. 10 см
Б. 5 см
C. 0,12 см
Д. 0,2 см
E. Недостаточно данных ответить на вопрос
Ответ и объяснение
Sol: опция A
Пояснение: A = 615 см 2 .База = 123 см.
Перпендикуляр =?
Также A = 1/2 * B * H
∴ 615 = 1/2 * 123 * H
⇒ H = 10 см.
A. 250 см 2
Б. 75 см 2
C. 125 см 2
Д. 150 см 2
E. Ни одного из этих
Ответ и объяснение
Sol: опция BПояснение: Длина сторон 12.5 см, 12,5 см и 20 см. ∴ s = (12,5 + 12,5 + 20) / 2 ⇒ s = 22,5.
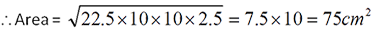
Обязательно читать статьи о треугольниках
Q.6. В равнобедренном прямоугольном треугольнике периметр составляет 20 метров. Найдите его область.A. 17,16 м 2
Б. 5,858 м 2
К. 34,32 м 2
Д. 9.320 м 2
E. 15,45 м 2
Ответ и объяснение
Sol: опция A
Пояснение: В равнобедренном прямоугольном треугольнике основание = высота.Пусть a — база, а b — гипотенуза.
∴ a + a + b = 20 ⇒ 2a + b = 20.
Также b 2 = a 2 + a 2
⇒ b 2 = 2a 2 .
∴ b = & redic; 2a. Итак, 2a + & redic; 2a = 20 ⇒ 3,41a = 20
∴ a = 5,86m.
Требуемая площадь = 1/2 a 2 = 1/2 * 5,86 * 5,86 = 17,16 м 2

A. KM Б.КМ C. LM D. KL E. Ни одного из этих Ответ и объяснение Sol: опция C A. 28 кв.м Б. 56/3 кв.м C. 8 кв.м Д.33.6 кв.м E. 30,7 кв.м Ответ и объяснение Sol: опция C A. 4 см Б. 4,5 см C. 5 см D. Недостаточно данных Ответ и объяснение Sol: опция A A. 64 & redic; 3 м 2 B. 80 & redic; 3 м 2 C. 75 & redic; 3 мес. 2 D. 72 & redic; 3м 2 E. 60 & redic; 3м 2 Ответ и объяснение Если вы думали, что ACT был большим поклонником кругов, то приготовьтесь к его абсолютно бесстыдной любви к треугольникам. На одном дыхании вы можете ожидать, что найдете различные размеры тупого треугольника, а на следующем — равнобедренного прямоугольного треугольника. Задачи треугольника ACT будут столь же многочисленны, как и разнообразны, поэтому убедитесь, что вы ознакомились со всеми типами перед экзаменом. Это будет ваше полное руководство по треугольникам ACT — типы треугольников, которые будут отображаться на ACT, формулы, которые вам нужно знать, чтобы их решить, и стратегии, которые вам нужно будет применить при приближении к вопрос о треугольнике.Мы также разберем настоящие математические задачи ACT и расскажем, как наиболее эффективно и действенно решать любые задачи треугольника, с которыми вы сталкиваетесь. Прежде чем мы рассмотрим, как решить задачу треугольника, давайте обсудим основы. Треугольник — это плоская фигура, состоящая из трех прямых линий, соединяющихся под тремя углами. Сумма этих углов составляет 180 °. Каждая из трех сторон треугольника называется «катетом» треугольника, а самый большой (самый длинный) катет называется «гипотенузой».«Угол, противоположный гипотенузе, всегда будет самым большим из трех углов. Сумма любых двух катетов треугольника всегда должна быть больше, чем размер третьей стороны. Зачем? Потому что, когда сумма двух линий меньше, чем размер третьей линии, они не могут все соединиться в треугольник. вопросов с треугольником составляют менее 10% всех вопросов SAT по математике. При этом вы все равно хотите правильно ответить на эти вопросы, поэтому вы должны быть готовы знать все виды треугольников: прямоугольные, равнобедренные треугольники, равнобедренные прямоугольные треугольники — SAT может проверить вас по любому из них. Поскольку задачи с треугольниками составляют лишь небольшой процент вопросов SAT по математике, вам не следует тратить все свое учебное время на треугольники. Эта статья должна быть всем, что вам нужно, чтобы подготовить вас к решению вопросов треугольника SAT. Я дам вам знать типы треугольников, которые будут отображаться на тесте SAT, их формулы и стратегии, которые вам нужно будет применить при решении вопроса о треугольнике. Я также разложу практические вопросы SAT по математике и объясню, как выбивать из общего числа вопросы с треугольниками. Сначала поговорим об основах. Треугольник — это плоская фигура, состоящая из трех прямых линий, соединяющихся под тремя углами.Сумма этих углов составляет 180 °. Каждая из трех сторон треугольника называется «катетом» треугольника, а самый длинный катет прямоугольного треугольника называется «гипотенузой». Угол напротив гипотенузы всегда будет 90 °, это самый большой из трех углов. Когда мы посмотрим на множество различных типов, вы заметите, что многие категории треугольников будут подмножествами других категорий треугольников, и определения будут продолжать сужаться. Существует несколько различных типов специальных треугольников, каждый из которых обычно появляется в SAT. В этом разделе
Пояснение: Поскольку M> ∠K, KL> LM

Пояснение: XY ∥ MN
Следовательно, ∆ LXY — ∆LMN …… .. (AA Test)
Площадь (∆LXY) / Площадь (∆ LMN) = LX 2 / LM 2 (Пусть площадь (∆LXY = x))
∴ x / (x + Area (XMNY)) = (LX / LM) 2
∴ x / (x + 42) = (2/5 ) 2
∴ x / (x + 42) = (4/25)
25x = 4x + 168
⇒ 21 x = 168
⇒ 8 кв.м
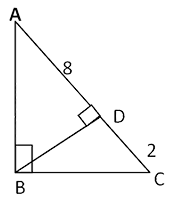
∆ADB — ∆BDC
∴ AD / BD = BD / DC
∴ BD 2 = AD * DC = 8 * 2
∴ BD 2 = 16 ∴ BD = 4 см
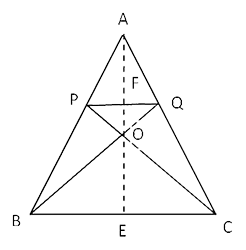
Здесь сторона равностороннего треугольника равна 60.В равностороннем треугольнике PQ ∥ BC,
(∴ P и Q — середины сторон)
Итак, BC = 2PQ ⇒ 2PQ = 30 м. Теперь AE = & redic; 3/2 * 60 = 30 & redic; 3 м
As, O — центроид. Итак, AO: OE = 2: 1
OE = 10 & redic; 3 м и AO = 20 & redic; 3 м
AF = 1/2 AE = 15 & redic; 3 м
FO = AO-AF = 5 & redic; 3 м 2
Следовательно, площадь ∆ PQO: 1/2 * PQ * FO
= 1/2 * 30 * 5 & redic; 3 = 75 & redic; 3 м 2 . Руководство по геометрии и практические задачи
Что такое треугольники?
Геометрические стратегии и практические задачи
Что такое треугольники?
Особые треугольники
c ++ — проблема треугольника — qaru.
Переполнение стека
.