Практика. Линейные уравнения и их системы. Часть 4. Решение задач с помощью систем линейных уравнений
Задача 4
Лодка за 3 ч движения по течению реки и 4 ч против течения проходит 114 км (Рис. 5). Найти скорость лодки по течению и ее скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как и за 5 ч по течению.

Рис. 5. Иллюстрация к задаче 4
Решение
Введем обозначения:
- Скорость лодки по течению:
 .
. - Скорость лодки против течения:
 .
.
Воспользуется формулой: 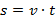
Лодка за 3 ч движения по течению реки и 4 ч против течения проходит 114 км, тогда 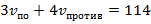 .
.
За 6 ч движения против течения она проходит такой же путь, как и за 5 ч по течению: 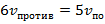 .
.
Запишем полученную систему линейных уравнений: 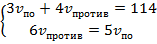 .
.
Воспользуется методом подстановки. Во втором уравнении выразим 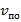 через
через 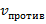
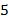 :
: 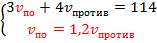 .
.Подставим полученное значение 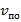 в первое уравнение:
в первое уравнение: 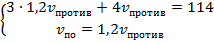 .
.
Выполним действие: 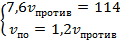 .
.
Найдем 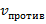 :
: 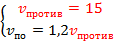
Найдем 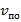 :
: 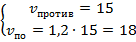 .
.
Ответ: 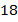 км/ч;
км/ч; 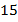 км/ч.
км/ч.
Задача 5
В двух ящиках лежат яблоки. Если из первого ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну (Рис. 6). Если же из второго ящика переложить в первый 20 яблок, то в первом станет в 3 раза больше яблок, чем во втором (Рис. 7). Сколько яблок лежит в каждом ящике?

Рис. 6. Иллюстрация к задаче 5

Рис. 7. Иллюстрация к задаче 5
Решение
Пусть изначально в первом ящике было 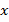 яблок, а во втором –
яблок, а во втором – 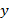 яблок. Если из первого ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну:
яблок. Если из первого ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну:
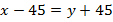
Если же из второго ящика переложить в первый  яблок, то в первом станет в
яблок, то в первом станет в 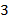 раза больше яблок, чем во втором:
раза больше яблок, чем во втором: 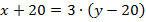 . Запишем полученную систему линейных уравнений:
. Запишем полученную систему линейных уравнений: 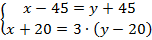 .
.
Раскроем скобки во втором уравнении: 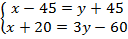 .
.
В обоих уравнениях выразим 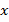
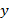 :
: 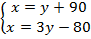 .
.Воспользуемся методом подстановки – подставим выражение во второе уравнение: 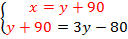 .
.
Во втором уравнении перенесем все слагаемые с переменной в левую часть, а без переменной – в правую: 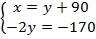 .
.
Найдем 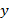 – количество яблок во втором ящике:
– количество яблок во втором ящике: 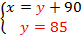
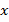 – количество яблок в первом ящике:
– количество яблок в первом ящике: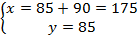
Ответ: 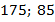 .
.
Задача 6
Один металлический сплав содержит 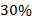 меди, другой –
меди, другой – 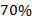 меди (Рис. 8). Сколько килограммов каждого сплава надо взять, чтобы получить 120 кг сплава, содержащего
меди (Рис. 8). Сколько килограммов каждого сплава надо взять, чтобы получить 120 кг сплава, содержащего 
Рис. 8. Иллюстрация к задаче 6

Рис. 9. Иллюстрация к задаче 6
Решение
Пусть необходимо взять 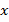 кг первого сплава и
кг первого сплава и 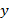 кг второго сплава. Тогда
кг второго сплава. Тогда 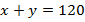
Теперь посчитаем массу меди, она составляет: 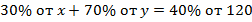 .
.
Мы знаем, что 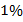 – это
– это 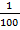 от чего-то (Рис. 10), значит,
от чего-то (Рис. 10), значит, 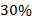 — это
— это 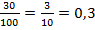 , т.е.
, т.е. 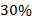
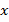 – это
– это  .Аналогично
.Аналогично 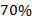 от
от 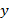 – это
– это 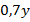 , а
, а 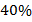 от
от 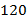 – это
– это 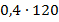

Рис. 10. Иллюстрация к задаче 6
Запишем уравнение: 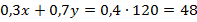 . Запишем полученную систему линейных уравнений:
. Запишем полученную систему линейных уравнений: 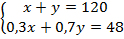 .
.
В первом уравнении выразим 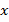 через
через 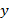 :
: 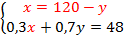 .
.
Воспользуемся методом подстановки – подставим первое уравнение во второе: 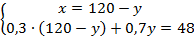 .
.
Раскроем скобки во втором уравнении: 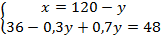 .
.
Во втором уравнении оставим слагаемые с переменной в левой части уравнения, а без переменной перенесем в правую: 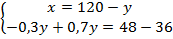 .
.
Выполним действия: 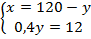 . Найдем
. Найдем 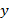 – количество кг второго сплава, которое необходимо взять:
– количество кг второго сплава, которое необходимо взять: 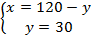 .
.
Найдем 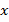 – количество кг первого сплава:
– количество кг первого сплава: 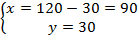 .
.
Ответ: 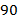 кг;
кг; 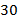 кг.
кг.
Задача 7
Сумма цифр двузначного числа равна 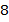 . Если поменять местами его цифры, то получим число, которое больше данного на
. Если поменять местами его цифры, то получим число, которое больше данного на 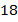 . Найти данное число.
. Найти данное число.
Решение
Обозначим двузначное число так: 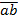 . Сумма цифр двузначного числа
. Сумма цифр двузначного числа 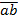 равна
равна 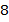 :
: 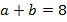 .
.
Если поменять местами его цифры, то получим следующее число: 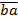 . Так как в числе
. Так как в числе 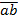
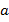 десятков и
десятков и 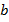 единиц, то
единиц, то 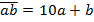 , а в числе
, а в числе 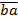
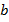 десятков и
десятков и 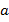 единиц, значит,
единиц, значит, 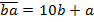 .
.
Число 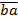 на
на 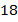 больше, чем
больше, чем 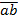 , поэтому
, поэтому 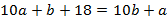 .
.
Перенесем все слагаемые с переменной в левую часть, а без переменной – в правую:
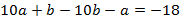
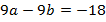
Запишем полученную систему линейных уравнений: 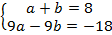 .
.
В первом уравнении выразим 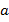 через
через 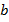 :
: 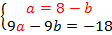 .
.
Воспользуемся методом подстановки – подставим это выражение во второе уравнение: 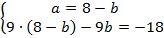 .
.
Во втором уравнении раскроем скобки: 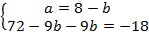 .
.
Перенесем все слагаемые с переменной в левую часть, а без переменной – в правую и выполним действия: 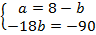 .
.
Найдем 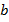 – число единиц в числе
– число единиц в числе 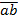 :
:
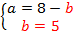
Найдем 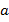 – число десятков в числе
– число десятков в числе 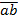 :
:
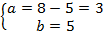
Таким образом, исходным числом является 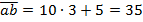 .
.
Ответ: 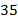 .
.
Заключение
На этом уроке мы потренировались решать различные уравнения и системы линейных уравнений, а также задачи, которые к ним сводятся.
Список рекомендованной литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, изд-во «Просвещение», 2017.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник, изд-во «Просвещение», 2014.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник, изд-во «Просвещение», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «school-assistant.ru» (Источник)
- Интернет-портал «yaklass.ru» (Источник)
- Интернет-портал «yaklass.ru» (Источник)
Домашнее задание
- Решите уравнение:
 .
. - Решите графически систему уравнений:
 .
. - Три утенка и четыре гусенка весят
 г, а четыре утенка и три гусенка весят
г, а четыре утенка и три гусенка весят  г. Сколько весит один гусенок?
г. Сколько весит один гусенок?
interneturok.ru
Тест: Решение задач с помощью уравнений
Выбери верный ответ
Математика 7 класс | ID: 243 | Дата: 24.10.2013
«;} else {document.getElementById(«torf1″).innerHTML=»»;}; if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;}; if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;}; if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;}; if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;}; if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;}; } }
Получение сертификата
о прохождении теста
testedu.ru
Урок алгебры «Решение задач на составление уравнений» для 7 класса
План-конспект урока
1. Ф.И.О. Чуприна Ольга Николаевна
2. Место работы МБОУ СОШ № 18 посёлка Паркового Тихорецкого района
3. Должность учитель математики
4. Предмет алгебра
5. Класс 7
6.Тема урока Решение задач на составление уравнений
7. Базовый учебник Алгебра. 7 класс: Г.В.Дорофеев, С.Б.Суворова, Е.А.Бунимович и др. – М.: Просвещение, 2017
8. Цель урока: Развить умения решать текстовые задачи алгебраическим способом: составлять уравнение по условию задачи, решать составленное уравнение.. проводить рассуждения, основанные на интерпретации условия поставленной задачи, для поиска целых корней некоторых несложных нелинейных уравнений
9. Планируемые результаты
личностные: вoспитание трудолюбия, коммуникабельности, интереса к умственной деятельности;
предметные: владеть базовым понятийным аппаратом по теме «Решение уравнений»
уметь применять свойства уравнений;
уметь решать уравнения;
уметь решать текстовые задачи способом составления уравнений.
Метапредметные: формировать умение создавать обобщение, развивать речь, внимание, мышление, память; решать задачи на составление линейного уравнения, по условию задачи
умение логически рассуждать; умение работать умение распознавать верные и неверные утверждения и решения; умение действовать в соответствии с предложенным алгоритмом; применение приёмов самоконтроля при решении учебных задач; умение видеть математическую задачу в несложных практических ситуациях.
Тип урока: изучение новой темы
1. Организационный моментПостановка цели и задач урока.
Тема урока определяется учащимися при помощи диалога с учителем:
Подписать число, тему
Регулятивные— постанoвка учебной цели
2. Устная работа
Повторение изученного ранее материала: алгоритм решения линейных уравнений
Карточка 1 на каждой парте. Дети работают в парах. Первые справившиеся с заданием пары показывают свое решение с помощью документ-камеры, отвечают на вопросы одноклассников и учителя
Регулятивные — определяют цель учебной деятельности, осуществляют поиск средств её достижения.
Познавательные -подведение под понятие, анализ объектов.
Коммуникативные-взаимоконтроль,
3. Объяснение нового материала.
Алгоритм решения задач с помощью уравнений:
I – х (ед.изм.) – это обычно то, что требуется узнать в задаче
II – через х выражается все остальное
III – составляется уравнение с помощью предложений в которых есть фразы «больше, меньше, во…, на…» Например: если х больше у на 10, то уравнение будет таким
х= у + 10
Цель учащихся научиться применять алгоритм решения задач с помощью уравнений для составления уравнения к любой задачи.
Познавательные-
выбор эффективных
способов решения задач, анализ
объектов для выделения свойств и признаков объектов, построение логической цепи рассуждения.
Регулятивные –
выявление объективной учебной информации
Коммуникативные—
использовать речевые средства для дискуссии и аргументации.
4. Разбор решения задачи 1 п.7.6 из учебника.
Решить задачи № №758(а), 759(а), 760(а), 762(а), 763(а).
Задачи №760 и 763 решают в парах
Карточка № 2 для каждой пары своя задача
Дети проводят работу по составлению и решению уравнений по условию задач на движение.
Карточку 2 решают дети в группах по 4 ученика. Затем защищают свое решение. Чтобы затратить меньше времени, дети свое решение показывают через документ- камеру
Познавательные-
выбор эффективных способов решения задачи,
рефлексия способов и условий действий.
Регулятивные-
контроль усвоения учебной информации
Коммуникативные-взаимоконтроль, работа в парах
5. Заключительный этап
Решаем старинную задачу: В 1881г. была найдена зарытой в земле близ Бахшали (северо-западная Индия) рукопись неизвестного автора, которая, как полагают, относится к VI-VIII вв. В этом памятнике, написанном на березовой коре и известным под названием ”Бахшалийской рукописи”, содержится такая задача:
“Из четырех жертвователей второй дал вдвое больше первого, третий – втрое больше второго, четвертый – вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?”
Решение:
Пусть первый дал х то следующие дали 2х, 6х, 24х, все же вместе дали 132.
х+2х+6х+24х=132
33х=132
х=4
Следовательно, первый дал 4, второй 8, третий 24, четвертый 96.
Познавательные-
выбор эффективных способов решения задачи,
рефлексия способов и условий действий.
Регулятивные-
самодиагностика и коррекция собственных учебных действий.
Коммуникативные-взаимоконтроль,
6. Подведение итогов урока. рефлексия
Ответы учащихся. В соответствии с целью урока
Познавательные—
рефлексия способов и условий действия.
Регулятивные-
оценивание результатов выполненной деятельности.
Коммуникативные-
использовать речевые средства для дискуссии и аргументации своей позиции.
7. Домашнее задание. №№№ №758(б), 759(б), 760(б), 762(б), 763(б).
Карточка 1. Решить уравнения:
1) 3х + 2 =11.
2) 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.
3) 2 (х + 3) = 5 – 6х.
4) – 6 (5 – 3х) = 8х – 7.
5) 5(x — 2) = 45
Карточка 2. Решить задачу:
I. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
II. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
III. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней второй догонит первого?
IV. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком расстоянии от турбазы был сделан привал?
V. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было орехов?
Решения:
№758(а)
х – (км/ч) – скорость туриста
(х + 10) –(км/ч) – скорость велосипедиста
0,5х(км) – прошел турист до встречи
0,5(х + 10)(км) – проехал велосипедист до встречи
0,5х + 0,5(х + 10) = 9
х = 4
4 км/ч – скорость туриста
Ответ: 4 км/ч
№759(а)
х – (км/ч) скорость пассажирского поезда
(х – 30) –(км/ч) – скорость электропоезда
2х –(км) — проехал до разъезда п.п.
2(х – 30) –(км) — проехал до разъезда эл.п.
2х + 2(х – 30) = 300
х = 90
2х = 180(км) – расстояние от А до разъезда
2(х – 30) = 120(км) — расстояние от В до разъезда
Ответ: 180 км от А, 120км от В
№ 760(а)
х – (км/ч) скорость 1 поезда
(х + 20) –(км/ч) – скорость 2 поезда
3х –(км) — проехал 1 поезд.
3(х + 20) –(км) — проехал до разъезда эл.п.
Всего проехали 480 км
3х + 3(х + 20) = 480
х = 70(км/ч) скорость 1 поезда
70 + 20 = 90(км/ч) – скорость 2 поезда
Ответ: 70 км/ч, 90км/ч.
№ 762(а)
х км/ч – скорость течения реки
(30 + х) (км/ч) – скорость катера по течению реки
(30 — х) (км/ч) – скорость катера против течения реки
3,5(30 + х) (км) – прошел катер по течению реки
4(30 — х) (км) – прошел катер против течения реки
3,5(30 + х) = 4(30 — х)
х = 2(км/ч) – скорость течения реки
3,5 * (30 + 2) = 112 (км) прошел катер по течению реки
Ответ: 2км/ч, 112км
№763(а)
х(ч) – плыла лодка по течению реки
(8 – х) (ч) – плыла лодка против течения реки
8 + 2 = 10(км/ч) –скорость лодки по течению реки
8 – 2 = 6(км/ч) – скорость лодки против течения реки
10х(км) – проплыла лодка по течению реки
6(8 – х) (км) — проплыла лодка против течения реки
10х = 6(8 – х)
х = 3(ч) – плыла лодка по течению реки
10 * 3 * 2 = 60(км) – проплыла лодка всего
Ответ: 3 часа, 60км.
Решение задач карточки 2
I.
х(км/ч) – собственная ск. теплохода
(х + 2)(км/ч) – скорость тепл-да по течению реки
(х – 2)(км/ч) – скорость тепл-да против течения реки
9(х + 2)(км) – прошел тепл-д по течению реки
11(х – 2)(км) – прошел тепл-д против течения реки
9(х + 2) = 11(х – 2)
х = 20(км/ч) – собственная скорость теплохода
Ответ: 20 км/ч.
II.
х(кошек) – грелось на солнышке
2х-было ушей
4х – было лап
4х = 2х + 10
х = 5(кошек) грелось на солнышке
Ответ: 5 кошек
III.
х (дней) – первый шел до встречи
(х -1) (дней) – второй шел до встречи
40х (верст) – прошел первый
45(х – 1) (верст) – прошел второй
40х = 45(х -1)
х = 9
через 9 дней после выхода первого второй его догонит
Ответ: через 9 дней
IV.
х(ч) – туристы шли до привала
(х + 15/60)(ч) = (х + 0,25) (ч) – туристы шли обратно
4,5х(км – туристы прошли до привала
4(х + 0,25)(км) – туристы прошли до турбазы
4,5х = 4(х + 0,25)
х = 2(км) от турбазы был сделан привал
Ответ: 2 км.
V.
х (учеников) всего
(х – 1) учеников получили по 5 орехов
3 + 5(х – 1)(орехов) – было всего
4х(орехов) — получили бы все ученики
3 + 5(х – 1) = 4х + 15
х = 17
4 * 17 + 15 = 83(ореха)
Ответ: 83 ореха.
infourok.ru
Решение задач с помощью уравнений. 7-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока:
- закрепление умения решать текстовые задачи с помощью уравнений;
- проверить уровень усвоения;
- развитие правильной математической речи;
- воспитание критичного отношения к себе.
Планируемые результаты:
- предметные: уметь применять алгоритм решения задач с помощью составления уравнений; уметь решать текстовые задачи с помощью уравнений; уметь работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи;
- личностные: уметь слушать собеседника и вести диалог, аргументировать свою точку зрения, дополнять и исправлять ответы других учащихся; способность сопереживать радость, удовольствие от верно решенной задачи; понимать смысл поставленной задачи;
- метапредметные: способность самостоятельно ставить цели учебной деятельности, планировать, осуществлять, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения, владение основами самоконтроля, самооценки.
Познавательные УУД: анализировать и осмысливать текст задачи, применять алгоритм решения текстовых задач с помощью уравнений.
Регулятивные УУД: работать по алгоритму, сверять свои ответы с ответами одноклассников.
Коммуникативные УУД: аргументировать свою точку зрения, участвовать в диалоге, работать в группах.
В результате у учащихся формируются такие качества личности, необходимые в современном обществе, как интуиция, логическое мышление, определение адекватных способов решения учебной задачи на основе заданных алгоритмов.
Задачи:
- образовательные: продолжить формировать умение решать текстовые задачи;
- воспитательные: умение слушать и вступать в диалог; формировать внимательность и аккуратность в вычислениях; прививать учащимся умение аргументировать свое мнение, повышая самооценку, самоконтроль, взаимоконтроль; требовательное отношение к себе и своей работе;
- развивающие: развитие навыков и способностей критического мышления; развитие у детей способности рассуждать.
Тип урока: урок закрепления знаний и умений.
Формы работы учащихся: фронтальная, индивидуальная, работа в группах.
Необходимое оборудование: доска, интерактивная доска, компьютер, карточки для коммуникации.
Ход урока
1. Организационный этап
Учитель приветствует учащихся, проверяет их готовность к уроку, предлагает обучающимся поделиться своим настроением с помощью карточек для коммуникации.
Доброе утро, садитесь. С каким настроением вы пришли ко мне на урок? Надеюсь, что с урока вы уйдёте с хорошим настроением и новыми знаниями.
Учащиеся слушают учителя, поднимают карточки.
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Кто может сказать, чем мы с вами занимались на прошлом уроке?
Правильно. Мы начали с вами применять уравнения для решения задач.
- Как вы считаете, достаточно ли вами решено задач? (Нет).
- Какая цель может быть у нас сегодня? (Закрепить умение решать текстовые задачи с помощью уравнений).
- Что для этого необходимо? (Продолжить решать текстовые задачи на эту тему).
Сегодня на уроке мы продолжим решать задачи с помощью уравнений. Работать вы будете в группах, а это значит, что нужно активно участвовать в совместной работе, внимательно выслушивать каждого члена группы, не перебивать собеседника, не смеяться над ошибками других, а помочь им в работе. В конце урока каждый получит оценку за свою работу.
Учащиеся отвечают на вопросы учителя и формулируют цель и задачи урока.
3. Устная работа
Проверим сначала, как вы научились решать линейные уравнения и составлять их по условию задачи? (Да).
Задания проецируются на экран. Презентация, слайд № 2.
№ 1. Составьте уравнение по условию задачи:
- В первой бригаде на 5 рабочих больше, чем во второй. Сколько рабочих в каждой бригаде, если всего в двух бригадах 77 человек?
- Длина прямоугольника в 2 раза больше ширины, а его периметр равен 138 см. Найдите размеры прямоугольника.
№ 2. Решите уравнение:
- 5 – 2х = 0;
- х – 8 = -4х – 9.
Учащиеся работают фронтально, выполняют предложенные задания.
4. Работа в группах
Повторение алгоритма решения задач с помощью уравнений. Перед вами на интерактивной доске алгоритм решения задач с помощью уравнения. Вам нужно найти ошибки и исправить их:
1. Обозначают все неизвестные числа буквой и, используя условие задачи, составляют уравнение.
2. Решают это уравнение.
3. Записывают полученный результат в ответ задачи.
Каждая из групп находит ошибки и подзывает учителя, даёт правильный ответ, потом ответ проверяется с помощью слайдов презентации.
5. Физкультминутка
Перед тем, как продолжить нашу работу, давайте немного передохнём.
— Встали. Потянулись. Поиграем в «Карлики – великаны».
6. Работа в группах
Решение задач
Каждая из групп решает задачу, показывает своё решение учителю, потом решение проверяется с помощью слайда презентации.
Задача 1: Три школы получили 70 компьютеров. Вторая школа получила на 6 компьютеров больше первой, а третья – на 10 компьютеров больше второй. Сколько компьютеров получила каждая школа?
Задача 2 (на движение): За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
7. Информация о домашнем задании
Решить задачи из учебника:
На свитер, шапку и шарф израсходовали 555 г шерсти, причём на шапку ушло в 5 раз меньше шерсти, чем на свитер, и на 5 г больше, чем на шарф. Сколько шерсти израсходовали на каждое изделие?
Можно ли 59 банок консервов разложить в три ящика так, чтобы в третьем было на 9 банок больше, чем в первом, а во втором – на 4 банки меньше, чем в третьем?
Тем, кому интересно, предлагаю решить старинную задачу:
Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 верст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 верст в день. Через сколько дней второй догонит первого?
8. Рефлексия
С каким настроением вы заканчиваете урок? Покажите карточкой.
Предлагаю каждой группе написать на листочках ответы на следующие вопросы:
- Что понравилось на уроке?
- Что не понравилось на уроке?
9. Подведение итогов
Оценивается работа каждого обучающегося, выставляются оценки.
Список литературы и источников Интернета.
- Учебник для общеобразовательных организаций. Алгебра. 7 класс: учеб. для общеобразоват. организаций с прил. на электрон. носителе / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В. Суворова; под ред. С.А.Теляковского. – М. : Просвещение, 2014.
- https://xn--80aa2aegbj2f.xn--p1ai/publications/igry-na-trave/%D1%88%D0%BA%D0%BE%D0%BB%D0%B0%D0%BC%D0%B0%D0%BC.%D1%80%D1%84/publications/igry-na-trave/
urok.1sept.ru
Конспект урока алгебры в 7 классе «Уравнения. Решение задач на составление уравнений»
Тема: Уравнения. Решение задач на составление уравнений
1) Организационный этап.
Приветствие, проверка присутствующих.
Давайте улыбнёмся друг другу и с хорошим настроением начнём наш урок.
2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Математику не зря называют «царицей наук», ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики — любознательность. Постараемся доказать это на уроке. Скажите, какую тему мы изучали на прошлом уроке? (Уравнения. Решения задач с помощью уравнений). Посмотрите на экран, решали ли мы такие уравнения? (Ответы учащихся: да, решали). А такие? А хотели бы проявить любознательность и решить похожее уравнение? Как вы думаете, какая цель нашего урока? (Предполагаемые цели ученика: научиться решать уравнения более сложные, чем те, способы решения которых ему известны.)
Мы изучили очень важную главу в курсе алгебры «УРАВНЕНИЯ». Вы знаете и умеете решать уравнения, приводимые к линейным, составлять различные уравнения по условию задачи. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу.
Итак, цель нашего урока: Повторение и закрепление полученных знаний по теме «Уравнения. Решение задач на составление уравнений», применение полученных знаний к решению уравнений и задач различного уровня сложности.
Откройте тетради, запишите число, тему. Сегодня на уроке мы продолжим работу по теме «Уравнения. Решение задач на составление уравнений».
3) Проверка домашнего задания, воспроизведение и коррекция опорных знаний учащихся. Актуализация знаний.
Начнём урок с проверки домашнего задания, потому что, чтобы узнать что-то новое, необходимо повторить уже изученный материал. У кого возникли трудности при решении домашнего задания? Все справились? Нет таких. А мне интересно, как вы справились с №157.
№157. Старинная задача. Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходит по 45 вёрст в день. Через сколько дней второй догонит первого?
Решение. Пусть второй человек догонит первого через х дней, тогда за эти дни он пройдет 45х верст. Первый человек, так как он шел на день дольше, пройдет 40(х + 1) верст. Зная, что они пройдут одинаковое расстояние, составим и решим уравнение:
х = 8.
Значит, второй человек догонит первого через 8 дней.
+ если ваши решения совпадают с решениями на доске
— если есть ошибки и вы не понимаете, почему не так
№150, №151, №153, №163.
4) Первичное закрепление в знакомой ситуации (типовые) в изменённой ситуации (конструктивные)
1. Корнем уравнения называется…
2. Решить уравнение — …
3. Равносильные уравнения — …
4. Линейное уравнение с одной переменной — …
Задание 1. Запишите в виде выражения:
г) произведение суммы чисел a и b и числа с.
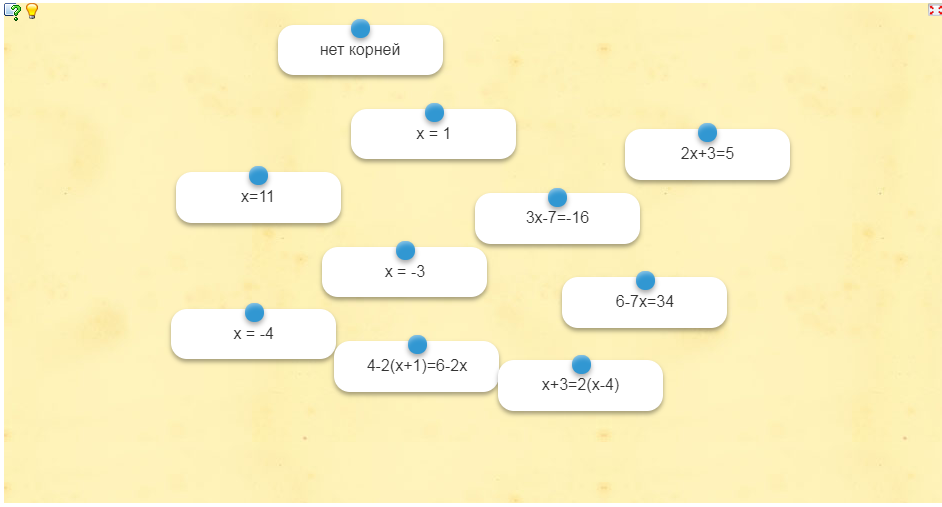
Задание 2. Установить соответствие между уравнением и его решением.
Ребята, у нас началась творческая работа. Был объявлен конкурс на составление уравнения. По итогам конкурса я предоставлю слово Мелешко Дарье, так как, на мой взгляд, её уравнение более сложное из всех представленных. Все остальные уравнения я также оценила, и мы будем рассматривать их на следующих уроках в качестве повторения темы.
(На слайде представлено уравнение, которое я составила самостоятельно. Так как в 5 классе мы решали уравнения с натуральными числами, дробями, в 6м – с использованием свойств сложения и вычитания, а также уравнения с пропорцией, у меня возникла идея, что получится, если соединить все те уравнения, которые мы решали в прошлых классах. И вот что у меня получилось:
Я предлагаю приступить к решению, в качестве подсказки на слайде выделено место для фиксирования промежуточного результата.)
Задание 3. Решить уравнение:
Ответ:
(57х — 6)/3 = 39 (х + 2)
Уравнение для Даши:
Ответ: 733/2000
Прежде чем приступить к решению задачи, давайте повторим этапы решения.
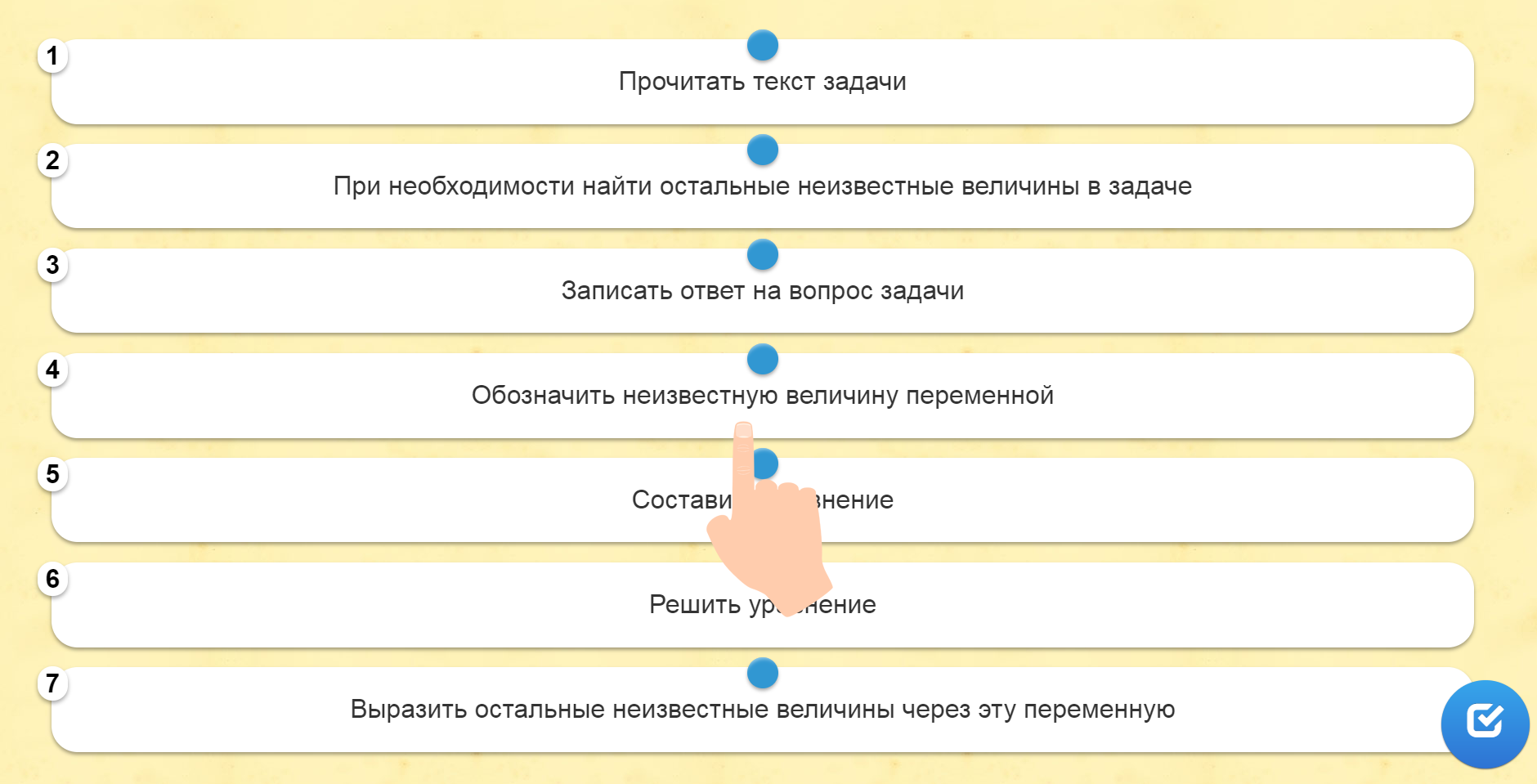
Задание 4. Расставить этапы решения задачи с помощью уравнения по порядку.
Задание 5. Задача. Из двух городов, расстояние между которыми равно 270 км, выехали одновременно навстречу друг другу автомобиль и автобус. Через 2 ч после начала движения расстояние между ними составляло 30 км. Найдите скорость автомобиля и автобуса, если скорость автомобиля на 10 км/ч больше скорости автобуса.
Решение с помощью презентации, уравнение решают самостоятельно.
(2х + 10) · 2 = 270 – 30,
(2х + 10) · 2 = 240,
2х + 10 = 120,
2х = 110,
х = 55.
Значит, скорость автобуса 55 км/ч, а скорость автомобиля – 65 км/ч.
Ответ: 55 км/ч, 65 км/ч.
Физкультминутка
Цель: снять утомление, обеспечить активный отдых и повысить умственную работоспособность учащихся.
Упражнения:
1) «Черепаха»: наклоны головы вперед -назад.
2) «Маятник»: наклоны головы вправо-влево.
3) «Собачка»: вращение головы вокруг воображаемой оси, проходящей через нос и затылок.
4) «Сова»: поворот головы вправо-влево.
5) «Весы»: левое плечо вверх, правое вниз. Поменять положение рук.
6) «Тянемся — потянемся»: руки вверх, вытягиваем позвоночник.
А теперь займемся решением задач
5) Творческое применение и добывание знаний в новой ситуации (проблемные задания)
Задача, составленная Соловьевой Юлией.
(Изучив все предложенные задачи в учебнике, я составила следующую задачу:
В магазин фруктов привезли ящики с бананами, апельсинами, грушами и персиками. Ящиков с грушами было на 20 штук меньше, чем ящиков с апельсинами и в 4 раза меньше, чем ящиков с персиками. Ящиков с бананами привезли в 3 раза больше, чем ящиков с апельсинами и грушами вместе. Найти, сколько всего ящиков привезли, если ящиков с бананами и грушами было на 50 штук больше, чем ящиков с персиками и апельсинами.
В качестве подсказки, я представляю схему условия, которую необходимо дополнить.)
Задача 6. В магазин фруктов привезли ящики с бананами, апельсинами, грушами и персиками. Ящиков с грушами было на 20 штук меньше, чем ящиков с апельсинами и в 4 раза меньше, чем ящиков с персиками. Ящиков с бананами привезли в 3 раза больше, чем ящиков с апельсинами и грушами вместе. Найти, сколько всего ящиков привезли, если ящиков с бананами и грушами было на 50 штук больше, чем ящиков с персиками и апельсинами.
Ответ: 140 ящиков
Уравнение (3(2х + 20) + х) – 50 = 4х + х + 20
Х = 5.
Груши – 5 шт., апельсины – 25 шт., персики – 20 шт., бананы – 90 шт.
Задача для Юли: Петя, Саша и Маша решали задачу. Петя решил её быстрее всех. Саша решил задачу только через 10 минут после того, как её решил Петя, а Маша решила задачу через 20 минут после того, как её решил Саша. Сколько минут решала задачу Маша, если эту задачу ребята решили ща 49 минут?
Уравнение: х + х + 10 + х + 10 + 20 = 49.
Ответ: Петя за 3 минуты, Саша за 13 минут, Маша за 33 минуты.
Самостоятельная работа
Ответы зафиксировать с помощью системы Mimio Vote.
1. Укажите уравнение, корнем которого является число 3.
А) (х — 3)(х + 3) = 2
Б) (х + 3)2 = 0
В) (х + 2)(х — 1) = 10
Г) |х| = -3
2. Какое из следующих уравнений имеет корни?
А) х + 2 = х + 3
Б) |x + 2| = -2
В) х2 = 0
Г) х2 = -4
3. Составьте по условию задачи уравнение, обозначив буквой х количество конфет, которые съела Алена.
Три подружки съели 23 конфеты. При этом Тамара съела в 3 раза больше конфет, чем Алена, но на 2 конфеты меньше, чем Наташа. Сколько конфет съела Алена?
А) 3х + 2 =23
Б) 7х + 2 = 23
В) 3х – 2 = 23
Г) 7х – 2 = 23
4. Укажите уравнение, которое не является линейным уравнением с одной переменной.
А) х(х — 5) = 0
Б) 2х + 3 (х — 4) = 5
В) 0,3 (х — 4) = 0,5 (х + 1)
В) x – 1 = 2 (x — 4)
5. Решите уравнение 0,3х – 0,45 = 0.
А) -15
Б) 15
В) 1,5
Г) -1,5
6. Укажите, при каком значении а уравнение ax – 5 = 0 имеет один корень.
А) а ≠ 0
Б) а = 0
В) а = 5
Г) нет таких значений а
7. Укажите, при каком условии уравнение a·x = 0 имеет бесконечно много корней.
А) а ≠ 0
Б) а = 0
В) а = 5
Г) нет условий
8. Выясните, какие из следующих уравнений равносильны:
1) х2 = 25; 2) х – 5 = 0; 3) (х — 5)(х + 5) = 0.
А) 2 и 3
Б) 1 и 2
В) 1, 2 и 3
Г) 1 и 3
9. Решите уравнение Укажите два целых числа, между которыми находится его корень.
А) 0; 1
Б) 3; 4
В) -4; -3
Г) -1; 0
10. Составьте уравнение к задаче, обозначив буквой х собственную скорость теплохода.
Расстояние от одной пристани на реке до другой теплоход проходит за 6 часов, а обратно за 5 часов. Найдите собственную скорость теплохода, если скорость течения реки равна 2 км/ч.
А) 6х = 5(х + 2)
Б) 6(х + 2) = 5(х — 2)
В) 6(х — 2) = 5х
Г) 6(х — 2) = 5(х + 2)
6) Информация о домашнем задании, инструктаж по его выполнению
I уровень — №246, №248, №252.
II уровень — №1188, №1189.
7) Рефлексия (подведение итогов занятия)
Наше занятие подходит к концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).
Вам для этого помогут слова:
1. Было интересно …
2. Было трудно …
3. Я выполнял задания …
4. Я понял, что …
5. Теперь я могу …
6. Я научился …
7. У меня получилось …
9. Я смог …
10. Меня удивило …
11. Мне захотелось …
12. Я попробую…
Резервные задания:
1. Верно ли решено уравнение


2. Правильно или неправильно составлено уравнение по условию задачи?
Обозначение неизвестногоУравнение
Верно/
неверно
1.
Расстояние от А до В автомобиль проехал за 2 часа, а грузовик за 2,5 часа. Чему равно расстояние от А до В, если известно, что скорость автомобиля была на 20 км/ч больше скорости грузовика?
х (км/ч) – скорость грузовика
2,5х = 2(х + 20)
+
2.
Сумма трёх чисел равна 92. Второе число меньше первого в 2 раза, больше третьего на 12. Найдите эти числа.
х – второе число
2х + х + (х + 12) = 92
—
3. Старинная задача
Уже около 4000 лет назад вавилоняне и египтяне решали разные задачи землемерия, строительства и военного дела с помощью уравнений. Уравнение первой и второй степеней умели решать в древности также китайские и индийские ученые.
Задача Бхаскара (крупнейший индийский математик и астроном XII века).
Некто сказал другу: «Дай мне 100 рупий, и я буду вдвое богаче тебя». Друг ответил: «Дай ты мне только 10, и я стану в 6 раз богаче тебя». Сколько было у каждого?
Решение:
170; 40. Вводя вспомогательное неизвестное, Бхаскара принимает, что первый имеет 2х – 100, тогда по условию задачи второй имеет х+100. Второе условие приводит к уравнению.
6(2х-100-10)=х+100+10, откуда х=70.
infourok.ru
Учебно-методический материал по алгебре (7 класс): Решение задач с помощью уравнений
ФИО: ЖиленкоЛилия Евгеньевна
Должность: учитель математики
Место работы: ГБОУ школа №480 г.Санкт-Петербург
Предмет: алгебра
Тема урока: «Решение задач с помощью уравнений»
Цель урока: создание условий для осознанного и уверенного владения навыком составления уравнений при решении текстовых задач.
Техническое обеспечение:
Алгебра 7 класс: учебник для учащихся общеобразовательных учреждений / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.:Вентана-Граф, 2018 г.
Задачи:
— образовательные (формирование познавательных УУД):
создать условия для формирования умений решать задачи с помощью уравнений, выполнять действия по нахождению неизвестных компонентов уравнений, составлять план решения задач по заданным условиям и в жизненных ситуациях составлять собственные задачи по заданным условиям; закрепить навыки и умения применять алгоритмы при решении уравнений и задач.
— развивающие (формирование регулятивных УУД)
определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий на уроке; фиксировать собственные затруднения на уроке; проводить рефлексию собственной деятельности и деятельности группы; находить информацию; осуществлять контроль правильности действий; выбирать способы решения задач в зависимости от конкретных условий; выявить качество и уровень овладения знаниями и умениями, полученными
— воспитательные (формирование коммуникативных и личностных УУД):
научить слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие;
уметь договариваться и приходить к общему решению в совместной деятельности, оценивать работу участников группы в тактичной форме, отражать результаты в устной и письменной речи, соблюдая правила речевого этикета, уметь использовать знаково-символические средства, воспитывать ответственность и аккуратность.
Тип урока – урок изучения нового материала.
Формы организации деятельности учащихся: фронтальная, групповая.
Ход урока
1. Организационный момент.
Мы урок начнем сейчас,
Интересен он для вас.
Слушайте внимательно,
Пойметё обязательно.
Давайте улыбнёмся друг другу и с хорошим настроением начнём наш урок.
2. Мотивация урока.
Начать урок я хочу с вопроса к вам. Как вы думаете, что самое ценное на Земле?
Выслушиваются варианты ответов учеников.
Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный писатель М. Горький: «Знание — это абсолютная ценность нашего времени. Нет силы более могучей, чем знание, человек, вооруженный знанием, — непобедим». Пусть эти слова станут девизом нашего урока.
3. Постановка целей урока.
Ребята. Сегодня мы с вами будем решать задачи. Это уже не ново для вас, мы решали задачи на вычисление периметра и площади прямоугольника, на нахождение части от числа и числа по его части, на движение и многие другие. А вот каким способом решения мы займемся сегодня – нам поможет узнать следующее задание.
Разгадайте ребус.
Итак, сегодня мы займемся решением задач с помощью уравнений. Как вы думаете, что нужно сделать, чтобы научиться правильно составлять уравнения? Такой приём мы уже применяли при решении задач «по действиям».
Ученики в процессе обсуждения приходят к мнению, что нужно попробовать самим составлять задачи.
Значит, сегодня на уроке перед нами стоят следующие задачи.
С помощью учеников учитель формулирует задачи урока. Вот возможные варианты.
- Учиться составлять уравнения к задачам.
- Учиться составлять задачи.
- Учиться определять тип задач.
Запишите в тетради тему урока: «Решение задач с помощью уравнений».
4. Устная работа.
Задание 1. Какое слово лишнее?
А) Километр, метр, сантиметр, длина, миллиметр, дециметр.
Б) Тонна, центнер, масса, грамм, пуд.
В каком отношении находится лишнее слово в каждом из списков?
Задание 2. Решить уравнения, повторяя правила нахождения неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя.
а) х + 23=48; в) 10 – х = 2; д) х : 10 = 4;
б) у – 10 = 28; г) 72 : у =9; е) 25х = 75.
5. Изучение нового материала.
Задание 1.
В одном бидоне х л, а в другом – у л молока.
1. Расшифруйте выражения:
а) х + у
б) x + 4
в) y – 1
г) x – y
2. Расшифруйте равенства:
а) х + у = 70
б) x + 9 = y
в) 3x = y
г) x – 15 = y + 25
Задание 2. Решите задачу.
Поле площадью 28 га разделили на два участка. Найдите площадь каждого участка, если известно, что один из участков на 4 га больше другого.
Разбор задачи.
О чем говориться в задаче? (Предполагаемый ответ: в задаче говорится о поле)
На какие части можно условно разделить поле в задаче? (I участок, II участок)
Какая величина характеризует поле? (Площадь поля)
В чем она измеряется? (Гектарах)
Какова площадь поля? (28 га)
Какова площадь первого участка? (Неизвестна)
Какова площадь второго участка? (Неизвестна)
Какова зависимость между неизвестными величинами? (Площадь первого поля на 4 га больше площади второго участка)
Если в задаче неизвестны значения каких-либо величин, но известна зависимость между ними, то задачу можно решать с помощью составления уравнения. Для этого необходимо ввести переменную и составить уравнение.
Решение.
Пусть х га площадь второго участка, тогда х + 4 площадь второго участка. Зная что, площадь всего поля 28 га, составим уравнение.
х + х + 4 = 28
х + х = 28 – 4
2х = 24
х = 24 : 2
х = 12
Значит 12 га площадь второго участка.
12+4 = 16 (га) площадь первого участка.
Ответ. 12 га и 16 га.
Ребята, каким образом поступают при решении задач с помощью уравнений?
- Обозначают некоторое неизвестное число буквой, и, используя условие задачи, составляют уравнение.
- Решают уравнение.
- Истолковывают полученный результат в соответствии с условием задачи.
6. Физкультминутка.
Быстро встали, улыбнулись.
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали. Сели, встали.
И на месте побежали.
7. Закрепление изученного материала.
Задание 1. Составьте несколькими способами уравнение для решения задачи.
Мотоциклист движется навстречу автобусу. Сейчас между ними расстояние 90 км. Они встретились через 1 час. Найдите скорость автобуса, если она больше скорости мотоциклиста в 2 раза.
Проверим решение задачи.
Пусть х км/ч- скорость мотоциклиста, тогда 2х км/ч – скорость автобуса.
Путь, который прошёл автобус: х∙1= х (км).
Путь, который проделал мотоциклист 2х∙1= 2х (км).
По условию задачи весь путь равен 90 км.
Возможные уравнения:
2х + х = 90
90 – х = 2х
90 – 2х = х
Какое из уравнений является самым простым для решения?
Решить № 34(чет),№37(чет)
8. Рефлексия.
Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).
Вам для этого помогут слова:
Я узнал…
Я почувствовал…
Я увидел…
Я сначала испугался, а потом…
Я заметил, что …
Я сейчас слушаю и думаю…
Мне интересно следить за…
9. Домашнее задание.
Для обязательного выполнения № 113,115
nsportal.ru
Решение задач с помощью уравнений (7 класс)

Решение задач с помощью уравнений-
7 кл.
Учитель Хренкова Г.Г.

Устный счет

Найди ошибку!
8х+40=8(х+2)+24;
8х+40=8х+16+24;
8х-8х=16+2 4 — 40;
0х=0;
х — любое число.
8х+40=8(х+2)+24;
8х+40=8х+16+24;
8х-8х=16+24 + 40;
0х=80.
уравнение корней не имеет.

Задача №1
Пусть Х- вес пустой коробки,
Пустая коробка в 4 раза легче коробки с сахаром
Тогда вес коробки с сахаром 4Х
Решение:
4х+4х+0,1=х+1+0,5;
С
С
А
А
Х
Х
А
А
р
р
4х+4х-х=1,5-0,1;
С
А
Х
А
р
1кг
7х=1,4;
500г
100г
х=1,4:7;
х=0,2;
0,2(кг) — пустая коробка,
Сколько весит сахар ?
0,2∙4=0,8(кг) -коробка с сахаром,
0,8-0,2=0,6(кг) — сахар.
Ответ: 0,6кг

Задача №2
Дано: АВСD – прямоугольник,
Р(АВСD)=64см,
АВ ‹ ВС на 8см.
1. 2х+2(х+8)=64;
Х+8
В
С
2. (х+х+8) 2=64 .
Х
D
А
Х = 12,
Значит одна сторона 12 см,
а вторая 12 + 8 = 20 (см)
Найти стороны ABCD
Составьте уравнение к задаче двумя способами.

Задача №3
Составить условие задачи по уравнению:
а) х+2х=15;
б) х +(х-2)=18.

По шоссе идут две автомашины с одной и той же скоростью.
Если первая увеличит скорость на 20 км/ч, а вторая уменьшит на 20 км/ч,
то первая за 2 ч пройдёт столько же, сколько вторая за 3 ч.
С какой скоростью идут автомашины?

Пусть х км/ч- скорость каждой машины.
1.
v,км/ч
t,ч
(х+20)
2.
(х-20)
S,км
2
3
(х+20)2
(х-20)2
По условию задачи, автомашины проехали одинаковое расстояние.
(х+20)2=(х-20)3;
2х+40=3х-60;
2х-3х=-60-40;
-х = -100;
Х=100;
100 км/ч-скорость каждой автомашины.
Ответ: 100 км/ч

Проверь себя!
В двух сараях сложено сено, причём, в первом сарае в 3 раза больше, чем во втором. После того, как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в сараях первоначально?

Пусть х т сена было во II сарае,
тогда (3х) т сена было в I сарае, а (3х-20) т стало в Iсарае,
(х+10)т стало во II сарае.
Известно, что в сараях сена стало поровну.
3х-20=х+10;
3х-х=10+20;
2х=30;
х=15; 15(т) было во II сарае;
15 ∙3=45(т) было в I сарае.
Ответ: 45 т

Дополнительные задания
Решите уравнения:
-2х=14;
3х=0;
0х=0;
0х=12;
(х-6)(х+11)=0;
Х(х+3)(х-1)=0.
kopilkaurokov.ru
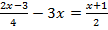 .
.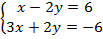 .
.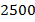 г, а четыре утенка и три гусенка весят
г, а четыре утенка и три гусенка весят 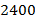 г. Сколько весит один гусенок?
г. Сколько весит один гусенок?