Решение основных задач по теме «Параллелограмм»
Задача 1.

По данным на рисунке докажите, четырёхугольник ABCD является параллелограммом.
Решение.
Так как BСА=CAD и они являются накрест лежащими при секущей АС, то прямые AD и ВС параллельны.
Имеем две стороны AD и BC четырёхугольника равны и параллельны, значит ABCD является параллелограммом.
Задача 2.
Дано: ABCD — параллелограмм; AB : BC = 4 : 5 см; PABCD = 10,8 см. Найти: AB; BC,CD,AD

Задача 3.
Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Решение.
Пусть меньший угол параллелограмма равен х, тогда больший угол будет равен (х + 40). Поскольку сумма односторонних углов равна 180 градусов, то составим уравнение:
x + x +40=180
2x=140
х=70
Таким образом, наименьший угол параллелограмма равен 70°.
Ответ: 70.
Задача 4.
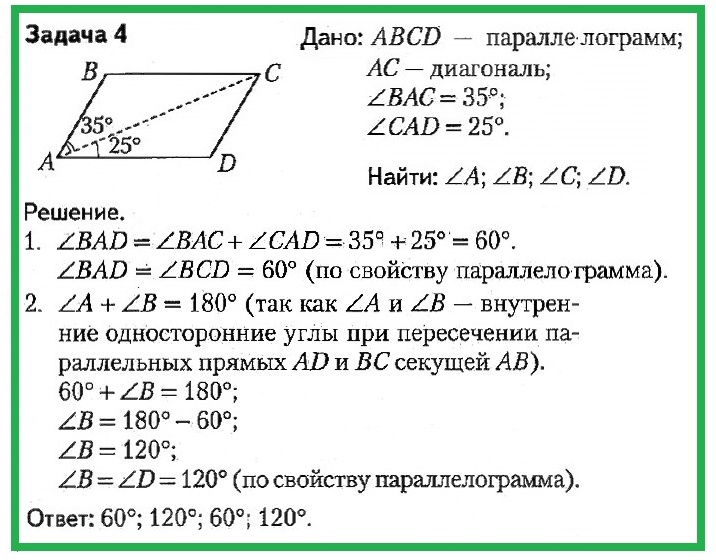
Дано: ABCD — параллелограмм; AC — диагональ; ∠BAC = 35°; ∠CAD = 25°. Найти: ∠A; ∠B; ∠C; ∠D.
Задача 5.
Дано: ABCD — параллелограмм; PABCD = 10 см; PABD = 8 см. Найти: BD.

Задача 6.
Дано: ABCD — параллелограмм; AK — биссектриса ∠A; BK : KC = 2 : 1; P ABCD = 50 см. Найти: AB; BC; CD; A

Задача 7.
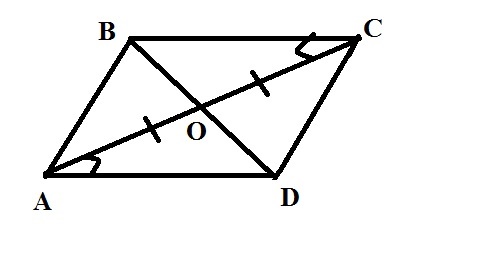
По данным на рисунке докажите, четырёхугольник ABCD является параллелограммом.
Решение.
Рассмотрим треугольники AOD и BOC. В них: ОAD= OCB по условию, AОD=COB ( как вертикальные) и AO=OC. Значит треугольники равны по второму признаку. Следовательно, BO=OD.
В четырёхугольнике диагонали AC и BD пересекаются и делятся точкой пересечения пополам, значит ABCD является параллелограммом.
Задача 8.
Высота LE параллелограмма KLRS делит сторону KS на отрезки KE и ES. Найти периметр параллелограмма, если известно, что KL=2 см, ES=4 см и K=60°.
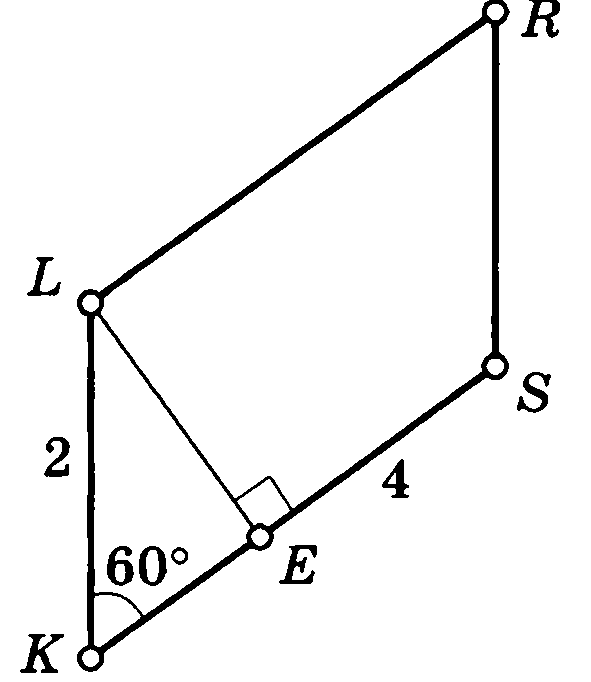
Решение. 1. В прямоугольном треугольнике KLЕ есть угол в 30° (KLЕ=180°-90°-60°=30°), значит катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, то есть KЕ=2:2=1см
2. KS= 1+4=5см
3. P KLRS =2+2+5+5=14 см.
Ответ: 14.
Задача 9.
Докажите, что биссектрисы односторонних углов параллелограмма – перпендикулярны.

Решение.
Пусть А=2х, а D=2у. А и D – односторонние, значит их сумма равна 180°. Поэтому 2х+2у=180 или х+у =90.
Так как АN и DM – биссектрисы, тоNAD=х, а MDA=у. По свойству суммы углов треугольника имеем: АOD = 180-(х+у) =180-90=90. А это значит, что прямые АN и DM – перпендикулярны.
infourok.ru
Задачи на параллелограмм. Видеоурок. Геометрия 8 Класс
На уроке мы, прежде всего, повторим уже изученные ранее свойства и признаки параллелограмма и все основные понятия, которые связаны с этой геометрической фигурой. Главной целью занятия будет рассмотрение нескольких примеров на применение знаний о параллелограмме. В процессе решения примеров познакомимся с важнейшей теоремой, связанной с параллельностью прямых, – теоремой Фалеса.
Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.
Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).
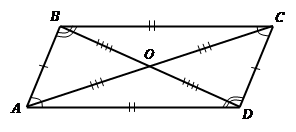
Рис. 1. Параллелограмм
Основные свойства параллелограмма:

Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм.  параллелограмм.
параллелограмм.

Рис. 2. Первый признак параллелограмма

Рис. 3. Второй признак параллелограмма
Теорема. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник – параллелограмм. 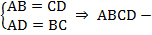 параллелограмм.
параллелограмм.
Теорема. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. 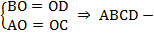 параллелограмм.
параллелограмм.
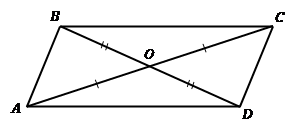
Рис. 4. Третий признак параллелограмма
Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.
Пример 1. В параллелограмме 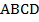 проведены биссектрисы
проведены биссектрисы 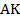 и
и  , которые пересекаются в точке
, которые пересекаются в точке 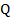 . Найти
. Найти 
Решение. Изобразим Рис. 5.
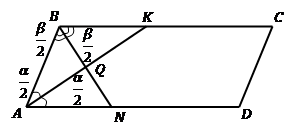
Рис. 5
Обозначим для удобства:  . Следовательно,
. Следовательно, 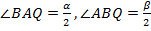 поскольку
поскольку  и
и  биссектрисы.
биссектрисы.
По теореме о сумме внутренних углов треугольника 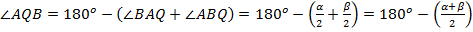 .
.
Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: 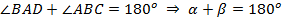
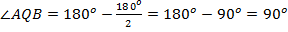 .
.
Ответ. 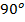 .
.
Пример 2. Прямая 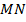 , проведенная через середину
, проведенная через середину 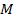 стороны
стороны 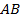 параллельно стороне
параллельно стороне 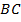
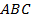 пересекает третью его сторону в середине. Доказать, что
пересекает третью его сторону в середине. Доказать, что 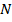 – это середина
– это середина 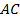 .
.Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем 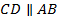 .
.

Рис. 6
Рассмотрим четырехугольник 
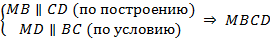 параллелограмм по определению. Тогда по свойству равенства противоположных сторон
параллелограмм по определению. Тогда по свойству равенства противоположных сторон  , но по условию еще известно, что
, но по условию еще известно, что 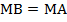 , следовательно,
, следовательно, 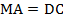 .
.
Рассмотрим треугольники 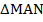 и
и 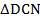 :
:
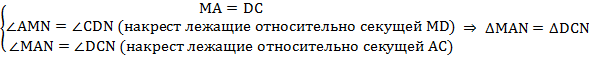 по второму признаку равенства треугольников (по стороне и прилежащим углам).
по второму признаку равенства треугольников (по стороне и прилежащим углам).
Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что 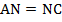 . Это означает, что точка
. Это означает, что точка 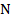 является серединой стороны
является серединой стороны 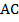 . Что и требовалось доказать.
. Что и требовалось доказать.
Доказано.
Теорема Фалеса. Если параллельные прямые, которые пересекают стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство. Изобразим Рис. 7.
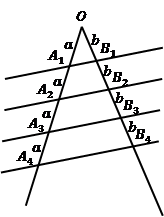
Рис. 7. Теорема Фалеса
Рассмотрим  . В нем точка
. В нем точка 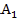 – середина стороны
– середина стороны 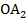 , а прямая
, а прямая 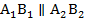 . Из предыдущего примера следует, что точка
. Из предыдущего примера следует, что точка  делит сторону
делит сторону 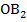 на две равные части, т.е.
на две равные части, т.е. 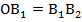 . Равенство двух отрезков, ближайших к вершине угла доказано. Аналогично доказывается попарное равенство всех остальных отрезков на второй стороне угла, если проводить прямые параллельные первой стороне угла через начало первого отрезка в любой рассматриваемой паре.
. Равенство двух отрезков, ближайших к вершине угла доказано. Аналогично доказывается попарное равенство всех остальных отрезков на второй стороне угла, если проводить прямые параллельные первой стороне угла через начало первого отрезка в любой рассматриваемой паре.
Доказано.
Рассмотрим пример на доказанную теорему.
Пример 3. Дан отрезок  , разделить его на три равные части.
, разделить его на три равные части.
Решение. Изобразим указанный отрезок на Рис. 8 и сделаем дополнительные построения: отложим три равных отрезка любой длины 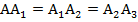 вдоль одной прямой, не совпадающей с указанным в условии отрезком.
вдоль одной прямой, не совпадающей с указанным в условии отрезком.
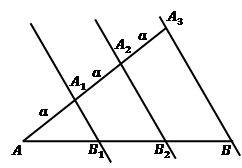
Рис. 8. Применение теоремы Фалеса
Соединим прямой точки 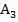 и
и 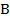 , а затем проведем прямые, параллельные прямой
, а затем проведем прямые, параллельные прямой 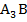 , через точки
, через точки  и
и 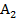 :
:  . Полученные при пересечении отрезка точки
. Полученные при пересечении отрезка точки  и
и 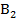 будут делить отрезок
будут делить отрезок  на три равных части по теореме Фалеса. Необходимое построение выполнено и задача решена.
на три равных части по теореме Фалеса. Необходимое построение выполнено и задача решена.
Ответ: построено.
Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях. А на следующем уроке мы познакомимся с таким видом четырехугольников, как трапеция, и обсудим ее свойства.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Narod.ru (Источник).
- Фестиваль педагогических наук «Открытый урок» (Источник).
Домашнее задание
- № 50 (г, д, е, ж, з, и), 51 (б, в, г, ж), 52 (б, в, е, ж). Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- В параллелограмме

 см,
см,  см, биссектрисы углов
см, биссектрисы углов  и
и  пересекают сторону
пересекают сторону  в точках
в точках  и
и  . Найдите длину отрезка
. Найдите длину отрезка  .
. - Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен
 . Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
. Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см. - ∗ Через середину
 диагонали
диагонали  параллелограмма
параллелограмма  проведена прямая, которая пересекает стороны
проведена прямая, которая пересекает стороны  и
и  в точках
в точках  и
и  соответственно. Докажите, что четырехугольник
соответственно. Докажите, что четырехугольник  параллелограмм.
параллелограмм.
interneturok.ru
Задачи с практическим содержанием по теме «Параллелограмм»
Малик Наталья Ивановна
учитель математики
первая категория
МБОУ – Займищенская СОШ им. Ф.Г. Светика
Г. Клинцы Брянской области
Задачи с практическим содержанием
по теме «Четырёхугольники»
Представленный ресурс можно использовать на уроке – практикуме
по теме Четырёхугольники»
Задача №1
Как найти расстояние между двумя недоступными для геодезиста точками А и В, используя признак параллелограмма.
Решение: 1случай
Расстояние до точек А и В измерить геодезист не может.

Отметим в доступном месте точки К, О и Е так, что КО=ОЕ.
Соединим АЕ и КВ (не измеряя) так, чтобы они пересеклись в доступной точке Р . Строим отрезок РО и равный ему ОМ . Получили параллелограмм КМЕР ( по признаку). Точку В1 получаем пересечением прямых КМ и АО, а точку А1 – пересечением МЕ и ВО.
Отрезок А1В1= АВ.
Докажем, что это верно. Точка О – центр параллелограмма, следовательно является центром симметрии. Действительно, при преобразовании симметрии относительно центра О точка К переходит в точку Е , точка Р — в точку М, прямая РЕ — в прямую КМ,
КР в МЕ, прямая РМ— в себя, а точка В — точка пересечения прямых КР и BО — в точку А1 пересечения ЕМ и BО. Аналогично точка А при этом преобразовании переходит в точку В1, поэтому отрезок АВ симметричен отрезку А1В 1 относительно точки О.

2 случай
С помощью приборов можно измерить расстояние ОА и ОВ. Достроить до параллелограмма АВРК, пользуясь признаком параллелограмма.
По свойствам параллелограмма КР=АВ. Измерить отрезок КР .
Задача №2
Школьная мастерская изготовила партию пластин четырёхугольной формы. Как проверить, будет ли иметь пластина форму прямоугольника, располагая лишь линейкой с делениями.
Решение:

1) Измерим пары противоположных сторон четырёхугольника.
Если они равны,то пластина имеет форму параллелограмма
(по признаку параллелограмма: Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник является параллелограммом).
2) Измерим диагонали данной пластины, если они равны, то параллелограмм является прямоугольником
(по признаку прямоугольника: Если диагонали параллелограмма равны, то он является прямоугольником)
Необходимо сделать 6 измерений
Задача №3

Фруктовый сад имеет форму прямоугольника, стороны которого относятся как 16:11, причём его ширина на 250 м меньше длины.
За сколько времени сторож может обойти вдоль забора весь участок, идя со скоростью 4км/ч?
Решение:
На ширину участка приходится 11 частей, а на длину – 16 частей.
16-11=5 частей приходится на 250 м
250:5 =50м приходится на одну часть
(16+11)*2= 54 части приходится на длину всего забора
54*50=2700м= 2,7км–длина забора
2,7:4=0,675ч=40,5 мин сторож может обойти вдоль забора весь участок, идя со скоростью 4км/ч
Ответ: за 40,5минут
Задача № 4
Разделите пополам угол, вершина которого недоступна
Решение:1способ

Проведём прямую ДР, получили ∆АДР, построим биссектрисы углов Д и Р. Точка К- точка пересечения биссектрис, а в треугольнике биссектрисы пересекаются в одной точке, следовательно искомая биссектриса должна проходить через эту точку.
Аналогично получаем точку О в ∆АВС.
Точки О и К – точки биссектрисы угла А.
Соединяем точки О и К.
Т.О. Прямая ОК делит угол пополам
2 способ

Проведём прямые АВ и ВС параллельно сторонам угла. Получили параллелограмм ХАВС с недоступной точкой Х.
Биссектриса АК отсекает от параллелограмма равнобедренный ∆ХАК,
По свойству равнобедренного треугольника биссектриса совпадает с медианой и высотой. Таким образом, можно построить серединный перпендикуляр к отрезку АК, который разделит данный угол Х пополам.
Задача №5
Столяру нужно изготовить подставку в форме четырёхугольника.
Сколько и какие размеры он должен измерить для выполнения заказа?
Решение этой проблемы дл столяра зависит от того, какие у него имеются инструменты



Рулетка
Циркуль
Угломер
А) Форма параллелограмма
1)
 Три измерения:
Три измерения:
смежные стороны и диагональ
( циркуль и рулетка)
2)

Три измерения:
смежные стороны и угол между ними
( угломер и рулетка)
Б) Форма прямоугольника
 Два измерения:
Два измерения:
смежные стороны
( при измерении используем только рулетку, при построении – угломер или другой инструмент для построения прямого угла)
В) Форма ромба

Два измерения:
диагонали ромба
( при измерении используем только рулетку, при построении – угломер или другой инструмент для построения прямого угла)
Г) Форма квадрата Д) равносторонний треугольник


Одно измерение: сторона
Задача №6
У плотника имеется только один инструмент – двусторонняя линейка без делений. Ему необходимо разделить кусок доски пополам. Как это сделать? (длина доски больше ширины линейки)
Решение:
Решение задачи основано на свойстве ромба: диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам





Задача №7
В старинном замке пол был покрыт паркетом. Каждая плитка имела форму равнобедренной трапеции, от которой остались лишь обломки. Среди них имеется обломок, у которого сохранилось меньшее основание и половина боковой стороны трапеции. Задача реставратора восстановить форму плитки (с помощью циркуля и линейки)
старинном замке пол был покрыт паркетом. Каждая плитка имела форму равнобедренной трапеции, от которой остались лишь обломки. Среди них имеется обломок, у которого сохранилось меньшее основание и половина боковой стороны трапеции. Задача реставратора восстановить форму плитки (с помощью циркуля и линейки)
Р ешение:
ешение:
Восстанавливаем боковую сторону АД. Строим прямую п перпендикулярную АВ, затем через точку Д прямую m перпендикулярную п. Прямые АВ и m параллельны. Далее воспользуемся свойством диагоналей равнобедренной трапеции ( диагонали равны), построим окружность с центром в точке В радиусом ВД. Восстановили четвёртую вершину трапеции.
АВСД- искомая трапеция.
Задача №8
На фотографии изображён образец паркета «Белочка».
Определить, какая фигура является основой для составления данного паркета, и вычислить площадь одной «белочки».


Решение: 1способ
По формуле Пика
Площадь многоугольника с целочисленными вершинами равна
S= В + Г/2 − 1,
Где В есть количество целочисленных точек внутри многоугольника,
а Г — количество целочисленных точек на границе многоугольника.

2 способ.
Площади равносоставленных фигур равны.
Выяснить перекраиванием, что данная фигура и квадрат равносоставлены, следовательно, их площади равны.
Определив сторону квадрата, находим площадь фигуры.
Литература:
1) Сборник задач по математике с решениями. 8—11 кл. / В. К. Егерев, В. В. Зайцев, Б. А. Кордемский и др.; Под ред. М. И. Сканави.
2) Задачи к урокам геометрии, 7-11 классы. (Зив Б.Г.) 1998
multiurok.ru
Задачи по геометрии параллелограмм. | Геометрия
Задачи по геометрии параллелограмм. | Геометрия — просто!
Добрый день, дорогие друзья!
Сегодня мы продолжим решение задач из сборника под редакцией М.И. Сканави.
И на этот раз мы будем решать задачи по геометрии параллелограмма.
Понятно, что прежде, чем приступать к решению таких задач, надо понимать, что такое параллелограмм и какие у него есть свойства.
Параллелограмм — выпуклый четырёхугольник, у которого противоположные стороны попарно параллельны.
У параллелограмма противоположные стороны и противоположные углы равны;
диагонали его делят параллелограмм на 2 равных треугольника,
а сами диагонали точкой пересечения делятся пополам.
И сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
Вот в основном те свойства, которые в первую очередь необходимы для понимания и решения задач по геометрии параллелограмма. А теперь задачи.
Задача 1. Периметр параллелограмма равен 90 см, а его острый угол равен 60°.
Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма.
Решение: Если угол А равен 60°, то угол В, лежащий рядом с ним , будет равен 180-60=120°.
Но диагональ BD делит его в соотношении 1:3, или на 4 равные части.
Получается, что одной части принадлежит 120:4 = 30°.
Следовательно, диагональ BD делит угол В на 2 угла 30° и 90°.
По рисунку угол 1 — прямой. Треугольник ABD — прямоугольный.
И угол 2 в треугольнике равен 30º, как накрест лежащий при параллельных прямых AB и CD и секущей BD.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, что АВ=1/2 AD.
Теперь составляем уравнение для периметра.
AB+BC+CD+AD=90
1/2AD+AD+1/2AD+AD= 90
3AD=90 AD=30 AB=1/2*30 = 15.
Ответ: стороны параллелограмма равны 30 см и 15 см.
Задача 2. Биссектриса острого угла параллелограмма делит его диагональ на отрезки длиной 3,2 см и 8,8 см.
Найти стороны параллелограмма, если его периметр равен 30 см.
Решение: Мы знаем, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные сторонам угла.
А именно, AB:AD = BO:OD, но BO и OD равны соответственно 3,2 см и 8,8 см.
Поэтому, можно принять, что АВ = 3,2х, а AD равно 8,8х.
Противоположные стороны параллелограмма равны.
Периметр это есть сумма всех сторон параллелограмма.
Составляем уравнение: 3,2х+8,8х+3,2х+8,8х = 30 24х = 30 х = 30/24 = 5/4.
Мы нашли коэффициент пропорциональности Х=5/4.
Отсюда, сторона АВ = 3,2х = 3,2 * 5/4 = 4 см.
Сторона AD равна 8,8х = 8,8 * 5/4 = 11 см.
Ответ: стороны параллелограмма равны 4 см, 4 см, 11 см, 11 см.
Задача 3. Параллелограмм с периметром 44 см разделён диагоналями на 4 треугольника.
Разность между периметрами двух смежных треугольников равна 6 см.
Найти стороны параллелограмма.
Решение: Рассмотрим два треугольника, лежащих выше диагонали d.
Периметр первого равен b+c+d.
Периметр второго равен a+c+d.
Разность периметров двух треугольников равна 6 см.
Составляем уравнение:
a+c+d — (b+c+d) = a+c+d-b-c-d = a-b = 6.
Получилось, что разность двух сторон параллелограмма равна 6 см.
Второе уравнение составляем из свойства периметра параллелограмма:
a+b+a+b = 44
2a+2b=44
a+b=22.
Получили систему двух уравнений с двумя неизвестными:
a — b = 6
a + b = 22 Решим её методом сложения. Сложим левые и правые части уравнений. Получим:
a — b + a + b = 6 + 22 2a = 28 a = 14.
a — b = 6 b = a — 6 = 14 — 6 = 8.
Ответ: Стороны параллелограмма равны 14 см, 14 см, 8 см, 8 см.
Задача 4. Перпендикуляр, опущенный из вершины параллелограмма на его диагональ, делит эту диагональ на отрезки АМ и МС длиной 6 см и 15 см соответственно.
Разность сторон параллелограмма равна 7 см.
Найти длины сторон и диагонали параллелограмма.
Решение: Примем сторону AB за a, сторону BC за b.
Из двух прямоугольных треугольников АВМ и ВМС выразим равный для них катет ВМ по теореме Пифагора.
АВ² — АМ² = ВС² — МС².
Подставляем вместо сторон известные выражения:
а² — 6² = b² — 15² или 15² — 6² = b² — а² (b — а) (b + а) = (15 — 6) (15 + 6),
но b — а = 7
7 (b + а) = 9 * 21 b + a = 9 * 3 = 27.
Имеем систему двух уравнений с двумя неизвестными, как в задаче 3.
b + a = 27
b — а = 7 Отсюда получаем 2b = 34 b = 17, a = 27 — 17 = 10.
Теперь, зная стороны параллелограмма, мы можем найти высоту ВМ.
ВМ² = 10² — 6² = 64. Отсюда ВМ = 8 см.
А теперь, из прямоугольного треугольника ВМО находим ВО.
ВМ = 8 см,
МО = АО — АМ = АС/2 — АМ = (6+15)/2 — 6 = 21/2 — 6 = 10,5 — 6 = 4,5 см.
По теореме Пифагора находим ВО.
ВО² = 8² + 4,5² = 64 + (9/2)² = 64 + 81/4 = 337/4. Или ВО = √337/2.
Поскольку BD в 2 раза больше, чем ВО, то её длина будет равна √337.
Ответ: Длины сторон параллелограмма 17 см, 17 см, 10 см, 10 см. Длина диагонали √337.
На сегодня всё. В следующий раз мы продолжим решение задач по геометрии из «Сборника для поступающих во ВТУЗы». Успехов!
Вам так же будет интересно:
Оставить комментарий
geometriyaprosto.ru
Задачи для самостоятельной работы на тему «Параллелограмм» (8 класс)
САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ №1 (8 КЛАСС)
Один из углов параллелограмма равен 400. Найдите остальные углы.
Один из углов параллелограмма равен 1050. Найдите остальные углы.
Найдите периметр параллелограмма, если его стороны равны 3,6 см и 5,8 см.
Найдите периметр параллелограмма, если его стороны равны 3,9 см и 7,6 см.
Найдите углы параллелограмма, зная, что один из них больше другого на 500.
Найдите углы параллелограмма, зная, что 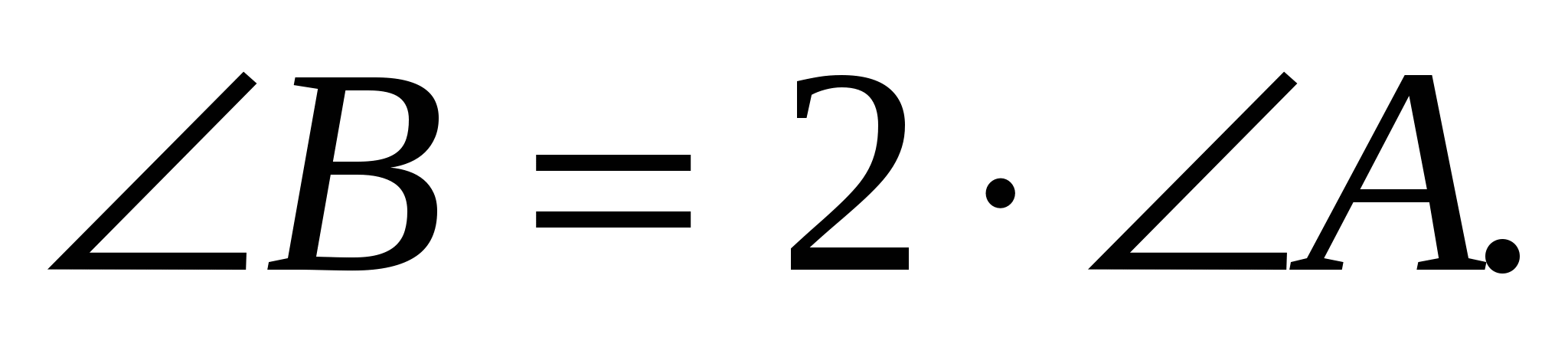
В параллелограмме биссектриса угла А делит сторону ВС на отрезки, равные 3 см и 5 см. Найдите его периметр.
В параллелограмме биссектриса угла В делит сторону АД на отрезки, равные 2 см и 6 см. Найдите его периметр.
Найдите все углы параллелограмма, если сумма двух из них равна 100 .
.
Найдите все углы параллелограмма, если сумма двух из них равна 2400.
Периметр параллелограмма равен 48 см. Найдите стороны, если одна из сторон в 2 раза больше другой.
Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если одна сторона на 3 см больше другой.
Существует ли параллелограмм, в котором одна сторона и две диагонали соответственно равны 10 см, 4 см, 8 см?
Существует ли параллелограмм, в котором одна сторона и две диагонали соответственно равны 7 см, 6 см, 8 см?
Найти углы параллелограмма, если неравные углы относятся, как 3:5.
Две стороны параллелограмма относятся как 3:4, а периметр его равен 2,8 м. Найдите стороны.
Найдите длину неизвестной стороны параллелограмма, если одна сторона равна 3,6 см и составляет 0,3 периметра.
Найдите длину неизвестной стороны параллелограмма, если одна сторона равна 5,4 м и составляет 40% периметра.
На диагонали ВД параллелограмма АВСД отмечены две точки P и Q так, что РВ=QД. Докажите, что четырехугольник АРСQ- параллелограмм.
Диагонали параллелограмма АВСД пересекаются в точке О. Докажите, что четырехугольник А1В1С1Д1, вершинами которого являются середины отрезков ОА, ОВ, ОС и ОД,- параллелограмм.
1 ВАРИАНТ- НЕЧЕТНЫЕ НОМЕРА, 2 ВАРИАНТ- ЧЕТНЫЕ НОМЕРА.
infourok.ru
Решение задач по теме: «Признаки параллелограмма»
Система задач на доказательство по теме «Признаки параллелограмма»
Гордеева М.Э. МКОУ Нижнечирская СОШ
Суровикинского района Волгоградской области.
Деятельностный подход в обучении математики позволяет выделить основные результаты обучения и воспитания, выраженные в терминах ключевых задач и способов действий, которые должны быть положены в основу выбора и структурирования содержания образования. Предложу конкретныq набор задач, позволяющиq реализовать вышеуказанные требования в одной отдельно взятой теме по геометрии в 8 классе. Важность рассмотрения решения задач на доказательство не надо описывать, данный вид задач постоянно встречается в заданиях ОГЭ в 9-х классах, во второй его части. Умение решать задачи такого типа, дает возможность учащемуся как можно дальше пройти процедуру ОГЭ и получить как можно больший балл. В своей работе успешно использую набор задач на доказательство того, что данный четырехугольник является параллелограммом.
На первом уроке совметно с учащимися разбираем и доказываем 6 признаков параллелограма: 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм. 2. Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник — параллелограмм. 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм. И дополнительные признаки: 4. Если биссектриса четырехугольника отсекает в нем равнобедренный треугольник, то этот четырехугольник — параллелограмм. 5. Есди биссектрисы соседних углов четырехугольника пресекаются под прямым углом, то этот четырехугольник — параллелограмм. 6. Если биссектрисы противолежащих углов четырехугольника параллельны, или лежат на одной прямой, то этот четырехугольник — параллелограмм.
К следующему уроку учащиеся учат все 6 признаков параллелограмма и решают систему задач на доказательство того, что данный четырехугольник является параллелограммом. Задачи привожу в порядке, соответствующем 1-6 признакам. Учитель может эти задачи дать учащимся для решения в тм порядке, кторый посчитает нужным сделать.
Задача №1.
Дано: АВСД — четырехугольникАВ=СД,
| Доказать: АВСД — параллелограмм |
Задача №2.
Дано: АВСД — четырехугольникΔАВС=ΔСДА
Доказать:
АВСД — параллелограмм
Задача №3.
Дано: АВСД — четырехугольникМА=МО=ОР=РС,
ВN=NO=OQ=QD
Доказать:
MNPQ — параллелограмм
Задача №4.
Дано: АВСД — четырехугольникАЕ- биссектриса ے А,
Доказать:АВСД — параллелограмм
Задача №5.
Дано: АВСД – четырехугольник,АN –биссектриса ےА
DK – биссектриса ےД
FN ∩DK=M
ےAMD=37º
ےADM=53º
Доказать:
ABCD — параллелограмм
Задача №6.
Дано: АВСД – четырехугольник,МС- биссектриса ےС,
AN – биссектриса ےА,
ےВМС=ےANC
Доказать:
ABCD — параллелограмм
В своей работе использую алгоритмы, которые позволяют облегчить учащимся их работу на различных этапах урока, занятия, при выполнении самостоятельной работы. В связи с переходом на стандарты второго поколения данная статья актуальна и востребована в педагогических кругах.
infourok.ru
Задачи по теме «Трапеция. Параллелограмм».
Задачи по теме «Трапеция. Параллелограмм».
I.
1. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.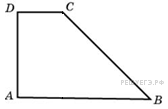

2.
Основания прямоугольной трапеции равны 13 и 21. Ее площадь равна 136. Найдите острый угол этой трапеции. Ответ дайте в градусах.
3.
Основания прямоугольной трапеции равны 6 и 18. Ее площадь равна 144. Найдите острый угол этой трапеции. Ответ дайте в градусах.
4.
Основания прямоугольной трапеции равны 21 и 29. Ее площадь равна 200. Найдите острый угол этой трапеции. Ответ дайте в градусах.
II.
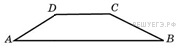
1. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
2. Основания трапеции равны 7 и 15. Боковая сторона, равная 6, образует с большим основанием трапеции угол, синус которого равен . Найдите площадь трапеции. 
3. Основания трапеции равны 10 и 18, боковая сторона, равная 2, образует с одним из оснований трапеции угол 60°. Найдите площадь трапеции.
4. Основания трапеции равны 13 и 5, боковая сторона, равная 3, образует с одним из оснований трапеции угол 45°. Найдите площадь трапеции.
III.
1. В параллелограмме из одной вершины проведены две высоты. Высота, проведенная к большей стороне равна 4, а высота, проведенная к меньшей стороне равна 8. Длина меньшей стороны равна 5. Найдите длину большей стороны. 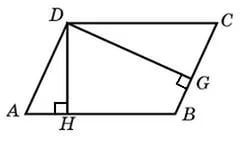
2. В параллелограмме АВСD высота DН проведена к стороне AВ, а высота DG проведена к стороне CВ. Найдите DG, если AВ=12см, ВC=8 см, DН=6 см.

3. Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны 2см и 3см. Найдите площадь этого параллелограмма.

4. АВСD — параллелограмм. Высота DН проведена к стороне AВ, а высота DG проведена к стороне ВC. Острый угол параллелограмма равен 60°, AD=6см, AH=0,3 AВ Найдите периметр параллелограмма АВСD . 
IV.
1. В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Чему равна длина отрезка ЕС, если АВ=9 см, AD=15 см?
2. Биссектриса угла D параллелограмме АВСD делит противоположную сторону на отрезки АL=7 см и LB=14 см. Найдите периметр параллелограмма.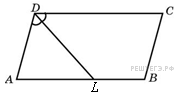
3. Биссектриса одного из углов прямоугольника делит противоположную сторону пополам. Найдите площадь прямоугольника, если его меньшая сторона равна 10 см.
4. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если его большая сторона 16 см, а один из углов равен 45°.
ОТВЕТЫ:
I. II.
III. IV.
infourok.ru
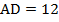 см,
см, 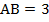 см, биссектрисы углов
см, биссектрисы углов  пересекают сторону
пересекают сторону 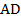 в точках
в точках 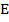 и
и 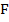 . Найдите длину отрезка
. Найдите длину отрезка 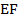 .
.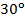 . Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
. Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см. диагонали
диагонали 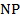 параллелограмма
параллелограмма 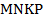 проведена прямая, которая пересекает стороны
проведена прямая, которая пересекает стороны 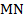 и
и  в точках
в точках 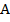 и
и 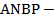 параллелограмм.
параллелограмм.