Задание №29 ЕГЭ по физике
Комбинированные задачи по механике
Особенность задания № 29 заключается в том, что в нем требуется использование материалов не менее чем из двух-трех разделов механики. Актуальные сведения, необходимые для решения задания, приведены в разделе теории. Законы сохранения, силы, действующие в макромире, и другая нужная информация содержится в разделах теории соответствующих типовых заданий по механике.
Теория к заданию №29 ЕГЭ по физике
Проекции сил, скорости, ускорения
При решении расчетных задач векторные величины требуется представлять в их скалярных (числовых) значениях. Для этого их выражают в виде проекций на оси выбранной инерционной с-мы координат, например: Fx, vY. Система координат может быть представлена единственной осью (Ox или Oy), если речь идет о движении по горизонтальной плоскости, о свободном падении тела и т.п. При перемещении тела под углом к горизонту и в других более или менее сложных случаях требуется прямоугольная система (Oxy).
Если направление вектора физ.величины совпадает с направлением координатной оси (или одной из осей, когда задача решается в рамках прямоугольной с-мы координат), то величина проекции совпадает с величиной ее модуля. К примеру, если тело бросают вертикально вниз с ускорением 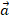
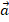 , то представив схему движения в системе Ox, ось которой направлена тоже вертикально вниз, получим для расчетов:
, то представив схему движения в системе Ox, ось которой направлена тоже вертикально вниз, получим для расчетов: 
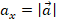 .
.Если векторная величина направлена по отношению к осям под углом, то вектор вместе со своими проекциями на оси прямоугольной системы координат образует прямоугольный треугольник, в котором вектор – гипотенуза, а проекции – катеты. Приняв угол между вектором и осью Оx равным α (на рисунке представлен пример для вектора ускорения),

величины проекций определяют таким образом:

 ;
;
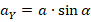
 .
.
Закон Архимеда
На помещенное в жидкость тело действует выталкивающая его сила. Эта сила традиционно обозначается как FA и вычисляется по формуле:

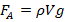 ,
,
где ρ – плотность жидкости, в которую помещено тело, 
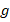 – ускорение свободного падения, V – объем погруженного тела. Относительно объема нужно отметить важный момент: если тело погружено полностью, то для расчета должен браться полный его объем; если тело погружено частично, то следует использовать объем части тела, находящейся в толще жидкости.
– ускорение свободного падения, V – объем погруженного тела. Относительно объема нужно отметить важный момент: если тело погружено полностью, то для расчета должен браться полный его объем; если тело погружено частично, то следует использовать объем части тела, находящейся в толще жидкости.Разбор типовых вариантов №29 по физике
Демонстрационный вариант 2018
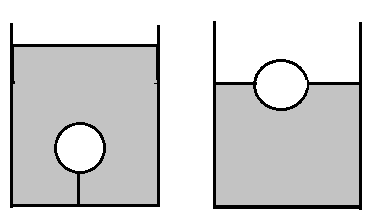
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S=100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой Т. Если нить перерезать, то шар всплывет, а уровень воды изменится на h=5 см. Найдите силу натяжения нити Т.
Алгоритм решения:
- Переводим числовые данные, приведенные в условии, в СИ. Записываем необходимое для решения табличное значение для плотности жидкости (воды).
- Анализируем начальную ситуацию (шар на нити). Определяем силы, действующие на шар.
- Анализируем ситуацию после перерезания нити. Определяем силы, действующие на шар. Составляем уравнение для вычисления объема вытесненной части шара.
- Применяя 3-й з-н Ньютона, составляем уравнения силы для начальной ситуации (1) и последующей (2). Из этой системы выражаем Т. Используя формулу з-на Архимеда и выражение для объема вытесненной части шара, находим Т.
- Записываем ответ.
Решение:
1. Переведем S и h в СИ:

 ,
,
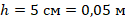
 . Плотность воды ρ равна:
. Плотность воды ρ равна: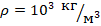
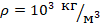 .
.2. Поскольку шар полностью погружен в воду, то он вытесняет объем воду, равный собственному объему. Обозначим его V1. На погруженный шар действуют: сила тяжести mg, сила Архимеда FA1, сила натяжения Т.
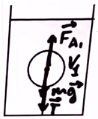
3. После перерезания нити уровень воды в сосуде понизился, поскольку шар всплыл и теперь занимает в толще воды только часть своего объема, вытесняя меньше воды. Обозначим этот объем через V2. Объем части шара, оказавшегося над поверхностью воды, составляет 
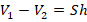 . Силы, действующие на шар: сила тяжести mg, сила Архимеда FT2.
. Силы, действующие на шар: сила тяжести mg, сила Архимеда FT2.

4. В обеих ситуациях шар находится в равновесии. Поэтому по 3-му з-у Ньютона:


(1) – (2) : 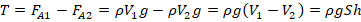
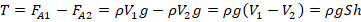 .
.
Отсюда: 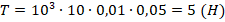
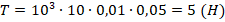 .
.
Ответ: 5 Н.
Первый вариант (Демидова, № 5)
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 100 г и m2 = 400 г, связанные нерастяжимой невесомой нитью длиной l. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). При вращении штанги с частотой 900 об/мин модуль силы натяжения нити, соединяющей грузы, T = 150 Н. Определите длину нити l.
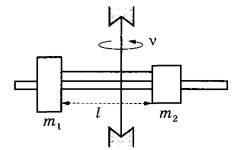
Алгоритм решения:
- Определяем для каждого из грузов инерциальную с-му отсчета, в которой, применив 2-й з-н Ньютона, записываем уравнения в соответствующих проекциях.
- Определяем вид ускорения и записываем формулы для его вычисления. Из предыдущих формул формируем уравнения для определения сил, действующих на грузы.
- Анализируем соотношения между входящими в уравнения величинами и после преобразований выводим формулу для вычисления искомой длины.
- Переводим в СИ несоответствующие ей значения из условия. Подставляем данные в результирующее уравнение, вычисляем длину нити.
- Записываем ответ.
Решение:
1. Выбираем системы отсчета для каждого из грузов так, чтобы их оси были направлены горизонтально (вдоль штанги) от края штанги к оси вращения:
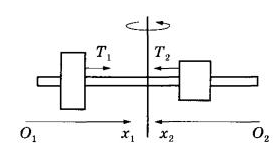
Т1 и Т2 на рисунке – силы, действующие соответственно на левый и правый грузы.
На основании 2-го з-на Ньютона запишем уравнения силы в проекции на оси с-м отсчета:
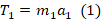
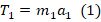 ;
;
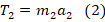
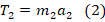 .
.2. Т.к. в данном случае имеет место вращательное движение, то грузы испытывают центростремительное ускорение. Для их вычисления используем формулу: 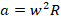
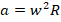 , где w – угловая скорость их вращательного движения, R – радиусы окружностей их вращения. Поскольку
, где w – угловая скорость их вращательного движения, R – радиусы окружностей их вращения. Поскольку 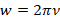
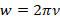 , то применив эту и предыдущую формулы для каждого груза, получим:
, то применив эту и предыдущую формулы для каждого груза, получим: 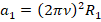
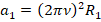 ,
, 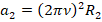
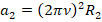 . Подставим формулы для
. Подставим формулы для 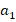
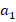 и
и 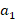
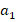 в (1) и (2). Получим:
в (1) и (2). Получим: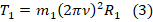
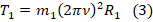 ;
;
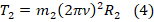
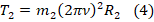 .
.
3. Если l – длина нити между грузами, то 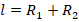
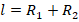 . Выразим радиус вращения одного из грузов (например, правого) через радиус другого:
. Выразим радиус вращения одного из грузов (например, правого) через радиус другого: 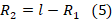
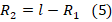 .Поскольку грузы связаны в единую систему, то
.Поскольку грузы связаны в единую систему, то 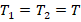
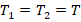 . Отсюда: (3)=(4) →
. Отсюда: (3)=(4) → 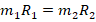
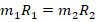 . Учтя при этом (5), имеем:
. Учтя при этом (5), имеем: 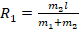
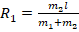 (6).
(6).
Приравняем Т к одной из сил, например: 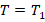
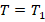 . Приняв при этом во внимание (6), получаем:
. Приняв при этом во внимание (6), получаем: 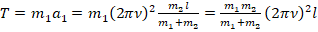
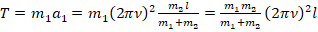 . Тогда:
. Тогда: 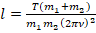
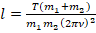 .
.
4. Переводим данные из условия в СИ: 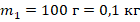
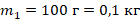 ;
; 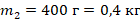
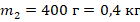 ;
; 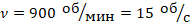
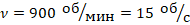 . Найдем l:
. Найдем l: 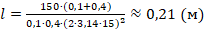
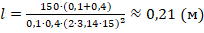
Ответ: 0,21 м.
Второй вариант (Демидова, № 11)
Снаряд, движущийся со скоростью 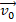
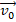 , разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счет энергии взрыва на величину ∆Е. Скорость осколка, движущегося вперед по направлению движения снаряда, равна
, разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счет энергии взрыва на величину ∆Е. Скорость осколка, движущегося вперед по направлению движения снаряда, равна 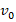
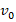 . Найдите массу m осколка.
. Найдите массу m осколка.
Алгоритм решения:
- На основании условия чертим схему движения описанных объектов.
- Используя з-н сохранения импульса, записываем уравнение для импульсов снаряда и осколков в проекции на ось Ох. Из него выразим модуль скорости для 2-го осколка (1).
- Приняв во внимание, что кинет.энергия осколков (по условию) увеличилась на ∆Е, запишем уравнение, описывающее соотношение энергий снаряда и осколков. Отсюда выразим массу осколка (2).
- Подставив (1) в (2) получим результирующее выражение для массы m.
- Записываем ответ.
Решение:
1. Схема движения снаряд и его осколков выглядит так:
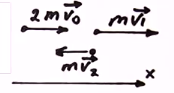
На схеме масса снаряда обозначена как 2m. Это следует из условия, что снаряд разорвался на равные части. Поскольку масса каждого из них составляет m, то их суммарная масса, являющаяся массой неразорвавшегося заряда, как раз и равна 2m. Обозначение на схеме « 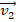
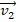 » – это скорость второго осколка, движущегося в противоположную снаряду сторону. Обозначения вида mv – импульсы, соответствующие снаряду и паре осколков.
» – это скорость второго осколка, движущегося в противоположную снаряду сторону. Обозначения вида mv – импульсы, соответствующие снаряду и паре осколков.
2. По з-ну сохранения импульса в момент разрыва снаряда 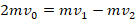
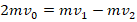 . Отсюда:
. Отсюда: 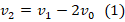
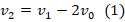 .
.
3. Выразим взаимосвязь энергий до и после разрыва снаряда: 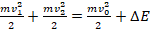
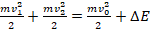 . Выполним преобразования и выразим m:
. Выполним преобразования и выразим m: 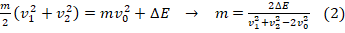
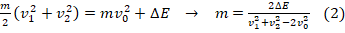
4. (1) → (2) : 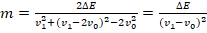
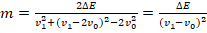 .
.
Ответ: 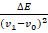
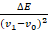 .
.
 Скачать PDF
Скачать PDF Распечатать
РаспечататьA1 | Зависимость координаты от времени для некоторого тела описывается уравнением Решение: По виду уравнения зависимости координаты от времени заключаем, что движение равноускоренное с отрицательной проекцией ускорения. Уравнение зависимости скорости от времени имеет вид: Верный ответ 2 | ||||
1) 6с | 2) 3 с | 3) 2с | 4) 0 | ||
A2 |
1 2 3 4
Верный ответ 3 | ||||
1) 1 | 2) 2 | 3) 3 | 4) 4 | ||
A3 | В каком случае потребуется большая сила, чтобы сдвинуть верхний брусок с места? Материал, из которых сделаны бруски, а также их массы одинаковы.
| ||||
1) в первом | 2) во втором | 3) в третьем | 4) во всех случаях сила одинакова | ||
Решение: Поскольку максимальная сила трения покоя примерно равна силе трения скольжения, то для того, чтобы сдвинуть брусок с места необходимо приложить силу по величине равную Fтр=μN, где N- сила нормальной реакции опоры. Поскольку тело находится на горизонтальной поверхности, N= mg. следовательно, Fтр=μ mg. Поскольку все бруски имеют одинаковую массу, то и сила, необходимая для т ого, чтобы сдвинуть их с места, должна быть одинаковой. Верный ответ 4 | |||||
A4 | Шарик массой m, двигаясь со скоростью V перпендикулярно стенке, упруго отскакивает от нее в обратную сторону с прежней по модулю скоростью. Чему равен модуль импульса силы, действовавшей на шарик в момент удара? Решение: Модуль импульса силы, действовавшей на шарик в момент удара, равняется модулю изменения импульса шарика |Dp|=2mv. Верный ответ 3 | ||||
1) 0 | 2) mV | 3) 2mV | 4) mV/2 | ||
A5 | Машина равномерно поднимает тело массой 20 кг на высоту h=10 м за время t=20 с. Чему равна ее мощность? Решение: Поскольку тело движется равномерно, работа силы тяги по модулю равна работе силы тяжести. А= mgh. Тогда мощность определится следующим образом: Верный ответ 1 | ||||
1) 100 Вт | 2) 10 Вт | 3) 1000 Вт | 4) 1 Вт | ||
A6 |
Решение: Скорость волны равна произведению ее длины волны на частоту колебаний частиц среды. Из рисунка видно, что половина длины волны равна 8 см, следовательно, длина волны 0,16 м. Умножая полученное значение на частоту (4 Гц), получим значение скорости, равное 0,64 м/с. Верный ответ 1 | ||||
1) 0,64 м/с | 2) 0,32 м/с | 3) 32 м/с | 4) 64 м/с | ||
A7 | На столе лежит книга массой 0,5 кг. Какая из указанных ниже сил, согласно третьему закону Ньютона, равна по модулю и противоположна по направлению силе тяжести, действующей на книгу? Решение: Сила тяжести обусловлена взаимодействием книги с Землей. По третьему закону Ньютона силой, равной по модулю и противоположной по направлению действующей на книгу силе тяжести, является сила тяготения, действующая на Землю со стороны книги. Верный ответ 3 | ||||
1) сила реакции опоры | |||||
2) вес книги | |||||
3) сила тяготения, действующая на Землю со стороны книги | |||||
4) сила трения покоя | |||||
A8 | Укажите пару веществ, скорость диффузии которых наибольшая при прочих равных условиях: Решение: Наибольшая скорость диффузии при прочих равных условиях наблюдается в газах. Верный ответ 2 | ||||
1) раствор медного купороса и вода | |||||
2) пары эфира и воздух | |||||
3) свинцовая и медная пластины | |||||
4) вода и спирт | |||||
A9 | Медь плавится при постоянной температуре 1085° C. Поглощается или выделяется энергия в этом процессе? Решение: Плавление меди происходит с поглощением энергии, поскольку внутренняя энергия расплава больше внутренней энергии меди в твердом состоянии. Верный ответ 1 | ||||
1) поглощается | |||||
2) выделяется | |||||
3) не поглощается и не выделяется | |||||
4) может поглощаться, может выделяться | |||||
A10 | 2 моль неона и 3 моль аргона находятся в разных сосудах при одинаковой температуре. Отношение значений внутренних энергий этих газов Решение: Внутренняя энергия неона и аргона определяется следующими с отношениями: Верный ответ 3 | ||||
1) 3/2 | 2) 4/3 | 3) 2/3 | 4) 1/3 | ||
A11 | В алюминиевый сосуд массой 100 г налито 200 г воды. Температура воды и стакана 750С. При опускании в воду серебряной ложки массой 80 г при температуре 150С температура воды в сосуде понизится на Решение: В теплообмене участвуют три тела: вода, алюминиевый стакан и серебряная ложка. При этом изменения агрегатного состояния не происходит. Уравнение теплового баланса имеет вид: Верный ответ 4 | ||||
1) 20С | 2) 1,50С | 3) 10С | 4) 1,20С | ||
A12 | Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,5 м3. При нагревании его давление возросло на 4∙103 Па. При этом внутренняя энергия газа увеличилась на Решение: Записывая уравнение Менделеева – Клапейрона Верный ответ 2 | ||||
1) 2 кДж | 2) 3 кДж | 3) 1,5 кДж | 4) 3 Дж https://5-ege.ru/ege-po-fizike-s-resheniyami-chast-a/ | ||
A13 | Расстояние между обкладками конденсатора уменьшили в 4 раза, не отключая его от источника зарядов. При этом напряжение на обкладках конденсатора Решение: Изменение расстояния между обкладками конденсатора без отключения его от источника зарядов приводит к изменению его емкости и заряда на обкладках конденсатора, напряжение при этом не меняется. Верный ответ 4 | ||||
1) уменьшилось в 4 раза | |||||
2) увеличилось в 4 раза | |||||
3) увеличилось в два раза | |||||
4) не изменилось | |||||
A14 |
Решение: Верный ответ 3 | ||||
1) 0,44 | 2) 0,67 | 3) 0,9 | 4) 1,5 | ||
A15 | При увеличении в 2 раза индукции однородного магнитного поля и площади неподвижной рамки поток вектора магнитной индукции Решение: Магнитный поток определяется следующим образом: Ф= B*S*cosa Следовательно, при увеличении в 2 раза индукции однородного магнитного поля и площади неподвижной рамки поток вектора магнитной индукции увеличится в 4 раза. Верный ответ 3 | ||||
1) не изменится | |||||
2) увеличится в 2 раза | |||||
3) увеличится в 4 раза | |||||
4) уменьшится в 4 раза | |||||
A16 | При прохождении электромагнитных волн в воздухе происходят колебания Решение: При прохождении электромагнитных волн в воздухе происходят колебания напряженности электрического и индукции магнитного полей Верный ответ 3 | ||||
1) молекул воздуха | |||||
2) плотности воздуха | |||||
3) напряженности электрического и индукции магнитного полей | |||||
4) концентрации кислорода | |||||
A17 | Дано: преломление светового пучка на границе стекло-воздух. Угол падения равен 60 градусов, а угол преломления – 30. Чему равен показатель преломления стекла? Решение: Показатель преломления Верный ответ 3 | ||||
1) 1 | 2) | 3) | 4) | ||
A18 | При прохождении света через стекло наибольшая скорость у лучей Решение: оранжевого цвета. Верный ответ 1 | ||||
1) оранжевого цвета | 2) синего цвета | 3) зеленого цвета | 4) голубого цвета | ||
A19 | Два точечных электрических заряда q1=4 мкКл и q2=10 мкКл находятся на расстоянии r друг от друга. Каким образом нужно перераспределить заряды, чтобы сила взаимодействия между ними была наибольшей? Решение: По закону Кулона сила взаимодействия двух точечных зарядов, находящихся на определенном неизменном расстоянии, прямо пропорциональна их произведению. При неизменном значении суммарного заряда наибольшее значение силы Кулона получается в случае равных зарядов. Наиболее просто в этом случае ответ может быть получен выбором произведения величин зарядов, приведенных в вариантах возможных ответов. Верный ответ 3 | ||||
1) q1=1 мкКл; q2=13 мкКл | |||||
2) q1=6 мкКл; q2=8 мкКл | |||||
3) q1=q2=7 мкКл | |||||
4) q1=14 мкКл; q2=0 мкКл | |||||
Задание №5 ЕГЭ по физике
Механика. Объяснение явлений.
В задании №5 ЕГЭ по физике необходимо выбрать верные варианты утверждений, характеризующие то или иное явление. Теория аналогична другим заданиям по механике, но мы напомним основные моменты.
Теория к заданию №5 ЕГЭ по физике
Колебания
Колебание – это многократно повторяющийся процесс, характеризующийся изменением значения некоторой физической величины около ее равновесного состояния.
Пружинный маятник
В пружинном маятнике сила упругости пропорциональна удлинению пружины F = –kx. Здесь k— коэффициент жесткости пружины, который не зависит от величины силы и смещения.
Максимальное отклонение от положения равновесия называется амплитудой. Сила упругости при этом отклонении максимальна, потому максимальным является и ускорение тела. При приближении к положению равновесия растяжение пружины уменьшается, что влечет за собой уменьшение ускорения тела, ведь оно зависит от силы упругости. Достигнув точки равновесия, тело не останавливается, хотя в этой точке сила и ускорение равны нулю. Скорость тела в точке равновесия пружины имеет наибольшее значение. По инерции тело продолжит движение мимо этого положения, деформируя пружину в противоположную сторону. Сила упругости, которая возникает при этом, тормозит маятник. Она направлена в сторону, противоположную движению маятника. Вновь достигнув амплитуды, тело останавливается, а потом начинает движение в обратную сторону, повторяя все описанное выше.
Период колебаний
Период колебаний такого маятника определяется формулой: 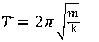
где m – масса тела (груза) на пружине
Потенциальная энергия
Потенциальная энергия равна произведению силы на отклонение, то есть 
где х – расстояние от точки, в которой находится груз маятника, до положения его равновесия
Кинетическая энергия
Кинетическая энергия зависит от скорости маятника и определяется формулой 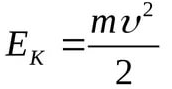 Здесь т – масса маятника, v – его скорость.
Здесь т – масса маятника, v – его скорость.
Ускорение тела
Модуль ускорения на отрезке пути определяется формулой 
где v, v0 – соответственно конечная и начальная скорости тела на указанном промежутке; t, t0 – конечное и начальное время соответственно.
Импульс тела
Импульс тела можно вычислить, используя формулу:
p=mv
где m – масса тела, v – его скорость
Сила Архимеда
Сила Архимеда является силой, с которой жидкость выталкивает тело, погруженное в нее. Она определяется формулой:
F=ρgV
где ρ – плотность погруженного физ.тела, g – ускорение своб.падения, V – объем тела.
Разбор типовых вариантов заданий №5 ЕГЭ по физике
Демонстрационный вариант 2018
В таблице представлены данные о положении шарика, прикрепленного к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
| t, с | 0,0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 |
| x, мм | 0 | 5 | 9 | 12 | 14 | 15 | 14 | 12 | 9 | 5 | 0 | -5 | -9 | -12 | -14 | -15 | -14 |
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера:
- Потенциальная энергия пружины в момент времени 1,0 с максимальна
- Период колебаний шарика равен 4,0 с
- Кинетическая энергия шарика в момент времени 2,0 с минимальна
- Амплитуда колебаний шарика равна 30 мм
- Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна
Алгоритм решения:
1. Анализируем таблицу данных движения шарика.
2–6. Определяем истинность утверждений 1–5.
7. Записываем ответ.
Решение:
- Максимальное значение потенц.энергии шарик имеет в моменты достижения амплитуды. Из таблицы видно, что наибольшее отклонение от состояния равновесия составляет – по модулю – 15 мм. Поскольку трением и сопротивление воздуха можем пренебречь (т.к. в условии не оговорено обратное), то состояние равновесия (когда пружина не деформирована) находится на одинаковом расстоянии от точек амплитуды, т.е. в нуле. Схематически движение такого маятника можно представить как:

- В момент t=1,0 c маятник отклоняется на 15 мм, т.е. достигает амплитуды. В таком положении шарик имеет максимальную потенц.энергию. Утверждение 1 верно.
- Периодом называют промежуток времени, за которое груз на пружине осуществляет 1 полное колебание. Пользуясь нашей схемой, можно утверждать, что полное колебание происходит, когда груз из точки амплитуды справа (15 мм) перемещается в точку амплитуды слева (–15 мм) и обратно. В таблице таким точкам соответствуют моменты времени t1=1 с, t2=3 c. Следовательно, чтобы переместиться между этими точками, требуется время ∆t=t2–t1=3–1=2 c. А чтобы вернуться обратно – еще столько же. Значит, Т=2∆t=2·2=4 c. Утверждение 2 верно.
- Смотрим в таблицу: при t= 2,0 с координата шарика равна 0 мм. Он в этот момент пролетает точку равновесия. И скорость его при этом максимальная. А кинетическая энергия равна полупроизведению массы на квадрат скорости. Следовательно, его кинетическая энергия максимальная. Значит, утверждение 3 неверно.
- Амплитуда равна 15 мм, поскольку это максимальное отклонение от положения равновесия. Следовательно, утверждение 4 неверно.
- Поскольку движение маятника происходит без трения, то выполняется з-н сохранения энергии, т.е. E=const. Поэтому полная механическая энергия не может быть в один момент времени быть большей или меньшей, чем в другой. Утверждение 5 неверно.
Ответ: 12
Первый вариант задания (Демидова, №3)
В инерциальной системе отсчёта вдоль оси Ох движется тело массой 20 кг. На рисунке приведён график зависимости проекции скорости vx этого тела от времени t. Из приведённого ниже списка выберите два правильных утверждения, описывающих движение тела.
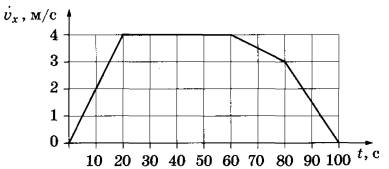
- Модуль ускорения тела в промежутке времени от 60 до 80 с в 3 раза больше модуля ускорения тела в промежутке времени от 80 до 100 с.
- В промежутке времени от 80 до 100 с тело переместилось на 30 м.
- В момент времени 90 с модуль равнодействующей сил, действующих на тело, равна 1,5 Н.
- В промежутке времени от 60 до 80 с импульс тела увеличился на 40 кг∙м/с.
- Кинетическая энергия тела в промежутке времени от 10 до 20 с увеличилась в 4 раза.
Алгоритм решения:
- Ищем модуль ускорения и проверяем истинность первого утверждения.
- Определяем расстояние, пройденное телом за указанный в утверждении 2 отрезок времени, и проверяем истинность его.
- Определяем величину равнодействующей всех сил, действующих на тело.
- Вычисляем изменение импульса в указанный промежуток.
- Находим кинетическую энергию в начале и конца проежутка и сравниваем их значения.
- Записываем ответ.
Решение:
1. Модуль ускорения на отрезке времени от 60 до 80 с равен 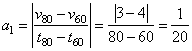 а на отрезке от 80 до100 с:
а на отрезке от 80 до100 с: 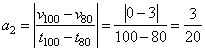 Как видим, утверждение неверно, (так как в условии сказано наоборот):
Как видим, утверждение неверно, (так как в условии сказано наоборот):
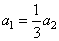
2. Используем только что найденное значение ускорения для вычисления координаты тела:
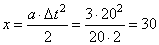 Это и есть пройденное расстояние. Утверждение верно.
Это и есть пройденное расстояние. Утверждение верно.
3. Равнодействующая всех сил, действующих на данное тело, равна F = ma. Вычислим ее, учитывая, что по условию масса тела m=20 кг, а ускорение a=3/20. Тогда F=20 ∙3/20 кг • м/с2 = 3 Н. Утверждение неверно.
4. Изменение импульса определяем таким образом: 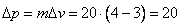 кг∙м/с. Утверждение неверное. 5. Кинетическую энергию тела в момент времени 10 с определяем по формуле:
кг∙м/с. Утверждение неверное. 5. Кинетическую энергию тела в момент времени 10 с определяем по формуле: 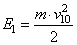 , а в момент 20 с
, а в момент 20 с 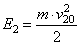 . Найдем их отношение:
. Найдем их отношение: 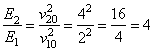 Значит, Е2=4Е1 — последнее утверждение верное.
Значит, Е2=4Е1 — последнее утверждение верное.
Ответ: 25
Второй вариант задания (Демидова, №27)
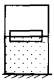
Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
- Если воду заменить на керосин, то глубина погружения брусков уменьшится.
- Сила Архимеда, действующая на бруски, равна 20 Н.
- Плотность материала, из которого изготовлены бруски, равна 500 кг/м3.
- Если на верхний брусок положить груз массой 0,7 кг, то бруски утонут.
- Если в стопку добавить ещё два таких же бруска, то глубина её погружения увеличится на 10 см.
Алгоритм решения:
- Анализируем условие задачи. Проверяем правильность первого утверждения.
- Определяем силу Архимеда, действующую на бруски. Сравниваем ее с указанным в утверждении 2.
- Находим плотность материала и определяем истинность утверждения 3.
- Проверяем истинность утверждения 4.
- Находим правильный ответ на последний вопрос.
- Записываем ответ.
Решение:
- На тела действует сила выталкивания F=ρgV. Плотность воды ρв=1000 кг/м3, ρк=800 кг/м3. Т.е. ρк<ρв. Поскольку ρ пропорционально F, то при снижении ρ сила тоже уменьшится. А это означает, что глубина погружения станет больше. Утверждение 1 неверно.
- На рисунке сила выталкивания удерживает нижнеетело погруженным полностью, но его верхняя грань находится награнице воды с воздухом. На бруски действуют сила тяжести нижнего бруска и сила тяжести верхнего тела. Т.к. массы брусков одинаковы, то F= 2mg. Эта сила уравновешена силой выталкивания. Тогда FА= 2mg= 2∙10∙1 = 20 Н. Утверждение 2 верно.
- Из формулы силы Архимеда, находим объем бруска (м3)
 Масса бруска по условию равна 1 кг. Тогда плотность каждого бруска определяется так (кг/м3):
Масса бруска по условию равна 1 кг. Тогда плотность каждого бруска определяется так (кг/м3): Утверждение 3 верно.
Утверждение 3 верно. - Если сверху на верхний брусок положить груз, массой 0,7 кг, верхний брусок не полностью погрузится в воду. Ведь нижний полностью погрузился, когда верхний брусок весил 1 кг. Эту массу в данном случае можно считать минимально необходимой для полного погружения. Значит, верхний брусок будет частично выступать из воды. Утверждение 4 неверно.
- Каждый следующий брусок массой в 0,7 кг будет частично погружать стопку нижних. Если сверху на бруски положить еще два таких же, то только два нижних бруска опустятся под воду, а верхние останутся над водой. Поскольку толщина каждого бруска равна 5 см, глубина, на которую будет погружено нижнее тело, будет больше на 5 см. Утверждение 5 неверно
Ответ: 23
 Скачать PDF
Скачать PDF Распечатать
РаспечататьМатериал для подготовки к ЕГЭ (ГИА) на тему: Методика решения задач по физике ЕГЭ части С (механика)
Слайд 1
МеханикаСлайд 2
Перед ребенком, решившим выбрать в своей жизни дорогу научно-технического направления, встают две задачи: ЭКЗАМЕНЫ (ГИА и ЕГЭ) . И для сдачи экзаменов в новых форматах успешной учебы в течение всех прошедших лет оказывается недостаточно. Проблема в том, что сдача экзаменов требует от ребенка особого алгоритма работы, повышенной интенсивности мыслительной деятельности, работы в измененном психофизическом стрессовом состоянии и работы с большим объемом информации. Можно уверенно сказать, что школьная программа на это не рассчитана.
Слайд 3
1. Поэтапно, в соответствии с последовательностью изучения 6 разделов школьного курса физики освоить все содержание основной триады (понятия-законы-границы применимости). Более того, в задачи школьной программы вовсе, не входит подготовка к ГИА и ЕГЭ. По действующему законодательству в задачи школы входит освоение учениками федеральных государственных образовательных стандартов (ФГОС) и не более. А экзамены ГИА и ЕГЭ – это уже проверка государством уровня подготовленности учеников по своим стандартам, которые попросту не связаны с ФГОС.
Слайд 4
2. После изучения триады соответствующего раздела физики освоить методы решения физических задач из этого раздела. 3. Проконтролировать освоение изученного раздела. «Подводные камни» Методика работает только при полной мотивации ребенка на обучение. Уговоры и принуждения при таком подходе попросту «не сработают». Школьнику необходимо выделить время на заучивание триады (понятия-законы-границы применимости), этого за него никто сделать не сможет. В случае же, если необходимые составляющие заучены не будут, все остальные учебные действия потеряют свою базовую опору и в сознании школьника не сохранятся.
Слайд 5
Существенные затруднения у учащихся ежегодно возникают при решении качественных задач. Порядка 70-75% экзаменуемых получали за ее решение ноль баллов. Дело в том, что примеры качественных заданий в пособиях для подготовки к экзамену и в опубликованном открытом сегменте КИМ присутствуют в минимальном количестве. Таким образом, возможности абитуриентов по целенаправленной подготовке к выполнению этой части экзаменационной работы были ограничены.. Результаты экзамены показали, что обучающиеся не умеют корректно использовать физические термины, ссылаясь при необходимости на физические законы.
Слайд 6
В качестве примера приведем подробное решение следующей задачи. Задача С1. Доказать, что крупные капли дождя падают быстрее, чем мелкие. Капли имеют форму шара, силу сопротивления воздуха считать пропорциональной площади поперечного сечения капли. Решение: Прежде всего, следует понять модель процесса. Совершенно ясно, что в данной задаче нельзя пренебречь силой сопротивления воздуха. Именно она и оказывает решающее влияние на скорость капли, и дело здесь не только в разной массе капель воды. Рассмотри силы, действующие на каплю при ее падении в воздухе
Слайд 7
На каплю вверх действует сила сопротивлении воздуха. пропорциональная квадрату радиуса (площади поперечного сечения), а вниз действует сила тяжести , пропорциональная массе тела, а следовательно объему тела, т.е. кубу радиуса капли. Таким образом, с ростом размера капли сила тяжести растет быстрее силы сопротивления воздуха., равнодействующая этих сил (направленная вниз) растет и растет ускорение капли. F т F сопр
Слайд 8
Основное затруднение при решении задач это создание алгоритма. К сожалению создать такой алгоритма невозможно. В некоторых разделах физики например в динамике некоторые элементы таких алгоритмов можно придумать. В динамике очень важно находить все силы. Действующие на тело и ускорение. Что является первичным в механике? Первичным является взаимодействие: гравитационное, электромагнитное, сильное и слабое. Результатом взаимодействия является сила. Определение сил и является построением модели задачи.
Слайд 9
Задача С2. Груз массой m располагается на поверхности клина с углом при основании α. К грузу прикреплена нить, другой конец которой привязан к гвоздю. Вбитому в вершину клина. Клин перемещается в горизонтальном направлении с ускорением а .Найти силу натяжения нити T силу давления груза на поверхность клина F д. Решение. На клин действует сила, вынуждающая его двигаться с ускорением а в горизонтальном направлении. Эта сила приложена именно к клину, но не к грузу на нем. Груз хоть и движется вместе с клином с таким же ускорением а , но под действием иных сил, приложенных к нему. Этими силами являются сила тяжести mg , сила натяжения нити Т и сила реакции опоры N . Совместное действие этих трех сил и сообщает грузу ускорение а .
Слайд 10
Y X N mg T cos α N sin α T N cos α T sin α α α α α α a
Слайд 11
Согласно второму закону Ньютона, применительно к грузу: ma = mg + T + N Запишем закон в скалярном виде. Спроецируем эти силы на оси координат ОХ и OY , сонаправив ось ОХ с ускорением груза и клин а . Тогда второй закон Ньютона в проекциях применительно к движению груза на клине имеет вид: ma = 0 + T cos α – N sin α ( 1 ) В этом уравнение есть две искомые величины N и T . Для их определения составим еще одно уравнение, спроецировав силы, приложенные к грузу , на ось OY : mg =T sin α +N cos α ( 2 ) Из уравнения ( 2 ) выразим силу N : N = (mg -T sin α ) / cos α ( 3 )
Слайд 12
и подставим в уравнение ( 1 ): ma = T cos α – (mg -T sin α ) sin α cos α преобразуем : ma cos α = T cos 2 α — mg sin α +T sin 2 α m (a cos α + g sin α ) = T ( sin 2 α + cos 2 α ) sin 2 α + cos 2 α = 1 отсюда: T = m (a cos α + g sin α ) – первая величина найдена. По третьему закону Ньютона сила давления груза F давл равна силе давления клина на груз, т.е. силе реакции опоры N , которая равна ( 3 ): N = (mg -T sin α ) / cos α – вторая величина найдена, Задача решена.
Слайд 13
Задача С3 . Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля, летящая навстречу шару. Она пробивает его и продолжает двигаться горизонтально. После попадания пули в шар он продолжает движение в прежнем направлении, пока нить не составит с вертикалью угол 39°. Определите массу пули, если в результате попадания в шар скорость пули уменьшилась на 100 м/с. (Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити, с os 39 ° = 0,778.
Слайд 14
1. По закону сохранения импульса Mu 1 — m υ 1 = Mu 2 — m υ 2 , где m – масса пули, u 1 , u 2 – скорости шара до и после взаимодействия с пулей соответственно. Отсюда ∆ υ = υ 2 — υ 1 = ( u 2 — u 1 ) ( 1 ) 2. По закону сохранения энергии скорость шара в нижней точке траектории до попадания в него пули равна: u 1 = √ 2gl(1- cosa ) . 3. По закону сохранения энергии скорость шара в нижней точке траектории после вылета из него пули равна: u 2 = √ 2gl(1- cos β ) . m M
Слайд 15
4. Подставляя в формулу ( 1 ) изменение скорости шара, получим: ∆ υ = υ 2 — υ 1 = M √ 2gl(1- cos β ) — √ 2gl(1- cosa ) , откуда: m = M √ 2gl(1- cos β ) — √ 2gl(1- cosa ) 5. Проводя вычисления, получим: m = 1 √ 2 . 10 . 0,9 (1 – 0,778) — √ 2 . 10 . 0,9 ( 1 – 0,5) = 0,01 кг Ответ: 0,01 кг υ 2 — υ 1 m — 100
Слайд 16
ЕЕЕЕЕЕ Е k Задача 4. Е k Е k Е P Задача решена.
Слайд 17
Задача 5. Тело массой m связано двумя пружинами одинаковой жесткости k , которые один раз соединяются параллельно, а второй- последовательно. В обеих случаях телу сообщается скорость υ . В каком отношении будут находится амплитуды колебаний грузов без учета трения и сопротивления ?
Слайд 18
Решение: 1. В первом случае пружины соединены параллельно, поэтому общая их жесткость равна k 1 = k + k = 2k . Закон сохранения энергии представится следующим образом: 2. При последовательном соединении пружин: 3.Отношение амплитуд собственных колебаний: Задача решена.
Слайд 19
Задача С6. Небольшой шар, надет на гладкую горизонтальную спицу, прикреплен к двум невесомым пружинам, вторые концы которых заделаны в неподвижную стену так, что в положении равновесия пружины не деформированы. Найти период колебаний тела, если при ее поочередном подвешивании к пружинам их удлинение составило ∆ x 1 и ∆ x 2 .
Слайд 20
Решение. 1. Жесткости пружин: 2. Пружины соединены параллельно. Поэтому их общая жесткость равна сумме жесткостей:
Слайд 21
3. Период колебания тела: Задача решена.
Слайд 22
Задача 6. Поднимая при помощи подвижного блока ведро с песком весом 200 Н на высоту 5 м, производят работу 1020 Дж. Какой процент составляет энергия, которая была затрачена непроизводительно? Решение: Полезная работа, которую нужно совершить, чтобы поднять груз весом Р на высоту h равна: А= Р . h = 200 . 5 = 1000 Дж . Общая совершенная работа составила А общ =1020 Дж. Таким образом, непроизводительно была затрачена энергия: ∆ А =А общ – А = 1020 — 1000 = 20 Дж. Эта величина составляет в процентном отношении: (∆ А /А общ ) . 100%= (20/100) . 100% = 2% То есть непроизводительно было затрачено 2% от общей энергии Задача решена.
 . В какой момент времени проекция скорости тела на ось равна нулю?
. В какой момент времени проекция скорости тела на ось равна нулю? . Определяем значения начальной скорости v0=12 м/с и ускорения, равного удвоенному коэффициенту при t2 (а=4 м/с2). Следовательно, уравнение скорости в нашем случае имеет вид:
. Определяем значения начальной скорости v0=12 м/с и ускорения, равного удвоенному коэффициенту при t2 (а=4 м/с2). Следовательно, уравнение скорости в нашем случае имеет вид:  . Подставляя v=0, находим t=3с.
. Подставляя v=0, находим t=3с. Тело движется вдоль оси Ох под действием силы F. Проекция скорости тела меняется по закону, представленному на рисунке. По какому закону изменяется проекция силы Fх?
Тело движется вдоль оси Ох под действием силы F. Проекция скорости тела меняется по закону, представленному на рисунке. По какому закону изменяется проекция силы Fх?
 Решение: Из анализа графика следует, что движение тела равноускоренное с отрицательной проекцией ускорения. Такое движение осуществляется под действием постоянной по модулю силы, проекция которой на направление движения отрицательна.
Решение: Из анализа графика следует, что движение тела равноускоренное с отрицательной проекцией ускорения. Такое движение осуществляется под действием постоянной по модулю силы, проекция которой на направление движения отрицательна.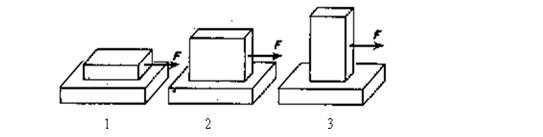
 . После подстановки и вычислений получим N=100 Вт.
. После подстановки и вычислений получим N=100 Вт. На рисунке изображена поперечная волна. Частота колебаний частиц среды, в которой она распространяется, 4 Гц. Чему равна скорость волны?
На рисунке изображена поперечная волна. Частота колебаний частиц среды, в которой она распространяется, 4 Гц. Чему равна скорость волны? равно
равно ,
, 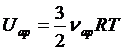 . Поскольку значения всех величин, входящих в правые части этих равенств, за исключением n, одинаковы, отношение значений внутренних энергий определяется отношением
. Поскольку значения всех величин, входящих в правые части этих равенств, за исключением n, одинаковы, отношение значений внутренних энергий определяется отношением 
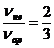 .
. , где mв, mст и mл – массы воды, стакана и ложки соответственно, св, сал и сс – удельные теплоемкости воды, алюминия и серебра, t1– начальная температура воды и стакана, t2 – начальная температура ложки, q – температура термодинамического равновесия. Из уравнения находим q = 73,80С. Следовательно температура воды в сосуде понизится на 1,20С.
, где mв, mст и mл – массы воды, стакана и ложки соответственно, св, сал и сс – удельные теплоемкости воды, алюминия и серебра, t1– начальная температура воды и стакана, t2 – начальная температура ложки, q – температура термодинамического равновесия. Из уравнения находим q = 73,80С. Следовательно температура воды в сосуде понизится на 1,20С. (1) для начального и конечного состояний и вычитая из второго уравнения первое, получим
(1) для начального и конечного состояний и вычитая из второго уравнения первое, получим  (2). Изменение внутренней энергии идеального одноатомного газа
(2). Изменение внутренней энергии идеального одноатомного газа  (3) или, с учетом (2),
(3) или, с учетом (2),  . Подставляя числовые значения, получим
. Подставляя числовые значения, получим кДж.
кДж.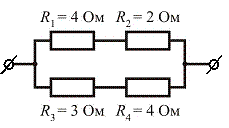 На рисунке представлен участок электрической цепи. Каково отношение количеств теплоты
На рисунке представлен участок электрической цепи. Каково отношение количеств теплоты 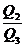 , выделившихся на резисторах R2 и R3 за одно и то же время?
, выделившихся на резисторах R2 и R3 за одно и то же время?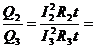
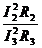 (1), где I2 и I3 – токи, которые текут на верхнем и нижнем участке цепи. Поскольку напряжение на параллельно соединенных участках одинаково, I2*(R1+R2)= I3*(R3+R4), а
(1), где I2 и I3 – токи, которые текут на верхнем и нижнем участке цепи. Поскольку напряжение на параллельно соединенных участках одинаково, I2*(R1+R2)= I3*(R3+R4), а 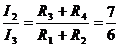 . Подставляя числовые значения в формулу (1), получим
. Подставляя числовые значения в формулу (1), получим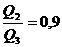
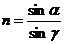 , где угол падения a=60о, а угол преломления g=30о. Подставляя значения синусов в формулу (1), получим n=
, где угол падения a=60о, а угол преломления g=30о. Подставляя значения синусов в формулу (1), получим n=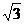
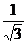
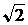
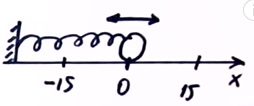
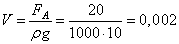 Масса бруска по условию равна 1 кг. Тогда плотность каждого бруска определяется так (кг/м3):
Масса бруска по условию равна 1 кг. Тогда плотность каждого бруска определяется так (кг/м3):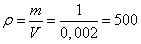 Утверждение 3 верно.
Утверждение 3 верно.