Относительность движения_9 класс — задачи — Каталог статей

1.     Скорость велосипедиста 10 м/с, а скорость встречного ветра 6 м/с. Определите скорость ветра относительно велосипедиста.

За тело в данной задаче лучше считать ветер, неподвижной системой отсчета – землю, подвижной – велосипедиста. Тогда 10 м/с – это скорость v₂ подвижной СО, 6 м/с – скорость v₁ тела относительно неподвижной СО. Так как ветер встречный, то v₁ и v₂  направлены в противоположные стороны.

Тогда v₁ = v_1,2 – v₂, откуда искомая v_1,2 = v₁  + v₂.

v_1,2 = 10 + 6 = 16 м/с.

2.     Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда?

Телом в данной задаче будем считать второй поезд, неподвижная СО – Земля, подвижная СО – первый поезд. 72 км/ч = 20 м/с – скорость v₂ подвижной СО, 54 км/ч = 15 м/с – скорость v₁ тела относительно неподвижной СО. Длина поезда – перемещение s_1,2 тела относительно подвижной СО. Так как поезда движутся навстречу друг другу, то v₁ = v_1,2 – v₂, откуда искомая v_1,2 = v₁  + v₂. А перемещение s_1,2 = t (v₁  + v₂).

s_1,2 = 14 ∙(20 + 15) = 490 м.

3.     Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору?

Телом будем считать пассажира, подвижной СО – эскалатор, неподвижной – Землю. Эскалатор и пассажир движутся в одном направлении. Поэтому         v₁ = v_1,2 + v₂

Скорость определяется как отношение пути ко времени движения. Тогда

Относительность движения и система отсчета в физике

Тело отсчета и система координат

Тело отсчета выбирают произвольно. Следует отметить, что движущееся тело и тело отсчета равноправны. Каждое из них при расчете движения в случае необходимости можно рассматривать или как тело отсчета, или как тело движущееся. Например, человек стоит на Земле и наблюдает, как по дороге едет автомобиль. Человек неподвижен относительно Земли и считает Землю телом отсчета, самолет и автомобиль в этом случае тела движущиеся. Однако, пассажир автомобиля, который говорит, что дорога убегает из-под колес, тоже прав. Он считает телом отсчета автомобиль (он неподвижен относительно автомобиля), Земля при этом – тело движущееся.

Чтобы фиксировать изменение положение тела в пространстве, с телом отсчета нужно связать систему координат. Система координат – это способ задания положения объекта в пространстве.

При решении физических задач наиболее распространенной является декартова прямоугольная система координат с тремя взаимно перпендикулярными прямолинейными осями – абсциссой (), ординатой () и аппликатой (). Масштабной единицей измерения длины в СИ является метр.

При ориентировании на местности пользуются полярной системой координат. По карте определяют расстояние до нужного населенного пункта. Направление движения определяют по азимуту, т.е. углу, который составляет нулевое направление с линией, соединяющей человека с нужным пунктом. Таким образом, в полярной системе координат координатами являются расстояние и угол .

В географии, астрономии и при расчетах движений спутников и космических кораблей положение всех тел определяется относительно центра Земли в сферической системе координат. Для определения положения точки в пространстве в сферической системе координат задают расстояние до начала отсчета и углы и — углы, которые составляет радиус-вектор с плоскостью нулевого гринвичского меридиана (долгота) и плоскостью экватора (широта).

Система отсчета

Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.

При решении любой задачи о движении прежде всего должна быть указана та система отсчета, в которой будет рассматриваться движение.

При рассмотрении движения относительно подвижной системы отсчета справедлив классический закон сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной:

   

Примеры решения задач по теме «Относительность движения»

Методическая разработка по физике (9 класс) по теме: Интегрированный урок «Решение задач на относительность движения»

План-конспект интегрированного урока с применением технологии личностно-ориентированного обучения: геометрия + физика.

Тема: «Векторы. Решение задач на относительность скоростей».

Кончакова Светлана Юрьевна

Учитель физики

 МОУ « ООШ с. Покровка Вольского

 района Саратовской области»

Цели:

Синтезировать и обобщить полученные теоретические и практические знания на уроках геометрии и физики.

Развивать умения использовать теоретические знания при решении практических задач, способность анализировать и обобщать полученные данные, работать с дополнительной литературой.

Развивать логическое мышление, память, самостоятельность. Формировать коммуникативную и эмоциональную культуру. Продолжать показ тесной связи точных наук.

Тип урока: урок  обобщения, повторения и коррекции знаний.

Ход урока.

I. Орг. момент

«Практика рождается от тесного соединения физики и математики»

II. Повторение теоретического материала из геометрии.

1. Что называется вектором?
2. Что такое абсолютная величина вектора?
3. Какие векторы называются равными?
4. Какие векторы называются сонаправленными?
5. Какие векторы называются коллинеарными?
6. Как сложить два сонаправленных вектора? Сделать чертеж.
7. Как сложить два противоположнонаправленных вектора? Сделать чертеж.
8. Как сложить неколлинеарные векторы с помощью правила параллелограмма? Сделать чертеж.

III. Повторение теоретического материала по физике.

1. Как понимать движение тела относительно?
2. Как понимать скорость тела относительна?
3. По дороге едут автомобиль и автобус с одинаковой скоростью 60км\ч. Укажите тело отсчета, относительно которого задана эта скорость. Относительно какого тела отсчета скорость автобуса равна нулю?
4. Почему говорят солнце всходит и заходит? Что в данном случае является  телом отсчета?

IV. Практическое применение понятия вектора и действий с векторами в физике.

 Одними  из самых сложных в физике являются задачи на относительность движения.

Сегодня на уроке, опираясь на знания по геометрии мы научимся их решать.

Ведь согласно известной пословице –«Легким делается все то, к чему приложишь старание!»

Задача 1.

Скорость пловца относительно воды 1,2м\с. Скорость течения реки 0,8м\с.Определите скорость пловца относительно берега: а) если он плывет по течению б) против течения?

 Задача 2.

Вертолет летел на север со скоростью 20м\с. С какой скоростью будет лететь вертолет, если подует западный ветер со скоростью 10м\с?

В физике имеет место понятие скорости сближения, которую необходимо учитывать в практической жизни человека.

Задача 3.

Скорость велосипедиста 36км\ч, а скорость ветра 4м\с. Какова скорость ветра в СО связанной с велосипедистом а) при встречном ветре б) при попутном ветре?

А теперь задачка посложнее.

Задача 4.

Легковой автомобиль движется со скоростью 20м\с за грузовым, скорость которого 16,5м\с. В момент начала обгона водитель легкового автомобиля увидел встречный автобус, движущийся со скоростью 25м\с. При каком минимальном расстоянии до автобуса можно начинать обгон, если в начале обгона легковая машина была в 15м от грузовой, а к концу обгона она должна быть впереди грузовой на 20м?

Почему при лобовом столкновении разрушения особенно сильные?

Не уверен – не обгоняй!

V.  Закрепление навыка решений задач по данному разделу.

— Выбрать одну задачу и решить в тетради.

1. Два поезда движутся равномерно друг за другом. Скорость первого 72км\ч, а второго 54км\ч. Какова скорость второго поезда относительно первого?
2. Скорость течения реки 1,5м\с. Каков модуль скорости катера относительно берега, если он движется перпендикулярно к берегу со скоростью 2м\с?
3. Два поезда движутся навстречу друг другу со скоростями 72 и 54км\ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14с. Какова длина второго поезда?

VI. Оценка работы.

Выставляются оценки за все работы, выполненные на уроке.

VII. Домашнее задание (по выбору, с учетом индивидуальных способностей учащихся)

Составить:

— задачу для решения на уроках математики и физики;

— кроссворд;

— тест для проверки практических навыков по теме “Вектор”;

— составить тест для проверки знаний, умений навыков в компьютерном

варианте на электронных носителях (по выбору).

— реферат “Применение вектора в учебных дисциплинах ”.

VIII. Итог урока.

-Итак, сегодня мы повторили основной теоретический материал по теме “Векторы” и научились решать задачи по физике.

-Работа с материалом на уроках физики и геометрии не только повысила вашу математическую культуру, но и способствовала прочному усвоению физических знаний.

 (Учащиеся подводят итог урока, делятся своими впечатлениями.)

Урок заканчивается словами Ф.Бекона

“Практика рождается из тесного соединения физики и математики”.

Список литературы:

1. А.В.Перышкин, Е.М.Гутник «Физика 9 класс», Дрофа 2009г
2. А.П.Рымкевич , Задачник по физике 10-11 классы, Дрофа 2004г
3. Н.И.Гольдфарб,Физика.Задачник 9-11 классы,Дрофа 2009г
4. Л.С.Атанасян,В.Ф.Бутузов и др., Геометрия 7-9 классы, М:Просвещение, 2009г

Урок по физике на тему «Относительность движения»(9 класс)

Урок решения задач по теме «Относительность движения» в 9 классе.

Рыбицкая В. А. МОУ «Лицей № 124» г. Барнаул.

Цель урока: Сформировать представление о механическом движении и его относительности, развить умение анализировать траекторию движения в различных системах отсчета.

Ход урока: ВВЕДЕНИЕ:

Слово учителя: На этом уроке мы попытаемся рассмотреть различные виды траектории на экспериментальных и виртуальных примерах. Попробуем сравнить их и выяснить, как они меняются в зависимости от тела отсчета.

АКТУАЛИЗАЦИЯ ЗНАНИЙ:

С помощью применения интерактивной доски Smart Board ребята знакомятся

с различными видами траектории, анализируют их и делают выводы.

ФОРМУЛИРОВКА ЦЕЛИ УРОКА:

Вопросы ученикам: Почему траектория меняется в разных системах отсчета? Как это объяснить? Для чего это нужно знать? (Учащиеся формулируют цели урока, а учитель конкретизирует эти цели).

РЕШЕНИЕ ЗАДАЧ НА ИНТЕРАКТИВНОЙ ДОСКЕ

1. Что можно сказать о движении самолетов, ядер, маятников относительно друг друга?

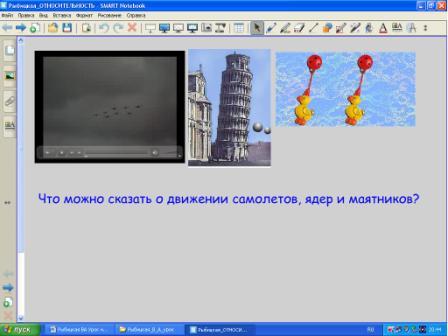
2. Нарисовать траекторию шара, падающего с мачты в системе отсчата «Земля» и «Яхта».

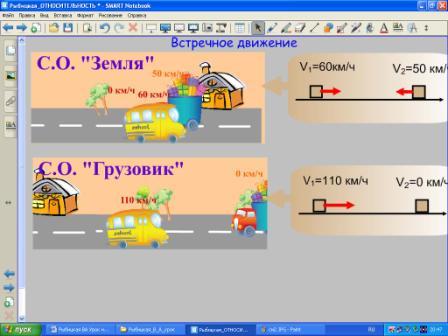
3. Проанализировать и вычислить относительную скорость встречного и попутного движения автомобилей в разных системах отсчета.

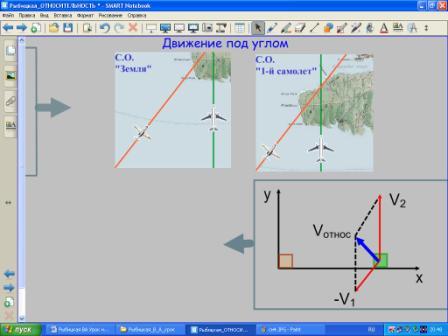
4. Рссмотреть пересекающиеся курсы самолетов и определить относительную скорость.

5. Используя модель из единой коллекции ЦОР вывести закон сложения скоростей лодки и реки.

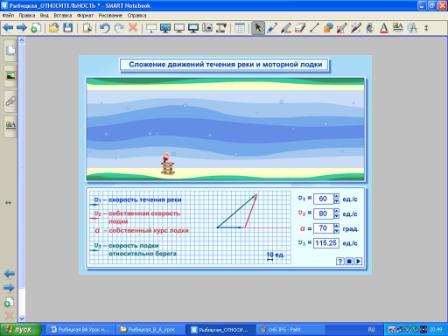
САМОСТОЯТЕЛЬНАЯ ДЕЯТЕЛЬНОСТЬ УЧАЩИХСЯ:

Задание 1: Провести карандашом линии вдоль неподвижной линейки и вдоль вращающейся линейки. Сравнить полученные траектории и ответить на вопрос: Какова траектория карандаша относительно неподвижной и относительно движущейся линейки.

Задание 2: Начертить в тетради траекторию жука, движущегося по линейке, расположенной над вращающимся диском, если за время движения жука по диаметру диск делает 1 оборот. Рассмотреть траекторию жука относительно диска.

Обсуждаем полученные результаты и проверяем их с помощью FLASH-анимации «Жук», которая позволяет изменять число оборотов и пояснить способ рисования такой траектории – перейти в систему отсчета «Диск».

Обсуждаем примеры из опорного конспекта ( Приложение 1) и записываем в тетрадь.

ПОДВЕДЕНИЕ ИТОГОВ

Ребята анализируют результаты лабораторного и виртуального эксперимента. Учитель комментирует и оценивает.

РЕФЛЕКСИЯ

Слово учителя: Ребята подумайте, для чего мы рассматривали движение тел в различных системах отсчета? Зачем проводили компьютерный эксперимент? Что нового вы узнали сегодня?

ДОМАШНЕЕ ЗАДАНИЕ

Начертить в тетради траектории точек колеса автомобиля относительно оси колеса и относительно дороги.

Статья по физике по теме: Относительность движения.

Относительность движения. Закон сложения скоростей.

Всякое движение относительно. Это означает, что одно и то же тело одновременно и движется, и покоится. Движется относительно одних тел и одновременно покоится относительно других. Мы все, земляне, можем покоиться относительно своего письменного стола и одновременно всегда движемся относительно Солнца.

В задачах на относительность движения часто приходится пользоваться правилом сложения скоростей. Правило сложения скоростей: 

скорость тела относительно неподвижной системы отсчета υ равна сумме скорости тела относительно подвижной системы отсчета  υ1 и скорости υ0 самой подвижной системы относительно неподвижной, где

 υ — скорость тела относительно НСО
υ1- скорость тела относительно ПСО

 υ0- скорость ПСО относительно НСО

Это правило применимо только к классическим скоростям, т.е. скоростям, значительно меньшим скорости света в вакууме (т.е. к скоростям порядка 106 м/с и меньше).

 

---

1) Если система отсчета и тело в ней движутся в одном направлении, то

v = v1 + v0.

Например, если поезд движется со скоростью 16 м/с относительно вокзала, а пассажир по ходу поезда бежит со скоростью 2 м/с относительно полок вагона, то скорость пассажира относительно вокзала равна 18 м/с.

---

2) Если система отсчета и тело в ней движутся в противоположных направлениях, то

v = v1- v0.

---

Например, если в предыдущем примере пассажир будет бежать навстречу ходу поезда, то скорость, с которой он будет удаляться от вокзала, будет равна 14 м/с.

---

---

3) Если в подвижной системе отсчета, движущейся со скоростью относительно неподвижной системы, тело станет двигаться со скоростью  относительно подвижной системы под углом  к направлению ее движения, то для определения модуля скорости тела относительно неподвижной системы придется применить теорему Пифагора или теорему косинусов — в зависимости от величины угла α (рис. 10 а и б).

Рисунок 10

Например, если скорость течения v0 =1 м/с, а лодка переплывает реку со скоростью v1 = 2 м/с относительно воды перпендикулярно берегу (рис. 10), то скорость лодки относительно берега будет, согласно теореме Пифагора, равна

!!! Если в условии сказано, что лодка переплывает реку по кратчайшему пути, значит, ее скорость относительно берега  υ направлена перпендикулярно берегу, а скорость лодки относительно воды   υ1 направлена под тупым углом к вектору скорости течения υ0 (рис. 11). В таком случае скорость лодки относительно берега можно определить по теореме Пифагора:

а время t, за которое лодка переплывет реку шириной Н, двигаясь с этой скоростью, можно найти как отношение этой ширины к скорости лодки относительно берега:

Если говорится о минимальном времени, за которое лодка переплывет реку, то теперь перпендикулярно берегу надо направить вектор скорости лодки относительно воды под прямым углом к течению, как на рис. 12. В этом случае минимальное время t будет равно отношению ширины реки к скорости лодки относительно течения:

Таким образом, если вам нужно переплыть реку как можно быстрее, значит, надо грести перпендикулярно течению.

4) Если два тела сближаются или удаляются друг от друга, т.е. движутся в противоположных направлениях со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга будет по модулю равна сумме их скоростей относительно неподвижных объектов:

v = v1+ v2.

---

5) Если два тела обгоняют друг друга, т.е. движутся в одном направлении со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга по модулю будет равна разности их скоростей относительно неподвижных объектов:

v = v2- v1.

Например, если два поезда едут по параллельным рельсам навстречу друг другу со скоростями 36 км/ч и 74 км/ч относительно вокзала, то скорость их взаимного сближения, т.е. скорость первого поезда относительно второго по модулю равна скорости второго относительно первого и равна:

36 км/ч + 74 км/ч = 110 км/ч.

А если они движутся по параллельным рельсам в одном направлении, т.е., например, если второй поезд, скорость которого равна 72 км/ч, обгоняет первый, скорость которого 36 км/ч, то скорость первого поезда относительно второго равна скорости второго минус скорость первого:

72 км/ч – 36 км/ч = 36 км/ч,

а скорость второго поезда относительно первого равна скорости

первого поезда минус скорость второго:

36 км/ч – 72 км/ч = –36 км/ч.

---

6) Если два тела движутся со скоростями v1 и v2 относительно неподвижных объектов и векторы этих скоростей направлены под углом α друг к другу, то, чтобы найти скорость второго тела относительно первого, надо найти векторную разность  υ2- υ1  (рис. 13, а), а чтобы найти скорость первого тела относительно второго, надо найти векторную разность υ1- υ2  (рис. 13, б).

Для нахождения модуля относительной скорости можно применить теорему косинусов:

Если α = 900, то удобно применить теорему Пифагора:

Если сказано, что два поезда длиной L1 и L2 каждый движутся навстречу друг другу со скоростями v1 и v2 относительно неподвижных объектов (деревьев, домов), то время t, в течение которого они будут проезжать мимо друг друга, можно найти, разделив сумму их длин на их скорость относительно друг друга, которая при встречном движении поездов равна сумме их скоростей:

А если эти поезда обгоняют друг друга, двигаясь в одном направлении, то время обгона равно:

Относительность движения. Закон сложения скоростей.

А1. Два тела движутся равномерно во взаимно перпендикулярных направлениях со скоростями 3 м/с и 4 м/с. Их скорость относительно друг друга равна…

1) 2 м/с         2) 3,5 м/с            3) 5 м/с           4) 7 м/с

А2. Два автомобиля движутся по взаимно перпендикулярным дорогам. Скорость первого автомобиля относительно дороги v, а модуль скорости второго автомобиля относительно первого равен v2. Чему равна скорость второго автомобиля относительно дороги?

1) 0,5v            2) 3v                 3) v                  4) 2v

А3. Два автомобиля движутся по прямым шоссе со скоростями 15 м/с и 20 м/с. Угол между шоссе составляет 600. Модуль относительной скорости автомобилей примерно равен…

1) 5 м/с          2) 18 м/с                3) 25 м/с          4) 35 м/с

А4. Два поезда движутся навстречу друг другу со скоростями 36 км/ч и 54 км/ч. Длина первого поезда 40 м, длина второго 50 м. В течение какого времени поезда будут проезжать мимо друг друга?

1) 10,5 c            2) 2,4 с             3) 8,4 с                 4) 3,6 с

А5. Поезд длиной 40 м движется со скоростью 54 км/ч. Его обгоняет поезд длиной 50 м, движущийся по параллельному пути со скоростью 72 км/ч. В течение какого времени второй поезд будет обгонять первый?

1) 9 с             2) 18 с             3) 24 с             4) 32 с

А6. Поезд длиной 60 м, движущийся со скоростью 36 км/ч, въехал на мост длиной 540 м. Он съедет с этого моста через

1) 6 с              2) 54 с              3) 1 мин           4) 4 мин

А7. Пловец должен переплыть реку по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения относительно берега v0 = 0,8 м/с, а скорость пловца относительно воды v1 = 1,2 м/с. Модуль скорости пловца относительно берега

при этом примерно равен

1) 0,9 м/с         2) 1,6 м/с          3) 2 м/с      4) 2,4 м/с

А8. Скорость течения реки относительно берега 0,8 м/с, скорость лодки относительно берега такая же. При этом лодка выдерживает курс, перпендикулярный берегу. Под каким углом к берегу должна быть направлена скорость лодки относительно течения, чтобы выдержать этот курс?

1) 300             2) 450               3) 600                     4) 1200

А9. Эскалатор метро поднимается со скоростью 1 м/с. Может ли человек, находящийся на нем, быть в покое в системе отсчета, связанной с Землей?

1) может, если движется в противоположную сторону со скоростью 1 м/с

2) может, если движется в ту же сторону со скоростью 1 м/с

3) может, если стоит на эскалаторе

4) не может ни при каких условиях

А10. Два автомобиля движутся по прямой дороге в одном направлении: один со скоростью 50 км/ч, а другой — со скоростью 70 км/ч. При этом они

1) сближаются    3) не изменяют расстояние друг от друга

2) удаляются      4) могут сближаться, а могут и удаляться

А11. Два автомобиля движутся по прямому шоссе: первый — со скоростью v, второй — со скоростью (-3v). Модуль скорости второго автомобиля относительно первого равен

1. v              2) 2v                        3) 3v                       4) 4v

А12. Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды v. Модуль скорости лодки относительно берега должен быть равен

1) v  + u           2) v — u             3)  v2+u2                 4)  v2-u2

  Рис. 1

А13. К перекрестку по взаимно перпендикулярным дорогам движутся два велосипедиста со скоростями v1 = 10 км/ч и v2 = 15 км/ч (рис. 1). Какое направление имеет скорость первого велосипедиста в системе отсчета, связанной со вторым (укажите номер стрелки)?

А14. Пешеход идет по прямолинейному участку дороги со скоростью v. Навстречу ему движется автобус со скоростью 10v. С какой скоростью должен двигаться навстречу пешеходу велосипедист, чтобы модуль его  скорости относительно пешехода и автобуса был одинаков?

1) 4,5v            2) 5,5v             3)9v                    4) 11v

   Рис. 2

А15. Капля дождя, летящая с постоянной скоростью v вертикально вниз, попадает на стекло вагона, движущегося с постоянной скоростью u (рис. 2, а). Какая из траекторий на рисунке 2, б соответствует следу капли на стекле (№ стрелки (б))?

А16. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с.

1) 1,5 м/с.              2) 3 м/с.         3) 4,5 м/с.         4) 9 м/с.

A17. Два корабля движутся под углом α = 600 друг к другу из одной точки ( v1 = 10 м/с и v2 = 15 м/с). Найдите относительную скорость кораблей и расстояние между ними (в км) в момент времени t = 5 мин.

1) v = 25 м/с, S = 7,5 км.            3) v = 5 м/с,   S =1,5 км.

2) v = 13,23 м/с, S = 3,97 км.      4) v = 25 м/с, S = 125 км.

A18. Две капли падают из крана одна вслед за другой. Как движется вторая капля в системе отсчета, связанной с первой каплей, после отрыва ее от крана?

1) Равноускоренно.                   3) Не движется.

2) Равнозамедленно.                 4) Равномерно вверх.

A19. Чему равна проекция скорости второй капли относительно первой на направление движения капель (см. задачу А18) если интервал отрыва капель 0,5 с?

1) -2,5 м/с.       2) 2,5 м/с.            3) -5 м/с.          4) 5 м/с.

A20.   Два корабля А и В движутся со скоростями v1, и v2 относительно Земли. (См. рис.) С какой по модулю скоростью корабль А движется относительно корабля В?                                                                                          1) v1       2) v1 – v2            3) v1+ v2         4)  v12+v22

A21. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.

1) 0,1 м/с          2) 0,25 м/с        3) 0,5 м/с         4) 0,7 м/с

        

Относительность движение. Сложение скоростей

1. В безветренную погоду капли дождя оставляют на окне равномерно движущегося со скоростью 10 м/с автобуса следы, направленные под углом 600 к вертикали. Определите скорость капель относительно Земли. Ответ: 5,8

2. Велосипедист и мотоциклист одновременно выезжают на шоссе и движутся в одну сторону. Скорость первого 12 м/с, второго — 54 км/ч. Расстояние между ними через 5 мин будет равно… Ответ: 900

3. Катер переплывает реку шириной 40 м. Скорость течения реки 3 м/с. Скорость катера относительно воды 5 м/с. За какое время катер переплывет реку по наикратчайшему пути (в с)? Ответ: 10

4. Через реку переправляется лодка, выдерживая курс перпендикулярно к течению реки. Скорость лодки относительно воды 1,4 м/с, скорость течения 0,7 м/с, ширина реки 308 м. Через какое время лодка достигнет другого берега? На какое расстояние вдоль берега отнесет ее течением? Ответ:  220 с, 154 м.  

5. При скорости горизонтального ветра 20 м/с скорость капель дождя относительно земли 40 м/с. Какой будет скорость капель при скорости ветра 5 м/с? Ответ: 35

6. Пловец плывет против течения реки. Определите скорость движения пловца относительно берега, если скорость пловца относительно воды 1,5 м/с, а скорость течения реки 0,5 м/с… Ответ: 1

7. Два поезда идут навстречу друг другу со скоростями 54 км/час и 36 км/час. Длина второго поезда 250м. Пассажир, сидящий и первом поезде, будет видеть проходящий мимо него встречный поезд в течение… Ответ: 10

8.  Из двух пунктов, расстояние между которыми 100м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела (в м/с), если они встретились через 4с? Ответ: 5.

9. Эскалатор поднимает стоящего человека за 2 мин. Человек поднимается по неподвижному эскалатору за 6 мин. Сколько времени  будет подниматься человек по движущемуся эскалатору? Ответ: 90

10. При скорости ветра 10 м/с капли дождя падают под углом 30° к вертикали. Под углом 45° капли будут падать при скорости ветра… Ответ: 17

11. Два поезда идут навстречу друг другу по двум параллельным путям со скоростью 36 и 54 км/ч. Длины поездов 125 и 150 м. Время, в течение которого поезда проходят мимо друг друга, равно… Ответ: 11 с

12. Скорость моторной лодки по течению реки равна 18 км/ч, против течения равна 4 м/с. Скорость течения реки равна… Ответ: 0,5

13. Катер проходит расстояние между двумя пристанями на реке по течению за 600 c, а против течения – за 900 с. Какое время потребуется катеру для преодоления этого расстояния в озере… Ответ: 720

14. Автоколонна длиной 600 м движется со скоростью 10 м/с. Мотоциклист выехал из конца колонны по направлению к ее началу со скоростью 20 м/с. Достигнув головной машины, мотоциклист повернул обратно к концу автоколонны. За какое время он вернется обратно? Ответ: 80

1. Две вагонетки катятся навстречу друг другу со скоростями 0,5 м /с и 0,4 м /с.  Через какое время вагонетки столкнутся, если первоначальное расстояние между ними 135 м? {150 с}

2. Автомобиль, двигаясь со скоростью 45 км/ч, в течение 10 с прошел такой же путь, какой автобус, двигающийся в том же направлении с постоянной скоростью, прошел за 25 с. Найдите величину их относительной скорости.   {7,5 м/с}

3. Сколько времени сидящий у окна пассажир поезда, идущего со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого равна 36 км/ч, а длина – 150 м?    {6 c}

4. Рыбак, плывя по течению реки с постоянной относительно воды скоростью, проплывая под мостом, потерял удочки. Через полчаса он заметил пропажу и повернул обратно. На расстоянии 4 км от моста он встретился с удочками. Определить скорость течения реки.   {4 км/ч}

5. Моторный катер проходит расстояние между двумя пристанями против течения за 1час. За такое же время это расстояние проходит по течению плот. За какое время пройдет это расстояние по течению катер? {20 мин}

6. Самолет летит их пункта А в пункт В и обратно со скоростью 600 км/час относительно воздуха. Сколько времени затратил самолет на весь полет, если вдоль линии полета непрерывно дует ветер постоянного направления со скоростью 20 м/с? Расстояние между пунктами 900 км. {3,04 часа}

7. Во сколько раз время проезда одного и того же расстояния на катере туда и обратно по реке больше, чем по озеру? Скорость течения реки 3 км/ч, скорость катера относительно воды в обоих случаях 10 км/ч. {2,2}

8. Скорость движения лодки относительно воды в два раза больше течения реки. Во сколько раз больше времени занимает поездка между двумя пунктами против течения, чем по течению?  {3}

9. В безветренную погоду капли дождя оставляют на окне равномерно движущегося поезда следы, направленные под углом 60º к вертикали. Определить скорость капель относительно Земли, если поезд движется со скоростью 36 км/ч?   {5,77 м/с}

10. При горизонтальном ветре, скорость которого 10 м/с, капли дождя падают под углом 30º к вертикали. При какой горизонтальной скорости ветра капли будут падать под углом 60º к вертикали?  {30 м/с}

11. Какую скорость должен сообщить мотор катеру, чтобы при скорости течения реки 1,2  м/с катер двигался перпендикулярно берегу со скоростью 3,2 м/с? Под каким углом к берегу должна быть направлена эта скорость?  {3,42 м/с; 69,40}

12. Лодка движется перпендикулярно берегу реки. Ее скорость относительно воды равна 2 м/с. Определите время движения лодки к другому берегу, если ширина реки 80 м, а скорость течения 1 м/с. {46,2 c}

13. Катер, переправляясь через реку шириной 600 м, двигался перпендикулярно течению реки со скоростью 4 м/с в системе отсчета, связанной с водой. На сколько метров будет снесен катер течением, если скорость течения 1,5 м/с?  {225 м}

14. Гребец сообщает лодке скорость 2 м/с относительно воды. Под каким углом к течению реки он должен направить лодку, чтобы плыть точно поперек реки, если скорость ее течения 1 м/с?  {1200}

15. Эскалатор метро спускает неподвижно стоящего человека за 90 с. По неподвижному эскалатору человек спускается за 2 мин. За какое время спустится человек по движущемуся эскалатору? Скорости движения человека и эскалатора во всех случаях неизменны.    {51,4 с}

16. Эскалатор метрополитена, двигаясь равномерно, поднимает неподвижно стоящего на нём человека в течение одной минуты. По неподвижному эскалатору пассажир, двигаясь равномерно, поднимается за три минуты. Сколько секунд будет подниматься пассажир по движущемуся вверх эскалатору?   {45 c}

17. Колонна автомашин длиной 2 км движется со скоростью 36 км/ч. Из начала колонны выезжает мотоциклист, который, достигнув ее конца, возвращается обратно. Скорость мотоциклиста постоянна и равна  54 км/ч. Сколько времени будет в пути и какой путь пройдет мотоциклист пока он снова нагонит начало колонны?  {8 мин; 7,2 км}

18. Два велосипедиста едут по взаимно перпендикулярным дорогам со скоростями 10,8 км/ч и 14,4 км/ч, соответственно. Чему равна их относительная скорость? {18 км/ч}

19. Две прямые дороги пересекаются под углом 60º. От перекрестка в одну сторону удаляются по ним две машины: одна со скоростью 60 км/ч, другая со скоростью 80 км/ч. Определить величину скорости, с которой одна машина удаляется от другой. Перекресток машины прошли одновременно.   {72,1 км/ч; 122 км/ч}

20. Пешехода, идущего со скоростью 3,6 км/ч, обгоняет велосипедист, движущийся в том же направлении со скоростью 6 м/с. Найдите проекцию па ось X скорости пешехода относительно велосипедиста. (Скорости пешехода и велосипедиста относительно земли считать положительными.) {-5 м/с}

21. По двум параллельным путям в одном направлении идут товарный поезд длиной L1 = 560 м со скоростью v1= 68,4 км/ч и электропоезд длиной L2 = 440 м со скоростью v2 = 104,4 км/ч. За какое время электропоезд обгонит товарный состав? {100 с}

22. Пловец переплывает реку по прямой, перпендикулярно берегу. Определите скорость течения реки, если скорость пловца относительно воды в 2 раза больше скорости течения. Скорость пловца относительно берега равна 0,87 м/с. {0,5 м/с}

23. Самолет летит из пункта А в пункт В, расположенный на расстоянии 300 км к востоку. Определите продолжительность полета (в мин), если ветер дуст с юга на север. Скорость ветра u = 25 м/с, скорость самолета относительно воздуха v2 = 600 км/ч (учесть, что самолет в ветреную погоду может менять курс, чтобы попасть из пункта А в пункт В по кратчайшему пути). {30,34 мин}

24. От перекрестка одновременно отъехали два автобуса: первый — со скоростью v1 = 40 км/ч, второй – со скоростью v2 = 60 км/ч, в направлении, перпендикулярном движению первого. С какой относительной скоростью (в км/ч) они удаляются друг от друга? {78,1 км/ч}

25. Человек бежит по движущемуся эскалатору. В первый раз он насчитал 60 ступенек, во второй раз, двигаясь со скоростью на 50% большей, он насчитал 70 ступенек. Сколько ступенек он насчитал бы на неподвижном эскалаторе? {105}