Повторение темы «Подобные треугольники». Решение задач
На этом уроке мы займемся повторением темы «Подобные треугольники. Решение задач». Занятие начнем с повторения понятия «подобные треугольники», вспомним все три признака подобия этих фигур. После решим несколько задач на эту тему, используя полученные ранее знания.
Тема: Подобные треугольники
Урок: Повторение темы «Подобные треугольники». Решение задач
На этом уроке мы повторим тему «Подобные треугольники».
Для начала вспомним определение подобных треугольников.
Определение
Треугольники 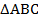 и
и 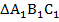 называются подобными треугольниками (
называются подобными треугольниками (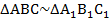
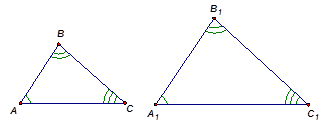
Рис. 1
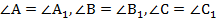 ;
; 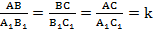 .
.
При этом коэффициент 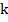 называется коэффициентом подобия.
называется коэффициентом подобия.
Если обозначить: 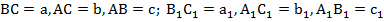 , можно получить следующие соотношения между сторонами подобных треугольников:
, можно получить следующие соотношения между сторонами подобных треугольников: 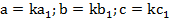
Кроме того, площади подобных треугольников относятся как квадрат коэффициента подобия: 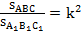 .
.
Для того чтобы определить, являются ли треугольники подобными, не прибегая к определению, существуют признаки подобия треугольников.
Всего существует три признака подобия. Перечислим их:
1. По равенству двух углов: если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны: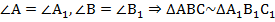 .
.
2. По пропорциональности двух сторон и равенству угла между ними:
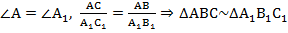 .
.3. По пропорциональности трёх сторон: если три стороны одного треугольника пропорциональны соответственно трём сторонам другого треугольника, то такие треугольники подобны: 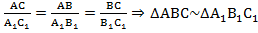 .
.
С помощью подобия треугольников доказывается свойство средней линии треугольника. Напомним определение средней линии треугольника.
Средняя линия треугольника – отрезо
interneturok.ru
Задачи по геометрии тема » Решение треугольников» 8 класс.

Теорема Пифагора
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
В режиме слайдов ответы появляются после кликанья мышкой

Синус и косинус
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе. Синус угла А обозначается sin A .
Кос инусом острого угла прямоугольного треугольника называется отношение п ри лежащего к этому углу катета к гипотенузе. Кос инус угла А обозначается cos A .
В режиме слайдов ответы появляются после кликанья мышкой

Тангенс и котангенс
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к прилежащему.Тангенс угла А обозначается tg A .
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему. Котангенс угла А обозначается с tg A .
В режиме слайдов ответы появляются после кликанья мышкой

Теорема косинусов
Теорема. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
В режиме слайдов ответы появляются после кликанья мышкой
c 2 = a 2 + b 2 – 2 ab cos C .

Теорема синусов
Теорема. Стороны треугольника пропорциональны синусам противолежащих углов. Причем отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.
В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 1
У прямоугольного треугольника один катет равен 8 см, а синус противолежащего ему угла равен 0,8. Найдите гипотенузу и второй катет.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10 см и 6 см.

Упражнение 2
В прямоугольном треугольнике ABC sin A = 1/3, AB = 6. Найдите BC .
Ответ: 2 .
В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 3
В прямоугольном треугольнике ABC sin A = 3/4, BC = 6. Найдите AB .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8 .

Упражнение 4
В прямоугольном треугольнике ABC cos A = 2/3, AB = 6. Найдите AC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4 .

Упражнение 5
В прямоугольном треугольнике ABC cos A = 2/3, AC = 6. Найдите AB .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 9 .

Упражнение 6
В прямоугольном треугольнике ABC tg A = 2/3, AC = 6. Найдите BC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4 .

Упражнение 7
В прямоугольном треугольнике ABC tg A = 3/4, BC =
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8 .

Упражнение 8
В прямоугольном треугольнике ABC , AC = 6. Найдите BC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4 .

Упражнение 9
Катеты прямоугольного треугольника равны 3 и 4. Найдите гипотенузу.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5 .

Упражнение 10
Гипотенуза прямоугольного треугольника равна 13. Один из его катетов равен 5. Найдите другой катет.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12 .

Упражнение 11
В треугольнике ABC AC = BC = 2, угол C равен 120 о . Найдите высоту, опущенную на сторону AB .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 1 .

Упражнение 12
В треугольнике ABC AC = BC = 2, угол A равен 30 о . Найдите высоту, опущенную на сторону BC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 1 .

Упражнение 13
В треугольнике ABC AC = BC , угол C равен 90 о , AB = 6. Найдите высоту, опущенную на сторону AB .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3 .

Упражнение 14
В треугольнике ABC AB = BC , угол B равен 120 о , AC = 4. Найдите высоту, опущенную из вершины C .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2 .

Упражнение 15
Боковые стороны равнобедренного треугольника равны 10. Высота, опущенная на основание, равна 8. Найдите основание.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12 .

Упражнение 16
В треугольнике ABC AB = 6, BC = 4, угол B равен 90 о . Найдите медиану, проведенную из вершины C .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5 .

Упражнение 17
Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3 .

Упражнение 18
В прямоугольном треугольнике ABC угол C равен 90 о , угол B равен 30 о , катет AC равен . Найдите биссектрису, проведенную из вершины A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2 .

Упражнение 19
В треугольнике ABC угол A равен 60 о , угол B равен 45 о , сторона AC равна . Найдите сторону BC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3 .

Упражнение 20
Найдите сторону треугольника, лежащую против угла в 120 о , если прилежащие к нему стороны равны 6 и 10.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 14 .

Упражнение 21
В прямоугольном треугольнике ABC AB = 6, Найдите BC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2 .

Упражнение 22
В прямоугольном треугольнике ABC AB = 6, Найдите AC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4 .

Упражнение 23
В прямоугольном треугольнике ABC AB = 5, Найдите AC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4 .

Упражнение 2 4
В прямоугольном треугольнике ABC Найдите 5 sin A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3 .

Упражнение 25
Гипотенуза прямоугольного треугольника равна 10, а разность катетов равна 2. Найдите меньший катет.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 6.

Упражнение 26
Найдите высоту, опущенную на гипотенузу, прямоугольного треугольника с катетами 15 и 20.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12 .

Упражнение 27
Гипотенуза прямоугольного треугольника равна 25, а высота, опущенная на нее, равна 12. Найдите больший катет этого треугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 20 .

Упражнение 28
В прямоугольном треугольнике проекции катетов на гипотенузу равны 1 и 3. Найдите его меньший острый угол.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 30 o .

Упражнение 29
В треугольнике ABC AB = 10, угол C равен 90 о . Найдите медиану, проведенную из вершины C .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5 .

Упражнение 30
В треугольнике ABC угол C равен 90 о , AC = 15, BC = 20, CH – высота. Найдите отрезок AH .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 9 .

Упражнение 31
В треугольнике ABC угол A равен 60 о , угол B равен 45 о , высота CH равна . Найдите сторону AB .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2 .

Упражнение 32
Боковые стороны равнобедренного треугольника равны 25, основание равно 30. Найдите высоту, проведенную к боковой стороне.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 24 .

Упражнение 33
В равнобедренном треугольнике высота, опущенная на боковую сторону, делит ее на отрезки равные 7 и 2, считая от вершины. Найдите основание треугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 6 .

Упражнение 34
В треугольнике ABC AC = BC , AB = 1, угол C равен 36 о . Найдите биссектрису, проведенную из вершины A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 1 .

Упражнение 35
Боковые стороны равнобедренного треугольника равны , основание равно . Найдите медиану, проведенную к боковой стороне.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3 .

Упражнение 36
Боковые стороны равнобедренного треугольника равны , основание равно . Найдите биссектрису, проведенную к боковой стороне.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10 .

Упражнение 37
В треугольнике ABC угол C равен 90 о , угол B равен 30 о , биссектриса, проведенная из вершины A , равна . Найдите сторону AB .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3 .

Упражнение 38
В треугольнике ABC сторона AC равна , сторона BC равна 3, угол A равен 60 о . Найдите угол B .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 45 o .

Упражнение 39
В треугольнике ABC AB = 7, BC = 5, AC = 3. Найдите угол C .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 120 o .

Упражнение 40
Одна из сторон треугольника равна 13, а угол, лежащий против этой стороны, равен 120 о , сумма двух других сторон треугольника равна 15. Найдите наименьшую сторону треугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 7 .

Упражнение 41
В прямоугольном треугольнике ABC cos A = 3/5 , AB = 10. Найдите AC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 6 .

Упражнение 42
У прямоугольного треугольника один катет равен 6 см, а синус противолежащего ему угла равен 2/3 . Найдите гипотенузу .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 9 .

Упражнение 43
Гипотенуза прямоугольного треугольника равна 10. Один из его катетов на 2 больше другого. Найдите больший катет.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8 .

Упражнение 44
В треугольнике ABC AC = 4, угол A равен 30 о . Найдите высоту, опущенную на сторону BC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2 .

Упражнение 45
Боковые стороны равнобедренного треугольника равны 13. Высота, опущенная на основание, равна 12. Найдите основание.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10 .

Упражнение 46
В прямоугольном треугольнике ABC AB = 10, tg A = 3/4 . Найдите AC .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8 .

Упражнение 47
В треугольнике ABC AC = 8, BC = 6, угол C равен 90 о . Найдите медиану, проведенную из вершины C .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5 .

Упражнение 48
В треугольнике ABC BC = 3, AB = , угол С равен 45 о . Найдите угол A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 60 o .

Упражнение 49
В треугольнике ABC AB = 3, AC = 2, BC = . Найдите угол A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 60 o .

Упражнение 50
В треугольнике ABC угол B равен 30 о , AB = , биссектриса, проведенная из вершины A , равна 1. Найдите угол C .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 90 o .
multiurok.ru
Урок 34. Решение задач на применение 1 признака подобия Δ
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 34. Решение задач на применение первого признака подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Урок 34. Решение задач на применение первого признака подобия треугольников
Основная дидактическая цель урока: сформировать у учащихся навыки решения задач на применение первого признака подобия треугольников.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности (Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся
- Теоретический опрос.
1) Доказать теорему, выражающую первый признак подобия треугольников. (Один ученик готовит доказательство теоремы у доски. Заслушать после проведения фронтального теоретического опроса.)
- Фронтальный теоретический опрос.
- Сформулируйте первый признак подобия треугольников.
- Чему равно отношение периметров подобных треугольников?
- Какие треугольники называются подобными?
- Сформулируйте теорему об отношении площадей подобных треугольников.
III. Решение задач по готовым чертежам
Решить задачи (самостоятельно).
(Один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки. Учитель индивидуально проверяет домашнее задание.)
- Рис. 7.17. Найти: ВС, MN.
- Дано: DE||АС (рис. 7.18). Найти: АВ, ВС.
- Дано: а||b (рис. 7.19). Найти: х, у.
- Рис. 7.20. Найти: BD.
- Рис. 7.21. Найти: СО, ВО.
- Рис. 7.22. Найти: ВС.

Ответы к задачам по готовым чертежам:
- ВС =3,2, MN= 22,4.
- АВ= 18, ВС= 12.
- х = 4, у = 5.
- BD = 8.
- СО = 4, ВО = 12.
- ВС= 15.
IV. Решение задач
- Работа в рабочих тетрадях.
Решить задачу № 58. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
- Решить задачу № 554 (работа в парах).

Наводящие вопросы.
- Есть ли на рисунке подобные треугольники? Почему вы так считаете?
- Найдите коэффициент подобия этих треугольников?
- Каким соотношением связаны сходственные стороны AM и BMP DM и СМ?
- Решить задачу № 556 (с последующим обсуждением решения).
Вопросы для обсуждения.
- Почему ∠O = ∠CАС1? (Это соответственные углы при параллельных прямых АС1 и OD и секущей ОА.)
- Почему ∠OAB = ∠C? (Это соответственные углы при параллельных прямых АВ и CD и секущей АС.)
- Почему ОА : АС = ОВ : АС1? (Это сходственные стороны подобных треугольников.)
- Докажите, что АС1 = BD. (BAC1D — параллелограмм, так как АВ||CD по условию задачи, АС1||BD как противолежащие стороны параллелограмма.)
- Объясните, каким образом из равенств ОА : АС = ОВ : AС1 и AC1 = BD получилось равенство OA : OB = АС : BD.
- Решить задачу N° 557 (а). (На доске подготовить рисунок. Записать краткое решение задачи.)

Наводящие вопросы.
- Есть ли на рисунке подобные треугольники? Докажите их подобие.
- Составьте отношение сходственных сторон и найдите АС.
V. Самостоятельное решение задач
- Решить задачи № 557 (б), 552 (в).

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены две задачи;
- оценка «4» — одна из задач решена правильно, а при решении второй задачи допущены незначительные ошибки;
- оценка «3» — правильно решена одна задача или при решении двух задач допущены незначительные ошибки;
- оценка «2» — не ставится.
- Решить дополнительную задачу.
Диагонали трапеции ABCD с основаниями AD и ВС пересекаются в точке О. Периметры треугольников ВОС и AOD относятся как 2 : 3, АС = 20. Найдите длины отрезков АО и ОС.

VI. Рефлексия учебной деятельности
- Сформулируйте первый признак подобия треугольников.
- Сколько пар равных углов нужно найти, чтобы доказать подобие треугольников?
- Сколько пар равных углов нужно найти у прямоугольных (равнобедренных) треугольников, чтобы данные треугольники были подобны?
- Могут ли быть подобными равносторонние треугольники?
Домашнее задание
- Повторить П. 61.
- Решить задачи № 552 (а, б), 557 (в), 558.
- Решить дополнительную задачу.
В трапеции ABCD (AD и ВС — основания) точка К лежит на стороне CD, причем СК : KD = 1 : 2. АК пересекает BD в точке О. Докажите, что если ВС : AD = 1 : 2, ВО = OD.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 34. Решение задач на применение первого признака подобия треугольников.
Вернуться к Списку уроков Тематического планирования.
uchitel.pro
Задачи на повторение курса геометрии в 8 классе. Базовый уровень
Дидактический материал для работы репетитора по математике с учеником 8 класса слабого и среднего уровня способностей. Базовый учебник по геометрии — Атанасян 7-9 кл. Почти все задачи составлены так, что первая решается в совместно с репетитором, а вторая остается для домашней работы. Вторая отличаются от первой только числами.
№1. В параллелограмме АВСD высота ВH равна 4 см, а сторона ВС=10см. Найти площадь параллелограмма.
№2. В трапеции ABCD CH – высота, BC=2см, AH=3см, HD=5см, CH=4см. Найдите площадь данной трапеции.
№3. В параллелограмме MNKP MT- биссектриса угла M. Известно, что NT=5см, TK=3см. Найти периметр данного параллелограмма.
№4.1 В трапеции MNKP верхнее основание NK и средняя линия AB равны соответственно 5 и 9 см.
Найти ее нижнее основание.
№4.2 В трапеции PQNE нижнее основание PE и средняя линия KN равны соответственно 10 и 7 см. Найти ее верхнее основание.
№5.1 В прямоугольнике ABCD проведены биссектрисы углов А и D, которые пересекаются в точке М, лежащей на стороне B. Найдите периметр ABCD , если АВ=6см.
№5.2 В прямоугольнике ABCD проведена биссектриса угла А, которая разбивает сторону ВС на отрезки длиной 5см и 3 см. Найти периметр прямоугольника ABCD.
№6.1 На окружности отмечены точки А,В,С,D так, что АВ ее диаметр, а угол АСD равен  . Найти угол DСВ.
. Найти угол DСВ.
№6.2 На окружности отмечены точки А,В,С,D так, что АС-диаметр, угол АСD равен  , а угол ВАС равен
, а угол ВАС равен  . Найдите угол ВСD.
. Найдите угол ВСD.
№7.1 На окружности отмечены точки В, N и D. Угол ВND равен  . Найдите угол ВОD.
. Найдите угол ВОD.
№7.2 На окружности отмечены точки В, К и C. Угол ВОС равен  . Найти угол ВКС.
. Найти угол ВКС.
№8.1 В прямоугольном треугольнике АСВ катет СВ равен 4 см, угол В равен 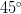 . Найти гипотенузу АВ.
. Найти гипотенузу АВ.
№8.2 В прямоугольном треугольнике АСВ катет СА равен 3 см, угол А равен 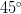 . Найти гипотенузу АВ.
. Найти гипотенузу АВ.
№9* В трапеции АВСD АВ=СD, АС=5см, СH=3см. Найти площадь трапеции.
№10.1 Найти площадь трапеции, стороны которой равны 16, 13, 6 и 13 см.
№10.2 Найти площадь трапеции, стороны которой равны 17, 10, 5 и 10 см.
№11.1 Найти площадь прямоугольного треугольника с катетами 2 и 4 см.
№11.2 Найти площадь прямоугольного треугольника с катетами 3 и 5 см.
№12.1 Найти площадь прямоугольного треугольника, гипотенуза которого равна 25 см, а один из катетов – 20 см.
№12.2 Найти площадь прямоугольного треугольника, гипотенуза которого равна 17 см, а один из катетов – 8 см.
№13.1 Найти площадь квадрата, диагональ которого равна 4 см.
№13.2 Найти площадь квадрата, диагональ которого равна 6 см.
№14.1 Найти площадь прямоугольного треугольника , гипотенуза которого равна 12 см, а один из острых углов cоставляет 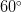 .
.
№15.1 Найти площадь прямоугольного треугольника , гипотенуза которого равна 16 см, а один из острых углов равен .
.
№16.1 В прямоугольном ∆ АВС :  – прямой, АВ=
– прямой, АВ= , АС=3, ВС=6. Найти sinA, cosA, tgA.
, АС=3, ВС=6. Найти sinA, cosA, tgA.
№16.2 В прямоугольном ∆ АВС :  – прямой, АВ=
– прямой, АВ= , АС=4, ВС=
, АС=4, ВС=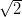 .
.
Заполнить таблицу:
№17.1 В прямоугольном ∆ АВС : ∠C – прямой, АВ=6, ∠B= . Найти АС, ВС.
. Найти АС, ВС.
№17.2 В прямоугольном ∆ АВС : ∠C – прямой, СВ=6, ∠B= . Найти АС, АВ.
. Найти АС, АВ.
Задачи по геометрии на рисунках:
№18-19 Найдите по данным рисунка стороны X и Y (левая задача разбирается с репетитором по математике совместно, а правая предназначена для домашней работы)

№20-21 Выразите через X и Y стороны а и b а и b (левая задача разбирается с репетитором по математике совместно, а права предназначена для домашней работы)

№22 Найдите по данным рисунка длины отрезков X, Y и Z:
Автор подборки задач — Николай Викторович, репетитор по математике в отставке.
Уважаемые преподаватели: присылайте на сайт для публикации ваши дидактические и методические материалы, отдельные задачи или тексты объяснений каких-то традиционно трудных для школьников тем. Я с радостью помогу оформить их для публичного просмотра. Если Вы — репетитор по математике, прошедший регистрацию на сайте, то с каждого присланного материала я поставлю ссылку на Вашу анкету. Это привлечет внимание к Вам со стороны родителей и учеников.
С уважением, владелец сайта Колпаков Александр Николаевич,
репетитор по математике в Москве.
Репетитор по математике в Строгино, м.Щукинская.
Метки: Геометрия, Задачник по геометрии
ankolpakov.ru
Задачи КДР по геометрии с решениями. 8 класс.
Предлагаю решение пятого варианта КДР по геометрии 2012 года, для учащихся 8 классов. Варианты КДР по геометрии 2012 года можно посмотреть здесьЗАДАЧА 1. ABCD – прямоугольник. О — точка пересечения АС и BD. Угол BOC=120º. Найдите угол DАО ( см. рис. 1 ).
| Рис.1 |
Решение. Угол DAO можно найти, рассмотрев треугольник DOA. Треугольник равнобедренный. Угол DOA равен углу BOC, так как они вертикальные. Сумма углов при основании треугольника DOA равна 180-120=60. Так как углы при основании равнобедренного треугольника равны, то искомый угол DAO равен 60/2=30. Ответ: 300.
ЗАДАЧА 2. Дан треугольник АВС. KF – средняя линия треугольника АВС. АВ=10, ВС=8, АС=12. Найдите периметр треугольника BKF (см. рис. 2).| Рис.2 |
| Рис. 3 |
| Рис.4 |
| Рис.5 |
Решение. По условию задачи составим чертеж (см. рис. 5). Проведем отрезок BK, параллельный отрезку CD. Рассмотрим получившийся прямоугольный треугольник ABK.
Теперь осталось найти меньшее основание BC= AD-AK=20-10=10.Задачу можно решить намного проще, если вспомнить, что в прямоугольном треугольнике катет, противолежащий углу 30º ( угол ABK) равен половине гипотенузы. Следовательно AK=10. Отсюда находим, что BC=10.
Ответ: 10 см. ЗАДАЧА 6. Катеты прямоугольного треугольника относятся как 8:15, гипотенуза равна 51. Найдите периметр этого треугольника. Решение. Приведу решение без предварительного составления чертежа. Катеты прямоугольного треугольника равны 8x и 15x. Используя теорему Пифагора, получим: 512=(8x)2+(15x)2. Решив данное уравнение, получим, что x=3. Следовательно стороны треугольника равны соответственно 24 и 45. Если у кого-то есть интересные задачи КДР по геометрии прошлых лет для восьмиклассников, то просьба поделиться. Порешаем… ЗАДАЧА 7. В параллелограмме большая сторона равна 25 . Меньшая высота равна 12. Меньшая диагональ — 20. Найдите угол между этой диагональю и меньшей стороной.| Рис.6 |
| Рис. 7 |
ЗАДАЧА, предложенная в комментариях к посту. На стороне АD параллелограмма АВСD взята точка Е так, что АЕ = 4, ЕD = 5, ВD = 13. Докажите, что треугольник ВЕD прямоугольный, и найдите площадь параллелограмма. Решение: Рассмотрим этот чертеж с пояснениями (рисунок можно увеличить)
solodenkovagalina.blogspot.com
Задачи с решениями 8класс( геометрия)
ЗАДАЧИ ДЛЯ УЧАЩИХСЯ 8 КЛАССА.( с решениями)
Задача № 1
Вычислите углы параллелограмма, если его углы, прилежащие к одной стороне, относятся как 2 : 3.
Д а н о: ABCD – параллелограмм; A: B = 2 : 3.
Н а й т и: A; B; C; D.

Задача №2
Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.
Д а н о: ABCD – параллелограмм; ВС – АВ = 25 см; PАВСD = 122 см.
Н а й т и: АВ; ВС; CD; AD.
Задача № 3
Постройте параллелограмм со сторонами 4 см и 6 см и углом 50° между ними.
Д а н о: A = 50°; АВ = 4 см; AD = 6 см.
П о с т р о и т ь параллелограмм ABCD.
Задача № 4
Меньшая сторона прямоугольника равна 4 см и образует с диагональю угол в 60°. Найдите диагонали прямоугольника.

Д а н о: ABCD – прямоугольник; АВ = 4 см; BAC = 60°; АС – диагональ.
Н а й т и: АС.
Задача № 5
Биссектриса угла А прямоугольника ABCD делит сторону ВС на части 2 см и 6 см. Найдите периметр прямоугольника.
Д а н о: ABCD – прямоугольник; АЕ – биссектриса A; BE = 2 см; ЕС = 6 см; (или BE = 6 см, ЕС = 2 см).
Н а й т и: PАВСD.


Задача № 6
Д а н о: ABCD – четырехугольник; ОА = ОС; 1 = 2.
Д о к а з а т ь, что ABCD – параллелограмм.

Задача № 7
Д а н о: EFCD – квадрат; DO = OF; ACD; BEF; CAO = 130°.
Н а й т и все неизвестные углы.

Задача № 1
Р е ш е н и е.
Если ABCD – параллелограмм, то A = C, B = D, A + B = 180° – как внутренние односторонние при AD || BC и секущей АВ. Если A : B = 2 : 3, то A = 2х, B = 3х и 2х + 3х = 180°, 5х = 180°, х = 180° : 5 = 36°. A = C = 36° 2 = 72°, B = D = 36°3 = 108°.
О т в е т: 72°; 108°.
Задача №2
Р е ш е н и е.
Пусть АВ = х, тогда ВС = х + 25. Так как CD = АВ и ВС = AD, то CD = х и AD = х + 25. По условию PАВСD = 122 см, значит, 2х + (х + 25) 2 = 122, х + (х + 25) = 61. 2х + 25 = 61, 2х = 61 – 25, 2х = 36, х = 18, тогда АВ = CD = 18 см, ВС = AD = 18 + 25 = 43 (см).
О т в е т: 18 см; 43 см.
Задача № 3
А н а л и з:

П о с т р о е н и е:

1. Строим A = 50°.
2. На одной из сторон A откладываем отрезок АВ = 4 см, на другой – AD = 6 см.
3. Через точку В проводим прямую a || AD, через точку D прямую в || АВ. а || в = С. ABCD – искомый параллелограмм.
Д о к а з а т е л ь с т в о.

Задача № 4
Р е ш е н и е.
CBA = 90°, т. к. ABCD – прямоугольник. В ΔАВС CBA = 90°, BAC = 60°, тогда ACB = 180° – (60° + 90°) = 30°, т. к. сумма углов треугольника 180°. Катет, лежащий против угла в 30°, равен половине гипотенузы, значит, если АВ = 4 см, то АС = 42 = 8 (см).
О т в е т: 8 см.
Задача № 5
Р е ш е н и е.
PАВСD = АВ 2 + ВС 2; ВС = 2 + 6 = 8 см. В ΔАВЕ BAE = 90 : 2 = 45°, т. к. АЕ – биссектриса A, значит, BEA = 180° – (90° + 45°) = 180° – 135° = 45° и ΔАВЕ – прямоугольный и равнобедренный, т. е. АВ = BE = 2 см (или АВ = ВЕ = 6 см), тогда PАВСD = 2 8 + 2 2 = 16 + 4 = 20 (см) [или PАВСD = 2 8 + 2 6 = 16 + 12 = 28 (см)].
О т в е т: 20 см или 28 см.
Задача № 6
Р е ш е н и е.
1. 1 = 2, но эти углы накрест лежащие при пересечении прямых ВС и AD секущей BD, значит, ВС||АО.
2. BC||AD, AC – секущая, значит, BCO = DAO.
3. BOC = AOD как вертикальные.
4.

5.

Задача № 7
Р е ш е н и е.
C = D = E = F = 90°, т. к. EFCD – квадрат. DF – диагональ, и по свойству диагоналей квадрата CDF = EDF = DFE = DFC = 45°. DAO = 180° – 130° = 50°. так как DAO и CAO – смежные, ABF = DAO = 50°, т. к. CD || FE и АВ – секущая, ABF и DAO – внутренние накрест лежащие, аналогично ABE = ВАС = 130°. В ΔAOD DAO = 50°, ADO = 45°, значит, AOD = 180° – (50° + 45°) = 85°, т. к. сумма углов треугольника равна 180°. AOD = BOF = 85°, т. к. эти углы вертикальные.
О т в е т: 90°; 45°; 130°; 50°; 85°.
infourok.ru
Урок геометрии в 8-м классе по теме «Решение задач на применение признаков подобия треугольников»
Цели урока:
- Образовательные:
- обобщить и систематизировать знания по теме: «Признаки подобия треугольников»;
- продолжить формирование у учащихся навыков применения признаков подобия треугольников при решении задач.
- развивать логическое мышление, умение сравнивать, обобщать, делать выводы;
- развивать культуру устной речи, познавательный интерес;
Оборудование:
- мультимедийный проектор, экран;
- презентация для сопровождения урока;
- дидактический материал для разноуровневой самостоятельной работы;
- планшет для регистрации баллов, полученных учащимися на каждом этапе урока;
- листы опроса.
Тип урока: урок-практикум по решению задач
Структура урока:
- Организационный момент.
- Актуализация опорных знаний:
а)повторение теоретического материала;
б)устное решение задач. - Практикум по решению задач:
а)решение задач базового уровня по готовым чертежам;
б)разноуровневая самостоятельная работа. - Итог урока.
- Домашнее задание.
»Геометрия является самым могущественным средством
для изощрения наших умственных способностей
и дает возможность правильно мыслить и рассуждать».
Г. Галилей
Ход урока
1. Организационный момент:
Приветствие учащихся, мобилизация внимания.
Учитель: Треугольник — самая простая геометрическая фигура, знакомая вам с детства. К треугольнику на уроках геометрии мы обращаемся чаще всего. Эта фигура таит в себе немало интересного и загадочного, как Бермудский треугольник, в котором бесследно исчезают корабли и самолеты. Один мудрец сказал: «Высшее проявление духа – это разум. Высшее проявление ума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная». Это одна из основных тем школьного курса планиметрии. Умение решать задачи на применение признаков подобия широко используется в геометрии, физике, астрономии.
Сегодняшний урок мы посвятим решению задач по теме: «Признаки подобия треугольников». Это урок-практикум, где мы проверим, как усвоена тема, узнаем, как вы научились решать задачи.
Чтобы урок был успешным, вам нужно будет преодолеть четыре этапа: (Приложение 1, слайд № 3).
- Теоретический этап
- Разминка
- Это должен знать каждый
- Реши, если силен
Оценка за урок будет складываться из набранных на каждом этапе урока баллов.
Критерии оценки:
- Выше 17 баллов — «5»
- 15-17 баллов — «4»
- 10-14 баллов — «3»
- Менее 10 баллов — «2»
(Приложение 1, слайд № 4).
2. Актуализация опорных знаний.
а) Повторение теоретического материала:
Вопросы:
- Какие треугольники называют подобными?
- Какие стороны треугольников называют сходственными?
- Что такое коэффициент подобия?
- Какие существуют признаки подобия треугольников?
- Как формулируется основная теорема о подобии?
- Назовите свойство подобных треугольников.
- Чему равно отношение площадей двух подобных треугольников?
б) Устное решение задач (разминка).
(Приложение 1, слайд № 5-11).
Учащиеся фронтально решают устные задачи по готовым чертежам (7 задач на слайдах), объясняя ход решения задачи.
Замечание: Все ответы, полученные в ходе повторения теоретического материала и устной работы по готовым чертежам, учителем фиксируются на планшете для регистрации ответов учащихся, а затем переводит в баллы. Полученные, на этом этапе, каждым учеником баллы учитываются при выставлении итоговой отметки. (Верный ответ – 1 балл)
Ф. И. |
Теоретический этап |
Разминка |
Это должен знать каждый |
Реши, если силен |
Итоговая оценка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Зачет по решению задач.
а) Решение задач базового уровня по готовым чертежам (Приложение № 2)
На закрытой части доски изображены чертежи к пяти задачам. Учащиеся решают каждую задачу на отдельном листочке и сдают учителю по мере решения, который их сразу проверяет. (Можно, для оказания помощи в проверке работ учащихся, создать «команду арбитров» из числа старших школьников.) Верное решение задачи оценивается 2 баллами. Учащиеся, справившиеся с задачами этого этапа, переходят к следующему этапу. (Задачи прилагаются.)
б) Разноуровневая самостоятельная работа (Приложение № 3)
На столе учителя конверты с задачами, оцененными в 3 балла, 5 баллов и 7 баллов. Учащиеся сами выбирают себе уровень сложности задания и решают задачи в тетрадях, набирая баллы.
Задачи, оцениваемые:
- в 3 балла – базовый уровень;
- в 5 баллов – продвинутый уровень;
- в 7 баллов — продвинутый уровень.
В конце урока учитель подсчитывает количество баллов, набранных каждым учащимся, и выставляет им оценки, учитывая критерии. (Задачи прилагаются)
4. Итог урока.
а) Результаты практикума (1 – 3 этапов).
б) «Рефлексия». Предложить учащимся определить уровень усвоения, данной темы, записав на полях своих тетрадей одно из следующих утверждений:
- всё усвоил хорошо;
- усвоил, но не всё;
- не совсем усвоил;
- не усвоил.
Сегодня на уроке вы работали с самой простой геометрической фигурой, названной «клеткой геометрии», Решая различные задачи на применение признаков подобия треугольников, вы учились правильно логически мыслить, сравнивать, обобщать, делать выводы, тем самым развивали свои умственные способности.
Закончить урок хочется словами Г. Галилея «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает возможность правильно мыслить и рассуждать». (Приложение 1, слайд № 2).
5. Домашнее задание.
а) Учащиеся I группы, показавшие через рефлексию, что тему усвоили, не достаточно хорошо, получают задание на индивидуальных карточках;
б) более подготовленным учащимся необходимо подобрать, в дополнительной литературе, три задачи на применение признаков подобия треугольников, решить их;
в) два ученика получают индивидуальное задание: оформить задачи в виде презентации в Power Point.
urok.1sept.ru