Различные геометрические задачи
В этой статье мы рассмотрим решение разных задач, которые показались мне нетривиальными, интересными, “с изюминкой”.
1. В трапецию АВСD, боковые стороны которой СD и AB равны соответственно 6 и 10, вписана окружность радиуса 3. Продолжения боковых сторон пересекаются в точке М. Требуется найти радиус окружности, описанной около треугольника AMD.
Задача 1
Диаметр вписанной в трапецию окружности равен 6. Так как вписанная окружность касается оснований трапеции, то ее диаметр является высотой нашей трапеции. Но боковая сторона ее тоже 6! Известно, что перпендикуляр – кратчайшее расстояние между любыми объектами, поэтому боковая сторона СD – перпендикулярна основаниям трапеции, иначе она была бы большей длины. Таким образом, трапеция прямоугольная и треугольник ADM – тоже прямоугольный. Тогда, чтобы найти радиус описанной около него окружности, нужно найти его гипотенузу – искомый радиус будет равен ее половине.
Дополнительные построения
Рассмотрим теперь рисунок справа: проведем высоту трапеции из вершины В, как это показано красной линией на рисунке. В треугольнике АОВ известны гипотенуза (10) и высота (6). Определим его основание АО по теореме Пифагора – это второй его катет, и он равен 8:
Теперь можем определить основания нашей трапеции. Если в четырехугольник вписана окружность, то такой четырехугольник является описанным, и по свойству описанного четырехугольника суммы его противоположных сторон равны. То есть сумма оснований равна сумме боковых сторон, BC +AD=16. Тогда, поскольку OD=BC, то
Зная основание треугольника AMD, можем найти его гипотенузу. Здесь можно воспользоваться подобием треугольников ABO и AMD, а можно – теоремой синусов. Также можно определить косинус угла А, и затем, зная его, найти гипотенузу треугольника AMD:
Итак, АМ=15. Радиус описанной около треугольника АMD окружности тогда 7.5
Ответ: 7.5
2. Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Задача 2
Нарисуем чертеж:
Чтобы определить тангенс искомого угла (рисунок справа), необходимо найти только расстояние между хордами.
Построения задачи
Это расстояние – прилежащий катет треугольника MNP, тангенс угла N которого мы ищем. Противолежащий катет – образующая цилиндра, и она нам известна. То есть нам достаточно найти расстояния KM и NO и сложить их. КM – высота равнобедренного треугольника ABK. NO – высота равнобедренного треугольника DOC. Равнобедренные они потому, что их боковые стороны – радиусы цилиндра. Найдем площади этих треугольников по формуле Герона, тогда мы сможем узнать их высоты. Формула Герона:
Здесь p – полупериметр треугольника. Тогда:
Так как основание треугольника AKB равно 6 (это известная нам хорда), то его высота, очевидно, равна 4. Итак, KM=4.
Теперь рассмотрим треугольник DNC:
Так как основание треугольника DNC равно 8 (это вторая известная нам хорда), то его высота, очевидно, равна 3, ON=3. Значит, NP=NO+KM=7.
Тогда тангенс искомого угла можно определить из прямоугольного треугольника NPM:
Ответ: тангенс угла равен 2.
3. Плоскость 
, параллельная , касается меньшего шара, а площадь сечения большего шара этой плоскостью равна 5. Найдите площадь сечения большего шара плоскостью .Рассмотрим чертеж:
Задача 3
Построения задачи 3
Красными линиями показаны плоскости, секущие шары. Зеленые линии – радиусы большего шара, серые – меньшего. Расставим буквы, чтобы обозначить необходимые расстояния:
Чтобы определить площадь сечения (которая является окружностью), необходимо знать радиус этой окружности. Нам нужно найти длину отрезка DB. Этот отрезок – катет прямоугольного треугольника DOB. Прямоугольный он потому, что плоскость по условию касается меньшего шара, значит, отрезок EO перпендикулярен ей, и, следовательно, перпендикулярен и плоскости
Рассмотрим треугольник EFO. Его гипотенуза – это также R, а один из катетов – EO – это радиус меньшего шара r. Тогда
Заметим, что 
– известная нам площадь, равная по условию 5.
В треугольнике DOC:
Из треугольника DBO выразим искомый радиус DB:
Тогда:
Здесь тоже фигурирует величина известная: 
– площадь, равная по условию 7. Умножим последнее уравнение на 
, и вот она – искомая площадь сечения!
Ответ: искомая площадь сечения – 12.
4. Найдите объем и площадь поверхности тела, полученного при вращении треугольника со сторонами 13, 14 и 15 вокруг прямой, проходящей через вершину среднего по величине угла треугольника параллельно средней его стороне.
Чтобы лучше представить себе, как может выглядеть подобная фигура, рассмотрим чертеж:
Задача 4
Средний угол треугольника лежит против его средней стороны – то есть это угол, противолежащий стороне с длиной 14. Тогда при вращении треугольника получится цилиндр, из которого “вырезаны” два конуса: сверху и снизу. Высота нашего цилиндра равна длине стороны – 14, а образующие конусов равны 13 и 15. Тогда объем такой фигуры равен объему цилиндра за вычетом объемов двух конусов, а площадь поверхности – это сумма боковых поверхностей обоих конусов и цилиндра.
Рассмотрим рисунок:
Сечение цилиндра
Здесь представлено осевое сечение цилиндра (вернее, его половина). Этот рисунок поможет определить радиус цилиндра R. Видно, что искомый радиус цилиндра – это высота треугольника ABC – AK. Чтобы определить высоту, найдем площадь треугольника ABC. Здесь можно воспользоваться формулой Герона:
Найдем половину периметра:
Теперь определим площадь:
Зная площадь треугольника, просто найти высоту, а в нашем случае это радиус цилиндра:
Определим теперь высоты конусов h и H. Это можно сделать по теореме Пифагора из треугольников ABD и ACM:
Теперь нам известны радиус цилиндра, образующие и высоты конусов, так что найти требуемые объем и площадь поверхности – дело техники, как говорится:
Определение полной поверхности
Площадь боковой поверхности цилиндра:
Площадь боковой поверхности конуса с меньшей высотой:
Площадь боковой поверхности конуса с большей высотой:
Общая площадь поверхности:
Объем цилиндра:
Объем меньшего конуса:
Объем большего конуса:
Искомый объем фигуры равен разнице объемов цилиндра и двух конусов:
Ответ: объем 4222, площадь 2111.
easy-physic.ru
Пять по геометрии
Хорошо ли вы помните школьную математику? А как с логикой и пространственным мышлением? Предлагаем вам попробовать свои силы и решить пять не самых очевидных задач по геометрии, которые подобрали для нас специалисты Московского центра непрерывного математического образования. Если вам понравится, вы можете продолжить — на сайте центра в открытом доступе выложены 10 тысяч геометрических задач.
1. По неподвижной окружности, касаясь ее изнутри, катится без скольжения окружность вдвое меньшего радиуса. Траектория фиксированной точки подвижной окружности лежит на:
- Окружности
- Прямой
- Ломаной линии
- Эллипсе
- Кривой четвертого порядка
Правильно!
Это прямая. Решается задача так: пусть O — центр неподвижной окружности, K0 — первоначальная точка касания окружностей, O1 — новый центр катящейся окружности, M — новая точка касания, K — движущаяся точка. Тогда дуга MK0 = дуге MK. Поэтому угол MO1K = двойному углу MOK0. Следовательно, точка K лежит на прямой OK0.
Неправильно!
Это прямая. Решается задача так: пусть O — центр неподвижной окружности, K0 — первоначальная точка касания окружностей, O1 — новый центр катящейся окружности, M — новая точка касания, K — движущаяся точка. Тогда дуга MK0 = дуге MK. Поэтому угол MO1K = двойному углу MOK0. Следовательно, точка K лежит на прямой OK0.
2. По стороне правильного треугольника катается окружность радиуса, равного высоте треугольника, причем противоположная этой стороне вершина треугольника все время находится внутри окружности. Как при этом меняется величина дуги, высекаемой на окружности сторонами треугольника?
3. На столе лежат двое плоских часов. И те, и другие идут точно, но не обязательно показывают одинаковое время. По какой линии движется середина M отрезка, соединяющего концы их минутных стрелок?
- Эллипс
- Ромб
- Окружность
- Отрезок
Правильно!
Это окружность. Пусть O1 и O2 — центры часов, P1 и P2 соответственно — концы минутных стрелок, O и M — середины отрезков O1O2 и P1P2 соответственно. Рассмотрим параллелограммы P1O1OA и P2O2OB. Из равенства треугольников MP2B и MP1A (по двум сторонам и углу между ними) следует равенство углов BMP2 и AMP
Неправильно!
Это окружность. Пусть O1 и O2 — центры часов, P1 и P2 соответственно — концы минутных стрелок, O и M — середины отрезков O1O2 и P1P2 соответственно. Рассмотрим параллелограммы P1O1OA и P2O2OB. Из равенства треугольников MP 2B и MP1A (по двум сторонам и углу между ними) следует равенство углов BMP2 и AMP1, поэтому точки A, M и B лежат на одной прямой, причем M — середина отрезка AB. Стороны OA и OB треугольника AOB соответственно равны и параллельны отрезкам O1P1 и O2P2. Эти отрезки с одинаковой угловой скоростью (1 оборот в час) вращаются вокруг точек O1 и O2, значит, медиана OM треугольника AOB вращается с той же угловой скоростью вокруг точки O. Следовательно, точка M движется по фиксированной окружности с центром O и радиусом, равным медиане OM.
4. Прямоугольный лист бумаги ABCD согнули так, что его вершина C совпала с серединой C1 стороны AD, как показано на рисунке. Чему равно отношение CK : KD?
- Однозначного ответа нет, он зависит от отношения сторон исходного прямоугольника
- 2
- 2,25
- √5
Правильно!
Отрезок СК вдвое длиннее. Из условия следует, что треугольники BC1K и BCK равны, значит, BC1 = BC, C1K = CK. В прямоугольном треугольнике ABC1 катет AC1 равен половине гипотенузы BC1, значит, ∠ABC1 = 30∘. Тогда ∠AC1B = 60∘, ∠DC1K = 180∘ − ∠AC1B − ∠BC1K = 180∘ − 60∘ − 90∘ = 30∘. В прямоугольном треугольнике KDC1 катет, лежащий против угла в 30∘, равен половине гипотенузы, то есть DK = 1/2 KC1 = 1/2 CK.
Неправильно!
Отрезок СК вдвое длиннее. Из условия следует, что треугольники BC1K и BCK равны, значит, BC1 = BC, C1K = CK. В прямоугольном треугольнике ABC1 катет AC1 равен половине гипотенузы BC1, значит, ∠ABC1 = 30∘. Тогда ∠AC1B = 60∘, ∠DC1K = 180∘ − ∠AC1B − ∠BC1K = 180∘ − 60∘ − 90∘ = 30∘. В прямоугольном треугольнике KDC1 катет, лежащий против угла в 30∘, равен половине гипотенузы, то есть DK = 1/2 KC1 = 1/2 CK.
5. Чему равна сумма углов при вершинах произвольной пятиконечной звезды? [Пятиконечная звезда — замкнутая пятизвенная ломаная, у которой каждое звено пересекает оба звена, не имеющих с ним общих вершин.]
Поздравляем, ваш результат: из
Одномерный геометрДвумерное пространство для вас пока слишком сложно, попробуйте попрактиковаться в одномерном.
Поделиться результатами
Поздравляем, ваш результат: из
Двумерный геометрНа плоскости вы уже почти освоились, нужно еще немного потренироваться.
Поделиться результатами
Поздравляем, ваш результат: из
Готов выйти в трехмерное пространствоС планиметрией вы уже разобрались, теперь можно переходить к стереометрии!
Поделиться результатами
nplus1.ru
Две сложные планиметрические задачи из части В
2017-06-02 | Автор: Анна
Задачи достаточно интересные. Первая заставила подумать над решением, вторая – над условием. Интересны они также тем, что присутствуют в части В – под номером 6, для которого в целом являются необычными.
Задача 1. В треугольнике 
, в котором угол 
и 
, проведена медиана 
. Найдите угол 
, ответ дайте в градусах.
К задаче 1
Решение. Определим угол 
:
![\[\angle C=180^{\circ}-105^{\circ}-30^{\circ}=45^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6052dc5f8dedaf72d377a0b056eed317_l3.png "Rendered by QuickLaTeX.com")
Такие углы – 
и 
– наталкивают на построение высоты треугольника. Построим 
, которая разобьет треугольник на два: равнобедренный 
и треугольник 
с углом в . Против угла в лежит катет, который вдвое короче гипотенузы. Поэтому 
, треугольник 
– правильный. А треугольник 
– равнобедренный, и, так как угол 
– то угол 
, и 
.
Ответ: 
.
Задача 2. Средняя линия треугольника образует со стороной углы, которые в три раза больше углов треугольника при этой стороне. Найдите углы треугольника.
К задаче 2
Рассмотрим треугольник и его среднюю линию 
. Пусть 
и 
. Пусть 
, тогда, чтобы условие было до конца соблюдено, то 
. Тогда, так как 
(как односторонние), то 
, 
. Тогда углы треугольника 
, 
, 
.
Ответ: , 
, 
.
easy-physic.ru
Разные геометрические задачи на доказательство
Все задачи взяты из книги “ОГЭ 2015. Математика. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко”
Задача 1. В треугольнике АВС с тупым углом ВАС проведены высоты 
и 
. Докажите, что треугольники 
и 
подобны.
К задаче 1
Дополнительные построения
Чтобы доказать подобие, нам потребуется доказать равенство хотя бы двух углов треугольников и . Один видно сразу: очевидно, что угол 
равен углу как вертикальный. Осталось доказать равенство еще каких-нибудь двух углов этих треугольников. Рассмотрим треугольники 
и 
. Они прямоугольные, и имеют равные гипотенузы. Значит, если провести окружность диаметром BC, то она будет описанной и для треугольника и для треугольника . Тогда угол 
– вписанный и угол 
– также, и опираются они на одну дугу. Вот мы и доказали равенство двух углов в треугольниках и , то есть, они подобны, ч.т.д.
Задача 2. Докажите, что биссектрисы смежных углов перпендикулярны.
К задаче 2
Рассмотрим углы ADB и BDC. Их сумма равна 
, так как они смежные. Биссектриса 
угла ADB делит его на равные углы 1 и 2, а биссектриса 
угла BDC делит его в свою очередь на равные углы 3 и 4. Тогда сумма всех малых углов 
, а так как угол 
, а угол 
, то можно записать, что 
, или 
, или, иначе, 
, ч.т.д.
К задаче 3
Задача 3. Докажите, что биссектрисы 
и 
внутренних накрест лежащих углов, образованных параллельными прямыми 
и 
и секущей 
, параллельны, то есть лежат на параллельных прямых.
Так как прямые параллельны, то внутренние накрест лежащие углы равны. Биссектрисы e и d делят пополам каждая свой угол. Но так как равны сами накрест лежащие углы, то равны и их половины (на рисунке все равные углы обозначены дугой одного цвета). Но углы 1 и 2 являются внутренними накрест лежащими для прямых d и e при пересечении их секущей с, а следовательно, прямые e и d параллельны, ч.т.д.
Задача 4. Докажите, что прямые и , изображенные на рисунке, параллельны.
К задаче 4
Рассмотрим рисунок. Из него видно, что угол вертикальным с углом 
, а значит, тоже равен . По той же причине угол равен 
. Тогда в треугольнике, образованном пересекающимися прямыми, нам известны два угла и мы можем определить третий – угол 
– из суммы углов треугольника. Тогда 
. Угол является соответственным с известным углом, равным 
, и, так как соответственные углы равны, то прямые a и b параллельны.
Задача 5. Докажите, что диагональ четырехугольника меньше его полупериметра.
К задаче 5
Рассмотрим треугольник ABC и запишем для него неравенство треугольника: 
. То же самое сделаем для треугольника ADC: 
. Теперь просто сложим два неравенства: 
. В правой части имеем не что иное, как периметр четырехугольника: 
, ну а теперь разделим наше неравенство пополам, и правую, и левую части: 
, ч.т.д.
Задача 6. Докажите, что два острых угла со взаимно перпендикулярными сторонами равны.
К задаче 6
Сторона CD угла ACD перпендикулярна стороне OD угла AOD, сторона CA угла ACD перпендикулярна стороне AO угла AOD. Рассмотрим образовавшиеся треугольники ABC и OBD. Их углы CBA и DBO вертикальные, а значит, равны. Кроме того, оба треугольника прямоугольные, значит, они подобны по двум углам, а в подобных треугольниках равны все углы, значит, угол ACB равен углу BOD, ч.т.д.
Задача 7. Стороны тупого угла А соответственно перпендикулярны сторонам угла В. Докажите, что сумма углов А и В равна 180 градусам.
К задаче 7
Рассмотрим треугольник ABC. Сумма его углов равна . Сумма углов треугольника ABD также равна . Тогда сумма всех углов четырехугольника ACBD равна 
. Два угла рассматриваемого четырехугольника прямые, их сумма 
. Тогда 
, ч.т.д.
Задача 8. В равностороннем треугольнике АВС точки M, N, K – середины сторон АВ, ВС и СА соответственно. Докажите, что треугольник MNK – равносторонний.
К задаче 8
Так как M и N – середины сторон AB и BC, то MN – средняя линия треугольника ABC, а значит, 
. Так как N и K – середины сторон BC и AC, то NK – средняя линия треугольника ABC, а значит, 
. Аналогично 
. Так как треугольник ABC равносторонний, то равны все его стороны, а следовательно, и половины сторон: 
, что, в свою очередь, означает, что треугольник MNK равносторонний, ч.т.д.
Задача 9. На стороне ВС квадрата АВСD взята точка К. Докажите, что площадь треугольника AKD равна половине площади квадрата.
К задаче 9
Площадь квадрата равна 
, так как его стороны равны. Площадь треугольника AKD равна произведению основания на высоту: 
. Высота треугольника равна 
, тогда 
, ч.т.д.
Задача 10. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
К задаче 10
Проведем доказательство от обратного. Предположим, что 
. Тогда треугольник ABH равнобедренный, и угол HBA равен углу BAH. В то же время треугольник HAC также равнобедренный, и угол HAC равен углу HCA. Сумма острых углов прямоугольного треугольника равна 
. Тогда и сумма углов BAH и HCA равна тоже , а это дано нам по условию. Следовательно, 
. Можно также поместить центр окружности в точку H и провести окружность радиусом HB. Она пройдет и через точку C. Тогда, поскольку угол BAC прямой, эта окружность должна пройти через точку A, так как угол BHC – развернутый и центральный, а угол, опирающийся на ту же дугу – прямой, и, следовательно, вписанный. Тогда AH – радиус окружности и .
easy-physic.ru
Геометрические задачи на доказательство. Признаки равенства треугольников.
Все задачи взяты из книги “ОГЭ 2015. Математика. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко”
Задача 1. Два отрезка 
и 
пересекаются в точке О, которая является серединой каждого из них. Докажите равенство треугольников 
и 
.
К задаче 1
Рассмотрим треугольники COB и AOD. Они имеют равные стороны: CO=OD, AO=OB – по условию. Угол COB равен углу AOD (вертикальные). Таким образом, треугольники COB и AOD равны по первому признаку. Тогда CB=AD.
Рассмотрим треугольники COA и BOD. Они имеют равные стороны: CO=OD, AO=OB – по условию. Угол COA равен углу BOD (вертикальные). Таким образом, треугольники COA и BOD равны по первому признаку. Тогда CA=BD.
Треугольники ACD и BDC имеют общую сторону – CD. Таким образом, они равны по третьему признаку, ч.т.д.
Задача 2. Лучи 
и 
пересекаются в точке О, угол 1 равен углу 2, 
. Докажите, что 
.
К задаче 2
Чтобы доказать, что ОА=ОВ, потребуется доказать равенство треугольников AOC и OBD. В этих треугольниках мы имеем один равный элемент: нам дано, что OC=OD. Также известно, что угол 1 равен углу 2. Тогда угол 
, а угол 
, а это значит, что угол 
. Добавим к этому еще равенство углов AOC и BOD – они вертикальные. Таким образом, имеем равную сторону и два равных прилегающих к ней угла – а это второй признак равенства треугольников. Раз треугольники равны, то равны и их элементы: OA=OB, ч.т.д.
Задача 3. В треугольнике ABC 
и угол 1 равен углу 2. Докажите, что угол 3 равен углу 4.
К задаче 3
Рассмотрим треугольник АВС. Нам дано, что он равнобедренный. А это значит, что углы при его основании равны: угол C равен углу В. Тогда треугольники CDA и ABE равны по второму признаку: угол 1 равен углу 2 по условию, CA=AB. Тогда в этих треугольниках равны соответствующие элементы: DA=AE. Это значит, что, в свою очередь, треугольник DEA тоже равнобедренный. А это означает, что углы при его основании равны, т.е. угол 3 равен углу 4, ч.т.д.
Задача 4. На рисунке 
и 
. Докажите, что 
.
К задаче 4
Равенство BD и CE можно доказать, если удастся доказать равенство треугольников ABD и AEC.
Поскольку и , то 
. Угол A у данных треугольников общий, таким образом, они равны по первому признаку. А это означает, что 
, ч.т.д.
Задача 5. Докажите, что у равных треугольников и 
медианы, проведенные из вершин 
и 
, равны.
Так как 
, то 
, то есть 
, а еще из равенства треугольников следует, что 
. Так как треугольники и равны по условию, то равны и углы: угол равен углу . Но тогда у треугольников 
и 
равны углы и прилегающие стороны, они равны по первому признаку. Тогда 
, ч.т.д.
К задаче 5
easy-physic.ru
Полезные факты для решения задач ЕГЭ по геометрии
Углы, треугольники, четырехугольники
1. Биссектрисы смежных углов перпендикулярны.
2. Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
3. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
4. Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними.
5. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
6. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
7. Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии.
8. Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, являющейся центром окружности, описанной вокруг треугольника.
9. Три биссектрисы треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник.
10. Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
11. Три высоты треугольника пересекаются в одной точке. В случае тупоугольного треугольника пересекаются продолжения высот.
Окружности
12. Диаметр, перпендикулярный хорде, делит ее пополам
13. Произведения отрезков пересекающихся хорд окружности равны.
14. Серединный перпендикуляр к хорде проходит через центр окружности
15. Равные хорды удалены от центра окружности на равные расстояния
16. Дуги окружности, заключенные между параллельными хордами, равны.
17. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
18. Теорема о касательной и секущей. Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
19. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
20. Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружности.
21 Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен .
22. Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
23. Если расстояние между центрами окружностей радиусами R и r равно а и , то отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно и
24. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусов.
25. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
26. Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии.
27. Если М – точка касания со стороной АС окружности, вписанной в треугольник АВС, то АМ = р – ВС, где р – полупериметр треугольника АВС.
28. Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС, то расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС.
29. Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен , то угол .
30. Если прямые, проходящие через точку А, касаются окружности S в точках В и С, то центр вписанной окружности треугольника АВС лежит на окружности S.
31. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна .
32. Свойство биссектрисы треугольника. Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.
При составлении списка полезных фактов использованы учебные пособия
Р. К. Гордина
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Решение треугольников. Более сложная задача. Видеоурок. Геометрия 9 Класс
На этом уроке мы будем находить элементы треугольника, используя основные теоремы синусов и косинусов и теоремы о площади.
Рассмотрим задачу, в которой заданы две стороны треугольника и угол не между ними, в этом случае число решений зависит от конкретных числовых данных.
Число решений может быть два:
предположим, что 
. В треугольнике может быть угол 
или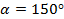 
(рис. 1)
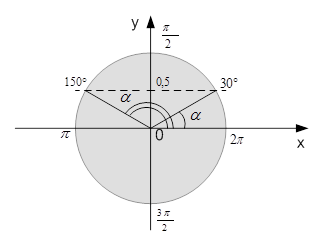
Рис. 1. Иллюстрация к задаче
Дано: треугольник ABC, a = 6, b =8, (рис. 2)
Найти: углы 
, γ; сторону с
Решение:
Воспользуемся теоремой синусов
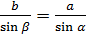
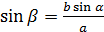
Рис. 2. Иллюстрация к задаче
Видим, что 
, следовательно, угол β существует и существует два угла.
Рисунок 3 иллюстрирует наличие двух углов β.
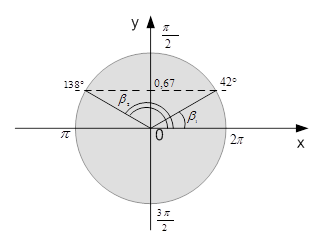
Рис. 3. Иллюстрация к задаче
Треугольник ABC (рис. 2) имеет определённый радиус описанной окружности.
По теореме синусов:
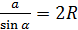
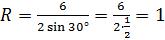
Рассмотрим два случая:
1. (рис. 4)
Тогда угол 
:
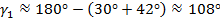
Следовательно,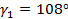 
, 
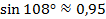
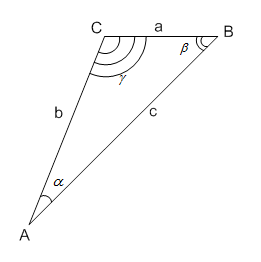
Рис. 4. Иллюстрация к задаче
Далее используем теорему синусов:
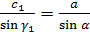
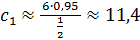
Для первого случая треугольник решён.
Ответ: β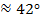 
, 
, 
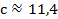
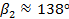(рис. 2)
Тогда угол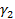 
:
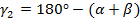
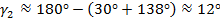
Следовательно,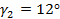 
, 
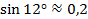
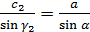
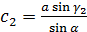
Ответ: 
, 
, 
Задача решена, получены два ответа. Дадим геометрическую интерпретацию ответа.
1. В окружности радиусом R = 6 проведём хорду a = 6, получим две точки B и C, которые являются вершинами искомого треугольника (рис. 5). Этот треугольник вписан в окружность с центром в точке O.
2. Проведём окружность с центром в точке C и радиусом b = 8.
3. Радиус второй окружности – 8, он меньше, чем удвоенный радиус первой окружности. Значит, существуют две точки пересечения (
этих окружностей.
4. Вписанные в окружность углы с вершинами 
одинаковые. 
. 
, так как треугольник BOC правильный (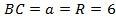
).
5. Получили два треугольника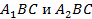 
. Это и есть искомые треугольники. В них:
, 
, 
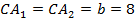– все заданные значения.
6. В треугольниках найдены точные значения искомых величин:
— треугольник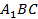 
: 
, 
, 
;
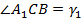— треугольник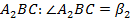 
, 
, 
.
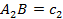Рис. 5. Иллюстрация к задаче
Четвёртый признак равенства треугольников и его частный случай
Также можно сделать замечание: угол α = 30
явно не наибольший угол в заданном треугольнике ABC, а из четвёртого признака равенства треугольников знаем, что треугольники равны по двум сторонам и наибольшему углу (этот наибольший угол может находиться не между двумя сторонами). Отсюда частный случай четвёртого признака равенства треугольников: равенство прямоугольных треугольников по катету и гипотенузе (прямой угол наибольший, он не лежит между катетом и гипотенузой).
[00:17:09 Разветвление: опорные факты из задачи 1]
Из задачи 1 можно выделить важные опорные факты.
1. Теорема о вписанном угле имеет важное следствие:
вписанные углы, опирающиеся на одну и ту же дугу, равны между собой.
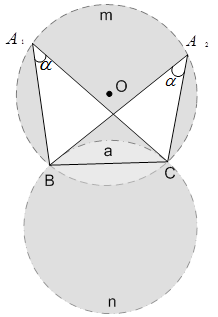
Рис. 6. Иллюстрация к следствию
(рис. 6)
Это означает, что из любой точки дуги 
отрезок BC = а виден под одним и тем же углом (α). Существуют также другие точки, с которых данный отрезок виден под этим же углом. Это точки на дуге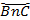 
. Таким образом, объединение этих двух дуг (исключая концы отрезка BC) даёт геометрическое место всех точек, с которых данный отрезок виден под данным углом.
2. Отрезок BC = a и противолежащий угол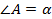 
задают семейство треугольников (
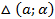). Эти треугольники часто не похожи друг на друга, но они имеют один и тот же элемент – радиус описанной окружности 
.
3. Также у семейства этих треугольников есть ещё один общий элемент – отрезок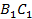 
(рис. 7), где точка 
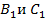– основание высот, опущенных из вершины B и вершины C. Для того чтобы в этом убедиться, попробуйте решить самостоятельно задачу:
Задан остроугольный треугольник ABC (рис. 7). В нём сторона BC = a, ,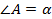
interneturok.ru