Задачи по теме «Комбинаторика»

Задачи для решения на закрепление нового материала

Задача № 1. Сколькими способами могут быть расставлены 5 участниц финального

забега на 5-ти беговых дорожках?

Решение: Р₅ = 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов.

Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая

цифра входит в изображение числа только один раз?

Решение: Число всех перестановок из трех элементов равно Р₃=3!, где 3!=1 * 2 * 3=6

Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.

Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шести

девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И

варианты, при которых одни и те же девушки танцуют с разными юношами,

считаются разными, поэтому: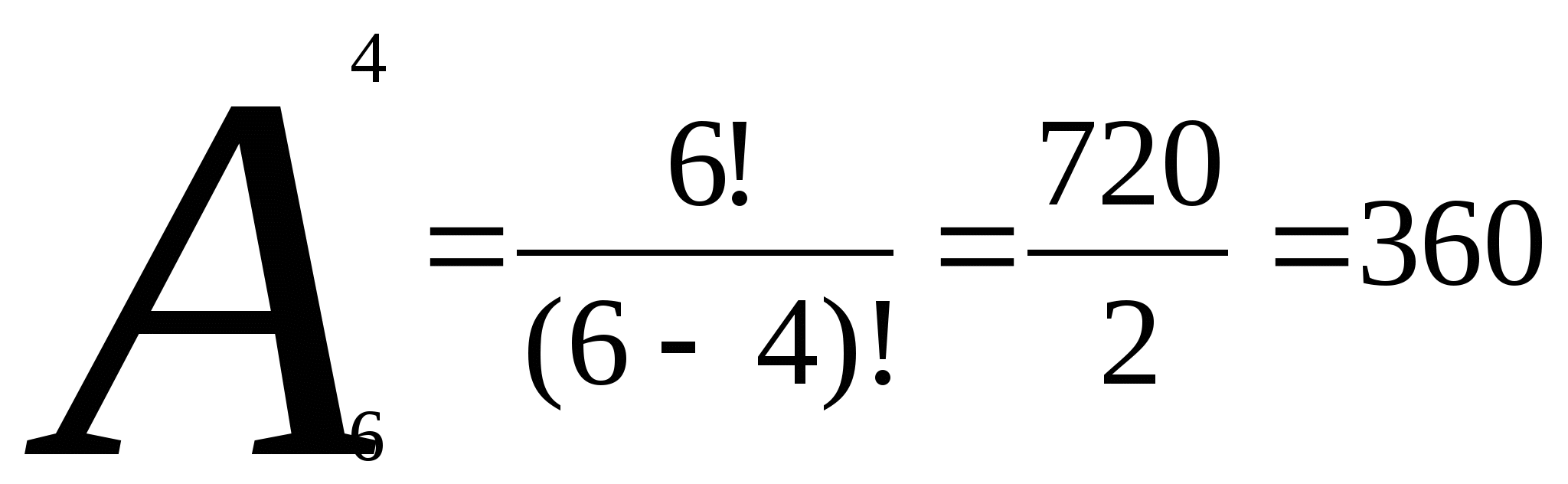

Задача № 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5,

6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только

один раз?

Решение: В условии задачи предложено подсчитать число всевозможных комбинаций из

трех цифр, взятых из предположенных девяти цифр, причём порядок

расположения цифр в комбинации имеет значение (например, числа 132)

и 231 различные). Иначе говоря, нужно найти число размещений из девяти

элементов по три.

По формуле числа размещений находим:

Ответ: 504 трехзначных чисел.

Задача №5 Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3

человек?

Решение: Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все

возможные 3 – элементные подмножества множества, состоящего из 7

человек. Искомое число способов равно

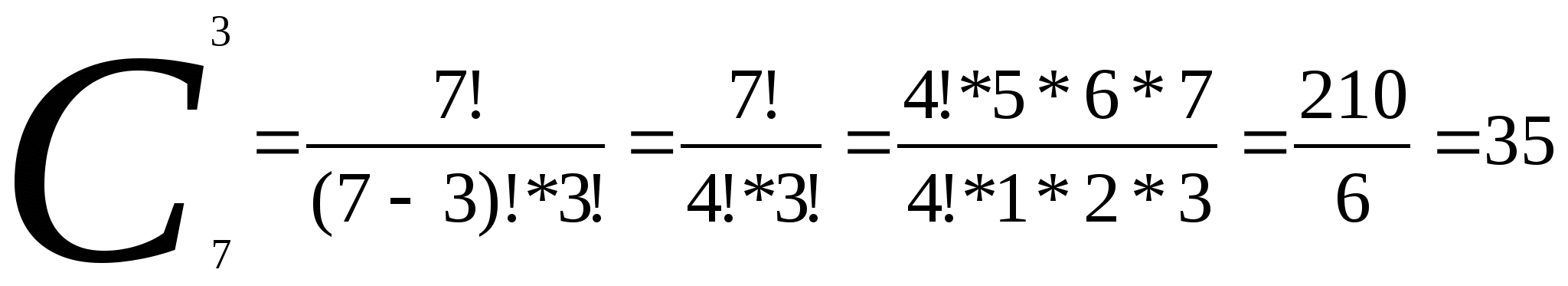
Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантов

распределения призовых (1, 2, 3) мест?

Решение: А₁₂³ = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест. Ответ: 1320 вариантов.

Задача № 7. На соревнованиях по лёгкой атлетике нашу школу представляла команда из

10 спортсменов. Сколькими способами тренер может определить, кто из них

побежит в эстафете 4100 м на первом, втором, третьем и четвёртом этапах?

Решение: Выбор из 10 по 4 с учётом порядка: 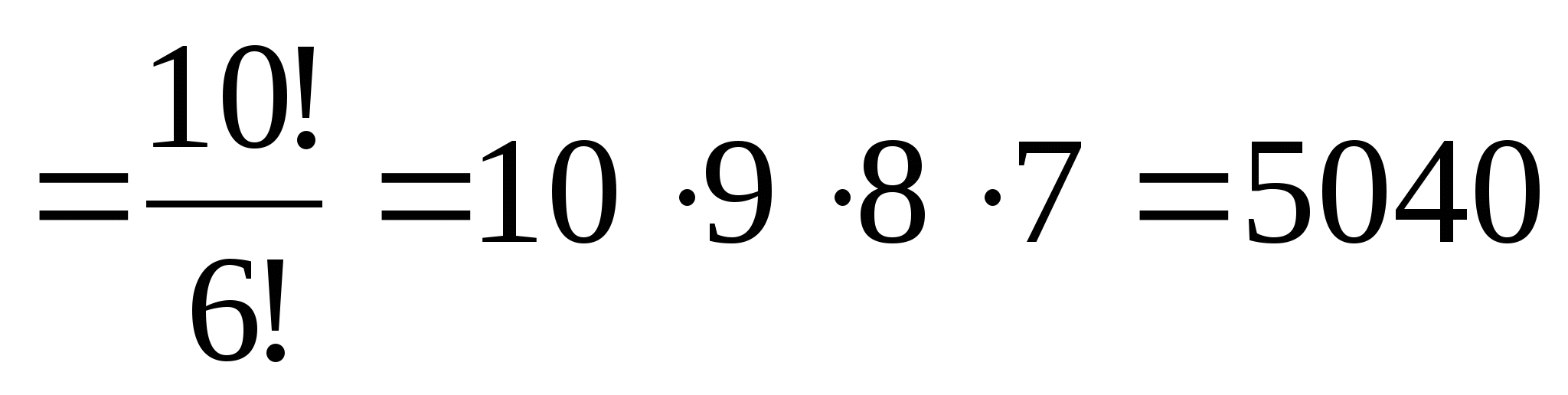способов.

Ответ: 5040 способов.

Задача № 8. Сколькими способами можно выложить в ряд красный, черный, синий и

зеленый шарики?

Решение: На первое место можно поставить любой из четырех шариков (4 способа), на

второе – любой из трех оставшихся (3 способа), на третье место – любой из

оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.

Всего 4 · 3 · 2 · 1 = 24 способа.

Р₄ = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.

Задача № 9. Учащимся дали список из 10 книг, которые рекомендуется прочитать во

время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Решение: Выбор 6 из 10 без учёта порядка: 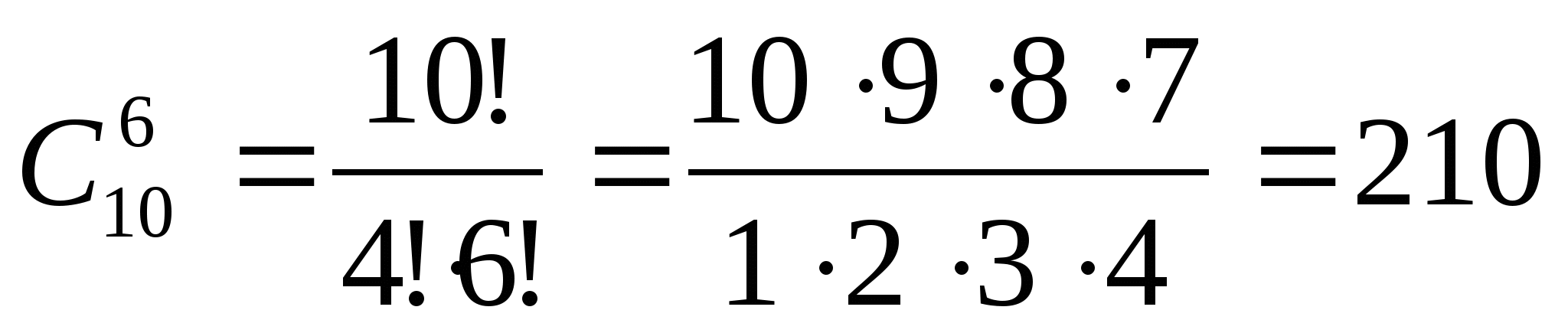способов.

Ответ: 210 способов.

Задача № 10. В 9 классе учатся 7 учащихся, в 10 — 9 учащихся, а в 11 — 8 учащихся. Для

работы на пришкольном участке надо выделить двух учащихся из 9 класса,

трех – из 10, и одного – из 11 . Сколько существует способов выбора

учащихся для работы на пришкольном участке?

Решение: Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из

первой совокупности (С₇²) может сочетаться с каждым вариантом выбора из

второй (С₉³) ) и с каждым вариантом выбора третьей (С₈¹) по правилу

умножения получаем:

Ответ: 14 112 способов.

Задача № 11. Девятиклассники Женя, Сережа, Коля, Наташа и Оля побежали на

перемене к теннисному столу, за которым уже шла игра. Сколькими

способами подбежавшие к столу пятеро девятиклассников могут занять

очередь для игры в настольный теннис?

Решение: Первым в очередь мог встать любой девятиклассник, вторым – любой из

оставшихся троих, третьим – любой из оставшихся двоих и четвёртым –

девятиклассник, подбежавший предпоследним, а пятым – последний. По

правилу умножения у пяти учащихся существует 5· 4321=120 способов

занять очередь.

infourok.ru

4.2 Простейшие комбинаторные задачи

Знакомство с новыми понятиями начнем с двух простых задач.

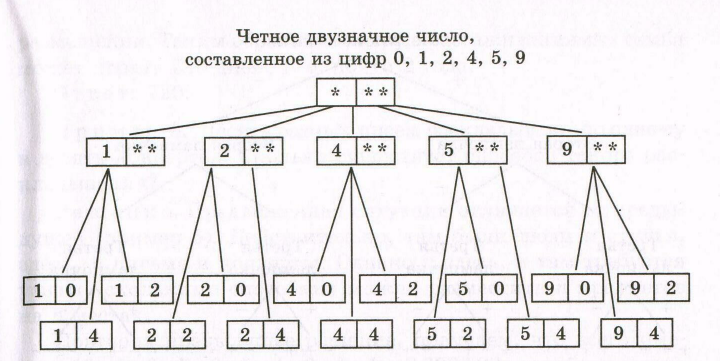
Пример 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 9?

Решение. Составим таблицу: слева от первого столбца поместим первые цифры искомых чисел, а выше первой строки – вторые цифры этих чисел. Так как в двузначном числе на первом месте может стоять любая цифра, кроме 0, то строки будут отмечены цифрами 1, 2, 4, 5, 9. Значит, в нашей таблице будет пять строк. На втором месте в искомом числе должна стоять четная цифра, значит, столбцы будут отмечены цифрами 0, 2, 4. Всего в таблице будет три столбца.

	0	2	4
1	10	12	14
2	20	22	24
4	40	42	44
5	50	52	54
9	90	92	94

Клетки таблицы заполняются следующим образом: первая цифра числа равна метке строки, а вторая цифра – метке столбца, поэтому каждое из интересующих нас чисел попадет в определенную клетку таблицы. По строкам и столбцам мы перечислили все возможные варианты, значит, искомых чисел будет столько же, сколько клеток в таблице, т. е. 5 • 3 = 15.

Ответ: 15.

Здесь был осуществлен полный перебор всех возможных вариантов или, как обычно говорят в таких случаях, всех возможных комбинаций. Поэтому подобные задачи называют комбинаторными.

Пример 2. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?

Решение. Соберем все варианты в такой таблице: в ней три строки и четыре столбца, они образуют 12 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоять один из возможных вариантов завтрака и, наоборот, любой вариант завтрака будет записан в одной из клеток. Значит, всего вариантов столько же, сколько клеток в таблице.

	Плюшка	Бутерброд	Пряник	Кекс
Кофе	Кофе, плюшка	Кофе, бутерброд	Кофе, пряник	Кофе, кекс
Сок	Сок, плюшка	Сок, бутерброд	Сок, пряник	Сок, кекс
Кефир	Кефир, плюшка	Кефир, бутерброд	Кефир, пряник	Кефир, пряник

Ответ: 12.

Мы видим, что, хотя примеры 1 и 2 очень разные, их решения совершенно одинаковые. Основаны они на общем правиле умножения.

4.3 Правила умножения и сложения

Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

Правило умножения для двух независимых испытаний удобно объяснять, используя прямоугольники, разбитые на квадратики, или прямоугольные таблицы. Но если проводятся три испытания, то для иллюстрации надо использовать и длину, и ширину, и высоту, и на картинке получится прямоугольный параллелепипед, разбитый на кубики. Здесь уже рисунок и объяснения становятся сложнее, поскольку, например, будут невидимые кубики. Еще хуже дело обстоит с четырьмя испытаниями. В этом случае для рисунка нам просто не хватит измерений, ведь окружающее нас пространство всего лишь трехмерно.

Оказывается, правило умножения для трех, четырех и т. д. испытаний можно объяснить, не выходя за рамки плоскости, с помощью геометрической модели, которую называют деревом возможных вариантов. Она, во-первых, наглядна как всякая картинка, и, во-вторых, позволяет все учесть, ничего не пропустив.

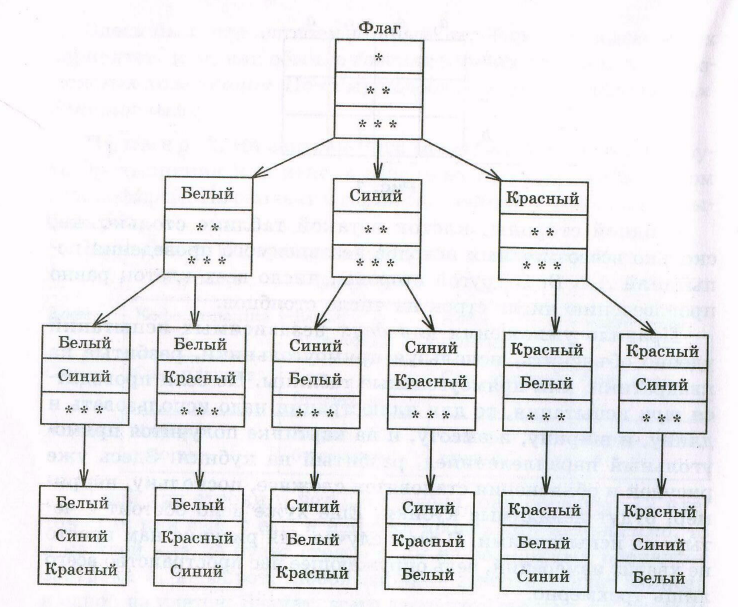Пример 3. Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?

Решение. Будем искать решение с помощью дерева возможных вариантов (рис. 4.1). Посмотрим на его левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя.

Пусть теперь верхняя полоса – синего цвета, это вторая «веточка».

Рисунок 4.1

Тогда средняя полоса может быть белой или красной, а нижняя – соответственно, красной или белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая.

Аналогично рассматривается случай для верхней полосы красного цвета. Получится еще два варианта: красная, белая, синяя и красная, синяя, белая полосы флагов. Всего 6 комбинаций.

Ответ: 6.

Построенная схема действительно напоминает дерево, только перевернутое. Видимо, поэтому ее и называют деревом возможных вариантов.

Вот как, например, выглядит дерево возможных вариантов для примера 1 (рисунок 4.2):

Для следующего примера мы приведем три различных способа решения: с помощью простого перебора, с помощью дерева вариантов и по правилу умножения.

Рисунок 4.2

Пример 4. В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?

Решение.

Первый способ. Пронумеруем лампочки и будем писать «+» или «-» в зависимости от того, горит или не горит очередная лампочка. Тогда все способы освещения можно просто перечислить: + + +, + + -, + — +, — + +, + — -, — + -, — — +,

Всего 8 способов.

Второй способ. Дерево возможных вариантов представлено на рисунке 4.3. С его помощью находим, что осветить коридор можно 8 способами.

Третий способ. Первая лампочка может или гореть, или не гореть, т.е. имеется два возможных исхода. То же самое относится и ко второй, и к третьей лампочкам. Мы предполагаем, что лампочки горят или нет независимо друг от друга. По

Рисунок 4.3 правилу умножения получаем, что число всех способов освещения равно 2 • 2 • 2 = 8.

Ответ: 8.

У каждого из этих трех способов решения в каждом конкретном случае есть свои преимущества и свои недостатки. Выбор способа решения – за вами! Отметим все же, что правило умножения позволяет в один шаг решать самые разнообразные задачи. Например, оно приводит к крайне важному в математике понятию факториала. Рассмотрим сначала примеры.

Пример 5. В семье – 6 человек, и за столом в кухне стоят 6 стульев. В семье решили каждый вечер, ужиная, рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?

Решение. Ответ оказывается неожиданно большим: почти два года! Объясним его. Для удобства рассуждений будем считать, что семья (бабушка, дедушка, мама, папа, дочь, сын) будет рассаживаться на стулья поочередно. Нас интересует, сколько всего существует различных способов их размещения на стульях.

Предположим, что первой усаживается бабушка. У нее имеется 6 вариантов выбора стула. Вторым садится дедушка и независимо выбирает стул из 5 оставшихся. Мама делает свой выбор третьей и выбор у нее будет из 4 стульев. У папы будет уже 3 варианта, у дочки – 2, ну а сын сядет на единственный незанятый стул. По правилу умножения получаем, что всего имеется 6·5·4·3·2·1 = 720 различных способов размещения. Таким образом, в «игру с рассаживаниями» семья может играть 720 дней, т. е. почти 2 года.

Ответ: 720.

Пример 6. Десять разных писем раскладывают по одному в десять конвертов. Сколько существует способов такого раскладывания?

Решение. Предложенная ситуация отличается от предыдущей (пример 5). Действительно, там были люди и стулья, здесь – письма и конверты. Однако и здесь, и там требуется узнать, сколькими способами можно разместить п предметов на п местах.

Повторяя предыдущее решение, получаем, что всего имеется 10·9·8·7·6·5·4·3·2·1=3 628 800 способов раскладывания писем по конвертам. Более 3,5 миллионов!

Ответ: 3628800.

Как мы видим, условия задач – разные, а решения, да и полученные ответы, по сути дела, одинаковы. Удобно поэтому ввести и одинаковые обозначения для таких ответов.

Определение. Произведение первых подряд идущих п натуральных чисел обозначают п!

п! = 1·2·3·…·(п-2)·(п-1)·п

Знак п! читается как «эн факториал», что в дословном переводе с английского языка означает «состоящий из п множителей». Приведем несколько первых значений для п:

1! = 1

2! = 1·2 = 2

3! = 1·2·3 = 6

4! = 1·2·3·4 = 24

5! = 1·2·3·4·5 = 120

6! = 1·2·3·4·5·6 = 720 и т.д.

Рассмотрим еще несколько примеров:

Пример 7. Вычислить: а) 3!; б) 7!5!; в) .

Решение. а) 3!=1∙2∙3=6.

б) т.к. 7!= 1∙2∙3∙4∙5∙6∙7 и 5!= 1∙2∙3∙4∙5, то 5! можно вынести за скобки, тогда получим 5!(6∙71)= 1∙2∙3∙4∙5∙41=4920.

в) .

Пример 8. Упростить выражение: .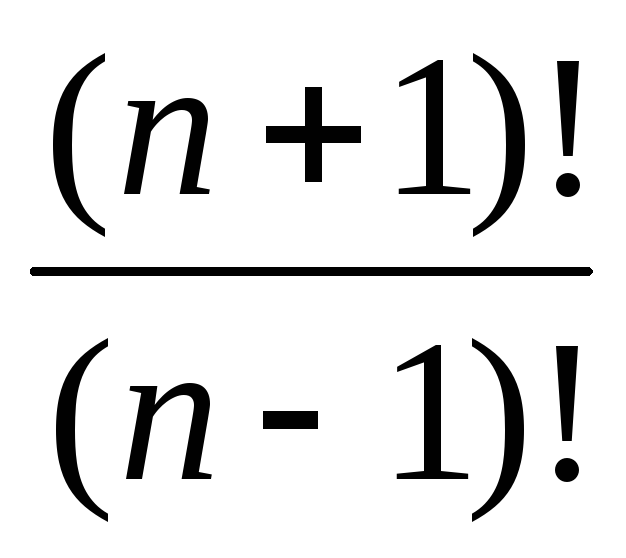

Решение. 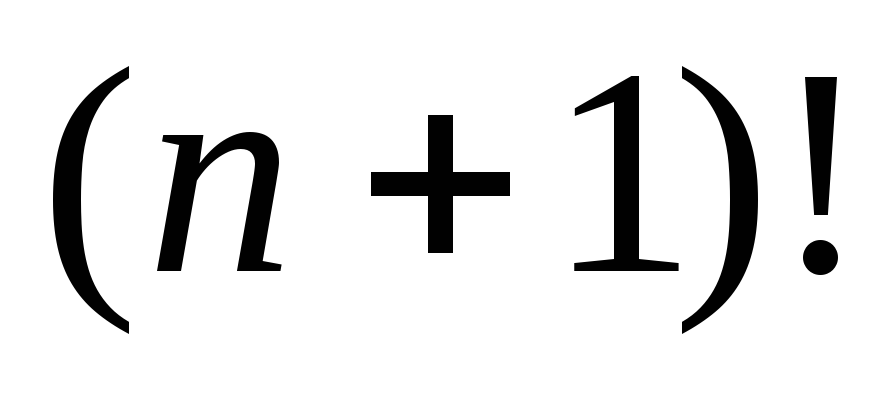=1∙2∙3∙…∙(п 1)∙п∙(п+1), а =1∙2∙3∙…∙(п1), после сокращения получим п∙(п+1).

Как же сформулировать общее утверждение, частными случаями которого являются решения примеров 3, 5 и 6? Вот один из возможных вариантов.

ТЕОРЕМА: п различным элементам можно присвоить номера от 1 до п ровно п! различными способами.

Каждый способ нумерации от 1 до п, о котором идет речь в теореме, часто называют перестановкой данного п-элементного множества. Действительно, можно считать, что каждая такая нумерация просто расставляет или переставляет все элементы множества в некотором порядке.

Перестановками из п элементов называют комбинации, которые отличаются друг от друга только порядком элементов.

Число перестановок множества из п элементов обозначают Р_п. Значит, приведенную теорему можно записать в виде формулы:

Р_п = п!

Кроме правила умножения в комбинаторике иногда используется еще правило сложения: Для того чтобы найти число всех возможных исходов независимого проведения одного из двух испытаний А или В, следует сложить число всех исходов испытания А и число всех исходов испытания В.

Пример 9. На столе в стаканчике стоит 5 карандашей и 3 ручки. Для того, чтобы написать записку (записать телефонный номер и т.п.), мы можем взять 1 из 5 карандашей или 1 из 3 ручек, то есть у нас имеется 5 возможностей выбора одного карандаша и 3 возможности выбора одной ручки. Так как мы выбираем только 1 предмет, карандаш или ручку, то число всех возможностей выбора равно: 5 + 3 = 8.

Правила умножения и сложения применимы для любого количества независимых испытаний.

Подведем итоги нашего знакомства с простейшими комбинаторными задачами. Мы получили основное правило – правило умножения, рассмотрели его геометрическую модель – дерево возможных вариантов, ввели новое понятие – факториал, сформулировали теорему о перестановках, в которой это понятие используется.

studfile.net

Элементы комбинаторики. Методы решения некоторых задач

1) Немного истории.

В математике и ее приложениях часто приходится иметь дело с различного рода множествами и подмножествами: устанавливать их связь между элементами каждого, определять число множеств или их подмножеств, обладающих заданным свойством. Такие задачи приходится рассматривать при определении наиболее выгодных коммуникаций внутри города, при организации автоматической телефонной связи, работы морских портов, при выявлении связей внутри сложных молекул, генетического кода, а также в лингвистике, в автоматической системе управления, значит и в теории вероятностей, и в математической статистике со всеми их многочисленными приложениями.

Поговорим об одном из разделов теории вероятности – комбинаторике.

Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в 17 веке. Долгое время она лежала вне основного русла развития математики.
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов — во время работы.
Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника.
Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж.Кардано, Н.Тарталье (1499-1557), Г.Галилею (1564-1642) и французс- ким ученым Б.Паскалю (1623-1662) и П.Ферма.
Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г.Лейбниц в своей работе “ Об искусстве комбинаторики ”, опубликованной в 1666 году. Он также впервые ввел термин “комбинаторика”. Значительный вклад в развитие комбинаторики внес Л.Эйлер. В современном обществе с развитием вычислительной техники комбинаторика “добилась” новых успехов. В настоящее время в образовательный стандарт по математике включены основы комбинаторики, решение комбинаторных задач методом перебора, составлением дерева вариантов (еще его называют “дерево возможностей”) с применением правила умножения. Так, например, “дерево возможностей” помогает решать разнообразные задачи, касающиеся перебора вариантов происходящих событий. Каждый путь по этому “дереву” соответствует одному из способов выбора, число способов выбора равно числу точек в нижнем ряду “дерева”. Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В. В задачах по комбинаторике часто применяется такое понятие как факториал (в переводе с английского “factor” - “множитель”).
Итак, произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут: n!=1 2 3 … (n-1) n
В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

2) ЗАДАЧИ

1. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе - мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье — чай и компот. Сколько различных обедов можно составить из указанных блюд?

1 способ. Перечислим возможные варианты

Чай(Ч) Компот (К)	Мясо с макаронами(М)	Рыба с картошкой(Р)	Курица с рисом(Кр)
Борщ (Б)	БМЧ/ БМК	БРЧ/БРК	БКрЧ/БКрК
Солянка(С)	СМЧ/ СМК	СРЧ/СРК	СКрЧ/СКрК
Грибной суп(Г)	ГМЧ/ГМК	ГРЧ/ГРК	ГКрЧ/ГКрК

18 вариантов.
2 способ. Дерево возможностей.

3 способ. Используя правило умножения, получаем: 3х3х2=1

2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу?

1 способ. Обозначим мячи — М1, М2, игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5.
Перечислим возможные варианты:

М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5,
М1-И2-К1, М1-И2-К2, М1-И2-К3, М1-И2-К4, М1-И2-К5,
М1-И3-К1, М1-И3-К2, М1-И3-К3, М1-И3-К4, М1-И3-К5,
М1-И4-К1, М1-И4-К2, М1-И4-К3, М1-И4-К4, М1-И4-К5
М2-И1-К1, М2-И1-К2, М2-И1-К3, М2-И1-К4, М2-И1-К5,
М2-И2-К1, М2-И2-К2, М2-И2-К3, М2-И2-К4, М2-И2-К5,
М2-И3-К1, М2-И3-К2, М2-И3-К3, М2-И3-К4, М2-И3-К5,
М2-И4-К1, М2-И4-К2, М2-И4-К3, М2-И4-К4, М2-И4-К5

Ответ: 40 вариантов.
2 способ. Используя правило умножения, получаем: 2х4х5= 40

3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?

1 способ.
Перечислим возможные варианты.

	0	2	6
2	20	22	26
3	30	32	36
6	60	62	66
7	70	72	76
9	90	92	96

2 способ. Дерево возможностей.

3 способ. Используя правило умножения, получаем: 5х3=15 .

4. Мисс Марпл, расследуя убийство, заметила отъезжающее от дома мистера Дэвидсона такси. Она запомнила первую цифру “2”. В городке номера машин были трехзначные и состояли из цифр 1,2,3,4 и 5. Скольких водителей, в худшем случае, ей придется опросить, чтобы найти настоящего убийцу?

1 способ. Перечислим возможные варианты номеров такси:

	1	2	3	4	5
1	211	212	213	214	215
2	221	222	223	224	225
3	231	232	233	234	235
4	241	242	243	244	245
5	251	252	253	254	255

Ответ: 25 человек.

2 способ. Используя правило умножения, получаем: 5х5=25

5. Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?

1 способ. Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:

№1 — Саша — есть возможность выбрать из 5 вариантов (стульев)
№2 — Петя — 4 варианта
№3- Денис — 3 варианта
№4- Оля — 2 варианта
№5 — Настя- 1 вариант

Используя правило умножения, получаем: 5х4х3х2х1=120

2 способ. Решаем, используя понятие факториала: 5!=120

6. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)?

1 способ. Перечислим возможные варианты состава пары:

11А-11Б, 11А-11В, 11А-11Г, 11А-11Д,
11Б-11В, 11Б-11Г, 11Б-11Д, 11В-11Г, 11В-11Д, 11Г-11Д

Ответ: 10 пар.

2 способ. Из пяти классов нужно выбрать 2 дежурных.
Число элементарных событий = = 10

7. В 8 “а” классе лучше всех математику знают 5 учеников: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами учительница может эту пару выбрать?

1 способ. Обозначим имена детей первыми заглавными буквами.
Получаем следующие пары:
В-К, В-А, Д-К, Д-А, О-К, О-А.

Ответ: 6 пар.

2 способ. Мальчиков 3, из них 1 можно выбрать , девочек 2, из них можно 1 выбрать , используя правило умножения, получаем:
х = 6

8. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы.

Сколькими способами могут распределится места по окончании соревнований?
Обозначим участников по первой заглавной букве страны и пронумеруем: Р1, И2, У3, Н4,К5, Ф6
Р1 — имеют возможность занять с1-6 места, т.е. 6 вариантов
И2 — 5 вариантов
У3- 4 варианта
Н4- 3 варианта
К5- 2 варианта
Ф6- 1 вариант
Используя правило умножения, получаем: 6х5х4х3х2х1= 720

2 способ. Используя понятие факториала, получаем: 6!=720

9. В 9 “б” классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Департамент образования премировал лучших учащихся путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора учеников на отдых?

Обозначим первыми заглавными буквами имен учащихся.
Возможны следующие тройки:
Г-С-К-О, Г-С-К-М, Г-С-К-В,
Г-С-О-М, Г-С-О-В, Г-С-М-В
С-К-О-М, С-К-О-В, С-К-М-В,
К-О-М-В, С-О-М-В, Г-К-О-В,
Г-К-О-В, Г-О-М-В, Г-К-М-В

2 способ. Из 6 человек нужно выбрать 4, число элементарных событий равно = 15

10. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого?

Вычислим, сколько четверок из 7 дисков можно составить у Пети:
=35, число четверок у Вали из 9 дисков -= 126
По правилу умножения находим число обменов 35х126=4410

11. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых?

Из 5 офицеров выбрать 2 можно с помощью числа сочетаний =10 способами, из 8 сержантов 4 — =70, из 70 рядовых 15 -. По правилу умножения находим число выбора отряда:
10х70х= 700х

12. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет?

Из 6 изумрудов 3 он может выбрать =20 способами, из 9 алмазов 5 -=126, из 7 сапфиров 2 — =21. По правилу умножения находим число вариантов 20х126х21=52920

13. На выборах победили 9 человек - Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать?

Здесь речь идет о размещениях
Можно было решать по-другому. На должность председателя выбираем из 9 человек, на заместителя — из 8, на профорга — из 7
По правилу умножения получаем 9х8х7=504

14. В районе построили новую школу. Из пришедших 25 человек нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими способами это можно сделать?

На должность директора выбираем из 25 человек, на завуча начальной — из 24, завуча среднего звена — из 23, завуча по воспитательной работе — 22. По правилу умножения получаем:
25х24х23х22 = 303600
Или, зная формулу размещения, получаем

15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)?

Для Пети набор можно набрать 6х8х10=480 способами, для Васи — 5х7х9=315, для Коли — 4х6х8=192. По правилу умножения получаем
480х315х192=29030400 способами.

16. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся?

В русском языке 9 гласных букв — а, е, е, и, о, у, э, ю, я. Выбрать из них 2 можно =36 способами. Из 10 цифр выбрать 3 можно=120 способами. Применяя правило умножения, получаем:
36х120=4320

17. Сколькими способами можно составить трехцветный флаг из полос разной ширины, если имеются материи из 8 тканей?
Эта задача на размещение

Другой способ решения.
1цвет выбирается из 8 тканей 8 способами
2цвет выбирается 7 способами
3 цвет — 6способами
Используя правило умножения, получаем 8х7х6=336 способов.

18. В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различные?

Из 15 предметов 5 любых можно выбрать

19. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета?

1 способ. Обозначим белые — Б1, Б2, Б3, алые — А1,А2, чайные — Ч1, Ч2, Ч3,Ч4
Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3, Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3, Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3, Б3-А2-Ч4

Ответ: 24 варианта.

2способ. Дерево возможностей

 3 способ. Используя правило умножения, получаем: 2х3х4=24

20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка-Быковка- Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М- пешком или на автобусе, из М в В — по реке, пешком или автобусе. Сколько вариантов похода есть у щкольников?

1 способ. Обозначим СБ — путь из Сосновки в Бытовку, ВГ — путь из Быковки в Масловку, МВ — путь из Масловки в Видово.
По реке -Р, пешком — П, на автобусе — А
Перечислим возможные варианты:
СБР- БМП-МВР, СБР- БМП-МВП, СБР- БМП-МВА
СБР-БМА-МВР, СБР-БМА-МВП, СБР-БМА-МВА
СБА- БМП-МВР, СБА- БМП-МВП, СБА- БМП-МВА
СБА-БМА-МВР, СБА-БМА-МВП, СБА-БМА-МВА
Ответ: 12 вариантов.

2 способ. Дерево возможностей

urok.1sept.ru

Задачи по комбинаторике в начальной школе.

Задачи на комбинаторику.

2 класс

3 класс

4 класс

1. У кошки Мурки родилось 8 котят. Из них 6 – пушистые, а 5 – рыжие. Может ли быть такое? Сколько одновременно рыжих и пушистых котят у Мурки?

Ответ: 6+5 – 8 = 3 котёнка.

2. Миша решил в воскресенье навестить дедушку, своего друга Петю и старшего брата Володю. Сколько вариантов визитов получится, если он может идти в гости в любом порядке?

ДПВ, ДВП, ВПД, ВДП, ПДВ, ПВД

Ответ: 6

3. Из цифр 2, 7, 3 составь все возможные двузначные числа (цифры могут в числе повторяться). Сколько и какие из них больше 30?

32, 33, 37, 72, 73, 77.

Ответ: 6 чисел

4. Начерти отрезок АО. Поставь внутри него 2 точки, обозначь их буквами М и К. Сколько всего получится отрезков?

А М К О

АМ, АК, АО, МК, МО, КО.

Ответ: 6 отрезков.

1. У Вити имеется 4 вида цветной бумаги (красная, синяя, желтая и зелёная) и 3 вида образца оригами животных (заяц, собака, голубь). Сколько вариантов одного любого животного он может сделать из любого цвета?

4 ∙ 3 = 12

Ответ: 12 различных вариантов.

2. Шесть семей уехали отдыхать в разные города. Приехав к месту отдыха, они поговорили друг с другом по телефону. Сколько звонков было сделано?

5 + 4 + 3 + 2 +1 = 15

Ответ: 15 звонков.

3.Как можно разместить на скамейке Настю, Таню, Мишу и Сережу, чтобы мальчики и девочки чередовались? Сколько способов получилось?

Ответ: НМТС, НСТМ, ТМНС, ТСНМ, МТСН, МНСТ, СТМН, СНМТ. 8 вариантов.

4. Из цифр 2, 7, 5, 0 составь все возможные трёхзначные числа так, чтобы цифры не повторялись. Сколько и какие из них больше 300?

507, 502, 570, 520, 705, 702, 720, 750

Ответ: 8

1.3. Сосчитай, сколько слов содержится в заклинании волшебника, если в словах по три буквы, первая из них – Щ или Ц, второй могут быть О, Е, И, а оканчиваются слова на Р, Х, К,

2 ∙ 3 ∙ 3 = 18

Ответ: 18

2. Из цифр 9, 7, 5, 0 составь все возможные четырёхзначные числа так, чтобы цифры не повторялись. Сколько их?

5079, 5097, 5709, 5790, 5907, 5970, 7059, 7095, 7507, 7509, 7905, 7950, 9057, 9075, 9507, 9570, 9705, 9750

Решение умножением: на первом месте может быть 3 цифры, кроме 0, но втором месте другие 3 цифры, на третьем месте только 2 цифры, на четвёртом месте – только одна оставшаяся, т.е.

3∙3∙2∙1 = 18

Если бы в условии разрешили повторять цифры, то решение выглядело бы так:

3∙4∙4∙4 = 192 варианта (т.е. на первом месте нельзя брать 0, на всех последующих местах можно брать все цифры)

Ответ: 18 чисел.

3. У клоуна четыре берета: красный (К), чёрный (Ч), жёлтый (Ж), зелёный (З) и две рубашки: клетчатая (1) и полосатая (2). Сможет ли клоун в течение недели надевать каждый день разные комплекты «берет — рубашка»? Докажи.
Сколько вариантов комплектов у тебя получилось?
4 ∙ 2 = 8, значит, на 1 неделю хватит.

Ответ: 8 комплектов, их хватит.

1. Начерти отрезок АО. Поставь внутри него 3 точки, обозначь их буквами М, К, Е.

Сколько всего получится отрезков?

А М К Е О

АМ, АК, АЕ, АО, МК, МЕ, МО, КЕ, КО, ЕО.

Ответ: 10

2).4 парусника готовились к соревнованиям. У каждого спортсмена был свой белый корабль, на корабле – два паруса. Судьи решили, что надо раскрасить паруса, чтобы парусники были видны издалека, и было ясно, кто из спортсменов идет впереди, кто запаздывает. Покажите, как по-разному раскрасили паруса, если были всего 2 краски красная и синяя?

Ответ:

3. Из цифр 1, 7, 6 составь все возможные двузначные числа (цифры могут в числе повторяться). Сколько и какие из них больше 20?

61, 66, 67, 71, 76, 77

Ответ: 6 чисел

4. У Алёши 12 кубиков. Из них 9 – синие, а на 7 написаны буквы. Сколько синих кубиков с буквами?

Ответ: 9+7 – 12 = 4 .

1. Из города А в город В ведут пять дорог, а из города В в город С — три дороги. Сколько путей, проходящих через В, ведут из А в С?

А

С

В

Ответ: 5 ∙ 3 = 15 вариантов пути.

2. Пять друзей после отдыха в лагере обменялись фотографиями на память (каждый подарил остальным одну свою). Сколько фотографий потребовалось?

4+4+4+4+4 = 20

Ответ: 20 фотографий.

3. Из цифр 9, 7, 5, 0 составь все возможные трёхзначные числа так, чтобы цифры не повторялись. Сколько и какие из них меньше 900?

507, 509, 570, 590, 705, 709, 750, 790

Ответ: 8

4.У Кати в четверг 2 лёгких предмета – физкультура и изо, и 2 трудных предмета – русский и математика. Как нужно составить расписание, чтобы лёгкие предметы чередовались с трудными? Найди все варианты.

Ответ: ФМИР, ФРИМ, РФМИ, РИМФ, ИМФР, ИРФМ, МИРФ, МФРИ.

8 вариантов.

1.В знаменитой басне Крылова “Квартет” “Проказница Мартышка, Осел, Козел да косолапый Мишка” герои пытались сесть, чтобы красиво сыграть музыку.

Сколько существует способов, чтобы рассадить четырех музыкантов?

ПОКМ ПОМК ПКОМ ПКМО ПМОК ПМКО

И т.д. каждый может быть впереди….

4 ∙ 3 ∙ 2 ∙ 1 = 24

Ответ: 24

2. Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?

Гласных – 3, согласных – 3

ЗА, ЗИ, ЗЕ, ДА, ДИ, ДЕ, НА, НИ, НЕ

3 ∙ 3 = 9

Ответ: 9

3. У Вити имеется 4 вида цветной бумаги (красная, синяя, желтая и зелёная) и 5 видов оригами животных (заяц, собака, лиса, голубь, кот) . Сколько вариантов одного любого животного он может сделать из разного цвета?

4 ∙ 5 = 20

Ответ: 20 различных вариантов.

4. Из цифр 9, 7, 2 составь все возможные трёхзначные числа так, чтобы цифры в числе повторялись. Сколько и какие из них меньше 900?

799, 797, 792, 779, 777, 772, 727, 729, 722, 277, 272,279, 227, 222, 229, 299, 292, 297.

Решение умножением: 2∙3∙3 = 18 – все числа, которые меньше 900

Ответ: 18 чисел.

1. Петя, Вася, Катя, Лиза и Миша участвуют в конкурсе чтецов. В каком порядке выступят дети, если Миша будет первым, а Катя идёт сразу за Мишей? Найди все варианты.

Ответ:

1) Миша, Катя, Лиза, Петя, Вася

2) Миша, Катя, Лиза, Вася, Петя

3) Миша, Катя, Петя, Вася, Лиза

4) Миша, Катя, Петя, Лиза, Вася

5) Миша, Катя, Вася, Петя, Лиза

6) Миша, Катя, Вася, Лиза, Петя

Всего 6 вариантов.

2. Как можно разместить на скамейке Настю, Таню, Мишу и Сережу, чтобы мальчики и девочки чередовались? Сколько способов получилось?

Ответ: НМТС, НСТМ, ТМНС, ТСНМ, МТСН, МНСТ, СТМН, СНМТ. 8 вариантов.

3. Из цифр 1, 7, 9, 0 составь все возможные двузначные числа (цифры не должны повторяться). Сколько и какие из них больше 20?

70, 71, 79, 90, 91, 97.

Ответ: 6 чисел

4. Начерти отрезок АО. Поставь внутри него 3 точки, обозначь их буквами М, К, Е.

Сколько всего получится отрезков?

А М К Е О

АМ, АК, АЕ, АО, МК, МЕ, МО, КЕ, КО, ЕО.

Ответ: 10

1. В классе 30 человек.19-ходят на кружок по математике, 10-на кружок по русскому языку, 1-человек ходит на русский и на математику. Сколько человек не посещают кружки?

30 – (19 +10 — 1) = 2

Ответ: 2

2. На цветочной клумбе сидели шмель, жук, стрекоза, бабочка и муха. Двое насекомых улетели. Какие пары насекомых могли улететь?Перечисли все варианты.

ШЖ, ШС, ШБ, ШМ, ЖС, ЖБ, ЖМ, СБ, СМ, БМ.

2 ∙ 5 = 10 вариантов.

Ответ: 10 вариантов.

3. Сосчитай, сколько слов содержится в заклинании волшебника, если в словах по три буквы, первая из них – Щ или Ц, второй могут быть О, Е, И, а оканчиваются слова на Р, Х, К.

2 ∙ 3 ∙ 3 = 18

Ответ: 18.

4. Из цифр 9, 7, 5, 0 составь все возможные трёхзначные числа так, чтобы цифры не повторялись. Сколько и какие из них меньше 900?

507, 509, 570, 590, 705, 709, 750, 790

Ответ: 8 чисел

1. На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и спуститься с нее, если по любой тропинке он может идти и вверх и вниз?

5∙ 5 = 25

Ответ:25

2. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета?

Обозначим белые — Б1, Б2, Б3, алые — А1,А2, чайные — Ч1, Ч2, Ч3,Ч4. Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3, Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3, Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3, Б3-А2-Ч4

Рациональное решение умножением:

3 ∙ 2 ∙ 4 = 24

Ответ: 24 варианта.

3. У клоуна четыре берета: красный (К), чёрный (Ч), жёлтый (Ж), зелёный (З) и три рубашки: клетчатая (1), полосатая (2), в горошек (3). Сможет ли клоун в течение двух недель надевать каждый день разные комплекты «берет — рубашка»? Докажи.

Сколько вариантов комплекта у тебя получилось?

Составили: учителя начальных классов школы-лицея №8 для одарённых детей Шафоренко Л. П., Соловьёва И. Ю.

infourok.ru

Задачи по комбинаторике. Часть 1

В этой статье использован материал из лекций Шарича Владимира Златковича и Максимова Дмитрия Васильевича на КПК foxford.

Очень рекомендую абитуриентам курсы foxford для подготовки к ЕГЭ и олимпиадам.

1. Сколько четырехзначных чисел содержит ровно одну семерку?

Решение.

Четырехзначное число имеет вид . Если четырехзначное число содержит ровно одну семерку, то она может стоять

1) на первом месте, и тогда на остальных трех местах могут стоять любые цифры от 0 до 9, кроме цифры 7, и по правилу произведения мы получаем  четырехзначных чисел, у которых семерка стоит на первом месте.

2) на любом месте, кроме первого, и тогда по правилу произведения мы получаем . У нас три возможности расположения цифры 7, на первом месте может стоять 8 цифр (все цифры, кроме нуля и 7), на тех местах, где не стоит цифра 7  — 9 цифр.

Сложим полученные варианты, и получим четырехзначных чисел, содержащих ровно одну семерку.

2. Сколько пятизначных чисел содержит ровно две семерки?

Решение.

Так же как в предыдущей задаче у нас две возможности:

1) Одна из семерок стоит на первом месте, а вторая на любом из оставшихся четырех мест. На трех местах, не занятых цифрой 7 может стоять любая из 9 цифр (все, кроме цифры 7). В этом случае мы получаем  чисел.

2) Ни одна из семерок не стоит на первом месте. В этом случае мы имеем возможностей расставить 2 семерки на оставшихся 4-х местах. У нас осталось 3 места, не занятых цифрой 7, одно из которых первое, и таким образом мы получаем чисел.

Сложим полученные варианты, и получим  пятизначных чисел, содержащих ровно две семерки.

3. Сколько существует пятизначных чисел, цифры которых различны и расположены в порядке возрастания?

Так как первой цифрой не может быть 0, рассмотрим последовательность цифр 1-9, расположенных в порядке возрастания.

1, 2, 3, 4, 5, 6, 7, 8, 9

Если мы выберем из этой последовательности 5 произвольных цифр, например так:

1, 2, 3, 4, 5, 6, 7, 8, 9

то получим пятизначное число, цифры которого различны и расположены в порядке возрастания.

Осталось посчитать, сколькими способами мы можем выбрать из 9 цифр 5:

   

Итак существует 126 пятизначных чисел, цифры которых различны и расположены в порядке возрастания.

Треугольник Паскаля и число сочетаний.

4. Задача о хромом короле. Пусть есть доска размером . Король находится в левом верхнем углу доски и может перемещаться по доске, двигаясь только вправо и вниз. Сколькими способами король может добраться до левого нижнего угла доски?

Решение.

Посчитаем, для каждой клетки, сколькими способами король может до нее добраться.

Так как король может двигаться только вправо и вниз, до любой клетки первого столбца и первой строки он может добраться единственным способом:

Рассмотрим произвольную клетку доски. Если в клетку, стоящую над ней можно добраться способами, а в клетку, стоящую слева от нее   способами, то в саму клетку можно добраться способами (это следует из того, что король может двигаться только вправо и вниз, то есть не может дважды зайти на одну клетку):

Заполним начальные клетки, пользуясь этим правилом:

Мы видим, что при заполнении клеток у нас получается треугольник Паскаля, только повернутый на бок.

Число в каждой клетке показывает, сколькими способами король может попасть в эту клетку из левой верхней.

Например, чтобы попасть в клетку (4;3)  — четвертая строка, третий столбец, король должен сделать 4-1=3 шага вправо, и 3-1=2 шага вниз. То есть всего 3+2=5 шагов. Нам нужно найти число возможных последовательностей этих шагов:

То есть найти, скольким способами мы можем расположить 2 вертикальные (или 3 горизонтальные) стрелки на 5-ти местах. Число способов равно:

   

—  то есть ровно то число, которое стоит в этой клетке.

Для того, чтобы попасть в последнюю клетку, король должен сделать всего шага, из которых по вертикали. Таким образом, он может попасть в последнюю клетку

   

способами.

Можно получить  рекуррентное соотношение для числа сочетаний:

   

Смысл этого соотношения следующий. Путь у нас есть множество, состоящее из n элементов. И нам нужно выбрать из этого множества l элементов.  Все способы, которыми мы можем это сделать делятся на две группы, которые не пересекаются. Мы можем:

а) зафиксировать один элемент, и из оставшихся n-1-го элемента выбрать l-1 элемент. Это можно сделать способами.

б) выбрать из оставшихся n-1-го элемента все l элементов. Это можно сделать способами.

Всего получаем

   

способов.

 

Также можно получить  соотношение:

   

Действительно, левая часть этого равенства показывает число способов выбрать какое-то подмножество из множества, содержащего n элементов. (Подмножество, содержащее 0 элементов, 1 элемент и так далее.) Если мы пронумеруем n элементов, то получим цепочку из n нулей и единиц, в которой 0 означает, что данные элемент не выбран, а 1 — что выбран. Всего таких комбинаций, состоящих из нулей и единиц .

Кроме того, число подмножеств с четным числом элементов равно числу подмножеств с нечетным числом элементов:

   

Докажем это соотношение. Для этого докажем, что между подмножествами с четным числом элементов и подмножествами с нечетным числом элементов существует взаимно однозначное соответствие.

Зафиксируем один элемент множества:

Теперь возьмем произвольное подмножество, и если оно не содержит этот элемент, то поставим ему в соответствие подмножество, состоящее из тех же элементов, что и выбранное, плюс этот элемент. А если выбранное подмножество уже содержит это элемент, то поставим ему в соответствие подмножество, состоящее из тех же элементов, что и выбранное, минус этот элемент. Очевидно, что из этих пар подмножеств одно содержит четное число элементов, а другое — нечетное.

5. Рассмотрим выражение

1. Сколько слагаемых имеет этот многочлен?

а) до приведения подобных членов

б) после приведения подобных членов.

2. Найти коэффициент при произведении

Решение. показать

При возведении суммы слагаемых в степень , мы должны эту сумму умножить на себя раз. Мы получаем сумму одночленов, степень каждого из которых равна m. Число всевозможных произведений, состоящих из  переменных из множества с учетом порядка и возможностью повторения равно числу размещений с повторениями из k по m:

   

Когда мы приводим подобные члены, мы считаем одинаковыми произведения, содержащие равное число множителей каждого вида. В этом случае, чтобы найти число слагаемых многочлена после приведения подобных членов, мы должны найти число сочетаний с повторениями из k по m:

   

Найдем коэффициент при произведении .

Выражение   представляет собой произведение m элементов из множества , причем элемент взят   раз, элемент взят   раз, и так далее, и, наконец, элемент взят   раз. Коэффициент при произведении равен числу возможных произведений:

   

Рассмотрим частный случай: — Бином Ньютона. И получим формулу для биномиальных коэффициентов.

Произвольный член многочлена, полученного возведением двучлена в степень имеет вид , где А — биномиальный коэффициент, . Как мы уже получили,

   

Таким образом,

   

   

Тогда если мы положим х=1 и y=1, то получим, что

   

 

6. Задача про кузнечика.

Есть n клеточек, расположенных последовательно. Кузнечик должен попасть из крайней левой клеточки в крайнюю правую, прыгая вправо на произвольное число клеток.

а) Сколькими способами он может это сделать?

Решение. показать

Изобразим условие задачи:

Кузнечик может попасть в крайнюю правую клетку, побывав, или не побывав в любой внутренней клетке. Присвоим клетке значение 1, если кузнечик в ней побывал, и 0, если нет, например, так:

Тогда у нас есть n-2 клеточек, каждая из которых может принимать значение 0 или 1. Задача сводится к нахождению числа последовательностей, состоящих из n-2 нулей и единиц. Таких последовательностей .

б) сколькими способами кузнечик может добраться в n-ю клетку, сделав k шагов?

Решение. показать

Чтобы попасть в n-ю клетку, сделав k шагов, кузнечик должен попасть ровно в k—1  клетку между первой и последней. Так как последний шаг он делает всегда в последнюю клетку. То есть стоит вопрос, сколькими способами можно выбрать k—1 клетку из n-2 клеток?

Ответ: .

в) сколькими способами кузнечик может добраться в n-ю клетку, двигаясь на одну или на две клетки вправо?

Решение.

Распишем, сколькими способами можно попасть в каждую клетку.

В первую и вторую клетки можно попасть единственным способом: в первую — никуда из нее не уходя, и во вторую из первой:

В третью можно попасть из первой или второй, то есть двумя способами:

В четвертую — из второй или третьей, то есть 1+2=3 способами:

В пятую — из третьей или четвертой, то есть 2+3=5 способами: Можно заметить закономерность: чтобы найти число способов, которыми кузнечик может попасть в клетку с номером k нужно сложить число способов, которыми кузнечик может попасть в две предыдущие клетки: 

 

 

Мы получили интересную последовательность чисел — числа  Фибоначчи — это линейная рекуррентная последовательность натуральных чисел, где первое и второе равно единице, а каждое последующее — сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…

 

ege-ok.ru

Задачи по комбинаторики для 11 класса

Задачи по комбинаторики

Задача 1: Сколькими способами можно составить список из 5 учеников?

Ответ: перестановки, 5! = 120.

Задача 2: В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Ответ: размещения из 11 по 2, А²₁₁= 110.

Задача 3: Расписание на день содержит 5 уроков. Определить количество возможных расписаний при выборе из 14 предметов, при условии, что ни один предмет не стоит дважды.

Ответ: размещения из 14 по 5, 1320.

Задача 4: Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета?

Ответ: перестановки, 6 способов.

Задача 5: В классе 24 ученика. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

Ответ: сочетания из 24 по 4,

Задача 6: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 6 способов.

Задача 7: Сколькими различными способами можно избрать из 15 человек делегацию в составе 3 человек?

Ответ: сочетания, 455 способами.

Задача 8: Из ящика, где находится 15 шаров, нумерованных последовательно от 1 до 15, требуется вынуть 3 шара. Определить число возможных комбинаций при этом?

Ответ: размещения, 2830 способами.

Задача 9: Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 4! – 3! =18.

Задача 10: Сколькими способами можно разместить 6 пассажиров в четырехместной каюте?

Ответ: размещения из 6 элементов по 4, 360 способами.

Задача 11: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Ответ: сочетания из 10 элементов по 2, 45 способами.

Задача 12: Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек?

Ответ: сочетания из 13 по 4, 715 бригад.

Задача 13: При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Ответ: сочетания из 16 по 2, 120 рукопожатий.

Задача 14: Группа учащихся в 30 человек пожелала обменяться своими фотокарточками. Сколько всего фотокарточек потребовалось для этого?

Ответ: сочетание из 30 по 2, 435 фотокарточек.

Задача 15: Сколько различных плоскостей можно провести через 10 точек, если никакие три из них не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости?

Ответ: сочетание из 10 по 3; 120 точек

Задача 16: Сколько существует различных семизначных телефонных номеров?

Ответ: 10⁷.

Задача 17: Сколько существует различных семизначных телефонных номеров, если в каждом номере нет повторяющихся цифр?

Ответ: размещение из 10 по 7.

Задача 18: Сколько существует таких перестановок 7 учеников, при которых 3 определенных ученика находятся рядом друг с другом? Ответ: 720 = 3! · 5!

Задача 19: На книжной полке стоит собрание сочинений в 30 томах. Сколькими различными способами их можно переставить, чтобы: а) тома 1 и 2 стояли рядом; б) тома 3 и 4 рядом не стояли?

Ответ: а)2∙29!; б)28∙29!

Задача 20: Сколько существует трёхзначных чисел, все цифры которых нечётные и различные?

Ответ: размещение из 5 по 3, 60.

Задача 21: У одного мальчика имеется 10 марок для обмена, а у другого – 8. Сколькими способами они могут обменять 2 марки одного на 2 марки другого?

Ответ: сочетания, С²₁₀·С²₈ = 1260.

multiurok.ru

Подготовка к ОГЭ. «Комбинаторные задачи» 9 класс

Решение комбинаторных задач.

Подготовила Стопичева Вера Ивановна, учитель математики МОУ Иловская СОШ им. Героя России В. Бурцева .

Задача 1. В классе 30 учащихся. Сколькими способами могут быть выбраны староста и физорг, если каждый учащийся может быть избран только на одну из этих должностей?

Решение:

Так как по условию задачи каждый учащийся может быть избран старостой, то, очевидно, существует 30 способов выбора старосты. Физоргом может стать каждый из оставшихся 29 человек. Любой из 30 способов выбора старосты может осуществляться вместе с любым из 29 способов выбора физорга. Поэтому существует 30 · 29 = 870 способов выбора старосты и физорга. Ответ: 870 способов.

Задача 2. Для дежурства в классе в течение недели (пятидневная учебная неделя) выделены 5 учащихся. Сколькими способами можно установить очерёдность дежурств, если каждый учащийся дежурит один раз?

Решение:

В понедельник может дежурить любой из выделенных пяти человек. Во вторник может дежурить каждый из ещё не дежуривших учащихся. К среде остаются три человека, которые ещё не дежурили, и поэтому на среду дежурного можно будет назначать тремя способами. Ясно, что число способов, которыми можно установить очерёдность дежурств, равно

5 · 4 · 3 · 2 · 1 = 120.

Ответ: 120 способов.

Задача 3. Для проверки олимпиадных работ создаётся комиссия из двух преподавателей. Сколько различных комиссий можно составить из шести преподавателей?

Решение:

Обозначим для удобства преподавателей буквами А, В, С, Д, Е, К. Теперь выпишем все возможные варианты состава комиссии, а именно:

АВ, АС, АД, АЕ, АК, ВС, ВД, ВЕ,ВК, СД, СЕ, ДЕ, ДК, ЕК.

Таким образом, видно, что число различных комиссий равно 15.

Эту задачу можно решить с помощью таблицы, если учесть, что АВ = ВА, АС = СА и тд:

Ответ: 15 составов комиссий.

Задача 4. Сколькими способами можно изготовить 3-х цветный флаг с горизонтальными полосами, если имеется материал 7-ми цветов.

Решение: А₇³ = 7(7 – 1) (7 – (3 – 1)) = 7 ∙6 ∙5 = 210 способов.

Ответ: 210 способов.

Задача 5. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8 при условии, что в записи числа каждая цифра используется только один раз?

Решение: В условии задачи предложено подсчитать число всевозможных комбинаций из двух цифр, взятых из предположенных восьми цифр, причём порядок расположения цифр в комбинации имеет значение (например, числа 13 и 31 различные). Иначе говоря, нужно найти число размещений из восьми элементов по два. По формуле числа размещений находим:

А₈² = 8 (8 – 1) = 8 ∙7 = 56.

Ответ: 56 двузначных чисел.

Задача 14. Сколько различных трёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4?

Решение: Первой цифрой трёхзначного числа может быть одна из четырёх цифр 1, 2, 3, 4, а второй и третьей – любая из пяти цифр 0,1, 2, 3, 4. Всего можно образовать

4 ∙5 ∙ 5 = 100 трёхзначных чисел.

Ответ: 100 чисел.

Задача 6. Сколькими способами можно разместить на полке 5 книг?

Решение: Задача сводится к подсчёту числа перестановок из пяти элементов:

Р₅ = 5! = 1 ∙2 ∙3 ∙4 ∙5 = 120 способов.

Ответ: 120 способов

Задача 13. Из числа учащихся, посещающих математический кружок, в котором занимаются 5 девушек и 3 юноши, нужно отправить на олимпиаду двоих: одну девушку и одного юношу. Сколько существует различных пар, которые можно отправить на олимпиаду?

Решение: Девушку из состава кружка можно выбрать пятью способами, а юношу – тремя. Пару (девушка с юношей) можно выбрать пятнадцатью различными способами

5 ∙3 = 15 способов.

Ответ: 15 способов.

Задача 14. Андрей, Борис, Владимир, Григорий, Дмитрий и Евгений при встрече обменялись каждый с каждым рукопожатием. Сколько всего было сделано рукопожатий?

Решение: Обозначим для удобства юношей буквами А, Б, В, Г, Д, Е. Теперь выпишем все возможные варианты рукопожатий, а именно:

АБ, АВ, АГ, АД, АЕ, БВ, БГ, БД, БЕ, ВГ, ВД, ВЕ, ГД, Г

Эту задачу можно решить с помощью таблицы, если учесть, что АВ = ВА, АС = СА и тд:

Таким образом, видно, что число различных рукопожатий равно 15.

Ответ: 15 рукопожатий.

Задача 15. Для подарков первоклассникам закупили книги пяти разных авторов и игрушки шести разных видов. Сколько различных подарков можно составить, если в каждый должна входить одна книга и одна игрушка?

Решение: В соответствии с правилом произведения всего можно составить 5 ∙6 = 30 подарков.

Ответ: 30 подарков.

Задача 16. Сколько различных смешанных пар для игры в теннис можно образовать из восьми юношей и шести девушек?

Решение: 8 ∙6 = 48 пар.

Ответ: 48 пар.

infourok.ru