| Сумма цифр | 15 |
| Произведение цифр | 54 |
| Произведение цифр (без учета ноля) | 54 |
| Все делители числа | 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96 |
| Наибольший делитель из ряда степеней двойки | 32 |
| Количество делителей | 12 |
| Сумма делителей | 252 |
| Простое число? | Нет |
| Полупростое число? | Нет |
| Обратное число | 0. 010416666666666666 010416666666666666 |
| Римская запись | XCVI |
| Индо-арабское написание | ٩٦ |
| Азбука морзе | —-. -…. |
| Факторизация | 2 * 2 * 2 * 2 * 2 * 3 |
| Двоичный вид | 1100000 |
| Троичный вид | 10120 |
| Восьмеричный вид | 140 |
| Шестнадцатеричный вид (HEX) | 60 |
| Перевод из байтов | 96 байтов |
| Цвет | RGB(0, 0, 96) или #000060 |
| Наибольшая цифра в числе (возможное основание) | 9 (10, десятичный вид) |
| Число Фибоначчи? | Нет |
| Нумерологическое значение | семья, любовь, доброта, забота, переживания, обида, гармония, равновесие, баланс |
| Синус числа | 0. 9835877454343449 9835877454343449 |
| Косинус числа | -0.18043044929108396 |
| Тангенс числа | -5.451340110823241 |
| Натуральный логарифм | 4.564348191467836 |
| Десятичный логарифм | 1.9822712330395684 |
| Квадратный корень | 9.797958971132712 |
| Кубический корень | 4.5788569702133275 |
| Квадрат числа | 9216 |
| Перевод из секунд | |
| Дата по UNIX-времени | Thu, 01 Jan 1970 00:01:36 GMT |
| MD5 | 26657d5ff9020d2abefe558796b99584 |
| SHA1 | 6fb84aed32facd1299ee1e77c8fd2b1a6352669e |
| Base64 | OTY= |
| QR-код числа 96 |
Алгоритм извлечения квадратного корня
Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нём исходное число и нажать клавишу корня
Для этого достаточно набрать на нём исходное число и нажать клавишу корня
Если калькулятора под рукой нет, то квадратный корень извлекают пользуясь алгоритмом извлечения квадратного корня.
Применение алгоритма может оказаться весьма полезным на контрольных и экзаменах. Ведь чаще всего на таких мероприятиях использовать калькулятор запрещено.
Предварительные навыкиКак пользоваться алгоритмом
Рассмотрим применение алгоритма извлечения квадратного корня на конкретных примерах. О том, почему алгоритм следует применять именно так, поговорим позже.
Пример 1. Извлечём квадратный корень из числа 4096 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 4096 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку:
Сгруппированные цифры исходного числа называют грáнями, а саму группировку по две цифры разделением на грáни. Количество грáней позволяет предположить сколько цифр будет содержаться в извлечённом корне. В нашем примере извлечённый корень будет содержать две цифры, поскольку исходное число содержит две грани.
Теперь нужно извлечь квадратный корень из числа 40 с точностью до целых, получаем 6. Записываем 6 после знака равенства:
Далее возвóдим число 6 в квадрат и полученный результат записываем под числом 40
Далее вычитаем из числа 40 число 36, получаем 4. Записываем это число под 36
Снóсим оставшиеся цифры из под корня, а именно 96. Получаем остаток 496
Теперь нужно найти следующую цифру корня. Её находят так. Первую найденную цифру корня, а именно 6 умножаем на 2, получаем 12. К числу 12 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 496 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 12 и умножим образовавшееся число 125 на 5
Получилось число 625, которое больше остатка 496. Значит цифра 5 не годится в качестве следующей цифры корня. Проверим тогда цифру 4. Допишем ее к числу 12 и умножим образовавшееся число 124 на 4
Получилось число 496, которое в точности является нашим остатком. Значит дописанная к числу 12 цифра 4 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 4 в ответе после цифры 6
А число 496, которое получилось в результате умножения 124 на 4 записываем под остатком 496
Выполняем вычитание 496 − 496 = 0. Ноль в остатке говорит о том, что решение окончено:
Для удобства поиска второй цифры, слева от остатка проводят вертикáльную линию и уже за этой линией записывают умножение. В нашем случае умножение 124 на 4. Результат умножение сразу записывают под остатком:
Итак, квадратный корень из числа 4096 равен 64
Пример 2. Извлечём квадрáтный корень из числа 441 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 441 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку. В данном случае в числе 441 только три цифры. Поэтому группируем цифры 4 и 1. Крайняя четвёрка слева будет сама по себе:
Теперь нужно извлечь квадратный корень из числа 4 с точностью до целых, получаем 2. Записываем 2 после знака равенства:
Далее возвóдим число 2 в квадрат и полученный результат записываем под числом 4
Вычитаем из числа 4 число 4, получаем 0. Ноль принято не записывать. Снóсим оставшиеся цифры корня, а именно 41
Теперь нахóдим следующую цифру корня. Первую найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить получившееся число на ту же самую дописанную цифру.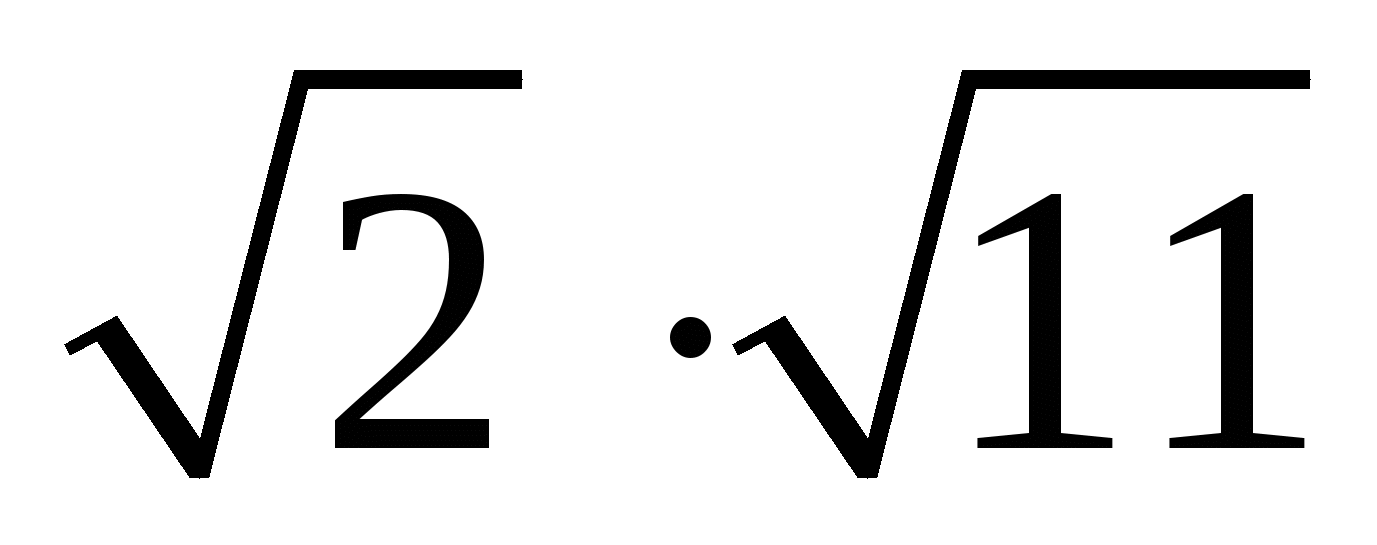 Полученное произведение должно быть равно остатку 41 или хотя бы максимально близким ему, но не превосходящим его.
Полученное произведение должно быть равно остатку 41 или хотя бы максимально близким ему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 4 и умножим получившееся число 42 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 41
Получилось число 84, которое больше остатка 41. Значит цифра 2 не годится в качестве следующей цифры корня. Проверим тогда цифру 1. Допишем ее к числу 4 и умножим получившееся число 41 на на ту же самую дописанную цифру 1
Получилось число 41, которое в точности является нашим остатком. Значит дописанная к числу 4 цифра 1 является следующей цифрой корня. Записываем цифру 1 после цифры 2
А число 41, которое получилось в результате умножения 41 на 1, записываем под остатком 41
Выполняем вычитание 41 − 41 = 0. Ноль в остатке говорит о том, что решение окончено:
Пример 3. Извлечём квадратный корень из числа 101761 с помощью алгоритма извлечения квадратного корня.
Разбиваем число 101761 на грани:
Получилось три грани. Значит корень будет состоять из трёх цифр.
Извлекáем квадратный корень из первой грани (из числа 10) с точностью до целых, получаем 3. Записываем 3 после знака равенства:
Далее возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 10)
Вычитаем из числа 10 число 9, получаем 1. Снóсим следующую грань, а именно число 17. Получаем остаток 117
Теперь нахóдим вторую цифру корня. Первую найденную цифру корня, а именно 3 умножаем на 2, получаем 6. К числу 6 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 117 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 6 и умножим образовавшееся число 62 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 117
Допишем её к числу 6 и умножим образовавшееся число 62 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 117
Получилось число 124, которое больше остатка 117. Значит цифра 2 не годится в качестве второй цифры корня. Проверим тогда цифру 1. Допишем ее к числу 6 и умножим образовавшееся число 61 на на ту же самую дописанную цифру 1
Получилось число 61, которое не превосходит остатка 117. Значит дописанная к числу 6 цифра 1 является второй цифрой корня. Записываем её в ответе после цифры 3
Теперь выполняем вычитание 117 − 61 = 56.
Снóсим следующую грань, а именно число 61. Получаем новый остаток 5661
Теперь нахóдим третью цифру корня. Первые две найденные цифры корня, а именно число 31 умножаем на 2, получаем 62. К числу 62 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 5661 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 9. Допишем её к числу 62 и умножим образовавшееся число 629 на ту же самую дописанную цифру 9. Результат умножения будем записывать сразу под остатком 5661
Получилось число 5661, которое в точности является нашим остатком. Значит дописанная к числу 62 цифра 9 является третьей цифрой корня. Записываем цифру 9 в ответе после цифры 1
Выполняем вычитание 5661 − 5661 = 0. Ноль в остатке говорит о том, что решение окончено:
Пример 4. Извлечём квадратный корень из числа 30,25 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. В данном случае на грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
Получилось по одной грани в каждой части. Это значит, что корень будет состоять из двух цифр: одна цифра будет в целой части корня и одна цифра в дробной.
Это значит, что корень будет состоять из двух цифр: одна цифра будет в целой части корня и одна цифра в дробной.
Извлечём квадратный корень из первой грани (из числа 30) с точностью до целых, получаем 5. Записываем 5 после знака равенства:
Далее возвóдим число 5 в квадрат и полученный результат записываем под первой гранью (под числом 30)
Вычитаем из числа 30 число 25, получаем 5.
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 30,25 с точностью до целых, получили ответ 5. Последний остаток 5 показывает, что целая часть 30 превосходит квадрат 52 на 5 квадратных единиц.
Чтобы дальше извлечь корень (с точностью до десятых), снесём следующую грань, а именно число 25, получим остаток 525. А в ответе после числа 5 следует поставить запятую, поскольку сейчас мы будем искать дробную часть корня.
Затем снóсим следующую грань, а именно число 25. Получаем остаток 525
Далее работаем по тому же принципу, что и раньше. Нахóдим следующую цифру корня. Для этого уже найденный корень, а именно число 5 умножим на 2 получим 10. К числу 10 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 525 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 10 и умножим получившееся число 105 на ту же самую дописанную цифру 5
Получилось число 525, которое в точности является нашим остатком. Значит дописанная к числу 10 цифра 5 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 5 после в ответе после запятой:
Выполняем вычитание 525 − 525 = 0. Ноль в остатке говорит о том, что решение окончено:
В подкоренном выражении можно было использовать следующий прием: умножить подкоренное число на 100 и получить под корнем число 3025.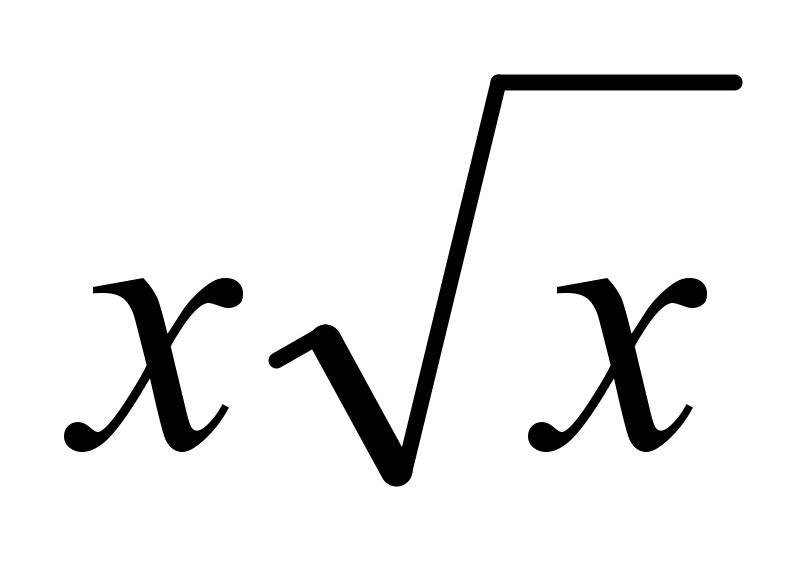 Далее извлечь из него квадратный корень, как из обычного целого числа. Тогда получился бы ответ 55
Далее извлечь из него квадратный корень, как из обычного целого числа. Тогда получился бы ответ 55
Затем можно обратно разделить 3025 на 100 (или сдвинуть запятую влево на две цифры). В результате под корнем полýчится прежнее число 30,25, а правая часть уменьшится в десять раз и полýчится квадратный корень из числа 30,25.
Пример 5. Извлечём квадратный корень из числа 632,5225 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. Разбиваем число на грани. На грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
Получилось четыре грани. При этом две грани в целой части, и две грани в дробной. Это значит, что корень будет состоять из четырёх цифр: две цифры будет в целой части корня, и две цифры после запятой.
Извлечём квадратный корень из первой грани (из числа 6) с точностью до целых, получаем 2. Записываем 2 после знака равенства:
Далее возвóдим число 2 в квадрат и полученный результат записываем под первой гранью (под числом 6)
Вычитаем из числа 6 число 4, получаем 2. Затем снóсим следующую грань, а именно число 32. Получаем остаток 232
Теперь нахóдим вторую цифру корня. Первую уже найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить получившееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 232 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 4 и умножим получившееся число 46 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 232
Получилось число 276, которое больше остатка 232. Значит цифра 6 не годится в качестве второй цифры корня. Проверим тогда цифру 5. Допишем ее к числу 4 и умножим получившееся число 45 на на ту же самую дописанную цифру 5
Проверим тогда цифру 5. Допишем ее к числу 4 и умножим получившееся число 45 на на ту же самую дописанную цифру 5
Получилось число 225, которое не превосходит остатка 232. Значит дописанная к числу 4 цифра 5 является второй цифрой корня. Записываем её в ответе после цифры 2
Теперь выполняем вычитание 232 − 225 = 7.
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 632,5225 с точностью до целых, получили ответ 25. Последний остаток 7 показывает, что целая часть 632 превосходит квадрат 252 на 7 квадратных единиц.
Чтобы дальше извлечь корень (с точностью до десятых и сотых), снесём следующую грань, а именно число 52, получим остаток 752. А в ответе после числа 25 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
Далее работаем по тому же принципу, что и раньше. Нахóдим первую цифру корня после запятой. Для этого уже найденные цифры, а именно 25 умножим на 2 получим 50. К числу 50 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 752 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 50 и умножим получившееся число 502 на ту же самую дописанную цифру 2. Можно интуитивно понять, что цифра 2 великá, поскольку 502 × 2 = 1004. А число 1004 больше остатка 752. Тогда очевидно, что первой цифрой после запятой будет цифра 1
Теперь выполняем вычитание 752 − 501 = 251. Сразу снóсим следующую грань 25. Полýчим остаток 25125
Теперь нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 502.
К числу 502 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 25125 или хотя бы максимально близким к нему, но не превосходящим его.
Полученное произведение должно быть равно остатку 25125 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 502 и умнóжим образовавшееся число 5026 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 25125
Получилось число 30156, которое больше остатка 25125. Значит цифра 6 не годится в качестве второй цифры корня после запятой. Проверим тогда цифру 5. Допишем ее к числу 502 и умножим получившееся число 5025 на на ту же самую дописанную цифру 5
Получилось число 25125, которое в точности является нашим остатком. Значит дописанная к числу 502 цифра 5 является второй цифрой корня после запятой. Записываем цифру 5 в ответе после цифры 1
Теперь выполняем вычитание 25125 − 25125 = 0. Ноль в остатке говорит о том, что решение окончено:
В этом примере можно было воспользоваться методом умножения подкоренного выражения на 10000. Тогда подкоренное число приняло бы вид 6325225. Его можно разделить на грани, двигаясь справа налево. В результате получился бы корень 2515
Затем подкоренное число 6325225 делят на 10000, чтобы вернуться к изначальному числу 632,5225. В результате этого деления ответ умéньшится в 100 раз и обратится в число 25,15.
Пример 4. Используя алгоритм извлечения квадратного корня, извлечь квадратный корень из числа 11 с точностью до тысячных:
В данном числе только одна грань 11. Извлечём из неё корень с точностью до целых, получим 3
Теперь возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 11)
Выполним вычитание 11 − 9 = 2
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 11 с точностью до целых, получили ответ 3. Последний остаток 2 показывает, что целая часть 11 превосходит квадрат 32 на две квадратные единицы.
Наша задача была извлечь корень из числа 11 с точностью до тысячных. Значит нужно снести следующую грань, но её в данном случае нет.
Если после целого числа поставить запятую и написать сколько угодно нулей, то значение этого числа не измéнится. Так, после 11 можно поставить запятую и написать несколько нулей (несколько граней), которые в последствии можно будет снóсить к остаткам.
Если корень извлекáется с точностью до тысячных, то в ответе после запятой должно быть три цифры. Поэтому в подкоренном выражении поставим запятую и запишем три грани, состоящие из нулей:
Теперь можно снести следующую грань, а именно два нуля. Получим остаток 200. А в ответе после числа 3 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
Теперь нахóдим первую цифру после запятой в ответе. Первую найденную цифру корня, а именно число 3 умножаем на 2, получаем 6. К числу 6 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 3
Выполним вычитание 200 − 189 и снесём следующую грань 00
Нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 66.
К числу 66 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 1100 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 1
Выполним вычитание 1100−661 и снесём следующую грань 00
Нахóдим третью цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умножим на 2. Получим 662.
Получим 662.
К числу 662 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 43900 или хотя бы максимально близким к нему, но не превосходящим его.
Проверим цифру 7
Получилось число 46389, которое больше остатка 43900. Значит цифра 7 не годится в качестве третьей цифры корня после запятой. Проверим тогда цифру 6. Допишем ее к числу 662 и умножим получившееся число 6626 на на ту же самую дописанную цифру 6
Получилось число 39756, которое не превосходит остатка 43900. Значит дописанная к числу 662 цифра 6 является третьей цифрой корня после запятой. Записываем цифру 6 в ответе после цифры 1
Выполним вычитание 43900 − 39756 = 4144
Дальнейшее вычисление не требуется, поскольку корень нужно было извлечь с точностью до тысячных.
Но в таких примерах как этот, цифры после запятой можно находить бесконечно. Например, так можно продолжить данный пример, найдя значение корня с точностью до десятитысячных:
Как работает алгоритм
Алгоритм извлечения квадратного корня основан на формуле квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Геометрически эту формулу можно представить так:
То есть сторона a увеличивается на b. Это приводит к увеличению изначального квадрата. Чтобы вычислить площадь такого квадрата, нужно по отдельности вычислить площади квадратов и прямоугольников, входящих в этот квадрат и сложить полученные результаты. Нужно хорошо понимать данный рисунок. Без его понимания невозможно понять как работает алгоритм извлечения квадратного корня.
Отметим, что формула квадрата суммы двух выражений позволяет возвести в квадрат любое число. Используя разряды, исходное число представляют в виде суммы чисел и далее эту сумму возвóдят в квадрат.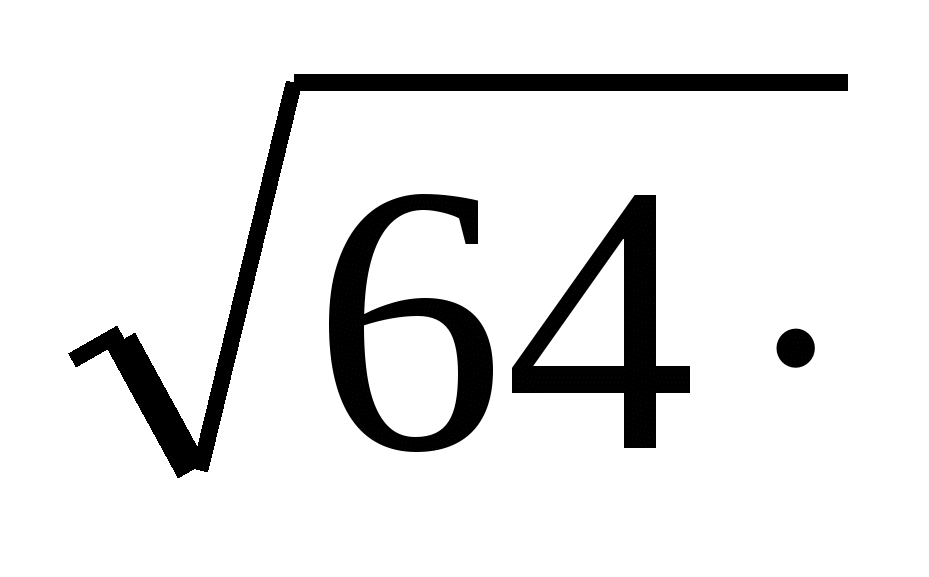
Например, так можно возвести число 21 в квадрат: представить данное число в виде суммы двух десятков и одной единицы, и далее эту сумму возвести в квадрат :
212 = (20 + 1)2 = 202 + 2 × 20 × 1 + 12 = 400 + 40 + 1 = 441
Геометрически это будет выглядеть так: сторона квадрата равная 21 разбивается на две составляющие: 20 и 1.
Затем по отдельности вычисляются площади квадратов и прямоугольников, входящих в большой квадрат. А именно: один квадрат со стороной 20 (получается площадь, равная 400), два прямоугольника со сторонами 20 и 1 (получается две площади по 20), один квадрат со стороной 1 (получается площадь, равная 1). Результаты вычисления площадей складываются и получается итоговое значение 441.
Заметим также, что при возведéнии десятков в квадрат получились сотни. В данном случае при возведéнии числа 20 в квадрат получилось число 400. Это позволяет предположить, что если корень является двузначным числом, то десятки этого корня следует искать в сотнях подкоренного числа. Действительно, . Десятки корня это цифра 2, является корнем числа 4, которое отвечает за сотни числа 441.
А при возведéнии сóтен в квадрат получаются десятки тысяч. Например, возведём в квадрат число 123, используя формулу квадрата суммы двух выражений. Число 123 это одна сотня, два десятка и три единицы:
1232 = (100 + 20 + 3)2
При изучении многочленов мы выяснили, что если многочлен содержит более двух членов и возникла необходимость применить формулу квадрата суммы, то некоторые из членов можно взять в скобки, чтобы получилось выражение вида (a + b)2
Рассмотрим подробное извлечение квадратного корня из числа 4096. Заодно пройдёмся по основным этапам алгоритма извлечения квадратного корня, рассмотренного в предыдущей теме.
Допустим, что число 4096 это площадь следующего квадрата:
Извлечь корень из числа 4096 означает найти длину стороны данного квадрата:
Для начала узнáем из скольких цифр будет состоять корень. Ближáйшие от 4096 известные нам квадраты это 3600 и 4900. Между ними располагается квадрат 4096. Запишем это в виде неравенства:
Ближáйшие от 4096 известные нам квадраты это 3600 и 4900. Между ними располагается квадрат 4096. Запишем это в виде неравенства:
Запишем каждое число под знáком корня:
Квадратные корни из чисел 3600 и 4900 нам известны. Это корни 60 и 70 соответственно:
Корни 60 и 70 являются двузначными числами. Если квадратный корень из числа 4096 располагается между числами 60 и 70, то этот корень тоже будет двузначным числом.
Двузначное число состоит из десятков и единиц. Это значит, что квадратный корень из числа 4096 можно представить в виде суммы a + b, где a — десятки корня, b — единицы корня. Сумма a + b во второй степени будет равна 4096
(a + b)2 = 4096
Тогда сторона квадрата будет разбита на две составляющие: a и b
Перепишем в равенстве (a + b)2 = 4096 левую часть в виде a2 + 2ab + b2
a2 + 2ab + b2 = 4096
Тогда рисунок, иллюстрирующий квадрат площадью 4096, можно представить так:
Если мы узнáем значения переменных a и b, то узнáем длину стороны данного квадрата. Проще говоря, узнáем сам корень.
Вернёмся к извлечению корня. Мы выяснили, что корнем будет двузначное число. Двузначное число состоит из десятков и единиц. При возведéнии десятков в квадрат, получаются сотни. Тогда десятки искомого корня следует искать в сотнях подкоренного числа. В подкоренном числе 40 сотен. Отделим их небольшой помéткой:
Извлечём корень из числа 40. Из числа 40 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых.
Ближáйший мéньший квадрат к числу 40 это 36. Извлечём корень из этого квадрата, получим 6. Тем сáмым полýчим первую цифру корня:
На самом деле корень извлечён не из числа 40, а из сорокá сотен. Метка, которая постáвлена после числа 40, отделяет разряды числа, находящегося под знáком корня. Нужно понимать, что в данном случае 40 это 4000.
Метка, которая постáвлена после числа 40, отделяет разряды числа, находящегося под знáком корня. Нужно понимать, что в данном случае 40 это 4000.
Из 4000 как и 40 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 4000. Но нужно принимать во внимание следующий момент. Десятки это числа с одним нулем на конце. Примеры:
10 — один десяток
30 — три десятка
120 — двенадцать десятков
При возведéнии таких чисел в квадрат, получаются числа с двумя нулями на конце:
102 = 100
302 = 900
1202 = 14400
Мы ищем десятки корня в сотнях числá 4096, то есть в числе 4000. Но нет такого числá с нулем на конце, вторая степень которого равна 4000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с двумя нулями на конце. Таковым является квадрат 3600. Корень следует извлекать из этого квадрата.
Вернемся к нашему рисунку. Большой квадрат со стороной a и площадью a2 это тот самый квадрат 3600. Укажем вместо a2 значение 3600
Теперь извлечём квадратный корень из квадрата 3600. Ранее мы говорили, что если число содержит уже знакомый нам квадрат и чётное количество нулей, то можно извлечь корень из этого числа. Для этого сначала следует извлечь корень из знакомого нам квадрата, а затем записать половину от количества нулей исходного числа:
Итак, мы нашли сторону квадрата, площадь которого 3600. Подпишем сторону a как 60
Но ранее в ответе мы написали не 60, а 6. Это является сокращённым вариантом. Число 6 в данном случае означает шесть десятков:
Итак, десятки корня найдены. Их шесть. Теперь нужно найти единицы корня. Единицы корня это длина оставшейся маленькой стороны квадрата, то есть значение переменной b.
Чтобы найти b, нужно из общего квадрата, площадь которого 4096 вычесть квадрат, площадь которого 3600. В результате останется фигура, площадь которой 4096 − 3600 = 496
В результате останется фигура, площадь которой 4096 − 3600 = 496
На рисунке видно как из квадрата, площадь которого 4096 отделился квадрат, площадь которого 3600. Осталась фигура, площадь которой 496.
Именно поэтому в процессе применения алгоритма первая найденная цифра корня возводится в квадрат, чтобы результат возведения вычесть из сотен подкоренного выражения.
Так, из 40 сотен вычитаются 36 сотен, остаётся 4 сотни плюс сносятся девяносто шесть единиц. Эти четыре сотни и девяносто шесть единиц вместе образуют 496 единиц:
Оставшаяся фигура есть ни что иное как удвоенное произведение первого выражение a плюс квадрат второго выражения b
Сумма площадей 2ab + b2 должна вмещаться в число 496. Запишем это в виде следующего равенства:
2ab + b2 = 496
Значение a уже известно. Оно равно 60. Тогда равенство примет вид:
2 × 60 × b + b2 = 496
120b + b2 = 496
Теперь наша задача найти такое значение b, при котором левая часть станет равна 496 или хотя близкой к этому числу. Поскольку b является единицами искомого корня, то значение b является однозначным числом. То есть значение b это число от 1 до 9. Это число можно найти методом подбора. В данном случае очевидно, что числом b является 4
120 × 4 + 42 = 496
480 + 16 = 496
496 = 496
Но для удобства поиска этой цифры, переменную b выносят за скобки. Вернёмся к выражению 120b + b2 = 496 и вынесем b за скобки:
b(120 + b) = 496
Теперь правую часть можно понимать так: к 120 следует прибавить некоторое число b, которое при умножении с тем же сáмым b даст в результате 496.
Именно поэтому при использовании алгоритма, уже найденную цифру умножают на 2. Так, 6 мы умножили на 2 получили 12 и уже к 12 дописывали цифру и умножáли образовавшееся число на ту же дописанную цифру, пытаясь получить остаток 496.
Так, 6 мы умножили на 2 получили 12 и уже к 12 дописывали цифру и умножáли образовавшееся число на ту же дописанную цифру, пытаясь получить остаток 496.
Но это опять же упрощённый вариант. На самом деле на 2 умножается не просто 6, а найденные десятки (в нашем случае число 60), получается число 120. Затем следует нахождение числá вида b(120 + b). То есть к 120 прибавляется число b, которое при перемножении с b даёт остаток 496.
Итак, b = 4. Тогда:
4(120 + 4) = 496
4 × 124 = 496
496 = 496
При подстановке числá 4 вместо b получается остаток 496. Это значит, что единицы корня найдены. Квадрат, площадь которого 4096, имеет сторону равную 60 + 4, то есть 64.
Если из общей площади вычесть 3600, затем 496, полýчим 0. Остаток, равный нулю, говорит о том, что решение завершено:
4096 − 3600 − 496 = 0
Пример 2. Извлечь квадратный корень из числа 54756
Пусть число 54756 это площадь следующего квадрата:
Извлечь корень из числа 54756 означает найти длину стороны данного квадрата:
Пока неизвестно является ли квадратный корень из числа 54756 целым либо дробным числом. Узнáем для начала из скольких цифр будет состоять целый корень.
Число 54756 больше числá 10000, но меньше числá 90000
10000 < 54756 < 90000
Корни из 10000 и 90000 являются трёхзначными числами.
Тогда корень из 54756 тоже будет трёхзначным числом. А трёхзначное число состоит из сотен, десятков и единиц.
Квадратный корень из числа 54756 можно представить в виде суммы a + b + с, где a — сотни корня, b — десятки корня, с — единицы корня. Сумма a + b + с во второй степени будет равна 54756
(a + b + c)2 = 54756
Тогда сторона квадрата будет разбита на три составляющие: a, b и c
Выполним в левой части равенства (a + b + c)2 = 54756 возведéние в квадрат:
Тогда рисунок иллюстрирующий квадрат, площадью 54756 можно представить так:
Два прямоугольника площадью ab в приведённом ранее равенстве заменены на 2ab, а два прямоугольника площадью (a + b)c заменены на 2ac + 2bc, поскольку (a + b)c = ac + bc. Если повторить выражение ac + bc дважды, то полýчится 2ac + 2bc
Если повторить выражение ac + bc дважды, то полýчится 2ac + 2bc
2(ac + bc) = 2ac + 2bc
Если мы узнáем значения переменных a, b и c, то узнáем длину стороны данного квадрата. Проще говоря, узнáем сам корень.
Вернёмся к извлечению корня. Мы выяснили, что корнем будет трёхзначное число. Трёхзначное число состоит из сотен, десятков и единиц.
При возведéнии сотен в квадрат, получаются десятки тысяч. Тогда сотни искомого корня следует искать в десятках тысяч подкоренного числа. В подкоренном числе 5 десятков тысяч. Отделим их мéткой:
Извлечём корень из числа 5. Из числа 5 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых Ближáйший мéньший квадрат к 5 это 4. Извлечём корень из этого квадрата, получим 2. Тем самым полýчим первую цифру корня:
На самом деле корень извлечён не из числа 5, а из пяти десятков тысяч. Метка, которая поставлена после числá 5, отделяет разряды числá, находящегося под знáком корня. Нужно понимать, что в данном случае 5 это 50000.
Из 50000 как и 5 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 50000. Но нужно принимать во внимание, что сотни это числа с двумя нулями на конце. Примеры:
100 — одна сотня
500 — пять сотен
900 — девять сотен
При возведéнии таких чисел в квадрат, получаются числа, у которых четыре нуля на конце:
1002 = 10000
5002 = 250000
9002 = 810000
Мы ищем сотни корня в десятках тысяч числа 54756, то есть в числе 50000. Но нет такого числá с двумя нулями на конце, вторая степень которого равна 50000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с четырьмя нулями на конце. Таковым является квадрат 40000.
Вернёмся к нашему рисунку. Большой квадрат со стороной a и площадью a2 это тот самый квадрат 40000. Укажем вместо a2 значение 40000
Укажем вместо a2 значение 40000
Теперь извлечём корень из квадрата 40000
Итак, мы нашли сторону квадрата, площадь которого 40000. Подпишем сторону a как 200
Но ранее в ответе мы написали не 200, а 2. Это является сокращённым вариантом. Число 2 в данном случае означает две сотни:
Теперь вытаскиваем остаток. Из пяти десятков тысяч корень извлечён только из четырёх десятков тысяч. Значит в остатке остался один десяток тысяч. Вытащим его:
Опять же надо понимать, что 4 это 40000, а 1 это 10000. С помощью рисунка это можно пояснить так: квадрат, площадь которого 40000, вычитается от общего квадрата, площадь которого 54756. Остаётся фигура, площадь которой 54756 − 40000 = 14756
Теперь нужно найти десятки корня. Рассмотрим на рисунке сумму площадей ab + ab + b2 (или 2ab + b2). В эту сумму будет входить один десяток тысяч, который остался в результате нахождения сóтен корня, удвоенное произведение сотен и десятков корня 2ab, а также десятки корня в квадрате b2.
Десятки в квадрате составляют сотни. Поэтому десятки корня следует искать в сотнях подкоренного числа. Под корнем сейчас 47 сотен. Снесём их к остатку 1, предварительно отделив их под корнем мéткой:
Один десяток тысяч это сто сотен, плюс снесено 47 сотен. Итого 100 + 47 = 147 сотен. В эти 147 сотен должна входить сумма 2ab + b2
2ab + b2 = 14700
Переменная a уже известна, она равна 200. Подставим это значение в данное равенство:
2 × 200 × b + b2 = 14700
400b + b2 = 14700
Теперь наша задача найти такое значение b, при котором левая часть станет равна 14700 или хотя близкой к этому числу, но не превосходящей его. Поскольку b является десятками искомого корня, то значение b является двузначным числом с одним нулём на конце. Такое число можно найти методом подбора. Для удобства вынесем в левой части за скобки b
Такое число можно найти методом подбора. Для удобства вынесем в левой части за скобки b
b(400 + b) = 14700
Теперь левую часть можно понимать так: к 400 следует прибавить некоторое число b, которое при умножении с тем же самым b даст в результате 14700 или близкое к 14700 число, не превосходящее его. Подставим например 40
40(400 + 40) = 14700
17600 ≠ 14700
Получается 17600, которое превосходит число 14700. Значит число 40 не годится в качестве десятков корня. Проверим тогда число 30
30(400 + 30) = 14700
12900 ≤ 14700
Получилось число 12900, которое не превосходит 14700. Значит число 30 подходит в качестве десятков корня. Числа, расположенные между 30 до 40 проверять не нужно, поскольку сейчас нас интересуют только двузначные числа с одним нулем на конце:
Вернемся к нашему рисунку. Сторона b это десятки корня. Укажем вместо b найденные десятки 30. А квадрат, площадь которого b2 это найденные десятки во второй степени, то есть число 900. Также укажем площади прямоугольников ab. Они равны произведению сотен корня на десятки корня, то есть 200 × 30 = 6000
Ранее в ответе мы написали не 30, а 3. Это является сокращённым вариантом. Число 3 в данном случае означают три десятка.
Теперь вытаскиваем остаток. В 147 сотен вместилось только 129 сотен. Значит в остатке осталось 147 − 129 = 18 сотен плюс сносим число 56 из подкоренного выражения. В результате образýется новый остаток 1856
С помощью рисунка это можно пояснить так: от фигуры, площадь которой 14756, вычитается площадь 12900. Остаётся фигура, площадь которой 14756 − 12900 = 1856
Теперь нужно найти единицы корня. Рассмотрим на рисунке сумму площадей 2(a + b)c + c2. В эту сумму и должен входить последний остаток 1856
2(a + b)c + c2 = 1856
Переменные a и b уже известны, они равны 200 и 30 соответственно.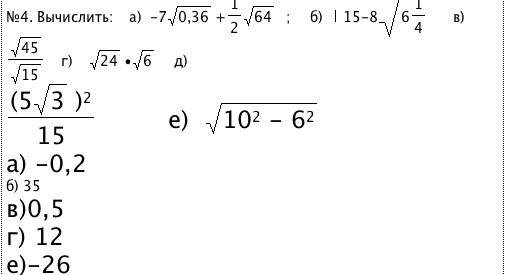 Подставим эти значения в данное равенство:
Подставим эти значения в данное равенство:
2(200 + 30)c + c2 = 1856
2 × 230c + c2 = 1856
460c + c2 = 1856
Теперь наша задача найти такое значение c, при котором левая часть станет равна 1856 или хотя близкой к этому числу, но не превосходящей его. Поскольку c является единицами искомого корня, то значение с является однозначным числом. То есть значение с это число от 1 до 9. Это число можно найти методом подбора. Для удобства вынесем в левой части за скобки с
с(460 + c) = 1856
Теперь левую часть можно понимать так: к 460 следует прибавить нéкоторое число с, которое при умножении с тем же сáмым с даст в результате 1856 или близкое к 1856 число, не превосходящее его. Подставим, например, число 4
4(460 + 4) = 1856
4 × 464 = 1856
1856 = 1856
Именно поэтому при использовании алгоритма первые найденные цифры умножают на 2. Так, 23 мы умнóжили на 2, получили 46 и уже к 46 дописывали цифру и умножáли образовавшееся число на ту же самую дописанную цифру, пытаясь получить остаток 1856
Итак, с = 4. При подстановке вместо с числá 4 получается остаток 1856. Это значит, что единицы корня найдены.
Квадрат, площадь которого 54756, имеет сторону равную 200 + 30 + 4, то есть 234.
Если из общей площади 54756 вычесть 40000, 6000, 6000, 900, 920, 920 и 16, то получим 0. Остаток равный нулю говорит о том, что решение завершено:
54756 − 40000 − 6000 − 6000 − 900 − 920 − 920 − 16 = 0
Пример 3. Извлечь квадратный корень из числа 3
Квадратный корень из числа 3 не извлекается. Ранее мы говорили, что квадратные корни из таких чисел можно извлекать только приближённо с определенной точностью.
Пусть 3 это площадь следующего квадрата:
Извлечь корень из числа 3 значит найти длину стороны данного квадрата:
Корень из 3 больше корня из 1, но меньше корня из 4
√1 < √3 < √4
Корни из 1 и 4 являются целыми числами.
√1 < √3 < √4
1 < √3 < 2
Между числами 1 и 2 нет целых чисел. Значит корень из числа 3 будет десятичной дробью. Найдём этот корень с точностью до десятых.
Квадратный корень из числа 3 можно представить в виде суммы a + b, где a — целая часть корня, b — дробная часть. Тогда сторону квадрата можно разбить на две составляющие: a и b
Сумма a + b во второй степени должна приближённо равняться 3.
(a + b)2 ≈ 3
Выполним в левой части данного равенства возведéние в квадрат:
a2 + 2ab + b2 ≈ 3
Тогда рисунок, иллюстрирующий квадрат площадью 3, можно представить так:
Найдём a. Извлечём корень из числа 3 с точностью до целых, получим 1
Если a2 это 1, а площадь всего квадрата равна 3, то в остатке останется 2. В этот остаток должна вмещаться площадь оставшейся фигуры:
Найдём b. Для этого рассмотрим сумму площадей 2ab + b2. Эта сумма должна приближённо равняться остатку 2, но не превосходить его
2ab + b2 ≈ 2
Значение a уже известно, оно равно единице:
2b + b2 ≈ 2
Вынесем за скобки b
b(2 + b) ≈ 2
Теперь в левой части к 2 следует прибавить нéкоторое число b, которое при умножении с тем же b будет приближённо равняться 2.
Значение b является дробным числом, а именно десятой частью. Оно равно какому-нибудь числу из промежутка [0,1; 0,9]. Возьмём любое число из этого промежутка и подставим его в равенство. Подставим к примеру 0,8
0,8(2 + 0,8) ≈ 2
2,24 ≈ 2
Получилось 2,24 которое превосходит 2. Значит 0,8 не годится в качестве значения b. Проверим тогда 0,7
0,7(2 + 0,7) ≈ 2
1,89 ≈ 2
Получилось 1,89 которое приближённо равно 2 и не превосходит его. Значит 0,7 является значением b
Значит 0,7 является значением b
Значит квадратный корень из 3 с точностью до десятых приближённо равен 1 + 0,7
К сожалению, понять механизм алгоритма извлечения квадратного корня намного сложнее, чем использовать сам алгоритм. Решите несколько примеров на применение алгоритма, и понимание механизма его работы будет даваться вам значительно проще.
Задания для самостоятельного решения
Задание 1. Извлечь квадратный корень из числа 169, используя алгоритм извлечения квадратного корня
Решение:
Задание 2. Извлечь квадратный корень из числа 289, используя алгоритм извлечения квадратного корня
Решение:
Задание 3. Извлечь квадратный корень из числа 1089, используя алгоритм извлечения квадратного корня
Решение:
Задание 4. Извлечь квадратный корень из числа 1764, используя алгоритм извлечения квадратного корня
Решение:
Задание 5. Извлечь квадратный корень из числа 4761, используя алгоритм извлечения квадратного корня
Решение:
Задание 6. Извлечь квадратный корень из числа 132496, используя алгоритм извлечения квадратного корня
Решение:
Задание 7. Извлечь квадратный корень из числа 157 с точностью до сотых, используя алгоритм извлечения квадратного корня
Решение:
Задание 8. Извлечь квадратный корень из числа 240,25 используя алгоритм извлечения квадратного корня
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Свойства числа 96 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Математические настройки для вашего сайта | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выберите язык: Deutsch English Español Français Italiano Nederlands Polski Português Русский 中文 日本語 한국어 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности. © 2021 numberempire.com Все права защищены | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Свойства числа 503 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Математические настройки для вашего сайта | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выберите язык: Deutsch English Español Français Italiano Nederlands Polski Português Русский 中文 日本語 한국어 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности. © 2021 numberempire.com Все права защищены | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Извлечение квадратного корня из многозначного числа
В предисловии к своему первому изданию “В царстве смекалки” (1908 год) Е. И. Игнатьев пишет: “… умственную самодеятельность, сообразительность и “смекалку” нельзя ни “вдолбить”, ни “вложить” ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью”.
В предисловии к изданию 1911 г “Роль памяти в математике” Е.И. Игнатьев пишет “… в математике следует помнить не формулы, а процесс мышления”.
Для извлечения квадратного корня существуют
таблицы квадратов для двухзначных чисел, можно
разложить число на простые множители и извлечь
квадратный корень из произведения. Таблицы
квадратов бывает недостаточно, извлечение корня
разложением на множители — трудоёмкая задача,
которая тоже не всегда приводит к желаемому
результату. Попробуйте извлечь квадратный
корень из числа 209764? Разложение на простые
множители дает произведение 2*2*52441. Методом проб и
ошибок, подбором – это, конечно, можно сделать,
если быть уверенным в том, что это целое число.
Способ, который я хочу предложить, позволяет
извлечь квадратный корень в любом случае.
Таблицы
квадратов бывает недостаточно, извлечение корня
разложением на множители — трудоёмкая задача,
которая тоже не всегда приводит к желаемому
результату. Попробуйте извлечь квадратный
корень из числа 209764? Разложение на простые
множители дает произведение 2*2*52441. Методом проб и
ошибок, подбором – это, конечно, можно сделать,
если быть уверенным в том, что это целое число.
Способ, который я хочу предложить, позволяет
извлечь квадратный корень в любом случае.
Когда-то в институте (Пермский государственный педагогический институт) нас познакомили с этим способом, о котором сейчас хочу рассказать. Никогда не задумывалась, есть ли у этого способа доказательство, поэтому сейчас пришлось некоторые доказательства выводить самой.
Основой этого способа, является состав числа =.
=&, т.е. &2=596334.
1. Разбиваем число (5963364) на пары справа налево (5`96`33`64)
2. Извлекаем квадратный корень из первой слева группы ( — число 2). Так мы получаем первую цифру числа &.
3. Находим квадрат первой цифры (22=4).
4. Находим разность первой группы и квадрата первой цифры (5-4=1).
5.Сносим следующие две цифры (получили число 196).
6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4).
7.Теперь необходимо найти вторую цифру числа &: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 — вторая цифра числа &.
8. Находим разность (196-176=20).
9. Сносим следующую группу (получаем число 2033).
10. Удваиваем число 24, получаем 48.
11.48 десятков в числе, при умножении которого на
число единиц, мы должны получить число меньшее 2033
(484*4=1936). Найденная нами цифра единиц (4) и есть
третья цифра числа &.
Найденная нами цифра единиц (4) и есть
третья цифра числа &.
Далее процесс повторяется.
Доказательство приведено мной для случаев:
1. Извлечение квадратного корня из трехзначного числа;
2. Извлечение квадратного корня из четырехзначного числа.
Приближенные методы извлечения квадратного корня (без использования калькулятора) [2].
1.Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а2+b, где а2ближайший к числу х точный квадрат натурального числа а (а2?х), и пользовались формулой . (1)
Извлечем с помощью формулы (1) корень квадратный, например из числа 28:
Результат извлечения корня из 28 с помощью МК 5,2915026.
Как видим способ вавилонян дает хорошее приближение к точному значению корня.
2. Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.
Пусть а1— первое приближение числа (в качестве а1 можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего х) .
Следующее, более точное приближение а2числа найдется по формуле .
Третье, еще более точное приближение и т.д.
(n+1)-е приближение найдется по формуле .
Нахождение приближенного значения числа методом Ньютона дает следующие результаты: а1=5; а2= 5,3; а3=5,2915.
- итерационная формула Ньютона для нахождения квадратного корня из числа х (n=2,3,4,…, аn — n-е приближение .
Указанный мною способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.
Литература:
- Пичугин Л.Ф. За страницами учебника алгебры. Книга для учащихся 7-9 классов средней школы. – М.: Просвещение, 1990.
- Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса общеобразовательных учебных заведений. – М.: Просвещение 1994.
Тест по алгебре с ответами
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 1 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 2 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 3 из 31. При каком, выраженном через а и b, значении m выражение будет полным квадратом?
- 1. 4/9a2b2
- 2. ±3/2ab
- 3. 9/4a2b2
- 4. Правильный ответ не приведен
- 1. х = 9
- 2. 9 ≤ х
- 3. х ≤ 8
- 4. х ≤ 9
3. Составьте квадратное уравнение, корни которого обратны корням уравнения х2 — 20х + 96 = 0.
- 1. 96х2 + 20х + 1 = 0
- 2. 96х2 — 20х + 1 = 0
- 3. 96х2 — 20х — 1 = 0
- 4. 96х2 + 20х — 1 = 0
4. При каких значениях х верно равенство |x2 — 49| = 49 — х2?
- 1. -7 ≤ х ≤ 7
- 2. х ≥ 7
- 3. х ≤ -7
- 4. х ≤ 7
5. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 4+√5 и 4-√5.
6. Один из корней квадратного уравнения х2 + 11х + q = 0 равен 8. Найдите второй корень.
7. Найдите значение x1x22 + x21x2, если x1 и х2 — корни квадратного уравнения х2 — 8х + 11 = 0.
8. Найдите значение x2 + x2x1 + x1, если x1 и х2 — корни квадратного уравнения 2х2 + 5х — 11 = 0.
9. Найдите значение x2 + x2x1 + x1, если x1 и х2 — корни квадратного уравнения 2х2 + 3х — 7 = 0.
10. Найдите значение x2 + x2x1 + x1, если x1 и х2 — корни квадратного уравнения 2х2 + 7х — 3 = 0.
11. Найдите значение x2 + x2x1 + x1, если x1 и х2 — корни квадратного уравнения 2х2 — 5х + 3 = 0.
12. Один из корней квадратного уравнения х2 — 11х + q = 0 равен 8. Найдите второй корень.
13. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 5+√3 и 5-√3.
14. Один из корней квадратного уравнения х2 + 13х + q = 0 равен 7. Найдите второй корень.
15. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 6+√2 и 6-√2.
16. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 3+√5 и 3-√5.
17. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 4+√3 и 4-√3.
18. Составьте квадратное уравнение, корни которого равны 6+√3 и 6-√3.
- 1. х2 + 12х — 33 = 0
- 2. х2 — 12х — 33 = 0
- 3. х2 + 12х + 33 = 0
- 4. х2 — 12х + 33 = 0
19. Составьте квадратное уравнение, корни которого равны 4+√5 и 4-√5.
- 1. х2 — 8х — 11 = 0
- 2. х2 + 8х — 11 = 0
- 3. х2 — 8х + 11 = 0
- 4. х2 + 8х + 11 = 0
20. Составьте квадратное уравнение, корни которого равны 3+√2 и 3-√2.
- 1. х2 — 6х — 7 = 0
- 2. х2 + 6х + 7 = 0
- 3. х2 — 6х + 7 = 0
- 4. х2 + 6х — 7 = 0
21. Составьте квадратное уравнение, корни которого равны 2+√5 и 2-√5.
- 1. х2 + 4х — 1 = 0
- 2. х2 — 4х — 1 = 0
- 3. х2 + 4х + 1 = 0
- 4. х2 — 4х + 1 = 0
22. Найдите значение x2 + x2x1 + x1, если x1 и х2 — корни квадратного уравнения 2х2 + 5х — 3 = 0.
23. Найдите значение x1x22 + x21x2, если x1 и х2 — корни квадратного уравнения х2 — 10х + 22 = 0.
- 1. -120
- 2. 220
- 3. 280
- 4. -220
24. Один из корней квадратного уравнения х2 — 13х + q = 0 равен 7. Найдите второй корень.
25. Один из корней квадратного уравнения х2 — 7х + q = 0 равен 11. Найдите второй корень.
26. Найдите значение x1x22 + x21x2, если x1 и х2 — корни квадратного уравнения х2 — 8х + 13 = 0.
- 1. 104
- 2. 94
- 3. -152
- 4. -104
27. Найдите значение x1x22 + x21x2, если x1 и х2 — корни квадратного уравнения х2 — 6х + 7 = 0.
28. Найдите значение x1x22 + x21x2, если x1 и х2 — корни квадратного уравнения х2 — 8х + 14 = 0.
- 1. -112
- 2. 112
- 3. -144
- 4. -92
29. Составьте квадратное уравнение, корни которого равны 2+√3 и 2-√3.
- 1. х2 + 4х + 1 = 0
- 2. х2 + 4х — 1 = 0
- 3. х2 — 4х — 1 = 0
- 4. х2 — 4х + 1 = 0
30. Найдите наименьшее целое значение k, при котором уравнение х2 — 2(k + 2)х + 11 + k2 = 0 имеет два различных действительных корня.
31. Найдите сумму корней уравнения:32. При каких значениях t уравнение х2 + (t — 2)х + 4 = 0 имеет два различных отрицательных корня?
- 1. t ≤ 1
- 2. t > 6
- 3. t
- 4. t
33. Корни уравнения х2 + рх + q = 0 вдвое больше корней уравнения х2 — 3х + 2 = 0. Чему равно р + q?
34. Найдите сумму корней уравнения:35. Найдите разность наибольшего и наименьшего корней уравнения х4 — 10х2 + 9 = 0.
36. Зная, что x1 и х2 — корни уравнения х2 + х — 1 = 0, найдите х31+х32.
37. Найдите наибольшее целое значение k, при котором уравнение kz2 + 2(k — 12)z + 6/5 = 0 не имеет действительных корней.
38. Сколько целых решений имеет уравнение |x2 — 3х| = 3х — х2?
39. Зная, что x1 и х2 — корни уравнения х2 — х + q = 0. Найдите q, если x31 + х32 = 19.
40. Найдите сумму корней уравнения |х| = х2 — х — 4.
- 1. 1 — 2√5
- 2. 2 — √5
- 3. —1 + √5
- 4. 1 + √5
41. x1 и х2 — корни уравнения x2 + mx + n = 0. Если каждый корень этого уравнения увеличить на 4 и из полученных чисел составить новое уравнение, то свободный член нового уравнения будет равен n — 32 (n — свободный член исходного уравнения). Чему будет равно m?
42. Найдите наибольшее значение выражения , если .43. Вычислите x1/х2 + x2/х1, если x1 и х2 — корни уравнения 3х2 — 8х — 15 = 0.
- 1. -3 19/45
- 2. -3 1/45
- 3. 5
- 4. -8/3
44. При каких значениях а уравнение ах2 — (а + 1)х + 2а + 2 = 0 имеет один корень?
- 1. 0; -1
- 2. -1; 0; 1/7
- 3. 1; -1/7
- 4. -1; 1/7
45. Чему равна сумма всех натуральных чисел, являющихся корнями уравнения |х2 — 8х + 7| = -7 + 8х — х2?
46. При каких значениях k уравнение х2 – 2k(х + 1) – k2 + 6k = 0 имеет отличное от нуля два совпадающих корня?
47. z1 и z2 — корни уравнения z2 + pz + q = 0. Если каждый корень этого уравнения увеличить на 4 и из полученных чисел составить новое уравнение, то свободный его член будет равен q + 68. Найдите р.
48. Найдите k в уравнении х2 + 3х + k + 8 = 0, если его корни x1 и х2 удовлетворяют условию x1/х2 = -1/4.
49. Найдите произведение корней уравнения .50. Найдите произведение корней уравнения 4|х — 2| = 3 + (х — 2)2.
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 1 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 2 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 3 из 3
Калькулятор настольный Casio JW-200SC-PK, премиум
Настольный калькулятор Casio JW-200SC-PK не только стильно выглядит, но и имеет необходимые для работы бухгалтера, товароведа, экономиста функции.
Casio JW-200SC-PK умеет конвертировать валюты, рассчитывать налоги и проценты, выводить итоговую сумму. У модели есть специальные кнопки для смены знаков и коррекции ввода. Можно выбрать режим десятичной точки.
Главным отличием этого настольного калькулятора, конечно, является яркий дизайн. Нежный розовый цвет привлекает внимание: Casio JW-200SC-PK не затеряется в сумке или среди бумаг! Корпус модели металлический, поэтому можно не бояться падений и ударов. Угол наклона дисплея можно регулировать.
РАСЧЕТ ПРОЦЕНТОВ: ЛОГИКА CASIO
Процент
Определите число, составляющее 5% от числа 200.
200 Х 5 % = 10
Увеличение
Увеличьте число 100 на 5%.
100 Х 5 % + = 105
Скидка
Уменьшите число 100 на 5%.
100 Х 5 % — = 96
Отношение
Сколько процентов составляет число 30 от числа 60. Найдите процентное соотношение.
30 ÷ 60 % = 50
Наценка
От какого числа нужно отнять 20%, чтобы получить число 100.
100 ÷ 20 % = 125
Например, Вы закупили товар и планируете в скором времени объявить на него 20% скидку, но не можете опустить цену ниже 100. Если Вы просто прибавите 20% к числу 100 (получится 120), а затем сделаете скидку 20%, то опуститесь ниже минимальной цены (получится 96). Если воспользоваться функцией «Наценка», то получится искомое число – 125.
Процентное изменение
На сколько процентов нужно увеличить число 10, чтобы получить число 12.
12 – 10 % = 20
Например, Вы хотите сделать размер торговой наценки такой, чтобы розничная цена была равна 12, закупая по оптовой цене 10. Эта функция поможет найти размер процента торговой наценки.
квадратный корень из 96 — как найти квадратный корень из 96?
Квадратный корень из числа 96 — это число, произведение которого на само себя дает 96. Квадратный корень числа может быть положительным или отрицательным, действительным или мнимым. Теперь мы вычислим квадратный корень из 96, используя различные методы, а также несколько интересных фактов и проблем.
- Корень квадратный из 96: √96 = 9,79796
- Квадрат 96: (96) 2 = 9216
Содержание
Что такое квадратный корень из 96?
- Квадратный корень из 96 записывается как √96 = 9.79796
- Квадратный корень из 96 можно также записать как 4√6 в упрощенной форме.
- Квадратный корень из числа 96 не является целым числом, поэтому это не полный квадрат.
Является ли квадратный корень из 96 рациональным или иррациональным?
Число называется рациональным, если его можно записать в форме p / q, где q 0.
Квадратный корень из 96 — это неповторяющееся и не завершающееся число.
Итак, квадратный корень из 96 — это иррациональное число.
Как найти квадратный корень из 96?
Теперь мы найдем квадратный корень из 96, используя следующие методы.
Квадратный корень из 96 с использованием метода простого факторизации
- Разложение на простые множители 96: 2 5 × 3
- Простые множители 96 в парах: (2 × 2) × (2 × 2) × 2 × 3
- Квадрат 96 равен √96: √ ((2 × 2) 2 × 6)
√96 = ± 4√6
Квадратный корень из 96 по длинному делению
Теперь мы найдем квадратный корень из 96 методом деления в столбик.
- Начните группировать цифры с места единицы в пары из двух цифр, помещая полосу / линию поверх них. В этом случае у нас есть пара (96).
- Найдите число (a) такое, что a × a ≤ 96. Итак, a будет 9, так как 9 × 9 = 81.
- Мы получаем 15 (96-81) как остаток и 9 как частное. Теперь сложите делитель a с самим собой, чтобы получить новый делитель (9 + 9 = 18).
- Поместите десятичную дробь в частное и делимое одновременно. Кроме того, поместите 3 пары нулей в делимую часть после десятичной дроби.
- Сбросьте одну пару зеро. Теперь наш новый дивиденд равен 1500. Теперь найдите такое число (b), что 18b × b ≤ 1500. Число m будет 7, так как 187 × 7 = 1309 ≤ 1500.
- Повторите вышеуказанный шаг для оставшихся двух пар нулей.
Итак, методом долгого деления мы получаем квадратный корень из √96 = 9,797.
Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров.
Часто задаваемые вопросы о квадратном корне из 96
Что такое отрицательный квадратный корень из 96?
Отрицательный квадратный корень из 96 равен -9.79796.
Что такое квадратный корень из 96 с точностью до 7 знаков после запятой?
Квадратный корень из 96 равен √96 = 9,7979589
Можем ли мы найти квадратный корень из 96, используя метод повторного вычитания?
Нет, мы не можем найти квадратный корень из 96, используя метод повторного вычитания.
Число 96 — не идеальный квадрат, и этот метод можно использовать только для полных квадратов.
Что такое квадрат 96?
Площадь 96 — 9216.
Как мы можем представить квадратный корень из 96 в экспоненциальной и радикальной форме?
- Квадратный корень из 96 записывается как √96 в радикальной форме.
- Квадратный корень из 96 записывается как (96) 1/2 в экспоненциальной форме.
- Корень квадратный из 96 — иррациональное число.
- Квадратный корень -96 — мнимое число.
- Число 96 — не идеальный квадрат.
Квадратный корень из 96 решенных примеров
Пример 1: Оцените квадратный корень из 96, используя метод аппроксимации.
Решение:
Число 96 находится между 81 и 100 (два последовательных полных квадрата).
Итак, целая часть квадратного корня 96 равна 9.
Для десятичной части воспользуемся формулой: (96 — 81) / (100 — 81) = 15/19 = 0,7894
Следовательно, квадратный корень из 96 составляет 9,7894 прибл.
Пример 2: Рио хочет найти связь между квадратным корнем из 96 и 6. Можете ли вы помочь Рио?
Решение:
Квадратный корень из 96 в упрощенном виде равен 4√6.
Мы видим, что квадратный корень из 96 в четыре раза больше квадратного корня из 6.
Итак, квадратный корень 96 = 4 × квадратный корень из 6.
Пример 3: Найдите наименьшее кратное 96, которое является полным квадратом?
Решение:
Полный квадрат — это число, делители которого являются квадратами числа.
Пара простых делителей 96 = (2 × 2) × (2 × 2) × 2 × 3
Следовательно, чтобы получился идеальный квадрат, нам нужно умножить его на 2.
Итак, 96 × 6 (576) кратно 96, что является полным квадратом.
- Найдите значение √√96.
- Найдите квадратный корень из всех множителей 96, кроме 1 и 96.
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Упростить квадратный корень из 96
Здесь мы покажем вам два метода, которые вы можете использовать, чтобы упростить квадратный корень из 96.Другими словами, мы покажем вам, как найти квадратный корень из 96 в его простейшей радикальной форме двумя разными способами.
Чтобы быть более конкретным, мы создали иллюстрацию ниже, показывающую, что мы хотим вычислить. Наша цель — сделать «A» вне радикала (√) как можно большим, а «B» внутри радикала (√) как можно меньше.
√96 = A√B
Метод наибольшего точного квадратного множителя
Метод наибольшего точного квадратного множителя использует наибольший коэффициент полного квадрата 96, чтобы упростить квадратный корень из 96.Вот как вычислить A и B с помощью этого метода:
A = Вычислить квадратный корень из наибольшего полного квадрата из списка всех множителей 96. Множители 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 и 96. Кроме того, наибольший полный квадрат в этом списке равен 16, а квадратный корень из 16 равен 4. Следовательно, A равно 4.
B = Вычислите 96, разделив его на наибольший полный квадрат из списка всех множителей 96. Выше мы определили, что наибольший полный квадрат из списка всех множителей 96 равен 16.Кроме того, 96, разделенное на 16, равно 6, поэтому B равно 6.
Теперь у нас есть A и B, и мы можем получить ответ на 96 в его простейшей радикальной форме следующим образом:
√96 = A√B
√96 = 4√6
Метод двойного основного коэффициента
Метод двойного простого множителя использует простые множители 96, чтобы упростить квадратный корень из 96 до его простейшей возможной формы. Вот как вычислить A и B с помощью этого метода:
A = Умножьте все двойные простые множители (пары) числа 96, а затем извлеките квадратный корень из этого произведения.Простые множители, которые умножаются вместе, чтобы получить 96, равны 2 x 2 x 2 x 2 x 2 x 3. Когда мы удаляем только пары, мы получаем 2 x 2 x 2 x 2 = 16, а квадратный корень из 16 равен 4. Следовательно, A равно 4.
B = Разделите 96 на число (A) в квадрате. 4 в квадрате равно 16, а 96, разделенное на 16, равно 6. Следовательно, B равно 6.
И снова у нас есть A и B, и мы можем получить ответ на 96 в его простейшей радикальной форме следующим образом:
√96 = A√B
√96 = 4√6
Упростить квадратный корень
Для упрощения введите еще один квадратный корень в поле ниже.
Упростить квадратный корень из 97
Вот следующий квадратный корень в нашем списке, который мы для вас упростили.
Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт
Квадратный корень из 96 (√96)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 96. Начнем с определения, а затем ответим на некоторые общие вопросы о квадратном корне из 96. Затем мы покажем вам различные способы вычисления квадратного корня из 96 с учетом и без компьютер или калькулятор.У нас есть чем поделиться, так что приступим!
Корень квадратный из 96 определения
Квадратный корень из 96 в математической форме записывается со знаком корня, например, √96. Мы называем это квадратным корнем из 96 в радикальной форме. Квадратный корень из 96 — это величина (q), которая при умножении сама на себя будет равна 96.
√96 = q × q = q 2
Является ли 96 идеальным квадратом?
96 — это полный квадрат, если квадратный корень из 96 равен целому числу.Как мы подсчитали дальше На этой странице квадратный корень 96 не является целым числом.
96 — не идеальный квадрат.
Квадратный корень из 96 является рациональным или иррациональным?
Квадратный корень из 96 является рациональным числом, если 96 — полный квадрат. Это иррациональное число, если оно не является полным квадратом. Поскольку 96 не является полным квадратом, это иррациональное число. Это означает, что ответ на «квадратный корень из 96?» будет бесконечное число десятичных знаков.Десятичные дроби не прерываются, и вы не можете преобразовать их в точную дробь.
√96 — иррациональное число
Можно ли упростить квадратный корень из 96?
Вы можете упростить 96, если можете сделать 96 внутри корня меньше. Мы называем этот процесс «упрощением сурда». Корень квадратный из 96 можно упростить.
√96 = 4√6
Как вычислить квадратный корень из 96 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 96 — использовать калькулятор! Просто введите 96, а затем √x, чтобы получить ответ.Мы сделали это с помощью нашего калькулятора и получили следующий ответ с 9 десятичными числами:
√96 ≈ 9,797958971
Как вычислить квадратный корень из 96 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT (96) в ячейку, чтобы получить квадратный корень из 96. Ниже приведен результат с 13 знаками после запятой. Мы называем это квадратным корнем из 96 в десятичной форме.
КОРЕНЬ (96) ≈ 9,7979589711327
Что такое квадратный корень из 96 с округлением?
Квадратный корень из 96, округленный до ближайшей десятой, означает, что вам нужна одна цифра после десятичной точки.Квадратный корень из 96, округленный до сотых, означает, что вы хотите две цифры после десятичной точки. Квадратный корень из 96, округленный до ближайшей тысячной, означает, что вам нужны три цифры после десятичной точки.
10-я: √96 ≈ 9,8
100-я: √96 ≈ 9,80
1000-я: √96 ≈ 9,798
Что такое квадратный корень из 96 в виде дроби?
Как мы уже говорили выше, поскольку квадратный корень из 96 является иррациональным числом, мы не можем превратить его в точную дробь.Однако мы можем преобразовать его в приблизительную дробь, используя квадратный корень из 96, округленный до ближайшей сотой.
√96
≈ 9,80 / 1
≈ 980/100
≈ 9 4/5
Что такое квадратный корень из 96, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробной степенью. Квадратный корень из 96 — не исключение. Вот правило и ответ в «квадратный корень из 96, преобразованный в основание с показателем степени?»:
√b = b ½
√96 = 96 ½
Как найти квадратный корень из 96 методом деления в длину
Здесь мы покажем вам, как вычислить квадратный корень из 96, используя метод деления в длину с точностью до одного десятичного знака.Это потерянный искусство того, как они вычисляли квадратный корень из 96 вручную до того, как были изобретены современные технологии.
Шаг 1)
Задайте 96 в парах по две цифры справа налево и присоедините один набор 00, потому что нам нужен один десятичный разделитель:
Шаг 2)
Начиная с первого набора: наибольший полный квадрат, меньший или равный 96, равен 81, а квадратный корень из 81 равен 9. Таким образом, поместите 9 вверху и 81 внизу следующим образом:
Шаг 3)
Вычислите 96 минус 81 и запишите разницу ниже.Затем перейдите к следующему набору чисел.
Шаг 4)
Удвойте число, выделенное зеленым сверху: 9 × 2 = 18. Затем используйте 18 и нижнее число, чтобы решить эту задачу:
18? ×? ≤ 1500
Знаки вопроса «пустые» и такие же «пустые». Методом проб и ошибок мы обнаружили, что наибольшее число «пробел» может быть 7. Теперь введите 7 сверху:
Это оно! Ответ сверху. Квадратный корень из 96 с точностью до одной десятичной дроби равен 9,7.
Квадратный корень числа
Введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 96 на этой странице.
Банкноты
Помните, что отрицательное умножение на отрицательное равняется положительному. Таким образом, квадратный корень из 96 не дает только положительного ответа. что мы объяснили выше, но также и отрицательный аналог.
На этой странице мы часто упоминаем точные квадратные корни. Вы можете использовать список идеальных квадратов для справки.
Квадратный корень из 97
Вот следующее число в нашем списке, о котором у нас есть столь же подробная информация о квадратном корне.
Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт
Коэффициенты квадратного корня из 96 (коэффициент √96)
Здесь мы покажем вам, как получить множители квадратного корня 96 (множители √96).Мы определяем множители квадратного корня 96 как любые целое число (целое число) или квадратный корень, который можно равномерно разделить на квадратный корень из 96. Кроме того, если вы разделите √96 на коэффициент √96, получится приводит к другому коэффициенту √96.
Сначала мы найдем все квадратные корни, которые можно без остатка разделить на квадратный корень из 96. Мы делаем это, находя все множители 96 и добавьте к ним радикал (√) следующим образом:
√1, √2, √3, √4, √6, √8, √12, √16, √24, √32, √48 , и √96
Затем мы найдем все целые числа, которые можно без остатка разделить на квадратный корень из 96.Мы делаем это, сначала определяя полные квадратные корни из приведенного выше списка:
√1, √4, √16
Затем мы извлекаем квадратный корень из полных квадратных корней, чтобы получить целые числа, которые мы можем равномерно разделить на квадратный корень из 96.
1, 2, 4
Множители квадратного корня 96 — это два приведенных выше списка, вместе взятых. Таким образом, множители квадратного корня из 96 (квадратные корни и целые числа) следующие:
1, 2, 4, √1, √2, √3, √4, √6, √8, √12, √16 , √24, √32, √48 и √96
Как мы сказали выше, квадратный корень 96, деленный на любой из его множителей, даст другой из его множителей.Следовательно, если разделить √96 на любой из
факторов, указанных выше, вы увидите, что это приводит к одному из других факторов.
Что вы можете сделать с этой информацией? Во-первых, вы можете получить квадратный корень из 96 в простейшей форме. Квадратный корень из 96 упрощенное — это наибольший целочисленный множитель, умноженный на квадратный корень из 96, деленный на наибольший полный квадратный корень. Таким образом, вот математика для получения квадратного корня из 96 в его простейшей радикальной форме:
√96
= 4 × (√96 ÷ √16)
= 4√6
Калькулятор коэффициента квадратного корня
Вам нужно множители другого квадратного корня? Хорошо, введите квадратный корень в поле ниже.
Коэффициенты квадратного корня из 97
Надеемся, эта информация была полезной. Хотите узнать больше? Если это так, перейдите сюда, чтобы получить множители следующего квадратного корня в нашем списке.
Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт
Упростите квадратные корни — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Используйте свойство продукта, чтобы упростить квадратный корень
- Используйте свойство Quotient для упрощения квадратного корня
Перед тем, как начать, пройдите тест на готовность.
- Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
В последнем разделе мы вычислили квадратный корень из числа между двумя последовательными целыми числами. Мы можем сказать, что это от 7 до 8. Это довольно легко сделать, когда числа достаточно малы, чтобы мы могли их использовать (рисунок).
Но что, если мы хотим оценить? Если мы сначала упростим квадратный корень, мы сможем легко его вычислить.Есть и другие причины для упрощения квадратного корня, как вы увидите далее в этой главе.
Квадратный корень считается упрощенным , если его подкоренное выражение не содержит точных квадратных множителей.
Упрощенный квадратный корень
считается упрощенным, если не имеет точных квадратов.
Так упрощено. Но это не упрощает, потому что 16 — это полный квадратный множитель 32.
Используйте свойство продукта для упрощения квадратного корня
Свойства, которые мы будем использовать для упрощения выражений с квадратными корнями, аналогичны свойствам показателей степени.Мы знаем это . Об этом говорит соответствующее свойство квадратных корней.
Продукт Свойство квадратного корня
Если a , b — неотрицательные действительные числа, то.
Мы используем свойство произведения квадратного корня, чтобы удалить все точные квадратные множители из радикала. Мы покажем, как это сделать, на (Рисунок).
Как использовать свойство продукта для упрощения квадратного корня
Упростить:.
Упростить:.
Упростить:.
Обратите внимание, что в предыдущем примере упрощенная форма — это произведение целого числа и квадратного корня. Мы всегда пишем целое число перед квадратным корнем.
Упростите извлечение квадратного корня с помощью свойства продукта.
- Найдите наибольший коэффициент полного квадрата подкоренного выражения. Перепишите подкоренное выражение как произведение, используя коэффициент полного квадрата.
- Используйте правило произведения, чтобы переписать радикал как произведение двух радикалов.
- Упростите квадратный корень из полного квадрата.
Упростить:.
Решение
Упростить:.
Упростить:.
Мы можем использовать упрощенную форму для оценки. Мы знаем, что 5 находится между 2 и 3, и это так. Так между 20 и 30.
Следующий пример очень похож на предыдущие, но с переменными.
Упростить:.
Решение
Упростить:.
Упростить:.
Мы выполняем ту же процедуру, когда в радикале есть коэффициент.
Упростить:
Решение
Упростить:.
Упростить:.
В следующем примере и константа, и переменная имеют точные квадратные множители.
Упростить:.
Решение
Упростить:.
Упростить:.
Упростить:.
Решение
Упростить:.
Упростить:.
Мы видели, как использовать порядок операций для упрощения некоторых выражений с помощью радикалов. Для упрощения мы должны сначала упростить каждый квадратный корень отдельно, а затем сложить, чтобы получить сумму 17.
Выражение нельзя упростить — для начала нам нужно упростить каждый квадратный корень, но ни 17, ни 7 не содержат точного квадратного множителя.
В следующем примере у нас есть сумма целого числа и квадратного корня. Мы упрощаем извлечение квадратного корня, но не можем прибавить полученное выражение к целому числу.
Упростить:.
Решение
Условия не похожи и поэтому мы не можем их добавить. Попытка сложить целое число и радикал подобна попытке сложить целое число и переменную — они не похожи на термины!
Упростить:.
Упростить:.
Следующий пример включает дробь с радикалом в числителе.Помните, что для упрощения дроби вам понадобится общий множитель в числителе и знаменателе.
Упростить:.
Решение
Упростить:.
Упростить:.
Используйте свойство Quotient для упрощения квадратного корня
Всякий раз, когда вам нужно упростить квадратный корень, первый шаг, который вы должны сделать, — это определить, является ли подкоренное выражение идеальным квадратом. Дробь полного квадрата — это дробь, в которой числитель и знаменатель являются точными квадратами.
Упростить:.
Решение
Упростить:.
Упростить:.
Если у числителя и знаменателя есть общие множители, удалите их. Вы можете найти идеальную квадратную дробь!
Упростить:.
Решение
Упростить:.
Упростить:.
В последнем примере нашим первым шагом было упростить дробь под радикалом, удалив общие множители.В следующем примере мы будем использовать свойство Quotient для упрощения под радикалом. Мы делим одинаковые основания, вычитая их показатели,.
Упростить:.
Решение
Упростить:.
Упростить:.
Упростить:.
Решение
Упростить:.
Упростить:.
Помните коэффициент мощности? В нем говорилось, что мы можем возвести дробь в степень, возведя числитель и знаменатель в степень по отдельности.
Мы можем использовать аналогичное свойство, чтобы упростить извлечение квадратного корня из дроби. После удаления всех общих множителей из числителя и знаменателя, если дробь не является полным квадратом, мы отдельно упрощаем числитель и знаменатель.
Фактор квадратного корня
Если a , b — неотрицательные действительные числа и, тогда
Упростить:.
Решение
Упростить:.
Упростить:.
Как использовать свойство Quotient для упрощения квадратного корня
Упростить:.
Упростить:.
Упростить:.
Упростите квадратный корень, используя свойство частного.
- По возможности упростите дробь в подкоренном выражении.
- Используйте свойство Quotient, чтобы переписать радикал как частное двух радикалов.
- Упростим радикалы в числителе и знаменателе.
Упростить:.
Решение
Упростить:.
Упростить:.
Обязательно сначала упростите дробь в подкоренном выражении, если это возможно.
Упростить:.
Решение
Упростить:.
Упростить:.
Упростить:.
Решение
Упростить:.
Упростить:.
Практика ведет к совершенству
Используйте свойство продукта для упрощения квадратного корня
Упростите следующие упражнения.
70)
Используйте свойство Quotient для упрощения квадратного корня
Упростите следующие упражнения.
Письменные упражнения
Объясните почему.Тогда объясните почему.
Объясните, почему не равно.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
кв. 96
кв. (96). Найдите квадратный корень из 96 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Sqrt 96 или что такое квадратный корень из 96? Используйте калькулятор квадратного корня ниже, чтобы найти квадратный корень любого действительного числа, положительного или отрицательного.См. Также на этой странице таблицу квадратного корня от 1 до 100.
Что такое квадратный корень? Определение квадратного корня
Квадратный корень из числа «x» — это такое число y, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 9 — это квадратный корень из 81, потому что 9 2 = 9 • 9 = 81, -9 — квадратный корень из 81, потому что (-9) 2 = (-9) • (-9) = 81. При написании математики люди часто используют sqrt (x) для обозначения квадратного корня из x. Узнайте больше о квадратном корне здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Квадратный символ?
Вот символ квадратного корня.Он обозначается символом √, известным как знак корня или основание системы счисления.
Таблица квадратного корня 1-100
Квадратные корни от 1 до 100 с округлением до тысячных.
| число | квадрат | квадрат корень | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.000 | ||||||
| 2 | 4 | 1.414 | ||||||
| 3 | 9 | 1.732 | ||||||
| 4 | ||||||||
| 4 | 00||||||||
| 5 | 25 | 2.236 | ||||||
| 6 | 36 | 2.449 | ||||||
| 7 | 49 | 2.646 | 81 | 3.000 | ||||
| 10 | 100 | 3.162 | ||||||
| 11 | 121 | 3.317 | ||||||
| 12 | 144.464 | |||||||
| 13 | 169 | 3.606 | ||||||
| 14 | 196 | 3,742 | ||||||
| 15 | 225 | 3,873106 | 3,873106 | 15 | 289 | 4,123 | ||
| 18 | 324 | 4,243 | ||||||
| 19 | 361 | 4,359 | ||||||
| 20 | 400 9110.472 | |||||||
| 21 | 441 | 4,583 | ||||||
| 22 | 484 | 4.690 | ||||||
| 23 | ||||||||
| 23 | 4,796 | 9106625 | 5.000 |
| число | квадрат | квадрат корень | ||||||
|---|---|---|---|---|---|---|---|---|
| 26 | 676 | 5.099 | ||||||
| 27 | 729 | 5,196 | ||||||
| 28 | 784 | 5,292 | ||||||
| 29 | ||||||||
| 29 | 5,385 | |||||||
| 961 | 5,568 | |||||||
| 32 | 1,024 | 5,657 | ||||||
| 33 | 1,089 | 5,745 | ||||||
| 34 | 1,156.831 | |||||||
| 35 | 1,225 | 5,916 | ||||||
| 36 | 1,296 | 6.000 | ||||||
| 37 | ||||||||
| 37 | 1,369 | 6,083106 | 1 | 1,521 | 6,245 | |||
| 40 | 1,600 | 6,325 | ||||||
| 41 | 1,681 | 6,403 | ||||||
| 42 | 1 764481 | |||||||
| 43 | 1,849 | 6,557 | ||||||
| 44 | 1,936 | 6,633 | ||||||
| 45 | 2,025 | 6,7011,1106 | 2,209 | 6,856 | ||||
| 48 | 2,304 | 6,928 | ||||||
| 49 | 2,401 | 7.000 | ||||||
| 50 | 7000 | |||||||
| 50 | 9110071
| число | квадрат | квадрат корень | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 51 | 2,601 | 7,141 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | 2,704 | 7,211 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | 2,809 | 7,280 | 7,280 | 7,416 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | 3,136 | 7.483 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | 3,249 | 7,550 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | 3,364 | 7,616 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | 3,481 | 3,721 | 7,810 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | 3,844 | 7,874 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | 3,969 | 7,937 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | 4,225 | 8,062 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | 4,356 | 8,124 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | 4,489 | 8,185 9106 | 4,761 | 8,307 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | 4,900 | 8,367 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | 5,041 | 8,426 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72,1106 | 72,1106 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | 5,329 | 8,544 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | 5,476 | 8,602 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | 5,625 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| число | квадрат | квадрат корень | ||
|---|---|---|---|---|
| 76 | 5,776 | 8,718 | ||
| 77 | 5,929 | 8,775 | ||
| 78 | 6,084 | 8.832 | ||
| 79 | 6,241 | 8,888 | ||
| 80 | 6,400 | 8,944 | ||
| 81 | 6,561 | 9116 | 91056,889 | 9,110 |
| 84 | 7,056 | 9,165 | ||
| 85 | 7,225 | 9,220 | ||
| 274 | ||||
| 87 | 7,569 | 9,327 | ||
| 88 | 7,744 | 9,381 | ||
| 89 | 7,921 | |||
| 8,281 | 9,539 | |||
| 92 | 8,464 | 9,592 | ||
| 93 | 8,649 | 9,644 | ||
| 9,644 | ||||
| 94,8106 | 695||||
| 95 | 9,025 | 9,747 | ||
| 96 | 9,216 | 9,798 | ||
| 97 | 9,409 | |||
| 9,801 | 9,950 | |||
| 100 | 10,000 | 10.000 |
Корень квадратный из значений около 96
| Число | Sqrt |
|---|---|
| 95.6 | 9,778 |
| 95,7 | 9,783 |
| 95,8 | 9,788 |
| 95,9 | 9,793 |
| 9105 | 9,808 |
| 96,3 | 9,813 |
| 96,4 | 9,818 |
| 96,5 | 9,823 |
Примеры квадратного корня
Корень квадратный из 96 | кв из 96
Факторинговая площадь 96 Решения
96√9216 = 9216
96√884736 =
.989878
96√84934656 = 884736
96√8153726976 = 8668607.02828
96√782757789696 = 84934656
2√192 = 27,7128129211
2√384 = 39,18845
2√768 = 55,4256258422
2√1536 = 78,3836717691
2√3072 = 110,851251684
3√288 = 50,
3√864 = 88,1816307402
3√2592 = 152,735064736
3√7776 = 264,544892221
3√23328 = 458,205194209
Вопрос: Является ли 96 рациональным числом?.
Ответ: Да 96 рациональное число, потому что это целое и целое число.Все числа и целые числа являются рациональными числами.
Вопрос: 96 — иррациональное число ?.
Ответ: Нет.
Вопрос: является ли sqrt 96 рациональным числом?
Ответ: Нет.
Этот калькулятор — два в одном, он вычисляет квадратные и кубические корни чисел. .
Квадратный корень из числа b — это такое число x, что x2 = b, что означает число x, квадрат которого является результатом умножения числа на себя, или x × x равен b.
Например, 5 и −5 являются квадратным корнем из 25, потому что 5² = (−5) ² = 25.
Каждое неотрицательное действительное число c имеет уникальный неотрицательный квадратный корень, называемый главным, который обозначается как √c, где √ называется радикальным знаком или основанием системы счисления. Например, главный квадратный корень 36 равен 6, обозначается √36 = 6, потому что 6² = 6 × 6 = 36 и 6 неотрицательно. Нет, корень которого рассматривается, известен как подкоренное выражение. Подкоренное выражение — это число или выражение под знаком радикала, в этом примере 36.
Каждое положительное число a имеет два корня: √b, положительный, и −√b, отрицательный. Эти два корня обозначены ± √b. Главный корень положительного числа — это только один из двух квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного корня. Для положительного b главный квадратный корень можно также записать в экспоненциальной записи как b1 / 2.
Система счисления. Система счисления в математике устроена так, что 2 (два) — наименьшее четное простое число.это единственное простое число, за которым следует еще одно простое число 3 (тройка). Все четные и целые числа делятся на 2. Два — это третье число последовательности Фибоначчи. Готфрид Вильгельм Лейбниц открыл двойную систему счета (двоичную систему), в которой для представления чисел используются только две цифры. Это помогло в развитии цифровых технологий для распространения. По этой причине это самая известная и самая важная система счисления в дополнение к обычно используемой десятичной системе.
Нулевая цифра.Цифра ноль — это количество элементов в пустой коллекции объектов. Математически мощность пустого множества Zero зависит от контекста других по-разному определенных объектов. но его можно отождествить с другими, принадлежащими тому же объекту, который сочетает в себе несколько свойств, совместимых друг с другом. Поскольку кардинальные числа, то есть количество элементов в наборе, идентифицируются специальными порядковыми числами, нулевая цифра — это просто наименьшее кардинальное число. ноль выбирается первым порядковым номером.Как конечный кардинал и порядковый номер, это зависит от определения, которое часто считается среди натуральных чисел. Нулевая цифра — это элемент идентичности для добавления во многие системы couting, такие как рациональные числа, комплексные числа и действительные числа, а также общее имя для нейтрального элемента во многих алгебраических процессах, даже если другие элементы не идентифицируются с общими числами.
 7979589711327
7979589711327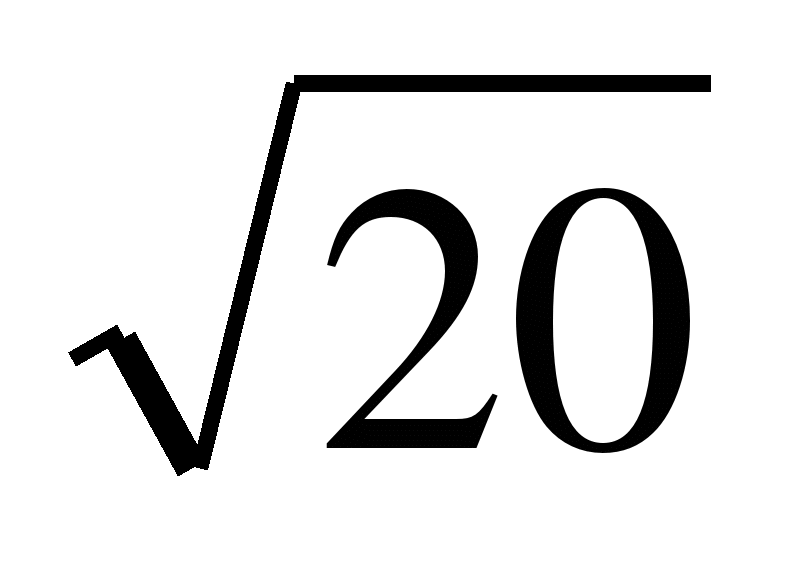 427661492006
427661492006