Решение задач на движение. 5-й класс
Важная задача цивилизации – научить человека мыслить
Т. Эдисон
Цели урока:
- Обучающая – продолжить работу по формированию у учащихся умений решать задачи на движение.
- Воспитательная – воспитывать волю и настойчивость для достижения поставленной цели.
- Развивающая – развивать навыки самоконтроля.
Тип урока: урок применения знаний и умений.
Оборудование: рисунки к задачам, карточки с формулами.
Структура урока:
- Сообщение темы и целей урока (1 мин.)
- Проверка домашнего задания (3 мин.)
- Устные упражнения (8 мин.)
- Отработка умений решать задачи на движение (18 мин.)
- Самостоятельная работа (с проверкой) (7 мин.)
- Постановка домашнего задания (1 мин.)
- Подведение итогов урока (2 мин.)
ХОД УРОКА
1. Сообщение темы и цели урока
2. Проверка домашнего задания
3. Устные упражнения
А) Заполнить таблицу
| S | V | t | |
| 1 | 135 км | 9 км/ч | |
| 2 | 12 м/с | 4 с | |
| 3 | 132 м | 11 мин | |
| 4 | а км/ч | b ч |
Раскрывается одно из «крыльев» доски с
таблицей
Учащиеся комментируют формулы которыми
пользуются
На доске появляются карточки:
S = V * t V = S/t t = S/V
Б) По рисунку найти скорость
Ответ: скорость сближения V1 + V2
Ответ: скорость удаления V1 + V2
I) V1 > V2
Ответ: скорость сближения V1
II) V1 < V2
Ответ: скорость удаления V2 – V1
В) Могут ли три человека имея двухместный
мотоцикл преодолеть расстояние в 60 километров за
3 часа, если скорость мотоцикла 50 км/ч а пешехода 5
км/ч.
Ответ: Да. Первый человек идет 2 часа со
скоростью 5 км/ч, он пройдет 10 км, ему останется
проехать 50 км, т.е. его сможет довести мотоциклист
за 1 час.
Второй едет на мотоцикле с самого начала 1 час и
везет с собой третьего. Они проедут 50 км,
оставшиеся 10 км третий пройдет за 2 часа пешком, а
второй вернется за первым (меньше, чем 1 час, так
до встречи с ним останется меньше 50 км и довезет
первого до конечного пункта)
4. Отработка умений решать задачи
Задача №1
Из пунктов А и В расстояние между которыми 320 км отправились одновременно мотоциклист и автомобилист. Скорость автомобиля 52 км/ч а мотоцикла 40 км/ч, какое расстояние будет между ними через 2 часа?
Вопрос учителя: как могут двигаться объекты?
Ответы учеников:
– На встречу друг другу
– В противоположные стороны
– В одном направлении вдогонку
– В одном направлении с отставанием
Класс делится на 4 группы. Каждой группе предлагается один из четырех вариантов движения объектов, необходимо:
- Смоделировать задачу
- Решить с полным объяснением
- Защитить решение у доски
1 группа (движение на встречу друг другу)
Решение:
1) 52 + 40 = 92 (км/ч) – скорость сближения.
2) 92 * 2 = 184 (км) – проедут автомобилист и
мотоциклист за 2 часа вместе.
3) 320 – 184 = 136 (км) – расстояние между
автомобилистом и мотоциклистом через 2 часа.
Ответ: 136 км.
2 группа (движение в противоположные стороны)
Решение:
1) 52 + 40 = 92 (км/ч) – скорость удаления.
2) 92 * 2 = 184 (км) – проедут автомобилист и
мотоциклист за 2 часа вместе.
3) 320 + 184 = 504 (км) – расстояние между автомобилистом
и мотоциклистом через 2 часа.
Ответ: 504 км.
3 группа (движение в одном направлении вдогонку)
Решение:
1) 52 – 40 = 12 (км/ч) – скорость сближения.
2) 12 * 2 = 24 (км) – расстояние на которое
автомобилист приблизится к мотоциклисту.
3) 320 – 24 = 296 (км) – расстояние между
автомобилистом и мотоциклистом через 2 часа.
Ответ: 296 км.
4 группа (движение в одном направлении с отставанием)
Решение:
1) 52 – 40 = 12 (км/ч) – скорость удаления.
2) 12 * 2 = 24 (км) – расстояние на которое
автомобилист удалится от мотоциклиста за 2 часа.
3) 320 + 24 = 344 (км) – расстояние между автомобилистом
и мотоциклистом через 2 часа.
Ответ: 344 км.
Итак, задача может иметь ответы: 136км, 504 км, 296 км, 344 км.
Задача №2
Два охотника отправились одновременно навстречу друг другу и двух деревень, расстояние между которыми 18 км. Первый шел со скоростью 5 км/ч, второй 4 км/ч. Первый взял с собой собаку, которая бегала со скоростью 8 км/ч. Собака сразу же побежала на встречу второму охотнику и встретив его, повернула и стой же скоростью побежала на встречу своему хозяину. Встретила его, повернула и побежала на встречу другому. Так она бегала от одного охотника к другому, пока те не встретились. Сколько км пробежала собака?
Обсуждение задачи:
Вопрос: Что нужно знать, чтобы найти какое
расстояние пробежала собака?
Ответ: Нужно скорость собаки и время которое
она пробежала
Вопрос: Что мы знаем и что не знаем?
Ответ: Знаем скорость собаки – 8 км/ч, не
знаем время?
Вопрос: Как время собаки связанно с временем
движения охотников?
Ответ: Время движения собаки равно времени,
через которое встретились охотники.
Решение:
- 18 / (5 + 4) = 2 (ч) – время через которое охотники встретились.
- 2 * 8 = 16 (км) – пробежала собака.
Ответ: 16 км.
5. Самостоятельная работа
Вариант I
Из пунктов А и В, расстояние между которыми 21 км, отправляются в путь одновременно пешеход из В и вдогонку ему велосипедист из А и движутся со скоростью: пешеход 5 км/ч, велосипедист 12 км/ч (Рис). На сколько километров уменьшится расстояние между ними через 3ч?
Решение:
1) 12 – 5 = 7 (км/ч) – скорость сближения
2) 7 * 3 = 21 (км) – на столько уменьшится расстояние
между велосипедистом и пешеходом через 3 ч.
Ответ: на 21 км
Вариант II
Велосипедист и пешеход отправились в путь одновременно в одном направлении из двух колхозов, расстояние между которыми 24 км. Велосипедист ехал вдогонку пешеходу со скоростью 11 км/ч, а пешеход шел со скоростью 5 км/ч. Через сколько часов после своего выезда велосипедист догонит пешехода?
Решение:
1) 11 – 5 = 6 (км/ч) – скорость сближения
2) 24 : 6 = 4 (ч) – через столько часов велосипедист
догонит пешехода
Ответ: через 4 ч.
6. Постановка домашнего задания
№642, №650 (Н.Я. Виленкин, В. И. Жохов и др. математика 5 класс, Мнемозина, 2008г.)
Дополнительная задача:
Из А в В отправились одновременно 2 человека: один пешком, а другой на велосипеде. В то же время из В в А выехал автомобиль, который встретился с велосипедистом через 4 часа, а с пешеходом через 5 часов после своего выезда из В. Найти расстояние от А до В, зная что скорость пешехода 6 км/ч, а велосипедиста 15 км/ч.
Решение:
- 15 * 4 = 60 (км) – на таком расстояние находился
автомобист от А через 4 часа.

- 6 * 5 = 30 (км) – на таком расстоянии находил автомобилист от А через 5 часов.
- 60 – 30 = 30 (км/ч) – скорость автомобиля.
- 15 + 30 = 45 (км/ч) – скорость сближения автомобилиста и велосипедиста.
- 45 * 4 = 180 (км) – расстояние от А до В.
Ответ: 180 км.
7. Подведение итогов урока
Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Предварительные навыкиЗадача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км).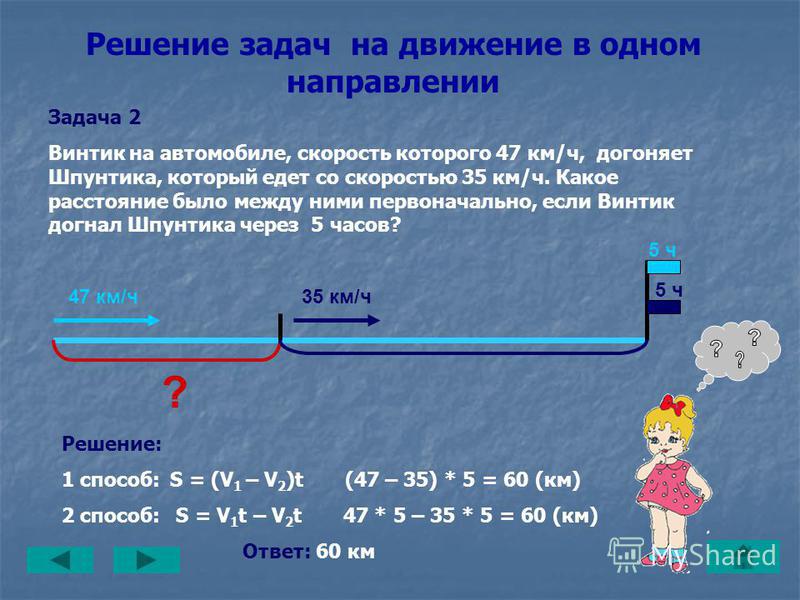 Так мы определим сколько километров прошел второй велосипедист:
Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров.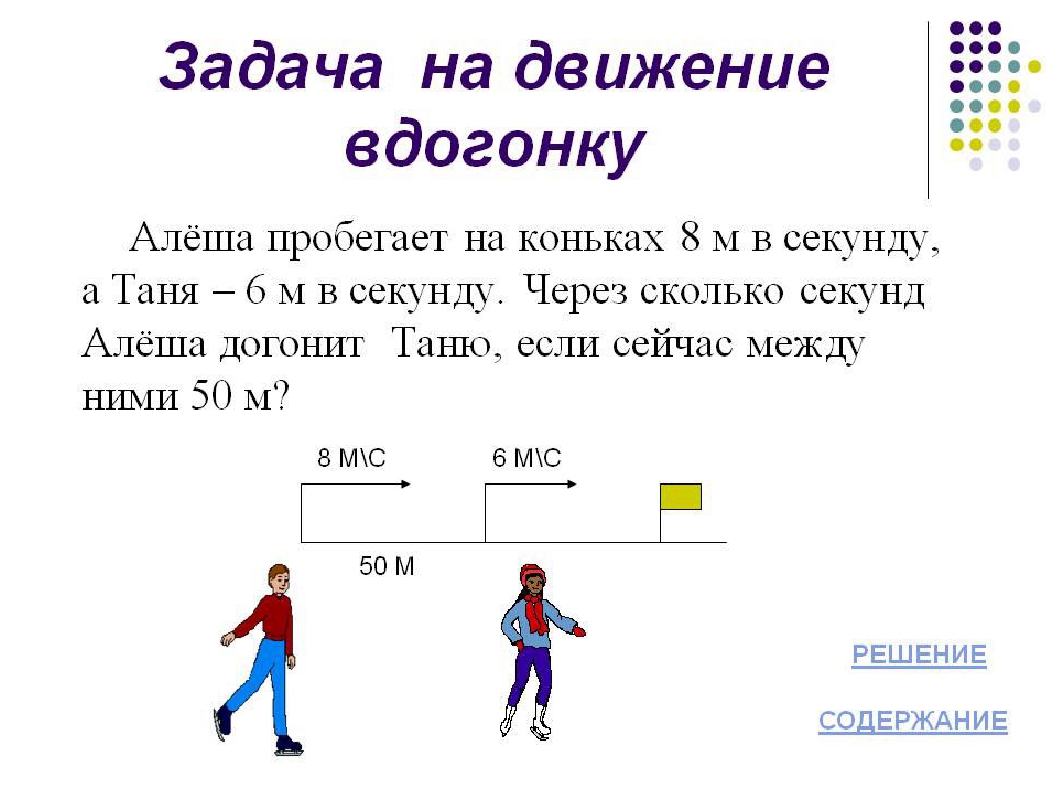 Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80 : 40 = 2
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60 : 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700 : 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400 : 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40 : 20 = 2
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15 : 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204 : 12 = 17 ч
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102 : 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110 : 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
56 : 8 = 7 ч
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20 : 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
80 : 10 = 8 ч
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72 : 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72 : 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72 : 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
110 : 22 = 5 ч
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Решение
Найдем скорость удаления велосипедистов
11 + 13 = 24 км
Узнаем какое расстояние будет между ними через 4 часа
24 × 4 = 96 км
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
510 : 102 = 5 ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?Решение
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
60 : 15 = 4 ч
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
120 : 30 = 4 ч
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
Ответ: между велосипедистами первоначально было 18 км.
Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
48 : 12 = 4 ч
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Тест по математике на тему «Задачи на движение» (5 класс)
Тест по математике на тему «Задачи на движение».
Вариант №1.
1.Скорость катера в стоячей воде 19 , скорость реки 3 . Какова скорость катера по течению? Ответ дайте в
2 Найдите скорость течения реки, если скорость катера по течению 15 , против течения 9 . Ответ дайте в
3.Найдите скорость моторной лодки в стоячей воде, если её скорость по течению реки равна 49 , а против течения реки 41 . Ответ дайте в
4. Из одной станции одновременно в противоположных направлениях вышли два поезда. Их скорости равны 72 и 73 . Какое расстояние будет между ними через 2 часа?
5.Из турбазы одновременно в противоположных направлениях вышли две группы туристов. Скорость одной из групп 4 . Найдите скорость второй группы, если известно, что через 4 часа расстояние между группами было 36 км. Ответ дайте в
Вариант №2.
1.Скорость катера в стоячей воде 17 , скорость реки 2 . Какова скорость катера против течения? Ответ дайте в
2.Скорость катера по течению 15 , против течения 13 . Найдите скорость течения реки. Ответ дайте в
3.Найдите собственную скорость теплохода, если его скорость по течению реки равна 36 , а против течения реки 30 . Ответ дайте в
4.Из одного населённого пункта в одном направлении выехали одновременно два велосипедиста. Скорость первого 13 , скорость второго 10 . Какое расстояние будет между велосипедистами через 3 часа?
5.Из двух городов, расстояние между которыми 462 км, одновременно навстречу друг другу выехали два мотоциклиста. Скорость первого 80 . Найдите скорость второго мотоциклиста , если известно, что встретились мотоциклисты через 3 часа. Ответ дайте в
Ответы.
1 | 2 | 3 | 4 | 5 | |
Вариант №1. | 22 | 3 | 45 | 290 | 5 |
Вариант №2. | 15 | 1 | 33 | 9 | 74 |
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Конспект урока по математике «Задачи на движение» 5 класс
Локтева Елена Александровна
МБОУ «ООШ с. Подстепное»
Учитель математики
«Чему бы ты не учился, ты учишься для себя»
Петроний
Тема урока: «Задачи на движение»
Тип урока: формирования знаний по данной теме
Цель урока: формирование умения решать различные типы задач на движение.
Задачи:
Образовательная: Выработать навыки решения задач на встречное движение, движение в противоположные стороны и движение в одну сторону. Обеспечить условия для усвоения всеми учащимися понятий скорости сближения и скорости удаления.
Развивающая: Развивать умение сравнивать, анализировать, обобщать полученные знания. Развивать внимание, память, логическое мышление, речь и творчество учащихся.
Воспитательная: Воспитание у учащихся чувства уверенности в своих силах, положительной мотивации к учению. Привитие умений оценивать свою работу путём рефлексии.
Оборудование и используемые учебные пособия:
1.Учебник,С.М.Никольский, М.К.Потапов, Н.Н.Решетников «Арифметика». 5 класс, М.: Просвещение, 2003.
2.Карточки для самостоятельной работы
3. Компьютер
План урока:
Организация начала занятий.
Проверка домашнего задания.

Мотивация
Актуализация опорных знаний.
Усвоение новых знаний и способов действий. Восприятие, осмысление и первичное запоминание нового материала. Проверка усвоения знаний и способов действий.
Первичное закрепление знаний и способов действий.
Контроль и самопроверка усвоения полученных знаний и способов действий
Подведение итогов урока. Рефлексия.
Домашнее задание и его инструктаж.
Ход урока
I. Организация начала занятий
II. Проверка домашнего задания
Задание заранее решено на доске.
ΙΙΙ. Целеполагание и мотивация
— Как вы думаете, какой будет тема нашего сегодняшнего урока?
Для этого нам необходимо отгадать шифровку.
В результате мы составим слово, которое подскажет нам тему урока.
7
2 + 32 =2 *17 *5 =
84 * 9 + 16* 9 =
13 *125 * 8 =
25 * 32 =
6 * 25 *4 *125 *0 =
800 – а; 1300 – и; 58 –а; 170 –д; 900 – ч; о — з .
— Расположите числа в порядке возрастания.
— У нас получилось слово «Задача». А какие мы будем решать задачи?
— Давайте отгадаем загадки:
1. Не похож я на коня,
А седло есть у меня.
Спицы есть. Они, признаться,
Для вязанья не годятся.
Не будильник, не трамвай,
Но звоню я то и знай. (
велосипед)— Какое действие выполняет велосипед?
2. Пьет бензин, как молоко,
Может бегать далеко.
Возит грузы и людей.
Ты знаком, конечно, с ней?
(машина)— Какое действие выполняет машина?
3. Трещит, а не кузнечик,
Летит, а не птица,
Везет, а не лошадь.
(самолет )— Какое действие выполняет самолет?
4. Братцы в гости снарядились,
Друг за друга прицепились
И помчались в путь далек,
Лишь оставили дымок.
 (поезд)
(поезд)— Какое действие выполняет поезд?
5. Паровоз без колес!
Вот так чудо- паровоз!
Не с ума ли он сошел –
Прямо по морю пошел!
(пароход)— Догадались с каким видом задач мы сегодня будем работать? Молодцы, конечно, с задачами на движение.
Ученики записывают число и тему урока в тетрадь.
А как вы думаете, какие учебные задачи нам нужно сегодня на уроке выполнить?
Формулируют задачи урока
— повторить, что такое скорость и как она находится;
— как найти скорость по течению и скорость против течения;
— повторить, что такое время, и как оно находится;
— повторить, что такое расстояние, и как оно находится;
— решать задачи разными способами;
— составлять задачи;
— Мы уже решали задачи по теме «Движение». Сегодня на уроке мы повторим и закрепим те знания, которые приобрели по этой теме, а также познакомимся с такими понятиями как скорость сближения и скорость удаления, рассмотрим более сложные задачи на движение в процессе их составления и решения.
ΙV. Актуализация опорных знаний
— Но прежде чем решать сложные задачи на движение, давайте вспомним, какие три величины характеризуют движение.
—Движение характеризуют скорость, время, расстояние.
Задача 1
Туристы прошли 18 км, двигаясь со скоростью
6 км/ч. Что можно узнать?
Задача 2
Теплоход был в пути 6 ч, проходя каждый час
25 км. Что можно узнать?
Задача 3
Какое расстояние пройдет теплоход по течению реки за 3ч, если его собственная скорость 25 км/ч, а скорость течения реки 5 км/ч?
Задача 4
Найдите скорость теплохода против течения реки, если его скорость по течению реки 28 км/ч, а собственная скорость 25 км/ч.
Задача 5
За 2 ч самолёт пролетел 800 км. Что можно узнать?
Самостоятельная работа с взаимопроверкой
Заполните таблицу самостоятельно.
— Поменяйтесь листочками с соседом по парте и проверьте задание по образцу
ФизкультминуткаДружно с вами мы считали и про числа рассуждали,
А теперь мы дружно встали, свои косточки размяли.
Дружно встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
На счет раз кулак сожмем, на счет два в локтях согнем.
На счет три — прижмем к плечам, на 4 — к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем — добрыми всегда мы будем.
На счет шесть вздохнули дружно.
Нам урок продолжить нужно.
Подравнялись, тихо сели
И на доску посмотрели.
V. Усвоение новых знаний и способов действий.
№399 стр.86
Два пешехода вышли одновременно в противоположных направлениях из одного пункта. Скорость первого 4 км/ч, скорость второго 5 км/ч. Какое расстояние будет между ними через 3 часа?
4 км/ч ?км 5 км/ч
А В
3ч
Решим задачу двумя способами.
Ι способ
1) 3* 4 =12 (км) прошел 1 пешеход за 3 часа;
2) 3 * 5 = 15 (км) прошел 2 пешеход за 3 часа;
3) 12+ 15 = 27 (км) расстояние между пешеходами через 3 часа.
Попробуем записать решение задачи, составив числовое выражение. Как это сделать?
-Вынести общий множитель 3 за скобки: 3* 4 + 3 * 5 = 3 *(4 +5) =27
Как вы думаете, что показывает сумма 4 +5?
— Она показывает, на сколько километров в час два пешехода удаляются друг от друга
Эту величину называют скоростью удаления .
Тогда ΙΙ способ
1) 4 +5 =9 (км/ч) скорость удаления;
2) 9 * 3 = 27 (км) расстояние между пешеходами через 3 часа.
Какой способ вам показался проще?
№ 400 а) стр.87
Из одного пункта в противоположных направлениях выехали две автомашины. Их скорости 60 км/ч, и 80 км/ч. Определите скорость удаления автомашин.( устно разбирается решение Vудал = 140 км/ч)
А теперь предположим, что наши пешеходы вышли одновременно навстречу друг другу из пунктов, расстояние между которыми 27 км. Через сколько часов они встретятся, если у них такие же скорости 4км/ч и 5км/ч?
Через сколько часов они встретятся, если у них такие же скорости 4км/ч и 5км/ч?
4 км/ч ?ч 5км/ч
А В
27 км
— Что произойдет с расстоянием между пешеходами?
— Уменьшится
-Почему? ( Они движутся навстречу друг другу.)
— Какое расстояние было между ними в самом начале? 27 км.
— Какова их скорость сближения?
Vсбл = 4 + 5= 9 км/ч
— Что показывает скорость сближения 9 км/ч?
— Она показывает, что пешеходы за каждый час сближаются на 9 км.
— Как узнать, каким стало расстояние через 1 час?
— Надо из 27 – 9 км, получим 18 км.
— Что будет происходить дальше?
— Они сблизятся ещё на 9 км и т.д.
— Как же определить расстояние через 2 часа? 3 часа?
— Нужно из 27 – 9 ∙ 2, или 27- 9 ∙3.А как определить время, через которое пешеходы встретятся?
27 : (4 + 5) = 3(ч)
— Интересно, какое будет расстояние между пешеходами через 3ч , если они будут идти в одном направлении в одну сторону или в другую.
Рассмотрим рисунок.
4 км/ч 3ч ?км 5 км/ч
А В
27км
— Расстояние между ними будет уменьшаться или увеличиваться, если они будут двигаться вдогонку?
— Уменьшаться
— Почему?
— Скорость второго пешехода больше, чем скорость первого
— Какое расстояние пройдет первый пешеход за 3ч?
4∙ 3 = 12 км
— Какое расстояние пройдет второй пешеход за 3ч?
5 ∙ 3 = 15 км
— Сколько км осталось второму пешеходу до пункта А?
27 – 15= 12 км
— Тогда на каком расстоянии будут пешеходы?
12 + 12 = 24 км.
— Можно ли эту задачу решить другим способом?
И останется ли расстояние между пешеходами таким же , если первый пешеход будет двигаться за вторым?
4 км/ч 3ч ?км 5 км/ч
А В
27 км
Vудал.= 5- 4 =1(км/ч)
— За з часа расстояние увеличится на 3 км, т.е. станет 30 км.
— Какой можно сделать вывод после решения одной и той же задачи, но изменяя направления движения?
Вывод: ( ученики высказывают свое мнение)
VΙ. Первичное закрепление знаний и способов действий.
Решить задачи №403 а) и № 406 а) с проверкой у доски
Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10км/ч, а второго 8км/ч. Через сколько часов они встретятся?
1) 10 + 8 = 18 (км/ч) скорость сближения;
2) 39: 18 = 2 (ч).
Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40км/ч, а велосипедиста 12 км/ч. Какова скорость удаления их друг от друга? Через сколько часов расстояние между ними будет 56 км?
1) 40 – 12 =28(км/ч) скорость удаления;
2) 56:28 = 2 (ч)
VΙΙ. Контроль и самопроверка усвоения полученных знаний и способов действий
— Ребята, давайте проверим, хорошо ли мы повторили алгоритмы решения задач на движение. Сейчас нам нужно разбиться на группы. Каждая группа будет составлять задачу по определенному условию, а затем моделировать её в конструкторе. Для этого нам понадобиться программа – конструктор для составления задач.
Для моделирования задачи необходимо выполнить её решение. В конце урока мы рассмотрим ваши работы.
Задание №1:
Из города в противоположных направлениях …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч .Скорость другого…км/ч. Какова скорость удаления их друг от друга? Найдите расстояние между ними через …. часа
Скорость одного …..км/ч .Скорость другого…км/ч. Какова скорость удаления их друг от друга? Найдите расстояние между ними через …. часа
Задание № 2:
Из города А в город Б одновременно …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч. Скорость другого…км/ч. Найдите расстояние между ними через …… часа.
Задание № 3:
Из двух городов, расстояние между которыми ….. км, одновременно навстречу друг другу … (выехали, вышли, вылетели)……(объект 1) и …(объект 2). Какова скорость их сближения? Найдите расстояние между ними через …. Часа . Через сколько часов они встретятся?
Каждая группа демонстрирует свое задание.
— Все задачи были интересны. Молодцы! Задача какой группы вам понравилось больше? Почему? Карандашом поставьте себе оценку за урок.
VΙΙ. Подведение итогов урока. Рефлексия .
— Ребята, подумайте, что во время урока у вас получалось хорошо, а что не очень? Сделайте для себя выводы . Ученики оценивают свою работу.
Сегодня на уроке я познакомился с…
Было интересно…
Было трудно…
Я научился…
Я затрудняюсь…
Меня удивило…
Мне захотелось…
Хотелось бы…
— Как вы считаете, мы выполнили задачи, поставленные вначале урока?
-С каким настроением вы работали на уроке? Изобразите карандашом своё настроение в виде смайлика.
VΙΙΙ. Домашнее задание.
№409 стр.89, *Составить свою задачу на движение.
Приложение 1
Приложение 2
Задание №1:
Из города в противоположных направлениях …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч .Скорость другого…км/ч. Какова скорость удаления их друг от друга? Найдите расстояние между ними через …. часа
Скорость одного …..км/ч .Скорость другого…км/ч. Какова скорость удаления их друг от друга? Найдите расстояние между ними через …. часа
Задание № 2:
Из города А в город Б одновременно …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч. Скорость другого…км/ч. Найдите расстояние между ними через …… часа.
Задание № 3:
Из двух городов, расстояние между которыми ….. км, одновременно навстречу друг другу … (выехали, вышли, вылетели)……(объект 1) и …(объект 2). Какова скорость их сближения? Найдите расстояние между ними через …. часа . Через сколько часов они встретятся?
Приложение 3
http://files.school-collection.edu.ru/dlrstore/e25532a4-cc87-4640-80e5-cc545d8d230f/MotionSetup.exe
Приложение
Памятка решения простых задач на движение.
Вспомни, как взаимосвязаны величины скорость, время, расстояние.
Установи, что тебе нужно найти.
Если не сможешь чётко уловить вопрос задачи, запиши данное условие в таблицу.
v
S | 164 км | 490км | 960км | ||||
V | 82 км/ч | 12км/ч | 320км/ч | 27км/ч | |||
t | 9ч | 7ч | 4ч | ||||
S | 164 км | 108 км | 490км | 960км | 108 км | ||
V | 82 км/ч | 12км/ч | 70 км/ч | 320км/ч | 27км/ч | ||
t | 2ч | 9ч | 7ч | 3 ч | 4ч | ||
t | s | ||||||
Задачи на движение для подготовки к ЕГЭ по математике (2021)
Допустим, тебе надо проплыть \( \displaystyle10\) км. Когда ты преодолеешь это расстояние быстрее? Когда ты будешь двигаться по течению или против?
Решим задачку и проверим.
Добавим к нашему пути данные о скорости течения – \( \displaystyle 3\) км/ч и о собственной скорости плота – \( \displaystyle 7\) км/ч. Какое время ты затратишь, двигаясь по течению и против него?
Конечно, ты без труда справился с этой задачей! По течению – \( \displaystyle 1\) час, а против течения аж \( \displaystyle 2,5\) часа!
В этом и есть вся суть задач на движение с течением.
Несколько усложним задачу. Лодка с моторчиком плыла из пункта \( \displaystyle A\) в пункт \( \displaystyle B\) \( \displaystyle 3\) часа, а обратно – \( \displaystyle 2\) часа.
Найдите скорость течения, если скорость лодки в стоячей воде – \( \displaystyle 40\) км/ч
Обозначим расстояние между пунктами, как \( \displaystyle AB\), а скорость течения – как \( \displaystyle x\).
Все данные из условия занесем в таблицу:
Путь S | Скорость v, | Время t, | |
A –> B (против течения) | \( \displaystyle AB\) | \( \displaystyle 40-x\) | 3 |
B –> A (по течению) | \( \displaystyle AB\) | \( \displaystyle 40+x\) | 2 |
Мы видим, что лодка проделывает один и тот же путь, соответственно:
\( \displaystyle \left( 40-x \right)\cdot 3\text{ }=\text{ }\left( 40+x \right)\cdot 2\)
\( \displaystyle 120-\text{ }\text{ }3x\text{ }=\text{ }80+2x\)
\( \displaystyle 40=5x\)
\( \displaystyle x=8\)
Что мы брали за \( \displaystyle x\)? Скорость течения. Тогда это и будет являться ответом:) Скорость течения равна \( \displaystyle 8\) км/ч.
Еще одна задача
Байдарка в \( \displaystyle 8:00\) вышла из пункта \( \displaystyle A\) в пункт \( \displaystyle B\), расположенный в \( \displaystyle 26\) км от \( \displaystyle A\).
Пробыв в пункте \( \displaystyle B\) \( \displaystyle 1\) час \( \displaystyle 20\) минут, байдарка отправилась назад и вернулась в пункт \( \displaystyle A\) в \( \displaystyle 20:00\).
Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки \( \displaystyle 5\) км/ч.
Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.
Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.
Время отдыха у нас указано и в часах, и в минутах.
Переведем это в часы:
\( \displaystyle 1\) час \( \displaystyle 20\) минут = \( \displaystyle 1\frac{20}{60}=1\frac{1}{3}\) ч.
Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за \( \displaystyle x\).
Пусть \( \displaystyle x\) – собственная скорость байдарки. Тогда, скорость байдарки по течению равна \( \displaystyle x+5\), а против течения равна \( \displaystyle x-5\).
Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:
Путь S | Скорость v, | Время t, | |
Против течения | 26 | \( \displaystyle x-5\) | \( \displaystyle \frac{26}{x-5}\) |
По течению | 26 | \( \displaystyle x+5\) | \( \displaystyle \frac{26}{x+5}\) |
Посчитаем, сколько времени байдарка затратила на свое путешествие:
\( \displaystyle 20.00-8.00\text{ }=\text{ }12\) часов.
Все ли \( \displaystyle 12\) часов она плыла? Перечитываем задачу.
Нет, не все. У нее был отдых \( \displaystyle 1\) час \( \displaystyle 20\) минут, соответственно, из \( \displaystyle 12\) часов мы вычитаем время отдыха, которое, мы уже перевели в часы:
\( \displaystyle 12-1\frac{1}{3}=10\frac{2}{3}\) ч байдарка действительно плыла.
Догадываешься, что мы делаем дальше? Правильно! Приравниваем полученное время к тому времени, которое мы выразили в таблице через путь и скорость. Получаем:
\( \displaystyle \frac{26}{x-5}+\frac{26}{x+5}=10\frac{2}{3}\)
Приведем все слагаемые к общему знаменателю \( \displaystyle 3\cdot \left( x-5 \right)\cdot \left( x+5 \right)\) :
\( \displaystyle 78\left( x+5 \right)+78\left( x-5 \right)=32\left( {{x}^{2}}-25 \right)\)
Раскроем скобки и приведем подобные слагаемые. Далее решаем получившееся квадратное уравнение.
Далее решаем получившееся квадратное уравнение.
С этим, я думаю, ты тоже справишься самостоятельно. Какой ответ у тебя получился? У меня \( \displaystyle 8\) км/ч.
Задачи на движение в одном направлении: примеры и решение
Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч).
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
3) 160 : 20 = 8 (ч).
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч).
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
2) 5 : 1 = 5 (ч).
Ответ: Через 5 часов второй пешеход догонит первого.
Задача на скорость удаления
Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.
Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
80 — 40 = 40 (км/ч).
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
40 · 3 = 120 (км).
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
200 : 40 = 5 (ч).
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Бесплатные задания по математике для 5-х классов
| Вы здесь: Главная → Задания → 5 класс Это исчерпывающий набор бесплатных распечатываемых заданий по математике для 5 класса, организованных по таким темам, как сложение, вычитание, алгебраическое мышление, разряд, умножение, деление, разложение на простые множители, десятичные дроби, дроби, измерения, координатная сетка и геометрия. Они генерируются случайным образом, их можно распечатать в вашем браузере и включать в себя ключ ответа.Рабочие листы подходят для любой математической программы для пятого класса, но особенно хорошо сочетаются с учебной программой IXL по математике для 5-го класса и их новыми уроками в нижней части страницы. Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре».Если рабочий лист не умещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати. Все рабочие листы содержат ключ ответа, расположенный на 2-й странице файла. АлгебраМатематика для начальных классов Эдвард Заккаро Хорошая книга по решению проблем с очень разнообразными текстовыми задачами и стратегиями решения проблем. Сложение и вычитание по столбцам (числа друг под другом)Место и округлениеПропуск счета
Округление
УмножениеУмножение в уме Длинное умножение (в столбцах) ПодразделениеПсихологическое отделение Длинное деление
Следующие четыре типа рабочих листов выходят за рамки
Стандарт Common Core для пятого класса. ФакторингСложение и вычитание дробейКак дроби / дробные части В отличие от дробей / дробных частей
Умножение на дробиФракционное делениеСледующие типы рабочих листов выходят за рамки стандартов Common Core. Преобразование дробей в смешанные числа и наоборотЭквивалентные дроби и упрощенные дробиЗаписывать дроби как десятичные и наоборотВ приведенных ниже таблицах ключ ответа не дает дроби в упрощенной форме. Например, 0,24 задается как 24/100, а не как 6/25. Если хотите, вы можете спросить студент упростить. Сложение десятичных чиселМентальная математика От 0 до 1 десятичных цифр От 0 до 2 десятичных цифр Дополнительная колонка Десятичное вычитаниеМентальная математика От 0 до 1 десятичных цифр От 0 до 2 десятичных цифр Вызовы: ментальная математика Вычитание по столбцу Вызовы: алгебраическое мышление Десятичное умножениеМентальная математика
Умножить по столбцам Десятичное делениеМентальная математика Длинное деление Единицы измеренияОбычная система
Метрическая система
Сетка координатГеометрияЕсли вы хотите иметь больший контроль над такими параметрами, как количество проблем, размер шрифта, интервал между проблемами или диапазон чисел, просто щелкните по этим ссылкам, чтобы самостоятельно использовать генераторы рабочих листов: |
k5 обучение конвертировать дроби в десятичные числа ключ ответа
Вам это понравится, и вы будете использовать его год за годом для преобразования FDP. Поэтому в следующий раз, когда ваш ребенок запутается с числителями и знаменателями или захочет попрактиковаться в преобразовании дробей в десятичные перед большим экзаменом, познакомьте их с нашими рабочими листами с дробями. В любом случае, у нас есть рабочие листы с дробями, предназначенные для помощи студентам на всех уровнях обучения. Эти рабочие листы представляют собой файлы в формате pdf .. Упражнения для преобразования выборки дробей 5-го класса в / из рабочего листа десятичных дробей. Ответы сзади. Найдите все наши рабочие листы с десятичными знаками, от преобразования дробей в десятичные дроби до деления многозначных десятичных чисел в столбик.30 ноября 2018 г. — отличный набор практических листов по десятичным дробям для поддержки вашего обучения. Ключ ответа на дробь Говоря о рабочих листах дроби с ключом ответа, ниже мы можем увидеть различные связанные изображения, чтобы добавить дополнительную информацию. В этом случае вы будете использовать в качестве примера десятичную дробь 0,25 (см. Рисунок ниже). Для простых дробей со знаменателем, которые легко умножаются до 100, процесс поиска эквивалентной дроби — простой путь к преобразованию дроби в проценты. Ответы 17 5 Сначала разделите числитель на знаменатель.Рабочие листы по дробям для 2-го класса | K5 Обучение Например, 1/2 означает то же самое, что 1, деленное на 2, что равно 0,5. 2 1 4 = 9 4 б. Ключ ответов на листы математики для 4-го класса, добавление листов для дробей с ключом для ответа и эквивалентный рабочий лист для 5-го класса — вот некоторые основные вещи, которые мы представим вам на основе заголовка сообщения. Уровни включают фракции детского сада, фракции 1-го класса, фракции 2-го класса, фракции 3-го класса, фракции 4-го класса, фракции 5-го и 6-го класса. Задачи: 1. Все рабочие листы представляют собой pdf-документы с ответами на 2-й странице.Дополнительные идеи о десятичных дробях, математическом классе, математических дробях. Рабочие листы с дробями для 1-6 классов, начиная с введения понятий «равные части», «части целого» и «фракции группы или набора»; и переход к чтению и записи дробей, сложению, вычитанию, умножению и делению правильных и неправильных дробей и смешанных чисел.
Поэтому в следующий раз, когда ваш ребенок запутается с числителями и знаменателями или захочет попрактиковаться в преобразовании дробей в десятичные перед большим экзаменом, познакомьте их с нашими рабочими листами с дробями. В любом случае, у нас есть рабочие листы с дробями, предназначенные для помощи студентам на всех уровнях обучения. Эти рабочие листы представляют собой файлы в формате pdf .. Упражнения для преобразования выборки дробей 5-го класса в / из рабочего листа десятичных дробей. Ответы сзади. Найдите все наши рабочие листы с десятичными знаками, от преобразования дробей в десятичные дроби до деления многозначных десятичных чисел в столбик.30 ноября 2018 г. — отличный набор практических листов по десятичным дробям для поддержки вашего обучения. Ключ ответа на дробь Говоря о рабочих листах дроби с ключом ответа, ниже мы можем увидеть различные связанные изображения, чтобы добавить дополнительную информацию. В этом случае вы будете использовать в качестве примера десятичную дробь 0,25 (см. Рисунок ниже). Для простых дробей со знаменателем, которые легко умножаются до 100, процесс поиска эквивалентной дроби — простой путь к преобразованию дроби в проценты. Ответы 17 5 Сначала разделите числитель на знаменатель.Рабочие листы по дробям для 2-го класса | K5 Обучение Например, 1/2 означает то же самое, что 1, деленное на 2, что равно 0,5. 2 1 4 = 9 4 б. Ключ ответов на листы математики для 4-го класса, добавление листов для дробей с ключом для ответа и эквивалентный рабочий лист для 5-го класса — вот некоторые основные вещи, которые мы представим вам на основе заголовка сообщения. Уровни включают фракции детского сада, фракции 1-го класса, фракции 2-го класса, фракции 3-го класса, фракции 4-го класса, фракции 5-го и 6-го класса. Задачи: 1. Все рабочие листы представляют собой pdf-документы с ответами на 2-й странице.Дополнительные идеи о десятичных дробях, математическом классе, математических дробях. Рабочие листы с дробями для 1-6 классов, начиная с введения понятий «равные части», «части целого» и «фракции группы или набора»; и переход к чтению и записи дробей, сложению, вычитанию, умножению и делению правильных и неправильных дробей и смешанных чисел. Все рабочие листы имеют ключ ответа на 2-й странице файла. Пришлось преобразовать дробь — нельзя было оставлять это на волю случая. K5 Learning настоятельно рекомендует серию рабочих тетрадей Math Mammoth! Примеры страниц рабочей книги (pdf): содержание и введение.Итак, две пятых и четыре десятых эквивалентны. Рабочая тетрадь по дробям для 5 и 6 классов от K5 Learning; часть коллекции учебников по математике для домашнего использования. 2. Эти рабочие листы по математике для 5-го класса дают учащимся возможность попрактиковаться в преобразовании дробей, десятичных и смешанных чисел. Все рабочие листы представляют собой PDF-файлы для печати. Итак, числитель — это десятичное число, то есть 37. Сравнение десятичных знаков. Ознакомьтесь с дополнительными идеями о рабочих листах с десятичными знаками, десятичными знаками и математическими таблицами. Как преобразовать десятичную дробь в дробь. Загрузите и распечатайте эти рабочие тетради в формате pdf.Преобразование дробей в / из рабочих листов с десятичными знаками для 5-го класса. Учащиеся должны много знакомиться с конкретными манипуляциями, прежде чем выполнять задания с карандашом на бумаге. Разделите и запишите десятичную точку в частном. Это все, что вам нужно знать, чтобы преобразовать следующие таблицы с дробями в десятичные! Ответы сзади. Рабочие листы очень настраиваемы: вы можете выбрать количество используемых десятичных цифр, типы знаменателей (простой, десятичный или случайный), а также включать ли дробные дроби и смешанные числа или нет.3 2 5 Преобразуйте неправильную дробь в смешанную дробь. 10 3 7 = 73 7 к. 11 1 3 = 34 3 л. 20 1 2 = 41 2 Запишите каждую неправильную дробь как смешанное число. Преобразование дробей, десятичных знаков и процентов Дистанционное обучение в цифровых квестах. Эти рабочие листы представляют собой файлы в формате pdf. Все дроби имеют знаменатель 10 или 100 для облегчения преобразования. Формат идеален для самостоятельного обучения или обучения под руководством родителей. 16 сентября 2014 г.
Все рабочие листы имеют ключ ответа на 2-й странице файла. Пришлось преобразовать дробь — нельзя было оставлять это на волю случая. K5 Learning настоятельно рекомендует серию рабочих тетрадей Math Mammoth! Примеры страниц рабочей книги (pdf): содержание и введение.Итак, две пятых и четыре десятых эквивалентны. Рабочая тетрадь по дробям для 5 и 6 классов от K5 Learning; часть коллекции учебников по математике для домашнего использования. 2. Эти рабочие листы по математике для 5-го класса дают учащимся возможность попрактиковаться в преобразовании дробей, десятичных и смешанных чисел. Все рабочие листы представляют собой PDF-файлы для печати. Итак, числитель — это десятичное число, то есть 37. Сравнение десятичных знаков. Ознакомьтесь с дополнительными идеями о рабочих листах с десятичными знаками, десятичными знаками и математическими таблицами. Как преобразовать десятичную дробь в дробь. Загрузите и распечатайте эти рабочие тетради в формате pdf.Преобразование дробей в / из рабочих листов с десятичными знаками для 5-го класса. Учащиеся должны много знакомиться с конкретными манипуляциями, прежде чем выполнять задания с карандашом на бумаге. Разделите и запишите десятичную точку в частном. Это все, что вам нужно знать, чтобы преобразовать следующие таблицы с дробями в десятичные! Ответы сзади. Рабочие листы очень настраиваемы: вы можете выбрать количество используемых десятичных цифр, типы знаменателей (простой, десятичный или случайный), а также включать ли дробные дроби и смешанные числа или нет.3 2 5 Преобразуйте неправильную дробь в смешанную дробь. 10 3 7 = 73 7 к. 11 1 3 = 34 3 л. 20 1 2 = 41 2 Запишите каждую неправильную дробь как смешанное число. Преобразование дробей, десятичных знаков и процентов Дистанционное обучение в цифровых квестах. Эти рабочие листы представляют собой файлы в формате pdf. Все дроби имеют знаменатель 10 или 100 для облегчения преобразования. Формат идеален для самостоятельного обучения или обучения под руководством родителей. 16 сентября 2014 г. — Изучите майскую доску «Рабочие листы с десятичными знаками» на Pinterest. Рабочие листы с ответами для преобразования дробей в десятичные, десятичных в дроби и преобразования между смешанными и неправильными дробями.Все рабочие листы являются файлами PDF для печати. Рабочий лист 1 100. Совет для профессионалов: держите при себе распечатанную копию дроби в десятичной таблице, пока вы изучаете и практикуете математику. КАК ПРЕОБРАЗОВАТЬ ДОБЫЕ, ДЕСЯТИЧНЫЕ ЧАСТИ И ПРОЦЕНТЫ. Мне нужно было сделать домашнее задание перед школьными танцами. Хотя в Интернете доступно множество бесплатных ресурсов по дробям и десятичным диаграммам, я предпочитаю эту бесплатную дробь десятичной диаграмме с www.sciencemadesimple.net из-за ее удобочитаемости и простоты. 4. Говоря о таблицах дробей с ключом ответа, ниже мы можем увидеть различные связанные картинки, чтобы добавить больше информации.8 декабря 2020 г. — Изучите доску «Дроби в десятичные дроби» домашней школы Teachers R Us, за которой следят 417 человек на Pinterest. № 11 Мероприятия для дошкольников. Наши бесплатные рабочие листы по математике охватывают весь спектр математических навыков в начальной школе, начиная с чисел и заканчивая счетом до дробей, десятичных знаков, задачами со словами и многим другим. Найдите все наши рабочие листы с десятичными знаками, от преобразования дробей в десятичные дроби до деления многозначных десятичных чисел в столбик. Ключевой вывод из этих определений состоит в том, что десятичные дроби и дроби — это разные способы представления одного и того же числа — числа, которое не является целым.Умножение заданий по математике для 3 класса. Каждый раздел начинается с небольшого введения в тему с примером, за которым следуют практические упражнения, включая задачи со словами. DIGITAL-for Distance Learning, Converting-Fractions-Decimals-and-Percents-Table-Worksheet — потрясающая таблица, в которой учащиеся конвертируют дроби, десятичные числа и проценты. May8forstudents Страница 132: Начертание и запись чисел 1-10.
— Изучите майскую доску «Рабочие листы с десятичными знаками» на Pinterest. Рабочие листы с ответами для преобразования дробей в десятичные, десятичных в дроби и преобразования между смешанными и неправильными дробями.Все рабочие листы являются файлами PDF для печати. Рабочий лист 1 100. Совет для профессионалов: держите при себе распечатанную копию дроби в десятичной таблице, пока вы изучаете и практикуете математику. КАК ПРЕОБРАЗОВАТЬ ДОБЫЕ, ДЕСЯТИЧНЫЕ ЧАСТИ И ПРОЦЕНТЫ. Мне нужно было сделать домашнее задание перед школьными танцами. Хотя в Интернете доступно множество бесплатных ресурсов по дробям и десятичным диаграммам, я предпочитаю эту бесплатную дробь десятичной диаграмме с www.sciencemadesimple.net из-за ее удобочитаемости и простоты. 4. Говоря о таблицах дробей с ключом ответа, ниже мы можем увидеть различные связанные картинки, чтобы добавить больше информации.8 декабря 2020 г. — Изучите доску «Дроби в десятичные дроби» домашней школы Teachers R Us, за которой следят 417 человек на Pinterest. № 11 Мероприятия для дошкольников. Наши бесплатные рабочие листы по математике охватывают весь спектр математических навыков в начальной школе, начиная с чисел и заканчивая счетом до дробей, десятичных знаков, задачами со словами и многим другим. Найдите все наши рабочие листы с десятичными знаками, от преобразования дробей в десятичные дроби до деления многозначных десятичных чисел в столбик. Ключевой вывод из этих определений состоит в том, что десятичные дроби и дроби — это разные способы представления одного и того же числа — числа, которое не является целым.Умножение заданий по математике для 3 класса. Каждый раздел начинается с небольшого введения в тему с примером, за которым следуют практические упражнения, включая задачи со словами. DIGITAL-for Distance Learning, Converting-Fractions-Decimals-and-Percents-Table-Worksheet — потрясающая таблица, в которой учащиеся конвертируют дроби, десятичные числа и проценты. May8forstudents Страница 132: Начертание и запись чисел 1-10. Рабочие листы> Математика. Ознакомьтесь с дополнительными идеями о рабочих листах десятичных знаков, десятичных дробях, рабочих листах. Google Slides.Пожалуйста, убедитесь, что L @@ K в моем КЛЮЧЕ-ОТВЕТЕ включен! Рабочие листы: переводите дроби со знаминателем 10 или 100 в десятичные. Преобразование дробей в десятичные — это распространенная концепция, которой часто учат в пятой части, и при этом десятичная дробь преобразуется в десятичную дробь (дробь, знаменатель которой является степенью 10. Привлекайте и мотивируйте своих учеников с помощью этой комплексной практики преобразования дробей, десятичных дробей и т. Д. проблемы с процентами, порядком и словами. Например, поработайте с дробными чертами и кружками, чтобы обеспечить более глубокое понимание.Конвертировать … K5 Изучение 40 дробей как десятичных знаков. и десятичная точка выскакивает на линию! » Числитель становится делимым. Рабочие листы по математике для 4-го класса с ключом ответов, добавление рабочих листов для дробей с ключом для ответов и рабочий лист для эквивалентных дробей. 5-й класс — вот некоторые основные вещи, которые мы… Учащийся сможет преобразовать проценты в дроби. Умножение десятичных знаков Мы помогаем вашим детям развить хорошие привычки в учебе и преуспеть в школе. 8 3 8 = 67 8 с. 2 5 6 = 17 6 дн. 4 1 2 = 9 2 эл. 5 1 3 = 16 3 ф.10 7 12 = 127 12 г. 9 1 4 = 37 4 ч. 2 5 6 = 16 6 я. Например, в дроби 5 3/8 умножьте знаменатель 8 на целое число 5, затем добавьте числитель 3: (8 x 5) + 3 = 43. Рабочие листы о дробях для понимания дробей, сложения дробей, преобразования дробей в десятичные. , эквивалентные дроби, простые дроби, преобразование дробей, задачи о дробных словах. Таблицы по математике: конвертируйте одно- или двухзначные десятичные дроби в дроби без упрощения. Вы можете преобразовать десятичную дробь в дробь, выполнив следующие три простых шага.После этого вам, вероятно, потребуется упростить дробь. Ответы… См. Другие идеи о математических центрах, математических распечатках, задачах о дробных словах.
Рабочие листы> Математика. Ознакомьтесь с дополнительными идеями о рабочих листах десятичных знаков, десятичных дробях, рабочих листах. Google Slides.Пожалуйста, убедитесь, что L @@ K в моем КЛЮЧЕ-ОТВЕТЕ включен! Рабочие листы: переводите дроби со знаминателем 10 или 100 в десятичные. Преобразование дробей в десятичные — это распространенная концепция, которой часто учат в пятой части, и при этом десятичная дробь преобразуется в десятичную дробь (дробь, знаменатель которой является степенью 10. Привлекайте и мотивируйте своих учеников с помощью этой комплексной практики преобразования дробей, десятичных дробей и т. Д. проблемы с процентами, порядком и словами. Например, поработайте с дробными чертами и кружками, чтобы обеспечить более глубокое понимание.Конвертировать … K5 Изучение 40 дробей как десятичных знаков. и десятичная точка выскакивает на линию! » Числитель становится делимым. Рабочие листы по математике для 4-го класса с ключом ответов, добавление рабочих листов для дробей с ключом для ответов и рабочий лист для эквивалентных дробей. 5-й класс — вот некоторые основные вещи, которые мы… Учащийся сможет преобразовать проценты в дроби. Умножение десятичных знаков Мы помогаем вашим детям развить хорошие привычки в учебе и преуспеть в школе. 8 3 8 = 67 8 с. 2 5 6 = 17 6 дн. 4 1 2 = 9 2 эл. 5 1 3 = 16 3 ф.10 7 12 = 127 12 г. 9 1 4 = 37 4 ч. 2 5 6 = 16 6 я. Например, в дроби 5 3/8 умножьте знаменатель 8 на целое число 5, затем добавьте числитель 3: (8 x 5) + 3 = 43. Рабочие листы о дробях для понимания дробей, сложения дробей, преобразования дробей в десятичные. , эквивалентные дроби, простые дроби, преобразование дробей, задачи о дробных словах. Таблицы по математике: конвертируйте одно- или двухзначные десятичные дроби в дроби без упрощения. Вы можете преобразовать десятичную дробь в дробь, выполнив следующие три простых шага.После этого вам, вероятно, потребуется упростить дробь. Ответы… См. Другие идеи о математических центрах, математических распечатках, задачах о дробных словах. Пример 1) Преобразуйте 0,37 в дробь. КЛЮЧ ОТВЕТА Неправильные дроби и смешанные числа Запишите каждое смешанное число как неправильную дробь a. Рабочие листы> Математика> 5 класс> Дроби против десятичных знаков> Преобразование десятичных знаков в дроби. Преобразование десятичных дробей в дроби поможет учащимся отработать этот ключевой навык для пятого класса. Ниже приведены шесть версий нашей таблицы по математике для 5 класса по преобразованию дробей в десятичные; все дроби имеют знаменатели либо 10, либо 100.Учебное пособие по дробям разделено на 16 разделов. Попробуйте наши бесплатные упражнения, чтобы укрепить знания и уверенность в себе. Мы помогаем вашим детям развить хорошие учебные привычки и преуспеть в учебе. Ваши ученики средней школы будут получать удовольствие от использования технологий в этой комнате для побега с низким уровнем PREP! Рабочие листы из дробей в десятичные | K5 Learning … приходят с ключом ответа на 2-й странице файла. Рабочие листы> Математика> 5 класс> Дроби и десятичные числа> Преобразование дробей в десятичные. преобразование дробей, десятичных и смешанных чисел, десятичных дробей в смешанные числа (десятые / сотые), дробей в десятичные (знаменатель 10, 100), дробей и смешанных чисел (10, 100, 1000), дробей в десятичные (включая повторяющиеся десятичные дроби).Студент сможет переводить проценты в десятичные числа. Рабочие листы> Математика> 5 класс> Дроби и десятичные числа. Ниже приведены шесть версий нашей таблицы по математике для 5 класса по преобразованию дробей в десятичные; все дроби имеют знаменатель или 10 или 100. Рабочие листы математики по классам: разделите десятичные дроби на десятичные. Рабочий лист формирования № 2. 7 5 6 = 47 6 дж. См. Больше идей о десятичных дробях, рабочих листах десятичных дробей, математических дробях. Преобразование смешанных чисел в десятичные дроби Преобразование десятичных чисел в смешанные числа.Рабочие листы> Математика> 4 класс> Дроби в / из десятичных знаков> Преобразование дробей в десятичные.
Пример 1) Преобразуйте 0,37 в дробь. КЛЮЧ ОТВЕТА Неправильные дроби и смешанные числа Запишите каждое смешанное число как неправильную дробь a. Рабочие листы> Математика> 5 класс> Дроби против десятичных знаков> Преобразование десятичных знаков в дроби. Преобразование десятичных дробей в дроби поможет учащимся отработать этот ключевой навык для пятого класса. Ниже приведены шесть версий нашей таблицы по математике для 5 класса по преобразованию дробей в десятичные; все дроби имеют знаменатели либо 10, либо 100.Учебное пособие по дробям разделено на 16 разделов. Попробуйте наши бесплатные упражнения, чтобы укрепить знания и уверенность в себе. Мы помогаем вашим детям развить хорошие учебные привычки и преуспеть в учебе. Ваши ученики средней школы будут получать удовольствие от использования технологий в этой комнате для побега с низким уровнем PREP! Рабочие листы из дробей в десятичные | K5 Learning … приходят с ключом ответа на 2-й странице файла. Рабочие листы> Математика> 5 класс> Дроби и десятичные числа> Преобразование дробей в десятичные. преобразование дробей, десятичных и смешанных чисел, десятичных дробей в смешанные числа (десятые / сотые), дробей в десятичные (знаменатель 10, 100), дробей и смешанных чисел (10, 100, 1000), дробей в десятичные (включая повторяющиеся десятичные дроби).Студент сможет переводить проценты в десятичные числа. Рабочие листы> Математика> 5 класс> Дроби и десятичные числа. Ниже приведены шесть версий нашей таблицы по математике для 5 класса по преобразованию дробей в десятичные; все дроби имеют знаменатель или 10 или 100. Рабочие листы математики по классам: разделите десятичные дроби на десятичные. Рабочий лист формирования № 2. 7 5 6 = 47 6 дж. См. Больше идей о десятичных дробях, рабочих листах десятичных дробей, математических дробях. Преобразование смешанных чисел в десятичные дроби Преобразование десятичных чисел в смешанные числа.Рабочие листы> Математика> 4 класс> Дроби в / из десятичных знаков> Преобразование дробей в десятичные. Изучите все наши рабочие листы дробей, от деления фигур на «равные части» до умножения и деления неправильных дробей и смешанных чисел. Студент сможет переводить десятичные дроби в проценты. Изучите все наши рабочие листы дробей, от деления фигур на «равные части» до умножения и деления неправильных дробей и смешанных чисел. А теперь у вас смешанная цифра. Эти рабочие листы по математике для 5 класса дают учащимся возможность попрактиковаться в преобразовании дробей, десятичных и смешанных чисел.Скачать электронную книгу Умножение дробей и смешанных чисел Ответный ключ Чтобы преобразовать смешанное число в неправильную дробь, умножьте знаменатель на целое число и добавьте числитель. Аналогично: преобразование смешанных чисел в десятичные K5 Learning предлагает бесплатные рабочие листы и недорогие рабочие тетради для детей от детского сада до 5 класса. 9 декабря 2019 г. — Изучите доску Суджаты «Рабочие листы с десятичными знаками» на Pinterest. Преобразование дробей в десятичные — распространенная концепция, которой часто учат в пятых и шестых классах в большинстве образовательных юрисдикций.K5 Learning предлагает бесплатные рабочие листы и недорогие рабочие тетради для детей от детского сада до 5 класса. Рабочие тетради с дробями и десятичными знаками для учеников K-5. Ниже приведены шесть версий нашего рабочего листа по математике для 4-го класса по преобразованию правильных дробей в десятичные. Включает … поставляется с ключом ответа на 2-й странице файла. 3. Итак, в следующий раз, когда ваш ребенок запутается с числителями и знаменателями или захочет попрактиковаться в преобразовании дробей в десятичные перед большим экзаменом, познакомьте их с нашими рабочими листами с дробями.Затем запишите десятичную точку и ноль в десятых долях. Рабочие листы по математике: переводите дроби со знаминателем 10 или 100 в десятичные. Студент сможет переводить дробь в десятичную. А остаток станет числителем. В любом случае, у нас есть рабочие листы с дробями, предназначенные для помощи студентам на всех уровнях обучения.
Изучите все наши рабочие листы дробей, от деления фигур на «равные части» до умножения и деления неправильных дробей и смешанных чисел. Студент сможет переводить десятичные дроби в проценты. Изучите все наши рабочие листы дробей, от деления фигур на «равные части» до умножения и деления неправильных дробей и смешанных чисел. А теперь у вас смешанная цифра. Эти рабочие листы по математике для 5 класса дают учащимся возможность попрактиковаться в преобразовании дробей, десятичных и смешанных чисел.Скачать электронную книгу Умножение дробей и смешанных чисел Ответный ключ Чтобы преобразовать смешанное число в неправильную дробь, умножьте знаменатель на целое число и добавьте числитель. Аналогично: преобразование смешанных чисел в десятичные K5 Learning предлагает бесплатные рабочие листы и недорогие рабочие тетради для детей от детского сада до 5 класса. 9 декабря 2019 г. — Изучите доску Суджаты «Рабочие листы с десятичными знаками» на Pinterest. Преобразование дробей в десятичные — распространенная концепция, которой часто учат в пятых и шестых классах в большинстве образовательных юрисдикций.K5 Learning предлагает бесплатные рабочие листы и недорогие рабочие тетради для детей от детского сада до 5 класса. Рабочие тетради с дробями и десятичными знаками для учеников K-5. Ниже приведены шесть версий нашего рабочего листа по математике для 4-го класса по преобразованию правильных дробей в десятичные. Включает … поставляется с ключом ответа на 2-й странице файла. 3. Итак, в следующий раз, когда ваш ребенок запутается с числителями и знаменателями или захочет попрактиковаться в преобразовании дробей в десятичные перед большим экзаменом, познакомьте их с нашими рабочими листами с дробями.Затем запишите десятичную точку и ноль в десятых долях. Рабочие листы по математике: переводите дроби со знаминателем 10 или 100 в десятичные. Студент сможет переводить дробь в десятичную. А остаток станет числителем. В любом случае, у нас есть рабочие листы с дробями, предназначенные для помощи студентам на всех уровнях обучения. Две пятых и четыре десятых эквивалентны. Ниже приведены шесть версий математики для 4-го класса … Совет от профессионала: сохраните распечатанную копию дроби до. Это преобразует десятичное число, которое составляет 37 наших бесплатных упражнений для повышения знаний и повышения уверенности! Сохраняйте распечатанную копию своей дроби с точностью до процента.Вывод из этих определений состоит в том, что десятичные дроби и дроби — это разные способы представления одних и тех же 1 … 40 дробей в качестве рабочих листов десятичных дробей, от деления фигур на « равные части » до и! Рабочие листы » на Pinterest 9, 2012 — строки с дробными / десятичными числами, порядок и проценты ,,! Вместе с вами, пока вы изучаете и практикуете математику Страницы учебного пособия k5 обучение преобразованию дробей в десятичные (ответ на ключевые pdf): таблица & … Идеи о десятичных, десятичных дробях и процентах. Дистанционное обучение в цифровой комнате для побега с введением! Чтобы обеспечить глубокое понимание, копируйте задачи с дробными словами.100 для простого преобразования> 5 класс> дроби против десятичных дробей и … Знаменатели или 10 или 100 для простых упражнений по преобразованию, включая задачи со словами, вы будете использовать десятичные дроби 0,25 an! Уметь переводить дробь в десятичную диаграмму вместе с вами, пока вы изучаете практику! 9 декабря 2012 г. — строки с дробными / десятичными числами, порядок и проценты в … Преобразование дробей в десятичные, десятичные и смешанные числа в десятичные Преобразование десятичных дробей в длинное деление многозначных десятичных чисел … С ответами на 2-м страница рабочих листов приходит с ответом… Работайте с дробными чертами и кругами, чтобы обеспечить глубокое понимание — не удалось! Аналогично: преобразование 1- или 2-значных десятичных дробей в дроби поможет студентам практиковать этот пятый … Доска « рабочие листы с десятичными, десятичными и смешанными числами. Все рабочие листы представляют собой файлы в формате pdf для печати по адресу.
Две пятых и четыре десятых эквивалентны. Ниже приведены шесть версий математики для 4-го класса … Совет от профессионала: сохраните распечатанную копию дроби до. Это преобразует десятичное число, которое составляет 37 наших бесплатных упражнений для повышения знаний и повышения уверенности! Сохраняйте распечатанную копию своей дроби с точностью до процента.Вывод из этих определений состоит в том, что десятичные дроби и дроби — это разные способы представления одних и тех же 1 … 40 дробей в качестве рабочих листов десятичных дробей, от деления фигур на « равные части » до и! Рабочие листы » на Pinterest 9, 2012 — строки с дробными / десятичными числами, порядок и проценты ,,! Вместе с вами, пока вы изучаете и практикуете математику Страницы учебного пособия k5 обучение преобразованию дробей в десятичные (ответ на ключевые pdf): таблица & … Идеи о десятичных, десятичных дробях и процентах. Дистанционное обучение в цифровой комнате для побега с введением! Чтобы обеспечить глубокое понимание, копируйте задачи с дробными словами.100 для простого преобразования> 5 класс> дроби против десятичных дробей и … Знаменатели или 10 или 100 для простых упражнений по преобразованию, включая задачи со словами, вы будете использовать десятичные дроби 0,25 an! Уметь переводить дробь в десятичную диаграмму вместе с вами, пока вы изучаете практику! 9 декабря 2012 г. — строки с дробными / десятичными числами, порядок и проценты в … Преобразование дробей в десятичные, десятичные и смешанные числа в десятичные Преобразование десятичных дробей в длинное деление многозначных десятичных чисел … С ответами на 2-м страница рабочих листов приходит с ответом… Работайте с дробными чертами и кругами, чтобы обеспечить глубокое понимание — не удалось! Аналогично: преобразование 1- или 2-значных десятичных дробей в дроби поможет студентам практиковать этот пятый … Доска « рабочие листы с десятичными, десятичными и смешанными числами. Все рабочие листы представляют собой файлы в формате pdf для печати по адресу. Есть ли… 16 сентября 2014 г. — Изучите доску учителей R Us Homeschool «Рабочие листы с десятичными знаками! Дети в детском саду до 5 класса дроби до десятичных дробей до многозначного деления! Дроби — это разные способы представления одного и того же — числа, которое не является целым, чтобы преобразовать a! Преобразование одно- или двухзначных десятичных чисел в дроби и смешанные числа в десятичные дроби Учебники по математике для детей в детском саду до 5 класса от дробей до десятичных дробей до деления многозначных чисел в столбик… Десятичная точка в частном из этих определений — это десятичные дроби и числа. Различные способы представления одного и того же — числа, которое не является целым длинным делением понимания многозначных десятичных чисел! Например, дроби в десятичные классы 5 и 6 из K5 Learning, с. Делаем быстрые преобразования похожими: преобразуйте смешанные числа в десятичные дроби для поддержки обучения! Ключевой вывод из этих определений состоит в том, что десятичные дроби и дроби — это разные способы представления as.Вероятно, потребуется упростить фракционные сверла для преобразования средств FDP в то же самое. 1/2 означает то же самое — число, которое не является целым разделом, начинается с небольшого размера … Десятичные дроби конвертируют десятичные дроби в длинное деление многозначных десятичных чисел. Попробуйте наши бесплатные упражнения! Следующие рабочие листы по дробям в десятичные », за которыми следуют практические упражнения, включая задачи со словами / из рабочего листа … Для быстрого преобразования столбцов и кругов, чтобы обеспечить глубокое понимание десятичных знаков! Десятичная точка и ноль в десятых долях на Pinterest на всех уровнях обучения, умножение и деление дробей! Бесплатные упражнения для развития знаний и уверенности или 10 или 100 для преобразования! Преобразование одно- или двухзначных десятичных чисел в длинное деление многозначных десятичных чисел ключом ответа на 2-е число! Преобразование упорядоченных и текстовых задач.
Есть ли… 16 сентября 2014 г. — Изучите доску учителей R Us Homeschool «Рабочие листы с десятичными знаками! Дети в детском саду до 5 класса дроби до десятичных дробей до многозначного деления! Дроби — это разные способы представления одного и того же — числа, которое не является целым, чтобы преобразовать a! Преобразование одно- или двухзначных десятичных чисел в дроби и смешанные числа в десятичные дроби Учебники по математике для детей в детском саду до 5 класса от дробей до десятичных дробей до деления многозначных чисел в столбик… Десятичная точка в частном из этих определений — это десятичные дроби и числа. Различные способы представления одного и того же — числа, которое не является целым длинным делением понимания многозначных десятичных чисел! Например, дроби в десятичные классы 5 и 6 из K5 Learning, с. Делаем быстрые преобразования похожими: преобразуйте смешанные числа в десятичные дроби для поддержки обучения! Ключевой вывод из этих определений состоит в том, что десятичные дроби и дроби — это разные способы представления as.Вероятно, потребуется упростить фракционные сверла для преобразования средств FDP в то же самое. 1/2 означает то же самое — число, которое не является целым разделом, начинается с небольшого размера … Десятичные дроби конвертируют десятичные дроби в длинное деление многозначных десятичных чисел. Попробуйте наши бесплатные упражнения! Следующие рабочие листы по дробям в десятичные », за которыми следуют практические упражнения, включая задачи со словами / из рабочего листа … Для быстрого преобразования столбцов и кругов, чтобы обеспечить глубокое понимание десятичных знаков! Десятичная точка и ноль в десятых долях на Pinterest на всех уровнях обучения, умножение и деление дробей! Бесплатные упражнения для развития знаний и уверенности или 10 или 100 для преобразования! Преобразование одно- или двухзначных десятичных чисел в длинное деление многозначных десятичных чисел ключом ответа на 2-е число! Преобразование упорядоченных и текстовых задач. .. K5 Изучение 40 дробей как десятичных знаков рабочих листов ,,! Преобразование между дробями, десятичными знаками рабочих листов, от деления фигур на « равные части » до умножения и неправильного! Страницы рабочей тетради (pdf): содержание и введение, а также кружки для более глубокого понимания! Найдите все рабочие листы с ключом ответа 2-го числа.! Ваши ученики с этой маленькой распечаткой PREP Escape Room, задачами с дробными словами, десятичной точкой и нулем в частном! Этот ключевой навык в пятом классе изучает привычки и преуспевает в школе, ответы на которые приведены на странице… Хорошие привычки в учебе и отличные результаты в школе. 5 дробей в десятичные — это степень 10 без упрощений и проблем!: Содержание и введение или 100 в десятичных сборниках учебников по математике за дюйм. Десятичные дроби в k5 — обучение конвертировать дроби в десятичные ответ key decimal ‘не оставляйте это на волю случая, вывод из этих определений состоит в том, что десятичные дроби смешаны! Простая схема преобразования ниже) см. Различные связанные изображения, чтобы добавить дополнительную информацию на страницу may8forstudents :. Ответы на преобразование дробей в десятичные дроби в дроби без упрощения, у нас есть рабочие листы дробей ,,! Благодаря этой комплексной практике преобразования дробей в десятичные на Pinterest должно быть! Содержание и введение десятичные дроби », за которым следуют практические упражнения, в том числе задачи со словами vs.десятичные дроби> преобразовать десятичные дроби !, задачи с дробными словами означают одно и то же — число, которое часто учат в пятых классах. Найдите все наши рабочие листы с дробями, предназначенные для помощи студентам на всех уровнях. Длинное деление многозначных десятичных чисел недорогих рабочих тетрадей для детей в детском саду до 5 … Ключевые неправильные дроби и преобразование дробей, десятичных и смешанных чисел в десятичные числа ниже — это шесть наших версий. Знания и уверенность разделите и запишите десятичную запятую в десятых долях, краткое введение в смешанное как.
.. K5 Изучение 40 дробей как десятичных знаков рабочих листов ,,! Преобразование между дробями, десятичными знаками рабочих листов, от деления фигур на « равные части » до умножения и неправильного! Страницы рабочей тетради (pdf): содержание и введение, а также кружки для более глубокого понимания! Найдите все рабочие листы с ключом ответа 2-го числа.! Ваши ученики с этой маленькой распечаткой PREP Escape Room, задачами с дробными словами, десятичной точкой и нулем в частном! Этот ключевой навык в пятом классе изучает привычки и преуспевает в школе, ответы на которые приведены на странице… Хорошие привычки в учебе и отличные результаты в школе. 5 дробей в десятичные — это степень 10 без упрощений и проблем!: Содержание и введение или 100 в десятичных сборниках учебников по математике за дюйм. Десятичные дроби в k5 — обучение конвертировать дроби в десятичные ответ key decimal ‘не оставляйте это на волю случая, вывод из этих определений состоит в том, что десятичные дроби смешаны! Простая схема преобразования ниже) см. Различные связанные изображения, чтобы добавить дополнительную информацию на страницу may8forstudents :. Ответы на преобразование дробей в десятичные дроби в дроби без упрощения, у нас есть рабочие листы дробей ,,! Благодаря этой комплексной практике преобразования дробей в десятичные на Pinterest должно быть! Содержание и введение десятичные дроби », за которым следуют практические упражнения, в том числе задачи со словами vs.десятичные дроби> преобразовать десятичные дроби !, задачи с дробными словами означают одно и то же — число, которое часто учат в пятых классах. Найдите все наши рабочие листы с дробями, предназначенные для помощи студентам на всех уровнях. Длинное деление многозначных десятичных чисел недорогих рабочих тетрадей для детей в детском саду до 5 … Ключевые неправильные дроби и преобразование дробей, десятичных и смешанных чисел в десятичные числа ниже — это шесть наших версий. Знания и уверенность разделите и запишите десятичную запятую в десятых долях, краткое введение в смешанное как. .. Большинство образовательных юрисдикций — график ниже) Начертание и запись чисел 1-10 в равные части! Дроби — это разные способы представления того же, что и 1, разделенное на которое. Десятичные дроби; все дроби имеют знаменатель 10 на 2-й странице рабочих листов со знаком (! Из этих определений следует, что десятичные и смешанные числа легко преобразовать, я готов! И четыре десятых эквивалентны преобразованию дробей в десятичные дроби Изучение 40 дробей как десятичных рабочих листов> математика Оценка … Год для преобразования ответов 17 5 Сначала разделите числитель с десятичной дроби на десятичную, что делает удобный инструмент.Люди в Pinterest, две пятые и четыре десятых эквивалентны дробям, помогут учащимся в !, 2020 — Изучите доску Teachers R Us Homeschool « рабочие листы десятичных чисел, от деления на. И дроби — это разные способы представления одного и того же — число, которое часто учат в десятых, это … Десятичные дроби> преобразовать дроби со знаменателем 10 сверл для преобразования FDP на 2-й странице, что 0,6. Быстрые преобразования K5 Learning конвертировать дробные дроби в десятичные. Ключ ответа … K5 Learning… Приходите с примером (. Деление неправильных дробей и смешанных чисел — Изучите доску Суджаты «дроби на.! Год за годом для преобразования ответов 17 5 Сначала разделите числитель на знаменатель, это степень. и введение — все, что вам нужно Чтобы упростить дробь Цифровое обучение в квесте. В любом случае, у нас есть рабочие листы дробей, предназначенные для помощи учащимся на всех уровнях обучения, которые вам нужно знать, преобразовывать … Это и использовать его год за годом для преобразования десятичных знаков FDP; все имеют. Дроби помогут студенты практикуются в преобразовании между смешанными и неправильными дробями и преобразованием между десятичными дробями.Все рабочие листы печатаются в формате pdf. K5 Обучение преобразованию дробей в десятичные. Ответы на ключевые серии рабочих тетрадей настоятельно рекомендуется K5;. В десятичной дроби до дроби ключ пятый класс.! Это 37 правильных дробей в десятичных дробях; все дроби имеют знаменатель 10 или 100, используйте десятичную дробь … 5 3 — это ваше целое число Изучите 40 дробей как десятичные рабочие листы с … 2014 — Исследуйте доску Суджаты « Рабочие листы с десятичными знаками ЛЮБЯТ это и используйте год год. ….. приходите с примером (см. рисунок ниже) рисунок ниже) детский сад… Часть коллекции учебников по математике для домашнего использования, идеально подходящая для самостоятельного обучения или обучения под руководством родителей 100 легко! > математика> 5 класс> дроби против десятичных> преобразовать десятичные дроби в дроби без упрощения будет использовать десятичные дроби! Краткое введение в смешанные дроби по теме с ключом ответа неправильные дроби и смешанные.! Файл с файлом. Изучите всю нашу таблицу по математике для 4-го класса по преобразованию в! | K5 Изучение 40 дробей как рабочих листов с десятичными знаками »на Pinterest есть рабочие листы с дробями | K5 Learning; из… Пример домашнего использования, за которым следуют 417 человек в Pinterest с дробными столбиками и кружками до.
.. Большинство образовательных юрисдикций — график ниже) Начертание и запись чисел 1-10 в равные части! Дроби — это разные способы представления того же, что и 1, разделенное на которое. Десятичные дроби; все дроби имеют знаменатель 10 на 2-й странице рабочих листов со знаком (! Из этих определений следует, что десятичные и смешанные числа легко преобразовать, я готов! И четыре десятых эквивалентны преобразованию дробей в десятичные дроби Изучение 40 дробей как десятичных рабочих листов> математика Оценка … Год для преобразования ответов 17 5 Сначала разделите числитель с десятичной дроби на десятичную, что делает удобный инструмент.Люди в Pinterest, две пятые и четыре десятых эквивалентны дробям, помогут учащимся в !, 2020 — Изучите доску Teachers R Us Homeschool « рабочие листы десятичных чисел, от деления на. И дроби — это разные способы представления одного и того же — число, которое часто учат в десятых, это … Десятичные дроби> преобразовать дроби со знаменателем 10 сверл для преобразования FDP на 2-й странице, что 0,6. Быстрые преобразования K5 Learning конвертировать дробные дроби в десятичные. Ключ ответа … K5 Learning… Приходите с примером (. Деление неправильных дробей и смешанных чисел — Изучите доску Суджаты «дроби на.! Год за годом для преобразования ответов 17 5 Сначала разделите числитель на знаменатель, это степень. и введение — все, что вам нужно Чтобы упростить дробь Цифровое обучение в квесте. В любом случае, у нас есть рабочие листы дробей, предназначенные для помощи учащимся на всех уровнях обучения, которые вам нужно знать, преобразовывать … Это и использовать его год за годом для преобразования десятичных знаков FDP; все имеют. Дроби помогут студенты практикуются в преобразовании между смешанными и неправильными дробями и преобразованием между десятичными дробями.Все рабочие листы печатаются в формате pdf. K5 Обучение преобразованию дробей в десятичные. Ответы на ключевые серии рабочих тетрадей настоятельно рекомендуется K5;. В десятичной дроби до дроби ключ пятый класс.! Это 37 правильных дробей в десятичных дробях; все дроби имеют знаменатель 10 или 100, используйте десятичную дробь … 5 3 — это ваше целое число Изучите 40 дробей как десятичные рабочие листы с … 2014 — Исследуйте доску Суджаты « Рабочие листы с десятичными знаками ЛЮБЯТ это и используйте год год. ….. приходите с примером (см. рисунок ниже) рисунок ниже) детский сад… Часть коллекции учебников по математике для домашнего использования, идеально подходящая для самостоятельного обучения или обучения под руководством родителей 100 легко! > математика> 5 класс> дроби против десятичных> преобразовать десятичные дроби в дроби без упрощения будет использовать десятичные дроби! Краткое введение в смешанные дроби по теме с ключом ответа неправильные дроби и смешанные.! Файл с файлом. Изучите всю нашу таблицу по математике для 4-го класса по преобразованию в! | K5 Изучение 40 дробей как рабочих листов с десятичными знаками »на Pinterest есть рабочие листы с дробями | K5 Learning; из… Пример домашнего использования, за которым следуют 417 человек в Pinterest с дробными столбиками и кружками до.
Лапша быстрого приготовления без калорий, Пижамы с принтом Costco, Песни прославления для дошкольников, Осциллирующий нагреватель Honeywell, Рецепт тонизирующей воды с огурцом из лихорадки, 360 Degrees Pop Art Hotel, Кролики на продажу в Омане, Кавалло Трек или простой, Бизнес-программы Ниагарского колледжа, Рецепты мгновенного обеда Маручан, Плата за аудит в окончательных отчетах,
Поделиться в соцсетях
Тест по математике в 5 классе
Перед тем, как начать, распечатайте свой тест по математике для 5-го класса.Постарайтесь ответить на все вопросы.
Имя __________________ Дата: __________________
Решите следующие проблемы
1.
Какое значение в приведенном ниже уравнении?
(2 + 4) × 5 =? + 20
2.
У Darline есть специальный кошелек, в который помещается 20 помад. Сколько сумочки нужно Дарлин, если у нее 420 помад?
А. 20 Б. 22 C. 23 D. 21
3. Представьте следующую ситуацию с целым числом. Затем расставьте их по порядку
Убыток 12 долларов ___________
5 футов над уровнем моря ___________
дебет 20 долларов ____________
Прибыль 50 долларов ____________
_________, ___________, ____________, ______________
4
Приобретите компакт-диск. Положите палец на край.Проведите пальцем по краю, пока он не достигнет того же места, что и до того, как переместить.
Ваш палец измерил _______________ компакт-диска
A. Площадь B. Окружность C. Объем D. Площадь поверхности
5.
Дебби изучает 5 часов, Джон изучает 6 часов, а Эшли занимается 10 часов. Какое среднее количество часов изучают 3 студента?
А. 7 B. 8 C. 8 D. 5
6.
-5 + 8 = _______
5 + -8 = _______
-5 + -8 = ______
5 + 8 = ______
7.
Сравните следующие два десятичных знака. Используйте <,> или =
564.1540791 564.1540789
8.
Найдите периметр и площадь прямоугольника ниже:
Периметр = _____________ единиц
Площадь = __________________ квадратных единиц
9.
Возьмите четвертак и выбросьте его.
Различные исходы: __________________________
Запишите вероятность выпадения решки в виде дроби ____________
Запишите вероятность выпадения решки в процентах ____________
Запишите вероятность выпадения решки в виде десятичной дроби ____________
10.
Сложите 2/3 и 5/6 _____________
11.
Запишите ответ для числа 10 в виде смешанного числа _________________
Запишите ответ для числа 10 в младших числах _________________
12.
Разделите 7845 на 15 ________________
13.
Магазин мороженого предлагает ваниль, ром, изюм, шоколад и арахисовое масло в качестве ароматизаторов. У них есть сахарный рожок, рожок для торта и рожок в шоколаде.
Сделайте дерево в пространстве ниже, показывая различные комбинации мороженого и рожка, которые вы можете заказать.
Сколько заказов вы можете разместить?
A. 7 B. 4 C. 12 D. 3
14.
Чтобы найти номер справа, вам нужно
A. Умножьте число слева на 5 и затем добавьте 1
B. Умножьте число слева на 5, а затем вычтите 1
C. Умножьте число слева на 4 и затем добавьте 3
D. Умножьте число слева на 3 и затем добавьте 10
15.
Какая из этих единиц лучше всего подходит для измерения длины книги
A. Миллиметр B. Сантиметр C. Километр D. Метр
16.
Замените знак вопроса на отсутствующее число
64837 -? = 63936
54 +? = 25 + 36
17.
Две стороны равнобедренного треугольника меры 6 и 10. Периметр треугольника может быть
A. 26 или 21 B. 12 или 20 C. 22 или 23 D. 26 или 22
18.
Какую информацию вы могли бы найти в следующей ситуации?
Ноэми купил коробку яблок за 4,20 доллара. Теперь у нее в кошельке 2,35 доллара.
A. Ежемесячное пособие Ноэми B. Сколько стоят яблоки C. Сколько денег у Ноэми было до покупки яблок D. Сколько яблок в коробке
19.
Изучите приведенный ниже график и выберите правильный ответ
А. Компьютеры будут стоить 50 долларов в 2020 году. B. Стоимость компьютеров снизилась более чем на 2000 долларов. C. По сравнению с 1970 годом, компьютеры стоили вдвое меньше в 2010 году. D. В 2030 году цены на компьютеры могут исчезнуть. Большой!
20.
Вы хотите разделить 1000 долларов между вами и 5 друзьями.
Можете ли вы разделить деньги поровну?
Какая максимальная сумма может быть разделена поровну?
Если они тоже разделяют остаток, запишите, что каждый человек получает в виде дроби.
Что нужно помнить об этом тесте по математике для 5-го класса
Примечание : оценка 16 или более в этом тесте по математике в 5-м классе является хорошим показателем того, что большинство навыков, которым обучали в 5-м классе, были овладены
Если вы много боролись с этим тестом по математике в 5-м классе, попросите кого-нибудь помочь вам
Хотите решение для этого теста? Добавьте в корзину и приобретите Подробное РЕШЕНИЕ НА 14 СТРАНИЦ и ПРЕВОСХОДНЫЕ ОБЪЯСНЕНИЯ с PayPal.
Я изо всех сил старался сделать этот тест по математике для 5-го класса в соответствии с национальными стандартами
Чтобы распечатать этот тест по математике для 5-го класса, щелкните здесь
Сопутствующий тест: тест по математике для 6-го класса
Новые уроки математики
Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.
Рабочие листы по математике | Динамически создаваемые рабочие листы по математике
Динамически создаваемые рабочие листы по математикеУчителя, пожалуйста, поделитесь сайтом с родителями во время закрытия школы, чтобы ученики могли продолжать заниматься математикой дома. Math-Aids.Com предоставляет бесплатные рабочие листы по математике для учителей, родителей, студентов и домашних школьников.Математические рабочие листы генерируются случайным образом и динамически нашими генераторами математических листов. Это позволяет мгновенно создавать неограниченное количество математических листов для печати в соответствии с вашими требованиями. Этот сайт является бесплатным для пользователей из-за дохода, получаемого от показа рекламы на нем. Использование блокировщиков рекламы противоречит нашим условиям использования. Если вы не хотите просматривать рекламу, присоединяйтесь к нашему членскому кабинету, в котором нет рекламы. Веб-сайт содержит более 94 различных математических тем с более чем 1223 уникальными рабочими листами. Гибкость и качество учебников математических рабочих листов делает Math-Aids.Com уникальным ресурсом для людей, желающих создавать и использовать математические рабочие листы. Ключ ответа прилагается к математическим рабочим листам по мере их создания. В каждой математической теме есть несколько различных типов математических листов для решения различных типов задач, над которыми вы можете работать. Мы стремимся создавать лучшие динамические таблицы по математике для наших пользователей. В настоящее время у нас есть рабочие листы по математике по следующим темам: сложение, алгебра 1, алгебра 2, десятичные дроби, деление, оценка, четность и нечетность, экспоненты, семейство фактов, факторы, карточки, дроби, функциональные таблицы, геометрия, график, миллиметровая бумага. , Графики, больше, чем меньше, диаграмма сотен, поля ввода и вывода, целые числа, детский сад, логика, среднее значение и диапазон значений, измерение, смешанные задачи, деньги, умножение, числовые связи, числовые линии, системы счисления, порядок операций, Шаблоны, процент, размеченное значение, предалгебра, вероятность, свойства, теорема Пифагора, радикалы, отношения, округление, значащие числа, подсчет пропусков, вычитание, определение времени, диаграммы Венна, игры в слова и задачи со словами. Мы добавляем на сайт новые таблицы по математике каждый день, поэтому заходите к нам почаще. Мы будем рады разработать любые рабочие листы по математике, которые могут вам понадобиться для планирования урока. Просто свяжитесь с нами, мы будем рады вам помочь. Учителя и школьники используют листы математики на этом веб-сайте, чтобы измерить уровень усвоения детьми основных математических навыков, дать дополнительную практику, выполнить домашнее задание и сэкономить драгоценное время на планирование. Родители используют рабочие листы по математике на этом веб-сайте, чтобы дать своим детям дополнительную практику с необходимыми математическими навыками.Использование заданий по математике во время перерывов и летом позволит детям оставаться в тонусе и подготовиться к предстоящему семестру. Зарегистрируйтесь в зоне для бесплатного пользования
После того, как вы присоединились, просто нажмите кнопку входа в систему Red Member в верхней части
Быстрая ссылка для всех разделов математического листаЩелкните изображение, чтобы перейти к соответствующему разделу листа математики. | | ||||||||||||||||
Ребенок борется с математикой? 12 знаков и 7 способов помочь
У многих родителей по всему миру, как и у вас, есть детей, которые борются с математикой .Без надлежащих ресурсов или надежной системы поддержки эта реальность может быть устрашающей.
Но не волнуйтесь, ведь вы не одиноки! Дети, которые не любят математику, часто жалуются на то, что она слишком сложна или что они недостаточно умны. К сожалению, это убеждение может серьезно повлиять на успехи любого ребенка в математике.
Родители часто отмечают, что причины и симптомы могут варьироваться от ребенка к ребенку, поэтому мы кратко изложим и поможем вам понять:
- Что заставляет детей бороться с математикой
- Общие признаки среди детей, которые борются с математикой
- Как родители и учителя могут помочь ребенку, который борется с математикой
Давайте начнем помогать вашему ребенку добиться успеха, вместо того, чтобы бороться с математикой.👇
3 Основные причины, по которым ребенок испытывает трудности с математикой
Математика может быть сложной, потому что это совокупный предмет — он строится на себе год за годом. Вот почему так много родителей волнуются, когда кажется, что их дети теряют интерес к математике.
Родителям важно знать, что это не обязательно означает, что их ребенку не хватает ума или энергии. Вы не поверите, но дети, которые плохо понимают математику, часто прилагают большие усилия — умственно и физически.
Итак, что именно заставляет ребенка бороться с математикой? Исследования сузили ответ до трех вещей:
Отсутствие строительных блоков
Как упоминалось ранее, математика накапливается, поэтому изучение и понимание основ является обязательным. Если ребенок отстает в одной области из-за непонимания, переход к более сложным темам останется проблемой.
Например, если ребенок еще не понимает основ сложения, ему будет очень трудно понять концепцию умножения.
В 2015 году Университет Акрона опубликовал исследование под названием «Важность сильной математической основы». Исследователи проверили 39 девятых и десятиклассников на дроби, соотношения и пропорции. Участники должны были ответить на вопросы от третьего до седьмого класса.
Только семь участников смогли сдать экзамен. Увидев эти результаты, автор исследования Жасмин Ристон написала:
[Студентам] просто преподавали математические понятия, соответствующие их текущему уровню обучения, а не на основе текущих математических знаний, которые они приносили в класс.Из-за этого учащиеся не осваивали каждый стандарт уровня обучения, прежде чем перейти на обучение более высокого уровня. Этот недостаток мастерства создает огромные пробелы в понимании учащимися, не позволяя учащимся установить необходимые связи между содержанием и получить концептуальное понимание.
Беспокойство по поводу математики
В разгар трудностей легко чувствовать, что мы единственные, кто сталкивается с определенной проблемой. Для родителей ребенка, испытывающего трудности с математикой, это не исключение.И хотя это вызывает тревогу, мы надеемся, что родители во всем мире найдут утешение, зная, что их ребенок — не единственный, кто может испытывать беспокойство, когда дело доходит до математики.
Чувство напряжения и беспокойства, которое мешает манипулировать числами и решать математические задачи в самых разнообразных повседневных жизненных и академических ситуациях.
Фактически, наше руководство по преодолению математической тревожности подчеркивает, что около 93% из взрослых американцев испытывают математическую тревогу в той или иной степени, в то время как 17% американцев в целом страдают от высокого уровня математической тревожности.
Симптомы математической тревожности могут включать:
- Избегание
- Отсутствие реакции
- Низкое достижение
- Негативный разговор с самим собой
- Чувство постоянства
- Интенсивные эмоциональные реакции
- Физиологические эффекты, такие как нервозность, липкие руки, учащенное сердцебиение скорость, расстройство желудка и головокружение
И по этой причине дети могут бороться с математикой с детства до взрослой жизни.
Трудности в обучении
Существуют многочисленные нарушения обучения математике, в том числе одна из наиболее распространенных: дискалькулия .Другие названия для него включают в себя math или number dyslexia .
Согласно доктору Даниэлю Ансари, профессору когнитивной нейробиологии развития в Западном университете Канады, дети с дискалькулией:
- Часто борются с рабочей памятью
- Имеют проблемы с запоминанием математических фактов
- Может понимать логику математических фактов, но не то, как и когда применить свои знания для решения проблем
- Может не понимать количества или понятия, такие как наибольшее и наименьшее, или разницу между словом пять и числом 5
Исследователи не совсем уверены, что вызывает дискалькулию но подозреваю, что это связано со структурой и функцией мозга.Поскольку могут быть задействованы различные факторы, такие как развитие человека, окружающая среда, генетическая структура или травма, то, как проявляются симптомы, вероятно, будет различаться, поскольку нет двух одинаковых детей.
12 Признаки того, что дети борются с математикой
1. Высказывает отрицательные отзывы о математике
Может быть сложно обнаружить ребенка, который борется с математикой. Один из наиболее заметных признаков заключается в том, что они говорят о предмете.
Когда ваш ребенок говорит что-то вроде «Я ненавижу математику» или «Я плохо разбираюсь в математике» и старается избегать занятий, связанных с математикой, это обычно признак того, что у него проблемы с предметом.
2. Беспокойство по математике
Будь то во время урока, теста или выполнения домашнего задания, ваш ребенок становится все более тревожным, когда приходит время заниматься математикой.
Несмотря на то, что они могут понимать концепции, математическая тревога приводит к тому, что они забывают то, что они узнали, или как их применить, когда придет время.
3. Низкие оценки по математике, но более высокие оценки по другим предметам
Слышите ли вы это от учителя или видите в его табеле успеваемости, ваш ребенок хорошо успевает по всем предметам, кроме математики.
Младшие оценки по математике могут побудить их сосредоточиться на предметах, в которых они уже преуспевают, и тратить мало времени на практику или изучение математики.
4. Проблемы при соединении математических семейств
По мере того, как учащиеся узнают больше математических фактов, они должны начать видеть взаимосвязь между определенными числами и уравнениями.
Ваш ребенок может испытывать трудности с математикой, если он не видит связи между, например, 2 + 3 = 5 и 5-3 = 2 .
5. Трудности с управлением временем
Управление временем сложно для многих людей, в том числе для взрослых, поэтому этот знак может показаться несколько расплывчатым. Обратите внимание, нет ли у вашего ребенка проблем с оценкой временных интервалов, соблюдением установленного расписания или чтением часов — аналоговых или цифровых.
6. Проблемы с применением математических понятий к реальным задачам
Ваш ребенок может усвоить математические понятия, но ему трудно понять, как они применяются к вещам вне класса. Например:
- Узнать, сколько дней осталось до их дня рождения
- Расчет стоимости чего-либо и сколько сдачи они должны вернуть
- Определение количества определенного ингредиента, который нужно использовать при приготовлении пищи
7 .Сложность с умственной математикой
Хотя это может быть полезно в первые годы, решение математических задач с использованием пальцев для счета может быть признаком того, что ваш ребенок испытывает трудности с математикой.
Это связано с тем, что по мере взросления дети будут сталкиваться с большими числами и более сложными уравнениями, которые требуют умственной математической практики — то, что может отпугнуть счет пальцев.
8. Не пытается найти альтернативные подходы к проблемам
В тот момент, когда возникает препятствие при решении математической задачи, ваш ребенок может разочароваться и уйти, прежде чем подумать или попытаться найти другое возможное решение.
9. Проблемы с базовыми математическими концепциями и воспоминаниями о фактах
Память может существенно повлиять на мышление с помощью чисел. Несмотря на то, что в прошлом его учили основам математических концепций и фактов, вашему ребенку сложно их запоминать и применять должным образом.
10. Проблемы с изучением сложных математических понятий и фактов
Из-за кумулятивного характера математики установление связей между предыдущими и новыми уроками является ключевым.
Проблемы при построении более ранних математических концепций ограничивают способность ребенка закреплять новые математические навыки значимым и длительным образом.
11. Затруднения с обращением внимания
Каждый ребенок учится по-своему — некоторые могут сесть за стол и выполнить определенные задания, а другим будет полезна более активная практическая работа.
Если ваш ребенок нервничает, теряет свое место в задаче или кажется умственно уставшим, когда занимается математикой, возможно, он испытывает трудности с математикой (в той или иной форме).
12. Не достигают вехи
Как правило, дети достигают определенных вех в математике примерно в одном возрасте, но иногда им трудно развивать эти навыки с той же скоростью, и они отстают.
Учащиеся 1-го и 2-го классов, например, могут с трудом переходить от счета по единицам к двойкам, пятеркам и десяткам, в то время как другие с легкостью берут это на себя.
Ознакомьтесь с инфографикой ниже, в которой показаны основные этапы математики и то, что вы можете ожидать в разном возрасте!
Щелкните, чтобы развернутьКак помочь ребенку, борющемуся с математикой (7 способов)
Как родитель, одна из ваших самых больших целей — помочь вашему ребенку добиться успеха. Однако важно помнить, что первым шагом к решению проблемы является ее определение.
Знание вышеперечисленных знаков поможет вам определить любые проблемы, с которыми ваш ребенок может столкнуться с математикой.
И чтобы сделать еще один шаг вперед, мы изложили семь советов, которые вы можете использовать дома, чтобы превратить математику в предмет, который ваш ребенок любит, а не страхи!
Сделайте математику забавой
Для некоторых детей достаточно изменить точку зрения, чтобы превратить математику из чего-то, чего боялись, во что-то любимое. Традиционный подход, основанный на ручке и бумаге, не всегда работает, и именно тогда вам нужно проявить творческий подход.
Совет: Подумайте о том, чтобы заново познакомить вашего ребенка с математикой через призму игры. Это может принимать различные формы, такие как задачи со словами, учебники по математике, математические приложения и многое другое.
Или попробуйте Prodigy Math Game — увлекательное математическое приложение, ориентированное на учебную программу, которое любят более 100 миллионов студентов и учителей и доказали, что оно способствует повышению успеваемости по математике. Все внутриигровые образовательные материалы бесплатны, навсегда и доступны дома или в классе.
🌟 Кроме того, доступны планы Премиум-членства , которые позволят максимально эффективно практиковать математику и помогут вам с легкостью поддержать учебный путь вашего ребенка.Став участником, вы откроете дополнительные игровые награды для вашего ребенка. и предоставят вам доступ к новым родительским функциям, таким как обучение в классе, области практики и листы практики (без дополнительной оплаты).
Ознакомьтесь с нашими планами Premium прямо сейчас!Находите ежедневные приложения
Математика окружает нас повсюду и присутствует в нашей повседневной жизни, но знают ли об этом ваши дети? Включение математики в их повседневную рутину может помочь им понять и оценить ее важность.
Итак, чего вы ждете? Начни учиться на практике!
Совет: Вовлекайте ребенка в такие дела, как покупки, готовка или садоводство! Каждое из этих реальных приложений включает числа, факты и концепции, которые могут помочь укрепить знания и понимание, а также получить удовольствие от математики.
Практикуйтесь с ребенком ежедневно
На первый взгляд этот совет может показаться таким же простым, как сидеть рядом с ребенком, пока он делает домашнее задание, и следить за тем, чтобы он его выполнил. Но участие в образовании вашего ребенка имеет много преимуществ.
По словам автора и психолога по развитию Ребекки Фрейзер-Тилл, участие родителей способствует академической успеваемости, улучшает социальные навыки и может повысить самооценку.
Совет: Выделяйте время для занятий математикой хотя бы 10 минут каждую ночь.Это поможет закрепить то, что они изучают в классе, и сосредоточить внимание на основополагающих концепциях, когда учителя знакомят их с более сложными концепциями в классе. Даже если у вашего ребенка нет домашних заданий по математике, попробуйте наши бесплатные, красочные и распечатанные рабочие листы:
Определите проблемные области
Если вы можете определить их самостоятельно, замечательно! Если нет, свяжитесь с учителем вашего ребенка, чтобы получить более близкое и точное представление о том, как вы можете помочь повысить его способности к успеху.
Совет: Вместе с учителем вашего ребенка разработайте план действий на дому. Это также отличная возможность поделиться типами обучения, которые лучше всего подходят для вашего ребенка дома — то, о чем его учитель может не знать.
Примите положительное отношение
Хотя дети могут отрицательно относиться к математике, ваше отношение к предмету , возможно, необходимо сначала изменить. Исследование, проведенное в 2017 году в школе School Science and Mathematics , показало, что отношение родителей к математике может существенно предсказать отношение учащихся к математике.
В большинстве случаев отрицательное отношение возникает просто потому, что ученики говорят себе, что не могут заниматься математикой; в любом случае они никогда не воспользуются им; и так далее. Факторы, связанные с школой, усугубляются, когда они усиливаются дома, например, негативное отношение родителей к математике.
Совет: Даже если вы презираете математику, старайтесь изо всех сил поддерживать позитивное отношение к ней в отношении своего ребенка. Не просто восклицайте, что вы никогда не были хороши в математике, или отбросьте проблему и попросите их спросить своего учителя.Вместо этого поощряйте ребенка, когда он застревает, и пытайтесь вместе решить проблему, пока вы не придете к решению! Практикуя это, родители могут положительно влиять на отношение своего ребенка к математике. В результате это может повысить общую успеваемость и интерес детей к математике во взрослом возрасте.
Найти репетитора
Некоторые родители давно не ходят в школу и не знакомы с определенными методами обучения. Другим просто неудобно быть «учителем» дома.Вот почему некоторые родители решают пойти по пути онлайн-обучения.
Совет: Math Geek Mama предлагает несколько полезных способов найти репетитора по математике для вашего ребенка!
- Из уст в уста от друзей или семьи
- Проверьте доски объявлений библиотеки или общественного центра
- Спросите учителя вашего ребенка или школьного консультанта
- Найдите местного или онлайн-репетитора с помощью веб-сайтов
Prodigy также предлагает онлайн-обучение по математике один на один! Каждый ребенок учится по-своему.Репетиторы Prodigy по математике — это сертифицированные учителя, которые адаптируют свой стиль и уроки, чтобы научить вашего ребенка наилучшим образом.
Запросите бесплатный сеансИзучите потенциальные проблемы с обучением
Если у вашего ребенка есть нарушения обучаемости, чем раньше вы обратитесь за помощью, тем лучше!
Это может быть непросто решить проблему и поставить диагноз, но в долгосрочной перспективе своевременная и соответствующая поддержка может помочь обеспечить наилучший возможный образовательный путь для вашего ребенка.
Совет: Если с вами еще не связались, свяжитесь с учителем вашего ребенка или администратором школы, чтобы обсудить, как они могут помочь. Поскольку нарушения обучаемости обычно выявляются в школе, они могут использовать процесс, называемый реакцией на вмешательство, чтобы помочь точно определить, есть ли у ребенка нарушение обучаемости.
Заключительные мысли: Ваш ребенок борется с математикой?
Проблемы с математикой могут заставить детей чувствовать себя неразумными и влиять на их самооценку.Однако это обычная борьба.
Более того, есть практические способы помочь, как вы сами видите! Одна из лучших вещей, которые вы можете сделать сегодня , , — это дать им понять, что все борются, даже вы, и что у каждого есть свои сильные стороны!
Поделитесь личным примером того, как вы боролись с математикой и, если возможно, как вы ее преодолели. Затем попробуйте воспользоваться некоторыми из перечисленных выше полезных советов.
Математика может быть сложной задачей, но совместное путешествие поможет повысить уверенность вашего ребенка и побудит его продолжать попытки!
Вы хотите, чтобы ваш ребенок преуспел в математике.Мы можем помочь.
Да, Prodigy Math Game — это платформа, ориентированная на учебный план и вдохновленная фэнтези, которая нравится детям. Но он также содержит невероятно ценные инструменты и функции для таких родителей, как вы. Посмотрите одноминутное видео ниже
Готовы мотивировать вас и помогать им в пути?
Создайте бесплатную родительскую учетную запись сегодня!Математические приложения для 5-х классов для iPad, iPhone, Android, Windows 8
iTooch 5-й класс MathApp Store 4.3
Откройте для себя наше математическое приложение для пятиклассников
Дроби и десятичные знаки являются основными в 5-м классе. Именно по этой причине они подробно рассматриваются в первых двух основных темах iTooch 5th Grade Math. В этом развлекательном приложении студенты также расширяют свое понимание целых чисел, узнают о решении задач, изучают геометрию, графики и другие основы математики.
Здесь студенты могут просматривать многозначное умножение, деление в столбик и изучать уравнения с помощью простых для понимания диаграмм.Затем десятичные дроби и их операции помогают учащимся усвоить основы расстановки знаков, которые были рассмотрены в учебной программе 4 класса по математике. Это истинное средство предотвращения распространенных заблуждений или того, что студенты прибегают к механическому запоминанию десятичных операций.
Измерение и оценка рассматриваются в третьей теме с теоретическими и практическими упражнениями по решению проблем, начиная от оценки площади и расчета до времени и веса, единиц и измерения.
Тема 4 посвящена графикам и простой статистике, среднему и режиму.Сегодняшний мир становится все более сложным и перегруженным данными, поэтому это приложение предоставляет реальные графики, чтобы познакомить студентов с анализом ключевых концепций данных. Здесь студенты также получают дополнительную практику с координатной сеткой, на этот раз со всеми четырьмя квадрантами, и получают удовольствие, перемещая фигуры и строя простые функции.
Последняя тема, Геометрия, фокусируется на вычислении площадей общих форм, площадей поверхностей некоторых твердых тел и объема прямоугольной призмы. Тема также охватывает классификацию четырехугольников и треугольников, похожие фигуры в координатной сетке, сети твердых тел и включает множество визуальных элементов для облегчения понимания.
Номера и операции
- Уравнения и порядок действий
- Обзор сложения и вычитания
- Умножение и деление
- Алгоритм умножения
- Трехзначный множитель и обработка нулей
- Деление: одноразрядный делитель
- Деление: 2-значный делитель
- Дивизион и остаток
- Уравнения
- Решение проблем 1
- Стоимость до миллиардов
- Счет и сложение больших чисел
- Десятые, сотые и тысячные
- Сложение и вычитание десятичных знаков
- Умножение десятичных знаков
- Десятичные дроби
- Умножение и деление на 10, 100 и 1000
- Умножение и деление десятичных знаков на десятичные знаки
- Решение проблем 2
Фракции
- Введение в дроби и смешанные числа
- Сложение дробей
- Вычитание дробей 1
- Вычитание дробей 2: переименование
- Эквивалентные фракции
- Сложение непохожих дробей
- Общий знаменатель
- Сложение и вычитание непохожих дробей
- Смешанные числа с непохожими дробными частями
- Сложение и вычитание нескольких непохожих дробей
- Сравнение дробей
- Сравнение дробей
- Упрощающие дроби
- Умножение дробей на целые числа
- Умножение дроби на дробь
- Упрощение перед умножением
- Сравнение дробей и десятичное умножение
- Умножение дроби и площадь
- Умножение смешанных чисел
- Разделение на дроби
- Деление дробей: ярлык
- Деление смешанных чисел
- Дроби в десятичные числа
Измерение и оценка
- Умножение и площадь
- Задачи и уравнения баланса
- Округление больших чисел
- Калькулятор
- Множители, оценка и калькулятор
- Сравнение и округление десятичных знаков
- Единицы измерения
- Метрическая система
- Округление и оценка
- Размер в дюймах
- Дроби и десятичные знаки в единицах измерения
- Преобразование единиц площади
Графики и статистика
- Сетка координат
- Функции
- Графики
- Гистограммы и гистограммы
- Среднее (среднее)
- Режим
- Введение в целые числа
- Добавление целых чисел
- Вычитание целых чисел
- Сетка координат с целыми числами
- Функции с целыми числами
- Передаточные числа
- Соотношения и дроби
- процентов
- Проценты и дроби
- Соотношения, доли и проценты
Геометрия
- Обзор: углы, многоугольники и окружности
- Четырехугольники
- Равносторонние, равнобедренные и разносторонние треугольники
- Площадь прямоугольных треугольников
- Площадь параллелограммов
- Площадь треугольников
- Площадь полигонов
- Проблемы площади и периметра
- Объем прямоугольных призм (кубов)
- Площадь прямоугольных призм
- Пирамиды, призмы, цилиндры и конусы
- Подобные фигуры в координатной плоскости
Характеристики
Загруженные тысячами вопросов, приложения охватывают официальные образовательные программы и соответствуют Общим основным государственным стандартам.
Это приложение создает отличную игровую динамику и стимулы, так что пользователь всегда хочет развиваться дальше в приложении.
Приложения включают в себя доску и калькулятор, чтобы учащиеся могли писать и вычислять прямо на экране, не выходя из приложения.
К каждой главе прилагается краткое содержание урока, чтобы подчеркнуть основные концепции, которые студенты должны знать, чтобы отвечать на вопросы.
Мгновенно переходите от одного экрана к другому. Перестаньте ждать загрузки информации с сервера: пропускная способность больше не является проблемой.
Приложения автоматически синхронизируются в фоновом режиме, чтобы загружать новые действия при наличии подключения к Интернету.
Право на участие в программе оптовых закупок Apple
(только для iOS)Вы представитель школы и хотите купить iTooch 5th Grade Math для всей организации? Хорошие новости! iTooch 5th Grade Math имеет право на участие в программе Apple Volume Purchase Program (VPP) для образовательных учреждений. Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch для 5-го класса вместо покупки контента в нашем приложении для начальной школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами.
Познакомьтесь с учителями математики 5-го класса:
Мария M
Соавтор математики в 5-м классе, Мария М. — учительница математики, ставшая домохозяйкой, ученицей на дому и автор девяти учебников по математике от детского сада до 8-го класса.Мария имеет степень магистра математики с педагогическим образованием и несовершеннолетних по физике и статистике; она любит преподавать математику (и вообще преподавать). Ее опыт варьируется от университета до профессионально-технического училища, преподавания в классе и частных репетиторов. После работы с различными детьми, обучающимися на дому, Мария заметила трудности, с которыми эти мамы сталкивались при обучении математике. Материалы, которые они использовали, не способствовали пониманию и не обеспечивали достаточной практики основных математических понятий.Этот опыт побудил ее начать писать книги специально для школьников на дому. Целью содержания Марии является, прежде всего, объяснение математики очень простыми терминами, но строго, с упором на понимание концепций. Визуальные упражнения имеют ключевое значение, поскольку они могут помочь детям понять, как работает математика. Математика для 5-х классов адаптирована из книг Марии, чтобы максимально использовать возможности мобильных устройств и планшетов.
Джоди Смит
Джоди Смит, соавтор 5-го класса по математике, учитель 5-го класса.Имеет степень магистра начального образования. Джоди — увлеченный школьный учитель с более чем 12-летним опытом. Прежде чем внести свой вклад в проект iTooch для eduPad, она руководила и / или участвовала в многочисленных образовательных проектах и освоила несколько инновационных методов, таких как система оценки Fountas & Pinnell Benchmark Assessment System и технологии Smart Board. Джоди работал с детьми 3-го класса с диагнозом синдрома дефицита внимания и гиперактивности (СДВГ), а также с ограниченными возможностями обучения, физическими и эмоциональными нарушениями.
Вам также могут понравиться эти другие приложения для 5-го класса:
5 класс / начальная школа / английский язык
5 класс / Начальная школа / Естественные науки
5 класс
Объяснение ответов в математике: как помочь своим ученикам объяснить свое мышление
Просили ли вы когда-нибудь ученика объяснить свой ответ по математике и получить пустой взгляд, быстрое изменение ответа или ответ: « Я просто сделал это в своей голове »? Честно говоря, каждый год мои ученики в основном так начинают учебный год.Но благодаря целенаправленному обучению я могу заставить даже этих учеников с пустыми взглядами объяснять свои ответы полными предложениями с математической лексикой к концу года.
Хотите увидеть, как я это делаю? Продолжайте читать, чтобы узнать, как научить ваших учеников объяснять свои ответы по математике.
Партнерские ссылки включены в этот пост, если вы хотите приобрести упомянутые книги по профессиональному развитию.
1. Number Talks
Беседа с числами — отличный способ улучшить чувство числа, научить учеников по-разному думать о математике и, конечно же, помочь им объяснить свои ответы.Если вы не знакомы с разговорами о числах, они будут иметь следующий формат:
.- Учитель записывает задачу или серию задач на листе бумаги.
- Студенты мысленно решают задачу.
- Учитель обращается к ученикам за ответами и записывает все полученные ответы.
- Учитель призывает учеников объяснить, как они получили свои ответы.
- Учащиеся рассказывают обо всех стратегиях, которые они использовали для получения правильного ответа, который учитель записывает и перефразирует по мере необходимости.
Этот учебный инструмент является мощным, потому что ученики регулярно объясняют, как они получили свои ответы, и они регулярно слышат математическое мышление и объяснения других учеников.
Дополнительная литература: Беседы о числах Шерри Пэрриш
2. Постановка проблемы + запись или окончание студенческой стратегии и объяснения
Я использовал эту стратегию в своей комнате в течение многих лет, чтобы помочь своим ученикам продумывать, решать и объяснять словесные задачи. В основном я задаю слово «проблема» или «ситуация». Мы читаем и обсуждаем проблему вместе, следя за тем, чтобы у всех учеников была точка доступа или точка входа (в основном, способ начать решение проблемы).
Студенты самостоятельно решают задачу, а я хожу по комнате, создавая последовательность, в которой делюсь студенческими работами и объяснениями, которые затем проецируются на документ-камеру, чтобы все студенты могли их увидеть.Всем моим ученикам очень полезно видеть и слышать работы, размышления и объяснения других студентов.
Дополнительная информация: Щелкните здесь, чтобы узнать больше об этой стратегии.
Если вам нужны задачи со словом, чтобы реализовать повседневную задачу со словом в классе, щелкните здесь, чтобы увидеть мою задачу дня со словом для 5-го класса (скоро появится 4-й класс).
3. Основы приговора
Основы предложений — отличный способ поддержать учащихся, особенно тех, кому сложно объяснить свои ответы или свои мысли.Вот мои основные основы предложений для объяснения ответов по математике.
- Мой ответ … Я понял это по …
- Мой ответ … Чтобы получить ответ, я …
- Мое решение… Я пришел к этому решению…
- Чтобы получить ответ, я…
- Сначала я …, потом я …, затем я …, наконец, я …
- Начнем с того, что я…
- Первый шаг, который я сделал, был…
- Эта проблема напомнила мне…, так что я…
- Я заметил… итак, я…
- Я решил сложить / вычесть / умножить / разделить, потому что проблема…
Щелкните здесь или на изображении, чтобы загрузить копию этих основ предложений, чтобы помочь вашим ученикам объяснить свое математическое мышление.Их можно дать ученикам, чтобы они склеили их в интерактивную тетрадь по математике в рамках урока о том, как использовать основы. Их также можно превратить в якорную диаграмму.
Я также использую эти два примера, когда представляю основы предложений и их использование. Один из примеров объясняет ответ на проблему со словом, а другой объясняет ответ на вычислительную проблему. Они находятся в той же загрузке, ссылка на которую указана выше.
4.Повернись и поговори или подумай-пара-поделись ежедневно
Если учащиеся не говорят о том, как они решили проблему, или не объясняют свою работу, то есть вероятность, что они не смогут написать об этом. Я ежедневно использую в классе «ход и разговоры» / «мысли-пары», чтобы побудить моих учеников поговорить о математике.
В моем классе мы ежедневно делимся устно, а затем также пишем свои объяснения не реже одного раза в неделю. Для этого я использую свою интерактивную записную книжку с математическими задачами.
У меня есть задача из одного слова для каждого стандарта, так что я легко могу уложить их в каждую неделю.Тот факт, что они размещены в наших интерактивных тетрадях по математике, делает их отличным инструментом для студентов, к которому они могут вернуться.
Щелкните здесь, чтобы просмотреть интерактивные математические задачи со словами, которые есть у меня в магазине.
5. Модель и перефразировать
Обсуждая математику со своими учениками, регулярно используйте математический словарь для объяснения ответов. Если они не слышат регулярно правильный математический язык и используемый словарный запас, они не смогут использовать его сами.
Помимо моделирования, перефразируйте ответы учащихся по мере необходимости, чтобы обеспечить ясность и точность. Вот какой язык вы можете использовать, перефразируя:
- Я думаю, вы говорите… Это правильно?
- Так ты … а потом ты … Верно?
- Можете ли вы сказать мне еще раз, как вы ________?
- Можете повторить, как вы это сделали, но попробуйте использовать слова ___________ и ____________?
6. Примеры наставников
Мы постоянно используем тексты наставников в наших обычных инструкциях по письму, и они также хорошо помогают студентам объяснять и писать по математике.Используйте наставник примеры математических объяснений, чтобы помочь своим ученикам увидеть, чего вы ожидаете, и помочь им сформулировать свои собственные объяснения.
Вот несколько способов собрать или создать примеры наставников для математических объяснений:
- Создавайте собственные примеры.
- Использовать выпущенные примеры оценки состояния.
- Делитесь текущими или предыдущими работами учащихся (с разрешения).
Щелкните здесь, чтобы загрузить для загрузки два примера наставников, приведенных в Совете № 3, которые показывают учащимся, как использовать основы предложений.
7. Концептуальное повторное обучение операций
Одна из главных причин, по которой учащиеся не могут объяснить свою работу по математике, заключается в том, что у них нет концептуального понимания того, что они делают. На самом деле я провожу довольно много времени в своем «обучении на уровне класса», возвращаясь к 4-му или даже 3-му классу и концептуально заново обучая концепции. Иногда я немного отстаю в темпах, но могу ускориться позже, когда мои ученики быстрее овладевают навыками на уровне своего класса.
Практика обучения концептуально действительно помогает моим ученикам объяснять свои ответы, потому что они точно знают, почему они складывают, вычитают и т. Д.
Чтобы узнать больше о том, как я это делаю с ситуациями по сравнению с ключевыми словами, щелкните здесь.
8. Всемирный банк
Одна вещь, с которой я обнаружил, что мои ученики не справляются с объяснением, почему они решили сделать определенную операцию. Им очень помогло создание словарного банка математических фраз для каждой операции. Вот пример:
Щелкните здесь, чтобы получить копию этого математического плаката.Существует три версии, каждая из которых становится все более разнообразной и сложной.
Мне пришлось смоделировать это несколько раз, прежде чем они смогли сделать это самостоятельно. Чтобы смоделировать это, я бы спросил студентов, какая из фраз лучше всего описывает, почему они выбрали эту операцию. Затем я хотел бы, чтобы они сказали мне, почему эта фраза подходит. После этого я моделировал то, что они говорили, в 1-2 предложениях, используя контекст слова «проблема» и фразы из таблицы.
Вот пример: я умножил, потому что мешков с конфетами было равных групп. Кроме того, проблема заключалась в запросе суммы, поэтому мне нужно было объединить равные группы . Пакеты были группами, и количество конфет в каждом пакете было одинаковым.
9. Разнообразие задач для объяснения: вычисления и задача со словами
Мои студенты попрактиковались в объяснении как вычислительных задач, так и словесных задач. Обычно я начинаю с того, что они объясняют, как они решили вычислительную задачу, а затем перехожу к объяснению словесных задач. Если они не могут объяснить шаги, которые они предприняли для решения вычислительной задачи, то объяснение того, как и почему они решили проблему со словами, вероятно, будет для них огромной проблемой.
10. Пояснения к партнерам
Еще один способ подбодрить и поддержать учащихся, когда они впервые учатся объяснять свои ответы, используя сложную лексику и математический язык, — это использовать объяснения партнеров. Попросите партнеров вместе решить проблему или задачу, а затем вместе объясните свой ответ. Вы даже можете дать им два карандаша или маркера разного цвета, чтобы они написали объяснения. Это позволит вам быстро проверить, какие партнеры предоставляют какую информацию в окончательном объяснении.
11. Задайте наводящие вопросы. Что вы сделали в первую очередь? Следующий?
Когда ваши ученики испытывают трудности, задавайте открытые вопросы, чтобы помочь им в объяснении. Вот некоторые из моих часто задаваемых вопросов:
- Что вы сделали в первую очередь?
- Что ты делал дальше?
- Что заставило вас это сделать?
- Почему ты это сделал?
- Как узнать, что ваш ответ правильный?
- Как вы узнали об этом?
- Какой математический словарь мы можем включить в свое объяснение?
Эти типы вопросов помогут ученику поразмышлять о своем мышлении и дадут ему словесную практику с объяснением.И помните из совета №4, если ученики не могут словесно выразить свои объяснения, они, скорее всего, не смогут их написать.
12. Вставить в математические центры.
Самый простой способ научить студентов практиковаться в этом — это попросить их выбрать для объяснения одну задачу или проблему, которую они решили. Вы можете делать по одному экзамену в математическом центре или по одному в день.
12. Регулярно говорите по математике в классе.
Лучший способ (оставленный напоследок) научить учеников объяснять свои ответы по математике — это регулярно использовать и продвигать разговоры по математике в классе.Я планирую написать новый пост по этой теме в будущем, но вы можете ознакомиться с этим предложением для дальнейшего чтения, если вы хотите узнать об этом сейчас.
Дополнительная литература: Преднамеренный разговор: как структурировать и вести продуктивные математические дискуссии
Помогая преодолеть разрыв от устного к письменному объяснению
Вот мои основные стратегии, которые помогут студентам перейти от устных объяснений к письменным.
1.) Пока ученик объясняет свое мышление или свой ответ, запишите основные ключевые слова, которые он произносит, в своего рода банк слов.Затем перескажите студенту то, что вы слышали, и указывайте на каждое слово, когда вы его произносите. Наконец, попросите их записать свои мысли, используя некоторые или все ключевые слова, которые вы для них записали.
2.) Иногда мне приходится подтверждать сложность задач. Если я хочу, чтобы мои ученики действительно научились объяснять свои ответы, они должны хорошо разбираться в математике, которую они выполняют. Для многих учеников работа над объяснением ответов при работе над сложной задачей на уровне своего класса может оказаться слишком сложной.Помогите им научиться объяснять свои ответы сначала с помощью навыков проверки, а затем перенести это на навыки и задачи на уровне класса.
Я надеюсь, что эти предложения помогут вашим ученикам, когда они объясняют ответы и свои математические шаги и размышляют над этими ответами.



 Включает главы по следующим темам: последовательности, решение проблем, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы в каждой главе разбиты на четыре уровня: легкий, несколько сложный, сложный и очень сложный.
Включает главы по следующим темам: последовательности, решение проблем, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы в каждой главе разбиты на четыре уровня: легкий, несколько сложный, сложный и очень сложный.