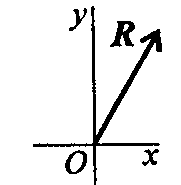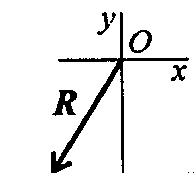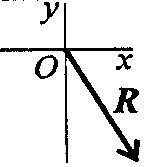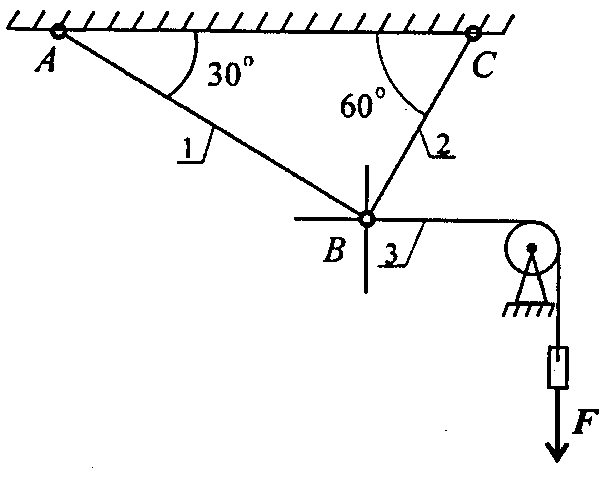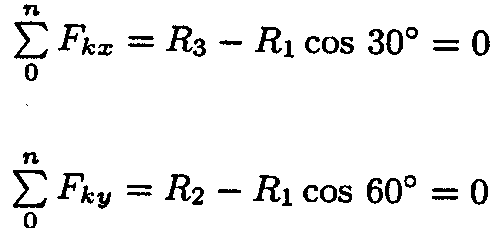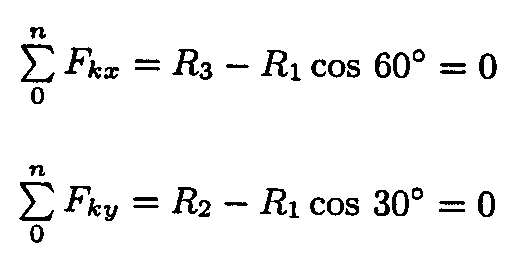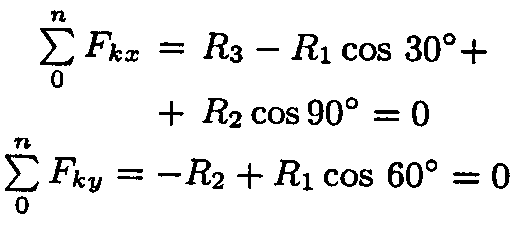Примеры решения задач по разделу «Статика» теоретической механики
Выберите предметМеханикаТеоретическая механикаСопротивление материаловТеория машин и механизмовДетали машинВысшая математикаФизикаНачертательная геометрияИнформатикаАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАрхитектура и строительствоБазы данныхВысшая математикаГеометрияГидравликаДетали машинИздательское делоИнформатикаИнформационная безопасностьИнформационные технологииМатериаловедениеМашиностроениеМеталлургияМетрологияМеханикаМорская техникаНаноинженерияНачертательная геометрияПолиграфияПриборостроение и оптотехникаПрограммированиеПроцессы и аппаратыРабота на компьютереРадиофизикаСопротивление материаловТелевидениеТеоретическая механикаТеория вероятностейТеория машин и механизмовТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТранспортные средстваФизикаХолодильная техникаЧертежиЧерчениеЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЯдерная энергетика и теплофизикаЯдерные физика и технологииАнализ хозяйственной деятельностиАнтикризисное управлениеБанковское делоБизнес-планированиеБухгалтерский учет и аудитВнешнеэкономическая деятельностьГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиИнвестицииИнновационный менеджментКредитЛогистикаМаркетингМеждународные рынкиМенеджментМенеджмент организацииМикро-, макроэкономикаНалогиОрганизационное развитиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментСервисСтандартизацияСтатистикаСтратегический менеджментСтрахованиеТаможенное делоТеория управленияТовароведениеТорговое делоТуризмУправление персоналомФинансовый менеджментФинансыЦенообразование и оценка бизнесаЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализАрхеологияАстрономияБезопасность жизнедеятельностиБиологияБиотехнологияВетеринарияВоспроизводство и переработка лесных ресурсовГеографияГеодезияГеологияГидрометеорологияЕстествознаниеКартография и геоинформатикаМедицинаНефтегазовое делоПочвоведениеПриродообустройство и водопользованиеСельское и рыбное хозяйствоХимияХирургияЭкологияБиблиотечно-информационная деятельностьДизайнДокументоведение и архивоведениеЖурналистикаИскусствоИсторияКонфликтологияКриминалистикаКультурологияЛитератураЛогикаМеждународные отношенияМузыкаПедагогикаПолитологияПраво и юриспруденцияПсихологияРежиссураРеклама и PRРелигияСвязи с общественностьюСоциальная работаСоциологияСтрановедениеТеатроведениеФизическая культураФилософияЭтикаЯзыки (переводы)Языкознание и филология
Выберите вид работы…Решение задачОнлайн помощьКонтрольная работаКурсовая работаПомощь на экзаменеОтветы на вопросыОтчёт по практикеЧертёжДипломная работаРефератМонографияБизнес-планТворческая работаЭссеСочиненияРецензияДокладНабор текстаМагистерская диссертацияКандидатская диссертацияСтатьяЛабораторная работаПереводПрезентацииПовышение уникальности текстаДругое
isopromat.ru
Термех_Статика
МОДУЛЬ 1
ОСНОВНЫЕ ПОНЯТИЯ РАЗДЕЛА «СТАТИКА»
1. НАУЧНО-ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ УЧЕБНО-МЕТОДИЧЕСКОГО КОМПЛЕКСА «СТАТИКА»
1.1. Глоссарий
Абсолютно твердое тело – тело, расстояния между точками которого не изменяются.
Активные – заданные силы, приложенные к телу, могущие вызвать его ускорение.
Внешние силы – силы, с которыми другие тела действуют на данное тело.
Внутренние силы – силы, с которыми части одного тела действуют друг на друга.
Главный вектор системы сил – величина R, равная геометри-
ческой сумме всех сил.
Главный момент системы сил относительно этого центра –
величина M0 , равная геометрической сумме моментов всех сил от-
носительно центра О.
Статика – раздел механики, в котором излагается общее учение о силах, изучается приведение сложных систем сил к простейшему виду иустанавливаются условия равновесия различных систем сил.
Равновесие – состояние покоя тела по отношению к другому телу, выбранному за неподвижное, или его равномерное прямолинейное движение.
Равнодействующая – сила, эквивалентная данной системе сил. Распределенная сила – силы, приложенные вдоль тела по ка- кому-либо закону. Величина силы, приходящейся на единицу дли-
ны, определяет интенсивность q распределенной нагрузки. Реакция связи – сила, с которой связь действует на тело, пре-
пятствуя перемещению тела.
Связь – все то, что препятствует перемещению тела в какомлибо направлении.
Сосредоточенная сила – сила, приложенная к какой-либо точке твердого тела.
5
Сила – мера механического взаимодействия тел, характеризующая его интенсивность и направленность.
Cходящиеся силы – силы, линии действия которых пересекаются в одной точке.
Свободное тело – тело, которому из данного положения можно сообщить любое перемещение в пространстве.
Уравновешенная (эквивалентная нулю) – система сил, под дей-
ствием которой свободное твердое тело может находиться в покое. Уравновешивающая – сила, равная равнодействующей по мо-
дулю, прямо противоположная ей по направлению и действующая вдоль той же прямой.
Эквивалентные системы – если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.
1.2.Темы лекций и их содержание
Тема 1. Равновесие тела, находящегося под действием произвольной плоской системы сил.
Введение в дисциплину. Понятие о силе, распределенные и сосредоточенные силы. Типы связей и их реакции. Проекция силы на ось и плоскость.
Аналитический способ сложения сходящихся сил. Момент силы относительно точки и оси.
Литература: [1], стр. 31–57; [2], стр. 15–33.
Тема 2. Системы сходящихся сил
Приведение системы сходящихся сил к равнодействующей. Теорема о равнодействующей системы сходящихся сил. Теорема о равновесии тела, находящегося под действиемсистемы сходящихся сил.
Литература: [1], стр. 62–69; [2], стр. 35–49.
Тема 3. Пара сил и ее момент
Свойства пары сил. Условия равновесия пар.
Литература: [1], стр. 88–94; [2], стр. 50–56.
6
studfile.net
Решение задач по теоретической механике
Здесь собраны избранные разделы теоретической механики и примеры решения задач.
СодержаниеИзбранные разделы по теоретической механике ⇓
Примеры решения задач по теоретической механике ⇓
Статика ⇓
Кинематика ⇓
Кинематика материальной точки ⇓
Поступательное и вращательное движение твердого тела ⇓
Кинематический анализ плоского механизма ⇓
Определение абсолютной скорости и абсолютного ускорения точки ⇓
Динамика ⇓
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил ⇓
Теорема об изменении кинетической энергии механической системы ⇓
Применение общего уравнения динамики к исследованию движения механической системы ⇓
Применение принципа Даламбера к определению реакций опор вращающегося тела ⇓
Избранные разделы по теоретической механике
Примеры решения задач по теоретической механике
Статика
Условия задач
Найти графическим способом реакции опор балки AB, на которую действует сила P, приложенная в точке C.
Дано: P = 55 kH, AB = 10 м, AC = 7 м, BC = 3 м.
Решение
Найти реакции опор для того способа закрепления, при котором момент MA в опоре A имеет наименьшее значение.Решение
Найти реакции опор составной конструкции.Решение
Найти реакции стержней, поддерживающих тонкую однородную горизонтальную плиту в трехмерном пространстве.Решение
Кинематика
Кинематика материальной точки
Определение скорости и ускорения точки по заданным уравнениям ее движения
Дано: Уравнения движения точки: x = 12 sin(πt/6), см; y = 6 cos2(πt/6), см.
Установить вид ее траектории и для момента времени t = 1 с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение задачи
Поступательное и вращательное движение твердого тела
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t3 – 6t (см).
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
Решение
Кинематический анализ плоского механизма
Дано:
R1, R2, L, AB, ω1.
Найти: ω2.
Решение с помощью
теоремы о проекциях скоростей
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна E. Стержни соединены с помощью цилиндрических шарниров. Точка D расположена в середине стержня AB.
Дано: ω1, ε1.
Найти: скорости VA, VB, VD и VE; угловые скорости ω2, ω3 и ω4; ускорение aB; угловое ускорение εAB звена AB; положения мгновенных центров скоростей P2 и P3 звеньев 2 и 3 механизма.
Решение
Определение абсолютной скорости и абсолютного ускорения точки
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6t 2 – 3t3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40(t – 2t 3) – 40 (s — в сантиметрах, t — в секундах). Расстояние b = 20 см. На рисунке точка M показана в положении, при котором s = AM > 0 (при s < 0 точка M находится по другую сторону от точки A).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с.
Решение задачи
Динамика
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Условие задачи
Груз D массой m, получив в точке A начальную скорость V0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV2, вектор R направлен противоположно скорости V груза).
Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция Fx которой на ось x задана.
Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.
Скачать решение задачи
Теорема об изменении кинетической энергии механической системы
Условие задачи
Механическая система состоит из грузов 1 и 2, цилиндрического катка 3, двухступенчатых шкивов 4 и 5. Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Каток (сплошной однородный цилиндр) катится по опорной плоскости без скольжения. Радиусы ступеней шкивов 4 и 5 равны соответственно R4 = 0,3 м, r4 = 0,1 м, R5 = 0,2 м, r5 = 0,1 м. Массу каждого шкива считать равномерно распределенной по его внешнему ободу. Опорные плоскости грузов 1 и 2 шероховатые, коэффициент трения скольжения для каждого груза f = 0.1.
Под действием силы F, модуль которой изменяется по закону F = F(s), где s — перемещение точки ее приложения, система приходит в движение из состояния покоя. При движении системы на шкив 5 действуют силы сопротивления, момент которых относительно оси вращения постоянный и равен M5.
Определить значение угловой скорости шкива 4 в тот момент времени, когда перемещение s точки приложения силы F станет равным s1 = 1,2 м. 
Скачать решение задачи
См. также: Теорема об изменении кинетической энергии. Пример решения задачи
Применение общего уравнения динамики к исследованию движения механической системы
Условие задачи
Для механической системы определить линейное ускорение a1. Считать, что у блоков и катков массы распределены по наружному радиусу. Тросы и ремни считать невесомыми и нерастяжимыми; проскальзывание отсутствует. Трением качения и трением скольжения пренебречь. 
Скачать решение задачи
См. также: Общее уравнение динамики. Пример решения задачи
Применение принципа Даламбера к определению реакций опор вращающегося тела
Условие задачи
Вертикальный вал AK, вращающийся равномерно с угловой скоростью ω = 10 с-1, закреплен подпятником в точке A и цилиндрическим подшипником в точке D.
К валу жестко прикреплены невесомый стержень 1 длиной l1 = 0,3 м, на свободном конце которого расположен груз массой m1 = 4 кг, и однородный стержень 2 длиной l2 = 0,6 м, имеющий массу m2 = 8 кг. Оба стержня лежат в одной вертикальной плоскости. Точки прикрепления стержней к валу, а также углы α и β указаны в таблице. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.
Пренебрегая массой вала, определить реакции подпятника и подшипника.
Скачать решение задачи
1cov-edu.ru
Примеры решения задач по теоретической механике.
Решение задач по технической механике
Примеры решения задач по теоретической механике
Принципы и способы решения задач теоретической механики рассмотрены на простейших примерах, где необходимо определить какие-либо силовые факторы, действующие на тело, скорость, ускорение, работу, мощность и другие физические величины. На основе результатов расчетов с использованием приемов теоретической механики приступают к решению задач методами сопротивления материалов, а затем переходят к расширенным практическим вопросам, которые ставит раздел «Детали машин».
Решение задачи с использованием метода кинетостатики
Определить силу натяжения в канате крановой установки, поднимающей груз G с ускорением а.
Исходные данные:
Масса груза m = 5 тонн;
Ускорение груза а = 2 м/сек2;
Ускорение свободного падения принять равным g = 10 м/сек2;
Силой сопротивления воздуха пренебречь.
Решение:
Для решения задачи используем метод кинетостатики (принцип Д’Аламбера), который основывается на введении понятия силы инерции и приведении подвижной системы к состоянию условного равновесия. Это позволяет использовать для решения задач Кинематики способы и методы Статики.
Чтобы понять сущность этого принципа, представьте себе просмотр киносюжета, кадры которого сняты при малой скоростью съемки, и движение тел на экране словно состоит из отдельных прерывистых фрагментов (или — как передвигается робот — урывками). Т. е. движение тела рассматривается состоящим из отдельных крохотных моментов, и в каждый такой микромомент тело находится в состоянии равновесия под действием движущей силы и силы инерции, сопротивляющейся движению.
Итак, для решения этой задачи следует рассмотреть условие равновесия груза, который поднимается с ускорением а под действием некоторой системы сил. Реально к грузу приложены две силы – сила натяжения каната, и сила тяжести груза. Очевидно, что эти силы не равны по величине, поскольку груз поднимается с ускорением, значит, сила натяжения в канате больше силы тяжести.
Введем в систему упомянутую выше силу инерции, которая условно уравнивает разницу между силой натяжения в канате и силой тяжести, тогда груз будет находиться в условном равновесии.
Составим уравнение этого равновесия: Fк – G – Fин = 0,
где: Fк – сила натяжения каната (тяга крановой установки), G – вес груза, Fин – сила инерции.
Очевидно, что условие равновесия будет соблюдаться, если искомая сила Fк будет равна сумме сил тяжести и инерции.
Силу тяжести G и силу инерции Fин можно вычислить, используя второй закон Ньютона, как произведение массы тела на ускорение, вызываемое этими силами:
G = mg, где m – масса тела в кг, g – ускорение свободного падения;
Fин = ma, тогда:
Fк = G + Fин = mg + ma = m(g + a) = 5000 × (10 + 2) = 60 000 Н = 60 кН.
Задача решена.
***
Решение задачи на на трение
Определить силу F, необходимую для равномерного перемещения бруса по горизонтальной шероховатой поверхности.
Исходные данные:
Коэффициент трения между брусом и поверхностью f = 0,6;
Масса бруса m = 12 кг;
Ускорение свободного падения g принять равным 10 м/сек2.
Решение:
Эта задача решается с использованием законов движения тел под действием сил трения скольжения.
Для того, чтобы тело равномерно перемещалось по поверхности без ускорения, сила трения должна быть равна силе тяги (т. е. искомой силе F): F = Fтр.
Поскольку поверхность горизонтальная, сила трения равна весу тела, умноженному на коэффициент трения:
Fтр = fG, где: G = mg — вес тела.
Тогда:
F = F
Задача решена.
***
Решение задачи из раздела Статика
Найти силу натяжения упругой нити, удерживающей груз в состоянии равновесия на идеально гладкой наклонной плоскости.
Исходные данные:
Вес груза G = 100 Н,
угол наклона поверхности указан на рисунке.
Решение:
Поскольку груз находится в равновесии, решение задачи возможно с применением методов Статики, т. е. с на основе анализа причин, по которым тело находится в неподвижном состоянии (в равновесии).
Итак, сначала необходимо определить – под влиянием каких сил груз находится в состоянии равновесия.
Кроме силы тяжести G, на груз наложены две связи, ограничивающие его перемещение: гибкая связь (упругая нить) и наклонная плоскость. Реакция гибкой связи Rн направлена вдоль линии этой связи (вдоль нити), а реакция плоскости Rп всегда перпендикулярна этой плоскости и приложена в точке касания телом плоскости (см. схему).
Задача может быть решена двумя методами.
Определив направление реакций, можно решить эту задачу графическим методом, построив силовой треугольник, который будет замкнутым, поскольку векторная сумма сил равна нулю (равновесие груза).
Для построения векторной цепочки (в нашем случае – треугольник) откладываем силу тяжести груза G в определенном масштабе (поскольку нам известны и направление, и величина этой силы).
Для реакций мы знаем лишь их направление (величина сил неизвестна). От концов вектора силы G откладываем отрезки прямых, параллельные реакциям, и точка пересечения этих прямых позволит нам получить искомый треугольник сил. Теперь можно определить величину любой из реакций, измерив ее длину на чертеже линейкой и умножив на масштаб чертежа, который задает сила G. Порядок построений показан на рисунке а).
Аналитическим методом эта задача решается с помощью уравнений равновесия, исходя из условия, что сумма проекций всех сил на любую координатную ось равна нулю. Разумеется, необходимо выбрать удобную систему координат, тогда для решения задачи потребуется минимальное количество уравнений.
В нашем случае можно любую из координат расположить так, чтобы одна из неизвестных реакций была ей перпендикулярна, тогда проекция этой силы на данную координатную ось будет равна нулю.
Поскольку нам необходимо найти силу натяжения нити (реакция Rн), то расположим координатную ось y так, чтобы реакция плоскости (Rп) была ей перпендикулярна (рис. в). Тогда реактивная сила Rп проецируется в точку, т. е. в ноль, и для решения задачи потребуется лишь сумма проекций сил G и Rн на ось y:
ΣFy = 0 => Rн – G cos60˚ = 0, откуда найдем искомую реакцию Rн:
Rн = G cos60˚ = 100×0,5 = 50 Н.
Задача решена двумя методами.
***
Пример решения задачи из раздела Динамика
Какую работу W необходимо совершить, чтобы повалить кубический предмет на боковую грань?
Исходные данные:
Длина грани кубического предмета (ящика) a = 1 м;
Масса кубического предмета m = 100 кг;
Центр тяжести кубического предмета расположен в точке пересечения диагоналей;
Ускорение свободного падения принять равным g = 10 м/сек2
Решение:
Как известно, работа любой силы равна произведению модуля этой силы на величину перемещения тела, вызванного действием этой силы.
Искомая работа W равна работе по преодолению силы тяжести при подъеме центра масс ящика на высоту Δh, равную разности между половиной диагонали боковой грани ящика и половиной длины его стороны, т.е. – вся работа заключается в постановке ящика на ребро А.
Длину диагонали грани можно найти по теореме Пифагора, или с применением тригонометрических зависимостей.
Тогда:
W = mgΔh = mgа(√2 – 1)/2 = 100×10×1×(1,414 — 1)/2 ≈ 207 Дж
***
Пример решения задачи из раздела кинематика
Автомобиль движется между городами Барнаул и Камень-на-Оби с постоянной скоростью v = 60 км/час.
Определить частоту вращения n колес автомобиля и сколько оборотов nl сделает каждое колесо в течение поездки, если диаметр колеса d = 0,6 м (считать, что колеса автомобиля катятся без пробуксовки).
Расстояние между городами принять равным l = 180 км.
Решение:
Для определения числа оборотов каждого колеса по пути следования, надо всю длину маршрута (180 км = 180 000 м) разделить на длину окружности колеса (lк = πd), тогда:
nl = 180 000/πd ≈ 95541 оборотов.
Для определения частоты вращения колеса можно определить время в пути автомобиля между городами
(t = S/v = 3 часа, т. е. 180 минут) и, разделив количество оборотов nl, совершенных колесом в пути на это время, определить число оборотов n колеса за одну минуту.
Получим:
n = 95541/180 ≈ 530 об/мин.
Задача решена.
***
Пример решения задачи из Статики
Балка висит на гибких связях горизонтально, нагружена собственным весом G, силой F и находится в состоянии равновесия.
Определить реакцию гибкой связи RА.
Исходные данные:
Вес балки G = 1200 Н;
Сила F = 600 Н;
Расположение гибких связей и силовых факторов приведено на схеме.
Решение:
Из условия равновесия балки: сумма моментов всех приложенных к ней сил относительно любой точки балки равна нулю.
Поскольку по условию задания нас интересует лишь реакция RA, то уравнение моментов составляем относительно точки В (момент неизвестной силы RВ относительно этой точки равен нулю), при этом силы, стремящиеся повернуть балку вокруг точки В по часовой стрелке, мы считаем положительными, против часовой стрелки – отрицательными.
Тогда:
4RA – 2G – F = 0, откуда: RA = (2G + F)/4 = 750 Н.
Задача решена.
***
Решение задачи из раздела Динамика
Для изображенной на схеме передачи определить вращающий момент Т2 на ведомом валу.
Исходные данные:
Мощность на ведущем валу Р1 = 8 кВт;
Угловая скорость ведущего вала ω1 = 40 рад/сек;
Коэффициент полезного действия передачи η = 0,97;
Передаточное число передачи u = 4.
Решение:
Сначала определим мощность Р2 на ведомом валу редуктора, с учетом потерь (исходя из величины КПД):
Р2 = ηР1 = 0,97×8000 = 7760 Вт
Для определения мощности ведомого вала необходимо знать его угловую скорость ω2, которая определяется из соотношения u = ω1/ω2, где u = 4 — передаточное число передачи. Получаем: ω2 = ω1/u = 10 рад/сек.
Вращающий момент равен отношению мощности ведомого вала к его угловой скорости:
Т2 = Р2/ω2 = 7760/10 = 776 Нм
Задача решена.
***
Задача из раздела динамика
Лебедка состоит из цилиндрической передачи и барабана, к которому посредством троса прикреплен груз G. Определить требуемую мощность Рм электродвигателя лебедки, если скорость подъема груза должна составлять v = 4 м/сек.
Исходные данные:
Вес груза G = 1000 Н;
Скорость подъема груза v = 4 м/сек;
КПД барабана лебедки ηб = 0,9;
КПД цилиндрической передачи ηц = 0,98;
Элементы конструкции приведены на схеме.
Решение:
Определим мощность на выходе из привода, необходимую для подъема груза с данной скоростью:
Р2 = Gv = 1000×4 = 4000 Вт.
Чтобы найти требуемую мощность электродвигателя для лебедки необходимо определить КПД всей передачи:
ηп = ηб×ηц = 0,9×0,98 = 0,882.
Требуемая мощность электродвигателя:
Рм = Р2 / ηп= 4000/0,882 ≈ 4535 Вт.
Задача решена.
***
Пример расчета пространственной конструкции или рамы
Правильные ответы на вопросы тестов:
Тест №1 2-4-1-3-4
Тест №2 1-3-4-4-1
Тест №3 3-1-1-2-2
Тест №4 4-2-2-3-3
Тест №5 2-1-1-1-4
Тест №6 3-2-4-2-3
Тест №7 2-2-1-1-3
Тест №8 1-4-1-2-2
Тест №9 3-2-4-4-1
Тест №10 1-1-4-2-3
k-a-t.ru
Ответы на задачи по технической механике
Рейтинг ↑ не забываем
Порядок действий при демонтаже кондиционеров (посмотреть)
Свод правил вентиляции и кондиционирования 2017 год (посмотреть)
Условные обозначения систем вентиляции и кондиционирования (посмотреть)
Ответы на задачи по технической механике
Задача № 29 Найти реакцию опор
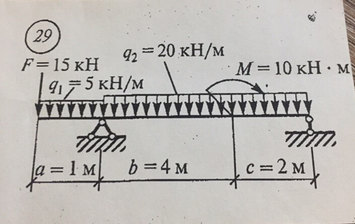
Ответ к задачи №29
Задача № 20 Натяжка троса
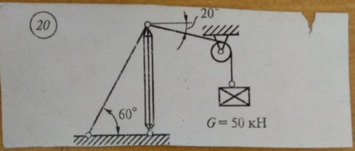
Ответ к задачи № 20
Задача №7 Найти реакцию опор
Ответ к задаче №7
Задача № 9 Распределение нагрузки
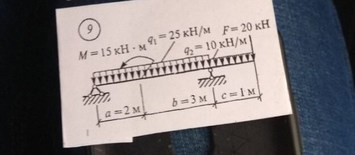
Ответ к задачи № 9
Задача № 11 Определить координаты центра тяжести сечения
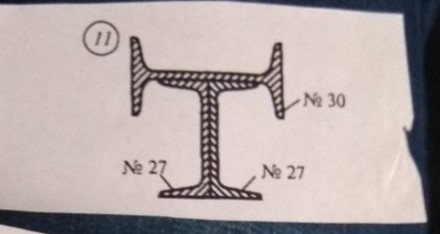
Ответ к задачи № 11 С решением
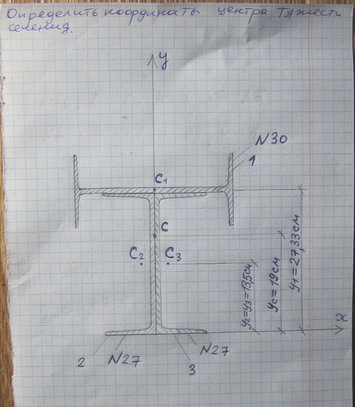
Задача № 12 Найти реакцию опор
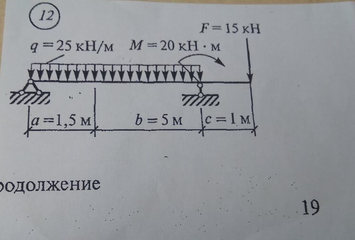
Ответ к задачи №12
Задача № 13 Решить графически
Ответ к задаче №13
Задача № 33 Решить графически
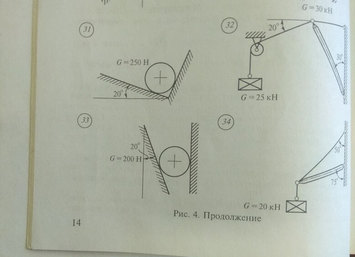
Ответ к задачи № 33
Задача № 33 Силы давящие на шар
Ответ к задачи № 33 Силы давящие на шар
Задача № Задача №21 Определить координат центра тяжести
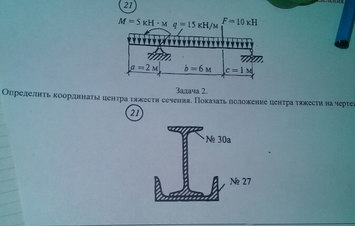
Ответ к задаче № 21 Определить координат центра тяжести
Ответ № 21 /2 Определить координат центра тяжести 30А Ответ на координат центр тяжести № 21 -27
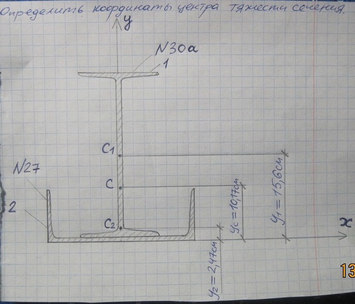
Задача № 20 Определить опорные реакции балки.Проверить правильность их определения
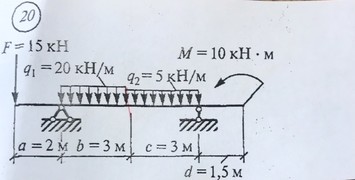
Ответ к задачи № 20 Определить опорные реакции балки.Проверить правильность их определения
Задача № 22 Задача № 22 найти R(a) и R(b)
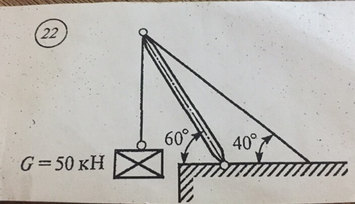
Ответ к задачи Задача № 22 найти R(a) и R(b)
Задача Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
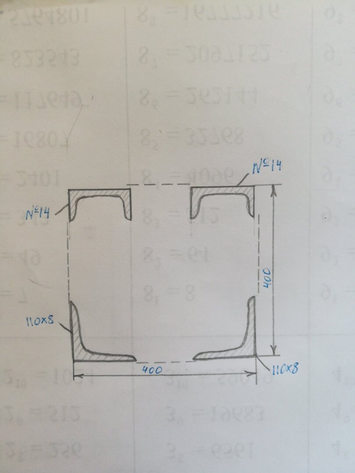
Ответ к задачи Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Задача № 10 Найти реакцию опор
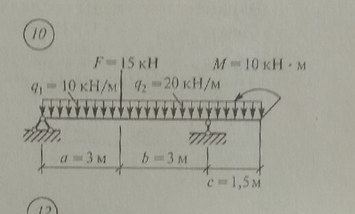
Ответ к задачи №10 Найти реакцию опор
Задача № 16 Определить опорные реакции балки.Проверить правильность их определения
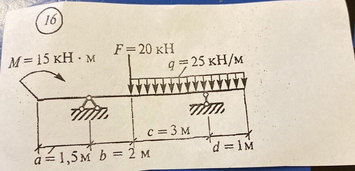
Ответ к задачи № 16
Задача № 22 Определить опорные реакции балки. Проверить правильность их определения
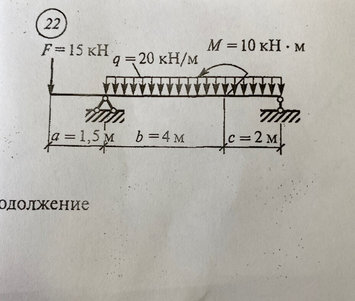
Ответ к задачи № 22 Определить опорные реакции балки Проверить правильность их определения
Задача № 27 Определить опорные реакции балки Проверить правильность их определения
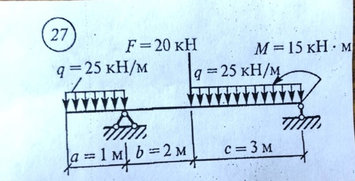
Ответ к задачи № 27 Определить опорные реакции балки Проверить правильность их определения
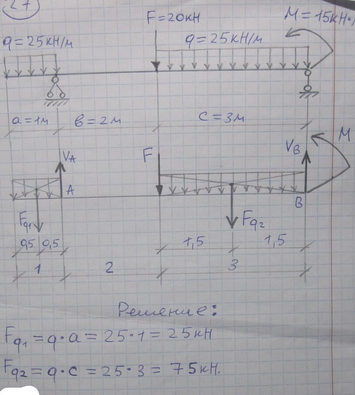
Задача № 26 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 26 Определить опорные реакции балки Проверить правильность их определения
Вариант 32 задача № 1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Ответ к варианту 32 задача №1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Вариант 32 задача №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
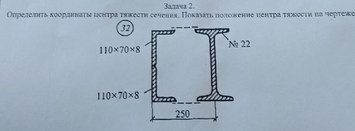
Ответ к варианту 32 №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Решение к варианту 32 № 2
Вариант 24 задача № 2 Определить координаты центра тяжести сечения Показать положения центра тяжести на чертеже
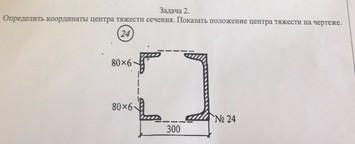
Ответ к варианту 24 задача № 2 Определить координаты центра тяжести сечения
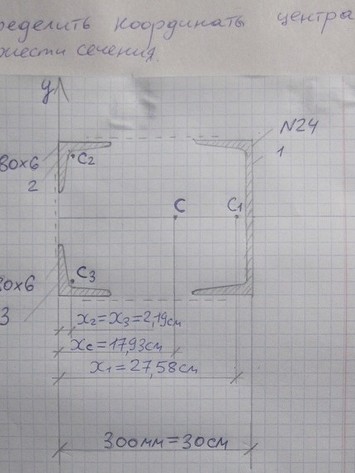
Задача Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
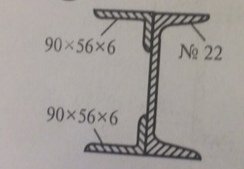
Ответ к задачи Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Задача — Определить величину и направления реакцию связей
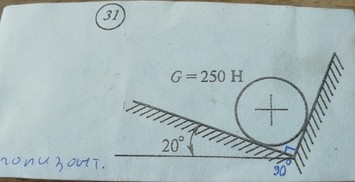
Ответ к задаче -Определить величину и направления реакций связей
Задача- Определить опорные реакции балки на 2-х опорах
Ответ к задачи Определить опорные реакции балки на 2-х опорах
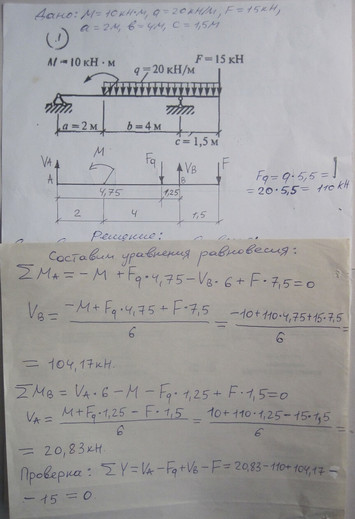
Задача № 9 Найти центр тяжести
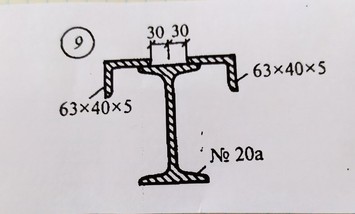
Ответ к задаче № 9 найти центр тяжести
Найти центр тяжести
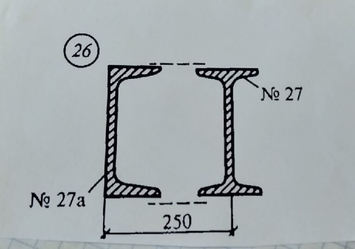
Решение к задаче Найти центр тяжести
Задача № 7
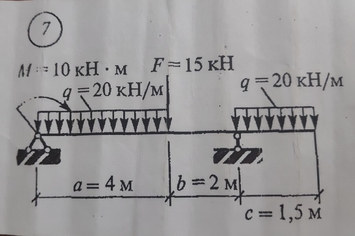
Решение к задаче № 7
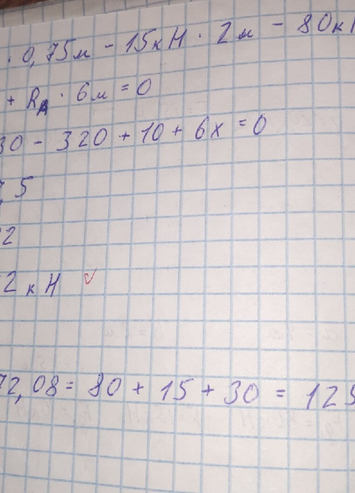
28 задача Определить положение координаты центра тяжести
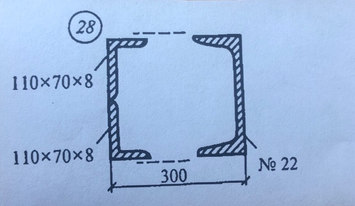
Ответ к 28 задачи Определить положение координаты центра тяжести
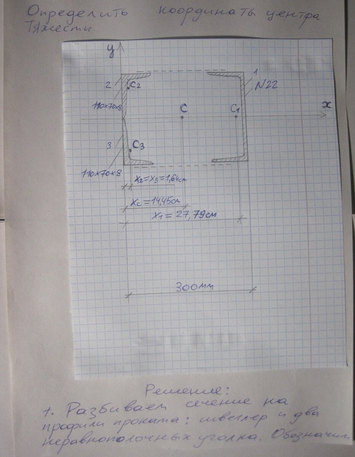
Задача Найти центр тяжести
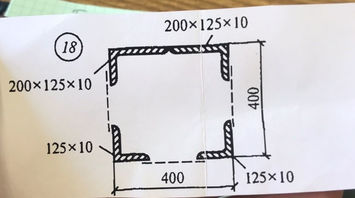
Ответ к задаче Найти центр тяжести
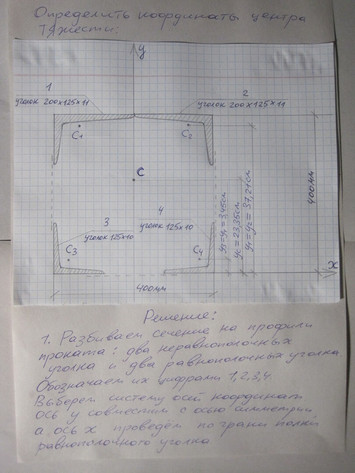
Задача № 16 Определить положение координаты центра тяжести
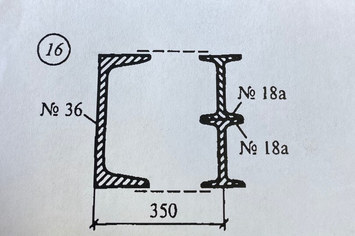
Ответ к задаче № 16 Определить положение координаты центра тяжести
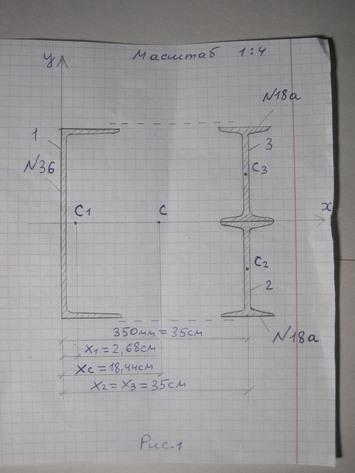
Ответ к задаче № 16 Определить положение координаты центра тяжести
Задача №23 Определить кординаты центра тяжести сечения
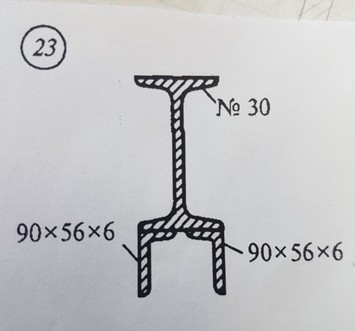
Ответ к задаче № 23 Определить координаты центра тяжести сечения
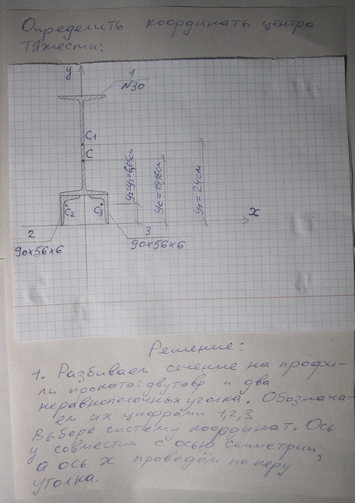
Определить опорные реакции балки
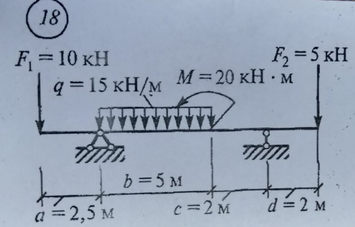
Ответ к задаче Определить опорные реакции балки
Определить опорные реакции балки
Ответ к задаче Определить опорные реакции балки
Определить координат центр тяжести
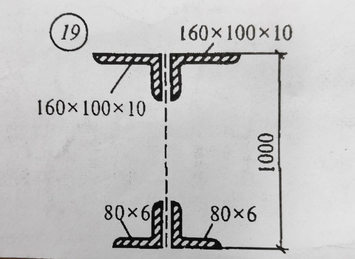
Ответ к задаче определить координат центр тяжести
Задача №20 Найти центр тяжести
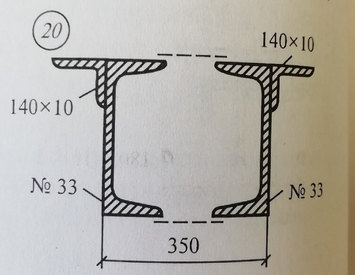
Ответ к Задаче №20 Найти центр тяжести
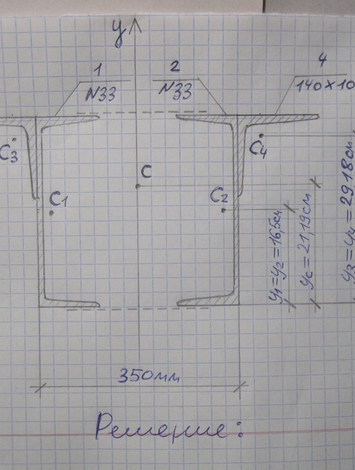
Задача: Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Ответ к задаче: Определить опорные реакции балки на двух опорах. Проверить правильность их определения 
Задача Определить центр тяжести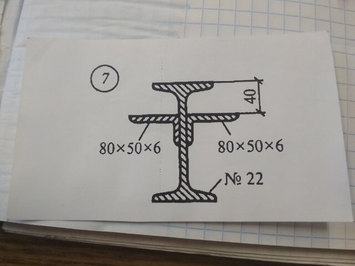 
Ответ к задаче — Определить центр тяжести
www.condei-chehov.ru
Раздел «Статика» теоретической механики — Лекции и примеры решения задач технической механики
Данный раздел учебно-методического пособия предназначен для оказания методической помощи студентам при выполнении контрольных работ и расчетно-графических заданий по разделу «Статика» дисциплины «Теоретическая механика».
В пособии приведены аксиомы статики, основные понятия и определения статики твердого тела, подробно разобраны примеры решения задач на равновесие твердого тела.
Данное пособие не исключает дополнительного изучения курса по учебникам, в которых более подробно изложены основные понятия, определения, доказательства теорем, что способствует развитию логического мышления и более успешному закреплению материала, необходимого для сдачи экзамена и изучения других разделов курса теоретической механики и родственных дисциплин, таких как сопротивление материалов и детали машин
Основные понятия статики
В окружающем нас пространстве тела могут перемещаться или покоиться, т.е. находиться в равновесии.
В разделе «Статика» устанавливаются условия равновесия сил, приложенных к твердому телу.
Исходя из этих условий рассчитываются опоры различных конструкций, сооружений, механизмов.
Основой для всех теорем являются аксиомы статики.
Содержание раздела
- Основные понятия и определения
- Аксиомы статики
- Связи и их реакции
- Проекция силы на ось
- Момент силы
- Плечо силы
- Момент силы относительно точки
- Теорема Вариньона
- Момент силы относительно оси
- Пара сил
- Распределенные нагрузки
- Равновесие системы
- Уравнения равновесия системы сил
- Cистема сходящихся сил
- Равновесие системы сходящихся сил
- Система сходящихся сил. Приведение к равнодействующей и ее вычисление
- Условия равновесия системы сходящихся сил
- Равновесие пространственной системы сходящихся сил
- Исследование равновесия тела под действием произвольной плоской системы сил
- Произвольная плоская система сил
- Равновесие произвольной плоской системы сил
- Первая форма условия равновесия
- Вторая форма условия равновесия (теорема о трех моментах)
- Третья форма условия равновесия
- Составные и соединенные конструкции
- Равновесие составных конструкций под действием плоской системы сил
- Равновесие твердого тела при наличии трения
- Сила трения
- Сила трения скольжения
- Сила трения качения
- Произвольная пространственная система сил
- Равновесие произвольной пространственной системы сил
- Момент относительно точки
- Момент относительно оси
- Связь момента силы относительно оси с моментом силы относительно точки
- Условия равновесия произвольной пространственной системы сил
- Центр тяжести
- Центр параллельных сил
- Центр тяжести
- Способы определения координат центра тяжести
- Центры тяжести простейших фигур
isopromat.ru
Контрольная работа №1 по разделу «Теоретическая механика»
Тема 1.2. Плоская система сходящихся сил
Знать способы сложения двух сил и разложение силы на составляющие, геометрический и аналитический способы определения равнодействующей силы, условия равновесия плоской сходящейся системы сил.
Уметь определять равнодействующую системы сил, решать задачи на равновесие геометрическим и аналитическим способом, рационально выбирая координатные оси.
Расчетные формулы
Равнодействующая системы сил
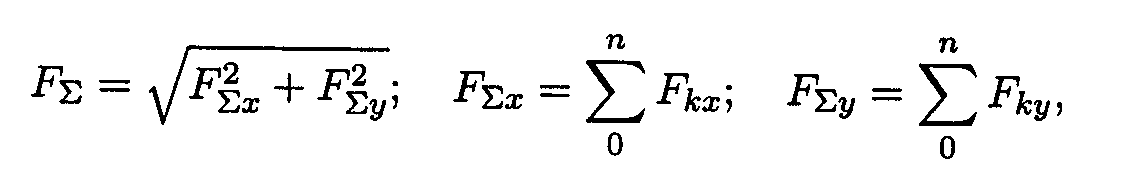
где PΣx, PΣy — проекции равнодействующей на оси координат; Pkx, Pky — проекции векторов-сил системы на оси координат.
Где αΣх — угол равнодействующей с осьюОх.
Условие равновесия
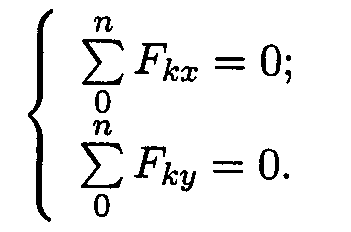
Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.
Пример 1.Определение равнодействующей системы сил
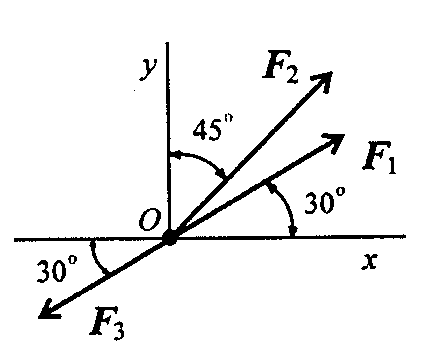
Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П 1.1).
Дано: F1 = 10кН;F2 = 15кН;F3 = 12кН;F4 = 8кН;F5 = 8кН;
αl = 30˚; α2 = 60˚; α3= 120˚; α4 = 180˚; α5 = 300˚.
Решение
1. Определить равнодействующую аналитическим способом (рис. П 1.1а).
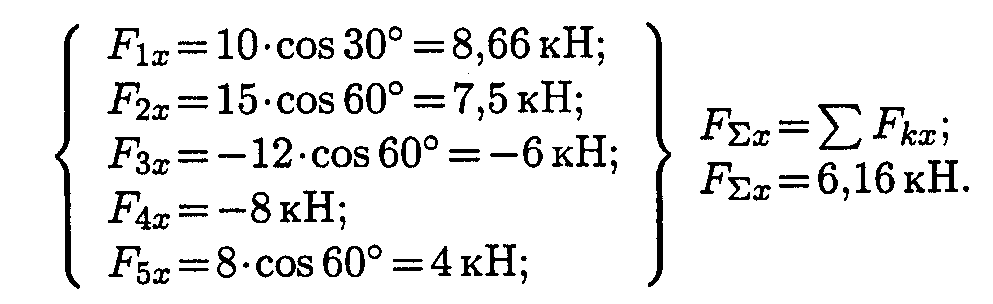
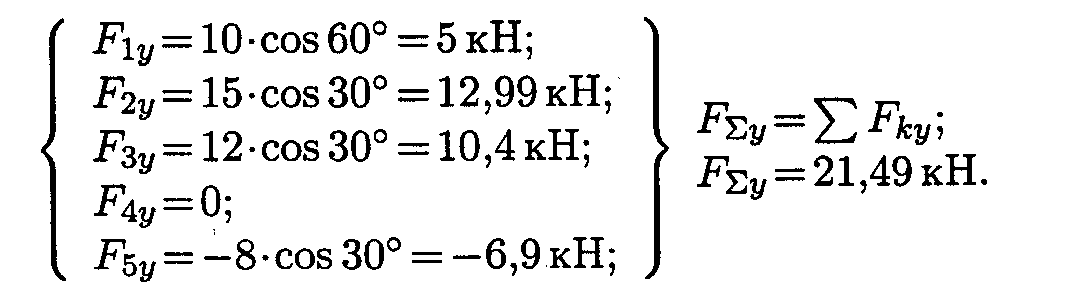
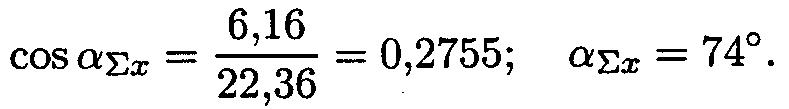
2. Определить равнодействующую графическим способом.
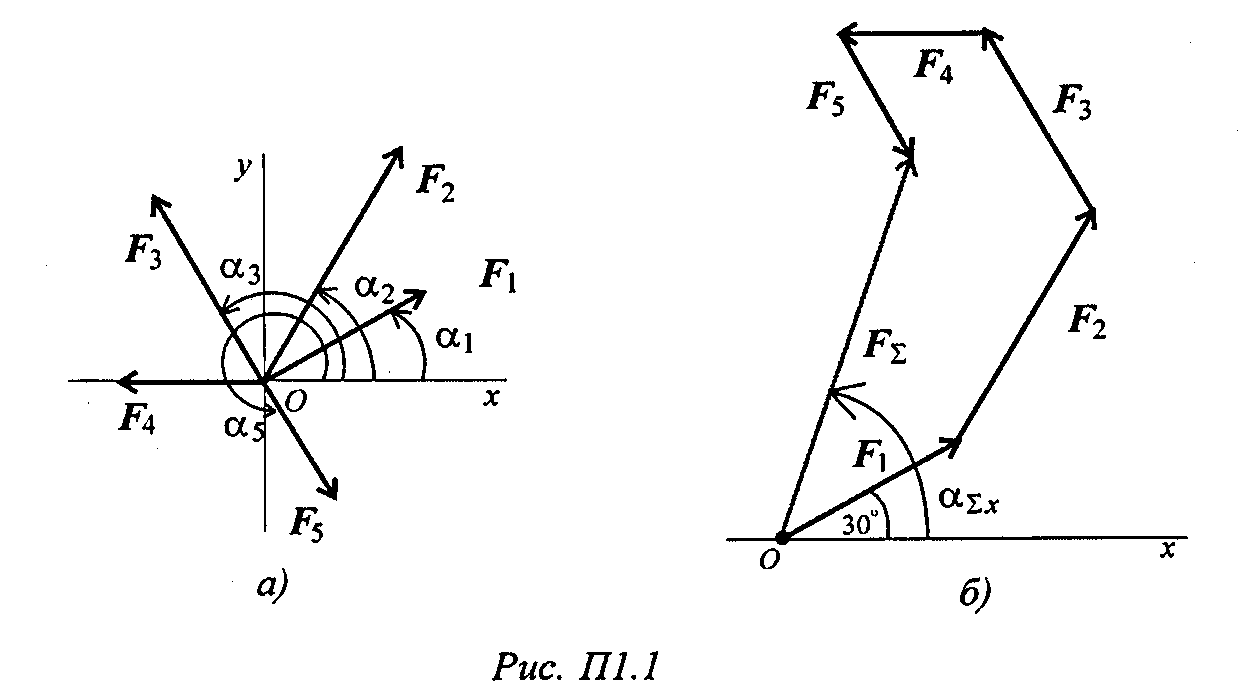
С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П l.l 6). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.
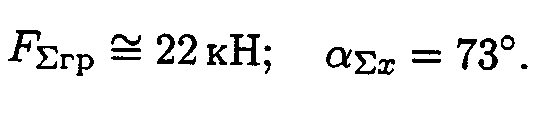
Результаты расчетов не должны отличаться более чем на 5 %:
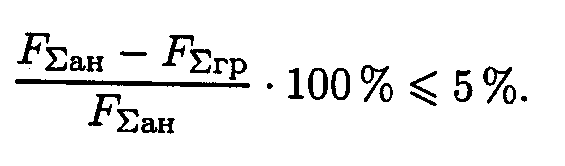
Задание № 1
Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами.
Задание. Используя схему рис. П. 1.1а, определить равнодействующую системы сил.
Параметр | Вариант | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
F1, кН | 12 | 8 | 20 | 3 | 6 | 8 | 20 | 12 | 8 | 3 |
F2, кН | 8 | 12 | 5 | 6 | 12 | 12 | 5 | 8 | 12 | 6 |
F3, кН | 6 | 2 | 10 | 12 | 15 | 2 | 10 | 6 | 2 | 12 |
F4, кН | 4 | 10 | 15 | 15 | 3 | 10 | 15 | 4 | 10 | 15 |
F5, кН | 10 | 6 | 10 | 9 | 18 | 6 | 10 | 10 | 6 | 9 |
| 30 | О | О | 15 | О | 30 | 30 | 30 | О | О |
| 45 | 45 | 60 | 45 | 15 | 45 | 45 | 45 | 60 | 60 |
| О | 75 | 75 | 60 | 45 | О | О | О | 75 | 75 |
| 60 | 30 | 150 | 120 | 150 | 60 | 60 | 60 | 50 | 15 |
| 300 | 270 | 210 | 270 | 300 | 300 | 300 | 300 | 10 | 20 |
1,град
2,град
3,град
4,град
5,градПараметр | Вариант | |||||||||
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
F1, кН | 20 | 12 | 3 | 20 | 8 | 10 | 8 | 2 | 3 | 16 |
F2, кН | 5 | 8 | 6 | 5 | 12 | 9 | 10 | 15 | 16 | 2 |
F3, кН | 10 | 6 | 12 | 10 | 2 | 6 | 2 | 11 | 10 | 12 |
F4, кН | 15 | 4 | 15 | 15 | 10 | 4 | 12 | 15 | 5 | 6 |
F5, кН | 10 | 10 | 9 | 10 | 6 | 12 | 7 | 10 | 7 | 8 |
| 15 | 30 | О | О | 30 | 30 | О | О | 15 | О |
| 45 | 45 | 15 | 15 | 45 | 45 | 45 | 60 | 45 | 15 |
| 60 | О | 45 | 45 | О | О | 75 | 75 | 60 | 45 |
| 120 | 60 | 150 | 150 | 60 | 60 | 30 | 150 | 0 | 90 |
| 270 | 300 | 300 | 300 | 300 | 300 | 270 | 210 | 270 | 30 |
1,град
2,град
3,град
4,град
5,градПараметр | Вариант | |||||||||
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
F1, кН | 8 | 2 | 13 | 9 | 3 | 4 | 6 | 2 | 20 | 8 |
F2, кН | 15 | 15 | 7 | 14 | 16 | 15 | 18 | 6 | 5 | 12 |
F3, кН | 13 | 14 | 15 | 16 | 17 | 20 | 1 | 2 | 3 | 2 |
F4, кН | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 | 5 | 10 |
F5, кН | 9 | 10 | 11 | 20 | 19 | 18 | 15 | 12 | 13 | 6 |
| 30 | 30 | 30 | О | О | 15 | 30 | О | О | 90 |
| 45 | 45 | 45 | 60 | 60 | 0 | 45 | 15 | 15 | 45 |
| О | О | О | 75 | 75 | 60 | О | 45 | 45 | 30 |
| 60 | 60 | 60 | 150 | 150 | 120 | 60 | 150 | 150 | 85 |
| 300 | 300 | 300 | 210 | 210 | 270 | 300 | 300 | 300 | 60 |
1,град
2,град
3,град
4,град
5,градПример 2. Решение задачи на равновесие аналитическим способом
Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рис. Пl.2).
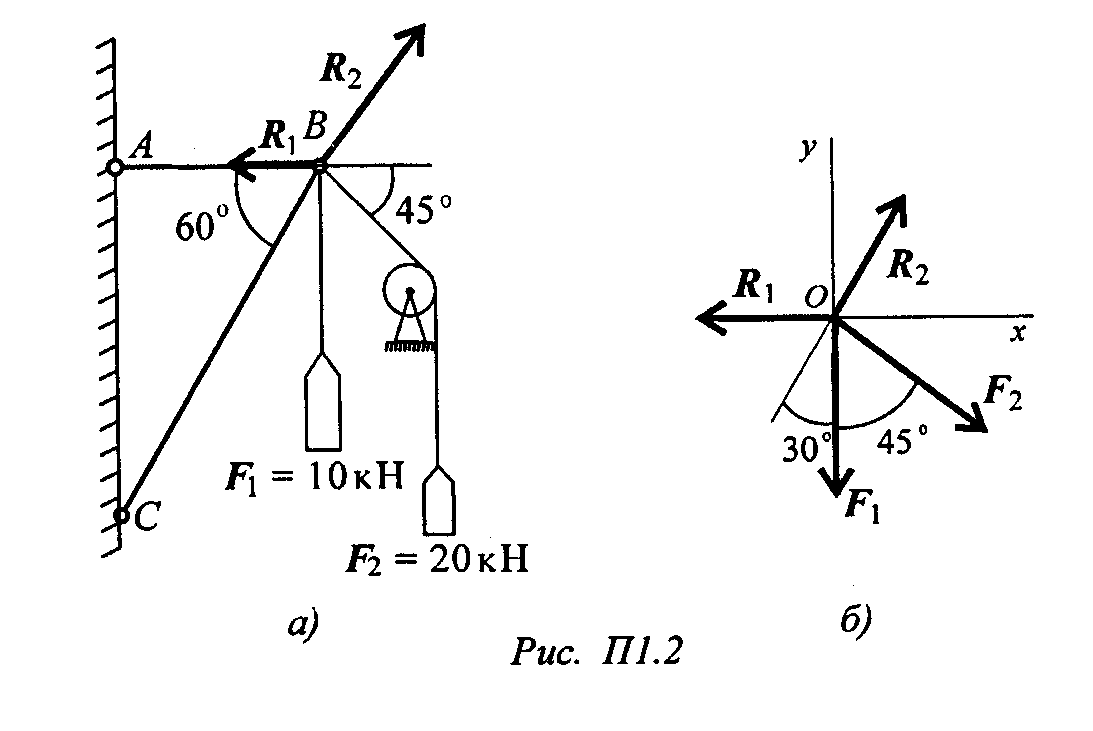
Решение.
1. Определяем вероятные направления реакций (рис. П1.2а).
Мысленно убираем стержень АВ, при этом стержень С В опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень С В поддерживает точку В снизу — реакция направлена вверх.
2. Освобождаем точку В от связи (рис. П1.2б).
3. Выберем направление осей координат, ось Ох совпадает с реакцией Rl.
4. Запишем уравнения равновесия точки В:
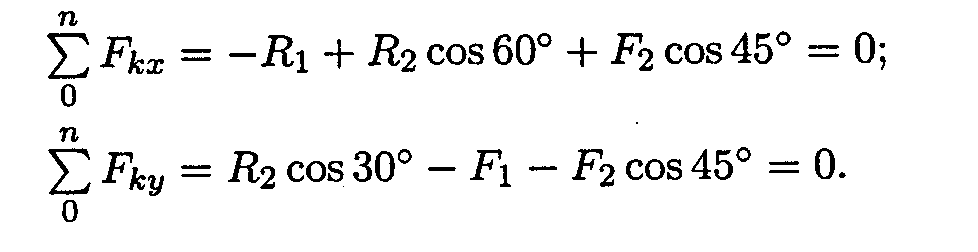
5. Из второго уравнения получаем:
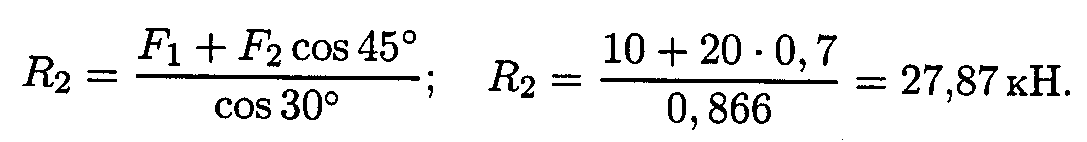
Из первого уравнения получаем:
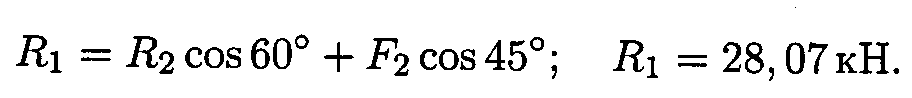
Вывод: стержень АВ растянут силой 28,07 кН, стержень СВ сжат силой 27,87 кН.
Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.
В данном случае реакции направлены, верно.
Задание № 2
Условие равновесия плоской системы сходящихся сил в аналитической форме.
З
адание.Определить реакции стержней АС и AD (рис.
П l.3).
Параметры | Варианты. | ||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 40 | 45 | 48 | 50 | 56 | 58 | 61 | 63 | 67 | 72 | 75 | 78 | 80 | 86 | 82 |
| 60 | 45 | 75 | 60 | 45 | 30 | 35 | 40 | 55 | 60 | 65 | 70 | 75 | 75 | 80 |
| 15 | 30 | 30 | 15 | 45 | 10 | 20 | 15 | 30 | 35 | 45 | 35 | 20 | 25 | 30 |
| 60 | 45 | 60 | 75 | 75 | 50 | 55 | 65 | 60 | 70 | 75 | 80 | 85 | 30 | 35 |
G,
кН.
,
град.
,
град.
,
град.Параметры | Варианты. | ||||||||||||||
16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 45 | 48 | 50 | 56 | 58 | 61 | 63 | 67 | 72 | 75 | 78 | 86 | 45 | 30 | 35 |
| 60 | 45 | 30 | 75 | 45 | 40 | 55 | 60 | 35 | 30 | 50 | 60 | 65 | 45 | 20 |
| 15 | 45 | 10 | 30 | 35 | 45 | 20 | 25 | 30 | 20 | 15 | 35 | 20 | 10 | 40 |
| 70 | 75 | 80 | 55 | 55 | 65 | 40 | 45 | 60 | 80 | 90 | 35 | 85 | 30 | 35 |
G,
кН.
,
град.
,
град.
,
град.Тест для самоконтроля:
Темы 1.1, 1.2. Статика.
Плоская сходящаяся система сил.
Вопросы | Ответы | Код |
1. Определить проекции равнодействующей на ось Ох при F1 = 10кН; F2 = 20кН; F3 = 30кН. | Rx = 4,99kH | 1 |
Rx = 7,89kH | 2 | |
Rx = -3,18kH | 3 | |
Rx =6,55kH | 4 | |
2. Определить величину равнодействующей силы по ее известным проекциям: Rx = 15 кН; Ry= 8,66 кН. | 23,66kH | 1 |
17,32kH | 2 | |
9,50kH | 3 | |
8,50kH | 4 | |
3. Как направлен вектор равнодействующей системы сил, если известно, что Rx = -4кН; Ry= 12кН? |
| 1 |
| 2 | |
| 3 | |
| 4 |
Вопросы | Ответы | Код |
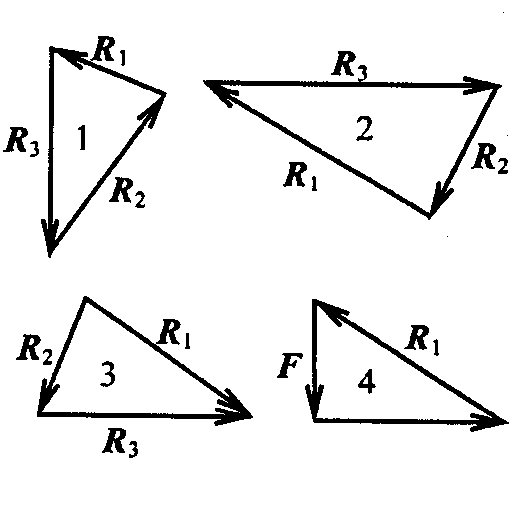
4. Груз находится в равновесии. Указать, какой из треугольников для шарнира В построен верно.
|
| 1 |
2 | ||
3 | ||
4 | ||
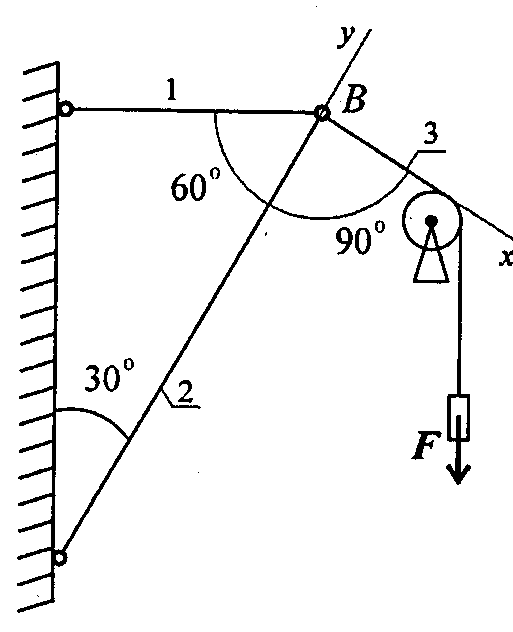
5. Груз F находится в равновесии. Указать, какая система уравнений равновесия для точки В верна.
|
| 1 |
| 2 | |
| 3 | |
Верный ответ не приведен | 4 |
studfile.net