Потенциальная энергия | Все Формулы

Потенциальная энергия — Чтобы увеличить расстояние тела от центра Земли (поднять тело), над ним следует совершить работу. Эта работа против силы тяжести запасается в виде потенциальной энергии тела.

   

Для того, чтоб понять что же такое потенциальная энергия тела найдем работу, совершаемую силой тяжести

   

при перемещении тела массой m вертикально вниз с высоты

   

над поверхностью Земли до высоты

   

.

Если разность

   

пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяготения

   

во время движения тела можно считать постоянной и равной mg.

Так как перемещение совпадает по направлению с вектором силы тяжести то получается, что

   

, работа силы тяжести равна

   

Из последней формулы видно, что работа силы тяжести при переносе материальной точки массой m в поле тяготения Земли равна разности двух значений некоторой величины

   

. Поскольку работа есть мера изменения энергии, то в правой части формулы стоит разность двух значений энергии этого тела. Это значит, что величина

   

представляет собой энергию, обусловленную положением тела в поле тяготения Земли.

Энергию, обусловленную взаимным расположением взаимодействующих между собой тел (или частей одного тела), называют потенциальной и обозначают Wp. Следовательно, для тела, находящегося в поле тяготения Земли,

   

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

   

Работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, то есть высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия тела, находящегося на высоте h над поверхностью Земли, равна произведению массы тела на Модуль ускорения свободного падения и расстояние его от поверхности Земли:

   

Из всего выше сказанного, можем сделать вывод: потенциальная энергия тела зависит всего от двух величин, а именно: от массы самого тела и высоты, на которую поднято это тело. Траектория движения тела никак не влияет на потенциальную энергию.

Потенциальная энергия упруго деформированного тела. Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

   

Потенциальная энергия упруго деформированного тела

   

Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Так же есть:

Кинетическая энергия

   

В формуле мы использовали :

   

— Потенциальная энергия

m — Масса тела

   

— Ускорение свободного падения

   

— Высота на которую поднято тело

A — Работа силы тяжести

   

— Сила тяжести

   

— Перемещение тела

k — Жесткость пружины

x — Деформация пружины

   

— Угол между направлением тела и силой тяжести

Потенциальная энергия: определение, виды, формулы

Определение потенциальной энергии

Энергия, говоря простым языком, это возможность что-либо сделать, возможность совершить работу. То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.

Энергию, связанную с взаимодействием тел, называют ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ. Иначе говоря, если тело за счёт взаимодействия с другим телом может совершить некоторую работу, то оно будет обладать потенциальной энергией, и при совершении работы будет происходить изменение этой энергии. Обозначают механическую потенциальную энергию чаще всего — Еп.

Виды потенциальной энергии

Существуют различные виды потенциальной энергии. К примеру, любое тело на Земле находится в гравитационном взаимодействии с Землёй, а значит обладает потенциальной энергией гравитационного взаимодействия. И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.

Далее мы рассмотрим только виды механической потенциальной энергии и формулы, по которым их можно рассчитать. Но в дальнейшем вы узнаете и о других видах потенциальной энергии — к примеру, о потенциальной энергии электрического взаимодействия заряженных тел, о потенциальной энергии взаимодействия электрона с атомным ядром.

Знакомьтесь: наш мир. Физика всего на свете.

Книга адресована школьникам старших классов, студентам, преподавателям и учителям физики, а также всем тем, кто хочет понять, что происходит в мире вокруг нас, и воспитать в себе научный взгляд на все многообразие явлений природы. Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.

Купить

Формулы потенциальной энергии

Перед тем как приступить к выводу формул потенциальной энергии, ещё раз вспомним, что совершённая телом или над телом работа равна изменению его энергии. При этом, если само тело совершает работу, то его энергия уменьшается, а если над телом совершают работу, то его энергия увеличивается. К примеру, если спортсмен поднимает штангу, то он сообщает ей потенциальную энергию гравитационного взаимодействия, а если он отпускает штангу и она падает, то потенциальная энергия гравитационного взаимодействия штанги с Землёй уменьшается. Также, если вы открываете дверь, растягивая пружину, то вы сообщаете пружине потенциальную энергию упругого взаимодействия, но если потом дверь закрывается, благодаря сжатию пружины в начальное состояние, то и энергия упругой деформации пружины уменьшается до нуля.

А) Чтобы вывести формулу потенциальной энергии гравитационного взаимодействия, рассмотрим, какую работу совершает тело, двигаясь под действием силы тяжести:

А = F*s = mg*s = mg*(h₁ — h₂) = mgh₁ — mgh₂ = Eп₁ — Еп₂, то есть, мы получили, что потенциальная энергия гравитационного взаимодействия тела с Землёй может быть вычислена по формуле: Еп = mgh.

Здесь важно отметить, что поверхность Земли принимается за начало отсчёта высоты, то есть для тела, находящегося на поверхности Земли Еп = 0, для тела, поднятого над Землёй Еп > 0, а для тела, находящегося в яме глубиной h, Еп < 0.

Отметим также и то, что в формуле работы отсутсвовал cosa. Это не случайно. Ведь если тело движется по сложной траектории, то, какой бы сложной она ни была, её можно разбить на множество вертикальных и горизонтальных участков. Но на горизонтальных участках работа силы тяжести будет равна нулю, так как угол между силой тяжести и перемещением будет прямым, а значит работа будет совершаться только на вертикальных участках траектории, для которых cosa = 1 или cosa = −1.

Тогда можно сделать ещё один важный вывод — работа силы тяжести не зависит от формы траектории, а только от расположения начальной и конечной точки. А это не случайность — это свойство любых сил, сообщающих телам потенциальную энергию. Такие силы называют потенциальными и сила тяжести — одна из них. К потенциальным силам относится и сила упругости.

Б) Чтобы вывести формулу потенциальной энергии упругой деформации, рассмотрим, какую работу нужно совершить, чтобы растянуть пружину, изменив её длину на х (х = l — l₀):

А = –Fупр(ср.)*s,

Во-первых, знак минус в формуле стоит потому, что угол между силой упругости и перемещением свободного конца пружины равен 180 градусов и cosa = −1.

Во-вторых, возникающая при растяжении пружины сила упругости является переменной силой, в отличие от силы тяжести, поэтому в формуле работы стоит средняя сила упругости. При этом величина силы упругости, в соответствии с законом Гука, прямо пропорциональна изменению длины пружины, а значит её среднее значение можно определить так:

Fупр(ср.) = (Fупр(нач.) + Fупр(конеч.))/2

И так как Fупр(нач.) = 0, а Fупр(конеч.) = kх, то:

А = —kх*s/2

Но s = x, поэтому: А = —kx²/2 = 0 — kх²/2 = Еп₁ — Еп₂.

В итоге, мы получили формулу потенциальной энергии упругой деформации: Еп = kx²/2.

Что еще почитать?

Методические советы учителям

1) Обязательно обратите внимание учащихся на связь энергии и работы.

2) Не давайте учащимся формулы потенциальной энергии без вывода.

3) Обратите внимание учащихся на то, что оба вида потенциальной энергии зависят от выбора начальной точки, то есть от системы координат.

4) При выводе формул потенциальной энергии обязательно поясните учащимся почему отсутствует cosa в формуле работы.

5) Отметьте, что и работа силы тяжести, и работа силы упругости не зависят от формы траектории и, следовательно равны нулю на замкнутой траектории — это общее и важное свойство всех потенциальных сил.

#ADVERTISING_INSERT#

Потенциальная энергия — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Потенциал.

Потенциальная энергия U(r→){\displaystyle U({\vec {r}})} — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения

материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении^[1]. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы и описывающая взаимодействие элементов системы

[2]. Помимо символа U{\displaystyle U}, для потенциальной энергии могут использоваться обозначения  Ep{\displaystyle \ E_{p}},  W{\displaystyle \ W} и другие.

Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в Международной системе единиц (СИ) является джоуль, а в системе СГС — эрг.

О физическом смысле понятия потенциальной энергии

В то время как кинетическая энергия всегда характеризует тело относительно выбранной системы отсчёта, потенциальная энергия всегда характеризует тело относительно источника силы (силового поля). Кинетическая энергия тела определяется его скоростью относительно выбранной системы отсчёта; потенциальная — расположением тел в поле.

Потенциальная энергия определяется с точностью до постоянного слагаемого^[3] (приводимые в следующем разделе выражения для Ep{\displaystyle E_{p}} могут быть дополнены произвольным фиксированным членом +Ep0{\displaystyle +E_{p0}}). Однако основной физический смысл имеет не само значение потенциальной энергии, а её изменение: например, сила, действующая со стороны потенциального поля на тело, записывается (∇{\displaystyle \nabla } — оператор набла) как

F→(r→)=−∇Ep(r→),{\displaystyle {\vec {F}}({\vec {r}})=-\nabla E_{p}({\vec {r}}),}

или, в простом одномерном случае,

F(x)=−dEp(x)/dx,{\displaystyle F(x)=-{\rm {d}}E_{p}(x)/{\rm {d}}x,}

так что произвол выбора Ep0{\displaystyle E_{p0}} не сказывается.

Виды потенциальной энергии

В поле тяготения Земли

Потенциальная энергия тела  Ep{\displaystyle \ E_{p}} в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

 Ep=mgh,{\displaystyle \ E_{p}=mgh,}

где  m{\displaystyle \ m} — масса тела,  g{\displaystyle \ g} — ускорение свободного падения,  h{\displaystyle \ h} — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

В электростатическом поле

Потенциальная энергия материальной точки, несущей электрический заряд  qp{\displaystyle \ q_{p}}, в электростатическом поле с потенциалом φ(r→){\displaystyle \varphi ({\vec {r}})} составляет:

 Ep=qpφ(r→).{\displaystyle \ E_{p}=q_{p}\varphi ({\vec {r}}).}

Например, если поле создаётся точечным зарядом  q {\displaystyle \ q\ } в вакууме, то будет  Ep=qpq/4πε0r{\displaystyle \ E_{p}=q_{p}q/4\pi \varepsilon _{0}r} (записано в системе СИ), где r{\displaystyle r} — расстояние между зарядами  q {\displaystyle \ q\ } и  qp{\displaystyle \ q_{p}}, а  ε0{\displaystyle \ \varepsilon _{0}} — электрическая постоянная.

В механической системе

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела и приближённо выражается формулой:

Ep=k(Δx)22,{\displaystyle E_{p}={\frac {k(\Delta x)^{2}}{2}},}

где k{\displaystyle k} — жёсткость деформированного тела, Δx{\displaystyle \Delta x} — смещение от положения равновесия.

См. также

Ссылки

§ 12. Кинетическая и потенциальная энергии

Кинетическая энергия механической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает рабо­ту, а энергия движущегося тела возраста­ет на величину затраченной работы. Таким образом, работа dA силы F на пути, кото­рый тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.

dA= dT.

Используя второй закон Ньютона F=mdv/dt

и умножая обе части равен­ства на перемещение dr, получим

Fdr =m(dv/dt)dr=dA

23

Таким образом, тело массой т, движущее­ся со скоростью v, обладает кинетической энергией

Т = тv²/2. (12.1)

Из формулы (12.1) видно, что кинети­ческая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее дви­жения.

При выводе формулы (12.1) предпола­галось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать за­коны Ньютона. В разных инерциальных системах отсчета, движущихся друг отно­сительно друга, скорость тела, а следова­тельно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетиче­ская энергия зависит от выбора системы отсчета.

Потенциальная энергия — механиче­ская энергия системы тел, определяемая их взаимным расположением и характе­ром сил взаимодействия между ними.

Пусть взаимодействие тел осуществля­ется посредством силовых полей (напри­мер, поля упругих сил, поля гравитацион­ных сил), характеризующихся тем, что работа, совершаемая действующими сила­ми при перемещении тела из одного поло­жения в другое, не зависит от того, по какой траектории это перемещение прои­зошло, а зависит только от начального и конечного положений. Такие поля на­зываются потенциальными, а силы, дей­ствующие в них,— консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является си­ла трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией II. Работа консервативных сил при элемен­тарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

dA=-dП. (12.2)

Работа dА выражается как скалярное произведение силы F на перемещение dr и выражение (12.2) можно записать в виде

Fdr=-dП. (12.3)

Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению.

Потенциальная энергия может быть определена исходя из (12.3) как

где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной по­стоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциаль­ную энергию тела в каком-то определен­ном положении считают равной нулю (вы­бирают нулевой уровень отсчета), а энер­гию тела в других положениях отсчитыва­ют относительно нулевого уровня. Для консервативных сил

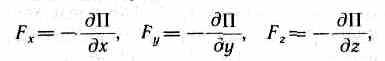
или в векторном виде

F=-gradП, (12.4) где

(i, j, k — единичные векторы координат­ных осей). Вектор, определяемый выраже­нием (12.5), называется градиентом ска­ляра П.

24

Для него наряду с обозначением grad П применяется также обозначение П.  («набла») означает символический вектор, называе­мый оператором Гамильтона или набла-оператором:

Конкретный вид функции П зависит от характера силового поля. Например, по­тенциальная энергия тела массой т, под­нятого на высоту h над поверхностью Зем­ли, равна

П = mgh, (12.7)

где высота h отсчитывается от нулевого уровня, для которого П₀ = 0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.

Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (ки­нетическая энергия всегда положитель­на!}. Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h’), П=—mgh’.

Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна дефор­мации:

F_{х упр}= -kx,

где F_xупр — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а знак минус ука­зывает, что F_{x упр} направлена в сторону, противоположную деформации х.

По третьему закону Ньютона, дефор­мирующая сила равна по модулю силе упругости и противоположно ей направле­на, т. е.

F_x=-F_{x упр}=kx Элементарная работа dA, совершаемая силой F_x при бесконечно малой деформации dx, равна

dA = F_x dx = kxdx,

а полная работа

идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела

П=kx²/2.

Потенциальная энергия системы, подо­бно кинетической энергии, является функ­цией состояния системы. Она зависит толь­ко от конфигурации системы и ее положе­ния по отношению к внешним телам.

Полная механическая энергия систе­мы — энергия механического движения и взаимодействия:

Е = Е+П,

т. е. равна сумме кинетической и потен­циальной энергий.

Электростатический потенциал — Википедия

У этого термина существуют и другие значения, см. Потенциал.

Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

φ=Wpqp.{\displaystyle \varphi ={\frac {W_{p}}{q_{p}}}.}

Напряжённость электростатического поля E{\displaystyle \mathbf {E} } и потенциал φ{\displaystyle \varphi } связаны соотношением^[1]

∫ABE⋅dl=φ(A)−φ(B),{\displaystyle \int \limits _{A}^{B}\mathbf {E} \cdot \mathbf {dl} =\varphi (A)-\varphi (B),}

или обратно^[2]:

E=−∇φ.{\displaystyle \mathbf {E} =-\nabla \varphi .}

Здесь ∇{\displaystyle \nabla } — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля ∇⋅E=ρε0{\displaystyle \mathbf {\nabla } \cdot \mathbf {E} ={\rho \over \varepsilon _{0}}}, легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:

∇2φ=−ρε0,{\displaystyle {\nabla }^{2}\varphi =-{\rho \over \varepsilon _{0}},}

где φ{\displaystyle \varphi } — электростатический потенциал (в вольтах), ρ{\displaystyle \rho } — объёмная плотность заряда (в кулонах на кубический метр), а ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная (в фарадах на метр).

Неоднозначность определения потенциала[править | править код]

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

φ1−φ2=Afq∗1→2q∗,{\displaystyle \varphi _{1}-\varphi _{2}={\frac {A_{f}^{q^{*}1\to 2}}{q^{*}}},}

где:

φ1{\displaystyle \varphi _{1}} — потенциал в точке 1,

φ2{\displaystyle \varphi _{2}} — потенциал в точке 2,

Afq∗1→2{\displaystyle A_{f}^{q^{*}1\to 2}} — работа, совершаемая полем при переносе пробного заряда q∗{\displaystyle q^{*}} из точки 1 в точку 2.

При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произволом выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

В СИ за единицу разности потенциалов принимают вольт (В).

Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT⁻³I⁻¹).

В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг.

Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ.

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов.

Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния 1r{\displaystyle {\frac {1}{r}}} (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:

φ=kqr,{\displaystyle \varphi =k{\frac {q}{r}},}

где k{\displaystyle k} обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ:

k=14πε0{\displaystyle k={\frac {1}{4\pi \varepsilon _{0}}}} = 9·10⁹ В·м/Кл,

q{\displaystyle q} — величина заряда, r{\displaystyle r} — расстояние от заряда-источника до точки, для которой рассчитывается потенциал.

• Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть, например, над поверхностью шара, а не внутри его.
• Кулоновский потенциал в приведенном выше виде используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

  W=∑i<jkqiqjrij=12∑i≠jkqiqjrij.{\displaystyle W=\sum _{i<j}k{\frac {q_{i}q_{j}}{r_{ij}}}={\frac {1}{2}}\sum _{i\neq j}k{\frac {q_{i}q_{j}}{r_{ij}}}.}

Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция ∫CE⋅dℓ{\displaystyle \textstyle \int _{C}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}} зависит от пути, потому что ∇×E≠0{\displaystyle \mathbf {\nabla } \times \mathbf {E} \neq \mathbf {0} } (см. Закон индукции Фарадея).

Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности, А определен так чтобы

B=∇×A,{\displaystyle \mathbf {B} =\mathbf {\nabla } \times \mathbf {A} ,\,}

где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. Учитывая это, величина

F=E+∂A∂t{\displaystyle \mathbf {F} =\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}}

является консервативным полем по закону Фарадея, и поэтому можно написать

E=−∇V−∂A∂t,{\displaystyle \mathbf {E} =-\mathbf {\nabla } V-{\frac {\partial \mathbf {A} }{\partial t}},\,}

где V — скалярный потенциал, определённый консервативным полем F.

Электростатический потенциал — это частный случай этого определения, где A не зависит от времени. С другой стороны, для изменяющихся во времени полей,

−∫abE⋅dℓ≠V(b)−V(a),{\displaystyle -\int _{a}^{b}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)},\,}

в отличие от электростатики.

Формула потенциальной энергии

ОПРЕДЕЛЕНИЕ

Потенциальная энергия — это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.

   

– потенциальная энергия тела, – его масса, – ускорение свободного падения, – высота тела над некоторым нулевым уровнем.

Условное обозначение —

Единица измерения энергии — Дж (джоуль).

Потенциальная энергия характеризует энергию тела в некотором поле тяготения. Это скалярная физическая величина. Чаще всего рассматривается поле тяготения, связанное с землёй, в нём м/с. Для других объектов величина различается.

Примеры решения задач по теме «Потенциальная энергия»

ПРИМЕР 1

Задание	Тело массой 12 кг находится на высоте 5 км над землёй. Найти его потенциальную энергию.
Решение	Подставим исходные данные в формулу. Не забываем, что км = м. Дж
Ответ	Потенциальная энергия тела относительно земли равна Дж.

ПРИМЕР 2

Задание	Астероид массой тонн вращается вокруг Солнца на расстоянии м. Известно, что м/с. Найти потенциальную энергию астероида относительно Солнца.
Решение	Помня, что т = кг подставим исходные данные в формулу: Дж
Ответ	Потенциальная энергия астероида приблизительно равна Дж.

Читайте также:

Все формулы по физике

Формула момента силы

Формула мощности

Формула силы тока

Формула массы тела

Формула давления

Формула силы выталкивания

Механическая работа — Википедия

Механическая работа

A=F⋅S=F⋅S⋅cos⁡φ{\displaystyle A={\mathbf {F}}\cdot {\mathbf {S}}=F\cdot S\cdot \cos \varphi } Работа силы

Ключевые статьи

Работа в физике

Известные учёные

См. также: Портал:Физика

Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)^[1].

Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).

Работа силы, приложенной к материальной точке[править | править код]

Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:

A=Fss=Fs cos(F,s)=F→⋅s→{\displaystyle A=F_{s}s=Fs\ \mathrm {cos} (F,s)={\vec {F}}\cdot {\vec {s}}}

Здесь точкой обозначено скалярное произведение, s→{\displaystyle {\vec {s}}} — вектор перемещения; подразумевается, что действующая сила F→{\displaystyle {\vec {F}}} постоянна в течение времени, за которое вычисляется работа.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки^[2]:

A=∫F→⋅ds→.{\displaystyle A=\int {\vec {F}}\cdot {\vec {ds}}.}

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений ds→,{\displaystyle {\vec {ds}},} если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[3], интеграл определяется^[4] следующим образом:

A=∫r→0r→1F→(r→)⋅dr→{\displaystyle A=\int \limits _{{\vec {r}}_{0}}^{{\vec {r}}_{1}}{\vec {F}}\left({\vec {r}}\right)\cdot {\vec {dr}}},

где r→0{\displaystyle {\vec {r}}_{0}} и r→1{\displaystyle {\vec {r}}_{1}} — радиус-векторы начального и конечного положения тела соответственно.

• Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.

Работа сил, приложенных к системе материальных точек[править | править код]

Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).

Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если Atotal{\displaystyle A_{total}} — полная работа, совершённая над частицей, определяемая как сумма работ, совершенных приложенными к частице силами, то она выражается как:

Atotal=Δ(mv22)=ΔEk,{\displaystyle A_{total}=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k},}

где Ek{\displaystyle E_{k}} называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как^[5]:

Ek=12mv2.{\displaystyle E_{k}={\frac {1}{2}}mv^{2}.}

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая Ep{\displaystyle E_{p}}, такая, что

F→=−∇Ep.{\displaystyle {\vec {F}}=-\nabla E_{p}.}

Если все силы, действующие на частицу, консервативны, и Ep{\displaystyle E_{p}} является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, тогда:

F→⋅Δs→=−∇→Ep⋅Δs→=−ΔEp⇒−ΔEp=ΔEk⇒Δ(Ek+Ep)=0{\displaystyle {\vec {F}}\cdot \Delta {\vec {s}}=-{\vec {\nabla }}E_{p}\cdot \Delta {\vec {s}}=-\Delta E_{p}\Rightarrow -\Delta E_{p}=\Delta E_{k}\Rightarrow \Delta (E_{k}+E_{p})=0}.

Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,

∑E=Ek+Ep{\displaystyle \sum E=E_{k}+E_{p}}

является постоянной во времени. Этот закон широко используется при решении задач классической механики.

В термодинамике работа, совершённая газом при расширении^[6], рассчитывается как интеграл давления по объёму:

A1→2=∫V1V2PdV.{\displaystyle A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV.}

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

dA=PdSh.{\displaystyle dA=PdSh.}

Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка M{\displaystyle M} движется по непрерывно дифференцируемой кривой G={r=r(s)}{\displaystyle G=\{r=r(s)\}}, где s — переменная длина дуги, 0≤s≤S{\displaystyle 0\leq s\leq S}, и на неё действует сила F(s){\displaystyle F(s)}, направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под F(s){\displaystyle F(s)} проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина F(ξi)△si,△si=si−si−1,i=1,2,…,iτ{\displaystyle F(\xi _{i})\triangle s_{i},\triangle s_{i}=s_{i}-s_{i-1},i=1,2,…,i_{\tau }}, называется элементарной работой силы F{\displaystyle F} на участке Gi{\displaystyle G_{i}} и принимается за приближённое значение работы, которую производит сила F{\displaystyle F}, воздействующая на материальную точку, когда последняя проходит кривую Gi{\displaystyle G_{i}}. Сумма всех элементарных работ ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} является интегральной суммой Римана функции F(s){\displaystyle F(s)}.

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} всех элементарных работ, когда мелкость |τ|{\displaystyle |\tau |} разбиения τ{\displaystyle \tau } стремится к нулю, называется работой силы F{\displaystyle F} вдоль кривой G{\displaystyle G}.

Таким образом, если обозначить эту работу буквой W{\displaystyle W}, то, в силу данного определения,

W=lim|τ|→0∑i=1iτF(ξi)△si{\displaystyle W=\lim _{|\tau |\rightarrow 0}\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}},

следовательно,

W=∫0sF(s)ds{\displaystyle W=\int \limits _{0}^{s}F(s)ds} (1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра t{\displaystyle t} (например, времени) и если величина пройденного пути s=s(t){\displaystyle s=s(t)}, a≤t≤b{\displaystyle a\leq t\leq b} является непрерывно дифференцируемой функцией, то из формулы (1) получим

W=∫abF[s(t)]s′(t)dt.{\displaystyle W=\int \limits _{a}^{b}F[s(t)]s'(t)dt.}

Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷Дж

1. ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
2. ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения ds→{\displaystyle {\vec {ds}}}, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях ds→{\displaystyle {\vec {ds}}} суммируется, что и дает в результате интеграл.
3. ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
4. ↑ По сути через предыдущий, поскольку здесь F→(t)=F→(r→(t)){\displaystyle {\vec {F}}(t)={\vec {F}}({\vec {r}}(t))}; вектор же малого перемещения ds→{\displaystyle {\vec {ds}}} совпадает с dr→{\displaystyle d{\vec {r}}}.
5. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
6. ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле ∫PdV{\displaystyle \int PdV} давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

• История механики с древнейших времен до конца XVIII в. В 2 т. М.: Наука, 1972.
• Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
• Льоцци М. История физики. М.: Мир, 1970.
• Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
• Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
• Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.