Задачи про рыцарей и лжецов
парадокс лжеца является высказывание Евбулида (4 век до н. э.): «Я лгу».
Если сказав «я лгу», я сказ истину, то значит я при этом солгал (т. е. сказал неправду), что противоречит, следовательно, произнося это высказывание, я сказал неправду, т. е. солгал. Итак, доказав, что произнеся это высказывание, я солгал, а т к именно это я и утверждал, произнося это высказывание, то я, тем самым, сказал при этом истину, т. е. док и то, что я (в том же слцчае) сказал истину. В этом протиоречиив и состоит парадокс.
Чел произносит: «Я лгу», или «То что я сейчас говорю, является ложью», или же «Это высказывание ложно». Если высказывание ложно, то говорящий сказал правду и, сказанное им не является ложью. Если же высказывание не является ложным, а говорящий утверждает, что оно ложно, то это его высказывание ложно. Таким образом, если говорящий лжёт, он говорит правду, и наоборот.
Парадокс лжеца демонстрирует расхождение разговорной речи с формальной логикой, вводя высказывание, которое одновременно истинно и ложно.
Утверждение, составляющее парадокс лжеца, в формальной логике не доказывается и не опровергается. Поэтому считается, что данное высказывание вообще не является логическим утверждением .Попытка разрешить парадокс прив к обобщениям классической логики: например, тройственной логике, комплексной логике или паранепротиворечивой логике
Задачи про рыцарей и лжецов
0) На острове живут рыцари и лжецы. Путник, встретив местного жителя, спросил его, кем он является. Что ответил житель?
1а)A утверждает: «Я говорю правду». Кто он рыцарь или лжец?
1б) А говорит «Или я лжец, или 2+2=5.
К какому заключению можно прийти на основании этого утверждения?
2) Путник на дороге, соединяющей город лжецов и город рыцарей. Он хочет узнать, в какой стороне находится каждый из городов. Какой вопрос он должен задать прохожему (не зная, рыцарь он или лжец), чтобы определить это?
3) А говорит: «По крайней мере, один из нас лжец».
Кто такой А (рыцарь или лжец) и кто такой В?
Реш Если А – лжец, тогда получается, что он говорит правду (действительно тогда хотя бы один из них лжец, а именно А). Это противоречие. Поэтому А не может быть лжецом. Поэтому А – рыцарь. Поэтому он говорит правду (как рыцарь). Поэтому среди них есть хотя бы один лжец. Но так как А – рыцарь, то лжец – В.
Ответ: А – рыцарь, В – лжец.
3а) A говорит: «Или я лжец, или B рыцарь». Кто из A и B рыцарь и кто лжец (4 вар отв)
3б) Из 2 жит A и B B утверждают: «Только один из нас двоих рыцарь». Кто эти жители?
3в) A утверждает: «Мы оба вместе с B лжецы». Кто есть A и кто есть B?
3г) A: B утверждает, что он рыцарь.
B: A утверждает, что он лжец.
К какой категории следует отнести каждого?
3д) двое людей A и B, о которых известно, что каждый из них либо рыцарь, либо лжец, либо нормальный человек, высказал утверждение
Доказать, что по крайней мере один из них говорит правду, но это не рыцарь. Доказать а)если A говорит правду, то он говорит правду, не будучи рыцарем; б)если A лжет, то B говорит правду, не будучи рыцарем.
3е) А и В. А говорит: «Я лжец, а В не лжец». Кто такой А (рыцарь или лжец), и кто такой В? Отв: А и В оба лжецы.
Решение: запишем высказывание формулой  тогда должно быть
тогда должно быть
 или
или  =1 или а)
=1 или а)  или б)
или б) случай б)
случай б)
В случае а) А рыцарь и он не может соврать (p=0). В случае б) подставив А=0 в 1-е уравнение имеем  т е В=0
т е В=0
4)В городе есть Р , все высказывания которых правда, Л – каждое высказывание которых – ложь. Г- может говорить правду, но может и солгать. Однажды встретился человек, который сказал о себе: «Я – лжец». Кем был тот человек, который встретился?
5) 3 жителя A, B и C. Двое из них (A и B) высказали утверждение:
A: Мы все лжецы. B: Один из нас рыцарь.
Кто из 3 островитян A, B и C рыцарь и кто лжец?
5а)На острове живут рыцари, кот всегда говорят правду, и лжецы, которые всегда лгут. Путник встретил 3 человек и спросил каждого из них: «Сколько рыцарей среди твоих спутников?». 1й ответил: «Ни одного». 2й сказал: «Один». Что сказал 3й?
5б)На острове живет 25 чел: рыцари, лжецы и хитрецы. Рыцари всегда гов правду, лжецы всегда лгут, а хитрецы отв на зад им вопросы по оч то правду, то ложь. Всем жит острова б задано 3 вопр: “Вы рыцарь?”, “Вы хитрец?”, “Вы лжец?”. На 1й вопр “Да” отв 15 чел, на 2й — 7 чел, на 3й — 5 чел. Сколько хитрецов живет на этом острове?
Нач реш.1) Рыцарь (R) на такие вопр ответит: «да, нет, нет»;2) Лжец (L) на такие вопросы ответит «да,да, нет»;3) Хитрец может ответить либо: «да, нет, да» (X1),
либо «нет, да, нет» (X2).
Теперь по задаче составим систему уравнений : R+L+X1+X2=25, R+L+X1=15, L+X2=7, X1=5. Поэтому X1=5, отсюда X2=10, но тогда L=-3. Вр бы верно все сделал, но получ противор. -На 1 и 3 вопр хитрецы д б отв одинак, отсюда R+L=15−5=10, а хитрецов всего 25−10=15.Для полноты решения надо проверить, что ответ на 2й вопрос не противоречит ответу.
5с) На острове живут 100 рыцарей и 100 лжецов, у каждого из них есть хотя б один друг. Однажды утром каждый житель произнес фразу «Все мои друзья — рыцари», либо «Все мои друзья — лжецы», причем каждая из фраз произнесена ровно 100 чел. Найдите мин возможное число пар друзей, один из которых рыцарь, а другой — лжец.
Решение: в паре рыцарь-лжец каждый д сказать, что другой лжец: рыцарь скажет правду, а лжец соврёт, в паре рыцарь-рыцарь оба скажут правду, а в паре лжец-лжец оба скажут неправильно. Значит фраза «Все мои друзья — лжецы» употребляется только в парах рыцарь-лжец. Минимальное количество пар рыцарь-лжец, когда фразу сказало 100 чел, это 50. Если пар было меньше, то и фраз тоже было меньше.
6в)). За круглым столом собр 2012 жит острова. Каждый из низ заяв : «Один из моих соседей — рыцарь, а др — лжец». М ли опр ск за столом рыцарей.
Реш. Соседи Рыцаря: Р-Р-Л Зн, посадка такая …—Р-Р-Л—Р-Р-Л—.. число, сидящих д дел на 3.
Рыцарей д б в 2 р больше, чем лжецов. 2012 на 3 не делится. Задача не корректная
7)человек спросил A: «Сколько рыцарей среди вас?» A ответил неразборчиво. человек спросил B: «Что сказал A?» B ответил: «А сказал, что среди нас 1 рыцарь». Тогда C закричал «Он лжет!» Кто из 2 B и C рыцарь и кто лжец?
B — лжец, а C — рыцарь. B — рыцарь, а C — лжец.
8) Предположим, что A и B высказали следующие утверждения:
A: Мы все лжецы. B: Ровно 1 из нас лжец.
Можно ли определить, кто такой B: рыцарь или лжец?
Можно ли определить, кто такой C?
9) На о-ве живут только рыцари , кот всегда гов правду, и лжецы , кот всегда лгут. В Думе о-ва — 11 депут. В целях сокр бюджета б решено сокр Думу на 1 депут. Но каждый из деп заявил, что, если его выведут из сост Думы, то среди оставя депут больш-во будут лжецами . Сколько рыцарей и сколько лжецов в Думе?
Изнач в Думе 5 рыцарей и 6 лжецов. Если убир рыцаря, то каждый из рыц вправе утв, что лжецов больше, если лжеца, то их с рыц будет поровну, но каждый лжец б утв, что их, лжецов, больше, т.е. лгать, как и положено
Сперва м предп, что рыцар , чем лжецов, и отсечь этот вар, потом, что рыц
10) 5) На острове, насел кот сост только рыцари, всегда гов правду, и лжецы, кот всегда лгут, нах НИИ. Каждый из его сотруд однажды сделал два заявления:
а) В инст нет и 10 чел, кот работают больше меня.
б) По кр мере 100 чел в инст получают зарплату большую, чем моя.
Известно, что нагрузка у всех работников разная, как и зарплата.
Сколько человек работает в НИИ?
53)Один из попугаев А, В, и С всегда говорит правду, другой всегда врет, а 3й – иногда говорит правду, а иногда врет. На вопрос: «Кто В?» они ответили :
А: — Лжец . В: — Я хитрец! С: — Абсолютно честный попугай.
Кто из попугаев лжец, а кто хитрец?
54)До Царя дошла весть, что кто-то из 3 богат убил Змея Горын. Приказал Царь им явиться ко двору. Илья Мур: — Змея убил ДН.Д Н: — Змея убил А П.А По: — Я убил змея.
Изв, что только 1 богатырь сказал правду, а двое других слукавили. Кто убил змея?
55)До царя Гороха дошла молва, что наконец кто-то убил Змея Горыныча. Царь догад, что это дело рук или Ильи Муромца, или Добр Никитича, или Алеши Поповича. Пригл их ко двору, стал расспр. Трижды каждый богатырь речь держал. И сказали они так:
И М: «Я не убив З Г. А змея Гор убил А П.»
Д Н: «З убил А П. Но я если бы и убил, то не созн бы.
А П: «Не я убил ЗГ. Я давно ищу, какой бы подвиг совершить. И взаправду И Муромец в заморские страны уезжал.»
Потом царь Горох узнал, что дважды каждый богатырь правду говорил, а 1 раз соврал. кто убил Змея Горыныча?
56)За круглый стол сели 7 братьев-гномов. Гномы всегда говорят правду всем старшим братьям, а младшие всегда врут. Каждый гном сказал своему правому соседу: «все здесь присутствующие говорят мне только неправду». В каком порядке сидят гномы?
57)За круглым столом сидят 8 чел, каждый из которых л рыцарь, либо лжец. Рыцарь всегда говорит правду, а лжецы – всегда лгут . На вопрос, кто их соседи, каждый из них ответил : « Мои соседи – лжец и рыцарь». Сколько среди них будет лжецов ?
59)В стране есть города А и В. Все жители гор А говорят только правду, а жителм города В всегда лгут. Жители этих гор ходят друг к другу в гости. Путник попал в один из этих городов, но не знает, в какой. Как он может, задав 1 вопрос первому попавшемуся жителю, узнать, в каком городе он находится?
60)В конференции участвуют 100 чел – химики и алхимики. Каждому был задан вопрос: « Если не считать Вас, то кого больше среди остальных уч-ков – химиков или алхимиков?» когда опросили 51 участника, и все ответили, что алхимиков больше, опрос прервали. Алхим всегда лгут, а химики всегда говорят правду.
Сколько химиков среди участников?(пересеч и объед множеств)
1)Путешеств посетил селение, в кот каждый человек либо всегда гов правду, либо всегда лжет. Жители стали в круг, и каждый сказал путеш про соседа справа, правдив тот или лжив. На осн этих сообщ путеш одноз опред, какую долю от всех жит селения сост правдивые. Опр и вы, чему она равна.
Реш Пусть x — доля правд жителей. Предст, что все правд жители стали лжецами, а все лжецы «исправ». Тогда путеш услышит то же самое! Действ, правдив любого жителя изм, но изм и правдив соседа, о кот он говорит. Но доля правд в этом круге = 1 — x. Таким обр, путеш не м отличить круг с долей правд жителей x от круга с долей правд жителей 1 — x. Зн, он м опр долю правдивых жит только при x = 1 — x. Но это значит, что x = 1/2.Комм. Занум жителей числами по час стрелке и поло xi = 1, если i-й житель лжец, и xi = 0 — в прот с. Тогда i-й житель сообщит путеше xi + xi + 1, где слож происх по модулю 2 (т. е. 0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 0). Поэтому информ, получ путеш, м понимать как систему лин уравн над полем из 2 элементов.
2)5 чел сидят за круглым столом каждый из них гов оба мои соседа слева и справа лжецы кроме того все присуств знают явл ли лжецами их соседи сколько лжецов за столом
Ответ 3 лжеца
multiurok.ru
Остров рыцарей и лжецов
Остров рыцарей и лжецов
Жигалов М.М. 11МБОУ «СОШ № 11» НМР РТ
Косова Н.В. 11МБОУ «СОШ № 11» НМР РТ
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Предмет математики настолько серьезен,
что нужно не упускать случая делать его
немного занимательным.
Паскаль
Занимательная математика – это направление в математике, проявляющееся в большей степени в рамках досуга, развлечения и самообразования. Элемент игры, который делает занимательную математику занимательной, может иметь форму головоломки, состязания, фокуса, ошибочного рассуждения или обычной математической задачи с «секретом» – каким-либо неожиданным или забавным поворотом мысли.
Задачи о рыцарях и лжецах – разновидность увлекательных математических задач, в которых фигурируют персонажи:
Лжец (плут, вампир, сумасшедший, оборотень) – человек, всегда говорящий ложь.
Рыцарь (человек, поступающий правдиво и правильно, правдец) – человек, всегда говорящий правду.
Решение подобных задач обычно сводится к перебору вариантов с исключением тех, которые приводят к противоречию.
Существуют задачи с тремя типами персонажей – рыцари, лжецы и нормальные люди (вариант – шпионы). Последние могут как лгать, так и говорить правду.
С задачами про рыцарей и лжецов я познакомился при подготовке к олимпиаде по математике. Это не простые, но веселые, увлекательные задачи. Они учат логически рассуждать и нестандартно мыслить. На уроках математики подобные задачи мы не решали и мне стало интересно, а знают ли о таких задачах мои одноклассники? Справятся ли с их решением? Узнать об этом я решил с помощью исследования, и назвал я его «Остров рыцарей и лжецов».
Актуальность изучения темы моей работы вижу в том, что решение логических задач способствует развитию у учеников интереса к математике, разностороннему раскрытию способностей школьников, умению самостоятельно организовать своё свободное время.
Цель моего исследования – повышение интереса к предмету математика у моих одноклассников, показать им, что решение логических задач в математике – это увлекательно.
Задачи моей исследовательской работы:
— рассмотреть задачи про рыцарей и лжецов и способы их решения;
— изучить интерес моих одноклассников к решению логических задач.
Объект исследования – занимательная математика, логические задачи.
Предмет работы – решение задач про рыцарей и лжецов для повышения наблюдательности и умения логически мыслить.
Практическая значимость моей исследовательской работы заключается в том, что результаты исследования могут быть использованы при подготовке к уроку, олимпиадам, экзаменам.
Структура работы: титульный лист, оглавление, введение, теоретическая и практическая части, заключение, список использованной литературы.
1. Логические задачи в математике
1.1. Задачи о рыцарях и лжецах
Логические задачи – пожалуй, самый эффективный инструмент для развития логики и мышления как у детей, так и у взрослых.
Решение задачи на логику предполагает сложный мыслительный процесс. Это последовательное совершение определённых логических действий, работа с понятиями, использование различных логических конструкций, построение цепочки точных рассуждений с правильными промежуточными и итоговыми умозаключениями.
Логические задачи от обычных отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Можно сказать, что логическая задача – это особая информация, которую не только нужно обработать в соответствии с заданным условием, но и хочется это сделать. Особое место логики, уделено в математике. Задачи, решение которых развивает логическое мышление, способствуют успешному изучению предмета. Эти задачи носят занимательный характер и не требуют большого запаса математических знаний, поэтому они привлекают даже тех учащихся, которые не очень любят математику.
Исходными данными в логических задачах являются высказывания. Высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов сложно. Основная идея метода рассуждений состоит в том, чтобы последовательно анализировать всю информацию, имеющуюся в задаче, и делать на этой основе выводы.
Наверняка большинство из нас хотя бы раз проходили тесты на уровень логики. Большинство из них составлено из одних вопросов с подвохом.
Существует множество хитроумных задач об острове, населенном рыцарями, всегда говорящими только правду и лжецами, говорящими только ложь. Предполагается, что каждый обитатель острова либо рыцарь, либо лжец.
Так же бывают задачи с третьим типам персонажей – нормальные люди (вариант – шпионы). Они могут как лгать, так и говорить правду.
Систематическое выполнение логических заданий, решение нестандартных задач развивает, совершенствует познавательные способности и познавательную деятельность учащихся. Кроме того, выполнение задач такого вида требует постоянных умственных усилий, более глубокого анализа взаимосвязей, догадки, активизации знаний, проявления творческой инициативы.
1.2. Решение задач о рыцарях и лжецах
Жили-были на одном небольшом островке в океане два племени – рыцари и лжецы. Рыцари были настолько горды и благородны, что не могли говорить ничего, кроме правды, правды и только правды. А лжецы за годы так привыкли оправдываться, выкручиваться и хитрить, что уже не могли говорить ничего, кроме лжи. Так же на острове жили «нормальные люди», они могли говорить как правду, так и ложь. Попробуем определить, кто из них кто.
Как, задав один вопрос, определить, кто перед нами – рыцарь или лжец? Можно, например, спросить: «Ты — человек?» или «Дважды два — четыре?» Рыцарь скажет «да», а лжец «нет».
Если спросить у жителя острова «Кто ты: рыцарь или лжец?», то, кем бы он ни был, он ответит «Я – рыцарь». Рыцарь скажет про себя правду, а лжец солжет про себя. А вот ответ «Я – лжец» не даст никто, так как для рыцаря это будет ложью, а для рыцаря правдой.
Решим задачи посложнее.
Задача 1.
На острове рыцарей и лжецов собралась компания из людей разного роста. Каждый заявил «Среди тех, кто выше меня, есть лжецы». Сколько лжецов могло быть среди них?
Решение: Самый высокий – точно лжец (ведь выше него вообще никого нет, а значит, и лжецов среди них нет). Любой, кто ниже него, автоматически говорит правду – значит он рыцарь. Лжец — один (самый высокий), все остальные — рыцари (сколько угодно).
Задача №2.
На острове живут 100 рыцарей и 100 лжецов, у каждого из них есть хотя бы один друг. Рыцари всегда говорят правду, а лжецы всегда лгут. Однажды утром каждый житель произнес фразу «Все мои друзья – рыцари», либо «Все мои друзья – лжецы», причем каждую из фраз произнесло ровно 100 человек. Найдите наименьшее возможное число пар друзей, один из которых рыцарь, а другой – лжец.
Решение: Заметим, что в паре рыцарь-лжец каждый должен сказать, что другой лжец: рыцарь скажет правду, а лжец соврёт, в паре рыцарь-рыцарь оба скажут правду, а в паре лжец-лжец оба скажут неправду. Значит фраза «Все мои друзья – лжецы» употребляется только в парах рыцарь-лжец. Минимальное кол-во пар рыцарь-лжец, когда фразу сказали 100 человек, это 50. Если пар будет меньше, то и фраз тоже будет меньше.
Задача №3.
На острове рыцарей и лжецов собралась компания из 12 человек, каждый заявил всем остальным: «Вы все лжецы!». Сколько лжецов может быть в этой компании?
Решение: Предположим, что все аборигены лжецы. Но тогда каждый из них говорит правду, чего он как лжец делать никак не может. Противоречие!
Значит, есть хотя бы один рыцарь. Рассмотрим этого рыцаря. Он должен был сказать правду. То есть все остальные 11 человек – лжецы. Каждый из них при этом говорит неправду, то есть этот пример подходит. Больше, чем один рыцарей быть не может, т.к. иначе каждый из них, сказав, что все остальные лжецы солгал бы.
Задача №4.
По кругу сидят рыцари и лжецы – всего 12 человек. Каждый из них сделал заявление: «Все кроме, быть может, меня и моих соседей – лжецы». Сколько рыцарей сидит за столом, если известно, что лжецы всегда врут, а рыцари всегда говорят правду?
Решение: Все не могут быть лжецами – тогда все заявления были бы истинными. Значит, есть рыцарь. Все, кроме, быть может, его двух соседей – лжецы. Оба соседа не могут быть лжецами – тогда они сказали бы правду; оба не могут быть рыцарями – тогда бы они солгали. Единственная оставшаяся возможность – один сосед – лжец, другой – рыцарь (то есть два рыцаря рядом, остальные – лжецы) удовлетворяет условиям задачи. Ответ: 2 рыцаря.
Задача №5.
Перед нами трое жителей острова A, B и C. Один из них рыцарь, другой лжец и третий – нормальный человек Эти люди высказывают следующие утверждения: A: Я нормальный человек; B: Это правда; C: Я не нормальный человек. Кто такие A, B и C?
Решение: Прежде всего заметим, что A не может быть рыцарем, потому что рыцарь не назвал бы себя нормальным человеком. Следовательно, получается, что A – либо лжец, либо нормальный человек. Тогда истинно высказывание человека B. Значит, B – либо рыцарь, либо нормальный человек. Но B не может быть нормальным человеком (так как A – нормальный человек), поэтому B – это доблестный рыцарь, а C – маленький лжец. Но лжец не может сказать о себе, что он не нормальный человек (так как любой лжец – не нормальный человек), и мы приходим к противоречию. Итак, A не может быть нормальным человеком. Следовательно, A – хитрый лжец. Это означает, что высказывание человека B ложно, в силу чего B должен быть нормальным человеком (лжецом он быть не может, так как лжец – человек A). Итак, A – хитрый лжец, а B – нормальный человек. Отсюда мы заключаем, что C – доблестный рыцарь.
Как видим, решение логических задач не требует глубокого знания математики. Эти непростые, но интересные задачи научат логически рассуждать и нестандартно мыслить, позволят приобщиться к радости самостоятельного открытия, глубже узнать окружающий мир. Их решение развивает находчивость, сообразительность, наблюдательность, умение анализировать, догадываться, доказывать, решать учебную задачу творчески.
2. Исследование уровня логического мышления учеников 5 класса
2. 1. Математика и логика на практике
Для изучения уровня логического мышления моих одноклассников, проведено небольшое исследование, в котором приняло участие двадцать человек. Всем им были предложены для решения два вида задач – математическая и логическая:
Задача №1.
В двух корзинах лежало 86 яблок. Когда из первой во вторую переложили 3 яблока, то яблок в корзинах стало поровну. Сколько яблок было в каждой корзине первоначально?
Решение:
Разделим пополам общее количество яблок:
1) 86 : 2 = 43 (яблока) − стало в каждой корзине;
Прибавим к половине яблок 3:
2) 43 + 3 = 46 (яблок) − было в первой корзине;
Отнимем от половины яблок 3:
3) 43 − 3 = 40 (яблок) − было во второй корзине.
Ответ: в первой корзине было 46 яблок, а во второй было 40 яблок.
Задача №2.
Вы попали на остров, на котором живут только рыцари и лжецы. Покинуть остров можно по одному из двух мостов (А или B). Один из мостов приведет вас на большую землю и вы спасены. Другой мост ведет на непроходимые болота. Для того, чтобы выбраться, у вас есть возможность обратиться с единственным вопросом к одному из двух жителей. Имеется достоверная информация: один из двух ваших собеседников рыцарь, а другой лжец. Какой вопрос следует выбрать?
а) Ты рыцарь? б) Твой друг рыцарь? в) Мне лучше выбрать мост А? г) Твой друг отправит на мост В?
Решение:
Правильный вопрос, который нужно задать одному из жителей –г) Твой друг отправит на мост В?
Если выход по мосту А, то рыцарь ответит: «Да», а лжец ответит: «Нет». Если выход по мосту B, то рыцарь ответит: «Нет», а лжец ответит «Да».
С математической задачей под №1 справились 18 человек из 20. Это задача из учебника по математики для пятого класса, подобные задачи мы решаем на уроках.
С задачей на логику под №2 справились только 5 человек из 20. Подобные задачи на уроках мы не решали, поэтому решить ее смогли только те ученики, которые занимаются математикой углубленно, решают олимпиадные задачи. Остальным ученикам задача показались сложной и непонятной.
Как видим, решение логических задач вызвало трудности и учеников. Многие, не смогли решить задачу про рыцарей и лжецов, так как никогда не решали подобные задачи.
Чтобы решить логическую задачу нужно оригинально мыслить, использовать смекалку, проявить находчивость, применить нестандартные подходы.
Развивать логическое мышление необходимо постоянно. Регулярные тренировки в решении головоломок, нестандартных задач, ребусов и задач на смекалку полезны и необходимы для ума школьников.
Считаю нужным заниматься решением логических задач не только при подготовке к олимпиадам, экзаменам, а так же на уроках математики, при выполнении домашних заданий и в свободное время для саморазвития. Так же решением логических задач можно заниматься на «классных часах», в форме командной игры. В процессе игры у ребят появится дух соперничества.
2.2. Математика – это интересно
Чтобы вызвать интерес у моих одноклассников к логическим задачам, я предложил решить две логические задачи на время.
Предварительно, я объяснил одноклассникам, кто такие рыцари и лжецы.
Задача №1.
Саша всегда говорит правду, а Паша всегда лжёт. Какой вопрос надо им задать, чтобы они дали на него одинаковые ответы (оба ответили «да» или оба ответили «нет»)?
Ответ: «Тебя зовут Саша?»
Правильный ответ дали 10 человек из 20.
Малыш спрятал от Карлсона банку с вареньем в одну из трех разноцветных коробок. На коробках Малыш сделал надписи: на красной – «Здесь варенья нет»; на синей – «Варенье — здесь»; на зеленой – «Варенье в синей коробке». Только одна из надписей правдива. В какой коробке Малыш спрятал варенье
Ответ: Варенье в зеленой коробке.
Правильный ответ дали 12 человек из 20.
Задача №2.
Путешественник вышел на дорогу, соединяющую город лжецов и город рыцарей. Он хочет узнать, в какой стороне находится каждый из городов. Путешественник вышел на дорогу, соединяющую город лжецов и город рыцарей. Он хочет узнать, в какой стороне находится каждый из городов. Какой вопрос он должен задать прохожему (не зная, рыцарь он или лжец), чтобы определить это?
Ответ: Ты живешь в этом городе?
Правильный ответ дали 15 человек из 20.
Решение задач на время развило у ребят дух соперничества, стремление дать правильный ответ первым. Все 20 человек сказали, что им было интересно решать такие задачи.
Логические задачи обладают высоким потенциалом. Они приучают к анализу воспринимаемой информации, её разносторонней оценке, повышают интерес к занятиям математикой.
Заключение
Математика – интересная, многогранная, занимательная и полезная наука. Занимательная математика – это направление в математике, которое может иметь форму головоломки, игры, состязания, фокуса, задачи с «секретом».
Одна из разновидностей увлекательных математических задач – задачи о рыцарях, лжецах и нормальных людях. Лжецы всегда лгут, рыцари – говорят правду, нормальные люди – могут как лгать, так и говорить правду. Решение подобных задач обычно сводится к перебору вариантов с исключением тех, которые приводят к противоречию.
Решение логических задач способствует развитию любознательности, сообразительности, развитию внимательности, настойчивости, целеустремлённости, умения преодолевать трудности – качеств весьма важных в практической деятельности любого человека
Таким образом, логика необходима и значима для любого человека. С помощью обоснования своих идей и взглядов логически, можно убеждать в своей правоте других людей. Логика формирует привычку анализировать свои и чужие суждения, позволяющие устранять ошибки в умозаключениях, отличать ложь от истины.
Логика улучшает память, ведь постигнув законы правильного мышления, можно более корректно обходиться с информацией. Логика упорядочивает нашу жизнь, она помогает отделить важное от неважного, отбрасывает все ненужные второстепенные вещи. Она помогает экономить наше время, что так важно человеку на сегодняшний день. Помимо этого, логика помогает шире смотреть на окружающий мир и глубже чувствовать и понимать его. Эти качества мышления имеют большое значение в любой области научной и практической деятельности.
Логические задачи будут одинаково интересны и увлечённым математикой детям, и «гуманитариям».
Список использованной литературы
Братусь Т.А. Все задачи «Кенгуру». / Братусь Т.А., Жарковская Н.А., Максимов Д.В. – СПб.: Левша, 2017. – 352 с.
Литвинов В.Л. 88 занимательных и олимпиадных задач по математике. Сборник занимательных задач, интересных загадок, головоломок, фокусов и игр. / В.Л. Литвинов. – Самара, 2017. – 43 с.
Никольский С.М. Математика 5 класс: учебник / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2018. – 269 с.
Смаллиан Р.М. Как же называется эта книга? / Р.М. Смаллиан. – М.: Мир, 2012. – 272 с.
Шарыгин И.Ф. Задачи на смекалку: учебное пособие для 5-6 классов общеобразовательных учреждений / И.Ф. Шарыгин, А.В. Шевкин. – М.: Просвещение, 2017. – 95 с.
Просмотров работы: 6700
school-science.ru
Сборник задач «В стране рыцарей и лжецов»
Сборник задач «В стране рыцарей и лжецов»
Предисловие
Я решил создать этот сборник, в то время, когда готовился к олимпиаде по математике. В него я включил все задачи, которые я когда либо встречал. Впервые, я познакомился с задачами логического типа и понял, что решать их не так то просто, нужно уметь рассуждать и делать правильные выводы. В моём сборнике задач я собрал задачи для 5-8 классов. Создавая его, я преследовал следующие цели: задачник поможет тем учащимся, которые готовятся к олимпиадам по математике и участвуют в разных математических конкурсах. Решая задачи ученики смогут развить свои нераскрытые таланты, логическое и образное мышление. При решении логических задач предоставляется возможность подумать над необычным условием. Задачи на нестандартное логическое мышление помогут и в повседневной жизни решать житейские проблемы нестандартным образом. В наше время очень часто успех человека зависит от его способности четко мыслить, логически рассуждать и ясно излагать свои мысли.
Вот что говорили знаменитые ученые. Мало иметь хороший ум, главное -его хорошо применять. (Р. Декарт). Прежде чем решать задачу-прочитай условие. (Ж. Адамар). Истина ничуть не страдает от того, что кто то ее признает. (Ф. Шиллер). Человека, умеющего наблюдать и анализировать, обмануть просто невозможно. Его выводы будут безошибочны, как теоремы Евклида. (Артур Конан Дойл)
Опираясь на эти высказывания, можно сделать вывод, что задачи на логическое мышление появились еще в глубокой древности, и многие великие ученые придавали большое значение мысли!
Называется сборник задач «В стране рыцарей и лжецов» не зря! В нем фигурируют следующие персонажи: Лжец (плут, вампир, сумасшедший, оборотень) — человек, всегда говорящий ложь. Рыцарь (человек, поступающие правдиво и правильно, правдец) — человек, говорящий всегда правду. Нормальный человек (шпион, человек говорящий, как правду, так и ложь). Решение подобных задач обычно сводится к перебору вариантов с исключением тех, которые приводят к противоречию.
Содержание
Предисловие 2
Содержание 3
Задачи для 5-ых классов 4
Задачи для 6-ых классов 4-5
Задачи для 7-ых классов 5-6
Задачи для 8-ых классов 6-7
Ответы на задачи для 5-ых классов 7-8
Ответы на задачи для 6-ых классов 8-9
Ответы на задачи для 7-ых классов 9-10
Ответы на задачи для 8-ых классов 11-12
Литература 13
Задачи для 5 классов
1.Трое жителей острова (А, B и C) разговаривали между собой в саду. Проходивший мимо незнакомец спросил у A: «Вы рыцарь или лжец?» Тот ответил, но так неразборчиво, что незнакомец не смог ничего понять. Тогда незнакомец спросил у B: «Что сказал A?» «А сказал, что он лжец», — ответил B. «Не верьте B! Он лжет! — вмешался в разговор островитянин C. Кто из островитян B и C рыцарь и кто лжец?
2. Перед нами снова три островитянина A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец. Двое из них (А и B) высказывают следующие утверждения: A: Мы все лжецы. B: Один из нас рыцарь. Кто из трех островитян A, B и C рыцарь и кто лжец?
3. Перед нами трое людей A, B и C. Один из них рыцарь, другой лжец и третий — нормальный человек (типы людей могут быть перечислены не в том же порядке, в каком выписаны их «имена» A, B и C). Наши знакомые высказывают следующие утверждения. A: Я нормальный человек. B: Это правда. C: Я не нормальный человек. Кто такие A, B и C?

Задачи для 6-ых классов
1. Трое людей A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец, либо нормальный человек, высказывают следующие утверждения: A:
B по рангу выше, чем C.
B: C по рангу выше, чем A.
Затем у C спрашивают: «Кто старше по рангу — A или B?» Что ответит C?
2. Как-то раз встретились два островитянина и один сказал другому: «По крайней мере один из нас – лжец». История умалчивает, ответил ли ему на это что-либо собеседник. Тем не менее определите, кем являются оба?
3. Двое людей A и B, о которых известно, что каждый из них либо рыцарь, либо лжец, либо нормальный человек, высказывают следующие утверждения: A: B — рыцарь. B: A — не рыцарь. Докажите, что по крайней мере один из них говорит правду, но это не рыцарь.

Задачи для 7-ых классов
1. Трое людей A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец, либо нормальный человек, высказывают следующие утверждения: A: B по рангу выше, чем C. B: C по рангу выше, чем A. Затем у C спрашивают: «Кто старше по рангу — A или B?» Что ответит C?
2. Давным-давно островитянин Дерб сказал своим друзьям: — Вчера мой сосед заявил мне, что он лжец! Кем является Дерб — рыцарем или лжецом?
3. Однажды в четверг после дождя между островитянами Тимом и Томом произошел следующий диалог: — Ты можешь сказать, что я рыцарь, — гордо заявил Тим. — Ты можешь сказать, что я лжец, — грустно ответил ему Том. Кем являются Тим и Том?

Задачи для 8-ых классов
1.Перед нами трое людей A, B и C. Один из них рыцарь, другой лжец и третий — нормальный человек. Эти люди высказывают следующие утверждения.
A: Я нормальный человек.
B: Это правда.
C: Я не нормальный человек.
Кто такие A, B и C?
2. По кругу сидят рыцари и лжецы – всего 12 человек. Каждый из них сделал заявление: «Все кроме, быть может, меня и моих соседей – лжецы». Сколько рыцарей сидит за столом, если известно, что лжецы всегда врут, а рыцари всегда говорят правду?
3. На острове живут 100 рыцарей и 100 лжецов, у каждого из них есть хотя бы один друг. Рыцари всегда говорят правду, а лжецы всегда лгут. Однажды утром каждый житель произнес фразу «Все мои друзья — рыцари», либо «Все мои друзья — лжецы», причем каждую из фраз произнесло ровно 100 человек. Найдите наименьшее возможное число пар друзей, один из которых рыцарь, а другой лжец.

Ответы на задачи для 5-ых классов
1. Решение: Ни рыцарь, ни лжец не могут сказать: «Я лжец» (высказав подобное утверждение, рыцарь солгал бы, а лжец изрек бы истину). Следовательно, A, кем бы он ни был, не мог сказать о себе, что он лжец. Поэтому B, утверждая, будто A назвал себя лжецом, заведомо лгал. Значит, B — лжец. А так как C сказал, что B лгал, когда тот действительно лгал, то C изрек истину. Следовательно, C — рыцарь. Таким образом, B — лжец, а C — рыцарь. (Установить, кем был A, не представляется возможным).
Ответ: С-рыцарь, В-лжец.
2. Прежде всего, заметим, что A должен быть лжецом. Действительно, если бы A был рыцарем, то из его высказывания следовало бы, что все трое лжецы. Но тогда A (по предположению, рыцарь) оказался бы лжецом, что невозможно. Следовательно, A — лжец. Но тогда его высказывание ложно и по крайней мере один из трех островитян A, B и C — рыцарь. Предположим теперь, что B — лжец. Тогда A и B — оба лжецы, поэтому C должен быть рыцарем (так как, по крайней мере, один из трех островитян рыцарь). Это означает, что ровно один из трех островитян рыцарь, и, следовательно, высказывание B истинно, но это невозможно, так как любое высказывание лжеца не истинно. Отсюда мы заключаем, что B должен быть рыцарем.
Итак, мы установили, что A — лжец, а B — рыцарь. Так как B — рыцарь, то его высказывание истинно, поэтому ровно один из трех островитян — рыцарь. Им должен быть B, следовательно, C должен быть лжецом. Итак, A — лжец, B — рыцарь и C — лжец. Ответ: А-лжец, В-рыцарь, С-лжец.3. Прежде всего заметим, что A не может быть рыцарем, потому что рыцарь не назвал бы себя нормальным человеком. Следовательно, A — либо лжец, либо нормальный человек. Тогда истинно высказывание островитянина B. Значит, B — либо рыцарь, либо нормальный человек. Но B не может быть нормальным человеком (так как A — нормальный человек), поэтому B — рыцарь, а C — лжец. Но лжец не может сказать о себе, что он не нормальный человек (так как любой лжец — не нормальный человек), и мы приходим к противоречию. Итак, A не может быть нормальным человеком. Следовательно, A — лжец. Это означает, что высказывание островитянина B ложно, в силу чего B должен быть нормальным человеком (лжецом он быть не может, так как лжец — островитянин A). Итак, A — лжец, а B — нормальный человек. Отсюда мы заключаем, что А-рыцарь, В-нормальный человек, С-лжец.
Ответы на задачи для 6-ых классов
1. Первый шаг. Прежде всего докажем, что в силу высказывания A островитянин C не может быть нормальным человеком. Действительно, если A — рыцарь, то B — особа более высокого ранга, чем C. Следовательно, B должен быть нормальным человеком, а C — лжецом. Таким образом, в этом случае C — не нормальный человек. Предположим, что A — лжец. Тогда B по рангу не выше C. Следовательно, B — особа более низкого ранга, поэтому B должен быть нормальным человеком, а C — рыцарем. Таким образом, и в этом случае C — не нормальный человек. Предположим, наконец, что A — нормальный человек. Тогда C — заведомо не нормальный человек (так как из трех островитян A, B и C только один – нормальный человек). Итак, C — не нормальный человек.
Второй шаг. При аналогичных рассуждениях из высказывания B можно вывести, что A — не нормальный человек. Таким образом, ни A, ни C не нормальны. Следовательно, B — нормальный человек.
Третий шаг. Поскольку C — не нормальный человек, то он может быть рыцарем или лжецом. Предположим, что он рыцарь. Тогда A — лжец (так как B — нормальный человек). Следовательно, B — особа более высокого ранга, чем A, и C, будучи рыцарем, даст правдивый ответ: «В по рангу выше A». С другой стороны предположим, что C — лжец. Тогда A должен быть рыцарем, поэтому B по рангу не выше A. В этом случае C, будучи лжецом, солгал бы и ответил так: «В по рангу выше A». Таким образом, независимо от того, кто такой островитянин C — рыцарь или лжец, он ответит, что B по рангу выше A
2. Пусть первый островитянин является лжецом. Тогда получается, что он сказал правду, чего быть не может.
Значит, он рыцарь. Тогда он сказал правду, значит, один из них лжец. Поскольку про первого уже знаем, что он рыцарь, то лжецом может быть только второй.
Эта задача обладает интересной особенностью. Условия ее не позволяют установить, кто из двух островитян говорит правду, не будучи рыцарем: A или B. Мы можем доказать более слабое утверждение: по крайней мере один из двух островитян A и B говорит правду, не будучи рыцарем. Островитянин A либо говорит правду, либо не говорит правду. Докажем два утверждения: 1) если A говорит правду, то он говорит правду, не будучи рыцарем; 2) если A лжет, то B говорит правду, не будучи рыцарем.
1) Предположим, что A говорит правду. Тогда B — рыцарь и, следовательно, говорит правду. Значит, A — не рыцарь. Таким образом, если A говорит правду, то A — лицо, говорящее правду, не будучи рыцарем. 2) Предположим, что A не говорит правду. Тогда B — не рыцарь. Но B должен говорить правду, так как A не может быть рыцарем (ведь A не говорит правду). Следовательно, в этом случае B говорит правду, не будучи рыцарем.
Ответы на задачи для 7-ых классов
1. Первый шаг. Прежде всего докажем, что в силу высказывания A островитянин C не может быть нормальным человеком. Действительно, если A — рыцарь, то B — особа более высокого ранга, чем C. Следовательно, B должен быть нормальным человеком, а C — лжецом. Таким образом, в этом случае C — не нормальный человек. Предположим, что A — лжец. Тогда B по рангу не выше C. Следовательно, B — особа более низкого ранга, поэтому B должен быть нормальным человеком, а C — рыцарем. Таким образом, и в этом случае C — не нормальный человек. Предположим, наконец, что A — нормальный человек. Тогда C — заведомо не нормальный человек (так как из трех островитян A, B и C только один – нормальный человек). Итак, C — не нормальный человек. Второй шаг. При аналогичных рассуждениях из высказывания B можно вывести, что A — не нормальный человек. Таким образом, ни A, ни C не нормальны. Следовательно, B — нормальный человек. Третий шаг. Поскольку C — не нормальный человек, то он может быть рыцарем или лжецом. Предположим, что он рыцарь. Тогда A — лжец (так как B — нормальный человек). Следовательно, B — особа более высокого ранга, чем A, и C, будучи рыцарем, даст правдивый ответ: «В по рангу выше A». С другой стороны предположим, что C — лжец. Тогда A должен быть рыцарем, поэтому B по рангу не выше A. В этом случае C, будучи лжецом, солгал бы и ответил так: «В по рангу выше A». Таким образом, независимо от того, кто такой островитянин C — рыцарь или лжец, он ответит, что B по рангу выше A.
2. Так как про соседа Дерба неизвестно, кем он является, то придётся рассмотреть два случая:
1) Если сосед Дерба — рыцарь, тогда то, что он заявил Дербу, должно быть правдой, то есть он должен быть лжецом. Но мы предположили, что он рыцарь. Значит, такого не может быть.
2) Если сосед Дерба — лжец, то он сказал Дербу неправду, то есть неправда, что он лжец. Снова противоречие.
Итак, если бы сосед Дерба сказал ему, что он лжец, то в любом случае получилось бы противоречие, то есть, такого быть не могло. Вывод: сосед Дерба этого вообще не говорил! Значит, Дерб лжёт.
3. Пусть Тим — рыцарь, то есть говорит правду. Тогда Том может сказать, что Тим рыцарь. Поскольку это правда, то получается, что Том может сказать правду, значит, Том тоже рыцарь. Но тогда сказанное Томом тоже должно быть правдой, но на самом деле Тим не сможет сказать, что он лжец, потому что он не лжец, а Тим не врёт. Противоречие.
Значит, Тим — лжец. Тогда Том не может сказать, что он рыцарь, то есть Том не может сказать неправду. Значит, Том рыцарь. И действительно, слова Тома — правда, потому что Тим может соврать, сказав, будто Том лжец.
Ответы на задачи для 8-ых классов
Прежде всего заметим, что A не может быть рыцарем, потому что рыцарь не назвал бы себя нормальным человеком. Следовательно получается, что, A — либо лжец, либо нормальный человек. Тогда истинно высказывание человека B. Значит, B — либо рыцарь, либо нормальный человек. Но B не может быть нормальным человеком (так как A — нормальный человек), поэтому B — это доблестный рыцарь, а C — маленький лжец. Но лжец не может сказать о себе, что он не нормальный человек (так как любой лжец — не нормальный человек), и мы приходим к противоречию. Итак, A не может быть нормальным человеком. Следовательно, A — хитрый лжец. Это означает, что высказывание человека B ложно, в силу чего B должен быть нормальным человеком (лжецом он быть не может, так как лжец — человек A). Итак, A — хитрый лжец, а B — нормальный человек. Отсюда мы заключаем, что C — доблестный рыцарь.
2. Все не могут быть лжецами – тогда все заявления были бы истинными. Значит, есть рыцарь. Все, кроме, быть может, его двух соседей – лжецы. Оба соседа не могут быть лжецами – тогда они сказали бы правду; оба не могут быть рыцарями – тогда бы они солгали. Единственная оставшаяся возможность – один сосед — лжец, другой – рыцарь (то есть два рыцаря рядом, остальные — лжецы) удовлетворяет условиям задачи.
Ответ: 2 рыцаря.
3. Прежде всего заметим, что A не может быть рыцарем, потому что рыцарь не назвал бы себя нормальным человеком. Следовательно получается, что, A — либо лжец, либо нормальный человек. Тогда истинно высказывание человека B. Значит, B — либо рыцарь, либо нормальный человек. Но B не может быть нормальным человеком (так как A — нормальный человек), поэтому B — это доблестный рыцарь, а C — маленький лжец. Но лжец не может сказать о себе, что он не нормальный человек (так как любой лжец — не нормальный человек), и мы приходим к противоречию. Итак, A не может быть нормальным человеком. Следовательно, A — хитрый лжец. Это означает, что высказывание человека B ложно, в силу чего B должен быть нормальным человеком (лжецом он быть не может, так как лжец — человек A). Итак, A — хитрый лжец, а B — нормальный человек. Отсюда мы заключаем, что C — доблестный рыцарь.

Литература
http://www.kakprosto.ru
https://yandex.ru/images
https://ru.wikipedia.org/wiki
https://yandex.ru/images
http://www.spishy-u-antoshki.ru/zadacha-pro-lzhecov-rycarej-i-hitrecov.htm
http://obuchonok.ru/
https://yandex.ru/video
http://mmmf.msu.ru
http://znaemna5.ucoz.ru
infourok.ru
§22. Логические задачи и способы их решения
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (ФГОС) | Логические задачи и способы их решения

 |
22.2. Задачи о рыцарях и лжецах |  |
||
| 22.1. Метод рассуждений |  |
22.3. Задачи на сопоставление. Табличный метод. 22.4. Использование таблиц истинности для решения логических задач |

22.2. Задачи о рыцарях и лжецах
Задачи о рыцарях и лжецах — это такой класс логических задач, в которых фигурируют персонажи:
• рыцарь — человек, всегда говорящий правду;
• лжец — человек, всегда говорящий ложь;
• обычный человек — человек, который в одних ситуациях может говорить правду, а в других — лгать.
Решение подобных задач сводится к перебору вариантов и исключению тех из них, которые приводят к противоречию.
Пример 2. Двое жителей острова А и В разговаривали между собой в саду. Проходивший мимо незнакомец спросил у А: «Вы рыцарь или лжец?». Тот ответил, но так неразборчиво, что незнакомец не смог ничего понять. Тогда незнакомец спросил у В: «Что сказал А?». «А сказал, что он лжец», — ответил В. Может ли незнакомец доверять ответу Б? Мог ли А сказать, что он лжец?
Если А — рыцарь, то он скажет правду и сообщит, что он рыцарь.
Если А — лжец, то он скроет правду и сообщит, что он рыцарь.
Это значит, что В, утверждающий, что «А сказал, что он лжец» заведомо лжёт; он — лжец. Определить же, кем является А, в данной ситуации невозможно.
Пример 3. Рядом стоят два города: город Лжецов (Л) и город Правдивых (П). В городе Лжецов живут лжецы, а в городе Правдивых — правдивые люди. Лжецы всегда лгут, а правдивые — всегда говорят правду. Лжецы и правдивые ходят друг к другу в гости.
Вы попали в один из городов, а в какой не знаете. Вам нужно у первого встречного, задав простой вопрос, узнать, в каком вы городе. Ответом на вопрос может быть только «Да» или « Нет ».
Нужен простой вопрос, ответ на который точно известен вашему респонденту. Например: «Вы находитесь в своём городе?».
Надо задать вопрос и проанализировать варианты ответов с учетом того, кто их мог дать.
Самостоятельно разберитесь с решением задачи, рассмотрев блок-схему на рис. 4.12.
Рис. 4.12. Блок-схема для анализа ответов
Пример 4. Перед нами три человека: А, В и С. Один из них рыцарь, другой — лжец, третий — нормальный человек. При этом неизвестно, кто есть кто. Эти люди утверждают следующее:
1) А: я нормальный человек;
2) В: это правда;
3) С: я не нормальный человек.
Кто такие А, В и С?
Для решения этой задачи следует рассмотреть все возможные варианты распределения ролей.
Начнём с А. Он может быть рыцарем (Р), лжецом (Л) или нормальным человеком (Н). Если А — рыцарь, то В может быть лжецом или нормальным человеком и т. д. Представим все варианты распределения ролей в таблице:
Проанализируем имеющиеся три утверждения, считая, что роли между А, В и С распределены в соответствии с первой строкой таблицы.
Итак, А утверждает, что он нормальный человек (1). Но, согласно первой строке таблицы, — он рыцарь, который не может так о себе сказать. Получено противоречие. Следовательно, первая строка не удовлетворяет условию задачи.
Самостоятельно проанализируйте оставшиеся строки таблицы и дайте ответ на вопрос, поставленный в задаче.
Cкачать материалы урока
xn—-7sbbfb7a7aej.xn--p1ai
Решение олимпиадных задач по математике онлайн. Задача про лжецов, рыцарей и хитрецов
Каждый из 10000 жителей острова лжец, хитрец или рыцарь. Лжецы всегда лгут, рыцари всегда говорят правду, хитрецы говорят как правду, так и ложь. На острове была проведена перепись. Для опроса населения было выбрано 100 человек, про которых известно, что среди них 75 рыцарей и 25 лжецов. Каждый из переписчиков обязан был опросить 100 человек, включая себя, записывая данные про одного человека в одну анкету. Анкеты были сданы в аналитический центр, где их обрабатывал рыцарь. Он разделил данные, записанные рыцарями и лжецами. Данные рыцарей: 4000 лжецов, 2000 хитрецов, 1500 рыцарей; данные лжецов: 500 хитрецов, 500 лжецов, 1500 рыцарей. По итогам переписи король острова заявил, что на острове более четверти жителей рыцари. Правда ли, что он рыцарь?
Решение:
Для удобства будем называть 75 рыцарей, выбранных в условии, «отборными рыцарями», а 25 лжецов из условия – «отборными лжецами». Всех остальных людей на острове будем называть «неизвестными лицами».
Проанализируем сначала анкеты, которые собрали отборные рыцари. Так как их собрали рыцари, то анкеты были сданы в аналитический центр в их первозданном виде, в том виде, в котором их заполняли неизвестные лица (ведь отборные рыцари всегда за правду и не будут подменивать результаты в анкетах). Всего отборные рыцари собрали 75 · 100 = 7500 анкет от неизвестных лиц. Среди них были четыре тысячи анкет, хозяинами которых были лжецы. Но настоящие ли это лжецы? Давайте поразмышляем. Настоящие лжецы всегда врут, поэтому не подписали свои анкеты, будто они от лжецов. Поэтому среди этих 4000 анкет не было ни одной анкеты лжеца. Но могли ли быть среди них анкеты рыцарей? Нет, ведь рыцари никогда не врут, они никогда не назовутся лжецами. Значит, 4000 анкет принадлежат лишь хитрецам, которые могут иногда приврать.
Также отборные рыцари упомянули про 2000 анкет, якобы принадлежащих хитрецам. Выясним, кто на самом деле мог скрываться под личиной хитреца. Хитрецы могли назвать себя так, лжецы – тоже, ведь это будет ложью, а вот рыцари себя хитрецами назвать не могли. Поэтому среди этих 2000 анкет не будет ни одной анкеты рыцаря. И последние данные от отборных рыцарей: 1500 анкет принадлежат рыцарям. Но рыцарями могли себя назвать кроме настоящих рыцарей, также лжецы и хитрецы. Подведём первый итог: всего из 7500 человек, опрошенных отборными рыцарями, настоящими рыцарями могли оказаться только неизвестные люди из последней категории, то есть обладатели указанных выше 1500 анкет. И при наилучшем стечении обстоятельств из 7500 жителей рыцарями могли оказаться ровно 1500 человек. И никак не больше.
Для того чтобы найти ответ в этой задаче, мы будем считать сколько анкет принадлежит рыцарям. Так мы вычислим, сколько на острове живёт рыцарей, и правду сказал король или нет. На самом деле, посчитать точное количество рыцарей на острове нам не удастся, однако мы оценим наибольшее количество рыцарей, которые могут проживать на острове с учётом всех данных в задаче. И если мы докажем, что максимально возможное количество рыцарей на острове менее четверти от общего количества жителей (именно такое число упомянул король), то тем самым мы докажем, что король соврал, поэтому не является рыцарем.
Теперь проанализируем 2500 анкет, собранных отборными лжецами. Тут рассуждения немного усложнятся, теперь информация в анкетах будет искажаться также отборными лжецами. Если, например, анкету заполнял рыцарь, он напишет, что он рыцарь, и никак иначе. Но так как анкету принимал отборный лжец, то в результате в анкете будет записано, что её обладатель либо хитрец, либо лжец (потому что сказать правду отборный лжец не сможет).
рассуждения немного усложнятся, теперь информация в анкетах будет искажаться также отборными лжецами. Если, например, анкету заполнял рыцарь, он напишет, что он рыцарь, и никак иначе. Но так как анкету принимал отборный лжец, то в результате в анкете будет записано, что её обладатель либо хитрец, либо лжец (потому что сказать правду отборный лжец не сможет).
Итак, отборные лжецы указали, что среди 2500 опрошенных оказалось 500 человек, указавших в своих анкетах, что они лжецы. Учитывая характер отборных лжецов, можно сделать вывод, что эти 500 человек указали в анкетах либо про хитрецов, либо про рыцарей. Выясним, кто мог быть среди этих 500 человек. Хитрецами себя могли назвать (как уже выяснилось выше) лишь хитрецы и лжецы. А рыцарями – лишь рыцари и хитрецы. Итого среди этих 500 человек могли оказаться в разной пропорции и лжецы, и рыцари, и хитрецы.
Также среди 2500 анкет 500 анкет якобы принадлежат хитрецам. Учитывая, кто составлял анкеты, 500 анкет могут принадлежать рыцарям и лжецам. Назвать себя рыцарями осмелились бы любые из жителей острова, в том числе рыцари. Назвать себя лжецами могли лишь хитрецы. Поэтому среди этих 500 человек могли в разной пропорции оказаться также лжецы, рыцари и хитрецы.
Осталось рассмотреть 1500 анкет, в которых указано, что их обладатели рыцари. Снова делая поправку на характер отборных лжецов, собиравших анкеты, делаем вывод: эти 1500 анкет могут принадлежать хитрецам и лжецам. Назваться хитрецами могли либо лжецы, либо хитрецы. Назваться лжецами – только хитрецы. Поэтому среди обладателей этих 1500 анкет могли быть лишь хитрецы и лжецы. Рыцарей среди них быть не могло.
Подведём второй итог: среди 2500 неизвестных людей, опрошенных отборными лжецами, настоящими рыцарями могли оказаться только люди из первой и второй категории. То есть в лучшем случае это 500 рыцарей из первой категории и 500 рыцарей из второй. Тогда вообще из 2500 опрошенных рыцарями могли быть не больше 500 + 500 = 1000 человек.
Последний итог: среди всех жителей острова может быть не больше, чем 1500 (столько человек мы нашли из первого итога) + 1000 (столько человек из второго итога) = 2500 человек. То есть на острове живёт не больше 2500 человек. Но король сказал наоборот, что на острове рыцарей строго больше чем четверть населения острова, то есть больше 2500 человек. Поэтому мы доказали, что король просто напросто соврал. Поэтому к числу рыцарей его отнести нельзя, то есть ответ в задаче – «неправда, король не может быть рыцарем». Эх, что же это за король, который не является рыцарем?!
Вот такая интересная задача по олимпиадной математике была решена на нашем сайте.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
1. На развилке двух дорог, одна из которых ведёт в город А, где живут правдивые люди, а другая ведёт в город В, где живут лгуны, математик встретил жителя одного из этих городов. Может ли математик за один вопрос выяснить у встреченного им жителя, какая из дорог ведёт в город А? 2. Пусть в условиях задачи 1 математик встретил на развилке не одного, а трёх человек, один из которых является жителем города А, второё – жителем города В, а третий – обманщиком. При этом математик знает, что среди этих троих – один житель города А, другой – житель города В, а третий – обманщик, но конкретно не знает, кто из них есть кто. Может ли математик за два вопроса выяснить дорогу в А? ОСТРОВ РЫЦАРЕЙ И ЛЖЕЦОВСуществует множество хитроумных задач об острове, населенном «рыцарями», всегда говорящими только правду, и лжецами, изрекающими только ложь. Предполагается, что каждый обитатель острова либо рыцарь, либо лжец. Мы начнем с одной хорошо известной задачи этого типа.
3. Трое жителей острова (А, B и C) разговаривали между собой в саду. Проходивший мимо незнакомец спросил у A: «Вы рыцарь или лжец?» Тот ответил, но так неразборчиво, что незнакомец не смог ничего понять. Тогда незнакомец спросил у B: «Что сказал A?» «А сказал, что он лжец», — ответил B. «Не верьте B! Он лжет! — вмешался в разговор островитянин C. Кто из островитян B и C рыцарь и кто лжец? 4. Предположим, что A говорит: «Или я лжец, или B рыцарь». Кто из двух персонажей A и B рыцарь и кто лжец? 5.Перед нами снова три островитянина A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец. Двое из них (А и B) высказывают следующие утверждения: 6.Перед нами в очередной раз три островитянина A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец. Условимся называть двух островитян однотипными, если они оба рыцари или оба лжецы. Пусть A и B высказывают следующие утверждения: 7.Перед нами снова трое островитян A, B и C. А высказывает утверждение: «В и C однотипны». Кто-то спрашивает у C: «А и B однотипны?» Что ответит островитянин C? РЫЦАРИ, ЛЖЕЦЫ И НОРМАЛЬНЫЕ ЛЮДИВ не менее увлекательном виде задач персонажи делятся на три типа: рыцарей, говорящих всегда только правду, лжецов, изрекающих только ложь, и нормальных людей, которые иногда лгут, а иногда говорят правду. 8.Перед нами трое людей A, B и C. Один из них рыцарь, другой лжец и третий — нормальный человек (типы людей могут быть перечислены не в том же порядке, в каком выписаны их «имена» A, B и C). Наши знакомые высказывают следующие утверждения. 9. Двое людей A и B, о которых известно, что каждый из них либо рыцарь, либо лжец, либо нормальный человек, высказывают следующие утверждения: 10. Табель о рангах. 11. Трое людей A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец, либо нормальный человек, высказывают следующие утверждения: A: |
znaemna5.ucoz.ru
Помогите решить / разобраться (М)
Известен тип логических задач о рыцарях и лжецах. Вариантов немало.Приведу 3 из них
(напомню что рыцари говорят всегда только правду, лжецы всегда лгут)
1)А говорит: «По кр мере, один из нас лжец». Кто такой А (рыцарь или лжец) и кто такой В?
2) A: B утверждает, что он рыцарь. B: A утверждает, что он лжец. Кто такой А и кто такой В?
3)На острове живет 25 чел: рыцари, лжецы и хитрецы. Рыцари всегда гов правду, лжецы всегда лгут, а хитрецы отв на зад им вопросы по очереди то правду, то ложь. Всем жителям острова б задано 3 вопроса: “Вы рыцарь?”, “Вы хитрец?”, “Вы лжец?”. На 1й вопр “Да” отв 15 чел, на 2й — 7 чел, на 3й — 5 чел. Сколько хитрецов живет на этом острове?
——————————————————————————————
Вопрос заключается в следующем: можно ли решать подобные задачи не устными логическими рассуждениями а путем составления и решения логических уравнений
И далее использование метода таблиц истинности или дерева выражений традиционных для задач на логические уравнения (ЕГ по информатике)?
Или в крайнем случае с использованием формулы включений-исключений (з-ча 3)?
например 1) можно записать в виде
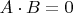
но это уравнение нельзя принять за окончательное так как А может врать. Может более верно пару систем:
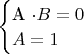
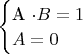
2)нельзя ли обобщить данный тип задач применительно к практическим задачам из практики юристов и следствия?
dxdy.ru