Ромб. Площадь, периметр, радиус
В школьном курсе в геометрии среди основных задач значительное внимание уделено примерам вычисления площади и периметра ромба. Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD. Ниже приведен рисунок на котором изображен ромб.
Свойства ромбаПоскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.
- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.
- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
P=4a.
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а).
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
r=h/2.
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S) ромба и величина острого угла (alpha) то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
Она достаточно проста для того чтобы запомнить, а также — для вычислений.
Третья формула площади имеет смысл когда известен угол между сторонами. Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Периметр ромба
Периметр ромба равен сумме всех его сторон. Учитывая то что они все равны периметр принимает значение
P=4a.
И в завершение запомните что периметр измеряется в единицах длины, а площадь в квадратных единицах. 2}}2\)
2}}2\)
- Формула стороны ромба через периметр:
\(a=\frac{P}{4}\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
ромб или не ромб? квадрат или не квадрат?: janemouse — LiveJournal
в четверг — на прошлом занятии нашего математического кружка в ДНТТМе — мы решили предложить детям задачки, связанные с подсчётом прямоугольников.но для того, чтоб сосчитать правильно, нужно всё-таки договориться, что же считать прямоугольником, а что — нет.
вот тут-то и началось самое весёлое!
ведь дети все эти геометрические фигуры в лицо узнают лет с трёх, а потому ко второму-третьему классу они уже уверены, что уж в чём-чём, а в этом они прекрасно разбираются!
Показали мы детям разные картинки, и попросили обвести на них все прямоугольники.
смотрим: ответы у всех разные!
Ага!
значит, будет отличный повод это обсудить.
даём следующие картинки, и просим обвести все ромбы.
тоже ответы не сходятся.
Ну ладно, начинаем собирать мнения о том, что же такое ромб, и что такое квадрат.
Быстро выяснили, что у квадрата 4 стороны, и все углы прямые.
Отлично!
рисую тогда такие картинки:
сразу откуда-то всплывает слово «замкнутый» — уже приятно 🙂
прошу выйти и дорисовать все эти фигуры до квадрата.
все дорисовать почему-то не получается, хотя сторон и 4, и все углы прямые, но из лесенки квадрат не выходит…
но в целом обсуждение движется в нужном направлении, и мы лишь подталкиваем детей.
нам кажется, что они уже почти во всём разобрались, и мы даём следующую картинку:
просим посчитать, сколько тут ромбов, и сколько — квадратов.
и тут часть детей впадает в ступор, и более того, они так увлечённо и страстно отстаивают свою точку зрения, что и остальные начинают сомневаться!
мамы, сидящие на последней парте, давятся от смеха.
Настя тем временем вырезала из бумаги квадрат, и показывает его детям.
-Квадрат?
-Да! Квадрат!
Настя поворачивает квадрат на 15 градусов, и интересуется:
-А так — квадрат?
-Да, так тоже квадрат!!!
Настя поворачивает квадрат ещё немного — и мнения разделяются. А при виде квадрата, повёрнутого на 45 градусов, все вслед за Денисом вопят:
-Ромб! Теперь — ромб!
Только Серёжа всё ещё сомневается, и пытается сказать, что так — и то, и другое. Но и в его голосе уже нет прежней уверенности.
-А ромб — это что такое? — интересуемся мы.
-Ромб, он такой длинненький, у него стороны одинаковые, и углы одинаковые.
-А у квадрата разве стороны не одинаковые?
-Одинаковые. Но у него же углы прямые!
Пытаемся дописать определение квадрата.
Мы уже договорились, что квадрат — замкнутый, у него 4 равные стороны, и все углы прямые.
Проверяем, что при повороте квадрата длина его сторон и углы, вроде бы, не меняются, но дети всё равно в сомнениях.
И тут Денис предлагает внести гениальное дополнение к определению:
-Квадрат стоит ровно на земле!
-Ты точно в этом уверен?
-Да, так в учебнике написано!
-Ой, принеси нам этот учебник, пожалуйста!
-Ну, может, не в учебнике, но нам так учительница говорила.
Договариваемся, что Денис попросит учительницу ему это написать, чтоб мы тоже не сомневались.
И — раз Денис так настаивает, — добавляем к определению фразу «стоит ровно на земле».
И тут Настя спрашивает:
-А если земля наклонная, если земля идёт вот так?
-Тогда квадрат! — уверенно говорит Денис.
Мамы на задней парте уже больше не могут сдерживаться, они уже почти стонут от смеха.
Тогда мы всё-таки вносим ясность, что некоторые фигуры могут быть одновременно и квадратами ромбами.
Заодно обсуждаем, что квадрат — он по совместительству ещё и четырёхугольник.
Приходим к выводу, что у четырёхугольника 4 угла, а у треугольника — три.
И тут меня осенило.
-Три угла? — переспрашиваю я.- Тогда вот тут есть треугольники? Много?
-Много!
И я им ещё гору разных фигур о трёх углах нарисовала, прежде, чем они сообразили, что стороны должны быть обязательно именно прямые!
Аналогично мы разбирались и с четырёхугольниками:
-А если уголок отрезать? а если звёздочка 4-угольная — это разве не четырёхугольник?
Потом мы наконец создали все определения, и перешли к подсчёту прямоугольников,
но только тогда, когда мы были уверены, что дети хорошо понимают, считать ли среди прямоугольников квадраты.
интересно будет спросить их ещё раз через месяц,
смогут ли они дать определение квадрата и ромба, и выбрать их среди других фигур.
про кружок — выношу из комментариев.
мы с Настей ведём кружок для начальной школы в ДНТТМ.
м Шаболовская, ул Донская 37
у нас сейчас 3 группы
16.00 — 3 класс
17.00 — 1-2 класс
18.00 — 2-3 класс
в этот четверг занятия не будет, поскольку в ДНТТМ будет проходить конференция, и наш класс, возможно, будет занят.
если вы хотите привести ребёнка к нам на занятия, напишите, пожалуйста, мне в почту
mouse точка jane собачка gmail точка com
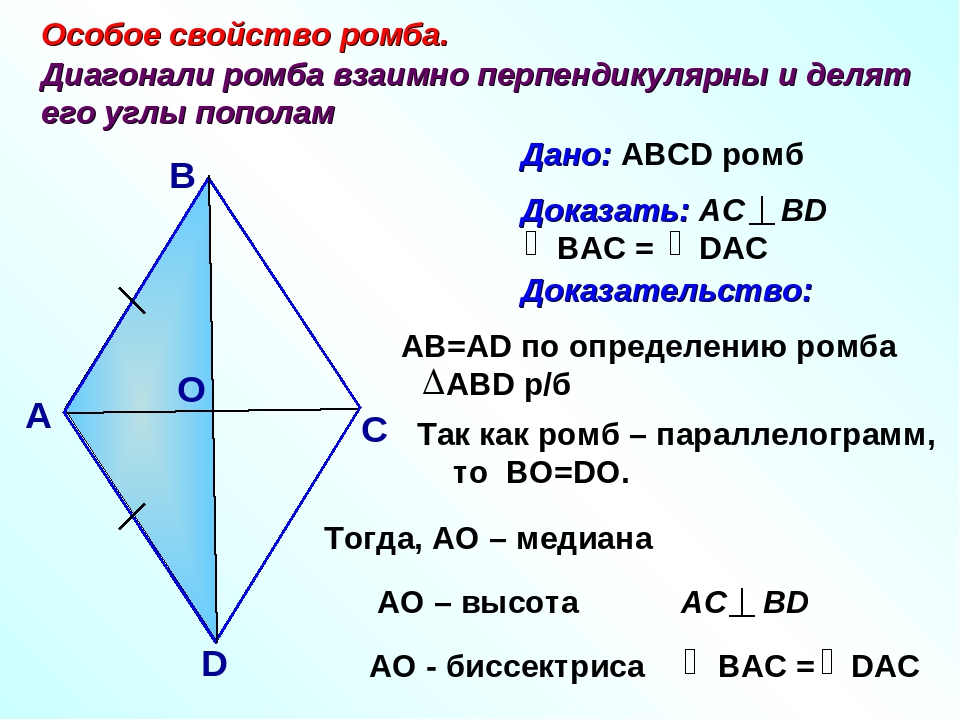
ТЕОРИЯ. Ромб — параллелограмм, у которого все стороны равны. Прямые, содержащие диагонали ромба, являются его осями симметрии. Задача №4 Докажите, что если центр вписанной в четырехугольник окружности совпадает с точкой пересечения
2«Ромб»
Историческая справка.
«Ромб» происходит от латинского слова «ромбус» — латинской формы греческого слова «ромбос», означающего бубен. Мы привыкли к тому, что бубен имеет круглую форму, но раньше бубны имели форму квадрата или ромба, о чём свидетельствуют изображения «бубен» на игральных картах.
Ромб — параллелограмм, у которого все стороны равны. Ромб обладает всеми свойствами параллелограмма и дополнительно к ним следующими свойствами:
Диагонали ромба взаимно перпендикулярны.
Диагонали ромба являются биссектрисами, его внутренних углов.

Прямые, содержащие диагонали ромба, являются его осями симметрии.
В любой ромб можно вписать окружность, центр которой лежит на пересечении диагоналей ромба.
S=ah
S=aІsinA
S=0.5 d1 d2
d1І + d2І=4 aІ
r=h/2
Задача №1 .
На сторонах выпуклого четырехугольника ABCD внешним образом построены подобные ромбы, причем их острые углы
· прилегают к вершинам A и C. Докажите, что отрезки, соединяющие центры противоположных ромбов, равны, а угол между ними равен
·.
Решение.
Пусть O1,O2,O3 и O4 центры ромбов, построенных на сторонах AB,BC,CD и DA; M середина диагонали AC. Тогда MO1 = MO2 и
·O1MO2 =
· (см. домашнюю задачу (1)) . Аналогично MO3 = MO4 и
·O3MO4 =
·. Следовательно, при повороте на угол
· относительно точки M треугольник O1MO3 переходит в O2MO4.
Задача №2.
Продолжения сторон AB и CD вписанного четырехугольника ABCD пересекаются в точке P, а продолжения сторон BC и AD- в точке Q. Докажите, что точки пересечения биссектрис углов AQB и BPC со сторонами четырехугольника являются вершинами ромба.
Решение. Обозначим точки пересечения и углы так, как показано на рисунок. Достаточно проверить, что x = 90°. Углы четырехугольника BMRN равны 180° –
·,
· +
·,
· +
· и x, поэтому равенство x = 90° эквивалентно равенству (2
· +
·) + (2
· +
·) = 180°. Остается заметить, что 2
· +
· =
·BAD и 2
· +
· =
·BCD.
Задача№3.
Из вершин A и B опущены перпендикуляры на CD, пересекающие прямые BD и AC в точках K и L соответственно. Докажите, что AKLB- ромб.
·BLP =
·BDC =
·BAP. Кроме того, AK
·
·BL и AL
·BK. Поэтому AKLB- ромб.
Задача №4
Докажите, что если центр вписанной в четырехугольник окружности совпадает с точкой пересечения диагоналей, то этот четырехугольник- ромб.
Решение. Пусть O центр вписанной окружности и точка пересечения диагоналей четырехугольника ABCD. Тогда
·ACB =
·ACD и
·BAC =
·CAD. Поэтому треугольники ABC и ADC равны, так как сторона AC у них общая. Следовательно, AB = DA. Аналогично AB = BC = CD = DA.
Задача №5.
Докажите, что середины сторон произвольного четырехугольника — вершины параллелограмма. Для каких четырехугольников этот параллелограмм является прямоугольником, для каких ромбом, для каких квадратом?
Д.З.
Четырехугольник ABCD вписанный. Докажите, что центры вписанных окружностей треугольников ABC, BCD, CDA и DAB образуют прямоугольник.
Решение. Пусть Oa,Ob,Oc и Od- центры вписанных окружностей треугольников BCD,ACD,ABD и ABC соответственно. Так как
·ADB =
·ACB, то
·AOcB = 90° + (
·ADB/2) = 90° + (
·ACB/2) =
·AOdB (см. задачу №3 урока №6,7). Поэтому четырехугольник ABOdOc вписанный, т.е.
·OcOdB = 180° –
·OcAB = 180° – (
·A/2). Аналогично
·OaOdB = 180° – (
·C/2). Так как
·A +
·OcOdB +
·OaOdB = 270°, а значит,
·OaOdOc = 90°. Аналогично доказывается, что и остальные углы четырехугольника OaObOcOd равны 90°.
15
Приложенные файлы
- 5204794
Размер файла: 38 kB Загрузок: 0
Ромб против параллелограмма — Технология
Содержание:
Есть много форм, которые создают впечатление сходства друг с другом, но когда вы смотрите на них, между ними очень мало различий. То же самое имеет место с ромбом и параллелограммом, которые тесно связаны, но все же отличаются.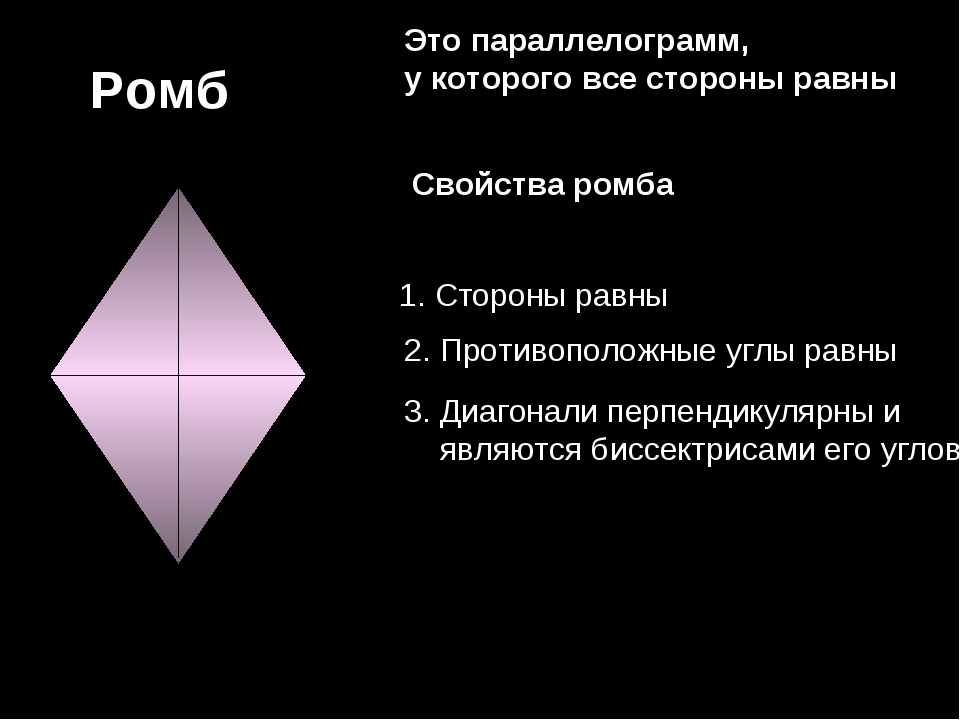 Основное различие между ними можно объяснить, например, ромб представляет собой четырехугольник, все стороны которого имеют одинаковую длину. С другой стороны, четырехугольник, противоположные стороны которого параллельны и равны по длине, будет называться параллелограммом. Ромб всегда будет параллелограммом, но это не так, наоборот.
Основное различие между ними можно объяснить, например, ромб представляет собой четырехугольник, все стороны которого имеют одинаковую длину. С другой стороны, четырехугольник, противоположные стороны которого параллельны и равны по длине, будет называться параллелограммом. Ромб всегда будет параллелограммом, но это не так, наоборот.
Содержание: Разница между ромбом и параллелограммом
- Сравнительная таблица
- Что такое ромб?
- Что такое параллелограмм?
- Ключевые отличия
- Видео Объяснение
Сравнительная таблица
| Основа отличия | Ромб | Параллелограмм |
| Определение | Четырехугольник, все стороны которого имеют одинаковую длину. | Четырехугольник, противоположные стороны которого параллельны и равны по длине. |
| формула | (х / а) + (у / б) = 1. | K = чч |
| происхождения | Латинское слово «ромб», означающее «вертеться». | Греческое слово «параллелограмм» на греческом языке означает «из параллельных линий». |
| Характерная черта | Все четыре стороны одинаковой длины, даже короткие или длинные. | Две длинные стороны одинаковой длины и две короткие стороны одинаковой длины. |
| Co-связь | Каждый ромб будет параллелограммом. | Каждый параллелограмм не будет ромбом. |
Что такое ромб?
Это можно определить как четырехугольник, все стороны которого имеют одинаковую длину. Само слово происходит от латинского языка и является одним из тех редких, кто остался таким же, каким он был с момента интеграции вго век и имел значение «поворачиваться и вращаться». У него также есть другое название, которое является равносторонним четырехугольником, поскольку равносторонний — это термин, который означает, что все стороны имеют одинаковую длину. Он также упоминается как алмаз, особенно при игре в карты, в которых ромбовидная форма, как известно, выглядит как восьмигранник или в некоторых случаях как ромб с углом 60 градусов. Можно с уверенностью сказать, что каждый объект, который является ромбом, также является параллелограммом и выглядит как воздушный змей. Можно также предположить, что каждый ромб с прямыми углами называется квадратом. Есть много способов его различения, первый из которых — самое простое определение, согласно которому четырехугольник со всеми четырьмя сторонами является ромбом. Любой четырехугольник, в котором диагонали делят пополам друг друга и являются перпендикулярными, также является определением ромба. Другой способ охарактеризовать его состоит в том, что любой четырехугольник, в котором каждая диагональ делит пополам две противоположные стороны внутренних углов, называется ромбом. Это также объясняется в отношении геометрии как четырехугольника ABCD, который имеет стандартную точку O на своей плоскости и образует четыре параллельных треугольника ABO, BCO, CDO и DAO. Это может быть выражено через уравнение, которое (x / a) + (y / b) = 1.
Можно с уверенностью сказать, что каждый объект, который является ромбом, также является параллелограммом и выглядит как воздушный змей. Можно также предположить, что каждый ромб с прямыми углами называется квадратом. Есть много способов его различения, первый из которых — самое простое определение, согласно которому четырехугольник со всеми четырьмя сторонами является ромбом. Любой четырехугольник, в котором диагонали делят пополам друг друга и являются перпендикулярными, также является определением ромба. Другой способ охарактеризовать его состоит в том, что любой четырехугольник, в котором каждая диагональ делит пополам две противоположные стороны внутренних углов, называется ромбом. Это также объясняется в отношении геометрии как четырехугольника ABCD, который имеет стандартную точку O на своей плоскости и образует четыре параллельных треугольника ABO, BCO, CDO и DAO. Это может быть выражено через уравнение, которое (x / a) + (y / b) = 1.
Что такое параллелограмм?
Его можно определить как четырехугольник, противоположные стороны которого параллельны и равны по длине. Это похоже на ромб, но отличается в то же время и имеет некоторые отличительные свойства, которые имеют свойства прямоугольника. Это можно объяснить как простой четырехсторонний объект, у которого две стороны параллельны друг другу. Стороны слева и справа будут равны друг другу, в то время как стороны сверху и снизу будут равны друг другу, но все четыре не будут иметь одинаковую длину. Слово произошло от греческого термина «параллелограмм» и означало «параллельные линии». Существуют некоторые особые случаи для этого термина, которые заключаются в том, что если две стороны имеют одинаковую длину, а две другие имеют разную длину, то оно известен как трапеция. Точно так же, если противоположные стороны параллельны друг другу, а соседние стороны неравны, то правых углов не будет, этот случай называется ромбоидом. Ромб — другая часть, которая вписывается в это, и как объяснено ранее, каждый ромб будет параллелограммом.
Ключевые отличия
- Все четыре стороны имеют одинаковую длину в случае ромба, в то время как все четыре стороны не имеют одинаковую длину в случае параллелограмма.
- Есть две стороны одинаковой длины, которые будут длинными, и две стороны одинаковой длины, которые будут короткими для параллелограмма, в то время как ромб имеет все четыре стороны, длинные или короткие, но равные.
- В ромбе будет два острых и два тупых угла, тогда как параллелограмм будет одинаковым.
- Каждый ромб будет параллелограммом, в то время как каждый параллелограмм не будет ромбом.
- В случае параллелограмма будет две пары параллельных линий, а в ромбе также будут две пары равной длины.
- Термин «ромб» произошел от латинского языка и остался тем же словом со значением «переворачиваться». Термин «параллелограмм» произошел от греческого слова «параллелограмм» со значением «параллельных линий».
- Термин ромб может быть объяснен в терминах уравнения как (x / a) + (y / b) = 1. С другой стороны, термин параллелограмм может быть выражен как K = bh.
Видео Объяснение
Разница между ромбом и параллелограммом
В геометрии существует много типов четырехугольника, то есть параллелограмма, ромба, квадрата, прямоугольника, трапеции и воздушного змея, которые имеют общие характеристики, из-за чего люди сталкиваются с проблемами в понимании этих фигур. Ромб можно назвать косым квадратом, соседние стороны которого равны. Напротив, параллелограмм — это наклонный прямоугольник с двумя наборами параллельных противоположных сторон.
Основное различие между ромбом и параллелограммом заключается в их свойствах, то есть все стороны ромба имеют одинаковую длину, тогда как параллелограмм представляет собой прямолинейную фигуру, противоположные стороны которой параллельны.
Сравнительная таблица
| Основа для сравнения | Ромб | Параллелограмм |
|---|---|---|
| Имея в виду | Ромб относится к плоской четырехгранной фигуре со всеми конгруэнтными сторонами. | Параллелограмм — это четырехсторонняя плоская фигура, противоположные стороны которой параллельны друг другу. |
| Равные стороны | Все четыре стороны имеют одинаковую длину. | Противоположные стороны имеют равную длину. |
| Диагонали | Диагонали делят пополам друг на друга под прямым углом, образуя разносторонний треугольник. | Диагонали делят пополам друг на друга, образуя два конгруэнтных треугольника. |
| Площадь | (pq) / 2, где p и q — диагонали | bh, где b = основание и h = высота |
| периметр | 4 а, где а = сторона | 2 (a + b), где a = сторона, b = основание |
Определение ромба
Четырехугольник, длина сторон которого совпадает, называется ромбом. Он имеет плоскую форму и имеет четыре стороны; причем лицевые стороны параллельны друг другу (см. рисунок, приведенный ниже).
Противоположные углы ромба равны, т.е. одинаковой степени. Его диагонали встречаются друг с другом под углом 90 градусов (под прямым углом), следовательно, перпендикулярны друг другу и образуют два равносторонних треугольника. Его смежные стороны являются дополнительными, что означает, что сумма их меры равна 180 градусам. Он также известен как равносторонний параллелограмм.Определение параллелограмма
Параллелограмм, как следует из его названия, описывается как плоская фигура, имеющая четыре стороны, чьи противоположные стороны параллельны и конгруэнтны (см. Рисунок ниже).
Мера его углов наклона равна, и последующие углы являются дополнительными, то есть сумма их меры равна 180 градусам. Его диагонали делят пополам, образуя два конгруэнтных треугольника.
Его диагонали делят пополам, образуя два конгруэнтных треугольника.Ключевые различия между ромбом и параллелограммом
Различие между ромбом и параллелограммом может быть четко показано на следующих основаниях:
- Мы определяем ромб как четырехгранный четырехугольник плоской формы, длина всех сторон которого совпадает. Параллелограмм — это четырехгранная плоская фигура, противоположные стороны которой параллельны друг другу.
- Все стороны ромба равны по длине, тогда как только противоположные стороны параллелограмма равны.
- Диагонали ромба делят друг на друга под прямым углом, образуя два разносторонних треугольника. В отличие от параллелограмма, диагонали которого делят пополам друг на друга, образуя два конгруэнтных треугольника.
- Математическая формула для площади ромба (pq) / 2, где p и q — диагонали. Наоборот, площадь параллелограмма может быть рассчитана путем умножения основания и высоты.
- Периметр ромба можно рассчитать с помощью следующей формулы — 4 a, где a = сторона ромба. Напротив, периметр параллелограмма можно рассчитать путем сложения базы и высоты и умножения суммы на 2.
Заключение
И параллелограмм, и ромб четырехугольные, у которых лицевые стороны параллельны, противоположные углы равны, сумма внутренних углов равна 360 градусам. Сам ромб — это особый параллелограмм. Поэтому можно сказать, что каждый ромб является параллелограммом, но обратное невозможно.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Типы четырёхугольников
Классификация треугольников изложена в разделе нашего справочника «Типы треугольников».
Целью данного раздела является классификация четырёхугольников.
Классификация четырёхугольников по типам представлена на схеме 1.
Схема 1
Рисунки и определения фигур, представленных на схеме 1, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Четырёхугольник | Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. | |
| Выпуклый четырёхугольник | Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках | |
| Невыпуклый четырёхугольник | Четырёхугольник называют невыпуклым, если он не является выпуклым. | |
| Параллелограмм | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны | |
| Трапеция | Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). | |
| Дельтоид | Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
| Четырёхугольник |
Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. |
| Выпуклый четырёхугольник |
Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках |
| Невыпуклый четырёхугольник |
Четырёхугольник называют невыпуклым, если он не является выпуклым. |
| Параллелограмм |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Трапеция |
Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). |
| Дельтоид |
Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
Типы параллелограммов
На схеме 2 представлена классификация параллелограммов.
Схема 2
Рисунки и определения фигур, представленных на схеме 2, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Прямоугольник | Прямоугольник – это параллелограмм, у которого все углы прямые. | |
| Ромб | Ромб – это параллелограмм, у которого все стороны равны. | |
| Квадрат | Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. | |
| Параллелограмм общего вида | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Прямоугольник |
Прямоугольник – это параллелограмм, у которого все углы прямые. |
| Ромб |
Ромб – это параллелограмм, у которого все стороны равны. |
| Квадрат |
Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. |
| Параллелограмм общего вида |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
Типы трапеций
На схеме 3 представлена классификация трапеций.
Схема 3
Рисунки и определения фигур, представленных на схеме 3, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Равнобедренная (равнобочная) трапеция | Равнобедренной называют трапецию, у которой боковые стороны равны. | |
| Прямоугольная трапеция | Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. | |
| Трапеция общего вида | Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
| Равнобедренная (равнобочная) трапеция |
Равнобедренной называют трапецию, у которой боковые стороны равны. |
| Прямоугольная трапеция |
Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. |
| Трапеция общего вида |
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Rhombus Facts for Kids
Ромб представляет собой параллелограмм со всеми сторонами равной длины. Ромб со всеми равными углами называется квадратом.
Слово ромб происходит от греческого слова ромб , что означает «волчок». Ромб иногда называют ромбом, но не все ромбы имеют форму ромба.
Чтобы найти периметр ромба, просто сложите все стороны. Также противоположные стороны параллельны и противоположные углы равны.
Еще одна интересная вещь: диагонали (пунктирные линии на втором рисунке) пересекаются посередине под прямым углом.
Характеристики
Простой (несамопересекающийся) четырехугольник является ромбом тогда и только тогда, когда он является одним из следующих:
- параллелограмм, в котором диагональ делит пополам внутренний угол
- Параллелограмм, у которого не менее двух последовательных сторон равны по длине
- параллелограмм, в котором диагонали перпендикулярны (ортодиагональный параллелограмм)
- четырехугольник с четырьмя сторонами одинаковой длины (по определению)
- четырехугольник, в котором диагонали перпендикулярны и делят друг друга пополам
- четырехугольник, каждая диагональ которого делит пополам два противоположных внутренних угла
- четырехугольник ABCD , имеющий точку P на своей плоскости, так что все четыре треугольника ABP , BCP , CDP и DAP совпадают.
- четырехугольник ABCD , в котором вписанные окружности в треугольники ABC , BCD , CDA и DAB имеют общую точку
Основные свойства
Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон.Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Отсюда следует, что любой ромб обладает следующими свойствами:
- Противоположные углы ромба имеют равную меру.
- Две диагонали ромба перпендикулярны; то есть ромб — это ортодиагональный четырехугольник.
- Его диагонали делят пополам противоположные углы.
Детские картинки
Ромб имеет квадрат как частный случай и является частным случаем воздушного змея и параллелограмма.
Ромб. Каждый угол, отмеченный черной точкой, является прямым. Высота h — это расстояние по перпендикуляру между любыми двумя несмежными сторонами, которое равно диаметру вписанной окружности. Диагонали длиной p и q представляют собой отрезки красной пунктирной линии.

Факты о параллелограммах для детей
Параллелограмм — многоугольник с четырьмя сторонами (четырехугольник). У него две пары параллельных сторон (стороны, которые никогда не пересекаются) и четыре ребра.Противоположные стороны параллелограмма имеют одинаковую длину (одинаковую длину). Слово «параллелограмм» происходит от греческого слова «параллелограммон» (, ограниченное параллельными линиями ). Прямоугольники, ромбы и квадраты — это параллелограммы.
Как показано на рисунке справа, поскольку треугольники ABE и CDE совпадают (имеют одинаковую форму и размер),
У всех параллелограммов противоположные углы равны друг другу.Углы, которые не противоположны параллелограмму, в сумме составляют 180 градусов.
Характеристики
Простой (не самопересекающийся) четырехугольник является параллелограммом тогда и только тогда, когда истинно любое из следующих утверждений:
- Две пары противоположных сторон равны по длине
- Две пары противоположных углов равны по мере
- Диагонали пересекают друг друга
- Одна пара противоположных сторон параллельна и равна длине
- Углы прилегающие дополнительные
- Каждая диагональ делит четырехугольник на два равных треугольника
- Сумма квадратов сторон равна сумме квадратов диагоналей.(Это закон параллелограмма)
- Обладает вращательной симметрией порядка 2
- Имеет две линии симметрии
Недвижимость
- Противоположные стороны параллелограмма параллельны.
- Любая линия, проходящая через середину параллелограмма, делит область пополам.
- Параллелограммы — это четырехугольники.
хороший факт параллелограмм параллелограмм в нем параллелограмм представляет собой многоугольник с четырьмя сторонами (четырехугольник). У него две пары параллельных сторон (стороны, которые никогда не пересекаются) и четыре ребра. Противоположные стороны параллелограмма имеют одинаковую длину (одинаковую длину). Слово «параллелограмм» происходит от греческого слова «параллелограммон» (ограниченный параллельными линиями). [1] Прямоугольники, ромбы и квадраты — это параллелограммы.
Противоположные стороны параллелограмма имеют одинаковую длину (одинаковую длину). Слово «параллелограмм» происходит от греческого слова «параллелограммон» (ограниченный параллельными линиями). [1] Прямоугольники, ромбы и квадраты — это параллелограммы.
Как показано на рисунке справа, поскольку треугольники ABE и CDE совпадают (имеют одинаковую форму и размер),
{\ displaystyle AE = CE} {\ displaystyle AE = CE} {\ displaystyle BE = DE.} {\ Displaystyle BE = DE.} Во всех параллелограммах противоположные углы равны друг другу.Углы, которые не противоположны параллелограмму, в сумме составляют 180 градусов.
Содержание 1 Характеристики 2 Свойства 3 Ссылки 4 Другие веб-сайты Характеристики Простой (не самопересекающийся) четырехугольник является параллелограммом тогда и только тогда, когда выполняется одно из следующих утверждений: [2] [3]
Две пары противоположных сторон равны по длине Две пары противоположных углов равны по размеру Диагонали делят друг друга пополам Одна пара противоположных сторон параллельны и равны по длине Соседние углы являются дополнительными Каждая диагональ делит четырехугольник на два равных треугольника Сумма квадратов сторон равняется сумме квадратов диагоналей.(Это закон параллелограмма) Он имеет вращательную симметрию 2-го порядка. Он имеет две линии симметрии. Свойства Противоположные стороны параллелограмма параллельны. Любая линия, проходящая через середину параллелограмма, делит область пополам. Параллелограммы — это четырехугольники. Список литературы
«Интернет-словарь этимологии». etymonline.com. Проверено 10 января 2011 года. Оуэн Байер, Феликс Лазебник и Дейдра Смелцер, Методы евклидовой геометрии, Математическая ассоциация Америки, 2010 г., стр. 51-52. Залман Усискин, Дженнифер Гриффин, «Классификация четырехугольников.Исследование определения ", Издательство информационного века, 2008 г., стр. 22.
Другие веб-сайты Викискладе есть медиафайлы по теме параллелограммов. Параллелограмм и ромб — анимированный курс (конструкция, окружность, площадь) Интерактивный параллелограмм — стороны, углы и наклон
Эту короткую математическую статью можно сделать длиннее.Вы можете помочь Википедии, добавив к ней.
это параллелограмм хороший факт параллелограмм параллелограмм в нем
Категория: Полигоны Меню навигации Вы не вошли в систему Обсуждение Вклад Создать учетную запись Войти PageTalk ПрочитатьИзменитьИсточник измененийПросмотреть историюПоиск Поиск в Википедии Главная страница Простой старт Простой разговор Новые изменения Показать любую страницу Помощь Связаться с нами Отправить в Википедию О Википедии Инструменты Какие ссылки здесь Связанные изменения Загрузить файл Специальные страницы Постоянная ссылка Информация о странице Цитировать эту страницу Элемент Викиданных Песочница Печать / экспорт Создать книгу Загрузить в формате PDF Страница для печати В других проектах Wikimedia Commons
На других языках Deutsch English Español Français 한국어 Italiano Tagalog Tiếng Việt 中文 79 еще Изменить ссылки Эта страница последний раз была изменена 12 января 2021 года в 14:46.Текст доступен по лицензии Creative Commons Attribution / Share-Alike и GFDL; могут применяться дополнительные условия. См. Подробности в Условиях использования.
Урок ромба для детей: определение и факты
Что делает ромб
Чтобы иметь ромб, должны быть определенные элементы, которые должна иметь форма.
- Все четыре стороны должны быть равны, поэтому я говорил о ударе по квадрату.Итак, ромб похож на квадрат, поскольку все стороны имеют одинаковую длину.
- Противоположные внутренние углы равны.
- Противоположные стороны параллельны. Это делает ромб особенным параллелограммом.
Определение периметра ромба выполняется так же, как и для любого другого четырехугольника; сложив четыре стороны. Однако поиск области — это другое дело.
Определение площади
Поскольку стороны наклонены, вы не можете умножить длину на ширину, как квадрат, чтобы найти площадь ромба. Вы должны найти высоту ромба, а затем умножить ее на длину. Для этого вы должны нарисовать прямую вертикальную линию от верхнего внешнего угла вниз и нарисовать горизонтальную линию, которая простирается от основания, пока не встретится с вертикальной линией, которую вы нарисовали. Затем измерьте вертикальную линию от точки, где она встречается с горизонтальной линией, которую вы нарисовали, до угла ромба. Это даст вам высоту. Затем умножьте высоту на длину верхней или нижней стороны.
Вы должны найти высоту ромба, а затем умножить ее на длину. Для этого вы должны нарисовать прямую вертикальную линию от верхнего внешнего угла вниз и нарисовать горизонтальную линию, которая простирается от основания, пока не встретится с вертикальной линией, которую вы нарисовали. Затем измерьте вертикальную линию от точки, где она встречается с горизонтальной линией, которую вы нарисовали, до угла ромба. Это даст вам высоту. Затем умножьте высоту на длину верхней или нижней стороны.
Интересные факты о ромбах
Знаете ли вы, что все ромбы — параллелограммы, но не все параллелограммы — ромбы? Это правда! Единственное различие между ромбом и параллелограммом состоит в том, что все стороны ромба должны быть равны.Итак, ромб — это всегда параллелограмм, но не наоборот.
Еще одна вещь, которую большинство людей не знает о ромбах, — это то, что квадрат на самом деле представляет собой особый вид ромба. Если вы посмотрите на то, что образует квадрат, это все, что составляет ромб. Единственное, что есть у квадрата, чего нет у ромба, — это четыре равных угла, которые составляют 90 градусов. Итак, квадрат — это не только особый прямоугольник, но и особый ромб.
Краткое содержание урока
Ромб — это особый вид четырехугольника, известный как четырехугольник . У ромба должны быть четыре равные стороны, противоположные стороны параллельны, а противоположные углы параллельны. Чтобы найти его площадь, вы должны сначала нарисовать линию высоты.
Классификация ромбов
Ромб — это четырехугольник, и его можно классифицировать в соответствии с иерархией четырехугольников, показанной ниже:
Вы можете видеть, что ромб классифицируется как параллелограмм и воздушный змей, и все три являются четырехугольниками. Как это может быть правдой? Давайте сделаем параллелограмм активности, чтобы выяснить это.
Как это может быть правдой? Давайте сделаем параллелограмм активности, чтобы выяснить это.
Активность
Для этого занятия вам понадобятся:
- Соломинки для питья, разрезанные пополам — так как соломинки для питья имеют длину около 9 дюймов, у вас будут секции длиной 4,5 или 2,25 дюйма (снова разрежьте их пополам, если не можете протянуть шнурок)
- Линейка для измерения соломинок
- Ножницы для резки соломки
- Тонкая эластичная нить или шнурок, проходящий через отверстие в соломке
Инструкция
1) Сначала свяжите четыре соломинки вместе на шнурке или резинке и свободно свяжите их, чтобы потом можно было расстегнуть.Сделайте все четыре угла одинакового размера.
- Каков ваш результат?
- Теперь наклоните квадрат в любую сторону. Какая у вас фигура сейчас?
2) Разрежьте одну из использованных выше соломок на две равные части. Соедините эти две короткие части, а затем две другие более длинные части.
- Сделайте угол между короткими частями менее 90 градусов. Какая у вас фигура сейчас?
- Можно ли сделать из воздушного змея ромб?
3) Развяжите резинку или шнурок и замените две короткие части еще двумя соломинками.
- Сделайте один угол меньше 90 градусов. Какая у вас фигура сейчас?
- Сделайте все углы равными. Какая у вас фигура сейчас?
Вопросы для размышления
- Всегда ли ромб параллелограмм? Квадрат?
- Ромб — это всегда воздушный змей? Квадрат?
- Посмотрите на иерархию. Что вы можете сказать о четырехугольнике, который находится под другим четырехугольником? Над другим четырехугольником?
Свойства ромба — Концепция — Геометрия Видео от Brightstorm
Свойства ромбов часто проявляются в геометрических доказательствах и многих других типах задач.Все свойства параллелограмма применимы к свойствам ромба , поскольку ромб является разновидностью параллелограмма. У ромба есть (1) две пары параллельных сторон, (2) четыре стороны, которые все конгруэнтны друг другу, (3) диагонали, которые делят углы пополам, и (4) диагонали, которые перпендикулярны биссектрисам друг друга.
У ромба есть (1) две пары параллельных сторон, (2) четыре стороны, которые все конгруэнтны друг другу, (3) диагонали, которые делят углы пополам, и (4) диагонали, которые перпендикулярны биссектрисам друг друга.
Важно знать свойства ромба.Почему? Потому что вы собираетесь использовать его в доказательствах, истинных и ложных вопросах, сопоставлении и многом другом, особенно когда вы пытаетесь найти недостающие углы и стороны внутри ромба. Итак, приступим.
Первое, что важно в ромбе, — это то, что он параллелограмм. Итак, все, что применимо к параллелограмму, применимо и к ромбу. Итак, у нас есть две пары параллельных сторон. У нас также есть четыре стороны, которые все конгруэнтны друг другу, а не две пары конгруэнтных сторон, как у прямоугольника.
Во-вторых, диагонали делят углы пополам. Итак, если я нарисую здесь диагональ, он разделит этот угол пополам на два совпадающих угла и сделает то же самое с этим углом. Итак, эти четыре угла будут соответствовать друг другу. Если я нарисую другую диагональ, она разделит этот угол пополам, а также этот угол.
Еще один ключевой момент — диагонали перпендикулярны биссектрисам друг к другу. Таким образом, они всегда будут пересекаться под углом 90 градусов и будут рассекать друг друга пополам.Таким образом, диагонали параллелограмма делят друг друга пополам, но не обязательно пересекаются под прямым углом. Ромб должен пересекаться под углом 90 градусов.
Напомню, что эти две вещи неверны для прямоугольников. Итак, для прямоугольника диагонали не делят свои углы пополам, а диагонали в прямоугольнике не перпендикулярны биссектрисам друг друга.
6 четырехугольников | Недвижимость | Площадь
17 декабря 2020
Время чтения: 3 минуты
ВведениеЧто такое четырехугольник?
Какие бывают четырехугольники?
Многоугольники с четырьмя ребрами и четырьмя вершинами называются четырехугольниками. В реальной жизни многие предметы напоминают четырехугольники. Четырехугольник имеет некоторые основные свойства, то есть он может быть правильной или неправильной формы, его внутренние углы в сумме составляют 360 °. Давайте посмотрим на типы четырехугольников с их свойствами и некоторыми примерами.
В реальной жизни многие предметы напоминают четырехугольники. Четырехугольник имеет некоторые основные свойства, то есть он может быть правильной или неправильной формы, его внутренние углы в сумме составляют 360 °. Давайте посмотрим на типы четырехугольников с их свойствами и некоторыми примерами.
Что такое четырехугольник? — PDF
Если вы когда-нибудь захотите прочитать его столько раз, сколько захотите, вот загружаемый PDF-файл, чтобы узнать больше.
| 📥 | Что такое четырехугольник? Различные типы, формулы и свойства — PDF | Загрузить |
Также читайте:
Как классифицируются четырехугольники?
Все четырехугольники могут иметь основные свойства, но в чем-то отличаться.У всех типов четырехугольников есть свои уникальные свойства.
Это следующие:
- Квадрат
- Прямоугольник
- параллелограмм
- Трапеция
- Ромб
- Воздушный змей
Все о квадратах Формулы квадрата
- Площадь квадрата = сторона \ (\ times \) сторона , длина стороны квадрата, умноженная на саму сторону.
- Периметр квадрата = 4 \ (\ times \) стороны , в четыре раза больше длины стороны.
- Диагональ квадрата = \ (a \ sqrt {2} \) , где a — сторона квадрата.
- Все внутренние углы составляют 90 °.
- Все стороны квадрата равны по длине.
 2)}, \), где l и b — длина и ширина прямоугольника.
2)}, \), где l и b — длина и ширина прямоугольника.
- Внутренний угол прямоугольника составляет 90 °.
- Противоположные стороны прямоугольника параллельны и равны.
- Диагональ — это линия, соединяющая противоположные вершины.
- Диагональ прямоугольника образует две пары разносторонних треугольников.
Пример:
Телевизоры, Мобильные телефоны, Коврики
Все о параллелограммах Формулы параллелограмма
- Площадь параллелограмма = b \ (\ times \) h , где b — основание основания параллелограмма, а h — высота параллелограмма.
- Периметр периметра = 2 \ (\ times \) (основание + длина стороны)
- Имеет две пары равных противоположных сторон, параллельных друг другу.
- Сумма их внутренних углов составляет 360 °.
- Смежные углы в сумме составляют 180 °.
- Их противоположные углы равны.
- Их диагонали пересекают друг друга.
Примеры:
танграм
Все о трапециях Формулы трапеции
- Площадь трапеции = ½ × h (a + b) , где h — высота, а a и b — две длины основания.
- Периметр трапеции = сумма всех сторон трапеции.
- Трапеции имеют две противоположные неравные параллельные стороны.
- Суммарные внутренние углы трапеции составляют 360 °.
Все о ромбе Формулы ромба:
Площадь ромба = высота \ (\ times \) сторона ромба
Другой способ рассчитать площадь ромба — разделить произведение двух диагоналей
Площадь \ (= P \ frac {Q} {2} \)
- Периметр ромба \ (= 4 \ times \) сторона ромба.

- Все четыре стороны равны.
- Диагонали пересекаются под углом 90 °.
Все о воздушных змеях Формулы воздушных змеев
- Периметр воздушного змея \ (= 2 \ times \) (a + b)
- Площадь воздушного змея \ (= h_1 × h_2 \)
- Диагонали пересекаются под углом 90 °.
- Две соседние стороны равны друг другу.
- Диагонали пересекают друг друга.
Сводка
В этом блоге рассказывается о различных четырехугольниках, их свойствах и формулах для определения их площади и периметра. Он подробно обсуждает и охватывает все основы четырехугольника.
Автор: Суганья Баладжи, учитель Cuemath
О компании Cuemath
Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков.Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.
Часто задаваемые вопросы о четырехугольниках
Как найти площадь параллелограмма?
Площадь параллелограмма \ (= b \ times h \)
Какова формула площади квадрата?
Площадь квадрата \ (= a × a \)
a = длина стороны
Какова формула площади прямоугольника?
Площадь прямоугольника \ (= w \ times h \)
W = ширина
h = высота
Какова формула площади параллелограмма?
Площадь параллелограмма \ (= b \ times h \)
b = основание
h = вертикальная высота
Какова формула площади трапеции?
Площадь трапеции \ (= ½ (a + b) \ times h \)
h = вертикальная высота
Какова формула площади ромба?
Площадь ромба \ (= P \ times \ frac {Q} {2} \)
Какова формула периметра квадрата?
«Периметр любого замкнутого геометрического объекта определяется как расстояние вокруг этого объекта. ”
”
Периметр квадрата \ (= 4 \ умноженный на \)
Какова формула периметра прямоугольника?
Периметр прямоугольника определяется как сумма всех сторон прямоугольника.
Периметр прямоугольника \ (= 2 \ times (l + b) \)
Какова формула периметра параллелограмма?
Сумма сторон параллелограмма равна периметру параллелограмма.
Какова формула периметра трапеции?
Сумма всех сторон трапеции называется периметром трапеции.
Какова формула периметра ромба?
Сумма всех сторон ромба составляет периметр ромба.
Периметр ромба \ (= 4 \ умножить на \)
Какова формула периметра воздушного змея?
У воздушного змея две пары равных сторон. Общее расстояние по внешней стороне называется периметром воздушного змея.
Внешние ссылки
Четырехугольник (Википедия)
Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция
ПОДАРИТЕ СВОЕМУ РЕБЕНКУ CUEMATH EDGE
Доступ к персонализированному обучению математике с помощью интерактивных рабочих листов, игровых концепций и курсов по уровням
Запишитесь на бесплатный урок
Узнайте больше о Cuemath
Rhombi at a Glance
Теперь, когда мы рассмотрели наиболее распространенный тип четырехугольника, с которым мы сталкиваемся, мы можем выкопать наши лопаты и копнуть немного глубже, чтобы найти более редкие четырехугольники.Как мы узнаем, является ли четырехугольник обычным или редким? Что ж, нам следует искать четырехугольники, которые чем-то отличаются и обладают особыми свойствами. Они будут выделяться, как оперные певцы на пантомиме.
Первый из этих параллелограммов — это ромб, или ромбы во множественном числе. Если это сбивает с толку, подумайте «осьминог → осьминоги». Конечно, споры об осьминоги и осьминоги еще более сбивают с толку.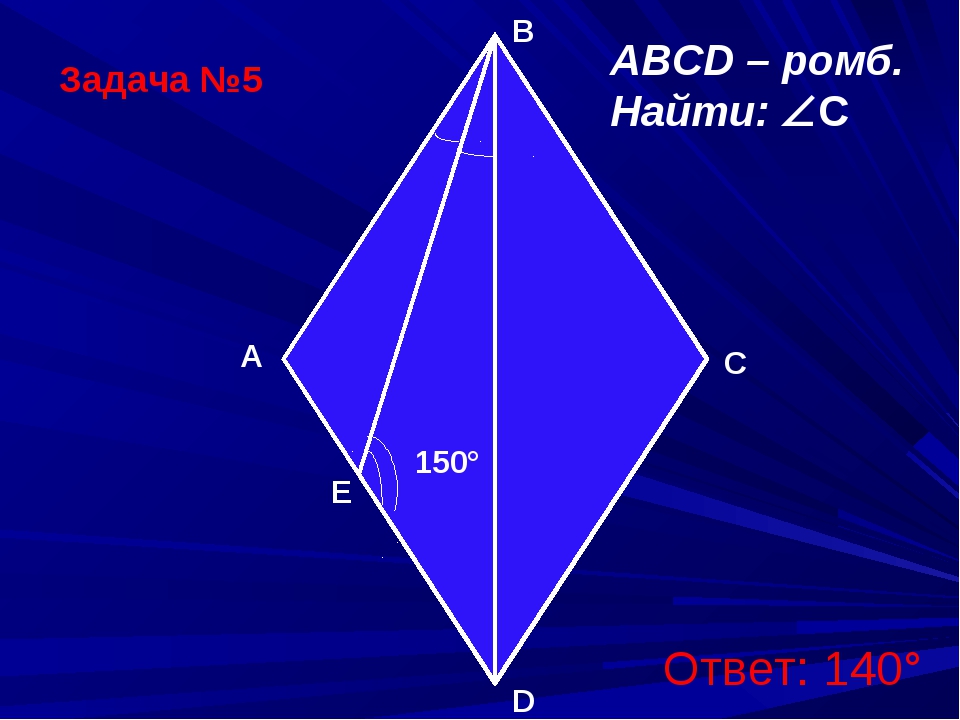 Мы бы предпочли не вдаваться в подробности.
Мы бы предпочли не вдаваться в подробности.
Ромб — это тип параллелограмма с четырьмя конгруэнтными сторонами.На нашем рисунке WX || YZ и XY || ZW (что делает его параллелограммом) и WX ≅ XY ≅ YZ ≅ ZW , (что делает его ромбом).
Пример задачи
Четырехугольник PQRS ромб?
PQRS — параллелограмм, но только противоположные стороны совпадают. Поскольку PQ ≅ RS ≇ QR ≅ PS , этот параллелограмм не является ромбом.
Ромби выходят за рамки того, что ожидается от параллелограммов. У них есть все свойства параллелограммов и многое другое. Намного больше.
Как известно, диагонали параллелограмма делят друг друга пополам. Это все хорошо, но диагонали ромбов продвигают этот хет-трик еще дальше. Они не только биссектрисы друг друга; они тоже перпендикулярны. Оооо, да.
Еще одна удивительная особенность диагоналей ромба состоит в том, что они разделяют его углы пополам.Другими словами, диагонали ромба — это тоже биссектрисы.
Ромб ABCD , ∠1 ≅ ∠2 ≅ ∠3 ≅ ∠4 и ∠5 ≅ ∠6 ≅ ∠7 ≅ ∠8. Итак, диагонали ромба — это биссектрисы угла и перпендикулярные биссектрисы . Поговорим о многозадачности.
Пример задачи
Каков размер ∠ HIA в виде ромба HIJK ?
Нам дано, что m∠ AHI = 80 °, и мы знаем, что диагонали ромба перпендикулярны друг другу.Это означает, что ∠ HAI имеет размер 90 °. Эти три угла образуют внутренние углы треугольника, которые в сумме должны составлять 180 °, согласно теореме суммы углов для треугольников. Это означает, что ∠ HIA составляет 180 — 80 — 90 = 10 °.
Пример задачи
Докажите, что диагонали ромба делят его на четыре равных треугольника.
Естественно, есть несколько способов сделать это. Мы могли бы использовать любое количество различных теорем и определений о ромбах, но прежде чем мы это сделаем, почему бы нам не нарисовать диагонали? Возможно, это нам немного поможет.
Мы могли бы использовать любое количество различных теорем и определений о ромбах, но прежде чем мы это сделаем, почему бы нам не нарисовать диагонали? Возможно, это нам немного поможет.
А теперь перейдем к доказательству.
| Заявления | Причины |
| 1. ABCD представляет собой ромб | Дано |
2. AB 9050 6 ≅| Определение ромба (1) | |
| 3. ABCD — параллелограмм | Ромб также является параллелограммом (1) |
| 4. AE ≅ CE и BE ≅ DE | Диагонали параллелограмма делят друг друга пополам (3) |
| 5. Δ BEC ≅ Δ DEC 50 Δ DEC 50 Δ 90 DEA | Постулат SSS (2, 4) |
Все, что нам нужно сделать, чтобы доказать наши теоремы о том, что диагонали перпендикулярны друг другу и делят внутренние углы пополам, — это продолжить это доказательство с использованием CPCTC и зная несколько определений .Вы, вероятно, сможете сделать это сами, поэтому мы не будем тратить на это ваше время.
Но что, если четырехугольники нужно доказать, что они ромбовидные? Например, MARK отчаянно пытается доказать Четырехстороннему комитету, что он больше, чем просто предсказуемый параллелограмм. Он ромб, но как он может проявить себя?
MARK нужно будет опуститься на его вершины и умолять. Но члены Четырехстороннего комитета довольно прямолинейны. Их нисколько не поколебали его унижения.Им понадобится доказательство того, что он настоящий ромб, поэтому сумма внутренних углов в 360 ° или деление диагоналей пополам не поможет. Любой старый параллелограмм мог бы легко удовлетворить этим требованиям, не так ли? Но MARK придется доказать немного больше, чтобы добиться ромбовидности. Ему нужно будет убедить их одним из следующих способов:
Ему нужно будет убедить их одним из следующих способов:
- Докажите, что он параллелограмм с 4 равными сторонами.
- Докажите, что это параллелограмм с перпендикулярными диагоналями.
Например, MARK может доказать, что он ромб, вот так:
| Заявления | Причины |
| 1. MARK — параллелограмм | Дано |
| 2. MA ≅ RK и AR ≅ KM | Противоположные стороны параллелограмма равны (1) | Дано |
| 4. m∠ AMK = 60 ° | Теорема суммы углов для треугольников (3) |
| 5. Δ MAK равно равносторонний | Определение равностороннего треугольника (3, 4) |
| 6.Δ MAK равносторонний | Все равносторонние треугольники равносторонние (5) |
| 7. MA ≅ KM ≅ AK | Определение равностороннего треугольника (6) |
| Замена (2, 7) | |
| 9. MARK представляет собой ромб | Определение ромба (8000) |
Все о поддержке Rhombus — Системы Rhombus
В Rhombus мы гордимся тем, что обеспечиваем отличную поддержку клиентов. Мы знаем, что возникнут вопросы и проблемы, и хотим быть уверены, что вы получите как можно более положительный опыт, когда это произойдет.
Комплект поставки
В Rhombus круглосуточная поддержка включена без дополнительных затрат. Независимо от того, есть ли у вас 5-минутный вопрос или вам нужен 5-часовой звонок, все это входит в нашу стандартную услугу.

 Вы можете помочь Википедии, добавив к ней.
Вы можете помочь Википедии, добавив к ней.
 2)}, \), где l и b — длина и ширина прямоугольника.
2)}, \), где l и b — длина и ширина прямоугольника.