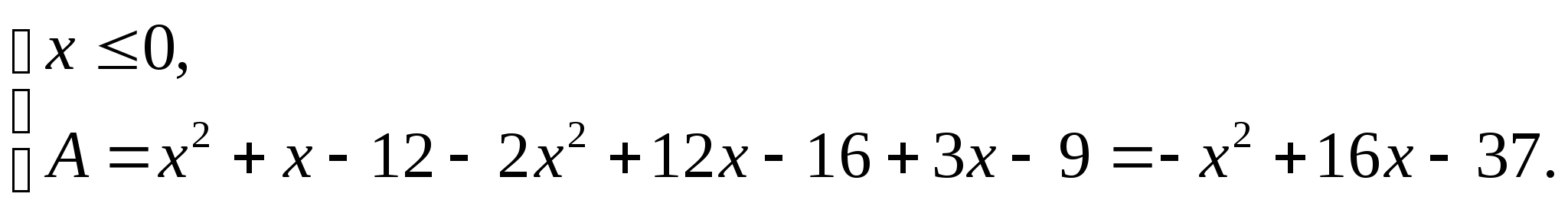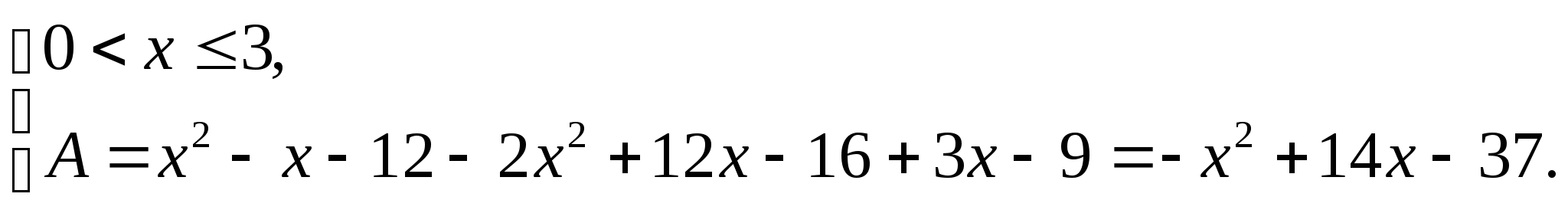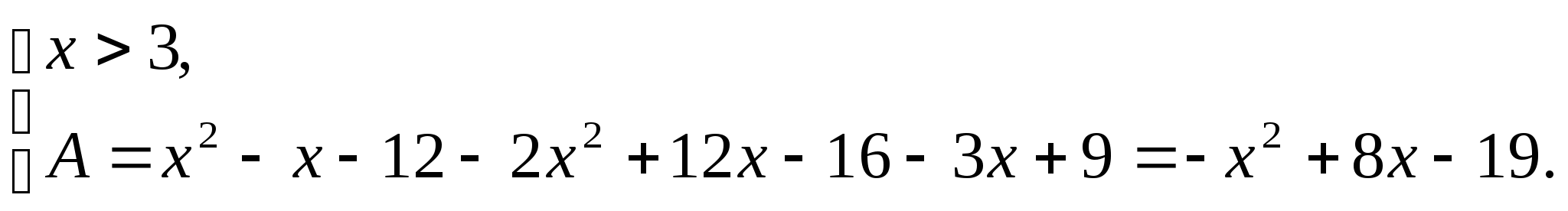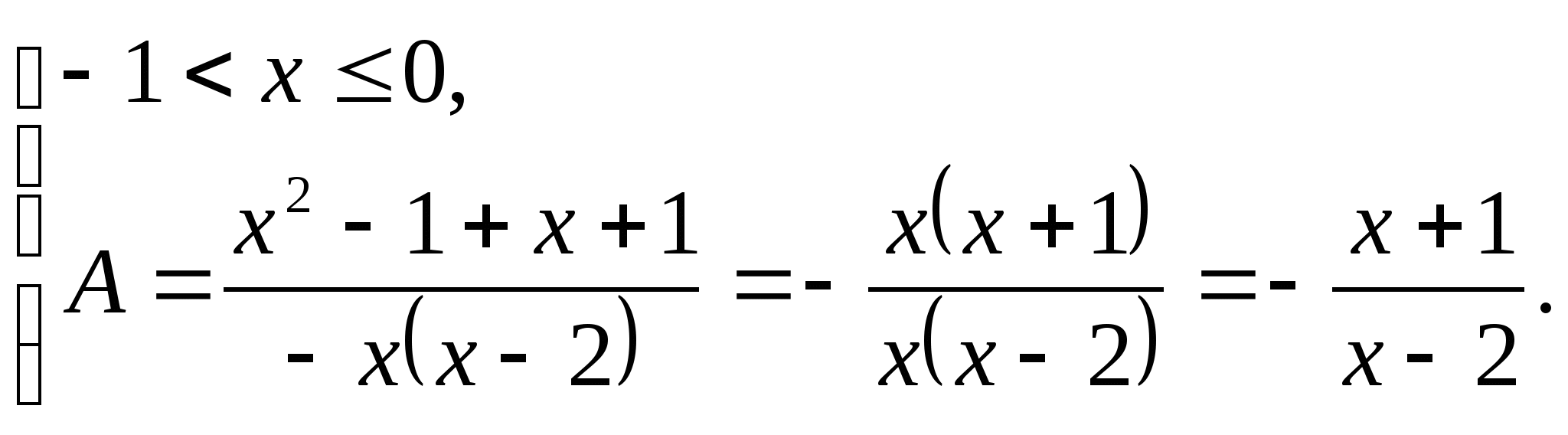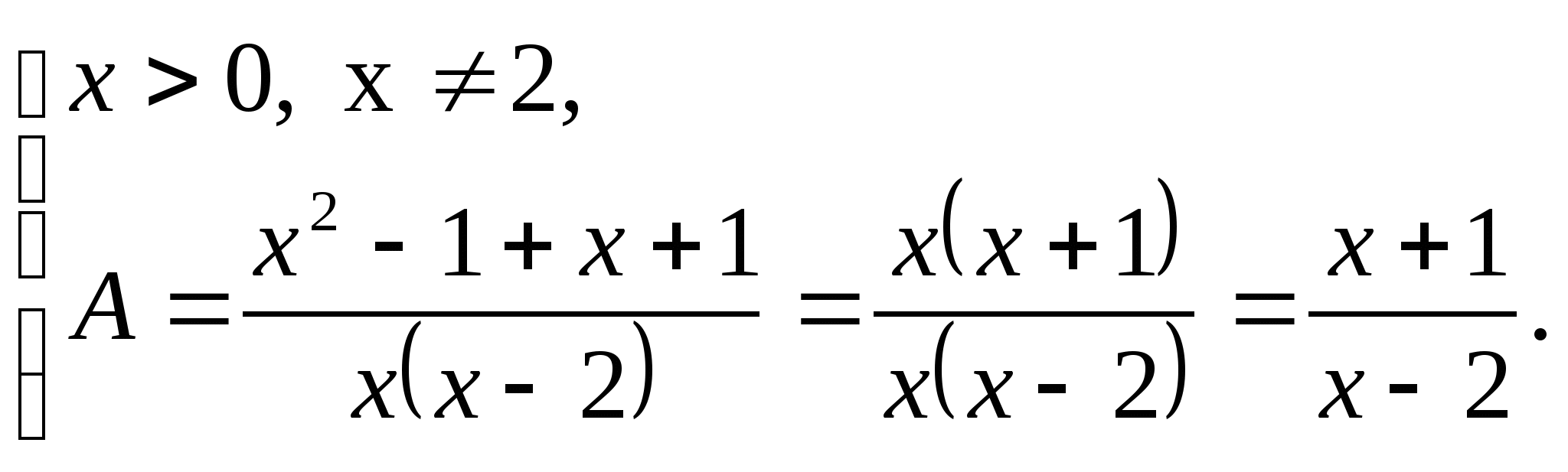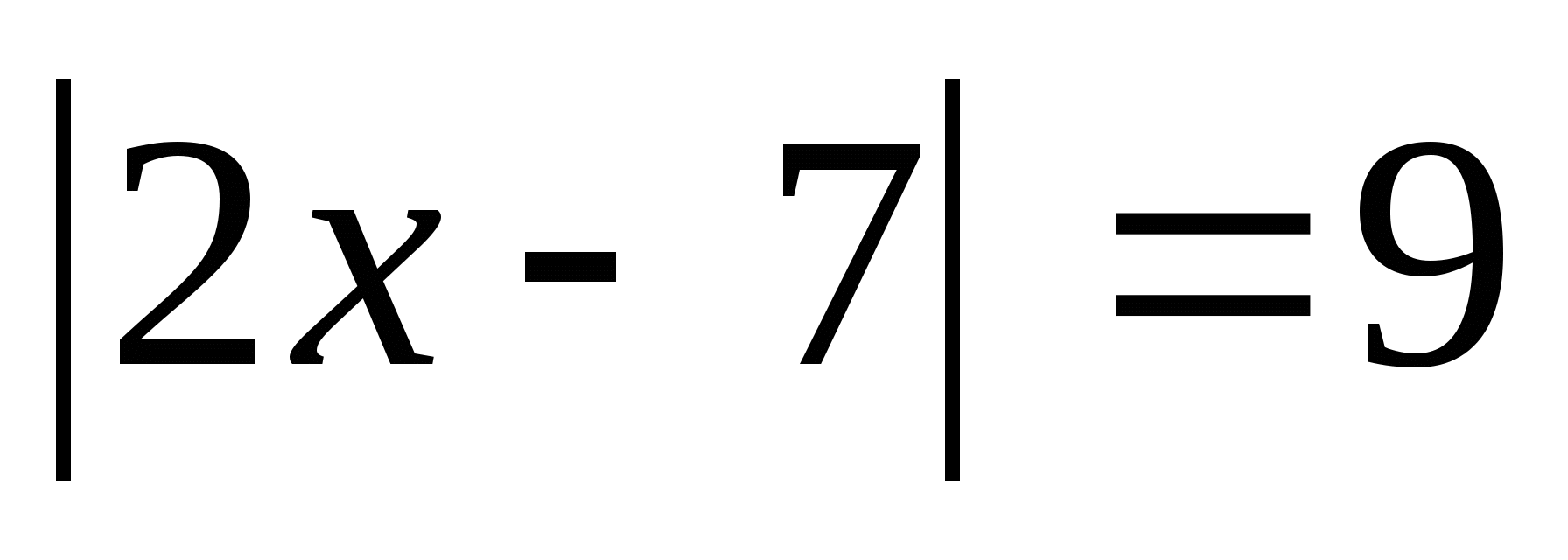Элективный курс «Задачи с модулем»
Программа
элективного курса:
«Задачи с модулем»
( в рамках предпрофильной подготовки)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
В соответствии с концепций модернизации российского образования на период до 2010 г. главная задача российской образовательной политики заключается в обеспечении современного качества образования на основе сохранения его фундаментальности и соответствия актуальным и перспективным потребностям личности, общества и государства.
Основная задача обучения математике в школе заключается в том, чтобы обеспечить прочное и сознательное овладение учащимися системой математических знаний, развивать их математическое мышление и нравственные черты личности.
Элективные курсы являются средством дифференциации и индивидуализации обучения, позволяющие за счет изменений в структуре, содержании и организации образовательного процесса более полно учитывать интересы, склонности и способности учащихся, создавать условия для обучения старшеклассников в соответствии с их профессиональными интересами и намерениями в отношении продолжения образования.
Элективный курс «Задачи с модулем» рассчитан на учеников 9 класса. Актуальность данного курса можно объяснить следующим. Понятие «модуль» традиционно относится к наиболее сложным разделам школьного курса математики.
Известно, что модуль используется при определении предела последовательности, предела функции, при изучении непрерывности и, вообще, при работе с отклонениями величин друг от друга, при изучении разрывных функций и построении графиков разрывных функций и построении графиков, являющихся ломанными с прямолинейными и криволинейными элементами. Применение модулей в условиях задачи нередко позволяет записать условие задачи более компактно, а включение модуля в условие почти любого примера из алгебры и начала анализа сразу заметно повышает трудность его решения.
С понятием модуля школьники знакомятся в курсе математики 6 класса при изучении тем «Положительные и отрицательные числа». Кроме этого, понятие модуля встречается в таких разделах как абсолютная погрешность приближённого числа, изучение свойств корня чётной степени, при решении уравнений и неравенств, их систем, построении графиков функций и в задачах с параметрами.
Задачи с параметрами постоянно присутствуют в материалах ЕГЭ по математике. В тоже время анализ результатов ЕГЭ и вступительных экзаменов по математике свидетельствуют о том, что наибольшие затруднения у школьников вызывают задачи на применение понятия модуля и его свойств.
Так, например, в 2004 задание В6 содержало задачу с модулем. Верно ответили 26 % тестируемых, дали неверный ответ 44 %, не дали ответа 30 %.
В 2005 году в части С (С2) надо было решить уравнение с модулем. Решаемость этих задач составила 11%.
В 2006 году с заданием С2 справились от 7% до 13% учащихся.
Названный элективный курс имеет следующие цели:
систематизировать знания учащихся по теме «Модуль»;
проанализировать содержания школьного курса математики и материалов ЕГЭ по данному типу задач;
познакомить учащихся с основными методами решения уравнений и неравенств с модулем и построения графиков функций содержащих переменную под знаком модуля;
выработать у школьников соответствующие умения и навыки.
Курс рассчитан на 34 часа, 9 класс.
Содержание элективного курса
Тема 1 Определение понятия «модуль» и основные свойства.
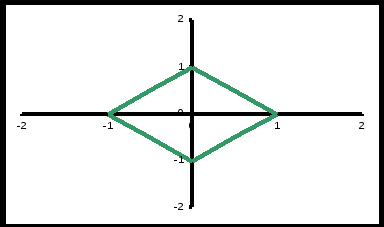
Определение понятия «модуль». Геометрическая интерпретация понятия .
.Простейшие операции над абсолютными величинами (в множестве действительных чисел).
Тема 2 Тождественные преобразования рациональных и иррациональных выражений.
Тема 3 Рациональные уравнения.
Уравнения вида 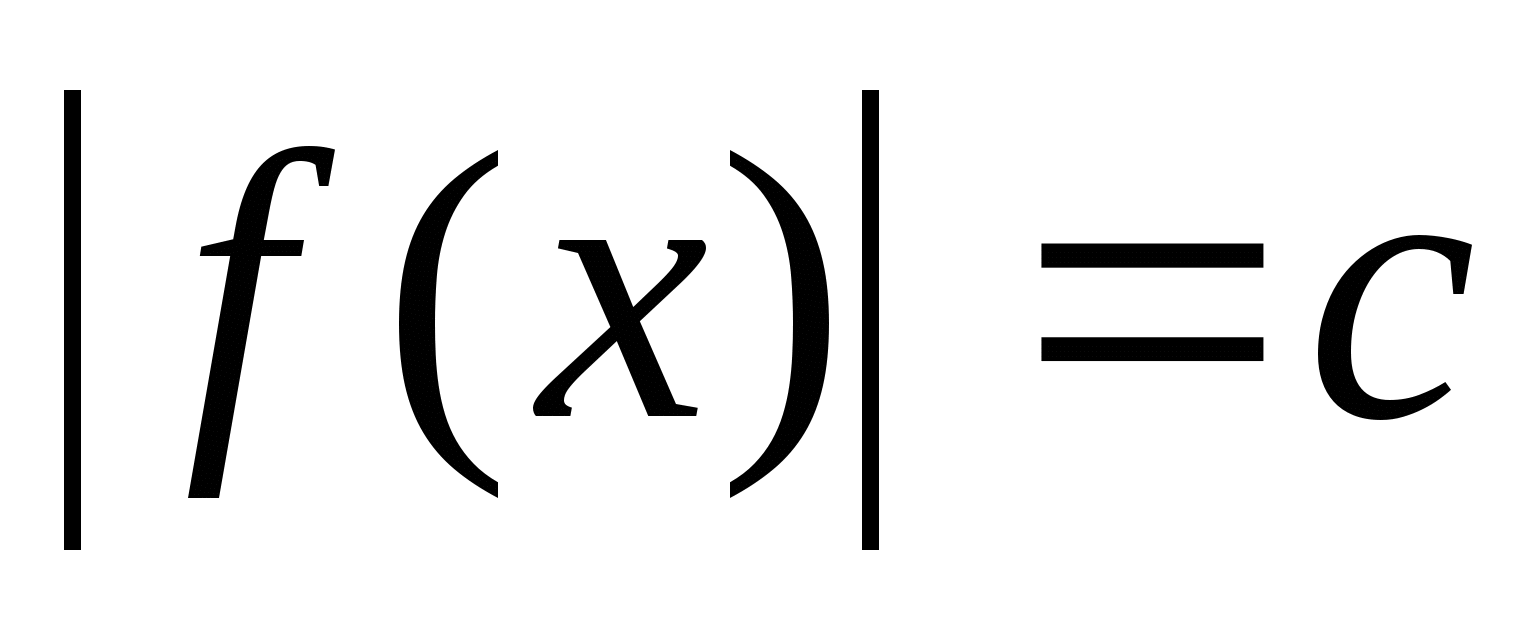 (с- число).
(с- число).
Уравнения вида 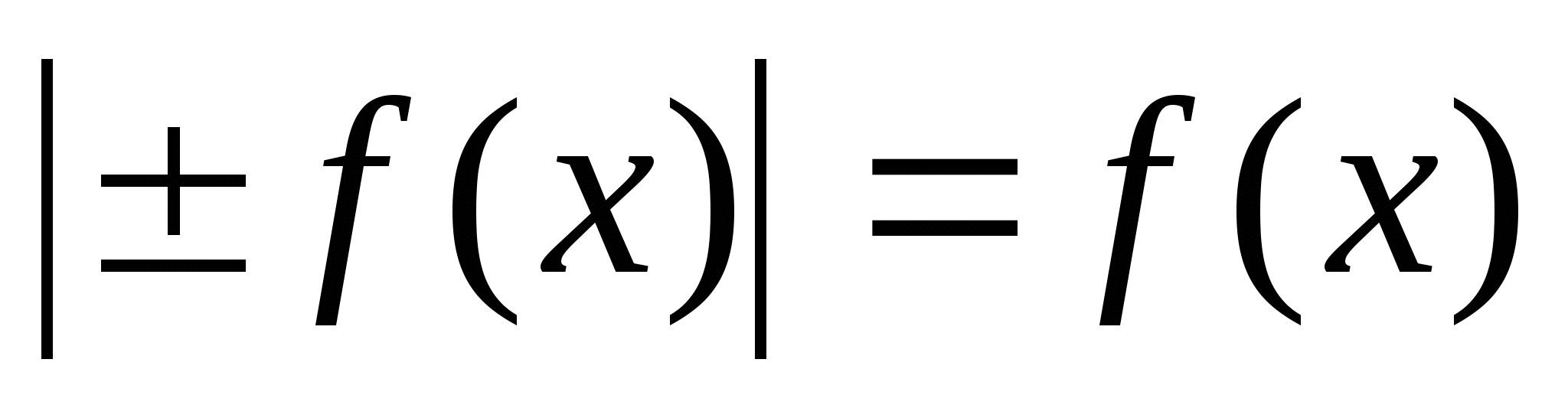 .
.
Уравнения вида 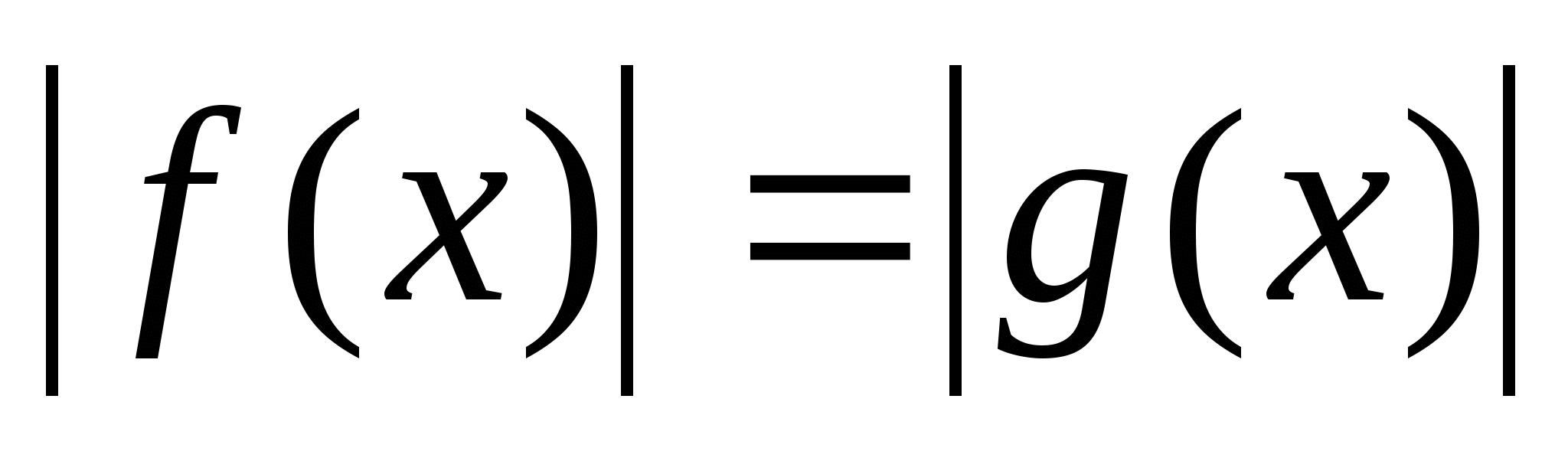
Уравнения вида 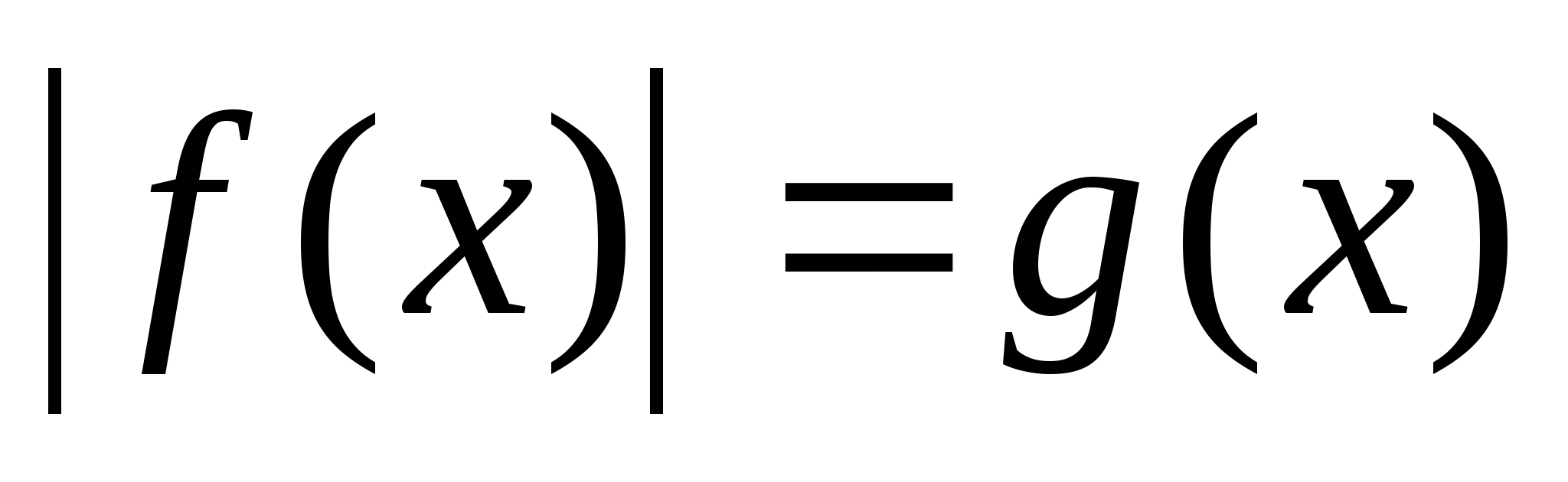 .
.
Уравнения вида 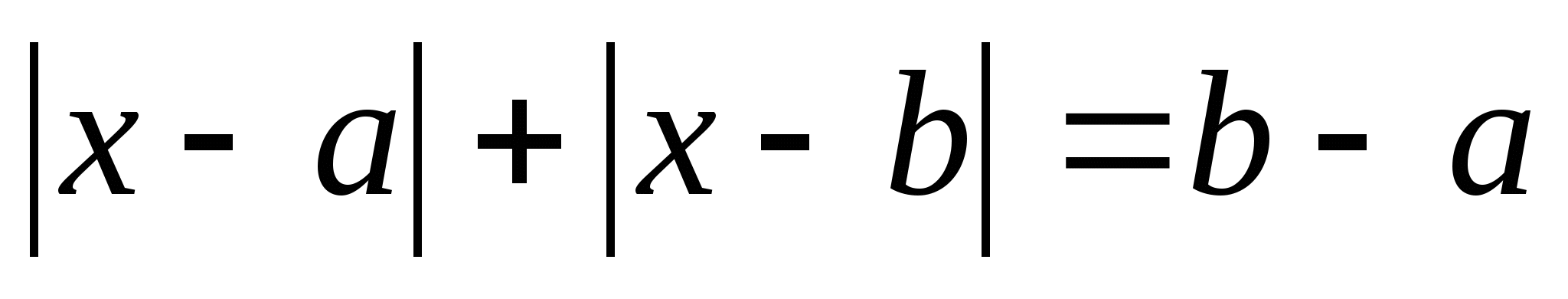 (b>a).
(b>a).
Уравнения общего вида.
Тема 4 Рациональные неравенства.
Неравенства вида 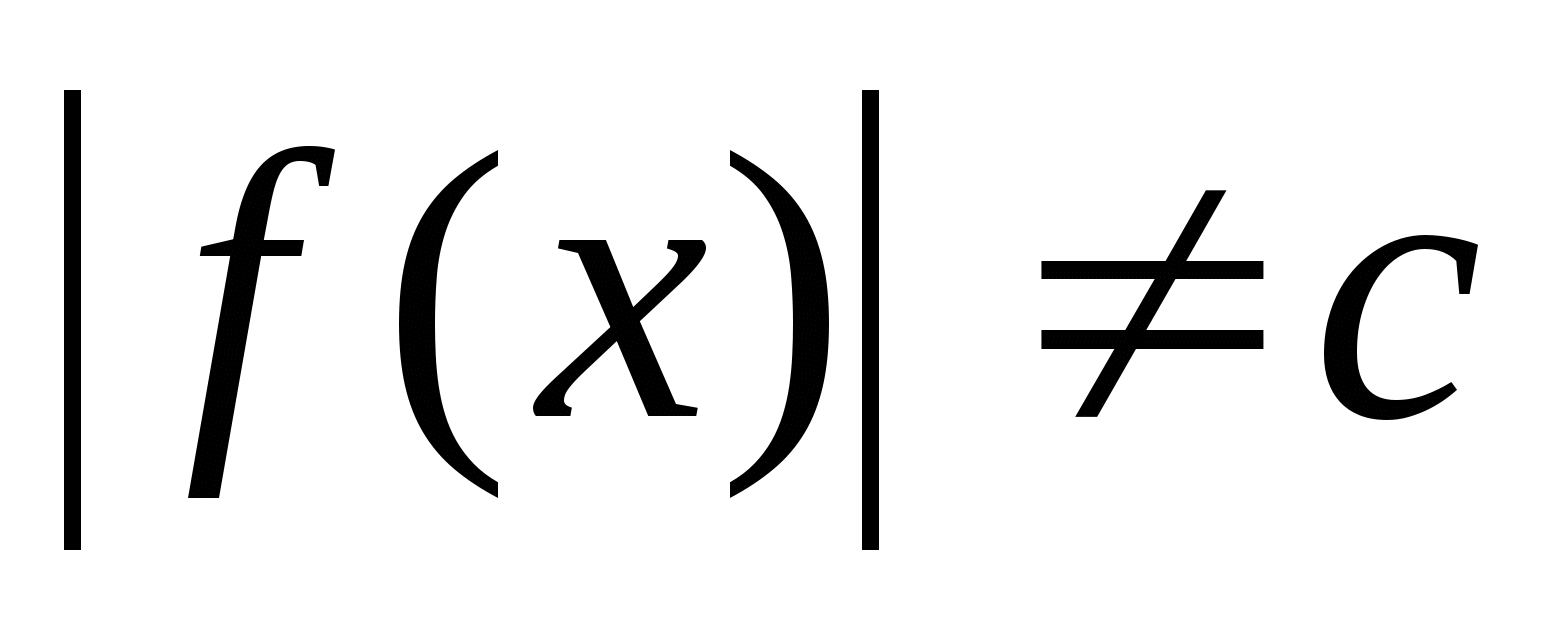 .
.
Неравенства вида 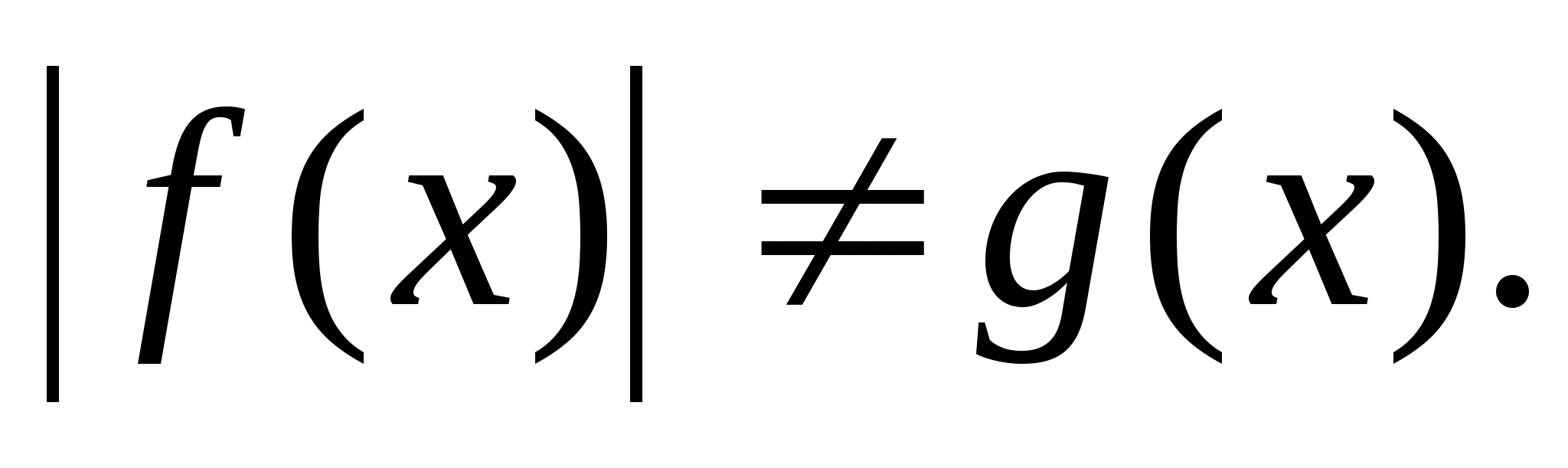
Неравенства вида 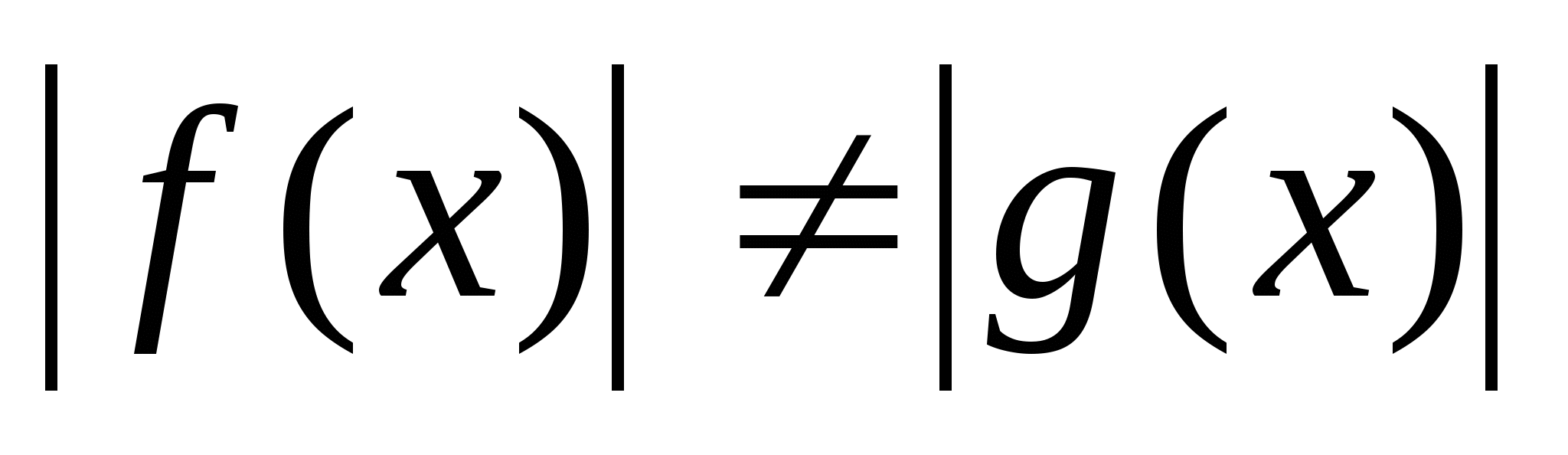
Неравенства вида 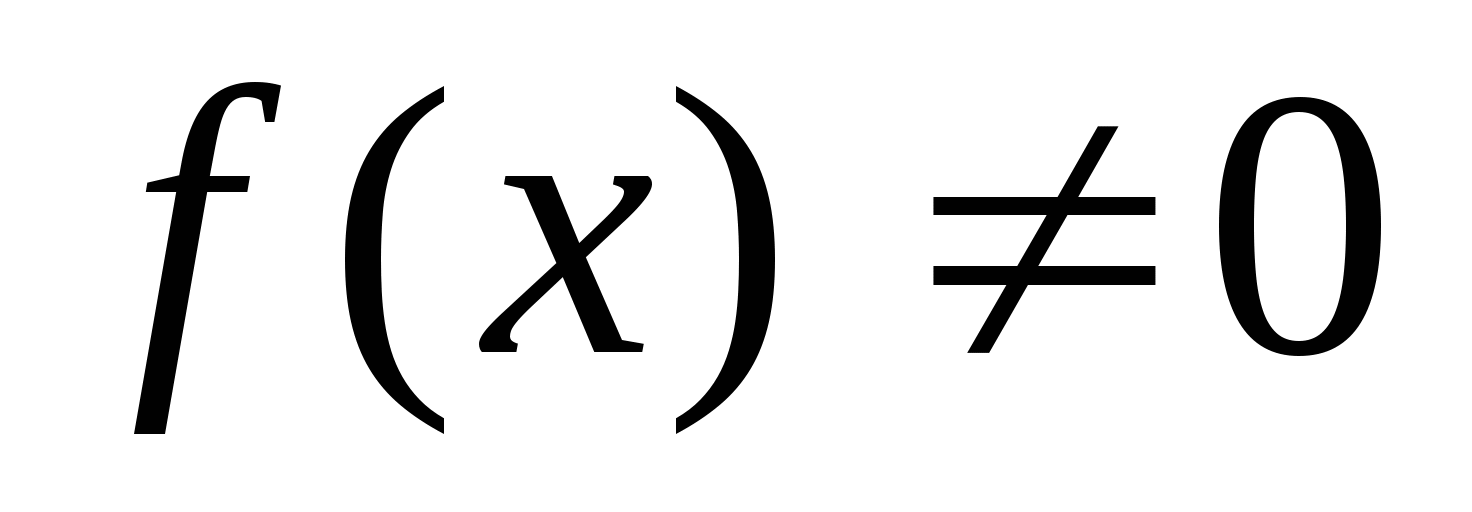 , решаемые разложением левой части на множители.
, решаемые разложением левой части на множители.
Тема 5 Функции и их свойства.
Определение числовой функции, область определения и множество значений функции, чётность и нечётность функции, периодические функции.
Тема 6 Построение графиков функций, содержащих переменную под знаком модуля.
График функции 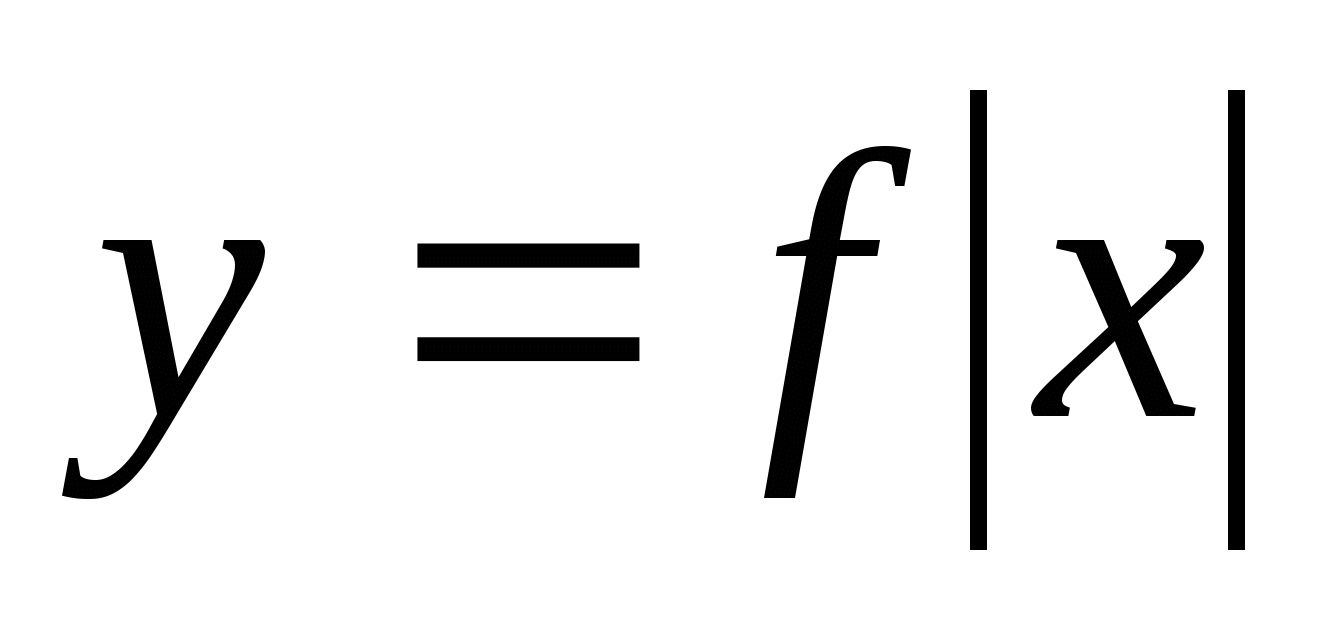 .
.
График функции 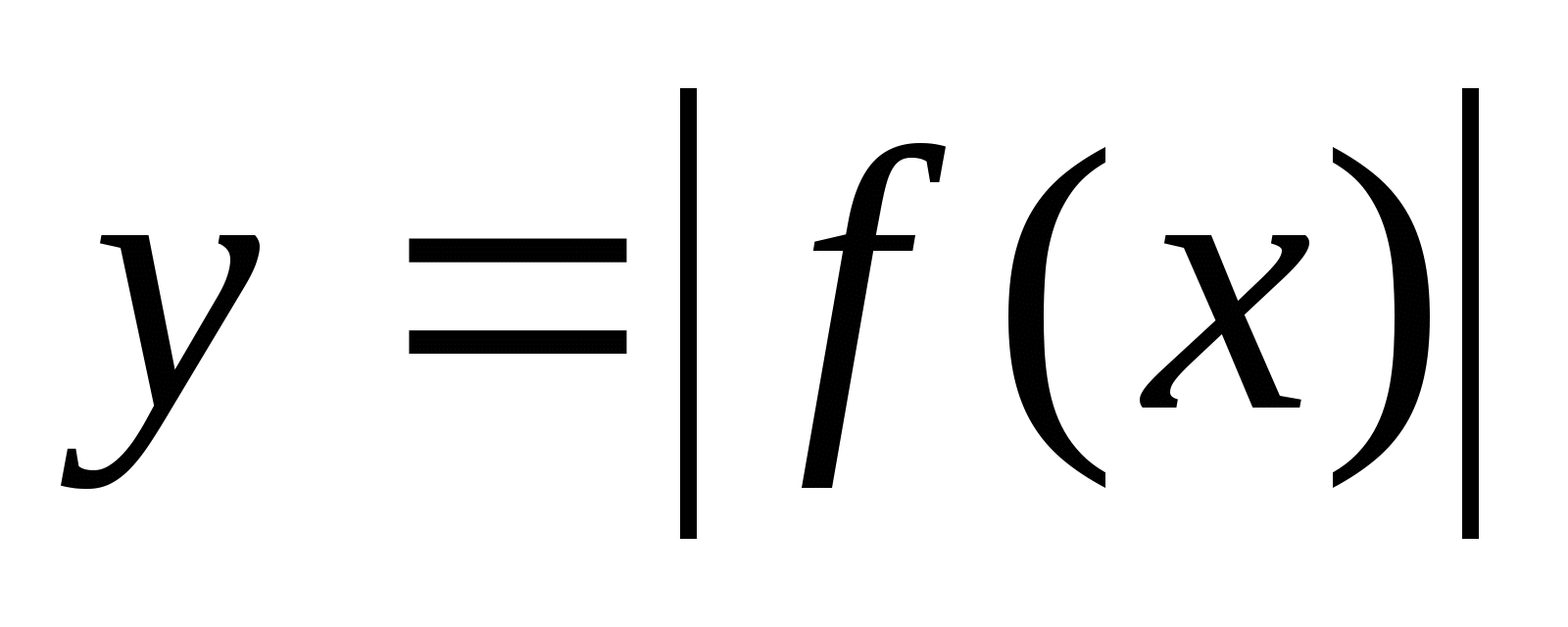 .
.
График функции 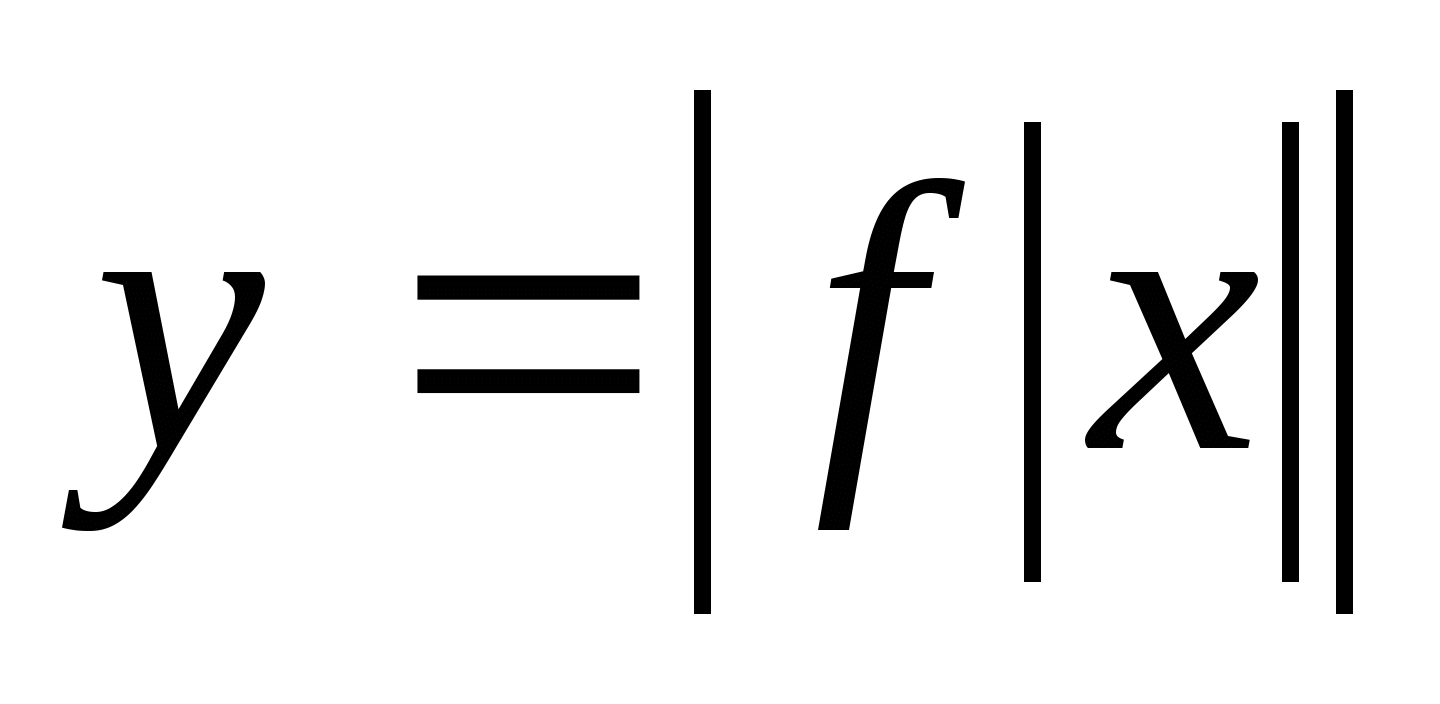
График функции 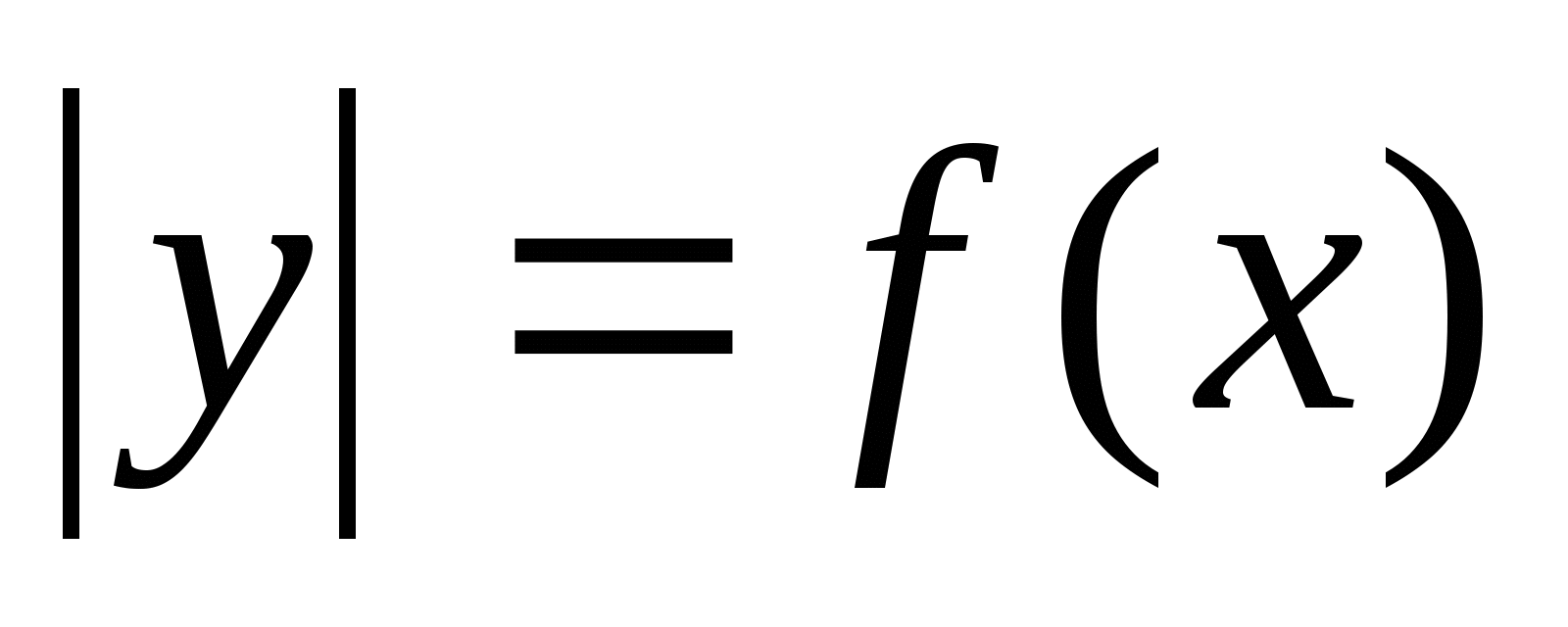 , где
, где 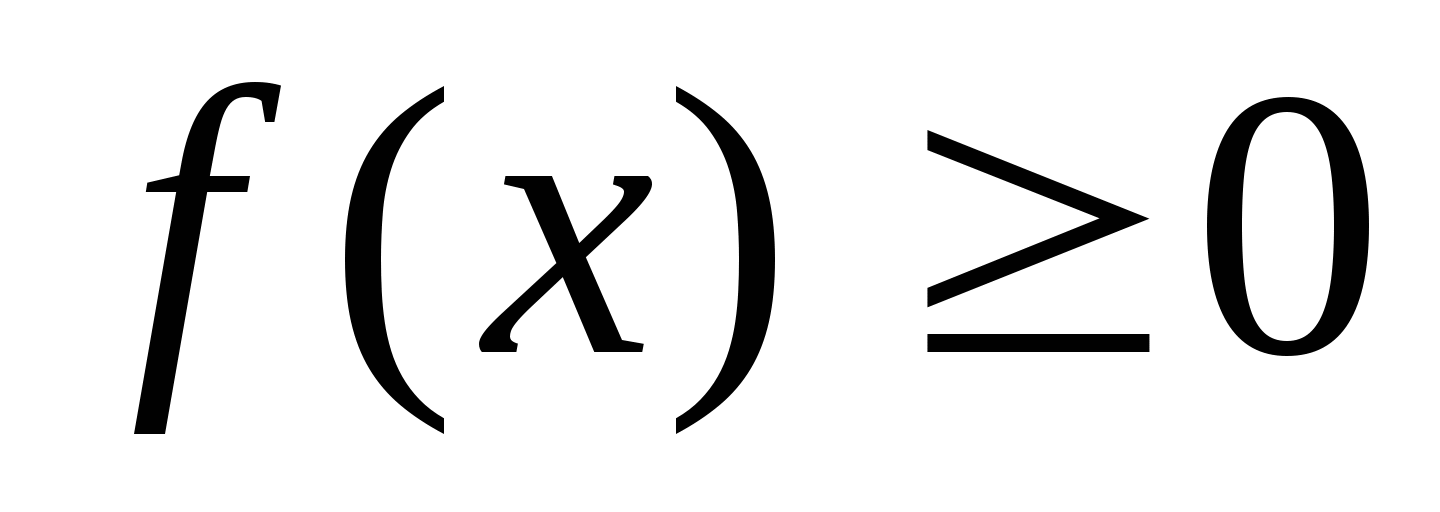 .
.
График функции 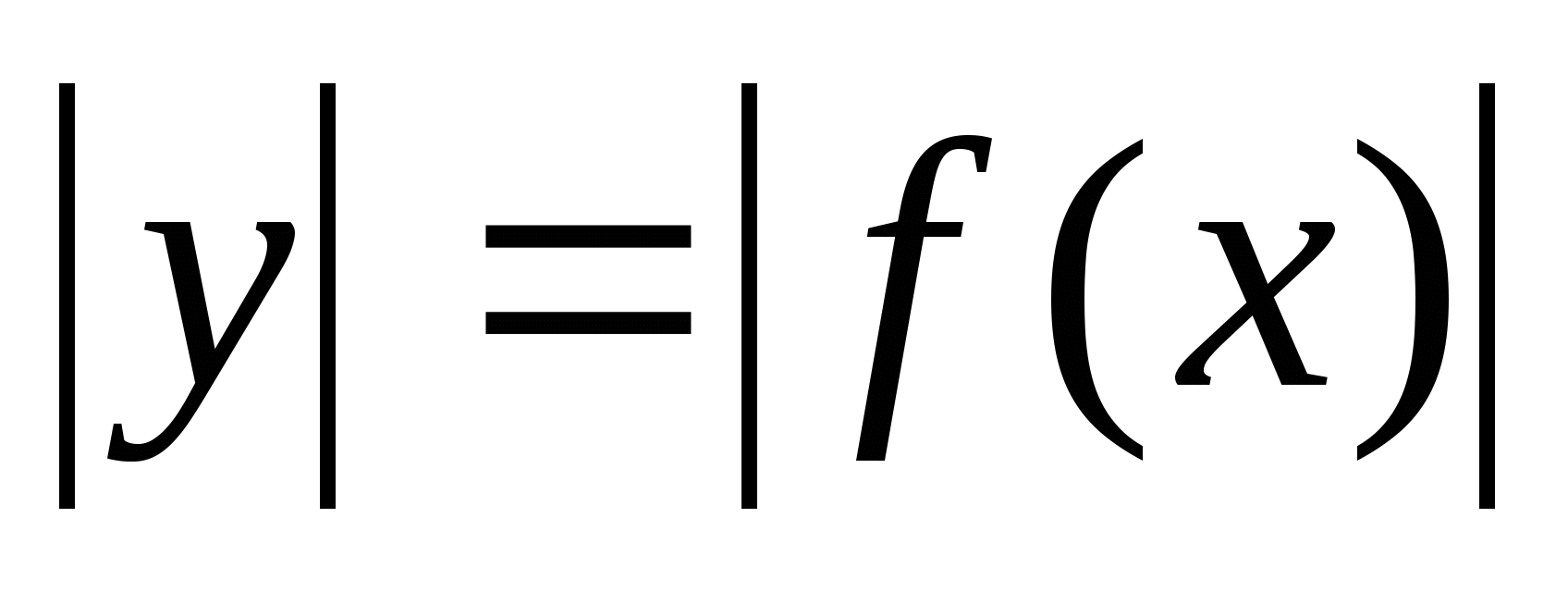 .
.
Тема 7 Построение графиков неявно заданных функций, аналитическое выражение которых содержит переменную под знаком модуля.
Тематический план
Количествочасов
Форма
поведения
Определение понятия «модуль» и основные свойства
1
Лекция
Тождественные преобразования рациональных и иррациональные выражения
2
Практикум
Рациональные уравнения
9
Практикум
Рациональные неравенства
10
Практикум
Функции и их свойства
1
Лекция
Построение графиков функций содержащих переменную под знаком модуля
8
Практикум
Построение графиков неявно заданных функций, аналитическое выражение которых содержит переменную под знаком модуля
3
Семинар
Литература
Гайдуков И.И. Абсолютная величина. Пособие для учителя – М.: Просвещение, 1968 .
Галицкий М.Л., Машкович М.М., Шварчбурд С.И. Углубленное изучение курса алгебры и математического анализа. Пособие для учителя – М.: Просвещение, 1990.
Галицкий М.Л., Машкович М.М., Шварчбурд С.И. Сборник задач по алгебре для 8-9 классов. Учебное пособие для учащихся школ и классов с углубленным изучением математики – М.: Просвещение, 1994.
Графики функций: Справочник Вирченко Н.А., Ляшко И.И. – Киев: Наук. Думка, 1980.
Литвиненков В.Н., Мордкович А.Г. Практикум по элементарной математике. Алгебра. Тригонометрия. М.: Просвещение, 1991.
Сборник задач по математике для поступающих в вузы. Под ред. М.И. Сканави. – М.: Высшая школа, 1994 .
Фельдман Я.С., Жаржевский А.Я. Математика. Решение задач с модулями. – С-Пб.: Оракул, 1997.
Методические рекомендации
Тема 1
Определение понятия «модуль». Основные свойства.
Абсолютной величиной (модулем) действительного числа называется само это число, если оно неотрицательное, и это число, взятое с противоположным знаком, если оно отрицательное:
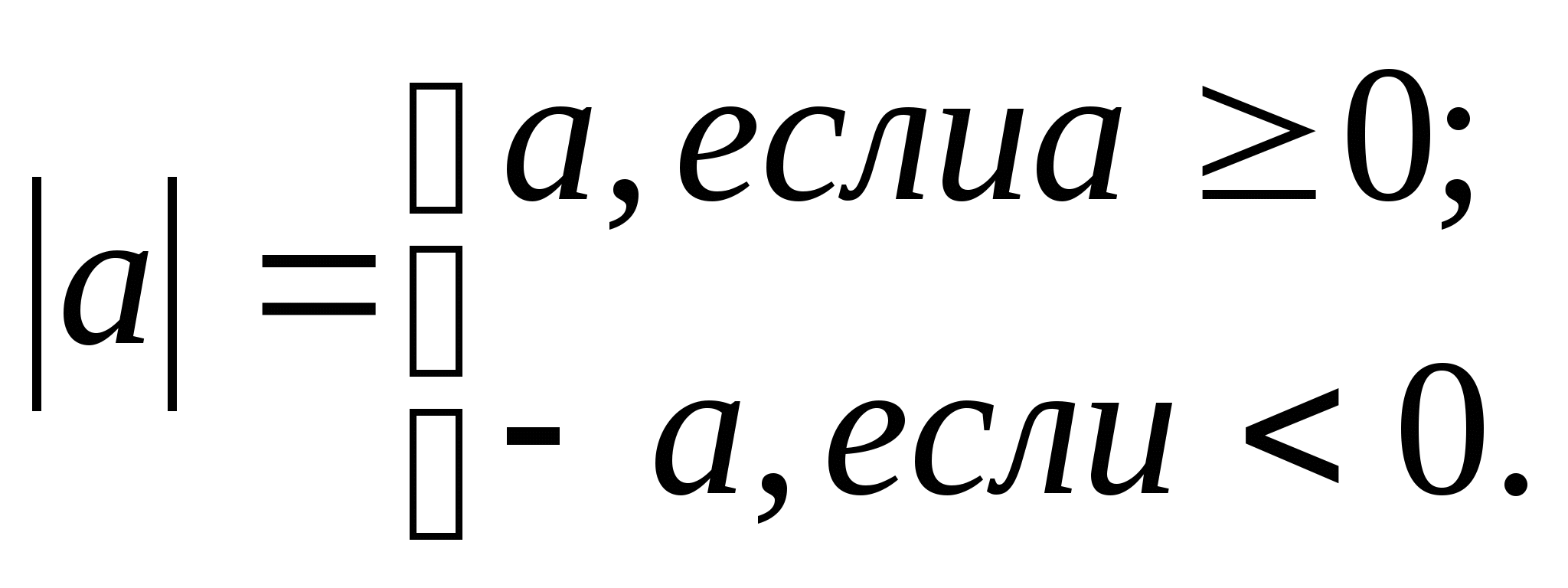
Основные свойства:
1.1. Противоположные числа имеют равные противоположные величины,
т.е. 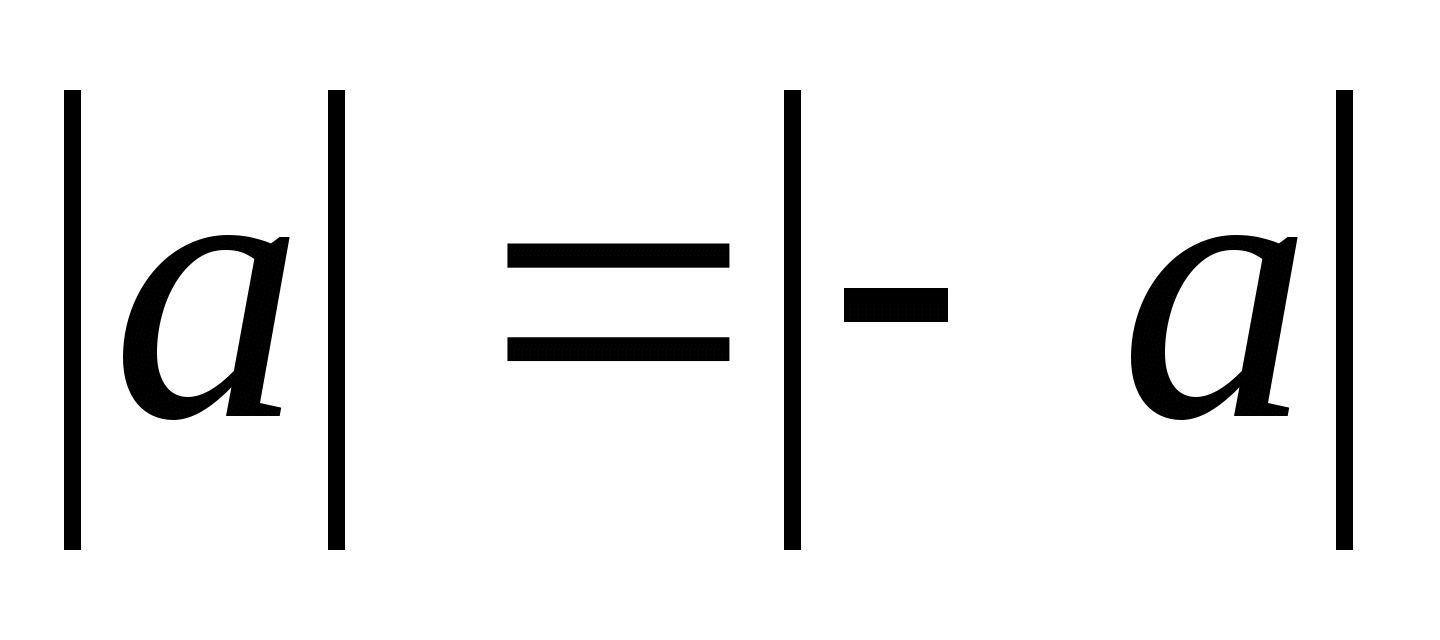
1.2. 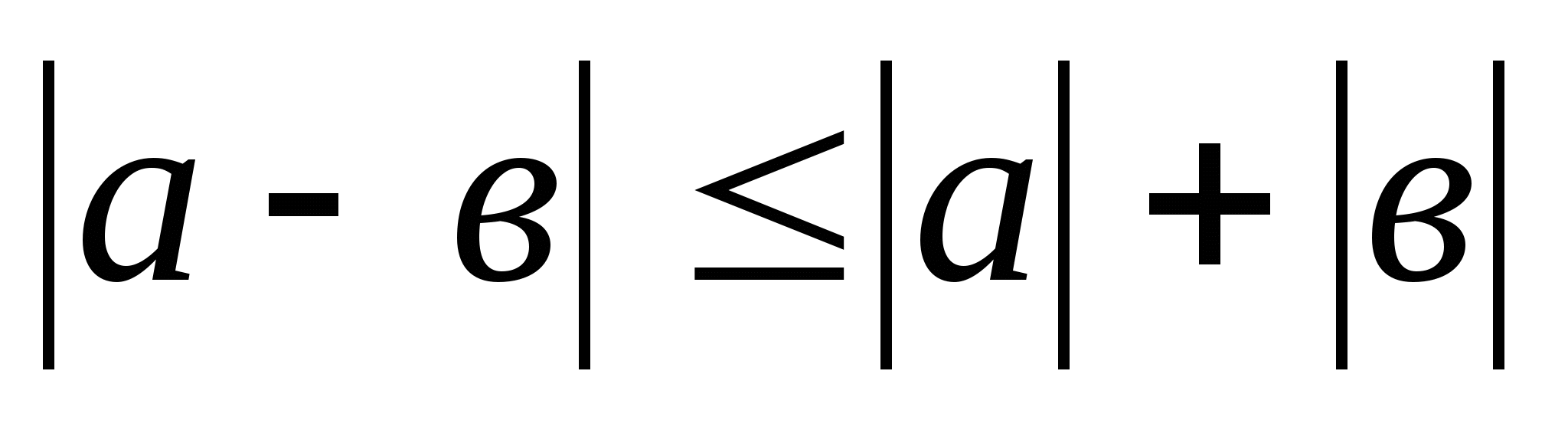 .
.
1.3. Для любых a и b справедливы неравенства
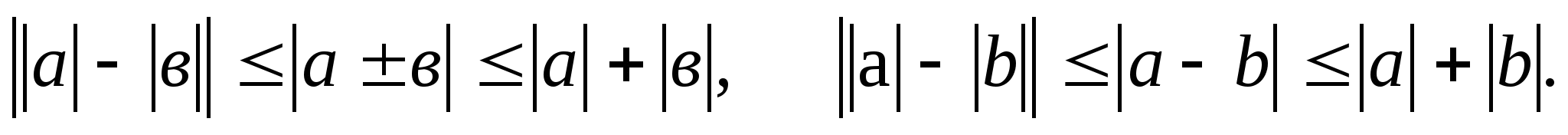
1.4. 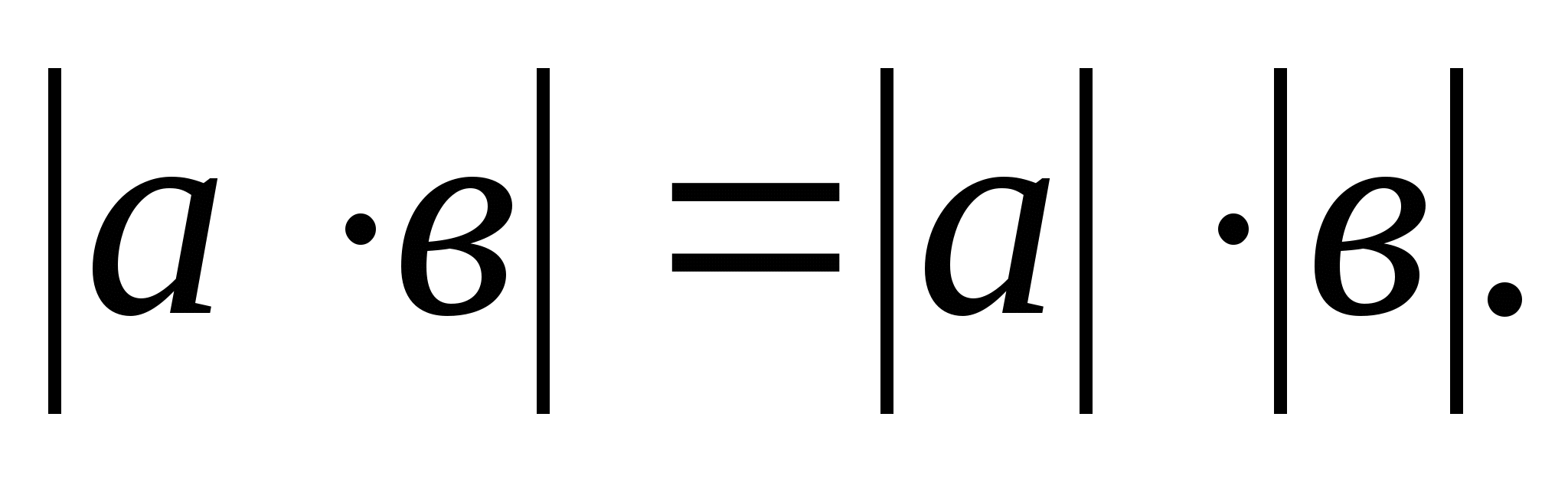
1.5. 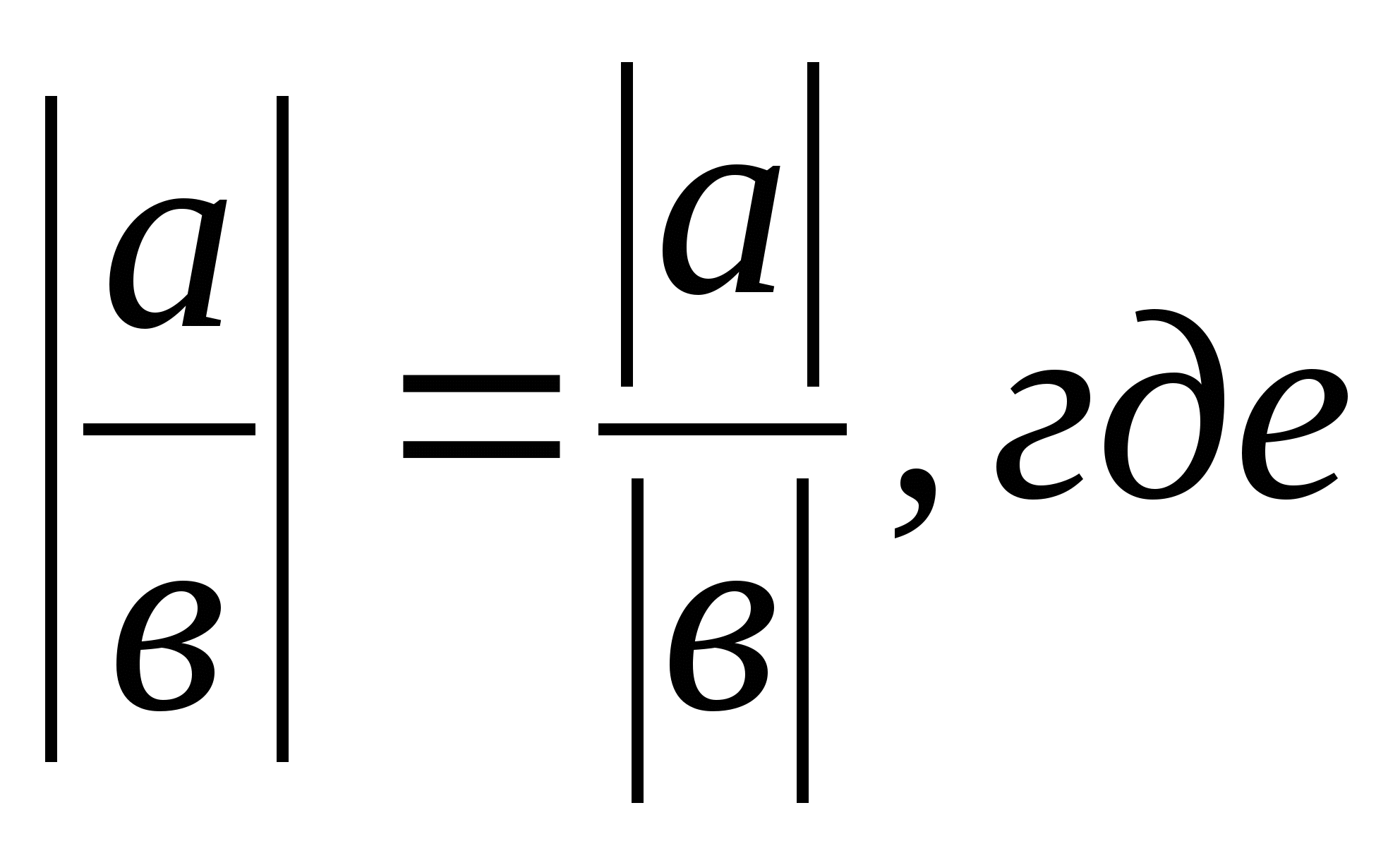
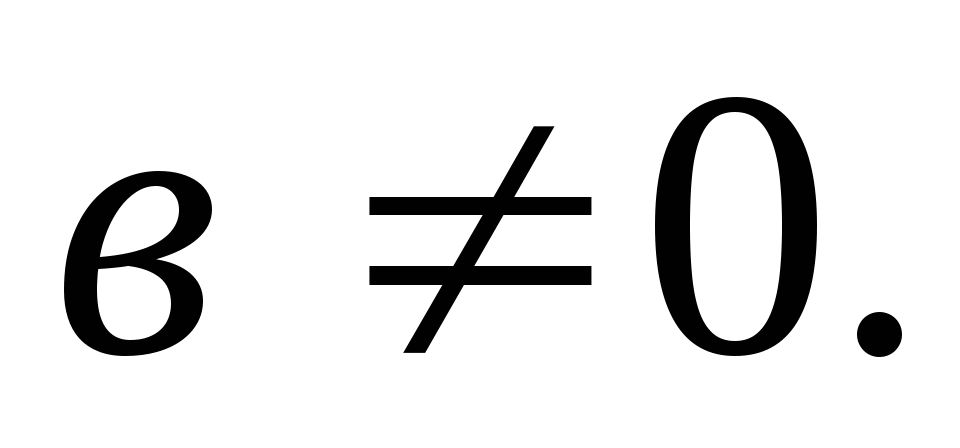

1.6. 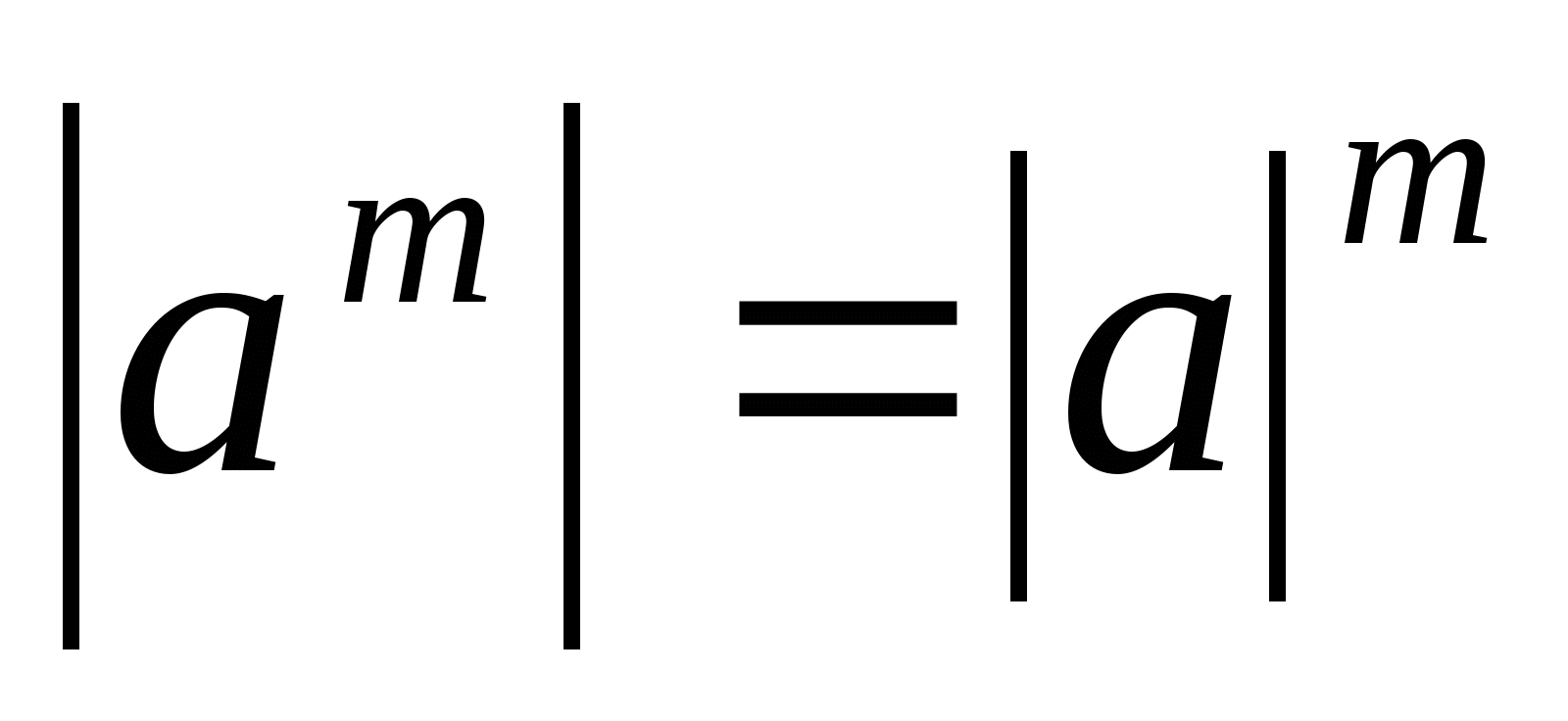 для любого целого значения m.
для любого целого значения m.
1.7. 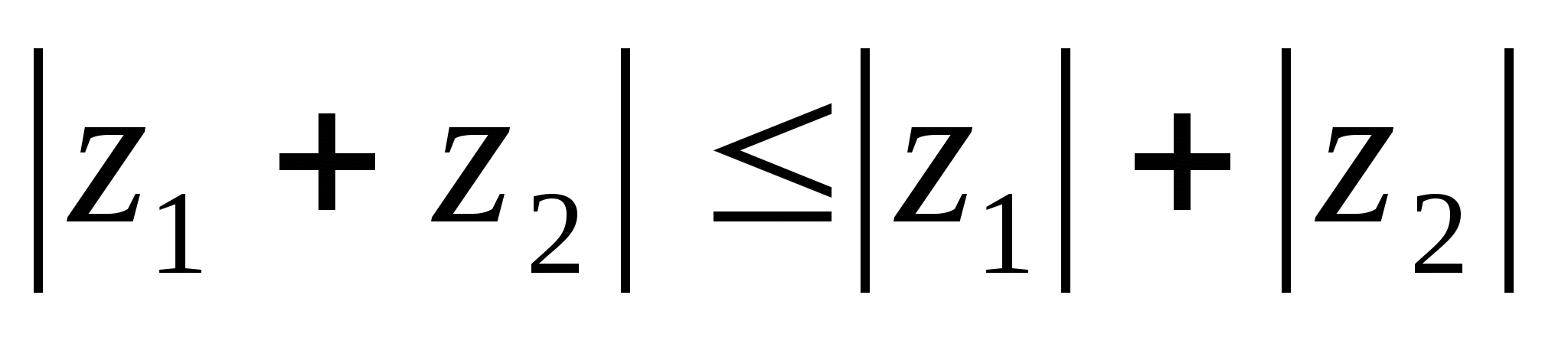 для любого конечного числа слагаемых.
для любого конечного числа слагаемых.
Тема 2
Тождественные преобразования рациональных и иррациональных выражений.
На уроке будут рассматриваться преобразования выражений, содержащих функции под знаком модуля, а также таких, в которых модули функций возникают при тождественных преобразованиях, например, при использовании соотношений
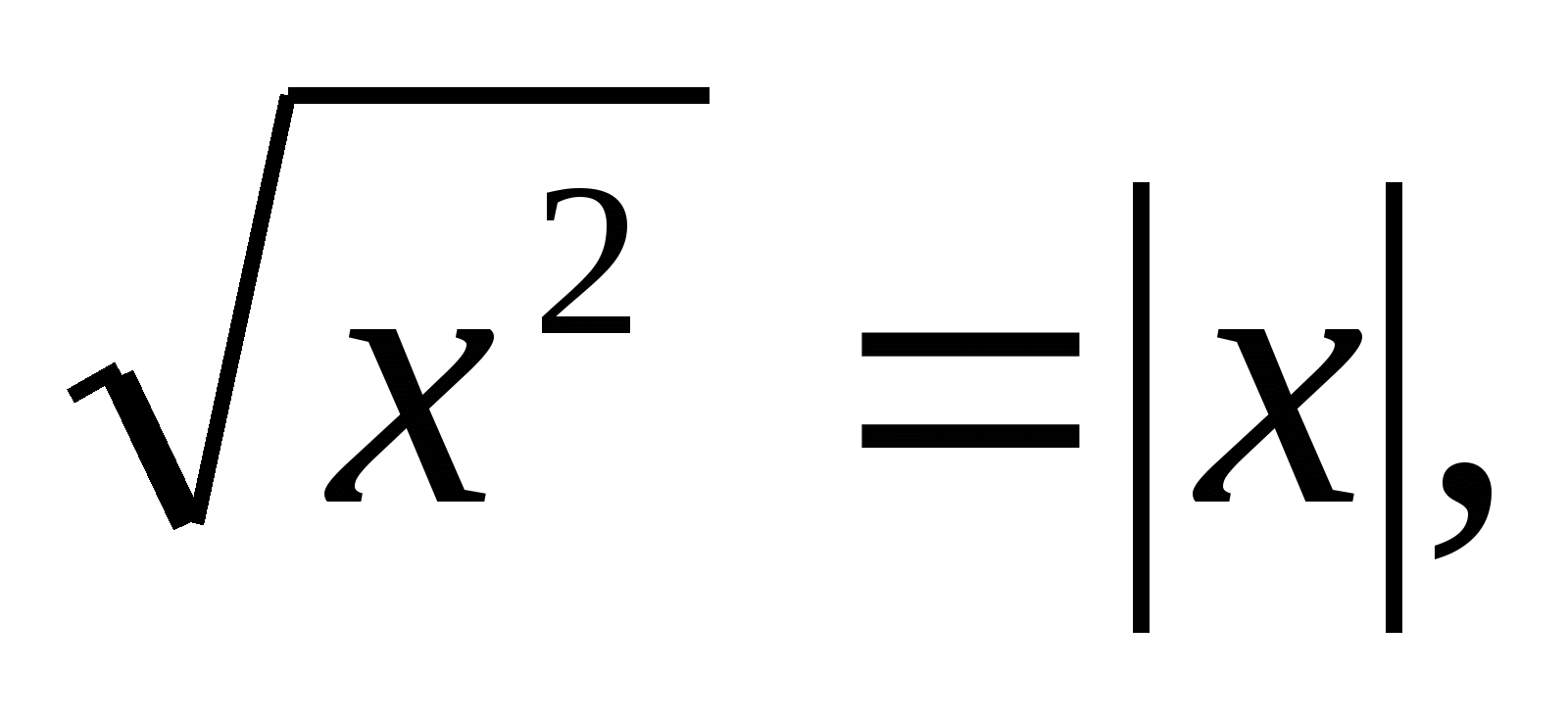
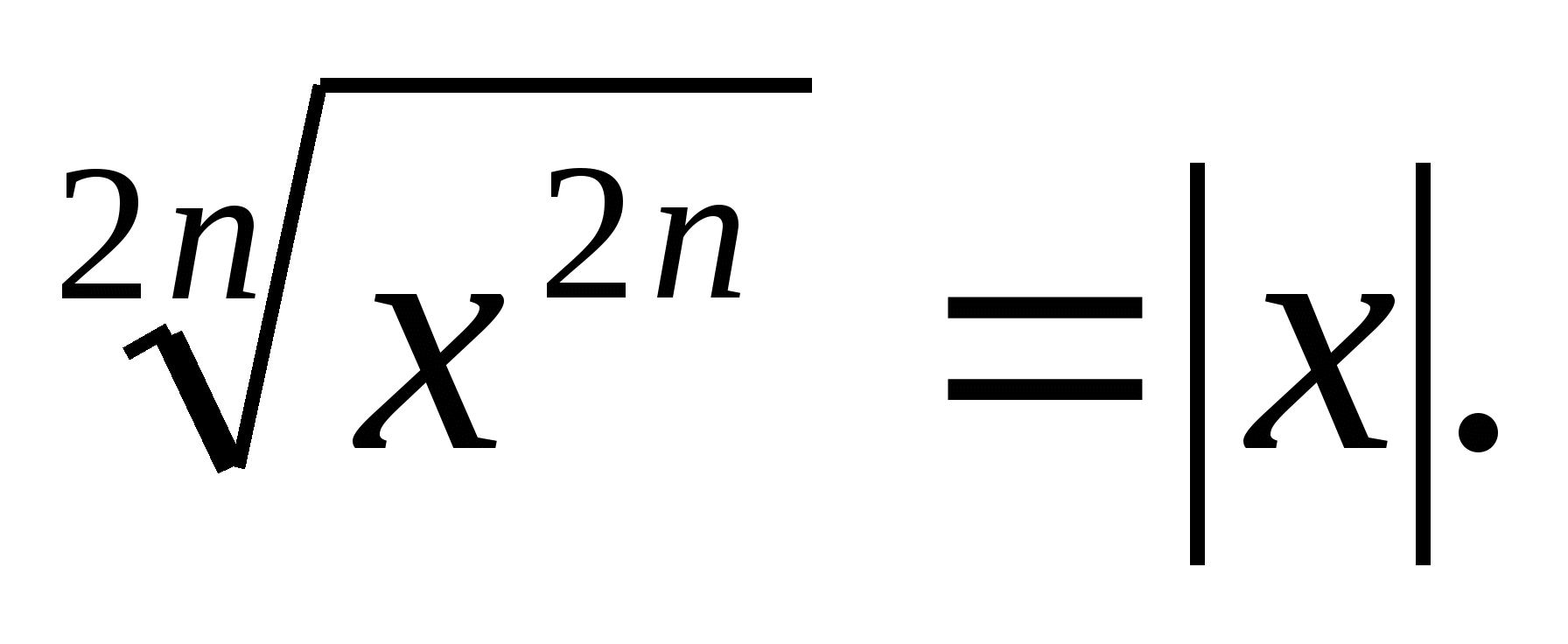
Тождественные преобразования таких выражений состоит в разбиении области их определения на промежутки знакопостоянства, в каждом из которых с использованием определения модуля производится освобождение от модуля и дальнейшее упрощение выражений.
Тема 3
Рациональные уравнения.
Определение. Рациональным называется уравнение вида 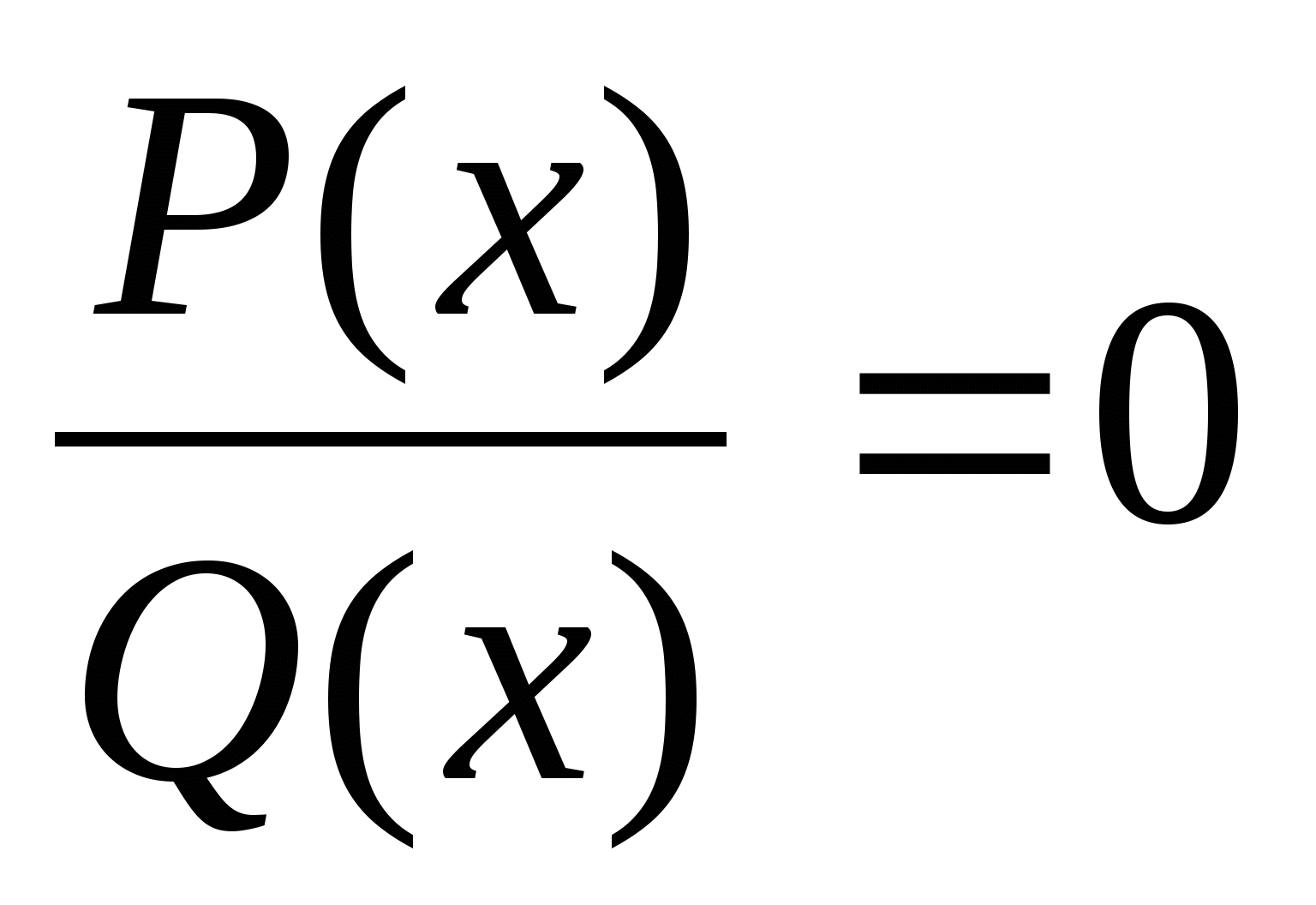 (1), где P(х) и Q(x) – многочлены.
(1), где P(х) и Q(x) – многочлены.
3.1. Уравнения вида 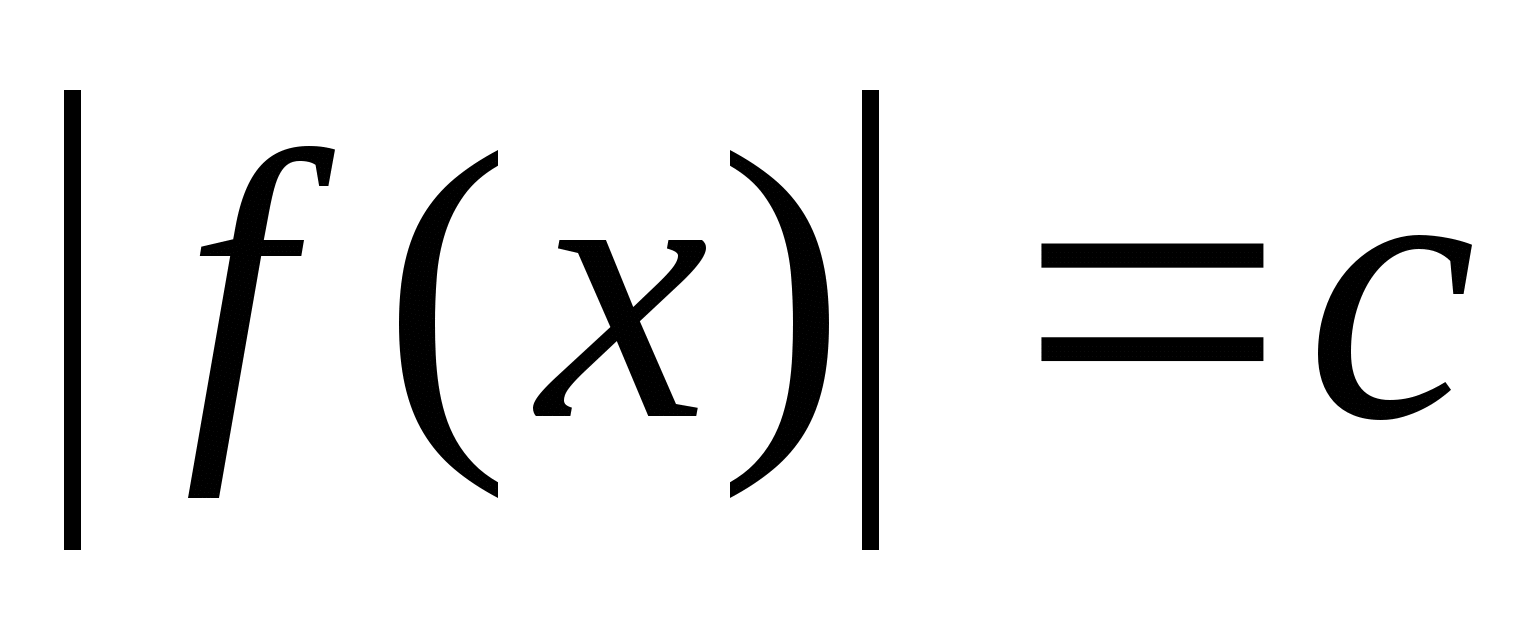 (с — число).
(с — число).
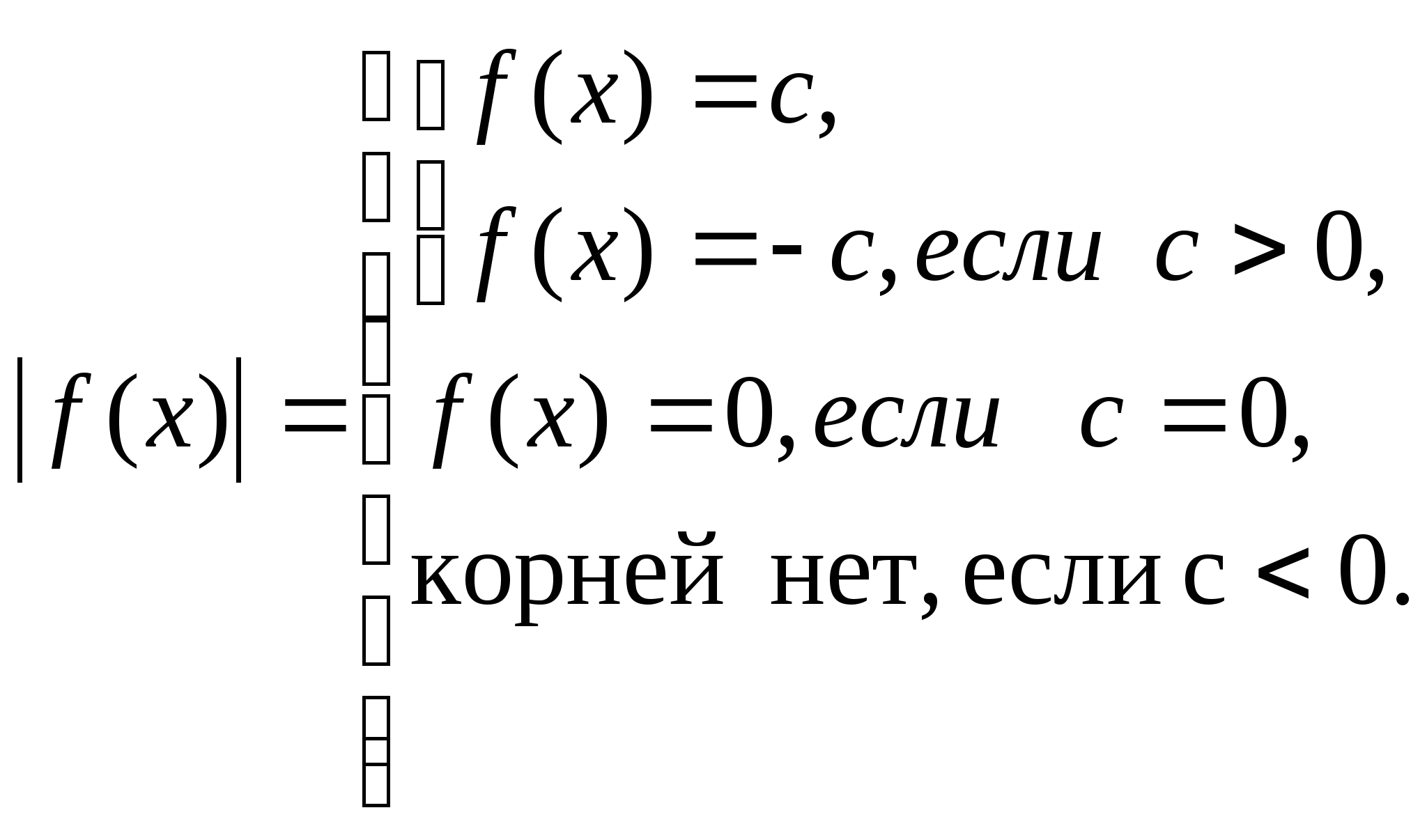 (1)
(1)
3.2. Уравнения вида 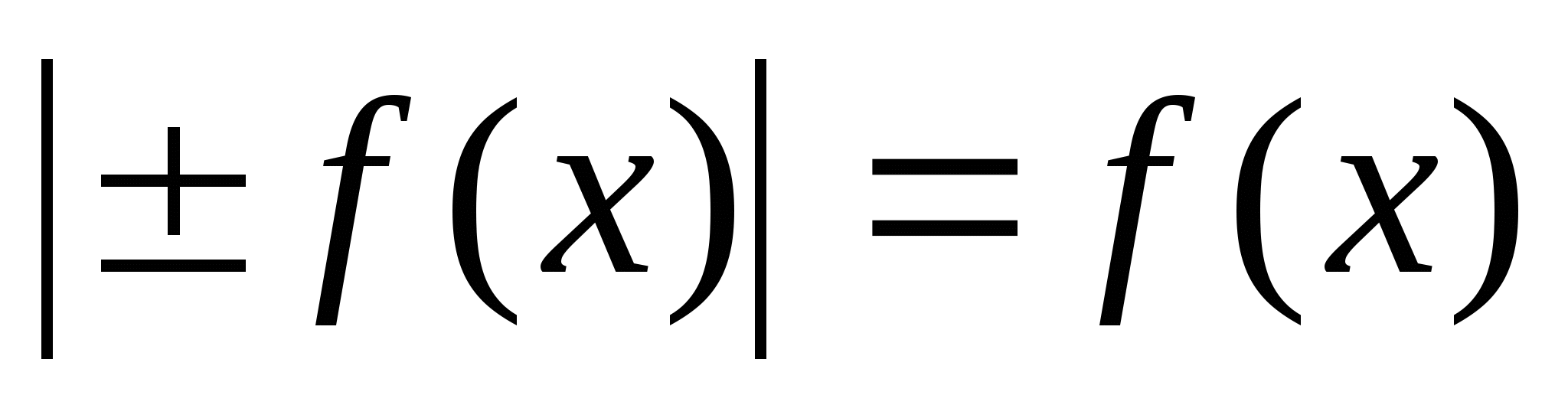 .
.
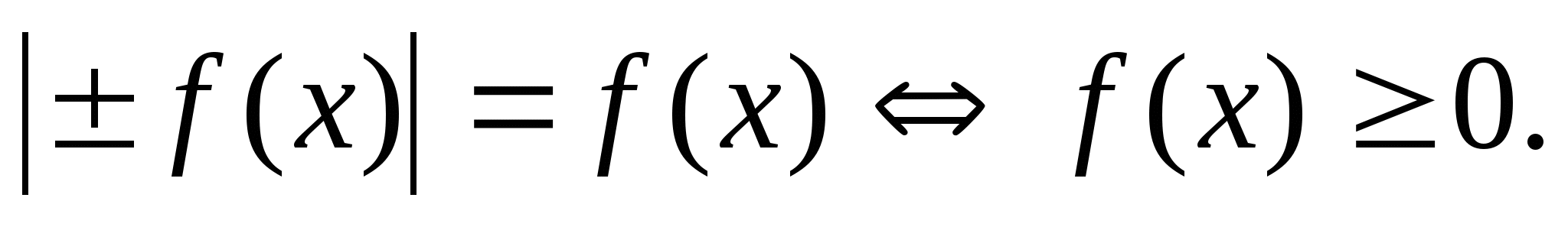 (2)
(2)
3.3 Уравнения вида 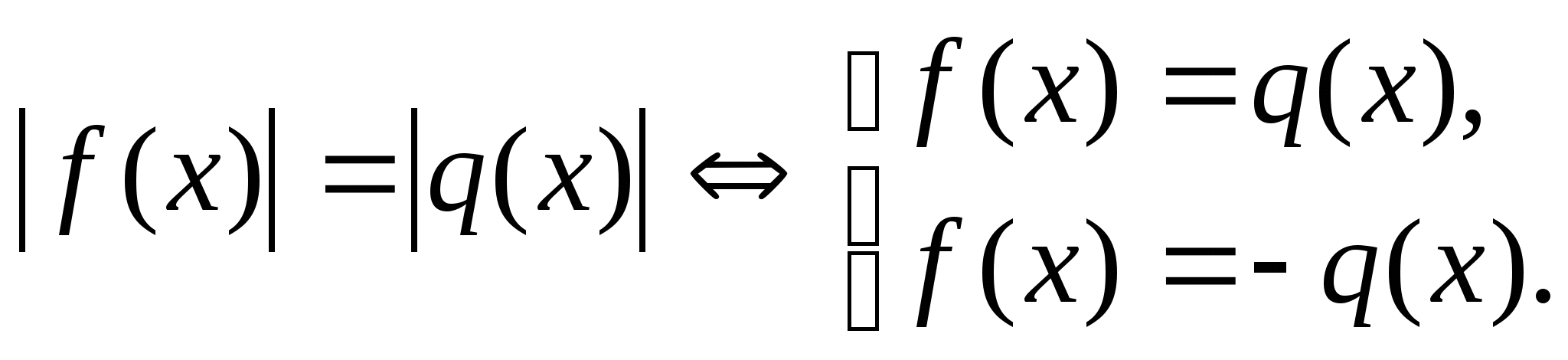 (3)
(3)
3.4. Уравнения вида 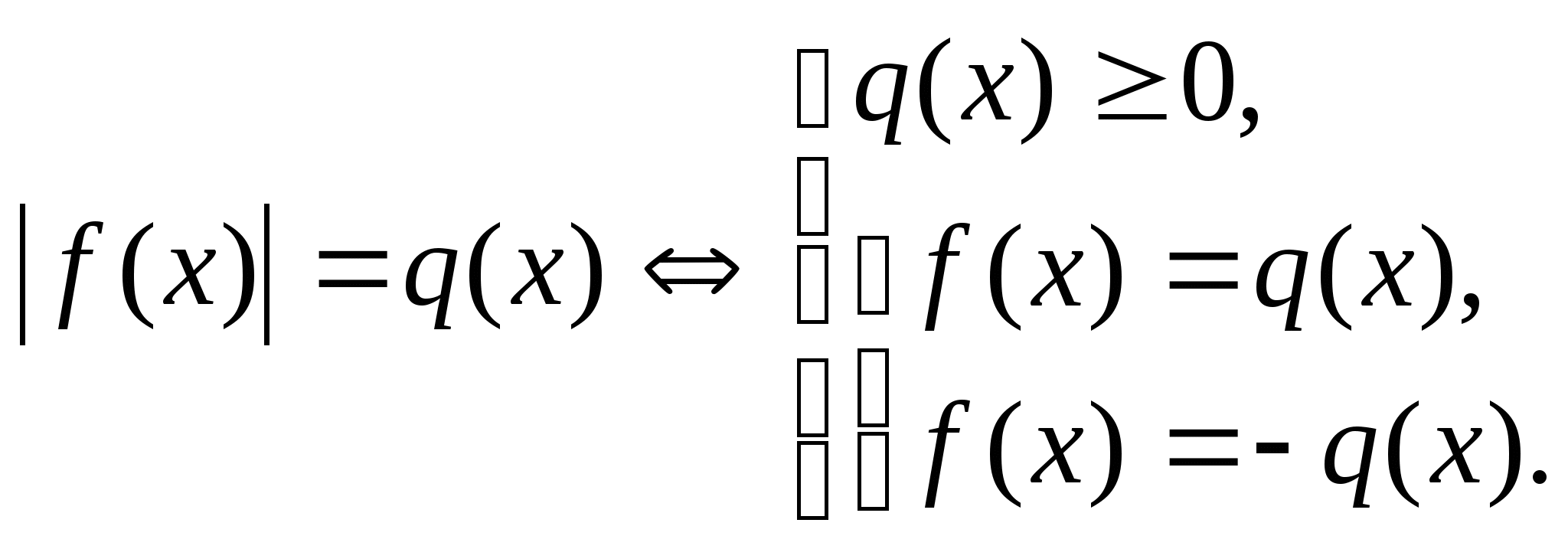 (4)
(4)
3.5. Уравнения вида 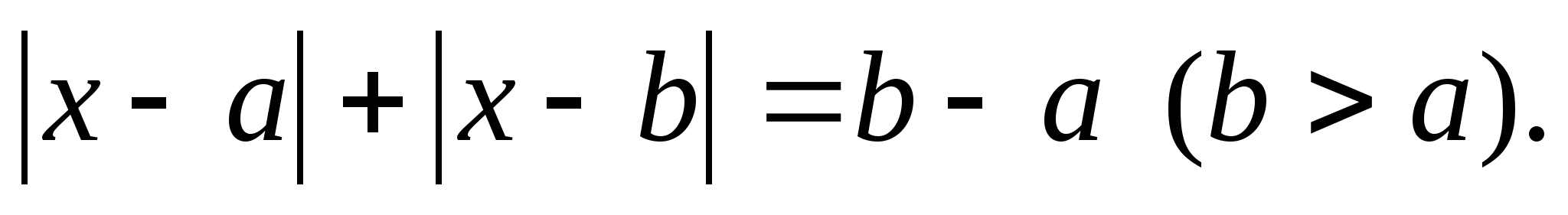
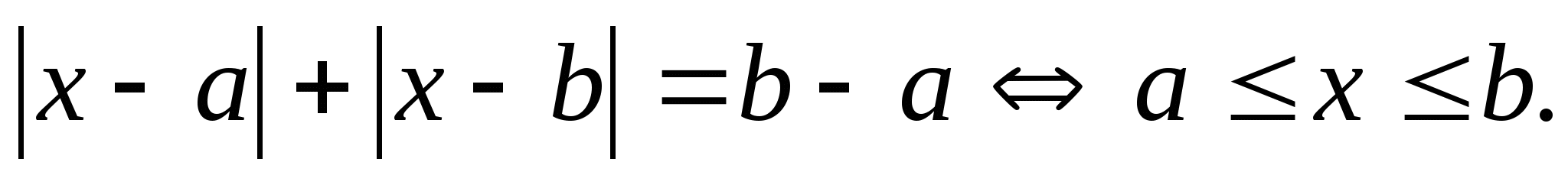 (5)
(5)
Тема 4
Рациональные неравенства.
4.1. Неравенства вида 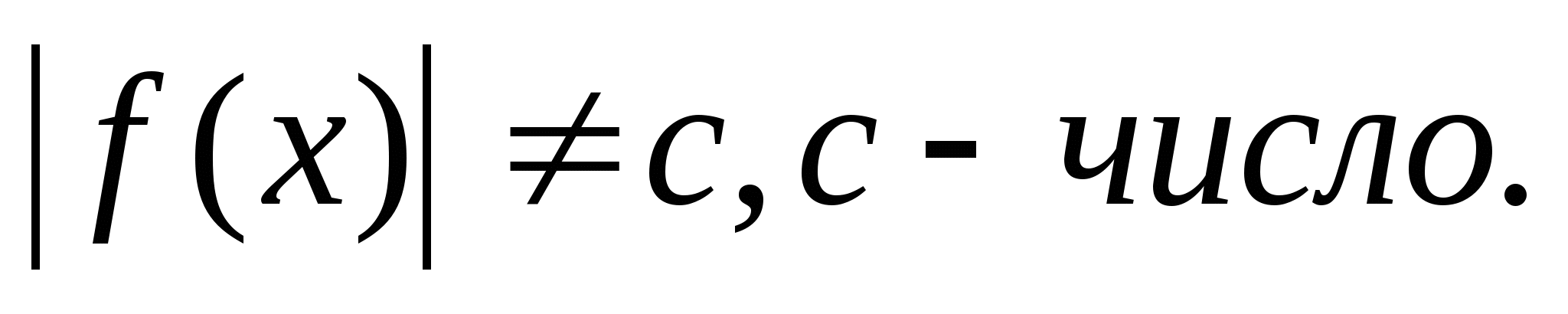
Приведём схемы решения неравенств указанного типа.
1. 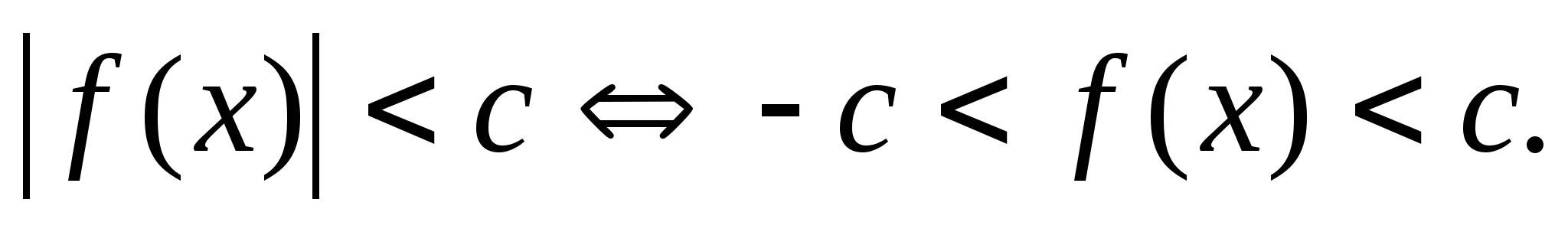
2. 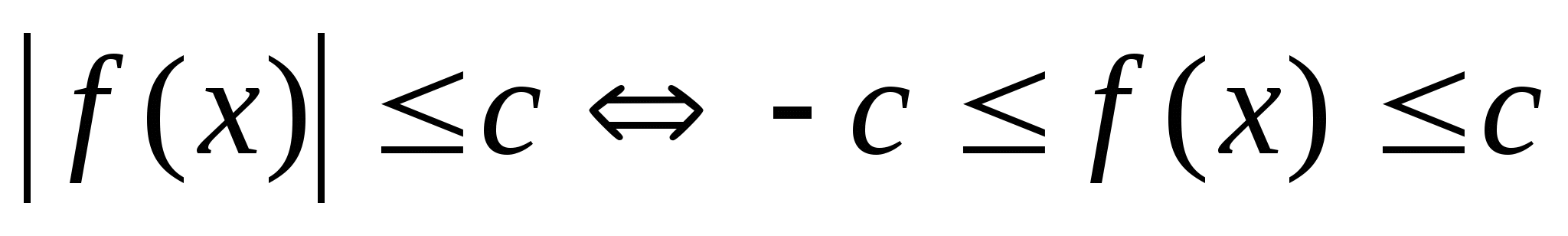
3. 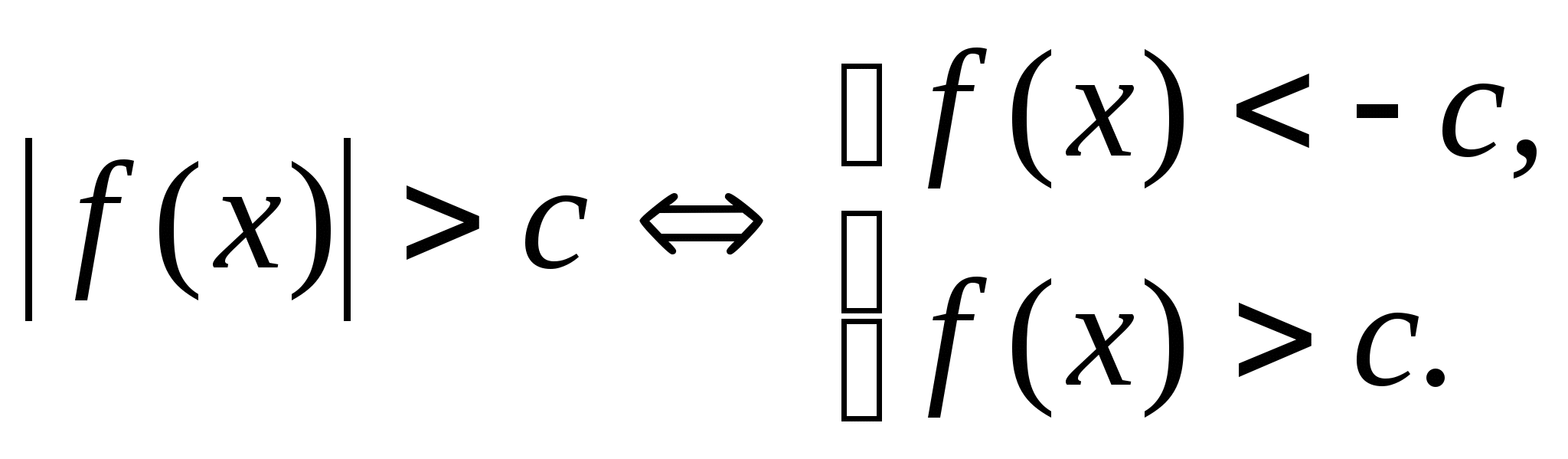
4. 
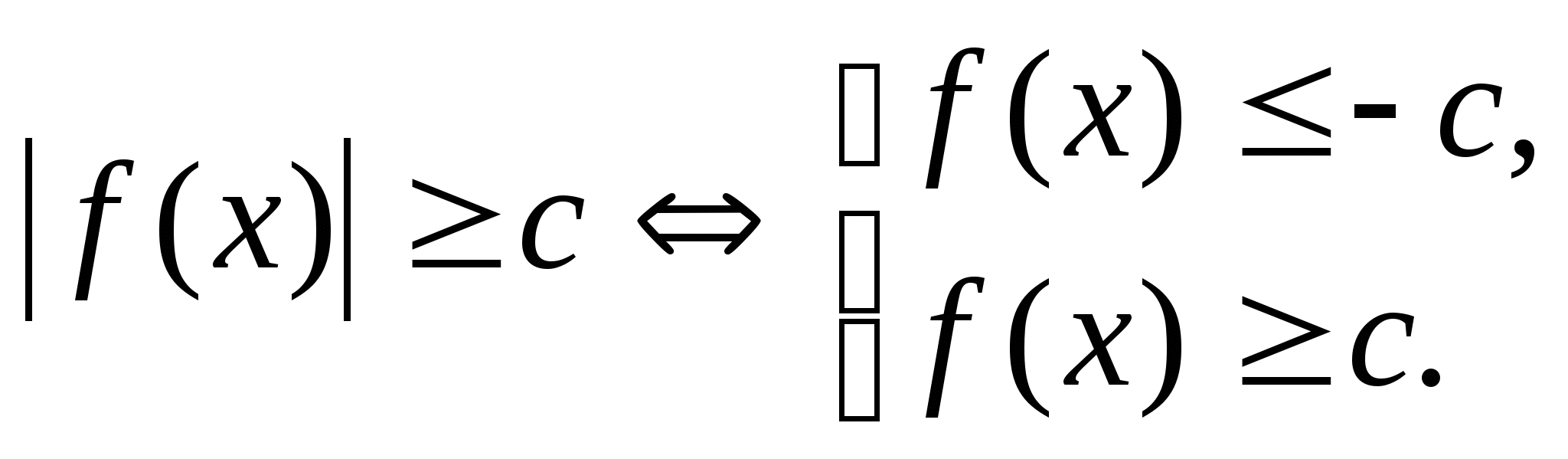
4.2. Неравенства вида 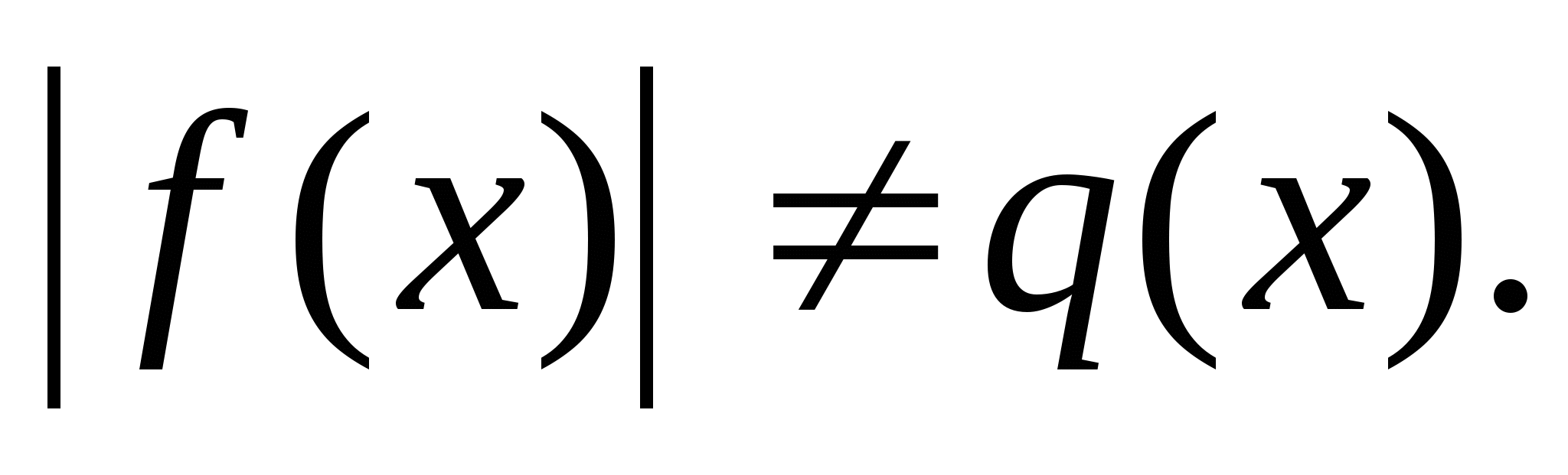
Приведём схемы решения неравенств этого вида
1. 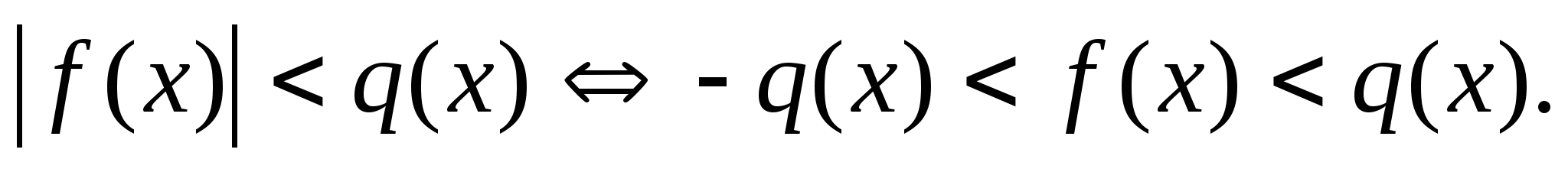

2. 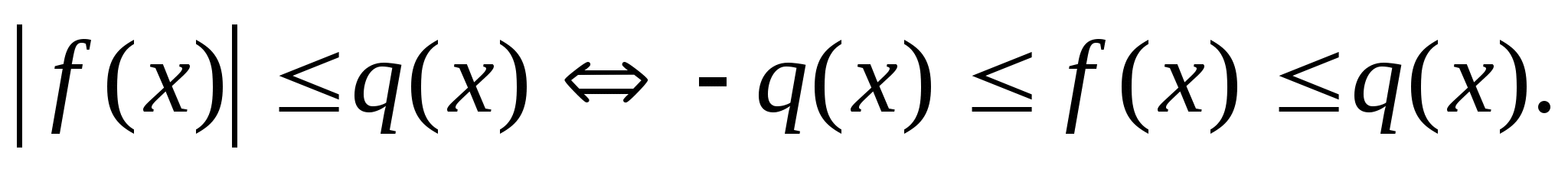
3.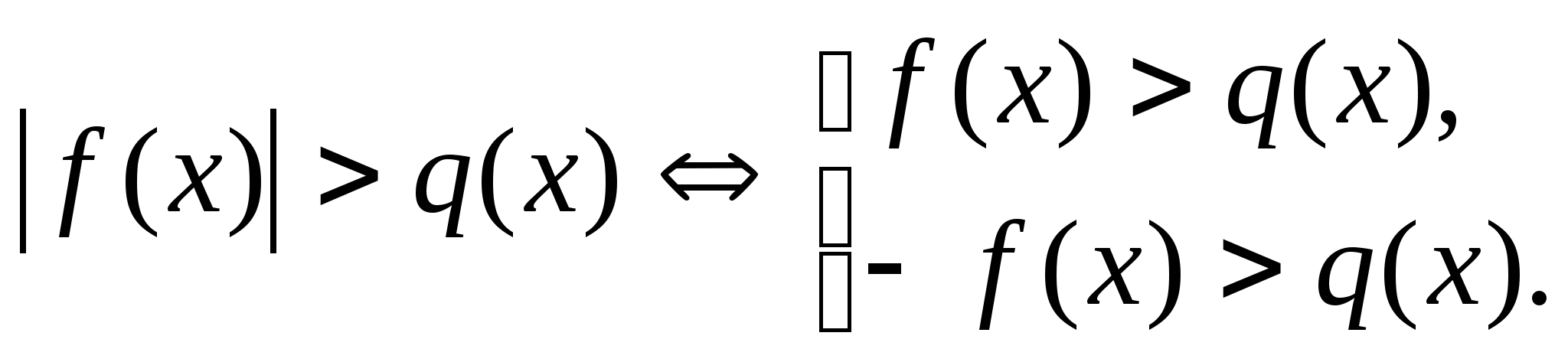
4.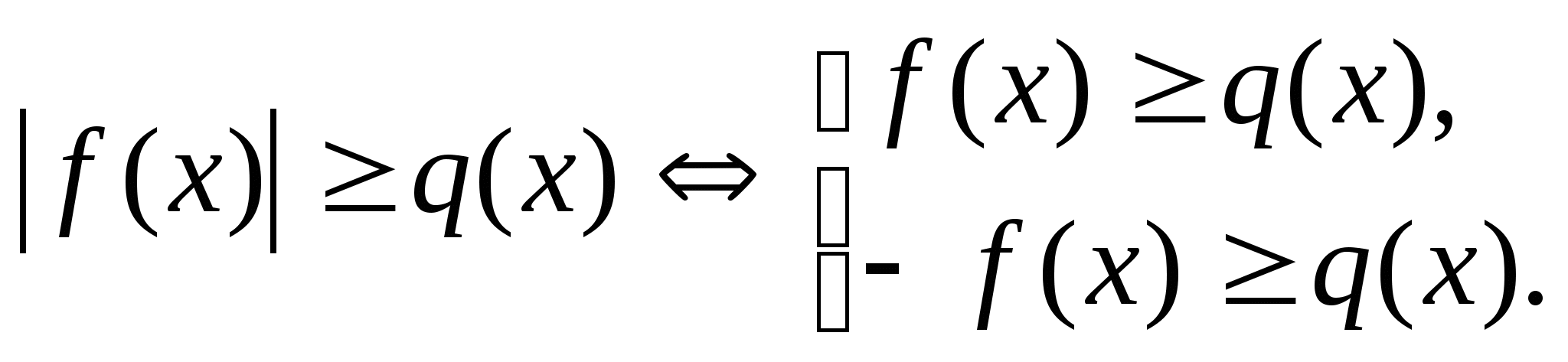
4.3. Неравенства вида 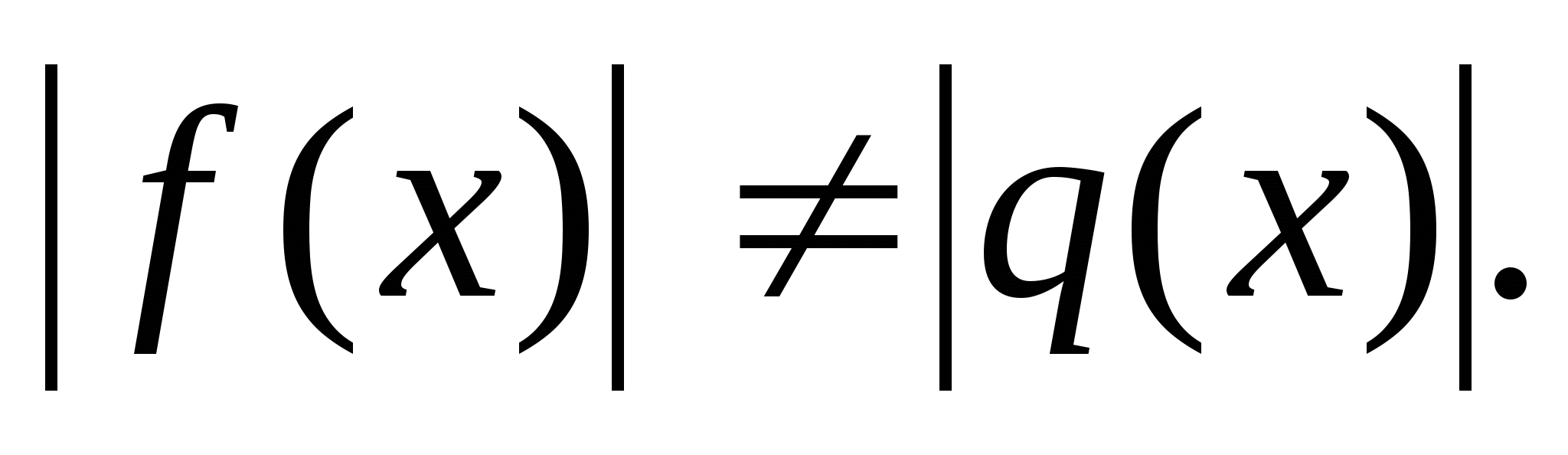
Приведём схемы решений неравенств этого вида
1. 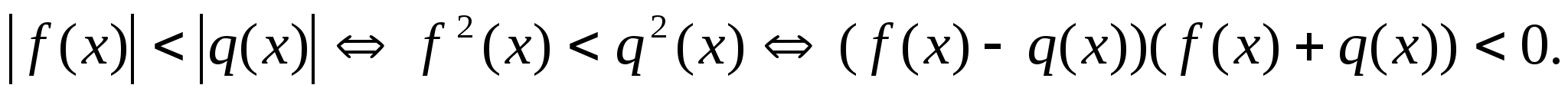
2. 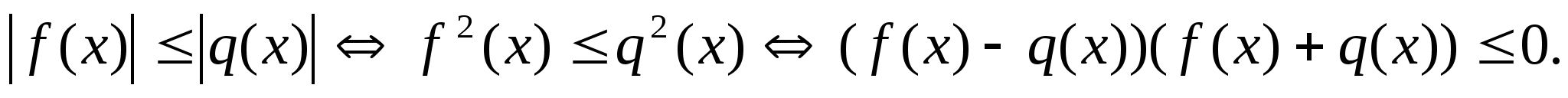
3. 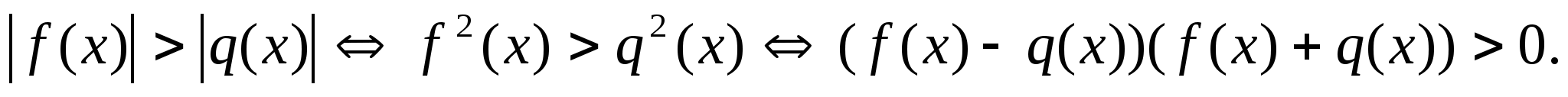
4. 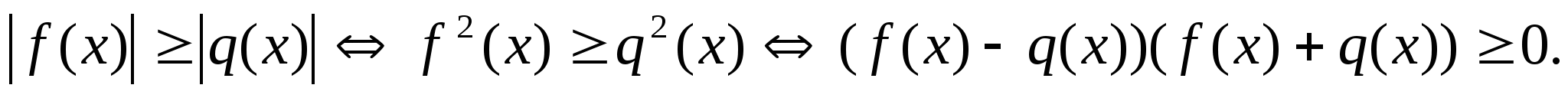
Тема 5
Функции и их свойства.
Тема 6
Построение графиков функций.
6.1. График функции 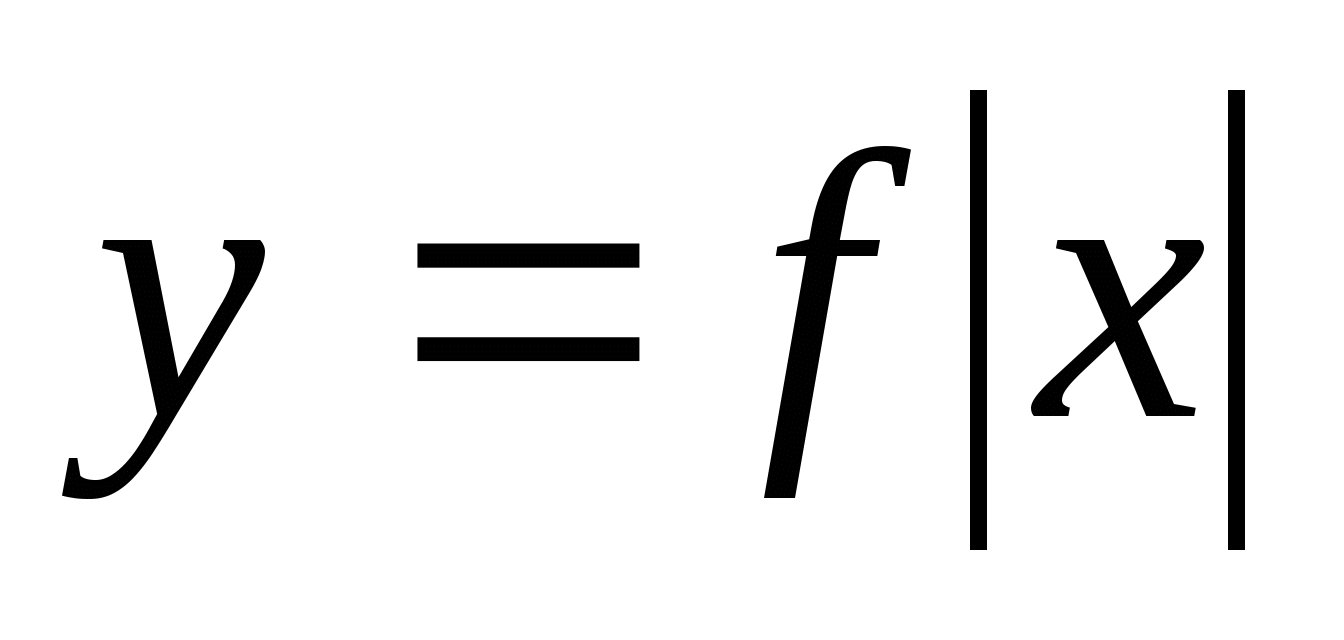


Функция 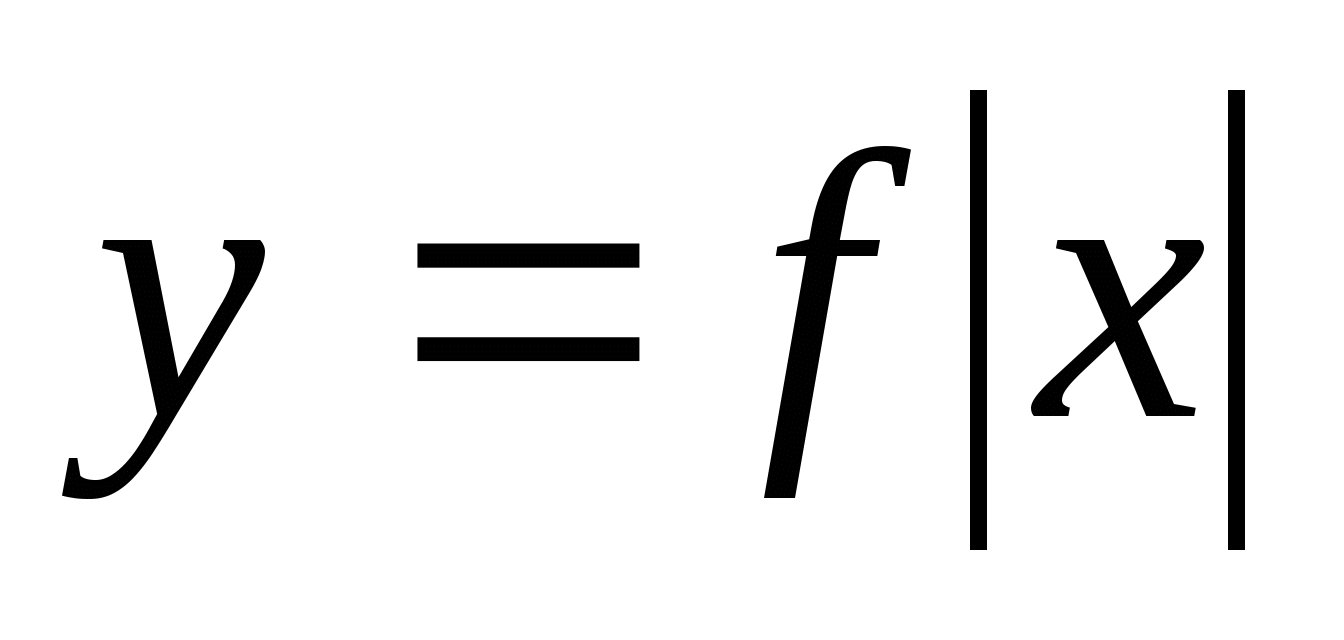 -чётная, следовательно график этой функции симметричен относительно оси ординат. Следовательно, достаточно построить график функции
-чётная, следовательно график этой функции симметричен относительно оси ординат. Следовательно, достаточно построить график функции 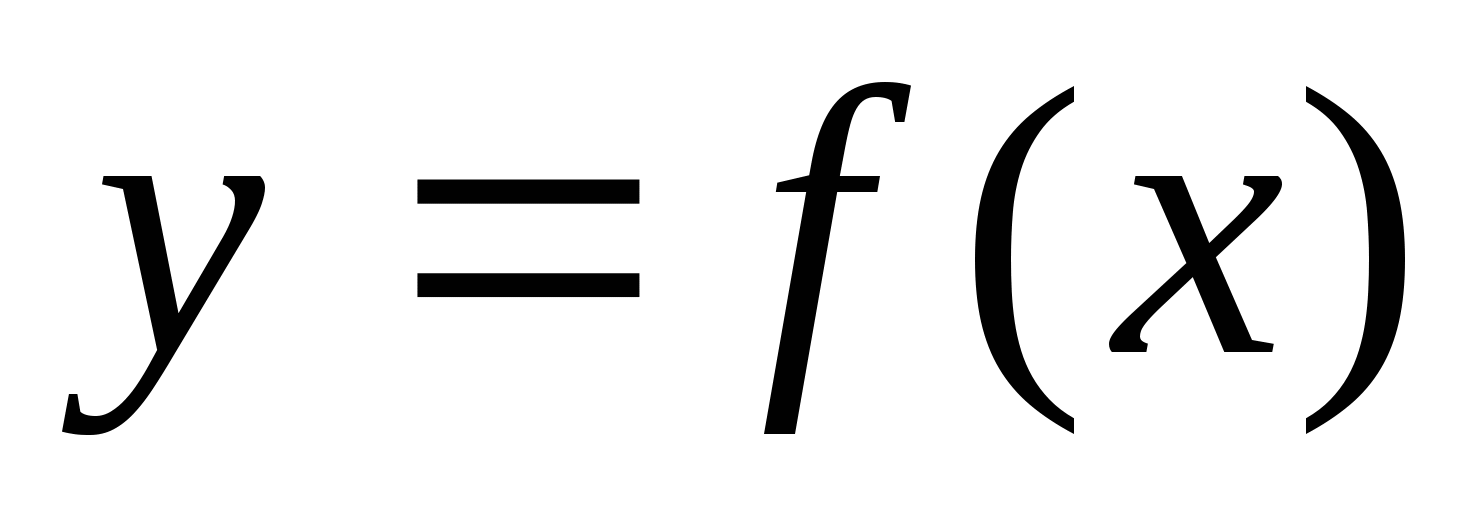 для
для 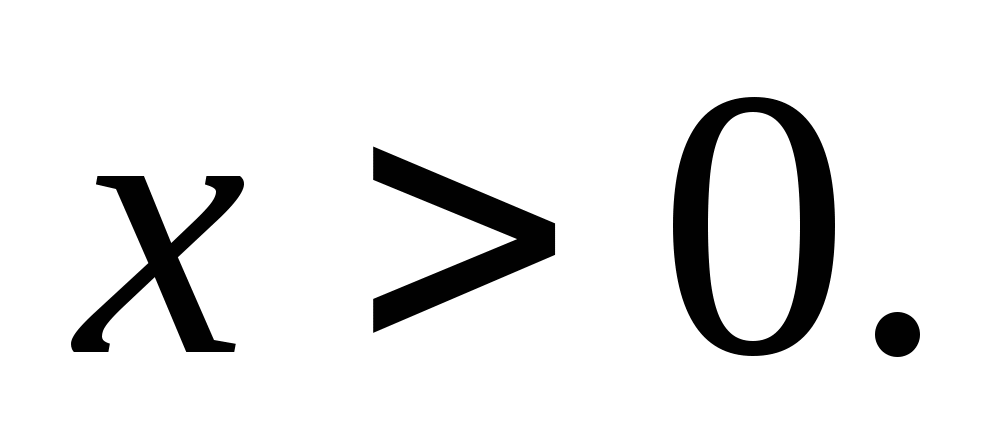 А затем достроить его левую часть, симметрично правой относительно оси ординат.
А затем достроить его левую часть, симметрично правой относительно оси ординат.
6.2. График функции 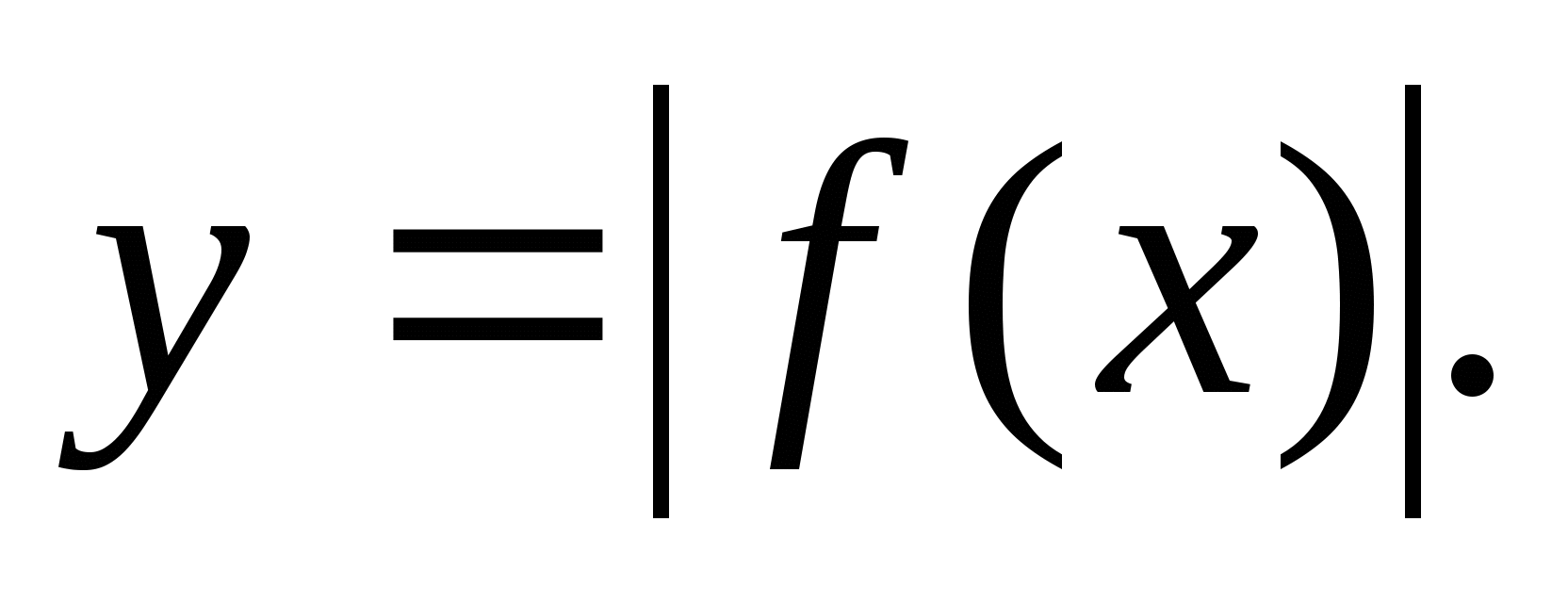
Правило построения графика функции:
Строим график функции
 .
.На участках, где график функции расположен в нижней полуплоскости, т. е. где
 , строим кривые симметричные построенным относительно оси абсцисс.
, строим кривые симметричные построенным относительно оси абсцисс.
6.3. График функции 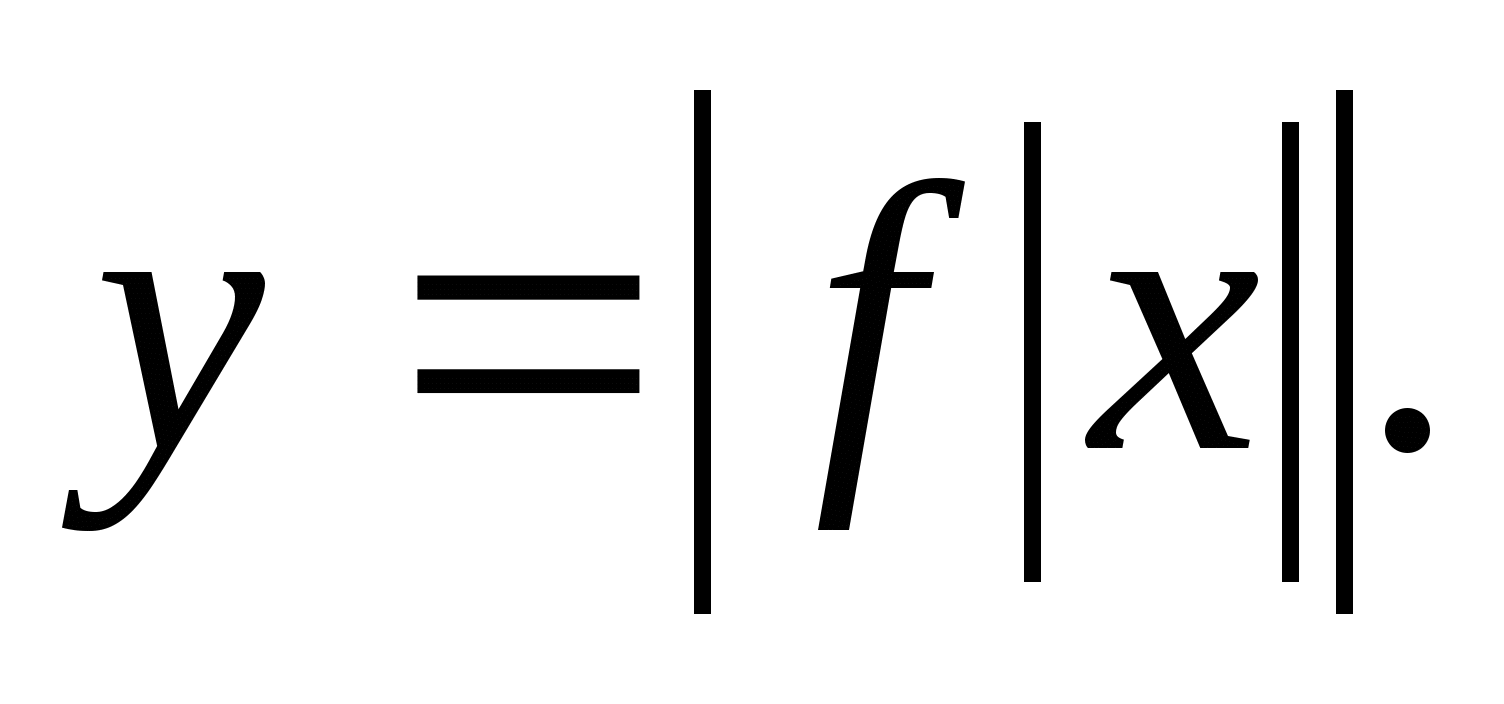
Порядок построения графика функции:
Строим график функции
 , для
, для  .
.Строим кривую графика функции, симметричную построенной относительно оси ординат (т.к. функция чётная).
Участки графика расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ординат.
6.4. График функции 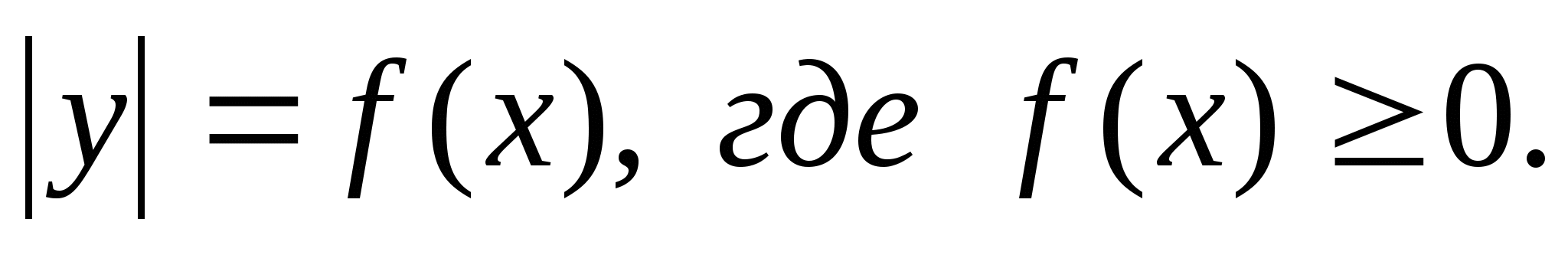
Порядок построения графика функции:
Находим область определения функции из условия
 .
.На промежутках определения функции строим график функции
 .
.Строим кривые симметричные построенному графику относительно оси ОХ.
6.5. График функции 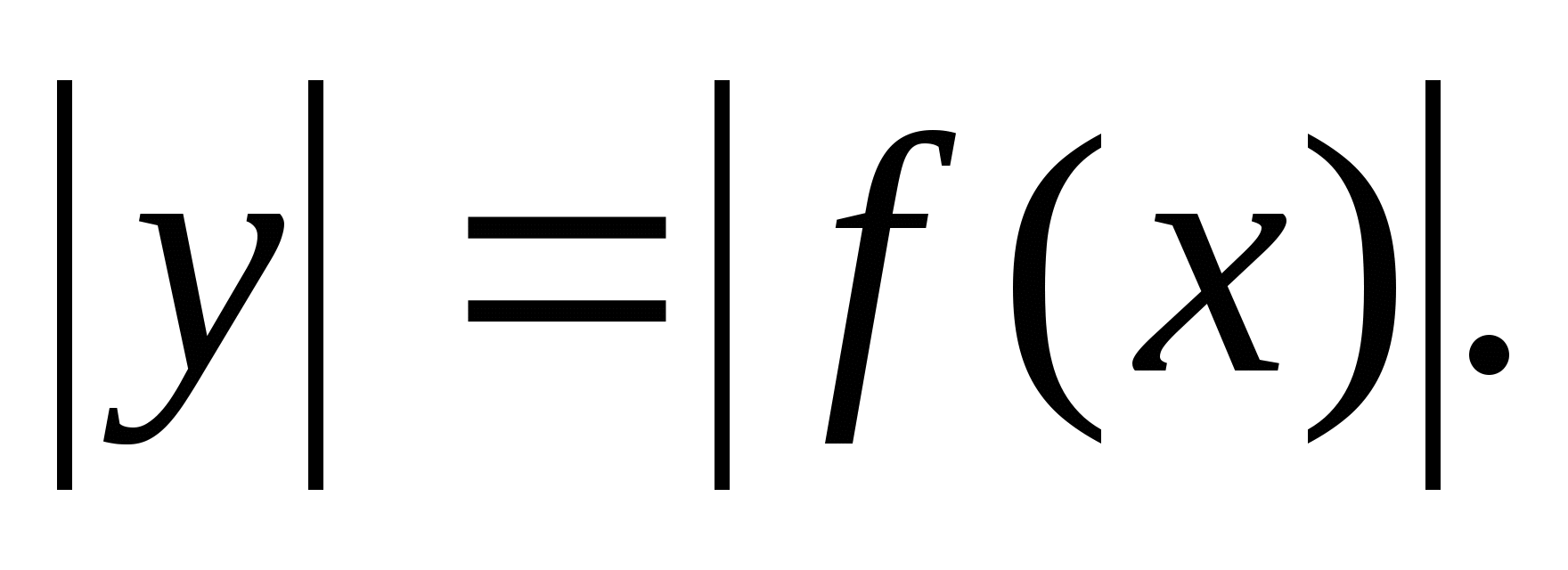
Порядок построения графика функции:
Строим график функции
 (он весь расположен в верхней полуплоскости).
(он весь расположен в верхней полуплоскости).Строим график функции
 . Он будет симметричен построенному относительно оси ОХ.
. Он будет симметричен построенному относительно оси ОХ.
Тема 7
Построение графиков неявно заданных функций, аналитическое выражение которых содержит переменную под знаком модуля.
При построении графиков данных функций основное внимание, мы уделяем функциям, аналитическое выражение которых содержит переменные х и у под знаком модуля. Поэтому функции будут чётными относительно координатных осей. Графики функций, как правило, представляют определённый «орнамент», что вызывает интерес школьников к указанной теме.
ПРИЛОЖЕНИЕ
Примеры
Тема 2
Упростить выражение:

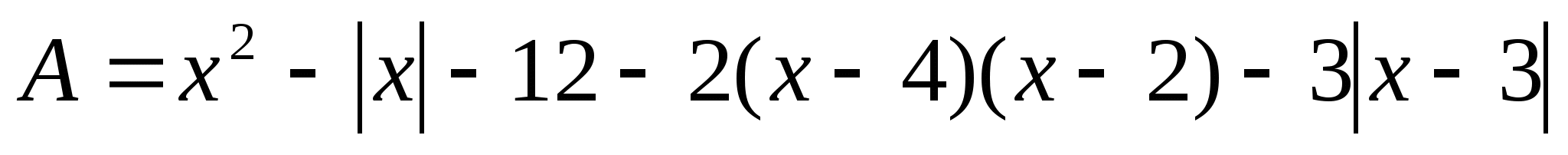
Ответ.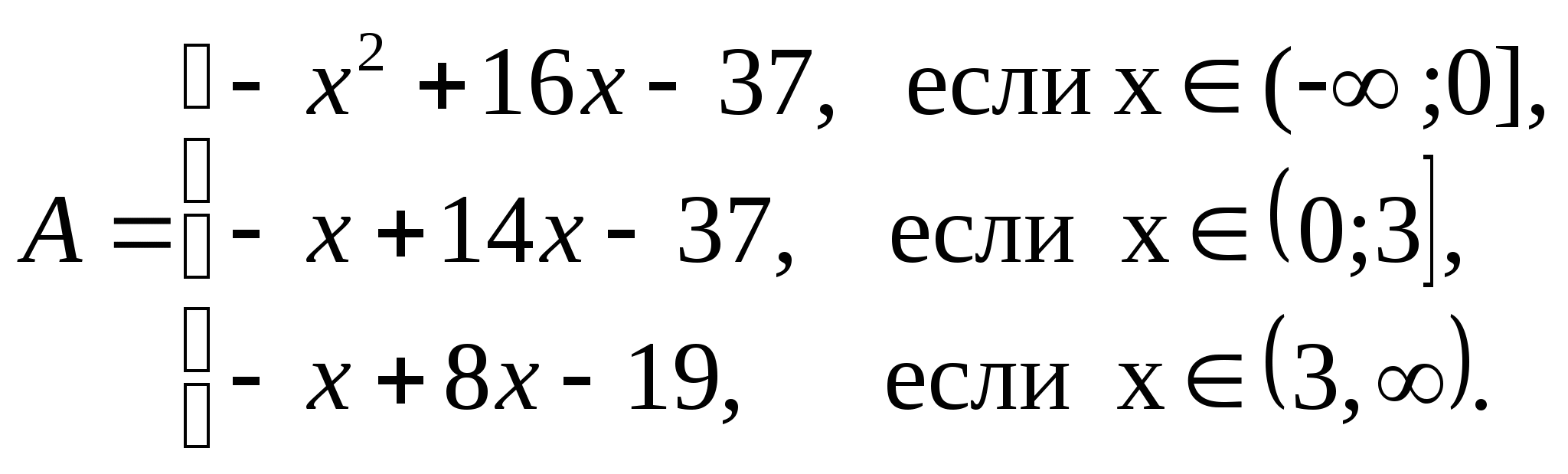
Упростить выражение:
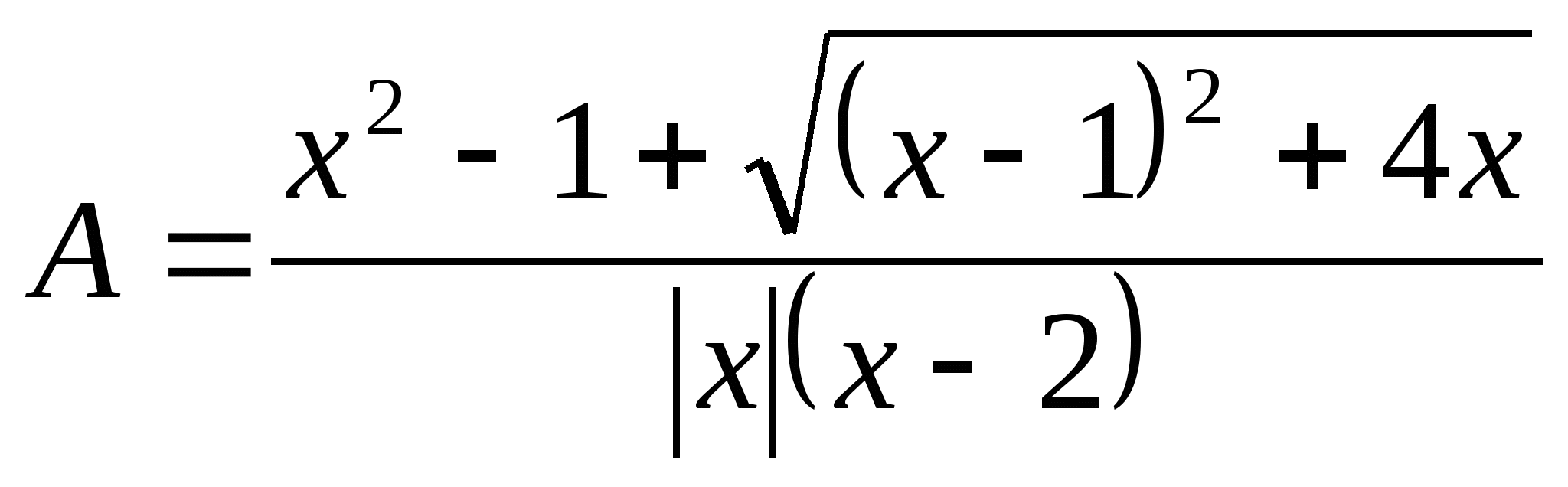
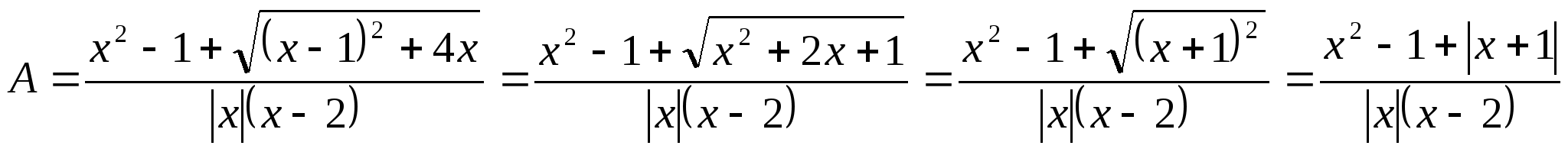
Ответ. 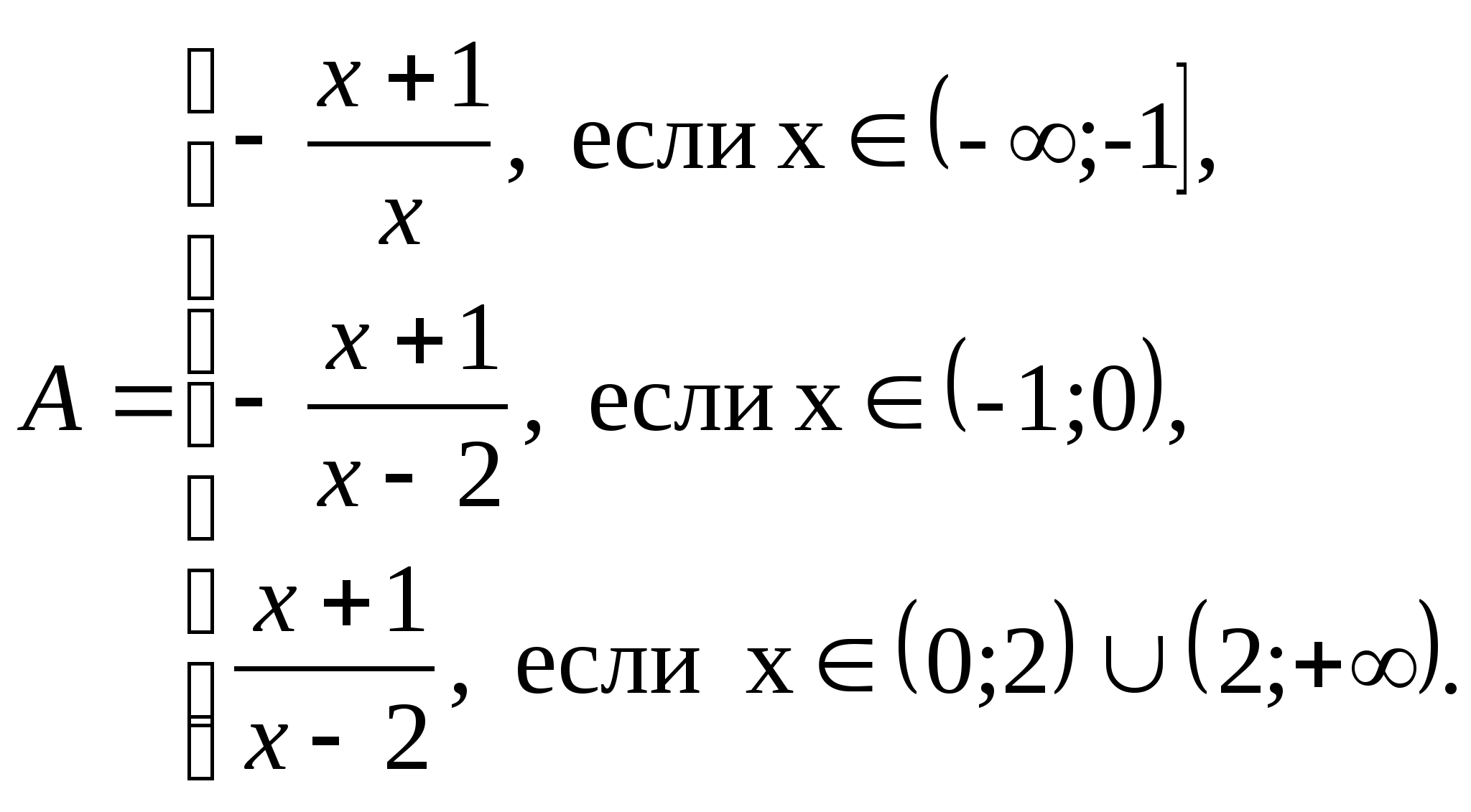
Тема 3
Решить уравнения:
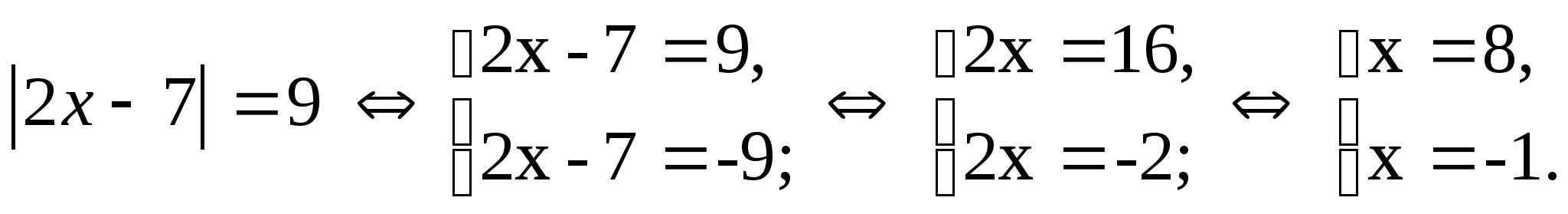
Ответ. -1; 8.
2) 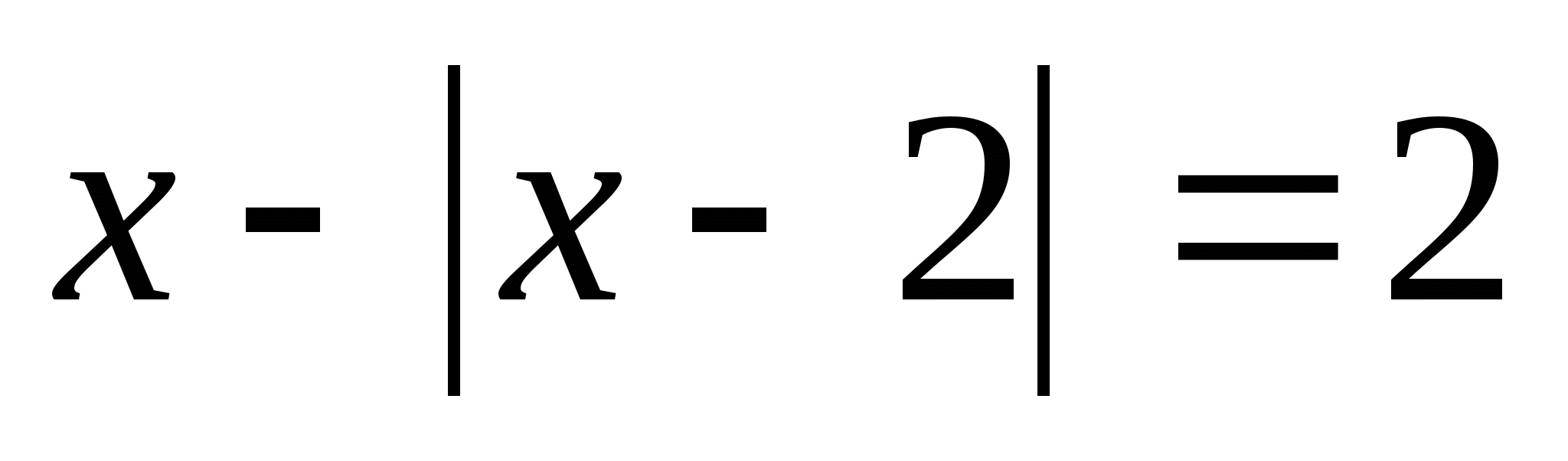
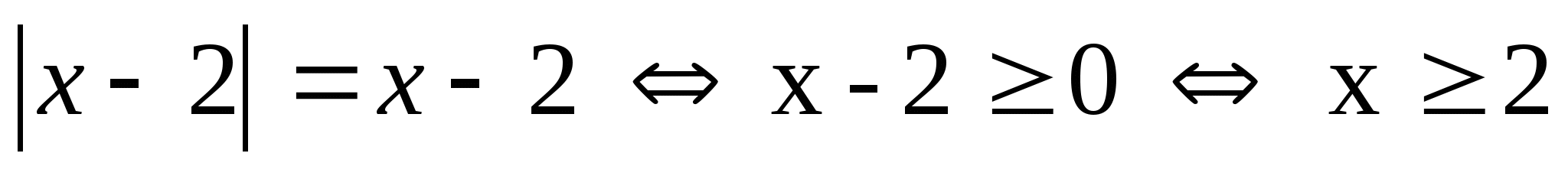
Ответ. 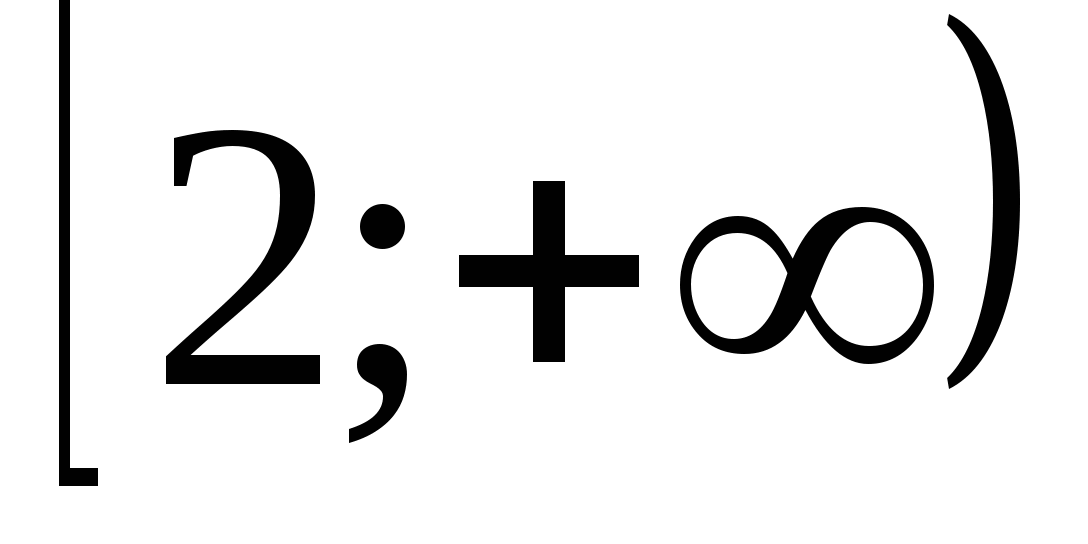
3) 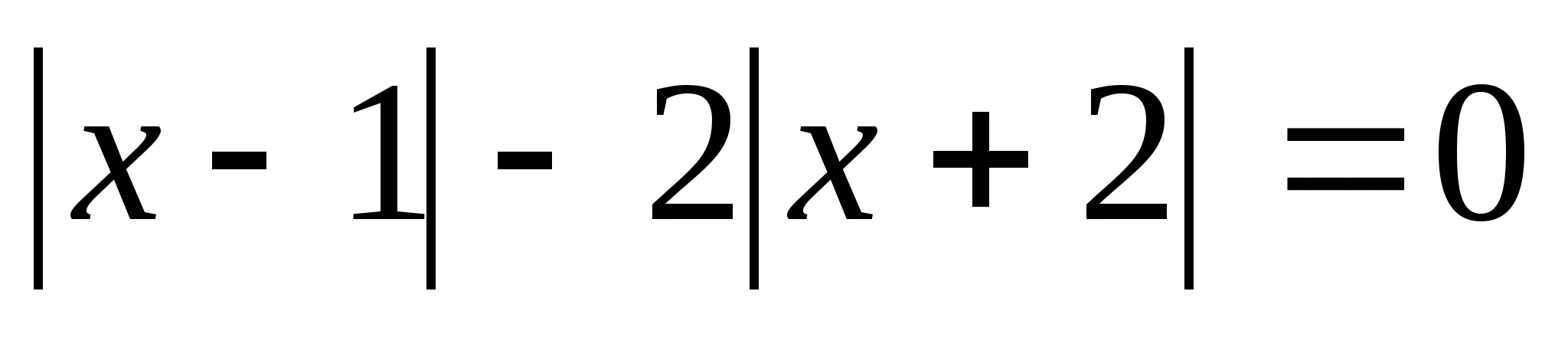
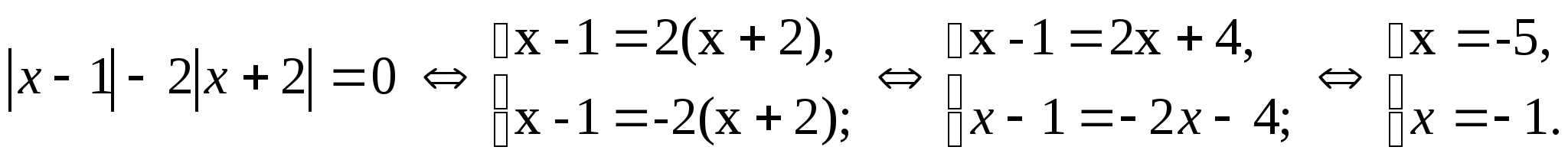
Ответ. -5; -1.
4) 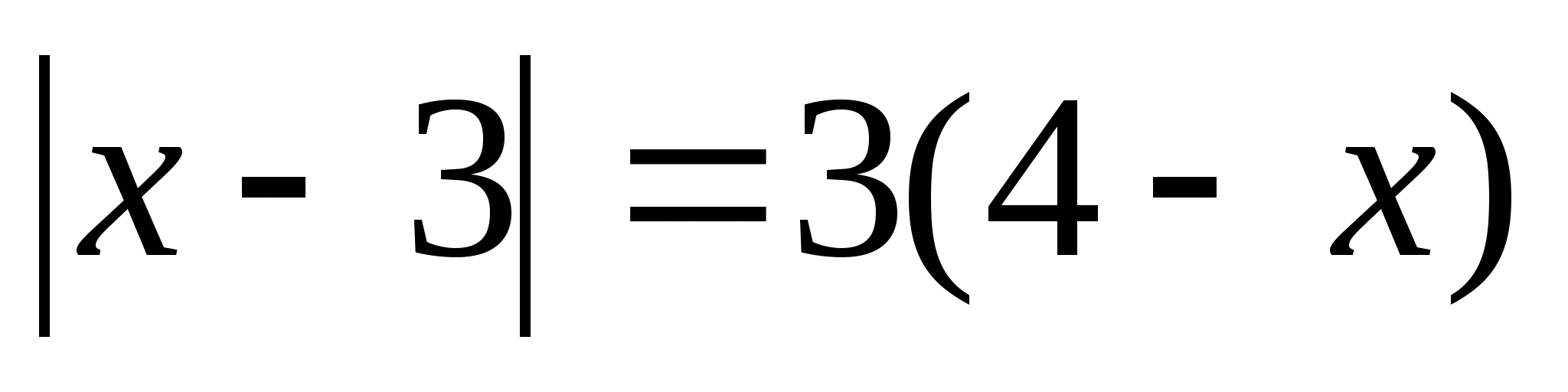
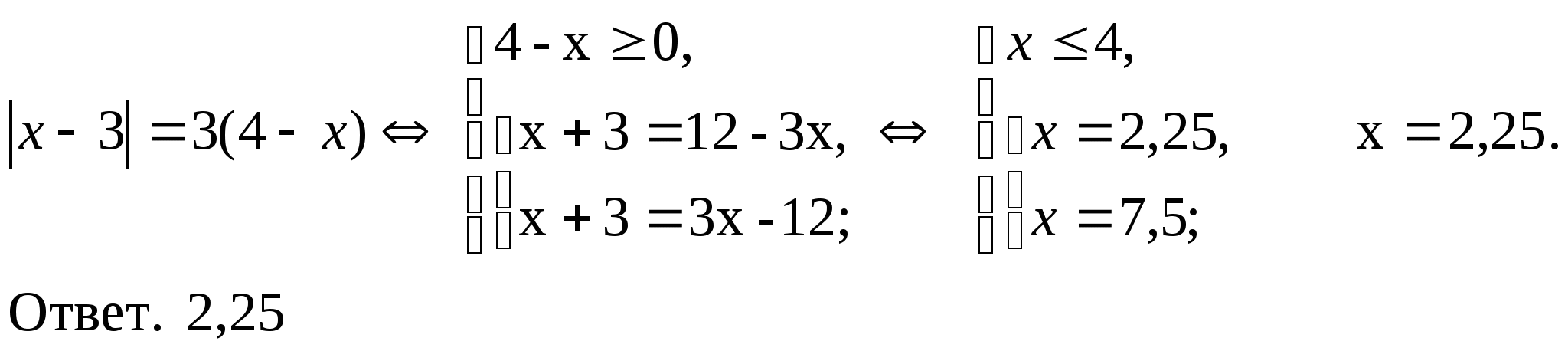
5) 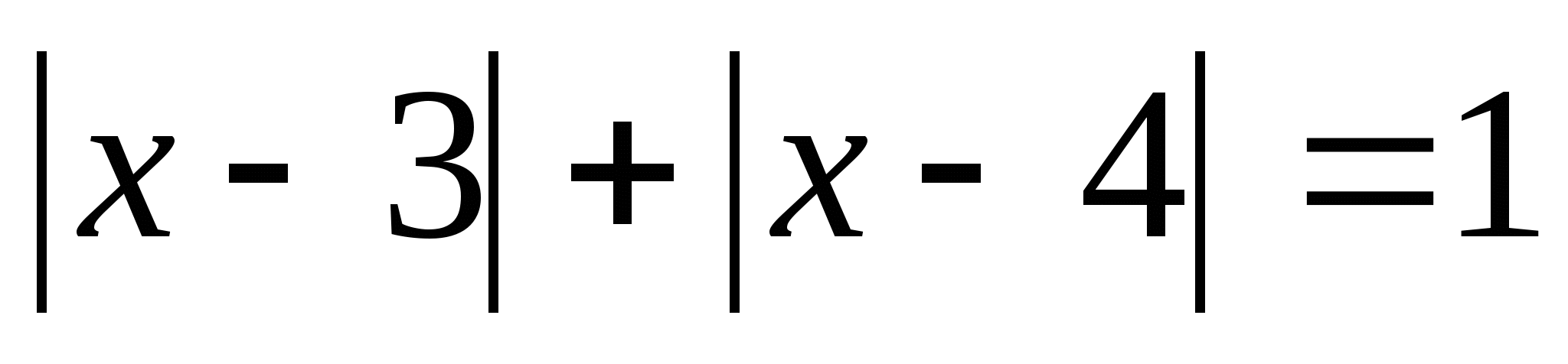
Согласно схеме, 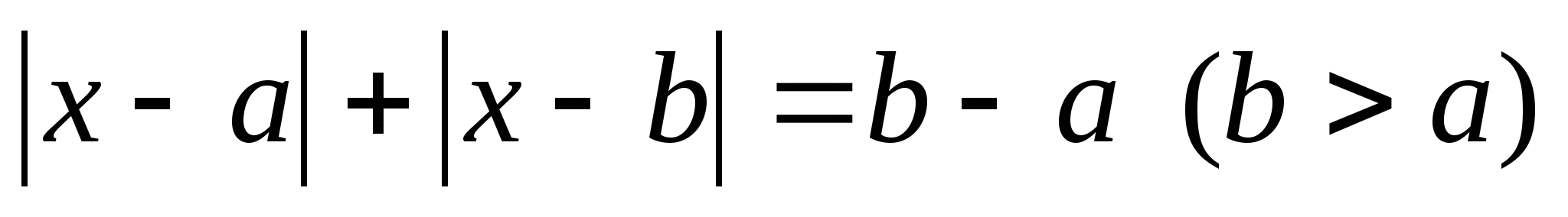
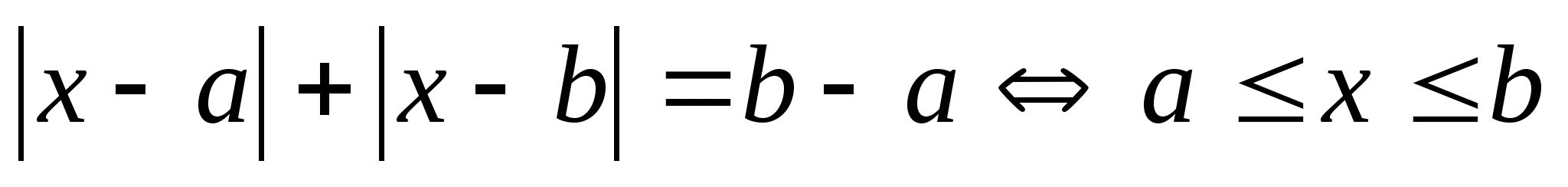 а=3, в=4, в-а=1. Поэтому решение уравнения:
а=3, в=4, в-а=1. Поэтому решение уравнения:
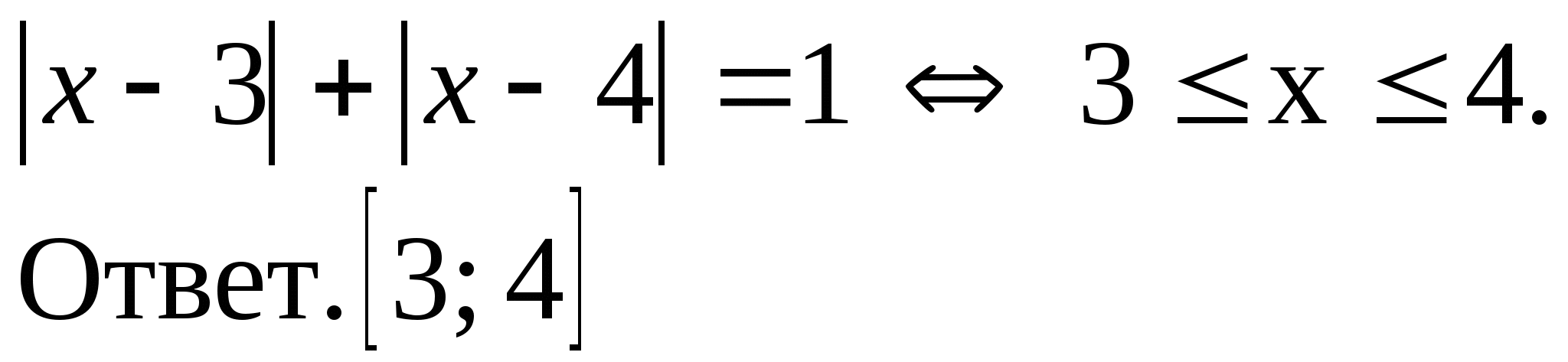
6)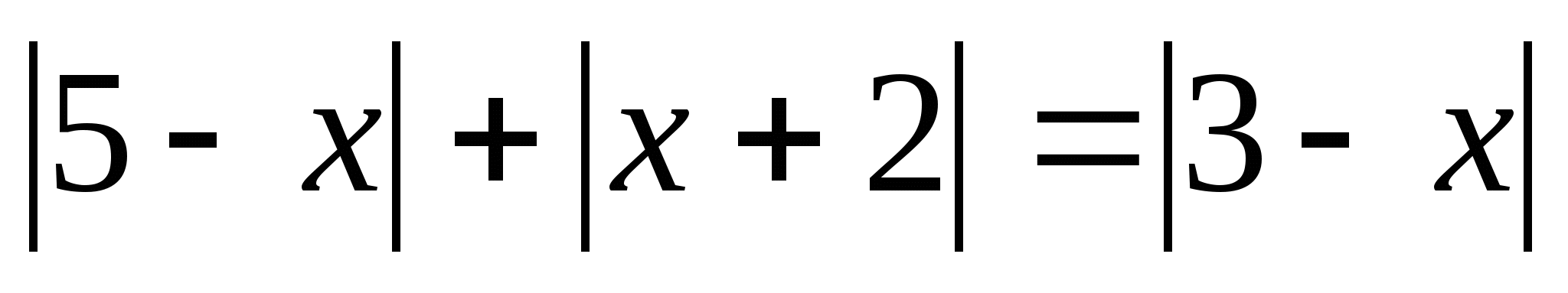
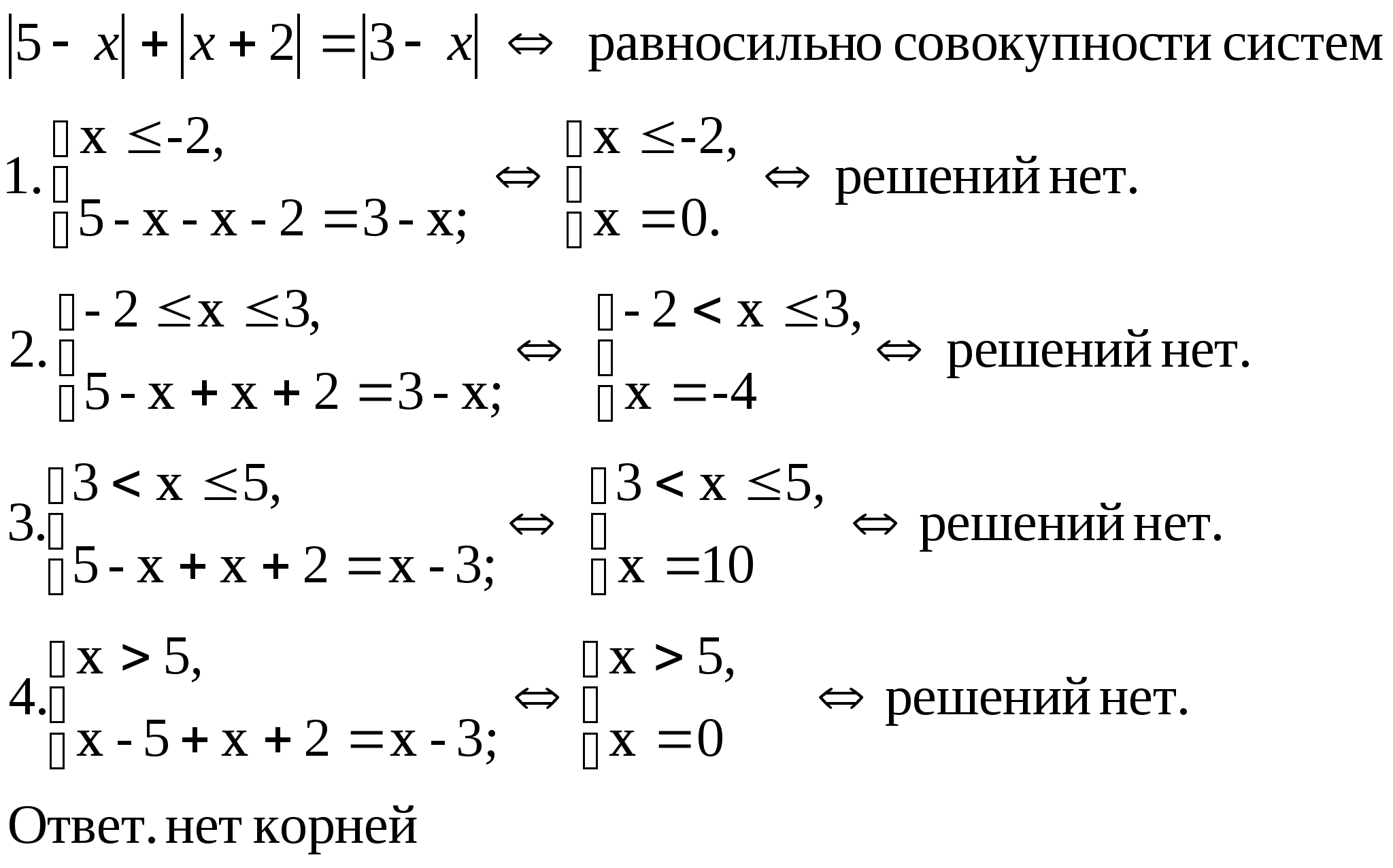
Тема 4
Решите неравенства:
1). 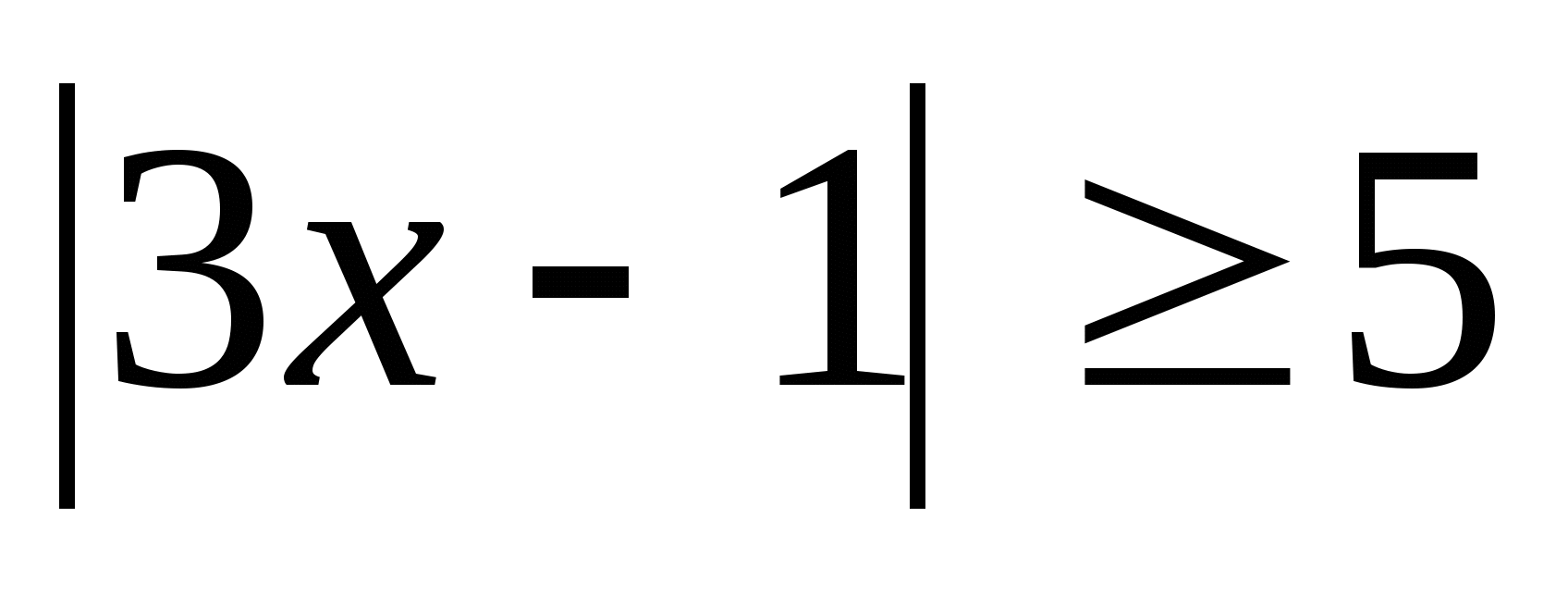
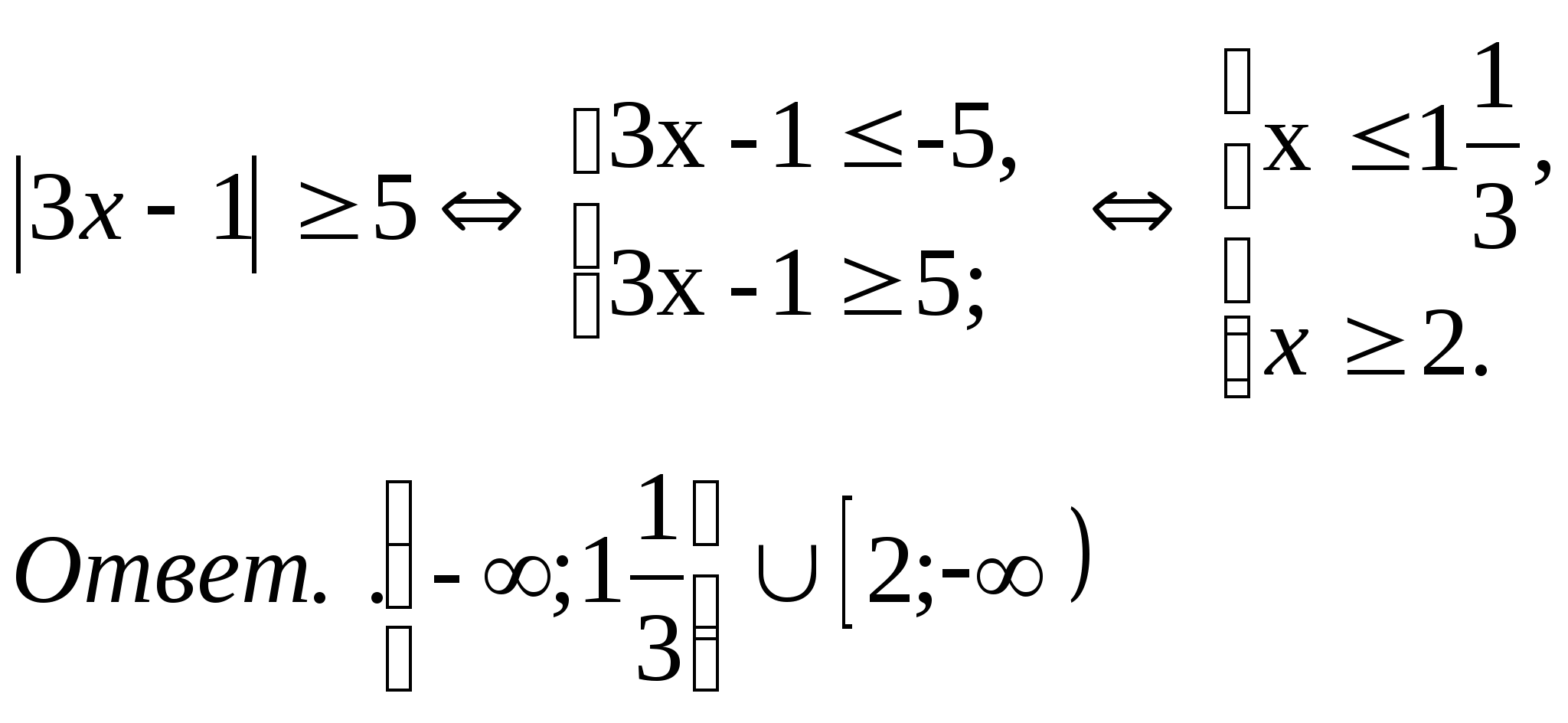
2). 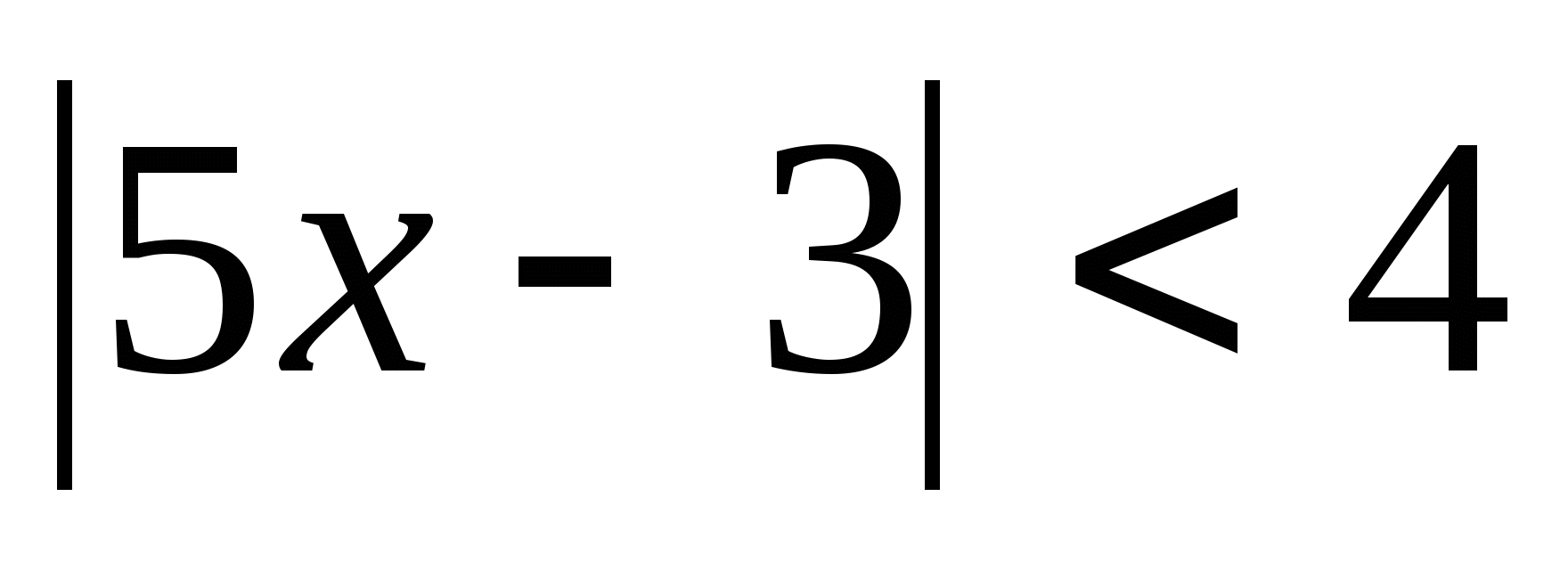
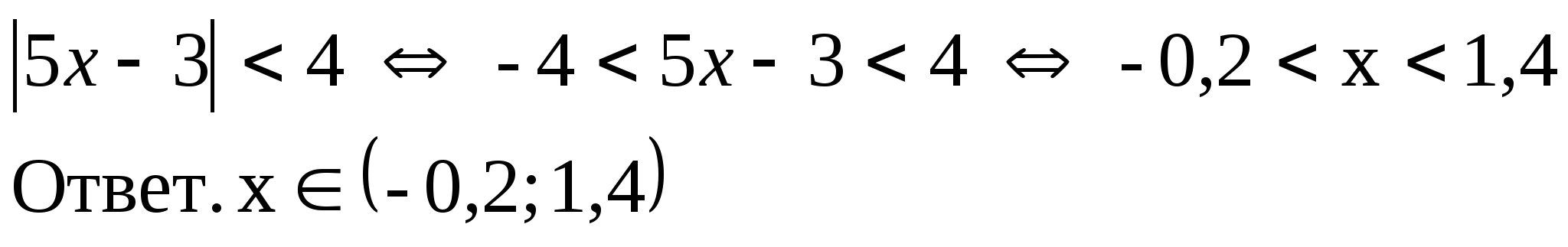
3). 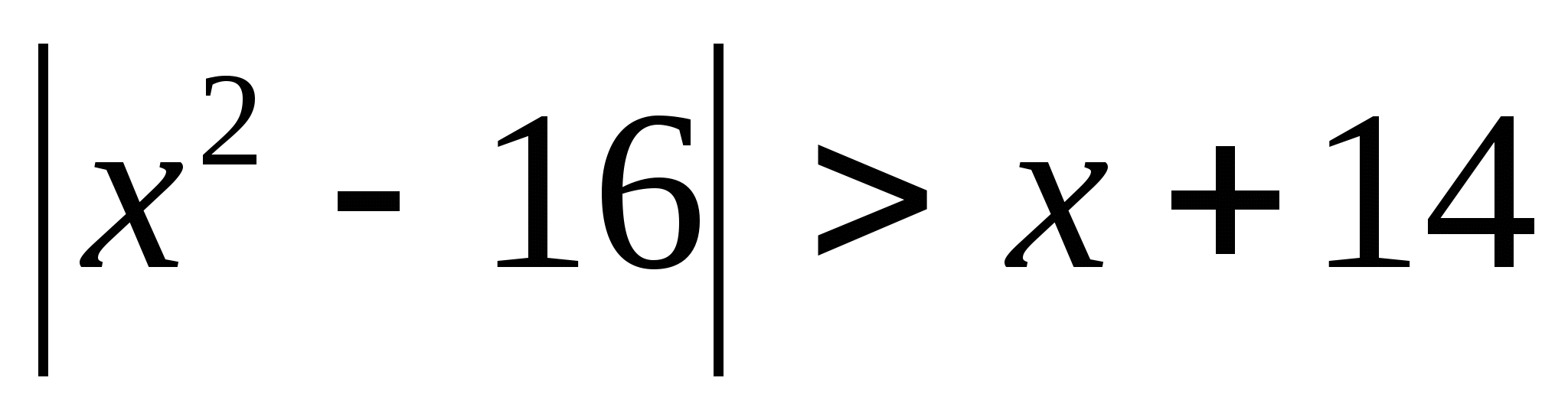
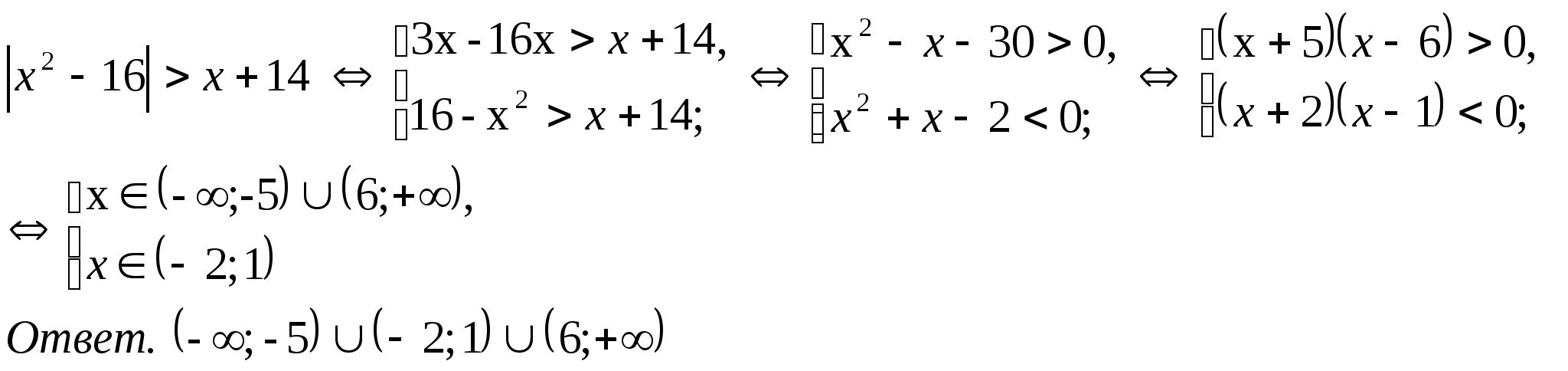
4) 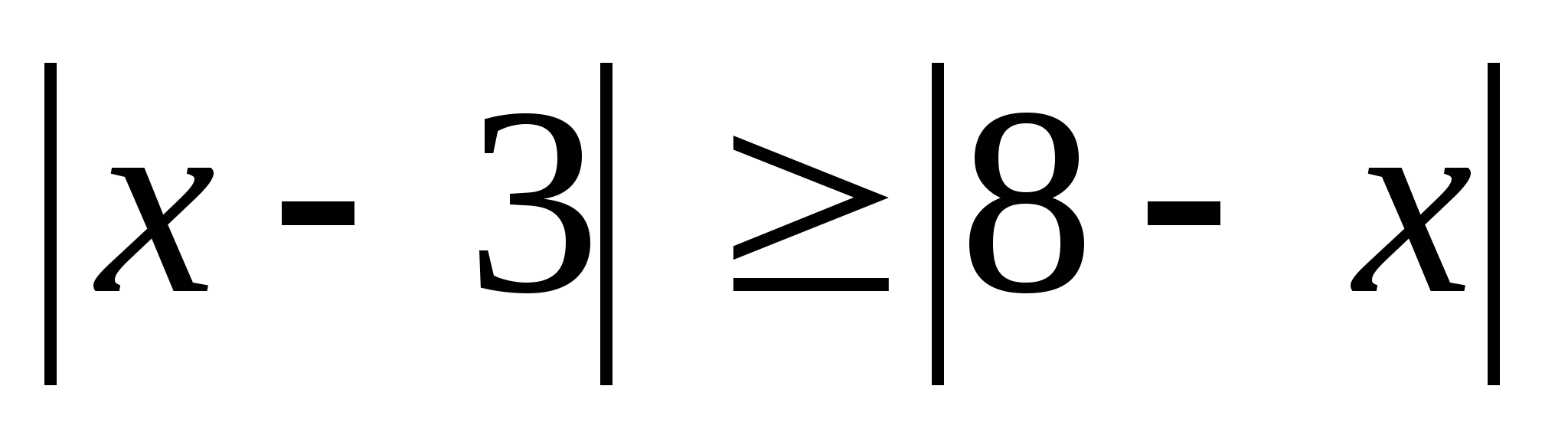
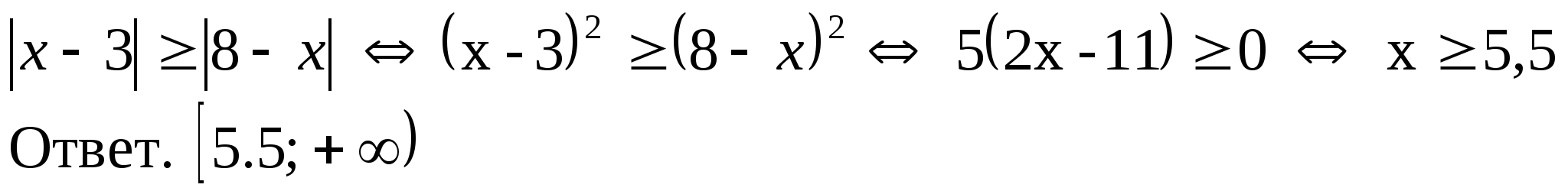
Тема 7
Построить графики функций:
1. 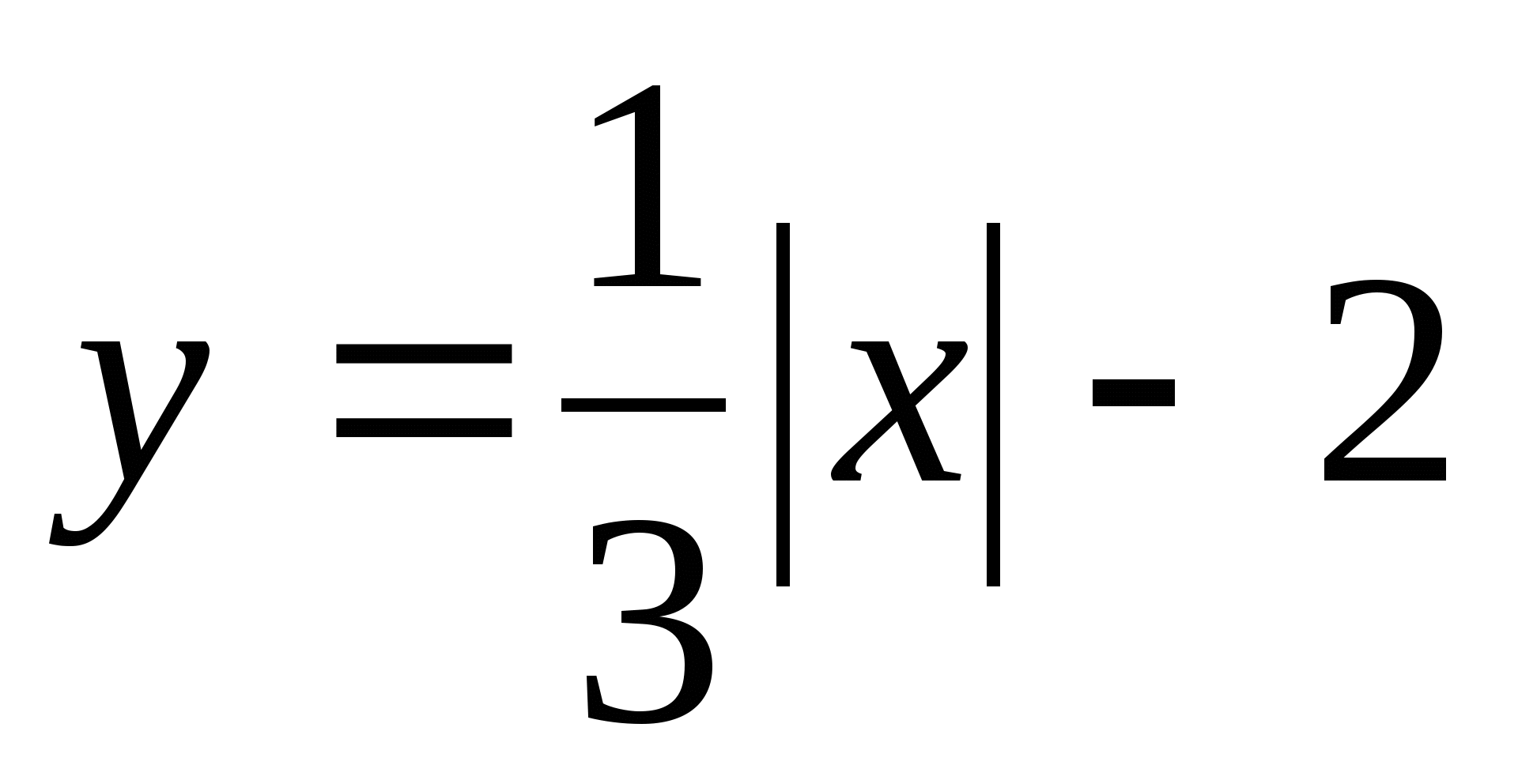
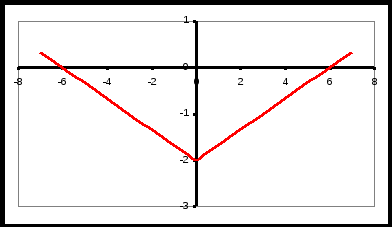
2. 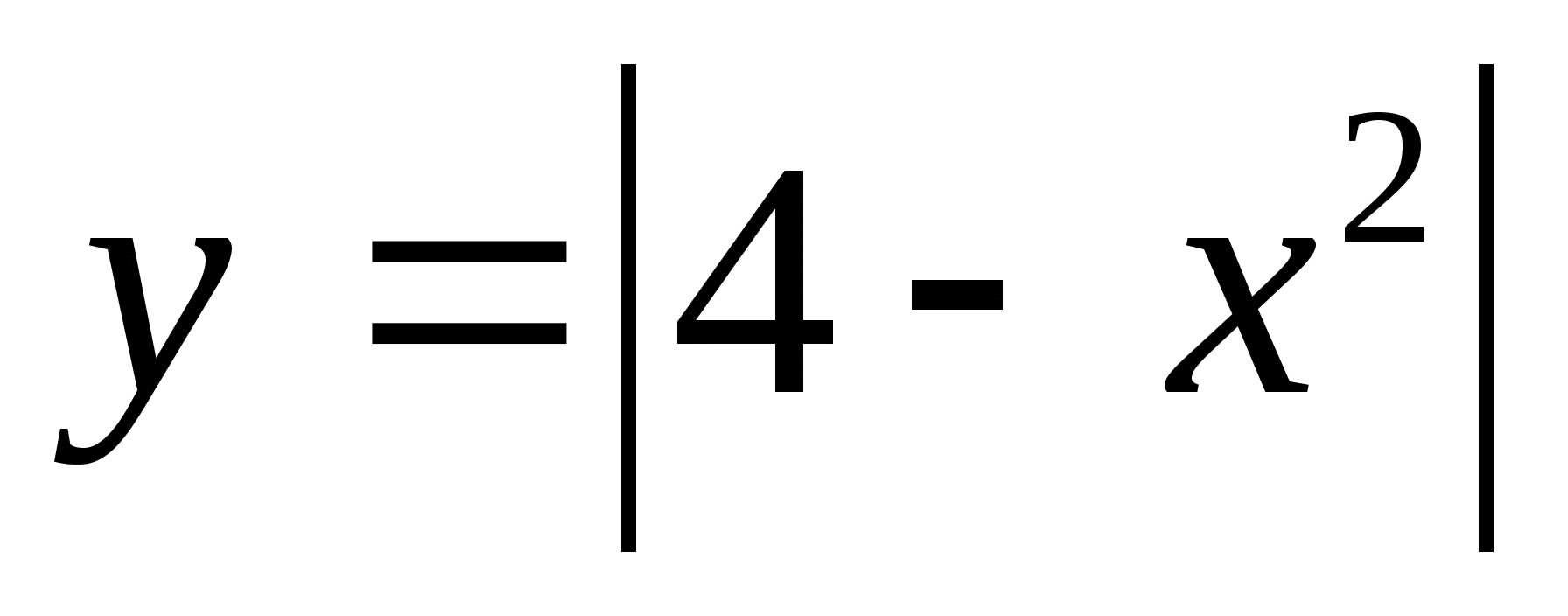
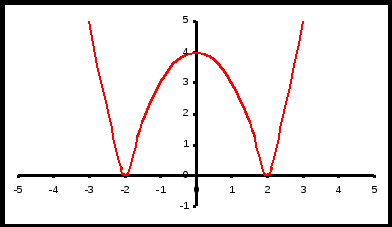
3.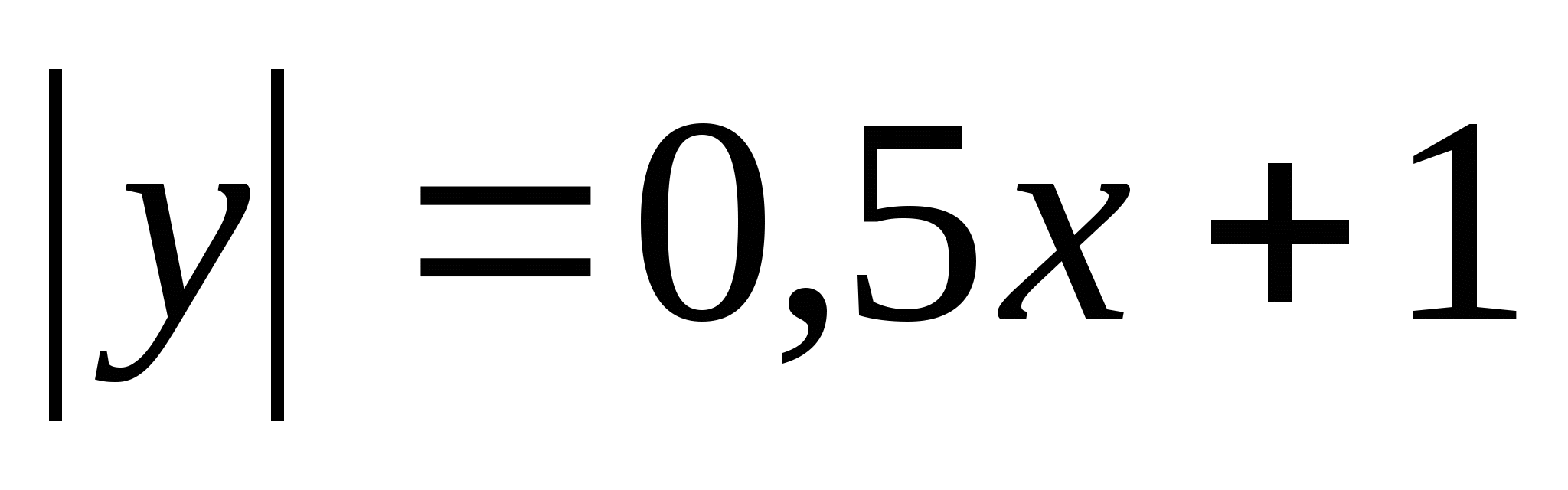
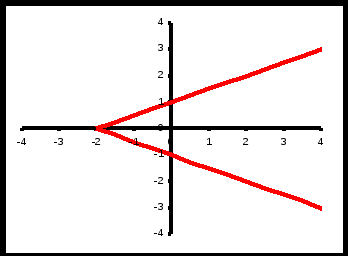
4. 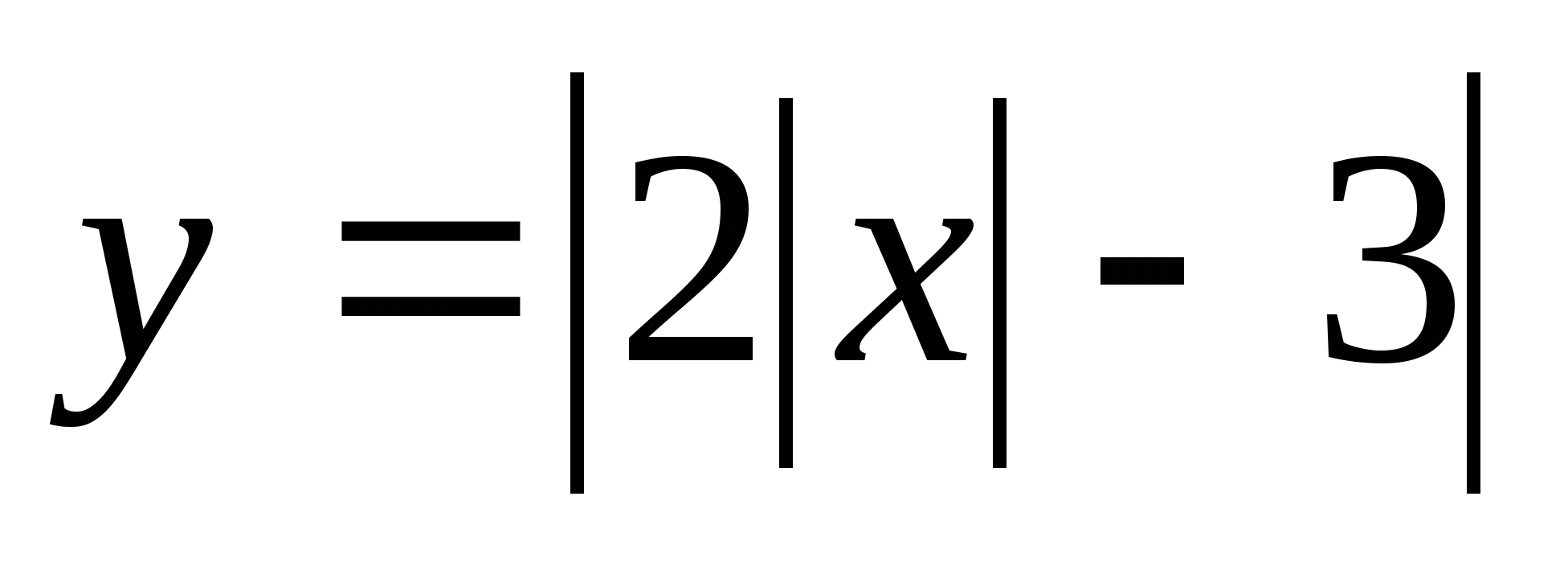
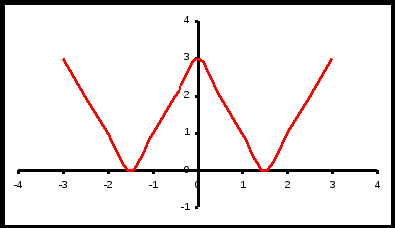
5. 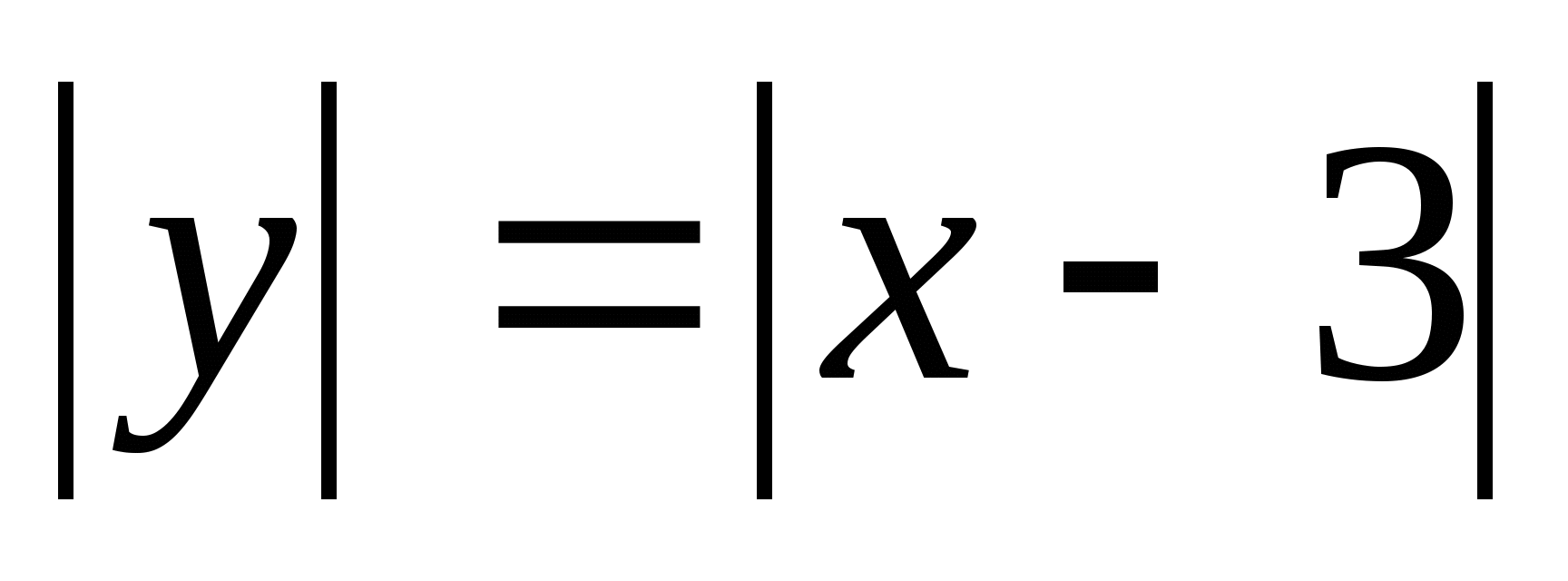
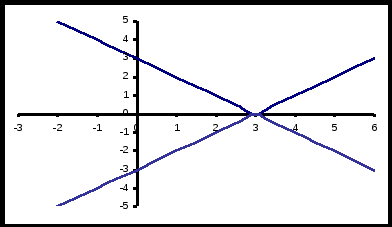
6. Построить множество точек 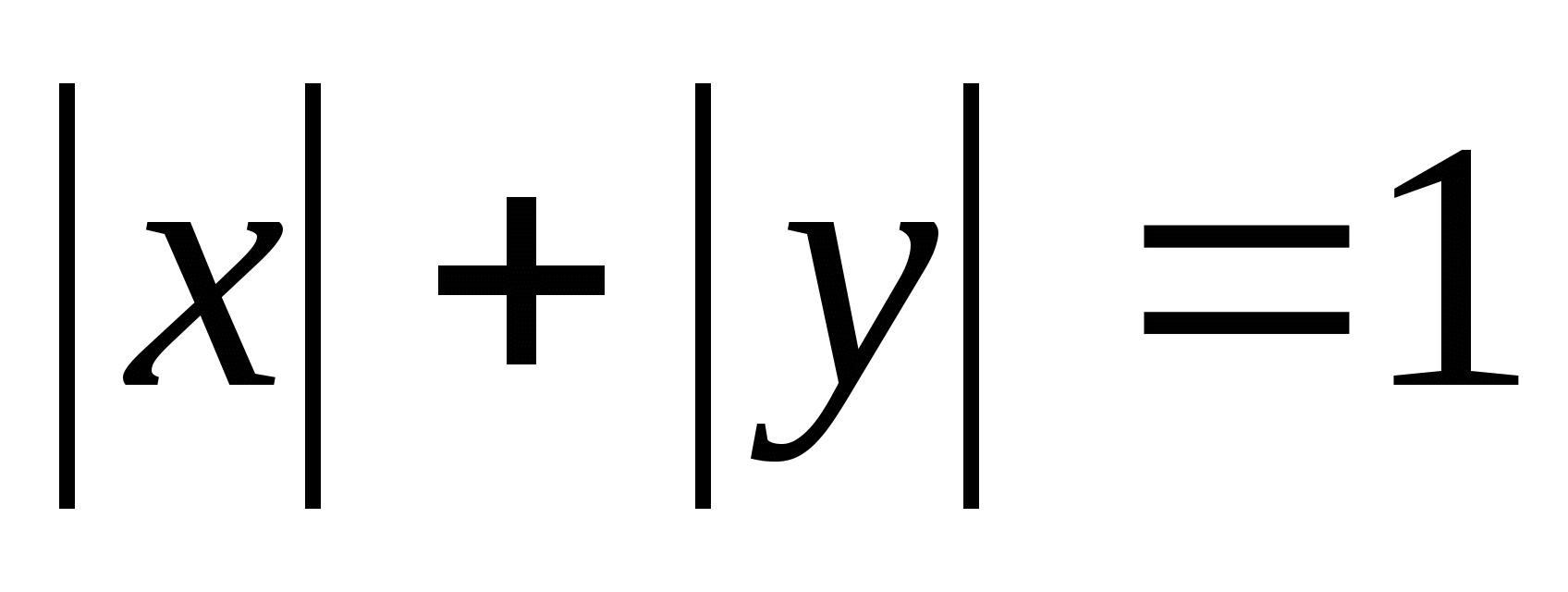 функция чётная относительно координатных осей. Если
функция чётная относительно координатных осей. Если 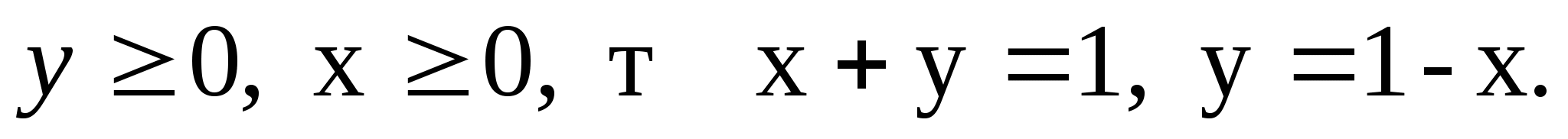
infourok.ru
Рабочая программа по алгебре (11 класс) по теме: рабочая Программа элективного курса «Задачи с модулями и параметрами»
Рассмотрено на заседании МО Протокол №___ от______ ________2009г. | Согласовано на заседании НМС Протокол №____ от______ ________2009г.
| Утверждаю Директор МОУ СОШ №46 _____________Н.Ф.Иванисов от______ ________2009г. |
Рабочая программа элективного курса
«Задачи с модулями и параметрами»
Ф. И. О. учителя: Гагинян Веры Алексеевны
Класс: 11-е
Количество часов: 34 час
Пояснительная записка.
Основная функция курсов по выбору в системе профильной подготовки по математике – выявление средствами предмета математики направленности личности, её профессиональных интересов.
Предметно-ориентированные курсы являются пропедевтическими по отношению к профильным курсам по математике, которые имеют более высокий уровень. Присутствие таких курсов в учебном плане учащегося повышает вероятность того, что выпускник после11-го класса сделает осознанный и успешный выбор вуза, связанного с математикой.
Программы предметно-ориентированных курсов по выбору включают углубление отдельных тем базовых общеобразовательных программ по математике, а также изучение некоторых тем, входящих за их рамки.
Курс «Задачи с модулями и параметрами» дополняет базовую программу, не нарушая её целостность.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования, а также в профессиональной деятельности, требующей достаточно высокой математической культуры.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющего в определённых умственных навыках. В процессе решения задач с параметрами и модулями в арсенал приёмов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ, классификация и систематизация, аналогия.
Именно задачи с параметрами обладают диагностической и прогностической ценностью, которые позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Как известно, в настоящее время практика вступительных экзаменов оторвалась от школы, настолько велики «ножницы» между требованиями, которые предъявляют к своему выпускнику школа, и требованиями, которые предъявляет к своему абитуриенту вуз, особенно вуз высокого уровня.
Очевидно одним из способов устранения указанных «ножниц» является изучение данного курса, посвященного трудным вопросам школьной математики, связанными с параметрами и модулями.
Задачи, предлагаемые в данном курсе, интересны и часто не просты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике, позволяет подготовить учащихся к поступлению в ВУЗ, тем самым исключая противоречие между требованиями системы высшего образования и итоговой подготовкой выпускников учреждений среднего образования. Вместе с тем, содержание курса позволяет ученику любого уровня активно включаться в учебно-познавательный процесс и максимально проявить себя: занятия могут проводиться на высоком уровне сложности, но включать в себя вопросы, доступные и интересные всем учащимся.
Изучение спецкурса способствует процессу самоопределения учащихся, помогает им адекватно оценить свои математические способности, обеспечивая системное включение ребёнка в процесс самостоятельного построения знаний.
Цель данного курса перейти от репродуктивного уровня усвоения материала к творческому. Научить применять знания при выполнении нестандартных заданий. При решении таких задач школьники учатся мыслить логически, творчески. Это хороший материал для учебно-исследовательской работы, что является пропедевтикой научно-исследовательской деятельности.
Основная задача курса как можно полнее развить потенциальные творческие способности каждого слушателя, не ограничивая заранее сверху уровень сложности задачного материала. Решение задач способствует систематическому углублению изучаемого материала и развитию навыка решения сложных задач.
Основная цель данного курса – подготовить учащихся таким образом, чтобы они смогли в жесткой атмосфере конкурсного экзамена успешно справиться с задачами, содержащими модули и параметры.
Воспитательное назначение курса.
Обучение задачам с параметрами потребует от учащихся умственных и волевых усилий, развитого внимания, воспитания таких качеств, как активность, творческая инициатива, умений коллективно-познавательного труда.
Основные задачи данного курса:
- углубить знания по математике, предусматривающие формирование у учащихся устойчивого интереса к предмету;
- выявить и развить их математические способности;
- расширить математические представления учащихся о приёмах и методах решения задач с модулями и параметрами;
- повышение уровня математического и логического мышления учащихся;
- развитие навыков исследовательской деятельности,
- обеспечить подготовку к поступлению в вуз и продолжению образования;
- обеспечить подготовку к профессиональной деятельности, требующей высокой математической культуры.
Работа элективного курса строится на принципах: — научности;
— доступности;
— опережающей сложности;
— вариативности;
— самоконтроля.
Формы контроля:
- Рейтинг – таблица
- Уроки самооценки и оценки товарищей
- Презентация учебных проектов
О том, что учащийся должен будет представить учебный проект по теме курса, нужно проинформировать его заблаговременно, познакомив с формами такого рода деятельности.
Для того чтобы урок – презентация получился интересным, виды проектов должны соответствовать уровню и интересам учащихся, а также должны быть интересными по форме и содержанию.
Работы могут быть как индивидуальные, так и парные, групповые. Данный урок можно провести в виде конкурса, где победителей определят сами учащиеся.
Административной проверки усвоения материала курса не предполагается, соответствующие задачи не будут включаться в административные контрольные работы.
В технологии проведения занятий присутствует этап самопроверки, который представляет учащимся возможность самим проверить, как ими усвоен изучаемый материал.
В свою очередь учитель может провести обучающие самостоятельные работы, которые позволят оценить уровень усвоения вопросов курса.
Формой итогового контроля может стать обучающая самостоятельная работа, собеседование или тестовая работа.
Требования к уровню подготовки учащихся:
- должны иметь элементарные умения решать задачи повышенного по сравнению с обязательным уровнем сложности;
- точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач;
- правильно пользоваться математической символикой и терминологией;
- применять рациональные приемы тождественных преобразований;
- использовать наиболее употребляемые эвристические приемы.
В результате изучения данного курса учащиеся должны знать:
-понятие параметра
-прочно усвоить понятие модуль числа;
-алгоритмы решений задач с модулями и параметрами;
-зависимость количества решений неравенств, уравнений и их систем от значений параметра;
-свойства решений уравнений, неравенств и их систем;
-свойства функций в задачах с параметрами.
должны уметь:
- уметь решать линейные, квадратные уравнения с модулем;
- уметь решать линейные, квадратные неравенства с модулем;
- строить графики уравнений, содержащие модули;
- уметь решать линейные, квадратные, рациональные уравнения с параметром;
- уметь решать неравенства с параметром;
- находить корни квадратичной функции;
- строить графики квадратичных функций;
- исследовать квадратный трехчлен;
- знать и уметь применять нестандартные приемы и методы решения уравнений, неравенств и систем.
Содержание обучения.
- Решение задач с модулем. (12 часов).
Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину. Уравнение и неравенства вида |х|= а, |ах+в|=0, |ах+в|≤0.
График функции у=|х|, у=| ах+в |. Построение графиков функций, связанных с модулем.
Методы решения уравнений вида: |ах+в|=с, где с — любое действительное число, |ах+в|=|сх+д|.
Графическое решение неравенства |ах+в|≤с, где с – любое действительное число.
Методы решения уравнений вида: |ах+в|+|сх+д|=т, |ах+в|+|сх+д|+пх=т. Методы решения неравенств вида: |ах+в|+|сх+д| сх+д|+ пх>т.
Методы решения неравенств вида: |ах+в|≤| сх+д|, |ах+в|≥| сх+д|, |ах+в|≤ сх+д, |ах+в|≥ сх+д. Графическая интерпретация.
Квадратное уравнение, содержащее абсолютную величину. Метод замены переменной. Решение уравнений.
2.Решение задач с параметрами. (12 часов).
Понятие параметра. Что значит — решить уравнение или неравенство с параметрами. Что значит — исследовать уравнение (определить количество решений, найти положительные решения и т.д.), содержащее параметры.
Линейное уравнение с параметрами. Общий метод решения уравнения вида ах= в, решение линейных уравнений с параметрами, сводящихся к виду ах=в. Линейные уравнения с параметрами, содержащие дополнительные условия (корень равен данному числу, прямая проходит через точку с заданными координатами, уравнение имеет отрицательное решение и т.д.).
Линейные неравенства с параметрами вида ах≤в, ах≥в.
Уравнения и неравенства с параметрами, сводящиеся к линейным.
Решение квадратных уравнений и неравенств с параметром. Исследование квадратного трехчлена.
Количество корней в зависимости от значений параметров. Параметр, как фиксированное число.
3. Нестандартные методы и приемы решения уравнений,
неравенств и систем, содержащих модули и параметры. (10 часов).
Графические и аналитические методы. Классификация задач. Ответ, как наперёд заданное подмножество множество действительных чисел. Параметр, как равноправная переменная. Свойства решений уравнений, неравенств и их систем.
Свойства функций в задачах с параметрами и модулями. Схема исследования функций. Область значений функции. Подстановки. Экстремальные свойства функций. Метод оценки. Свойства монотонных функций.
Список литературы.
Литература для учащихся
- Макарычев Ю.Н. Миндюк Н.Г. Алгебра 8. Алгебра 9. Дополнительные главы к школьному учебнику. Москва. «Просвещение». 2001год.
- Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре 8-9. Москва. «Просвещение». 2001год.
Литература для учителя
- Литвиненко В.Н., Мордкович А. Г. Практикум по решению математических задач.
- Ястрибинецкий Г.А Задачи с параметрами.
- Горнштейн П.И., Полонский В.Б., Якир М.С.
Задачи с параметрами.
«Необходимые условия в задачах с параметрами».
- Родионов Е.М. Решение задач с модулями и параметрами. Пособие для поступающих в вузы.
- Голубев В.И., Гольдман А.М., Дорофеев Г.В. «О параметрах – с самого начала».
- Дорофеев Г.В., Затахавай В.В. «Решение задач, содержащих модули и параметры».
- Дорофеев Г.В. «Квадратный трёхчлен в задачах».
- Марков В.К. «Метод координат и задачи с параметрами».
- Шарыгин И.Ф. «Факультативный курс по математике. Решение задач».
Учебно-тематический план.
№ №п/п | Тема занятия | Беседа, лекция | Сообщения учащихся | Практикум | Творческое исследование | Конкурсы | Викторины | Тренажер | Формы контроля |
Решение задач с модулем 12ч. |
1-2 | Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину. Уравнение и неравенства вида |х|= а, |ах+в|=0, |ах+в|≤0. | 1 ч. | 1 ч. |
3-4 | График функции у=|х|, у=| ах+в |. Построение графиков функций, связанных с модулем. | 1 ч. | 1 ч. |
5-8 | Решение уравнений и неравенств различных видов, содержащих модули. Графическая интерпретация. | 1 ч. | 1 ч. | 1 ч. | 1 ч. |
9-12 | Квадратное уравнение, содержащее абсолютную величину. Метод замены переменной. Решение уравнений. | 1 ч. | 1 ч. | 1 ч. | Сам. работа 1 ч. |
Решение задач с параметрами 12ч. |
13 | Понятие параметра. | 1 ч. |
14-15 | Линейное уравнение с параметрами. Общий метод решения уравнения вида ах= в, решение линейных уравнений с параметрами, сводящихся к виду ах=в. | 1 ч. | 1 ч. |
16-17 | Линейные неравенства с параметрами вида ах≤в, ах≥в. | 1 ч. | 1 ч. |
18-19 | Уравнения и неравенства с параметрами, сводящиеся к линейным. | 1 ч. | 1 ч. |
20-22 | Решение квадратных уравнений и неравенств с параметром. Исследование квадратного трехчлена. | 1 ч. | 1 ч. | 1 ч |
23-24 | Количество корней в зависимости от значений параметров. | 1 ч. | 1 ч. | Сам. работа |
Нестандартные методы и приемы решения уравнений, неравенств и систем, содержащих модули и параметры 10ч. |
25-28 | Графические и аналитические методы. Классификация задач. | 1 | 1 | 1 | 1 |
29-31 | Свойства решений уравнений, неравенств и их систем. | 1 | 1 | 1 |
32-34 | Свойства функций в задачах с параметрами и модулями. | 1 | 1 | 1 |
nsportal.ru
Элективный курс «Задачи с модулями и параметрами»
Филиал муниципального бюджетного общеобразовательного учреждения
Староюрьевской средней общеобразовательной школы в с. Новоюрьево
Староюрьевского района Тамбовской области
РЕКОМЕНДОВАНОМетодическим советом школы
Протокол №___
от «___» _____2016г
УТВЕРЖДЕНО
приказ № _______от_____
Директор школы_________
Т.И. Киселёва
Элективный курс
9 класс
«Задачи с модулями
и параметрами»
на 2016-2017 учебный год
Предпрофильная
подготовка обучающихся
Автор программы: Братищева А.С.
Пояснительная записка
Основная функция курсов по выбору в системе предпрофильной подготовки по математике – выявление средствами предмета математики направленности личности, её профессиональных интересов.
Предметно-ориентированные курсы являются пропедевтическими по отношению к профильным курсам по математике, которые имеют более высокий уровень. Присутствие таких курсов в учебном плане учащегося повышает вероятность того, что выпускник после окончания 9-го класса сделает осознанный и успешный выбор профиля, связанного с математикой.
Программы предметно-ориентированных курсов по выбору включают углубление отдельных тем базовых общеобразовательных программ по математике, а также изучение некоторых тем, выходящих за их рамки.
Курс «Задачи с модулями и параметрами» дополняет базовую программу, не нарушая её целостность. Курс рассчитан на 17 часов и является курсом предпрофильной подготовки (синтез предметно-ориентированного и межпредметного курсов), осуществляет учебно-практическое знакомство с особенностями профиля.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования, а также в профессиональной деятельности, требующей достаточно высокой математической культуры.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющего в определённых умственных навыках. В процессе изучения избранных вопросов математики как решение задач с параметрами и модулями в арсенал приёмов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ, классификация и систематизация, аналогия.
Именно задачи с параметрами обладают диагностической и прогностической ценностью, которые позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Как известно, в настоящее время практика вступительных экзаменов оторвалась от школы, настолько велики «ножницы» между требованиями, которые предъявляют к своему выпускнику школа, и требованиями, которые предъявляет к своему абитуриенту ВУЗы, особенно ВУЗы высокого уровня.
Очевидно одним из способов устранения указанных «ножниц» является изучение данного курса, посвященного трудным вопросам школьной математики, связанными с параметрами и модулями.
Задачи, предлагаемые в данном курсе, интересны и часто непросты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике, позволяет подготовить учащихся к поступлению в ВУЗы, тем самым исключая противоречие между требованиями системы высшего образования и итоговой подготовкой выпускников учреждений среднего образования. Вместе с тем, содержание курса позволяет ученику любого уровня активно включаться в учебно-познавательный процесс и максимально проявить себя: занятия могут проводиться на высоком уровне сложности, но включать в себя вопросы, доступные и интересные всем учащимся.
Изучение спецкурса способствует процессу самоопределения учащихся, помогает им адекватно оценить свои математические способности, обеспечивая системное включение ребёнка в процесс самостоятельного построения знаний.
Цель данного курса перейти от репродуктивного уровня усвоения материала к творческому. Научить применять знания при выполнении нестандартных заданий. При решении таких задач школьники учатся мыслить логически, творчески. Это хороший материал для учебно-исследовательской работы, что является пропедевтикой научно-исследовательской деятельности.
Основная задача курса как можно полнее развить потенциальные творческие способности каждого слушателя, не ограничивая заранее сверху уровень сложности задачного материала. Решение задач способствует систематическому углублению изучаемого материала и развитию навыка решения сложных задач.
Основная цель данного курса – подготовить обучающихся таким образом, чтобы они смогли в жесткой атмосфере конкурсного экзамена успешно справиться с задачами, содержащими модули и параметры.
Воспитательное назначение курса
Обучение задачам с параметрами потребует от учащихся умственных и волевых усилий, развитого внимания, воспитания таких качеств, как активность, творческая инициатива, умений коллективно-познавательного труда.
Основные задачи данного курса:
углубить знания по математике, предусматривающие формирование у учащихся устойчивого интереса к предмету;
выявить и развить их математические способности;
расширить математические представления учащихся о приёмах и методах решения задач с модулями и параметрами;
повышение уровня математического и логического мышления учащихся;
развитие навыков исследовательской деятельности,
обеспечить подготовку к поступлению в вуз и продолжению образования;
обеспечить подготовку к профессиональной деятельности, требующей высокой математической культуры.
Работа элективного курса строится на принципах:
— научности;
— доступности;
— опережающей сложности;
— вариативности;
— самоконтроля.
Формы контроля
Рейтинг – таблица
Уроки самооценки и оценки товарищей
Презентация учебных проектов
О том, что учащийся должен будет представить учебный проект по теме курса, нужно проинформировать его заблаговременно, познакомив с формами такого рода деятельности. Для того чтобы урок-презентация получился интересным, виды проектов должны соответствовать уровню и интересам учащихся, а также должны быть интересными по форме и содержанию. Работы могут быть как индивидуальные, так и парные, групповые. Данный урок можно провести в виде конкурса, где победителей определят сами учащиеся. Административной проверки усвоения материала курса не предполагается, соответствующие задачи не будут включаться в административные контрольные работы. В технологии проведения занятий присутствует этап самопроверки, который представляет учащимся возможность самим проверить, как ими усвоен изучаемый материал. В свою очередь учитель может провести обучающие самостоятельные работы, которые позволят оценить уровень усвоения вопросов курса. Формой итогового контроля может стать обучающая самостоятельная работа, собеседование или тестовая работа.
Требования к уровню подготовки учащихся:
должны иметь элементарные умения решать задачи повышенного по сравнению с обязательным уровнем сложности;
точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач;
правильно пользоваться математической символикой и терминологией;
применять рациональные приемы тождественных преобразований;
использовать наиболее употребляемые эвристические приемы.
В результате изучения данного курса учащиеся
должны знать:
понятие параметра, прочно усвоить понятие модуль числа;
алгоритмы решений задач с модулями и параметрами;
зависимость количества решений неравенств, уравнений и их систем от значений параметра;
свойства решений уравнений, неравенств и их систем;
свойства функций в задачах с параметрами.
должны уметь:
уметь решать линейные, квадратные уравнения с модулем;
уметь решать линейные, квадратные неравенства с модулем;
строить графики уравнений, содержащие модули;
уметь решать линейные, квадратные, рациональные уравнения с параметром;
уметь решать неравенства с параметром;
находить корни квадратичной функции;
строить графики квадратичных функций;
исследовать квадратный трехчлен;
знать и уметь применять нестандартные приемы и методы решения уравнений, неравенств и систем.
Содержание курса
Решение задач с модулем (9 часов).
Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину. Уравнение и неравенства вида |х|= а, |ах+в|=0, |ах+в|≤0.
График функции у=|х|, у=| ах+в |. Построение графиков функций, связанных с модулем.
Методы решения уравнений вида: |ах+в|=с, где с — любое действительное число, |ах+в|=|сх+д|.
Графическое решение неравенства |ах+в|≤с, где с – любое действительное число.
Методы решения уравнений вида: |ах+в|+|сх+д|=т, |ах+в|+|сх+д|+пх=т. Методы решения неравенств вида: |ах+в|+|сх+д|<т,|ах+в|+| сх+д|+ пх>т.
Методы решения неравенств вида: |ах+в|≤| сх+д|, |ах+в|≥| сх+д|, |ах+в|≤ сх+д, |ах+в|≥ сх+д. Графическая интерпретация.
Квадратное уравнение, содержащее абсолютную величину. Метод замены переменной. Решение уравнений.
Решение задач с параметрами (7 часов).
Линейное уравнение с параметрами. Общий метод решения уравнения вида ах= в, решение линейных уравнений с параметрами, сводящихся к виду ах=в. Линейные неравенства с параметрами вида ах≤в, ах≥в.
Уравнения и неравенства с параметрами, сводящиеся к линейным.
Решение квадратных уравнений и неравенств с параметром.
Исследование квадратного трехчлена. Количество корней в зависимости от значений параметров.
Урок защиты проектов (1час).
Учебно-тематический план
Тема
Беседа, лекция
Сообщения
учащихся
Практикум
Творческое исследование
Конкурсы
Викторины
Тренажер
Формы
контроля
Решение задач с модулем (9ч)
1.
Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину. Уравнение и неравенства вида |х|= а, |ах+в|=0, |ах+в|≤0.
1 ч.
1 ч.
2.
Решение уравнений и неравенств различных видов, содержащих модули.
Графическая интерпретация.
1 ч.
1 ч.
1 ч.
1 ч.
3.
Квадратное уравнение, содержащее абсолютную величину. Метод замены переменной.
1 ч.
1 ч.
1 ч.
Сам. работа
Решение задач с параметрами (7ч)
4.
Линейное уравнение с параметрами. Общий метод решения уравнения вида ах= в, решение линейных уравнений с параметрами, сводящихся к виду ах=в.
1 ч.
1 ч.
5.
Линейные неравенства с параметрами вида ах≤в, ах≥в. Уравнения и неравенства с параметрами, сводящиеся к линейным.
1 ч.
1 ч.
6.
Решение квадратных уравнений и неравенств с параметром.
1 ч.
7.
Исследование квадратного трехчлена. Количество корней в зависимости от значений параметров.
1 ч.
1 ч.
Сам. работа
8.
Урок защиты проектов
1ч
Всего: 17ч
Список литературы
Голубев В.И., Гольдман А.М., Дорофеев Г.В. «О параметрах – с самого начала».
Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. «Необходимые условия в задачах с параметрами».
Дорофеев Г.В. «Квадратный трёхчлен в задачах».
Литвиненко В.Н., Мордкович А. Г. Практикум по решению математических задач.
Марков В.К. «Метод координат и задачи с параметрами».
Родионов Е.М. Решение задач с модулями и параметрами. Пособие для поступающих в вузы.
Шарыгин И.Ф. «Факультативный курс по математике. Решение задач».
Ястрибинецкий Г.А Задачи с параметрами.
Приложение
Календарно-тематическое планирование
п\п
Тема
К-во
часов
Дата
план
Дата
факт
1.
Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину. Уравнение и неравенства вида |х|= а, |ах+в|=0, |ах+в|≤0.
1
2.
Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину. Уравнение и неравенства вида |х|= а, |ах+в|=0, |ах+в|≤0.
1
3.
Решение уравнений и неравенств различных видов, содержащих модули.
Графическая интерпретация.
1
4.
Решение уравнений и неравенств различных видов, содержащих модули.
Графическая интерпретация.
1
5.
Решение уравнений и неравенств различных видов, содержащих модули.
Графическая интерпретация.
1
6.
Решение уравнений и неравенств различных видов, содержащих модули.
Графическая интерпретация.
1
7.
Квадратное уравнение, содержащее абсолютную величину.
Метод замены переменной. Решение уравнений.
1
8.
Квадратное уравнение, содержащее абсолютную величину.
Метод замены переменной. Решение уравнений.
1
9.
Квадратное уравнение, содержащее абсолютную величину.
Метод замены переменной. Решение уравнений.
1
10.
Линейное уравнение с параметрами. Общий метод решения уравнения вида ах= в, решение линейных уравнений с параметрами, сводящихся к виду ах=в.
1
11.
Линейное уравнение с параметрами. Общий метод решения уравнения вида ах= в, решение линейных уравнений с параметрами, сводящихся к виду ах=в.
1
12.
Линейные неравенства с параметрами вида ах≤в, ах≥в. Уравнения и неравенства с параметрами, сводящиеся к линейным.
1
13.
Линейные неравенства с параметрами вида ах≤в, ах≥в. Уравнения и неравенства с параметрами, сводящиеся к линейным.
1
14.
Решение квадратных уравнений и неравенств с параметром.
1
15.
Исследование квадратного трехчлена. Количество корней в зависимости от значений параметров.
1
16.
Исследование квадратного трехчлена. Количество корней в зависимости от значений параметров.
1
17.
Урок защиты проектов
1
infourok.ru
Решение задач с модулем и параметром
Принята Утверждена
на заседании приказом директора
педагогического совета МКОУ Черноземная СОШ
МКОУ Черноземная СОШ от _________20 г №_____
от г Директор школы:_________
протокол № /Гревцев В.Т./
Рабочая программа
по элективному курсу
«Задачи с модулями и параметрами»
для учащихся 9 класса
Колесниковой Елены Федоровны
учителя I квалификационной категории
МКОУ Черноземная СОШ
Калачеевского муниципального района
Воронежской области
Пояснительная записка
Основная функция курса по выбору направлена на повышение интереса к математике. Общеизвестно, что на вступительных экзаменах в ВУЗы довольно часто предлагаются задачи с параметрами, которые содержатся также в заданиях ГИА и ЕГЭ по математике. Нередко учащиеся не могут справиться с простейшими задачами, содержащими параметры и модули, что свидетельствует об отсутствии у части их навыков решения такого типа задач. Известно, что в программах по математике для неспециализированных школ этим задачам отводится совсем незначительное место.
Элективный курс «Задачи с модулями и параметрами» предназначен для предпрофильной подготовки учащихся 9 классов общеобразовательной школы. Данный элективный курс направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого класса задач. Он расширяет и углубляет отдельные темы базовых общеобразовательных программ по математике, не нарушая ее целостности, а также предполагает изучение некоторых тем, выходящих за их рамки. Навыки в решении уравнений, неравенств, содержащих модуль и параметры, совершенно необходимы любому ученику, желающему хорошо подготовиться к сдаче экзаменам и поступлению в дальнейшем в высшие учебные заведения. Программа элективного курса применима для различных групп школьников, независимо от выбора их будущей профессии, профиля в старшей школе. Курс рассчитан на 35 часов.
Наряду с основной задачей обучения математики — обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющего в определённых умственных навыках. В процессе решения задач с параметрами и модулями в арсенал приёмов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ, классификация и систематизация, аналогия.
Именно задачи с параметрами обладают диагностической и прогностической ценностью, которые позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Задачи, предлагаемые в данном курсе, интересны и часто не просты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике. Вместе с тем, содержание курса позволяет ученику любого уровня активно включаться в учебно-познавательный процесс и максимально проявить себя.
При решении таких задач школьники учатся мыслить логически, творчески. Это хороший материал для учебно-исследовательской работы, что является пропедевтикой научно-исследовательской деятельности.
Курс разработан следующим образом. Учащиеся на нескольких уроках знакомятся на уровне формулировок и иллюстраций с основными понятиями, которые на каждом уроке закрепляются при решении задач. В конце каждого занятия для работы дома предлагается несколько задач, часть из них имеет одинаковое решение с классными задачами, а одна или две требуют понимания изложенного материала. Таким образом, достигается дифференциация учашихся. После изложения всего материала предлагается 1-2 урока решения задач по всей теме, затем дифференцированное домашнее задание. Завершает тему зачетный урок, на котором вновь каждый учащийся в составе группы, равного с ним уровня усвоения материала, получает индивидуальное задание. Обязательно контролируется решение домашних задач, тестирование, контрольные и самостоятельные работы.
Основной упор делается не на изложение теоретического материала (он для большей части учашихся, посещающих курс по выбору, очень труден для понимания и усвоения), а на формирование навыков решения задач простейшего и повышенного уровня (дифференцированно) и развитие логического мышления. В данном курсе не будут излагаться строгие доказательства вводимых формул. Предполагается, что «правдоподобные рассуждения» и аналогии являются достаточно убедительными и будут легче восприняты. Строгие доказательства (если они окажутся необходимыми) лучше отложить для индивидуальной работы с одаренными учащимися. Основной методический прием заключается в использовании задач для выяснения математической сути в рассматриваемых ситуациях. Использование задач с различной фабулой позволяет обратить внимание учащихся на то, что в этих задачах общего с математической точки зрения.
Цели курса:
изучение методов решения задач избранного класса и формирование умений, направленных на реализацию этих методов;
восполнить некоторые содержательные пробелы основного курса.
продолжить формирование качеств мышления, необходимых человеку для жизни в современном обществе.
сформировать у учащихся представление о задачах с параметрами и модулем как задачах исследовательского характера, показать их многообразие;
научить применять аналитический метод в решении задач с параметрами и модулем;
научить приемам выполнения изображений на плоскости и их использованию в решении задач с параметрами и модулем;
научить осуществлять выбор рационального метода решения задач и обосновывать сделанный выбор;
способствовать подготовке учащихся к успешной сдаче ГИА и ЕГЭ, к вступительному экзамену по математике.
перейти от репродуктивного уровня усвоения материала к творческому. Научить применять знания при выполнении нестандартных заданий.
Задачи курса:
Образовательные:
формирование у учащихся умений решать нестандартные задания;
углубить знания по математике, предусматривающие формирование у учащихся устойчивого интереса к предмету;
расширить математические представления учащихся о приёмах и методах решения задач с модулями и параметрами;
обеспечить подготовку к поступлению в вуз и продолжению образования;
обеспечить подготовку к профессиональной деятельности, требующей высокой математической культуры.
Развивающие:
выявить и развить математические способности, продолжить развитие математической культуры;
как можно полнее развить потенциальные творческие способности каждого учащегося;
повышение уровня математического и логического мышления учащихся;
развитие навыков исследовательской деятельности.
Воспитательные:
обучение задачам с параметрами потребует от учащихся умственных и волевых усилий, развитого внимания;
воспитание таких качеств, как активность, творческая инициатива, умений коллективно-познавательного труда.
Работа элективного курса строится на принципах:
— научности;
— доступности;
— опережающей сложности;
— вариативности;
— самоконтроля.
Формы и методы обучения.
1) Использование лекции учителя (если материал неизвестен школьникам), которая сопровождается записью учащимися основных её положений. Полезно заранее записать план сообщения учителя.
2) При знакомстве с материалом, частично известным, используется составление конспекта, умение собирать материал по теме из печатных источников (по указанию учителя).
3) Самостоятельная работа по опорным конспектам при изучении нового материала.
4) Для закрепления новых знаний используются такие формы работы:
— дифференцированное домашнее задание;
— толкование новых терминов.
5) При повторении материала использовать групповую работу по интересам, индивидуальную повышенной сложности.
6) Тестирование (задания для тестирования давать дифференцированно).
Формы контроля
Ø Рейтинг – таблица
Ø Уроки самооценки и оценки товарищей
Ø Самостоятельные работы
Ø Презентация учебных проектов (индивидуальные, групповые, коллективные)
Ø Тестирование
Ø Контрольные работы
Ø собеседование
Требования к уровню подготовки учащихся:
должны иметь элементарные умения решать задачи повышенного по сравнению с обязательным уровнем сложности;
точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач;
правильно пользоваться математической символикой и терминологией;
применять рациональные приемы тождественных преобразований;
использовать наиболее употребляемые эвристические приемы.
В результате изучения данного курса учащиеся
должны знать:
понятие параметра
прочно усвоить понятие модуль числа;
алгоритмы решений задач с модулями и параметрами;
зависимость количества решений неравенств, уравнений и их систем от значений параметра;
свойства решений уравнений, неравенств и их систем;
свойства функций в задачах с параметрами.
должны уметь:
уметь решать линейные, квадратные уравнения с модулем;
уметь решать линейные, квадратные неравенства с модулем;
строить графики уравнений, содержащие модули;
уметь решать линейные, квадратные, рациональные уравнения с параметром;
уметь решать неравенства с параметром;
находить корни квадратичной функции;
строить графики квадратичных функций;
исследовать квадратный трехчлен;
Компетенции при изучении курса.
Познавательные.
— Умение самостоятельно и мотивированно организовывать свою познавательную деятельность (от постановки цели до получения и оценки результата).
— Участие в организации и проведении учебно-исследовательской работы. Самостоятельное создание алгоритмов познавательной деятельности для решения задач творческого и поискового характера.
— Создание собственных текстов с использованием разнообразных средств.
Информационные.
— Поиск нужной информации по заданной теме в источниках различного типа.
— Извлечение необходимой информации из текстов, таблиц, графиков.
— Отделение основной информации от второстепенной.
— Передача содержания информации адекватно поставленной цели (сжато, полно, выборочно).
— Развернутое обоснование суждения, приведение обоснования (доказательства), примеров.
Коммуникативные.
— Владение навыками организации и участия в коллективной деятельности; восприятие иных мнений, объективное определение своего вклада в общий результат.
— Оценивание своего поведения в группе, выполнение требований в совместной практической деятельности.
— Умение отстаивать свою точку зрения.
— Развитие готовности к сотрудничеству.
Содержание обучения
1.Решение задач с модулем. (12 часов).
1)Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину. Преобразование выражений, содержащих модуль.
2)Решение уравнений и неравенств вида |х|= а, |ах+в|=0, |ах+в|≤0.
3)Графики функций, содержащих модули. Построение графиков функций вида у=|f(х)|, у=| ах+в|, y= f|x|, |y| =f(x) b |y|=|f(x). Построение графиков функций, связанных с модулем.
4)Методы решения уравнений вида: |ах+в|=с, где с — любое действительное число, |ах+в|=|сх+д|.
5)Графическое решение неравенства |ах+в|≤с, где с – любое действительное число.
6)Методы решения уравнений вида: |ах+в|+|сх+д|=т, |ах+в|+|сх+д|+пх=т. Методы решения неравенств вида: |ах+в|+|сх+д|<т,|ах+в|+| сх+д|+ пх>т.
7)Методы решения неравенств вида: |ах+в|≤| сх+д|, |ах+в|≥| сх+д|, |ах+в|≤ сх+д, |ах+в|≥ сх+д. Графическая интерпретация.
8)Квадратное уравнение, содержащее абсолютную величину. Метод замены переменной. Решение уравнений.
2.Решение задач с параметрами. (13 часов).
1)Понятие параметра. Что значит — решить уравнение или неравенство с параметрами. Что значит — исследовать уравнение (определить количество решений, найти положительные решения и т.д.), содержащее параметры.
2)Линейное уравнение с параметрами. Общий метод решения уравнения вида ах= в, решение линейных уравнений с параметрами, сводящихся к виду ах=в. Линейные уравнения с параметрами, содержащие дополнительные условия (корень равен данному числу, прямая проходит через точку с заданными координатами, уравнение имеет отрицательное решение и т.д.).
3)Линейные неравенства с параметрами вида ах≤в, ах≥в.
4)Уравнения и неравенства с параметрами, сводящиеся к линейным.
5)Решение квадратных уравнений и неравенств с параметром. Исследование квадратного трехчлена.
6)Количество корней в зависимости от значений параметров. Параметр, как фиксированное число.
3. Нестандартные методы и приемы решения уравнений, неравенств и систем, содержащих модули и параметры. (10 часов).
1)Графические и аналитические методы. Классификация задач. Ответ, как наперёд заданное подмножество множество действительных чисел. Параметр, как равноправная переменная. Свойства решений уравнений, неравенств и их систем.
2)Свойства функций в задачах с параметрами и модулями. Схема исследования функций. Область значений функции. Подстановки. Экстремальные свойства функций. Метод оценки. Свойства монотонных функций.
Календарно-тематическое планирование
Тема занятия
Кол-во часов
Форма контроля
Дата проведения
План
Факт
Решение задач с модулем 12ч
1
Модуль действительного числа. Геометрическая интерпретация. Линейное уравнение, содержащее абсолютную величину
1
2
Уравнение и неравенства вида |х|=а, |ах+в|=0, |ах+в|≤0, |ах+в|≥0
1
3-4
График функции у=|f(х)|, у=|ах+в| и др. построение графиков функций, связанных с модулем
2
с/р
5-8
Решение уравнений и неравенств различных видов, содержащих модули. Графическая интерпретация.
4
с/р
9-11
Квадратное уравнение, содержащее абсолютную величину. Метод замены переменной. Решение уравнений.
3
конкурс
12
Контрольное тестирование
1
тест
Решение задач с параметрами 13ч
13
Понятие параметра
1
14-15
Линейное уравнение с параметрами. Общий метод решения уравнения вида ах=в, решение линейных уравнений с параметрами, сводящихся к виду ах=в
2
16-17
Линейные неравенства с параметрами вида ах≥в, ах≤в
2
с/р
18-19
Уравнения и неравенства с параметрами, сводящиеся к линейным
2
с/р
20-22
Решение квадратных уравнений и неравенств с параметром. Исследование квадратного трехчлена
3
собеседо вание
23-24
Количество корней в зависимости от значений параметров
2
с/р
25
Контрольное тестирование
1
тест
Нестандартные методы и приемы решения уравнений, неравенств и систем, содержащих модули и параметры 10ч
26-27
Графические и аналитические методы. Классификация задач
2
с/р
28-30
Свойства решений уравнений, неравенств и их систем
3
с/р
31-32
Свойства функций в задачах с параметрами и модулями
2
презентация проектов
33
Итоговая контрольная работа
1
к/р
34-35
Резервный урок
2
Перечень учебно- методических средств
Литература для учащихся
Алгебра. 9 класс. Пособие для самостоятельной подготовки к итоговой аттестации 2006. под ред. Ф.Ф.Лысенко, Ростов-на-Дону, изд. «Легион», 2009г.
Виленкин Н.Я.и др. «Алгебра и математический анализ» учебное пособие для уч-ся школ и классов с углублен. изуч. матем.» . М., «Просвещение», 1995
Галицкий М.Л., Гольдман А.М., Звавич Л.И. «Сборник задач по алгебре 8-9». -М. «Просвещение», 2001
Кузнецова Л.В. и др. «Алгебра. Сборник заданий для подготовки к ГИА в 9 классе», М., «Просвещение», 2009
Лаппо, Л.Д. ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ: учебно-методическое пособие / Л.Д. Лаппо, М.А. Попов. — М.: «Экзамен», 2010
Макарычев Ю.Н. и др.«Алгебра 8. Алгебра 9. Дополнительные главы к школьному учебнику».- М. «Просв-е», 2001.
Литература для учителя
Литвиненко В.Н., Мордкович А. Г. «Практикум по решению математических задач.»,М., «Просвещение», 1995
Ястрибинецкий Г.А. «Задачи с параметрами», М., «Дрофа», 2003
Шарыгин И.Ф. «Факультативный курс по математике. Решение задач».
Рязановский А.Р. «Алгебра и начала анализа: 500 способов и методов решения задач по математике для школьников и поступающих в вузы», М., «Дрофа», 2001
Электронные приложения
— Электронный практикум по теме «Параметры» из коллекции ОМС и Единой коллекции ЦОР
— Сайты ФЦИОР http://eor.edu.ru/ , http://fcior.edu.ru/,
— http://www.college.ru/ (Открытый колледж) ,
— http://www.school.edu.ru/default.asp (Российский общеобразовательный портал)
— сайт «Открытый класс» (Сетевые образовательные сообщества) http://www.openclass.ru/collection
— Диск «Функции и графики» из серии «Открытая математика» изд. ООО«Физикон», Москва
— Диск «Математика 5-11 классы. Практикум», «1С: Школа», Москва
— Диск «ЕГЭ 2008. Математика. Интенсивный тренинг-курс.», «ЭКСМО»,М., ФИПИ
— On-line тестирование на сайтах http://uztest.ru , http://fipi.ru
infourok.ru
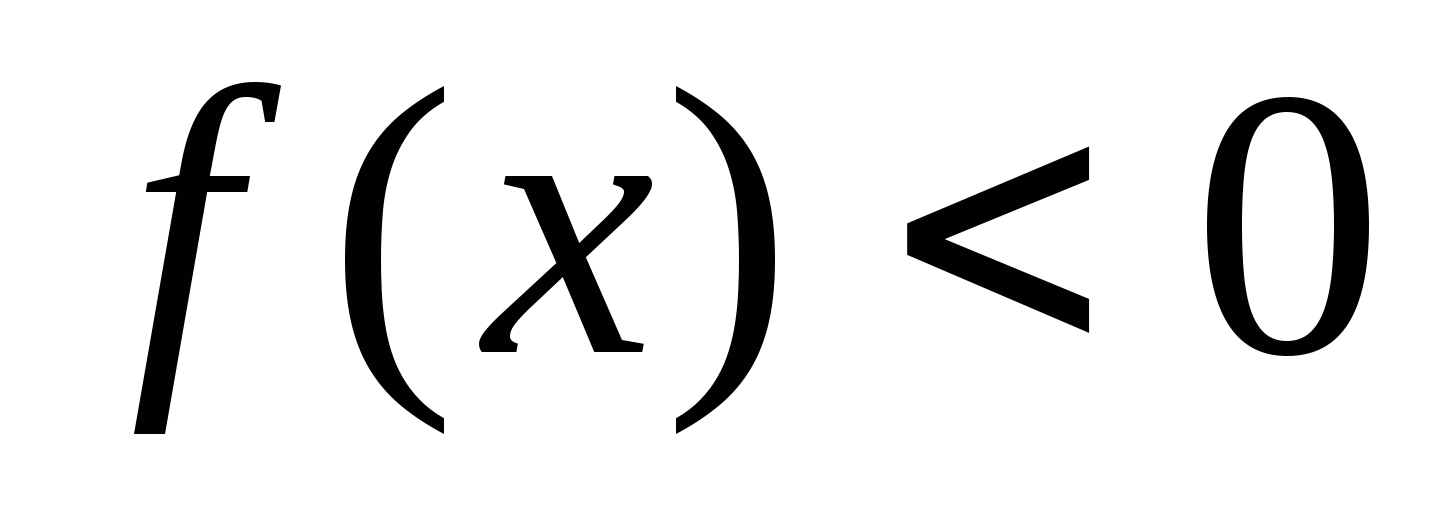 , строим кривые симметричные построенным относительно оси абсцисс.
, строим кривые симметричные построенным относительно оси абсцисс.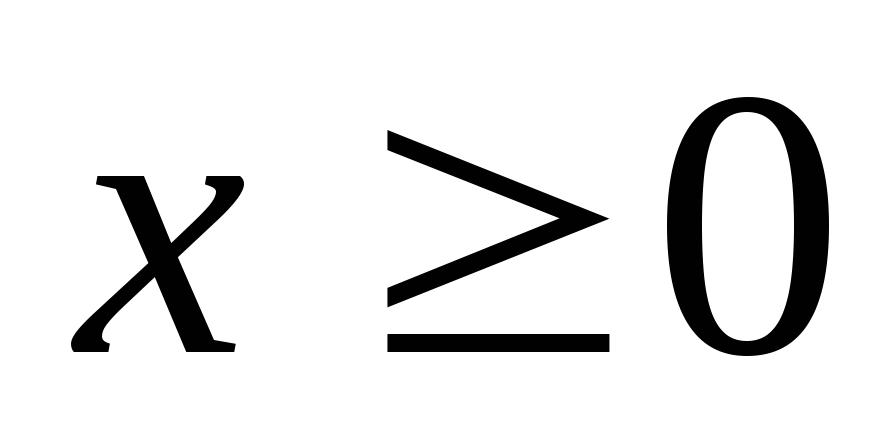 .
.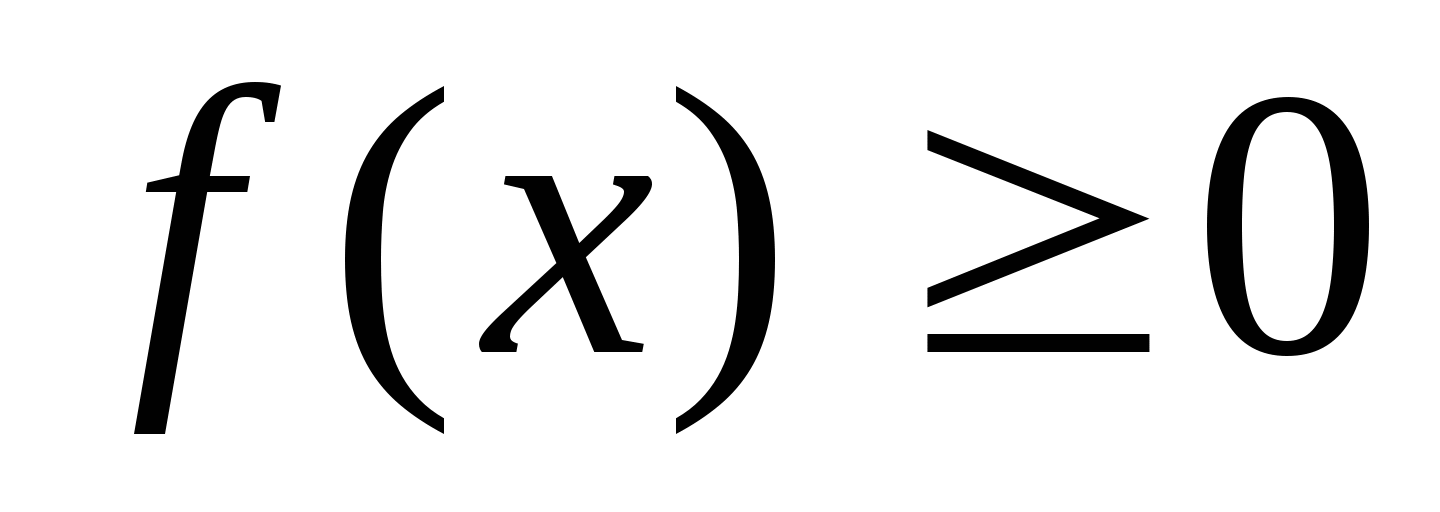 .
.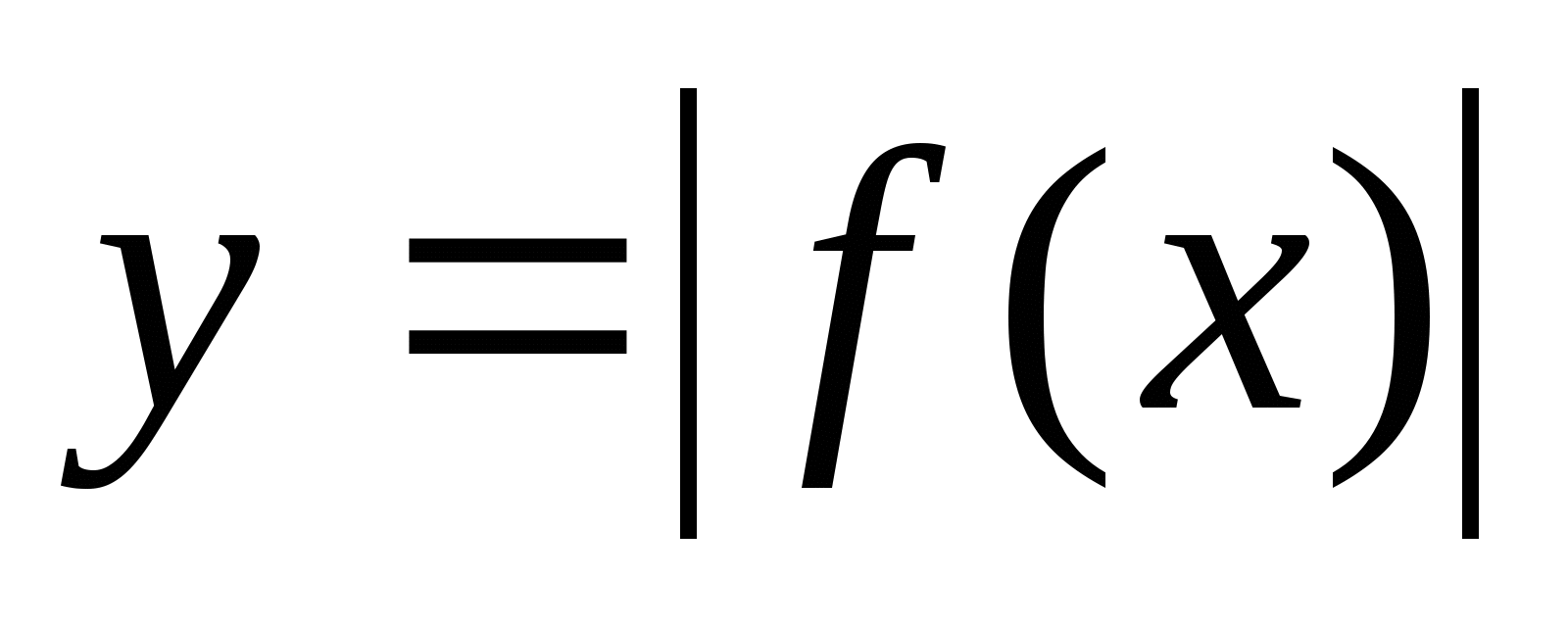 (он весь расположен в верхней полуплоскости).
(он весь расположен в верхней полуплоскости).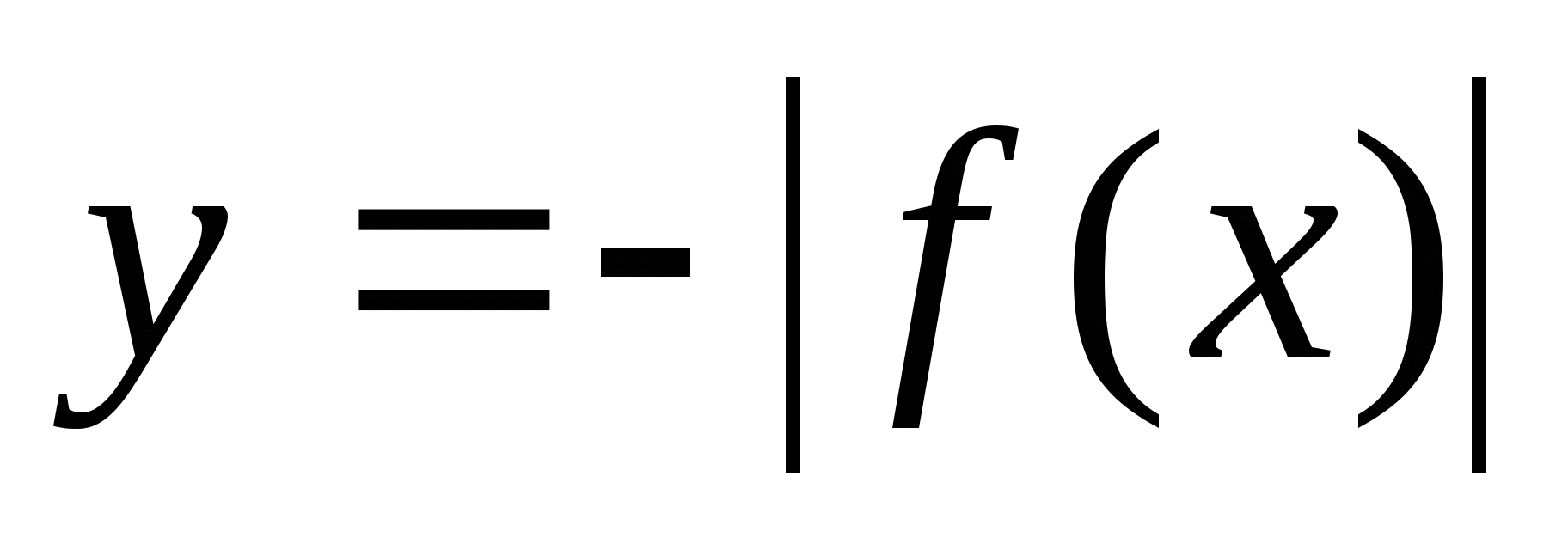 . Он будет симметричен построенному относительно оси ОХ.
. Он будет симметричен построенному относительно оси ОХ.