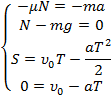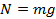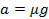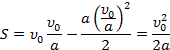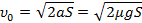Решение задач по теме «Прямолинейное равномерное и неравномерное движение»
Давайте рассмотрим две задачи, причем решение одной из них – в двух вариантах.
Условие
Самолет, летящий со скоростью 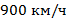 , совершает посадку. Время до полной остановки самолета
, совершает посадку. Время до полной остановки самолета 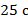 . Необходимо определить длину взлетной полосы.
. Необходимо определить длину взлетной полосы.
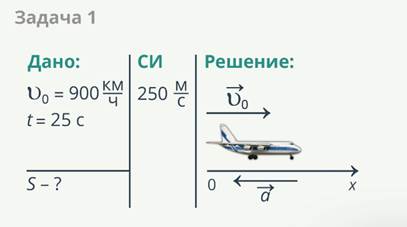
Рис. 1. К условию задачи 1
Решение
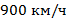 надо перевести в СИ, т. обр. начальная скорость самолета при посадке
надо перевести в СИ, т. обр. начальная скорость самолета при посадке 
На рисунке ускорение имеет направление против оси 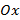 , тем самым мы должны понимать, что проекция ускорения на ось
, тем самым мы должны понимать, что проекция ускорения на ось 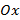 будет иметь отрицательное значение.
будет иметь отрицательное значение.
В данном случае движение прямолинейное (в одну сторону), поэтому модуль перемещения равен пройденному пути и определяется по формуле Галилея:
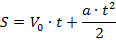
Чтобы решить окончательно эту задачу, надо определить ускорение:
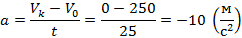
Обратите внимание, что ускорение получилось со знаком минус. В данном случае мы понимаем, что движение замедленное. Скорость с течением времени уменьшается.
Стоит сделать акцент на том, что в решении мы не использовали обозначение векторов. Вспомните: в начале рассуждения мы уже нарисовали рисунок, где точно поставили направление векторных величин, связанных с выбранной системой отсчета, т. е. с осью 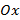 . Подставляем в формулу, в уравнение движения Галилея, все нам известные величины:
. Подставляем в формулу, в уравнение движения Галилея, все нам известные величины:
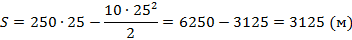
Ответ: .
.
Вторая задача, которую мы рассмотрим, несколько сложнее.
Условие
Автобус начинает свое дви
interneturok.ru
Задачи. Равноускоренное движение — PhysBook
Уровень А
1. Куда направлены ускорения следующих тел:
а) у поезда, который начинает тормозить;
б) у поезда, который отходит от станции?
Решение
2. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?
Рис. 1.
Решение
3. Скорость движения автомобиля за 40 с возросла от 5 м/с до 15 м/с. Определите ускорение автомобиля.
Решение
4. С каким ускорением двигался автобус, если, трогаясь с места стоянки, он развил скорость 15 м/с за 50 с?
Решение
5. Двигаясь со скоростью 72 км/ч, мотоциклист притормозил и через 20 с достиг скорости 36 км/ч. С каким ускорением он тормозил?
Решение
6. Поезд подходит к станции со скоростью 21,6 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?
Решение
7. В начале измерения скорость тела равнялась 5 м/с и направлена была на север. Через 50 с измерения показали, что тело двигается со скоростью 15 м/с на юг. Считая движения тела равноускоренным прямолинейным, определите его ускорение.
Решение
8. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с2. Через сколько времени он приобретет скорость 54 км/ч?
Решение
9. Через сколько времени останавливается автобус, если его начальная скорость 20 м/с, а ускорение 1,25 м/с2?
Решение
10. Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
Решение
11. Какую скорость приобретает отходящий от станции поезд через 7 с от начала движения, если его ускорение равно 0,9 м/с2?
Решение
12. Какую скорость приобретает автомобиль при торможении с ускорением 0,5 м/с2 через 10 с от начала торможения, если начальная скорость его была равна 72 км/ч?
Решение
13. Определите скорость тела при торможении с ускорением 0,2 м/с2 через 30 с от начала торможения, если начальная скорость его была равна 2 м/с.
Решение
14. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался с ускорением 9,8 м/с2?
Решение
15. Тело движется прямолинейно равнозамедленно с начальной скоростью 10 м/с и ускорением 2 м/с2. Определите перемещение тела через 5 с после начала движения.
Решение
16. Чтобы оторваться от земли, самолет должен набрать скорость 180 м/с. На каком расстоянии от места старта на взлетной полосе самолет достигает этого значения скорости, если его ускорение постоянно и равно 2,5 м/с2?Решение
17. Пассажирский поезд тормозит с ускорением 0,2 м/с2. На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 54 км/ч?
Решение
18. Автобус движется со скоростью 36 км/ч. На каком расстоянии от остановки водитель должен начать тормозить, сообщая автобусу ускорение, не превышающее 1,2 м/с2?
Решение
19. Автомобиль движется прямолинейно с постоянным ускорением 2,0 м/с2, имея в данный момент скорость 10 м/с. Где он был 4,0 с назад?
Решение
20. Поезд, движущийся после начала торможения с ускорением 0,40 м/с2, через 15 с имел скорость 10 м/с. Найдите пройденный путь за это время.
Решение
21. Снаряд, летящий со скоростью 1000 м/с, пробивает стенку блиндажа за 0,001 с, и после этого его скорость оказывается равной 200 м/с. Считая движение снаряда в толще стенки равноускоренным, найдите ее толщину.
Решение
22. После старта гоночный автомобиль достиг скорости 360 км/ч за 25 с. Какое расстояние он прошел за это время?
Решение
23. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найдите тормозной путь.
Решение
Уровень B
1. Шарик скатывается по желобу длиной 1,25 м с ускорением 1,6 м/с2. Какова скорость шарика в конце жалоба?
Решение
2. Хоккейная шайба пересекла ледяное поле длиной 60 м за 3,0 с и остановилась. Какая скорость была сообщена шайбе клюшкой хоккеиста?
Решение
3. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с 2, пройдет 30 м?
Решение
4. Самолет при отрыве от земли имеет скорость 252 км/ч и пробегает по бетонированной дорожке расстояние 700 м. Сколько времени продолжает разбег самолет? Движение считайте равноускоренным.
Решение
5. Ножной тормоз грузового автомобиля считается исправным если при торможении автомобиля, движущегося со скоростью 30 км/ч по сухой и ровной дороге, тормозной путь не превышает 9,0 м. Найдите соответствующее этой норме тормозное ускорение.
Решение
6. При какой начальной скорости поезд пройдет путь 1260 м в течении 60 с, замедляя ход с ускорением 1,5 м/с2?
Решение
7. Электропоезд тормозит с ускорением 0,40 м/с2. Определите, за какое время он остановится, если тормозной путь равен 50 м.
Решение
8. Лифт Останкинской телевизионной башни заканчивает свое движение после прохождения 49 м за 14 с. Найдите ускорение и начальную скорость лифта.
Решение
9. Поезд, двигаясь с горы с ускорением 0,2 м/с2, прошел путь 340 м и развил скорость 19 м/с. Сколько времени двигался поезд и какой была его скорость в начале отсчета?
Решение
10. Поезд, движущийся после начала торможения с ускорением 0,40 м/с2, через 25 с остановился. Найдите скорость в момент начала торможения и тормозной путь.
Решение
www.physbook.ru
Решение задач по теме «Равномерное движение»
План-конспект урока по теме «Решение задач по теме «Равномерное движение»»
Дата:
Тема: «Решение задач по теме «Равномерное движение»»
Цели:Образовательная: формирование практических умений по решению задач на тему «Равномерное движение»;
Развивающая: совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), развивать познавательный интерес;
Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.
Тип урока: обобщение и систематизация знаний
Оборудование и источники информации:
Исаченкова, Л. А. Физика : учеб. для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2015
Структура урока:
Организационный момент (5 мин)
Актуализация опорных знаний (5 мин)
Закрепление знаний(30 мин)
Итоги урока (5 мин)
Содержание урока
Организационный момент
Здравствуйте, садитесь! (Проверка присутствующих). Сегодня на уроке мы должны научиться решать задачи по теме «Равномерное движение». А это значит, что Тема урока: «Решение задач по теме «Равномерное движение»»
Актуализация опорных знаний
Дайте определение скорости равномерного прямолинейного движения.
Что показывает модуль скорости равномерного прямолинейного движения?
Как направлена скорость при равномерном прямолинейном движении?
Как зависит координата тела от времени при равномерном прямолинейном движении? Какой будет эта зависимость, если начальное положение тела совпадает с началом координат?
В каком случае проекция скорости движения будет отрицательной? Равной нулю?
Закрепление знаний
А сейчас перейдем к решению задач из сборника:
№ 58
Птица летит с постоянной скоростью, модуль которой v = 36 . За какой промежуток времени она преодолеет путь s = 200 м?
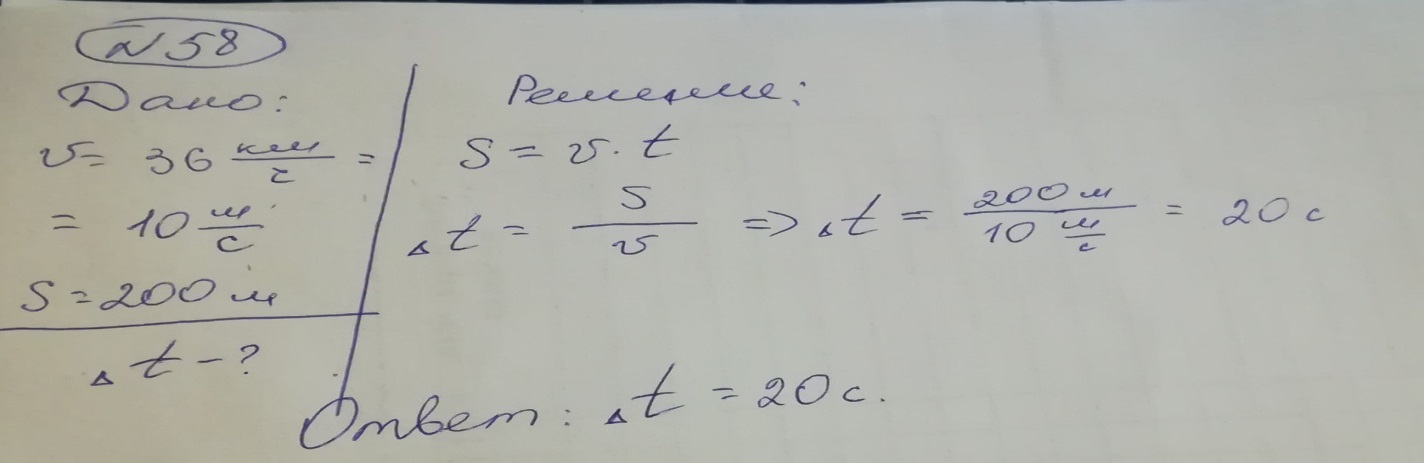
№ 59
Водитель легкового автомобиля, движущегося равномерно и прямолинейно со скоростью, модуль которой = 90 , отвлекся на время Δt = 2,0 с от дороги (смотрел в сторону). Какой путь за это время проехал автомобиль? Почему опасно отвлекать водителя во время движения?

№ 60
Электропоезд длиной = 150 м, движущийся равномерно со скоростью, модуль которой v = 45 , въезжает в тоннель длиной = 300 м. Через какой промежуток времени электропоезд полностью выйдет из тоннеля?
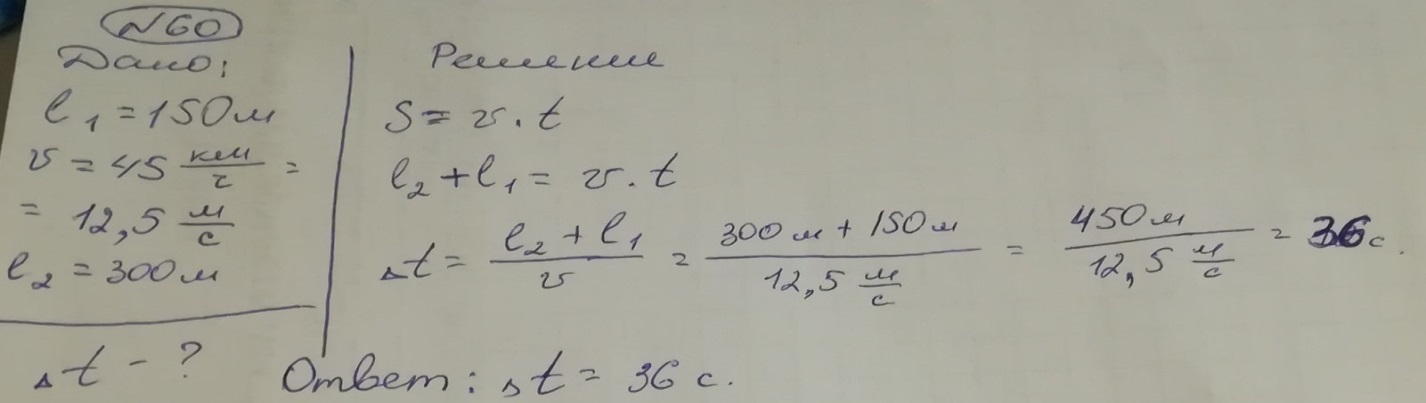
№ 61
Один из автомобилей, двигаясь со скоростью, модуль которой =18, в течение промежутка времени Δtt = 10 с совершил такое же перемещение, как и другой за промежуток времени Δt2 = 15 с. Определите модуль скорости движения другого автомобиля, если оба двигались равномерно.

№ 66
Два бегуна двигались по пересекающимся под углом = 60° прямым дорожкам со скоростями, модули которых равны. Через промежуток времени Δt = 30 с после их встречи в месте пересечения дорожек расстояние между бегунами стало = 90 м. Определите модуль скорости движения бегунов.

№ 73
Равномерное прямолинейное движение туриста относительно турбазы задано уравнением x = A + Bt, где А = 200 м, В = 2,5 . Определите начальную координату туриста и проекцию скорости его движения вдоль оси Ох.
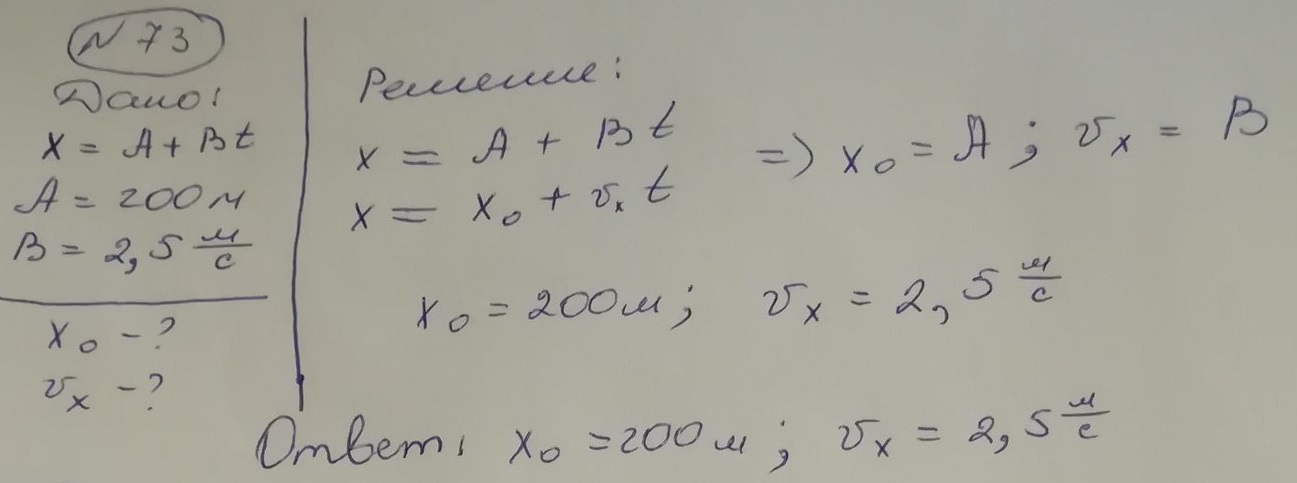
№ 75
Прямолинейное движение вдоль оси Ох лодки задано уравнением х = А + Bt, где А = 100 м, Б = 7,20. Чему равна проекция скорости движения лодки? Найдите координату лодки в момент времени t= 10,0 с.

№ 80
Начальная координата лыжника х0 = 200 м, проекция скорости его движения на ось Ох постоянна и равна = 36 . Запишите кинематический закон движения лыжника. Найдите по формуле и по графику координату лыжника в момент времени t = 5,0 с от начала движения.
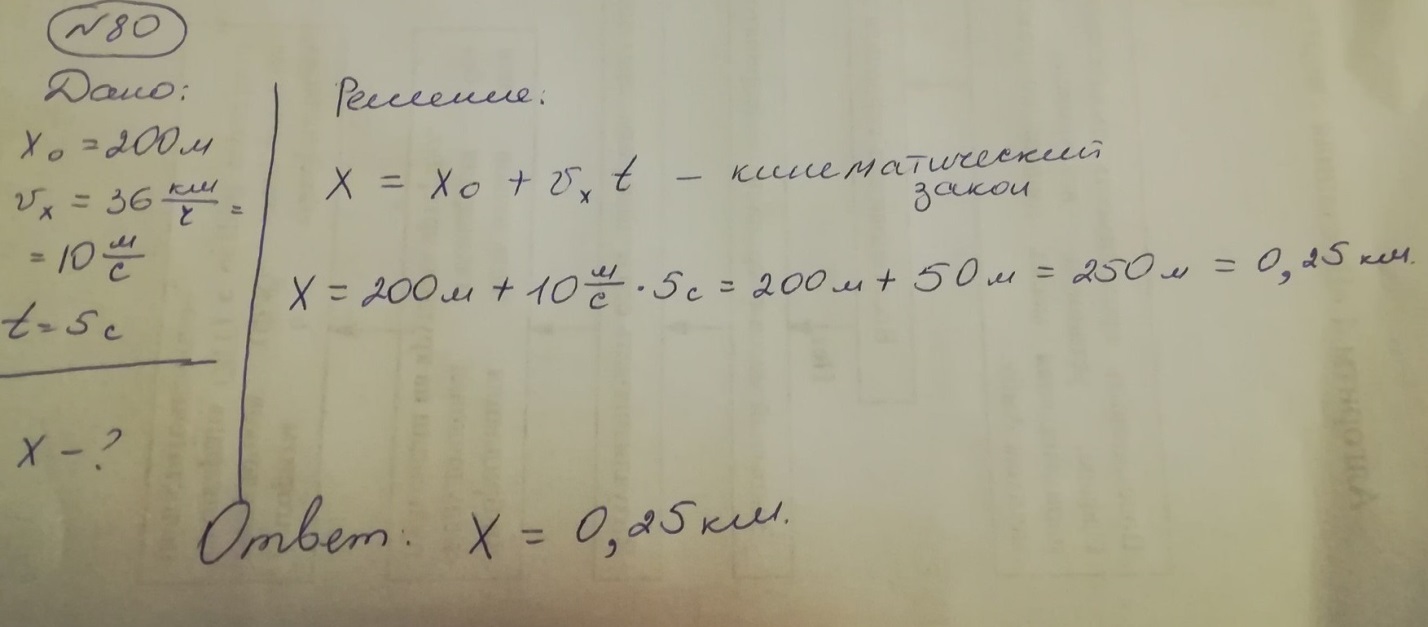
Закрепление знаний
Для равномерного прямолинейного движения график проекции скорости — прямая, параллельная оси времени.
Графики проекции перемещения и координаты — прямые, наклон которых к оси времени определяется проекцией скорости.
Площадь фигуры между графиком проекции скорости и осью времени определяет проекцию перемещения.
Итоги урока
Итак, подведем итоги. Что вы сегодня узнали на уроке?
Организация домашнего задания
§6,7,8, упр. 3 № 4, упр.4 № 3.
Рефлексия.
Продолжите фразы:
Сегодня на уроке я узнал…
Было интересно…
Знания, которые я получил на уроке, пригодятся
infourok.ru
Задачи на движение с ускорением свободного падения. Видеоурок. Физика 11 Класс
Этот урок посвящён решению задач на криволинейное движение с ускорением свободного падения. Они обычно связаны с движением тела, брошенного под углом к горизонту или горизонтально. Мы рассмотрим основные формулы для решения подобных заданий и решим три задачи различной сложности, взятые из сборника задач для подготовки к единому государственному экзамену
Задачи на криволинейное движение с ускорением свободного падения чаще всего представлены в ЕГЭ как задачи на движение тела, брошенного под углом к горизонту. Рассмотрим общий вид таких задач и формулы для их решения.
Из точки, расположенной на высоте h (см. Рис. 1), со скоростью 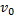 под углом к горизонту
под углом к горизонту 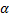 брошено тело.
брошено тело.
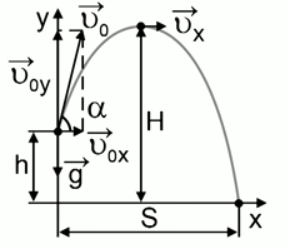
Рис. 1. Движение тела, брошенного под углом к горизонту
1. Для того чтобы узнать, как выглядит уравнение движения тела, нужно представить начальную скорость 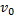 в виде составляющих:
в виде составляющих: 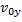 и
и 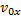 .
.
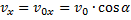
Скорость по оси x не меняется с течением времени, так как ускорение направлено по оси y (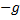 ) и имеет только одну составляющую. Следовательно, с течением времени изменяется скорость по оси y.
) и имеет только одну составляющую. Следовательно, с течением времени изменяется скорость по оси y.
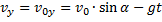
2. В решении таких задач также нужно пользоваться уравнением для координат.
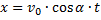 – уравнение равномерного движения
– уравнение равномерного движения
Координата y в выбранной системе координат изменяется по закону равнопеременного движения с отрицательным ускорением:
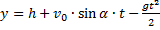
3. Модуль скорости равен:
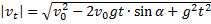
4. Уравнение траектории (зависимость координаты x от y):
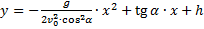 – уравнение параболы, ветви которой опущены вниз, смещённой по оси x в положительном направлении.
– уравнение параболы, ветви которой опущены вниз, смещённой по оси x в положительном направлении.
5. Время полёта (падения) тела:
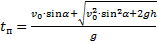
6. Дальность полёта:
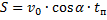
7. При 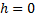 дальность полёта:
дальность полёта:
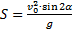
8. Наивысшая высота подъёма:
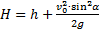
Снаряд вылетел из ствола со скоростью 200 м/с под углом 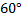 к плоскости горизонта. Определить дальность полёта снаряда. Ответ выразить в километрах.
к плоскости горизонта. Определить дальность полёта снаряда. Ответ выразить в километрах.
Дано: 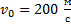 ;
; 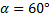 ;
; 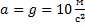 (см. Рис. 2)
(см. Рис. 2)
Найти: S
Решение
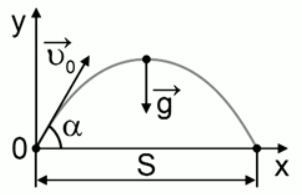
Рис. 2. Иллюстрация к задаче
В данной задаче начальная и конечная точка полёта снаряда лежат на одной высоте, поэтому воспользуемся следующей формулой дальности полёта:
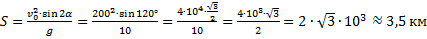
Ответ: 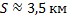
С вышки бросили камень в горизонтальном направлении. Через 2 с камень упал на землю на расстоянии 30 м от основания вышки. Определить конечную скорость камня.
Дано: 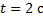 ;
; 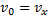 – начальная скорость имеет направление только по оси x;
– начальная скорость имеет направление только по оси x; 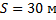 (см. Рис. 3)
(см. Рис. 3)
Найти: 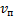
Решение
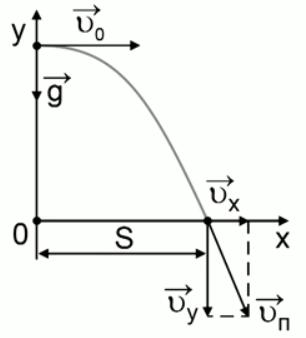
Рис. 3. Иллюстрация к задаче
Конечная скорость находится по следующей формуле (как модуль вектора):
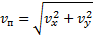
Скорость по оси x равна:
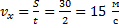
Начальной скорости по оси y не было, а далее она увеличивается с ускорением свободного падения:
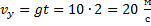
Следовательно:
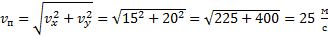
Ответ: 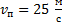
Мяч, брошенный под углом 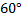 к горизонту, достиг максимальной высоты 17,3 м. Какова дальность полёта мяча?
к горизонту, достиг максимальной высоты 17,3 м. Какова дальность полёта мяча?
Дано: 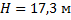 ;
; 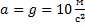 ;
; 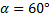 (рис. 4)
(рис. 4)
Найти: S
Решение
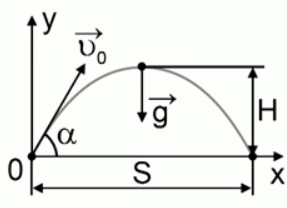
Рис. 4. Иллюстрация к задаче
H– максимальная высота подъёма, то есть высота, на которую тело поднимается и с которой падает.
Тело падает с высоты H за время 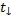 , которое равно времени подъёма
, которое равно времени подъёма 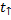 , следовательно:
, следовательно:
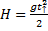
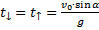
Поэтому:

Формула для дальности полёта:
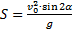
Отношение дальности полёта к максимальной высоте:
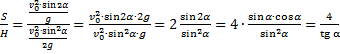
Следовательно:
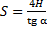
Полученную формулу дальности полёта можно использовать и в других задачах, в которых тело движется по симметричной траектории.
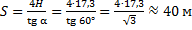
Ответ: 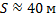
Домашнее задание
- Упражнение 4 (2, 3) стр. 43 – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы)
- Из точки А свободно падает тело. Одновременно из точки В под углом
 к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Показать, что угол
к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Показать, что угол  не зависит от начальной скорости
не зависит от начальной скорости  тела, брошенного из точки В, и определить этот угол, если
тела, брошенного из точки В, и определить этот угол, если  . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь. - С башни брошено тело в горизонтальном направлении со скоростью 40 м/с. Какова скорость тела через 3 с после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А.П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А.В. Пёрышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
- Орлов В.А., Демидова М.Ю., Никифоров Г.Г., Ханнанов Н.К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Eduspb.com (Источник).
- Интернет-портал Youtube.com (Источник).
- Интернет-портал Fizportal.ru (Источник).
interneturok.ru
Прямолинейное равноускоренное движение. Примеры решениЯ задач по физике. 9-10 класс
Прямолинейное равноускоренное движение. Примеры решениЯ задач по физике. 9-10 класс
Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Решение задач на прямолинейное равноускоренное движение. При решении задачи обязательно делаем чертеж, на котором показываем все вектора, о которых идет речь в задаче. В условии задачи, если не оговорено иное, даются модули величин. В ответе задачи также должен стоять модуль найденной величины.
Задача 1
Автомобиль, двигавшийся со скоростью 30 м/с, начал тормозить. Чему будет равна его скорость через 1 минуту, если ускорение при торможении равно 0,3 м/с2?
Обратите внимание! Проекция вектора ускорения на ось t отрицательна.
Задача 2
Санки начинают двигаться с горы с ускорением 2 м/с2. Какое расстояние они пройдут за 2 секунды?
Не забудьте в ответе перейти от проекции к модулю вектора ускорения!
Задача 3
Каково ускорение велосипедиста, если его скорость за 5 секунд изменилась от 7 до 2 м/с ?
Из условия задачи видно, что в процессе движения скорость тела уменьшается. Исходя из этого, определяем направление вектора ускорения на чертеже. В результате расчета должно получиться отрицательное значение вектора ускорения.
Задача 4
Санки начинают двигаться с горы из состояния покоя с ускорением 0,1 м/с2. Какую скорость будут они иметь через 5 секунд после начала движения?
Задача 5
Поезд, двигавшийся с ускорением 0,4 м/с2, через 20 секунд торможения остановился. Чему равен тормозной путь, если начальная скорость поезда 20 м/с ?
Внимание! В задаче поезд тормозит, не забудьте о минусе при подстановке числового значения проекции вектора ускорения.
Задача 6
Автобус, отходя от остановки, движется с ускорением 0,2 м/с2. На каком расстоянии от начала движения его скорость станет равной 10 м/с ?
Задачу можно решить в 2 действия.
Это решение аналогично решению системы из двух уравнений с двумя неизвестными. Как в алгебре: два уравнения — формулы для Vx и Sx, два неизвестных — t и Sx.
Задача 7
Какую скорость разовьет катер, пройдя из состояния покоя 200 метров с ускорением 2 м/с2?
Не забудьте, что не всегда все данные в задаче задаются числами!
Здесь надо обратить внимание на слова «из состояния покоя» — это соответствует начальной скорости, равной 0.
При извлечении корня квадратного: время может быть только больше 0!
Задача 8
При аварийном торможении мотоцикл, двигавшийся со скоростью 15 м/с, оставовился через 5 секунд. Найти тормозной путь.
Продолжение смотри здесь
class-fizika.ru
Примеры решения задач по теме «Равномерное прямолинейное движение»
Примеры решения задач по теме «Равномерное прямолинейное движение»
«Физика — 10 класс»
При решении задач по данной теме необходимо прежде всего выбрать тело отсчёта и связать с ним систему координат. В данном случае движение происходит по прямой, поэтому для его описания достаточна одна ось, например ось ОХ. Выбрав начало отсчёта, записываем уравнения движения.
Задача I.
Определите модуль и направление скорости точки, если при равномерном движении вдоль оси ОХ её координата за время t1 = 4 с изменилась от х1 = 5 м до х2 = -3 м.
Р е ш е н и е.
Модуль и направление вектора можно найти по его проекциям на оси координат. Так как точка движется равномерно, то проекцию её скорости на ось ОХ найдём по формуле
Отрицательный знак проекции скорости означает, что скорость точки направлена противоположно положительному направлению оси ОХ. Модуль скорости υ = |υх| = |-2 м/с| = 2 м/с.
Задача 2.
Из пунктов А и В, расстояние между которыми вдоль прямого шоссе l0 = 20 км, одновременно навстречу друг другу начали равномерно двигаться два автомобиля. Скорость первого автомобиля υ1 = 50 км/ч, а скорость второго автомобиля υ2 = 60 км/ч. Определите положение автомобилей относительно пункта А спустя время t = 0,5 ч после начала движения и расстояние I между автомобилями в этот момент времени. Определите пути s1 и s2, пройденные каждым автомобилем за время t.
Р е ш е н и е.
Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.14). Движение автомобилей будет описываться уравнениями
x1 = х01 + υ1xt, x2 = х02 + υ2xt.
Так как первый автомобиль движется в положительном направлении оси ОХ, а второй — в отрицательном, то υ1x = υ1, υ2x = —υ2. В соответствии с выбором начала координат х01 = 0, х02 = l0. Поэтому спустя время t
x1 = υ1t = 50 км/ч • 0,5 ч = 25 км;
х2 = l0 — υ2t = 20 км — 60 км/ч • 0,5 ч = -10 км.
Первый автомобиль будет находиться в точке С на расстоянии 25 км от пункта А справа, а второй — в точке D на расстоянии 10 км слева. Расстояние между автомобилями будет равно модулю разности их координат: l = |х2 — x1| = |—10 км — 25 км| = 35 км. Пройденные пути равны:
s1 = υ1t = 50 км/ч • 0,5 ч = 25 км,
s2 = υ2t = 60 км/ч • 0,5 ч = 30 км.
Задача 3.
Из пункта А в пункт В выезжает первый автомобиль со скоростью υ1 Спустя время t0 из пункта В в том же направлении со скоростью υ2 выезжает второй автомобиль. Расстояние между пунктами A и В равно l. Определите координату места встречи автомобилей относительно пункта В и время от момента отправления первого автомобиля, через которое они встретятся.
Р е ш е н и е.
Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.15). Движение автомобилей будет описываться уравнениями
x1 = υ1t, х2 = l + υ2( t — t0).
В момент встречи координаты автомобилей равны: х1 = х2 = хв. Тогда υ1tв = l + υ2( tв — t0) и время до встречи
Очевидно, что решение имеет смысл при υ1 > υ2 и l > υ2t0 или при υ1 < υ2 и l < υ2t0. Координата места встречи
Задача 4.
На рисунке 1.16 представлены графики зависимости координат точек от времени. Определите по графикам: 1) скорости точек; 2) через какое время после начала движения они встретятся; 3) пути, пройденные точками до встречи. Напишите уравнения движения точек.
Р е ш е н и е.
За время, равное 4 с, изменение координаты первой точки: Δx1 = 4 — 2 (м) = 2 м, второй точки: Δх2 = 4 — 0 (м) = 4 м.
1) Скорости точек определим по формуле υ1x = 0,5 м/с; υ2x = 1 м/с. Заметим, что эти же значения можно было получить по графикам, определив тангенсы углов наклона прямых к оси времени: скорость υ1x численно равна tgα1, а скорость υ2x численно равна tgα2.
2) Время встречи — это момент времени, когда координаты точек равны. Очевидно, что tв = 4 с.
3) Пути, пройденные точками, равны их перемещениям и равны изменениям их координат за время до встречи: s1 = Δх1= 2 м, s2 = Δх2 = 4 м.
Уравнения движения для обеих точек имеют вид х = х0 + υxt, где х0 = x01 = 2 м, υ1x = 0,5 м/с — для первой точки; х0 = х02 = 0, υ2x = 1 м/с — для второй точки.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»
class-fizika.ru
Решение задач по динамике. Движение по горизонтали и вдоль наклонной плоскости
Мы продолжаем изучать динамику. Это раздел физики, который изучает причины механического движения.
Сегодня мы займемся решением задач на движение по горизонтали и вдоль наклонной плоскости. Как решать такие задачи?
У нас есть тело, которое находится на горизонтальной или наклонной плоскости. На него в любом случае действует сила тяжести и сила реакции опоры. Если поверхность не гладкая, на тело действует сила трения, направленная против направления движения. Тело могут тащить за нить, в таком случае на него будет действовать сила натяжения нити. Наличие той или иной силы зависит от условия задачи, но равнодействующая всех сил, действующих на тело, в общем случае вызывает ускорение тела,  . Это следствие из второго закона Ньютона – главного инструмента решения задач по динамике.
. Это следствие из второго закона Ньютона – главного инструмента решения задач по динамике.
Итак, мы разобрали, что происходит при движении тела вдоль плоскости, определили действующие на тело силы и описали процесс математически, применив второй закон Ньютона. На этом физика заканчивается, и остается математика.
Решать уравнения в векторной форме математически сложно, поэтому нужно переписать следствие из второго закона Ньютона в проекциях на оси координат.
Если плоскость наклонная, она ориентирована под определенным углом к горизонту, а значит, сила тяжести будет направлена под углом к плоскости, знаем мы этот угол или нет. Это делает важным выбор системы координат.
Мы свободны в выборе, результат не будет зависеть от выбора системы координат, но нужно выбрать такую, при которой математические преобразования будут максимально простыми. Мы увидим это на примере одной из задач.
И только теперь, когда получена система уравнений, описывающая физический процесс, мы решаем задачу математически: решаем уравнения и находим неизвестное.
Приступим к решению задач.
Камень, скользивший по горизонтальной поверхности льда, остановился, пройдя расстояние S =48 м. Найдите начальную скорость  камня, если сила трения скольжения камня о лед составляет 0,06 силы нормального давления камня на лед.
камня, если сила трения скольжения камня о лед составляет 0,06 силы нормального давления камня на лед.
Анализ условия:
— в задаче описано тело, которое движется под действием сил, значит, будем применять второй закон Ньютона;
— на камень действует сила тяжести, сила реакции опоры и сила трения. Отметим их (см. рис. 1).
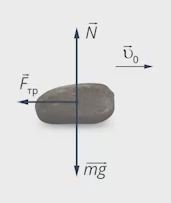
Рис. 1. Действующие на камень силы
— сила трения равна 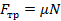 ;
;
— камень останавливается, движется с ускорением, которое по второму закону Ньютона вызвано равнодействующей силой;
-при равноускоренном движении тело проходит путь 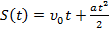 и приобретает скорость
и приобретает скорость 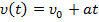 .
.
Решение
Выберем систему координат. Удобно направить ось х в направлении движения камня, а ось у перпендикулярно оси х (см. рис. 2).

Рис. 2. Выбор системы координат
Применим второй закон Ньютона:

Учитывая, что сила трения равна 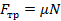 , запишем в проекциях на выбранные оси координат. Сила трения направлена против движения камня, туда же направлено и ускорение (камень замедляется) (см. рис. 3):
, запишем в проекциях на выбранные оси координат. Сила трения направлена против движения камня, туда же направлено и ускорение (камень замедляется) (см. рис. 3):
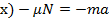
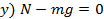
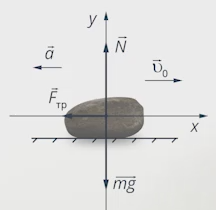
Рис. 3. Направление ускорения
За время остановки  камень по условию задачи пройдет расстояние
камень по условию задачи пройдет расстояние 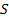 . Начальная скорость направлена в направлении оси х, ее проекция будет иметь знак «+», ускорение – против оси х, ставим знак «-»:
. Начальная скорость направлена в направлении оси х, ее проекция будет иметь знак «+», ускорение – против оси х, ставим знак «-»:
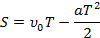
Тело остановится, то есть его скорость через время  будет равна нулю:
будет равна нулю:
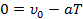
Получили систему уравнений, которую остается решить и получить начальную скорость камня, равную 7,6 м/с:
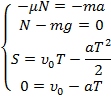
Математическая часть решения задачи
|
Выразим из второго уравнения силу реакции опоры:
Подставим ее в первое уравнение:
Выразим из четвертого уравнения время Т:
Подставим его в третье уравнение:
Выразим скорость и подставим найденное выше ускорение:
|
Теперь решим задачу на движение вдоль наклонной плоскости.
Тело массы m без начальной скорости соскальзывает с наклонной плоскости с углом 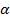 с высоты h (см. рис. 4).
с высоты h (см. рис. 4).
Рис. 4. Рисунок к условию задачи 2
Коэффициент трения тела о поверхность равен  . За какое время тело достигнет подножья?
. За какое время тело достигнет подножья?
Анализ условия
— Задан прямоугольный треугольник, в котором известна одна сторона и угол. Значит, известны все стороны, и определен путь, который проходит тело.
— На тело действуют сила тяжести, сила реакции опоры и сила трения (см. рис. 5).
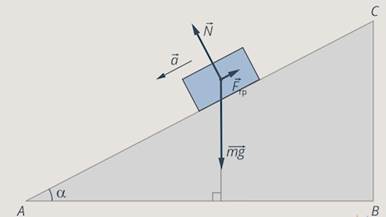
Рис. 5. Силы, которые действуют на тело
Равнодействующая этих сил создает ускорение – будем применять второй закон Ньютона.
— В задаче нужно найти время движения тела, которое движется с ускорением, равноускоренное движение описывается уравнениями кинематики.
Решение
Выберем систему координат. Здесь есть своя особенность: движение бруска происходит вдоль наклонной плоскости, сила трения направлена противоположно направлению движения, сила реакции опоры перпендикулярна плоскости, а сила тяжести направлена под углом к плоскости. Нам особенно важно выбрать удобную систему координат. Для математических расчетов удобно направить оси координат, как показано на рисунке: ось х вдоль в направлении движения бруска, ось у перпендикулярно поверхности (см. рис. 6).

Рис. 6. Выбор системы координат
Применим второй закон Ньютона:

Учитывая, что сила трения равна 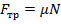 , запишем в проекциях на выбранные оси координат.
, запишем в проекциях на выбранные оси координат.
Сила тяжести направлена под углом к обеим осям координат. Треугольники АВС и авс подобны, и угол 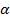 равен углу cab. Следовательно, проекция силы тяжести на ось х равна
равен углу cab. Следовательно, проекция силы тяжести на ось х равна 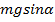 , на ось у –
, на ось у – 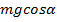 (см. рис. 7).
(см. рис. 7).

Рис. 7. Проекции сил на оси координат
Тогда:
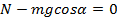
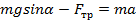
Нахождение проекций силы тяжести
interneturok.ru
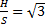 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.