ФИЗИКА: Задачи Закон всемирного тяготения — Ответы и решения
Задачи Закон всемирного тяготения с решениями
Формулы, используемые на уроках «Задачи закон всемирного тяготения».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. На каком расстоянии друг от друга находятся два одинаковых шара массами по 20 т, если сила тяготения между ними 6,67•10-5 Н?

Задача № 2. Масса Сатурна 5,7•1026 кг, а его радиус— 6•107 м. Определите ускорение свободного падения на Сатурне.

Задача № 3. Чему равно ускорение свободного падения на высоте над поверхностью Земли, равной двум ее радиусам?

Задача № 4. На какой высоте над поверхностью Земли сила тяготения в 2 раза меньше, чем на поверхности Земли?

Задача № 5. С какой силой притягивается к центру Земли тело массой m, находящееся в глубокой шахте, если расстояние от центра Земли до тела равно г? Плотность Земли считайте всюду одинаковой и равной р.

Задача № 6. Экипаж поднимающегося аэростата периодически проводит измерения ускорения свободного падения. На сколько уменьшилось значение g на высоте h = 6,4 км?

Ответ: на 0,02 м/с2
Задача № 7. Вычислите ускорение свободного падения и первую космическую скорость у поверхности Луны.

Задача № 8. Ракета стартует с Луны вертикально вверх с ускорением а = 20 м/с2. Сколько весит во время старта космонавт, масса которого m = 90 кг?

Задача № 9. (повышенной сложности) Во сколько раз сила притяжения между Луной и Солнцем больше, чем сила притяжения между Луной и Землей?

Краткая теория для решения Задачи Закон всемирного тяготения.

Это конспект по теме «ЗАДАЧИ закон всемирного тяготения с решениями». Выберите дальнейшие действия:
Сила тяжести. Задачи по физике Григория Остера — 7 класс
Сила тяжести. Задачи по физике Григория Остера — 7 класс
Посмейся и сообрази!
Перед тобой занимательные задачи по физике Григория Остера!
89. Почему американцы, которые живут прямо под нами на другой стороне земли, не сыплются с планеты как горох? И почему не сыплемся мы, когда вращающаяся земля переворачивается?
Ответ.Потому что и мы, и американчы, и земля — все взаимно притягиваемся друг к другу. Это называется всемирным тяготением. Вот почему нас всех так и тянет в Америку.
90. Масса листика, сорвавшегося с березы, — 0,1 г, а масса кота Яшки, размечтавшегося о птичках и сорвавшегося с той же самой березы, 10 кг. Во сколько раз сила тяжести, действующая на планирующий листик, меньше силы тяжести, действующей на планирующего кота?
Ответ. В 10000 раз. Во столько же раз, во сколько масса листика меньше массы кота. Птички считают, что это справедливо.
95. Как, не понимая ни бельмеса в физике, все-таки научиться вычислять действующую на тебя силу тяжести?
Ответ.Не снимая ботинок и не вынимая из карманов гайки и гвозди, встань на весы. Помотри, сколько килограммов весы показывают — это твоя масса. Не вес, а масса. Запомни, не ВЕС, а МАССА! Запомнил? Теперь быстро умножай свою массу на девять и восемь десятых. Только не спрашивай, зачем. Так надо! Умножил? Теперь припиши к тому что получилось буковку «н» и можешь хвастаться, что на тебя действует сила тяжести в столько-то ньютонов.
96. Массы голубого большого воздушного шарика и мелкого ржавого железного гвоздика, который мечтает этот шарик когда-нибудь проткнуть, одинаковы. Как отличаются силы тяжести, действующие на шарик и гвоздик?
Ответ.Никак не отличаются. Один голубой и воздушный, другой мелкий и ржавый. Ну и что? Массы у них одинаковы? Одинаковы! Значит одинаковы и действующие на обоих силы тяжести.
97. Перестала ли действовать сила тяжести на Вовочку, который уже долетел с крыши сарая до поверхности планеты Земля?
Ответ.Нет, не перестала. Хотя Вовочка и кричит, что лежачих не бьют.
100. Какая сила тяжести действует на один килограмм картошки, висящий у дяди Пети в авоське за окном?
Ответ.На этот килограмм, как и на всякое другое висящее за окошком тело массой в один килограмм, действует сила тяжести, равная 9,8 ньютонов.
101. Когда один килограмм картошки, висевший у дяди Пети за окном в авоське, сорвался и полетел вместе с авоськой вниз, скорость его под действием силы тяжести с течением времени все увеличивалась и увеличивалась. За что принимают физики силу, которая за 1 секунду изменяет скорость летящего килограмма картошки на 1 м/с?
Ответ.Физики принимают такую силу за единичу измерения силы тяжести — 1 ньютон. Кстати, разные другие физические силы физики тоже любят измерять в ньютонах. Чтоб никто не обижался.
104. Талантливый мальчик, на которого действует сила тяжести, равная 200-м ньютонам, стоит на стуле и читает гостям свои стихи. Каков вес мальчика?
Ответ. Если ножки у стула одинаковые, и сидение (опора, на которой стоит мальчик) расположено горизонтально относительно поверхности родной планеты, и если стул не шатается (опора неподвижна), тогда вес мальчика равен действующей на него силе тяжести, то есть тем же 200-м ньютонам.
107. Тяжелоатлет, масса которого 60 кг, замахнулся на легкоатлета гирей, масса которой 10 кг. В свою очередь легкоатлет массой в 70 кг челится в тяжелоатлета копьем массой 1 кг. На кого из них действует меньшая сила тяжести?
Ответ.На тяжелоатлета с гирей действует сила тяжести в 686 ньютонов, а на легкоатлета с копьем — 695,8 ньютонов. Тяжелоатлету легче.
110. Великовозрастный Вася, масса которого 60 кг, сидит на шее у своей престарелой бабушки. Вычислите силу тяжести и вес Васи и объясните — к чему приложены эти вес и сила тяжести.
Ответ. Васин вес и сила его тяжести одинаковы. И то и другое приблизительно равно 600-м ньютонам. А вот приложены они по-разному. Сила тяжести к самому васе, а его вес — к горизонтальной опоре, то есть к бабушкиной шее.
112. На обеденном столе, в тарелке, обложенный со всех сторон солеными огурчиками, лежит крупный кирпич массой 4 кг. Вычислите действующую на кирпич силу тяжести и скажите, как действует вес кирпича на огурчики?
Ответ.На огурчики вес кирпича физически не действует, он действует на тарелку. Но вес кирпича действует огурчикам на нервы. Они завидуют кирпичу, что он такой тяжелый. А на сам кирпич в тарелке действует сила тяжести в 39,2 ньютона. Приятного аппетита.
Ответ: за то, что вес мальчика меньше веса жидкости, взятой в объеме его тела.
Физика 7 класс. Решение задач по теме «Сила тяжести» — РазборЗадач.COM

Мы рады приветствовать Вас на сайте РазборЗадач.com! В этой статье мы решим основные задачи по теме «Сила тяжести» !
Другие задачи с решениями на тему «сила тяжести» смотрите тут!
Как всегда, мы начнем свой разбор с наиболее простых задач этой темы:
1) На тело действуют две вертикально направленные силы — 10 Н и 15 Н. Изобразите эти силы. Сколько вариантов рисунка вы можете сделать? Чему равна равнодействующая этих сил в каждом случае?
Вариантов расположения вертикально направленных сил не так уж и много — их всего два. Либо вверх направлена сила 10 Н, либо 15 Н. Равнодействующую находим путем вычитания из большей меньшую: 15-10=5 Н. Направление равнодействующей силы 5 Н будет зависеть от того, куда направленная большая сила 15 Н.
2) Два человека тянут груз, прикладывая горизонтальные силы F1=100 Н и F2=150 Н, направленные вдоль одной прямой. Каким может быть модуль равнодействующей R этих сил? Рассмотрите все возможные случаи.
Равнодействующая может быть направленна в двух направлениях, в зависимости от того, куда тянут груз. Всего вариантов расположения четыре: 1) Влево тянет 100 Н вправо 150 Н 2) Вправо 100 Н, а влево 150 Н 3) Они вместе тянут влево 4) они вместе тянут вправо. Тк как спрашивают только модуль (численное значение), то рассмотрим два случая. 1) силы приложены в разные стороны, тогда равнодействующая R= 150-100=50 Н. 2) силы приложены в одну сторону, тогда R= 150+100=250 Н.
3) Одна из двух сил, действующих на тело вдоль одной прямой, равна 5 Н. Равнодействующая этих сил равна 8 Н. Какой может быть по модулю другая сила? Как она должна быть направлена по отношению к первой силе?
Ситуация такая же, как и в предыдущей задаче. Тк как спрашивают только модуль (численное значение), то рассмотрим два случая. 1) силы приложены в разные стороны 2) силы приложены в одну сторону. 1) можно составить уравнение, взяв за x искомую силу: х-5=8; х=8+5=13 Н 2) х+5=8; х=8-5=3Н
4) На тело действуют три силы, направленные вдоль одной прямой: 3 Н, 12 Н и 6 Н соответственно. Каким может быть модуль равнодействующей R этих сил?
5) Какой объем воды находится в сосуде, если на нее действует сила тяжести 150 Н?
Для решения задачи нам потребует таблица плотности веществ и знание: что такое сила тяжести.

Для начала, найдем массу воды: 150=m*10; m=150/10=15 кг. Теперь мы можем определить объем по формуле плотности: m=p*V; V=m/p; V= 15/ 1000 (кг/ куб м) = 0,015 куб м
Итак, мы рассмотрели основные задачи по теме «Сила тяжести». Если у Вас есть вопросы по разбору — пишите в комментарии! Если Вы хотите, чтобы мы разобрали конкретную задачу, то отправьте ее в разделе «Задать вопрос«. Успехов в учебе!
Сила тяготения: простые задачи
В этой статье рассмотрены самые простые задачи на тему “Сила тяготения”. Мы научимся определять ускорение свободного падения на поверхности планеты и на некоторой высоте, рассчитывать первую космическую скорость, и вспомним закон сохранения импульса.
Задача 1. Определить ускорение свободного падения на поверхности Марса, если отношение масс Марса и Земли равно 0,107, а отношение радиусов Марса и Земли равно 0,53.
Ускорение свободного падения определяется формулой
![Rendered by QuickLaTeX.com \[g=G\cdot \frac{M}{R^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-45290a8a957ee40012db8176386079ba_l3.png)
Где  – масса планеты, а
– масса планеты, а  – ее радиус. Тогда для земли можем записать:
– ее радиус. Тогда для земли можем записать:
![Rendered by QuickLaTeX.com \[g_Z=G\cdot \frac{M_Z}{R_Z^2}~~~~~~~~~~~~~~~~(1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f7e14053b988a2e39b5913eeb1ed7d5c_l3.png)
А для Марса тогда
![Rendered by QuickLaTeX.com \[g_M=G\cdot \frac{M_M}{R_M^2}~~~~~~~~~~~~~~~(2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-04f312c04456b5eb95553416dc4f0070_l3.png)
Разделим (2) на (1):
![Rendered by QuickLaTeX.com \[\frac{ g_M }{ g_Z }=\frac{ M_M }{ R_M^2}\cdot \frac{ R_Z^2}{ M_Z }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b0d9c3afc573ac18e0425fd0363cc1c9_l3.png)
Или
![Rendered by QuickLaTeX.com \[\frac{ g_M }{ g_Z }=\frac{ M_M }{ M_Z }\cdot \frac{ R_Z^2}{ R_M^2 }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-22dfbc7212a9f1a6018284d3c0912245_l3.png)
![Rendered by QuickLaTeX.com \[\frac{ g_M }{ g_Z }=\frac{ M_M }{ M_Z }\cdot \left(\frac{ R_Z}{ R_M }\right)^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-02df83156dee6712cd9e8afcfef12111_l3.png)
![Rendered by QuickLaTeX.com \[g_M= g_Z \frac{ M_M }{ M_Z }\cdot \left(\frac{ R_Z}{ R_M }\right)^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-522ef84af81cab1d9f3c1be7fbf258b0_l3.png)
Подставляем известные величины:
![Rendered by QuickLaTeX.com \[g_M =\frac{0,107\cdot 9,8 }{\left(0,53\right)^2}=3,7\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e3bb1c47994b17771b0223c52ba7ec8c_l3.png)
Ответ: 3,7 м/с .
.
Задача 2. На какой высоте  ускорение свободного падения будет в
ускорение свободного падения будет в  раз меньше ускорения свободного падения у поверхности Земли?
раз меньше ускорения свободного падения у поверхности Земли?
Ускорение свободного падения у поверхности определяется формулой
![Rendered by QuickLaTeX.com \[g=G\cdot \frac{M}{R^2}~~~~~~~~~~~~~~~~(3)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-978d7c8ad04f1b99f9fcb2314eb43304_l3.png)
Тогда на некоторой высоте мы можем его записать как
![Rendered by QuickLaTeX.com \[g_h=G\cdot \frac{M}{(R+h)^2}~~~~~~~~~~~~~~~~(4)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fb227cc4f7bb85d261cf1402d2ef1bf1_l3.png)
Так как по условию  , то разделим (3) на (4):
, то разделим (3) на (4):
![Rendered by QuickLaTeX.com \[\frac{g}{g_h}=n=\frac{(R+h)^2}{R^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a5ad21afafb9aa0ea682292dd2293452_l3.png)
Извлечем корень из правой и левой частей:
![Rendered by QuickLaTeX.com \[\sqrt{ n}=\frac{(R+h)}{R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b53210049b4f44db8057ff97ec96b115_l3.png)
![Rendered by QuickLaTeX.com \[R+h=\sqrt{ n}R\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a7a5b4cd6e42bef8fa63abecc0c0cd82_l3.png)
![Rendered by QuickLaTeX.com \[h=\sqrt{ n}R-R=R(\sqrt{ n}-1)=2R\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a7da22496adcb0effe442848bc5defd7_l3.png)
Ответ: на высоте, равной двум земным радиусам.
Задача 3. На каком расстоянии от центра земли тело в первую секунду свободного падения проходит расстояние  м?
м?
Из формулы пути при свободном падении тела находим, что
![Rendered by QuickLaTeX.com \[S=\frac{g_h t^2}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0b2738b2b551eb6e8cbf9b6cf671ecd8_l3.png)
![Rendered by QuickLaTeX.com \[g_h=\frac{2S}{t^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b260be9c86d8170f6cc8ee21e0603eff_l3.png)
С другой стороны, так как  в данном случае – расстояние от центра земли, то
в данном случае – расстояние от центра земли, то
![Rendered by QuickLaTeX.com \[g_h=G\cdot \frac{M}{h^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b92b9c19ba6849e6d3257dd8c36ba040_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[\frac{2S}{t^2}= G\cdot \frac{M}{h^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c55585525902e81ed75a79553e374892_l3.png)
![Rendered by QuickLaTeX.com \[h^2= G\cdot \frac{M t^2}{2S}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bd35e2fe0a4ea64dbc4498f5755a2759_l3.png)
![Rendered by QuickLaTeX.com \[h=t\sqrt{ G\cdot \frac{M}{2S}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f21f6168b456f3f52b27fee02ea00b27_l3.png)
Подставим числовые данные:
![Rendered by QuickLaTeX.com \[h=1\sqrt{ 6,67\cdot10^{-11} \frac{5,976 \cdot10^{24}}{2\cdot 0,55}}=\sqrt{ \frac{398,6 \cdot10^{12}}{1,1}}=1,9\cdot 10^7\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0e95405c97bc1612b0949f59a470b565_l3.png)
Ответ:  м
м
Задача 4. Космонавт массой  кг находится на поверхности шаровидного астероида радиусом
кг находится на поверхности шаровидного астероида радиусом  км и держит в руках камень массой
км и держит в руках камень массой  кг. С какой максимальной скоростью
кг. С какой максимальной скоростью  относительно поверхности астероида космонавт может бросить камень, не рискуя превратиться в спутник астероида? Средняя плотность астероида
относительно поверхности астероида космонавт может бросить камень, не рискуя превратиться в спутник астероида? Средняя плотность астероида  кг/м
кг/м .
.
По закону сохранения импульса, если вы сообщаете камню скорость, то камень сообщает скорость вам также. Поскольку речь о ма-аленьком астероиде, то и первая космическая скорость у него небольшая. Определим, какая. Для этого определим ускорение свободного падения на астероиде массой  :
:
![Rendered by QuickLaTeX.com \[g=G\cdot \frac{M_p}{R^2}= G\cdot \frac{\rho V}{R^2}= G\cdot \frac{4\rho \pi R^3 }{3R^2}=\frac{4}{3}\pi GR \rho\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e514a7fafd140d8ecca4b73e9d8f084f_l3.png)
Тогда первая космическая скорость равна
![Rendered by QuickLaTeX.com \[\upsilon_1=\sqrt{gR}=\sqrt{\frac{4}{3}\pi GR^2 \rho }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2cc04d9cc1999f3673a93a2471c385bf_l3.png)
По закону сохранения импульса имеем:
![Rendered by QuickLaTeX.com \[M \upsilon_1=m \upsilon\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-34f1e0ada20e3ef5541caa09ee0a30d1_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[\upsilon=\frac{ M \upsilon_1}{m}=\frac{M}{m}\sqrt{\frac{4}{3}\pi GR^2 \rho }=\frac{2MR}{m}\sqrt{\frac{\pi G\rho}{3} }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1551ccc43acba5e6a45fce71663409ff_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon=\frac{2 \cdot 100\cdot 1000}{10}\sqrt{\frac{3,14 \cdot 6,67\cdot10^{-11}\cdot 5\cdot10^3}{3}}=11,8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-02c289297f3cfd6f149972edd25b49b3_l3.png)
Ответ: 12 м/c
Задачи. Сила всемирного тяготения — PhysBook
Уровень А
1. С какой силой притягиваются:
а) два вагона массой по 80 т, если между ними расстояние 3,0 км;
б) Луна и Земля, массы которых равны 7,35·1022 кг и 5,98·1024 кг соответственно, а среднее расстояние между ними 3,84·108 м;
в) два протона массой 1,67·10-27 кг, находящихся на расстоянии 1,00·10-10 м друг от друга?
Решение
2. На каком расстоянии сила притяжения между двумя телами массой по 200 кг каждое будет равна 3,00·10-14 Н?
Решение
3. Два шарика находятся на расстоянии 0,20 м друг от друга и притягиваются силой 6,0·10-13 Н. Какова масса первого шарика, если масса второго равна 20 г?
Решение
4. Космический аппарат массой 750 кг достиг поверхности Луны. Найдите силу тяжести, действующую на аппарат:
а) на поверхности Земли;
б) на поверхности Луны.
Решение
5. Какова масса тела, если сила тяжести, действующая на него, равна 49 Н? Тело находится вблизи поверхности Земли.
Решение
6. Масса мальчика 50,0 кг. Определите силу тяжести, действующую на него на поверхности:
а) Меркурия;
б) Юпитера.
Решение
7. Тело имеет массу 10 кг. Какая сила тяжести действует на это тело на высоте трех земных радиусов от поверхности Земли?
Решение
8. Вычислите ускорение свободного падения тел вблизи поверхности Марса.
Решение
9. Каково ускорение свободного падения Земли на высоте, равной радиусу Земли?
Решение
10. Средний радиус планеты 2420 км, а ускорение свободного падения 3,72 м/с2. Найдите массу планеты.
Решение
11. Найдите первую космическую скорость для следующих тел Солнечной системы:
а) Венера,
б) Земля,
в) Луна.
Решение
12. Какую скорость должен иметь спутник Земли, движущийся по круговой орбите, на высоте 1700 км от поверхности Земли?
Решение
Решение задач по теме «Сила тяжести. Сила упругости. Вес тела»
План-конспект урока по теме «Решение задач по теме «Сила тяжести. Сила упругости. Вес тела»
Дата:
Тема: «Решение задач по теме «Сила тяжести. Сила упругости. Вес тела»
Цели:
Образовательная: формирование практических умений по решению задач на тему «Сила тяжести. Сила упругости. Вес тела»;
Развивающая: совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), развивать познавательный интерес;
Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.
Тип урока: обобщение и систематизация знаний
Оборудование и источники информации:
Исаченкова, Л. А. Физика : учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2017.
Структура урока:
Организационный момент (5 мин)
Актуализация опорных знаний (5 мин)
Закрепление знаний(30 мин)
Итоги урока (5 мин)
Содержание урока
Организационный момент
Здравствуйте, присаживайтесь! (Проверка присутствующих).Сообщение темы урока.
Актуализация опорных знаний

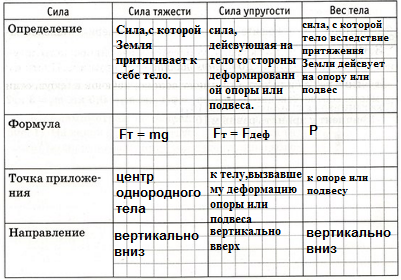
Закрепление знаний
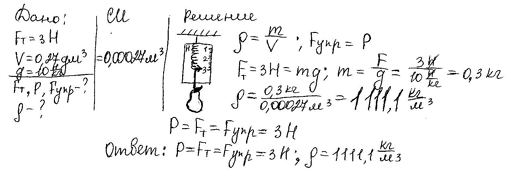
А сейчас перейдем к решению задач на карточках по теме «Решение зада по теме «Сила тяжести. Сила упругости. Вес тела» (приложение 1):

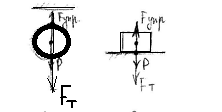
Вес шарика приложен к подвесу, а вес кубика- к опоре. Вес обоих тел направлен вниз.



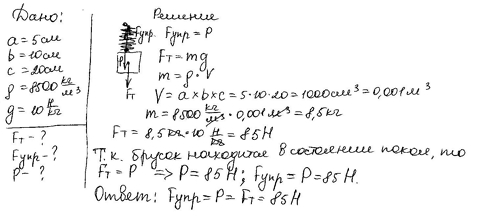

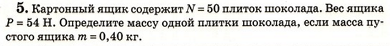
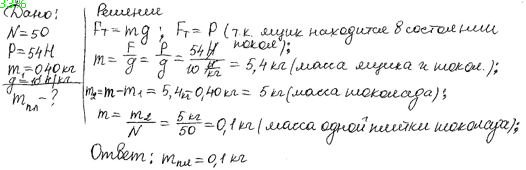

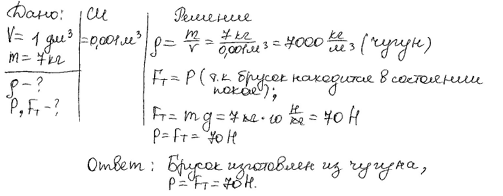
Итоги урока
Итак, подведем итоги. Что вы сегодня узнали на уроке?
Организация домашнего задания
§22-25(повт.),упр.9 (№4,6)
Рефлексия.
Продолжите фразы:
Сегодня на уроке я узнал…
Было интересно…
Знания, которые я получил на уроке, пригодятся…
Приложение 1
Карточка по теме «Решение зада по теме «Сила тяжести. Сила упругости. Вес тела»
Заполните таблицу







Решение задач. Сила тяжести. Сила упругости. Вес тела
- Дидактическая цель:
Основные знания и умения: уметь описывать характеристики сил, решать задачи, производить расчеты физических величин и графически изображать силы.
Тип урока: комбинированный.
Метод урока: иллюстративно-объяснительный, проблемно-поисковый.
Оборудование: 2 штатива, груз с нитью, динамометр, брусок, пластиковая линейка, шарик с водой, проволоки.
Мультимедийная технология. Презентация в Power Point.
Ход урока
I. Организационный момент и мотивация учащихся
Девиз урока:
“Используйте свою силу для защиты природы!”
– Ребята! Мы с вами познакомились с одной из физических величин – силой. Узнали о существовании силы тяжести и силы упругости, а также о весе тела. Сегодня продолжим систематизировать наши знания полученные в ходе изучения данных тем. Перед нами стояли следующие вопросы:
Какова природа сил? Когда возникает? К чему приложена? Как направлена? От чего зависит?
II. Проверка домашнего задания:
а) два человека решают у доски задачи из Лукашика № 336 и 338 и работа с рисунками №354 и 357
б) выступление учащихся (Биография Ньютона и Гука) Информацию о Ньютоне и можно посмотреть в Википедии:
http://ru.wikipedia.org/wiki/Роберт_Гук.
III. Систематизация изученного материала:
– Напоминаю вам, что мы должны в ходе урока закрепить знания о силах; научиться решать задачи.
Запишите в тетрадях число и тему урока. “Решение задач. Сила тяжести. Сила упругости. Вес тела”.
Фронтальный опрос.
в) класс отвечает на вопросы, выведенные на экран с помощью проектора. (Слайд 1)
- Напишите обозначение всех физических величин и их единицы измерения, которые вы знаете. (В тетрадях.)
- В результате чего может меняться скорость тела?
- Что такое сила?
- Какую называют силой тяжести? Как она направлена? К чему она приложена?
- Какую силу называют весом тела? К какому телу приложен вес тела?
- В каком случае вес тела по своему числовому значению равен силе тяжести?
- Чем объясняется возникновения силы упругости? Каково направление силы упругости?
- Как формулируется закон Гука?
- Какие величины называют векторными, а какие скалярные? Примеры.
- Дайте определение единицы силы 1 Н.
– Начнем с простых экспериментов:
А) представим, что это модель моста (пластиковая линейка закреплена в лапках штативов горизонтально). Насколько безопасно перемещаться по такому мосту? Поставим на мост груз (деревянный брусок, нагруженный 1–2 грузами по 100 г). Что мы наблюдаем?
Вопросы: Почему мост прогнулся? Изменил форму только мост или брусок тоже изменил форму?
– Конечно, мы не видим изменения формы бруска (можем об этом только догадываться). Но давайте изменим эксперимент.
Б) положим на “мост” воздушный шар, заполненный водой. Обратите внимание на формы этих взаимодействующих тел.
– Что мы видим теперь?
В) закрепим воздушный шар на пружине.
Вопросы:
– Я поддерживаю шар рукой. Что произойдет, если руку убрать?
– Куда и почему будет двигаться шар?
– Почему шар не падает вниз на Землю?
– Что произошло с пружиной?
– Что можно сказать о формах пружины и шара?
Вывод: При взаимодействии деформируются оба тела.
Поговорим немного о деформации:
– Деформация – это изменение формы и размеров тела под действием силы.
– Найдите силы, которые проявились в последнем опыте (со стороны каких тел и на
какие они действовали).
– Какие виды деформации существуют?
– Посмотрите, пружину растягиваю влево, сила упругости заставит ее вернуться в
первоначальное положение, значит, сила упругости направлена…
– Изгибаю линейку вверх, сила упругости направлена…
– Попробуйте ответить, а почему эта сила относится к электромагнитному
взаимодействию? Подсказка: из чего состоят тела? Что происходит с частицами при
деформации тел?
– Как выдумаете, будет ли изменяться сила упругости, если я буду растягивать или
сжимать пружину? Как?
0 Проведем эксперимент: линейка и пружина с указателем закреплены на штативе.
Будем поочередно подвешивать грузы на пружину и фиксировать ее удлинение.
Заносим данные в таблицу. Для расчета силы упругости используем равенство сил,
действующих на груз:
Fупр = Fтяж = mg. По данным таблицы строим график
зависимости Fупр(∆l).
– Какую линию получили на графике?
– Как называется такая зависимость в математике?
– Что происходит с силой упругости, если длина пружины увеличивается?
Уменьшается?
– Как изменится сила упругости, если длина пружины увеличится в 2 раза?
Посмотрим на график.
– Найдем отношение силы упругости к удлинению пружины (первый результат считаю
я, остальные вы – по вариантам):
– Какой вывод можно сделать об отношении силы упругости к удлинению пружины?
Модуль силы упругости при растяжении или сжатии тела прямо пропорционален
изменению длины тела.
Коэффициент жесткости зависит от длины образца, его площади поперечного сечения, а также от материала образца.
– Мы с вами получили закон, открытый английским физиком Робертом Гуком в 166 г. Информацию о Гуке и его биографию можно посмотреть в Википедии: http://ru.wikipedia.org/wiki/Роберт_Гук.
Продолжение урока по слайдам.
– Сила тяжести. Слайд 3-6. Приложение 1
– Сила упругости. Слайд 7–19.
– Вес тела. Слайд 20–25.
Решение задач по вариантам Слайд 17–22.
Решение задач из Лукашика.
Итог урока. Оценки ученикам.
IV. Домашнее задание: §27, упр. 9. Лукашик № 341– 343 записывать в дневниках.
Спасибо за урок!
Литература:
- Перышкин А.В. Учебник физика – 7-й класс.
Интернет ресурсы.
Приложение