Тесты по математике. ОГЭ 2018. Геометрия, 1 часть (9 класс)
Задание 15. Две сосны растут на расстоянии 15 м одна от другой. Высота одной сосны 30 м, а другой — 22 м. Найдите расстояние (в метрах) между их верхушками.
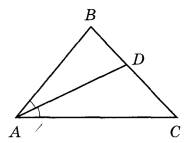
Задание 16. В треугольнике ABC известно, что угол BAC = 48°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
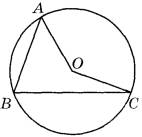
Задание 17. Точка О — центр окружности, на которой лежат точки А, В и С. Известно, что углы ABC = 69° и OAB = 48°. Найдите угол ВСО. Ответ дайте в градусах.
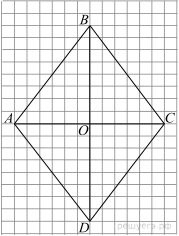
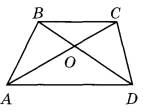
Задание 18. Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 7, AD = 9, АС = 32. Найдите АО.
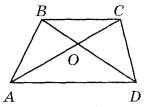
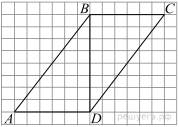
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
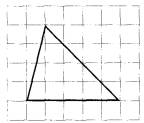
Задание 20. Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой
Задание 15. Две сосны растут на расстоянии 20 м одна от другой. Высота одной сосны 27 м, а другой — 12 м. Найдите расстояние (в метрах) между их верхушками.
Задание 16. В треугольнике ABC известно, что угол BAC = 84°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
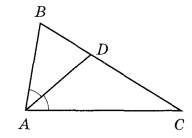
Задание 17. Точка О — центр окружности, на которой лежат точки А, В и С. Известно, что углы ABC = 56° и OAB = 15°. Найдите угол ВСО. Ответ дайте в градусах.
Задание 18. Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 6, AD = 13, АС = 38. Найдите АО.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
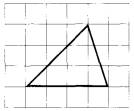
Задание 20. Какое из следующих утверждений верно?
1) Все равнобедренные треугольники подобны.
2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3) Сумма углов прямоугольного треугольника равна 90 градусам.
Задание 15. Две сосны растут на расстоянии 16 м одна от другой. Высота одной сосны 27 м, а другой — 15 м. Найдите расстояние (в метрах) между их верхушками.
Задание 16. В треугольнике ABC известно, что угол BAC = 28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
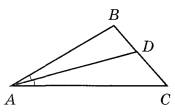
Задание 17. Точка О — центр окружности, на которой лежат точки А, В и С. Известно, что углы ABC = 54° и OAB = 41°. Найдите угол ВСО. Ответ дайте в градусах.
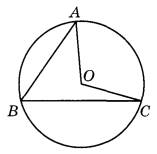
Задание 18. Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 2, АВ = 5, АС = 28. Найдите АО.
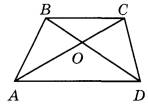
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
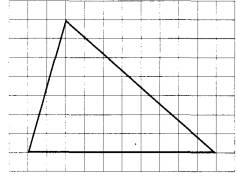
Задание 20. Какое из следующих утверждений верно?
1) Сумма острых углов прямоугольного треугольника равна 90 градусам.
2) Средняя линия трапеции равна сумме её оснований.
3) В любой четырёхугольник можно вписать окружность.
Задание 15. Проектор полностью освещает экран А высотой 70 см, расположенный на расстоянии 140 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран В высотой 150 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
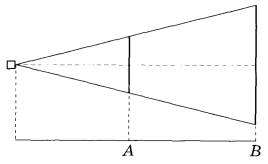
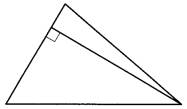
Задание 16. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
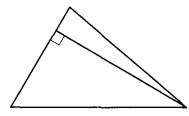
Задание 17. Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
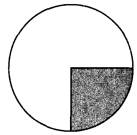
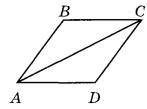
Задание 18. В ромбе ABCD угол ABC равен 134°. Найдите угол ACD. Ответ дайте в градусах.
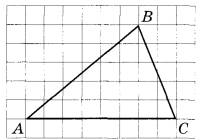
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне АС.
Задание 20. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Средняя линия трапеции равна сумме её оснований.
3) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Задание 15. Проектор полностью освещает экран А высотой 240 см, расположенный на расстоянии 300 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран В высотой 80 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Задание 16. Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.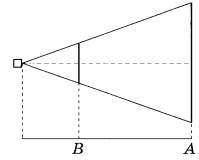
Задание 17. Площадь круга равна 72. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
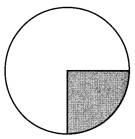
Задание 18. В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах.
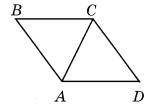
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне АС.
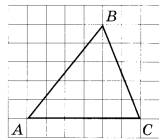
Задание 20. Какие из следующих утверждений верны?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
Задание 15. Проектор полностью освещает экран А высотой 50 см, расположенный на расстоянии 140 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран В высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
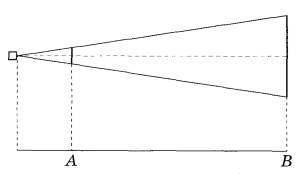
Задание 16. Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.
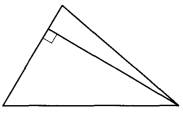
Задание 17. Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°.
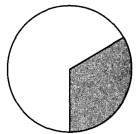
Задание 18. В ромбе ABCD угол ABC равен 84°. Найдите угол ACD. Ответ дайте в градусах.
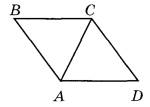
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне АС.
Задание 20. Какое из следующих утверждений верно?
1) Касательная к окружности параллельна радиусу, проведённому в точку касания.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Внешний угол треугольника равен сумме его внутренних углов.
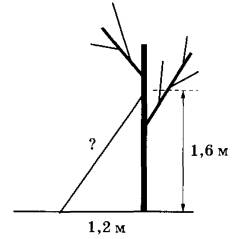
Задание 15. Найдите длину лестницы, которую прислонили к дереву, если её верхний конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м. Ответ дайте в метрах.
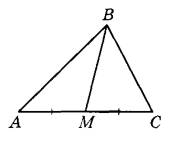
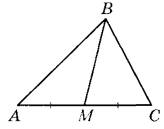
Задание 16. В треугольнике ABC известно, что АС = 32, ВМ — медиана, ВМ = 23. Найдите AM.
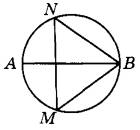
Задание 17. На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что угол NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.
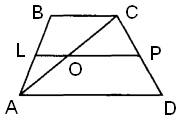
Задание 18. Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
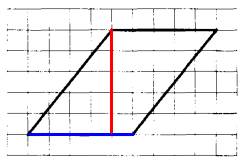
Задание 20. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Площадь квадрата равна произведению его диагоналей.
Задание 15. Две сосны растут на расстоянии 24 м одна от другой. Высота одной сосны 17 м, а другой — 10 м. Найдите расстояние (в метрах) между их вершинами.
Задание 16. В треугольнике ABC известно, что АС = 52, ВМ — медиана, ВМ = 36. Найдите AM.
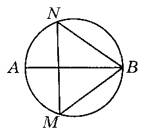
Задание 17. На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что угол NBA = 32°. Найдите угол NMB. Ответ дайте в градусах.
Задание 18. Основания трапеции равны 16 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
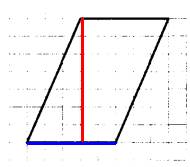
Задание 20. Какие из следующих утверждений верны?
1) Две прямые, перпендикулярные третьей прямой, перпендикулярны.
2) В любой прямоугольной трапеции есть два равных угла.
3) Все диаметры окружности равны между собой.
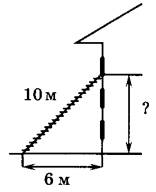
Задание 15. Пожарную лестницу длиной 10 м приставили к окну третьего этажа дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.
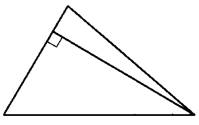
Задание 16. Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 22. Найдите площадь этого треугольника.
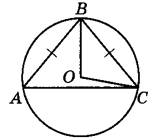
Задание 17. Окружность с центром в точке О описана около равнобедренного треугольника ABC, в котором АВ =ВС и угол ABC = 88°. Найдите угол ВОС. Ответ дайте в градусах.
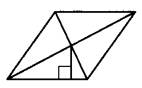
Задание 18. Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
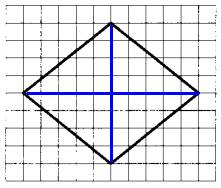
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Задание 20. Какие из следующих утверждений верны?
1) Диагонали ромба равны.
2) Всякий равносторонний треугольник является равнобедренным.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Задание 15. Две сосны растут на расстоянии 36 м одна от другой. Высота одной сосны 25 м, а другой — 10 м. Найдите расстояние (в метрах) между их вершинами.
Задание 16. Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
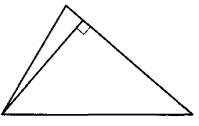
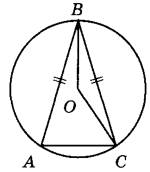
Задание 17. Окружность с центром в точке О описана около равнобедренного треугольника ABC, в котором АВ = ВС и угол ABC = 25°. Найдите угол ВОС. Ответ дайте в градусах.
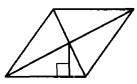
Задание 18. Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
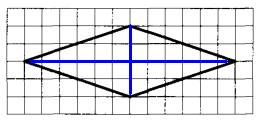
Задание 20. Какие из следующих утверждений верны?
1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) Все квадраты имеют равные площади.
3) Один из углов треугольника всегда не превышает 60 градусов.
Признаки равенства треугольников | |
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны. | |
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны. | |
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны. | |
Признаки равенства прямоугольных треугольников | |
1. По двум катетам
| 3. По катету и острому углу |
2. По катету и гипотенузе | 4. По гипотенузе и острому углу |
Теорема о сумме углов треугольника и следствия из неё. | |
1. Сумма внутренних углов треугольника равна . |
|
2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов. | |
3. Внешний угол треугольника больше любого угла треугольника, не смежного с ним | |
Неравенство треугольника. Следствия из неравенства треугольника | |
1. Сумма двух сторон треугольника больше третьей стороны. | AB AC BC |
2. Против большего угла треугольника лежит большая сторона. 3. Против большей стороны треугольника лежит больший угол. | |
4. Гипотенуза прямоугольного треугольника больше катета. |
AB > AC, AB > BC |
Основные свойства и признаки равнобедренного треугольника. | |
Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием. |
|
1. В равнобедренном треугольнике углы при основании равны. | |
2. Если в треугольнике два угла равны, то он равнобедренный. | |
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. | |
4. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный. | |
Средняя линия треугольника. | |
Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника. | |
Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна ее половине. | |
Теоремы о медианах треугольника. | |
1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины. | |
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный. |
|
3. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. | |
Свойство серединных перпендикуляров к сторонам треугольника. | |
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника. | |
Теорема о высотах треугольника. | |
Прямые, содержащие высоты треугольника, пересекаются в одной точке. |
|
Свойство биссектрисы треугольника. | |
Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник. | |
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам. | |
Квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения отрезков третьей стороны, на которые она разделена биссектрисой. | |
Прямоугольный треугольник | |
1. Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. |
|
2. Теорема, обратная теореме Пифагора. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный. | |
3. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла. |
|
4. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к этому катету острого угла. | |
5. Катет, лежащий против угла в 30 градусов, равен половине гипотенузы. | |
6. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 300 . | |
7. ; , где — катеты, — гипотенуза, и — радиусы соответственно вписанной и описанной окружности. |
|
8. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, | |
9. Катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу. | |
Метрические соотношения в треугольнике. | |
1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. |
|
2. Формула для медианы треугольника. Если mс — медиана треугольника, проведенная к стороне c, то , где a и b — остальные стороны треугольника. | |
3. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. | , где R – радиус, описанной около треугольника окружности |
4. Обобщенная теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника. | |
Формулы площади треугольника. | |
1. Площадь треугольника равна половине произведения основания на высоту. | 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. |
4. Площадь треугольника равна произведению трех его сторон, деленному на учетверенный радиус описанной окружности. | 3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. |
5. Формула Герона. | |
Элементы равностороннего треугольника. | |
Пусть h ,S, r, R — высота, площадь, радиусы описанной и вписанной окружности равностороннего треугольника со стороной a. | , , , , |
Подобие треугольников | |
1. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны. | и — подобны |
2. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны. | и — подобны |
3. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то треугольники подобны. | и — подобны |
Отношение соответствующих линейных элементов подобных треугольников равно коэффициенту подобия. | и — подобны |
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. | |
Тренажёр по геометрии (9 класс) на тему: Окружность. Касательная. Вписанные углы. ОГЭ (ГИА) задание 10 модуль «Геометрия»
МКОУ «Тугулымская В(С)ОШ»
Окружность. Касательная. Вписанные углы.
ОГЭ (ГИА) задание 10 модуль «Геометрия»
Составитель:
учитель математики
первой категории Т.Н.Сидорова
Окружность. Касательная. Вписанные углы.
Рассмотрим решение некоторых прототипов задач из Задания 10 ОГЭ (ГИА) по математике (или Задания 7 ЕГЭ по математике).
Предлагаю вам решить эти задачи самостоятельно, а затем свериться с решением.
Вспомним свойства вписанного угла.
Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписанным углом. Вписанный угол измеряется половиной дуги, на которую он опирается:
∠∠
Важно: вписанные углы, опирающиеся на равные дуги равны между собой. В частности, вписанные углы, опирающиеся на одну дугу, равны между собой.
Рассмотрим решение задач.
Решение.
Рассмотрим треугольник :
, следовательно, треугольник — равнобедренный.
∠∠
Угол и угол — вертикальные. Вертикальные углы равны.
∠∠
Ответ: 104
Решение.
∠∠∠:
∠ и ∠ опираются на дугу ,
поэтому ∠∠:
отсюда ∠∠∠
Ответ: 70
Решение.
Чтобы решить эту задачу нам нужно вспомнить два факта:
1. Вписанный угол, который опирается на диаметр равен . И наоборот, если вписанный угол равен , то он опирается на диаметр. Следовательно, гипотенуза прямоугольного треугольника является диаметром описанной около треугольника окружности, то есть
2. центр описанной около прямоугольного треугольника окружности лежит в середине гипотенузы.
Найдем по теореме Пифагора гипотенузу :
Отсюда и
Ответ: 2,5
Решение.
∠ опирается на дугу . Найдем величину этой дуги.
∠ опирается на дугу . Вписанный угол равен половине величины дуги, на которую он опирается, следовательно, .
диаметр окружности, следовательно, угловая величина дуги
Отсюда
Тогда ∠
Ответ: 54
Решение.
скрыть
Центральный угол опирается на ту же дугу, что и вписанный угол , следовательно, ∠∠
Проведем прямую и рассмотрим треугольник
Угол в сумме с углом дает ( так как они смежные), следовательно, ∠
Угол — внешний угол треугольника и равен сумме двух углов, не смежных с ним.
∠
тогда по теореме о сумме углов треугольника ∠∠
Ответ: 32
Решение.
Проведем диагональ ромба . Отрезки являются радиусами окружности, поэтому .
Стороны ромба равны между собой, поэтому треугольники и — равносторонние, и все углы этих треугольников равны :
Следовательно, ∠
Ответ: 120
Решение.
Вспомним свойства касательных.
1. Отрезки касательных, проведенные к окружности из одной точки равны между собой. То есть
2. Радиус окружности, проведенный к точке касания перпендикулярен касательной.
То есть ∠ ∠:
Получаем, что∠∠
Найдем ∠. Для этого рассмотрим равнобедренный треугольник .
В равнобедренном треугольнике углы при основании равны и сумма углов треугольника равна 180 градусов:
Отсюда ∠
Следовательно, ∠
Ответ: 36
Решение.
Длина дуги пропорциональна величине центрального угла, который на нее опирается.
Центральный угол, который опирается на большую дугу равен
Пусть длина большей дуги равна .
Составим пропорцию:
отсюда
Ответ: 441
Решение.
Для решения это задачи нам понадобится еще одна теорема:
Квадрат касательной равен произведению секущей на ее внешнюю часть. То есть
Найдем .
Следовательно,
Отсюда
Ответ: 40
Решение.
Квадрат касательной равен произведению секущей на ее внешнюю часть. То есть
Пусть радиус окружности равен . Тогда
Получаем уравнение:
Ответ: 75
Решение.
Радиус окружности, проведенный к точке касания перпендикулярен касательной. Хорда параллельна касательной, следовательно, перпендикулярна .
Нам нужно найти длину .
Найдем . Для этого рассмотрим треугольник . , то есть этот треугольник равнобедренный. В равнобедренном треугольнике высота является медианой, то есть
найдем по теореме теореме Пифагора из прямоугольного треугольника :
Ответ: 160
Подготовка к ОГЭ, геометрия, 8-9 класс. Тестовые задания и ответы.
Подготовка к ГИА. Раздел Геометрия. 9 класс.
1. Средняя линия трапеции равна 45, а меньшее основание равно 37. Найдите большее основание трапеции.

2. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 72°? Ответ дайте в градусах.
3. Найдите высоту ромба, сторона которого равна  , а острый угол равен 60°.
, а острый угол равен 60°.
5. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 15. Найдите периметр этого квадрата.
6. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 11. Найдите диагональ данного прямоугольника.
7. Меньшая сторона прямоугольника равна 56, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
8. Диагональ параллелограмма образует с двумя его сторонами углы 29° и 58°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
9. В треугольнике ABC AC = BC, угол C равен 120o,  . Найдите AB.
. Найдите AB.

10. В треугольнике ABC  , угол C равен 120o. Найдите высоту AH.
, угол C равен 120o. Найдите высоту AH.

11. В треугольнике ABC AC = BC = 6, высота AH равна 3. Найдите угол C. Ответ дайте в градусах.
12. В равностороннем треугольнике ABC высота CH равна  . Найдите стороны этого треугольника.
. Найдите стороны этого треугольника.
13. В треугольнике ABC угол C равен 90
14. В треугольнике ABC угол C равен 90o, угол A равен 30o,  . Найдите AB.
. Найдите AB.
15. На рисунке угол 1 равен 48o, угол 2 равен 26o, угол 3 равен 40o. Найдите угол 4. Ответ дайте в градусах.

16. В треугольнике ABC угол A равен 60o, угол B равен 82o. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

17. В треугольнике ABC угол A равен 30o, угол B равен 86o, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах.

18. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 4o. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

19. Острые углы прямоугольного треугольника равны 69oи 21o

20. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

21. Острый угол прямоугольного треугольника равен 40o. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

 .
. 
23. Основания равнобедренной трапеции равны 76 и 48. Тангенс острого угла равен . Найдите высоту трапеции.
. Найдите высоту трапеции.
24. Большее основание равнобедренной трапеции равно 56. Боковая сторона равна 9. Синус острого угла равен  . Найдите меньшее основание.
. Найдите меньшее основание.
25. Основания равнобедренной трапеции равны 3 и 27. Боковые стороны равны 15. Найдите синус острого угла трапеции.
26. В параллелограмме ABCD AB=5, AD=8, . Найдите большую высоту параллелограмма.
. Найдите большую высоту параллелограмма.
27. В треугольнике ABC AC=BC=5, . Найдите синус внешнего угла при вершине A.
. Найдите синус внешнего угла при вершине A.
28.В треугольнике ABC угол C равен 90o, CH — высота, AH = 49,  . Найдите BH.
. Найдите BH.
ОТВЕТЫ:
1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. |
53 | 126 | 4,5 | 11 | 120 | 22 | 112 | 93 | 6 | 3 |
11. | 12. | 13. | 14. | 15. | 16. | 17. | 18. | 19. | 20. |
30 | 4 | 1,5 | 4 | 114 | 49 | 56 | 41 | 48 | 36 |
21. | 22. | 23. | 24. | 25. | 26. | 27. | 28. | ||
65 | 2 | 17 | 42 | 0,6 | 7 | 0,4 | 25 |
Самостоятельная работа по геометрии. ОГЭ 9 класс
Вариант № 1.
Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.


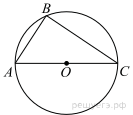
Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на
 .
.
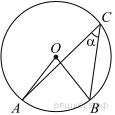
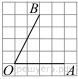
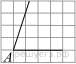
Найдите тангенс угла AOB, изображенного на рисунке.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Вариант № 2.
Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.

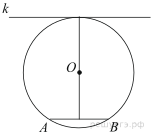
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на

 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
Вариант № 3.
Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см
 40 см?
40 см? ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.В треугольнике ABC угол C равен 90°, AC = 30 , BC =
 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на

 Найдите тангенс угла B треугольника ABC, изображённого на рисунке.
Найдите тангенс угла B треугольника ABC, изображённого на рисунке.Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Если утверждений несколько, запишите их номера в порядке возрастания.
Вариант № 4.
 Определите, сколько необходимо закупить пленки
Определите, сколько необходимо закупить пленки  для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
 Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.

На рисунке изображена трапеция  . Используя рисунок, найдите
. Используя рисунок, найдите 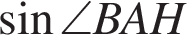 .
.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов любого треугольника равна 180° .
Если утверждений несколько, запишите их номера в порядке возрастания.
Вариант № 5.
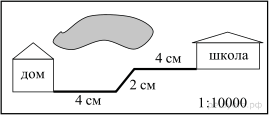
 На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите, длину пути (в м), если масштаб 1 см: 10000 см.
На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите, длину пути (в м), если масштаб 1 см: 10000 см.Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.

На рисунке изображен ромб 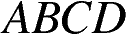 . Используя рисунок, найдите
. Используя рисунок, найдите 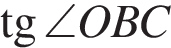 .
.
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
Вариант № 6.
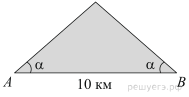
Склоны горы образуют с горизонтом угол  , косинус которого равен 0,8. Расстояние по карте между точками A и B равно 10 км. Определите длину пути между этими точками через вершину горы.
, косинус которого равен 0,8. Расстояние по карте между точками A и B равно 10 км. Определите длину пути между этими точками через вершину горы.
Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.

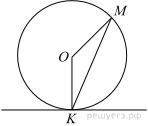
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.

На квадратной сетке изображён угол 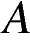 . Найдите
. Найдите  .
.
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
Если утверждений несколько, запишите их номера в порядке возрастания.
Вариант № 7.
Глубина бассейна составляет 2 метра, ширина — 10 метров, а длина — 25 метров. Найдите суммарную площадь боковых стен и дна бассейна (в квадратных метрах).
 В выпуклом четырехугольнике ABCD
В выпуклом четырехугольнике ABCD  ,
,  ,
,  ,
,  . Найдите угол A. Ответ дайте в градусах.
. Найдите угол A. Ответ дайте в градусах.Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.

На рисунке изображен параллелограмм 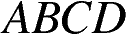 . Используя рисунок, найдите
. Используя рисунок, найдите 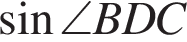 .
.
Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
3) Стороны треугольника пропорциональны косинусам противолежащих углов.
4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Если утверждений несколько, запишите их номера в порядке возрастания.
Вариант № 8.
Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.

На рисунке изображен ромб 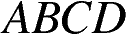 . Используя рисунок, найдите
. Используя рисунок, найдите  .
.
Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Если утверждений несколько, запишите их номера в порядке возрастания.
Материал для подготовки к ЕГЭ (ГИА) по геометрии (9 класс) по теме: Тренажеры по геометрии по подготовке к ОГЭ
Какое из следующих утверждений верно? 1.1.Площадь квадрата равна произведению двух его смежных сторон. 2)Диагональ трапеции делит её на два равных треугольника. 3)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2.1)Каждая из биссектрис равнобедренного треугольника является его медианой. 2)Диагонали прямоугольника равны. 3)У любой трапеции боковые стороны равны
3 1)Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2)Диагонали ромба равны. 3)Тангенс любого острого угла меньше единицы.
4.1)Все квадраты имеют равные площади. 2)Основания равнобедренной трапеции равны. 3)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
5.1)Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов. 2)Любой прямоугольник можно вписать в окружность. 3)Через заданную точку плоскости можно провести единственную прямую.
6.1)Вертикальные углы равны. 2)Две прямые, параллельные третьей прямой, перпендикулярны друг другу. 3)Диагонали любого прямоугольника делят его на 4 равных треугольника.
7.1)Один из двух смежных углов острый, а другой тупой. 2)Площадь квадрата равна произведению двух его смежных сторон. 3)Все хорды одной окружности равны между собой.
8.1)Отношение площадей подобных треугольников равно коэффициенту подобия. 2)Диагонали прямоугольника точкой пересечения делятся пополам. 3)Биссектриса треугольника делит пополам сторону, к которой проведена.
9.1)Треугольника со сторонами 1, 2, 4 не существует. 2)Медиана треугольника делит пополам угол, из которого проведена.
3)Все диаметры окружности равны между собой.
.
10.1)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. 2)Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб. 3)Площадь круга меньше квадрата длины его диаметра. .
11.1)В тупоугольном треугольнике все углы тупые. 2)В любом параллелограмме диагонали точкой пересечения делятся пополам. 3)Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
12.1)Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. 2)У любой трапеции боковые стороны равны. 3)Один из углов треугольника всегда не превышает 60 градусов.
13.1)Площадь квадрата равна произведению двух его смежных сторон. 2)Диагональ трапеции делит её на два равных треугольника. 3)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
14.1)Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны. 2)Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой 3)Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
15.1Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов. 2)Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла. 3)Если диагонали параллелограмма равны, то он является ромбом.
16.1)Все углы ромба равны. 2)Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны. 3)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
17.1)Площадь параллелограмма равна половине произведения его диагоналей. 2)Сумма углов прямоугольного треугольника равна 90 градусам. 3)Биссектрисы треугольника пересекаются в центре его вписанной окружности.
18.1)Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов. 2)В тупоугольном треугольнике все углы тупые .3)Средняя линия трапеции равна полусумме её оснований.
19.1)Если диагонали параллелограмма равны, то он является ромбом. 2)Тангенс любого острого угла меньше единицы. 3)Сумма углов равнобедренного треугольника равна 180 градусам
20.1 )Все хорды одной окружности равны между собой. 2)Диагональ равнобедренной трапеции делит её на два равных треугольника. 3)Сумма углов равнобедренного треугольника равна 180 градусам.
21.1)Все хорды одной окружности равны между собой. 2)Диагональ равнобедренной трапеции делит её на два равных треугольника. 3)Сумма углов равнобедренного треугольника равна 180 градусам.
22.1)Все углы ромба равны. 2)Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны. 3)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
23.1)Если диагонали параллелограмма равны, то он является ромбом. 2)Тангенс любого острого угла меньше единицы. 3)Сумма углов равнобедренного треугольника равна 180 градусам.
24.1)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. 2)Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб. 3)Площадь круга меньше квадрата длины его диаметра.
25.1)В тупоугольном треугольнике все углы тупые. 2)В любом параллелограмме диагонали точкой пересечения делятся пополам. 3)Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
26 1)Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. 2)У любой трапеции боковые стороны равны. 3)Один из углов треугольника всегда не превышает 60 градусов.
27.1)Площадь квадрата равна произведению двух его смежных сторон. 2)Диагональ трапеции делит её на два равных треугольника. 3)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Подготовка к ОГЭ, модуль «Геометрия», 9 класс
Подготовка к ОГЭ, модуль «Геометрия», 9 класс
Цель урока:
формировать навыки решения геометрических задач; выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; продолжать подготовку к экзамену в новой форме в процессе планового урока;
развивать логическое мышление, интерес к познавательной деятельности, творческие способности обучающихся, самоконтроль и взаимоконтроль, опыт работы в парах;
воспитание интереса к предмету, умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, настойчивости в достижении цели и заинтересованности в конечном результате труда.
Ход урока
I. Организационный момент. Мотивация учебной деятельности.
На доске эпиграф к уроку «Приобретать знания – это храбрость, приумножать знания – это мудрость, а умело применять – великое искусство» (Восточная мудрость).
Здравствуйте ребята и уважаемые гости!
Прозвенел уже звонок
Начинается урок
Мы сегодня не одни
Гости на урок пришли!
Ребята, у нас сегодня гости, давайте улыбнемся им!
Актуализация опорных знаний.
В последнее время мы с вами вплотную занимаемся подготовкой к ОГЭ, но проблемы до сих пор остаются, это подтверждают результаты последнего пробного экзамена. Сегодня на уроке мы повторим и проверим, как вы применяете геометрические знания на практике.
Итак, тема нашего урока «Подготовка к ОГЭ. Модуль «Геометрия»». Знания по этой теме вам понадобятся не только на экзамене, но и в 10, 11 классах, в специальных и высших учебных заведениях. Поэтому цель нашего урока: повторить и проверить геометрические знания и умения. А эпиграфом нашего урока будет восточная мудрость: «Приобретать знания – это храбрость, приумножать знания – это мудрость, а умело применять – великое искусство».
А начнем мы с теоретической разминки.
II. Теоретическая разминка
Сколько геометрических задач в варианте ОГЭ?
Прямоугольный треугольник, равнобедренный треугольник, медианы, биссектрисы, высоты треугольника, средняя линия.
Окружность
Площадь
Что нужно знать, чтобы правильно выполнить задание «на клетках»?
Что необходимо для выбора верного или неверного высказывания?
На каждый вопрос обучающиеся строят модель (на карандашах).
III. Устный счет
1)На клетчатой бумаге с размером клетки 1см×1см изображен параллелограмм. Найдите длину его большей высоты. Ответ дайте в квадратных сантиметрах.
2)
Найдите длину средней линии трапеции, если её основания равны 44 см и 60 см.
МК = (AD + ВС) / 2 = (44 + 60) / 2 = 104/2=52; Ответ: 52.
Средняя линия трапеции равна полусумме её оснований.
3) АВС вписан в окружность, АС=6, ВС=8, С=900. Найдите радиус окружности, описанной около этого треугольника.
Вписанный угол, опирающийся на полуокружность, — прямой.
Радиус окружности, описанной около прямоугольного треугольника равен половине гипотенузы.
Теорема Пифагора
Квадрат гипотенузы равен сумме квадратов катетов.
4) Периметр квадрата равен 100. Найдите площадь квадрата.
5) Найдите площадь квадрата, если радиус вписанной в него окружности равен 5.
IV. Математический диктант с последующей взаимопроверкой
1) Укажите номер верного утверждения
1) Сумма вертикальных углов равна 1800
2) Сумма двух смежных углов равна 1800
3) Сумма углов прямоугольного треугольника равна 900
2) Укажите номер верного утверждения
1). Площадь квадрата равна произведению двух его смежных сторон.
2). Диагональ трапеции делит её на два равных треугольника.
3). Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
3) Какое из следующих утверждений верно?
1) У любой трапеции боковые стороны равны.
2) Площадь прямоугольника равна произведению длин его смежных сторон.
3) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
4) Укажите номер неверного утверждения
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
5) Укажите номер неверного утверждения
Если две прямые перпендикулярны третьей, то эти прямые перпендикулярны.
Через любую точку плоскости можно провести прямую.
Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то прямые параллельны.
Проверка
1)2)
3)
4)
5)
2
1
2
2
1
V. Тест с последующей самопроверкой.
«Математику нельзя изучать, наблюдая, как это делает сосед»
Айвен Нивен
ТЕСТ «Решение задач по геометрии»
1)
а) 250 б) 600 в) 300 г) 150
Ответ: 300
2)а) 42 б) 112 в) 110 г) 68
Ответ: 420
3)
а) 17,5 б) 19 в) 20 г) 21
Ответ: 19
4)
а) 24 б) 48 в) 72 г) 36
Ответ: 36
5) а) 1 б) 2 в) 3 г) 13
Проверка теста
12
3
4
5
в
а
б
г
а
VI. Физкультминутка (Офтальмо пауза).
А теперь давайте проведём небольшую офтальмо паузу и дадим отдохнуть нашим глазам.
VII. Задание на дом: Повторить тему «Центральные и вписанные углы», вариант ОГЭ, online (по желанию)
VIII. Поиграем!
Различные игры со словами – одно из самых известных и любимых развлечений многих. В этих задачах нужна наблюдательность, эрудиция, собранность, развивающая конструктивное мышление. В течение 1 минуты составьте как можно больше слов, состоящих из букв слова ГЕОМЕТРИЯ (время). У кого получилось самое длинное слово?
Метеор, терем, метро, метр, темя, море, гиря, ярмо…
Метео́р (др.-греч.μετέωρος, «небесный»), «падающая звезда» — явление, возникающее при сгорании в атмосфере Земли мелких метеорных тел.
IX. Работа в парах (ОГЭ). «Величие человека в его способности мыслить» Блез Паскаль.
Два угла вписанного в окружность четырехугольника равны 880 и 720.
Найдите больший из оставшихся углов. Ответ дайте в градусах
А=880 ,В=720,А+С=1800, В+Д=1800 .
А>В, значит С<Д.Находим наибольший угол, значит Д.
X. Самостоятельная работа
1) В АВС АС=ВС, высота АН=50, С=300 . Найдите АС.
Из ∆АНС, АС = 2АН = 2 * 50 = 100 Ответ: 100.
Катет, лежащий напротив угла в 30о, равен половине гипотенузе.
В равнобедренном ∆АВС АВ=ВС, А=550 . Найдите В.
, А=С, В=1800-2∙550 =700
Ответ: 70
В треугольнике сумма углов равна 180°
В равнобедренном треугольнике углы при основании равны
3)
Найдите площадь треугольника АВС
Найдите площадь параллелограмма.
На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.
Найти радиус окружности
Найти угол ВОС, если угол ВАС = 70°
В окружность с центром O вписан =. Найдите .
Найдите тангенс угла AOB.
На клетчатой бумаге с клетками размером 1 см*1 см изображена трапеция. Найдите ее площадь в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см * 1 см изображен треугольник. Найдите его площадь в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.
Найти площадь трапеции
Найти площадь трапеции
Меньшая сторона прямоугольника равна 42, диагонали пересекаются под углом 600. Найдите диагонали прямоугольника.
Найдите площадь четырёхугольника.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найти углы ромба.
Углы В и С ∆АВС равны соответственно 710 и 790.Найти ВС, если радиус окружности, описанной около ∆АВС равен 8.
Высота АН ромба АВСД делит сторону СД на отрезки ДН=16 и СН=4.Найти высоту ромба.
Окружность с центром на стороне АС ∆АВС проходит через вершину С и касается прямой АВ в точке В.Найдите АС, если диаметр окружности равен 16, а АВ=15.
Дополнительное задание: решить задачу на карточке «ОГЭ II часть»
XI. Итог урока.
Критерии:
8 — 11 баллов- «3»;
Больше 13 баллов- «4»;
Больше 15 баллов, с учетом, что решена задача из II части — «5».
Стадия рефлексии. Осуществляется с использованием компьютера и проектора.
Вопросы учителя:
Что сегодня на уроке мы повторили?
Что показалось наиболее интересным?
Чему научились?
Для чего вы это делали?
Какие из задач оказались наиболее трудными?
Сегодня вы еще больше убедились, как важно уметь применять полученные знания, ведь они вам нужны будут на выпускных экзаменах. Не беда, если у вас сегодня что – то не получилось. Не зря говорится: «Не стыдно не знать, стыдно не учиться». Но я считаю, что вы сегодня хорошо потрудились. И получили заслуженные отметки (оценить). У кого–то сегодня хорошие результаты, а у кого — то и ошибки. Но не надо огорчаться. Ошибка – это всего лишь подсказка – над чем нужно ещё поработать. Поэтому помните слова Цицерона:
“Ошибаться может каждый, – оставаться при своей ошибке – только безумный”, и следуйте им.
Отметьте смайликом ваше отношение к уроку, прикрепив его на доске, возле своего имени.
– урок полезен, все понятно.
– лишь кое-что чуть-чуть неясно, ещё придется потрудиться.
– да, трудно все-таки учиться!
И закончить урок мне хочется притчей. Ребята послушайте, пожалуйста, притчу: Шел мудрец, а навстречу ему три человека, везли под горячим солнцем тележки с камнями для строительства Храма. Мудрец остановился и задал каждому по вопросу.
У первого спросил: « Что ты делал целый день?» И тот с ухмылкою ответил, что целый день возил проклятые камни.
У второго спросил: « А ты что делал целый день? И тот ответил: « Я добросовестно выполнял свою работу».
А третий улыбнулся ему, лицо засветилось радостью и удовольствием, и ответил «А я принимал участие в строительстве Храма».
-Ребята! Кто работал, так как первый человек?
-Кто работал добросовестно?
-А кто принимал участие в строительстве Храма знаний?
Спасибо за урок!
ИмяТ.Р.
У.С.
М.Д
Тест
Игра
Г. Р.
С.Р. (дополнительно)
Итог
Женя
Кирилл
Снежана
Денис
ТЕСТ «Решение задач по геометрии»
1)
а) 250 б) 600 в) 300 г) 150
2)а) 42 б) 112 в) 110 г) 68
3)
а) 17,5 б) 19 в) 20 г) 21
4)
а) 24 б) 48 в) 72 г) 36
5) а) 1 б) 2 в) 3 г) 13
Проверка теста
12
3
4
5
Математический диктант с последующей взаимопроверкой
ОГЭ, № 20
1) Укажите номер верного утверждения
1) Сумма вертикальных углов равна 1800
2) Сумма двух смежных углов равна 1800
3) Сумма углов прямоугольного треугольника равна 900
2) Укажите номер верного утверждения
1). Площадь квадрата равна произведению двух его смежных сторон.
2). Диагональ трапеции делит её на два равных треугольника.
3). Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
3) Какое из следующих утверждений верно?
1) У любой трапеции боковые стороны равны.
2) Площадь прямоугольника равна произведению длин его смежных сторон.
3) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
4) Укажите номер неверного утверждения
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
5) Укажите номер неверного утверждения
Если две прямые перпендикулярны третьей, то эти прямые перпендикулярны.
Через любую точку плоскости можно провести прямую.
Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то прямые параллельны.
Проверка
1)2)
3)
4)
5)
Модуль «Геометрия» содержит 8 заданий:
в I части — 5 заданий, вo II части — 3 задания.
ОГЭ № 24, 1 вариантРасстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найти углы ромба.
ОГЭ № 24, 2 вариант
Углы В и С ∆АВС равны соответственно 710 и 790.Найти ВС, если радиус окружности, описанной около ∆АВС равен 8.
ОГЭ № 24, 3 вариант
Высота АН ромба АВСД делит сторону СД на отрезки ДН=16 и СН=4.Найти высоту ромба.
ОГЭ № 24, 4 вариант
Окружность с центром на стороне АС ∆АВСпроходит через вершину С и касается прямой АВ в точке В.Найдите АС, если диаметр окружности равен 16, а АВ=15.
ОГЭ № 9, 1 вариант
В АВС АС=ВС, высота АН=50, С=300. Найдите АС.
ОГЭ № 9, 2 вариант
В равнобедренном ∆АВС АВ=ВС, А=550 . Найдите В.
ОГЭ № 9, 3 вариант
Найдите площадь треугольника АВС
ОГЭ № 9, 4 вариант
Найдите площадь параллелограмма.
ОГЭ № 10, 1 вариант
На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.
ОГЭ № 10, 2 вариант
Найти радиус окружности
ОГЭ № 10, 3 вариант
Найти угол ВОС, если угол ВАС = 70°
ОГЭ № 10, 4 вариант
В окружность с центром O вписан =. Найдите .
ОГЭ № 12, 1 вариант
Найдите тангенс угла AOB.
ОГЭ № 12, 2 вариант
На клетчатой бумаге с клетками размером 1 см*1 см изображена трапеция. Найдите ее площадь в квадратных сантиметрах.
ОГЭ № 12, 3 вариант
На клетчатой бумаге с клетками размером 1 см * 1 см изображен треугольник. Найдите его площадь в квадратных сантиметрах.
ОГЭ № 12, 4 вариант
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура. Найдите ее площадь в квадратных сантиметрах.
ОГЭ № 11, 1 вариант
Найти площадь трапеции
ОГЭ № 11, 2 вариант
Найти площадь трапеции
ОГЭ № 11, 3 вариант
Меньшая сторона прямоугольника равна 42, диагонали пересекаются под углом 600. Найдите диагонали прямоугольника.
ОГЭ № 11, 4 вариант
Найдите площадь четырёхугольника.
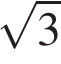 .
.
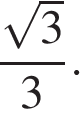
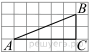 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке. 40 см?
40 см?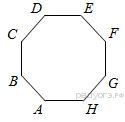 ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.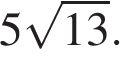 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.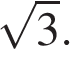
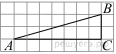 Найдите тангенс угла B треугольника ABC, изображённого на рисунке.
Найдите тангенс угла B треугольника ABC, изображённого на рисунке.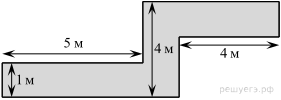 Определите, сколько необходимо закупить пленки
Определите, сколько необходимо закупить пленки  для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова. Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.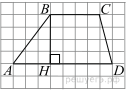
 На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите, длину пути (в м), если масштаб 1 см: 10000 см.
На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите, длину пути (в м), если масштаб 1 см: 10000 см.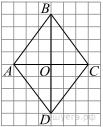
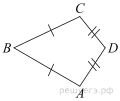 В выпуклом четырехугольнике ABCD
В выпуклом четырехугольнике ABCD  ,
,  ,
,  ,
,  . Найдите угол A. Ответ дайте в градусах.
. Найдите угол A. Ответ дайте в градусах.