Гидростатический парадокс — Википедия
Материал из Википедии — свободной энциклопедии
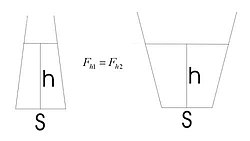
 Схема опыта Паскаля
Схема опыта ПаскаляГидростатический парадокс или парадокс Паскаля — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равна весу жидкости лишь для сосуда цилиндрической формы. Математическое объяснение парадоксу было дано Симоном Стевином в 1612 году[1].
Причина гидростатического парадокса состоит в том, что по закону Паскаля жидкость давит не только на дно, но и на стенки сосуда.
Если стенки сосуда вертикальные, то силы давления жидкости на его стенки направлены горизонтально и не имеют вертикальной составляющей. Сила давления жидкости на дно сосуда в этом случае равна весу жидкости в сосуде. Если же сосуд имеет наклонные стенки, давление жидкости на них имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда, поэтому он и отличается от давления на дно[2].
В 1648 году парадокс продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Гидростатический парадокс и закон Архимеда[править | править код]
Похожий кажущийся парадокс возникает при рассмотрении закона Архимеда. Согласно распространённой формулировке закона Архимеда, на погружённое в воду тело действует выталкивающая сила, равная весу воды, вытесненной этим телом. Из такой формулировки можно сделать неверное умозаключение, что тело не сможет плавать в сосуде, не содержащем достаточное количество воды для вытеснения.
Однако на практике тело может плавать в резервуаре с таким количеством воды, масса которой меньше массы плавающего тела. Это возможно в ситуации, когда резервуар лишь ненамного превышает размеры тела. Например, когда корабль стоит в тесном доке, он остаётся на плаву точно так же, как в открытом океане, хотя масса воды между кораблём и стенками дока может быть меньше, чем масса корабля[3].
Объяснение парадокса заключается в том, что архимедова сила создаётся гидростатическим давлением, которое зависит не от веса воды, а только от высоты её столба. Как в гидростатическом парадоксе на дно сосуда действует сила весового давления воды, которая может быть больше веса самой воды в сосуде, так и в вышеописанной ситуации давление воды на днище корабля может создавать выталкивающую силу, превышающую вес этой воды
Более корректной формулировкой закона Архимеда является следующая: на погружённое в воду тело действует выталкивающая сила, эквивалентная весу воды в погружённом объёме тела[3].
- Бутиков Е.И., Кондратьев А.С, Бобкин В.В. Физика. Книга 1. Механика. — М.: Наука, 1994. — 367 с.
Исследование границ применимости закона Архимеда
li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc8809912 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc8809912 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc8809912 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc8809912 ul.lst-kix_list_1-0{list-style-type:none}#doc8809912 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc8809912 .lst-kix_list_2-5>li:before{content:»» counter(lst-ctn-kix_list_2-5,lower-roman) «. «}#doc8809912 .lst-kix_list_2-8>li:before{content:»» counter(lst-ctn-kix_list_2-8,lower-roman) «. «}#doc8809912 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc8809912 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc8809912 ul.lst-kix_list_1-3{list-style-type:none}#doc8809912 ul.lst-kix_list_1-4{list-style-type:none}#doc8809912 ul.lst-kix_list_1-1{list-style-type:none}#doc8809912 ul.lst-kix_list_1-2{list-style-type:none}#doc8809912 ul.lst-kix_list_1-7{list-style-type:none}#doc8809912 ul.lst-kix_list_1-8{list-style-type:none}#doc8809912 ul.lst-kix_list_1-5{list-style-type:none}#doc8809912 ul.lst-kix_list_1-6{list-style-type:none}#doc8809912 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc8809912 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc8809912 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc8809912 .lst-kix_list_2-6>li{counter-increment:lst-ctn-kix_list_2-6}#doc8809912 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc8809912 ol.lst-kix_list_2-2{list-style-type:none}#doc8809912 ol.lst-kix_list_2-3{list-style-type:none}#doc8809912 ol.lst-kix_list_2-4{list-style-type:none}#doc8809912 ol.lst-kix_list_2-5{list-style-type:none}#doc8809912 ol.lst-kix_list_2-0{list-style-type:none}#doc8809912 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc8809912 ol.lst-kix_list_2-1{list-style-type:none}#doc8809912 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc8809912 .lst-kix_list_1-0>li:before{content:»\0025cf «}#doc8809912 ol.lst-kix_list_2-6{list-style-type:none}#doc8809912 .lst-kix_list_1-1>li:before{content:»o «}#doc8809912 .lst-kix_list_1-2>li:before{content:»\0025aa «}#doc8809912 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc8809912 ol.lst-kix_list_2-7{list-style-type:none}#doc8809912 ol.lst-kix_list_2-8{list-style-type:none}#doc8809912 .lst-kix_list_1-3>li:before{content:»\0025cf «}#doc8809912 .lst-kix_list_1-4>li:before{content:»o «}#doc8809912 .lst-kix_list_1-7>li:before{content:»o «}#doc8809912 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc8809912 .lst-kix_list_1-5>li:before{content:»\0025aa «}#doc8809912 .lst-kix_list_1-6>li:before{content:»\0025cf «}#doc8809912 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «. «}#doc8809912 .lst-kix_list_2-1>li:before{content:»» counter(lst-ctn-kix_list_2-1,lower-latin) «. «}#doc8809912 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc8809912 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc8809912 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc8809912 .lst-kix_list_1-8>li:before{content:»\0025aa «}#doc8809912 .lst-kix_list_2-2>li:before{content:»» counter(lst-ctn-kix_list_2-2,lower-roman) «. «}#doc8809912 .lst-kix_list_2-3>li:before{content:»» counter(lst-ctn-kix_list_2-3,decimal) «. «}#doc8809912 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc8809912 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc8809912 ol{margin:0;padding:0}#doc8809912 .c1{padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;text-align:justify;direction:ltr}#doc8809912 .c5{padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;direction:ltr}#doc8809912 .c27{padding-top:0pt;padding-bottom:36pt;line-height:1.0;orphans:2;widows:2;direction:ltr}#doc8809912 .c25{vertical-align:baseline;font-size:18pt;font-family:»Times New Roman»;font-weight:bold}#doc8809912 .c6{vertical-align:baseline;font-size:16pt;font-family:»Times New Roman»;font-weight:bold}#doc8809912 .c8{vertical-align:sub;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc8809912 .c7{vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»;font-weight:bold}#doc8809912 .c0{vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc8809912 .c15{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc8809912 .c32{vertical-align:baseline;font-size:16pt;font-family:»Times New Roman»;font-weight:normal}#doc8809912 .c30{vertical-align:baseline;font-size:18pt;font-family:»Times New Roman»;font-weight:normal}#doc8809912 .c31{vertical-align:baseline;font-size:13pt;font-family:»Times New Roman»;font-weight:normal}#doc8809912 .c10{background-color:#ffffff;max-width:506.5pt;padding:45pt 42.5pt 56.7pt 63pt}#doc8809912 .c11{margin-left:6.2pt;text-indent:7.7pt;margin-right:7.2pt}#doc8809912 .c19{margin-left:6.2pt;text-indent:9.4pt;margin-right:6.7pt}#doc8809912 .c2{margin-left:5pt;text-indent:9.1pt;margin-right:7.2pt}#doc8809912 .c23{margin-left:132.5pt;text-indent:200.5pt}#doc8809912 .c12{margin-left:333pt;text-indent:2.5pt}#doc8809912 .c3{text-indent:9.1pt;height:11pt}#doc8809912 .c9{text-decoration:underline;font-style:italic}#doc8809912 .c13{margin-left:1.4pt;text-indent:9.1pt}#doc8809912 .c4{height:11pt}#doc8809912 .c20{margin-left:0.5pt}#doc8809912 .c28{font-style:italic}#doc8809912 .c24{text-align:center}#doc8809912 .c22{text-decoration:underline}#doc8809912 .c16{text-indent:9.1pt}#doc8809912 .c17{text-indent:8.8pt}#doc8809912 .c18{margin-right:12.9pt}#doc8809912 .c21{text-indent:9.3pt}#doc8809912 .c26{margin-left:333pt}#doc8809912 .c14{text-indent:10.1pt}#doc8809912 .c29{text-indent:9.6pt}#doc8809912 .title{padding-top:24pt;color:#000000;font-weight:bold;font-size:36pt;padding-bottom:6pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 .subtitle{padding-top:18pt;color:#666666;font-size:24pt;padding-bottom:4pt;font-family:»Georgia»;line-height:1.15;page-break-after:avoid;font-style:italic;orphans:2;widows:2;text-align:left}#doc8809912 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc8809912 p{margin:0;color:#000000;font-size:11pt;font-family:»Arial»}#doc8809912 h2{padding-top:24pt;color:#000000;font-weight:bold;font-size:24pt;padding-bottom:6pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h3{padding-top:18pt;color:#000000;font-weight:bold;font-size:18pt;padding-bottom:4pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h4{padding-top:14pt;color:#000000;font-weight:bold;font-size:14pt;padding-bottom:4pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h5{padding-top:12pt;color:#000000;font-weight:bold;font-size:12pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h5{padding-top:11pt;color:#000000;font-weight:bold;font-size:11pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h6{padding-top:10pt;color:#000000;font-weight:bold;font-size:10pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 ]]>МОУ Краснореченская ООШ
Исследование границ применимости закона Архимеда
Выполнил: ученик 8 класса
Ширинкин Виктор
Руководитель: учитель физики
Санин Ю.В.
2015
Оглавление:
1.Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3
2. Погрешности узкого сосуда. . . . . . . . . . . . . . . . . . . . . . . . .4-6
3. «Прилипание» к дну и стенкам . . . . . . . . . . . . . . . . . . . ….6-7
4. Закон Архимеда в невесомости . . . . .. . . . . . . . . . . . . . . . 7-8
5. Ускорение и сила Архимеда . . . . . . . . . . . . . . . . . . . . . . . 8-9
6. Выводы . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . .. . 9
7. Литература . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . .. . . 10
1. Введение
В школе изучается много различных законов. Большинство из них имеют те или иные границы применимости. Знания о границах применимости позволяют безошибочно применять законы в различных ситуациях. Проводя некоторые опыты и получая не совпадающие с теорией результаты, возникла идея о выяснении условий, при которых закон гидростатики не выполняется. Чтобы тщательно изучить этот вопрос, необходимо было найти и обработать большое количество информации, провести ряд опытов. Вся эта работа- внесение своего вклада в науку. Возможно, данный материал не имеет практической значимости, но работать над этим материалом было очень интересно.
2. Чтобы детально разобраться в вопросе о границах применимости закона Архимеда, нужно начать с рассмотрения необходимой, возможно знакомой всем, информации.
Закон Архимеда впервые был упомянут им в трактате «О плавающих телах». Архимед писал: » тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела».
Этот закон, едва ли не первый физический закон, с которым мы знакомимся в школе. Он справедлив не только для жидкостей, но и для газов. Сила, выталкивающая погруженное тело, называется архимедовой, или гидростатической, подъемной силой. Появляется она потому, что верхняя и нижняя поверхности тела находятся на разной глубине и, следовательно, испытывают разные силы давления со стороны выше лежащих слоев газа или жидкости.
Воздух сжимаем, у поверхности Земли его плотность заметно выше, чем на высоте нескольких километров. Поэтому воздушный шар, увлекаемый вверх архимедовой силой, остановится, дойдя до некоторой высоты, на которой вес вытесненного воздуха станет равным весу шара. Вода практически несжимаема, поэтому в ней такой картины наблюдать нельзя: если тело начало тонуть, то оно опустится до самого дна.
Всё кажется простым и знакомым. Но всё ли так просто, как кажется? Чтобы ответить на этот вопрос, попробуем объяснить результаты одного эксперимента.
Эксперимент. Оборудование: широкий сосуд (таз), песок, два сосуда, вода.
Ход выполнения: 1. Наполним широкий сосуд водой на ¾ объема.
Два других сосуда необходимо подобрать таких размеров, чтобы один входил в другой с небольшим зазором. Для наглядности эксперимента можно взять градуированную стеклянную банку и цилиндрическую мензурку, но можно использовать и два любых сосуда, для которых выполняются те же условия (небольшой зазор).
2. В меньший сосуд (банку) насыплем такое количество песка, чтобы она держалась на плаву в широком сосуде с водой.
3.Отметим на стенке мензурки глубину её погружения.
4.Определим примерное значение веса банки с песком.
Если в эксперименте используется сосуд с делениями, то объём вытесненной воды можно примерно принять равным величине деления на сосуде, до которого произошло погружение. (В др.случае можно воспользоваться измерительным цилиндром и отливным сосудом для определения объёма вытесненной жидкости.)
Поскольку банка находится в состоянии равновесия, плавает, то, значит, ее вес скомпенсирован выталкивающей силой, равной весу вытесненной жидкости. По количеству вытесненной воды можно определить вес банки с песком. (Примерное значение.)
5. Наполним цилиндрическую мензурку водой так, чтобы её вес был в 1,5-2 раза меньше веса банки с песком и опустим в неё банку с песком. Будет ли плавать эта банка с песком в сосуде (мензурке) немного большего диаметра, в который налито воды меньше, чем необходимо для плавания тела по закону Архимеда? (снимок I)
Естественно предположить, что выталкивающей силы уже не хватит на то, чтобы скомпенсировать вес банки и что банка с песком просто встанет на дно. Чтобы выяснить это, продолжим эксперимент.
7. Наблюдая за банкой убеждаемся в том, что банка, как и в опыте с широким сосудом плавает, погрузившись до того же, деления, что и при плавании в широком сосуде.
Это неожиданный результат. В чем же здесь дело? Почему она плавает?
Чтобы ответить на эти вопросы, нужно вспомнить другой закон гидростатики, открытый в XVII веке французским ученым Б. Паскалем и носящий его имя: «Давление, создаваемое внешними силами, передаетcя без изменения в каждую точку жидкости». В жидкости, находящейся под действием только одной силы тяжести, давление одинаково во всех точках любой горизонтальной плоскости. Эти плоскости называются поверхностями уровня или поверхностями равного давления. Пример такой плоскости — горизонтальная поверхность уровня в сообщающихся сосудах, например, в чайнике и его носке. Давление на любом уровне зависит только от высоты столба жидкости над ним и не зависит от ее массы. Поэтому общая сила F, которая давит на дно сосуда (она равна произведению давления Р на площадь дна S), может быть и больше и меньше веса воды, налитой в сосуд (см, рисунок), в зависимости от формы сосуда. Это на первый взгляд странное явление, открытое Б. Паскалем, получило название «гидростатический парадокс». Оно наводит на мысль, что в сосуде определённой формы можно получить огромные силы давления очень малым количеством жидкости. Сам Паскаль демонстрировал это с помощью бочки с водой и присоединённой к ней тонкой вертикальной трубки, длиной несколько метров. Когда в трубку влили пару кружек воды, наполнив ее доверху, бочка лопнула под действием силы давления F, равной весу столба воды высотой в несколько метров
(давление Р) и диаметром с бочку (площадь S)! Давление в жидкости передается во все стороны одинаково, поэтому струи воды из щелей хлынули во все стороны практически с равной силой,
Гидростатический парадокс приводит к разгадке «неправильного» поведения банки с песком в опыте с «узким» сосудом. Тонкий слой воды, оставшийся между стенками сосудов (банки с песком и мензурки), оказывает такое же давление на дно банки с песком, что и столб воды той же высоты в сосуде большого объема. Именно это давление и заставляет банку плавать.
Следовательно, чем уже зазор между стенками, тем меньшее количество воды вытеснит плавающее тело, тем сильнее нарушается закон Архимеда. Если бы не силы поверхностного натяжения, которые могут играть заметную роль при очень узком зазоре, любое тело можно было бы заставить плавать, в любом, сколь угодно малом количестве воды. Кажется непонятным, что о столь заметном нарушении закона Архимеда не упоминается ни в одном из многочисленных учебников и справочников по физике. Ведь это явление следовало бы, наверное, учитывать при гидростатическом взвешивании, когда определяют вес тела, погруженного в жидкость, при работе с ареометром, которым измеряют плотность жидкости и в других случаях.
Возникает вопрос о поправках к закону Архимеда, о границах его применимости. Но при более детальном рассмотрении этого вопроса становится ясно, что на самом деле эти поправки не нужны.
Если в опыте с «узким» сосудом мензурку наполнить водой до краев и опустить в него банку с песком, то собранной вылившейся воды будет столько, сколько и должно было быть вытеснено по закону Архимеда.
Учитывая это можно прийти к общепризнанному выводу о том, что закон Архимеда — частный случай закона Паскаля, справедливый только для больших объемов жидкости. Поэтому определение выталкивающей силы (равна весу вытесненной жидкости), которое дал Архимед, не подходит к случаю плавания тел в малых объёмах жидкости. Следовательно, в случае с малыми объёмами жидкости, применение закона Архимеда ограничено.
3.Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем одной из сторон прижато ко дну или стенке сосуда.
При рассмотрении закона Архимеда мы считали, что тело полностью погружено в жидкость и вся его поверхность соприкасается с жидкостью. Если же часть поверхности тела плотно прилегает к стенке или дну сосуда, так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Яркой иллюстрацией сказанного служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Брусок не всплывает, так как со стороны воды на него действует сила, не выталкивающая его вверх, а прижимающая ко дну (рис.)
Это явление учитывается при подъёме затонувших кораблей. Прежде чем приступить к подъёму, затонувшее судно вначале «отрывают» от дна и только затем приступают непосредственно к подъёму.
4. Тело, погруженное в жидкость, вытеснит часть этой жидкости. На нее, со стороны окружающей жидкости будет действовать такая же выталкивающая сила, как и на погруженное тело. По третьему закону Ньютона выделенная в объеме тела жидкость будет действовать на окружающую жидкость с той же самой по модулю, но противоположно направленной силой. Это — вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета, называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.
Итак, выталкивающая сила, действующая на погруженное в жидкость тело, равна по модулю и противоположна по направлению весу вытесненной жидкости. Это и есть закон Архимеда. Заметим, что в формулировке закона говорится именно о весе вытесненной жидкости, а не о силе тяжести. И это весьма существенно, так как вес тела (по модулю) не всегда совпадает с силой тяжести. Например, ящик массой m в кабине поднимающегося с ускорением а лифта давит на пол с силой m(g + a). Это значит, что вес ящика равен Р = m(g + a), в то время как сила тяжести, действующая на ящик, равна mg. Когда же кабина лифта опускается с тем же ускорением, вес ящика оказывается равным Р = m(g — a).
Из последнего выражения ясно, что выталкивающая сила появляется тогда, когда нет состояния невесомости, то есть любое тело (в том числе и жидкость) имеет вес. Если сосуд с жидкостью свободно падает, то жидкость находится в состоянии невесомости и на погруженное в нее тело сила Архимеда не действует. Не действует эта сила и в космическом корабле, движущемся с выключенными двигателями. Подтверждением этого служит отсутствие в невесомости явления естественной конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.
В земных условиях убедиться в том, что закон Архимеда в невесомости не действует, можно с помощью опыта с «картезианским водолазом». Нажмите на корпус бутылки так, чтобы водолаз опустился на дно. Затем «поместите его в невесомость»: подбросив (или уронив) бутылку, не изменяя её вертикального положения. Следите за поведением водолаза во время свободного полёта: всплывёт он или нет. В эти краткие мгновения на бутылку действует только сила тяжести (силой сопротивления воздуха можно пренебречь) и её содержимое находится в невесомости. Для получения более точных данных нужно повторить опыт несколько раз и можно самостоятельно сделать вывод о действии закона Архимеда в невесомости.
5. Рассмотрим ситуацию, в которой сила Архимеда девствует на тело, движущееся с ускорением внутри жидкости. Будет ли в этом случае выполняться закон Архимеда? Представим себе легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= ρ Vg и сила натяжения нити T, а вверх — сила гидростатического давления F=FАрх= -ρVg, (*)
где ρт- плотность тела, ρ — плотность жидкости. Условие равновесия тела
-ρVg +T+ ρтVg =0. (1)
Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вверх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения
F+ ρтV g = ρV a. (2)
Предположив, что в этом случае можно использовать закон Архимеда, подставим — -ρVg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение
a = — g (ρ- ρт)/ ρт (3)
Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.
Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости)
6. Выводы:
В окружающем нас мире происходит огромное количество различных по своей природе явлений. Некоторые из них, даже при современном уровне развития науки, остаются загадками для человека. Много тайм хранит в себе бескрайняя вселенная и микромир. Но всё это многообразие явлений подчиняется вполне определённым законам, которые мы уже открыли и которые ещё предстоит открыть. Поэтому при изучении законов не может быть мелочей и выяснение границ применимости – тоже очень важно. Эти знания помогут понять, где и как можно применять тот или иной закон, расширят кругозор.
Выполняя данную работу можно сделать следующие выводы:
1. Применение закона Архимеда ограничено к случаю плавания тел в малых объёмах жидкости.
2. Закон Архимеда не распространяется на тела, находящиеся в состоянии невесомости.
3.При ускоренном движении тела, находящегося в жидкости или газе, расчёт силы Архимеда затруднён.
7.Литература:
Учебно-методическое пособие. ИДУ Татьянкин Б.А. и др
Журнал «Наука и жизнь» №7 1983г.
portfolio.1september.ru
elementy.ru›Энциклопедия›21067
http://www.physbook.ru/index.php/Kvant._Выталкивающая_сила
http://www.phys.spbu.ru/library/schoollectures/manida
Файл:Закон Архимеда.webm — Википедия

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поискуКраткое описание
| ОписаниеЗакон Архимеда.webm | Русский: Видеоурок: Закон Архимеда |
| Дата | |
| Источник | GetAClass channel on Youtube |
| Автор | GetAClass |
Лицензирование
  | Этот файл доступен по лицензии Creative Commons Attribution 3.0 Unported | |
| Атрибуция: «GetAClass» web project | ||
https://creativecommons.org/licenses/by/3.0 CC BY 3.0 Creative Commons Attribution 3.0 truetrue |
История файла
Нажмите на дату/время, чтобы посмотреть файл, который был загружен в тот момент.
| Дата/время | Миниатюра | Размеры | Участник | Примечание | |
|---|---|---|---|---|---|
| текущий | 12:50, 6 октября 2014 | 3 м 36 с, 1920 × 1080 (20,7 Мб) | Rubin16 | Videoconvert upload from toollabs |
Использование файла
Следующие 2 страницы используют данный файл:
- Архимед
- Закон Архимеда
Файл содержит дополнительные данные, обычно добавляемые цифровыми камерами или сканерами. Если файл после создания редактировался, то некоторые параметры могут не соответствовать текущему изображению.
Файл:Закон Архимеда.webm — Википедия

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поискуКраткое описание
| ОписаниеЗакон Архимеда.webm | Русский: Видеоурок: Закон Архимеда |
| Дата | |
| Источник | GetAClass channel on Youtube |
| Автор | GetAClass |
Лицензирование
  | Этот файл доступен по лицензии Creative Commons Attribution 3.0 Unported | |
| Атрибуция: «GetAClass» web project | ||
https://creativecommons.org/licenses/by/3.0 CC BY 3.0 Creative Commons Attribution 3.0 truetrue |
История файла
Нажмите на дату/время, чтобы посмотреть файл, который был загружен в тот момент.
| Дата/время | Миниатюра | Размеры | Участник | Примечание | |
|---|---|---|---|---|---|
| текущий | 12:50, 6 октября 2014 | 3 м 36 с, 1920 × 1080 (20,7 Мб) | Rubin16 | Videoconvert upload from toollabs |
Использование файла
Следующие 2 страницы используют данный файл:
- Архимед
- Закон Архимеда
Файл содержит дополнительные данные, обычно добавляемые цифровыми камерами или сканерами. Если файл после создания редактировался, то некоторые параметры могут не соответствовать текущему изображению.