определение и формула :: SYL.ru
Часто научные открытия становятся следствием простой случайности. Но только люди с подготовленным умом могут оценить важность простого совпадения и сделать из него далеко идущие выводы. Именно благодаря цепи случайных событий в физике появился закон Архимеда, объясняющий поведение тел в воде.
Предание
В Сиракузах об Архимеде слагали легенды. Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Архимед установил, что в воздухе и в воде тела имеют разный вес, причем разность прямо пропорциональна плотности измеряемого тела. Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.
 По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.
По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.Формулировка
Результаты своих опытов Архимед изложил в труде «О плавающих телах», который, к сожалению, дошел до наших дней лишь в виде отрывков. Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.

Действие жидкостей и газов на погруженное тело
Любой предмет, погруженный в жидкость, испытывает на себе силы давления. В каждой точке поверхности тела данные силы направлены перпендикулярно поверхности тела. Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.
Физическая формула
Наглядно силу Архимеда можно продемонстрировать простым взвешиванием. Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
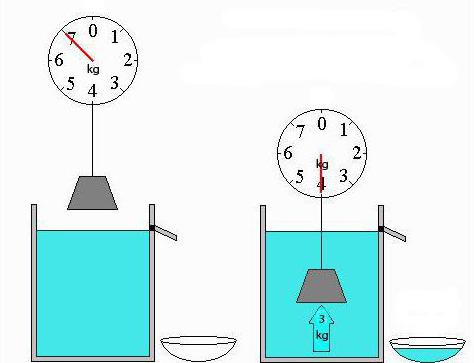
Если принять вес тела в вакууме за Ро, то его вес в воздушной среде может быть описан такой формулой: Рв=Ро — Fа;
здесь Ро – вес в вакууме;
Fа — сила Архимеда.
Как видно из рисунка, любые действия со взвешиванием в воде значительно облегчают тело, поэтому в таких случаях сила Архимеда обязательно должна учитываться.
Для воздуха эта разность ничтожна, поэтому обычно вес тела, погруженного в воздушную среду, описывается стандартной формулой.
Плотность среды и сила Архимеда
Анализируя простейшие опыты с весом тела в различных средах, можно прийти к выводу, что вес тела в различных средах зависит от массы объекта и плотности среды погружения. Причем чем плотнее среда, тем больше сила Архимеда. Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Формула
Архимедову силу и силы, которые на нее влияют, можно определить при помощи простых логических умозаключений. Предположим, что тело определенного объема, погруженное в жидкость, состоит из тоже же самой жидкости, в которую оно погружено. Это предположение не противоречит никаким другим предпосылкам. Ведь силы, действующие на тело, никоим образом не зависят от плотности этого тела. В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.
Таким образом, равновесие тела в воде будет описываться так.
Но сила тяжести, из условия, равна весу жидкости, которую она вытесняет: масса жидкости равна произведению плотности на объём. Подставляя известные величины, можно узнать вес тела в жидкости. Этот параметр описывается в виде ρV * g.
Подставляя известные значения, получаем:
F = ρV * g.
Это и есть закон Архимеда.
Формула, выведенная нами, описывает плотность, как плотность исследуемого тела. Но в начальных условиях было указано, что плотность тела идентична плотности окружающей его жидкости. Таким образом, в данную формулу можно смело подставлять значение плотности жидкости. Визуальное наблюдение, согласно которому в более плотной среде сила выталкивания больше, получило теоретическое обоснование.
Применение закона Архимеда
Первые опыты, демонстрирующие закон Архимеда, известны еще со школьной скамьи. Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило — важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.

Закон Архимеда необходим и подводникам. Дело в том, что плотность морской воды меняет свое значение в зависимости от глубины погружения. Правильный расчет плотности позволит подводникам правильно рассчитать давление воздуха внутри скафандра, что повлияет на маневренность водолаза и обеспечит его безопасное погружение и всплытие. Закон Архимеда должен учитываться также и при глубоководном бурении, огромные буровые вышки теряют до 50% своего веса, что делает их транспортировку и эксплуатацию менее затратным мероприятием.
www.syl.ru
Закон Архимеда Википедия
Видеоурок: закон АрхимедаЗако́н Архиме́да — один из законов статики жидкостей (гидростатики) и газов (аэростатики): на тело, погружённое в жидкость или газ, действует выталкивающая или подъёмная сила, равная весу объёма жидкости или газа, вытесненного частью тела, погружённой в жидкость или газ. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой или гидростатической подъёмной силой[1][2].
Так как сила Архимеда обусловлена силой тяжести, то в невесомости она не действует.
В соответствии с законом Архимеда для выталкивающей силы выполняется[3]:
- FA=ρgV,{\displaystyle F_{A}=\rho gV,}
где:
Описание
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.
FA=Fp;{\displaystyle F_{A}=F_{p};}
ρж g Vж = ρт g Vт
Например, воздушный шарик объёмом V{\displaystyle V}, наполненный гелием, летит вверх из-за того, что плотность гелия (ρH{\displaystyle \rho _{H}}) меньше плотности воздуха (ρO{\displaystyle \rho _{O}}):
FA>Fp;{\displaystyle F_{A}>F_{p};}
ρOgV>ρHgV.{\displaystyle \rho _{O}gV>\rho _{H}gV.}
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (PA{\displaystyle P_{A}}) и сила давления (FA{\displaystyle F_{A}}), действующие на верхнюю грань тела, равны:
- PA=ρghA;{\displaystyle P_{A}=\rho gh_{A};}
- FA=ρghAS,{\displaystyle F_{A}=\rho gh_{A}S,}
где:
Давление (PB{\displaystyle P_{B}}) и сила давления (FB{\displaystyle F_{B}}), действующие на нижнюю грань тела, равны:
- PB=ρghB;{\displaystyle P_{B}=\rho gh_{B};}
- FB=ρghBS,{\displaystyle F_{B}=\rho gh_{B}S,}
где:
- PB{\displaystyle P_{B}} — давление, оказываемое жидкостью или газом на нижнюю грань тела, Па;
- FB{\displaystyle F_{B}} — сила давления, действующая на нижнюю грань тела и направленная вверх, Н;
- hB{\displaystyle h_{B}} — расстояние между поверхностью жидкости или газа и нижней гранью тела, м.
Сила давления жидкости или газа на тело определяется разностью сил FB{\displaystyle F_{B}} и FA{\displaystyle F_{A}}:
- FB−FA=ρghBS−ρghAS=ρg(hB−hA)S=ρghS=ρgV,{\displaystyle F_{B}-F_{A}=\rho gh_{B}S-\rho gh_{A}S=\rho g\left(h_{B}-h_{A}\right)S=\rho ghS=\rho gV,}
где:
- h=hB−hA{\displaystyle h=h_{B}-h_{A}} — расстояние между верхней и нижней гранями тела (в случае частичного погружения высота части тела, погружённой в жидкость или газ), м;
- V{\displaystyle V} — объём тела, погружённого в жидкость или газ (в случае частичного погружения объём части тела, погружённой в жидкость или газ), м3.
Разница давлений:
- PB−PA=ρghB−ρghA=ρgh.{\displaystyle P_{B}-P_{A}=\rho gh_{B}-\rho gh_{A}=\rho gh.}
В отсутствие гравитационного поля, то есть, в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление p{\displaystyle p} на глубине h{\displaystyle h}, оказываемое жидкостью плотностью ρ{\displaystyle \rho } на тело, есть p=ρgh{\displaystyle p=\rho gh}. Пусть плотность жидкости (ρ{\displaystyle \rho }) и напряжённость гравитационного поля (g{\displaystyle g}) — постоянные величины, а h{\displaystyle h} — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxyz{\displaystyle Oxyz}, причём выберем направление оси z совпадающим с направлением вектора g→{\displaystyle {\vec {g}}}. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку dS{\displaystyle dS}. На неё будет действовать сила давления жидкости, направленная внутрь тела, dF→A=−pdS→{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
- F→A=−∫SpdS→=−∫SρghdS→=−ρg∫ShdS→=∗−ρg∫Vgrad(h)dV=∗∗−ρg∫Ve→zdV=−ρge→z∫VdV=(ρgV)(−e→z).{\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z}).}
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
- ∗h(x,y,z)=z;{\displaystyle {}^{*}h(x,y,z)=z;}
- ∗∗grad(h)=∇h=e→z.{\displaystyle ^{**}grad(h)=\nabla h={\vec {e}}_{z}.}
Получаем, что модуль силы Архимеда равен ρgV{\displaystyle \rho gV}, и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Замечание. Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погружённого тела на жидкость, приводит к изменению её потенциальной энергии:
A=−F∗(h2−h3)=−ΔEp=−mжgΔh{\displaystyle \ A=-F*(h2-h3)=-\Delta E_{p}=-m_{\text{ж}}g\Delta h},
где mж−{\displaystyle m_{\text{ж}}-}масса вытесненной части жидкости, Δh{\displaystyle \Delta h} — перемещение её центра масс. Отсюда модуль вытесняющей силы:
F=mжg{\displaystyle \ F=m_{\text{ж}}g}
По третьему закону Ньютона эта сила, равна по модулю и противоположна по направлению силе Архимеда, действующей со стороны жидкости на тело. Объём вытесненной жидкости равен объёму погруженной части тела, поэтому массу вытесненной жидкости можно записать как:
mж=ρжVт,{\displaystyle \ m_{\text{ж}}=\rho _{\text{ж}}V_{\text{т}},} где Vт−{\displaystyle V_{\text{т}}-}объем погружённой части тела.
Таким образом для силы Архимеда имеем:
FA= F=mжg=ρжgVт.{\displaystyle \ F_{A}=\ F=m_{\text{ж}}g=\rho _{\text{ж}}gV_{\text{т}}.}
Условие плавания тел
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести FT{\displaystyle F_{T}} и силы Архимеда FA{\displaystyle F_{A}}, которые действуют на это тело. Возможны следующие три случая:
- FT>FA{\displaystyle F_{T}>F_{A}} — тело тонет;
- FT=FA{\displaystyle F_{T}=F_{A}} — тело плавает в жидкости или газе;
- FT<FA{\displaystyle F_{T}<F_{A}} — тело всплывает до тех пор, пока не начнёт плавать.
Другая формулировка (где ρt{\displaystyle \rho _{t}} — плотность тела, ρs{\displaystyle \rho _{s}} — плотность среды, в которую тело погружено):
- ρt>ρs{\displaystyle \rho _{t}>\rho _{s}} — тело тонет;
- ρt=ρs{\displaystyle \rho _{t}=\rho _{s}} — тело плавает в жидкости или газе;
- ρt<ρs{\displaystyle \rho _{t}<\rho _{s}} — тело всплывает до тех пор, пока не начнёт плавать.
Примечания
Ссылки
wikiredia.ru
Закон Архимеда | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Закон (Сила) Архимеда — На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.
В интегральной форме
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами
В формуле мы использовали :
— Сила Архимеда
— Плотность жидкости
— Объем погруженного тела
— Ускорение свободного падения
— Давление в произвольной точке
xn--b1agsdjmeuf9e.xn--p1ai
ЗАКОН АРХИМЕДА | Энциклопедия Кругосвет
ЗАКОН АРХИМЕДА – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
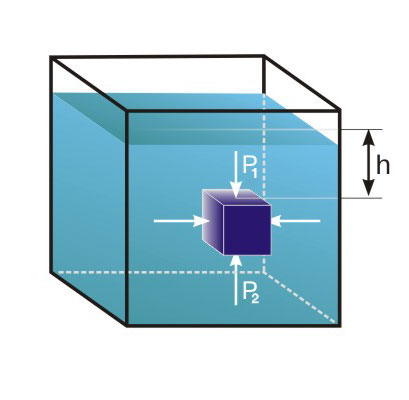
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.
Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть
r · g · h = p1
а на нижнюю
r · g(h+a) = p2
Сила давления равна давлению, умноженному на площадь, т.е.
F1 = p1 · a\up122, F2 = p2 · a\up122 , где a – ребро кубика,
причем сила F1 направлена вниз, а сила F2 – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – F1 и F2 и определяется их разностью, которая и является выталкивающей силой:
F2 – F1 =r · g · (h+a) a\up122 – rgha ·a2 = pga2
Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина F2 – F1= pga3 равна объему тела (кубика) a3, умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли.Если тело произвольной формы (рис. 2) занимает внутри жидкости объем V, то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).
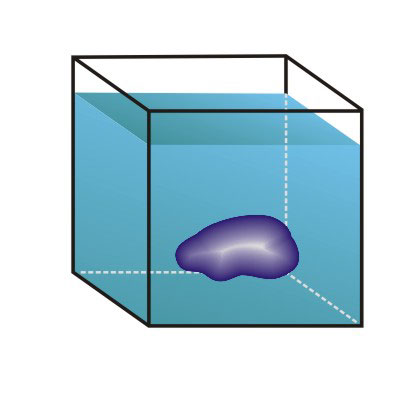
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема V – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема V. Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V, т.е. pgV.
Сделав мысленно обратную замену – поместив в объеме V данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема V, можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.
Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» g, т.е. веса единицы объема вещества: g = pg; если принять, что для воды g = 1, то сплошное тело из вещества, у которого g > 1 утонет, а при g < 1 будет плавать на поверхности; при g = 1 тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
Владимир Кузнецов
www.krugosvet.ru
СИЛА АРХИМЕДА (ВЫТАЛКИВАЮЩАЯ СИЛА)
СИЛА АРХИМЕДА (ВЫТАЛКИВАЮЩАЯ СИЛА)
1МО Г.о. Подольск МОУ СОШ пос. МИС
Яшина В.В. 11МО, Г.о. Подольск, МОУ СОШ пос. МИС
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Актуальность: Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»
Моя исследовательская работа направлена на то, чтобы углубить полученные на уроке знания об архимедовой силе. Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук — это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Гипотеза: Я предполагаю, что в домашних условиях можно рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело и определить зависит ли она от свойств жидкости, объема и формы тела.
Объект исследования: Выталкивающая сила в жидкостях.
Цель: Рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело.
Задачи:
— изучить историю открытия архимедовой силы;
— изучить учебную литературу по вопросу действия архимедовой силы;
— выработать навыки проведения самостоятельного эксперимента;
— доказать, что значение выталкивающей силы зависит от плотности жидкости.
Методы исследования:
— исследовательские;
— расчетные;
— информационного поиска;
— наблюдений
1. Открытие силы Архимеда
Существует знаменитая легенда о том, как Архимед бежал по улице и кричал «Эврика!» Это как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.
В III веке до нашей эры жил Гиерон — царь древнегреческого города Сиракузы и захотел он сделать себе новую корону из чистого золота. Отмерил его строго сколько нужно, и дал ювелиру заказ. Через месяц мастер вернул золото в виде короны и весила она столько, сколько и масса данного золота. Но ведь всякое бывает и мастер мог схитрить, добавив серебро или того хуже – медь, ведь на глаз не отличишь, а масса такая, какая и должна быть. А царю узнать охота: честно ль сделана работа? И тогда, попросил он ученого Архимеда, проверить из чистого ли золота сделал мастер ему корону. Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: . Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Из истории известно, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Опыты, проведенные Архимедом, были описаны в сочинении «О плавающих телах», которое дошло до нас. Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом: тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Открытие основного закона гидростатики — крупнейшее завоевание античной науки.
2. Формулировка и пояснения закона Архимеда
Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является одним из главных законов гидростатики и статики газов.
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела – эта сила называется силой Архимеда:
,
где – плотность жидкости (газа), — ускорение свободного падения, — объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).
Следовательно, архимедова сила зависит только от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погруженного в жидкость, так как эта величина не входит в полученную формулу.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
3. Определение силы Архимеда
Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно определить на опыте используя данный прибор:
Небольшое ведерко и тело цилиндрической формы подвешиваем на пружине, закрепленной в штативе. Растяжение пружины отмечаем стрелкой на штативе, показывая вес тела в воздухе. Приподняв тело, под него подставляем стакан с отливной трубкой, наполненный жидкостью до уровня отливной трубки. После чего тело погружают целиком в жидкость. При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
На основании этого опыта можно заключить, что сила, выталкивающая тело, целиком погруженное в жидкость, равна весу жидкости в объёме этого тела. Зависимость давления в жидкости (газе) от глубины погружения тела приводит к появлению выталкивающей силы (силы Архимеда), действующей на любое тело, погруженное в жидкость или газ. Тело при погружении двигается вниз под действием силы тяжести. Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Данный опыт подтверждает, что архимедова сила равна весу жидкости в объёме тела.
4. Условие плавания тел
На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
При этом возможны три случая:
1) Если сила тяжести больше архимедовой силы, то тело опускается вниз, то есть тонет:
, то тело тонет;
2) Если модуль силы тяжести равен модулю архимедовой силы, то тело может находиться в равновесии внутри жидкости на любой глубине:
, то тело плавает;
3) Если архимедова сила больше силы тяжести, то тело будет поднимается из жидкости – всплывать:
, то тело плавает.
Если всплывающее тело частично выступает над поверхностью жидкости, то объем погруженной части плавающего тела такой, что вес вытесненной жидкости равен весу плавающего тела.
Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела, если
1) =— тело плавает в жидкости или газе,2) >— тело тонет,3) < — тело всплывает до тех пор, пока не начнет плавать.
Именно эти принципы соотношения силы тяжести и силы Архимеда применяются в судоходостронии. Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Для воздухоплавания вначале использовали воздушные шары, которые раньше наполняли нагретым воздухом, сейчас – водородом или гелием. Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
5. Проведение эксперимента
-
Исследовать поведение сырого яйца в жидкостях разного рода.
Задача: доказать, что значение выталкивающей силы зависит от плотности жидкости.
Я взял одно сырое яйцо и жидкости разного рода (приложение 1):
— вода чистая;
— вода, насыщенная солью;
— подсолнечное масло.
Сначала я опустил сырое яйцо в чистую воду – яйцо утонуло — «пошло ко дну» (приложение 2). Потом в стакан с чистой водой я добавил столовую ложку поваренной соли, в результате яйцо плавает (приложение 3). И наконец, я опустил яйцо в стакан с подсолнечным маслом — яйцо опустилось на дно (приложение 4).
|
Название жидкости |
Плотность жидкости, |
Поведение тела в жидкости |
|
Чистая вода |
1000 |
Тело утонуло |
|
Соленая вода |
1030 |
Тело плавает |
|
Подсолнечное масло |
930 |
Тело утонуло |
Вывод: в первом случае плотность яйца больше плотности воды и поэтому яйцо утонуло. Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло. Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
2. Действие Архимедовой силы на тело человека в воде.
Задачи:
— определить на опыте плотность тела человека, сравнить ее с плотностью пресной и морской воды и сделать вывод о принципиальной возможности человека плавать;
— вычислить вес человека в воздухе, архимедову силу, действующую на человека в воде.
Для начала с помощью весов я измерил массу своего тела. Затем измерил объем тела (без объема головы). Для этого я налил в ванну воды столько, чтобы при погружении в воду я был полностью в воде (за исключением головы). Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ1, а затем – при погружении в воду ℓ2. После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ1 до уровня ℓ2 – так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:
.
Сила тяжести, действующая на тело в воздухе, была рассчитана по формуле: , где – ускорение свободного падения ≈ 10 . Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
|
Масса испытуемого (без учета массы головы), кг |
53 |
|
Объем тела человека (без объема головы), м3 |
0,052 |
|
Плотность тела человека (без учета головы), |
1019 |
|
Плотность пресной воды, |
1000 |
|
Плотность морской воды, |
1030 |
|
Сила тяжести, действующая на тело в воздухе, Н |
530 |
|
Значение выталкивающей силы в пресной воде, Н |
520 |
|
Значение выталкивающей силы в морской воде, Н |
536 |
Вывод:Тело человекаплотнее пресной воды, а, значит, оно в ней тонет. Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.
Заключение
В процессе работы над этой темой мы узнали для себя много нового и интересного. Круг наших познаний увеличился не только в области действия силы Архимеда, но и применении ее в жизни. Перед началом работы мы имели о ней далеко неподробное представление. При проведении опытов мы подтвердили экспериментально справедливость закона Архимеда и выяснили, что выталкивающая силазависит от объема тела и плотности жидкости, чем больше плотность жидкости, тем архимедова сила больше. Результирующая сила, которая определяет поведение тела в жидкости, зависит от массы, объёма тела и плотности жидкости.
Помимо проделанных экспериментов, была изучена дополнительная литература об открытии силы Архимеда, о плавании тел, воздухоплавании.
Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.
Список литературы
1.Большая книга экспериментов для школьников – М.: Росмэн, 2009. – 264 с.
2. Википедия: https://ru.wikipedia.org/wiki/Закон_Архимеда.
3. Перельман Я.И. Занимательная физика. — книга 1. — Екатеринбург.: Тезис, 1994.
4. Перельман Я.И. Занимательная физика. — книга 2.- Екатеринбург.: Тезис, 1994.
5. Перышкин А.В. Физика: 7 класс: учебник для общеобразовательных учреждений / А.В. Перышкин. — 16-е изд., стереотип. — М.: Дрофа, 2013. – 192 с.: ил.
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Просмотров работы: 10218
school-science.ru
ФИЗИКА: Задачи на силу Архимеда с решениями
Задачи на силу Архимеда с решениями
Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».
Название величины | Обозначение | Единица измерения | Формула |
Объем тела | V | м3 | Vт = FA / pg |
Плотность жидкости | p | кг/м3 | pж = FA / (Vg) |
Сила Архимеда | FA | Н | FA = pж Vт g |
Постоянная | g ≈ 10 Н/кг | Н/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Тело объемом 2 м3 погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2. Определить выталкивающую силу, действующую на деревянный плот объемом 12 м3, погруженный в воду на половину своего объема.

Задача № 3. Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4. Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5. Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6. Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

Задача № 7. Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?

Задача № 8. Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.

Задача № 9 (повышенной сложности). Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности). Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».
Следующая тема: «Задачи на механическую работу».
uchitel.pro
Ответы@Mail.Ru: Напишите закон Архимеда!
Закон Архимеда: на тело, погружённое в жидкость (или газ) , действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа) (называемая силой Архимеда) Математическое выражение закона: FA = ρgV, где ρ — плотность жидкости (газа) , g — ускорение свободного падения, а V — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности) . Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа) , и приложена к центру тяжести этого объёма.
Который? Тело погруженное в жидкость — вытесняет такой, же объем воды, какой имеет само. Этот?
Всяко тело, впёрто в воду, Выпирает на свободу Силой выпертой воды, Тела, впёртого туды. Тело впертое под воду Выперает и воды, Силой выпертой воды Тела впертого туды. Тело впёрнутое в воду Выпирает на свободу С силой выпертой воды Тела впёртого туды. Если ТЕЛО вперто в воду, Не потонет оно сроду. Отопрет из-под воды Силой выпертой воды. Тело, впернутое в воду — Выпирает на свободу. Сколько выперто воды — Столько впернуто туды. Тело, втиснутое в воду Не теряет весу сроду, Оно прется из туды Весом выпертой воды. Ежли тело впэрто в воду — Воно чуэ там невзгоду. И вылазэ вин туды Силой выпертой воды. Тело, впернутое в воду, Выпирает на свободу Объем выпертой воды, Равный впертому туды. Всяко тело, вперто в воду, Не утонет вон и с роду. Ибо прется из туды Силой выпертой воды. Тело всунутуе в воду, Выпирает на свободу, С силой выпертой воды, Тела впёртого туды Тело, впёрнутое в воду Выпирает на свободу С силой выпертой воды Телом, впёрнутым туды.. . Якщо тіло вперто в воду — Воно чуэ там невзгоду. И вилазе від туди Силою випертої води. Кожне тіло, вперте в воду, Не витримує незгоди Так и пнеться із води З силою випертої води
Следствие из принципа наименьшего действия в потенциальном поле: интеграл d (Fl) -> min можно перефразировать: «система стремится к состоянию с наименьшей потенциальной энергией». Применительно к равномерному полю (F = const = mg) и постоянной плотности (m = ро*V) получается закон Архимеда. Читай принцип экстремального действия. Это — один из базовых законов физики. Именно благодаря ему всё тяжёлое (т. е. плотное) падает вниз и выталкивает вверх более лёгкое.
Закон (Сила) Архимеда — На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа
Я тебе не Архимед, что-бы писАть
После плотного обеда, по закону Архимеда, что-бы жиром не заплыть, полагается курить 🙂
touch.otvet.mail.ru