Закон сохранения механической энергии. Видеоурок. Физика 9 Класс
Темой урока является один из фундаментальных законов природы – закон сохранения механической энергии.
Мы ранее говорили о потенциальной и кинетической энергии, а также о том, что тело может обладать вместе и потенциальной, и кинетической энергией. Прежде чем говорить о законе сохранения механической энергии вспомним, что такое полная энергия. Полной механической энергией называют сумму потенциальной и кинетической энергий тела.

Также вспомним, что называют замкнутой системой. Замкнутая система – это такая система, в которой находится строго определенное количество взаимодействующих между собой тел и никакие другие тела извне на эту систему не действуют.
Когда мы определились с понятием полной энергии и замкнутой системы, можно говорить о законе сохранения механической энергии. Итак, полная механическая энергия в замкнутой системе тел, взаимодействующих друг с другом посредством сил тяготения или сил упругости (консервативных сил), остается неизменной при любом движении этих тел.
Мы уже изучали закон сохранения импульса (ЗСИ):

Очень часто случается так, что поставленные задачи можно решить только с помощью законов сохранения энергии и импульса.
Рассмотреть сохранение энергии удобно на примере свободного падения тела с некоторой высоты. Если некоторое тело находится в состоянии покоя на некоторой высоте относительно земли, то это тело обладает потенциальной энергией. Как только тело начинает свое движение, высота тела уменьшается, уменьшается и потенциальная энергия. При этом начинает нарастать скорость, появляется энергия кинетическая. Когда тело приблизилось к земле, то высота тела равна 0, потенциальная энергия тоже равна 0, а максимальной будет являться кинетическая энергия тела. Вот здесь и просматривается превращение потенциальной энергии в кинетическую (рис. 1). То же самое можно сказать о движении тела наоборот, снизу вверх, когда тело бросают вертикально вверх.

Рис. 1. Свободное падение тела с некоторой высоты
Дополнительная задача 1. «О падении тела с некоторой высоты»
Задача 1
Условие
Тело находится на высоте 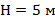 от поверхности Земли и начинает свободно падать. Определите скорость тела в момент соприкосновения с землей.
от поверхности Земли и начинает свободно падать. Определите скорость тела в момент соприкосновения с землей.
Решение 1:
Начальная скорость тела 
 .
.Рассмотрим закон сохранения энергии.

Рис. 2. Движение тела (задача 1)
В верхней точке тело обладает только потенциальной энергией:  . Когда тело приблизится к земле, то высота тела над землей будет равна 0, а это означает, что потенциальная энергия у тела исчезла, она превратилась в кинетическую:
. Когда тело приблизится к земле, то высота тела над землей будет равна 0, а это означает, что потенциальная энергия у тела исчезла, она превратилась в кинетическую:
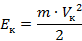
Согласно закону сохранения энергии можем записать:

Масса тела сокращается. Преобразуя указанное уравнение, получаем:  .
.
Окончательный ответ будет:  . Если подставить все значение, то получим:
. Если подставить все значение, то получим: .
.
Ответ: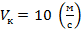 .
.
Пример оформления решения задачи:

Рис. 3. Пример оформления решения задачи № 1
Данную задачу можно решить еще одним способом, как движение по вертикали с ускорением свободного падения.
Решение 2:
Запишем уравнение движения тела в проекции на ось  :
:

Когда тело приблизится к поверхности Земли, его координата будет равна 0:

Перед ускорением свободного падения стоит знак «-», поскольку оно направлено против выбранной оси  .
.
Подставив известные величины, получаем, что тело падало на протяжении времени 

Полагая ускорение свободного падения равным  получаем:
получаем:

Знак минус означает, что тело движется против направления выбранной оси.
Ответ: .
.
Пример оформления решения задачи № 1 вторым способом.

Рис. 4. Пример оформления решения задачи № 1 (способ 2)
Также для решения данной задачи можно было воспользоваться формулой, которая не зависит от времени:

Конечно, нужно отметить, что данный пример мы рассмотрели с учетом отсутствия сил трения, которые в реальности действуют в любой системе. Обратимся к формулам и посмотрим, как записывается закон сохранения механической энергии:
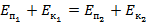
Дополнительная задача 2
Тело свободно падает с высоты 
 кинетическая энергия равна трети потенциальной (
кинетическая энергия равна трети потенциальной (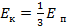 ).
).
Рис. 5. Иллюстрация к задаче № 2
Решение:
Когда тело находится на высоте  , оно обладает потенциальной энергией, и только потенциальной. Эта энергия определяется формулой:
, оно обладает потенциальной энергией, и только потенциальной. Эта энергия определяется формулой:  . Это и будет полная энергия тела.
. Это и будет полная энергия тела.
Когда тело начинает двигаться вниз, уменьшается потенциальная энергия, но вместе с тем нарастает кинетическая. На высоте, которую нужно определить, у тела уже будет некоторая скорость V. Для точки, соответствующей высоте h, кинетическая энергия имеет вид: 
Потенциальная энергия на этой высоте будет обозначена следующим образом:  .
.
По закону сохранения энергии, у нас полная энергия сохраняется. Эта энергия  остается величиной постоянной. Для точки
остается величиной постоянной. Для точки  мы можем записать следующее соотношение:
мы можем записать следующее соотношение: 
Вспоминая, что кинетическая энергия по условию задачи составляет  , можем записать следующее:
, можем записать следующее:  .
.
Обратите внимание: масса и ускорение свободного падения сокращается, после несложных преобразований мы получаем, что высота, на которой такое соотношение выполняется, составляет 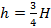 .
.
Ответ: 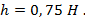
Пример оформления задачи 2.

Рис. 6. Оформление решения задачи № 2
Представьте себе, что тело в некоторой системе отсчета обладает кинетической и потенциальной энергией. Если система замкнутая, то при каком-либо изменении произошло перераспределение, превращение одного вида энергии в другой, но полная энергия остается по своему значению той же самой (рис. 7).

Рис. 7. Закон сохранения энергии
Представьте себе ситуацию, когда по горизонтальной дороге движется автомобиль. Водитель выключает мотор и продолжает движение уже с выключенным мотором. Что в этом случае происходит (рис. 8)?

Рис. 8. Движение автомобиля
В данном случае автомобиль обладает кинетической энергией. Но вы прекрасно знаете, что с течением времени автомобиль остановится. Куда девалась в этом случае энергия? Ведь потенциальная энергия тела в данном случае тоже не изменилась, она была какой-то постоянной величиной относительно Земли. Как произошло изменение энергии? В данном случае энергия пошла на преодоление сил трения. Если в системе встречается трение, то оно также влияет на энергию этой системы. Посмотрим, как записывается в данном случае изменение энергии.


Изменяется энергия, и это изменение энергии определяется работой против силы трения. Определить работу силы трения мы можем с помощью формулы, которая известна из 7 класса (сила и перемещение направлены противоположно):
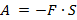

Итак, когда мы говорим об энергии и работе, то должны понимать, что каждый раз мы должны учитывать и то, что часть энергии расходуется на преодоление сил трения. Совершается работа по преодолению сил трения. Работа является величиной, которая характеризует изменение энергии тела.
В заключение урока хотелось бы сказать, что работа и энергия по сути своей связанные величины через действующие силы.
Дополнительная задача 3
Два тела – брусок массой  и пластилиновый шарик массой
и пластилиновый шарик массой 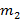 – движутся навстречу друг другу с одинаковыми скоростями (
– движутся навстречу друг другу с одинаковыми скоростями ( ). После столкновения пластилиновый шарик прилип к бруску, два тела продолжают движение вместе. Определить, какая часть механической энергии
). После столкновения пластилиновый шарик прилип к бруску, два тела продолжают движение вместе. Определить, какая часть механической энергии  превратилась во внутреннюю энергию этих тел, с учетом того что масса бруска в 3 раза больше массы пластилинового шарика (
превратилась во внутреннюю энергию этих тел, с учетом того что масса бруска в 3 раза больше массы пластилинового шарика ( ).
).
Решение:
Изменение внутренней энергии можно обозначить  . Как вы знаете, существует несколько видов энергии. Кроме механической, существует еще и тепловая, внутренняя энергия.
. Как вы знаете, существует несколько видов энергии. Кроме механической, существует еще и тепловая, внутренняя энергия.

Рис. 9. Иллюстрация к задаче № 3
Запишем в выбранной системе отсчета закон сохранения импульса (с учетом направления скоростей и оси 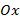 ):
):

Вместо  мы подставим
мы подставим  :
:

Массы сокращаются. Преобразуя это выражение, получаем, что конечная скорость этих тел будет определяться следующим образом:

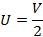
Это означает, что скорость бруска и пластилинового шарика вместе будет в 2 раза меньше, чем скорость до соударения.
Следующий шаг – это закон сохранения энергии.

В данном случае полная энергия – это сумма кинетических энергий двух тел. Тел, которые еще не соприкоснулись, не ударились. Что произошло после соударения? Посмотрите на следующую запись:

В левой части мы оставляем полную энергию, а в правой части мы должны записать кинетическую энергию тел после взаимодействия 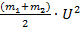 и учесть, что часть механической энергии превратилась в тепло
и учесть, что часть механической энергии превратилась в тепло  .
.
Таким образом, имеем:

Определим отношение  :
: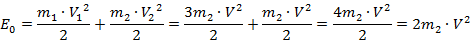

В итоге получаем ответ  .
.
Обратите внимание: в результате такого взаимодействия большая часть энергии превращается в тепло, т. е. переходит во внутреннюю энергию.
Ответ: 
Список литературы
- А так ли хорошо знакомы вам законы сохранения? // Квант. – 1987. – № 5. – с. 32–33.
- Городецкий Е.Е. Закон сохранения энергии // Квант. – 1988. – № 5. – с. 45–47.
- Соловейчик И.А. Физика. Механика. Пособие для абитуриентов и старшеклассников. – СПб.: Агенство ИГРЕК, 1995. – с. 119–145.
- Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «fizikaklass.ru» (Источник)
- Интернет-портал «eduspb.com» (Источник)
- Интернет-портал «msk.edu.ua» (Источник)
Домашнее задание
- Тело массой 10 г колеблется по закону
 . Найдите полную энергию колеблющегося тела.
. Найдите полную энергию колеблющегося тела. - Какие превращения энергии происходят при колебаниях? Что такое полная механическая энергия?
- Тело с некоторой высоты начало свободно падать, и в момент удара о землю его скорость была равна 20 м/с. С какой высоты упало тело?
Закон сохранения энергии | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Закон сохранения энергии — один из наиболее важных законов, согласно которому физическая величина — энергия сохраняется в изолированной системе. Этому закону подчиняются все без исключения известные процессы в природе. В изолированной системе энергия может только превращаться из одной формы в другую, но ее количество остается постоянным.
Для того, чтоб понять что же представляет из себя закон и откуда это получается возьмем тело массой m, которое уроним на Землю. В точке 1 тело у нас находится на высоте h и покоится (скорость равна 0). В точке 2 тело тело имеет некоторую скорость v и находится на расстоянии h-h2. В точке 3 тело имеет максимальную скорость и оно почти лежит на нашей Земле, то есть h=0
В точке 1 тело имеет только потенциальную энергию, так как скорость тела равно 0,так что полная механическая энергия равна.
После того как мы тело отпустили, оно стало падать. При падении потенциальная энергия тела уменьшается, так как уменьшается высота тела над Землей, а его кинетическая энергия увеличивается, так как увеличивается скорость тела. На участке 1-2 равном h2 потенциальная энергия будет равна
А кинетическая энергия будет равная в тот момент ( — скорость тела в точке 2):
Чем ближе тело становится к Земле, тем меньше его потенциальная энергия, но в тот же момент увеличивается скорость тела, а из-за этого и кинетическая энергия. То есть в точке 2 работает закон сохранения энергии: потенциальная энергия уменьшается, кинетическая растет.
В точке 3 (на поверхности Земли) потенциальная энергия равна нулю (так как h = 0), а кинетическая максимальна (где v3 — скорость тела в момент падения на Землю). Так как , то кинетическая энергия в точке 3 будет равна Wk=mgh. Следовательно, в точке 3 полная энергия тела W3=mgh и равна потенциальной энергии на высоте h. Конечная формула закона сохранения механической энергии будет иметь вид:
Формула выражает закон сохранения энергии в замкнутой системе, в которой действуют только консервативные силы: полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию и обратно.
В Формуле мы использовали :
— Полная энергия тела
— Потенциальная энергия тела
— Кинетическая энергия тела
— Масса тела
— Ускорение свободного падения
— Высота на которой находится тело
— Скорость тела
Зако́н сохране́ния эне́ргии — фундаментальный закон природы
Закон сохранения энергии – фундаментальный закон природы
 Содержание этого закона в наиболее краткой формулировке формулируется так : “Энергия любой замкнутой системы при всех процессах, происходящих в системе, остается постоянной. Энергия может только превращаться из одной формы в другую и перераспределяться между частями системы. Для незамкнутой системы увеличение/уменьшение ее энергии равно убыли/возрастанию энергии взаимодействующих с ней тел и физических полей.”
Содержание этого закона в наиболее краткой формулировке формулируется так : “Энергия любой замкнутой системы при всех процессах, происходящих в системе, остается постоянной. Энергия может только превращаться из одной формы в другую и перераспределяться между частями системы. Для незамкнутой системы увеличение/уменьшение ее энергии равно убыли/возрастанию энергии взаимодействующих с ней тел и физических полей.”
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени.
Некоторые авторы не согласны с тем, что энергия является скалярной величиной. Ведь энергия — это физическая величина, характеризующая движение материи, а понятие движение очевидно связано с понятием направления. Закон сохранения энергии в современной трактовке ничего не говорит о сохранении направления движения, так как энергия трактуется как скалярная величина. Поскольку энергия является характеристикой движения, то закон сохранения энергии является частным случаем более общего закона сохранения движения, учитывающего не только сохранение количества энергии, но и сохранение направления движения. Именно закон сохранения движения отражает не только вечное существование материи, но и вечное ее движение. Впрочем, наш сайт — не место для научных споров и мы ограничимся наиболее распространенным понятием энергии как скалярной величины.
Закон сохранения энергии говорит, что энергия не создается из ничего и не теряется бесследно. При всех происходящих в природе процессах один вид энергии превращается в другой. Химическая энергия батареек фонарика превращается в электрическую, в лампочке электрическая энергия превращается в тепловую и световую — это простой пример «энергетической цепочки», показывающий как один вид энергии превращается в другой.
Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
Коэффициент полезного действия
На первый взгляд закон сохранения энергии как бы утверждает, что энергия при любых преобразованиях не должна теряться. Но все мы знакомы с понятием коэффициента полезного действия, то есть знаем, что превращение энергии одного вида в другой связано с потерями энергии. Противоречия тут нет, поскольку речь идет о «полезном действии». Когда мы говорим о коэффициенте полезного действия мы всегда, явно или неявно, имеем в виду некоторый процесс преобразования энергии в работу, причем сравниваем при этом количество затраченной энергии с полученной работой. Но коэффициент полезного действия ни одного реального (необратимого) процесса не может быть 100% при преобразовании энергии в работу (этот принцип известен как второй закон термодинамики). Причина в том, что в ходе любого такого процесса имеют место неизбежные потери энергии, в основном на трение и нагревание участвующих в процессе тел. Трение — это в результате тоже нагревание, то есть часть затраченной энергии всегда переходит в теплоту.
Коэффициент полезного действия (КПД) выражают в процентах.
КПД механизма тем больше, чем большая часть потребляемой энергии превращается в необходимую энергию. Например, а среднем автомобиль преобразует лишь 15% химической энергии бензина в кинетическую энергию. Вся остальная энергия превращается в тепло. КПД флуоресцентных ламп выше КПД обычных электрических лампочек, поскольку во флуоресцентных лампах больше электричества превращается в свет и меньше уходит на производство тепла.
Но при описании таких устройств как тепловые насосы мы встречаемся с утверждениями, что их КПД превышает 100%. На первый взгляд может показаться, что тут есть какое-то противоречие с законом сохранения энергии. В действительности же тут просто некорректно используется понятие КПД. Действительно, достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса. Но для характеристики эффективности теплового насоса нужно применять не КПД, а коэффициент преобразования или отопительный коэффициент СОР (coefficient of performance), равный отношению энергии, отдаваемой потребителю теплоты к мощности, потребляемой компрессором. Поскольку энергия, отдаваемая потребителю перекачивается от источника этой теплоты, значение коэффициэнта преобразования может быть и больше 100%.
Энтропия
Итак, мы видим, что при любом преобразовании энергии в работу количество «полезной» энергии уменьшается, то есть количество энергии для преобразования в работу или теплоту непрерывно уменьшается со временем, так как теплота спонтанно переходит из более теплой области к более холодной. Но первый закон термодинамики гласит, что энергию невозможно создать или уничтожить. Следовательно, количество энергии во вселенной всегда такое же, как было и при ее создании. Другими словами, количество энергии во вселенной остается постоянным, но возможность использования ее для того, чтобы проделать полезную работу, уменьшается при каждой теплопередаче и выполнении работы. Это явление в науке принято характеризовать величиной, которая называется энтропией.
Энтропия — это сокращение доступной энергии вещества в результате передачи энергии. Энтропия используется для измерения уменьшения пригодности энергии в результате процесса.
Термин «энтропия» используется для описания количества хаотичности в любой системе. В термодинамике энтропия указывает расположение молекул вещества или организацию энергии системы. Системы или вещества с высоким значением энтропии более дезорганизованы, чем с низким. Например, у молекул в твердых телах определенная кристаллическая структура, благодаря чему они лучше организованы, и у них ниже значение энтропии. При сообщении телу теплоты и изменении его состояния на жидкое увеличивается уровень его энтропии, так как кинетическая энергия увеличивает колебания молекул, в результате чего их положение становится случайным.
Энтропия увеличивается, когда жидкость изменяет состояние на газообразное при потреблении большего количества тепловой энергии. Такая же аналогия существует при описании порядка источников энергии. Если энергия заключена в ограниченном источнике, у нее низкое значение энтропии. Если она распределена среди большого количества молекул, ее интенсивность уменьшается, увеличивая энтропию. Например, если 1,05 кДж энергии у 1000 молекул передать 1 миллиону молекул, интенсивность энергии уменьшится, а энтропия возрастет.
Энтропию трудно понять, так как это абстрактное понятие беспорядка энергии во вселенной. Этот беспорядок связан с уменьшением пригодности энергии для преобразования в работу. Энергия всегда становится недоступной, если процессы уменьшают ее интенсивность, распространяя ее по вселенной. Если энергия распределена среди бесчисленных молекул вселенной, разница температур самых холодных и самых теплых участков уменьшается. Если разница температур уменьшается, тепловая энергия, которую можно преобразовать в полезную работу, также уменьшается. Следовательно, любой процесс, который производит увеличение энтропии, уменьшает энергию для будущих процессов. В конечном счете наступит момент, когда энтропия вселенной приблизится к максимальному значению, и преобразование теплоты в работу станет невозможным.
Абсолютная энтропия (S) вещества или процесса — это изменение доступной энергии при теплопередаче при данной температуре (Btu/R, Дж/К). Математически энтропия равняется теплопередаче, деленной на абсолютную температуру, при которой происходит процесс. Следовательно, процессы передачи большого количества теплоты больше увеличивают энтропию. Также изменения энтропии увеличатся при передаче теплоты при низкой температуре. Так как абсолютная энтропия касается пригодности всей энергии вселенной, температуру обычно измеряют в абсолютных единицах (R, К).
Удельную энтропию (S) измеряют относительно единицы массы вещества. Температурные единицы, которые используются при вычислении разниц энтропии состояний, часто приводятся с температурными единицами в градусах по Фаренгейту или Цельсию. Так как различия в градусах между шкалами Фаренгейта и Ренкина или Цельсия и Кельвина равные, решение в таких уравнениях будет правильным независимо от того, выражена энтропия в абсолютных или обычных единицах.
Все процессы преобразования энергии в конечном счете увеличивают энтропию вселенной. Вывод отсюда — полезная работа может производиться только до тех пор, пока не иссякли запасы доступной нам энергии.
Вечный двигатель
 Люди веками мечтали (некоторые все еще мечтают) создать устройство, способное бесконечно совершать работу без затрат топлива или других энергетических ресурсов. Но согласно закону сохранения энергии, все попытки создать такой двигатель обречены на провал. К выводу о невозможности создания вечного двигателя ученые пришли после того, как многочисленные попытки создать такой двигатель оказались безуспешными.
Люди веками мечтали (некоторые все еще мечтают) создать устройство, способное бесконечно совершать работу без затрат топлива или других энергетических ресурсов. Но согласно закону сохранения энергии, все попытки создать такой двигатель обречены на провал. К выводу о невозможности создания вечного двигателя ученые пришли после того, как многочисленные попытки создать такой двигатель оказались безуспешными.
Проекты вечных двигателей разделяют на два типа по характеру совершаемой работы:
Вечный двигатель первого рода (физический \ механический, гидравлический, магнитный) — непрерывно действующая машина, которая, будучи запущенной один раз, совершает работу без получения энергии извне. Это устройства механического характера, принцип действия которых основывается на использовании некоторых физических явлений, например, на действии силы тяжести, законе Архимеда, капиллярных явлениях в жидкостях. Возможность работы такой машины неограниченное время означала бы получение энергии из ничего.
Вечный двигатель второго рода (естественный) — тепловая машина, которая в результате совершения цикла полностью преобразует в работу тепло, получаемое от какого- либо одного «неисчерпаемого» источника (океана, атмосферы и т. п.). Классический вечный двигатель второго рода предусматривает возможность накопления тепла за счет работы, затраты которой меньше полученного тепла, и использования части этого тепла для повторного совершения работы в новом цикле. Таким образом, должен образоваться избыток работы. Другой вариант этого двигателя подразумевает упорядочение хаотического теплового движения молекул, в результате чего возникает направленное движение вещества, сопровождаемое понижением его термодинамической температуры.
В результате бесконечных попыток создать вечный двигатель были сформулированы так называемые первое и второе начала термодинамики, которые являются следствиями закона сохранения энергии:
Первое начало термодинамики гласит: изменение внутренней энергии термодинамической системы при переходе ее из одного состояния в другое равно сумме работы внешних сил над системой и количества теплоты, переданного системе, и не зависит от способа, которым осуществляется этот переход, т. е. Q = ΔU + A. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.
Второе начало термодинамики утверждает: невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему. Что также означает, что в замкнутой системе энтропия при любом реальном процессе либо возрастает, либо остается неизменной (т. е. ΔS ≥ 0). Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.
Несмотря на то, что наука давно и окончательно пришла к выводу о невозможности создания вечного двигателя, существует множество энтузиастов, которые продолжают разрабатывать различные проекты такого рода. Чтобы убедиться в этом, достаточно создать запрос на Youtube.com на тему «вечный двигатель».
Решение задач на тему «Закон сохранения энергии». Видеоурок. Физика 7 Класс
На предыдущем уроке мы изучили, какая бывает энергия, и выяснили, в чем заключается закон сохранения энергии. В этом уроке применим эти знания при решении задач
Закон сохранения энергии – в замкнутых системах энергия ниоткуда не берется, никуда не исчезает. Она может только переходить от одного тела к другому и превращаться из одного вида в другой.
Виды механической энергии
Кинетическая энергия (обладают любые движущиеся тела):
 ;
;
где m – масса тела, V – скорость.
Потенциальная энергия (для тела, поднятого над землей):

где h – высота поднятия тела над землей, g – ускорение свободного падения (9,8 Н/кг).
Потенциальная энергия (для упругодеформированных тел):
 ;
;
где k – жесткость тела, х – величина деформации.
Условие
На какую высоту поднимется тело, подброшенное вертикально вверх, с начальной скоростью 20 м/с? При решении задачи не учитывается сопротивление воздуха.
Дано: V=20 м/c; h=?
Решение
Кинетическая энергия, полученная в броске, будет переходить постепенно в потенциальную энергию:


упрощаем это выражение до:

При упрошенных расчетах принято величину ускорения свободного падения (g) рассчитывать как 10 Н/кг.
Математически преобразуем формулу для нахождения h:

Ответ: высота подъема тела 20 метров.
Условие
Необходимо рассчитать жесткость пружины, если известно, что при растяжении ее на 20 см пружина приобрела потенциальную энергию упругодеформированного тела 20 Дж.
Дано: х=20 см=0,2 м; Ер=20 Дж; k=?
Решение
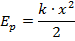
умножаем правую и левую часть на 2, для получения промежуточной формулы:

выражаем величину k:

проверим размерность величины, которую получили:


Ответ: жесткость пружины равна  .
.
Условие
Спусковую пружину игрушечного пистолета сжали на 5 см, при вылете шарик массой 20 г приобрел скорость 2 м/с. Необходимо рассчитать, какова жесткость пружины.
Дано: х=5 см=0,05 м; m=20 г=0,02 кг; V=2 м/с; k=?
Решение
По закону сохранения энергии, потенциальная энергия упругодеформированной пружины перейдет в кинетическую энергию движения шарика:


упрощаем данное выражение:

выражаем величину k:

Ответ: жесткость пружины равна  .
.
При решении задач на этом уроке мы применяли закон сохранения энергии, но не учитывали сопротивление среды, так как считали систему замкнутой. Вспомнили формулировку этого закона и формулы нахождения потенциальной и кинетической энергии.
Список литературы
- Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
- Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
- Перышкин А.В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
Домашнее задание
- Привести пример тела, которое обладает только кинетической энергией.
- С какой скоростью должен двигаться автомобиль массой 7,2 т, чтобы обладать кинетической энергией 8,1 кДж?
- Определите, какой кинетической энергией будет обладать пуля, вылетевшая из винтовки. Скорость пули при вылете равна 500 м/с, масса – 7 г.
- На какую высоту нужно поднять тело массой 5 кг, чтобы его потенциальная энергия увеличилась на 40 Дж?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал School-collection.edu.ru (Источник).
- Интернет-портал School-collection.edu.ru (Источник).
- Интернет-портал Sfiz.ru (Источник).
- Интернет-портал Pskgu.ru (Источник).
- Интернет-портал Docs.google.com (Источник).
Закон сохранения энергии
Во всех явлениях, происходящих в природе, энергия не возникает и не исчезает. Она только превращается из одного вида в другой, при этом ее значение сохраняется.
Закон сохранения энергии — фундаментальный закон природы, заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
Закон сохранения энергии
В электродинамике закон сохранения энергии исторически формулируется в виде теоремы Пойтинга.
Изменение электромагнитной энергии, заключенной в неком объеме, за некий интервал времени равно потоку электромагнитной энергии через поверхность, ограничивающую данный объем, и количеству тепловой энергии, выделившейся в данном объеме, взятой с обратным знаком.
$ \frac{d}{dt}\int_{V}\omega_{em}dV=-\oint_{\partial V}\vec{S}d\vec{\sigma}-\int_V \vec{j}\cdot \vec{E}dV $
Электромагнитное поле обладает энергией, которая распределяется в пространстве, занятом полем. При изменении характеристик поля меняется и распределение энергии. Она перетекает из одной области пространства в другую, переходя, возможно, в другие формы. Закон сохранения энергии для электромагнитного поля является следствием полевых уравнений.
Внутри некоторой замкнутой поверхности S, ограничивающей объем пространства V, занятого полем, содержится энергия W — энергия электромагнитного поля:
W = Σ(εε0Ei2 / 2 + μμ0Hi2 / 2)ΔVi.
Если в этом объеме имеются токи, то электрическое поле производит над движущимися зарядами работу, за единицу времени равную
N = Σij̅i ×E̅i • ΔVi.
Это величина энергии поля, которая переходит в другие формы. Из уравнений Максвелла следует, что
ΔW + NΔt = -Δt∮SS̅ × n̅ • dA, [1]
где ΔW — изменение энергии электромагнитного поля в рассматриваемом объеме за время Δt, а вектор S̅ = E̅ × H̅ называется вектором Пойнтинга.
Это закон сохранения энергии в электродинамике.
Через малую площадку величиной ΔA с единичным вектором нормали n̅ за единицу времени в направлении вектора n̅ протекает энергия S̅ × n̅ • ΔA, где S̅ — значение вектора Пойнтинга в пределах площадки. Сумма этих величин по всем элементам замкнутой поверхности (обозначена знаком интеграла), стоящая в правой части равенства [1], представляет собой энергию, вытекающую из объема, ограниченного поверхностью, за единицу времени (если эта величина отрицательна, то энергия втекает в объем). Вектор Пойнтинга определяет поток энергии электромагнитного поля через площадку, он отличен от нуля всюду, где векторное произведение векторов напряженности электрического и магнитного полей отлично от нуля.
Можно выделить три главных направления практического применения электричества: передача и преобразование информации (радио, телевидение, компьютеры), передача импульса и момента импульса (электродвигатели), преобразование и передача энергии (электрогенераторы и линии электропередачи). И импульс, и энергия переносятся полем через пустое пространство, наличие среды приводит лишь к потерям. Энергия не передается по проводам! Провода с током нужны для формирования электрического и магнитного полей такой конфигурации, чтобы поток энергии, определяемый векторами Пойнтинга во всех точках пространства, был направлен от источника энергии к потребителю. Энергия может передаваться и без проводов, тогда ее переносят электромагнитные волны. (Внутренняя энергия Солнца убывает, уносится электромагнитными волнами, в основном светом. Благодаря части этой энергии поддерживается жизнь на Земле.)
Закон сохранения энергии
В механике закон сохранения энергии утверждает, что в замкнутой системе частиц, полная энергия, которая является суммой кинетической и потенциальной энергии и не зависит от времени, то есть является интегралом движения. Закон сохранения энергии справедлив только для замкнутых систем, то есть при отсутствии внешних полей или взаимодействий.
Силы взаимодействия между телами, для которых выполняется закон сохранения механической энергии называются консервативными силами. Закон сохранения механической энергии не выполняется для сил трения, поскольку при наличии сил трения происходит преобразование механической энергии в тепловую.
Математическая формулировка
Эволюция механической системы материальных точек с массами \( m_i\) по второму закону Ньютона удовлетворяет системе уравнений
\[ m_i\dot{\mathbf{v}_i} = \mathbf{F}_i \]
где
\( \mathbf{v}_i \) — скорости материальных точек, а \( \mathbf{F}_i \) — силы, действующие на эти точки.
Если подать силы, как сумму потенциальных сил \( \mathbf{F}_i^p \) и непотенциальных сил \( \mathbf{F}_i^d \), а потенциальные силы записать в виде
\[ \mathbf{F}_i^p = — \nabla_i U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) \]
то, домножив все уравнения на \( \mathbf{v}_i \) можно получить
\[ \frac{d}{dt} \sum_i \frac{mv_i^2}{2} = — \sum_i \frac{d\mathbf{r}_i}{dt}\cdot \nabla_i U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) + \sum_i \frac{d\mathbf{r}_i}{dt} \cdot \mathbf{F}_i^d \]
Первая сумма в правой части уравнения является ни чем иным, как производной по времени от сложной функции, а следовательно, если ввести обозначения
\[ E = \sum_i \frac{mv_i^2}{2} + U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) \]
и назвать эту величину механической энергией, то, интегрируя уравнения с момента времени t=0 до момента времени t, можно получить
\[ E(t) — E(0) = \int_L \mathbf{F}_i^d \cdot d\mathbf{r}_i \]
где интегрирование проводится вдоль траекторий движения материальных точек.
Таким образом, изменение механической энергии системы материальных точек со временем равно работе непотенциальных сил.
Закон сохранения энергии в механике выполняется только для систем, в которых все силы потенциальные.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
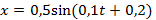 . Найдите полную энергию колеблющегося тела.
. Найдите полную энергию колеблющегося тела.