Інтеграл — Вікіпедія

Інтегра́л — центральне поняття інтегрального числення, узагальнення поняття суми для функції, визначеній на континуумі. Виникає під час розв’язування задач про знаходження площі кривої, знаходження пройденого шляху при нерівномірному русі та інших подібних задачах.
Ви́значений інтегра́л — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
Подальші узагальнення поняття дозволяють розширити його на кратні, поверхневі, об’ємні інтеграли, а також на інтеграли на об’єктах ширшої природи з мірою. Існує кілька різновидів визначених інтегралів: інтеграл Рімана, інтеграл Лебега, інтеграл Стілтьєса тощо.
Невизначений інтеграл[ред. | ред. код]
Нехай дано функцію f(x){\displaystyle f(x)} — функцію дійсної змінної. Неви́значеним інтегра́лом функції f(x){\displaystyle f(x)}, або первісною, називають таку функцію F(x){\displaystyle F(x)}, похідна якої дорівнює f(x){\displaystyle f(x)}, тобто, F′(x)=f(x){\displaystyle F'(x)=f(x)}. Позначається це так: ∫f(x)dx=F(x){\displaystyle \int f(x)\,{\rm {d}}x=F(x)}. Слід зазначити, що первісна існує не для будь-якої функції. Легко бачити, що первісна існує для будь-якої неперервної функції. Оскільки похідні двох функцій, які відрізняються лише на сталу, збігаються, при знаходженні невизначеного інтегралу включають невизначену сталу C,{\displaystyle C,} наприклад
∫x2dx=x33+C,∫cosxdx=sinx+C.{\displaystyle \int x^{2}\,{\rm {d}}x={\frac {x^{3}}{3}}+C,\qquad \int \cos x\,{\rm {d}}x=\sin x+C.}
Що таке інтеграл (анімація)Процес знаходження інтеграла називається інтегрува́нням. Цей процес зазвичай використовується при знаходженні таких величин як площа, об’єм, маса, зсув тощо, коли задана швидкість або розподіл змін цієї величини по відношенню до деякої іншої величини (розташування, час тощо).
Існує декілька різних визначень операції інтегрування, що відрізняються в технічних деталях. Проте всі вони сумісні, тобто будь-які два способи інтегрування, якщо їх можна застосувати до даної функції, дадуть той самий результат.
Інтегрування — операція, обернена до диференціювання, див. основна теорема аналізу. В результаті невизначеного інтегрування виходить функція, яка називається первісною. Першим інтегралом є число (або, принаймні, не залежна від змінної інтегрування частина).
Інтеграл в давнину[ред. | ред. код]
Інтеграція простежується ще в давньому Єгипті, приблизно у 1800 до н.е., Московський математичний папірус демонструє знання формули об’єму січної піраміди. Першим відомим методом для розрахунку інтегралів є метод вичерпування Евдокса (приблизно 370 до н. е.), який намагався знайти площі і об’єми, розриваючи їх на нескінченну безліч частин, для яких площа або об’єм вже відомий. Цей метод був підхоплений і розвинутий Архімедом, і використовувався для розрахунку площ парабол і наближеного розрахунку площі круга. Аналогічні методи були розроблені незалежно в Китаї в 3-м столітті н.е Лю Хуейєм, який використовував їх для знаходження площі круга. Цей метод був згодом використаний Цзу Чунчжи для знаходження об’єму сфери.
Ньютон і Лейбніц[ред. | ред. код]
Основне досягнення в області інтегрування відбулося в 17-му столітті із відкриттям фундаментальної теореми числення (відомої як формула Ньютона — Лейбніца) Ньютоном і Лейбніцем, незалежно один від одного. Теорема встановлює зв’язок між інтегруванням і диференціюванням. Зокрема, фундаментальна теорема числення дозволила вирішувати більш широкий клас задач. Ньютон і Лейбніц створили комплексну математичну теорію, що є не менш важливим. Ця теорія має назву — числення нескінченно малих величин, і дозволила здійснювати точний аналіз неперервних функцій. Ці основоположні роботи зрештою стали сучасним численням, в якому була використана нотація для інтегралів, що на пряму спирається на роботи Лейбніца.
Знак інтеграла (∫), був вперше використаний Лейбніцом наприкінці XVII століття. Цей символ утворився з букви ſ («довга s») — скорочення слова лат. ſumma (summa, сума).
Формальні визначення[ред. | ред. код]
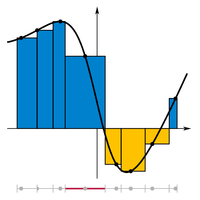
Приклад інтеграла із нерівномирним розділенням (найбільша ділянка відмічена червоним)
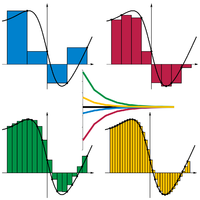
Збіжність ріманової суми
Існує багато способів формального визначення інтеграла, і не всі з них є еквівалентними один одному. Існують відмінності в основному пов’язані із різними особливими випадками, які можуть бути не інтегровані в рамках якихось визначень. Найбільш поширеними і загальними визначеннями інтеграла є ітеграл Рімана і інтеграл Лебега.
Інтеграл Рімана[ред. | ред. код]
Інтеграл Рімана — найпростіший із визначених інтегралів, є границею інтегральної суми. Для функції однієї змінної f(x){\displaystyle f(x)}, визначеній на відрізку [a,b]{\displaystyle [a,b]} та певного розбиття R{\displaystyle R} цього відрізку на відрізки [xi,xi+1]{\displaystyle [x_{i},x_{i+1}]} інтегральна сума визнається як
- σx=∑i=1nf(ξi)Δxi,{\displaystyle \sigma _{x}=\sum \limits _{i=1}^{n}{f(\xi _{i})\Delta x_{i}},}
де xi≤ξi≤xi+1{\displaystyle x_{i}\leq \xi _{i}\leq x_{i+1}} — будь-яка точка з відрізку.
Якщо існує границя таких сум при прямуванні найбільшої довжини відрізку [xi,xi+1]{\displaystyle [x_{i},x_{i+1}]} до нуля, то функція f(x){\displaystyle f(x)} називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку [a,b]{\displaystyle [a,b]} і позначається
- I=∫abf(x)dx{\displaystyle I=\int _{a}^{b}f(x)dx}.
Інтеграл Рімана можна також визначити як границю сум Дарбу.
Інші визначення інтегралу розширюють клас інтегрованих функцій, включаючи в них функції, для яких границі інтегральних сум не існує.
Лінійний функціонал[ред. | ред. код]
На певній області визначення D{\displaystyle D} інтеграл є лінійним функціоналом на просторі функцій:
- ∫Daf=a∫Df{\displaystyle ~\int _{D}af=a\int _{D}f}
- ∫Df+g=∫Df+∫Dg{\displaystyle ~\int _{D}f+g=\int _{D}f+\int _{D}g}
тут f{\displaystyle ~f} і g{\displaystyle ~g} — функції, a{\displaystyle ~a} — число.
Адитивність по області[ред. | ред. код]
Якщо області D{\displaystyle D} та E{\displaystyle E} не перетинаються (або «перетинаються в точці»), інтеграл по об’єднаній області D∪E{\displaystyle D\cup E} є сумою інтегралів по D{\displaystyle D} та E{\displaystyle E}:
- ∫D∪Ef=∫Df+∫Ef{\displaystyle ~\int _{D\cup E}f=\int _{D}f+\int _{E}f}
Монотонність[ред. | ред. код]
Якщо hn(x){\displaystyle h_{n}(x)} незростаюча послідовність (тобто h2≥⋯≥hk≥⋯{\displaystyle h_{1}\geq \cdots \geq h_{k}\geq \cdots }) функцій, які збігаються до нуля для всіх x{\displaystyle x} на області інтегрування, тоді ∫hn→0{\displaystyle \int h_{n}\to 0}.
Нормованість[ред. | ред. код]
Інтеграл сталої функції-константи f(x)=C{\displaystyle ~f(x)=C} розраховується «як площа прямокутника»
- ∫DC=μ(D)C{\displaystyle ~\int _{D}C=\mu (D)C}
де μ(D){\displaystyle \mu (D)} — це «міра» області інтегрування, в простішому випадку просто довжина інтервала, або ж «площа» області інтегрування.
Головна теорема інтегрального числення[ред. | ред. код]
Якщо у функції f(x){\displaystyle f(x)} на відрізку [a,b]{\displaystyle [a,b]} існує первісна F(x){\displaystyle F(x)}, то
- I=∫abf(x)dx=F(b)−F(a){\displaystyle I=\int _{a}^{b}f(x)dx=F(b)-F(a)}
Ця формула називається формулою Ньютона-Лейбніца, або основною формулою інтегрального числення. Вона дає практичний і зручний спосіб обчислення визначеного інтеграла за значеннями первісної на кінцях відрізку інтегрування. Багатовимірні інтеграли обчислюються за допомогою теореми про зведення кратних інтегралів до повторного.
Узагальнення визначеного інтеграла[ред. | ред. код]
Невласний інтеграл[ред. | ред. код]
 Інтеграл «першого роду» на необмеженій області визначення
Інтеграл «першого роду» на необмеженій області визначення 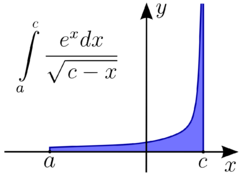 Інтеграл «другого роду» від необмеженої функції
Інтеграл «другого роду» від необмеженої функціїНевласний інтеграл є розширенням поняття визначеного інтегралу; він дозволяє в деяких випадках обраховувати «інтеграл на нескінченості» або «інтеграл від необмеженої функції». В математичному аналізі невласним інтегралом називають границю послідовності визначених інтегралів, коли інтервал інтегрування збільшується до нескінченості, або коли інтервал наближається до особливої точки інтегрованої функції, де та йде у нескінченість.
Невласним інтегралом «першого роду» ∫a+∞f(x)dx{\displaystyle \int \limits _{a}^{+\infty }f(x)dx} називається границя limA→+∞∫aAf(x)dx{\displaystyle \lim _{A\to +\infty }\int \limits _{a}^{A}f(x)dx}, якщо вона існує.
Невласний інтеграл «другого роду» дозволяє в деяких випадках визначити «інтеграл від функції, необмеженої на інтервалі». А саме, нехай функція f(x){\displaystyle f(x)} визначена на (a,b]{\displaystyle (a,b]}, і для кожного малого δ>0{\displaystyle \delta >0} існують інтеграли ∫a+δbf(x)dx=I(δ){\displaystyle \int \limits _{a+\delta }^{b}f(x)dx={I}(\delta )}. Тоді якщо існує дійсна границя limδ→0+0I(δ)=I{\displaystyle \lim _{\delta \to 0+0}I(\delta )=I}, то вона зветься невласним інтегралом «другого роду».
Кратний інтеграл[ред. | ред. код]
 Подвійний інтеграл як об’єм під поверхнею z = x² − y². Прямокутний регіон у основі тіла є областю інтегрування, а поверхня графіка функції двох зміних буде інтегруватися
Подвійний інтеграл як об’єм під поверхнею z = x² − y². Прямокутний регіон у основі тіла є областю інтегрування, а поверхня графіка функції двох зміних буде інтегруватисяКратний інтеграл або ж багатократний інтеграл степеня n, це визначений інтеграл по n змінних з функції n змінних:
- ∫∫∫⋯∫f(x1,x2,x3,⋯xn)dx1dx2dx3⋯dxn{\displaystyle \int \int \int \cdots \int f(x_{1},x_{2},x_{3},\cdots x_{n})\;dx_{1}\;dx_{2}\;dx_{3}\cdots \;dx_{n}}.
Кратний інтеграл — це саме визначений інтеграл, при його обчисленні завжди виходить число
Окремі випадки багатократного інтеграла це:
Для геометричної інтерпретації розглянемо випадок n=2{\displaystyle n=2}. Нехай функція f(x,y){\displaystyle f\left(x,y\right)} приймає в області D{\displaystyle \ D} тільки позитивні значення. Тоді подвійний інтеграл ∬Df(x,y)dσ{\displaystyle \iint \limits _{D}{f\left(x,y\right)d\sigma }} чисельно дорівнює об’єму V{\displaystyle \ V} вертикального циліндрового тіла, побудованого на основі D{\displaystyle \ D} і обмеженого зверху відповідним шматком поверхні z=f(x,y){\displaystyle z=f\left(x,y\right)}.
Головним методом для розрахунку кратного інтеграла є зведення кратного інтеграла до повторних
Хай D⊂Rd−1{\displaystyle D\subset {{\mathbb {R} }^{d-1}}} — вимірна множина, G={(x1,…,xd):(x1,…,xd−1)∈D;φ(x1,…,xd−1)≤xd≤
Інтегрування частинами — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Інтегрування частинами — один із способів знаходження інтеграла.
Суть методу в наступному: якщо підінтегральна функція подана у виді добутку двох неперервних і гла́дких функцій (кожна з яких може бути як елементарною функцією, так і композицією), то справедливі формули:
- для невизначеного інтеграла:
- ∫udv=uv−∫vdu{\displaystyle \int u\,dv=u\,v-\int v\,du}
- для визначеного:
- ∫abudv=uv|ab−∫abvdu{\displaystyle \int \limits _{a}^{b}u\,dv=u\,v\,{\bigg |}_{a}^{b}-\int \limits _{a}^{b}v\,du}
Передбачається, що знаходження інтеграла ∫vdu{\displaystyle \int v\,du} простіше, ніж ∫udv{\displaystyle \int u\,dv\,}. У іншому випадку застосування методу не виправдано.
Для невизначеного інтеграла[ред. | ред. код]
Функції u{\displaystyle \textstyle {\mathit {u}}} і v{\displaystyle \textstyle {\mathit {v}}} гладкі, отже, можливе диференціювання:
- d(uv)=duv+udv{\displaystyle d(u\,v)=du\,v+u\,dv}
Ці функції також неперервні, одже можна взяти інтеграл від обох частин рівності:
- ∫d(uv)=∫duv+∫udv{\displaystyle \int d(u\,v)=\int du\,v+\int u\,dv}
Операція інтегрування протилежна диференціюванню:
- uv=∫duv+∫udv{\displaystyle u\,v=\int du\,v+\int u\,dv}
Після перестановок:
- ∫udv=uv−∫vdu{\displaystyle \int u\,dv=u\,v-\int v\,du}
Для визначеного[ред. | ред. код]
У цілому аналогічно випадку для невизначеного інтеграла:
- d(uv)=duv+udv{\displaystyle d(u\,v)=du\,v+u\,dv}
- ∫abd(uv)=∫abduv+∫abudv{\displaystyle \int \limits _{a}^{b}d(u\,v)=\int \limits _{a}^{b}du\,v+\int \limits _{a}^{b}u\,dv}
- ∫abudv=uv|ab−∫abvdu{\displaystyle \int \limits _{a}^{b}u\,dv=u\,v\,{\bigg |}_{a}^{b}-\int \limits _{a}^{b}v\,du}
- ∫xcosxdx=∫xd(sinx)=xsinx−∫sinxdx=xsinx+cosx+C{\displaystyle \int x\cos x\,dx=\int x\,d(\sin x)=x\sin x-\int \sin x\,dx=x\sin x+\cos x+C}
- ∫exxdx=∫x(exdx)=∫xdex=xex−∫exdx=xex−ex+C{\displaystyle \int e^{x}\,x\,dx=\int x\,(e^{x}\,dx)=\int x\,de^{x}=x\,e^{x}-\int e^{x}\,dx=x\,e^{x}-e^{x}+C}
- Іноді цей метод застосовується кілька разів:
- ∫x2sinxdx=∫x2d(−cosx)=−x2cosx−∫−2xcosxdx={\displaystyle \int x^{2}\sin x\,dx=\int x^{2}\,d(-\cos x)=-x^{2}\cos x-\int -2x\cos x\,dx=}
- =−x2cosx+∫2xd(sinx)=−x2cosx+2xsinx−∫2sinxdx=−x2cosx+2xsinx+2cosx+C{\displaystyle =-x^{2}\cos x+\int 2x\,d(\sin x)=-x^{2}\cos x+2x\sin x-\int 2\sin x\,dx=-x^{2}\cos x+2x\sin x+2\cos x+C}
- Цей метод також використовується для знаходження інтегралів від елементарних функцій:
- ∫lnxdx=xlnx−∫1xxdx=xlnx−x+C{\displaystyle \int \ln x\,dx=x\ln x-\int {\frac {1}{x}}x\,dx=x\ln x-x+C}
- ∫arctgxdx=xarctgx−∫x1+x2dx=xarctgx−12ln(1+x2)+C{\displaystyle \int \operatorname {arctg} \,x\,dx=x\,\operatorname {arctg} \,x-\int {\frac {x}{1+x^{2}}}\,dx=x\,\operatorname {arctg} \,x-{\frac {1}{2}}\ln(1+x^{2})+C}
- У деяких випадках інтегрування частинами не дає прямої відповіді:
- I1=∫eαxsinβxdx={\displaystyle I_{1}=\int e^{\alpha x}\,\sin {\beta x}\,dx=}
- =∫eαxd(−1βcosβx)=−1βeαxcosβx+αβ∫eαxcosβxdx=−1βeαxcosβx+αβI2{\displaystyle =\int e^{\alpha x}\,d{\Big (}-{\frac {1}{\beta }}\cos {\beta x}{\Big )}=-{\frac {1}{\beta }}\,e^{\alpha x}\,\cos {\beta x}+{\frac {\alpha }{\beta }}\int e^{\alpha x}\,\cos {\beta x}\,dx=-{\frac {1}{\beta }}\,e^{\alpha x}\,\cos {\beta x}+{\frac {\alpha }{\beta }}\,I_{2}}
- I2=∫eαxcosβxdx={\displaystyle I_{2}=\int e^{\alpha x}\,\cos {\beta x}\,dx=}
- =∫eαxd(1βsinβx)=1βeαxsinβx−αβ∫eαxsinβxdx=1βeαxsinβx−αβI1{\displaystyle =\int e^{\alpha x}\,d{\Big (}{\frac {1}{\beta }}\sin {\beta x}{\Big )}={\frac {1}{\beta }}\,e^{\alpha x}\,\sin {\beta x}-{\frac {\alpha }{\beta }}\int e^{\alpha x}\,\sin {\beta x}\,dx={\frac {1}{\beta }}\,e^{\alpha x}\,\sin {\beta x}-{\frac {\alpha }{\beta }}\,I_{1}}
- У такий спосіб один інтеграл виражається через інший:
- {I1=−1βeαxcosβx+αβI2I2=1βeαxsinβx−αβI1{\displaystyle {\begin{cases}I_{1}=-{\frac {1}{\beta }}\,e^{\alpha x}\,\cos {\beta x}+{\frac {\alpha }{\beta }}\,I_{2}\\I_{2}={\frac {1}{\beta }}\,e^{\alpha x}\,\sin {\beta x}-{\frac {\alpha }{\beta }}\,I_{1}\end{cases}}}
- Вирішивши отриману систему, одержуємо:
- I1=eαxα2+β2(αsinβx−βcosβx)+C{\displaystyle I_{1}={\frac {e^{\alpha x}}{\alpha ^{2}+\beta ^{2}}}{\Big (}\alpha \sin {\beta x}-\beta \cos {\beta x}{\Big )}+C}
- I2=eαxα2+β2(αcosβx+βsinβx)+C{\displaystyle I_{2}={\frac {e^{\alpha x}}{\alpha ^{2}+\beta ^{2}}}{\Big (}\alpha \cos {\beta x}+\beta \sin {\beta x}{\Big )}+C}
Приклади
Знайти невизначений інтеграл функцій:
f(x) = 1

f(x) = ex

f(x) = sinx

f(x) =


f(x) =

 ,
припустивши, щох
,
припустивши, щох 0,
підінтегральну функцію можна записати
так:
0,
підінтегральну функцію можна записати
так:
Властивості невизначеного інтегралу
Послідовне виконання операції диференціювання та інтегрування в будь-якому порядку з точністю до довільної сталої приводить до початкової функції d(
 )=
f(x)dx
)=
f(x)dx = F(x)+c. Розглянуту властивість можна
сформулювати ще так: операції
диференціювання та інтегрування з
точністю до сталої є взаємно обернені.
= F(x)+c. Розглянуту властивість можна
сформулювати ще так: операції
диференціювання та інтегрування з
точністю до сталої є взаємно обернені.Якщо число а
 0,
то
0,
то =a
=a .
Дана властивість формулюється так:
сталий множник можна виносити за знак
невизначеного інтегралу.
.
Дана властивість формулюється так:
сталий множник можна виносити за знак
невизначеного інтегралу.Невизначений інтеграл від суми (різниці) функції дорівнює сумі (різниці) невизначених інтегралів від кожної функції:
 .
.
Основна таблиця інтегралів
1.

2.

3.

4.

5.

6.

7.
 ;
;
8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

Методи інтегрування
Усі методи інтегрування функцій зводять невизначений інтеграл до інтегралу, який знаходиться в основній таблиці інтегралів або, як кажуть, до табличного інтегралу. Одним із найбільш сильних методів є так званий метод підстановки. В основі цього методу лежить заміна перемінної функції. Звернемо увагу читача на те, що заtтреба вибирати таку функціюt = w(x), щоб:
під інтегралом був явний диференціал від w(x)(w′(x)dx)або якщо даного диференціалу й немає, то його можна легко утворити за допомогою множення або ділення на стале число, відмінне від нуля;
інтеграл
 був
би табличним.
був
би табличним.
Якщо одночасно ці два пункти не виконуються, то інтеграл треба обчислювати іншими методами.
Приклади
Користуючись методом підстановки, обчислити невизначені інтеграли:

Підстановка: t = sinx; dt = cosxdx.
2. 
Підстановка: t = lnx; dt =  .
.
 .
.
Підстановка: t =x 2; dt = 2xdx.
Підстановка: t = tg .
.
Інтегрування за частинами
Розглянемо дві функції u = (x),
v = g(x), які на деякому проміжку(а;b)є
неперервні і мають неперервні похідні
першого порядкуφ′(x),g′(x). Тоді
функціїuтаv мають диференціали
du = φ′(x)dx, dv = g′(x)dx, причому виконується
рівність d(uv) = udv+vdu. Візьмемо від обох
частин цієї рівності невизначений
інтеграл. Тоді внаслідок рівності
диференціалів невизначені інтеграли
відрізнятимуться тільки на сталу
величину. Отже, маємо рівність з точністю
до сталої
(x),
v = g(x), які на деякому проміжку(а;b)є
неперервні і мають неперервні похідні
першого порядкуφ′(x),g′(x). Тоді
функціїuтаv мають диференціали
du = φ′(x)dx, dv = g′(x)dx, причому виконується
рівність d(uv) = udv+vdu. Візьмемо від обох
частин цієї рівності невизначений
інтеграл. Тоді внаслідок рівності
диференціалів невизначені інтеграли
відрізнятимуться тільки на сталу
величину. Отже, маємо рівність з точністю
до сталої =
=
 але
але =
=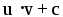 .
Тому дістаємо формулу:
.
Тому дістаємо формулу: =
uv –
=
uv –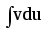 .
Зазначимо, що у формулі ми не пишемо
сталої, адже стала міститься в інтегралі
.
Зазначимо, що у формулі ми не пишемо
сталої, адже стала міститься в інтегралі ,
а сума двох сталих є сталою. Формула, що
написана, називаєтьсяформулоюінтегрування за частинами.
,
а сума двох сталих є сталою. Формула, що
написана, називаєтьсяформулоюінтегрування за частинами.Приклади
Знайти невизначені інтеграли, користуючись методом інтегрування за частинами:
= uv–
 .
.
Введемо позначення u=x;dv=sinxdx.
Знаходимо =
= .v
= –cosx – сталої при знаходженніvне
пишемо. Сталу запишемо при обчисленні
інтегралу
.v
= –cosx – сталої при знаходженніvне
пишемо. Сталу запишемо при обчисленні
інтегралу .
Оскількиuє відома функція: u = x, то
du = u′dx = dx. Отже,
.
Оскількиuє відома функція: u = x, то
du = u′dx = dx. Отже, = –xcosx –
= –xcosx – =
–xcosx+sinx+c. Якби ми взяли заu=sinx, то ми
приклад не розв’язали б.
=
–xcosx+sinx+c. Якби ми взяли заu=sinx, то ми
приклад не розв’язали б.
2.
Введемо позначення: u =lnx ; du =
;
dv = xdx, v = .
.
 .
.
Введемо позначення: u = ln2x; du = 2lnx ;
dv =dx; dv =
;
dv =dx; dv = .
.
Невизначений інтеграл  будемо
інтегрувати за частинами.
будемо
інтегрувати за частинами.
Нехай u = lnx; dv = dx. Тоді du = dx, v =
dx, v = =
x.
=
x.
Отже,  xlnx –
xlnx – =
xlnx – x + с.
=
xlnx – x + с.
Остаточно знаходимо  =
xln2x –2(xlnx – x) + c.
=
xln2x –2(xlnx – x) + c.
 =
еах
=
еах
Позначимо в цьому інтегралі u = eax , dv = sinbxdx. Звідки du = aeaxdx,
v =  = –
= –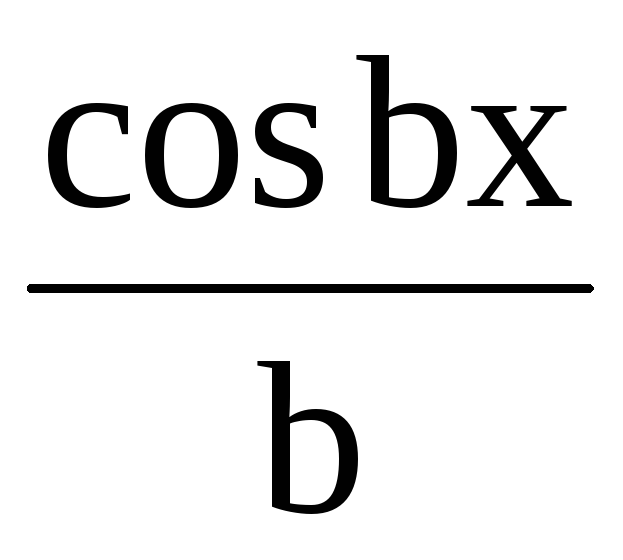 .
.
Тоді  .
.
Інтеграл у правій частині цієї рівності
теж обчислюється за частинами. Введемо
позначення: u = eax;dv = cos bxdx,
звідки du = eaxdx v = =
= =
= .
Скориставшись формулою метода інтегрування
за частинами, маємо
.
Скориставшись формулою метода інтегрування
за частинами, маємо .
.
Підставивши значення цього інтегралу в рівність, дістанемо:
 .
.
У правій частині цієї рівності маємо той самий інтеграл, що у лівій. Тому, розв’язуючи цю рівність відносно інтегралу, знаходимо:
 .
.
9.Застосування визначеного інтеграла до знаходження площі фігури та об’єму тіла обертання
Формула Ньютона – Лейбніца
1.Нехай
на інтервалі [a,
b]
задана неперервна невідємна
функція у=f(x).
Тоді
згідно з геометричним змістом визначеного
інтеграла площа криволінійної трапеції,
обмеженої даною функцією, віссю ОХ та
прямими х=а, х=b,
чисельно
дорівнює визначеному інтегралу.
Знаходження об`ємів фігур обертання
12. Диференціальні рівняння зі сталими коефіцієнтами. Теореми про структуру розвязків о.Л. Д.Р і н.Л.Д.Р.
Лінійне диференційне рівняння зі сталими коефіцієнтами з правою частиною спеціального виду — диференційне рівняння виду
, 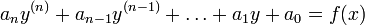
де коефіцієнти — певні сталі, — довільна функція.

Однорідне лінійне диференційне рівняння зі сталими коефіцієнтами
14. Ознаки збіжності додатніх рядів
Сформулюємо дві ознаки збіжності додатніх рядів, що ґрунтуються на порівнянні рядів між собою. Ці ознаки полягають в порівнянні членів досліджуваного ряду з членами іншого ряду, поведінка якого вже вияснена.
1.
Нехай  1)
1)
І 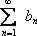 2)
2)
— два додатніх ряди, причому члени першого, починаючи з деякого місця, не більші відповідних членів другого:. Тоді, якщо ряд (2) збігається, то збігається і ряд (1), якщо ж ряд (1) розбігається, то розбігається і ряд (2) ( із збіжності ряду з більшими членами випливає збіжність ряду з меншими членами, із розбіжності ряду з меншими членами випливає розбіжність ряду з більшими членами).
2.
Якщо ряди (1) і (2) строго додатні і границя
відношення їх загальних членів є обмежене
додатнє число то
ряди (1) і (2) збігаються або розбігаються
одночасно.
то
ряди (1) і (2) збігаються або розбігаються
одночасно.
В
багатьох випадках для порівняння
досліджуваного ряду зручно використовувати
ряди виду Ми
будемо називати такі ряди гармонійними,
хоч частіше цю назву відносять лише до
ряду
Ми
будемо називати такі ряди гармонійними,
хоч частіше цю назву відносять лише до
ряду Пізніше
ми розглянемо ознаки збіжності, з
допомогою яких можна буде показати, що
гармонійні ряди збігаються при
Пізніше
ми розглянемо ознаки збіжності, з
допомогою яких можна буде показати, що
гармонійні ряди збігаються при >1
і розбігаються при 0<
>1
і розбігаються при 0< ≤1
≤1
Розглянемо декілька прикладів.
Приклад
1.  При
всіх
При
всіх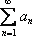 очевидна
нерівність
очевидна
нерівність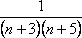 <
< Оскільки
ряд з більшими членами
Оскільки
ряд з більшими членами збігається,
то за ознакою 1 збігається і розглядуваний
ряд.
збігається,
то за ознакою 1 збігається і розглядуваний
ряд.
(ознака
Даламбера). Якщо для ряду з додатними членами
з додатними членами існує границя тоді:
існує границя тоді:
приряд збігається;
при ряд
розбігається;
ряд
розбігається;
при  питання
про збіжність ряду ознака не вирішує.
питання
про збіжність ряду ознака не вирішує.
15. Знакозмінні ряди. Абсолютна та умовна збіжність. Теорема Лейбніца
Теорема.
Якщо в ряді з додатними членами загальний
член, починаючи з певного значення п,
задовольняє нерівність  деq – стале
число, менше за одиницю, то ряд збігається.
деq – стале
число, менше за одиницю, то ряд збігається.
Коли
ж навпаки, починаючи з певного значення п,
маємо  то
ряд розбігається.
то
ряд розбігається.
Наслідок.
Якщо існує  ,
то приr < 1
ряд напевне збігається. Випадок r = 1
і тут взагалі є сумнівний.
,
то приr < 1
ряд напевне збігається. Випадок r = 1
і тут взагалі є сумнівний.
Теорема.
Ряди 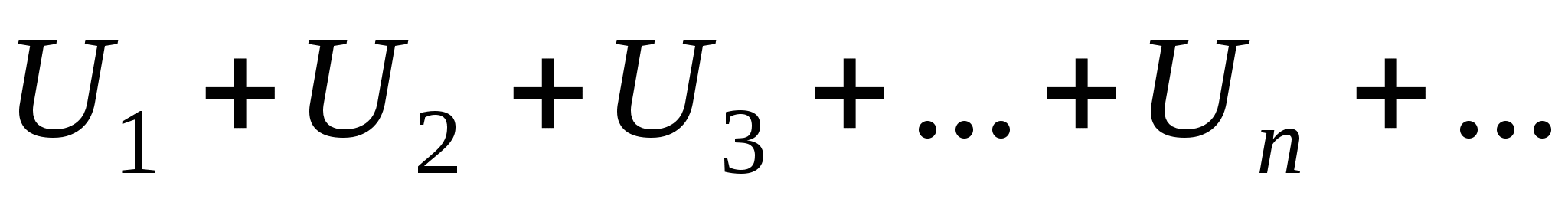 напевне
збігається, якщо збігається ряд
напевне
збігається, якщо збігається ряд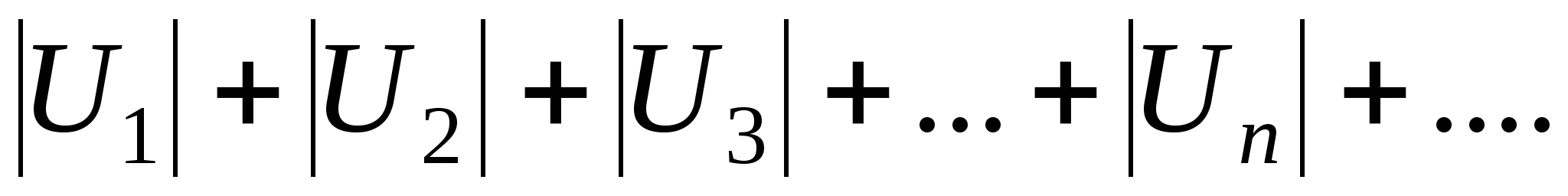
Означення. Збіжний ряд  називається
абсолютно збіжним. Якщо збігається
також і ряд
називається
абсолютно збіжним. Якщо збігається
також і ряд
Означення.
Якщо ряд  (*)
збіжний, а ряд
(*)
збіжний, а ряд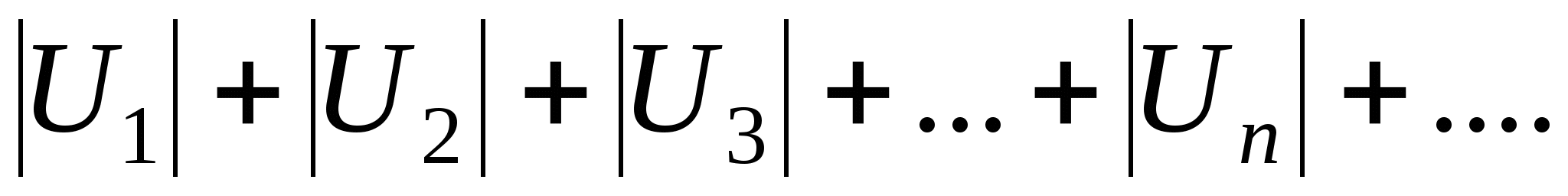 розбіжний,
то даний ряд (*) називається умовно
збіжним.
розбіжний,
то даний ряд (*) називається умовно
збіжним.
Означення. Знакозмінними рядами називаються ряди виду:

де  —
додатні числа.
—
додатні числа.
Теорема
Лейбніца.
Якщо в знакозмінному ряді абсолютне
значення загального члена монотонно
прямує до нуля (тобто  до
того ж
до
того ж ),
тоді знакозмінний ряд збігається,
причому сума його має числове значення,
проміжне між нулем та першим членом
),
тоді знакозмінний ряд збігається,
причому сума його має числове значення,
проміжне між нулем та першим членом
16. Степеневі ряди. Теорема Абеля. степеневим
рядом називається нескінченний
ряд виду:  де an —
коефіцієнти n —
го доданку, c —
деяка константа,
а x —
змінна визначена в деякій області, що
містить c.
На практиці часто c рівне
нулю і степеневі ряди мають простіший
вид:
де an —
коефіцієнти n —
го доданку, c —
деяка константа,
а x —
змінна визначена в деякій області, що
містить c.
На практиці часто c рівне
нулю і степеневі ряди мають простіший
вид:

Перша теорема Абеля: якщо степеневий ряд є розбіжним при , він є розбіжним при всіх
 ,
таких що .
,
таких що .
Друга
теорема Абеля:
Нехай степеневий ряд є збіжним в точці  .
Тоді він є рівномірно збіжним по
.
Тоді він є рівномірно збіжним по на
відрізку, що сполучає точки 0 і
на
відрізку, що сполучає точки 0 і .
.
-Степеневий
ряд називається збіжним в точці x0,
якщо збіжним
є
відповідний числовийряд 
Степеневий ряд є збіжним в деякій області, якщо він є збіжним в кожній точці цієї області.
Метод інтегрування частинами. Практичне застосування
Із формули диференціала добутку інтегруванням двох частин рівності одержуємо формулу інтегрування частинами
За цією формулою знаходження інтеграла зводиться до знаходження іншого інтеграла Застосовувати цю формулу потрібно в тих випадках, коли інтеграл легко знаходитися. Якщо неправильно вибрати , то завдання навпаки може ускладнитись. Для застосування формули інтегрування частинами до інтегралу необхідно підінтегральний вираз представити в вигляді добутку двох множників та . За диференціал завжди вибирають такий вираз, що містить . Його інтегруванням можна знайти . За в більшості випадків приймається функція, яка при диференціюванні спрощується.
В такий спосіб на перший погляд важкі і незрозумілі, з точки зору обчислень, інтеграли можна швидко звести до табличного вигляду.
Поширені приклади інтегрування частинами
Приклад 1. Обчислити інтеграли
а)
Розв’язок: Даний інтеграл один з класичних в курсі вищої математики. Функції підбираємо таким чином
Згідно формул інтегрування частинами маємо
б)
Розв’язок: Для даного інтеграла функції для підстановки вибираємо у вигляді
За формулою отримаємо
На цьому прикладі добре видно ефективність методу підстановки. Ніяка інша методика не дозволяє так швидко обчислити інтеграл.
в)
Розв’язок: Для заданого заміни вибираємо наступними
Підставляємо в інтеграл та обчислюємо його
Бачимо, що знову отримали інтеграл до якого потрібно застосувати правило інтегрування частинами. За схемою вибираємо функцію
Формли для беремо з попереднього інтегрування. Підставляємо в інтеграл та знаходимо
Останній доданок потребує повторного інтегрування частинами. Для цього записуємо заміну змінних
Друга змінна залишається без змін. Залишився один крок до повного обчислення значення інтегралу.
Всі внутрішні інтеграли підставляємо у початкову формулу
Це і є відповіддю до завдання.
г)
Розв’язок: Вибираємо функції для застосування правила заміни змінних у вигляді
За правилами інтегрування отримаємо
Останній інтеграл знайдемо за правилом розкладу, для цього чисельник доповнюємо до вигляду знаменника
Остаточно інтеграл матиме вигляд
д)
Розв’язок: За функції u,v вибираємо наступні
За правилом інтегрування частинами знаходимо неозначений інтеграл
Для останнього доданку необхідно повторно застосувати інтегрування частинами.
Першу функцію вибираємо так
— залишається без змін. Обчислюємо інтеграл
Значення інтегралу підставимо в попередній вираз
В цьому завдання застосовувати правило доводилося повторно. Це не складно, адже Ви тепер знаєте, яку робити заміну змінних при інтегруванні частинами.
е)
Розв’язок:Вибираємо функції u,v для заміни змінних наступними
Здійснимо інтегрування частинами
Далі u залишаємо без змін, а v знаходимо інтегруванням
Повторно інтегруємо косинус
Необхідно зауважити, що шуканий інтеграл та останній однакові. Позначимо їх
При цьому отримуємо рекурентну залежність
З рівняння виражаємо невідомий інтеграл
Інтеграли на подобі останнього зустрічаються доволі рідко, проте вимагають особливої уваги при їх розв’язанні. Найменша помилка може призвести до ускладнення інтегралу і красивого рівняння Ви можете не отримати. Тому будьте уважні при обчисленнях.
Сподіваюсь, що з даного уроку Ви багато потрібного для себе почерпнули. Практикуйте в розв’язуванні задач і до зустрічі в наступних уроках.
Приклади інтегрування функцій
Нижче наведені приклади інтегрування, які охоплюють значну частину різноманітних способів знаходження невизначеного інтегралу. Такого типу приклади інтегрування функцій Ви найчастіше побачите на 1,2 курсах навчання з вищої математики. Наведені нижче відповіді одночасно і пояснюють методику взяття інтегралів, і слугують інструкцією з обчислень. Щоб зекономити час та місце самих умов до прикладів ми не виписували.
Приклад 1. Якщо перед інтегралом мали б множником «ікс», то його можна було б внести під диференціал і провести заміну змінних. Однак інтеграл дещо складніший, тому вирази в дужках підносимо до кубу, а далі виконуємо інтегрування кожного з доданків.
Приклад 2. Задано дробову функцію в знаменнику якої міститься ірраціональність. Щоб її позбутися функцію під коренем позначимо за нову змінну, далі знаходимо її диференціал та підставляємо в інтеграл. Після незначних маніпуляцій з показниками обчислюємо інтеграл, і замість змінної підставляємо виконану заміну.
Приклад 3. Хто часто обчислює інтеграли або добре знає теорію інтегралів, то в цьому та подібних завданнях за нову змінну вибирає логарифм. При диференціюванні логарифма отримуємо одиницю розділену на «ікс», що значно спрощує подальше інтегрування. Вкінці не забувайте в прикладах на заміну змінних перейти до початкової змінної «ікс».
Приклад 4. Виконуємо інтегрування частинами, для цього синус вносимо під диференціал
Після першого разу знову отримаємо інтеграл, який обчислюємо інтегруванням частинами.
Приклад 5. Маємо завдання під правило інтегрування частинами u*dv. За змінну вибираємо експоненту, а синус вносимо під диференціал.
Після повторного інтегрування частинами прийдемо до рекурентної формули, з якої і визначаємо інтеграл.
Приклад 6. В цьому інтегралі квадратний тричлен, що стоїть в знаменнику треба звести до суми чи різниці квадратів.
Далі за формулами інтегрування отримаємо арктангенс.
Приклад 7. Інтегрування добутку тригонометричних функцій дається не всім студентам, і тут потрібно враховувати як степені, так і сам вигляд функцій. В цьому прикладі один косинус потрібно внести під диференціал і звести завдання до інтегрування функції від синуса.
Сам інтеграл не складний і знаходиться за правилом для степеневих функцій.
Приклад 8. Якщо маємо синуси чи косинуси у показниках більших одиниці, то за тригонометричними формулами їх треба порозписувати аж до першого степеня. Далі застосовують формули інтегрування синусів або косинусів.
Приклад 9. Щоб знайти інтеграл від дробової функції спершу розділимо чисельник на знаменник, та отриманий в остачі дріб розпишемо на найпростіші дроби. Після цього, використовуючи формули інтегрування, обчислюємо значення кожного з інтегралів.
Приклад 10. Маємо інтеграл від дробової функції
Записуємо її через найпростіші дроби першого та другого типів.
Далі зводимо дроби під спільний знаменник та з умови рівності чисельників складаємо систему лінійних рівнянь для обчислення невідомих сталих.
Після її розв’язування повертаємося до дробу, підставляємо сталі та виконуємо інтегрування.
Приклад 11. Маємо інтеграл від дробової ірраціональної функції. Для розкриття ірраціональності виконуємо наступну заміну змінних під інтегралом
Таблиця інтегралів — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Інтегрування є одною з двох основних операцій математичного аналізу. Тоді як диференціювання має прості правила, за якими можна знайти похідну складних функцій через диференціювання її складових функцій, для інтегралів це не так, і тому таблиці відомих первісних виявляються часто дуже корисними. На цій сторінці представлено список основних первісних.
C вживається як довільна константа інтегрування, яку можна визначити якщо відомо значення інтеграла в якій-небудь точці.
Правила інтегрування функцій[ред. | ред. код]
- ∫cf(x)dx=c∫f(x)dx{\displaystyle \int cf(x)\,dx=c\int f(x)\,dx}
- ∫f(ax+b)dx=1aF(ax+b)+C{\displaystyle \int f(ax+b)\,dx={1 \over a}F(ax+b)\,+C}
- ∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx{\displaystyle \int [f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx}
- ∫[f(x)−g(x)]dx=∫f(x)dx−∫g(x)dx{\displaystyle \int [f(x)-g(x)]\,dx=\int f(x)\,dx-\int g(x)\,dx}
- ∫f(x)g(x)dx=f(x)∫g(x)dx−∫(d[f(x)]∫g(x)dx)dx{\displaystyle \int f(x)g(x)\,dx=f(x)\int g(x)\,dx-\int \left(d[f(x)]\int g(x)\,dx\right)\,dx} , або, що те ж саме:
- ∫u(x)v′(x)dx=u(x)v(x)−∫u′(x)v(x)dx{\displaystyle \int u(x)v'(x)\,dx=u(x)v(x)-\int u'(x)v(x)\,dx}
Інтеграли простих функцій[ред. | ред. код]
Раціональні функції[ред. | ред. код]
- ∫dx=x+C{\displaystyle \int \,dx=x+C}
- ∫xndx=xn+1n+1+C,{\displaystyle \int x^{n}\,dx={\frac {x^{n+1}}{n+1}}+C,} якщо n≠−1{\displaystyle n\neq -1}
- ∫dxx=ln|x|+C{\displaystyle \int {\frac {dx}{x}}\,=\ln {\left|x\right|}+C}
- ∫dxa2+x2=1aarctgxa+C{\displaystyle \int {dx \over {a^{2}+x^{2}}}={1 \over a}\operatorname {arctg} {x \over a}+C}
- ∫dxx2−a2=12aln|x−ax+a|+C{\displaystyle \int \!{dx \over {x^{2}-a^{2}}}={1 \over 2a}\ln \left|{x-a \over {x+a}}\right|+C}
Логарифмічні функції[ред. | ред. код]
- ∫lnxdx=xlnx−x+C{\displaystyle \int \ln {x}\,dx=x\ln {x}-x+C}
- ∫logbxdx=xlogbx−xlogbe+C{\displaystyle \int \log _{b}{x}\,dx=x\log _{b}{x}-x\log _{b}{e}+C}
Показникові функції[ред. | ред. код]
- ∫exdx=ex+C{\displaystyle \int e^{x}\,dx=e^{x}+C}
- ∫axdx=axlna+C{\displaystyle \int a^{x}\,dx={\frac {a^{x}}{\ln {a}}}+C}
Ірраціональні функції[ред. | ред. код]
- ∫dxa2−x2=arcsinxa+C{\displaystyle \int {dx \over {\sqrt {a^{2}-x^{2}}}}=\arcsin {x \over a}+C}
- ∫−dxa2−x2=arccosxa+C{\displaystyle \int {-dx \over {\sqrt {a^{2}-x^{2}}}}=\arccos {x \over a}+C}
- ∫dxxx2−a2=1aarcsec|x|a+C{\displaystyle \int {dx \over x{\sqrt {x^{2}-a^{2}}}}={1 \over a}{\mbox{arcsec}}\,{|x| \over a}+C}
- ∫dxx2+a2=ln|x+x2+a2|+C{\displaystyle \int \!{dx \over {\sqrt {x^{2}+a^{2}}}}=\ln \left|{x+{\sqrt {x^{2}+a^{2}}}}\right|+C}
- ∫dxx2−a2=ln|x+x2−a2|+C{\displaystyle \int \!{dx \over {\sqrt {x^{2}-a^{2}}}}=\ln \left|{x+{\sqrt {x^{2}-a^{2}}}}\right|+C}
Тригонометричні функції[ред. | ред. код]
- ∫sinxdx=−cosx+C{\displaystyle \int \sin {x}\,dx=-\cos {x}+C}
- ∫cosxdx=sinx+C{\displaystyle \int \cos {x}\,dx=\sin {x}+C}
- ∫tgxdx=−ln|cosx|+C{\displaystyle \int \operatorname {tg} x\,dx=-\ln {\left|\cos {x}\right|}+C}
- ∫ctgxdx=ln|sinx|+C{\displaystyle \int \operatorname {ctg} x\,dx=\ln {\left|\sin {x}\right|}+C}
- ∫secxdx=ln|secx+tgx|+C{\displaystyle \int \sec {x}\,dx=\ln {\left|\sec {x}+\operatorname {tg} x\right|}+C}
- ∫cosecxdx=−ln|cosecx+ctgx|+C{\displaystyle \int \operatorname {cosec} x\,dx=-\ln {\left|\operatorname {cosec} x+\operatorname {ctg} x\right|}+C}
- ∫sec2xdx=tgx+C{\displaystyle \int \sec ^{2}x\,dx=\operatorname {tg} x+C}
- ∫cosec2xdx=−ctgx+C{\displaystyle \int \operatorname {cosec} ^{2}x\,dx=-\operatorname {ctg} x+C}
- ∫secxtgxdx=secx+C{\displaystyle \int \sec {x}\,\operatorname {tg} x\,dx=\sec {x}+C}
- ∫cosecxctgxdx=−cosecx+C{\displaystyle \int \operatorname {cosec} x\,\operatorname {ctg} x\,dx=-\operatorname {cosec} x+C}
- ∫sin2xdx=12(x−sinxcosx)+C{\displaystyle \int \sin ^{2}x\,dx={\frac {1}{2}}(x-\sin x\cos x)+C}
- ∫cos2xdx=12(x+sinxcosx)+C{\displaystyle \int \cos ^{2}x\,dx={\frac {1}{2}}(x+\sin x\cos x)+C}
- ∫sec3xdx=12secxtgx+12ln|secx+tgx|+C{\displaystyle \int \sec ^{3}x\,dx={\frac {1}{2}}\sec x\operatorname {tg} x+{\frac {1}{2}}\ln |\sec x+\operatorname {tg} x|+C}
- ∫sinnxdx=−sinn−1xcosxn+n−1n∫sinn−2xdx{\displaystyle \int \sin ^{n}x\,dx=-{\frac {\sin ^{n-1}{x}\cos {x}}{n}}+{\frac {n-1}{n}}\int \sin ^{n-2}{x}\,dx}
- ∫cosnxdx=−cosn−1xsinxn+n−1n∫cosn−2xdx{\displaystyle \int \cos ^{n}x\,dx=-{\frac {\cos ^{n-1}{x}\sin {x}}{n}}+{\frac {n-1}{n}}\int \cos ^{n-2}{x}\,dx}
- ∫dxcos2x=tgx+C{\displaystyle \int \!{dx \over \cos ^{2}x}=\operatorname {tg} \,x+C}
- ∫dxsin2x=−ctgx+C{\displaystyle \int \!{dx \over \sin ^{2}x}=-\operatorname {ctg} \,x+C}
Обернені тригонометричні функції[ред. | ред. код]
- ∫arcsinxdx=xarcsinx+1−x2+C{\displaystyle \int \arcsin {x}\,dx=x\,\arcsin {x}+{\sqrt {1-x^{2}}}+C}
- ∫arccosxdx=xarccosx−1−x2+C{\displaystyle \int \arccos {x}\,dx=x\,\arccos {x}-{\sqrt {1-x^{2}}}+C}
- ∫arctgxdx=xarctgx−12ln|1+x2|+C{\displaystyle \int \operatorname {arctg} x\,dx=x\,\operatorname {arctg} x-{\frac {1}{2}}\ln {\left|1+x^{2}\right|}+C}
- ∫arcsecxdx=xarcsecx+x2−1ln(x+x2−1)x1−1×2+C{\displaystyle \int \operatorname {arcsec} {x}\,dx=x\,\operatorname {arcsec} {x}+{\frac {{\sqrt {x^{2}-1}}\ln {(x+{\sqrt {x^{2}-1}})}}{x\,{\sqrt {1-{\frac {1}{x^{2}}}}}}}+C}
- ∫arccosecxdx=xarccosecx+x2−1ln(x+x2−1)x1−1×2+C{\displaystyle \int \operatorname {arccosec} x\,dx=x\,\operatorname {arccosec} x+{\frac {{\sqrt {x^{2}-1}}\ln {(x+{\sqrt {x^{2}-1}})}}{x\,{\sqrt {1-{\frac {1}{x^{2}}}}}}}+C}
- ∫arcctgxdx=xarcctgx+12ln|1+x2|+C{\displaystyle \int \operatorname {arcctg} x\,dx=x\,\operatorname {arcctg} x+{\frac {1}{2}}\ln {\left|1+x^{2}\right|}+C}
Гіперболічні функції[ред. | ред. код]
- ∫shxdx=chx+C{\displaystyle \int \operatorname {sh} x\,dx=\operatorname {ch} x+C}
- ∫chxdx=shx+C{\displaystyle \int \operatorname {ch} x\,dx=\operatorname {sh} x+C}
- ∫thxdx=ln|chx|+C{\displaystyle \int \operatorname {th} x\,dx=\ln |\operatorname {ch} x|+C}
- ∫cschxdx=ln|thx2|+C{\displaystyle \int \operatorname {csch} x\,dx=\ln \left|\operatorname {th} {x \over 2}\right|+C}






 )=
f(x)dx
)=
f(x)dx = F(x)+c. Розглянуту властивість можна
сформулювати ще так: операції
диференціювання та інтегрування з
точністю до сталої є взаємно обернені.
= F(x)+c. Розглянуту властивість можна
сформулювати ще так: операції
диференціювання та інтегрування з
точністю до сталої є взаємно обернені. 0,
то
0,
то =a
=a .
Дана властивість формулюється так:
сталий множник можна виносити за знак
невизначеного інтегралу.
.
Дана властивість формулюється так:
сталий множник можна виносити за знак
невизначеного інтегралу.

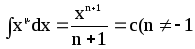
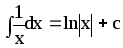


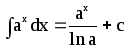 ;
;
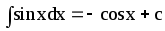
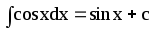










 був
би табличним.
був
би табличним. .
.

 .
. .
. =
еах
=
еах ,
таких що .
,
таких що .