После auch порядок слов: Сложносочинённые предложения в немецком языке
Сложносочинённые предложения в немецком языке
И.Г. Князева, учитель немецкого языка МБОУ СОШ №15 ст. Роговской
Сложносочинённые предложения в немецком языке
(сложность 11 класс)
Сложносочинённое предложение в немецком языке (Satzreihe) состоит из двух или более самостоятельных предложений, объединённых по смыслу. В сложносочинённых предложениях связь между предложениями может быть союзной и бессоюзной.
Der Vorgang ging auf, die Auffűhrung begann.
Gestern wollten wir einen Ausflug machen, aber es regnete den ganzen Tag und wir mussten zu Hause bleiben.
Основным средством связи между предложениями в немецком языке являются сочинительные союзы: und (и,а), aber (но, однако), denn (так как, потому что), oder (или, либо), sondern (а, но), sowie (а также, как и), а также наречия с временными, следственными и другими значениями: dann, danach (затем, потом, после того), doch (всё-таки, всё же), jedoch (однако, тем не менее), deshalb (потому), deswegen (поэтому, по этой причине), darum (поэтому), also (итак, следовательно, стало быть), sonst (иначе, а то), dabei (к тому же, вместе с тем), dazu (сверх этого, сверх того), zwar (правда, хотя), und zwar (а именно), űbrigens (впрочем), auβerdem (кроме того), trotzdem (несмотря на это).
Порядок слов в сложносочинённых предложениях немецкого языка, входящих в его состав, зависит от союза или союзного слова.
Большинство сочинительных союзов не оказывают влияния на порядок слов. К ним относятся союзы: und, aber, auch, denn, oder, sondern.
Die Eltern gehen ins Theater, aber ich bleibe zu Hause.
На порядок слов влияют союзы и союзы – наречия: darum, deshalb, deswegen, dann, trotzdem, zwar, sonst, dabei, dazu, űbrigens.
Например: Meine Schwester erzählte mir sehr viel von diesem Film, deshalb möchte ich mir ihn ansehen.
Im Foyer betrachteten sie die Bilder der Schauspieler, dann gingen asie in den Zuschauerraum.
Союзы, допускающие колебания в порядке слов:doch, jedoch, also. Например:Sie ist schon 80 Jahre alt, doch arbeitet sie bis heute im Theater.
Союзы, не влияющие на порядок слов | und (и,а), aber (но, однако), denn (так как, потому что), oder (или, либо), sondern (а, но), sowie (а также, как и), nicht nur … sondern auch ( не только … но и), sowohl … als auch (как … так и) |
Союзы, союзы- наречия, влияющие на порядок слов | deshalb (потому), deswegen (поэтому, по этой причине), darum (поэтому), auβerdem (кроме того), trotzdem (несмотря на это), zwar (правда, хотя), und zwar (а именно), halb … halb, teils … teils ( то… то) |
Союзы, допускающие колебания в порядке слов | doch (всё-таки, всё же), jedoch (однако, тем не менее), also (итак, следовательно, стало быть), entweder … oder ( или … или), weder … noch ( ни … ни) |
Уступки в немецком языке: разница между trotzdem и obwohl
Уровень B1
Время чтения: 9 мин
Как в немецком языке передается смысл русских союзов несмотря на, хотя, вопреки? Obwohl или trotzdem, что выбрать? Какими синонимами можно их заменить? Сегодня разбираемся, что из себя представляют уступительные придаточные предложения, как с их помощью разнообразить свою речь, и, конечно, тренируемся на примерах.
В немецком языке, как и в русском, существуют предложения, которые передают так называемый уступительный смысл, их называют Konzessivsätze. Если выразиться проще, эти предложения указывают на препятствия, вопреки которым совершается действие, описываемое в главном предложении.
Для того, чтобы выразить уступительный смысл, используются такие союзы или конструкции, как: aber – но; obwohl (obgleich, obschon, obzwar) – хотя; trotzdem (dennoch, gleichwohl) — несмотря на, однако, все же; ungeachtet dessen, dass — невзирая на то, что и многие другие.
Очень часто эти союзы в предложении сопровождаются частицами doch или so. Сегодня мы рассмотрим наиболее популярные варианты придаточных предложений, а также потренируемся в самостоятельном составлении предложений уступки.
Для начала давайте рассмотрим, каким именно образом выражается так называемый уступительный смысл.
Obwohl или trotzdemObwohl (можно также использовать его синонимы obschon, obzwar или obgleich) der Urlaub kurz war, habe ich mich doch gut erholt. – Хотя отпуск был короткий, я все же хорошо отдохнул.
Здесь мы видим обычное придаточное предложение. Смысл предложения можно выразить иначе, не образуя при этом придаточного предложения:
Der Urlaub war kurz. Trotzdem (синонимы dennoch, allerdings) habe ich mich gut erholt. – Отпуск был коротким. Несмотря на это (все же, однако) я хорошо отдохнул.
Само слово trotzdem не вводит придаточного предложения, а является просто второстепенным членом предложения, как, например, heute или deshalb. Поэтому в данной конструкции после trotzdem будет обычный (прямой) порядок слов.
Ich mag keine Restaurants, trotzdem gehe ich mit den Kollegen hin. – Я не люблю рестораны, несмотря на это, я иду туда с коллегами.
О том, что такое прямой порядок слов и как строится немецкое повествовательное предложение, мы рассказывали ранее.
У trotzdem есть синонимы — allerdings (однако), dennoch (всё же):
Sie war ein freundliches und hübsches Mädchen, allerdings liebte er sie nicht. – Она была дружелюбной и красивой девушкой, однако он ее не любил.
Er hatte die besten Zeugnisse, dennoch bekam er diese Arbeit nicht. – У него был лучший аттестат, и все же он не получил эту работу.
Der Urlaub war kurz. Aber ich habe mich gut erholt. – Отпуск был коротким. Но я хорошо отдохнул.
Der Urlaub war kurz. Ich habe mich doch (dennoch) gut erholt. – Отпуск был коротким. Я все же (однако) хорошо отдохнул.
Важно помнить, что после aber (как и после und) порядок слов не меняется, то есть остается прямым.
Zwar… aber (doch) Еще один способ выразить уступку с помощью двойного предлога zwar … aber … (doch):Zwar war der Urlaub kurz, aber ich habe mich doch (= dennoch) gut erholt. – Хотя отпуск был коротким, но я все же хорошо отдохнул.
Es ist zwar Morgen, aber ich habe schon alles gemacht. – Хотя сейчас и утро, но я уже всё сделал.
Zwar также является просто второстепенным членом предложения, как и в случае с trotzdem. Поэтому после него будет обычный порядок слов.
Уже звучит запутанно и сложно? Хотите разобрать тему с преподавателем, но никогда не пробовали заниматься онлайн? Мы проводим День бесплатных онлайн-уроков для начинающих и продолжающих, чтобы вы могли попробовать формат онлайн-обучения и научиться пользоваться современным приложением для дистанционных занятий. Участвовать можно из любой точки мира, нужен только компьютер, планшет или телефон. Запишитесь прямо сейчас! Это абсолютно бесплатно, а присоединиться можно всего в несколько кликов.
Wenn auch… so Придаточные предложения могут также вводиться в основное предложение с помощью слова wenn. В этом случае противопоставление будет звучать более выразительно:Wenn auch er kein Geld habe, so muss er das kaufen. – Хотя (даже если) у него нет денег, он должен это купить.
Или:
Wenn auch der Urlaub kurz war, so habe ich mich doch gut erholt. – Хотя (даже если) отпуск был короткий, я все же хорошо отдохнул.
Возможен и другой вариант:
Wenn der Urlaub auch kurz war, so habe ich mich doch gut erholt.
В данном случае, в главном предложении может быть и прямой порядок слов, хотя оно и следует за придаточным (такое возможно только после уступительных предложений с auch):
Wenn der Urlaub auch kurz war, ich habe mich doch gut erholt.
В случае, когда на место wenn (если) встает глагол, это слово может выпадать из предложения:
War der Urlaub auch kurz, ich habe mich doch gut erholt.
Обратите внимание, что в данной конструкции это уже не будет считаться придаточным предложением, ведь в конце придаточного предложения должен стоять глагол. Построение сложных предложений в немецком языке (с придаточными различных типов) само по себе является важной и непростой темой для всех, кто изучает немецкий. Предлагаем вам освежить свои знания, пройдя по ссылке.
Вопросительное слово + auch Такая комбинация дает значение как бы ни (было)…, куда бы ни (ездил) и т.д.Wie kalt es auch war, die Sportler mussten trainieren. – Как бы ни было холодно, спортсмены должны были тренироваться.
Wohin er auch reiste, er nahm immer seinen Sohn mit. – Куда он только ни ездил, он всегда брал с собой своего сына.
Вместо auch (также) при этом можно использовать immer (всегда) или noch (еще):
Woran er immer arbeitete, seine Arbeit war ausgezeichnet. – Над чем бы он ни работал, его работа была отличной. (Immer подчеркивает здесь многократность действия.)
Wohin du noch gehst, ich folge dir. – Куда бы ты ни пошел, я следую за тобой.
Обратите внимание, что придаточные предложения вводятся как вопросительными словами, так и вводным словом wenn. Для выражения уступительного смысла к этим вводным словам добавилось лишь auch.
Noch so Если в речи вам важно подчеркнуть, что какое-либо событие не может произойти ни при каком условии, то нужно употребить конструкцию noch so (как бы ни …):Da kannst du noch so viel trainieren, gegen ihn hast du keine Chance! – Как бы ты ни тренировался, против него у тебя нет шансов!
Глагол mögen В уступительных предложениях довольно часто используется глагол mögen:Mag das Wetter auch noch so kalt sein, wir gehen doch in den Park. – Какой бы холодной ни была погода, мы все же пойдем в парк.
В уступительных предложениях может употребляться и Konjunktiv 1 (сослагательное наклонение в форме бы):
Möge das Ziel auch noch so sehr entfernt sein, wir werden es erreichen. – Как бы ни была еще далека цель, мы ее достигнем.
Подробнее о том, как образуется условная форма Konjunktiv 1 в немецком языке, читайте в нашей отдельной статье.
Следует также запомнить оборот Wie dem auch sei… – Как бы то ни было.
Ungeachtet dessen, dass Эта часто употребляемая конструкция переводится как несмотря на то, что…Ungeachtet dessen, dass das Problem so kompliziert war, hat er eine Lösung gefunden. – Несмотря на то, что проблема была такой сложной, он нашел решение.
Ungeachtet dessen, dass wir keine Chance haben, werden wir weiter kämpfen. – Несмотря на то, что у нас нет шансов, мы будем бороться дальше.
А теперь давайте закрепим новую тему и попробуем связать два предложения в одно, используя конструкции, приведенные выше (возможны различные варианты):
Упражнение 1
- Mein Freund war krank. Еr ging zur Arbeit. – Мой друг был болен. Он пошел на работу.
- Das Wasser ist noch kalt. Wir gehen schwimmen. – Bода еще холодная. Мы пойдем купаться.
- Ich habe wenig Zeit. Ich helfe Ihnen. – У меня мало времени. Я Вам помогу.
- Das Bild ist teuer. Das Museum kauft es. – Картина дорогая. Музей купит ее.
- Du bist ein kluger Kopf. Du verstehst nicht alles. – Ты умная голова. Ты не все понимаешь.
- Deutschland gefällt mir ganz gut. Die Schweiz gefällt mir besser. – Германия мне очень нравится. Швейцария нравится мне больше.
- Der Patient ist sehr schwach. Er muss sofort operiert werden. – Пациент очень слаб. Его нужно сейчас же оперировать.
- Die Sonne schien. Es war kalt. – Солнце светило. Было холодно.
- Sie verdient wenig bei dieser Firma. Das Arbeitsklima gefällt ihr gut. – Она мало зарабатывает на этой фирме. Рабочая атмосфера ей нравится.
- Das Geschäft hatte noch auf. Es war schon zehn nach acht. – Магазин был еще открыт. Было уже десять минут девятого.
Материал готовила
Лилия Дильдяева, команда Deutsch Online
Урок 54. Doppelkonjunktionen — двойные союзы в немецком.
Hallo! С вами Егор, сегодня я расскажу вам о приеме, который может здорово упростить вам жизнь. Вы никогда не задумывались, как в немецком языке сказать: “мне нравится и то, и то” или “я хочу не вот это, а вот это”. Переводить такие двойные коннекторы буквально с русского нет смысла — вас не поймут. Для таких случаев в немецком есть так называемые Doppelkonjunktionen или или zweiteilige Konnektoren — двойные союзы или двойные коннекторы. О них я вам сегодня и расскажу.
Итак, дорогие друзья, двойные союзы нужны нам, чтобы соединять две части предложения или два отдельных предложения в одно. Выступать они могут как для объединения: “как это, так и то”, “не только это, но и то”, так и для противопоставления: “ни это, а то”, “либо это, либо то”.
Эти союзы могут связывать как отдельные слова: “я поеду или в Италию, или в Испанию”, так и целые предложение: “либо они делают музыку тише, либо мы вызываем полицию”.
Давайте наконец перейдем к первому такому двойному союзу: sowohl… als auch…
• Ich trinke sowohl Tee, als auch Kaffee — я пью как чай, так и кофе;
• Maria lernt Deutsch sowohl selbst, als auch mit einem Lehrer — Мария учит немецкий как сама, так и с преподавателем.
Особенность этого союза в том, что когда с помощью него мы хотим не просто объединить два слова, а два предложение, то у нас не может меняться ни подлежащее, ни сказуемое во второй части предложения. Во втором примере у нас было: “Maria lernt Deutsch sowohl selbst, als auch…” и дальше у нас будет то же действие (Deutsch lernen) и тот же исполнитель (Maria). То есть мы можем говорить: “Maria lernt Deutsch sowohl selbst, als auch mit einem Lehrer”, либо же “als auch in der Schule”, либо же “als auch in der Uni” и т.д. И это всегда будет относится к Марии и к изучению немецкого. Но мы не можем сказать, к примеру: “Maria lernt sowohl Deutsch, als auch trinke ich Tee”.
Идем дальше. Второй наш двойной союз: “nicht nur… sondern auch…” — “не только… а и…”:
• Er benutzt nicht nur Handy, sondern auch Tablet — он использует не только мобильный, но и планшет;
• Ich spreche nicht nur Deutsch, sondern auch Französisch — я говорю нетолько по-немецки, аи по-французски;
• Er kümmert sich nicht nur um sie, sondern er glaubt auch an sie — он нетолько о ней заботится, нои верит в нее.
Заметили, у нас в последнем примере изменилось действие во второй половине предложения, с “заботиться” на “верить”. С этим коннектором так делать уже можно: глагол во второй половине не обязательно тот же, что и в первой.
Следующий двойной союз: “entweder…oder…” — “или… или…”:
• Ich fahre entweder nach Spanien, oder nach Italien — я поеду или в Испанию, илив в Италию;
• Du kannst entweder mich, oder meine Schwester anrufen — ты можешь позвонить либо мне, либо моей сестре;
• Ich werde dich entweder am Bahnhof abholen, oder du kannst ein Taxi nehmen — или я заберу тебя на вокзале, или ты можешь взять такси.
Опять же, на последнем примере мы видим, что с этими коннекторами у нас может меняться не только сказуемое, а и подлежащее. В первой части у нас было: “я заберу”, а во второй “ты возьмешь”. То есть изменилось и действие и тот, кто его исполняет.
В предыдущих союзах мы были ограничены. Мы либо вообще не могли ничего менять, либо могли изменить только действие. Как это было в “nicht nur… sondern auch…”. А вот здесь мы уже можем изменить все. Обращайте, пожалуйста, на это внимание.
Следующий наш союз — это “weder… noch…” — “ни то… ни то…”:
• Peter trinkt weder Tee, noch Kaffee — Петер не пьет ни чай, ни кофе;
• Weder ich, noch meine Kollegin können die Aufgabe verstehen — ни я, ни моя коллега не понимаем задание;
• Sie schaut weder Filme, noch hört sie Musik — она не смотрит фильмы и не слушает музыку.
А здесь стоит обратить внимание на любопытную деталь: во всех предыдущих примерах у нас коннектор занимал нулевую позицию. После союза шло подлежащее, а потом сказуемое: “Ich werde dich entweder am Bahnhof abholen, oder du kannst ein Taxi nehmen”. Так вот после noch в конструкции “weder… noch…” сразу идет глагол: “noch hört sie Musik”.
Обращайте внимание на порядок слов в придаточном предложении, это очень важно для грамотной речи.
Также обратите внимание, что употребляя “weder… noch…” вам не нужно употреблять дополнительные отрицания. Иногда хочется сказать: “Ich trinke weder keinen Tee, noch keinen Kaffee”. Но это не правильно, “weder… noch…” уже и так содержит в себе отрицания и, по сути, являются аналогом английского “neither… nor…”. Никаких дополнительных отрицаний не требуется.
Дальше у нас идет двойной коннектор “teils… teils…” — “частично так, частично так”:
• Er arbeitet teils zu Hause, teils im Büro — он работает частично дома, частично в офисе;
• Der Tisch ist teils aus Holz, teils aus Stahl — стол частично изготовлен из дерева, частично из стали.
Следующая пара: “zwar… aber…” — “хотя… но”:
• Er ist zwar sehr net, aber ein bisschen merkwürdig — он, хотяи милый, новсёже немного странный;
• Zwar mag sie ihn, aber sie möchte ihn nicht heiraten — хотя он ей нравится, но все же она не хочет на нем жениться.
Предпоследним в нашем списке двойных союзов идет “einerseits… andererseits…” — “с одной стороны… с другой стороны…”:
• Lukas ist einerseits sehr nett, andererseits sehr anstrengend — с одной стороны Лукас очень милый, но с другой напряжный;
• Einerseits bin ich müde, andererseits will ich ins Kino gehen — с одной стороны я уставший, с другой стороны, я хочу пойти в кино.
И последним союзом у нас идет “je… desto…” или же “je… umso…” — “чем что-то там, тем то-то там”:
• Je mehr man isst, desto dicker wird man — чем больше кушаешь, тем толще становишься;
• Je schneller ein Auto fährt, desto gefährlicher kann es sein — чем быстрее едет машина, тем опаснее это может быть.
Здесь я попрошу вас обратить внимания на довольно странный порядок слов. В первой части предложения после союза je глагол ставится у нас в конец предложения: “Je mehr man isst…”. А во второй части предложения у нас идет desto, дальше на первой позиции идет прилагательное в сравнительной степени: быстрее, толще, выше, а лишь затем идет глагол: desto dicker wird man.
Подобный порядок слов достаточно нетипичен для немецкого языка, ведь обычно, когда у нас есть Nebensatz, которое заканчивается на глагол, то после него сразу следует глагол. К примеру:
• Weil ich heute müde bin, bleibe ich zu Hause.
А вот в случае с desto наш глагол стоит аж на 3 позиции. После прилагательного в сравнительной степени.
Если с этим двойным коннектором у нас используются какие-то имена существительные с артиклями, тогда эти артикли будут стоять перед je и перед desto:
• Eine je teurere Wohnung man kauft, ein desto dickers Konto muss man haben — чем дороже покупаешь квартиру, тем толще счет нужно иметь.
Видите? У нас глагол стал аж на 4 позицию, что крайне нестандартно для немецкого языка.
Ах да, чуть не забыл, разницы между “je… desto…” и “je… umso…” нет никакой. Это синонимы, которые вы можете использовать равноправно.
Что же, это были все союзы на сегодня, надеюсь, вы будете их использовать, ведь они позволяют здорово облегчить жизнь и сказать в одном предложении то, что без них вы бы объясняли целым абзацем.
На сегодня наш урок окончен. Тем, кто только присоединился, я советую подписаться на мой канал, ведь это Урок №54, а это значит, что у меня за спиной уже больше 50 уроков немецкого как по базовой грамматике, так и по более продвинутой. Спасибо вам за внимание. Пока-пока!
Если разобрались в теме, добро пожаловать в упражнения:
https://docs.google.com/document/d/1As8Fei7dyoUFiCbOdo__k3sIimp1jR6J-qZ5V0yPfRU/edit?usp=sharing
P.S.: для того, чтобы выполнить упражнения, скопируйте этот документ (откройте ссылку, нажмите в левом верхнем углу «Файл» — «Создать копию»)
Ответы:
https://docs.google.com/document/d/1YjW2i3Uanl48FLkB_LsPZfwXCSLAc2oG6LELKjdf2Mc/edit?usp=sharing
Видео:
Сложносочиненные предложения в немецком языке
Самостоятельные предложения, образующие сложносочиненное предложение, в немецком языке могут соединяться между собой как при помощи союзов, так и без них.
| Die Straßen waren von Menschen überfüllt, Berlin jubelte, alles strömte zum Brandenburger Tor. | Улицы были переполнены людьми, Берлин ликовала, все стремились к Бранденбургским воротам. |
Наиболее распространенными в немецком языке являются сложносочиненные предложения с союзами und (и, а), aber (но, однако), oder (или), denn (так как) и союзами-наречиями auch (также), zuerst (сначала), dann (затем, потом), doch (однако, но), außerdem (кроме того), sonst (иначе), darum, deshalb (потому, поэтому), trotzdem (несмотря на то, что; все же).
Союзы und, aber, denn не являются членами немецкого предложения (они служат только для связи предложений) и поэтому не влияют на порядок слов в предложении, т. е. после них на первом месте стоит подлежащее или второстепенный член предложения, а на втором — всегда сказуемое.
| Die Sonne ging unter, und wir fuhren nach Hause. | Солнце зашло, и мы поехали домой. |
| Die Sonne ging unter, und bald wurde es kalt. | Солнце зашло, и скоро стало холодно. |
| Die Sonne ging unter, aber es war noch sehr warm. | Солнце зашло, но было еще очень тепло. |
| Wir fuhren nach Hause, denn es war schon spät. | Мы поехали домой, так как было уже поздно. |
Союз aber может стоять и в середине предложения.
| Wir fuhren nach Hause, sie aber gingen ins Institut (… sie gingen aber ins Institut). | Мы поехали домой, а они пошли в институт. |
Союзы-наречия, являясь, как правило, членами немецкого предложения, занимают первое место в предложении, а за ними следует сказуемое или его изменяемая часть.
| Es war schon spät, deshalb (darum) fuhren wir nach Hause. | Было уже поздно, поэтому мы поехали домой. |
| Zuerst besichtige ich alle Pavillons dieser Ausstellung, dann kaufe ich einige Bücher. | Вначале я осматриваю все павильоны этой выставки, потом покупаю несколько книг. |
| Wir verbrachten dort nicht viel Zeit, doch war ich sehr müde. | Мы провели там не много времени, но я очень устал. |
Для соединения самостоятельных предложений в сложносочиненные в немецком языке могут употребляться также и парные союзы bald … bald (то… то), entweder … oder (или … или), nicht nur … sondern auch (не только … но и), sowohl … als auch (как … так и), teils … teils (отчасти … отчасти), weder … noch (ни … ни).
| Entweder gewinnt er dieses Spiel, oder er muss auf den Kampf um den ersten Platz verzichten. | Или он выигрывает эту игру, или он должен отказаться от борьбы за первое место. |
| Bald schneite es, bald regnete es wieder. | То шел снег, то снова шел дождь. |
| Nicht nur unsere Wissenschaftler arbeiten an dem Problem der Erschließung von Ölvorkommen, sondern auch die Wissenschaftler der anderen Länder helfen ihnen dabei. | Не только наши ученые работают над проблемой освоения нефтяных месторождений, но им помогают и ученые других стран. |
Также будет полезно прочитать:
Сочинительные союзы в немецком языке
|
Автор: София Стальская Высшее лингвистическое образование. Опыт работы 5 лет. |
Союзов в немецком языке достаточно много, и все они используются в разных типах предложений.
По своему составу немецкие союзы делятся на:
1. односложные или простые: «und», «dass», «weil» и др.;
2. составные или сложные: «nachdem», «solange» и др;
3. состоящие из двух элементов: «so dass», «und zwar» и др.;
4. парные: «weder…noch», «entweder…oder», «bald…bald», «nicht nur … sondern auch» и другие.
Союзы в немецком языке
Союзы бывают сочинительными и подчинительными.
Сочинительные — соединяют однородные члены предложения, подчинительные — образуют связь между частями предложения, зависимыми друг от друга. Этот урок будет посвящен сочинительным союзам.
К часто встречающимся союзам относятся такие простые союзы как und (и), sondern (а), aber (но), oder (или).
Вы с ними уже встречались:
Ich habe einen Bruder und zwei Schwestern.
Magst du Tee oder Kaffee?
Gehen wir ins Kino heute oder morgen?
Er ist aber nicht so klug.
Эти союзы могут соединять не только однородные члены предложения, но и простые предложения в составе сложного. Они служат соединительным элементом и не влияют на порядок слов: Ich studiere Deutsch, und mein Bruder studiert English.
C парными союзами происходит то же самое: они могут связывать и простые предложения в составе сложного, и однородные члены предложения. Например: Ich studiere nicht nur Deutsch, sondern auch English.
К наиболее распространенным парным союзам относятся:
| weder … noch… | ни …, ни … |
| sowohl … als auch/wie | как …, так и … |
| nicht nur … sondern auch | не только …, но и … |
| entweder … oder | или …, или … |
| bald … bald | то …, то … |
| teils … teils | частично …, частично … |
Рассмотрим еще несколько примеров употребления парных союзов. Обратите внимание на порядок слов:
Sowohl ich als auch meine Schwester studieren an der Universität. — Как я, так и моя сестра учимся в университете.
Sie gehen heute abend etweder ins Kino oder zum Konzert. — Сегодня вечером они идут или в кино, или на концерт.
С союзом «weder … noch» не используется отрицание — этот союз является отрицательным сам по себе: Ich esse weder Fisch noch Fleisch. — Я не ем ни рыбу, ни мясо.
Союзные слова
Помимо союзов, в немецком языке употребимы и союзные слова. Отличаются от союзов они тем, что влияют на порядок слов в предложении — после союзных слов следует подлежащее, т.е используется инверсия.
К союзным словам относятся:
| dann | тогда, потом |
| deshalb, darum, deswegen | поэтому, потому |
| außerdem | кроме того |
| trotzdem | несмотря на это, все же |
| sonst | иначе |
| doch, jedoch | однако, все-таки |
| also | итак, следовательно, таким образом |
Рассмотрим несколько примеров употребления союзных слов:
Das Wasser war kalt, trozdem schwammen wir. — Вода была холодной, несмотря на это, мы искупались.
Zuerst gehen wir zur Post, dann müssen wir nach Hause fahren. — Сначала мы пойдем на почту, потом мы должны поехать домой.
После союзных слов «doch», «jedoch» порядок слов может быть как прямым, так и обратным.
Потренируйтесь использовать разные союзы, выполнив следующее упражнение.
Задания к уроку
Упражнение 1. Переведите на немецкий.
1. Мои родители идут в театр, но я остаюсь дома.
2. Я болен, поэтому я не иду завтра на работу.
3. Погода была хорошей, несмотря на это, мы остались дома.
4. Ты должен сделать это сегодня, иначе завтра у тебя не будет времени.
5. Несмотря на мою просьбу, она не позвонила.
6. Я был в школе, а ты уже ушел.
7. То снег идет, то солнце светит.
8. Я хотел (möchte) купить эту книгу, однако она была слишком дорогой.
9. Сегодня вечером я или почитаю книгу, или посмотрю телевизор.
10. Я переводил текст, но это было слишком сложно для меня.
Ответ 1.
1. Meine Eltern gehen ins Theater, aber ich bleibe zu Hause.
2. Ich bin krank, deshalb gehe ich morgen nicht zur Arbeit.
3. Das Wetter war sehr schön, trotzdem blieben wir zu Hause.
4. Du musst das heute machen, sonst hast du morgen keine Zeit.
5. Trotz meiner Bitte hat sie nicht anrufen.
6. Ich war in derSchule,sondern du bist schon weggegangen.
7. Bald regnet es, bald scheint es.
8. Ich möchte dieses Buch kaufen, doch es war sehr teuer.
9. Heute abend ich entweder lese ein Buch oder sehe fern.
10. Ich überzetzte den Text, aber es war zu schwierig für mich.
Частицы в немецком языке: значение и употребление
Если вы уже начали изучать немецкий язык, вы наверно знаете, что он довольно сложный не только с грамматической, но и с лексической точки зрения – глаголы спрягаются, существительные и прилагательные склоняются, глагол ставится на второе место в предложении или же в его конец в зависимости от структуры фразы, а короткие существительные часто объединяются в одно очень длинное слово, которое нужно разделить на части, чтобы понять его смысл…
Одной из трудных лексических тем немецкого языка являются частицы, т.к. они могут иметь несколько разных значений. Сегодня мы с вами поговорим об основных частицах и их значениях, а также посмотрим несколько видео, чтобы повторить пройденное и выучить новые частицы.
1. Aber: “да”, “же” и “ну”, часто эта частица подчеркивает неожиданность, необычность и усиливает ответ на вопрос, в котором что-то предлагается
Er kommt aber spät! Ну он и поздно пришёл!
Aber sicher! Да, безусловно!
Kommst du mit? Aber ja!Ты идешь со мной? Конечно же!
Dieses Buch ist aber gut! Это книга оказалась хорошей!
2. Auch: “в самом деле”, “действительно”
Du wiederholst es auch immer! Вечно ты это повторяешь!
So ist es auch: Это и в самом деле так.
3. Bloß: “вот только”, “же”
Was ist bloß mit meinen Männern los? Что же происходит с моими мужчинами?
Lass uns bloß zu oft sehen! Вот только нам не нужно встречаться слишком часто.
4. Denn: “же”, выражает интерес говорящего к информации собеседника или к какому-либо событию или человеку
Was ist denn los? Что же случилось?
Wo ist er denn? Где же он?
5. Doch: “же”, ведь”, выражает недовольство, настойчивую просьбу, приказ
Ich habe es ihm doch gesagt: Я же ему это говорила.
Sprechen sie doch! Говорите же!
6. Eben: “именно”, обозначает сохранение определенной ситуации или констатацию факта
Das ist eben so: Это именно так.
Er will eben nicht arbeiten: Он и вправду не хочет работать.
7. Eigentlich: “в сущности”, “собственно”, “вообще-то”
Ich bin eigentlich neu hier: Вообще-то я тут новенький.
Er hat es eigentlich nicht gemacht: Вообще-то он этого не делал.
8. Etwa: “разве”, выражает уточнение, используется в вопросах, на которые подразумевается положительный ответ
Wissen sie es etwa nicht? Разве они этого не знают?
Hast du es etwa die Hausaufgabe nicht gemacht? Ты что же, не сделал домашнее задание?
9. Halt: “ведь”, “уж”, “именно”. синоним частицы “eben”
Es ist halt (eben) so: Это так и есть.
Ich bin halt auch aufgeregt: Я ведь тоже волнуюсь!
10. Ja: используется для усиления положительных и отрицательных высказываний
Er ist ja auch eine gute Person! Он же тоже хороший человек!
Komm ja nicht so spät: Только не опаздывай!
11. Kaum: “едва”, “почти не”
Peter kann kaum atmen: Петер почти не может дышать.
Nach der Operation konnte ich kaum laufen: После операции я почти не мог ходить.
12. Mal: “совсем нет”, “уж”, употребляется для подбадривания повелительном наклонении и для его смягчение
Man kann mal nichts ändern: Здесь уже ничего не поделаешь.
Er ist nicht mal klug: Он совсем не умный.
Sehen wir mal! Давайте посмотрим!
13. Nun: “ну”, “итак”. также выражает нетерпение
Nun, was machen wir jetzt? Ну, что сейчас будем делать?
Nun gut, ich werde dir helfen: Ну ладно, я тебе помогу.
14. Nur: “только”, “же”, в повелительном наклонении означает подбадривание
Sieh nur, was du gemacht hast! Посмотри-ка, что ты наделал!
Nur keine Fragen! Только без вопросов!
15. Schon: подчеркивает согласие, уверенность говорящего в действии
Ich denke schon: Я так и думаю
Sie wird schon ein Baby haben! У неё обязательно будет ребенок!
16. Selbst: “даже”, используется по отношению к лицам, совершающим определенные действия
Selbst Otto wusste es nicht: Даже Отто об этом не знал.
Selbst Anna lernt die Regeln: Даже Анна учит эти правила.
17. Sogar: “даже”. используется по отношению к фактам, предметам или действиям
Er hat sogar den Computer repariert: Он даже компьютер отремонтировал.
Sie kann sogar Japanisch! Она и японский знает!
18. Vielleicht: “пожалуй”, используется также во фразах, выражающих отрицательное отношение к чему-либо
Du bist mir vielleicht ein Faulpelz! Ну ты и лентяй!
Er ist vielleicht ein Spinner: Он, пожалуй, врун.
19. Wohl: “вероятно”, “скорее всего”, усиливает предположение
Wass werden sie wohl antworten? Что же они ответят?
Wie alt ist sie wohl? Сколько же ей может быть лет?
Итак, мы повторили значения основных немецких частиц. А теперь давайте посмотрим 2 видео, в которых носители языка объясняют употребление частиц:
Конечно, это лишь теория; чтобы непринужденно употреблять частицы в разговорной речи, вам нужно больше смотреть немецкое телевидение, слушать радио, а также разговаривать с носителями языка.
Парные союзы
Союз
Союз – часть речи, которая не склоняется и образует сочетания между словами, группами слов, членами предложений или целыми предложениями и заодно выражает их логические и грамматические связи.
Парные союзы (= двойные союзы), как их название подсказывает, состоят из двух частей. Первая часть стоит перед первым соединяющимся элементом, вторая – между обоими соединяющимися элементами.
В данной статье представлены чаще всего употребляемые и классифицированные по категориям парные союзы в немецком языке с примерами их употребления.
1. Перечисление
<sowohl – als auch, wie auch>
→ Ich spreche sowohl Spanisch als/wie auch Französisch.
(Я говорю и/как по-испански, (так) и по-французски.)
<nicht nur – sondern auch>
→ Ich spreche nicht nur Spanisch, sondern auch Französisch.
(Я говорю не только по-испански, но также и по-французски.)
<teils – teils>
→ Teils spreche ich Spanisch, teils Französisch.
(Частично/Отчасти я говорю по-испански, частично/отчасти – по-французски.)
2. Отрицание
<weder – noch>
→ Ich spreche weder/ Weder spreche ich Spanisch noch Französisch.
(Я не говорю ни по-испански, ни по-французски.)
3. Пропорция
<je – desto/umso>
→ Je mehr Sprachen du lernst, desto/umso leichter fallen sie dir.
(Чем больше языков ты изучаешь, тем легче они тебе даются.)
4. Ограничение
<insofern – als>
→ Er war insofern schuld, als er nicht geholfen hat.
(Он был виноват постольку, поскольку он не помог.)
5. Условие
<wenn – dann>
→ Wenn das wahr ist, dann tut es mir sehr leid.
(Если это правда, то мне очень жаль.)
6. Альтернатива, исключение
<entweder – oder>
→ Entweder Sie gehen/ gehen Sie, oder ich rufe die Polizei!
(Или/Либо Вы уйдёте, или/либо я вызову полицию!)
7. Противительность
<nicht – sondern>
→ Ich spreche nicht Spanisch, sondern Französisch.
(Я говорю не по-испански, а по-французски.)
<einerseits – andererseits>
→ Einerseits freue ich mich, andererseits bin ich traurig.
(С одной стороны, я рада, с другой стороны, мне грустно.)
<zwar – aber>
→ Ich bin zwar kein Profi, aber ich helfe dir.
(Я (хоть и) не профессионал, но я помогу тебе.)
<halb – halb>
→ Er ist halb deutsch, halb russisch.
(Он наполовину немец, наполовину русский.)
<mal – mal>
→ Mal funktioniert es, mal funktioniert es nicht.
(Раз/То работает, раз/то не работает.)
<bald – bald>
→ Bald lacht er, bald weint er.
(То он смеётся, то он плачет.)
| Примечания: ► Запомните, что некоторые парные союзы относятся к подчинительным союзам, т.е. порядок слов в предложении, которое вводится соответствующей частью парного союза, соответствует порядку слов в придаточном предложении: → Je mehr Sprachen du lernst, desto leichter fallen sie dir. → Wenn das wahr ist, dann tut es mir sehr leid. → Er war insofern schuld, als er nicht geholfen hat. ► Запомните также, что некоторые парные союзы рассматриваются как обычные наречия, следовательно, порядок слов в предложении, которое вводится одной частью парного союза, соответствует порядку слов в повествовательном предложении с обстоятельством: → Teils spreche ich Spanisch, teils (spreche ich) Französisch. → Weder spreche ich Spanisch noch (spreche ich) Französisch. → Einerseits freue ich mich, andererseits bin ich traurig. → Mal funktioniert es, mal funktioniert es nicht. → Bald lacht er, bald weint er. |
Есть замечания, отзывы или пожелания относительно данной статьи? Пишите!
Как правильно употреблять немецкое наречие ‘Auch’
Иногда самые маленькие слова могут иметь большое значение. Возьмем немецкое наречие auch . В простейшей форме это слово означает «также». Но это также (понятно?) Имеет большее значение.
Auch может означать «даже». Это также может быть модальная частица и подразумевать что угодно от «Я надеюсь» до «Вы уверены». Вот более подробный взгляд на силу, стоящую за этим обычным маленьким наречием.
Когда акцентируется внимание на «Auch»
Этот тип auch относится к предмету предложения и обычно находится перед вербальной группой.Его значение — «также». Например:
Mein Sohn будет выпускать все студии Klavier.
Мой сын теперь тоже хочет учиться игре на фортепиано.
Meine Oma isst gerne Bockwurst und auch Bratwurst.
Моя бабушка также любит есть Боквурст и Братвурст.
Когда не акцентируют внимание на « Auch »
Этот тип auch имеет прямое отношение к элементам фразы, которые следуют за ним. Обычно это означает «даже». Например:
Auch für einen fleißigen Schüler, war dies eine große Hausaufgabe.
Даже для трудолюбивого студента это было большим домашним заданием.
Ihr kann auch kein Arzt helfen.
Даже врач ей не поможет.
Обратите внимание, что в приведенных выше предложениях безударный auch привлекает внимание к слову с ударением: fleißigen или Arzt, соответственно.
«Аух» Can Express Mood
auch без акцента также может использоваться для обозначения настроения говорящего.В таких случаях вы найдете auch , чтобы подчеркнуть раздражение или успокоение говорящего. Например:
Du kannst auch nie still sein!
Ты никогда не сможешь оставаться в покое, не так ли?
Hast du deine Brieftasche auch nicht vergessen?
Надеюсь, вы не забыли свой кошелек.
Контекст — это все
Рассмотрим следующие два диалога и значение, подразумеваемое контекстом.
Sprecher 1: Die Freunde deines Sohnes können gut schwimmen. / Друзья твоего сына очень хорошо умеют плавать.
Sprecher 2: Mein Sohn ist auch ein guter Schwimmer. / Мой сын тоже хорошо плавает.
Sprecher 1: Mein Sohn treibt gerne Basketball und Fußball. Er ist auch ein guter Schwimmer. / Мой сын любит играть в баскетбол и футбол. Еще он хороший пловец.
Sprecher 2: Ihr Sohn ist sehr sportlich. / Ваш сын очень спортивный.
Как видите, в обоих диалогах фразы с auch практически одинаковы, но подразумевается разное значение.Тон и контекст значат все. В первом случае auch ставится с ударением и служит предметом предложения: Sohn. Во втором случае auch без акцента и акцент делается на guter Schwimmer , подразумевая, что сын, помимо прочего, также хорошо плавает.
Структура предложения— Правильно ли я использую слово «auch»?
Ваши вторые альтернативы с auch между подлежащим — здесь: местоимения — слева и глагол справа искажены.Эта частица, как и другие, идет после глагола, но, поскольку синтаксис немецкого языка более гибкий, чем английский, вы иногда будете видеть или слышать, как она появляется перед подлежащим (и глаголом), обычно для выделения.
- Auch ich komme mit der U-Bahn zur Schule.
Это подчеркивает важность предмета предложения ( ich ), вероятно, по отношению к предыдущим утверждениям других людей: не только вы / они, но и я тоже . В исходном положении это не может быть понято иначе, тогда как при стандартном среднем положении auch может относиться к субъекту:
- Ich komme auch mit der U-Bahn zur Schule.
Вместо этого он может изменить значение глагола:
- Ich komme auch mit der U-Bahn zur Schule.
- Ich kann mit der U-Bahn zur Schule kommen . (Автобус Ich nehme aber normalerweise den)
Это также может относиться к первому объекту, следующему за ним:
- Ich komme auch mit der U-Bahn zur Schule.
- Ich komme nicht nur mit der U-Bahn zur Schule.(Ich muss außerdem den Bus nehmen.)
Разницу между этими двумя нюансами можно смело считать продвинутой придиркой и неприменимо ко второму примеру в вопросе. Они разделяют возможное репозиционирование, что делает его в остальном однозначным:
- Auch mit der U-Bahn komme ich zur Schule.
Если частица должна применяться ко второму объекту¹, auch должно появиться непосредственно перед ним, независимо от его синтаксической позиции:
- Ich komme mit der U-Bahn (zum Training, aber) auch zur Schule .
- Auch zur Schule komme ich mit der U-Bahn.
Короткое утвердительное утверждение без глагола заставит частицу сразу же следовать за подлежащим:
- Алиса: Ich komme mit der U-Bahn zur Schule.
Bob: Ich auch ! — «я тоже», «я тоже».
¹ Я использую здесь , объект в очень широком смысле, который включает предложные фразы.
Грамматика— самый общий порядок слов в немецком языке
Чтобы расширить ответ Em1, потому что мне было скучно, я подсчитал порядок слов в одном случайном длинном сообщении австрийца на этом сайте, известного своими длинными и подробными ответами.Я считал только основные статьи.
«Стандартное» предложение с субъектом и глаголом, где субъект — первое, глагол — второе, и мне было все равно, что за ним последовало, (SV_) встречается 23 раза (включая два подзаголовка).
Вытягивание наречия, аппозиции или чего-либо еще в первую позицию с глаголом, следующим за вторым (AdvVS_), произошло 8 раз.
Предмет был вытянут перед глаголом (OVS) 3 раза.
Относительное или иное подчиненное предложение занимало первую позицию два раза, заставляя ScVSO.
Однажды я заметил VSO вне вопроса, хотя это, вероятно, спорно, и то, что я увидел, действительно было условным подчиненным предложением. ( Wird […], kann […] или что-то в этом роде.)
Наконец, конъюнкция в нулевой позиции (ConjSV_) случилась всего 4 раза.
Таким образом, исключая особый случай VSO, в 58% всех случаев порядок слов составляет субъект — глагол — объект, , чему учат в школе, и ожидаемый порядок слов в большинстве случаев.Можно добавить 10% случаев, когда SVO предшествует конъюнкция.
В 32% случаев порядок слов — something — глагол — подлежащее , т.е. что-то было перемещено в первую позицию, чтобы выделить это, что требует перемещения подлежащего на позицию после глагола. (Некоторые предложения не включали подлежащее в этой конструкции. Однако я не включил это в свои соображения, потому что я также не считал ругательства, которые иногда присутствуют в предложениях SVO.)
Но гораздо лучше сказать, что 90% всех основных предложений имели глагол на втором месте, независимо от того, что ему предшествовало. 10% были вышеупомянутыми соединениями в нулевой позиции ( Aber es gibt Ausnahmen ).
68% предложений в выборке имели SVO, но 90% следовали за V2 (то есть не имело значения, что предшествовало глаголу, если было или ).
4 быстрых совета по изучению немецкого языка Порядок слов
Что самое сложное в изучении немецкого языка?
Для англоговорящих это может быть просто немецкий порядок слов.
Немецкий порядок слов, если перевести его буквально на английский, выглядит как какой-то причудливый шекспировский узел, который нужно серьезно развязать.
Это одно из многих препятствий, которые необходимо преодолеть изучающим немецкий язык.
Надеюсь, этот пост поможет вам изменить порядок слов в немецком языке.
Загрузить: Эта запись в блоге доступна в виде удобного и портативного PDF-файла, который вы можете можно взять куда угодно. Щелкните здесь, чтобы получить копию. (Скачать)
4 быстрых совета по порядку слов на немецком языке
Мы подробно рассмотрим каждый совет всего за секунду.Чтобы лучше понять порядок слов на немецком и попрактиковаться, попробуйте FluentU.
Благодаря интерактивным субтитрам, которые дают мгновенные определения, произношения и дополнительные примеры использования, а также веселые викторины и мультимедийные карточки, FluentU представляет собой полноценный учебный пакет. Вы можете проверить это в бесплатной пробной версии и попробовать некоторые из упражнений по составлению предложений, чтобы проверить свое мастерство в немецком порядке слов.
1. Узнайте, какие союзы изменяют порядок слов в немецком языке, а какие нет Существуют разные виды союзов, которые по-разному влияют на предложение.
«Нормальный» порядок слов, как мы ожидаем, — это Subject Verb Object.
Ich werfe den Ball.
Координационные союзы не влияют на порядок слов: und , denn , sondern , aber , и oder .
Ich renne vorwärts und ich werfe den Ball.
Ich kann den Ball nicht gut treten, aber ich werfe den Ball ziemlich gut.
Entweder sagst du mir die Wahrheit, или ich werfe dir den Ball ins Gesicht!
Ich bin stark, denn ich werfe jeden Tag im Basketball-Training den Ball.
Подчиняющие союзы делают нечто гораздо более запутанное — они отбрасывают первый глагол в предложении до конца предложения. Наиболее распространенные подчиненные союзы: während , bis, als , wenn , da , weil , ob , obwohl , и dass .
Ich kann ihn nicht leiden, weil er so ein egoistischer Idiot ist.
Обычно порядок слов следующий:
Er ist so ein egoistischer Idiot.
Но если вы используете подчинительный союз, то глагол перемещается в конец предложения:
Ich habe auch schon immer gedacht, dass er ein egoistischer Idiot ist .
Obwohl er ein egoistischer Idiot ist , sollten wir nett zu ihm sein.
В знаменитом эссе «Ужасный немецкий язык» Марк Твен приводит хороший пример того, насколько нелепым может быть это правило:
«Но когда он на улице, жена государственного советника (в атласе и шелке, теперь очень непринужденно одетая по последней моде) встретила »,
Wenn er aber auf der Strasse der in Samt und Seide gehüllten jetzt sehr ungenirt nach der neusten Mode gekleideten Resräthin begegnet .
Помните, даже если это кажется трудным, это всего лишь немецкий язык! Придерживаться.
2. Научитесь удерживать глаголы до концаВ немецком языке есть много ситуаций, когда глагол обязательно должен стоять в конце предложения. Это одна из причин, почему немецкий считается таким странным и сложным языком.
Модальные глаголы
В немецком языке инфинитив глагола обычно легко определить — почти каждый глагол во всем языке оканчивается на «-en». (есть такие, как sammeln — собирать, и segeln — ходить, что немного отличается!)
Laufen, gehen, sagen, singen, lieben, führen, usw.(und so weiter…)
Модальные глаголы — очень распространенный вид «помогающих глаголов», и в немецком языке вы всегда будете встречать их в различных формах.
müssen, können, sollen, möchten
Когда вы используете модальный глагол, второй глагол в предложении всегда находится в инфинитиве, а стоит в конце предложения .
Поначалу вам покажется неестественным ставить бесконечность в конце предложения! Только представьте, что вы поднимаете его, жонглируете и кладете в нужное место.
Müssen wir ihm mit seinem blöden Umzug nochmal helfen ?
НИКОГДА: Müssen wir helfen mit seinem blöden Umzug?
Относительные статьи
В немецком языке в каждом относительном предложении ( Nebensatz) глагол стоит в конце.
Kommt auch der Idiot, der mich so nervt , zur Party?
Kommt Magdalena, die letztes Wochenende so witzig war , auch ins Kino?
Если в относительном предложении есть два глагола, глагол, который загружается в конец предложения, всегда является первым глаголом.Это означает « habe » в « habe…. geschlafen »или« ist »в« ist… gegangen »или« muss »в« muss… lernen ». Другой глагол остается в своем обычном положении. (причастие прошедшего времени — это жаргон, но я могу понять, что вы опускаете его!)
Das Geschenk, das ich meinem Vater gekauft habe, ist nicht mehr in meinem Auto!
Ich möchte nur Mitarbeiter in meinem Café haben, die richtig gut Latte Art machen können .
Эти инверсии в стиле Йоды — еще одна причина, по которой немцы, плохо знающие английский, могут говорить такие вещи, как «Сегодня мы можем пойти в магазин?» Каждый раз, когда в начале предложения появляется временное наречие или предложная фраза, глагол должен стоять во второй позиции.
Morgen gehen wir feiern.
1914 fing der Erste Weltkrieg an.
Вы по-прежнему можете помещать наречия в другую часть предложения:
Wir gehen morgen feiern.
Но не напутайте! Вы даже можете поместить объект в начало предложения и перевернуть его, чтобы выделить объект.
Seine Umzüge habe ich niemals gemocht — Er hat einfach zu viele Möbel!
Вы видите? habe предшествует ich в предложении.
Вот несколько примеров предложных фраз в начале предложения, которые помещают глагол в конец:
G western hat sie mir etwas unglaublicheerzählt.
Gegenüber von mir sitzen zwei andere Deutsche.
Основное правило немецкого предложения: Предмет, Глагол, Косвенный объект (дательный падеж), Прямой объект
Ich warf ihm den Ball.
Sie gab mir ein Geschenk.
Наконец, когда вы объединяете длинную строку информации в предложение, вся информация должна поступать в следующем порядке: Time Manner Place (TMP) . Это означает, что сначала должны идти наречия, описывающие , когда что-то произошло, затем , как наречия, и, наконец, , где наречия.
Попробуйте просмотреть длинные предложения на немецком языке, которые вы найдете в газетах или на FluentU, чтобы получить несколько реальных примеров того, как правильно использовать наречия.
Использование FluentU для этой цели дает вам огромное преимущество перед использованием газет, потому что FluentU имеет так много встроенных средств обучения.
Ich ging gestern gelangweilt in die Uni.
Toby kam heute morgen ins Büro gelaufenund sagte, dass Tanja heute Kuchen mitgebracht hat. Ich musste mich beeilen, weil ich noch etwas davon kriegen wollte!
Здесь модальный глагол wollte загружается до конца предложения, потому что w eil является таким соединением. Dass делает то же самое, перемещая га t на после mitgebracht .
- Время: heute Morgen
- Маннер — laufend
- Place- in das Büro (обратите внимание, что здесь это in das Büro , а не im Büro , потому что вбежал Тоби, поэтому это глагол с движением, и это означает, что из занимает винительный падеж)
Давайте попробуем найти несколько примеров этих правил в предложениях, которые я взял из этой статьи Spiegel Online о группе Steel Panther:
Offenbar nicht ohne Grund muss man in Deutschland volljährig sein, um Ihre Konzerte zu besuchen.
В этом предложении Offenbar nicht ohne Grund занимает первую позицию, что означает, что muss предшествует man . Sein , инфинитив глагола для быть , стоит в конце предложения.
Ich habe mich heute mit Interesse im Zug von Köln nach Hamburg mit einem Steel-Panther-Fan unterhalten
- Время: heute
- Образ жизни: mit Interesse
- Место: im Zug von Köln nach Hamburg
Как и в 1981 году Diese Band gründete, wollte ich nicht nur einen Sänger.Ich suchte auch jemanden, der die ganze Zeit genau das tut, was ich will.
Als , подчиненное соединение, перемещает gründete в конец предложения. В относительном предложении , der die ganze Zeit genau das tut , глагол tut также стоит в конце предложения.
Jetzt sind wir fertig! Wenn du noch dringend mehrGrammatik-Tipps brauchst, stöbere weiter im FluentU-Blog.
Загрузить: Эта запись в блоге доступна в виде удобного и портативного PDF-файла, который вы можете можно взять куда угодно. Щелкните здесь, чтобы получить копию. (Скачать)
И еще кое-что …
Хотите узнать ключ к эффективному изучению немецкого языка?
Он использует правильный контент и инструменты, , как и FluentU, предлагает ! Просматривайте сотни видео, проходите бесконечные викторины и овладевайте немецким языком быстрее, чем вы когда-либо могли себе представить!
Смотрите забавное видео, но не можете его понять? FluentU предоставляет доступ к родным видео с интерактивными субтитрами.
Вы можете нажать на любое слово, чтобы мгновенно его найти. Каждое определение содержит примеры, которые помогут вам понять, как используется это слово. Если вы видите интересное слово, которого не знаете, вы можете добавить его в список словаря.
И FluentU не только для просмотра видео. Это полноценная платформа для обучения. Он разработан, чтобы эффективно научить вас всем словарям из любого видео. Проведите пальцем влево или вправо, чтобы увидеть больше примеров того слова, которое вы используете.
Самое приятное то, что FluentU отслеживает словарный запас, который вы изучаете, и дает вам дополнительную практику со сложными словами. Он даже напомнит вам, когда придет время повторить то, что вы узнали.
Начните использовать веб-сайт FluentU на своем компьютере или планшете или, что еще лучше, загрузите приложение FluentU из магазинов iTunes или Google Play.
Если вам понравился этот пост, что-то мне подсказывает, что вам понравится FluentU, лучший способ выучить немецкий с помощью реальных видео.
Испытайте погружение в немецкий онлайн!
Английские Соответствия немецкому наречию auch
Английские соответствия немецкому наречию «auch»
В английском языке наречия тоже , также и также соответствуют немецкому наречию auch . В то время как тоже и , а также всегда располагаются в конце предложения (как в a, b), также встречается либо перед основным глаголом (как в c), либо между вспомогательным и основным глаголом (например, в г).
а) Джон тоже едет в Лондон / тоже.
* Джон тоже / тоже едет в Лондон.
б) Джон тоже уехал в Лондон / тоже.
c) Джон тоже едет в Лондон.
* Джон тоже едет в Лондон.
г) Джон тоже уехал в Лондон.
В английском языке наречия подчеркивают, что кроме Джона в Лондон ходит по крайней мере еще один человек. Но наречие вводит альтернативы, и поэтому предложение неоднозначно: либо есть альтернатива человеку (как в е), либо есть альтернатива месту Лондона (как в f).
д) Джон тоже едет в Лондон / тоже. {что x тоже едет в Лондон / тоже x ℮ D}
е) Джон тоже едет в Лондон / тоже. {что Джон тоже идет к x / тоже x ℮ D}
Какая из двух возможностей выражена предложением, зависит от того, на каком слове идет речь. Фокус устраняет двусмысленность этого предложения и, следовательно, исключает одно из прочтений.
То же самое с наречием и :
г) Джон тоже едет в Лондон. {что x также идет в Лондон x ℮ D}
з) Джон также отправляется в Лондон.{что Джон также идет к x x ℮ D}
В немецком языке наречие auch не имеет определенного места, но в зависимости от его положения в предложении оно имеет разные смысловые ссылки. Это из-за явления скремблирования.
В немецком языке предложения с наречием auch не являются двусмысленными, потому что положение auch не фиксировано. В зависимости от предполагаемого значения auch встречается в определенной позиции.
i) Auch John geht nach London.
j) John geht auch nach London.
Составляющая после наречия всегда подчеркнута и, таким образом, содержит наиболее важную информацию в предложении. [1] В i) это существительное «Джон», которое следует за наречием auch и поэтому подвергается ударению. Это означает, что есть по крайней мере еще один человек, помимо Джона, который также едет в Лондон, тогда как в j) основное внимание уделяется Лондону, потому что здесь существительное «Лондон» следует за наречием auch и, таким образом, сфокусировано.Согласно этим наблюдениям в немецком языке у нас нет двусмысленных предложений с наречием auch , и поэтому мы получаем только одно прочтение для каждого предложения:
k) Auch John geht nach London. {auch x geht nach London x ℮ D}
л) John geht auch nach London. {John geht auch nach x x ℮ D}
Как мы видели выше, в немецком языке положение наречия auch не так фиксировано, как положение его английских соответствий. Это из-за явления скремблирования, которое позволяет нам изменять порядок слов в немецких предложениях.Таким образом, в английском языке фокус более важен, потому что на каком слове делается акцент и какое чтение мы получаем, решается на основе интонации предложения, тогда как в немецком языке позиция auch определяет часть информации, на которой сосредоточено внимание. . Таким образом, мы получаем только одно прочтение каждого предложения на немецком языке, но у нас есть двусмысленность в этих предложениях на английском языке.
[…]
[1] Питтнер К. и Берман Дж. (2004).Немецкий синтаксис. Ein Arbeitsbuch. Тюбинген: Гюнтер Нарр Верлаг. 24-25.
Немецкие соединения (Konjunktionen): полное руководство
- «Это платье такое красивое, , но оно слишком короткое».
- «Мне пришлось ехать домой , потому что я плохо себя чувствовал».
- «Он не очень усердно учился и, следовательно, он не учился».
Что общего у всех этих предложений? Если вы внимательно посмотрите на то, как структурированы эти операторы, вы увидите, что все они объединены такими словами, как , но , , потому что , и или , следовательно, .
Эти слова позволяют нам строить длинные и сложные предложения вместо того, чтобы общаться только с помощью коротких и простых, таких как «Я люблю рисовать. Мне нравится живопись.»
Так что же это за волшебные слова, которые позволяют нам связать два разных утверждения или объяснить причинно-следственные связи?
Ответ: Союзы.
И, как и в любом другом языке, немецкие союзы являются жизненно важной частью немецкого языка.
В этом посте мы подробнее рассмотрим магию немецких союзов!
Типы немецких союзов
Есть два типа немецких союзов: координирующих союзов и подчиненных союзов .
Подчиняющие союзы влияют на структуру предложения, изменяя положение глагола, в то время как координирующие союзы оставляют положение глагола неизменным.
Давайте подробнее рассмотрим эти два типа немецких союзов!
Координационные союзы на немецком языкеКак уже говорилось, координирующее соединение в немецком языке не влияет на глагол (или его положение).
Если вы встретите следующие выражения, вы можете быть уверены, что имеете дело с координирующим союзом.
| и | и |
| абер | но |
| denn | потому что |
| или | или |
| зонд | , но (как , а скорее ) |
| beziehungsweise | или, точнее |
| док | , но, тем не менее, |
| джедох | , но, тем не менее, |
| аллен (редкое выражение) | но, к сожалению, |
Если вы наткнетесь на слова, перечисленные выше в предложении, вы знаете, что эти координирующие союзы связывают вместе два предложения равной важности.
Поскольку союзы (координирующие, а также подчиняющие) объясняют корреляции между двумя предложениями и / или определяют отношения между двумя (или более) утверждениями, очень важно, чтобы вы ознакомились со значением каждого конкретного союза.
Приведу несколько примеров немецких координационных союзов!
Примеры :
→ und, aber oder, sondern, denn
Andy ist sehr intelligent, aber er hat einfach keinen Ehrgeiz.- Энди очень умен, но у него нет никаких амбиций .
Sie ist nicht nur Mutter von drei Kindern, sondern [ sie ] schreibt auch Kinderbücher. — Она не только мама троих детей, но и пишет детские книги .
(В данном случае слово «sie» заключено в круглые скобки, так как технически его можно не указывать)
Er wurde nach Hause geschickt, denn er war krank. — Его отправили домой, потому что он был болен .
Ich mag es, zu zeichnen und zu malen. — Я люблю рисовать и рисовать .
Интересный факт : Лингвистическое общество Америки при Мичиганском университете предлагает, чтобы для запоминания некоторых немецких координирующих союзов вы можете спеть их на музыку « Stayin ‘Alive » Bee Gees .
(Я могу гарантировать вам, что это очень эффективно. Кроме того, песня останется в вашей голове до конца дня.Но все, что помогает, правда?)
Позвольте показать вам:
| и | денн | сын — | дерн | абер — или | абер — или |
| ах | га | га | га | остаться в живых | остаться в живых |
Создание таких запоминаний очень важно, особенно при изучении немецких союзов.
После координирующего союза вы продолжите с тем же порядком слов, что и в предыдущем предложении. Это означает, что обе части согласованного предложения действуют как независимые предложения (которые были связаны вместе), и их структура не изменяется.
Когда дело доходит до положения спряженного глагола в координирующем союзе, глагол будет на втором месте:
“ Sie ist nicht nur Mutter von drei Kindern, sondern schreibt auch Kinderbücher .”
Здесь спряженный глагол («schreiben» — «sie schreibt») находится во второй позиции, то есть во втором «слоте» предложения, связанном с первым согласованным спряжением.
Еще несколько полезных советов по немецким координирующим соединениям :- За фразой « nicht nur » всегда следует « sondern auch ».
- Разница между словами « sondern » и « aber » заключается в том, что вы используете « sondern », где вы должны использовать «но скорее» (что означает: вместо ) в английском языке.
- Перед словом « sondern » должно стоять отрицание.
- « Aber » может предшествовать отрицание, но не обязательно.
- « Denn » против « weil »: оба слова объясняют причинно-следственную связь и предоставляют причину, но между ними есть одно существенное различие — они требуют разного порядка слов. « denn » — clause никогда не может быть в начале предложения. Если вы хотите начать предложение с объяснения причины, используйте « weil ».
- « Jedoch » обычно более сильное слово, чем « doch », и может использоваться для добавления акцента. Ударение слова может меняться в зависимости от того, какое место оно занимает в предложении:
→ Er war verärgert, jedoch zeigte er es nicht. — Разозлился, но не показал .
→ Er war verärgert, er zeigte es jedoch nicht. — Разозлился, но не показал .
В первом предложении позиция слова « jedoch » делает гораздо больший акцент на его контроле над своим гневом.
Немецкий язык не был бы немецким, если бы не было «особого случая» для каждого случая. К счастью для вас, это довольно просто: я говорю о двухчастном координирующем соединении .
С двухчастными согласованиями это почти то же самое, что и с обычными координирующими союзами: они оставляют глагол в том же положении, что и в предыдущем предложении.
| энтведер… или | либо… либо |
| sowohl… als auch | и… и |
| Ведер… Ночь | ни… ни |
| einerseits,… andererseits | с одной стороны… с другой |
| mal… mal | иногда… иногда |
| teils… teils | частично… частично |
Примеры :
Entweder wir gehen heute ins Kino или wir gehen morgen.- Пойдем сегодня в кино или пойдем завтра .
Ich mag sowohl Richard Wagner as auch Richard Strauss. — Мне нравятся и Рихард Вагнер, и Рихард Штраус .
Es ist weder eine besonders schöne Stadt noch sind ihre Bewohner freundlich. — Это неприятный город, и его жители не особенно дружелюбны .
Einerseits würde ich wirklich gerne auf die Party gehen, andererseits bin ich sehr müde.- С одной стороны я бы хотел пойти на вечеринку, с другой стороны очень устал .
Mal kann ihr Hund sehr ruhig sein, mal ist er sehr anstrengend. — Иногда ее собака очень спокойна, иногда очень утомительна .
Der Film war teils sehr schön, teils etwas langweilig. — Фильм был отчасти очень красивым, отчасти несколько скучным .
Подчиненные союзы в немецком языкеВ отличие от координирующих союзов, немецкие подчинительные союзы изменяют положение глагола в предложении.Столкнувшись с подчинительным союзом, вы увидите, что глагол перемещен в конец предложения.
Как определить подчиненное соединение, спросите вы?
Эти слова означают, что вы имеете дело с одним:
| до | до |
| начдем | после |
| ehe | до |
| seit, seitdem | , поскольку (указывает время, а не причинно-следственную связь) |
| während | пока, в то время как |
| как | когда (при описании прошлых событий) |
| Венн | when (описание настоящего и будущего), если, когда бы то ни было |
| WANN | когда (только для вопросов) |
| до | до, по |
| obwohl | хотя |
| als ob, als wenn, als | как будто |
| софт | так часто, как (когда) |
| собальд | как только |
| соланж | до |
| da | потому что |
| индем | от… -ing |
| Вейл | потому что |
| об | ли *, если (* используется только тогда, когда можно сказать «ли» и на английском языке) |
| водопад | в случае, если |
| Венн | если, когда |
| мм… zu | Отдо |
| дасс | , что |
| натренированный | так что |
| плотина | так что |
Признаюсь: по сравнению с координирующими соединениями это гораздо больший список.
К сожалению, на этот раз у меня также нет броского запоминания, но я уверен, что у вас в мгновение ока будет ключевой , подчиняющий союзы !
Когда использовать «
wenn » и « als »?Если вы имеете в виду событие в прошлом, которое было завершено, вам нужно будет использовать слово « als »:
- Als ich ein Kind war, mochte ich keinen Brokkoli. — В детстве не любила брокколи .
Слово « wenn » может использоваться для описания повторяющегося события:
- [Immer] wenn ich nach Heidelberg gehe, schaue ich mir das Schloss an. — [Всегда /] Когда я еду в Гейдельберг, я посещаю замок .
Как видите, слово « wenn » может означать как «когда», так и «когда».
Разница между «
wenn » и « ob »И « wenn », и « ob » переводятся как «, если », но их нельзя использовать взаимозаменяемо.Уловка памяти здесь довольно проста: если вы можете использовать «ли» на английском языке, вам придется использовать « ob » на немецком языке.
- Ob estimmt, weiß ich nicht. — Верно ли , не знаю .
- Wenn das wahr ist, will ich mir die Konsequenzen nicht ausmalen. — Если это правда, я не хочу представлять себе последствия .
Вместо использования « wenn » для обозначения возможности вы также можете использовать « падает »:
- Falls das wahr ist, will ich mir die Konsequenzen nicht ausmalen.- Если это правда, я не хочу представлять себе последствия .
Использование «
wann »Как указано выше, « wann » используется только для вопросов.
- Wann gehst du nach Stuttgart? — Когда вы собираетесь в Штутгарт ?
«
Nach » и « Nachdem »Существует простое правило, которому вы можете следовать, когда дело доходит до использования « nach » и « nachdem »: « Nachdem » используется с действиями, а « nach » используется с существительными.
- Wir haben uns nach der Arbeit getroffen. — Встретились после работа . (Die Arbeit = существительное)
- Mir ging es nicht gut, nachdem ich zu viel Kuchen gegessen hatte. — Я плохо себя чувствовал после съел слишком много торта . (Эссен = глагол / действие).
«
Seit » и « seitdem »Использование « seit » и « seitdem » аналогично « nach » и « nachdem »: вы можете использовать « seit » и « seitdem » как с действиями, так и с существительными, но встречаясь с существительными, вы можете использовать только « seit ».
- Seitdem er mit seiner neuen Freundin zusammen ist, hat er sich sehr verändert. — С познакомился со своей новой девушкой, много поменял .
- Er schläft seit Beginn des Films. — Спит с начало фильма .
Различия между «
da » и « weil »Между этими двумя словами нет различий, за одним исключением: « da » более формально, чем « weil » (оба означают , потому что ).Поэтому, если вы пишете официальное письмо или находитесь в ситуации, требующей менее неформального языка, выбор « da » вместо « weil », вероятно, будет более подходящим решением.
«
Bevor » и « ehe »То же, что и выше: « ehe » более формально, чем « bevor ». Следует отметить, что « bevor » используется с действиями, но более короткая форма « vor » может использоваться только с существительными.
- Wir sollten uns treffen, bevor es dunkel wird.- Мы должны встретиться до стемнеет . (Дункель Верден = действие)
- Wir treffen uns vor dem Theater. — Встречаемся перед театром. (театр = существительное)
«Während» может означать «во время» или «во время»:
- Während des Vortrages ist er eingeschlafen. — Во время лекции заснул .
- Er hat blonde Haare, während sein Bruder rote Haare hat. — У него светлые волосы, , тогда как у его брата рыжие волосы .
- Er hat bis um acht Uhr geschlafen. — Он спал до восемь часов .
- Bis er das merkt werden Stunden vergangen sein. — К , когда он понимает, что часов пройдет .
- Obwohl er nur zwölf Jahre alt ist, ist er ein beginnadeter Schlagzeuger. — Хотя ему всего двенадцать лет, он очень талантливый барабанщик .
- Um ihr eine Freude zu machen, hat er ihr Blumen gekauft. — Чтобы сделать ее счастливой, он купил ей цветов .
Как и в английском переводе « that », « dass » можно опустить в предложении:
- Er glaubt, dass die Erde eine Scheibe sei.- Он считает , что Земля — это диск .
- Er glaubt, die Erde sei eine Scheibe. — Он считает, что Земля — это диск .
- Erbeeuptete, eine Erkältung zu haben, sodass er seinen Aufsatz nicht vor der Klasse vorlesen musste. — Он утверждал, что у него простуда , так что ему не пришлось читать свое эссе перед классом .
- Hans sicherte sich eine gute Note, indem er sich beim Lehrer einschleimte. — К подхлебнув учителя, Ганс удостоверился, что он получил хорошую оценку .
- Sooft er sich auch bemühte, seine Französischkenntnisse wurden nicht besser. — Как часто он пытался , его французские навыки не улучшались .
- Sobald wir genug Geld gespart haben, wollen wir nach Bali reisen. — Как только , так как мы накопили достаточно денег, мы хотим поехать на Бали .
- Solange sie ihre Einstellung nicht ändert, wird sie keinen Erfolg haben. — Пока она не изменит своего отношения, она не добьется успеха .
- Er hat die Prüfung bestanden, als ob es nichts wäre.- Экзамен сдал как будто ничего не .
- Er tat so, als ob er davon noch nie gehört hatte. — Он притворился , как будто он никогда не слышал об этом до .
- Dieser Grashüpfer sieht so aus als wäre er ein Zweig. — Этот кузнечик выглядит как , как если бы это была веточка .
- Er stellte er sich zwei Wecker, damit er nicht verschlief.- Поставил две будильники, чтобы не проспал .
Это было — надо признать — много информации для одного сообщения в блоге. Немецкие союзы (как вы можете видеть) — это довольно обширная область, полная неточностей и слов, которые меняют значение в зависимости от того, как используются .
Так что не волнуйтесь, если вы не избавитесь от них в одно мгновение — это то, с чем даже некоторые немцы борются!
Как только вы почувствуете, что готовы заняться темой немецких союзов, вы можете проверить свои знания с Clozemaster!
Viel Erfolg !
Испытайте себя с Clozemaster
Проверьте свои навыки и узнайте, что вы узнали из этой статьи, проиграв несколько предложений со всеми видами немецких союзов.
Зарегистрируйтесь здесь, чтобы сохранить свой прогресс и начать бегло говорить с тысячами немецких предложений в Clozemaster.
Clozemaster был разработан, чтобы помочь вам изучать язык в контексте, заполняя пробелы в аутентичных предложениях. Благодаря таким функциям, как Grammar Challenges, Cloze-Listening и Cloze-Reading, приложение позволит вам подчеркнуть все навыки, необходимые для свободного владения немецким языком.
Поднимите свой немецкий на новый уровень.Нажмите здесь, чтобы начать практиковаться с настоящими немецкими предложениями!
Грамматика по Гримму: порядок слов: Wortstellung
Союзы: Wortstellung
Порядок слов (также называемый синтаксисом) в немецком языке обычно определяется расположением глагола. Глагол в немецком языке может быть во второй позиции (наиболее часто встречается), в начальной позиции (сначала глагол) и в конце предложения.
Конечный глагол во второй позиции
а) общие положения
Самый простой порядок слов в немецком языке, как и в английском, — это последовательность подчиненного-глагола-прямого объекта:
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Die Zwerge lieben die junge Prinzessin. | Гномы любят юную принцессу. |
| Warum auch nicht? Sie putzt ihr Haus und kocht ihr Essen! | А почему бы и нет? Она убирает их дом и готовит им еду! |
Как видите, конечный глагол (спряжение глагола) стоит на втором месте в каждом предложении. Это самая распространенная, базовая позиция для спряженных глаголов.
б) вопросы с вопросительными словами
При наличии вопросительных слов (wer, wann, wo, wie и т. Д.) Конечный глагол все еще остается на второй позиции, а подлежащее перемещается на третью позицию.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Wohnen sie nochmal? | Где они снова живут? |
| Был ли тег tut sie den ganzen? | Что она делает целый день? |
Конечный глагол в первой позиции
Конечный глагол может стоять на первом месте в вопросах да / нет и в командах (повелительное наклонение).
а) да / нет вопросы
Конечный глагол переходит в начало вопросов типа да-нет:
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Wohnen die 7 Zwerge und Schneewittchen in der Mitte des Waldes? | Семь гномов и Белоснежка живут посреди леса? |
| Soll ich sie besuchen? Ха-ха! | Может мне пойти навестить ее? Ха-ха! |
б) команды
Точно так же при подаче команд спряженный глагол стоит на первой позиции.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Mach die Tür auf, mein Schatz! Кауф майне Варен! | Открой дверь, дорогая! Купи мой товар! |
| Siehe diesen Apfel! Probier ihn mal! | Посмотрите на это яблоко! Попробуйте, продолжайте! |
Конечный глагол в конечном положении предложения
В некоторых случаях конечный глагол также может стоять в конце предложения, в конце зависимого предложения.Это происходит, когда предложение вводится подчинительным союзом (например, weil, ob, nachdem).
а) подчинительные союзы
Обычно (если это не во время продолжающейся устной дискуссии) подчиненные союзы являются частью более крупного предложения, которое также имеет главное (независимое) предложение. Зависимое предложение, введенное подчинительным союзом, объясняет, расширяет или изменяет информацию, представленную в независимом предложении. Придаточное предложение может предшествовать независимому предложению или следовать за ним.
В каждом предложении будет конечный глагол. Конечный глагол независимого предложения будет на второй позиции. Конечный глагол зависимого предложения будет в последней позиции предложения.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Ich hoffe, dass sie bald in den Apfel beißt! Ich kann kaum warten, bis siegotibt! | Надеюсь, что она скоро откусит яблока! С нетерпением жду пока она умрет ! |
Каждое предложение начинается с независимого (основного) предложения.Первую позицию занимает подлежащее «ich» (в обоих предложениях), а вторую — конечный глагол независимого придаточного предложения «hoffe» и «kann».
После запятой идет придаточное предложение, введенное подчинительным союзом dass и bis. Конечный глагол придаточного предложения beisst и stibt находятся в конечном положении предложения.
Сравните это расположение со следующим примером, в котором зависимое предложение начинается с предложения:
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Nachdem du meinen Apfel gegessen hast, willst du nie wieder irgendwas anderes essen! Ха-ха! | После того, как вы съедите мое яблоко, вы больше не захотите есть что-нибудь еще! Ха-ха! |
Это предложение начинается с придаточного предложения (вводится подчинительным союзом nachdem). Конечный глагол gegessen hast стоит в конце предложения, непосредственно перед запятой, разделяющей зависимые и независимые предложения.
Второй пункт — независимый пункт. Конечный глагол willst стоит во второй позиции; первая позиция предложения занята всем придаточным предложением!
б) относительные придаточные предложения
Эффект относительных местоимений такой же, как и подчинительных союзов: конечный глагол идет до конца предложения, которое вводится относительным местоимением.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Ach, dies ist das Mädchen, das mir so viele schlaflose Nächte bereitet! Ich bin aber keine böse Königin, die so etwas ohne weiteres erlaubt! | Ах, это та девушка, которая вызвала у меня столько бессонных ночей! Я, однако, не злая королева, которая просто позволяет этим вещам происходить без лишних слов! |
Переход от основного глагола к второстепенному
Бывают случаи, когда исходный конечный глагол из простого утверждения вытесняется новым компаньоном.
Модальные глаголы
Конечные глаголы могут быть заменены модальными глаголами (которые, как следует из названия, изменяют значение предыдущего основного глагола). В результате входящего модального глагола (который спрягается и является новым конечным глаголом) исходный глагол превращается в инфинитив.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Ха-ха! Ich bin die allerschönste Frau in der ganzen Welt! | Ха-ха! Я самая красивая женщина в мире! |
| Tja, dastimmt doch nicht.Ich möchte nur die allerschönste Frau in der ganzen Welt sein! | Ну, на самом деле это неправда. Я только хочу быть самой красивой женщиной на свете! |
Вспомогательные глаголы
Вспомогательные глаголы, такие как ‘haben’ или ‘sein’, образующие перфект настоящего времени, ‘hätte’ или ‘wäre’, образующие сослагательное наклонение прошедшего времени или ‘werden’, образующее будущее время, также наталкивают исходный конечный глагол в придаточное предложение. -конечное положение.С haben / sein и hätte / wäre исходный конечный глагол становится причастием. С werden оно становится инфинитивом.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Ich habe mich daran gewöhnt, die allerschönste Frau der ganzen Welt zu sein. | Я привыкла к тому, что я самая красивая женщина на свете. |
| Vielleicht, wenn ich das nicht gemacht hätte, müsste sie jetzt nicht sterben, aber so ist das Leben.Абсолютно несправедливо! | Может быть, если бы я этого не сделал, ей бы не пришлось умереть прямо сейчас, но это жизнь. Совершенно несправедливо! | |
| Weil ich eine böse Königin bin, werde ich keine winzige Sekunde damit verschwenden, meine schreckliche Tat zu bereuen! Das Leben ist ganz einfach, wenn man böse ist! | Поскольку я злая королева, я не потрачу ни секунды на сожаление о своем ужасном поступке! Жизнь действительно проста, когда человек злой! |
Последовательность существительных и местоимений
Винительный и дательный падеж
Хорошие новости! Единственное, что вы должны помнить в отношении размещения существительных, — это последовательность прямых и косвенных объектов, т.е.д., дательный и винительный существительные и возможные местоимения, которые их заменяют.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | ОК. Wie war das noch mal? Ich gebe der Prinzessin einen Apfel, und sie isst ihn. Ага. Das darf ich nicht vergessen! | ОК. Как все прошло снова? Я даю принцессе яблоко, и она его ест. Ага. Я не могу этого забыть! |
| Также ich gebe ihr einen Apfel.Ich gebe ihn der Prinzessin. Ich gebe ihn ihr! Wenn ich das pausenlos wiederhole, werde ich es bestimmt nicht vergessen, wem ich was geben soll. | Итак, я даю ей яблоко. Отдаю принцессе. Даю ей! если я буду повторять это без остановки, я точно не забуду, кому и что давать! |
Обратите внимание на :
- если у вас есть два существительных (винительный и дательный), то существительное предшествует винительному падению !
- местоимений предшествуют существительным
- местоимение винительного падежа предшествует местоимению дательного падежа
| Дательное существительное | Винительный падеж существительного |
| Местоимение | Существительное |
| Винительный падеж | Дательный падеж |
Когда вы приобретете больше уверенности в немецком языке, вы сможете поэкспериментировать с порядком слов существительных и местоимений и увидеть, как смешивание элементов приводит к дифференцированию акцентов в предложении.Секрет: вы можете поменять местами дательный и винительный падеж существительных, если вы действительно хотите подчеркнуть получателя действия — если есть необычное расположение элементов, они, как правило, привлекают к себе дополнительное внимание!
Последовательность наречий
Время / место: от меньшей к более конкретной информации
При использовании выражений времени или места сначала идет более общая информация, а затем более конкретная.
Ваш браузер не поддерживает аудио элементы.| die böse Königin | Ich bin letzten Monat jeden Donnerstag um 3 Uhr am Zwergenhaus vorbeigegangen, und versuchte sie zu töten. Und ich gehe gar nicht gern in den Wald zu diesem miesen Häuschen! Ich habe Angst vor der Dunkelheit! Дуф, ничт? | В прошлом месяце Я ходил в дом гномов каждый четверг в 3 часа дня и пытался убить ее. И мне очень не нравится ходить в тот убогий домик в лесу ! Боюсь темноты! Глупо, а? |
Последовательность других наречий
Типичная пословица гласит, что наречия времени предшествуют наречиям способа, которые предшествуют наречиям места (т.е., время — способ — место). На самом деле наречия должны быть в следующем порядке:
время — место — способ
Манера всегда в последнюю очередь, так как дает самую новую информацию — а новая информация подчеркивается тем, что помещается самой первой или самой последней.
Однако наречия гораздо более гибкие с точки зрения последовательности, и их порядок действительно зависит от того, какую информацию вы хотите выделить.
Ваш браузер не поддерживает аудио элементы.| Место I (предмет или компонент выделения) | Место II (спряженный глагол) | Место III | Место IV | Место V | Выделение |
| Die 7 Zwerge und Schneewittchen (тема) | wohnen | am Anfang (наречие времени) | friedlich (наречие образа) | in der Mitte des Waldes (предложная фраза, место) | Wer (кто)? |
| Am Anfang (наречие времени) | wohnen | die 7 Zwerge und Schneewittchen (тема) | friedlich (наречие образа) | in der Mitte des Waldes.(место) | Ванн (когда)? |
| Фридлих (наречие манеры) | wohnen | die 7 Zwerge und Schneewittchen (тема) | am Anfang (наречие времени) | in der Mitte des Waldes. (место) | Wie (как)? |
| In der Mitte des Waldes (место) | wohnen | die 7 Zwerge und Schneewittchen (тема) | am Anfang (наречие времени) | фридлих.(наречие манеры) | Wo (где)? |
Вам нужно будет хранить наречия места отдельно от словесных дополнений, которые являются описанием места.
Вербальные дополнения важны для значения глагола (например, она пошла домой — «пошла» не имеет смысла без «дома»).
Наречия места на самом деле не нужны для определения значения глагола, они просто дают дополнительную информацию о месте события (например,g., она пошла к себе домой к лесу — «дом» имеет важное значение для «пошел», а «у леса» нет — это наречие вместо словесного дополнения).
Позиция nicht
Последняя информация, касающаяся порядка слов, с которой мы здесь поговорим, — это размещение отрицательной частицы nicht (и других отрицательных элементов, таких как nie или kaum — никогда не и вряд ли ).
Нихт …
- помещается в конец предложения (НО перед любыми глагольными дополнениями, такими как причастие или инфинитив после модального глагола или прямого объекта)
- следует за всеми наречиями, кроме наречий типа (schnell, gut, gern и т. Д.).)
- предшествует элементу, если это единственное, что в предложении должно отрицать (в отличие от отрицания всего предложения или предложения)
| 1. | die böse Königin: Mein Schatz, kauf ruhig diesen schönen Apfel, ich habe ihn nicht vergiftet! Warum isst du ihn nicht? | Дорогая, не волнуйся, покупай это яблоко, я не травил ! Почему не едят ? |
| 2. | Magst du Äpfel nicht? | Разве не любишь яблоки? |
| 1. | Du willst meinen Apfel nicht essen? Был ли soll dass denn heißen? | Ты, , не хочешь съесть мое яблоко? Что это должно значить? |
| 3. | Хммм … Венн Нихт Дизен Шёнен Апфель, Данн Кауф mindestens Diesen Wunderbaren Kamm! | Хммм … если не это красивое яблоко, то купите хотя бы эту чудесную расческу! |
| 1. | Эй, hast du meine Frage nicht gehört? Warum antwortest du nicht? Ого! Sie ist tot !!!! Ich bin die schönste Frau im ganzen Land — oder vielleicht auch nicht … | Эй, разве ты не слышал мой вопрос? Почему не отвечает ? Ага, она мертва !! Я самая красивая женщина во всей стране — а может, , а не … |

 Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
 И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
 Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
Компактно и можно посчитать функцию при произвольном значении аргумента из области определения. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
Чтобы найти их координаты для функции y = x2, нужно составить таблицу: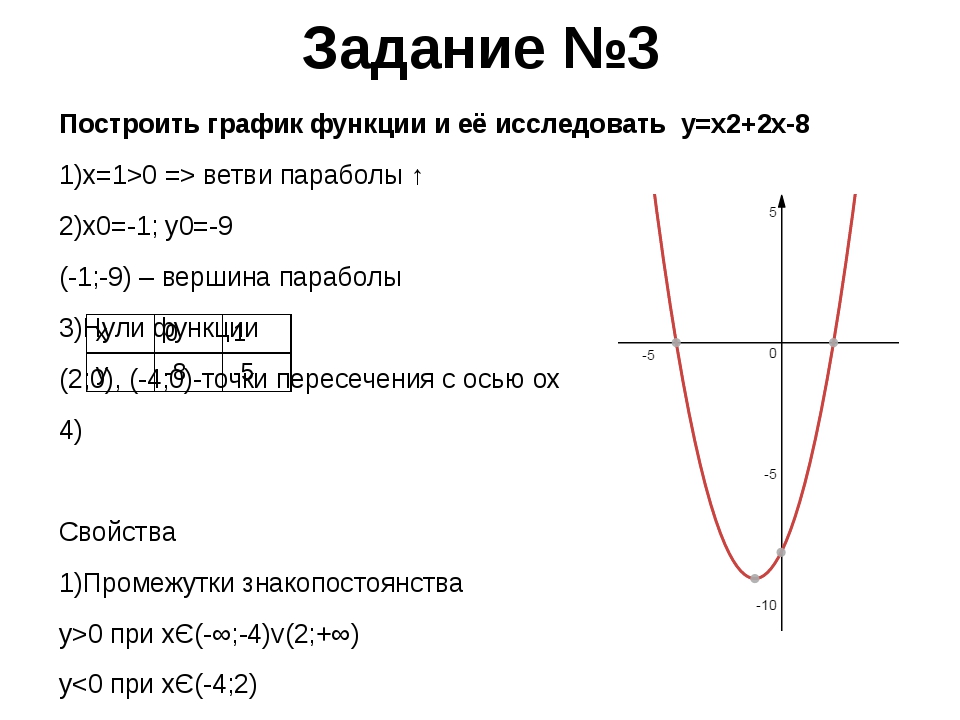 Отметим важные выводы:
Отметим важные выводы: Если a > 0,то график выглядит так:
Если a > 0,то график выглядит так: То есть координаты этой точки будут соответствовать: (0; c).
То есть координаты этой точки будут соответствовать: (0; c).

 Например, «1 2 производная».
Например, «1 2 производная». На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 производная. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2x производная).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 производная. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2x производная). 1 (стр.
244) текста.
1 (стр.
244) текста.
 2-5.Начнем с графика y = x 2 , сдвинем на 4 единицы вправо, затем
5 единиц вниз.
2-5.Начнем с графика y = x 2 , сдвинем на 4 единицы вправо, затем
5 единиц вниз.
 Когда мы
решая уравнение, мы просто добавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9
так что мы не меняем функцию.
Когда мы
решая уравнение, мы просто добавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9
так что мы не меняем функцию.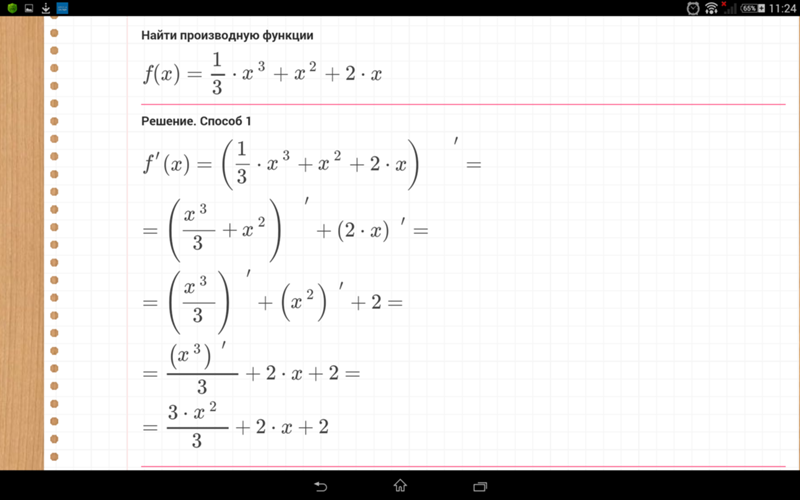
 Нарисуйте график функции f, найдите его вершину и найдите
нули f. Ответ
Нарисуйте график функции f, найдите его вершину и найдите
нули f. Ответ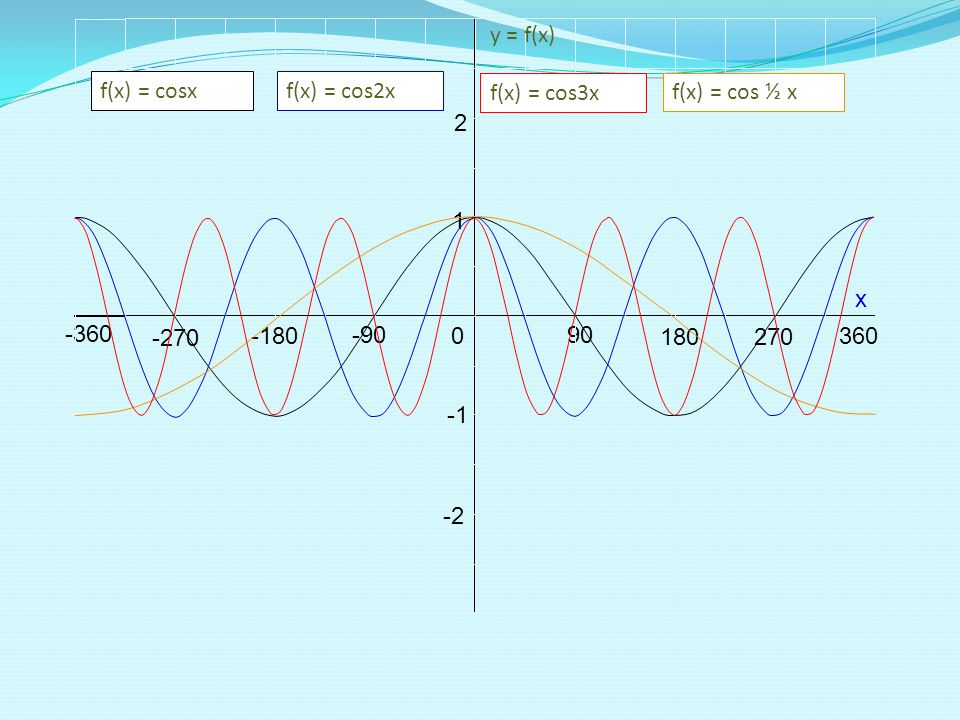 Итак, линия симметрии x = -2 и первая координата
вершины -2.
Итак, линия симметрии x = -2 и первая координата
вершины -2. Тем не мение,
Тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому должны удовлетворять x и y.
Тем не мение,
Тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому должны удовлетворять x и y.