Умножения и деление отрицательных чисел. Решение примеров.

 

 

В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел.

• \(«—«-\) при умножении минус на минус результат становится положительным;
• \(«-+»-\) при умножении минуса на плюс результат становится отрицательным;
•  \(«+-«-\) при умножении плюса на минус результат становится отрицательным;
• \(«++»-\)  при умножении плюса на плюс результат становится положительным.

---

Примеры умножения отрицательных чисел. 

Задача 1. Вычислить: \((-4)*(-4)\) и \((-6)*(-5).\)

Решение.

Отрицательное число при умножении на отрицательное станет положительным согласно правилу.

1. \((-4)*(-4)=16\)
2. \((-6)*(-5)=30\)

Ответ: \(16;30.\)

Задача 2. Вычислить: \((-10)*12\) и \((-7)*4.

\)

Решение.

Отрицательное при умножении на положительное число станет отрицательным согласно правилу.

-10 * 12= -120

(-7)*4=-28

 

Ответ: \(-120; -28\)

---

Задача 3. Вычислить: \(11*(-11)\) и \(13*(-6).\)

Решение.

Положительное при умножении на отрицательное число станет отрицательным согласно правилу.

1. \(11*(-11)=-121\)
2. \(13*(-6)=-78\)

Ответ: \(-121;-78.\)

Деление отрицательных чисел

 

При делении действуют те же правила знаков, что и при умножении. Делить на ноль нельзя.

• ​\(«—«-\)​ при делении минус на минус результат становится положительным;
•  ​\(«-+»-\)​при делении минуса на плюс результат становится отрицательным;
•  \(«+-«-\)при делении плюса на минус результат становится отрицательным;
• \(«++»-\) при делении плюса на плюс результат становится положительным.

Задача 4. Вычислить: \((-16)*(-4)\) и \((-6)*(-2)\).

Решение.

1. \(-16:(-4)=4\)
2. \((-6):-2=3\)

Ответ: \(4;3.\)

Задача 5. Вычислить: \((-10):5\) и \((-12):6\).

Решение.

1.  \((-10):5=-2\)
2. \((-12):6=-2\)

Ответ: \(-2;-2.\)

Задача 3. Вычислить:  \(121:(-11)\) и  \(169:(-13)\).

Решение.

1.  \(121:(-11)=-11\)
2.  \(169:(-13)=-13\)

Ответ: \(-11;-13.\)

 

 

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Новосибирский государственный технический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-9 классов. Люблю математику за её простоту и точность. Считаю, что каждый ребёнок может её освоить, нужно лишь немного его направить. Благодаря своему опыту работы, могу найти подход к каждому ученику и стать хорошим другом и наставником.

Оставить заявку

Репетитор по математике

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-6 классов. Я люблю математику за то, что математика- царица точных наук. Она не только интересна и «красива», она еще и полезна, как для других наук, так и в быту. Стараюсь прививать и поддерживать интерес детей к предмету.

Оставить заявку

Репетитор по математике

БГПУ им. Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-6 классов. Математика сложна, но интересна и увлекательна! При обучении настраиваю на позитивное восприятие всего нового и непонятного и впоследствии мои ученики испытывают радость новых открытий в этом удивительном мире цифр и знаков.

Математика по Skype

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Векторы

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Решение уравнений

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Похожие статьи

Почему минус на минус дает плюс? | Математика

Как известно, уже в школе всем говорят, что минус на минус дает плюс. Можно даже привести примеры: $$x-(-y)=x+y; (-x)\cdot (-y)=x\cdot y; -x/\left(-y \right)=x/y$$ Но самое интересное в другом. Если у кого угодно спросить а почему так, то мало кто сможет ответить. Вам скажут — так принято или так должно быть по правилам. А ответить почему такие правила и откуда они появились еще труднее. И даже если задать такой же вопрос в поисковой системе, то можно прочитать все что угодно, начиная с дурацких примеров и заканчивая попытками объяснения из области теории групп. Ну как школьнику или даже студенту можно объяснить что такое кольца из теории групп? Поэтому требуется нормальное объяснение, основанное на понятных и легко проверяемых понятиях и правилах. Как оказалось, это можно сделать фактически в одну строку. Смотрите выкладки: $$A-(-B)=X\Rightarrow A=X+(-B)\Rightarrow A=X-B\Rightarrow A+B=X\Rightarrow A-(-B)=A+B$$ Тут тоже могут возникать вопросы: «Почему при переносе слагаемого меняется знак на противоположный?» Ответ будет такой: «Мы ничего никуда не переносим, а просто добавляем в левую и правую части выражения одну и ту же величину»: $$A-(-B)=X\Rightarrow A-\left(-B \right)+(-B)=X+(-B)$$ А вот теперь обозначим: $$-B=Z$$ и после подстановки все становится очевидным: $$A-Z=X\Rightarrow A-Z+Z=X+Z\Rightarrow A=X+Z$$ Теперь осталось вернуться к старой (заменной переменной), используя выражение: $$-B=Z$$ И в результате получим, что при «переносе вправо слагаемого его знак поменялся на противоположный»: $$ A=X-B$$ Вот и все преобразования, объясняющие почему если в выражении идет два минуса подряд, то в итоге их надо заменить на плюс. Теперь займемся случаем умножения двух отрицательных чисел. $$(-A)\cdot (-B)=X\Rightarrow (-A)\cdot (-B)+\left(A\cdot B \right)-\left(A\cdot B \right)=X\Rightarrow …$$ $$… \Rightarrow (-A)\cdot (-B)+\left(A\cdot B \right)+ \left(-A \right) \cdot B=X\Rightarrow …$$ $$…\Rightarrow \left(-A \right)\left[\left(-B \right)+B \right]+A\cdot B=X\Rightarrow \left(-A\ \right) \cdot 0+A\cdot B=X\Rightarrow A\cdot B=X$$ Теперь осталось приравнять, с одной стороны: $$\left(-A \right)\cdot \left(-B \right)=X$$ а с другой стороны: $$A \cdot B =X$$ Тогда, окончательно: $$\left(-A \right)\cdot \left(-B \right)=A \cdot B$$ Как вам понятно, с делением двух отрицательных чисел уже не возникает проблем, так как операцию деления можно легко заменить операцией умножения на обратное. Остается выяснить почему минус из знаменателя можно поднимать в числитель. Один из вариантов: $$\frac{1}{-A}=\frac{1\cdot \left(-1 \right)}{-A\cdot \left(-1 \right)}=\frac{-1}{A}$$ Предлагаем все высказываться в комментариях, если что кому не понравилось. Эта статья подготовлена студенческой лабораторией для любознательных школьников и их учителей.
 

© Studlab.com

Узнаем как понять, почему «плюс» на «минус» дает «минус» ?

Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.

Законы математики

Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель. ..

Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».

Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.

Аксиома кольца

Существует несколько математических законов.

• Первый из них переместительный, согласно ему, C + V = V + C.
• Второй называется сочетательным (V + C) + D = V + (C + D).

Им же подчиняется и умножение (V х C) х D = V х (C х D).

Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.

Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.

Выведение аксиом для отрицательных чисел

Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.

Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.

Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.

Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.

Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).

Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.

Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.

Умножение и деление двух чисел со знаком «-»

Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.

Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.

(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.

Вспомная о правилах работы со скобками, получаем:

1) (-C) х (-V) + (C х V) + (-C) х V = D;

2) (-C) х ((-V) + V) + C х V = D;

3) (-C) х 0 + C х V = D;

4) C х V = D.

Из этого следует, что C х V = (-C) х (-V).

Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.

Общие математические правила

Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.

Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.

Раскрытие скобок: правила, примеры, решения

Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.

Что называется раскрытием скобок?

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2·(3+4) на выражение вида 2·3+2·4без скобок. Этот прием носит название раскрытия скобок.

Определение 1

Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:

• знаки «+» или «-» перед скобками, в которые заключены суммы или разности;
• произведение числа, буквы или нескольких букв и суммы или разности, которая помещена в скобки.

Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5+(−3)−(−7) к 5−3+7. Фактически, это тоже раскрытие скобок.

Точно также мы можем заменить произведение выражений в скобках вида (a+b)·(c+d) на сумму a·c+a·d+b·c+b·d. Такой прием также не противоречит смыслу раскрытия скобок.

Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x2·1a-x+sin(b)  будет соответствовать выражение без скобок вида x2·1a-x2·x+x2·sin(b) .

Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5−(3−(2−1))=5−(3−2+1)=5−3+2−1 или 5−(3−(2−1))=5−3+(2−1)=5−3+2−1.

Правила раскрытия скобок, примеры

Приступим к рассмотрению правил раскрытия скобок.

У одиночных чисел в скобках

Отрицательные числа в скобках часто встречаются в выражениях. Например, (−4) и 3+(−4). Положительные числа в скобках тоже имеют место быть.

Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а, +(а) на +а, -(а) на –а. Если вместо а взять конкретное число, то согласно правилу: число (5) запишется как 5, выражение 3+(5) без скобок примет вид 3+5, так как +(5) заменяется на +5, а выражение 3+(−5) эквивалентно выражению 3−5, так как +(−5) заменяется на −5.

Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.

Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. +(−a) мы заменяем на −a,  −(−a) заменяется на +a. Если выражение начинается с отрицательного числа (−a), которое записано в скобках, то скобки опускаются и вместо (−a) остается −a.

Приведем примеры:  (−5) можно записать как  −5,  (−3)+0,5 принимает вид −3+0,5,  4+(−3) превращается в 4−3, а −(−4)−(−3) после раскрытия скобок принимает вид 4+3, так как −(−4) и −(−3) заменяется на +4 и +3.

Следует понимать, что записать выражение 3·(−5) как 3·−5 нельзя. Об этом речь пойдет в следующих пунктах.

Давайте посмотрим, на чем основываются правила раскрытия скобок.

Согласно правилу разность a−b равна a+(−b). На основе свойств действий с числами мы можем составить цепочку равенств (a+(−b))+b=a+((−b)+b)=a+0=a, которая будет справедлива. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a+(−b)  — это разность a−b.

Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что −(−a)=a, a−(−b)=a+b.

Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть −(−((−(5)))). Раскроем скобки, продвигаясь изнутри наружу: −(−((−(5))))=−(−((−5)))=−(−(−5))=−(5)=−5. Также этот пример можно разобрать и в обратном направлении: −(−((−(5))))=((−(5)))=(−(5))=−(5)=−5.

Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком «+» впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.

К примеру, после раскрытия скобок выражение −(−2·x)−(x2)+(−1x)−(2·x·y2:z) примет вид 2·x−x2−1x−2·x·y2:z. Как мы это сделали? Мы знаем, что −(−2·x) есть +2·x, а так как это выражение стоит вначале, то +2·x можно записать как 2·x, −(x2)=−x2, +(−1x)=−1x и −(2·x·y2:z)=−2·x·y2:z.

В произведениях двух чисел

Начнем с правила раскрытия скобок в произведении двух чисел.

Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел −a и −b вида (−a)·(−b) мы можем заменить на (a·b), а произведения двух чисел с противоположными знаками вида (−a)·b и a·(−b) заменить на (−a·b). Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.

Рассмотрим несколько примеров.

Пример 1

Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел -435 и -2, вида(-2)·-435 . Для этого заменим исходное выражение на 2·435 . Раскроем скобки и получим 2·435 .

А если мы возьмем частное отрицательных чисел (−4):(−2), то запись после раскрытия скобок будет иметь вид 4:2

На месте отрицательных чисел −a и −b могут быть любые выражения со знаком минус впереди, которые  не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.

Раскроем скобки в выражении  -3·xx2+1·x·(ln5). Согласно правилу, мы можем произвести следующие преобразования:   -3·xx2+1·x·(ln5)=-3·xx2+1·x·ln5=3·xx2+1·x·ln5.

Выражение (−3)·2 можно преобразовать в выражение (−3·2). После этого можно раскрыть скобки: −3·2.

 23·-45=-23·45=-23·45

 Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок:  (−5):2=(−5:2)=−5:2 и  234:(-3,5)=-234:3,5=-234:3,5.

Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два  примера.

-1x+1:x-3=-1x+1:x-3=-1x+1:x-3

и 

sin(x)·(-x2)=(-sin(x)·x2)=-sin(x)·x2

В произведениях трех и большего количества чисел

Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.

Пример 2

Для примера, возьмем выражение 5·(−3)·(−2), которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как  (5·3·2) и затем окончательно раскрыть скобки, получив выражение 5·3·2.

В произведении (−2,5)·(−3):(−2)·4:(−1,25):(−1)  пять чисел являются отрицательными. поэтому (−2,5)·(−3):(−2)·4:(−1,25):(−1)=(−2,5·3:2·4:1,25:1). Окончательно раскрыв скобки, получаем  −2,5·3:2·4:1,25:1.

Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и -1 или -1 заменяем на (−1)·a.

Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные −1, в начало выражения. Произведение четного числа минус единиц равно 1, а нечетного – равно −1, что позволяет нам использовать знак минус.

Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении -23:(-2)·4:-67 выглядела бы следующим образом:

-23:(-2)·4:-67=-23·-12·4·-76==(-1)·23·(-1)·12·4·(-1)·76==(-1)·(-1)·(-1)·23·12·4·76=(-1)·23·12·4·76==-23·12·4·76

Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение

 x2·(-x):(-1x)·x-3:2.

Его можно привести к выражению без скобок  x2·x:1x·x-3:2 .

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Раскрытие скобок, перед которыми стоит знак «+»

Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.

Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.

Пример 3

Для примера приведем выражение (12−3,5)−7.  Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид (12−3,5)−7=+12−3,5−7. В приведенном примере знак перед первым слагаемым ставить не обязательно, так как +12−3,5−7=12−3,5−7.

Пример 4

Рассмотрим еще один пример. Возьмем выражение  x+2a-3×2+1-x2-4+1x и проведем с ним действия  x+2a-3×2+1-x2-4+1x==x+2a-3×2+1-x2-4+1x

Вот еще один пример раскрытия скобок:

Пример 5

2+x2+1x-x·y·z+2·x-1+(-1+x-x2)==2+x2+1x-x·y·z+2·x-1-1+x+x2

Как раскрываются скобки, перед которыми стоит знак минус

Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение. Согласно правилу раскрытия скобок, перед которыми стоит знак «-», скобки со знаком «-» опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.

Пример 6

К примеру:

—12=12,-1x+1=-1x+1,-(-x2)=x2

Выражения с переменными могут быть преобразованы с использованием того же правила:

—x+x3-3—2·x2+3·x3·x+1x-1-x+2,

получаем x-x3-3+2·x2-3·x3·x+1x-1-x+2.

Раскрытие скобок при умножении числа на скобку, выражения на скобку

Здесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида (a1±a2±…±an)·b=(a1·b±a2·b±…±an·b) или b·( a1±a2±…±an)=(b·a1±b·a2±…±b·an), где a1, a2, …, an и b – некоторые числа или выражения.

Пример 7

Например, проведем раскрытие скобок в выражении (3−7)·2. Согласно правилу, мы можем провести следующие преобразования: (3−7)·2=(3·2−7·2). Получаем 3·2−7·2.

Раскрыв скобки в выражении 3·x2·1-x+1x+2, получаем  3×2·1-3·x2·x+3·x2·1x+2.

Умножение скобки на скобку

Рассмотрим произведение двух скобок вида (a1+a2)·(b1+b2). Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку.

Для того, чтобы решить приведенный пример, обозначим выражение (b1+b2) как b. Это позволит нам использовать правило умножения скобки на выражение. Получим (a1+a2)·(b1+b2)=(a1+a2)·b=(a1·b+a2·b)=a1·b+a2·b. Выполнив обратную замену b на (b1+b2), снова применим правило умножения выражения на скобку:  a1·b+a2·b==a1·(b1+b2)+a2·(b1+b2)==(a1·b1+a1·b2)+(a2·b1+a2·b2)==a1·b1+a1·b2+a2·b1+a2·b2

Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки.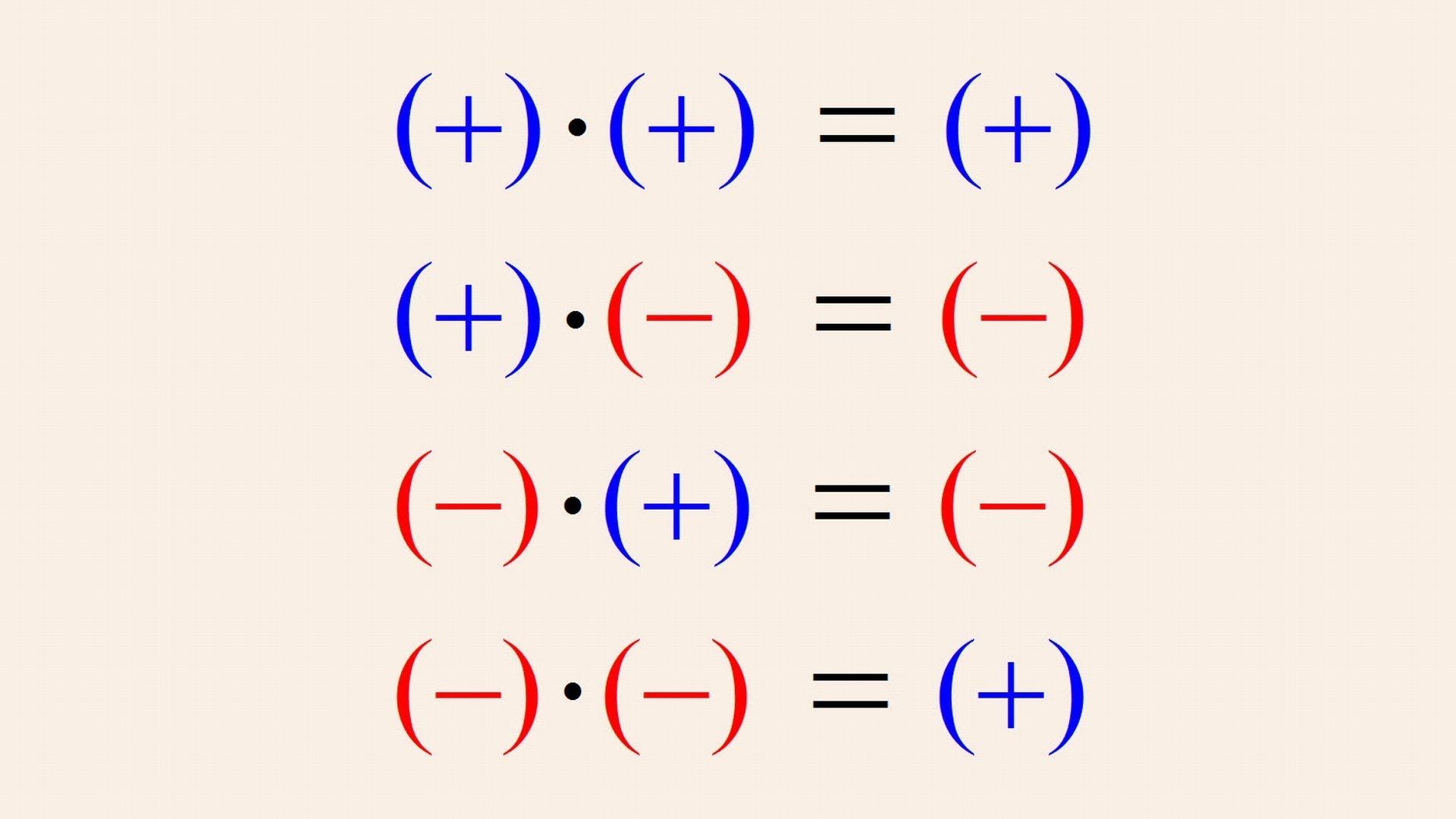 Правило можно распространить на любое количество слагаемых внутри скобок.

Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.

Формула будет иметь вид:

(a1+a2+…+am)·(b1+b2+…+bn)==a1b1+a1b2+…+a1bn++a2b1+a2b2+…+a2bn++…++amb1+amb1+…ambn

Проведем раскрытие скобок в выражении (1+x)·(x2+x+6) Оно представляет собой произведение двух сумм.  Запишем решение: (1+x)·(x2+x+6)==(1·x2+1·x+1·6+x·x2+x·x+x·6)==1·x2+1·x+1·6+x·x2+x·x+x·6

Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение  (1−x)·(3·x·y−2·x·y3).

Сначала представим выражения в скобках в виде сумм: (1+(−x))·(3·x·y+(−2·x·y3)). Теперь мы можем применить правило: (1+(−x))·(3·x·y+(−2·x·y3))==(1·3·x·y+1·(−2·x·y3)+(−x)·3·x·y+(−x)·(−2·x·y3))

Раскроем скобки: 1·3·x·y−1·2·x·y3−x·3·x·y+x·2·x·y3.

Раскрытие скобок в произведениях нескольких скобок и выражений

При наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2+4)·3·(5+7·8).

В выражении содержится сразу три множителя (2+4), 3 и (5+7·8). Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: (2+4)·3·(5+7·8)=((2+4)·3)·(5+7·8).

В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ((2+4)·3)·(5+7·8)=(2·3+4·3)·(5+7·8).

Умножаем скобку на скобку: (2·3+4·3)·(5+7·8)=2·3·5+2·3·7·8+4·3·5+4·3·7·8.

Скобка в натуральной степени

Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.

Рассмотрим процесс преобразования выражения  (a+b+c)2. Его можно записать в виде произведения двух скобок  (a+b+c)·(a+b+c).  Произведем умножение скобки на скобку и получим a·a+a·b+a·c+b·a+b·b+b·c+c·a+c·b+c·c.

Разберем еще один пример:

Пример 8

1x+23=1x+2·1x+2·1x+2==1x·1x+1x·2+2·1x+2·2·1x+2==1x·1x·1x+1x·2·1x+2·1x·1x+2·2·1x+1x·1x·2++1×2·2+2·1x·2+2·2·2

Деление скобки на число и скобки на скобку

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые. Например, (x2-x):4=x2:4-x:4 .

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x+2):23 . Для этого сначала заменим деление умножением на обратное число (x+2):23=(x+2)·23. Умножим скобку на число (x+2)·23=x·23+2·23.

Вот еще один пример деления на скобку:

Пример 9

1x+x+1:(x+2) .

Заменим деление умножением: 1x+x+1·1x+2.

Выполним умножение:  1x+x+1·1x+2=1x·1x+2+x·1x+2+1·1x+2.

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок выполнения действий:

• первым делом необходимо выполнить возведение скобок в натуральную степень;
• на втором этапе производится раскрытие скобок в произведениях и частных;
• заключительным шагом будет раскрытие скобок в суммах и разностях.

Рассмотрим порядок выполнения действий на примере выражения  (−5)+3·(−2):(−4)−6·(−7). Намнем преобразование с выражений 3·(−2):(−4) и 6·(−7), которые должны принять вид (3·2:4) и (−6·7). При подстановке полученных результатов в исходное выражение получаем: (−5)+3·(−2):(−4)−6·(−7)=(−5)+(3·2:4)−(−6·7). Раскрываем скобки:−5+3·2:4+6·7.

Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.

Урок 28. частное целых чисел. часть 2 — Математика — 6 класс

Математика

6 класс

Урок № 28

Частное целых чисел. Часть 2.

Перечень рассматриваемых вопросов:

1. Деление рациональных чисел.
2. Правила знаков при делении.

Глоссарий по теме

Чтобы разделить (или умножить) два числа с разными знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «минус».

Чтобы разделить (или умножить) два числа с одинаковыми знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «плюс»

В выражениях, где есть только действия умножения и деления чисел с разными знаками, знак можно определить по числу сомножителей. Если число знаков «минус» чётное, то значение выражения будет положительным, а если нечётное, то отрицательным.

Чтобы сложить два числа одинакового знака, надо сложить их модули и поставить перед суммой знак слагаемых.

Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем.

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения.

На предыдущем занятии мы узнали правило нахождения частного двух чисел одного знака и двух чисел разных знаков. Но таких выражений, содержащих только одно действие деления, на самом деле очень мало. Чаще всего встречаются более громоздкие выражения, которые содержат несколько действий.

Сегодня мы поговорим о вычислительной операции деления в таких случаях.

Для начала давайте вспомним все правила деления чисел с одинаковым и разными знаками. Стоит отметить, что аналогичное правило есть и при умножении.

Чтобы разделить (или умножить) два числа с разными знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «минус».

45 : (– 5) = – 9

Чтобы разделить (или умножить) два числа с одинаковыми знаками, надо разделить (или перемножить) модули этих чисел и поставить перед полученным частным (или произведением) знак «плюс».

– 35 : (– 7) = 5

В выражениях, где есть только действия умножения и деления чисел с разными знаками, знак можно определить по числу сомножителей. Если число знаков «минус» чётное, то значение выражения будет положительным, а если нечётное, то отрицательным.

Например:

– 5 ∙ 6 : (– 10) ∙ (– 4) = ?

В данном выражении сначала можно посчитать число знаков «минус», их оказалось 3, следовательно, ответ будет отрицательный. Далее выполним вычисления, взяв числа по модулю. В результате, объединив оба рассуждения (о знаке результата и сами вычисления), получаем ответ:

1. 5 ∙ 6 : 10 ∙ 4 = 12
2. – 5 ∙ 6 : (– 10) ∙ (– 4) = – 12

Обратите внимание, что если отрицательное число стоит после какого-либо знака, то его надо заключать в скобки, как и было представлено в наших примерах.

Если в вычислениях содержится не только умножение и деление, но и сложение с вычитанием, то нужно воспользоваться еще правилами сложения целых чисел.

Вспомним их.

Чтобы сложить два числа одинакового знака, надо сложить их модули и поставить перед суммой знак слагаемых.

Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем.

Вычислим значение выражения, состоящего из нескольких действий.

25 : (– 5) + 16 ∙ (– 2) = ?

В данном выражении 3 действия.

Первое действие деление, второе умножение, третье сложение.

Выполним первое действие:

1) 25 : (– 5) = – 5, ответ в этом действии будет с минусом так как «плюс» на «минус» даст знак «минус» и при делении модулей чисел получим ответ пять, следовательно, в этом действии ответ минус пять.

Выполним второе действие:

2) 16 ∙ (– 2) = – 32

Здесь знак определим по тому же правилу, это будет «минус» и умножим модули чисел, в итоге получим минус 32.

И последним действием сложим минус 5 и минус 32. Так как числа с одним знаком, следовательно, будем складывать результаты, но в ответе запишем «минус», следуя правилу сложения чисел, рассмотренному ранее. Получаем ответ данного выражения минус 37.

3) – 5 + (– 32) = – 37

25 : (– 5) + 16 ∙ (– 2) = – 37

Итак, сегодня мы получили представление о применении свойств деления для чисел с одинаковыми и разными знаками при вычислении значений выражений, содержащих разные действия.

Сравним значения выражений, не вычисляя их.

38 : (– 19) ? 52 · (– 4) : (– 13)

– 35 + (– 18) : 2 ? – 735 : (– 5)

Решение:

Для сравнения данных выражений достаточно посмотреть на знаки, которые будут получаться при вычислениях.

Сравним выражения в первой строке. В первом выражении, знак будет минус, т. к. число отрицательных знаков в нём нечётное. Во втором выражении ответ будет иметь положительное значение, т. к. число отрицательных знаков в нём чётное. Следовательно, первое выражение меньше второго.

Сравним выражения во второй строке. Сначала рассмотрим первое выражение по действиям. При делении у частного получается знак «минус» т. к. число отрицательных знаков в первом действии нечётное. Во втором действии при сложении двух чисел с одинаковым знаком получается результат с таким же знаком, следовательно, в ответе будет отрицательное число. Во втором выражении ответ будет иметь положительное значение, т. к. число отрицательных знаков в нём чётное. Следовательно, первое выражение меньше второго.

38 : (– 19) < 52 · (– 4) : (– 13)

– 35 + (– 18) : 2 < – 735 : (– 5)

Тренировочные задания

Какой знак имеет выражение?

28 : (– 4) · 8

Решение: Для нахождения знака используем правило нахождения частного (произведения) чисел с разными знаками. Если число знаков «минус» чётное, то значение выражения будет положительным, а если нечётное, то отрицательным.

Следовательно, в нашем примере ответ будет со знаком минус, т. к. число знаков «минус» нечётное – равное единице.

Решите уравнение

5 · х + 8 · х = – 65

Решение:

Вначале найдём, сколько x содержится в левой части уравнения: сложим 5x и 8x, получается 13x. Далее найдём x, как частное (– 65) от 13. Далее находим знак, используя правило нахождения частного двух чисел с разными знаками. Частное чисел а и b равно частному их модулей, со знаком «минус», если они разных знаков. Следовательно, частное будет со знаком минус. Далее выполним деление данных чисел по модулю, результат равен 5, но с учетом знака:

x = – 5

%d0%bc%d0%b8%d0%bd%d1%83%d1%81 на корейский — Русский-Корейский

В настоящий 83-й год правления Царства, возглавляемого Иисусом, некоторые, возможно, думают, что сейчас как раз период замедления.

금년은 예수의 왕국 통치의 83년째 되는 해이기 때문에, 어떤 사람들은 우리가 바로 지금, 그 더딘 것처럼 보이는 기간에 살고 있다고 생각할지 모릅니다.

jw2019

Она распространяет миллионы [19 миллионов каждого выпуска] экземпляров своего материала примерно на 60 [в настоящее время на 81] языках, в том числе на языках пиджин, хилигайнон и зулу.

그 단체는 자료를 수백만 부[매호 1900만 부]에 실어 피진어, 힐리가이논어, 줄루어를 포함하여 약 60개[실제로는 81개] 언어로 배포한다.

jw2019

83 И их решение по его делу должно положить конец спорам о нём.

83 그리고 그의 머리 위에 내려질 그들의 판결은 그에 대한 논쟁의 끝이 되어야 하느니라.

LDS

Если вы желаете получить новый выпуск «Пробудитесь!», который издается сейчас на 81 языке, обратитесь к Свидетелям Иеговы, живущим с вами по соседству, или напишите по одному из адресов, указанных на странице 5.

현재 81개 언어로 발행되는 「깨어라!」 지의 최근호를 받아 보기 원하신다면, 이웃에 사는 여호와의 증인을 만나 보시거나 5면에 나오는 주소 가운데 가장 가까운 주소로 연락하시기 바랍니다.

jw2019

Из них 81 человек был 65 лет и старше.

이들 중 81명은 65세 이상이었습니다.

jw2019

Учение и Заветы 81 можно читать сегодня не только, как откровение члену Церкви ранней эпохи Церкви, но также как совет любому человеку, который желает поддерживать Пророка.

현재의 교리와 성약 81편은 교회의 한 초기 회원에게 주어진 개인적인 계시이자 선지자를 기꺼이 지지하는 모든 이에게 주는 권고로도 볼 수 있다.

LDS

Секущая BD пересекает окружность в точках С и D

할선 BD는 원과 C, D 이렇게 두 점에서 만나요.

QED

Иисус даже цитировал из Псалмов, чтобы показать, что мощные люди назывались «богами» (Псалом 81:1—6; Иоанна 10:34, 35).

예수께서는 권세 있는 인간들이 “신”이라고 불린 일이 있음을 보여주기 위해 시편을 인용하기까지 하셨읍니다.

jw2019

MBI нашла 83 процента.

MBI는 83% 이었습니다.

ted2019

Порошковые огнетушители, на которых изображена желтая звездочка с буквой D, применяются только при пожарах класса D, когда горят металлы, в то время как порошковые химические огнетушители можно использовать для пожаров класса ABC или BC.

분말 소화기는 노란 별표에 알파벳 D자가 적혀 있는 것으로 금속 화재에만 사용할 수 있는 반면, 건식 화학 약품 소화기는 ABC나 BC형 화재에 사용할 수 있습니다.

jw2019

Поскольку кинно́р был по своей сути «приятным» инструментом, сопровождавшим «ликование», его звук умолкал во времена, когда вершился суд или совершалось возмездие (Пс 81:2; Иез 26:13; Иса 24:8, 9).

(시 81:2; 겔 26:13; 사 24:8, 9) 이스라엘인들은 바빌론 유배로 인해 슬퍼하였으므로, 수금을 연주하고 싶지 않아서 미루나무에 수금을 걸어 두었다.—시 137:1, 2.

jw2019

Учение и Заветы 81:5 (Учение и Заветы, страница 174)

교리와 성약 81:5(교리와 성약, 180쪽)

LDS

(Воспользуйся вопросником «Твой гардероб» на страницах 82 и 83. )

(잠언 15:22)—82, 83면에 나오는 “옷에 대한 의견을 교환해 보세요”를 사용해 본다.

jw2019

Те, кто полагаются на Иегову, «приходят от силы в силу» (Псалом 83:6, 8).

그 힘이 여호와에게 있는 사람들은 “활력에서 활력으로 계속 걸어”갈 것입니다.

jw2019

83:12). Происходит ли подобное в наши дни?

(시 83:12) 오늘날에도 그와 비슷한 일이 있었습니까?

jw2019

◆ 83:4 — Почему здесь упоминаются птицы?

◆ 84:3—새를 언급한 이유는 무엇인가?

jw2019

Об этом императоре говорили, что в последние три года своего правления, длившегося с 81 по 96 год н. э., он действовал как безумный.

도미티아누스 황제는 재위 마지막 3년 간 미친 사람처럼 행동하였다고 하는데, 그의 통치 기간은 기원 81-96년이다.

jw2019

Желаю лучше быть у порога в доме Божием, нежели жить в шатрах нечестия» (Псалом 83:11).

“주의 궁정에서 한 날이 다른 곳에서 천 날보다 나은즉 악인의 장막에 거함보다 내 하나님 문지기로 있는 것이 좋사[옵나이다. ]”

jw2019

Поясняя записанное в Коране 2:81 (87), ал-Байда̄вӣ сказал в своих знаменитых комментариях, что Иисус «воскрешал мертвых с помощью величайшего имени Бога».

(요한 17:6, 26) 바이다위는 자기의 유명한 코란 주해서에서 코란 2:87을 해설하면서, 예수께서 “하나님의 가장 위대한 이름으로 죽은 자들을 살리”시곤 하였다고 말한다.

jw2019

Современные читатели Учения и Заветов 81 могут найти имя Джесси Гауса только в предисловии к разделу.

교리와 성약 81편을 읽어보면 제시 고즈가 편 머리말에만 나온다는 것을 알 수 있다.

LDS

Они чтят Божье имя (Псалом 83:18).

(시편 83:18) 그리고 인류를 위한 유일한 희망으로 하느님의 왕국을 옹호하며 널리 알립니다.

jw2019

Вскоре ее муж и дочь тоже начали изучать Библию (Псалом 83:18; Луки 22:41, 42).

얼마 안 있어 그 여자의 남편과 딸도 성경을 공부하게 되었지요.—시편 83:18; 누가복음 22:41, 42.

jw2019

«Чтобы люди знали, что ты, чье имя Иегова, Ты один Всевышний над всей землей» (Псалом 83:18).

“그 이름이 여호와이신 당신, 당신만이 홀로 온 땅을 다스리는 가장 높으신 분임을 사람들이 알게 하십시오.”—시편 83:18.

jw2019

Наша серьезная обязанность… – «помога[ть] слабым, поднима[ть] опустившиеся руки и укрепля[ть] ослабевшие колени» (У. и З. 81:5).

“약한 자를 [돕고] 처진 손을 일으켜 세우며, 연약한 무릎을 강건하게 하[는]”(교리와 성약 81:5) 것은 우리의 숭고한 의무이자 책임입니다.

LDS

Ему 81 год, и утешает то, что болезнь прогрессирует очень медленно…

남편은 현재 81세인데 고맙게도 병세의 악화 속도가 매우 느립니다.

jw2019

Отрицательные дроби. Действия с отрицательными дробями

Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.

Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:

-2 : 7    и    2 : (-7),

каждое из них равно отрицательному числу

Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:

-2 : 7	=	-2	и	2 : (-7)	=	2	.
		7				-7

Следовательно, при записи отрицательных дробей знак минус можно ставить перед дробью, перед числителем или перед знаменателем:

Сложение и вычитание

Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.

Пример.

Приведём дроби к общему знаменателю:

—	2	+  (-	1	)  =	-8	+	-5	.
	5		4		20		20

Теперь сложим числители дробей по правилам сложения рациональных чисел:

-8	+	-5	=	-8 + (-5)	=	-13	=	—	13	.
20		20		20		20			20

Таким образом:

—	2	+  (-	1	)  =	-8	+	-5	=
	5		4		20		20

=	-8 + (-5)	=	-13	=	—	13	.
	20		20			20

Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.

Пример.

—	5	— (-	11	)  =	—	5	+ (+	11	)  =
	12		12			12		12

=	—	5	+	11	=	-5 + 11	=	6	.
		12		12		12		12

Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.

Умножение и деление

Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.

Пример.

—	2	· (-	4	)  =	-2	·	-4	=	-2 · (-4)	=	8	.
	3		5		3		5		3 · 5		15

Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:

—	2	· (-	4	)  =	2	·	4	=	2 · 4	=	8	.
	3		5		3		5		3 · 5		15

При умножении отрицательной дроби на положительную результат будет отрицательным.

Пример.

—	2	·	4	=	—	2 · 4	=	—	8	.
	3		5			3 · 5			15

К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:

4	·  (-	2	)  =	—	4 · 2	=	—	8	.
5		3			5 · 3			15

То есть при умножении положительной дроби на отрицательную результат будет отрицательным.

Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.

Пример.

—	2	: (-	4	)  =	-2	:	-4	=
	3		5		3		5

=	-2 · 5	=	-10	=	10	.
	3 · (-4)		-12		12

Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.

Умножение отрицательных чисел дает положительный результат

GCfiIBPG7Aw

Когда мы умножаем:

Да, действительно, два отрицания дают положительный результат, и мы объясним , почему , на примерах!

Знаки

Давайте поговорим о знаков .

«+» — положительный знак, «-» — отрицательный.

Когда число имеет без знака , это обычно означает, что положительное .

И мы можем поставить () вокруг чисел, чтобы избежать путаницы.

Пример: 3 × −2 можно записать как (+3) × (−2)

Два знака: правила

«Два одинаковых знака образуют положительный знак,
два разных знака образуют отрицательный знак»

Пример: (−2) × (+5)

Знаки — и + (отрицательный знак и положительный знак), поэтому они в отличие от знаков (они отличаются друг от друга)

Таким образом, результат должен быть отрицательным :

(−2) × (+5) = −10

Пример: (−4) × (−3)

Знаки — и — (оба являются отрицательными знаками), поэтому они похожи на знаки (похожи друг на друга)

Таким образом, результат должен быть положительным :

(−4) × (−3) = +12

Почему умножение двух отрицательных чисел дает положительное?

Ну, сначала объяснение «здравого смысла»:

Когда я говорю «Ешь!» Я призываю вас поесть (положительный результат)

Но когда я говорю «Не ешь!» Я говорю об обратном (отрицательном).

Теперь, если я скажу: « НЕ , не ешь!», Я говорю, что не хочу, чтобы ты умирал с голоду, поэтому я снова говорю «Ешь!» (положительный).

Итак, два негатива дают положительный результат, и если это вас устраивает, то вам больше не нужно читать.

Направление

Все дело в направлении. Помните числовую черту?

Итак, малыш Стивен делает свои первые шаги. Он делает 2 шага за раз и делает это три раза, поэтому он делает 2 шага x 3 = 6 шагов вперед:

Теперь Малыш Стивен тоже может отступить (он умный маленький парень).Его отец ставит его в исходное положение, а затем Стивен делает два шага назад и делает это три раза:

И снова папа Стивена ставит его на старт, но лицом в другую сторону. Стивен делает 2 шага вперед (для него!), Но движется в отрицательном направлении. Он делает это 3 раза:

Снова на старте (спасибо, папа!), Все еще глядя в отрицательном направлении, он пытается ходить задом, снова делая два шага за раз, и он делает это три раза:

Итак, идя назад, смотря в отрицательную сторону, он движется в положительном направлении.

Попробуйте сами! Попробуйте идти вперед и назад, затем снова, но лицом в другую сторону.

Играй с ним

Но, может быть, вы хотели бы увидеть это в действии? Используйте ползунки ниже:

числа / изображения / номер-строка-mult.js

Другие примеры

Пример: деньги

Сэм дает вам три купюры по 10 долларов:		+3 × +10 = вы получаете 30 долларов
Сэм дает вам три долга по 10 долларов:		+3 × −10 = вы теряете 30 долларов
Сэм берет у вас три купюры по 10 долларов:		−3 × +10 = вы теряете 30 долларов
Сэм берет у вас три долга по 10 долларов:		−3 × −10 = вы получаете 30 долларов

Пример: видео бегущих людей

Люди бегут вперед, видео нормальное:

Все нормально, люди бегут вперед: +1 × +1 = +1

Люди бегут вперед, а видео — — назад :

Похоже, люди бегут задом наперед: +1 × −1 = −1

Люди бегут Назад , видео нормальное:

Вы видите людей, бегущих назад: -1 × +1 = -1

Люди бегут назад , но видео в назад :

Похоже, люди бегут вперед: -1 × -1 = +1

Пример: повышение / понижение уровня в резервуаре

В баке 30 000 литров, каждый день вывозится 1000 литров.Сколько было воды в баке 3 дня назад ?

Мы знаем, что количество воды в резервуаре меняется на -1000 каждый день, и нам нужно вычесть это 3 раза (чтобы вернуться на назад на 3 дня ), поэтому изменение составит:

−3 × −1,000 = +3,000

Полный расчет:

30 000 + (−3 × −1 000) = 30 000 + 3 000 = 33 000

Итак, 3 дня назад в баке было 33 000 литров воды.

Таблица умножения

Вот с другой стороны, посмотреть на это.

Начните с таблицы умножения (достаточно 4 × 4):

×	1	2	3	4
1	1	2	3	4
2	2	4	6	8
3	3	6	9	12
4	4	8	12	16

Теперь посмотрим, что произойдет, когда мы перейдем к негативам !

Поехали назад через ноль:

×	1	2	3	4
-4	-4	-8	-12	-16
-3	-3	-6	-9	-12
-2	-2	-4	-6	-8
-1	-1	-2	-3	-4
0	0	0	0	0
1	1	2	3	4
2	2	4	6	8
3	3	6	9	12
4	4	8	12	16

Посмотрите на столбец «4»: он идет -16, -12, -8, -4, 0, 4, 8, 12, 16 .Каждый раз становясь на 4 больше.

Посмотрите еще раз на эту таблицу, убедитесь, что вам удобно, как она работает, потому что …

… теперь идем левее , через ноль:

×	-4	-3	-2	-1	0	1	2	3	4
-4	16	12	8	4	0	-4	-8	-12	-16
-3	12	9	6	3	0	-3	-6	-9	-12
-2	8	6	4	2	0	-2	-4	-6	-8
-1	4	3	2	1	0	-1	-2	-3	-4
0	0	0	0	0	0	0	0	0	0
1	-4	-3	-2	-1	0	1	2	3	4
2	-8	-6	-4	-2	0	2	4	6	8
3	-12	-9	-6	-3	0	3	6	9	12
4	-16	-12	-8	-4	0	4	8	12	16

Тот же образец: мы можем следовать по строке (или столбцу), и значения меняются последовательно:

• Следуйте за строкой «4»: она идет -16, -12, -8, -4, 0, 4, 8, 12, 16 .Каждый раз становясь на 4 больше.
• Следуйте за строкой «-4»: это идет 16, 12, 8, 4, 0, -4, -8, -12, -16 . Каждый раз становится на 4 меньше.
• и т.д …

Так что все идет по аккуратной схеме!

Как насчет умножения 3 и более чисел вместе?

Умножьте два за раз и следуйте правилам.

Пример: Что такое (−2) × (−3) × (−4)?

Сначала умножим (−2) × (−3). Два подобных знака означают положительный знак, поэтому:

(−2) × (−3) = +6

Далее умножаем +6 × (−4).Два непохожих знака образуют отрицательный знак, поэтому:

+6 × (−4) = −24

Результат: (−2) × (−3) × (−4) = −24

330, 1615, 1616, 1617, 3447, 3448 331, 1618, 3170, 3171

по математике — Кто записал минус, умноженный на минус, равен плюсу?

О Диофанте (родился, вероятно, где-то между 201 и 215 годом нашей эры; умер в возрасте 84 лет, вероятно, где-то между 285 и 299 годом нашей эры) Arithmetica, см .:

Минус, умноженный на минус, дает плюс; минус, умноженный на плюс, дает минус; а знак минуса — усеченный $ \ Psi $, перевернутый вверх ногами, таким образом, $ \ Lambda $ [с третьей центральной ножкой].[ Сноска . Буквальный перевод был бы таким: «Желание, умноженное на желание, порождает грядущее».]

См. Также:

Используется только знак вычитания. Полный термин для , желающего , — λείψις в отличие от ύπαρξις, a , предстоящий , который обозначает положительный член . Для обозначения и , соответствующего нашему знаку минус , используется символ $ \ Lambda $ [с третьей центральной ножкой], который описывается в тексте как «$ \ Psi $, повернутый вниз и усеченный».Описание очевидно интерполированы, и теперь ясно, что этот знак не имеет ничего общего с $ \ Psi $. И не ограничивается Диофантом, поскольку он появляется практически в той же форме в метрике Герона […].

---

Очевидно, что также, если правило «правильно описано», нет никакого намека на его современную символическую формулировку из-за отсутствия современных символов, которые датируются концом XVI — началом XVII веков.

Современную версию см .:

Unde patet ratio tum hujus regulae, $ + $ в $ + $ facit $ + $; tum hujus $ — $ in $ + $ facit $ — $.[…] Indeque patet ratio tum hujus regulae, $ + $ в $ — $ facit $ — $; tum hujus, $ — $ в $ — $ facit $ + $.

«Обоснование» состоит в том, что для умножение заданного количества на положительный коэффициент составляет ponendi («ubi $ + 2 $ значимое bis ponere «), а для умножение на отрицательный коэффициент . — tollendi («ibidem $ -2 $ est bis tollere , seu bis ponere contrarium «).

Contra vero, $ -A $ за $ -2 $ multiplicare, est bis tollere $ -A $, seu defectum $ -A $ bis Supplere, quod est $ + A $ bis ponere, facitque $ + 2A $, (adeoque $ — $ в $ — $ facit $ + $.)

Умножение отрицательных значений — знаки, примеры, правила, решаемые примеры и часто задаваемые вопросы

Числа меньше нуля называются отрицательными числами. Числа выше нуля — положительные числа. Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел.

Знаки

Мы знаем, что «+» — это положительный знак, «-» — отрицательный знак. Когда перед числом не ставится знак, это обычно означает, что он положительный.

Пример: 8 на самом деле +8

Примечание: Чтобы избежать путаницы в знаках, мы можем поместить () вокруг чисел. Например, 5 × −8 может быть записано как 5 × (−8)

Правила умножения отрицательных

У нас могут быть положительные и отрицательные целые числа при работе с целыми числами при умножении. Существуют правила умножения целых чисел и деления целых чисел, которые очень похожи на правила сложения и вычитания.

• Если знаки разные, ответ отрицательный.

• Если знаки одинаковые, ответ положительный.

Для лучшего понимания см. Описание ниже.

[Изображение будет загружено в ближайшее время]

Plus Times Plus is Plus

Пример: 2 × 5 = 10

(Мы уже обсуждали, что когда у числа нет знака, это обычно означает, что оно положительное.)

[Изображение будет загружено в ближайшее время]

Минус Умножить Минус равно Плюс

Пример: (-10) × (-5) = 50

Отрицательное, умноженное на Отрицательное, является положительным числом, что означает, что произведение двух отрицательных целых чисел равно всегда позитивный.

[Изображение будет загружено в ближайшее время]

Плюс Время Минус равно Минус

Пример: 5 x (-5) = — 25

Умножение отрицательного числа на положительное всегда приводит к отрицательному числу.

[Изображение будет загружено в ближайшее время]

Минус Время Плюс равно Минус

Примечание. Эти правила работают таким же образом для правил деления целых чисел; вам просто нужно заменить «раз» на «деленное на».

Деление отрицательных чисел

Деление отрицательных чисел работает так же, как и деление положительных чисел, за исключением того, что результаты иногда бывают отрицательными.От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательно. Если оба числа отрицательны, результат будет положительным.

9116

+

9253

—

—

Выражение	Частное	Пример
Положительное ÷	+	Отрицательный ÷ Отрицательный	Положительный	-25 ÷ — 5 = +5
Отрицательный ÷ Положительный	Отрицательный
Положительное ÷ Отрицательное	Отрицательное	25 ÷ -5 = — 5

Что происходит, когда мы умножаем отрицательные с помощью матриц?

Целочисленная матрица — это матрица, каждая из которых является целочисленной записью.Отрицательный результат матрицы получается умножением на -1.

Итак, если A — заданная матрица

Тогда — A = — 1 [A]

Решенные примеры

1. Что такое −6 × 3?

Ответ: 6 x 3 равно 18. Но здесь у нас есть одно отрицательное и одно положительное число. Значит, знак ответа будет минус.

Следовательно, ответ — 18.

2. Что такое −80 ÷ 8?

Ответ: 80 ÷ 8 равно 10. Опять же, у нас есть положительное и отрицательное число. Следовательно, в окончательном ответе знак будет отрицательным.

Следовательно, ответ -10.

3. Что такое −50 x −5?

Ответ: 50 x 5 равно 250. На этот раз у нас есть 2 отрицательных числа. Значит, знак в ответе будет положительным. Следовательно, ответ — 250.

Заключение

Помните только 2 вещи, когда умножаете отрицательные числа.

1. Два отрицательных числа всегда дают положительный результат.

2. Ваш ответ также будет отрицательным, если у вас есть только одно отрицательное значение. Запомните только эти два правила, а остальные легко вычислить.

Умножение положительных и отрицательных чисел: 3 простых правила

При умножении положительных и отрицательных чисел существует меньше правил, чем при сложении и вычитании положительных и отрицательных чисел. Следует запомнить всего три правила:

Правило 1. Положительное число, умноженное на положительное, равняется положительному числу.

Это умножение, которое вы делали все время: положительные числа, умноженные на положительные числа, равны положительным числам.

Например, 5 x 3 = 15.5 — положительное число, 3 — положительное число, а умножение дает положительное число: 15.

Ответ: 5 x 3 = 15.

Правило 2: Отрицательное число, умноженное на положительное, равняется отрицательному числу.

Когда вы умножаете отрицательное число на положительное, ваш ответ — отрицательное число. Не имеет значения, в каком порядке вы умножаете положительные и отрицательные числа, ответ всегда будет отрицательным.

Например: -2 x 4, что по сути то же самое, что -2 + (-2) + (-2) + (-2)

Ответ: -2 х 4 = -8.

И, как мы уже сказали, если наоборот 4 x -2, ответ все тот же: -8.

Ответ: 4 х -2 = -8.

Правило 3. Отрицательное число, умноженное на отрицательное, равняется положительному числу.

Два отрицательных числа дают положительное число, поэтому отрицательное число, умноженное на отрицательное число, дает положительное число. Если вы посмотрите на него на числовой прямой, идя назад и повернувшись лицом в отрицательном направлении, вы двинетесь в положительном направлении.

Например.-2 x -4 отрицательны, поэтому мы знаем, что ответ будет положительным.

Ответ: -2 x -4 = 8.

Вот общее правило, которое следует помнить при умножении положительных и отрицательных чисел:

Два одинаковых знака дают положительный знак:

Два непохожих знака образуют отрицательный знак:

Если вы все еще не понимаете, почему отрицательное число, умноженное на отрицательное число, дает положительное число, Диана Браун с факультета математики Университета Джорджии объясняет это разными способами в этой статье.

Скотт из About.com также собрал удобное видео о том, как создать шпаргалку для умножения отрицательных и положительных чисел (прокрутите страницу вниз, и вы найдете видео).

Почему отрицательное число, умноженное на отрицательное, положительное? номер?

Автор: Диана Браун

Это частый вопрос от многие студенты изучают математику в средней и даже старшей школе. это Для большинства неудивительно, что это трудное понятие для понимания учащимися.Отрицательные числа не так легко понять большинству людей. Сложность понимания негатива Иногда отрицательным является то, что мы не делаем этого в повседневной жизни. Ниже несколько методов, которые можно использовать, чтобы помочь учащимся лучше понять значение отрицательного умножить на отрицательное.

Метод первый: денежные представления

Мы можем начать объяснять отрицательное умножение, помогая ученику понять более простые концепции например, положительное умноженное на положительное или положительное умноженное на отрицательное.Например, в случае с деньгами мы можем представляют положительное значение, умноженное на отрицательное, говоря, что каждый раз вычитается 700 долларов. месяц для выплаты ипотечного платежа. Через шесть месяцев, сколько денег было вынули из платы по ипотеке? Мы можем выяснить ответ, выполнив умножение.

6 * — 700 долларов = — 4200 долларов. Это иллюстрация положительного времени отрицательный результат отрицательный.

Мы можем использовать тот же метод чтобы представить отрицательное значение, умноженное на отрицательное:

Теперь предположим, что в качестве бонуса работодатель решает выплатить ипотеку сроком на один год.Работодатель снимает ипотечный вычет из ежемесячной зарплаты. Сколько денег получает сотрудник в нашем примере? Мы можем представить «удаляет» отрицательным число и вычислим ответ умножением.

–12 * — 700 долларов = 8 400 долларов

Это иллюстрация отрицательный умноженный на отрицательный, что приводит к положительному результату. Если думать о умножения как группировки, то мы создали положительную группу, убрав отрицательное число двенадцать раз.

Метод Два: математическая иллюстрация

Большинство студентов быстро соглашаются с тем, что отрицательное число может быть представлено как количество раз -1. Легче понять иллюстрацию отрицательного и положительного. Итак, если мы возьмем число и умножим количество раз -1 представлено ниже:

(-1) х = -х. Два отрицательных перемножаемые числа можно представить следующим образом:

(-x) (-y) = (-1) (x) (-1) (y) = (-1) (-1) (x) (y), Итак, что такое (-1) (- 1)?

Первая мы начнем с того, что мы знаем.Например, мы знаем, что -1 (0) = 0.

ср можно переписать (-1) (0) = (-1) (- 1 + 1), затем используя по распределительному свойству в правой части уравнения получаем:

(-1) (-1) + (-1) (1)

Сейчас мы знаем, что (-1) (1) = -1, но мы не уверены, что такое (-1) (- 1), но мы знаем что что бы это ни было, уравнение равно нулю, так как оно не может быть -1 для этого сделало бы уравнение равным -2, тогда оно должно быть +1. Увидеть математика ниже:

0 = (-1) (0) = (-1) (- 1 + 1) = (-1) (-1) + (-1) (1) =? + (-1) поэтому

0 знак равно + (-1), из нашего утверждения выше (-1) (- 1) должно быть +1, чтобы завершить утверждение: 0 =? + (-1).Который может помочь сделать вывод, что отрицательное умножение на отрицательное равняется положительному.

Метод Три: Доказательство

Пусть a и b произвольные два действительных числа. Рассмотрим число x, определенное как

х = ab + (-a) (b) + (-a) (- b).

Мы можем написать

 x = ab + (-a) [(b) + (-b)] (множитель -a) 

 = ab + (-a) (0) 

 = ab + 0 

 = ab. 

Также,

 x = [a + (-a)] b + (-a) (- b) (вычесть b) 

 = 0 * b + (-a) (- b) 

 = 0 + (-a) (-b) 

 = (-a) (- b).

Итак, у нас

х = ab
и
x = (-a) (- b)

Следовательно, по транзитивности равенства имеем

ab = (-a) (- b).

Метод Четвертое: использование слов для обозначения отрицательного числа

Некоторые люди думают о слове НЕ как о негативном значении. Можно сказать, я НЕ пойду к своим друзьям жилой дом. Это похоже на отрицательную версию о том, чтобы сказать, что я иду в дом моих друзей.Так что, если я сказал это двумя NOTS. Я не собираюсь не ходить в дом к друзьям. Кажется, два НОТА отменяют друг друга и я иду в дом моих друзей выведено. Кажется, что двойное отрицательное утверждение действительно дает положительный утверждение. Еще примеры:

отрицательный * отрицательный	Положительно
Он не может просто сделать ничего	Он должен что-то сделать
нередкий посетитель	частый посетитель
Я никогда не пойду	Я иду

Метод Пятерка: Распознавание образов

Давайте посмотрим на последовательность ниже.Обратите внимание, что происходит с правой стороной уравнение при уменьшении первого числа на единицу:

4 х 5 = 20

3 х 5 = 15

2 х 5 = 10

1 х 5 = 5

0 x 5 = 0 Мы замечаем, что числа уменьшаются на 5. Продолжаем:

-1 х 5 = -5

-2 х 5 = -10

-3 х 5 = -15

-4 х 5 = -20. Теперь давайте проделаем ту же последовательность, заменив 5 на -5.

4 х -5 = -20

3 х -5 = -15

2 х -5 = -10

1 х -5 = -5

0 x -5 = 0 Мы замечаем, что числа увеличиваются на 5. Если мы используем ту же логику, что и раньше, мы увидим, что:

-1 х -5 = 5

-2 х -5 = 10

-3 х -5 = 15

-4 x -5 = 20. Следовательно, кажется, что отрицательный результат снова отрицательный положительный.

Метод Шесть: Использование технологии

ср можно использовать систему координат в Geometry Sketchpad для создания линии. Помните, что наклон линии — это подъем за пробегом. Если мы нанесем точку на координатной плоскости и используйте наклон, чтобы построить вторую точку, мы посмотрим на наклон, чтобы определить если линия имеет положительный или отрицательный наклон.

В На следующей диаграмме мы построили точку (2, 2):

Давайте используйте наклон 1/2, чтобы найти следующие три точки.

Сейчас если мы проведем линию через точки, мы увидим, что в результате получится линия с положительным наклоном.

Давайте попробуйте то же самое, начиная с точки (2, 2) и используя наклон -1 / -2. См. Диаграмму ниже для результатов.

Уведомление что линия такая же, как и раньше, наклон положительный. Следовательно, это может быть графический подход. чтобы показать взаимосвязь двух отрицательных чисел.

Сайтов используется для помощи в открытии различных методов:

www.mathforum.org

www.ncsu.edu

www.math.toronto.edu

www.mathcentral.com

www.newton.dep.anl.gov

plato.stanford.edu

Вернуться на мою домашнюю страницу 6690

1.5 Почему ОТРИЦАТЕЛЬНО ВРЕМЯ ОТРИЦАТЕЛЬНО ПОЛОЖИТЕЛЬНО?

Когда мы открываем отрицательные числа, мы, естественно, даже без сомнения, предполагаем, что они подчиняются тем же законам арифметики, что и обычные положительные счетные числа.То есть нам нравится верить, что основные законы, такие как \ (a \ times b = b \ times a \) и \ (a \ times 1 = a \) и \ (a \ times 0 = 0 \), выполняются для всех числа, как положительные, так и отрицательные, и что мы можем раскрывать скобки даже с отрицательными записями и т. д. Конечно, эти правила предполагают, что мы знаем, что априори умеют умножать на отрицательные числа.

УМНОЖЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ НОМЕРОВ

В начальной учебной программе умножение вводится в контексте целых счетных чисел и соответственно определяется как повторное сложение.Например, \ (4 \ times 5 \) читается как «четыре группы по пять» и вычисляется следующим образом: \ (4 \ times 5 = 5 + 5 + 5 + 5 = 20 \).

На самом деле довольно удивительно, что \ (5 \ times 4 \), «пять групп по четыре», дает тот же числовой ответ, что и четыре группы по пять. Вычисление совершенно иное с числами 5 и 4, выполняющими смену ролей.

Вопрос: Как бы вы убедили молодого студента в том, что 193 группы из 307 человек обязательно будут иметь такую ​​же ценность, как 307 групп из 193 человек? Почему мы хотим, чтобы верили, что \ (a \ times b = b \ times a \) для подсчета чисел? (ПОДСКАЗКА: расставьте точки в прямоугольные массивы.)

Повторное сложение позволяет нам умножить положительное число и отрицательное число. Например, \ (2 \ times \ left (-3 \ right) \) может быть прочитано как «две группы отрицательных трех» и поэтому вычисляется как \ (2 \ times \ left (-3 \ right) = — 3 + \; — 3 = -6 \). По сваям и ямкам это выглядит так:

Однако интерпретация отрицательного числа, умноженного на положительное, и отрицательного, умноженного на отрицательное, путем повторного сложения проблематична.

Что может означать \ (\ left (-2 \ right) \ times 3 \)? «Отрицательные две группы по три» не имеет смысла.

И \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) одинаково странно: «две отрицательные группы из трех отрицательных».

На самом деле умножение здесь не имеет значения в контексте повторяющегося сложения. Мы вступили на новую территорию, и если мы хотим открыть наш мир для новых типов чисел, неудивительно, что ранее конкретные, буквальные определения начинают ошибаться. Итак, мы должны провести изощренный сдвиг мышления, отказавшись от вопроса Что такое умножение? вместо этого спросить:

Как бы мы хотели, чтобы вело себя умножение?

Комментарий: Позвольте мне подчеркнуть этот момент.На вопрос: «Что означает умножение отрицательных чисел?» Это вводящий в заблуждение вопрос, и это не тот вопрос, который нужно задавать на данном этапе нашей работы: мы все еще пытаемся решить проблему того, каким может быть умножение в мире отрицательных чисел. Чтобы приблизиться к этому, мы сначала должны четко определить, какие особенности арифметики, по нашему мнению, должны оставаться верными.

ДУМАЯ НАШЕ ЧЕРЕЗ ВЕЩИ

Положительные, умноженные на Отрицательные : Кажется убедительным придерживаться понятия «повторное сложение» для произведения отрицательного и положительного:

\ (2 \ times \ left (-3 \ right) = \) две группы отрицательных трех \ (= — 3 + -3 = -6 \).

Большинство людей согласны с тем, что мы должны придерживаться этой идеи.

Отрицательное время Положительное : Это проблематично: \ (\ left (-2 \ right) \ times 3 =? \)

Но кажется убедительным сказать, что закон коммутативности \ (a \ times b = b \ times a \) должен выполняться для всех типов чисел, включая отрицательные числа. В этом случае мы можем написать:

\ (\ left (-2 \ right) \ times 3 = 3 \ times \ left (-2 \ right) \) три группы отрицательных двоек \ (= — 2 + -2 + -2 = -6 \).

Отрицательное время Отрицательное : Как нам вычислить \ (\ left (-2 \ right) \ times \ left (-3 \ right) \)?

Применение закона коммутативности и представление об этом как о \ (\ left (-3 \ right) \ times \ left (-2 \ right) \) в этом случае не помогает.Итак, какая математика могла бы направить нас в нашем мышлении?

Мы действительно сказали, что нам нравится верить, что все обычные законы арифметики (\ (a \ times b = b \ times a \), \ (a \ times 1 = a \), \ (a \ times 0 = 0 \), раскрывающиеся скобки и т. д.) должны выполняться для всех типов чисел. Поскольку модель площади — это всего лишь представление, которое мы верим в расширяющиеся скобки, модель площади должна работать и для отрицательных чисел!

КЛЮЧЕВОЙ ПРИМЕР: Вот три способа вычислить \ (17 \ times 18 \), считая \ (17 \) либо \ (10 ​​+ 7 \), либо \ (20+ \ left (-3 \ right) \) и \ (18 \) как \ (10 ​​+ 8 \) или \ (20 + \ left (-2 \ right) \).Несмотря на то, что геометрически нет смысла иметь отрицательную длину стороны геометрической фигуры, мы видим, что математика, которую представляет каждая диаграмма, по-прежнему является правильной математикой.

Но есть четвертая возможная картина!

Математика раскрывающихся скобок предполагает, что правильное значение \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) равно \ (+ 6 \). (У продукта должен быть ответ \ (306 \).)

УПРАЖНЕНИЕ: Нарисуйте четыре диаграммы, представляющие \ (26 \ times 35 \), и используйте последнюю, чтобы продемонстрировать, почему мы должны установить \ (\ left (-4 \ right) \ times \ left (-5 \ right) = +20 \).

ТОЧНЫЙ ЛОГИЧЕСКИЙ АРГУМЕНТ, ПОЧЕМУ ОТРИЦАТЕЛЬНЫЙ ВРЕМЯ ОТРИЦАТЕЛЬНЫЙ ДОЛЖЕН БЫТЬ ПОЛОЖИТЕЛЬНЫМ

Как только мы договоримся, что \ (2 \ times \ left (-3 \ right) = — 6 \) (посредством повторного сложения) и \ (\ left (-3 \ right) \ times 2 = -6 \) (через a убежденность в коммутативности), что отрицательное умножение на отрицательное — положительное, является вынужденным логическим следствием следующих двух основных арифметических убеждений: \ (a \ times 0 = 0 \) и \ (a \ left (b + c \ right) = ab + ас \). Вот почему:

Докажем \ (\ left (-2 \ right) \ times \ left (-3 \ right) = + 6 \).

По первому правилу мы должны сказать: \ (\ left (-2 \ right) \ times 0 = 0 \).

Переписывая первый ноль, мы должны договориться, что: \ (\ left (-2 \ right) \ times \ left (3+ \ left (-3 \ right) \ right) = 0 \).

При распределении мы также должны согласиться с тем, что: \ (\ left (-2 \ right) \ times 3 + \ left (-2 \ right) \ times \ left (-3 \ right) = 0 \).

Это читается так: \ (- 6 + \ left (-2 \ right) \ times \ left (-3 \ right) = 0 \).

Отсюда следует, что \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) должно быть \ (+ 6 \).

УПРАЖНЕНИЕ: Создайте аналогичный аргумент, чтобы установить, что \ (\ left (-4 \ right) \ times \ left (-5 \ right) = + 20 \).

ТАК… ЧТО ТАКОЕ УМНОЖЕНИЕ?

В контексте положительных целых чисел это повторное сложение.

В контексте положительных и отрицательных целых чисел я лично не знаю, что это такое, кроме математически согласованной операции, установленной так, что если \ (a \) и \ (b \) являются положительными целыми числами, то \ ( a \ times \ left (-b \ right) = — ab \), и с логическими следствиями \ (\ left (-a \ right) \ times b = b \ times \ left (-a \ right) = — ab \) и \ (\ left (-a \ right) \ times \ left (-b \ right) = ab \).

Люди пытаются придать всему этому конкретный смысл с помощью моделей солдат, идущих по числовым линиям, меняющих направление, систем прибыли и долга, работы с температурами выше и ниже нуля и т. Д. Каждая модель хороша для иллюстрации НЕКОТОРЫХ аспектов арифметики отрицательных чисел, но не всех. Например, идея «убрать пять градусов холода — это то же самое, что добавить пять градусов тепла» может сработать для некоторых, чтобы объяснить, почему \ (- \ left (-5 \ right) \) должно равняться \ (5 \) , но это не объясняет само по себе, почему отрицательное, умноженное на отрицательное, дублируется положительным.

С педагогической точки зрения нам нужно отойти от начинающих учеников думать об умножении отрицательных чисел с помощью моделей, которые пытаются, но в какой-то момент должны потерпеть неудачу, «объяснить», что такое умножение отрицательных чисел. Вместо этого мы должны начать с обсуждения того, что, по нашему мнению, должно быть правдой в отношении умножения в целом и как оно ведет себя. Расширение скобок с помощью модели площади дает студентам убедительную иллюстрацию того, что математика «хочет», чтобы отрицательные значения, умноженные на отрицательные, были положительными.(А для студентов, готовых к этому, это подтверждает аксиоматический подход.) Что на самом деле означает «отрицательное, умноженное на отрицательное, — положительное» — я понятия не имею. Я просто знаю, что это алгебраически непротиворечиво.

УПРАЖНЕНИЕ: a) Докажите, что \ (- a \) и \ (\ left (-1 \ right) \ times a \) — одно и то же число. (ПОДСКАЗКА: \ (a + \ left (-1 \ right) \ times a = 1 \ times a + \ left (-1 \ right) \ times a = \ ldots \).)

b) Если вы считаете, что \ (- \ left (-5 \ right) = 5 \), объясните, почему теперь следует, что \ (\ left (-1 \ right) \ times \ left (-1 \ right) = 1 \).

Присоединяйтесь к обсуждению в Facebook и Twitter и любезно поделитесь этой страницей с помощью кнопок ниже.

Facebook

Twitter

Правила отрицательных и положительных чисел

Целые числа, десятичные дроби и дроби могут быть положительными или отрицательными. Отрицательное число — это любое число меньше нуля, а положительное число — любое число больше нуля. Ноль не является ни положительным, ни отрицательным. Вы можете складывать, вычитать, умножать и делить как положительные, так и отрицательные числа, комбинируя отрицательные, положительные числа или их комбинацию.

Сложение чисел

При добавлении положительного к положительному или отрицательного к отрицательному, сложите их вместе и дайте им одинаковый знак. Например, 5 + 5 равно 10, а -5 + -7 равно -12. При сложении положительного числа и отрицательного числа используйте вычитание, взяв абсолютное значение — числа без их знаков — и вычтите меньшее из большего. Затем дайте ответ знак большего числа. Например, -7 + 4 означает, что вы берете 7, вычитаете 4 и даете ответ отрицательный знак, поскольку абсолютное значение -7 больше 4.

Вычитание

Для вычитания измените знак вычитаемого числа на противоположный и следуйте правилам сложения. В 12–9 возьмите 9 и преобразуйте его в отрицательное значение, затем сложите их вместе, получив 12 + (-9). Сложите два новых значения вместе, чтобы получить 3. При вычитании отрицательного значения из отрицательного, например -6 ​​- -4, переключите -4 на положительное 4 и сложите значения вместе, чтобы получить -6 + 4, получив -2 после сложения. правила. Чтобы вычесть положительное и отрицательное число, 12 — -9, переключите -9 на 9 и сложите значения, чтобы получить 21.

Умножение

При умножении положительного и положительного числа вместе или отрицательного и отрицательного вместе сохраняйте один и тот же знак.