Параллельные прямые — Википедия

Материал из Википедии — свободной энциклопедии

Паралле́льные прямы́е (от греч. παράλληλος, буквально — идущий рядом) — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны.

На чертежах параллельные линии выделяются одинаково направленными стрелками.

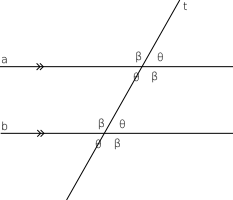
В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются^[1]. В другом варианте определения совпадающие прямые также считаются параллельными^[2][3].

Преимущество последнего определения состоит в том, что параллельность становится отношением эквивалентности

[4].

Параллельность прямых m{\displaystyle m} и n{\displaystyle n} обычно обозначается:

m∥n{\displaystyle m\parallel n}

Свойства[править | править код]

• Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского (см. ниже).
• Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
  • Соответственные углы равны (Рис.1).
  • Накрест лежащие углы равны (Рис.2).
  • Внутренние односторонние углы в сумме составляют 180° (Рис.3).

• Если считать совпадающие прямые параллельными, то параллельность будет бинарным отношением эквивалентности, которое разбивает всё множество прямых на классы параллельных между собой прямых.
• Множество точек плоскости, расположенных на некотором фиксированном расстоянии от данной прямой, по одну сторону от неё, есть прямая, параллельная данной.

Построение параллельных прямых[править | править код]

В стереометрии[править | править код]

В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.

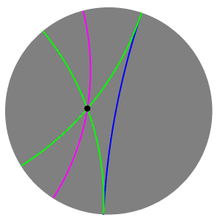Параллельные прямые в модели Пуанкаре: две зелёные прямые равнобежны (асимптотически параллельны) синей прямой, а фиолетовая ультрапараллельна к ней

В геометрии Лобачевского в плоскости через точку C{\displaystyle C} вне данной прямой AB{\displaystyle AB} проходит бесконечное множество прямых, не пересекающих AB{\displaystyle AB}. Прямая CE{\displaystyle CE} называется равнобежной прямой AB{\displaystyle AB} в направлении от A{\displaystyle A} к B{\displaystyle B}, если:

1. точки B{\displaystyle B} и E{\displaystyle E} лежат по одну сторону от прямой AC{\displaystyle AC};
2. прямая CE{\displaystyle CE} не пересекает прямую AB{\displaystyle AB}, но всякий луч, проходящий внутри угла ACE{\displaystyle ACE}, пересекает луч AB{\displaystyle AB}.

Аналогично определяется прямая, равнобежная AB{\displaystyle AB} в направлении от B{\displaystyle B} к A{\displaystyle A}.

Равнобежные прямые называются также асимптотически параллельными или просто параллельными. Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися^[5].

Свойства[править | править код]

Расходящиеся параллельные прямые имеют единственный общий перпендикуляр. Этот перпендикуляр соединяет ближайшую пару точек на этих прямых.

Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.

ru.wikipedia.org

Планиметрия. Страница 2

	Главная > Учебные материалы > Математика:  Планиметрия. Страница 2
	1.Параллельность прямых. 2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.Единственность перпендикуляра к прямой. 6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника. 8.Примеры.
1 2 3 4 5 6 7 8 9 10 11 12
	1.Параллельность прямых
	Теорема: если две прямые параллельны третьей прямой, то они параллельны.    Доказательство. Пусть даны две прямые а и b. Допустим, что они не параллельны между собой. (Рис.1) Тогда они пересекаются в некоторой точке С. Следовательно, через точку С проходят две прямые, параллельные прямой с. А это невозможно согласно аксиоме: через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Следовательно, прямые а и b не пересекаются. Они параллельны.		Рис.1 Теорема. Параллельность прямых.
	2.Признаки параллельности прямых
	Теорема. Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 градусов, то прямые параллельны.     Доказательство. Пусть даны две прямые a и b, которые образуют с секущей АВ внутренние накрест лежащие углы (Рис. 2 а). Допустим, что прямые a и b не параллельны. Тогда они пересекаются в одной точке С. Секущая АВ разбивает плоскость на две полуплоскости. И, следовательно, точка С лежит в одной из них и образует треугольник АВС. Сторона АС принадлежит прямой а. Сторона ВС принадлежит прямой b. (Рис. 2 б)    Отложим равный треугольник ABC1 в другой полуплоскости с вершиной С1 так, чтобы угол А треугольника АВС совпал с углом В треугольника АВС1. Так как по условию задачи сумма внутренних односторонних углов равна 180 градусов, то сторона АС1 ляжет на прямую а, ВС1 — на прямую b. Тогда точка С1 принадлежит двум прямым: а и b. Т.е. две точки С и С1 одновременно принадлежат двум прямым. А это невозможно. Следовательно прямые a и b не пересекаются, они параллельны.		Рис.2 Теорема. Признаки параллельности прямых.
	3.Свойство углов при пересечении параллельных прямых
	Теорема. Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны и сумма внутренних односторонних углов равна 180 градусов.     Доказательство. Пусть a и b параллельные прямые. Прямая с пересекает их в точках А и В. (Рис. 3)    Проведем через точку А прямую а1 так, чтобы внутренние накрест лежащие углы, образованные между прямыми а1 и b и секущей с, были равны. Тогда по признаку параллельности прямых они параллельны. А так как согласно аксиоме о единственной параллельной прямой, проходящей через точку не лежащей на данной прямой, такая прямая может быть только одна, то прямые а и а1 совпадают. А следовательно внутренние накрест лежащие углы, образованные между прямыми а,b и секущей с, равны.		Рис.3 Теорема. Свойство углов при пересечении параллельных прямых.
	4.Сумма углов треугольника
	Теорема. Сумма углов треугольника равна 180 градусов.     Доказательство. Пусть АВС данный треугольник. Проведем через вершину В прямую BD, параллельную стороне АС (Рис. 4).    Тогда углы α и α’, γ и γ’ равны как внутренние накрест лежащие. А так как прямая BD представляет собой развернутый угол с вершиной угла в точке В, который равен 180°, т.е. α’ + β + γ’ = 180°, то сумма углов треугольника равна также 180°. Таким образом, мы пришли к выводу, что сумма углов треугольника, т.е. α + β + γ = 180°.		Рис.4 Теорема. Сумма углов треугольника.
	5.Единственность перпендикуляра к прямой
	Теорема. Из любой точки, не лежащей на данной прямой, можно опустить только один перпендикуляр на данную прямую.     Доказательство. Пусть дана прямая а и не лежащая на ней точка А. Отметим на прямой а произвольную точку, например D. И проведем через нее перпендикуляр.(Рис. 5)    Теперь проведем через точку А прямую, параллельную нашей перпендикулярной прямой. Она также будет перпендикулярна прямой а. Так как прямая а, перпендикулярна одной из параллельных прямых, перпендикулярна и второй прямой. Отрезок АВ и есть перпендикуляр. Если допустить, что существует другой перпендикуляр, допустим в точке С. То в треугольнике АВС образуются два угла 90 градусов, а это невозможно. Следовательно отрезок АВ — это единственный перпендикуляр, проходящий через точку А.		Рис.5 Теорема. Единственность перпендикуляра к прямой.
	6. Высота, биссектриса и медиана треугольника
	Высотой треугольника, проведенной из данной вершины, называется перпендикуляр, опущенный из данной вершины на противолежащую сторону.    Биссектрисой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину угла и противолежащую сторону, и делящий данный угол пополам.    Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину и противолежащую сторону, и делящий ее пополам. (Рис.6)
	Рис.6 Высота, биссектриса и медиана треугольника.
	7. Свойство медианы равнобедренного треугольника
	Теорема. В равнобедренном треугольнике медиана, проведенная из вершины угла к основанию, является биссектрисой и высотой.    Доказательство:     Пусть АВС — данный равнобедренный треугольник с основанием АС. Боковые стороны АВ и ВС равны, ВD — медиана. Необходимо доказать, что BD является биссектрисой и высотой.    Рассмотрим треугольники ABD и BDC. Они равны по третьему признаку равенства треугольников. АВ = ВС по условию, AD = DC, так как BD медиана, а сторона BD у них общая. Следовательно, углы при вершине D равны, а так как они являются смежными, то ∠ADB = ∠CDB = 90°.     Из равенства треугольников ABD и BDC следует равенство углов при вершине В, т.е. ∠AВD = ∠CВD = α.     Отсюда можно сделать вывод, что медиана BD является биссектрисой и высотой.		Рис.7 Свойство медианы равнобедренного треугольника.
	8. Пример 1
	Даны прямая а и точка С, не лежащая на этой прямой. Необходимо доказать, что через точку С можно провести прямую, параллельную прямой а. (Рис.8)
	Доказательство:     Проведем прямую b, параллельную прямой а. Тогда, согласно аксиоме 9, (через точку, не лежащую на данной прямой, можно провести только одну прямую) проведем прямую с через точку С, параллельную прямой b.     Таким образом, получается, что прямая с параллельна прямой b, и прямая a также параллельна прямой b по построению. Следовательно, по теореме о двух прямых, параллельных третьей прямой, имеем, что две прямые a и c параллельны прямой b и, следовательно, они (прямые а и с) параллельны. Т.е. через точку С можно провести прямую, параллельную прямой а.		Рис.8 Задача. Даны прямая а и точка С …
	Пример 2
	Даны две параллельные прямые а и b, и секущая с. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных этими прямыми, параллельны (Рис.9)
	Доказательство:     Так как прямые а и b параллельны, то углы α и β, образованные этими параллельными прямыми и секущей с, равны как внутренние накрест лежащие, т.е. ∠α = ∠β. Согласно определению, биссектриса — это луч, исходящий из вершины угла между его сторонами, который делит этот угол пополам. Следовательно, биссектрисы d1 и d2 делят углы α и β пополам.    Таким образом, так как углы α и β равны, то и углы α/2 и β/2 также равны. А если углы α/2 и β/2 равны, то они являются внутренними накрест лежащими углами, между секущей с и прямыми, на которых лежат лучи d1 и d2, и согласно теореме: признак параллельности прямых, лучи d1 и d2 лежат на параллельных прямых.		Рис.9 Задача. Даны две параллельные прямые а и b и секущая с…
	Пример 3
	Один из углов равнобедренного треугольника АВС равен 100° (Рис.10). Найти остальные углы треугольника.
	Решение:    Так как сумма углов треугольника составляет 180°, а два угла у равнобедренного треугольника равны, то они не могут равняться 100°. Следовательно, углы при вершинах А и С равны, а угол при вершине В = 100°.    Отсюда следует, что можно составить соотношение:     2α + β = 180°     2α + 100° = 180°     2α = 80°     α = 40°     Ответ: углы равнобедренного треугольника составляют: 100°, 40°, 40°.		Рис.10 Задача. Найти углы треугольника.
	Пример 4
	Сумма внешних углов треугольника АВС при вершиах А и В равна 240° (Рис.11). Найдите угол С треугольника АВС.
	Решение:    Так как сумма углов α + β + α1 + β1 = 360°, а    α1 + β1 = 240° по условию задачи, то    α + β = 120°    А так как сумма углов треугольника составляет 180°, то    α + β + γ = 180°, т.е.    120° + γ = 180°    И следовательно, γ = 60°    Ответ: угол при вершине С = 60°.		Рис.11 Задача. Найти угол треугольника.
	Пример 5
	В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD. Угол при вершине В составляет 36° (Рис.12). Докажите, что треугольники CDA и ADB равнобедренные.
	Доказательство:    Так как по условию задачи треугольник АВС равнобедренный, то углы при вершинах А и С равны:    α = (180°-36°)/2    α = 72°, а так как AD биссектриса, то ∠BAD = ∠DAC, т.е.    α / 2 = 36°    Следовательно, треугольник ADB равнобедренный. Углы при вершинах А и В равны 36°.    Теперь рассмотрим треугольник ADC. Угол λ равен:    λ = 180° — (α / 2 + α)    λ = 180° — (36° + 72°)    λ = 72°    Таким образом, треугольник ADC равнобедренный. Углы при вершинах С и D равны 72°.		Рис.12 Задача. В равнобедренном треугольнике АВС …
1 2 3 4 5 6 7 8 9 10 11 12
	Содержание
	Страница 1		Страница 7
	1.Основные фигуры планиметрии. 2.Аксиомы планиметрии. 3.Смежные углы. 4.Вертикальные углы. 5.Перпендикулярные прямые. 6.Признаки равенства треугольников.		1.Движение и его свойства. 2.Симметрия относительно точки. 3.Симметрия относительно прямой. 4.Параллельный перенос и его свойства.
	Страница 2		Страница 8
	1.Параллельность прямых. 2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.Единственность перпендикуляра к прямой. 6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника.		1.Вектор и его абсолютная величина. 2.Сложение векторов. 3.Умножение вектора на число. 4.Разложение вектора по двум неколлинеарным векторам. 5.Скалярное произведение векторов.
	Страница 3		Страница 9
	1.Окружность. 2.Окружность описанная около треугольника. 3.Окружность вписанная в треугольник. 4.Геометрическое место точек.		1.Преобразование подобия и его свойства. 2.Подобие фигур. Подобие треугольников по двум углам. 3.Подобие треугольников по двум пропорциональным сторонам и углу между ними. 4.Подобие треугольников по трем пропорциональным сторонам. 5.Подобие прямоугольных треугольников.
	Страница 4		Страница 10
	1.Параллелограмм. 2.Свойства диагоналей параллелограмма. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках.		1.Углы, вписанные в окружность. 2.Пропорциональность хорд и секущих окружности. 3.Теорема косинусов. 4.Теорема синусов. 5.Соотношение между углами и сторонами в треугольнике.
	Страница 5		Страница 11
	1.Теорема Пифагора. 2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества.		1.Многоугольники. Правильные многоугольники. 2.Радиус вписанной и описанной окружностей правильных многоугольников. 3.Подобие многоугольников. 4.Длина окружности.
	Страница 6		Страница 12
	1.Декартова система координат. 2.Расстояние между точками. 3.Уравнение окружности. 4.Уравнение прямой. 5.Координаты точки пересечения.		1.Площадь прямоугольника. 2.Площадь параллелограмма. 3.Площадь треугольника. 4.Площадь круга. 5.Площадь подобных фигур. 6.Площадь трапеции.

www.mathtask.ru

Признаки параллельности прямых | Треугольники

Признаки параллельности прямых:

1) Если внутренние накрест лежащие углы равны, то прямые параллельны.

 

   

 

 

2) Если соответственные углы равны, то прямые параллельны.

 

   

 

 

3) Если сумма внутренних односторонних углов равна 180, то то прямые параллельны.

 

   

 

 

4) Если две прямые параллельны третьей прямой, то они параллельны между собой.

   

 

 

5) Если две прямые перпендикулярны третьей прямой, то они параллельны между собой.

   

Виды углов

www.treugolniki.ru

Признаки и свойства параллельных прямых

Признаки параллельных прямых

1. Если две прямые параллельны третьей прямой, то они являются параллельными:

Если  a||c  и  b||c, то  a||b.

2. Если две прямые перпендикулярны третьей прямой, то они параллельны:

Если  a⊥c  и  b⊥c, то  a||b.

Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.

3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:

Если ∠1 + ∠2 = 180°, то  a||b.

4. Если соответственные углы равны, то прямые параллельны:

Если ∠2 = ∠4, то  a||b.

5. Если внутренние накрест лежащие углы равны, то прямые параллельны:

Если ∠1 = ∠3, то  a||b.

Свойства параллельных прямых

Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.

1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:

Если  a||b, то  ∠1 + ∠2 = 180°.

2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:

Если  a||b, то  ∠2 = ∠4.

3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:

Если  a||b, то  ∠1 = ∠3.

Следующее свойство является частным случаем для каждого предыдущего:

4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

Если  a||b и  c⊥a, то  c⊥b.

Пятое свойство – это аксиома параллельности прямых:

5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:

naobumium.info

Условие параллельности прямых | matematicus.ru

Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:

y₁=k₁x+b₁

y₂=k₂x+b₂

служит равенство их угловых коэффициентов, то есть

k₁=k₂

Если прямые заданы уравнениями в общем виде, то есть

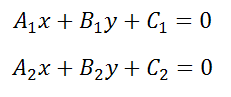
то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:

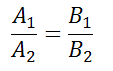
или в другом представлении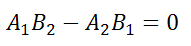

Также это равенство можно записать в виде

Если свободные члены пропорциональны, то есть,

то прямые не только параллельны, но и совпадают.

---

Пример 1

Уравнения

4x+2y-8=0 и 8x+4y-16=0

представляют одну и ту же прямую, то есть совпадают.

---

Пример 2
Прямые у=4x-3 (на графике синего цвета) и y=4x+7 (прямая красного цвета) параллельны, так как у них угловые коэффициенты равны k₁=k₂=4

 

---

Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k₁=5, k₂=3

---

Пример 4
Прямые 2x+4y+7=0 и 3x+6y-5=0 параллельны, так как выражение равно нулю

$\left| {\begin{array}{*{20}{c}} {{A_1}}&{{B_1}} \\ {{A_2}}&{{B_2}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}} 2&4 \\  3&6 \end{array}} \right| = 2 \cdot 6 — 3 \cdot 4 = 0$

---

Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю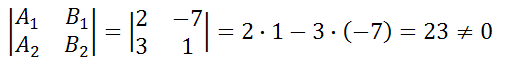

www.matematicus.ru

Параллельность прямой и плоскости. Видеоурок. Геометрия 10 Класс

Данный урок посвящен теме «Параллельность прямой и плоскости». На этом уроке мы обсудим параллельность прямой и плоскости как один из трех возможных вариантов их взаимного расположения в пространстве, рассмотрим ситуацию плоскость параллельная прямой. Сформулируем теорему и докажем ее и два утверждения, которые часто используются при решении задач на эту тему.

Тема: Параллельность прямых и плоскостей

Урок: Параллельность прямой и плоскости

Аксиома А2: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.

Отсюда следуют три случая взаимного расположения прямой и плоскости в пространстве.

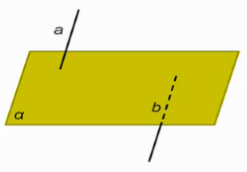
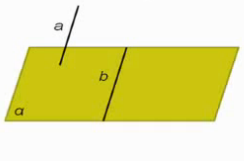
1. Прямая лежит в плоскости (рис. 1).

Рис. 1

2. Прямая и плоскость имеют только одну общую точку, то есть пересекаются (рис. 2).

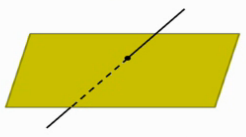
Рис. 2

3. Прямая и плоскость не имеют ни одной общей точки (рис. 3).

Рис. 3

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Параллельность прямой а и плоскости α обозначается так: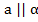 (рис. 4)

Рис. 4 Плоскость параллельная прямой

Наглядное представление о прямой, параллельной плоскости дают натянутые троллейбусные или трамвайные провода. В идеале, они параллельны плоскости земли (рис. 5).

Рис. 5

Другой пример дает линия пересечения стены и потолка (рис. 6). Эта линия параллельна плоскости пола. А пол — это плоскость параллельная прямой. Заметим, что в плоскости пола имеется прямая, параллельная этой линии. Такой прямой является, например, прямая пересечения пола с той же самой стеной. На рисунке указанные прямые обозначены как а и b.

Рис. 6

Оказывается, что если в плоскости α имеется прямая b, параллельная прямой а, не лежащей в плоскости α, то прямая а и плоскость α параллельны (рис. 7). Другими словами, наличие в плоскости α прямой b, параллельной прямой а, является признаком, по которому можно сделать вывод о параллельности прямой а и плоскости α. Сформулируем это утверждение в виде теоремы.

Рис. 7

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Доказательство:

Рассмотрим плоскость α и две параллельные прямые а и b, прямая b лежит в плоскости α, а прямая а не лежит в этой плоскости (рис. 7). Докажем, что прямая а параллельна плоскости α.

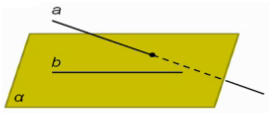
Рис. 8

Предположим, это не так, то есть что прямая а пересекается с плоскостью α (рис. 8). Значит, по лемме о пересечении плоскости параллельными прямыми (лемма приведена ниже), прямая b тоже пересекается с плоскостью α. Но это невозможно, так как прямая b по условию лежит в плоскости α. Итак, прямая а не пересекает плоскость α, поэтому она параллельна плоскости. Теорема доказана.

Лемма: если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Докажем еще два утверждения, которые часто используются при решении задач.

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

           

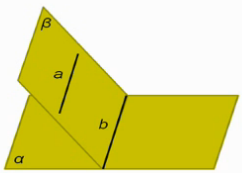
Рис. 9

Доказательство:

Итак, пусть через прямую а, параллельную плоскости α, проходит плоскость 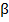, пересекающая плоскость α по прямой b (рис. 9). Докажем, что прямые а и b параллельны.

Действительно, прямые а, b лежат в одной плоскости 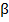 и не пересекаются, ведь в противном случае прямая а пересекала бы плоскость α, что невозможно, так как по условию прямая а параллельна плоскости α. Значит прямые а и b параллельны, что и требовалось доказать.

Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Рис. 10

Рис. 11

Доказательство:

Пусть а и b – параллельные прямые, причем прямая а параллельна плоскости α. Следовательно, прямая а не пересекает плоскость α. Тогда, по лемме о пересечении плоскости параллельными прямыми, прямая b тоже не пересекает плоскость α. А это значит, что прямая b либо параллельна плоскости α (рис. 10), либо лежит в ней (рис. 11), что и требовалось доказать.

 

Список литературы по теме «Плоскость параллельная прямой»

1. И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
2. Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3. Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.

 

Домашнее задание по теме «Параллельность прямой и плоскости», «Плоскость параллельная прямой»

1. Дайте определение параллельности прямой и плоскости.
2. Дана прямая и две точки вне прямой. Можно ли провести плоскость, которая проходит через эти точки и параллельна данной прямой?
3. Вершины A, B, C, D не лежат в одной плоскости. Параллельна ли прямая АС плоскости, которая проходит через середины отрезков AB, BC, CD?
4. И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
5. Задания 3, 6, 8 стр. 26

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. ЕГЭ (Источник).
2. Математика (Источник).
3. Якласс (Источник).
4. ФМ Класс (Источник).

interneturok.ru

Параллельные плоскости. Видеоурок. Геометрия 10 Класс

Тема: Параллельность прямых и плоскостей

Урок: Параллельные плоскости

На этом уроке мы дадим определение параллельных плоскостей и вспомним аксиому о пересечении двух плоскостей.

Определение. Две плоскости называются параллельными, если они не пересекаются.

Обозначение: .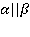

Иллюстрация параллельных плоскостей (Рис. 1.)

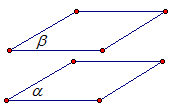
Рис. 1.

Существуют ли параллельные плоскости?

Вспомним аксиому А3.

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (Рис. 2.).

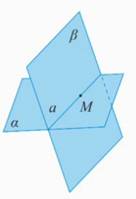
Рис. 2.

То есть, еще остается случай, если две плоскости не имеют общей точки. Такие плоскости называются параллельными.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны.

Доказательство

Проведем в плоскости  две пересекающиеся прямые а и b в точке М, а в плоскости  пересекающиеся прямые а₁ и b₁, причем прямая а₁ параллельна прямой а, а прямая b₁ параллельна прямой b (Рис. 3.). Докажем, что плоскости  и параллельны.

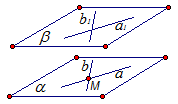
Рис. 3.

Прямая а принадлежит плоскости , прямая а₁ принадлежит плоскости , а прямая а параллельна прямой а₁. Значит, прямая а параллельна плоскости , по признаку параллельности прямой и плоскости.  Аналогично, прямая b параллельна прямой b₁ из плоскости . Значит, прямая b параллельна плоскости .

Предположим, что плоскости  и  не являются параллельными, то есть они пересекаются по некоторой прямой, назовем ее с (Рис. 4.).

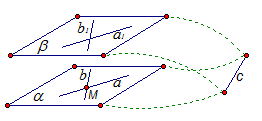
Рис. 4.

Плоскость  проходит через прямую а, параллельную плоскости , и пересекает эту плоскость по прямой с. Согласно опорному факту, прямая а параллельна прямой с. Аналогично, плоскость  проходит через прямую b, параллельную плоскости , и пересекает эту плоскость по прямой с. Согласно опорному факту, прямая b параллельна прямой с. Получаем, что через одну точку М проходит две прямые, параллельные прямой с, что невозможно. Получили противоречие. Значит, предположение о том, что плоскости пересекаются, было неверным. Значит, плоскости не пересекаются, то есть параллельны, что и требовалось доказать.

Плоскости  и  параллельны, прямая m лежит в плоскости .

Докажите, что прямая m параллельна плоскости .

Доказательство

Предположим, что прямая mпересекается с плоскостью  в некоторой точке М (Рис. 5.). Тогда точка М принадлежит и плоскости , и плоскости  (так как точка М лежит на прямой m, а прямаяmпринадлежит плоскости). Но это невозможно, так как плоскости  и  по условию параллельны. Значит, прямая mпараллельна плоскости .

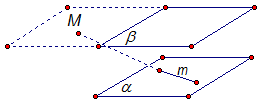
Рис. 5.

Докажите, что плоскости  и  параллельны, если прямые m и nплоскости  параллельны плоскости .

Доказательство

Предположим, что плоскости  и  пересекаются по прямой с (Рис. 6.). Плоскость  проходит через прямую m, параллельную плоскости , и пересекает эту плоскость по прямой с. Значит, прямая m параллельна прямой с. Аналогично, плоскость  проходит через прямую n, параллельную плоскости , и пересекает эту плоскость по прямой с. Согласно опорному факту, прямая n параллельна прямой с. Получаем, что через одну точку М проходит две прямые m и n, параллельные прямой с, что невозможно. Получили противоречие. Значит, предположение о том, что плоскости пересекаются, было неверным. Значит, плоскости  и  не пересекаются, то есть параллельны, что и требовалось доказать.

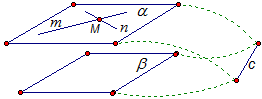
Рис. 6.

Две стороны треугольника параллельны плоскости . Докажите, что и третья сторона параллельна плоскости .

Доказательство

Дан треугольник АВС и плоскость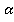. Стороны АВ и АС параллельны плоскости  (Рис. 7.). Докажем, что и сторона ВС параллельна плоскости .

Через две пересекающиеся прямые АС и АВ проходит плоскость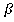 и притом только одна. Плоскость  параллельна плоскости , так как прямые АС и АВ параллельны плоскости  (из задачи 2). Но прямая ВС лежит в плоскости , а значит ВС параллельна плоскости  (из задачи 1).

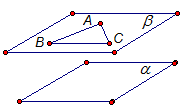
Рис. 7.

Итак, мы рассмотрели определение и признак параллельных плоскостей. На следующем уроке мы рассмотрим свойства параллельных плоскостей.

 

Список рекомендованной литературы

1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил.

2. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.

3. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил.

 

Рекомендованные ссылки на ресурсы интернет

1. Фестиваль педагогических идей «Открытый урок» (Источник)

2. Математика (Источник)

3. Шпаргалки (Источник)

 

Рекомендованное домашнее задание

1. Какие плоскости называются параллельными?

2. Могут ли быть параллельными плоскости, проходящие через непараллельные прямые?

3. Каким может быть взаимное расположение двух прямых, каждая из которых лежит в одной из двух различных параллельных плоскостей?

4. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил.

Задания 1, 2, 5 стр. 29

interneturok.ru