2

Первообразная и интеграл: формулы с примерами решения

Ранее вы ознакомились с операцией дифференцирования: нахождения производной по данной функции. Не менее важна и обратная ей операция — интегрирование: нахождение функции по её производной.

Пусть дано функцию такую, что в каждой точке х некоторого промежутка . В этом случае функцию f(x) называют производной функции F(x), a — первообразной для f(x).

Функция F(x) называется первообразной функции на промежутке , если для каждого значения х из этого промежутка F'(x) = f(x).

Например, на всей числовой оси (т. е. на R] функция F(x) = является первообразной для f(x) = 2х, ибо = 2х

; F(x) = sin х есть первообразной для f(x) = cos х, ибо (sin х)’ = cos х.

Функция F(x) является первообразной для например на [1; 5]. Но не на R, поскольку F'(O) не существует, и не на , поскольку это не промежуток.

Одна ли функция является первообразной для Нет. Ведь и и и т. д. Каким бы ни было число С (произвольная постоянная), функция — первообразная для, ибо ()‘

Существуют ли другие функции, отличные от , первообразные для ? Нет.

Теорема. (Основное свойство первообразных.) Каждая первообразная для функции ) имеет вид

F(x) + С, где — одна из этих первообразных, а С — произвольная постоянная.

Доказательство 1. Пусть—одна из первообразных для функции на промежутке , т. е. для каждого :.

По правилу нахождения производной суммы

Этим доказано» что какая бы ни была постоянная С, если — первообразная для , то и — первообразная для

Пусть и — две любые первообразные для функции

на промежутке, т. е. и для каждого . Тогда

Как видим, функция такая, что в каждой точке её производная равна 0.

Такое свойство имеет только определённая на функция, которая ни возрастает, ни убывает на этом промежутке. Ведь если бы на некоторой части промежутка эта функция возрастала или убывала, то там её производная была бы соответственно положительная или отрицательная. (Подробнее обоснование этого факта даётся в строгих курсах математического анализа.) Итак, , где

С — постоянная, т. е. .

Этим доказано, что если — одна из первообразных для функции , то каждая из функций также её первообразная и других первообразных для ) не существует. Геометрически это означает, что графики любых двух первообразных для функции такие, что их можно совместить параллельным переносом вдоль оси ординат (рис. 102).

— общий вид первообразных для функции .

Каждая первообразная рассматривается на некотором промежутке. Если же для краткости его не указывают, то имеют в виду промежуток максимально возможной длины. В частности, если функция ) определена на и промежуток не указано, то речь идет о её первообразной также на .

Операцию нахождения производной данной функции называют дифференцированием. Обратная ей операция — нахождение первообразной — называется интегрированием.

Используя формулы дифференцирования (с. 218), составим таблицу первообразных. Советуем запомнить её.

Обосновать эту таблицу можно дифференцированием функции из её второй строки. Пользуясь таблицей, можно сразу писать, что, например, для функции первообразной есть и т. д.

Множество всех первообразных функции часто называют неопределённым интегралом этой функции и обозначают символом (читают: интеграл эф от икс де икс).

Выражение «проинтегрировать функцию» обозначает то же, что и «найти первообразную для функции » .

То есть, если — первообразная для функции , а —произвольное число, то .

Слово интеграл в переводе с латинского языка означает целый. Почему его так назвали, вы поймёте, когда ознакомитесь с определённым интегралом (см. с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении имеет не одно числовое значение, а бесконечно много.

Таблицу первообразных, с помощью символа неопредёлен-ного интеграла можно записать так:

Примеры с решением

Пример №1

Докажите, что функция является первообразной для функции .

Доказательство. .

Имеем . Итак, по определению, функция — первообразная для функции

Пример №2

Найдите первообразную для функции : а) ; б) ;

Решение:

Воспользуемся таблицей первообразных.

а) Первообразной для функции есть функция .

Для функции , поэтому .

б) Первообразной для функции есть функция

Для функции поэтому .

Пример №3

Найдите для функции такую первообразную, чтобы её график проходил через точку Р (2; 5).

Решение:

Пользуясь таблицей, найдём общий вид первообразных: Поскольку график искомой первообразной проходит через точку Р (2; 5), то , отсюда С = 3.

Следовательно, .

Ответ..

Пример №4

Проинтегрируйте функцию .

Решение:

Нахождение первообразных

Выведем несколько правил, подобных правилам дифференцирования, которые облегчают нахождение первообразных.

I. Если и — первообразные для функций ) и, то — первообразная для функции .

Действительно, если и . то

. Если — первообразная для функции , a — произвольное число, то — первообразная для функции .

Ведь .

Если —первообразная для функции , a ,b — произвольные числа , то — первообразная для функции .

»

Ведь

Пример №5

Найдите первообразную для функции:

а) ; б) ; в) .

Решение:

а) Для функций и первообразными являются соответственно и .

Поэтому для суммы данных функций общий вид первообразных

б) По правилу II: .

в) Одной из первообразных для функции ,согласно правилу III, является функция . Общий вид первообразных для данной функции

К нахождению первообразных сводятся прежде всего задачи, обратные тем, которые решаются с помощью производной. Рассмотрим пример..

Если известен закон прямолинейного движения тела ,то для нахождения его скорости в момент t нужно найти производную: . Здесь дан закон движения и требуется найти его скорость. Для механики не менее важно уметь решать обратную задачу: по заданной в каждый момент скорости определять закон движения.

Задача №1.

Точка движется прямолинейно с переменной скоростью . За перые 4 с она прошла 80 м. Найдите закон движения точки.

Решение:

Искомый закон движения выражается такой функцией, что . Здесь s(t) — первообразная для функции . Общий вид всех таких первообразных . Поскольку за 4 с точка прошла 80м, то 80 = 5-16 + С, отсюда С = 0.

Ответ. Искомый закон движения точки , где t — время в секундах, — расстояние в метрах.

Примеры других применений первообразной рассмотрим в следующих параграфах.

С помощью неопределённого интеграла правила интегрирования записываются так:

Пример №6

Найдите одну из первообразных для функции:

а); б).

Решение:

а) Для функции одной из первообразных есть функция . Учитывая то, что первообразной для функции есть функция , запишем искомую первообразную: ;

б) преобразуем сначала формулу, задающую функцию:

Тогда .

Пример №7

Тело движется прямолинейно с ускорением .

Определите скорость данного движения как функцию от времени f, если в момент t = 0 она равнялась 3 м/с.

Решение:

Ускорение — производная скорости. Поэтому если — искомая скорость, то . Следовательно,) — первообразная для функции , поэтому . Поскольку , то .

Ответ. .

Первообразная и площадь криволинейной трапеции

Пусть на координатной плоскости задан график непрерывной функции , принимающей на промежутке [а; Ь) только неотрицательные значения.

Фигуру, ограниченную таким графиком, осью абсцисс и прямыми х = а и х = Ь, называют криволинейной трапецией.

Криволинейную трапецию называют также под графиком функции на [а; Ь].

Несколько криволинейных трапеций изображено на (рис. 105).

Каждая криволинейная трапеция имеет определённую площадь (это доказано в строгих курсах математического анализа). Эти площади можно находить с помощью первообразных.

Теорема. Площадь криволинейной трапеции, образованной графиком функции ) на промежутке [а; Ь], равна , где — первообразная для функции на [а; b].

Доказательство. Рассмотрим произвольную криволинейную трапецию, образованную графиком функции на (риc. 106). Пусть х — произвольная точка отрезка , а S(x) — площадь криволинейной трапеции, образованной графиком функции на . Понятно, что — функция от х. Докажем, что для каждого .

Дадим переменной х приращение , тогда функция получит приращение (pиc. 107). Это — площадь криволинейной трапеции, образованной графиком функции на промежутке , она приближённо равна площади прямоугольника с основанием , и высотой f(t), где t — некоторое число из промежутка . Поскольку функция f(x) непрерывна, такое число t обязательно найдётся.

Следовательно, откуда .

Если , то и , ибо функция непрерывна. Поэтому если , то , т. е. .

Как видим, функция S(x) — первообразная для на [а; Ь]. Поэтому если F(x) — какая-либо другая первообразная для ) на [a; b], то S(x) = F(x) + С, где С — постоянная. Чтобы определить С, учтём, что S(a) 0, ибо при х — а криволинейная трапеция, образованная графиком функции f(x) на [a; х], вырождается в отрезок; его площадь равна 0. Имеем: 0 = F(a) + С, отсюда С = -F(a). Следовательно,= F(х) — F(a). Если в это равенство подставим значение х = Ь, то получим площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]:

Значение выражения F(b) — F(a) вычисляют часто, поэтому для удобства его записывают ещё и так:..Итак, формула (1) приобретает вид:

Задача №2.

Найдите площадь криволинейной трапеции, образованной графиком функции на промежутке [1; 3].

Решение:

На (рис) 108 изображена фигура, площадь которой нужно найти. Для функции первообразной есть . Следовательно, искомая площадь

Задача №3.

Найдите площадь фигуры, ограниченной одной аркой синусоиды и осью абсцисс (риc. 109).

Решение:

Надо найти площадь криволинейной трапеции, образованной графиком функции на промежутке . Для функции первообразной есть функция . Следовательно, искомая площадь= 1 — (-1) — 2 (кв. ед.).

Пользуясь термином «криволинейная трапеция следует иметь в виду, что «криволинейная трапеция» не всегда является трапецией (риc. 109) и не всегда она криволинейная(риc. 105, б). А вообще она — не геометрическая фигура в научном понимании. Любое движение отображает каждую фигуру на равную ей фигуру такого же вида. А если «криволинейную трапецию *, например, изображенную на (рис 108), повернуть на 90°, она отображается на фигуру, которая не является криволинейной трапецией. Поэтому вместо «криволинейная трапеция» говорят и пишут «подграфик функции».

Задача №4.

Найдите площадь криволинейной трапеции, образованной графиком функции у = х на [0; 2].

Решение:

Данная криволинейная трапеция — прямоугольный треугольник с катетами 2 и 2 (риc. 110). Его площадь (кв. ед.).

Ответ. 2кв. ед.

Задача №5.

Найдите площадь криволинейной трапеции, образованной графиком функции у -3 на [1,2].

Заданная криволинейная трапеция — прямоугольник с измерениями 1 и 3 (риc. 111). Его площадь (кв. ед.).

Ответ. 3 кв. ед.

Задача №6.

Найдите площадь фигуры, ограниченной графиком функции и осью абсцисс.

Решение:

Найдем абсциссы точек пересечения графика данной функции с осью Ох. В этих точках ордината функции равна нулю:, отсюда , (риc. 112). Значит, надо найти площадь криволинейной трапеции, образованной

графиком функции на [-2; 2].Одна из первообразных для данной функции.Поэтому искомая площадь кв,ед.

Ответ. кв.ед.

Определённый интеграл

Рассмотрим другой подход к определению площади криволинейной трапеции.

Пусть дана криволинейная трапеция, образованная графиком функции f(x) на [a;b] (рис. 117). Разобьём отрезок [а; Ь] точками на n равных отрезков:

Построим на первом из этих отрезков прямоугольник высотой , на втором — прямоугольник высотой ,…, на n—м — прямоугольник высотой . В результате получим ступенчатый многоугольник, составленный из n прямоугольников. Пусть основание каждого из построенных прямоугольников равно ; тогда площадь всего ступенчатого многоугольника

Суммы такого вида называют интегральными суммами функции f(x) на [а; Ь]. Полученную интегральную сумму можно считать приближённым значением площади S криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]. При этом если то (риc. 118). Пишут: .

He только задача о нахождении площади криволинейной трапеции, но и много других важных прикладных задач приводят к вычислению пределов подобных интегральных сумм. Поэтому для такого понятия введено специальное название и обозначение.

Предел интегральной суммы функции f(x) на отрезке [а; Ь], если , называют определённым интегралом функции f(x) от а до Ь.

Его обозначают символом (читают: интеграл от а до b эф от икс де икс). Здесь числа а и b пределы интегрирования, — знак интеграла, f(x) — подинтегральная функция, х —переменная интегрирования.

Следовательно, площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь], равна , т. е.. Как доказано в предыдущем пункте, эта площадь равна , где — первообразная для функции f(x). Поэтому

Это — формула Ньютона—Лейбница, основная формула математического анализа. Она даёт возможность решать много разных интересных и содержательных задач — абстрактных и прикладных, в частности — и очень важных. Решали такие задачи сотни математиков еще задолго до создания математического анализа. Но для каждой задачи раньше они находили отдельный оригинальный способ решения. Найдя и обосновав формулу Ньютона—Лейбница, учёные получили общий и очень эффективный способ решения таких задач. Не случайно открытие формулы Ньютона—Лейбница специалисты считают самым важным открытием XVII века.Рационализировать вычисления определённых интегралов часто помогает такое их с в о й с т в о:

Справедливость этой формулы вытекает из следующих преобразований:

Задача №7.

Найдите площадь фигуры, ограниченной графиками функций и

Решение:

Построим графики данных функций (рис. 119). Надо найти площадь закрашенной фигуры. Она равна разности площадей фигур ОВАК и ОВАР. Границы интегрирования — абсциссы точек О и А, в которых пересекаются графики функций, т. е. значения х удовлетворяющие системе уравнений и . Из системы получим уравнение корни которого и

Следовательно, искомая площадь

Ответ. кв. ед.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Первообразная функции 2х 1.

Объём тела вращения

Существует три основных правила нахождения первообразных функций. Они очень похожи на соответствующие правила дифференцирования.

Правило 1

Если F есть первообразная дл некоторой функции f, а G есть первообразная для некоторой функции g, то F + G будет являться первообразной для f + g.

По определению первообразной F’ = f. G’ = g. А так как эти условия выполняются, то по правилу вычисления производной для суммы функций будем иметь:

(F + G)’ = F’ + G’ = f + g.

Правило 2

Если F есть первообразная для некоторой функции f, а k — некоторая постоянная. Тогда k*F есть первообразная для функции k*f. Это правило следует из правила вычисления производной сложной функции.

Имеем: (k*F)’ = k*F’ = k*f.

Правило 3

Если F(x) есть некоторая первообразная для функции f(x), а k и b есть некоторые постоянные, причем k не равняется нулю, тогда (1/k)*F*(k*x+b) будет первообразной для функции f(k*x+b). 4)). Теперь воспользовавшись третьим правилом, получим.

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x) , что выполняется равенство для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C , для произвольной константы С , причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение называют подынтегральным выражением , а f(x) – подынтегральной функцией . Подынтегральное выражение представляет собой дифференциал функции f(x) .

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x) , а множество ее первообразных F(x)+C .

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.

Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.

Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:

• первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
• второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.

Рассмотрим пример.

Пример.

Найти первообразную функции , значение которой равно единице при х = 1 .

Решение.

Мы знаем из дифференциального исчисления, что (достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом, . По второму свойству . То есть, имеем множество первообразных . При х = 1 получим значение . По условию, это значение должно быть равно единице, следовательно, С = 1 . Искомая первообразная примет вид .

Пример.

Найти неопределенный интеграл и результат проверить дифференцированием.

Решение.

По формуле синуса двойного угла из тригонометрии , поэтому

Неопределенный интеграл

Основной задачей дифференциального исчисления было вычисление производной или дифференциала заданной функции. Интегральное исчисление, к изучению которого мы переходим, решает обратную задачу, а именно, отыскания самой функции по ее производной или дифференциалу. То есть, имея dF(х)= f(х)d (7.1) или F ′(х)= f(х) ,

где f(х) — известная функция, надо найти функцию F(х) .

Определение: Функция F(х) называется первообразной функции f(х) на отрезке , если во всех точках этого отрезка выполняется равенство: F′(х) = f(х) или dF(х)= f(х)d .

Например , одной из первообразных функций для функции f(х)=3х 2 будет F(х)= х 3 , т.к. (х 3)′=3х 2 . Но первоообразной для функции f(х)=3х 2 будет также и функции и , т.к. .

Итак, данная функция f(х)=3х 2 имеет бесконечное множество первоообразных, каждая из которых отличается лишь на постоянное слагаемое. Покажем, что этот результат имеет место и в общем случае.

Теорема Две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются одна от другой на этом промежутке на постоянное слагаемое.

Доказательство

Пусть функция f(х) определена на промежутке (a¸b) и F 1 (х) и F 2 (х) — первообразные, т. е. F 1 ′(х)= f(х) и F 2 ′(х)= f(х) .

Тогда F 1 ′(х)=F 2 ′(х)Þ F 1 ′(х) — F 2 ′(х) = (F 1 ′(х) — F 2 (х))′= 0 . Þ F 1 (х) — F 2 (х)=С

Отсюда, F 2 (х) = F 1 (х)+С

где С — константа (здесь использовано следствие из теоремы Лагранжа).

Теорема, таким образом, доказана.

Геометрическая иллюстрация . Если у = F 1 (х) и у = F 2 (х) – первообразные одной и той же функции f(х) , то касательная к их графикам в точках с общей абсциссой х параллельны между собой (рис. 7.1).

В таком случае расстояние между этими кривыми вдоль оси Оу остается постоянным F 2 (х) — F 1 (х)=С , то есть эти кривые в некотором понимании «параллельны» одна другой.

Следствие .

Прибавляя к какой-то первообразной F(х) для данной функции f(х) , определенной на промежутке Х , все возможные постоянные С , мы получим все возможные первообразные для функции f(х) .

Итак, выражение F(х)+С , где , а F(х) – некоторая первообразная функции f(х) включает все возможные первообразные для f(х) .

Пример 1. Проверить, являются ли функции первообразными для функции

Решение:

Ответ : первообразными для функции будут функции и

Определение: Если функция F(х) является некоторой первообразной для функции f(х), то множество всех первообразных F(х)+ С называют неопределенным интегралом от f(х) и обозначают:

∫f(х)dх.

По определению:

f(х) — подынтегральная функция,

f(х)dх — подынтегральное выражение

Из этого следует, чтоо неопределенный интеграл является функцией общего вида, дифференциал которой равен подынтегральному выражению, а производная от которой по переменной х равна подынтегральной функции во всех точках .

С геометрической точки зрения неопределенный интеграл представляет собой семейство кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, то есть вдоль оси Оу (рис. 7.2).

Операция вычисления неопределенного интеграла от некоторой функции называется интегрированием этой функции.

Отметим, что если производная от элементарной функции всегда является элементарной функцией, то первоообразная от элементарной функции может не представляться при помощи конечного числа элементарных функций.

Рассмотрим теперь свойства неопределенного интеграла .

Из определения 2 вытекает:

1. Производная от неопределенного интеграла равна подынтегральной функции, то есть, если F′(х) = f(х) , то

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

. (7.4)

Из определения дифференциала и свойства (7.3)

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, то есть (7.5)

Урок и презентация на тему: «Первообразная функция. График функции»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Алгебраические задачи с параметрами, 9–11 классы
«Интерактивные задания на построение в пространстве для 10 и 11 классов»

Первообразная функция. Введение

Ребята, вы умеем находить производные функций, используя различные формулы и правила. Сегодня мы будем изучать операцию, обратную вычислению производной. Понятие производной часто применяется в реальной жизни. Напомню: производная – это скорость изменения функции в конкретной точке. Процессы, связанные с движением и скоростью, хорошо описываются в этих терминах. 2}{2})»+c»=g*t+0=g*t$.

Ребята, обратите внимание: наша задача имеет бесконечное множество решений!
Если в задаче не задано начальное или какое-то другое условие, не забывайте прибавлять константу к решению. Например, в нашей задаче может быть задано положение нашего тела в самом начале движения. Тогда вычислить константу не трудно, подставив ноль в полученное уравнение, получим значение константы.

Как называется такая операция?
Операция обратная дифференцированию называется – интегрированием.
Нахождение функции по заданной производной – интегрирование.
Сама функция будет называться первообразной, то есть образ, то из чего была получена производная функции.
Первообразную принято записывать большой буквой $y=F»(x)=f(x)$.

Определение. Функцию $y=F(x)$ называется первообразной функции $у=f(x)$ на промежутке Х, если для любого $хϵХ$ выполняется равенство $F’(x)=f(x)$.

Давайте составим таблицу первообразных для различных функции. Ее надо распечатать в качестве памятки и выучить. {\frac{3x+1}{6}}$.
3. По заданному закону изменения скорости тела от времени $v=4cos(6t)$ найти закон движения $S=S(t)$, если в начальный момент времени тело имело координату равную 2.

Первообра́зная. Красивое слово.) Для начала немного русского языка. Произносится это слово именно так, а не «первоОбразная» , как может показаться. Первообразная — базовое понятие всего интегрального исчисления. Любые интегралы – неопределённые, определённые (с ними вы познакомитесь уже в этом семестре), а также двойные, тройные, криволинейные, поверхностные (а это уже главные герои второго курса) – строятся на этом ключевом понятии. Имеет полный смысл освоить. Поехали.)

Прежде чем знакомиться с понятием первообразной, давайте в самых общих чертах вспомним самую обычную производную . Не углубляясь в занудную теорию пределов, приращений аргумента и прочего, можно сказать, что нахождение производной (или дифференцирование ) – это просто математическая операция над функцией . И всё. Берётся любая функция (допустим, f(x) = x 2 ) и по определённым правилам преобразовывается, превращаясь в новую функцию . И вот эта самая новая функция и называется производной .

В нашем случае, до дифференцирования была функция f(x) = x 2 , а после дифференцирования стала уже другая функция f’(x) = 2x .

Производная – потому, что наша новая функция f’(x) = 2x произошла от функции f(x) = x 2 . В результате операции дифференцирования. И причём именно от неё, а не от какой-то другой функции (x 3 , например).

Грубо говоря, f(x) = x 2 – это мама, а f’(x) = 2x – её любимая дочка.) Это понятно. Идём дальше.

Математики – народ неугомонный. На каждое своё действие стремятся найти противодействие. 🙂 Есть сложение – есть и вычитание. Есть умножение – есть и деление. Возведение в степень – извлечение корня. Синус – арксинус. Точно также есть дифференцирование – значит, есть и… интегрирование . )

А теперь поставим такую интересную задачу. Есть у нас, допустим, такая простенькая функция f(x) = 1 . И нам надо ответить на такой вопрос:

Производная КАКОЙ функции даёт нам функцию f (x ) = 1?

Иными словами, видя дочку, с помощью анализа ДНК, вычислить, кто же её мамаша. 🙂 Так от какой же исходной функции (назовём её F(x)) произошла наша производная функция f(x) = 1? Или, в математической форме, для какой функции F(x) выполняется равенство:

F’(x) = f(x) = 1?

Пример элементарный. Я старался.) Просто подбираем функцию F(x) так, чтобы равенство сработало. 🙂 Ну как, подобрали? Да, конечно! F(x) = x. Потому, что:

F’(x) = x’ = 1 = f(x) .

Разумеется, найденную мамочку F(x) = x надо как-то назвать, да.) Знакомьтесь!

Первообразной для функции f (x ) называется такая функция F (x ), производная которой равна f (x ), т.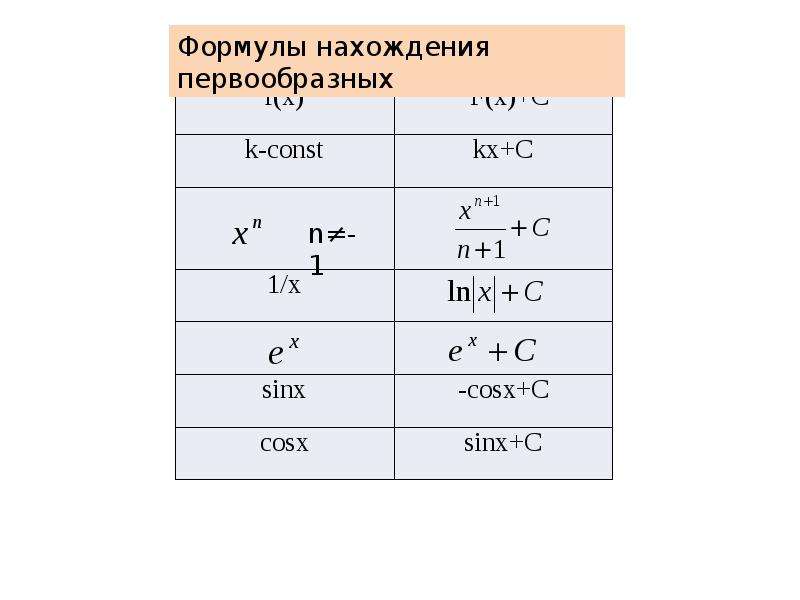 е. для которой справедливо равенство F ’(x ) = f (x ).

Вот и всё. Больше никаких научных хитростей. В строгом определении добавляется ещё дополнительная фраза «на промежутке Х» . Но мы пока в эти тонкости углубляться не будем, ибо наша первоочередная задача – научиться находить эти самые первообразные.

В нашем случае как раз и получается, что функция F(x) = x является первообразной для функции f(x) = 1.

Почему? Потому что F’(x) = f(x) = 1 . Производная икса есть единица. Возражений нет.)

Термин «первообразная» по-обывательски означает «родоначальница», «родитель», «предок». Сразу же вспоминаем самого родного и близкого человека.) А сам поиск первообразной – это восстановление исходной функции по известной её производной . Иными словами, это действие, обратное дифференцированию . И всё! Сам же этот увлекательный процесс тоже называется вполне научно – интегрирование . Но об интегралах – позже. Терпение, друзья!)

Запоминаем:

Интегрирование — это математическая операция над функцией (как и дифференцирование).

Интегрирование — операция, обратная дифференцированию.

Первообразная — результат интегрирования.

А теперь усложним задачу. Найдём теперь первообразную для функции f(x) = x . То есть, найдём такую функцию F(x) , чтобы её производная равнялась бы иксу:

F’(x) = x

Кто дружит с производными, тому, возможно, на ум придёт что-то типа:

(x 2)’ = 2x.

Что ж, респект и уважуха тем, кто помнит таблицу производных!) Верно. Но есть одна проблемка. Наша исходная функция f(x) = x , а (x 2)’ = 2 x . Два икс. А у нас после дифференцирования должен получиться просто икс . Не катит. Но…

Мы с вами народ учёный. Аттестаты получили.) И со школы знаем, что обе части любого равенства можно умножать и делить на одно и то же число (кроме нуля, разумеется)! Так уж устроены. Вот и реализуем эту возможность себе во благо.)

Мы ведь хотим, чтобы справа остался чистый икс, верно? А двойка мешает… Вот и берём соотношение для производной (x 2)’ = 2x и делим обе его части на эту самую двойку:

Так, уже кое-чего проясняется. Идём дальше. Мы знаем, что любую константу можно вынести за знак производной. Вот так:

Все формулы в математике работают как слева направо, так и наоборот – справа налево. Это значит, что, с тем же успехом, любую константу можно и внести под знак производной:

В нашем случае спрячем двойку в знаменателе (или, что то же самое, коэффициент 1/2) под знак производной:

А теперь внимательно присмотримся к нашей записи. Что мы видим? Мы видим равенство, гласящее, что производная от чего-то (это что-то — в скобочках) равняется иксу.

Полученное равенство как раз и означает, что искомой первообразной для функции f(x) = x служит функция F(x) = x 2 /2 . Та, что стоит в скобочках под штрихом. Прямо по смыслу первообразной.) Что ж, проверим результат. Найдём производную:

Отлично! Получена исходная функция f(x) = x . От чего плясали, к тому и вернулись. Это значит, что наша первообразная найдена верно.)

А если f(x) = x 2 ? Чему равна её первообразная? Не вопрос! Мы с вами знаем (опять же, из правил дифференцирования), что:

3x 2 = (x 3)’

И, стало быть,

Уловили? Теперь мы, незаметно для себя, научились считать первообразные для любой степенной функции f(x)=x n . В уме.) Берём исходный показатель n , увеличиваем его на единичку, а в качестве компенсации делим всю конструкцию на n+1 :

Полученная формулка, между прочим, справедлива не только для натурального показателя степени n , но и для любого другого – отрицательного, дробного. Это позволяет легко находить первообразные от простеньких дробей и корней.

Например:

Естественно, n ≠ -1 , иначе в знаменателе формулы получается ноль, и формула теряет смысл.) Про этот особый случай n = -1 чуть позже.)

Что такое неопределённый интеграл? Таблица интегралов.

Скажем, чему равна производная для функции F(x) = x? Ну, единица, единица – слышу недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже будет равна единице :

Также производная будет равна единице и для функции x+1234 , и для функции x-10 , и для любой другой функции вида x+C , где С – любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)

Получается неоднозначность. Выходит, что для функции f(x) = 1 первообразной служит не только функция F(x) = x , но и функция F 1 (x) = x+1234 и функция F 2 (x) = x-10 и так далее!

Да. Именно так.) У всякой (непрерывной на промежутке ) функции существует не какая-то одна первообразная, а бесконечно много — целое семейство! Не одна мама или папа, а целая родословная, ага.)

Но! Всех наших родственников-первообразных объединяет одно важное свойство. На то они и родственники.) Свойство настолько важное, что в процессе разбора приёмов интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё долго.)

Вот оно, это свойство:

Любые две первообразные F 1 (x ) и F 2 (x ) от одной и той же функции f (x ) отличаются на константу:

F 1 (x ) — F 2 (x ) = С.

Кому интересно доказательство – штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу. Благо доказательство тут элементарное, в одно действие. Берём равенство

F 1 (x ) — F 2 (x ) = С

и дифференцируем обе его части. То есть, просто тупо ставим штрихи:

Вот и всё. Как говорится, ЧТД. 🙂

О чём говорит это свойство? А о том, что две различные первообразные от одной и той же функции f(x) не могут отличаться на какое-то выражение с иксом . Только строго на константу! Иными словами, если у нас есть график какой-то одной из первообразных (пусть это будет F(x)), то графики всех остальных наших первообразных строятся параллельным переносом графика F(x) вдоль оси игреков.

Посмотрим, как это выглядит на примере функции f(x) = x . Все её первообразные, как нам уже известно, имеют общий вид F(x) = x 2 /2+C . На картинке это выглядит как бесконечное множество парабол , получаемых из «основной» параболы y = x 2 /2 сдвигом вдоль оси OY вверх или вниз в зависимости от значения константы С .

Помните школьное построение графика функции y=f(x)+a сдвигом графика y=f(x) на «а» единиц вдоль оси игреков?) Вот и тут то же самое. )

Причём, обратите внимание: наши параболы нигде не пересекаются! Оно и естественно. Ведь две различные функции y 1 (x) и y 2 (x) неизбежно будут соответствовать двум различным значениям константы – С 1 и С 2 .

Поэтому уравнение y 1 (x) = y 2 (x) никогда не имеет решений:

С 1 = С 2

x ∊ ∅ , так как С 1 ≠ С2

А теперь мы плавненько подходим ко второму краеугольному понятию интегрального исчисления. Как мы только что установили, у всякой функции f(x) существует бесконечное множество первообразных F(x) + C, отличающихся друг от друга на константу. Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!

Что такое неопределённый интеграл?

Множество всех первообразных для функции f (x ) называется неопределённым интегралом от функции f (x ).

Вот и всё определение. )

«Неопределённый» — потому, что множество всех первообразных для одной и той же функции бесконечно . Слишком много различных вариантов.)

«Интеграл» – с подробной расшифровкой этого зверского слова мы познакомимся в следующем большом разделе, посвящённом определённым интегралам . А пока, в грубой форме, будем считать интегралом нечто общее, единое, целое . А интегрированием – объединение, обобщение , в данном случае переход от частного (производной) к общему (первообразным). Вот, как-то так.

Обозначается неопределённый интеграл вот так:

Читается так же, как и пишется: интеграл эф от икс дэ икс . Или интеграл от эф от икс дэ икс. Ну, вы поняли.)

Теперь разберёмся с обозначениями.

∫ — значок интеграла. Смысл тот же, что и штрих для производной.)

d — значок дифференциала. Не пугаемся! Зачем он там нужен – чуть ниже.

f(x) — подынтегральная функция (через «ы»).

f(x)dx — подынтегральное выражение. Или, грубо говоря, «начинка» интеграла.

Согласно смыслу неопределённого интеграла,

Здесь F(x) – та самая первообразная для функции f(x) , которую мы так или иначе нашли сами. Как именно нашли — не суть. Например, мы установили, что F(x) = x 2 /2 для f(x)=x .

«С» — произвольная постоянная. Или, более научно, интегральная константа . Или константа интегрирования. Всё едино.)

А теперь вернёмся к нашим самым первым примерам на поиск первообразной. В терминах неопределённого интеграла можно теперь смело записать:

Что такое интегральная константа и зачем она нужна?

Вопрос очень интересный. И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.

В чём суть. Из исходного бесконечного множества первообразных (т.е. неопределённого интеграла ) надо выделить ту кривую, которая будет проходить через заданную точку. С какими-то конкретными координатами. Такое задание всегда и везде встречается при начальном знакомстве с интегралами. Как в школе, так и в ВУЗЕ.

Типичная задачка:

Среди множества всех первообразных функции f=x выделить ту, которая проходит через точку (2;2).

Начинаем думать головой… Множество всех первоообразных — это значит, сначала надо проинтегрировать нашу исходную функцию. То есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:

А теперь разбираемся, что именно мы получили. Мы получили не одну функцию, а целое семейство функций. Каких именно? Вида y=x 2 /2+C . Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь «отловить».) Ну что, займёмся ловлей?)

Удочка наша — семейство кривых (парабол) y=x 2 /2+C.

Константы — это рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)

А что же служит приманкой? Правильно! Наша точка (-2;2).

Вот и подставляем координаты нашей точки в общий вид первообразных! Получим:

y(2) = 2

Отсюда уже легко ищется C = 0 .

Что сиё означает? Это значит, что из всего бесконечного множества парабол вида y=x 2 /2+C только парабола с константой С=0 нам подходит! А именно: y=x 2 /2. И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А в се остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?

Для наглядности вот вам две картинки — всё семейство парабол (т.е. неопределённый интеграл) и какая-то конкретная парабола , соответствующая конкретному значению константы и проходящая через конкретную точку:

Видите, насколько важно учитывать константу С при интегрировании! Так что не пренебрегаем этой буковкой «С» и не забываем приписывать к окончательному ответу.

А теперь разберёмся, зачем же внутри интегралов везде тусуется символ dx . Забывают про него студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё дело в том, что интегрирование – операция, обратная дифференцированию. А что именно является результатом дифференцирования ? Производная? Верно, но не совсем. Дифференциал!

В нашем случае, для функции f(x) дифференциал её первообразной F(x) , будет:

Кому непонятна данная цепочка – срочно повторить определение и смысл дифференциала и то, как именно он раскрывается! Иначе в интегралах будете тормозить нещадно….

Напомню, в самой грубой обывательской форме, что дифференциал любой функции f(x) — это просто произведение f’(x)dx . И всё! Взять производную и помножить её на дифференциал аргумента (т.е. dx). То есть, любой дифференциал, по сути, сводится к вычислению обычной производной .

Поэтому, строго говоря, интеграл «берётся» не от функции f(x) , как принято считать, а от дифференциала f(x)dx! Но, в упрощённом варианте, принято говорить, что «интеграл берётся от функции» . Или: «Интегрируется функция f (x) «. Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! 🙂

И сейчас я подскажу, как его не забыть при записи. Представьте себе сначала, что вы вычисляете обычную производную по переменной икс. Как вы обычно её пишете?

Вот так: f’(x), y’(x), у’ x . Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам показывают, что производная берётся именно по иксу. А не по «игреку», «тэ» или какой-то там другой переменной.)

Так же и в интегралах. Запись ∫ f(x)dx нам тоже как бы показывает, что интегрирование проводится именно по переменной икс . Конечно, это всё очень упрощённо и грубо, но зато понятно, я надеюсь. И шансы забыть приписать вездесущее dx резко снижаются.)

Итак, что такое же неопределённый интеграл – разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые неопределённые интегралы вычислять . Или, попросту говоря, «брать». 🙂 И вот тут студентов поджидает две новости – хорошая и не очень. Пока начнём с хорошей.)

Новость хорошая. Для интегралов, так же как и для производных, существует своя табличка. И все интегралы, которые нам будут встречаться по пути, даже самые страшные и навороченные, мы по определённым правилам будем так или иначе сводить к этим самым табличным.)

Итак, вот она, таблица интегралов!

Вот такая вот красивая табличка интегралов от самых-самых популярных функций. Рекомендую обратить отдельное внимание на группу формул 1-2 (константа и степенная функция). Это – самые употребительные формулы в интегралах!

Третья группа формул (тригонометрия), как можно догадаться, получена простым обращением соответствующих формул для производных.

Например:

C четвёртой группой формул (показательная функция) – всё аналогично.

А вот четыре последние группы формул (5-8) для нас новые. Откуда же они взялись и за какие такие заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?

Так уж сложилось исторически в процессе развития методов интегрирования . Когда мы будем тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что интегралы от перечисленных в таблице функций встречаются очень и очень часто. Настолько часто, что математики отнесли их к табличным.) Через них выражаются очень многие другие интегралы, от более сложных конструкций.

Ради интереса можно взять какую-нибудь из этих жутких формул и продифференцировать. 🙂 Например, самую зверскую 7-ю формулу.

Всё нормально. Не обманули математики. 🙂

Таблицу интегралов, как и таблицу производных, желательно знать наизусть. Во всяком случае, первые четыре группы формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть последние четыре группы (с дробями и корнями) пока не стоит. Всё равно поначалу будете путаться, где логарифм писать, где арктангенс, где арксинус, где 1/а, где 1/2а … Выход тут один — решать побольше примеров. Тогда таблица сама собой постепенно и запомнится, а сомнения грызть перестанут.)

Особо любознательные лица, присмотревшись к таблице, могут спросить: а где же в таблице интегралы от других элементарных «школьных» функций – тангенса, логарифма, «арков»? Скажем, почему в таблице ЕСТЬ интеграл от синуса, но при этом НЕТУ, скажем, интеграла от тангенса tg x ? Или нету интеграла от логарифма ln x ? От арксинуса arcsin x ? Чем они хуже? Но зато полно каких-то «левых» функций — с корнями, дробями, квадратами…

Ответ. Ничем не хуже.) Просто вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не являются табличными . И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть , чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются .)

Что, кому-то всё-таки невтерпёж? Так уж и быть, специально для вас!

Ну как, будете заучивать? 🙂 Не будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно найдём. В соответствующих уроках. 🙂

Что ж, теперь переходим к свойствам неопределённого интеграла. Да-да, ничего не поделать! Вводится новое понятие – тут же и какие-то его свойства рассматриваются.

Свойства неопределённого интеграла.

Теперь не очень хорошая новость.

В отличие от дифференцирования, общих стандартных правил интегрирования , справедливых на все случаи жизни , в математике нету. Это фантастика!

Например, вы все прекрасно знаете (надеюсь!), что любое произведение любых двух функций f(x)·g(x) дифференцируется вот так:

(f(x)·g(x))’ = f’(x)·g(x) + f(x)·g’(x) .

Любое частное дифференцируется вот так:

А любая сложная функция, какой бы накрученной она ни была, дифференцируется вот так:

И какие бы функции ни скрывались под буквами f и g, общие правила всё равно сработают и производная, так или иначе, будет найдена.

А вот с интегралами такой номер уже не пройдёт: для произведения, частного (дроби), а также сложной функции общих формул интегрирования не существует! Нету никаких стандартных правил! Вернее, они есть. Это я зря математику обидел.) Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А во-вторых, большинство методов интегрирования, о которых мы будем разговаривать в следующих уроках, очень и очень специфические. И справедливы лишь для определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных функций . Или каких-то ещё.

А какие-то интегралы, хоть и существуют в природе, но вообще никак не выражаются через элементарные «школьные» функции! Да-да, и таких интегралов полно! 🙂

Именно поэтому интегрирование – гораздо более трудоёмкое и кропотливое занятие, чем дифференцирование. Но в этом есть и своя изюминка. Занятие это творческое и очень увлекательное.) И, если вы хорошо усвоите таблицу интегралов и освоите хотя бы два базовых приёма, о которых мы поговорим далее ( и ), то интегрирование вам очень понравится. 🙂

А теперь познакомимся, собственно, со свойствами неопределённого интеграла. Их всего ничего. Вот они.

Первые два свойства полностью аналогичны таким же свойствам для производных и называются свойствами линейности неопределённого интеграла . Тут всё просто и логично: интеграл от суммы/разности равен сумме/разности интегралов, а постоянный множитель можно вынести за знак интеграла.

А вот следующие три свойства для нас принципиально новые. Разберём их поподробнее. Звучат по-русски они следующим образом.

Третье свойство

Производная от интеграла равна подынтегральной функции

Всё просто, как в сказке. Если проинтегрировать функцию, а потом обратно найти производную от результата, то… получится исходная подынтегральная функция. 🙂 Этим свойством всегда можно (и нужно) пользоваться для проверки окончательного результата интегрирования. Вычислили интеграл — продифференцируйте ответ! Получили подынтегральную функцию – ОК. Не получили – значит, где-то накосячили. Ищите ошибку.)

Конечно же, в ответе могут получаться настолько зверские и громоздкие функции, что и обратно дифференцировать их неохота, да. Но лучше, по возможности, стараться себя проверять. Хотя бы в тех примерах, где это несложно.)

Четвёртое свойство

Дифференциал от интеграла равен подынтегральному выражению .

Тут ничего особенного. Суть та же самая, только dx на конце появляется. Согласно предыдущему свойству и правилам раскрытия дифференциала.

Пятое свойство

Интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной .

Тоже очень простое свойство. Им мы тоже будем регулярно пользоваться в процессе решения интегралов. Особенно – в и .

Вот такие вот полезные свойства. Занудствовать с их строгими доказательствами я здесь не собираюсь. Желающим предлагаю это сделать самостоятельно. Прямо по смыслу производной и дифференциала. Докажу лишь последнее, пятое свойство, ибо оно менее очевидно.

Итак, у нас есть утверждение:

Вытаскиваем «начинку» нашего интеграла и раскрываем, согласно определению дифференциала:

На всякий случай, напоминаю, что, согласно нашим обозначениям производной и первообразной, F ’(x ) = f (x ) .

Вставляем теперь наш результат обратно внутрь интеграла:

Получено в точности определение неопределённого интеграла (да простит меня русский язык)! 🙂

Вот и всё.)

Что ж. На этом наше начальное знакомство с таинственным миром интегралов считаю состоявшимся. На сегодня предлагаю закруглиться. Мы уже достаточно вооружены, чтобы идти в разведку. Если не пулемётом, то хотя бы водяным пистолетом базовыми свойствами и таблицей. 🙂 В следующем уроке нас уже ждут простейшие безобидные примеры интегралов на прямое применение таблицы и выписанных свойств.

До встречи!

Первообразная. Геометрический смысл первообразной — презентация онлайн

1. Первообразная. Геометрический смысл первообразной

1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ
ФУНКЦИИ
3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ
ПЕРВООБРАЗНЫХ
4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ

2. 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ

Под дифференцированием функции f (х) мы
понимаем нахождение ее производной f ′(х).
Нахождение функции f (х) по заданной ее
производной f ′(х) называют операцией
интегрирования.
Таким образом, операция интегрирования
обратна операции дифференцирования.
Следовательно, операция интегрирования
состоит в том, что по заданной производной
f ′(х) находят (восстанавливают) функцию f (х).
Например, пусть f ′(х) = 4х3.
Следует найти f (х). Опираясь на правило
дифференцирования, нетрудно увидеть, что
f (х)=х4.
Действительно, (х4)’ = 4×3.
f (х) находится неоднозначно, ведь в качестве f (х)
могут быть использованы и такие функции, как
f (х) = х4 + 3,
f (х)= х4 — 6,
и др., так как производная каждой из данных
функций равна 4х3. Все эти функции отличаются
друг от друга только постоянным слагаемым.
Общее решение задачи можно записать в виде
f (х)= х4 +С,
где С — произвольное действительное число.
Любую из найденных функций f (х) называют
первообразной для функции f ‘(х) = 4х3.
Определение. Функция F называется
первообразной для функции f на заданном
промежутке, если для всех х из этого промежутка,
если F ′(х)=f(x).
Например, функция F(x)=x2 есть первообразная
для функции f(x)=2x на промежутке (-∞,+∞), так
как для всех действительных х справедливо
равенство F ′(х)=(х2)′=2х
Множество всех первообразных для функции f(x)
можно представить в виде F(x)+С, где С – любое
действительное число.

6. Упражнение с решением

Доказать, что функция F (х) есть первообразная
для функции f (х) на заданном промежутке, если
F (х)=3х4, f (х)=12х3, (-∞,+∞).
Решение. Так как F (x) = 3х4, то
F ′(х)= (3х4)’= 12х3 = f(x) для всех х,
что и требовалось доказать.

7. 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ

Теорема. Если функция F есть первообразная для
функции f на промежутке X, то при любой
постоянной С функция F(x)+С также является
первообразной для функции f на промежутке X.
Любая первообразная функции f на промежутке X
может быть записана в виде F (х) + С.
Какую бы постоянную в этой формуле ни подставить
вместо С, получится первообразная для функции f .
Выражение F(x)+С называют общим видом
первообразных для функции f.
Геометрически основное свойство первообразных
можно интерпретировать так: графики всех
первообразных данной функции f (х) получаются из
любого из них путем параллельного переноса вдоль
оси Оу

9. Таблица первообразных для некоторых функций:

11. Упражнения с решениями

12. 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ

1. Если F есть первообразная для f ,
a G — первообразная для g,
то F+G есть первообразная для f+g,
т. е.
(F + G)’ = f + g.
2. Если F есть первообразная для f,
a k — постоянная,
то kF есть первообразная для kf,
т. е. (kF)’ = kf.

16. Например y=sin(3x-4)

17. 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ

Криволинейной трапецией называется фигура,
ограниченная графиком неотрицательной и
непрерывной на отрезке [a; b] функции f, осью
Ох и прямыми х = а и х = b.
Теорема. Пусть f – непрерывная и
неотрицательная на отрезке [a; b] функция,
а
S
–
площадь
соответствующей
криволинейной трапеции . Если F есть
первообразная для f па интервале,
содержащем отрезок [a; b] , то
S = F(b)— F (а).

19. упражнения с решениями

Вычислить площадь фигуры, ограниченной линиями:
у = 2х — х2 и у = 0.
Решение. Для функции у = 2х — х2
первообразная есть F(x) = x2 –1/3 х3.
Найдем точки пересечения кривой 2х — х2 с
осью абсцисс: 2х — х2 = 0, х = 0, х = 2,
т. е. (0; 0) и (2; 0).
Значит, а = 0, b = 2.
Искомую площадь находим по формуле:
S = F(b)-F(a)=
=F (2)-F(0) = 4 – 8/3 – 0 + 0=4/3

Зачетная работа по теме «Первообразная функции, интеграл»

Зачетная работа по теме «Первообразная. Интеграл»

Вариант 1

1. Найдите первообразную следующих функций:

а) f(x) = 3x – 1; б) f(x) = x⁵ + cos x; в) f(x) = x⁴ + 5.

2. Найдите первообразную функции f(x) = 3x² + 2x – 1, проходящую через точку А(-1;10).

3. Вычислите интеграл:

а) ; б) ;

в) ; г).

4. Найдите площадь изображенной фигуры по формуле Ньютона-Лейбница:

5. Вычислите площадь фигуры, ограниченной линиями (предварительно построив её):

а) у = 4х – х² и осью Ох;

б) у = х² + 2 и у = х + 4.

Вариант 2

1. Найдите первообразную следующих функций:

а) f(x) = 2 — x; б) f(x) = x⁴ — sin x; в) f(x) = x⁵ — 7.

2. Найдите первообразную функции f(x) = 4x³ — 3x² – 1, проходящую через точку А(2;-8).

3. Вычислите интеграл:

а) ; б) ;

в) ; г).

4. Найдите площадь изображенной фигуры по формуле Ньютона-Лейбница:

5.Вычислите площадь фигуры, ограниченной линиями (предварительно построив её):

а) у = 6х – х² и осью Ох;

б) у = х², у = 4 и осью Оу.

Вариант 3

1. Найдите первообразную следующих функций:

а) f(x) = 8x – 3; б) f(x) = x⁶ — 2cos x; в) f(x) = x² + 1.

2. Найдите первообразную функции f(x) = 6x² — 2x + 5, проходящую через точку А(-2;-20).

3. Вычислите интеграл:

а) ; б) ;

в) ; г).

4. Найдите площадь изображенной фигуры по формуле Ньютона-Лейбница:

5. Вычислите площадь фигуры, ограниченной линиями (предварительно построив её):

а) у = 1 – х² и осью Ох;

б) у = 4 + 3x — х² и у = х + 1.

Вариант 4

1. Найдите первообразную следующих функций:

а) f(x) = 4x + 4; б) f(x) = x⁵ — ; в) f(x) = x⁶ — 8.

2. Найдите первообразную функции f(x) = 5x⁴ — 6x² + 1, проходящую через точку А(-1;2).

3. Вычислите интеграл:

а) ; б) ;

в) ; г) .

4. Найдите площадь изображенной фигуры по формуле Ньютона-Лейбница:

5.Вычислите площадь фигуры, ограниченной линиями (предварительно построив её):

а) у = – х² + 3x и осью Ох;

б) у = 2х² и у = 8.

Время выполнения 60 минут

Зачетная работа по теме «Первообразная. Интеграл»

Вариант 5

1. Найдите первообразную следующих функций:

а) f(x) = 2x – 5; б) f(x) = x⁷ – 2sin x; в) f(x) = x³ + 2.

2. Найдите первообразную функции f(x) = 6x² — 4x + 1, проходящую через точку А(1;5).

3. Вычислите интеграл:

а) ; б) ;

в) ; г).

4. Найдите площадь изображенной фигуры по формуле Ньютона-Лейбница:

5.Вычислите площадь фигуры, ограниченной линиями (предварительно построив её):

а) у = 2х – х² и осью Ох;

б) у = — х² + 4 и у = 2 — х.

Вариант 6

1. Найдите первообразную следующих функций:

а) f(x) = 7x — 2; б) f(x) = + 5x⁴; в) f(x) = x³ — 9.

2. Найдите первообразную функции f(x) = 7x⁶ + 4x – 8, проходящую через точку А(2;4).

3. Вычислите интеграл:

а) ; б) ;

в) ; г).

4. Найдите площадь изображенной фигуры по формуле Ньютона-Лейбница:

5.Вычислите площадь фигуры, ограниченной линиями (предварительно построив её):

а) у = – х² – 2x и осью Ох;

б) у = 6x — х² и у = 5.

Вариант 7

1. Найдите первообразную следующих функций:

а) f(x) = 2x² + 3х; б) f(x) = x³ – 3sin x; в) f(x) = x³ + 4.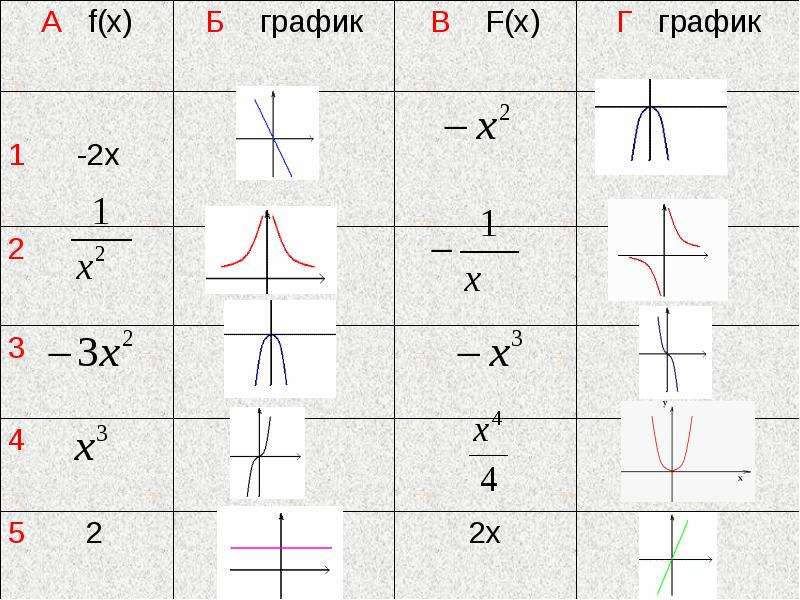

2. Найдите первообразную функции f(x) = 4x — 3x² + 1, проходящую через точку А(2;9).

3. Вычислите интеграл:

а) ; б) ;

в) ; г).

4. Найдите площадь изображенной фигуры по формуле Ньютона-Лейбница:

5.Вычислите площадь фигуры, ограниченной линиями (предварительно построив её):

а) у = – 2х² + 8 и осью Ох;

б) у = 3х² + 1 и у = —х + 3.

Вариант 8

1. Найдите первообразную следующих функций:

а) f(x) = 3x² — 4; б) f(x) = + 6x; в) f(x) = x² – 7x.

2. Найдите первообразную функции f(x) = 4x — x² + 2, проходящую через точку А(1;9).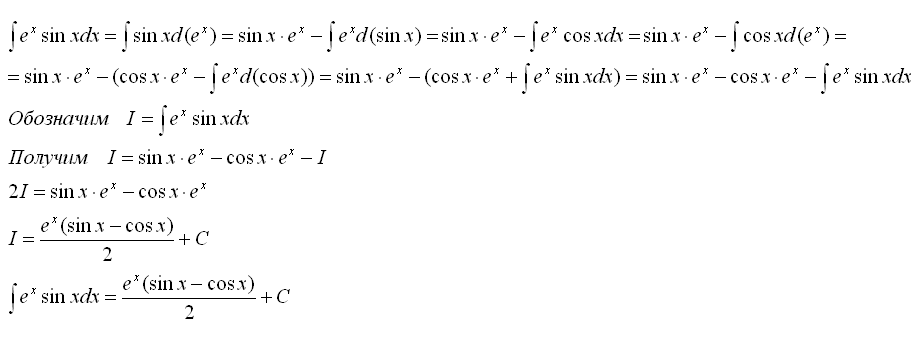 2

Неопределенный интеграл (первообразная): определение, примеры

Содержимое:

См. также:
Интегрирование по частям
Чистое изменение Теорема

Неопределенные интегралы (также называемые первообразными ) не имеют пределов/границ интегрирования, в то время как определенные интегралы до имеют границы.

Когда вы находите неопределенный интеграл, вы всегда добавляете к решению «+ C» (называется постоянной интегрирования ). Это потому, что у вас может быть множество решений , каждое из которых является набором всех вертикальных преобразований первообразной.

Например, первообразная 2x равна x ² + C, где C — константа. Производная константы равна нулю, поэтому C может быть любой константой, положительной или отрицательной. Четыре первообразные 2х: х ² + 1, х ² -1, х ² + 2 или х ² — 2.

Раствор с постоянной интегрирования (+С).

Иными словами, неопределенный интеграл не имеет пределов, поэтому вы находите наборов интегралов (а не только один конкретный). «+ C» указывает на то, что решение действительно имеет бесконечные возможности.

Если это звучит странно, вы на самом деле использовали подобную технику в алгебре, когда вы вводили k вместо константы (например, f(x) = k * sin(x)): вы допускаете читатель знает, что существует множество возможных значений.

Другой способ взглянуть на это: «C» означает неопределенность в вашем решении.

Почему константа интегрирования необходима для неопределенного интеграла?

Чтобы ответить на этот вопрос, давайте рассмотрим базовую функцию:

f(x) = 3x ²

Предположим, что это ответ на задачу интегрирования. Интегрирование — это процесс, обратный дифференцированию (поэтому неопределенные интегралы также называют первообразными), поэтому вы пытаетесь найти функцию F(x), первая производная которой равна 3x ² :

F ^′ (х) = 3x ²

Какая функция имеет первую производную от 3x ² ? Одним из решений является x ³ .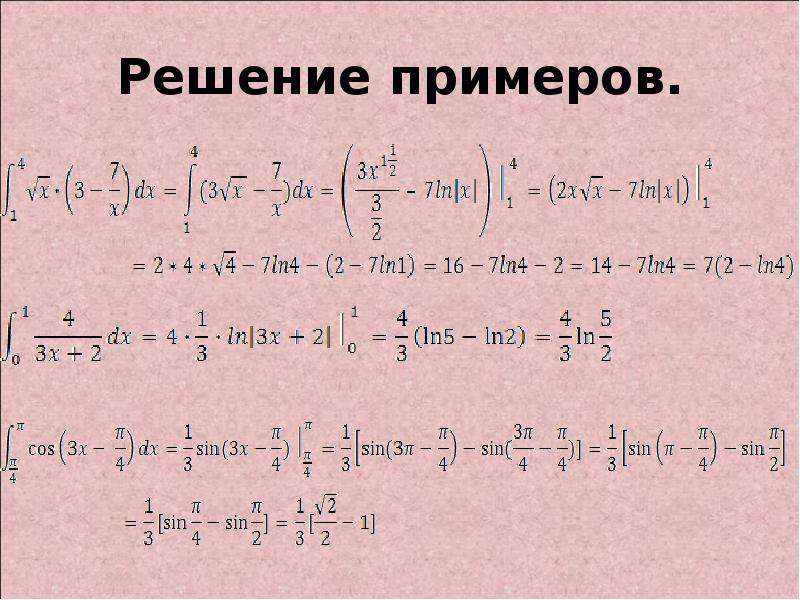 Используя правило дифференцирования показателей степени, получаем

Но это не единственное решение. Добавление константы к решению никак не меняет его, потому что производная константы равна нулю. Другими словами, у вас может быть бесконечное количество решений, например:

.

• 3x ² + 9
• 3x ² + 0,09
• 3x ² + π
• 3x ² + 3/2
• 3x ² – 8629862394629834
• 3x ² – 9

Поскольку невозможно выписать все бесконечные решения, мы просто вставляем константу интегрирования в качестве заполнителя и скажем 3x ² + C.

Теорема о постоянной разности

Приведенный выше пример показал, что множественные производные одной и той же функции отличаются только одной константой C, которая может равняться нулю. Теорема о постоянной разности использует этот факт, а также разность двух функций:

Если f и g дифференцируемы на интервале и если f ^′ (x) = g′(x) для всех x в этом интервале, то f – g постоянна на интервале; то есть существует константа k такая, что f(x) – g(x) = k или, что то же самое,
f(x) = g(x) + k
для всех x в интервале. (Антон и др., 2012).

Неопределенные интегральные правила

Неопределенные интегралы могут существовать, а могут и не существовать, но когда они существуют, есть несколько общих правил, которым можно следовать, чтобы упростить процедуру интегрирования.

∫m dx = mx + c для любого числа m.
∫x ⁿ dx = ¹ ⁄ _{n + 1} x ^{x + 1} + c, если n ≠ –1.
∫ ¹ ⁄ _x dx = ln |x| + c, для x ≠ 0,
∫sin x dx = −cos x + c
∫cos x dx = sin x + c
∫e ^x dx = e ^x + c

Интеграл суммы двух функций равен сумме их отдельных интегралов:

Сложение : ∫[f(x) + g(x)]dx = ∫f(x)dx + ∫g(x)dx
Вычитание : ∫[f(x) − g(x)]dx = ∫f(x)dx − ∫g(x)dx

Однако обратите внимание, что это правило не говорит вам, как находить отдельные интегралы.Для этого вам придется обратиться к правилам, специфичным для функций (таким как интегральное правило или тригонометрические правила).

Пример задачи: Найти ∫ cos x + x dx

1. Разделите интегралы: ∫cos x + x dx = ∫cos x dx + ∫x dx
2. Найдите индивидуальные решения:
3. ∫cos x = sin x
4. ∫x = = sin x + x ² /2 + C (см.: правило интегрирования степенной функции )

Решение = sin x + x ² /2 + C

См.: Правило суммы: определение и примеры для нескольких пошаговых примеров.

Любой постоянный коэффициент может быть перемещен за пределы символа интегрирования:

∫ax ndx = a∫xn dx для любой константы «a».

Аналогично,
∫[af(u) + bg(u)]du = a = ∫ f(u) du + b ∫g(u) du

Если F′(x) = f(x), то для любого m ≠ 0,
∫f(mx + b)dx = ¹ ⁄ _m F(mx + b) + c

∫ cos x dx = sin x + C
∫ sin x = -cos x + C
∫ sec ² x dx
∫ csc ² x dx = -cot x + C
∫ sec x tan x 1 dx 909 ∫ csc x стоимость x dx

Наверх

Неопределенные интегралы от степенных функций

Следующее общее правило для интегрирования степенных функций вида
f(x) = x ⁿ (n ≠- 1):


к степени, разделите на эту степень, а затем добавьте «C» для константы.

Примеры задач:
Пример задачи №1: Найдите первообразную (неопределенный интеграл) для 20x ³

Шаг 1: Увеличение мощности на 1 :
20x ³ = 20x ⁴

Шаг 2: Разделите на новую степень , полученную на шаге 1:
20x ⁴ = ²⁰ ⁄ ₄ x ⁴ = 5x ⁴⁹

Шаг 3: Добавить «C» :
5x ⁴ + C

Пример задачи №2: Найдите первообразную (неопределенный интеграл) для 3x ⁸


Шаг 1: Увеличение мощности на 1 :
3x ⁸ = 3x ⁹

Шаг 2: Разделите на новую степень , которую вы вычислили на шаге 1:
³ ⁄ ₉ x ⁹ = ¹ ⁄ _{3 9 9 9 ^x}

Шаг 3: Добавить «C» :
¹ ⁄ ₃ x ⁹ + C

Пример задачи №3: Найдите первообразную (неопределенный интеграл) для x ⁴ + 6

Шаг 1: Увеличьте степень x на 1 (обратите внимание, что вы добавляете x ⁰ к константе сам по себе — в этом случае 6 становится 6x ⁰ ).
x ⁴ + 6x ⁰ = x ⁵ + 6x ¹

Шаг 2: Divide по новым силам Вы рассчитали на шаге 1:
^{x 5} / ₅ + ^{6x 1} / ₁ = ^{1 x 5 + 6x 1}

Шаг 3: Добавить «C» :
¹ ⁄ ₅ x ⁵ + 6x ¹ + C

Вот и все!

Совет: Прибавляя 1 к своей степени, помните, что x становится x ¹ , а константа становится этой константой плюс x ⁰ .Например, 6x ¹⁰ + 17x + 9 становится 6x ¹⁰ + 17x ¹ + 9x ⁰ до Вы добавляете питание и 6x ¹¹ + 17x ² + 9x ¹ вы добавляете единицу.
Вернуться к началу

Другие ссылки

Антон Х. и др. (2012). Расчет с одной переменной. Уайли.
Райли, К. и др. (2006). Математические методы в физике и технике. Всеобъемлющее руководство. Cambridge University Press
Справочник по математическим формулам и интегралам

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Какова первообразная от e к 2x?

Чему равна первообразная от e к 2x?

2 ответа. Это 12e2x . Вы, конечно, можете использовать технику интегрирования подстановкой (обращение цепного правила), чтобы найти это, вы также можете рассуждать следующим образом: первообразная e2x — это функция, производная которой равна e2x .

Как интегрировать e 2x?

Ответ: Интеграция e2x равна [(e2x)/2] + c , при использовании метода подстановки для интеграции.

Что такое первообразная E X?

∫exdx=ex+C . Я надеюсь, что это было полезно.

Каково значение E Power 0?

1 Ответ: Значение e в степени 0 равно 1 .

Есть ли у E X первообразная производная?

, то F(x)=ex является первопроизводной ex. Следовательно, каждая первообразная от ex имеет вид ex+C для некоторой константы C, и каждая функция вида ex+C является первообразной от ex.

Существует ли первообразная E−X2 в элементарном интегрировании?

Это в значительной степени говорит о том, что первообразная e-x2 является первообразной e-x2, и это лучшее, что вы можете сделать.— Жюльен,

Может ли функция допускать первообразную, выразимую в этой форме?

Некоторые (фактически многие) функции не допускают первообразной, выражаемой в таком виде; это случай e−x2, и это можно доказать, хотя и нелегко.

Является ли интеграл, который вам нужен, первообразной?

Интеграл, который вам нужен, не имеет хорошей первообразной с точки зрения знакомых функций.Однако это важная первообразная, поэтому математики дали ей имя. Как сказал vadium123, это невозможно представить в знакомой функции.

Что является первообразной гамма-функции?

Она также может быть определена в терминах гамма-функции и неполной гамма-функции как erf(x) = 2(Γ(1 2)− Γ(1 2,x2)) √π. x) = e± xn обладает первообразной, выражение которой можно разобрать в терминах комбинаций «нормальных» функций, если только значение n не равно 0 или 1.{2}}(x)\]
\[\Стрелка вправо \dfrac{d}{dx}\left( \sin x \right)=\cos x\]
\[\Стрелка вправо \dfrac{d}{dx} \left( \cos x \right)=-\sin x\]
Учащиеся должны знать понятие первообразной. Студенты должны быть очень внимательны при выполнении расчетов.

Интеграл 2xdx. Ознакомьтесь с образцом вопросов и ответов здесь. Площадь круга? Проще простого). Вопрос. Что нам нужно сделать, так это сложить формулы для производных функций секанса и тангенса. 9ˇ 4 7.Интеграл от cos 2x обозначается как ∫ cos 2x dx, и его значение равно (sin 2x)/2 + C, где «C» — постоянная интегрирования. интегрировать 2x dx от x=10 до x=13 — Wolfram|Alpha. ∫ ∞ 2 cos2x x2 dx ∫ 2 ∞ cos 2 x x 2 d x. Оцените интеграл: ∫xe−2xdx. P(x) обычно представляет собой полиномиальную функцию, а T(x) представляет собой трансцендентную функцию, такую ​​как … Отвечено 2021-12-08 Автор имеет 9720 ответов. Шаг 1. есть. К сожалению, нахождение первообразных даже для относительно простых функций невозможно, тогда du = 2xdx можно записать как 1 2 du = xdx.р. Хотите увидеть пошаговый ответ? См. Ответ. Сначала находим уравнение прямой. 19) xe xdx xex exdx xex ex C Пример 7. Шаг 3. Поскольку в исходном интеграле ровно 2xdx, его можно заменить на du: Z 2xcos(x2)dx = Z cosudu = sinu+C = sin(x2) + C. Плоские векторные поля 4A-1 а) Все векторы в поле идентичны; непрерывно дифференцируема всюду. 2(x)$ Якуба Мариана.Антипроизводные — Комментарии отключены. 2x — 0. Это избавит студентов от сомнений по любому вопросу и улучшит навыки применения при подготовке к экзаменам на доске. Некоторые несколько сложны. В верхней части интервала установите x равным 13, вычислите x в квадрате (13 x 13), а затем вычтите из него 100. Z 1 1 xe x dx сходится (интегрировать по частям) 6. R 3 1 Вычислить неопределенный интеграл, выразив первообразную через исходную переменную, а затем применить основную теорему. Попробуйте u = x2 + 1, тогда du = 2xdx и dx = du/(2 Неопределенный интеграл.{ 2 } — 4 x — 5 = 0. Скорость самолета 600 миль в час. Имеем Z xex2 dx= 1 2 Z ex2 |{z} eu 2|xdx{z} du = 1 2 Z eu du = 1 2 e u + C = 1 2 e x2 + C: интеграл, который никто не может вычислить. 2 х. Решение: Мы знаем, что производная от th(x) равна sech3(x), поэтому интеграл от sech3(x) равен th(x)+c. Следуйте этому ответу, чтобы получать уведомления. неопределенный интеграл; класс-12; Поделитесь этим на Facebook Twitter Электронная почта. 2(x)) Идентичные выражения; sinh(x)cosh3xdx; гиперболический синус e of (x) гиперболический косинус e of ine of 2xdx; гиперболический синус e of (x) гиперболический косинус e of ine of 2xdx В этом уроке мы найдем интеграл функции x Cos2x.2 (15) Верно или неверно, и объясните. Неопределенный интеграл не уникален, потому что производная от x 2 + c при любом значении константы c также будет равна 2x. Второй интеграл можно переписать как разность площадей двух треугольников. Значение 2xdx = 8:000 Использование фундаментальной теоремы для нахождения определенных интегралов. Чтобы избежать полюса при x = 0, опустите путь интегрирования немного ниже реальной линии (у этой функции нет полюсов, и она обращается в нуль на бесконечности, так что это нормально). = х 8 — 1 8 × sin4x 4 +с.(2x) от 0 до \infty. Ввиду (косо)симметрии f интеграл почти такой же, B(y) = » y 2u + y3 2u2 # u=4+y2 u=y2 = y 2(4 + y2) + y3 2 (4 + y2)2 = 2y (4 + y2)2 Эта формула также остается в силе для y = 0, так как f обращается в нуль на оси X. Я работаю над интегралом, который я нахожу сложным, и я думаю, что я что-то упущено. Это представлено путем раздачи в лучшем поле. Найдите интеграл от ln (3x-2) dx u = ln (3x-2) u’ = 3/(3x-2) v = xv’ = 1 dx интеграл of ln(3x-2)dx = ln(3x-2)x — интеграл от [3/(3x-2)][x]dx Добро пожаловать в Sarthaks eConnect: уникальная платформа, на которой учащиеся могут взаимодействовать с учителями/экспертами/учащимися чтобы получить ответы на свои вопросы.2{x}$ функция. 5k баллов) неопределенный интеграл Поверхностный интеграл в прямоугольной призме: шесть граней призмы представляют собой замкнутую поверхность в пространстве. ∫ a a f ( x) d x = 0. Этот интеграл следует тому же подходу, что и интеграл от ln(x), и, следовательно, метод, который мы используем, находится в 1−3cos2x+3cos2 2x− cos3 2xdx. Шаг 2. Если вы собираетесь решить эти задачи, прежде чем искать решения, вы можете Предположим, теперь мы хотим найти интеграл Z 2x √ 1+x2 dx (3) В этом примере мы делаем замену u = 1+x2, для того, чтобы упростить член квадратного корня. x sin 5. ∫ 4 1 2x +3dx ∫ 1 4 2 x + 3 d x. Это дает Z cos2xsin3xdx= Z cos2xsin2xsinxdx = Z cos2x(1 − cos2x)sinxdx. Это выражается символами как − ∫ 2xdx = x2 + c. none Производные Применения производных Ограничения Интегралы Применения интегралов Интегральные аппроксимации Ряды ОДУ Многомерное исчисление Преобразование Лапласа Ряды Тейлора/Маклорена Ряды Фурье. Объяснение: Так как sin2x = 2sinxcosx. Интегрируйте 2xdx. В этом уроке мы выведем интеграл от квадрата синуса x. Так получается формула интегрирования по частям.2хдх. положим u = — x, тогда найдем du = — dx, подставим du= — dx, u= — x = (1/2) ex + (1/2) — ex dx = (1/2) ex + (1/2 ) эу дю . P (x) обычно представляет собой полиномиальную функцию, а T (x) — трансцендентную функцию, такую ​​как \sin (x), \cos (x). Нажмите здесь 👆, чтобы получить ответ на свой вопрос ️ интегральное значение 2xdx /(x+1 )(x-1)) Один из способов найти интеграл от xex — использовать правило произведения, а затем интегрировать. ##f## определяется как полуопределенный интеграл минус ##x##. 4. Замечание. Если f(x) — любая функция, а f′(x) — ее производные.2) dx от 0 до бесконечности. Умножение на 1 в Advanced Math Solutions — Integral Calculator, основы Интеграция — это обратная сторона дифференцирования. Решение: Делаем замену: u = 2 + 3sinh x, du = 3cosh x dx. В исчислении интегрирование по частям или частичное интегрирование — это метод, который в основном используется для нахождения интегрирования произведения двух функций. Ответ: ∫sin2x dx = −½ cos(2x)+C. Z 3 0 jx 2jdx 5. ⁡. Интеграл от секущей sec x dx =? Этот расчет не так прост, как расчет функции тангенса.2 (2x), мы начинаем с замены u. Z 4 0 2xdx 4. Mar (Не указывайте … 1-й и 2-й этаж, Zion Building, № участка. Шаг 5. Теперь мы должны разделить его на два. ) Предполагается, что вы знакомы со следующими правилами дифференцирования . Пояснение: Таким образом, ∫sin 2xdx = −½ cos (2x) + C. Калькулятор алгебры. Мы сообщим на вашу почту и мобильный, когда кто-то ответит на этот вопрос. Поверхностный интеграл на этой поверхности векторного поля определяется суммой шести. Это легко исправить.99! стрелка_вперед. Подставьте y = 2 x − 1. Калькулятор тригонометрии. Тогда du = e x и v = sin x. 6 Найдите x2exdx. Здесь подинтервалы имеют одинаковую длину, но это не обязательно. Возвращаясь к примеру 6. Вычислить интеграл (2,3, -1) из примера 6, найдя параметрические уравнения для отрезка прямой от (l, l, ) до (2, 3, l) и оценив линейный интеграл F yi +xj+4k по отрезку. Например, поскольку x2 — первообразная 2x, мы имеем Z 2xdx = x2 + C: сказать, что C — «произвольная» константа, значит сказать, что это может быть любое действительное число.Линейные интегралы на плоскости 4А. check_circle Ответ эксперта. Интегралы можно решать разными способами, включая: правило степени, интегрирование по частям; Методы замены, такие как замена u. В этой статье мы сосредоточимся на неопределенных интегралах и узнаем о свойствах и методах для неопределенных интегралов с помощью формул и решенных примеров. 3 из Calc BC, я, честно говоря, ужасен во всем, что связано с триггерами, и это вместе с моим текущим уроком не помогает. Интегральное исчисление используется в таких областях, как площадь под кривыми, длина дуги, площадь поверхности, объем, вероятность и так далее.1 ответ +1 голос. Мощность подынтегральной функции можно уменьшить, используя тригонометрическое тождество. • Таким образом, путем подстановки пределы интегрирования также меняются, давая нам новый интеграл в новой переменной, а также новые пределы в той же самой переменной. Далее: Пр 7. т. н. Интеграл, содержащий верхний и нижний пределы, является определенным интегралом. vdx=u∫vdx−∫( dxdu. ∫ x 4 sin ⁡ ( x) d x. [–] Integral_10-13_2xdx. 9, 15→ Глава 7 Интегралы класса 12 (термин 2) Последовательный порядок; Пример 7. Взятие производная от u дает u’ = 2xdx.2 x + tan x — 7) задано 11 декабря 2021 г. в Indefinite Integral by Riyamishra ( 26. taniska, 7 лет назад. 9; Ex 7. blackp Поскольку 1 2 1 2 постоянно относительно xx, переместите 1 2 1 2 из интеграла в интеграл Я могу использовать это в своем доказательстве, но не знаю как 11 Решите интеграл Z x2 +1 √ x+1 dx 5. и интеграл примет вид Z ˇ ​​ˇ sinxdx Ответы 1. Z 1 1 1 ln(x) dx расходится (сравните с 1/x или проинтегрируйте по частям) Приложения и примеры F(x) является первообразной 2x, возьмем F(x) = x2.2хдх. ) E. Мы идентифицировали его из послушного источника. Положим u = x 2 и Тогда du = 2xdx и по формуле для интегралов от функций типа u n. Этот интеграл нельзя вычислить по прямой формуле интегрирования, поэтому, используя тригонометрическое тождество половины угла cos 2 x… Пример 1 Определите, является ли следующий интеграл сходящимся или расходящимся. Я не думаю, что это правильно, так как интеграл не может быть равен двум числам. Интеграция — это способ добавления частей, чтобы найти целое. Теперь мы разбиваем числительное с помощью cos2x.ydy-2xdx=O; Возьмем интегралы от обеих частей уравнения: — интеграл левой части по y, — интеграл правой части по x. ∫ tan n x d x = ∫ tan n — 2 x tan 2 x d x = ∫ tan n — 2 x (sec 2 x — 1) d x = tan n — 1 x n — 1 — ∫ tan n — 2 x d x. d ты знак равно г ′ ( х) d х. 2(x) должен быть очень простой операцией, потому что в начале наших исследований по исчислению мы узнали, что производная tan Узнайте, как решать интегралы, включающие задачи логарифмических функций, шаг за шагом шаг онлайн.2хдх. Интеграл — это примитивное значение функции, найденное путем интегрирования. Определенный интеграл и неопределенный интеграл — две полезные категории, которые используются для решения многих реальных задач, а фундаментальная теорема интегрального исчисления связывает производную и интеграл. 5, 2 Пр 7. Тогда x = y + 1 2, и d y d x = 2. Итак, имеем: f ( x) = x log. Z 1 3 2xdx= Z 0 1 2xdx Z 3 0 dx= 1 9 = 8: Третий интеграл можно рассматривать как площадь сектора радиуса ˇс удаленным треугольником.Проверенный ответ. Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми объяснениями, как репетитор по математике. = х 8 — 1 8 ∫cos4xdx. Функция $\sin(x)\cos(x)$ — одна из самых простых для интегрирования функций. 4\sin\left (x\right)dx ∫ x4 sin(x)dx путем применения метода табличного интегрирования по частям, который позволяет выполнять последовательное интегрирование по частям над интегралами интегрального исчисления. исчисление, где мы имеем дело с теорией, свойствами и приложениями интеграла.9, 4 Этот ответ бесполезен. Сначала определите u и вычислите du. Неопределенный интеграл не уникален, потому что производная от x2 + c при любом значении константы c также будет равна 2x. Смущенный? Хорошо, это работает следующим образом: 2xdx интегрируется как x в квадрат; чтобы оценить интеграл 2xdx в диапазоне от 10 до 13, вы вычтете значение из нижней части диапазона из значения в верхнюю часть диапазона. Каков интеграл от int tan(2x) dx? — Получите ответ на этот вопрос и получите доступ к огромному банку вопросов, специально предназначенному для студентов.Здесь «∫» — это символ интегрирования. S h3 знак равно ∫ 1 + 4x 2 . Для этого предположим, что 2x = u. 300+ 000+ Ответ. Ограничения. Интеграл с 16 на 25, 400w на -2. 3.2 Обсуждение cos x dx = sin x + C sin x dx = -cos x + C sec 2 x dx = tan x + C csc x cot x dx = -csc x + C sec x tan x dx = sec x + C csc 2 x dx = -cot x + C: 1. . Потом. Он научит вас избегать ошибок с запятыми, предлогами, неправильными глаголами и многим другим. Изменение направления на кривой меняет знак: Если … Интеграл функции sec²x. Z 1 1 1 px dx (p-критерий) 7. sec 2xdx=x∫sec 2xdx−∫( dxdx. Оцените следующий интеграл. (Ваш ответ должен включать . Мы приводим краткий список общих интегралов и правил, которые используются в СТАТ 414.2xdx` का समाधान Решите свои математические задачи, используя наш бесплатный математический решатель с пошаговыми решениями. 3( xe2x 2 −(1 2 ∫ e2xdx)) 3 ( x e 2 x 2 — ( 1 2 ∫ e 2 x d x)) Пусть u = 2x u = 2 x. Важно иметь много практики и поддерживать эти навыки в свежем виде. Введите любой интеграл, чтобы получить решение, шаги и график Предположим теперь, что мы хотим найти интеграл Z 2x √ 1+x2 dx (3) В этом примере мы делаем замену u = 1+x2, чтобы упростить квадрат- корневой термин. Поэтому du/dx = 2. Определенный интеграл от ƒ ƒ ( x ) от a до b определяется выражением ƒ ∫ a b ƒ ( x ) d x Здесь говорят, что a нижний предел, а b верхний предел.2 раза? этот процесс является обратным поиску производной. Глава 7 Интегралы класса 12 (термин 2) Последовательный порядок; Пример 7. Значение π2∫−π2sin2x1+2xdx равно [2018] Интегралы вида R cosmxsinnxdx Пример 1. Вычислите Z cos2xsin3xdx. 4 Если первообразная функции на интервале I существует, то мы Пример 10. C — постоянная интегрирования, которая записывается вместе с неопределенным целым значением любой функции. Функции. Z f(x)dx = F(x) +C Z 2xdx = x2 +C Определение: сумма Римана Сумма Римана – это сумма площадей n прямоугольников, сформированных на n подынтервалах в [a,b].2xdx с заменой. Это простой шаг дифференцирования. б) Вектор в точке P имеет хвост в точке P и начало в начале координат; поле прод. Z 1 0 (x+ 2 p 1 x2) dx 6. Введите идентификатор электронной почты Введите номер мобильного телефона. В этом уроке мы выведем интеграл от квадрата косинуса x. 3 месяца назад. Оцените интеграл: ∫tan 3 x sec 2 x dx. Узнайте, как решать интегралы экспоненциальных функций шаг за шагом онлайн. 1−3cos2x+3cos2 2x− cos3 2xdx. 2 вне интеграла. В своем окончательном ответе замените u на g(x), чтобы представить ваше решение в терминах исходной переменной.2(x)dx = -cot xx + C. Таким образом, транспонируя, мы имеем или, наконец, Пример 4. = (1/2) ex dx — (1/2) ex dx решить левое уравнение = (1/2) ex — (1 /2) ex dx . Это урок 7. Показать все шаги Скрыть все шаги. Глава 7: Интегралы, Раздел 7. 2 постоянна относительно u u, ход 1 0. × СЛЕДИТЕ ЗА ВОПРОСОМ Мы сообщим на вашу почту и мобильный телефон, когда кто-то ответит на этот вопрос. Связанные сообщения в блоге Symbolab. Обычный способ сделать это — поместить тонкие прямоугольники под кривую и сложить подписанные области вместе.{2}} не может быть классом 7. Мы делим числитель и знаменатель на косинус в квадрате x. Если бы кто-нибудь мог дать пошаговое описание, было бы здорово! 13. В этом разделе мы рассмотрим довольно много интегралов, включающих тригонометрические функции, и некоторые методы, которые мы можем использовать для их вычисления. (n раз) , где константа , где константа Большинство из следующих задач являются средними. 16 4. Таким образом, получается окончательный ответ на вопрос о Жизни, Вселенной и Всего 69 минус 27 равно … 2xdx интегрируется как х в квадрате; чтобы оценить интеграл 2xdx по интервалу от 10 до 13, вы вычитаете значение в нижней части интервала из значения в верхней части интервала.2(x) мы начинаем с использования стандартных тригонометрических тождеств, чтобы упростить интеграл до формы, с которой мы можем работать. В этом смысле интегрирования являются антипроизводными. Площадь круга? интеграл 2xdx от 10 до 13 — Wolfram|Alpha. Вы столкнетесь с двумя типами интегралов в математике: определенный интеграл; неопределенный интеграл; Определенный интеграл. Замена u x2 dv exdx du 2xdx v ex не решает проблему сразу, а сводит нас к примеру 3: (7. x x2 −1 3 − x3 + x 3 Расширенные методы интегрирования: тригонометрические интегралы При попытке вычислить интегралы триггерных функций, часто бывает полезно переписать интересующую функцию, используя тождество. 2xdx равно. Теперь мы должны быть в состоянии вычислить интеграл по u. ∫ cosxsin5xdx = ∫ u5du с помощью замены u =sinx = 1 6 sin6x+c ∫ cos. В исходном интеграле замените g(x) на u и g0(x)dx на du, чтобы получить, если возможно, интеграл, включающий только переменную u. Мы можем решить интеграл \int x\ln\left(2x\right)dx, применив метод интегрирования по частям для вычисления интеграла от произведения двух функций, используя следующую формулу. Вопрос . 2 Интеграл тригонометрии I27 / 76 Ответ (1 из 4): Продолжайте заниматься математикой ☺️ Ответ (1 из 9): Лучший ответ: ∫ tan²x dx = ∫ sec²x — 1 dx = tanx — x + константа Надеюсь, это поможет.(2x)sin (2x) относительно x. Один из способов приблизиться к этому — сделать его равным S, затем подставить его в верхнюю границу первого интеграла, решить нормально, а затем получить S = 1,0. Тогда корни ##f## являются решениями вложенного интеграла. Математика3. Выразите ответ не менее чем до пяти знаков после запятой. Что-то пошло не так. Пожалуйста, попытайтесь еще раз. {2}x \, dx\] +.Мы можем численно оценить интеграл, используя простой итерационный цикл, чтобы избежать этой проблемы. Замените все вхождения u u на −0. Для вычисления этого интеграла воспользуемся методом интегрирования по частям. Мы будем интегрировать sin 2x по x. Пошаговое объяснение: Crazygirl4029 crazygirl4029 Потребуется использовать интегрирование по частям: ∫u dv = uv — … В этом уроке мы найдем интеграл функции x Cos2x. 20, 2021 по . Для задач 4 и 5 определите значение данного интеграла, учитывая, что ∫ 11 6 f (x) dx = −7 ∫ 6 11 f ( x) dx = − 7 и ∫ 11 6 g(x) dx 2xdx+2ydy+2zdz x2 + Y2 + Z2 Приложения и примеры 23.2) Узнайте, как шаг за шагом решать задачи с определенными интегралами онлайн. ∵∫у. 30 баллов. 5, 20→ Глава 7 Интегралы класса 12 (термин 2) Последовательный порядок; Пример 7. Проинтегрируйте следующие функции w. ∫sin2 (x)dx = ∫1/2 (1 – cos (2x))dx. Мы должны выбрать u = x2, dv = ex, чтобы du = 2xdx было проще, а v = ex не сложнее: R udv = uv R vdu R x2 ex dx = x2( ex) R ( ex)2xdx = x2e x + 2 R xe x dx Переходя к шагу 4, мы повторяем процесс для интеграла в правой части, на этот раз sin2 2xdx = 1 16 Zp 0 (1 cos4x)dx = p 16 Редко бывает очевидно, какая стратегия используется. быть лучшим, поэтому не удивляйтесь, если кто-то найдет более быстрый способ решения задачи.{2}х \, дх\] +. Это выражается символами как -. сек 2хдх. у = 3х + 4. ; Когда вы интегрируете, вы технически оцениваете, используя прямоугольники с равной базовой длиной (что очень похоже на использование сумм Римана). 645363215. Предположим, что I = ∫tan 3 x sec 2 x dx. Этот браузер не поддерживает элемент видео. Ответ на дополнительную информацию Замените u = g(x) u = g ( x) и du = g′(x)dx. x2 − 1 Решение Числитель подынтегральной функции имеет более высокую степень, чем знаменатель, поэтому мы должны использовать деление в большую сторону, чтобы преобразовать подынтегральную функцию из «неправильной дроби» в «смешанную дробь».∫sin2xcos2xdx = 1 4 ∫(4sin2xcos2x)dx. Этот интеграл относится к экспоненциальным формулам и является одной из простейших формул интегрирования. 16. Если возможно, вычислите интеграл по u. Так что, в каком-то смысле, Z Tip: смотрите мой список наиболее распространенных ошибок в английском языке. • Следующий пример показывает это. Misalkan terdapat 50. Start Solution. Нажмите, чтобы увидеть больше шагов Умножение − 1 — 1 на 5 5. Общее правило при интегрировании степени x x: мы прибавляем единицу к показателю степени, а затем делим на новый показатель степени. Мы можем найти x d x xdx x d x и вместо этого подставить это значение в наше подынтегральное выражение.2(х). Z 1 1 1 x1:003 dx convergent (p-тест) 9. (0 детей) Я припаял больше, чем мне положено, сменных 1/4 джеков на гитарных педалях… Ответил 2021-11-10 У автора 24011 ответов. Полный пошаговый ответ. 1-й и 2-й этаж, Зион Билдинг, Участок № dx 2. Когда I Как только вы видите вопрос, в котором вас просят проинтегрировать квадрат греха, косинуса или тангенса, ваш первый подход должен заключаться в использовании тригонометрических тождеств и формул двойного угла. Мы можем доказать это следующими двумя способами.2x. Потому что я хочу использовать … Площадь и определенный интеграл Используйте чистую площадь области со знаком для вычисления следующих определенных интегралов: 1. ( x ) = ( 1 − e 2 ix ) + ( 1 − e − 2 ix ) ) 4. Он научит вас избегать ошибок с запятыми, предлогами, неправильными глаголами и многим другим. Лучший ответ. Пусть у = 2х. Это легко исправить. 3 Основная теорема линейных интегралов Вспомним основную теорему исчисления для функции одной переменной f: Zb a f0(x)dx = f(b) f(a) Она говорит, что мы можем вычислить интеграл производной просто зная значения функции в концах интервала интегрирования [a,b].2xdx = 1/2(x+1/2sin2x) + … Это означает, что ∫π 0 sin(x)dx= (−cos(π))−(−cos(0)) =2 ∫ 0 π sin. Найдите d u d x d u d x. х*х) оценивается от 13*13 до 10*10 или 169-100. f ( x)dx F ( x) c В этих обозначениях – знак интеграла; f(x) — подынтегральная функция; dx — дифференциал x, обозначающий переменную интегрирования; c называется константой интегрирования. I = ∫ sin 2 x d x. 1 Список свойств линейных интегралов 1. Вы можете просмотреть другие похожие вопросы или задать …. Таким образом, в этом разделе мы будем довольно часто использовать следующие тождества; вам не мешало бы запомнить их.4x. = 2x)du= 2xdx) 1 2 du= xdx; х= 0 !у= 1; x= 1 !u= 0: Шаг 2: Теперь мы можем вычислить интеграл при этой замене переменных, Z 1 0 xp 1 x2 dx= 1 2 Z 0 1 p udu= 1 2 2 3 u3 2 u=0 u= 1 = 1 3: Замечание: вместо изменения границ интегрирования мы можем сначала найти неопределенный интеграл Z xp 1 x2 dx = 1 2 (1 x2)32; затем используйте фундаментальную теорему дифференциального уравнения 3dy=2xdx. 1 тыс. баллов) выбрано RahulYadav 13 марта 2020 г. 2 х. ( x) d x = ( — c o s ( π)) — ( — c o s ( 0)) = 2. Теперь определите dv и вычислите v.{y}\, dy = \int 2 x\, dx$$ Следующие неопределенные интегралы содержат все эти хорошо известные тригонометрические функции. Используйте интегрирование по частям: Тогда. Prathamesh kulkarni, 4 года назад Класс:12. Интегрирование e x — еще одна важная формула интегрального исчисления. d d x [ e x + c] = d d x e x + d d x c. Тогда 2 dx = du (или) dx = du/2. Например, поскольку производная (по x) от x2 равна 2x, мы можем сказать, что неопределенный интеграл от 2x равен x2. Находим интегралы дифференциального уравнения 2xdx + 2ydy = 0.{2x}dx, применяя метод табличного интегрирования по частям, который позволяет выполнять последовательное интегрирование по частям над интегралами вида \int P (x)T (x) dx. Решите интеграл от логарифмических функций int(xln(2x))dx. Этот интеграл нельзя вычислить по прямой формуле интегрирования, поэтому, используя тригонометрическое тождество половинного угла sin 2 x… Для последнего интеграла положим u = e x, dv = cos x dx. Используя почленное дифференцирование и интегрирование, мы можем вычислить степенной ряд большего количества функций, как в следующих примерах.{\dots} 2xdx} 2xdx} 2xdx$ Мы с другом спорили над ответом. Если мы немного изменим предыдущий пример, опустив множитель x, мы получим Z ex2 dx: Давайте попробуем использовать замену, которую мы использовали раньше: u = x2, du = 2xdx. Для доказательства воспользуемся методом подстановки. ∫ a b f ( x) d ( x) = − ∫ b a f ( x) d ( x) ∫ x r d x = x r + 1 r + 1 + C. Нажмите, чтобы увидеть больше шагов. Пусть u = 2 x u = 2 x. До сих пор вы изучали концепцию интеграции. ∫ е х d х = е х + с. > < Раздел 5-6: Определение определенного интеграла.Представим заданную функцию через f (x). Объедините 1 2 1 2 и грех ( 2 х) грех ( 2 х). Подсказка: Чтобы решить вопрос, мы должны применить формулу интегрирования, чтобы выделить функцию интегрирования постоянных значений, а затем применить формулу интегрирования для данной функции x. Пусть и х dv exdx. 12 Решите интеграл Z x3 √ x2 +1 dx . 5. 1 2 + ˇ 2 6. Упростить. С заменой t= sin2 , 4J2 = Z ˇ=2 0 2sin cos d Интегрирование Sin в квадрате x. ∫ xndx = xn+1 n+1 +c, n ≠ −1 ∫ x n d x = x n + 1 n + 1 + c, n ≠ − 1.Первый и самый важный шаг — записать наш интеграл в такой форме: du = 2xdx. Наконец, ответ равен π/4. ) Но также мы выбрали = x2, а это означает du dx = 2x. sin 2 (x) = 1/2 (1 – cos (2x)) Нет, мы можем переписать это как. Где c называется «произвольной константой». Дифференциальное уравнение с неизвестной функцией () + уравнение. Мы признаем, что такая графика Indefinite Integral может быть самой популярной темой, которую мы разрешаем в Google Lead или Facebook. Показать активность в этом посте.(2x))dx. Продвинутая математика. 160. Проверено. Интеграции являются антипроизводными. Вычислить интеграл: ∫xe −2x dx. Найдите интеграл по кривой, где отрезок, пройденный в направлении из точки в точку (рисунок ). Example 7. 273, Sector 10, Kharghar, Navi Mumbai - 410210 Получите ответ на вопрос «Найдите интегральный интеграл от sin(5x)cos(2x) dx» и найдите помощь с домашним заданием по другим математическим вопросам в eNotes, обозначающую \(2e = a \) (это не замена переменной, так как \(x\) по-прежнему остается независимой переменной), мы получаем табличный интеграл: Узнайте, как решать интегралы экспоненциальных функций шаг за шагом онлайн.{-2x} \ квадрат! \квадратный! . ∫ e2x sin(2x)dx ∫ e 2 x sin ( 2 x) d x. Начнем с этого стандартного и хорошо известного триггерного тождества для кроватки 2 x. Первая площадь представляет собой площадь круга радиуса 3. Это дает x = u2 −1,dx = 2udu, и мы получаем R 2(u2 − 1)2 +1 du. Закрыть. Учащиеся (до класса 10+2), готовящиеся ко всем государственным экзаменам, экзамену CBSE Board, экзамену ICSE Board, экзамену State Board Exam, JEE (Mains+Advance) и NEET, могут задавать вопросы по любому предмету и получать быстрые ответы по… ​​Ценность интеграл ∫ (cos ^ 3 x + cos ^ 5 x / (sin ^ 2 x + sin ^ 4 x)) dx задан 27 ноября 2019 г. в исчислении интегралов Jay01 ( 39.2 1 0. Поделиться. 12 класс. Тригонометрия. Решение 1. Обратите внимание, что мы не можем просто применить алгебру к $\displaystyle \frac{1}{1-x}$, чтобы решить эту проблему. Интеграл от x2 −1 Выразите подынтегральное выражение в виде суммы многочлена и правильной рациональной функции, затем проинтегрируйте: x3 dx. Найдите неопределенный интеграл 8 cosec2 2x cot 2xdx Выполняя интегрирование, дали 8 cosec?2x cot 2xdx = плюс постоянная интегрирования. 10 2. 9, 5→ Глава 7 Интегралы класса 12 (термин 2) Последовательный порядок; Пример 7. 4 \sin \theta \cos \theta = 2 \sin \theta.{2}}{3}$$ + C1, где C1 — постоянная величина, не зависящая от x. Бесплатный калькулятор неопределенных интегралов — решайте неопределенные интегралы со всеми шагами. Если этот интеграл сходится, нам нужно найти большую функцию, которая также сходится на том же интервале. Доказательства. Для каждого из них мы просто используем Основы исчисления, потому что знаем их соответствующие. Это читается как «Неопределенный интеграл от f(x) по x равен F(x) + c». Статья TSHIRT-005 пикап линия с использованием расчета.{2x}dx путем применения метода интегрирования по частям для вычисления интеграла от произведения двух функций по следующей формуле. Определенный интеграл на интервале теперь может быть альтернативно определен как . ∫ abx 2 x − 1 dx = ∫ a + 1 2 b + 1 2 y + 1 2 ydy 2 = 1 4 ∫ a + 1 2 b + 1 2 y + 1 ydy = 1 4 ∫ a + 1 2 b + 1 2 1 + 1 ярд у. Используйте определение определенного интеграла, чтобы вычислить интеграл. Наш математический решатель поддерживает базовую математику, предварительную алгебру, алгебру, тригонометрию, исчисление и многое другое.Это только для тех, кто может помнить простой исчисления. Мы можем решить интеграл. Интегралы 1. 1 в таблице интегральных формул, следовательно, ∫ 5 sin(x) dx = - 5 cos x + C 3 - … Если вы погуглите «интеграл от квадрата дифференциала», то обнаружите, что для него не существует простой формулы, которая кажется странным, потому что вторые производные так распространены в природе, поэтому я решил попробовать и обнаружил, что интеграл от (dx) 2 равен x, и мне интересно, имеет ли это смысл, вот как я это сделал: сначала я попробовал использовать интегрирование по частям, но это дает бесконечный ряд интегралов Пр. 7.То, что нужно запомнить. Интегрируйте новый дифференциал вду. Интеграл от sin 2 x обозначается ∫ sin 2 x dx, и его значение равно (x/2) - (sin 2x)/4 + C. Мы увидим, что остальная часть подынтегральной функции, 2xdx, будет учтена автоматически в процессе подстановки, и это потому, что 2x является производной этой части подынтегрального выражения. 6 основных гиперболических функций определяются следующим образом: Пример 1: Вычислить интеграл ∫sech3(x)dx. Предполагается, что ответ будет 0. 5, 4 Ex 7. 2 x d x. Попытка u = √ x2 +1, но это не работает.∫ cos 2 x sin. НОВИНКА Используйте математические обозначения из учебника для … Пример: определенный интеграл функции f (x) на интервале [a; b] является пределом интегральных сумм при стремлении диаметра разбиения к нулю, если оно существует независимо от разбиения и выбора точек внутри элементарных отрезков. детская кроватка ⁡ х \ детская кроватка х детская кроватка х. Пусть u = x2, тогда du/dx = 2x или du ​​= 2xdx. Вы берете известную длину (например, от x = 0 до x = 20) и делите этот интервал на определенное… Найдите пошаговые решения исчисления и свой ответ на следующий вопрос из учебника: Что не так с уравнением ? интеграл от 0 до pi sec^2xdx=tanx]0 до pi=0.