Задания по геометрии 6 класс
Тема: СИММЕТРИЯ
Задача 1
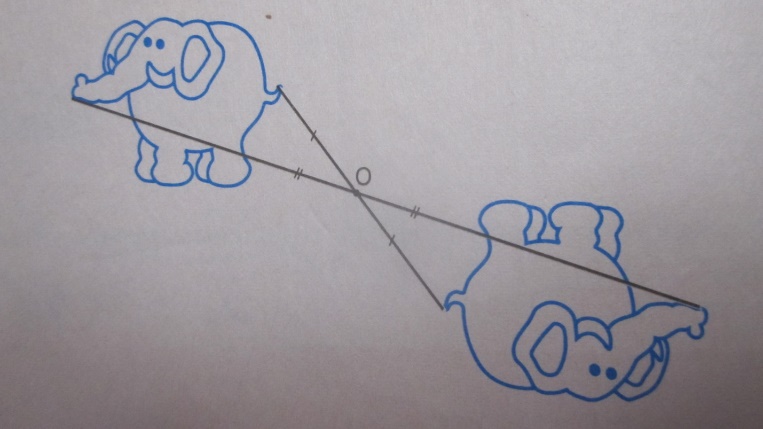
Посмотрите, какой занимательный рисунок может проиллюстрировать центральную симметрию. Придумайте рисунок, иллюстрирующий центральную симметрию и изобразите его на отдельном листе.
.
Задача 2
Придумайте и нарисуйте окружающие предметы, которые имеют оси симметрии.
Например:

Задача 3
Нарисуйте окружность и прямоугольник так, чтобы они имели общую ось симметрии
Задача 4
Запишите номера фигур , симметричных относительно
а) оси OY
б) оси OX
в) начала координат
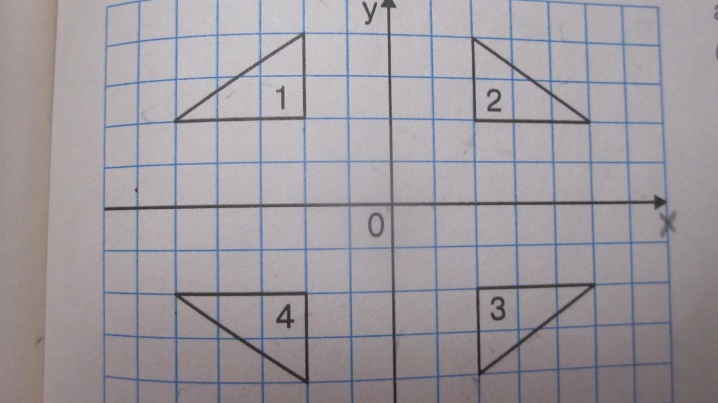
Задача 5
Придумайте рисунок из жизни, иллюстрирующий осевую симметрию, и изобразите его на отдельном листе.
Перед нами занимательная иллюстрация осевой симметрии
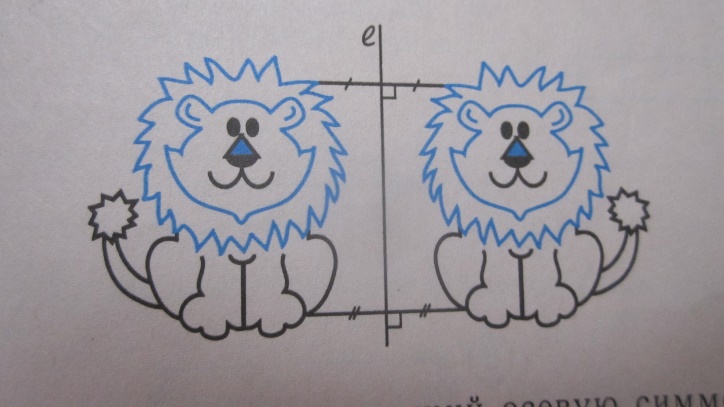
Задача 6
Разгадайте ребуса)
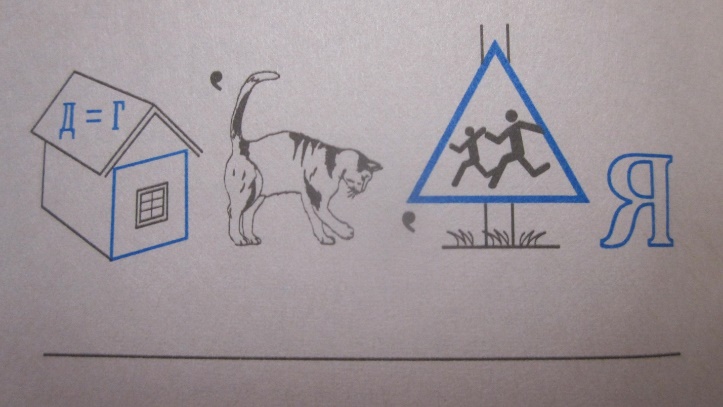
б)

Тема: ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Задача 1
На рисунке изображен прямоугольный параллелепипед Запишите название его…
А) вершин
Б) ребер
В) граней
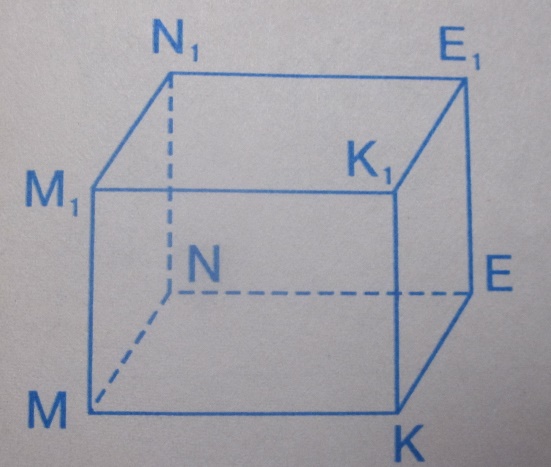
Задача 2
Определите объем прямоугольного параллелепипеда
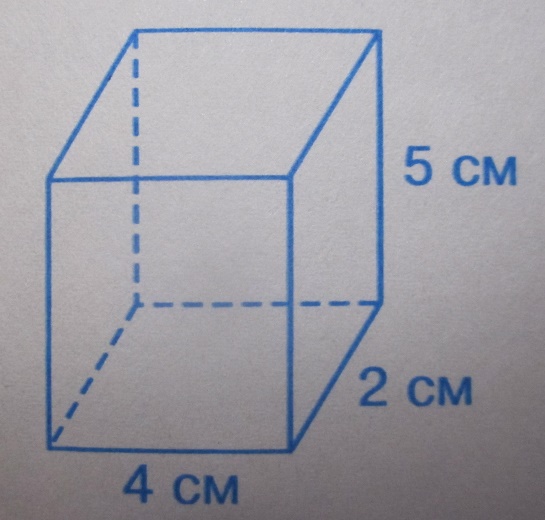
Задача 3
Вычислите объем прямоугольного параллелепипеда, если его измерения а=7 см, b=6 см, с=4 см.
Задача 4
Измерения прямоугольного параллелепипеда 3см, 2 см и 4,5 см. Вычислите его объем. Попробуйте определить , чему равна длина ребра куба, равновеликого данному прямоугольному параллелепипеду.
Задача 5
Разгадайте ребусы.
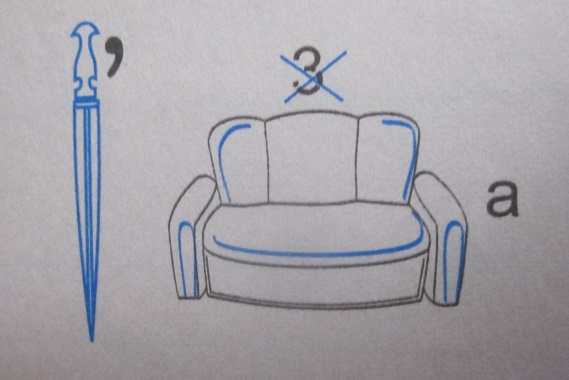
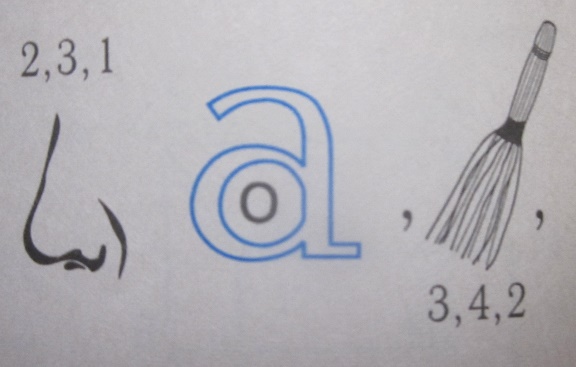
Тема: ФИГУРЫ В ПРОСТРАНСТВЕ
Задача 1
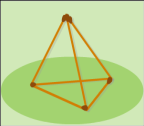
Обозначьте данную на рисунке треугольную пирамиду и укажите…
А) вершины
Б) ребра
В) грани
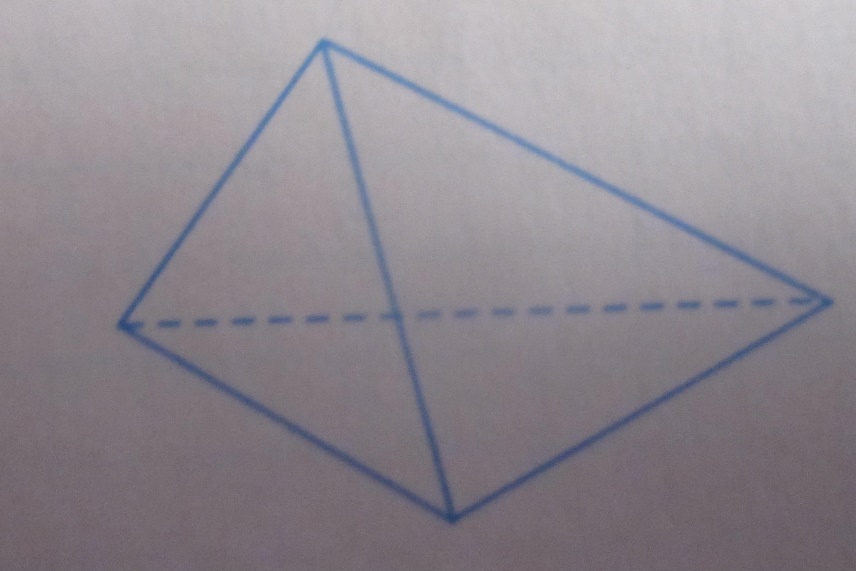
Задача 2
Постройте две пирамиды, в основании которых лежат
А) четырехугольник
Б) пятиугольник
Выделите другим цветом основания пирамид. Перечислите названия боковых граней и ребер.
А) Название пирамиды………………….
Боковые ребра………………………….
Боковые грани………………………….
Б) Название пирамиды………………….
Боковые ребра………………………….
Боковые грани………………………….
Задача 3
Дорисуйте пирамиду, в основании которой лежит шестиугольник.
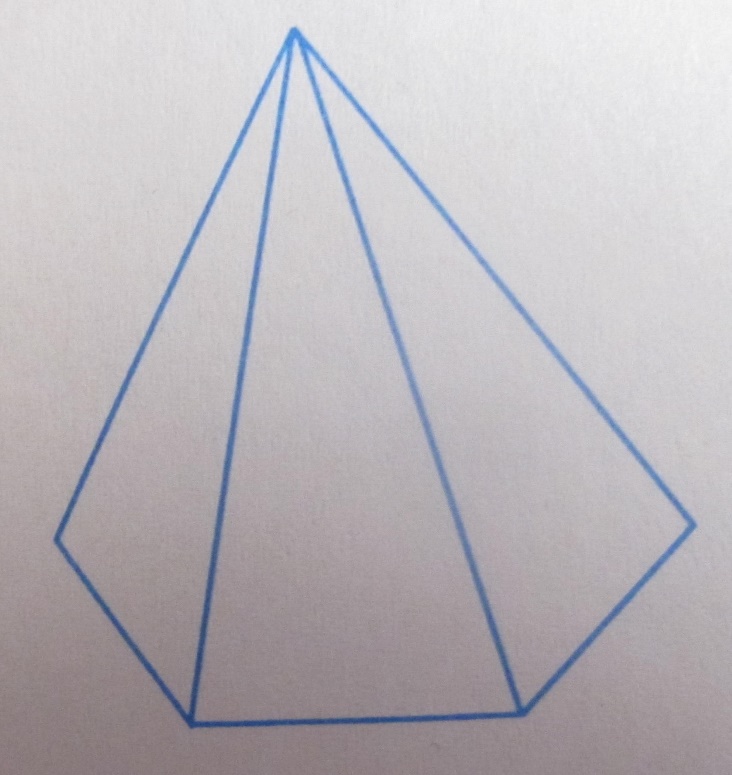
Задача 4
Форму пирамид имели гробницы фараонов в Древнем Египте. Они сохранились до наших дней. Одна из самых знаменитых- пирамида Хеопса, высота которой достигает 147 м. Дорисуйте пирамиду до:
А) четырехугольной
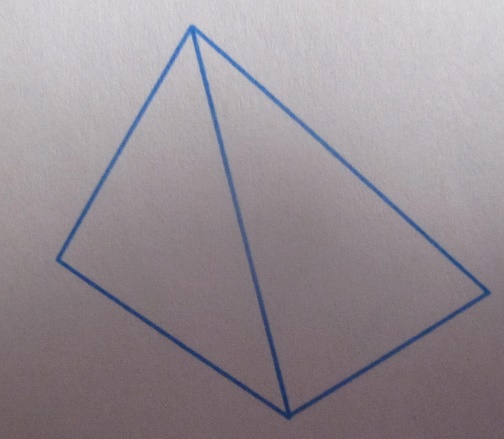
Б) треугольной
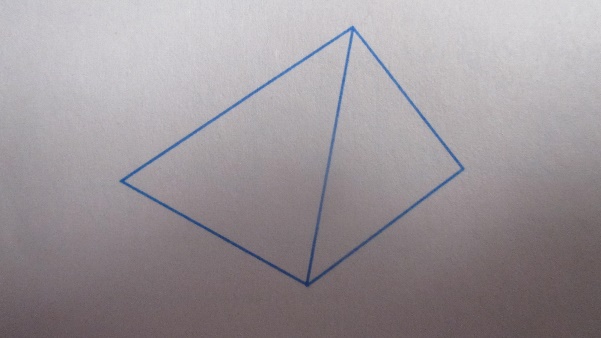
Задача 5
Ответьте на вопросы.
А) У пирамиды 12 вершин, сколько вершин в основании пирамиды?
Б) У пирамиды 15 граней, сколько у нее вершин?
В) У пирамиды 16 ребер, какая это пирамида?
Тема : Тела вращения
Задача 1
Названия некоторых геометрических тел идут из глубокой древности , причем произошли они от соответствующих предметов. Например, из Древней Греции пришли термины «конус» (conus- предмет, которым затыкали бочку), «пирамида» (pura- огонь, костер), «цилиндр»( cylindrus-валик)
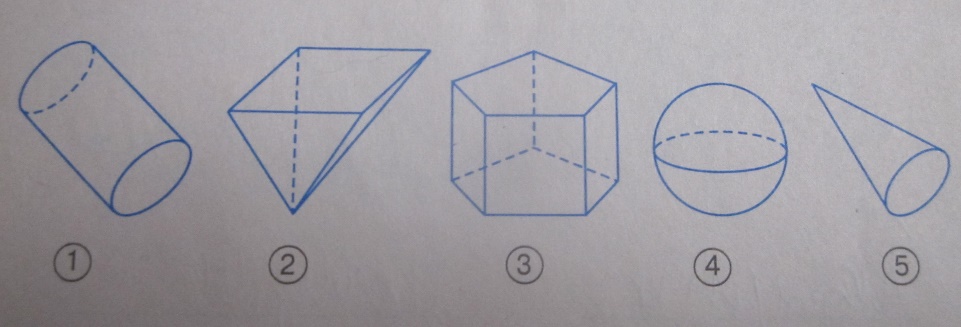
Из изображенных геометрических тел укажите…
А) номера многогранников:_____________________________
Б) названия по номерам остальных тел:___________________
Задача 2
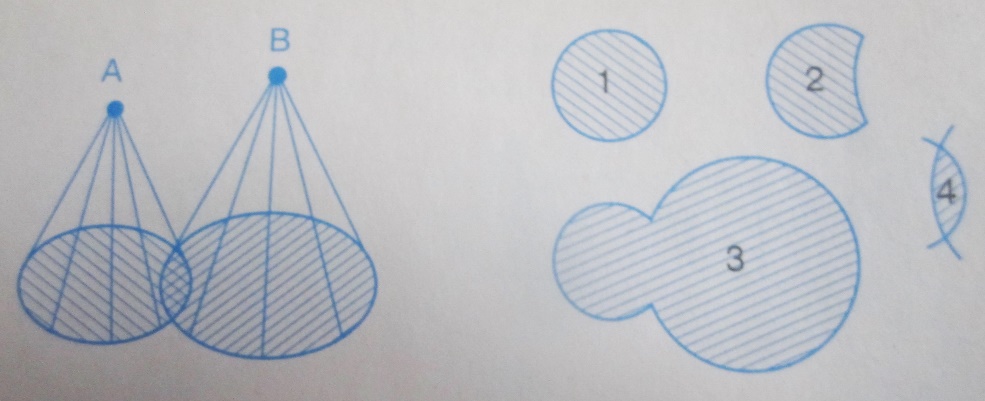
Электролампами А и В освещают заштрихованные площадки. Какая из заштрихованных областей освещается:
А) лампой А_______________________
Б) только лампой А_________________
В) лампами А и В___________________
Г) одновременно лампами А и В______
Задача 3
Разгадайте ребусы.

infourok.ru
Методическая разработка по геометрии (6 класс) по теме: тестовые задания по геометрии
Министерство науки и образования Р.Б.
МОУ Баргузинская средняя общеобразовательная школа
Т е м а т и ч е с к и е
т е с т ы п о г е о м е т р и и
К учебнику Г.В.Дорофеева, Л.Г.Петерсона «Математика. 6 класс. Часть 3» |
Разработчик Ухинова С.Б., учитель математики.
Эксперт по предметной части Эксперт по теории тестов
2008
Введение
В комплект включены тематические тесты по геометрии для текущего контроля знаний, умений и навыков учащихся 6-х классов по разделу «Геометрия», изучаемому в III – IV четвертях.
Продолжительность тестирования по всем тестам составляет 20 минут.
В ходе выполнения теста учащиеся фиксируют ответы в специальной таблице ответов. Отсутствие необходимости оформлять решение заданий приводит к существенной экономии времени учащихся. Наличие таблицы ответов обеспечивает оперативность контроля и проверки.
Разработанные тесты рекомендуется использовать для диагностики усвоения основных понятий после изучения соответствующих тем.
Рубежный контроль по разделу «Геометрия» осуществляется в виде письменной контрольной работы.
ЭЛЕМЕНТЫ СОДЕРЖАНИЯ РАЗДЕЛОВ.
Раздел № 1. Геометрические фигуры на плоскости.
Тест №1. Варианты 1 и 2.
Тема 1. Свойства геометрических фигур.
Тема 2. Замечательные точки в треугольнике.
Тема 3. Рисунки и определения геометрических понятий.
КОНТРОЛИРУЕМЫЕ ЗНАНИЯ, УМЕНИЯ И НАВЫКИ.
- Умение распознавать виды треугольников по сторонам и по углам.
- Умение различать медиану, высоту и серединные перпендикуляры в треугольнике.
- Умение распознавать замечательные точки в треугольнике.
- Знание определений геометрических понятий и фигур.
- Умение соотносить геометрические понятия и их графическое изображение.
Раздел № 2. Геометрические фигуры в пространстве.
Тест №2. Варианты 1 и 2.
Тема «Пространственные фигуры и их изображение».
Тест №3. Варианты 1 и 2.
Тема «Многогранники».
Тест №4. Варианты 1 и 2.
Тема «Тела вращения».
КОНТРОЛИРУЕМЫЕ ЗНАНИЯ, УМЕНИЯ И НАВЫКИ
Тест №2.
- Умение различать пространственные и плоские фигуры.
- Знание элементов пространственных фигур.
- Умение различать понятия проекции, развертки и секущей.
- Умение различать полные и усеченные пространственные фигуры.
Тесты №3 и №4.
- Различать многогранники и тела вращения.
- Знание элементов многогранников и тел вращения.
- Умение определять видимые и невидимые элементы многогранников и тел вращения.
- Умение строить развертки многогранников.
- Умение узнавать в предметах окружающего мира многогранники и тела вращения.
- Знать определение основных понятий тел вращения.
Раздел №3. Геометрические величины и их измерения.
Тест №5. Варианты 1 и 2.
Тема 1. Измерение величин.
Тема 2. Измерение углов.
КОНТРОЛИРУЕМЫЕ ЗНАНИЯ, УМЕНИЯ И НАВЫКИ
- Умение выделять среди различных величин геометрические величины.
- Знание единиц измерения длины, площади и углов.
- Умение переводить одни единицы измерения в другие.
- Умение измерять длину отрезка в различных единицах измерения, включая условные.
- Умение вычислять площади сложных плоских фигур.
- Умение вычислять объемы куба и параллелепипеда.
- Умение различать углы по видам.
- Умение вычислять величину углов в плоских фигурах.
Раздел №4. Симметрия фигур.
Тест №6. Варианты 1 и 2.
Тема 1. Преобразование плоскости.
Тема 2. Правильные многоугольники.
Тема 3. Правильные многогранники.
КОНТРОЛИРУЕМЫЕ ЗНАНИЯ, УМЕНИЯ И НАВЫКИ
- Умение различать симметрии по видам.
- Знание свойств симметрии.
- Умение различать правильные многогранники от правильных многоугольников.
- Уметь вычислять периметры правильных многоугольников.
- Уметь вычислять величину угла правильных многоугольников.
6. Умение узнавать в предметах окружающего мира симметричные фигуры.
Геометрические фигуры на плоскости
Т е с т 1.
Вариант 1.
Ребята! Вам предлагается выполнить 8 заданий , состоящих из частей А, В, С. На его выполнение отводится 15 минут.
Инструкция к выполнению заданий А1-А3: к каждому заданию даны варианты ответов, из которых только один верный. Выберите правильный ответ и запишите в таблицу ответов.
А 1. На рисунке изображенный треугольник является
1) равнобедренным 2) прямоугольным 3) равносторонним.
А 2. В изображенном треугольнике проведена
1) высота 2) медиана 3) серединный перпендикуляр.
А 3. В точке О пересекаются
о
1) высоты 2) медианы 3) серединные перпендикуляры.
Инструкция к заданиям В1-В3: допишите пропущенное слово и запишите в таблицу ответов.
В 1. Отрезок, соединяющий середины двух сторон треугольника, называется ________ _______.
В 2. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется __________.
В 3. Часть круга, ограниченная двумя радиусами, называется ___________.
Инструкция к заданию С 1-С 2: установите соответствие между геометрическими понятиями и их изображениями. Одному элементу левого списка соответствует один элемент правого списка. В таблице ответов запишите к номерам геометрических понятий индексы изображений, например: 1г,2в.
С 1. Геометрические понятия графические изображения
1) луч а)
2) прямая б)
3) прямоугольник в)
4) окружность г)
д)
Вариант 2.
Ребята! Вам предлагается выполнить 8 заданий , состоящих из частей А, В, С. На его выполнение отводится 15 минут.
Инструкция к выполнению заданий А1-А3: к каждому заданию даны варианты ответов, из которых только один верный. Выберите правильный ответ и запишите в таблицу ответов.
А 1. На рисунке изображенный треугольник является
1) равнобедренным 2) прямоугольным 3) равносторонним.
А 2. В изображенном треугольнике проведена
1) высота 2) медиана 3) серединный перпендикуляр.
А 3. В точке О пересекаются
О
1) высоты 2) медианы 3) серединные перпендикуляры.
Инструкция к заданиям В1-В3: допишите пропущенное слово и запишите в таблицу ответов.
В 1. Хордой называется отрезок, соединяющий две точки ____________.
В 2. Треугольник называется прямоугольным, если у него один из _______ прямой.
В 3. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется _________.
Инструкция к заданию С 1: установите соответствие между геометрическими понятиями и их изображениями. Одному элементу левого списка соответствует один элемент правого списка. В таблице ответов запишите к номерам геометрических понятий индексы изображений, например: 1г,2в.
С 1.Геометрические понятия графические изображения
1) угол а)
2) отрезок б)
3) квадрат в)
4) прямая г)
д)
Эталоны ответов.
Вариант 1.
№ заданий | А 1 | А 2 | А 3 | В 1 | В 2 | В 3 | С 1 |
ответ | 2 | 1 | 2 | Средней линией | медианой | сектором | 1б, 2г, 3а, 4в. |
Вариант 2.
№заданий | А 1 | А 2 | А 3 | В 1 | В 2 | В 3 | С 1 |
ответ | 1 | 2 | 2 | окружности | углов | медианой | 1г, 2б, 3а, 4в. |
Геометрические фигуры в пространстве.
Т е с т 2. Пространственные фигуры и их изображение..
Вариант 1.
Инструкция к выполнению заданий А1-А5: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запишите в таблицу ответов.
А 1. Запишите индексы пространственных фигур в таблицу ответов
1) 2) 3) 4) 5)
А 2. В изображенной пирамиде выберите количество ребер
1) 6 2) 7 3) 8
А 3. Дана фигура и ее проекция. Определите вид проекции.
1) сверху 2) слева 3) спереди.
А 4. Треугольник MNK для куба является
1) проекцией 2) секущей 3) разверткой.
А 5. Усеченная пирамида- это
1) 2) 3) 4)
Вариант 2.
Инструкция к выполнению заданий А1-А5: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запиши в таблицу ответов.
А 1. . Запишите индексы пространственных фигур в таблицу ответов
1) 2) 3) 4) 5)
А 2. В изображенной пирамиде выберите количество граней
1) 5 2) 6 3) 8
А 3. Дана фигура и ее проекция. Определите вид проекции.
1) сверху 2) слева 3) спереди.
А 4. Треугольник MNK для куба является
1) проекцией 2) секущей 3) разверткой.
А 5. Усеченный конус- это
1) 2) 3) 4)
Эталоны ответов.
Вариант 1.
№ заданий | А 1 | А 2 | А 3 | А 4 | А 5 |
ответы | 1; 3; 5. | 3 | 1 | 2 | 4 |
Вариант 2.
№ заданий | А 1 | А 2 | А 3 | А 4 | А 5 |
ответы | 1; 3; 5. | 1 | 1 | 2 | 2 |
Тест 3. Многогранники.
Вариант 1.
Инструкция к выполнению заданий А1-А5: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запиши в таблицу ответов.
А 1. Многогранниками являются
1) 2) 3) 4)
А 2.Выберите количество граней параллелепипеда
1) 8 2) 4 3) 6
А 3. Выберите количество невидимых ребер из задания А2:
1) 6 2) 3 3) 9
А 4. Выберите правильную развертку пирамиды
1) 2) 3)
А 5. Выберите многогранники в предметах вашего класса:
1) глобус 2) доска 3) аквариум 4) стол 5) шкаф
Вариант 2.
Инструкция к выполнению заданий А1-А5: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запиши в таблицу ответов.
А 1. Многогранниками являются
1) 2) 3) 4) 5)
А 2. Выберите количество ребер параллелепипеда
1) 6 2) 8 3)12
А 3. Выберите количество невидимых граней из задания А2:
1) 6 2) 3 3) 9
А 4. Выберите правильную развертку параллелепипеда
1) 2) 3)
А 5. Выберите многогранники в предметах ваших учебных принадлежностей:
1) пенал 2) книга 3) ранец 4) карандаш 5) циркуль
Эталоны ответов.
Вариант 1.
№ заданий | А 1 | А 2 | А 3 | А 4 | А 5 |
ответы | 2; 4 | 3 | 2 | 2 | 3; 5 |
Вариант 2.
№ заданий | А 1 | А 2 | А 3 | А 4 | А 5 |
ответы | 3; 5 | 3 | 2 | 1 | 1; 2 |
Т е с т 4. Тела вращения.
Вариант 1.
Инструкция к выполнению задания А 1: к заданию даны варианты ответов, из которых только один верный. Выберите правильный ответ и запишите в таблицу ответов.
А 1.Телом вращения является
1) 2) 3)
Инструкция к выполнению заданий В1-В5: допишите пропущенное слово и запишите в таблицу ответов.
В1. Осевым сечением конуса является _________.
В2. Запиши элементы конуса:
? ?
1) 2)
В3. Глобус, звезды, яблоко имеют форму ________.
В4. Большие полуокружности, котрые получаются при пересечении поверхности Земли плоскостями, проходящими через полюса, называются ______________.
В5. Запишите элементы шара:
1) АВ-________ 2) ОС-_________
Вариант 2.
Инструкция к выполнению задания А 1: к заданию даны варианты ответов, из которых только один верный. Выберите правильный ответ и запишите в таблицу ответов.
А1. Телом вращения является:
1) 2) 3)
Инструкция к выполнению заданий В1-В5: допишите пропущенное слово и запишите в таблицу ответов.
В1. Осевым сечением цилиндра является _________.
В2. Запишите элементы цилиндра:
?
?
1) 2)
В3. Арбуз, мяч, планеты имеют форму _________.
В4. Сечения поверхности Земли параллельными плоскостями, называются________.
В5. Поверхность шара называется ________.
Эталоны ответов.
Вариант 1.
№ заданий | А1 | В1 | В2 | В3 | В4 | В5 |
ответы | 3 | треугольник | 1) основание 2) боковая поверхность | шара | меридианами | 1) диаметр 2)радиус |
Вариант 2.
№ заданий | А1 | В1 | В2 | В3 | В4 | В5 |
ответы | 3 | прямоугольник | 1)основание 2)боковая поверхность | шара | параллелями | сферой |
§3 Геометрические величины и их измерения.
a
b
c
a
Тест 5.
Вариант 1.
Инструкция к выполнению заданий А1-А6: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запишите в таблицу ответов.
А1. Выберите геометрические величины:
1) градус 2) длина 3) масса 4) площадь 5) работа
А2. Площадь квартиры измеряется в :
1) м 2) м2 3)м3
А3. Высота дерева измеряется в :
1) м 2)м2 3) м3
А4. Найдите объем куба с высотой 5 см:
1) 12см 2) 125см 3) 125см3
А5. Укажите формулу объема прямоугольного параллелепипеда:
1) S=4 2) C=2 3) V= 4) V= abc
А6. Величина угла С равна
В
45
А 35 С 1) 80° 2) 90° 3) 100°
Инструкция к выполнению заданий В1-В5: выполните необходимые вычисления и запишите в таблицу ответов.
В1.Вычислите длину отрезка АВ в единицах измерения е1.. е1
А В
1) 7 2) 1 3) 4 4) 5
В2.Переведите заданные величины в указанные:
1) 2м4см=___см 2) 2м24см2=___см2 3)2м34см3=___см3
В3. Вычислите площадь фигуры:
1) 12см 2 2) 16см 2 3) 24см2
В4. Подсчитайте количество острых углов:
1) 3 2) 4 3) 5
В5. Вычислите величину угла АОС, если известно, что ОВ- биссектриса:
А
О 22° В 1)44° 2) 22° 3) 88°
С
Вариант 2.
Инструкция к выполнению заданий А1-А5: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запишите в таблицу ответов.
А1. Выберите геометрические величины:
1) площадь 2) скорость 3) температура 4) объем.
А2.Площадь поля измеряется в :
1) см2 2)га 3) км3 4)м
А3. Объем аквариума измеряется в :
1) м2 2) см3 3) км3 4) мм
А4.Найдите объем прямоугольного параллелепипеда с высотой 3м., длиной 4м., шириной 5м.
1)12м3 2)60м3 3) 60см3 4) 60м2
А5. Укажите формулу длины окружности:
1) 2) 4) C=2r
А6. Величина угла Д равна:
1)150° 2) 30° 3) 120° 4)180°
Инструкция к выполнению заданий В1-В5: выполните необходимые вычисления и запишите в таблицу ответов.
В1. Вычислите длину отрезка АВ в единицах измерения е1.. е1
А В
1) 5 2) 2 3) 1 4) 4
В2. Переведите заданные величины в указанные:
1) 3 м 5 см =___см 2) 3 м2 5 см2 = ___ 3) 3 м3 5 см3 = ___см3
В3. Вычислите площадь заштрихованной фигуры, если сторона квадрата 3 см.
1) 4 см2 2) 9 см2 3) 8 см2
В4. Подсчитайте количество тупых углов
1) 1 2) 2 3) 3 4) 4
В5. Вычислите величину угла ВОС, если известно, что угол АОВ = 110°
В
110°
А О С
1) 70° 2) 80° 3)180° 4) 60°
Эталоны ответов.
Вариант 1.
№ заданий | А1 | А2 | А3 | А4 | А5 | А6 | В1 | В2 | В3 | В4 | В5 | |
ответы | 1,2,4. | 2 | 1 | 3 | 4 | 3 | 7 | 1) 204 2)20004 3) 2000004 | 2 | 1 | 1 |
Вариант 2.
№ заданий | А1 | А2 | А3 | А4 | А5 | А6 | В1 | В2 | В3 | В4 | В5 |
ответы | 1, 4 | 2 | 2 | 2 | 4 | 1 | 1 | 1) 305 2) 30005 3)3000005 | 3 | 3 | 1 |
§4. Симметрия фигур
Тест 6.
Вариант 1.
Инструкция к выполнению заданий А1-А7: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запишите в таблицу ответов.
А1.Количество граней, которые сходятся в вершине тетраэдра, равно
1) 3 2) 4 3) 5 4) 6
А2. Правильные многогранники – это
1) икосаэдр 2) гексаэдр 3) пирамида 4) тетраэдр
А3. Составить паркет из одинаковых ромбов
1) можно 2) невозможно 3) не могу ответить
А4. Величина угла правильного пятнадцатиугольника равна
1) 150° 2) 156° 3) 210° 4) 24°
А5. Периметр правильного шестиугольника со стороной 4,5 см равен
1) 20,25 см2 2) 27 см 3) 22,5 см2 4) 18 см
А6. Ось симметрии имеют буквы
1) А 2) Б 3) Г 4) О 5) Т
А7. Центральную симметрию имеют
1) отрезок 2) прямая 3) луч 4) квадрат
Инструкция к заданию А8: установите соответствие между рисунками первого столбца и понятиями второго столбца. Ответ запишите в виде связанных индексов элементов. Например, 1а, 2с и тд.
А8. рисунки: виды симметрии:
1) а) поворот
2) б) параллельный перенос
3) в) осевая симметрия
4) г) центральная симметрия
Вариант 2.
Инструкция к выполнению заданий А1-А7: к каждому заданию дано от 3 до 5 вариантов ответов, из которых верными могут быть 1 и более ответов. Индексы верных ответов запишите в таблицу ответов.
А1. Количество ребер, которые сходятся в вершине тетраэдра, равно
1) 3 2)4 3)5 4)6
А2. Правильные многогранники – это
1) тетраэдр 2) октаэдр 3) додекаэдр 4) параллелепипед
А3. Составить паркет из одинаковых треугольников
1) можно 2) невозможно 3) не могу ответить
А4. Величина угла правильного двенадцатиугольника:
1) 120° 2) 210° 3) 150° 4) 135°
А5.Периметр правильного пятиугольника со стороной 1,8 см равен:
1) 9см 2) 3,24см2 3) 10,8см 4) 90см
А6.Осевую симметрию имеют:
1) отрезок 2) прямая 3) луч 4) квадрат
А7. Центр симметрии имеют буквы:
1) А 2) О 3) М 4) Х 5) К
Инструкция к заданию А8: установите соответствие между рисунками первого столбца и понятиями второго столбца. Ответ запишите в виде связанных индексов элементов. Например, 1а, 2с и тд.
А8. Действия : Виды симметрии:
1) совмещение двух половинок а) поворотная
одной фигуры
2) поворот на 180° б) параллельный перенос
3) поворот на 20° в) осевая
4) сдвиг на расстояние г) центральная
Эталоны ответов.
Вариант1.
№ заданий | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 |
ответы | 1 | 3,4 | 1 | 2 | 2 | 1,4,5 | 1,2,4 | 1в, 2а, 3г, 4б |
Вариант2
№ заданий | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 |
ответы | 1 | 1,2,3 | 1 | 3 | 1 | 1,2,4 | 2,4 | 1в, 2г, 3а, 4б |
nsportal.ru
Геометрические задачи на этапе подготовки к олимпиадам
Статистика итогов математических олимпиад различного уровня показывает, что к решению геометрических задач приступают буквально единицы конкурсантов. Даже решение простых задач из школьного учебника вызывает затруднения у многих учащихся.
Чтобы приобщить учащихся к решению геометрических задач, убедить их в полезности таких занятий, необходимо уделять внимание разбору геометрических задач на уроках математики в 5 – 6 классах, на внеурочных занятиях, на этапе подготовки к олимпиадам.
Олимпиадные геометрические задачи полезны не только для проверки математических способностей и уровня математической подготовленности учащихся в жестких соревновательных условиях. На занятиях математического кружка, в спокойной обстановке, конкурсная задача является источником небольшого самостоятельного исследования, творческого открытия. Известный педагог-математик Д. Пойа писал: «Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия».
Для расширения кругозора и конструктивных навыков хороши практические задания, связанные с разрезаниями, проведениями построений. В таких задачах не используются знакомые алгоритмы решения, они требуют нестандартного подхода. Необходимо учить ребят находить пути к решению проблемы, а это значит – формировать у них способность к самостоятельному, творческому мышлению.
Представляю разработку кружкового занятия по теме «Решение геометрических задач». Занятие может быть организовано как для учащихся 5 – 6 классов, так и для более старших школьников. Главной целью его является приобщение учащихся к миру математики, убеждение учащихся в том, что размышление, рассуждение, выдвижение идей приводит к удивительным и полезным открытиям. Занятие построено так, что рассматривая задачи различного уровня и содержания, учащиеся постепенно, от простого к сложному, продвигаются в своем развитии, совершенствуют навыки решения олимпиадных задач. Разнообразные теоретические факты вытекают из практических упражнений и экспериментов. Это занятие составлено в соответствии с авторской модульной программой работы с математически способными детьми. Использованы задачи из различных сборников олимпиадных заданий:
- Евдокимов М.А. От задачек к задачам. М.: МЦНМО, 2004
- Игнатьев Е.И. В царстве смекалки. М.: «Наука», 1987
- Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. М.: «Просвещение», 1988
- Материалы международного конкурса «КЕНГУРУ»
Методическая разработка занятия математического кружка
Класс:
5 – 6
Тема:
Решение геометрических задач
Цели:
- развивать пространственное воображение, конструкторские навыки;
- способствовать развитию интереса к предмету;
- учиться ведению логически стройного доказательства;
- способствовать самореализации и самосовершенствованию каждого ученика.
Оборудование:
- карточки с заданиями;
- наглядные иллюстрации к задачам;
- сборники олимпиадных заданий;
- материалы международного математического конкурса «КЕНГУРУ»;
- бумага, ножницы для практических экспериментов.
Этапы занятия:
- Организационные моменты (1 мин)
- Разминка (5 мин)
- Разбор интересных задач на проведение линий, разбиение фигур, перекраивания (20 мин)
- Решение задач математического конкурса «Кенгуру» (15 мин)
- Творческое домашнее задание (2 мин)
- Подведение итогов занятия (2 мин)
Ход занятия:
1 этап. (Организационный)
Учитель: – Для работы разобьемся на группы, чтобы вам было интереснее работать с товарищами. Постарайтесь быть активными, полезными для своей команды. Вносите свои предложения, прислушивайтесь к мнению других.
(Класс разбивается на группы, в составе которых оказываются учащиеся с разной математической подготовкой. Это необходимо для того, чтобы каждый нашел себе применение, и «слабый» имел возможность тянуться за «сильным»)
II этап. Разминка
1) Учащиеся получают три рисунка:
Рисунок 1.
Вопросы:
Сравните длины отрезков на рисунках 1 и 2. На сколько сантиметров один отрезок больше другого?
Сравните длины диагоналей параллелограммов на рисунке 3. У какого параллелограмма диагональ длиннее? (Для учащихся 5 – 6 классов пояснить, что называют параллелограммом, его диагоналями).
(После обсуждения в группах учащиеся высказывают предположения. Затем непосредственным измерением отрезков выясняют, правы ли они. Почему возникает такая иллюзия, что один отрезок кажется длиннее другого?)
2) Как, не отрывая карандаша от бумаги, разделить фигуру на рисунке 2 на шесть равных треугольников?
Рисунок 2. Рисунок 3. Рисунок 4.
III этап.Разбор интересных задач на проведение линий, разбиение фигур, перекраивания.
Задача 1
Постройте замкнутую ломаную линию, состоящую из трех звеньев и проходящую через четыре данные точки (Рисунок 3).
Задача 2
Как ломаной линией, состоящей из четырех отрезков, не отрывая карандаша от бумаги, перечеркнуть девять точек, расположенных так, как показано на рисунке 4?
(Обсудить все предложенные ребятами варианты решения. Обратить внимание учащихся на то, что задача считается решенной, если выполнены все требования условия, то есть ломаная состоит из четырех звеньев, звенья ломаной не должны накладываться друг на друга, линия должна быть без разрывов).
Задача 3
Как тремя прямолинейными разрезами разделить круглый торт на:
а) семь,
б) восемь частей (Рисунок 5)?
Рисунок 5.
Возможные варианты решения (Рисунок 6, Рисунок 7):
Рисунок 6. Рисунок 7.
Задача 4Рисунок 8.
Как из набора «уголков» сложить прямоугольник (Рисунок 8)?
Решение:
Подсчитаем, какую площадь займут все «уголки» 3+4+5+6+7+8=11*3=33. Значит, стороны прямоугольника могут быть равны 3 и 11. Остается заполнить прямоугольник 3*11 данными «уголками». Например, как на рисунке 9:
Рисунок 9.
Задача 5
Разрежьте фигуру на две части и сложите из них квадрат (Рисунок 10).
Рисунок 10.
Вопросы для обсуждения:
– Какова площадь первоначальной фигуры?
12*9-8=108-8=100
– Значит, сложив части, мы получим квадрат размером 10*10.
– На сколько нужно увеличить сторону длиной 9 клеток и на сколько уменьшить другую сторону? (на 1 и на 2)
Вариант разрезания (Рисунок 11):
Рисунок 11.
IV этап. Решение задач математического конкурса «Кенгуру»
Задачи «Кенгуру»
- (2006 год) Какая из линий самая короткая (Рисунок 12)? Объясните.
Рисунок 12.
Решение: Заметим, что линия, составленная из горизонтальных и вертикальных отрезков, имеет наибольшую длину.
Сравним (Рисунок 13)Рисунок 13.
Таким образом, в порядке убывания длины: (D) – (C) – (A) или (E) – (B).
Самая короткая линия – В. - Для того, чтобы покрасить кубик, изображенный на левом рисунке (Рисунок 14), понадобится 9 кг краски. Сколько краски потребуется, чтобы покрасить фигуру, изображенную на правом рисунке?
Рисунок 14.
(А) 4 кг (В) 5 кг (С) 6 кг (Д) 9 кг (Е) 12 кг
Решение: Площадь поверхности первой фигуры равна 9*6=54, правой – 9+9+9+5+5+5+12=54. Так как площади равны, то краски понадобится столько же, т.е. 9 кг. - Если бумажный кубик разрезать по некоторым ребрам и развернуть, то получится развертка I (Рисунок 15), а если стереть некоторые буквы и потом разрезать кубик иначе, получится развертка II. Какая буква стояла на месте вопросительного знака?
Рисунок 15.
(A) А (B) В (C) С (D) Е (E) невозможно определить
Решение: «Соберем» первый (Рисунок 16) кубик и расставим на нем буквы (можно использовать модель кубика)
Рисунок 16. Рисунок 17.
Перевернем его на себя (Рисунок 17):
Если полученный кубик разрезать, то на месте вопросительного знака , то есть справа от D , будет буква Е.
Ответ: (D)
V этап.Творческое домашнее задание
- У одной хозяйки было два клетчатых коврика: один размером 60х60 см, другой 80х80 см. Она решила сделать из них один клетчатый коврик размером 100х100 см. Мастер взялся выполнить эту работу и пообещал, что каждый коврик будет разрезан не более чем на две части и при этом не будет разрезана ни одна клетка. Обещание свое он сдержал. Как он поступил?
- Изображенную на рисунке 18 фигуру требуется разделить на 6 частей, проведя всего лишь 2 прямые. Как это сделать?
Рисунок 18.
VI этап. Подведение итогов занятия.
- Узнали ли вы сегодня на занятии что-то новое? Что именно?
- Понравилась ли вам работа в группах? Какую роль в группе играли вы? (Активно обсуждал, предлагал идеи, слушал других, старался не привлекать к себе внимания и т.п.)
- Какие интересные элементы можно добавить в организацию занятия?
Ответы ребят помогут учителю оценить проведенное занятие, спланировать дальнейшую работу.
urok.1sept.ru
Олимпиада по математике. Геометрические задачи, ч. 1. 5-6 класс.
Олимпиады по математике. 5-6 класс. Геометрические задачи. Часть 1
Часть 1. Самые простые задачи.
Многие из них можно предложить и ученикам начальной школы, которые увлекаются математикой.
Задача 1.
В какой из изображённых в ответах фигур закрашена ровно половина площади?
Варианты ответа:
А: 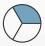 ; Б:
; Б: 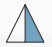 ; В:
; В:  ; Г:
; Г: 
Решение
Легко видеть, что ровно половина площади закрашена в ответе Б. В ответе А закрашена одна третья часть. В ответе Б — одна вторая, в ответе В — три четверти, в ответе Г — одна четверть.
Правильный ответ: Б
Задача 2
Разрежьте квадрат на 2 неравные части и сложите из них треугольник .
Решение:
Отрезать от квадрата треугольник, одна из сторон которого равна стороне квадрата, а другая-половине стороны квадрата. Из полученных треугольника и трапеции сложить треугольник.
Задача 3.
Миша разрисовал 9 квадратиков белым, серым и чёрным цветами так, как показано на рисунке. Какое наименьшее количество квадратиков надо перекрасить, чтобы никакие два квадратика, у которых общая сторона, не были одного цвета?

Решение
В правом верхнем углу есть 2 смежных серых квадратика. Чтобы выполнялось требование задачи, нужно перекрасить правый верхний квадратик в чёрный цвет, а в группе трёх чёрных квадратиков нужно нижний левый перекрасить в серый цвет. Итого 2 квадратика .
Задача 4
Квадрат со стороной 5 см разрезали на 25 равных квадратов. Составьте из них 2 квадрата.
Решение:
Один квадрат можно составить из 9 квадратов, а другой из 16.
Задача 5. Зелёная линия .
На рисунке изображена часть клетчатой доски. Площадь каждой клетки на ней равна 4 см2. Чему равна длина толстой зеленой линии?

Решение
Если площадь квадрата равна 4 см2, то его сторона равна 2 см (так как 2х2 = 4). Внимательно подсчитаем, через сколько сторон квадратиков пройдёт зелёная линия. Она проходит через 9 сторон. Значит, её длина равна 9х2 = 18 см.
Задача 6
Можно ли шахматную доску разрезать на равные фигуры, состоящие из трех клеточек, образующих «уголок»?
Решение:
Нельзя.
Шахматная доска состоит из 64 клеток. 64:3=21 ( ост 1). Одна клетка лишняя.
Задача 7.
Летела стая гусей. Впереди вожак, затем 2 гуся, затем 3 гуся и т. д. ( Построение стаи напоминало треугольник). Вечером гуси остьановились на ночлегш. Их расположение напоминало квадрат. В каждом ряду одинаковое количество гусей, причем число гусей в каждом ряду равно числу рядов. Гусей в стае меньше 50. Сколько гусей в стае?
Ответ:
36 гусей.
Использованы задачи из различных сборников олимпиадных заданий:
Евдокимов М.А. От задачек к задачам. М.: МЦНМО, 2004
Игнатьев Е.И. В царстве смекалки. М.: «Наука», 1987
Русанов В. Н. Математические олимпиады младших школьников.
Материалы международного конкурса «КЕНГУРУ»
infourok.ru
Конспект урока по математике «Наглядная геометрия.Введение» (6 класс)
Тема урока: «Наглядная геометрия. Введение»
Цели урока:
Образовательные: познакомить учащихся с историей возникновения геометрии; систематизировать знания учащихся о простейших геометрических фигурах; начать формировать геометрическое мышление.
Развивающие: развивать математическое мышление, пространственное воображение; развивать математическую речь; развивать творческую и мыслительную деятельность учащихся с помощью решения задач.
Воспитательные: прививать учащимся интерес к предмету с помощью изучения истории и развития науки, применения информационных технологий; расширять кругозор учащихся;
Задачи урока:
— сформировать умения приводить примеры геометрических фигур; обозначать точки, отрезки, прямые, углы; проводить прямую по заданному условию;
— способствовать развитию мыслительных процессов;
— воспитывать творческую, всесторонне-развитую личность.
Оборудование: компьютер, проектор, мультимедийная презентация.
Ход урока:
Организационный момент.
1. Мы начинаем урок математики. Наука математика делится на разделы: арифметика, алгебра, геометрия. Что вы изучаете сейчас?. На следующий год вы начнете изучать алгебру и геометрию. Я предлагаю начать готовиться к этому уже сейчас. Глядя на эти картинки, скажите о каком разделе пойдет речь? Геометрия.
2. Исторический материал. Занятия людей в древности:
Строительство храмов и домов; Украшение орнаментом посуды и жилищ;
Разметка земли, измерение расстояний и площадей, объемов сосудов.
3. Планиметрия и стереометрия.
4. Какие инструменты понадобятся на уроках геометрии? (загадки).
Палочка волшебная
Есть у меня, друзья.
Палочкою этой
Могу построить я
Башню, дом и самолет,
И большущий пароход.
Ноги очень интересны
У таинственного друга:
Если первая на месте,
То другая ходит кругом!
Я люблю прямоту, Я сама прямая.
Сделать новую черту
Вам я помогаю.
Что-нибудь без меня
Начертить сумей-ка.
Угадайте-ка, друзья. Кто же я?
Смотрите: мы раскрыли пасть,
В неё бумагу можно класть.
Бумага в нашей пасти
Разделится на части.
5. С какой самой первой простой фигуры начинается изучение этого предмета?
Я-невидимка! В этом суть моя.
Хотя меня нельзя измерить,
Фигурою считаюсь я. (Точка).
Задание: отметить точки в тетради и обозначить.
Без начала и без края
Линия прямая.
Хоть сто лет по ней иди,
Не найдешь конца пути. (Прямая).
Начертить прямую в тетради. Сколько прямых можно провести через точку К? Сколько прямых можно провести через точки К и N?
Он от солнца прилетает,
Пробивая толщу туч
И в тетрадочке бывает,
А зовется просто — …
Три вершины тут видны,
Три угла, три стороны, —
Ну, пожалуй, и довольно! —
Что ты видишь? — …
6. Мы можем измерить прямую, луч, сторону треугольника. Измерьте, то что можно измерить.
7. Физкультминутка. Берегите зрение.
8 .На уроках геометрии нужно уметь не только строить и измерять. На наших уроках будет много заданий на умение рассуждать, думать логично, делать выводы. Предлагаю потренироваться в играх со спичками. Слайды.
из 10-ти спичек сложена форма ключа. Передвиньте 4 спички так, чтобы получилось три квадрата. 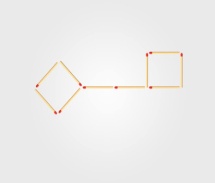
Корова на рисунке смотрит влево. Переложите ровно две спички так, чтобы она смотрела вправо. 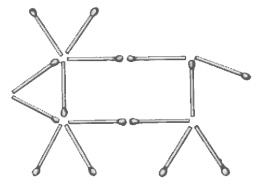
Как нужно переместить «бокал» , переложив две спички, чтобы вишенки оказались снаружи? 
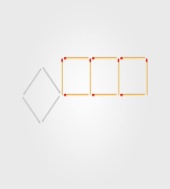
Переложи три спички так, чтобы получилось три квадрата
 Переместите всего две спички и получите 7 квадратов
Переместите всего две спички и получите 7 квадратов

Сложите шесть спичек так, чтобы образовалось четыре треугольника (сторона каждого треугольника должна быть равной длине спички) 
9. А еще геометрия помогает фантазировать, развивать воображение. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Дорисуй каждую из этих фигур так, чтобы превратить её в тот или иной предмет?
Сделайте рисунки, используя фигуры: прямоугольник, овал, окружность, треугольник, квадрат.
10.Итог. Рефлексия. Познакомились с разделом математики: геометрия; учились строить простые фигуры; развивали воображение, фантазировали.
Домашнее задание. Сделать аппликацию из геометр. Фигур. Из цветной бумаги вырежи геометрические фигуры и составь из них аппликацию.
infourok.ru
Открытый урок по математике в 6 классе « Повторение. Простейшие геометрические фигуры. Площади, объёмы»
 Муниципальное общеобразовательное учреждение «Клёмовская средняя общеобразовательная школа» Серебряно-Прудского района Московской области
Муниципальное общеобразовательное учреждение «Клёмовская средняя общеобразовательная школа» Серебряно-Прудского района Московской области
Открытый урок
по математике в 6 классе
« Повторение. Простейшие геометрические фигуры. Площади, объёмы»
( РМО учителей математики)
Учитель: Белинской О.И
Апрель. 2015г.
План открытого урока
Тема урока: Повторение. Простейшие геометрические фигуры. Площади, объёмы.
Тип урока: повторительно- обобщающий.
Цели урока:
1. Обобщить и систематизировать знания учащихся по теме «Простейшие геометрические фигуры. Площади, объёмы».
2. Сформировать умение применять полученные знания при решении задач.
3. Закрепить ранее изученный материал.
Задачи урока:
Обучающие:
Уметь различать простейшие геометрические фигуры, знать их определения и свойства.
Применять полученные знания при решении задач и практических заданий.
Развивающие:
Развивать познавательный интерес учащихся через знакомство с материалом наглядной геометрии.
Прививать навык к самостоятельности в работе.
Развивать такие качества ума, как гибкость, быстрота и логичность мышления.
Воспитательные:
Способствовать воспитанию сотрудничества между учащимися.
Воспитывать настойчивость и упорство в достижении цели.
Воспитывать внимание, любовь к науке математике.
Оборудование: презентация, проекционный экран, мультимедиапроектор, чертёжный инструмент, раздаточный материал для каждого ученика.
Методическая цель: использование нетрадиционных форм обучения при повторении и закреплении изученного материала.
Технология урока.
1. Организационный момент.
2. Вводное слово учителя. Постановка цели урока. (Сегодня на уроке математики мы закрепим ваши знания о простейших геометрических фигурах).
Презентация: «Зачем нужна геометрия».
3. Проведение игры «Путешествие в страну геометрию».
Учащимся предлагается отправиться в путешествие. На классной доске закрепляется несколько дорожек (полоски из бумаги) по количеству учащихся в классе. Каждый ученик выбирает себе дорогу (по цвету). На дорожках подвешивается по 4 конверта с заданиями. Игра проводится в 4 этапа. В каждом конверте два задания: теоретическое и практическое, которое соответствует отдельному геометрическому модулю.
4. Блиц – опрос.
1. Этап – простейшие геометрические фигуры. Танграм..
В теоретическом задании предлагается назвать изображённую фигуру и дать ей определение; и, наоборот, изобразить заданную фигуру. Практическое задание: составить из кусочков танграма изображённую на рисунке фигуру. Рассказать о танграме.
2. Этап – Вычисление площадей и объёмов (прямоугольник, квадрат, прямоугольный параллелепипед, куб).
В теоретическом задании каждому ученику предлагается тест из 4 заданий и по три вопроса. Практическое задание: каждый ученик получает по одной модели (параллелепипед или куб), производит соответственные измерения и вычисляет площадь и объём данной фигуры.
5. Гимнастика для глаз.
3. Этап – окружность и круг. Оригами.
Теоретическое задание: учащиеся изображают окружность по заданному радиусу, окружность по точкам.
Практическое задание: складывают из бумаги фигурки (оригами), рассказывают об оригами.
4. Этап – зашифрованная переписка.
Каждый ученик получает зашифрованное письмо, которое он должен расшифровать с помощью специального шаблона и прочитать (это будет высказывание о геометрии).
За каждое задание учитель присуждает количество баллов, набранное учеником (каждому этапу соответствуют определённые баллы, которые учитель озвучивает перед каждым этапом, либо они написаны на классной доске). На магнитной доске фиксируются баллы, полученные каждым учеником в течение всего урока.
Подводятся итоги. Тот ученик, который набрал максимальное количество баллов, объявляется почётным жителем страны «Геометрия», а остальные ученики просто жителями этой замечательной страны. Соответственно полученным баллам выставляются отметки за урок.
6. Домашнее задание. Повторить материал пунктов
7. Итог урока. Заключительное слово учителя.
Учитель: Решать задачи можно вечно.
Вселенная ведь бесконечна.
Спасибо всем вам за урок,
А главное, чтоб был он впрок!
Мне очень понравилось с вами работать.
А теперь давайте подведем итоги вашей работы на сегодняшнем уроке.
1.Психологическая разгрузка и снятие напряжения.
Учитель: Закройте глазки и вспомните всё, что у нас сегодня было на
уроке.
2. Беседа.
Учитель:
–Какой была тема урока?
–Что нового для себя узнали?
–Что было интереснее всего? Выскажите своё впечатление.
3.Оценка деятельности.
Учитель: У меня в коробочке лежат сердечки трёх цветов.
Если вам не понятен урок, то выберете синее сердечко;
если понятна тема урока, но не очень, то – зелёное сердечко;
если всё понятно – красное.
Приложение.
Блиц-опрос.
1. Сколько углов у треугольника? (три)
2. Как называется отрезок, соединяющий точку окружности с центром этой окружности? (радиус)
3. Сколько градусов содержит прямой угол? (90о), половину какого угла он составляет?
4. Какой угол называется острым?
5. На какой угол поворачивается солдат по команде “кругом”? (1800) , как он называется?
6. Какая фигура называется окружностью?
7. Треугольник, у которого все стороны равны.
8. Какой треугольник называется равнобедренным?
9. Угол больше 90о, но меньше 180о градусов? (тупой)
10. Что такое луч?
11. Какая плоская фигура не имеет площади? (окружность)
12. Какая фигура носит имя Хеопса? (пирамида)
13. В каких единицах измеряется величина угла? (градусы)
14. Старинные меры длины.
15. Сумма длин сторон многоугольника? (периметр)
16. Луч, делящий угол пополам? (биссектриса)
17. Какая фигура называется прямоугольным параллелепипедом?
18. Сколько вершин у куба? (8)
19. Инструмент для построения окружности? (циркуль)
20. Какая фигура лежит в грани куба? (квадрат)
21. Назовите фигуру, для которой любимым числом является «3»? (треугольник), что она означает?
22. Прямоугольник с равными сторонами (квадрат)
23. Чему равна длина окружности? Площадь круга?
24. С помощью какого инструмента измеряют величину угла? (транспортир)
25. Что можно вычислить, перемножив длину, ширину и высоту прямоугольного параллелепипеда? (объем)
26. Угол в 1 градус, рассматриваемый в лупу с четырёхкратным увеличением, имеет величину…? (в 1 градус)
Карточки с заданием 1 этапа:
Теоретическая часть (вопросы):
Практическая часть: с помощью танграма сложить нарисованную фигуру; выполнить задание по карточке — сложить треугольник с помощью некоторых частей танграма.
Карточки с заданием 2 этапа:
Теоретическая часть.
Тесты.
1. Найдите площадь квадрата, сторона которого равна 11см.
1) 44см 2) 121 см 3) 22 см 4) 121 см.
2. Найдите площадь фигуры:
1) 14см 2) 35см 3) 26см 4)27 см
3. Найдите объём прямоугольного параллелепипеда, длина-
-6см, ширина-2см, высота-3см.
1) 16см 2) 11см 3) 36см 4)15см
4. Найдите объём куба с ребром, равным 4м
1) 16м 2) 12м 3) 4м 4) 64м
Практическая часть. Предлагается модель прямоугольного параллелепипеда или куба. Произвести измерения и вычислить площадь поверхности фигуры и её объём.
Карточки с заданием 3 этапа:
Теоретическая часть.
Изобразить окружность по точкам.
Построить окружность диаметром 6 см и найти её длину.
Практическая часть.
Сложить из бумаги фигуру птицы (оригами).
Карточки с заданием 4 этапа:
Прочитать зашифрованное высказывание
о геометрии с помощью специального шаблона.
Варианты высказываний:
1. «Окружающий нас мир — это мир геометрии» А.Д.Александров.
2. «Математика полезна тем, что она трудна» А.Д.Александров
3. «Нет царского пути в геометрию» Евклид.
4. «Всё что превышает геометрию, превышает нас» Паскаль.
5. «Вдохновение нужно в геометрии, как и в поэзии» (не меньше, чем в поэзии) А.С.Пушкин.
6. «Математика – это язык, на котором написана книга природы» Г.Галилей.
7. «Математика – царица наук, арифметика – царица математики» К.Гаусс.
Танграм. Занимательных задач на разрезание квадрата — множество. Если разрезать квадрат на семь частей определённых фигур, то получится популярная китайская головоломка ТАНГРАМ, которую в Китае называют» чи чао ту», т. е. Умственная головоломка из семи частей. Название танграм возникло в Европе, вероятнее всего от слова «тянь» (что означает «китаец» и корня «грамма» ( в переводе с греческого «буква»)
Оригами. Оригами — это складывание фигурок из бумаги. Все фигурки складываются из прямоугольных листов бумаги (одного или двух), без помощи ножниц или клея. Оригами распространилось по всему свету. Во многих странах есть клубы оригамистов, членами которых являются люди самых разных профессий и возрастов. Придумывание их — настоящее искусство!
infourok.ru
Материал (геометрия, 5 класс) по теме: Сборник задач для учащихся 5-6 классов на развитие мышления, логики и пространственного мышления.
Сборник задач для учащихся 5-6 классов на развитие мышления, логики и пространственного мышления.
§ 1. Задачи на разрезание и складывание фигур
Задача 1. На рисунке 1, показан способ разрезания квадрата со стороной в четыре клетки по сторонам клеток на две равные части. Найдите пять других способовсколько существует способов разрезания квадрата на две равные части линиями, идущими по сторонам маленьких квадратиков?
Рис. 1
Задача 2. Эта задача посложнее, так как фигура на рисунке, которую также нужно разрезать на две равные части, не такая простая.
Рис. 2
Задача 3. Над разрезанием этих фигурок (рис. 3) на две равные части подумайте на досуге. Это очень хороший и полезный отдых, гораздо лучше сидения перед телевизором.
Замечание. Разрезать можно не только по сторонам, но и по диагоналям клеточек.
Рис. 3
Задача 4.
М.Артемьев .Разрезалка. Разрежьте фигуру с вырезанным квадратиком на две одинаковые части, из которых можно составить вторую фигуру. Части разрешается и поворачивать, и переворачивать.
Рис. 5
Задача 5. Д.Калинин. Цветной куб. Найдите наибольшее число цветов, в которые можно покрасить ребра куба (каждое ребро одним цветом) так, чтобы для каждой пары цветов нашлись два соседних ребра, покрашенные в эти цвета. Соседними считаются ребра , имеющие общую вершину.
Задача 6. Д Шноль, А. Хачатурян. Квадрат. Квадрат разрезали на двенадцать прямоугольных треугольников. Могут ли десять из них оказаться равными друг другу, а два оставшихся- отличаться от них, и друг от друга?
Задача 7. Д. Шноль. Жесть. Иван Иванович построил сруб, квадратный в основании, и собирается покрывать его крышей. Он выбирает между двумя крышами одинаковой высоты: двускатной и четырехскатной. На какую из этих крыш понадобиться больше жести?
Задача 8. А.В. Шевкин. Фигура изображена на клетчатой бумаге ( рис. 1).
Рис. 6
а) Покажите, как можно разрезать ее на 4 равные части, если резать разрешается только по линейкам клетчатой бумаги.
б) Найдите все возможные фигуры, которые можно получить при таком разрезании.
в) Можно ли ту же фигуру разрезать на 5 равных частей по тем же правилам?
Задача 9. А.В. Шевкин.
а) Покажите, как можно разрезать прямоугольник 9 х 4 (рис. 7) на 2 равные части, если резать разрешается только по линейкам клетчатой бумаги.
б) В каком из найденных случаев из полученных частей можно сложить квадрат?
Рис. 7
Задача 10. А.В. Шевкин.
Фигура изображена на клетчатой бумаге (рис.8)
а) Покажите, как можно разрезать ее на 2 равные части. Если резать разрешается только по линейкам клетчатой бумаги.
б) Найдите все возможные способы разрезания.
Рис. 8
Задача 11. А.В. Шевкин.
а) Покажите, как можно разрезать на 2 равные части фигуру, изображенную на клетчатой бумаге рис. 9, если резать разрешается только по линиям клетчатой бумаги.
б) В каком из найденных случаев из двух полученных равных частей можно сложить квадрат?
Рис. 9
Задача 12. А.В. Фарков.
Квадрат разрезали по ломаной линии, состоящей из трех равных отрезков. Начало разреза в точке А . Получили две равные фигуры. Как это сделали?
Рис. 10
Задача 13. А.В. Фарков.
Как разрезать квадрат 5 х 5 прямыми линиям
Задача 14.
А теперь мы предлагаем вам не задачу, а игру. И она называется ПЕНТАМИНО.
Эта игра была придумана в 50-х годах ХХ в. американским математиком С. Голомбом и очень быстро увлекла не только школьников и студентов, но и профессоров математики. Она заключается в складывании различных фигур из заданного набора ПЕНТАМИНО. Набор ПЕНТАМИНО содержит 12 фигурок, каждая из которых составлена из пяти («пента» в переводе с греческого означает «пять») одинаковых квадратов, причём квадраты «соседствуют» друг с другом только сторонами.
Составьте из пяти квадратов все 12 фигур ПЕНТАМИНО. Сравните свои результаты с рисунком 4.
Изготовьте из картона набор ПЕНТАМИНО со стороной квадратика, равной 2 см.
Уложите все 12 фигур ПЕНТАМИНО в прямоугольник 6 х 10. Сколько разных вариантов вы можете предложить? Фигурки ПЕНТАМИНО можно переворачивать.[1]
Перемешайте фигуры ПЕНТАМИНО на столе, чтобы они лежали произвольно, а затем сложите прямоугольник 6 х 10, не переварачивая ни одной фигурки.[2]
Постройте два прямоугольника 5 х 6.
Рис.4
Задача 15. Головоломка «Танграм»
Задача I. Можно ли составить треугольник, используя только две фигуры танграма? Три? Пять? Шесть? Все семь фигур?
Задача II. Сложите такой же треугольник , используя:
а) один большой треугольник, два маленьких треугольника и параллелограмм.
в) один большой треугольник, один треугольник средний и два маленьких.
Задача III. Очевидно, что из всех семи фигур составляется квадрат. Можно ли составить квадрат из двух фигур? Из трех?
Задача IV. Из каких различных фигур танграма можно составить прямоугольники? Какие еще многоугольники можно составить? [3]
Задача V. Соберите предложенные фигуры из элементов танграма
(приложение 4).
§ 2 Занимательные и старинные задачи.
Задача 1. Основание Карфагена.
Об основании древнего города Карфагена существует следующее предание. Дидона, дочь тирского царя, потеряв мужа, убитого рукой ее брата, бежала в Африку и высадилась со многими жителями Тира на ее северном берегу. Здесь она купила у нумидийского царя столько земли, «сколько занимает воловья шкура». Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, к которой впоследствии был пристроен город.
Попробуйте вычислить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что воловья шкура имеет поверхность 4 кв. м, а ширину ремешков, на которые Дидона ее разрезала, принять равной 1 мм
Задача 2. Четыре куба.
Из одного и того же материала изготовлено четыре сплошных куба различной высоты (рис. 1), а именно в 6 см, 8 см, 10 см и 12 см. надо разместить их на весах так, что бы чашки были в равновесии.
Рис. 1
Какие кубы или какой куб положите вы на одну чашку и какие (или какой) на другую?
Задача 3. Кирпичик.
Строительный кирпич весит 4 кг.
Сколько весит игрушечный кирпичик из того же материала, все размеры которого в четыре раза меньше?
Задача 4. Путь мухи
На внутренней стенке стеклянной цилиндрической банки виднеется капля меда в 3 см от верхнего края сосуда. А на наружной стенке, в точке, диаметрально противоположной, уселась муха (рис. 2).
Укажите мухе кратчайший путь, по которому она может добежать до медовой капли.
Высота банки 20 см; диаметр 10 см.
Рис. 2
Задача 5. Путь жука.
У дороги лежит тесаный гранитный камень в 30 см длины, 20 см высоты и такой же толщины (рис. 3). В точке А — жук, намеревающийся кратчайшим путем направиться к углу В. Как пролегает этот кратчайший путь и какой он длины?
Рис. 3
Задача 6. Число граней
Вот вопрос, который, без сомнения, покажется многим слишком наивным или, напротив, чересчур хитроумным: сколько граней у шестигранного карандаша?
Задача 7.Сколько прямоугольников?
Сколько прямоугольников можете вы насчитать в этой фигуре (рис.4)?
Не спешите с ответом. Обратите внимание на то, что спрашивается не о числе квадратов, а о числе прямоугольников вообще — больших и малых, — какие
Рис.4
можно насчитать в этой фигуре.
Задача 8. Путешествие шмеля
Шмель отправляется в дальнее путешествие. Из родного гнезда он летит прямо на юг, пересекает речку и наконец после целого часа пути спускается на косогор, покрытый душистым клевером. Здесь, перелетая с цветка на цветок, шмель остается полчаса.
Теперь надо посетить сад, где шмель вчера заметил цветущие кусты крыжовника. Сад лежит на запад от косогора, и шмель спешит прямо туда. Спустя 3/4 часа он был уже в саду. Крыжовник в полном цвету, и, чтобы посетить все кусты, понадобилось шмелю 1 1/2 часа.
А затем, не отвлекаясь в стороны, шмель кратчайшей дорогой полетел домой, в родное гнездо.
Сколько времени шмель пробыл в отсутствие родного гнезда?
Рис. 5
Задача 9. ЛЕНТА МЕБИУСА
Рис. 6
Но известно, что лист Мёбиуса — поверхность односторонняя. Пройдя вдоль всей его с поднятым вверх флажком, мы вернёмся в исходную точку — но флажок будет теперь «поднят» в другую сторону (рис. 8)! Это значит, что флажок, не пересекая проективную плоскость, попал из «внешности» во «внутренность» дополнения к ней.[4]
Задача 1. Вырежьте из бумаги три одинаковые полоски в форме прямоугольника со сторонами 200 мм и 20 мм и
а) склейте кольцо, повернув один из концов полоски на 180 ;
б) склейте кольцо, дважды повернув один из концов полоски на 180 ;
в)склейте кольцо , трижды повернув один из концов полоски на 180 .
Маршрут движения мухи начинается и заканчивается на месте склейки кольца, причем она всегда ползет на ровном расстоянии от краев кольца.Для каждого из пунктов а — в определите расстояние, которое проползла муха.[5]
Задача 10. Индийского математика XII века Бхаскары.
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Задача 11. Из китайской «Математики в девяти книгах»
«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша?»
Задача 12. Из учебника «Арифметика» Леонтия Магницкого
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти иметь.»
Задача № 13. Парадокс с разрезанием ковра.
Один фокусник (имя его за давностью забылось) нашел способ, как разрезать квадратный ковер на 4 части, а затем сложить из этих частей прямоугольный ковер большей площади.
Способ этот такой: разобьем каждую сторону квадрата (квадратного ковра) на 8 равных частей, проведем прямые линии, как указано на рис. 7 и разрежем по ним квадрат на 4 части. Затем сложим эти части так, как показано на рис. 8, получим прямоугольный ковер. Площадь прямоугольного ковра больше площади квадратного ковра, т. к. 13 х 5 = 65, а 8 х 8 = 64. В чем же дело? Почему увеличилась площадь?
Вы сможете ответить на этот вопрос самостоятельно, если нарисуете большой квадрат (чем больше, тем лучше), разрежете его по «выкройке» рис.7 и сложите по «выкройке» рис. 8.
Задача 14. Пифагорова головоломка.
Из семи частей квадрата составить снова квадрат, прямоугольник, равнобедренный треугольник, трапецию. Квадрат разрезается так: E, F, K, L – середины сторон квадрата, О – центр квадрата, ОМ ⊥ EF, NF ⊥ EF.[6]
§ 3.Задачи на неравенство треугольника и геометрические преобразования
Задача 1: Грибник выходит из леса в заданной точке. Ему надо дойти до шоссе, которое представляет собой прямую линию, и зайти обратно в лес в другой заданной точке. Как ему сделать это, пройдя по самому короткому пути?
Задача 2. Полуостров представляет собой острый угол, внутри которого находится дом лесника. Как леснику, выйдя из дома, добраться до одного берега полуострова, затем до другого и вернуться домой, пройдя при этом по самому короткому пути?
Задача 3. Точку A, лежащую внутри острого угла, отразили симметрично относительно сторон угла. Полученные точки B и C соединили и точки пересечения отрезка BC со сторонами угла обозначили через D и E. Докажите, что BC/2 > DE.
Задача 4. Точка C лежит внутри данного прямого угла, а точки A и B лежат на его сторонах. Докажите, что периметр треугольника ABC не меньше удвоенного расстояния OC, где O – вершина данного прямого угла.
Задача 5. Муха сидит в вершину X деревянного куба. Как ей переползти в противоположную вершину куба Y, двигаясь по самому короткому пути?
Задача 6. На середине ребра молочного пакета сидит паук, которому необходимо добраться до середины противоположного ребра. Как ему это сделать за наименьшее время?[7]
Список используемой литературы
1. Ресурсы интернет, ru.wikipedia.org
2. Гершинзон М.А. Головоломки профессора Головоломки. М. дет.лит., 1994, с-10.
3. Шевкин А.В. Школьная математическая олимпиада. илекса 2008, с 28-
4. Перельман Я.И. Живая математика, Пилигрим, 1999 г., с-76-150.
5. Олехник С.Н., Нестеренко Ю.В. Потапов М.К. Старинные занимательные задачи. Дрофа, 2002 г.
6. Фарков А.В. готовимся к олимпиаде оп математике. Экзамен, Москва, 2007.
7. А.Д.Блинков, А.В.Семенов, Т.А.Баранова, М.М.Горшкова, К.П.Кочетков, М.Г.Потапова Математика: Интеллектуальные марафоны, турниры, бои. Изд.»Первое сентября» 2003,с.69.
[1] Шевкин А.В. Школьная математическая олимпиада. илекса 2008, с 28-35.
[2] Шарыгин И.Ф. Ерганжиева Л.Н. Наглядная геометрия 5-6 классы, Дрофа, М., 2010 с. 22-25.
[3] Гершинзон М.А. Головоломки профессора Головоломки. М. дет.лит., 1994, с-10.
[4] Перельман Я.И. Живая математика, Пелегрим, 1999 г., с-76-150.
[5] А.Д.Блинков, А.В.Семенов, Т.А.Баранова, М.М.Горшкова, К.П.Кочетков, М.Г.Потапова Математика: Интеллектуальные марафоны, турниры, бои. Изд.»Первое сентября» 2003,с.69.
[6] Олехник С.Н., Нистеренко Ю.В. Потапов М.К. Старинные занимательные задачи. Дрофа, 2002 г.
[7] Фарков А.В. готовимся к олимпиаде по математике. Экзамен, Москва, 2007.
nsportal.ru