Таблица квадратов
Таблица квадратов| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
— версия для печати
- Определение
- Квадрат числа — результат умножения числа на себя.
 Также квадратом числа называется результат возведения числа в степень 2 (во вторую степень).
Также квадратом числа называется результат возведения числа в степень 2 (во вторую степень).
- Пример:
- 92 = 9×9 = 81
- Дополнительно:
- Расширенная таблица квадратов (числа от 1 до 210)
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Таблица квадратов чисел от 1 до 210
Таблица квадратов чисел от 1 до 210| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 |
| 225 | 256 | 289 | 324 | 361 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 |
| 841 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | 1600 | 1681 | 1764 | |
| 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 |
| 3249 | 3364 | 3481 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | 4900 |
| 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | 6400 | 6561 | 6724 | 6889 | 7056 |
| 7225 | 7396 | 7569 | 7744 | 7921 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 |
| 9801 | 10000 | 10201 | 10404 | 10609 | 10816 | 11025 | 11236 | 11449 | 11664 | 11881 | 12100 | 12321 | 12544 |
| 12769 | 12996 | 13225 | 13456 | 13689 | 13924 | 14161 | 14400 | 14641 | 14884 | 15129 | 15376 | 15625 | |
| 16129 | 16384 | 16641 | 16900 | 17161 | 17424 | 17689 | 17956 | 18225 | 18496 | 18769 | 19044 | 19321 | 19600 |
| 19881 | 20164 | 20449 | 20736 | 21025 | 21316 | 21609 | 21904 | 22201 | 22500 | 22801 | 23104 | 23409 | 23716 |
| 24025 | 24336 | 24649 | 24964 | 25281 | 25600 | 25921 | 26244 | 26569 | 26896 | 27225 | 27556 | 27889 | 28224 |
| 28561 | 28900 | 29241 | 29584 | 29929 | 30276 | 30625 | 30976 | 31329 | 31684 | 32041 | 32400 | 32761 | 33124 |
| 33489 | 33856 | 34225 | 34596 | 34969 | 35344 | 35721 | 36100 | 36481 | 36864 | 37249 | 37636 | 38025 | 38416 |
| 38809 | 39204 | 39601 | 40000 | 40401 | 40804 | 41209 | 41616 | 42025 | 42436 | 42849 | 43264 | 43681 | 44100 |
— версия для печати
- Пояснение к таблице:
2209 — квадрат числа [47] — само число
- Определение
- Квадрат числа — результат умножения числа на самого себя.
 Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
- Пример:
- 972 = 97×97 = 9409
- Дополнительно:
- Таблица квадратов двузначных чисел
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Таблицы квадратов чисел от 1 до 300
Квадрат чисел — это число умноженное на само себя или возведение его во вторую степень.
На данной странице можно познакомиться или вспомнить квадраты натуральных чисел от 1 до 300. Так же под каждой таблицей есть возможность сохранения таблицы на компьютер простым перетаскиванием.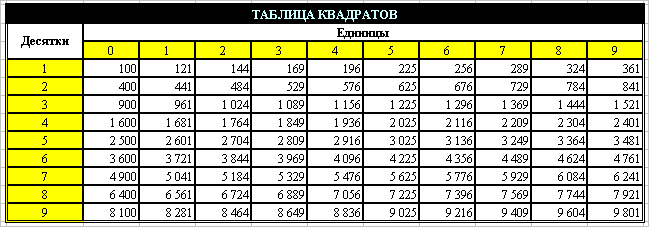
На калькуляторе можно вычислить квадрат любого натурального числа.
Аналогичным образом можно найти и более сложные квадраты, таблица квадратов натуральных чисел от 1 до 10000.
Таблица квадратов натуральных чисел 1 до 100
| 12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 72 = 49 82 = 64 92 = 81 102 = 100 |
112 = 121 122 = 144 132 = 169 142 = 196 152 = 225 162 = 256 172 = 289 182 = 324 192 = 361 202 = 400 |
212 = 441 222 = 484 232 = 529 242 = 576 252 = 625 262 = 676 272 = 729 282 = 784 292 = 841 302 = 900 |
312 = 961 322 = 1024 332 = 1089 342 = 1156 352 = 1225 362 = 1296 372 = 1369 382 = 1444 392 = 1521 402 = 1600 |
412 = 1681 422 = 1764 432 = 1849 442 = 1936 452 = 2025 46 472 = 2209 482 = 2304 492 = 2401 502 = 2500 |
| 512 = 2601 522 = 2704 532 = 2809 542 = 2916 552 = 3025 562 = 3136 572 = 3249 582 = 3364 592 = 3481 602 = 3600 |
612 = 3721 622 = 3844 632 = 3969 642 = 4096 652 = 4225 662 = 4356 672 = 4489 682 = 4624 692 = 4761 702 = 4900 |
712 = 5041 722 = 5184 732 = 5329 742 = 5476 752 = 5625 762 = 5776 772 = 5929 782 = 6084 792 = 6241 802 = 6400 |
812 = 6561 822 = 6724 832 = 6889 842 = 7056 852 = 7225 862 = 7396 872 = 7569 882 = 7744 892 = 7921 902 = 8100 |
912 = 8281 922 = 8464 932 = 8649 942 = 8836 952 = 9025 962 = 9216 972 = 9409 982 = 9604 992 = 9801 1002 = 10000 |
Таблица квадратов натуральных чисел 100 до 200
1022 = 10 404
1032 = 10 609
1042 = 10 816
1052 = 11 025
1062 = 11 236
1072 = 11 449
1082 = 11 664
1092 = 11 881
1102 = 12 100
1122 = 12 544
1132 = 12 769
1142 = 12 996
1152 = 13 225
1162 = 13 456
1172 = 13 689
1182 = 13 924
1192 = 14 161
1202 = 14 400
1222 = 14 884
1232 = 15 129
1242 = 15 376
1252 = 15 625
1262 = 15 876
1272 = 16 129
1282 = 16 384
1292 = 16 641
1302 = 16 900
1322 = 17 424
1332 = 17 689
1342 = 17 956
1352 = 18 225
1362 = 18 496
1372 = 18 769
1382 = 19 044
1392 = 19 321
1402 = 19 600
1422 = 20 164
1432 = 20 449
1442 = 20 736
1452 = 21 025
1462 = 21 316
1472 = 21 609
1482 = 21 904
1492 = 22 201
1502 = 22 500
1522 = 23 104
1532 = 23 409
1542 = 23 716
1552 = 24 025
1562 = 24 336
1572 = 24 649
1582 = 24 964
1592 = 25 281
1602 = 25 600
1622 = 26 244
1632 = 26 569
1642 = 26 896
1652 = 27 225
1662 = 27 556
1672 = 27 889
1682 = 28 224
1692 = 28 561
1702 = 28 900
1722 = 29 584
1732 = 29 929
1742 = 30 276
1752 = 30 625
1762 = 30 976
1772 = 31 329
1782 = 31 684
1792 = 32 041
1802 = 32 400
1822 = 33 124
1832 = 33 489
1842 = 33 856
1852 = 34 225
1862 = 34 596
1872 = 34 969
1882 = 35 344
1892 = 35 721
1902 = 36 100
1922 = 36 864
1932 = 37 249
1942 = 37 636
1952 = 38 025
1962 = 38 416
1972 = 38 809
1982 = 39 204
1992 = 39 601
2002 = 40 000
Таблица квадратов натуральных чисел 200 до 300
2022 = 40 804
2032 = 41 209
2042 = 41 616
2052 = 42 025
2062 = 42 436
2072 = 42 849
2082 = 43 264
2092 = 43 681
2102 = 44 100
2122 = 44 944
2132 = 45 369
2142 = 45 796
2152 = 46 225
2162 = 46 656
2172 = 47 089
2182 = 47 524
2192 = 47 961
2202 = 48 400
2222 = 49 284
2232 = 49 729
2242 = 50 176
2252 = 50 625
2262 = 51 076
2272 = 51 529
2282 = 51 984
2292 = 52 441
2302 = 52 900
2322 = 53 824
2332 = 54 289
2342 = 54 756
2352 = 55 225
2362 = 55 696
2372 = 56 169
2382 = 56 644
2392 = 57 121
2402 = 57 600
2422 = 58 564
2432 = 59 049
2442 = 59 536
2452 = 60 025
2462 = 60 516
2472 = 61 009
2482 = 61 504
2492 = 62 001
2502 = 62 500
2522 = 63 504
2532 = 64 009
2542 = 64 516
2552 = 65 025
2562 = 65 536
2572 = 66 049
2582 = 66 564
2592 = 67 081
2602 = 67 600
2622 = 68 644
2632 = 69 169
2642 = 69 696
2652 = 70 225
2662 = 70 756
2672 = 71 289
2682 = 71 824
2692 = 72 361
2702 = 72 900
2722 = 73 984
2732 = 74 529
2742 = 75 076
2752 = 75 625
2762 = 76 176
2772 = 76 729
2782 = 77 284
2792 = 77 841
2802 = 78 400
2822 = 79 524
2832 = 80 089
2842 = 80 656
2852 = 81 225
2862 = 81 796
2872 = 82 369
2882 = 82 944
2892 = 83 521
2902 = 84 100
2922 = 85 264
2932 = 85 849
2942 = 86 436
2952 = 87 025
2962 = 87 616
2972 = 88 209
2982 = 88 804
2992 = 89 401
3002 = 90 000
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица квадратов натуральных (целых) чисел от 1 до 999. Таблица квадратных корней. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Квадратное число — это… Что такое Квадратное число?
Квадрат или квадратное число — целое число, которое может быть записано в виде квадрата некоторого другого целого числа (иными словами, число, квадратный корень которого целый). Геометрически такое число может быть представлено в виде площади квадрата с целочисленной стороной.
Например, 9 — это квадратное число, так как оно может быть записано в виде 3 × 3 (может быть представлено в виде квадрата 3 × 3 точки).
Примеры
Последовательность квадратов начинается так:
- 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, … (последовательность A000290 в OEIS)
| _0 | _1 | _2 | _3 | _4 | _5 | _6 | _7 | _8 | _9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0_ | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1_ | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2_ | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3_ | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4_ | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5_ | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6_ | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7_ | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8_ | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9_ | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Свойства
- Четыре различных квадрата не могут образовывать арифметическую прогрессию.
 [1] Арифметические прогрессии из трёх квадратов существуют — например: 1, 25, 49.
[1] Арифметические прогрессии из трёх квадратов существуют — например: 1, 25, 49. - Каждое натуральное число может быть представлено как сумма четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).
- 4900 — единственное число > 1, которое является одновременно квадратным и пирамидальным.
- Суммы пар последовательных треугольных чисел являются квадратными числами.
- Последняя цифра квадрата в десятичной записи может быть равной 0, 1, 4, 5, 6 или 9 (квадратичные вычеты по модулю 10).
- Квадрат не может оканчиваться нечётным количеством нолей.
- Квадрат либо делится на 4, либо при делении на 8 даёт остаток 1. Квадрат либо делится на 9, либо при делении на 3 даёт остаток 1.
- Две последние цифры квадрата в десятичной записи могут принимать значения 00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89 или 96 (квадратичные вычеты по модулю 100). Зависимость предпоследней цифры квадрата от последней можно представить в виде следующей таблицы:
последняя
цифрапредпоследняя
цифра0 0 5 2 1, 4, 9 чётная 6 нечётная
Геометрическое представление
| 1 | |
|---|---|
Обобщения
Понятие квадрата обобщается на произвольные мультипликативные группы.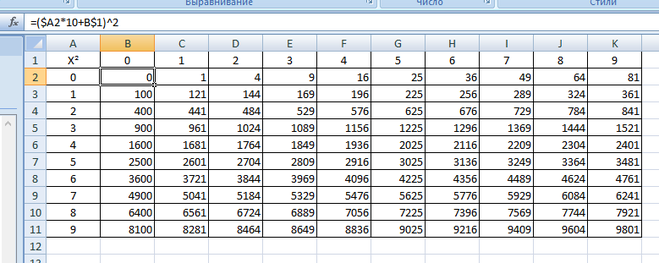 В частности, в кольцах вычетов квадратам соответствуют квадратичные вычеты.
В частности, в кольцах вычетов квадратам соответствуют квадратичные вычеты.
См. также
Примечания
Ссылки
| Сумма цифр | 13 |
| Произведение цифр | 0 |
| Произведение цифр (без учета ноля) | 56 |
| Все делители числа | 1, 2, 4, 8, 13, 16, 26, 52, 104, 169, 208, 338, 676, 1352, 2704 |
| Наибольший делитель из ряда степеней двойки | 16 |
| Количество делителей | 15 |
| Сумма делителей | 5673 |
| Простое число? | Нет |
| Полупростое число? | Нет |
| Обратное число | 0. 0003698224852071006 0003698224852071006 |
| Римская запись | MMDCCIV |
| Индо-арабское написание | ٢٧٠٤ |
| Азбука морзе | ..— —… —— ….- |
| Факторизация | 2 * 2 * 2 * 2 * 13 * 13 |
| Двоичный вид | 101010010000 |
| Троичный вид | 10201011 |
| Восьмеричный вид | 5220 |
| Шестнадцатеричный вид (HEX) | A90 |
| Перевод из байтов | 2 килобайта 656 байтов |
| Цвет | RGB(0, 10, 144) или #000A90 |
| Наибольшая цифра в числе (возможное основание) | 7 (8, восьмеричный вид) |
| Перевод восьмеричной записи в десятичную | 1476 |
| Число Фибоначчи? | Нет |
| Нумерологическое значение | 4 энергия земли, постоянство, однообразие, практичность, упорство, надежность, терпеливость, усердие, стойкость |
| Синус числа | 0. 7902854647755708 7902854647755708 |
| Косинус числа | -0.6127388384658345 |
| Тангенс числа | -1.289759054206968 |
| Натуральный логарифм | 7.902487437162855 |
| Десятичный логарифм | 3.4320066872695985 |
| Квадратный корень | 52 |
| Кубический корень | 13.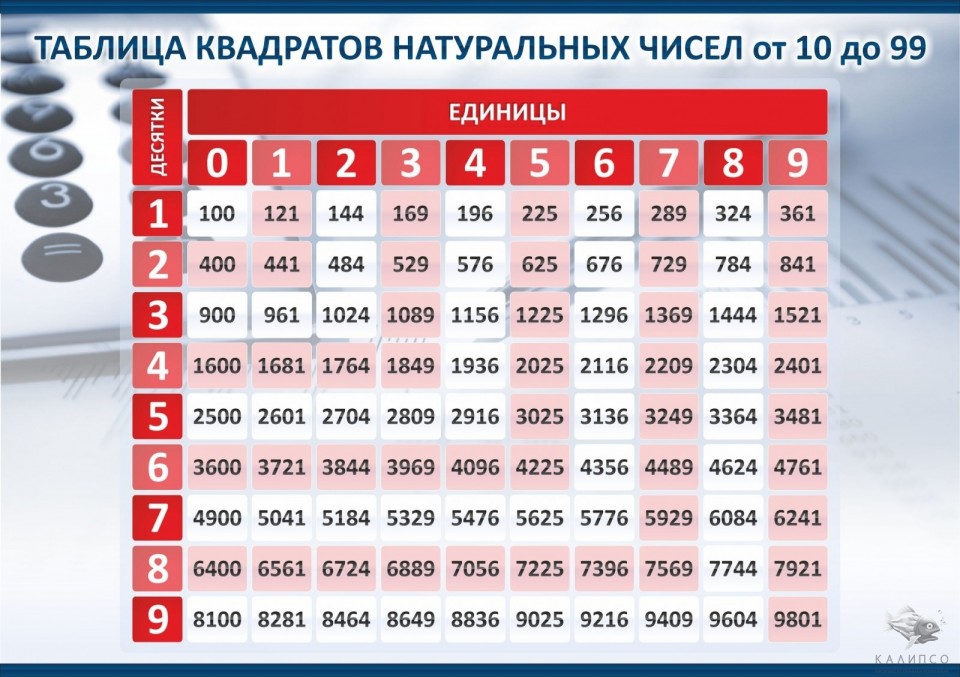 93163953576523 93163953576523 |
| Квадрат числа | 7311616 |
| Перевод из секунд | 45 минут 4 секунды |
| Дата по UNIX-времени | Thu, 01 Jan 1970 00:45:04 GMT |
| MD5 | 81c2f886f91e18fe16d6f4e865877cb6 |
| SHA1 | 326ebca10f7d586cf0cc96fe960636824b717d45 |
| Base64 | MjcwNA== |
| QR-код числа 2704 |
Как извлекать квадратный корень.
 Как найти квадратный корень? Свойства, примеры извлечения корня
Как найти квадратный корень? Свойства, примеры извлечения корняУченики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 9 2 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676 .
Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26 .
Еще пример: √6889 .
Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.
Проверяем: 83 2 = 6889.
Ответ: √6889 = 83 .
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025 .
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Еще пример: √20736 . Разложим число 20736 на множители:
Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах.
Вычислите √279841 .
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример . Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается .
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Для вычисления квадратного корня без калькулятора существует несколько методов.
Как найти корень из числа – 1 способ
- Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
- Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.
- Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
- Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
- В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
- Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
- Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18. - Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.
Как найти корень из числа – 2 способ
- Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
- В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
- Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
- При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень . Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней .
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.
Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
…
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа .
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 20 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
900 30 2
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 50 2
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 60 2
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.
При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.
К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Один из простейших способов вычисления корней заключается в использовании специальной таблицы . Что же она собой представляет и как ей правильно воспользоваться?
При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.
Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.
Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.
Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.
Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.
Разложение на простые множители
Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители . Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.
Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона . Его суть заключается в использовании приближённой формулы:
√R = √a + (R — a) / 2√a,
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.
Теперь проверим точность метода :
10,55² = 111,3025.
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
10,536² = 111,0073.
После повторного применения формулы погрешность стала совсем незначительной.
Вычисление корня делением в столбик
Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора .
Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой. Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
- Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
- Повторим шаги 3-6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
- Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.
Поразрядное вычисление значения квадратного корня
Метод обладает высокой точностью . Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.
Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.
- Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10²
- Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20
- Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27
- Каждый последующий разряд (десятые, сотые и т. д.) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.
Корнем n -ой степени натурального числа a называется такое число, n -ая степень которого равна a . Корень обозначается так: . Символ √ называется знаком корня или знаком радикала , число a — подкоренное число , n — показатель корня .
Действие, посредством которого находится корень данной степени, называется извлечением корня .
Так как, согласно определению понятия о корне n -ой степени
то извлечение корня — действие, обратное возведению в степень , при помощи которого по данной степени и по данному показателю степени находят основание степени.
Квадратный корень
Квадратным корнем из числа a называется число, квадрат которого равен a .
Действие, с помощью которого вычисляется квадратный корень, называется извлечением квадратного корня.
Извлечение квадратного корня — действие обратное возведению в квадрат (или возведению числа во вторую степень). При возведении в квадрат известно число, требуется найти его квадрат. При извлечении квадратного корня известен квадрат числа, требуется по нему найти само число.
Поэтому для проверки правильности проведённого действия, можно найденный корень возвести во вторую степень и, если степень будет равна подкоренному числу, значит корень был найден правильно.
Рассмотрим извлечение квадратного корня и его проверку на примере. Вычислим или (показатель корня со значением 2 обычно не пишут, так как 2 — это самый маленький показатель и следует помнить, что если над знаком корня нет показателя, то подразумевается показатель 2), для этого нам нужно найти число, при возведении которого во вторую степень получится 49. Очевидно, что таким числом является 7, так как
7 · 7 = 7 2 = 49.
Вычисление квадратного корня
Если данное число равно 100 или меньше, то квадратный корень из него можно вычислить с помощью таблицы умножения . Например квадратный корень из 25 — это 5, потому что 5 · 5 = 25.
Теперь рассмотрим способ нахождения квадратного корня из любого числа без использования калькулятора. Для примера возьмём число 4489 и начнём поэтапно вычислять.
- Определим, из каких разрядов должен состоять искомый корень. Так как 10 2 = 10 · 10 = 100, а 100 2 = 100 · 100 = 10000, то становится ясно, что искомый корень должен быть больше 10 и меньше 100, т.е. состоять из десятков и единиц.
- Находим число десятков корня. От перемножения десятков получаются сотни, в нашем числе их 44, поэтому корень должен содержать столько десятков, чтобы квадрат десятков давал приблизительно 44 сотни. Следовательно в корне должно быть 6 десятков, потому что 60 2 = 3600, а 70 2 = 4900 (это слишком много). Таким образом мы выяснили, что наш корень содержит 6 десятков и несколько единиц, так как он находится в в диапазоне от 60 до 70.
- Определить число единиц в корне поможет таблица умножения. Посмотрев на число 4489, мы видим, что последняя цифра в нём 9. Теперь смотрим в таблицу умножения и видим что 9 единиц может получится только при возведении в квадрат чисел 3 и 7. Значит корень числа будет равен 63 или 67.
- Проверяем полученные нами числа 63 и 67 возводя их в квадрат: 63 2 = 3969, 67 2 = 4489.
квадратный корень из 676 — Как найти квадратный корень из 676?
676 можно получить возведением в квадрат 26. Следовательно, это точное квадратное число. Следовательно, квадратный корень из 676 является рациональным числом. В этом мини-уроке мы научимся находить квадратный корень из 676 вместе с решенными примерами. Давайте посмотрим, что такое квадратный корень из 676.
- Квадратный корень из 676 : √ 676 = 26
- Квадрат из 676: 676 2 = 4,56,976
Что такое квадратный корень из 676?
Число 676 в квадрате равно 26.Следовательно, квадратный корень из 676 равен 26. Он записывается как
.√ 676 = 26
Ответ, который получается при возведении в квадрат 26: 676. Следовательно, 676 — это полный квадрат.
Является ли квадратный корень из 676 рациональным или иррациональным?
Поскольку 676 равно √ 676 = 26, можно легко выразить √ 676 в форме p / q. Это делает √ 676 рациональным числом.
Как найти квадратный корень из 676?
Существуют разные методы определения квадратного корня из любого числа.Щелкните здесь, чтобы узнать об этом подробнее. Мы можем определить квадратный корень из 676 двумя способами:
- Квадратный корень из 676 по длинному делению
- Квадратный корень из 676 по простому факторизации
Квадратный корень из 676 по длинному делению
Квадратный корень из 676 можно найти следующим образом.
- Шаг 1 : Мы объединяем цифры заданного числа в пары, начиная с цифры на месте. Поставьте горизонтальную полосу, чтобы обозначить сопряжение.
- Шаг 2 : Теперь мы находим число, которое при умножении на само себя дает произведение, меньшее или равное 6. Как мы знаем, 2 × 2 = 4 <6. Следовательно, делитель равен 2, а частное равно 2.
- Шаг 3 : Теперь нам нужно уменьшить 00 и умножить частное на 2. Это дает нам 4. Следовательно, 4 — это начальная цифра нового делителя.
- Шаг 4 : 6 помещается на место нового делителя, потому что, когда 46 умножается на 6, мы получаем 276.Полученный ответ равен 0. Теперь получен новый делитель 52.
- Шаг 5 : Следовательно, квадратный корень из 676 равен 26.
Квадратный корень из 676 путем простого факторизации
676 — это идеальный квадрат, следовательно, мы также можем выразить его как (2 × 2 × 13 × 13). Повторяющиеся числа в квадратном корне — 2 и 13. Следовательно, квадратный корень из 676 равен 2 × 13 = 26.
Квадратный корень из 676 равен 26.
Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров
Важные примечания:
- 676 — это точный квадрат, поскольку значение, полученное после извлечения квадратного корня, является целым числом.
- Квадратный корень из 676 можно упростить до 26, используя разложение на простые множители 676 или выразив 676 как квадрат 26.
Аналитический центр:
- Может ли квадратный корень 676 быть десятичным?
- Являются ли — √ 676 и √ -676 одинаковыми?
Часто задаваемые вопросы о квадратном корне из 676
Каковы два квадратных корня из 676?
Квадратные корни из 676 равны -26 и 26.
Является ли 676 идеальным квадратом?
Да, 676 — правильный квадрат.
Есть ли у 676 квадратный корень?
Да, 676 имеет квадратный корень. √ 676 — это 26.
Можно ли упростить квадратный корень из 676?
676 можно разбить как произведение 2 × 2 × 13 × 13. Квадратный корень из 676 дает результат 26.
Является квадратный корень из 676 рациональным или иррациональным?
Квадратный корень из 676 является рациональным.
Является ли квадратный корень из 676 действительным числом?
Да, квадратный корень из 676 — действительное число.
Является ли 676 идеальным квадратом?
Почему 676 — идеальный квадрат?
Полный квадрат — это число, которое может быть выражено как произведение двух равных целых чисел.
Единственный способ точно вычислить, является ли число точным квадратом, — это найти множители. Прежде чем мы приступим к поиску факторов, есть небольшой трюк: можно использовать, чтобы определить, нужна ли вам дополнительная работа.
Сначала попробуйте эти шаги:
- Число, которое является идеальным квадратом, никогда не заканчивается на 2, 3, 7 или 8. Если ваше число заканчивается любым из этих чисел, вы можете остановиться здесь, потому что ваше число не является точным квадратом.
- Получите цифровой корень числа. Цифровой корень по сути представляет собой сумму всех цифр. Если вы заблудились, не волнуйтесь, мы рассмотрим каждый шаг более подробно ниже.
- Все возможные числа, представляющие собой полный квадрат, имеют цифровой корень из 1, 4, 7, 9.
Давай попробуем …
Шаг 1:
Какое последнее число из 676? Это номер: 676. Ответ: 6. Есть ли 6 в списке чисел, которые никогда не бывают полными квадратами (2, 3, 7 или 8)?
Ответ: НЕТ, 6 нет в списке чисел, которые никогда не бывают полными квадратами. Перейдем к следующему шагу.
Шаг 2:
Теперь нам нужно получить цифровой корень числа.Вот как это сделать:
- Разделите число и сложите каждую цифру вместе:
6 + 7 + 6 = 19
Если ответ состоит из более чем одной цифры, вы должны снова сложить каждую цифру ответа:
1 + 9 = 10
Ответ снова состоит из нескольких цифр, нам нужно добавить каждую цифру еще раз:
1 + 0 = 1
Какой цифровой корень у числа 676?
Ответ: 1
Шаг 3:
Итак, теперь мы знаем, что цифровой корень 676 1 .Находится ли 1 в списке цифровых корней, которые всегда являются квадратным корнем (1, 4, 7 или 9)?
Ответ: ДА, 1 находится в списке цифровых корней, которые всегда являются точными квадратами. Мы можем сделать вывод, что 676 может быть идеальным квадратом!
Факторинг
Итак, теперь мы знаем, что 676 может быть точным квадратом. Мы должны найти множители числа, чтобы быть уверенными.
Вот все множители 676:
1 x 6762 x 3384 x 16913 x 5226 x 26
Выше оранжевым цветом выделена комбинация факторов, которая делает 676 точным квадратом. Вы понимаете почему? Число может быть полным квадратом только в том случае, если произведение двух точно таких же чисел равно исходному числу.
Вот доказательство: 26 х 26 = 676
Другие примеры
Найдите квадратный корень из следующих чисел по математике класса 10 CBSE
Подсказка: Сначала мы разложим заданные числа на их простые множители, а затем объединим аналогичные множители.Затем мы выберем по одному для каждой пары и, наконец, возьмем их продукт, чтобы получить ответ. Полный пошаговый ответ:
В этом вопросе нам даны некоторые числа, и мы должны найти квадратный корень из каждого из них, используя метод разложения на простые множители. Мы выполним определенные шаги, чтобы найти квадратный корень путем разложения на простые множители следующим образом:
1. Мы должны сначала разделить данное число на его простые множители.
2. Теперь мы должны сопоставить одинаковые факторы, которые равны друг другу.
3. Теперь возьмем по одному множителю из каждой пары.
4. Затем мы возьмем произведение множителей, полученных таким образом на шаге 3.
Например, мы найдем квадратный корень из 256. Итак, мы сначала разложим его на множители, как указано ниже,
$ \ begin {align}
& 2 \ влево | \! {\ underline {\,
256 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
128 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
64 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
32 \,}} \ right.\\
& 2 \ left | \! {\ underline {\,
16 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
8 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
4 \,}} \ right. \\
& \ text {} 2 \\
\ end {align} $
Итак, мы можем записать 256 как, $ 2 \ times 2 \ times 2 \ times 2 \ times 2 \ times 2 \ times 2 \ times 2 $ . Теперь мы составим пары этих факторов, так что мы получим $ \ overline {2 \ times 2} \ times \ overline {2 \ times 2} \ times \ overline {2 \ times 2} \ times \ overline {2 \ times 2} $.Теперь мы возьмем один множитель из каждой из этих пар, так что мы получим $ 2 \ times 2 \ times 2 \ times 2 $. Таким образом, мы получаем произведение этого числа как 16. Следовательно, квадратный корень из 256 равен 16. Точно так же мы теперь найдем квадратные корни всех заданных чисел один за другим.
(i) 121
Сначала мы разложим его на множители, как показано ниже:
$ \ begin {align}
& 11 \ left | \! {\ underline {\,
121 \,}} \ right. \\
& \ text {} 11 \\
\ end {align} $
Итак, мы записываем множители как $ 11 \ times 11 $.И мы получим пару как $ \ overline {11 \ times 11} $. Теперь возьмем один множитель пары, то есть 11.
Итак, мы получаем квадратный корень из 121 как 11.
(ii) 225
Сначала мы разложим его на множители, как показано ниже:
$ \ begin {align}
& 3 \ left | \! {\ underline {\,
225 \,}} \ right. \\
& 3 \ left | \! {\ underline {\,
75 \,}} \ right. \\
& 5 \ left | \! {\ underline {\,
25 \,}} \ right. \\
& \ text {5} \\
\ end {align} $
Итак, множители равны $ 3 \ times 3 \ times 5 \ times 5 $.Соединяя их, мы получим $ \ overline {3 \ times 3} \ times \ overline {5 \ times 5} $. Итак, вычитая по одному множителю из каждой пары, мы получаем $ 3 \ умноженные на 5 $. Теперь мы найдем их произведение, равное 15.
Итак, квадратный корень из 225 равен 15.
(iii) 441
Сначала мы разложим его на множители следующим образом:
$ \ begin {align}
& 3 \ left | \! {\ underline {\,
441 \,}} \ right. \\
& 3 \ left | \! {\ underline {\,
147 \,}} \ right. \\
& 7 \ left | \! {\ underline {\,
49 \,}} \ right.\\
& \ text {7} \\
\ end {align} $
Итак, множители 441 равны $ 3 \ times 3 \ times 7 \ times 7 $. Теперь мы можем получить пары как $ \ overline {3 \ times 3} \ times \ overline {7 \ times 7} $. И, взяв по одному множителю из каждой пары, мы получаем $ 3 \ умножить на 7 $. Произведение $ 3 \ умножить на 7 $ равно 21.
Итак, квадратный корень из 441 будет 21.
(iv) 484
Итак, мы разложим его на множители следующим образом:
$ \ begin {align}
& 2 \ left | \! {\ underline {\,
484 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
242 \,}} \ right.\\
& 11 \ left | \! {\ underline {\,
121 \,}} \ right. \\
& \ text {11} \\
\ end {align} $
Итак, мы получаем множители как $ 2 \ times 2 \ times 11 \ times 11 $. Мы объединим их в пары как $ \ overline {2 \ times 2} \ times \ overline {11 \ times 11} $. Мы возьмем 2 и 11 из этой пары и получим их произведение как 22.
Итак, квадратный корень из 484 будет 22.
(v) 676
Факторизуем его как
$ \ begin {align}
& 2 \ слева | \! {\ underline {\,
676 \,}} \ right.\\
& 2 \ left | \! {\ underline {\,
338 \,}} \ right. \\
& 13 \ left | \! {\ underline {\,
169 \,}} \ right. \\
& \ text {13} \\
\ end {align} $
Мы получаем множители 676 как, $ 2 \ times 2 \ times 13 \ times 13 $. Соединяя их, мы получаем $ \ overline {2 \ times 2} \ times \ overline {13 \ times 13} $. Итак, взяв по одному из пары, мы получим $ 2 \ умножить на 13 $, а их произведение равно 26.
Итак, квадратный корень из 676 будет равен 26.
(vi) 900
Мы разложим его на множители следующим образом:
$ \ begin {align}
& 2 \ left | \! {\ underline {\,
900 \,}} \ right.\\
& 2 \ left | \! {\ underline {\,
450 \,}} \ right. \\
& 3 \ left | \! {\ underline {\,
225 \,}} \ right. \\
& 3 \ left | \! {\ underline {\,
75 \,}} \ right. \\
& 5 \ left | \! {\ underline {\,
25 \,}} \ right. \\
& \ text {5} \\
\ end {align} $
Итак, множители равны $ 2 \ times 2 \ times 3 \ times 3 \ times 5 \ times 5 $, а их пары равны $ \ overline {2 \ times 2} \ times \ overline {3 \ times 3} \ times \ overline {5 \ times 5} $.Взяв по одной из каждой пары, мы получим $ 2 \ times 3 \ times 5 $. Их произведение равно 30.
Итак, квадратный корень из 900 равен 30.
(vii) 1296
Мы разложим 1296 на множители как,
$ \ begin {align}
& 2 \ left | \! {\ underline {\,
1296 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
648 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
324 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
162 \,}} \ right. \\
& 3 \ left | \! {\ underline {\,
81 \,}} \ right.\\
& 3 \ left | \! {\ underline {\,
27 \,}} \ right. \\
& 3 \ left | \! {\ underline {\,
9 \,}} \ right. \\
& \ text {3} \\
\ end {align} $
Итак, множители: $ 2 \ times 2 \ times 2 \ times 2 \ times 3 \ times 3 \ times 3 \ times 3 $ и мы можно соединить их как, $ \ overline {2 \ times 2} \ times \ overline {2 \ times 2} \ times \ overline {3 \ times 3} \ times \ overline {3 \ times 3} $. Теперь мы возьмем по одному множителю из пар, так что получим $ 2 \ times 2 \ times 3 \ times 3 $. Мы получаем их продукт как, 36.
Итак, квадратный корень из 1296 равен 36.
(viii) 1024
Мы найдем множители следующим образом:
$ \ begin {align}
& 2 \ left | \! {\ underline {\,
1024 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
512 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
256 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
128 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
64 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
32 \,}} \ right.\\
& 2 \ left | \! {\ underline {\,
16 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
8 \,}} \ right. \\
& 2 \ left | \! {\ underline {\,
4 \,}} \ right. \\
& \ text {2} \\
\ end {align} $
Итак, множители: $ 2 \ times 2 \ times 2 \ times 2 \ times 2 \ times 2 \ times 2 \ times 2 \ times 2 \ раз 2 $. Мы можем соединить их следующим образом: $ \ overline {2 \ times 2} \ times \ overline {2 \ times 2} \ times \ overline {2 \ times 2} \ times \ overline {2 \ times 2} \ times \ overline {2 \ times 2} $.Теперь мы берем один множитель из пар, поэтому получаем $ 2 \ times 2 \ times 2 \ times 2 \ times 2 $, и их произведение равно 32.
Итак, квадратный корень из 1024 будет 32.
Примечание. :
Ученики должны внимательно выбирать одинаковые факторы при выборе из пар, иначе они могут получить неправильный ответ. Этот метод используется для меньших чисел, а для больших чисел квадратный корень находится методом деления.
Вы в одном шаге от ответа!
Подпишитесь бесплатно!
Регистрируясь, вы также получаете доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам БЕСПЛАТНО!
Калькулятор квадратного корня
О калькуляторе квадратного корня
Калькулятор квадратного корня используется для нахождения квадратного корня из введенного числа.
Квадратный корень
В математике квадратный корень из числа x — это такое число r, что r 2 = x.
Например:
1. Квадратный корень из 25 равен 5, потому что 5 2 = 25.
3. Квадратный корень из 2 приблизительно равен 1,41421356237.
3. Квадратный корень числа пи (π) приблизительно равен 1,77245385102.
Таблица квадратного корня
Ниже приводится таблица квадратного корня от 1 до 1000 с округлением до 5 цифр:
| x | √x | |||
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | 1.41421 | |||
| 3 | 1.73205 | |||
| 4 | 2 | |||
| 5 | 2.23607 | |||
| 6 | 2.44932 7 | 2.44949 | ||
| 9 | 3 | |||
| 10 | 3,16228 | |||
| 11 | 3,31662 | |||
| 12 | 3,4641 | |||
| 60555 | ||||
| 14 | 3,74166 | |||
| 15 | 3,87298 | |||
| 16 | 4 | |||
| 17 | 4,12311 | |||
| 20 | 4.47214 | |||
| 21 | 4.58258 | |||
| 22 | 4.69042 | |||
| 23 | 4.79583 | |||
| 24 | 4,89898 | |||
| 25 | 5 | |||
| 26 | 5,09902 | |||
| 27 5,3 | 5,19615 | 5,3 | ||
| 30 | 5,47723 | |||
| 31 | 5,56776 | |||
| 32 | 5,65685 | |||
| 33 | 5.74456 | |||
| 34 | 5.83095 | |||
| 35 | 5. | |||
| 36 | 6 | |||
| 37 | 6.08276 | 6.08276 | 37 | 6.08276 |
| 40 | 6.32456 | |||
| 41 | 6.40312 | |||
| 42 | 6.48074 | |||
| 43 | 6.55744 | |||
| 44 | 6,63325 | |||
| 45 | 6,7082 | |||
| 46 | 6,78233 | |||
| 47 | 6,85565 | |||
| 48 | 6,9282 | |||
| 49 | 7 | |||
| 50 | 7.07107 | |||
| 51 | 7.14143 | |||
| 52 | 7.2111 | |||
| 53 | 7.28011 | |||
| 54 | 7,34847 | |||
| 55 | 7,4162 | |||
| 56 | 7,48331 | |||
| 57 | 7,54983 | 57 | 7,54983 | |
| 60 | 7.74597 | |||
| 61 | 7.81025 | |||
| 62 | 7.87401 | |||
| 63 | 7. | |||
| 64 | 8 | |||
| 65 | 8.06226 | |||
| 66 | 8.12404 | |||
| 67 | 8.18535 | |||
| 70 | 8.3666 | |||
| 71 | 8.42615 | |||
| 72 | 8.48528 | |||
| 73 | 8.544 | |||
| 74 | 8.60233 | |||
| 75 | 8.66025 | |||
| 76 | 8.7178 | |||
| 77 | 8.74354 904 | |||
| 80 | 8. | |||
| 81 | 9 | |||
| 82 | 9.05539 | |||
| 83 | 9.11043 | |||
| 84 | 9.16515 | |||
| 85 | 9.21954 | |||
| 86 | 9.27362 | |||
| 87 | ||||
| 87 | 9.32735 9034 9034 | |||
| 90 | 9,48683 | |||
| 91 | 9,53939 | |||
| 92 | 9,59166 | |||
| 93 | 9.64365 | |||
| 94 | 9.69536 | |||
| 95 | 9.74679 | |||
| 96 | 9.79796 | |||
| 97 | ||||
| 100 | 10 | |||
| 101 | 10,04988 | |||
| 102 | 10,0995 | |||
| 103 | 10.14889 | |||
| 104 | 10.19804 | |||
| 105 | 10.24695 | |||
| 106 | 10.29563 | |||
| 107 | 4 1035435 | 9034 9034|||
| 4 109354 9034 9034 9034 | ||||
| 110 | 10.48809 | |||
| 111 | 10.53565 | |||
| 112 | 10.58301 | |||
| 113 | 10.63015 | |||
| 114 | 10.67708 | |||
| 115 | 10.72381 | |||
| 116 | 10.77033 | |||
| 117 | ||||
| 117 | ||||
| 117 | 10.841665 | |||
| 120 | 10. | |||
| 121 | 11 | |||
| 122 | 11.04536 | |||
| 123 | 11.09054 | |||
| 124 | 11.13553 | |||
| 125 | 11.18034 | |||
| 126 | 11.22497 | |||
| 127 | ||||
| 127 | 11.269435 | 11.2694|||
| 130 | 11.40175 | |||
| 131 | 11.44552 | |||
| 132 | 11.48913 | |||
| 133 | 11.53256 | |||
| 134 | 11,57584 | |||
| 135 | 11,61895 | |||
| 136 | 11,6619 | |||
| 137 | ||||
| 137 | ||||
| 137 | ||||
| 137 | 11.70435 903 | |||
| 140 | 11.83216 | |||
| 141 | 11.87434 | |||
| 142 | 11. | |||
| 143 | 11. | |||
| 144 | 12 | |||
| 145 | 12.04159 | |||
| 146 | 12.08305 | |||
| 147 | 12.124354 904 | |||
| 150 | 12.24745 | |||
| 151 | 12.28821 | |||
| 152 | 12.32883 | |||
| 153 | 12.36932 | |||
| 154 | 12,40967 | |||
| 155 | 12,4499 | |||
| 156 | 12,49 | |||
| 157 | 12,52996 | |||
| 158 | 12,56981 | |||
| 159 | 12,60952 | |||
| 160 | 12.64911 | |||
| 161 | 12.68858 | |||
| 162 | 12.72792 | |||
| 163 | 12.76715 | |||
| 164 | 12.80625 | |||
| 165 | 12.84523 | |||
| 166 | 12.8841 | |||
| 167 | 904 904 904 904 904 904 904 904 904 354 904 904 904 904 904 904 904 904 904 904 354||||
| 170 | 13.0384 | |||
| 171 | 13.0767 | |||
| 172 | 13.11488 | |||
| 173 | 13.15295 | |||
| 174 | 13,19091 | |||
| 175 | 13,22876 | |||
| 176 | 13,2665 | |||
| 177 | 13,30413 | |||
| 178 | 13,34166 | |||
| 179 | 13,37909 | |||
| 180 | 13.41641 | |||
| 181 | 13.45362 | |||
| 182 | 13.49074 | |||
| 183 | 13.52775 | |||
| 184 | 13,56466 | |||
| 185 | 13,60147 | |||
| 186 | 13,63818 | |||
| 187 | 13,67479 | |||
| 188 | 13,71131 | |||
| 189 | 13,74773 | |||
| 190 | 13.78405 | |||
| 191 | 13.82027 | |||
| 192 | 13.85641 | |||
| 193 | 13.89244 | |||
| 194 | 13. | |||
| 195 | 13. | |||
| 196 | 14 | |||
| 197 | 14.0435 | |||
| 197 | 14.043567 | |||
| 200 | 14.14214 | |||
| 201 | 14.17745 | |||
| 202 | 14.21267 | |||
| 203 | 14.24781 | |||
| 204 | 14,28286 | |||
| 205 | 14,31782 | |||
| 206 | 14,3527 | |||
| 207 | 14,38749 | |||
| 208 | 14,42221 | |||
| 209 | 14,45683 | |||
| 210 | 14.49138 | |||
| 211 | 14.52584 | |||
| 212 | 14.56022 | |||
| 213 | 14.59452 | |||
| 214 | 14,62874 | |||
| 215 | 14,66288 | |||
| 216 | 14,69694 | |||
| 217 | 14,73092 | |||
| 218 | 14,76482 | |||
| 219 | 14,79865 | |||
| 220 | 14,8324 | |||
| 221 | 14,86607 | |||
| 222 | 14,89966 | |||
| 223 | 14. | |||
| 224 | 14. | |||
| 225 | 15 | |||
| 226 | 15.0333 | |||
| 227 | ||||
| 227 | 154354 9034 9034 | |||
| 230 | 15.16575 | |||
| 231 | 15.19868 | |||
| 232 | 15.23155 | |||
| 233 | 15.26434 | |||
| 234 | 15,29706 | |||
| 235 | 15,32971 | |||
| 236 | 15,36229 | |||
| 237 | 15,3948 | |||
| 238 | 15,42725 | |||
| 239 | 15,45962 | |||
| 240 | 15,49193 | |||
| 241 | 15,52417 | |||
| 242 | 15,55635 | |||
| 243 | 15.58846 | |||
| 244 | 15,6205 | |||
| 245 | 15,65248 | |||
| 246 | 15,68439 | |||
| 247 | 15,71623 | |||
| 248 | 15,74802 | |||
| 249 | 15,77973 | |||
| 250 | 15.81139 | |||
| 251 | 15.84298 | |||
| 252 | 15.87451 | |||
| 253 | 15. | |||
| 254 | 15. | |||
| 255 | 15. | |||
| 256 | 16 | |||
| 257 | 164122 | 9034|||
| 260 | 16.12452 | |||
| 261 | 16.15549 | |||
| 262 | 16.18641 | |||
| 263 | 16.21 727 | |||
| 264 | 16,24808 | |||
| 265 | 16,27882 | |||
| 266 | 16,30951 | |||
| 267 | 16,34013 | |||
| 268 | 16,37071 | |||
| 269 | 16,40122 | |||
| 270 | 16.43168 | |||
| 271 | 16.46208 | |||
| 272 | 16.49242 | |||
| 273 | 16.52271 | |||
| 274 | 16,55295 | |||
| 275 | 16,58312 | |||
| 276 | 16,61325 | |||
| 277 | 16,64332 | |||
| 278 | 16,67333 | |||
| 279 | 16,70329 | |||
| 280 | 16.7332 | |||
| 281 | 16.76305 | |||
| 282 | 16.79286 | |||
| 283 | 16.8226 | |||
| 284 | 16,8523 | |||
| 285 | 16,88194 | |||
| 286 | 16, | |||
| 287 | 16, | |||
| 288 | 16, | |||
| 289 | 17 | |||
| 290 | 17.02939 | |||
| 291 | 17.05872 | |||
| 292 | 17.08801 | |||
| 293 | 17.11724 | |||
| 294 | 17,14643 | |||
| 295 | 17,17556 | |||
| 296 | 17,20465 | |||
| 297 | 17,23369 | |||
| 298 | 17,26268 | |||
| 299 | 17,29162 | |||
| 300 | 17.32051 | |||
| 301 | 17.34935 | |||
| 302 | 17.37815 | |||
| 303 | 17.4069 | |||
| 304 | 17,4356 | |||
| 305 | 17,46425 | |||
| 306 | 17,49286 | |||
| 307 | 17,52142 | |||
| 308 | 17,54993 | |||
| 309 | 17,5784 | |||
| 310 | 17.60682 | |||
| 311 | 17.63519 | |||
| 312 | 17.66352 | |||
| 313 | 17.69181 | |||
| 314 | 17,72005 | |||
| 315 | 17,74824 | |||
| 316 | 17,77639 | |||
| 317 | 17,80449 | |||
| 318 | 17,83255 | |||
| 319 | 17,86057 | |||
| 320 | 17.88854 | |||
| 321 | 17. | |||
| 322 | 17. | |||
| 323 | 17.9722 | |||
| 324 | 18 | |||
| 325 | 18.02776 | |||
| 326 | 18.05547 | |||
| 327 | 18.08314 | |||
| 330 | 18.1659 | |||
| 331 | 18.19341 | |||
| 332 | 18.22087 | |||
| 333 | 18.24829 | |||
| 334 | 18,27567 | |||
| 335 | 18,30301 | |||
| 336 | 18,3303 | |||
| 337 | 18,35756 | |||
| 338 | 18,38478 | |||
| 339 | 18,41195 | |||
| 340 | 18.43909 | |||
| 341 | 18.46619 | |||
| 342 | 18.49324 | |||
| 343 | 18.52026 | |||
| 344 | 18,54724 | |||
| 345 | 18,57418 | |||
| 346 | 18,60108 | |||
| 347 | 18,62794 | |||
| 348 | 18,65476 | |||
| 349 | 18,68154 | |||
| 350 | 18.70829 | |||
| 351 | 18.73499 | |||
| 352 | 18.76166 | |||
| 353 | 18.78829 | |||
| 354 | 18,81489 | |||
| 355 | 18,84144 | |||
| 356 | 18,86796 | |||
| 357 | 18,89444 | |||
| 358 | 18, | |||
| 359 | 18,9473 | |||
| 360 | 18.97367 | |||
| 361 | 19 | |||
| 362 | 19.0263 | |||
| 363 | 19.+05256 | |||
| по ремонту 364 | 19,07878 | |||
| 365 | 19,10497 | |||
| 366 | 19,13113 | |||
| 367 | 19,15724 | |||
| 368 | 19,18333 | |||
| 369 | 19,20937 | |||
| 370 | 19.23538 | |||
| 371 | 19.26136 | |||
| 372 | 19.2873 | |||
| 373 | 19.31321 | |||
| 374 | 19,33908 | |||
| 375 | 19,36492 | |||
| 376 | 19,39072 | |||
| 377 | 19,41649 | |||
| 378 | 19,44222 | |||
| 379 | 19,46792 | |||
| 380 | 19.49359 | |||
| 381 | 19.51922 | |||
| 382 | 19.54482 | |||
| 383 | 19.57 039 | |||
| 384 | 19,59592 | |||
| 385 | 19,62142 | |||
| 386 | 19,64688 | |||
| 387 | 19,67232 | |||
| 388 | 19,69772 | |||
| 389 | 19,72308 | |||
| 390 | 19.74842 | |||
| 391 | 19.77372 | |||
| 392 | 19.79899 | |||
| 393 | 19.82423 | |||
| 394 | 19,84943 | |||
| 395 | 19,87461 | |||
| 396 | 19,89975 | |||
| 397 | 19, | |||
| 398 | 19, | |||
| 399 | 19,97498 | |||
| 400 | 20 | |||
| 401 | 20.02498 | |||
| 402 | 20.04994 | |||
| 403 | 20.07486 | |||
| 404 | 20,09975 | |||
| 405 | 20,12461 | |||
| 406 | 20,14944 | |||
| 407 | 20,17424 | |||
| 408 | 20,19901 | |||
| 409 | 20,22375 | |||
| 410 | 20.24846 | |||
| 411 | 20.27313 | |||
| 412 | 20.29778 | |||
| 413 | 20.3224 | |||
| 414 | 20,34699 | |||
| 415 | 20,37155 | |||
| 416 | 20,39608 | |||
| 417 | 20,42058 | |||
| 418 | 20,44505 | |||
| 419 | 20,46949 | |||
| 420 | 20.4939 | |||
| 421 | 20.51828 | |||
| 422 | 20.54264 | |||
| 423 | 20.56696 | |||
| 424 | 20,59126 | |||
| 425 | 20,61553 | |||
| 426 | 20,63977 | |||
| 427 | 20,66398 | |||
| 428 | 20,68816 | |||
| 429 | 20,71232 | |||
| 430 | 20.73644 | |||
| 431 | 20.76054 | |||
| 432 | 20.78461 | |||
| 433 | 20.+80865 | |||
| 434 | 20,83267 | |||
| 435 | 20,85665 | |||
| 436 | 20,88061 | |||
| 437 | 20, | |||
| 438 | 20, | |||
| 439 | 20, | |||
| 440 | 20.97618 | |||
| 441 | 21 | |||
| 442 | 21.0238 | |||
| 443 | 21.+04757 | |||
| 444 | 21,07131 | |||
| 445 | 21,09502 | |||
| 446 | 21,11871 | |||
| 447 | 21,14237 | |||
| 448 | 21,16601 | |||
| 449 | 21,18962 | |||
| 450 | 21.2132 | |||
| 451 | 21.23676 | |||
| 452 | 21.26029 | |||
| 453 | 21.2838 | |||
| 454 | 21,30728 | |||
| 455 | 21,33073 | |||
| 456 | 21,35416 | |||
| 457 | 21,37756 | |||
| 458 | 21,40093 | |||
| 459 | 21,42429 | |||
| 460 | 21.44761 | |||
| 461 | 21.47091 | |||
| 462 | 21.49419 | |||
| 463 | 21.51743 | |||
| 464 | 21,54066 | |||
| 465 | 21,56386 | |||
| 466 | 21,58703 | |||
| 467 | 21,61018 | |||
| 468 | 21,63331 | |||
| 469 | 21,65641 | |||
| 470 | 21.67948 | |||
| 471 | 21.70253 | |||
| 472 | 21.72556 | |||
| 473 | 21.74 856 | |||
| 474 | 21,77154 | |||
| 475 | 21,79449 | |||
| 476 | 21,81742 | |||
| 477 | 21,84033 | |||
| 478 | 21,86321 | |||
| 479 | 21,88607 | |||
| 480 | 21.9089 | |||
| 481 | 21. | |||
| 482 | 21.9545 | |||
| 483 | 21.97726 | |||
| 484 | 22 | |||
| 485 | 22,02272 | |||
| 486 | 22,04541 | |||
| 487 | ||||
| 487 | 9034 9034 9034 9034 | |||
| 490 | 22.13594 | |||
| 491 | 22.15852 | |||
| 492 | 22.18107 | |||
| 493 | 22.2036 | |||
| 494 | 22,22611 | |||
| 495 | 22,2486 | |||
| 496 | 22,27106 | |||
| 497 | 22,2935 | |||
| 498 | 22,31591 | |||
| 499 | 22,33831 | |||
| 500 | 22.36068 | |||
| 501 | 22.38303 | |||
| 502 | 22.40536 | |||
| 503 | 22.42766 | |||
| 504 | 22,44994 | |||
| 505 | 22,47221 | |||
| 506 | 22,49444 | |||
| 507 | 22,51666 | |||
| 508 | 22,53886 | |||
| 509 | 22,56103 | |||
| 510 | 22.58318 | |||
| 511 | 22.60531 | |||
| 512 | 22.62742 | |||
| 513 | 22.6495 | |||
| 514 | 22,67157 | |||
| 515 | 22,69361 | |||
| 516 | 22,71563 | |||
| 517 | 22,73763 | |||
| 518 | 22,75961 | |||
| 519 | 22,78157 | |||
| 520 | 22.80351 | |||
| 521 | 22.82542 | |||
| 522 | 22.84732 | |||
| 523 | 22.86919 | |||
| 524 | 22.89105 | |||
| 525 | 22. | |||
| 526 | 22. | |||
| 527 | ||||
| 527 | ||||
| 530 | 23.02173 | |||
| 531 | 23.04344 | |||
| 532 | 23.06513 | |||
| 533 | 23.+08679 | |||
| 534 | 23,10844 | |||
| 535 | 23,13007 | |||
| 536 | 23,15167 | |||
| 537 | 23,17326 | |||
| 538 | 23,19483 | |||
| 539 | 23,21637 | |||
| 540 | 23.2379 | |||
| 541 | 23.25941 | |||
| 542 | 23.28089 | |||
| 543 | 23.30236 | |||
| 544 | 23,32381 | |||
| 545 | 23,34524 | |||
| 546 | 23,36664 | |||
| 547 | 23,38803 | |||
| 548 | 23,4094 | |||
| 549 | 23,43075 | |||
| 550 | 23.45208 | |||
| 551 | 23.47339 | |||
| 552 | 23.49468 | |||
| 553 | 23.51595 | |||
| 554 | 23,5372 | |||
| 555 | 23,55844 | |||
| 556 | 23,57965 | |||
| 557 | 23,60085 | |||
| 558 | 23,62202 | |||
| 559 | 23,64318 | |||
| 560 | 23.66432 | |||
| 561 | 23.68544 | |||
| 562 | 23.70654 | |||
| 563 | 23.72762 | |||
| 564 | 23,74868 | |||
| 565 | 23,76973 | |||
| 566 | 23,79075 | |||
| 567 | 23,81176 | |||
| 568 | 23,83275 | |||
| 569 | 23,85372 | |||
| 570 | 23.87467 | |||
| 571 | 23.89561 | |||
| 572 | 23. | |||
| 573 | 23. | |||
| 574 | 23.9583 | |||
| 575 | 23.97916 | |||
| 576 | 24 | |||
| 577 | 9034 | 903 | ||
| 580 | 24.08319 | |||
| 581 | 24.10394 | |||
| 582 | 24.12468 | |||
| 583 | 24.14539 | |||
| 584 | 24,16609 | |||
| 585 | 24,18677 | |||
| 586 | 24,20744 | |||
| 587 | 24,22808 | |||
| 588 | 24,24871 | |||
| 589 | 24,26932 | |||
| 590 | 24.28992 | |||
| 591 | 24.31049 | |||
| 592 | 24.33105 | |||
| 593 | 24.35159 | |||
| 594 | 24,37212 | |||
| 595 | 24,39262 | |||
| 596 | 24,41311 | |||
| 597 | 24,43358 | |||
| 598 | 24,45404 | |||
| 599 | 24,47448 | |||
| 600 | 24,4949 | |||
| 601 | 24,5153 | |||
| 602 | 24,53569 | |||
| 603 | 24.55606 | |||
| 604 | 24,57641 | |||
| 605 | 24,59675 | |||
| 606 | 24,61707 | |||
| 607 | 24,63737 | |||
| 608 | 24,65766 | |||
| 609 | 24,67793 | |||
| 610 | 24.69818 | |||
| 611 | 24.71841 | |||
| 612 | 24.73863 | |||
| 613 | 24.75884 | |||
| 614 | 24,77902 | |||
| 615 | 24,79919 | |||
| 616 | 24,81935 | |||
| 617 | 24,83948 | |||
| 618 | 24,85961 | |||
| 619 | 24,87971 | |||
| 620 | 24,8998 | |||
| 621 | 24, | |||
| 622 | 24, | |||
| 623 | 24. | |||
| 624 | 24,97999 | |||
| 625 | 25 | |||
| 626 | 25,01999 25,01999 | |||
| 627 | ||||
| 627 | ||||
| 627 | ||||
| 630 | 25.0998 | |||
| 631 | 25.11971 | |||
| 632 | 25.13961 | |||
| 633 | 25.15949 | |||
| 634 | 25,17936 | |||
| 635 | 25,19921 | |||
| 636 | 25,21904 | |||
| 637 | 25,23886 | |||
| 638 | 25,25866 | |||
| 639 | 25,27845 | |||
| 640 | 25.29822 | |||
| 641 | 25.31798 | |||
| 642 | 25.33772 | |||
| 643 | 25.35744 | |||
| 644 | 25,37716 | |||
| 645 | 25,39685 | |||
| 646 | 25,41653 | |||
| 647 | 25,43619 | |||
| 648 | 25,45584 | |||
| 649 | 25,47548 | |||
| 650 | 25.4951 | |||
| 651 | 25.5147 | |||
| 652 | 25.53429 | |||
| 653 | 25.55386 | |||
| 654 | 25,57342 | |||
| 655 | 25,59297 | |||
| 656 | 25,6125 | |||
| 657 | 25,63201 | |||
| 658 | 25,65151 | |||
| 659 | 25,671 | |||
| 660 | 25.69047 | |||
| 661 | 25.70992 | |||
| 662 | 25.72936 | |||
| 663 | 25.+74879 | |||
| 664 | 25,7682 | |||
| 665 | 25,78759 | |||
| 666 | 25,80698 | |||
| 667 | 25,82634 | |||
| 668 | 25,8457 | |||
| 669 | 25,86503 | |||
| 670 | 25.88436 | |||
| 671 | 25. | |||
| 672 | 25. | |||
| 673 | 25. | |||
| 674 | 25. | |||
| 675 | 25.98076 | |||
| 676 | 26 | |||
| 677 | ||||
| 680 | 26.07681 | |||
| 681 | 26.09598 | |||
| 682 | 26.11513 | |||
| 683 | 26.13427 | |||
| 684 | 26,15339 | |||
| 685 | 26,1725 | |||
| 686 | 26,1916 | |||
| 687 | ||||
| 687 | 264354 9034 9034 | |||
| 690 | 26.26785 | |||
| 691 | 26.28688 | |||
| 692 | 26.30589 | |||
| 693 | 26.32489 | |||
| 694 | 26,34388 | |||
| 695 | 26,36285 | |||
| 696 | 26,38181 | |||
| 697 | 26,40076 | |||
| 698 | 26,41969 | |||
| 699 | 26,43861 | |||
| 700 | 26.45751 | |||
| 701 | 26.4764 | |||
| 702 | 26.49528 | |||
| 703 | 26.51415 | |||
| 704 | 26,533 | |||
| 705 | 26,55184 | |||
| 706 | 26,57066 | |||
| 707 | 26,58947 | |||
| 708 | 26,60827 | |||
| 709 | 26,62705 | |||
| 710 | 26.64583 | |||
| 711 | 26.66458 | |||
| 712 | 26.68333 | |||
| 713 | 26.70206 | |||
| 714 | 26,72078 | |||
| 715 | 26,73948 | |||
| 716 | 26,75818 | |||
| 717 | 26,77686 | |||
| 718 | 26,79552 | |||
| 719 | 26,81418 | |||
| 720 | 26.83282 | |||
| 721 | 26.85144 | |||
| 722 | 26.87006 | |||
| 723 | 26.88866 | |||
| 724 | 26, | |||
| 725 | 26, | |||
| 726 | 26, | |||
| 727 | 26, | |||
| 728 | 26,98148 | |||
| 729 | 27 | |||
| 730 | 27.01851 | |||
| 731 | 27.03701 | |||
| 732 | 27.0555 | |||
| 733 | 27.07 397 | |||
| 734 | 27,09243 | |||
| 735 | 27,11088 | |||
| 736 | 27,12932 | |||
| 737 | 27,14774 | |||
| 738 | 27,16616 | |||
| 739 | 27,18455 | |||
| 740 | 27.20294 | |||
| 741 | 27.22132 | |||
| 742 | 27.23968 | |||
| 743 | 27.25803 | |||
| 744 | 27,27636 | |||
| 745 | 27,29469 | |||
| 746 | 27,313 | |||
| 747 | 27,3313 | |||
| 748 | 27,34959 | |||
| 749 | 27,36786 | |||
| 750 | 27.38613 | |||
| 751 | 27.40438 | |||
| 752 | 27.42262 | |||
| 753 | 27.44085 | |||
| 754 с | 27,45906 | |||
| 755 | 27,47726 | |||
| 756 | 27,49545 | |||
| 757 | 27,51363 | |||
| 758 | 27,5318 | |||
| 759 | 27,54995 | |||
| 760 | 27,5681 | |||
| 761 | 27,58623 | |||
| 762 | 27.60435 | |||
| 763 | 27.62245 | |||
| 764 | 27,64055 | |||
| 765 | 27,65863 | |||
| 766 | 27,67671 | |||
| 767 | 27,69476 | |||
| 768 | 27,71281 | |||
| 769 | 27,73085 | |||
| 770 | 27.74887 | |||
| 771 | 27.76689 | |||
| 772 | 27.78489 | |||
| 773 | 27.80288 | |||
| 774 | 27,82086 | |||
| 775 | 27,83882 | |||
| 776 | 27,85678 | |||
| 777 | 27,87472 | |||
| 778 | 27,89265 | |||
| 779 | 27, | |||
| 780 | 27. | |||
| 781 | 27. | |||
| 782 | 27. | |||
| 783 | 27.98214 | |||
| 784 | 28 | |||
| 785 | 28.01785 | |||
| 786 | 28.03569 | |||
| 787 | 44 | |||
| 790 | 28.10694 | |||
| 791 | 28.12472 | |||
| 792 | 28.14249 | |||
| 793 | 28.16026 | |||
| 794 | 28,17801 | |||
| 795 | 28,19574 | |||
| 796 | 28,21347 | |||
| 797 | 28,23119 | |||
| 798 | 28,24889 | |||
| 799 | 28,26659 | |||
| 800 | 28.28427 | |||
| 801 | 28.30194 | |||
| 802 | 28.3196 | |||
| 803 | 28.33725 | |||
| 804 | 28,35489 | |||
| 805 | 28,37252 | |||
| 806 | 28,39014 | |||
| 807 | 28,40775 | |||
| 808 | 28,42534 | |||
| 809 | 28,44293 | |||
| 810 | 28.4605 | |||
| 811 | 28.47806 | |||
| 812 | 28.49561 | |||
| 813 | 28.51315 | |||
| 814 | 28,53069 | |||
| 815 | 28,5482 | |||
| 816 | 28,56571 | |||
| 817 | 28,58321 | |||
| 818 | 28,6007 | |||
| 819 | 28,61818 | |||
| 820 | 28.63564 | |||
| 821 | 28.6531 | |||
| 822 | 28.67054 | |||
| 823 | 28.68798 | |||
| 824 | 28,7054 | |||
| 825 | 28,72281 | |||
| 826 | 28,74022 | |||
| 827 | 28,75761 | |||
| 828 | 28,77499 | |||
| 829 | 28,79236 | |||
| 830 | 28.80972 | |||
| 831 | 28.82707 | |||
| 832 | 28.84441 | |||
| 833 | 28.86174 | |||
| 834 | 28,87906 | |||
| 835 | 28,89637 | |||
| 836 | 28, | |||
| 837 | 28, | |||
| 838 | 28, | |||
| 839 | 28,9655 | |||
| 840 | 28.98275 | |||
| 841 | 29 | |||
| 842 | 29.01724 | |||
| 843 | 29.03446 | |||
| 844 | 29,05168 | |||
| 845 | 29,06888 | |||
| 846 | 29,08608 | |||
| 847 | 29,10326 | |||
| 848 | 29,12044 | |||
| 849 | 29,1376 | |||
| 850 | 29.15476 | |||
| 851 | 29.1719 | |||
| 852 | 29.18904 | |||
| 853 | 29.20616 | |||
| 854 | 29,22328 | |||
| 855 | 29,24038 | |||
| 856 | 29,25748 | |||
| 857 | 29,27456 | |||
| 858 | 29,29164 | |||
| 859 | 29,3087 | |||
| 860 | 29.32576 | |||
| 861 | 29.3428 | |||
| 862 | 29.35984 | |||
| 863 | 29.37 686 | |||
| 864 | 29,39388 | |||
| 865 | 29,41088 | |||
| 866 | 29,42788 | |||
| 867 | 29,44486 | |||
| 868 | 29,46184 | |||
| 869 | 29,47881 | |||
| 870 | 29.49576 | |||
| 871 | 29.51271 | |||
| 872 | 29.52965 | |||
| 873 | 29.54657 | |||
| 874 | 29,56349 | |||
| 875 | 29,5804 | |||
| 876 | 29,5973 | |||
| 877 | 29,61419 | |||
| 878 | 29,63106 | |||
| 879 | 29,64793 | |||
| 880 | 29.66479 | |||
| 881 | 29.68164 | |||
| 882 | 29.69848 | |||
| 883 | 29.71532 | |||
| 884 | 29,73214 | |||
| 885 | 29,74895 | |||
| 886 | 29,76575 | |||
| 887 | 29,78255 | |||
| 888 | 29,79933 | |||
| 889 | 29,8161 | |||
| 890 | 29.83287 | |||
| 891 | 29.84962 | |||
| 892 | 29.86637 | |||
| 893 | 29.+88311 | |||
| 894 | 29,89983 | |||
| 895 | 29, | |||
| 896 | 29, | |||
| 897 | 29, | |||
| 898 | 29, | |||
| 899 | 29,98333 | |||
| 900 | 30 | |||
| 901 | 30.01666 | |||
| 902 | 30.03331 | |||
| 903 | 30.04 996 | |||
| 904 | 30,06659 | |||
| 905 | 30,08322 | |||
| 906 | 30,09983 | |||
| 907 | 30,11644 | |||
| 908 | 30,13304 | |||
| 909 | 30,14963 | |||
| 910 | 30.16621 | |||
| 911 | 30.18278 | |||
| 912 | 30.19934 | |||
| 913 | 30.21589 | |||
| 914 | 30,23243 | |||
| 915 | 30,24897 | |||
| 916 | 30,26549 | |||
| 917 | 30,28201 | |||
| 918 | 30,29851 | |||
| 919 | 30,31501 | |||
| 920 | 30.3315 | |||
| 921 | 30.34798 | |||
| 922 | 30.36445 | |||
| 923 | 30.38092 | |||
| 924 | 30,39737 | |||
| 925 | 30,41381 | |||
| 926 | 30,43025 | |||
| 927 | 30,44667 | |||
| 928 | 30,46309 | |||
| 929 | 30,4795 | |||
| 930 | 30,4959 | |||
| 931 | 30,51229 | |||
| 932 | 30,52868 | |||
| 933 | 30.54505 | |||
| 934 | 30,56141 | |||
| 935 | 30,57777 | |||
| 936 | 30,59412 | |||
| 937 | 30,61046 | |||
| 938 | 30,62679 | |||
| 939 | 30,64311 | |||
| 940 | 30.65942 | |||
| 941 | 30.67572 | |||
| 942 | 30.69202 | |||
| 943 | 30.70831 | |||
| 944 | 30,72458 | |||
| 945 | 30,74085 | |||
| 946 | 30,75711 | |||
| 947 | 30,77337 | |||
| 948 | 30,78961 | |||
| 949 | 30,80584 | |||
| 950 | 30.82207 | |||
| 951 | 30.83829 | |||
| 952 | 30.8545 | |||
| 953 | 30.8707 | |||
| 954 | 30,88689 | |||
| 955 | 30, | |||
| 956 | 30, | |||
| 957 | 30, | |||
| 958 | 30, | |||
| 959 | 30, | |||
| 960 | 30.98387 | |||
| 961 | 31 | |||
| 962 | 31.01612 | |||
| 963 | 31.03224 | |||
| 964 | 31,04835 | |||
| 965 | 31,06445 | |||
| 966 | 31,08054 | |||
| 967 | 31,09662 | |||
| 968 | 31,1127 | |||
| 969 | 31,12876 | |||
| 970 | 31.14482 | |||
| 971 | 31.16087 | |||
| 972 | 31.17691 | |||
| 973 | 31.19295 | |||
| 974 | 31.20897 | |||
| 975 | 31.22499 | |||
| 976 | 31.241 | |||
| 977 | 9034 9034||||
| 4 | ||||
| 980 | 31.30495 | |||
| 981 | 31.32092 | |||
| 982 | 31.33688 | |||
| 983 | 31.35283 | |||
| 984 | 31,36877 | |||
| 985 | 31,38471 | |||
| 986 | 31,40064 | |||
| 987 | 31,41656 | |||
| 988 | 31,43247 | |||
| 989 | 31,44837 | |||
| 990 | 31.46427 | |||
| 991 | 31.48015 | |||
| 992 | 31.49603 | |||
| 993 | 31.5119 | |||
| 994 | 31,52777 | |||
| 995 | 31,54362 | |||
| 996 | 31,55947 | |||
| 997 | 31,57531 | |||
| 998 | 31,59114 | |||
| 999 | 31,60696 | |||
| 1000 | 31.62278 |
Связанные
Часто используемые Miniwebtools:
Все минивеб-инструменты (отсортировано по названию):
PWA (прогрессивное веб-приложение) Инструменты (17) Финансовые калькуляторы (121) Здоровье и фитнес (31) Математика (161) Случайность (17) Спорт (8) Текстовые инструменты (30) Время и Дата (27) Инструменты для веб-мастеров (10) Хеш и контрольная сумма (8) Разное (108)1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100 | 11 2 = 121 12 2 = 144 13 2 = 169 14 2 = 196 15 2 = 225 16 2 = 256 17 2 = 289 18 2 = 324 19 2 = 361 20 2 = 400 | 21 2 = 441 22 2 = 484 23 2 = 529 24 2 = 576 25 2 = 625 26 2 = 676 27 2 = 729 28 2 = 784 29 2 = 841 30 2 = 900 | 31 2 = 961 32 2 = 1024 33 2 = 1089 34 2 = 1156 35 2 = 1225 36 2 = 1296 37 2 = 1369 38 2 = 1444 39 2 = 1521 40 2 = 1600 | 41 2 = 1681 42 2 = 1764 43 2 = 1849 44 2 = 1936 45 2 = 2025 46 2 = 2116 47 2 = 2209 48 2 = 2304 49 2 = 2401 50 2 = 2500 | 51 2 = 2601 52 2 = 2704 53 2 = 2809 54 2 = 2916 55 2 = 3025 56 2 = 3136 57 2 = 3249 58 2 = 3364 59 2 = 3481 60 2 = 3600 | 61 2 = 3721 62 2 = 3844 63 2 = 3969 64 2 = 4096 65 2 = 4225 66 2 = 4356 67 2 = 4489 68 2 = 4624 69 2 = 4761 70 2 = 4900 | 71 2 = 5041 72 2 = 5184 73 2 = 5329 74 2 = 5476 75 2 = 5625 76 2 = 5776 77 2 = 5929 78 2 = 6084 79 2 = 6241 80 2 = 6400 | 81 2 = 6561 82 2 = 6724 83 2 = 6889 84 2 = 7056 85 2 = 7225 86 2 = 7396 87 2 = 7569 88 2 = 7744 89 2 = 7921 90 2 = 8100 | 91 2 = 8281 92 2 = 8464 93 2 = 8649 94 2 = 8836 95 2 = 9025 96 2 = 9216 97 2 = 9409 98 2 = 9604 99 2 = 9801 100 2 = 10000 |
Оценка квадратного корня
Когда мы оцениваем квадратный корень числа, сначала мы найдем два значения, между которыми лежит квадратный корень данного числа.
Например, квадратный корень из числа 40 находится между 6 и 7.
Поскольку квадратный корень из 36 равен 6, а квадратный корень из 49 равен 7. Данное число находится между 36 и 49. Таким образом, мы можем сказать, что квадратный корень из заданного числа от 6 до 7.
√1 = 1
√4 = 2
√9 = 3
√16 = 4
√25 = 5
√36 = 6
√49 = 7
√64 = 8
√ 81 = 9
√100 = 10
√121 = 11
√144 = 12
√169 = 13
√196 = 14
√225 = 15
√256 = 16
√289 = 17
√324 = 18
√ 361 = 19
√400 = 20
√441 = 21
√484 = 22
√529 = 23
√576 = 24
√625 = 25
√676 = 26
√729 = 27
√784 = 28
√ 841 = 29
√900 = 30
Из приведенных выше квадратных корней мы можем узнать, что
(i) Если полный квадрат имеет n цифр, где n четно, его квадратный корень состоит из n / 2 цифр.
(ii) Если полный квадрат состоит из n цифр, где n нечетно, его квадратный корень состоит из (n + 1) / 2 цифр.
Пример 1:
Оцените значение следующего до ближайшего целого числа.
√80
Решение:
√64 <√80 <√81
8 <√80 <9
Поскольку данное число находится между 64 и 81, приблизительный квадратный корень из данного числа равен 8
Итак, приблизительное значение √80 равно 8.
Пример 2:
Оцените значение следующего до ближайшего целого числа.
√1000
Решение:
Данное число больше 900. Если мы умножим 32 x 32, мы получим 1024, что больше 1000. Таким образом, мы должны попробовать число меньше 32, но больше 30
31 x 31 = 961 <1000
Итак, приблизительное значение √1000 равно 31.
Пример 3:
Оцените значение следующего до ближайшего целого числа.
√172
Решение:
Данное число больше 169 и меньше 196. Таким образом, квадратный корень из данного числа лежит между 16 и 17.
Таким образом, приблизительное значение √172 равно 16
Пример 4:
Оцените значение следующего до ближайшего целого числа.
√5928
Решение:
Количество цифр в данном числе = 4
Итак, квадратный корень из 5928 будет иметь 2 цифры.
70 x 70 = 4900
75 x 75 = 5625
77 x 77 = 5929
Итак, приблизительное значение √5928 равно 76.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебра
Алгебра
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по скорости за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Проблемы со словами по простым процентам
Проблемы со словами по сложным процентам
Проблемы со словами по типам ngles
Проблемы со словами с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи о словах с уравнениями
Проблемы со словами с линейными неравенствами
900o18 ЗадачиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций
Домен и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с использованием длинного di видение
Л.Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
математических упражнений.com 404 Страница
Страница не найдена (ошибка 404)
Извините, но запрошенная вами страница не существует. Пока ты здесь, ты можешь узнать почему. Эта страница займет у несколько опытного читателя 111 секунд. читать вслух с небольшим выражением лица, так что вы можете использовать это измерение, чтобы оценить, сколько времени вам потребуется, и вы можете узнать что-то интересное. Если вы торопитесь, вы можете использовать меню навигации или посетить нашу страницу поиска.
А, вы все еще читаете.Вы попали на эту страницу по ряду причин, которые описаны ниже.
- Ссылка, которую вы использовали для перехода сюда, была закодирована неправильно. Мы знаем, что их несколько сотен на разных веб-сайтах, но мы бы предпочли создать новые математические рабочие листы, чем тратить время на то, чтобы связываться со всеми этими веб-сайтами и обучать их кодированию правильных ссылок. Вы можете сказать им, если хотите; мы были бы признательны.
- Ссылка, которую вы использовали, вполне могла быть сделана экспертом, но произошла опечатка из-за того, что чей-то кот шел по клавиатуре в то время, когда он вставлял ссылку в код веб-сайта.
- Ссылка, которую вы использовали для перехода сюда, могла быть действующей ссылкой в прошлом, но мы переместили или удалили элемент. Иногда мы обновляем что-то и удаляем старый контент или ссылки.
- Мог быть глюк. Если это так, попробуйте еще раз, и это может сработать. Как мог бы сказать Доктор: «Люди предполагают, что время — это строгое следование причинно-следственной связи. Но на самом деле с нелинейной, несубъективной точки зрения это больше похоже на большой шар шаткой-шаткой-вайми… прочее. «
- Очевидно, вы могли перейти на страницу 404 непосредственно по ссылке или введя ее в адресную строку.
- Есть небольшая вероятность, что мы несовершенны, и это произошло. Вы узнаете, что это была наша вина, потому что ссылка, которую вы использовали для перехода сюда, была на Math-Drills.com. Мы будем признательны, если вы сообщите нам об этом, и мы сможем это исправить.
Что ж, мы надеемся, что вам понравилась наша страница 404, и, конечно же, надеемся, что вы найдете то, что хотите.
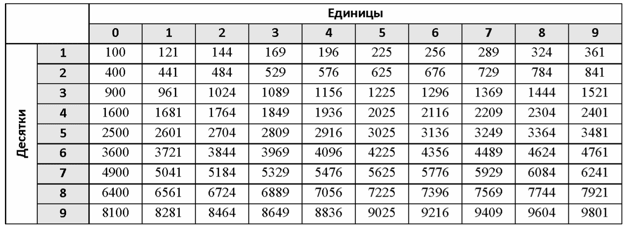 Также квадратом числа называется результат возведения числа в степень 2 (во вторую степень).
Также квадратом числа называется результат возведения числа в степень 2 (во вторую степень). Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
Также квадратом числа называется результат его возведение в степень 2 (во вторую степень) Таблица квадратных корней.
Таблица квадратных корней. То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129.
То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129. То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат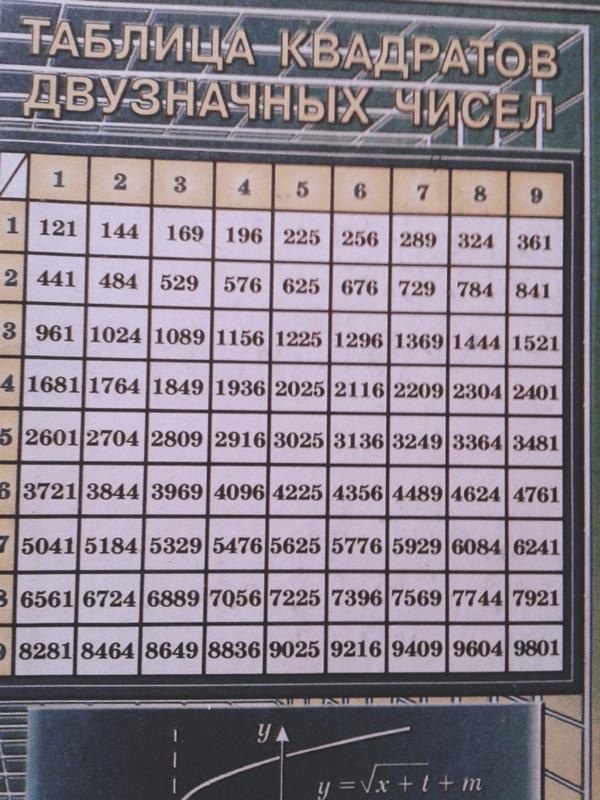 [1] Арифметические прогрессии из трёх квадратов существуют — например: 1, 25, 49.
[1] Арифметические прогрессии из трёх квадратов существуют — например: 1, 25, 49.