Иррациональные уравнения
Иррациональным уравнением называется уравнение, в котором переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Например,
 ,
,
 ,
,
 ….
….
Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.
Итак, давайте перечислим основные методы решения иррациональных уравнений.
1 метод: возведение обеих частей уравнения в одну и ту же степень.
2 метод: замена переменной.
3 метод: умножение обеих частей уравнения на одну и ту же функцию.
4 метод: применение свойств функций, входящих в уравнение.
Чаще всего при решении иррациональных уравнений применяют 1метод, то есть обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного. Следует не забывать, что уравнение-следствие наряду с корнями исходного уравнения может содержать и другие корни, которые называются посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.
Давайте докажем, что при возведении обеих частей уравнения в натуральную степень получается уравнение — следствие данного.
Доказательство:
пусть у нас есть уравнение  и
и
 —
корень этого уравнения. То есть
—
корень этого уравнения. То есть  —
верное числовое равенство.
—
верное числовое равенство.
Тогда
по свойствам верных числовых равенств равно  ,
где
,
где 
 —
корень уравнения
—
корень уравнения  .
В свою очередь, уравнение
.
В свою очередь, уравнение  –
это уравнение-следствие.
–
это уравнение-следствие.Что и требовалось доказать.
Напомним, что при возведении обеих частей уравнения в чётную натуральную степень может получиться уравнение, не равносильное данному.
Например,
решим уравнение  .
.
Решение.
Возведём в квадрат обе части уравнения 
 .
.
Обратите
внимание: второе уравнение не равносильно исходному, так как первое уравнение
имеет только один корень —  ,
а второе — два корня –
,
а второе — два корня –  и
и
 .
.
В этом случае второе уравнение называют следствием первого уравнения. Отметим, что второй корень является
Как видим, при возведении иррационального уравнения в натуральную степень могут появиться посторонние корни, поэтому проверка обязательна.
Если
обе части уравнения  неотрицательны
на множестве
неотрицательны
на множестве ,
то уравнение
,
то уравнение  равносильно
уравнению
равносильно
уравнению  при
при

При решении иррациональных уравнений необходимо учитывать основные свойства иррациональных уравнений:
1. Если показатель радикала – чётное число, то подкоренное выражение должно быть неотрицательным, при этом значение радикала также является неотрицательным. Проще говоря, все корни чётной степени, входящие в уравнение, являются арифметическими, то есть если подкоренное выражение отрицательно, то корень лишён смысла; если подкоренное выражение равно 0, то корень также равен 0; если подкоренное выражение положительно, то значение корня – положительно.
2. Если показатель радикала – нечётное число, то подкоренное выражение может быть любым действительным числом. В этом случае знак радикала совпадает со знаком подкоренного выражения. Говоря другими словами, все корни нечётной степени, входящие в уравнение определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения.
А теперь давайте приступим к практической части нашего урока.
Задание
1.
Решите уравнение  .
.
Решение.
Отметим, что при  уравнение
не имеет корней, так как правая часть нашего уравнения будет принимать
отрицательные значения. А мы знаем, что значение корня не может быть отрицательным
числом. Значит, нам будут подходить только корни больше либо равные 3.
уравнение
не имеет корней, так как правая часть нашего уравнения будет принимать
отрицательные значения. А мы знаем, что значение корня не может быть отрицательным
числом. Значит, нам будут подходить только корни больше либо равные 3.
Итак,
возведём в квадрат обе части уравнения 
 .
.
Перенесём
все слагаемые из правой части уравнения в левую  .
Получим уравнение
.
Получим уравнение  .
.
Теперь
вынесем общий множитель х за скобки. Получим уравнение  .
В скобках квадратный многочлен разложим на множители.
.
В скобках квадратный многочлен разложим на множители.
Имеем

Чтобы данное уравнение равнялось 0, нужно чтобы хотя бы один из множителей равнялся 0.
Отсюда
полученное уравнение имеет корни  ,
, ,
, .
.
Вначале
решения мы с вами оговаривали, что корни меньше –3 нам не подходят. Проверим,
подходят ли корни  и
и

 левая
часть исходного уравнения равна
левая
часть исходного уравнения равна  ,
а правая – 3. Имеем верное равенство. Значит,
,
а правая – 3. Имеем верное равенство. Значит,  является
корнем уравнения. При
является
корнем уравнения. При  левая
часть исходного уравнения равна
левая
часть исходного уравнения равна  ,
правая – 4. Тоже имеем верное равенство.
,
правая – 4. Тоже имеем верное равенство.Следовательно,

Запишем
ответ:  ,
,
 .
.
Задание
2.
Решите уравнение  .
.
Решение.
Возведём обе части уравнения в квадрат  .
.
Получим
равносильное исходному уравнение  .
.
Приведём
подобные члены и перенесём слагаемые без знака корня в правую часть уравнения  .
.
Получим
уравнение  .
.
Возведём обе части получившегося уравнения в квадрат.

Получим
уравнение  .
.
Раскроем скобки. Перенесём все слагаемые из правой части уравнения в левую. Приведём подобные.
 .
.
 .
.
Получим
уравнение  .
.

 ,
, .
.
Последнее
уравнение является следствием исходного уравнения. Вычислим его корни. Имеем  ,
,
 .
.
Выполним проверку.
При выражение
выражение
 .
Имеем верное равенство. Значит,
.
Имеем верное равенство. Значит,  является
корнем нашего уравнения.
является
корнем нашего уравнения.
При
 выражение
выражение
 .
Видим: имеем неверное равенство.
.
Видим: имеем неверное равенство.
Следовательно,
 не
является корнем нашего уравнения. Запишем ответ.
не
является корнем нашего уравнения. Запишем ответ.
videouroki.net
Решение иррациональных уравнений (10 класс)
Урок алгебры и начала анализа
в 10 классе

Учитель:
Семендяева Людмила Вячеславовна
ГБОУ ЛНР
«Ровеньковская общеобразовательная школа №8»
Основные цели:
-обобщить и систематизировать знания и умения решать иррациональные уравнения различного вида и различными способами.
-развивать у учащихся внимание и аккуратность
-воспитывать усидчивость и трудолюбие
Одной из задач данного урока является повторение пройденного по теме «Иррарациональные уравнения» материала, подготовка учащихся к контрольной работе по данной теме.
1. Организационный момент.
2. Проверка домашнего задания:
а) Раздать карточки учащимся, которые садятся на первые парты, с индивидуальным заданием.
В этих карточках- часть домашней работы (для слабых учащихся).
Карточка №1 Карточка №2 Карточка №3
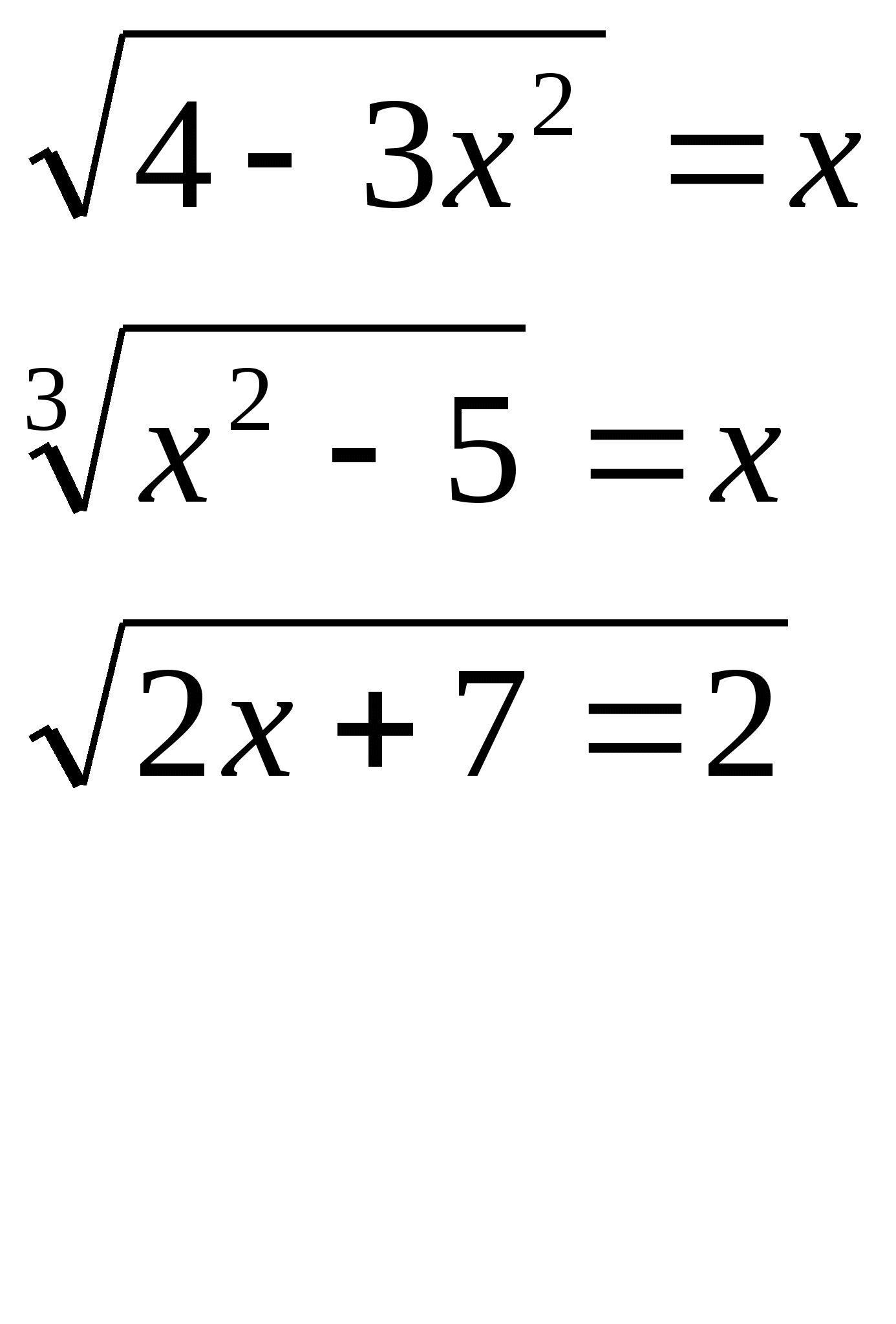
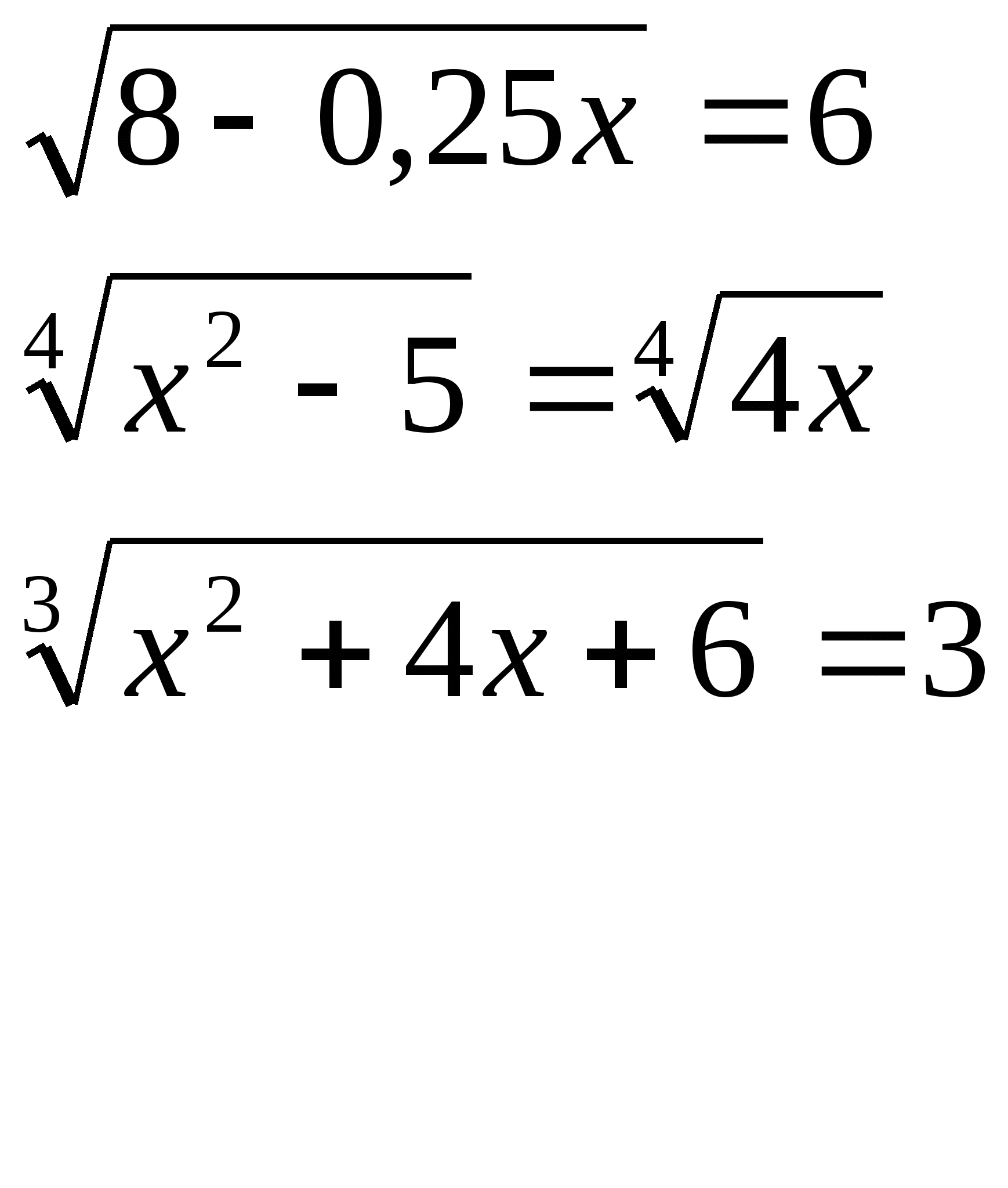
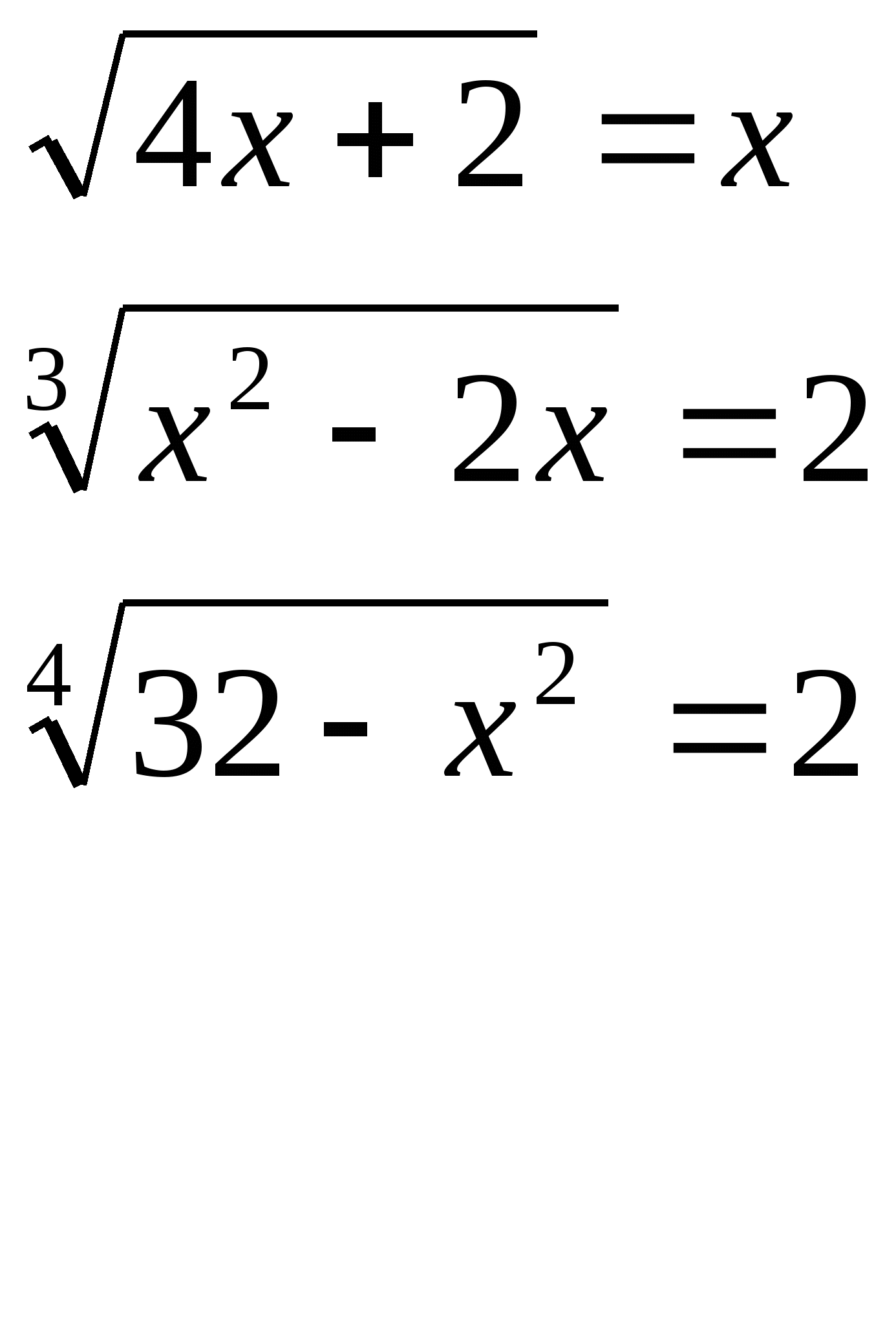
б) Вторая часть домашней работы проверяется на электронной доске. На доске выведены примеры с решением. Учащимся предлагается найти ошибку в решении, исправить её и объяснить.
№644(1) №644(3) №644(5)
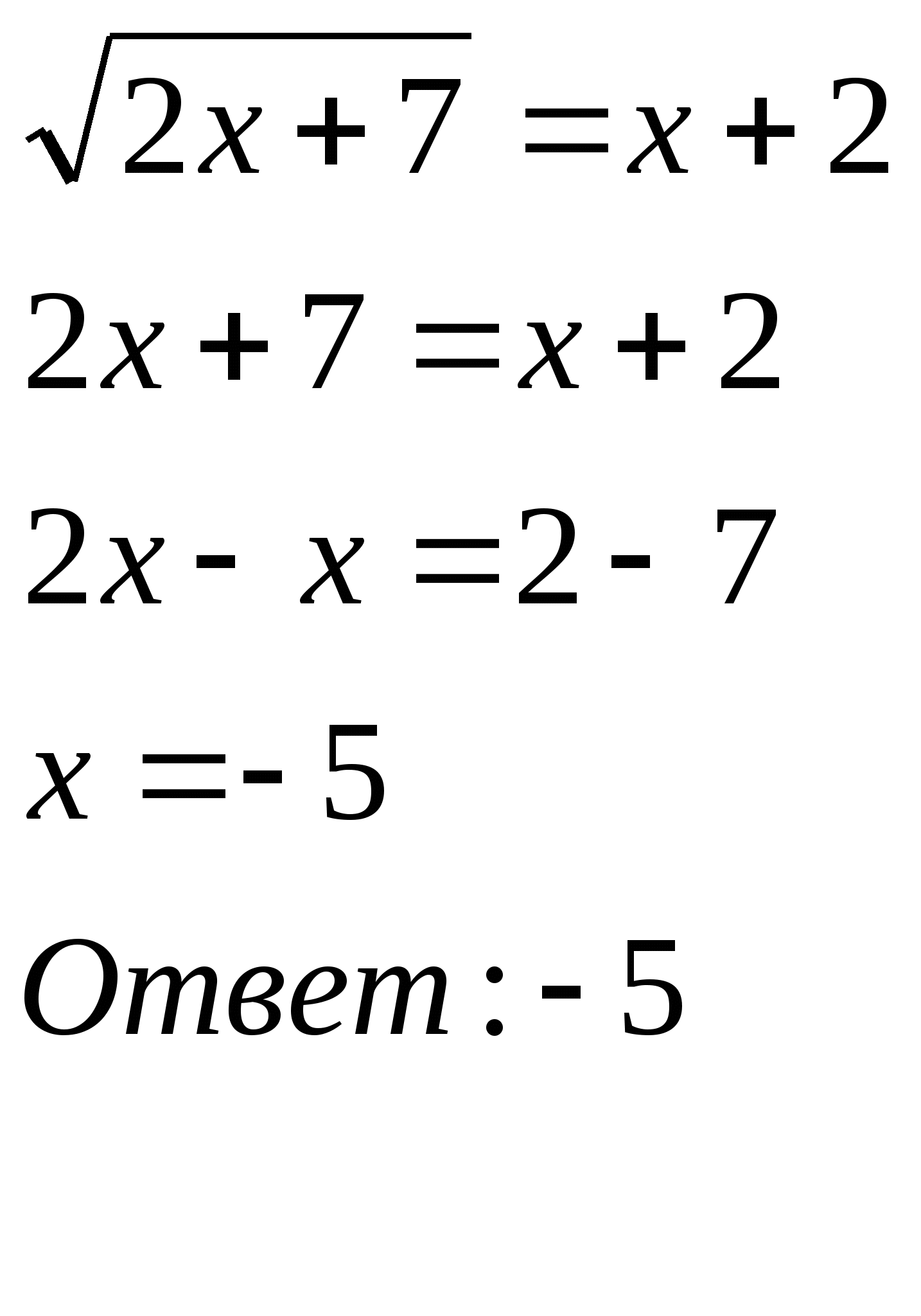
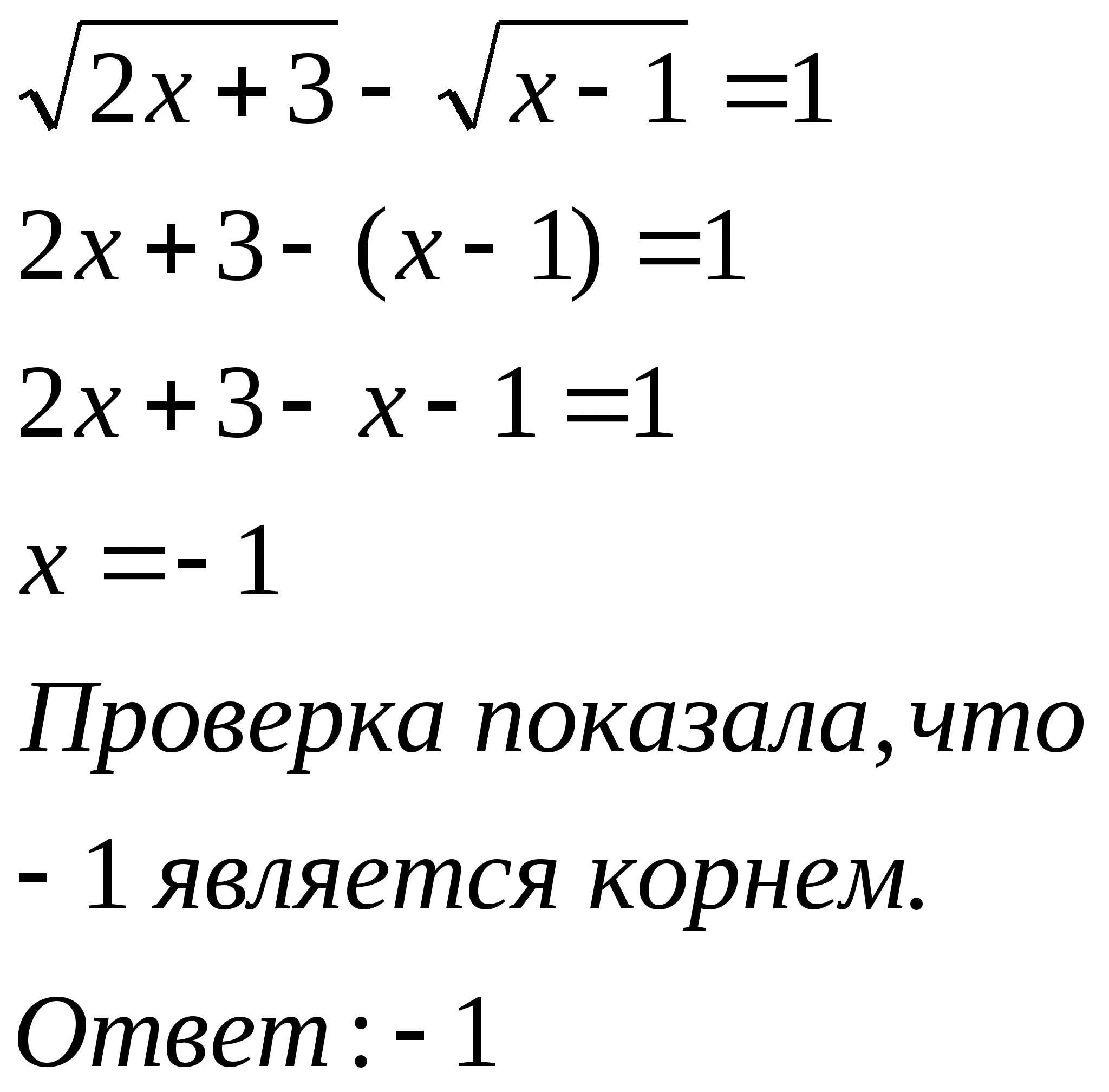
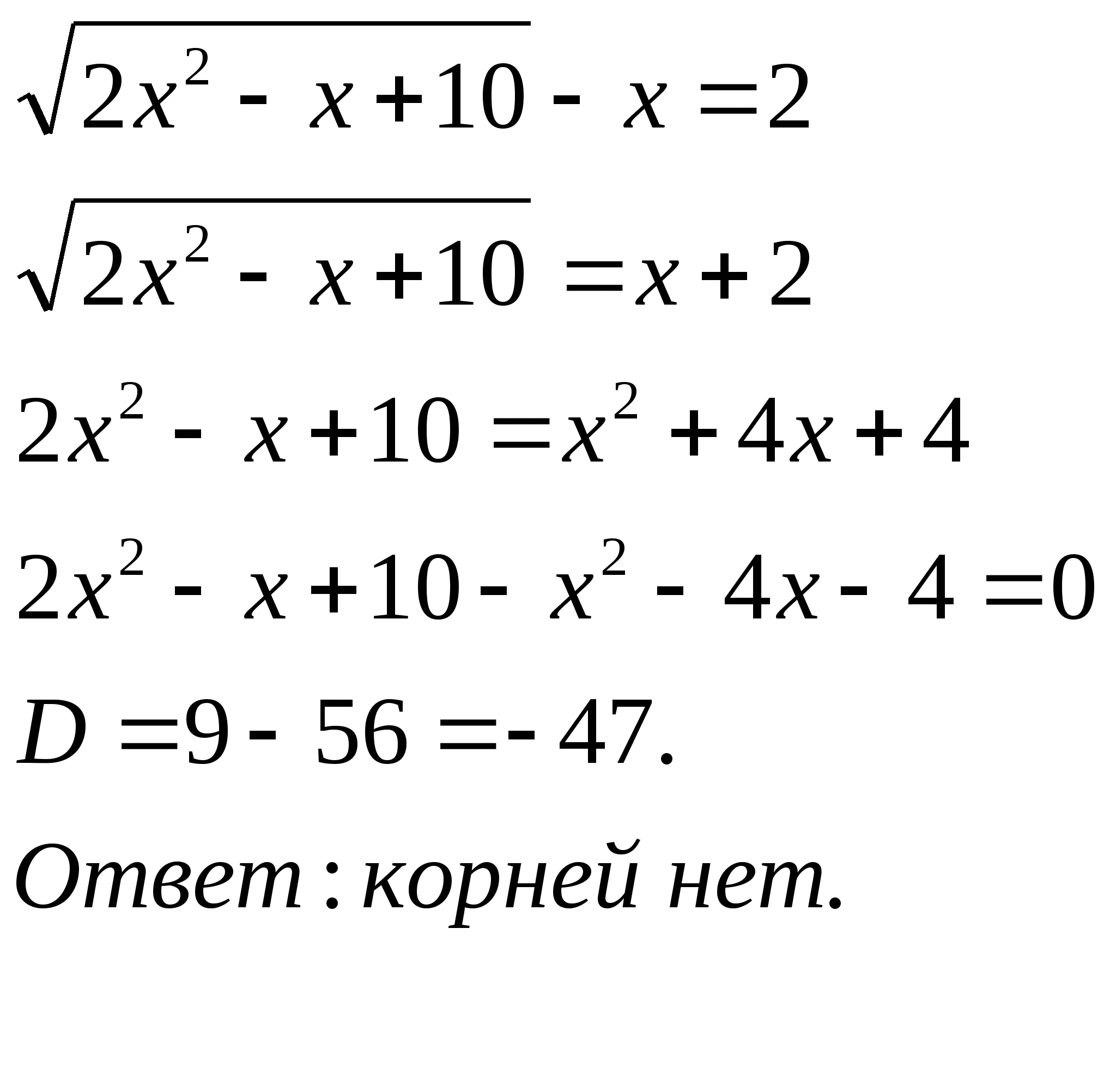
Вызванные 3 ученика исправляют ошибки:
№644(1) №644(3) №644(5)
2х+7=(х+2)² 2х+3-2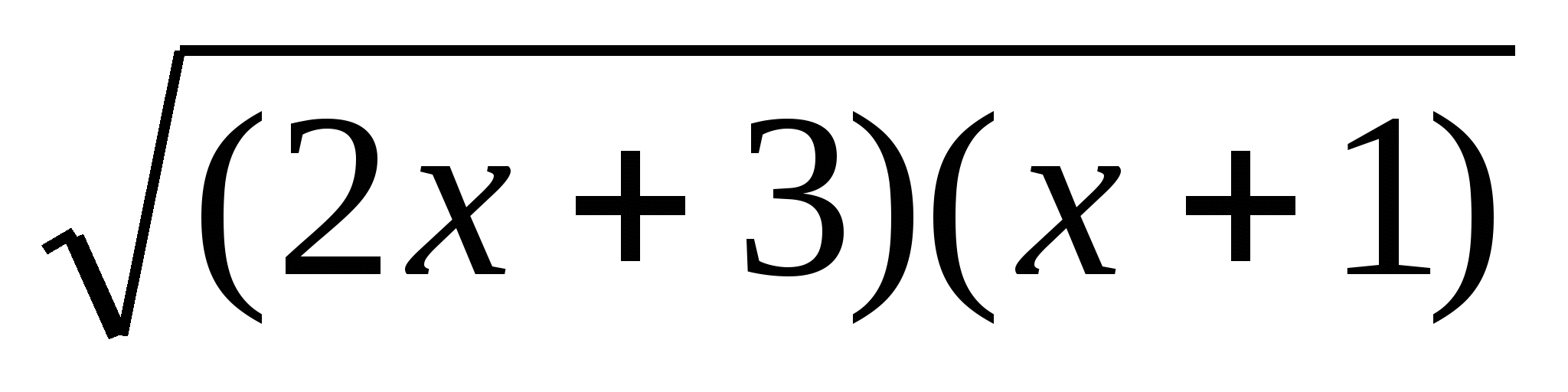 +(х+1)=1 2x²-х+10-x²-4х-4=0
+(х+1)=1 2x²-х+10-x²-4х-4=0
2х+7=x²+4х+4 3х+4-2 =1 x²-5х+6=0
=1 x²-5х+6=0
x²+2х-3=0 3х+3=2 х1=3 х2=2
х1=3 х2=2
Проверка показывает 9x²+18х+9=8x²+20х+12 с учётом проверки
что, х=-3 не является x²-12х-3=0 Ответ: 3; 2
корнем х1=3 х2=-1
Ответ: 1 Проверка показывает,
что оба корня подходят
Ответ: 3 ; -1
3.Объявление темы: сегодня мы повторим способы решения иррациональных уравнений и начнем с самых простых.
4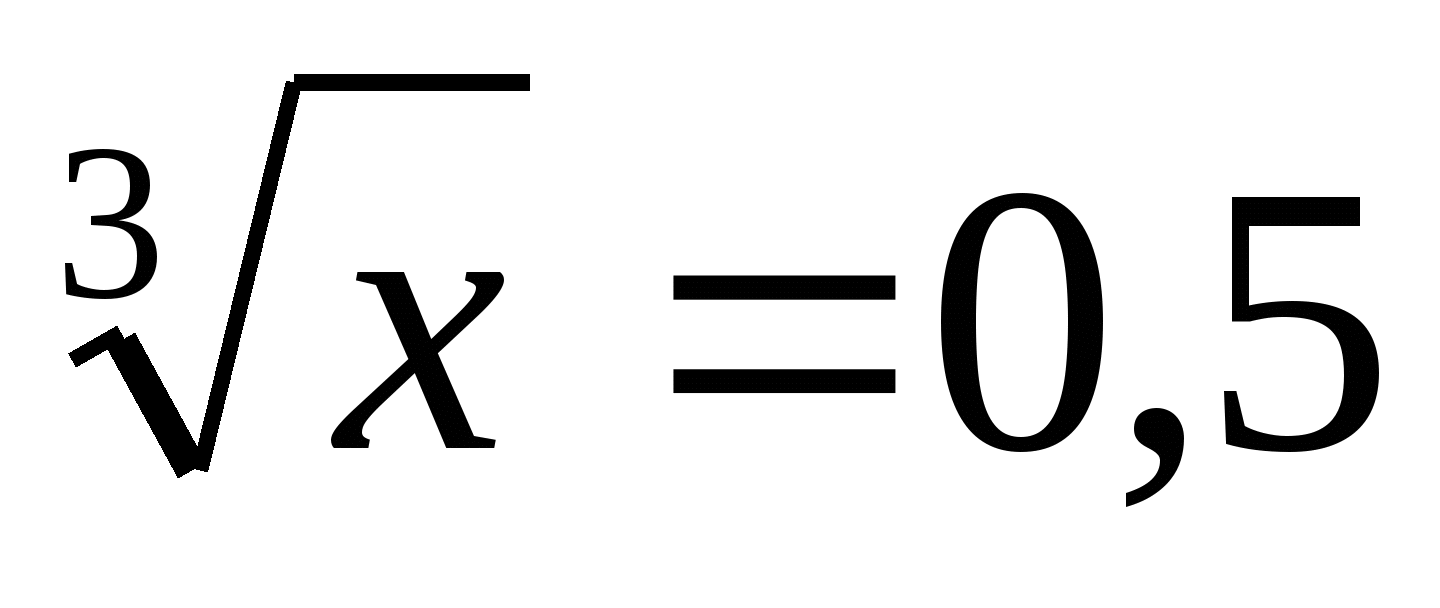 .Устный счет: 1) Решить уравнения:
.Устный счет: 1) Решить уравнения:
а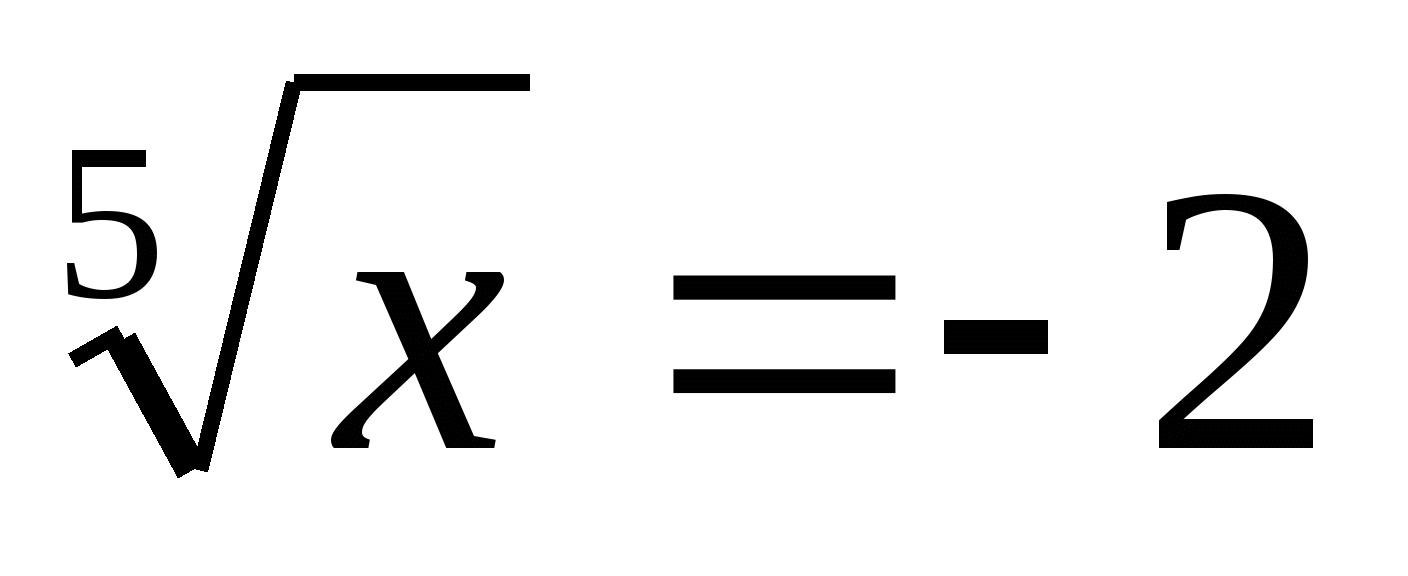 ) (0,125) Что общего в этих уравнениях?
) (0,125) Что общего в этих уравнениях?
(-32) (корни нечётной степени)
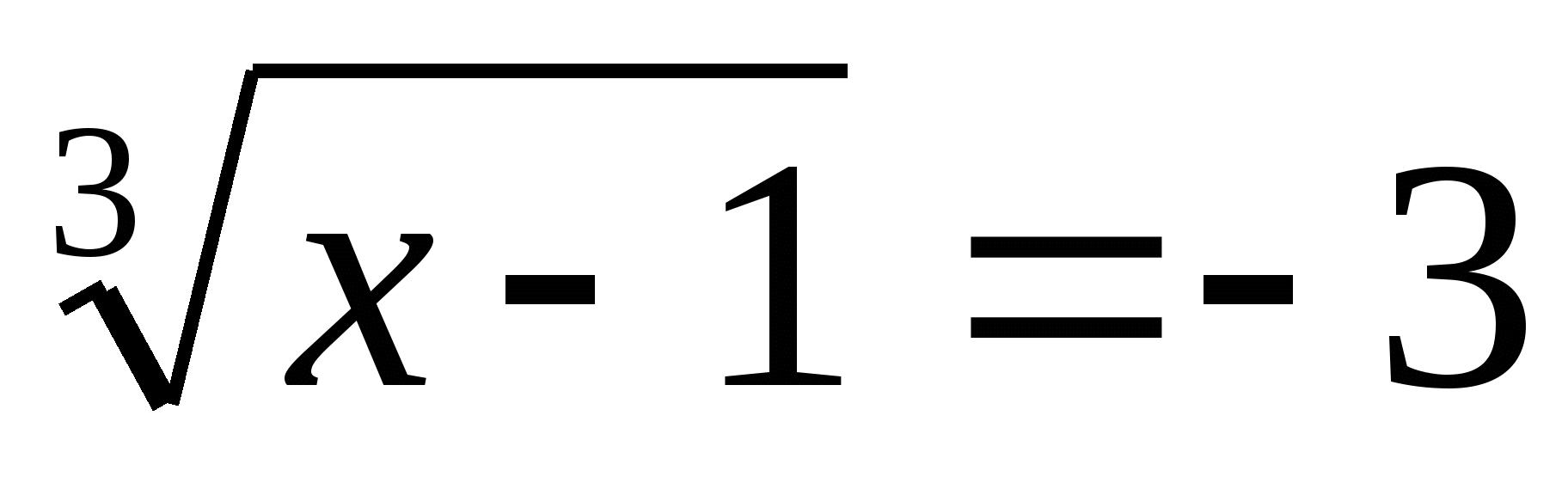 (-26) Что можно сказать про подкоренное выражение?
(-26) Что можно сказать про подкоренное выражение?
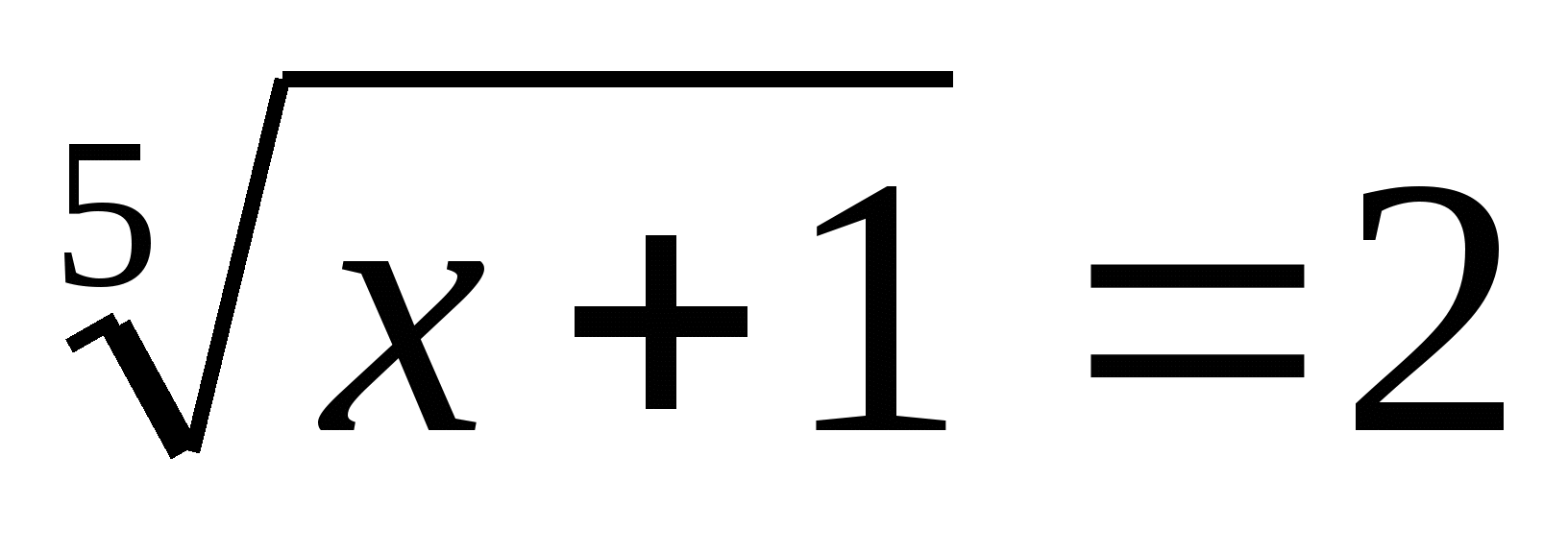 (может быть любым числом)
(может быть любым числом)
(31) Что можно сказать про значение этого корня?
(может быть любым действительным числом)
б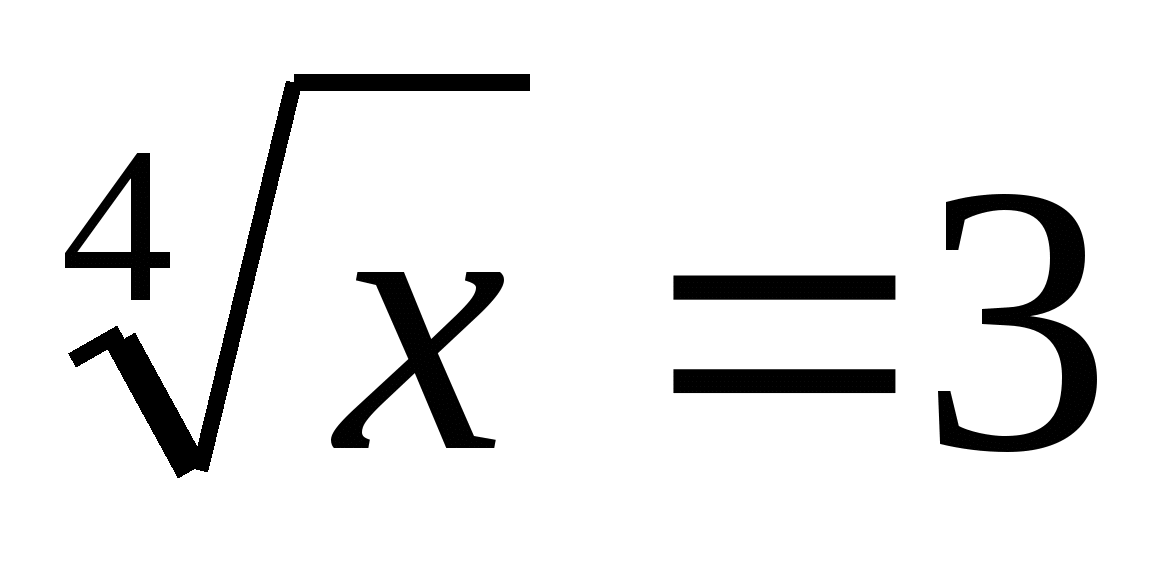 ) (81) Что общего в этих уравнениях?
) (81) Что общего в этих уравнениях?
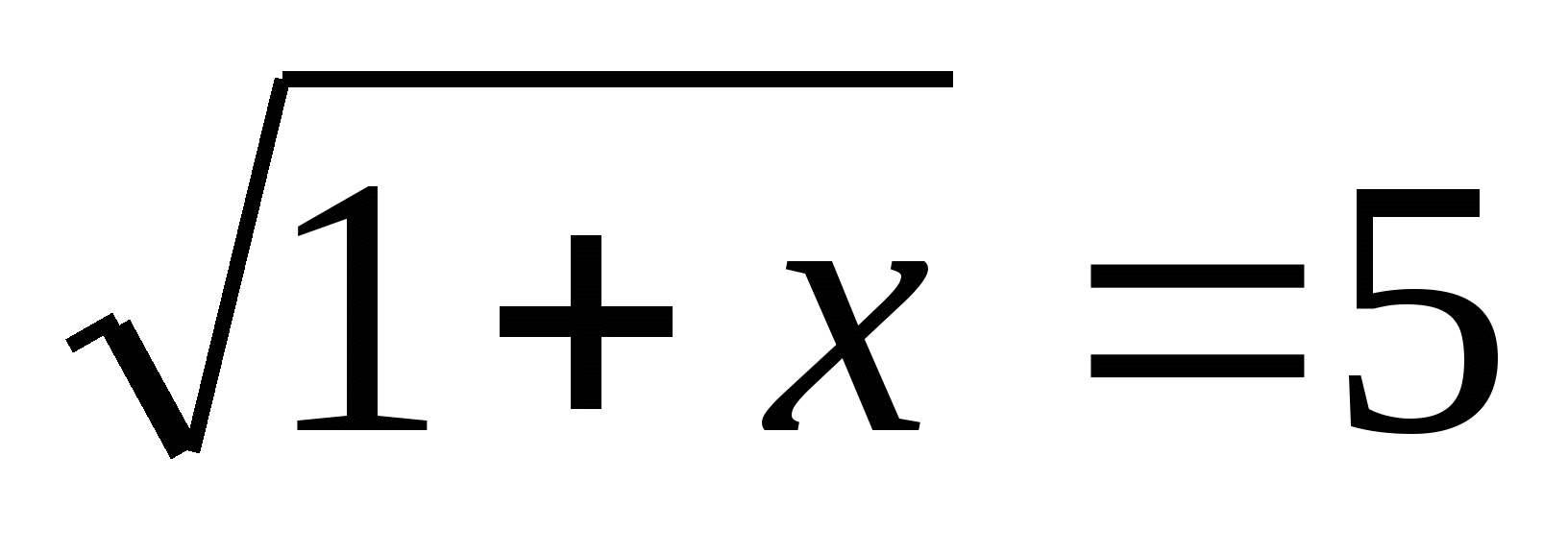
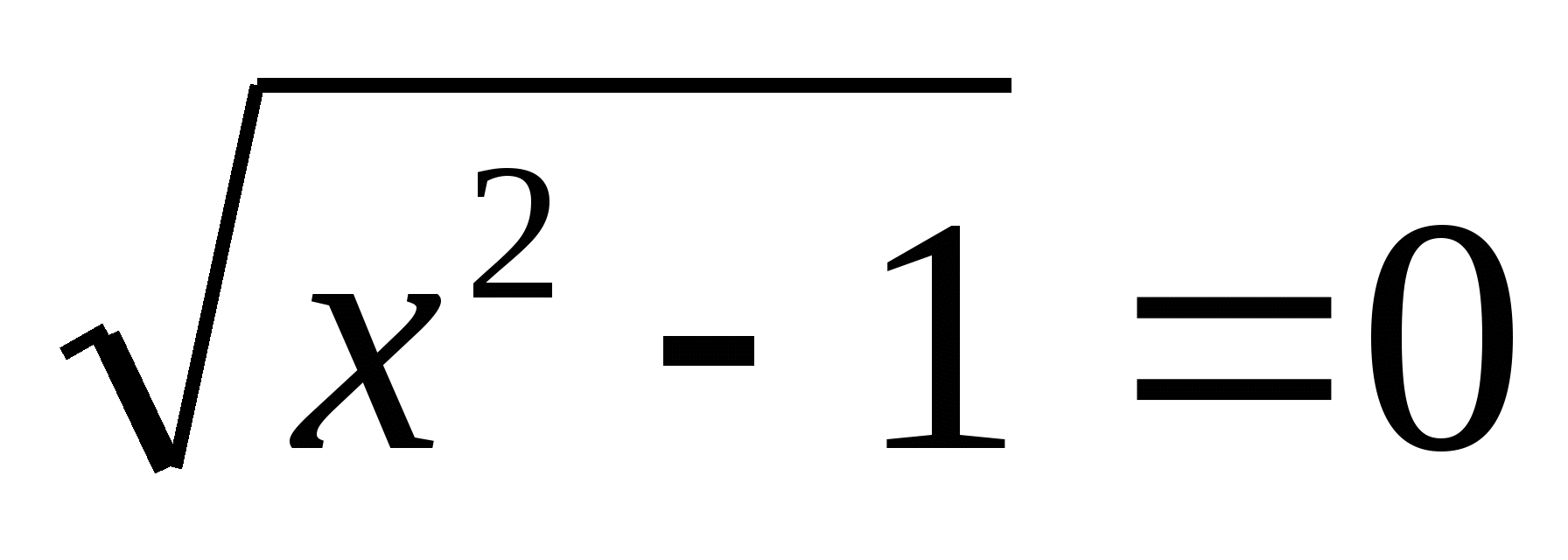 (24) (корни чётной степени)
(24) (корни чётной степени)
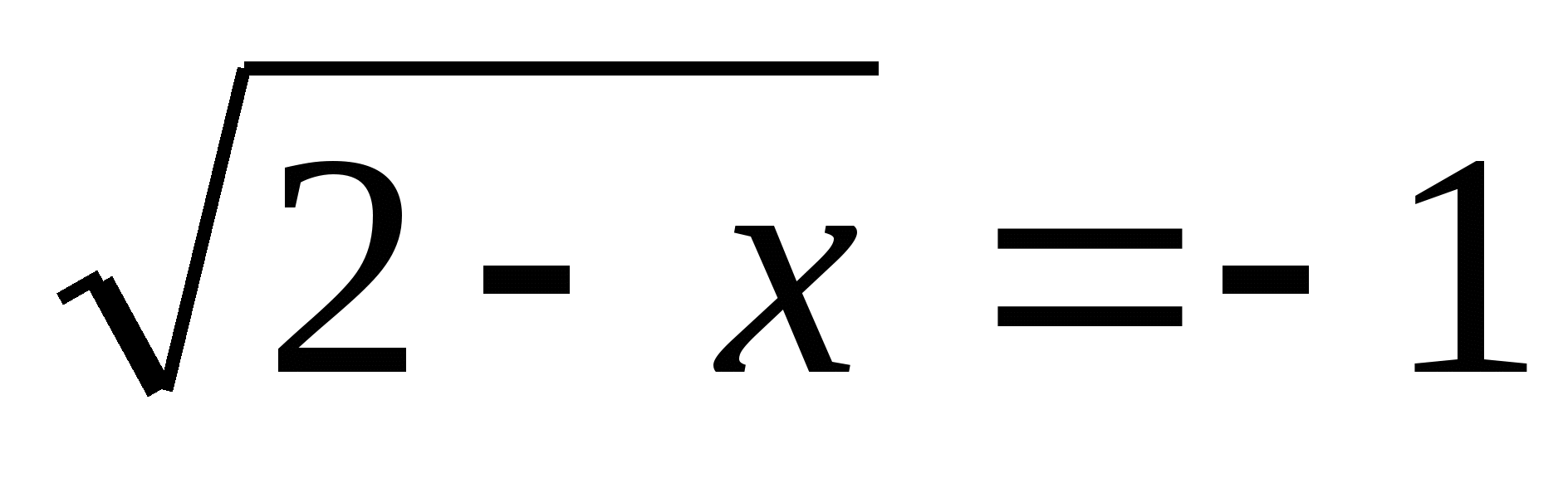 (+1 и -1) Что можно сказать про подкоренное выражение?
(+1 и -1) Что можно сказать про подкоренное выражение?
(корней нет) (положительное или 0)
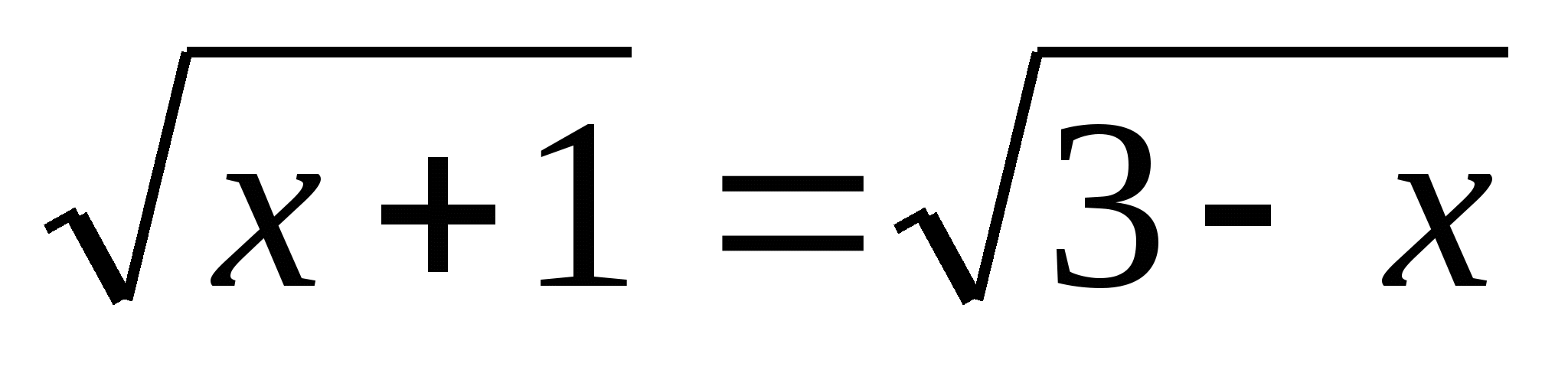 (1) Что можно сказать про значение этого корня?
(1) Что можно сказать про значение этого корня?
(положительное или 0)
2) Представить в виде квадрата следующие выражения:
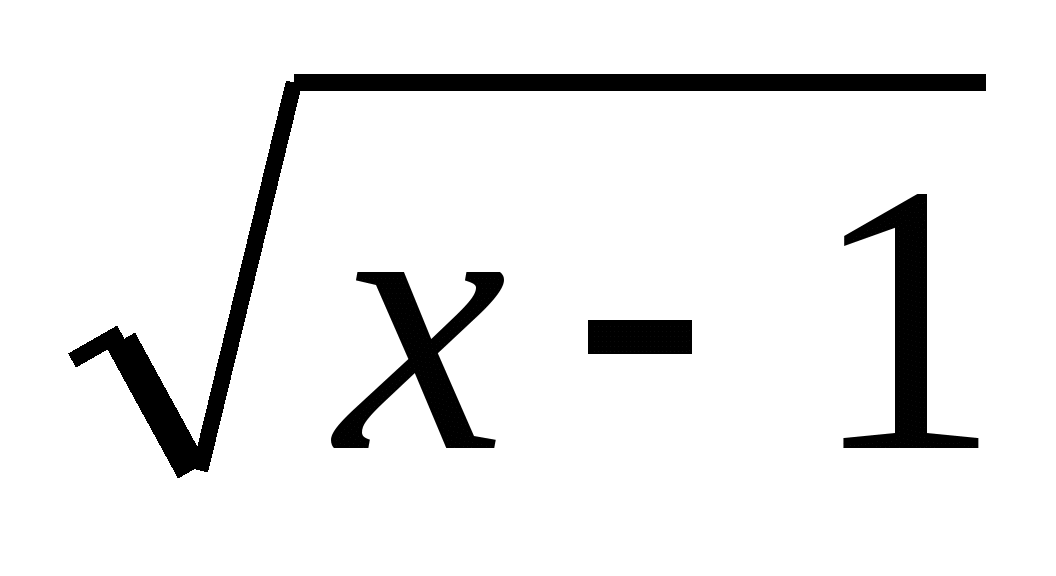
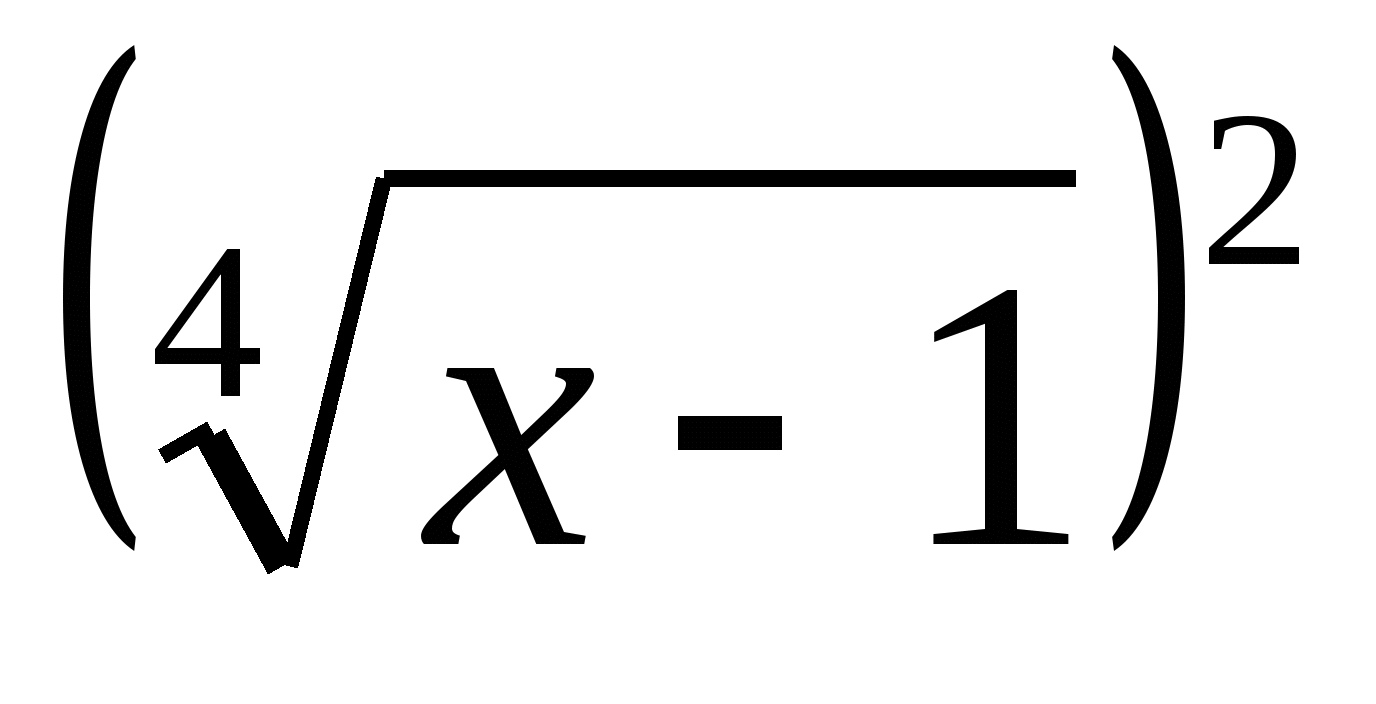
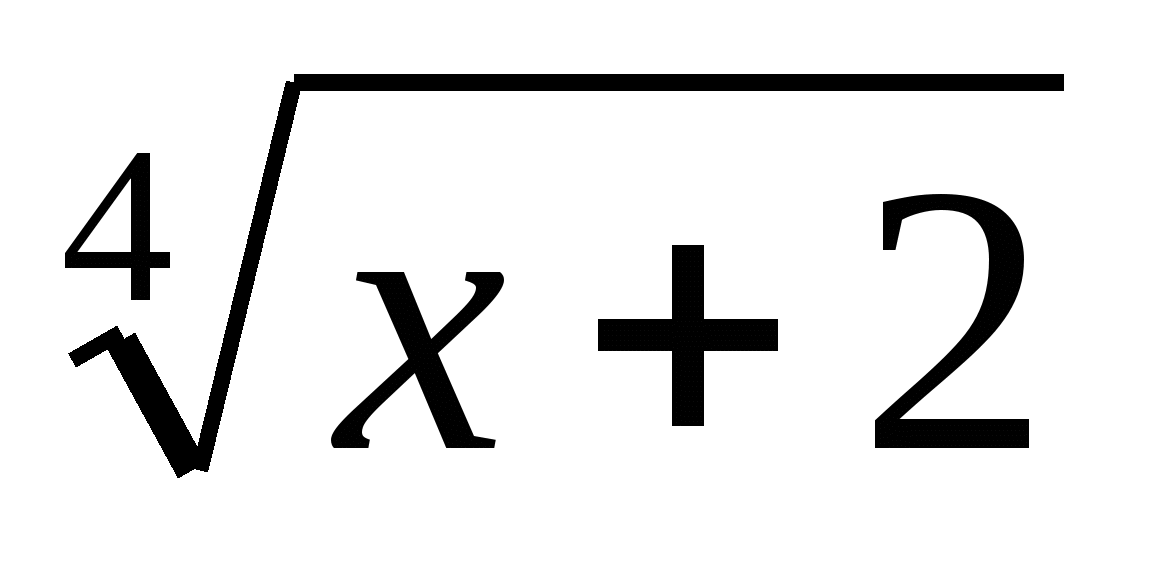
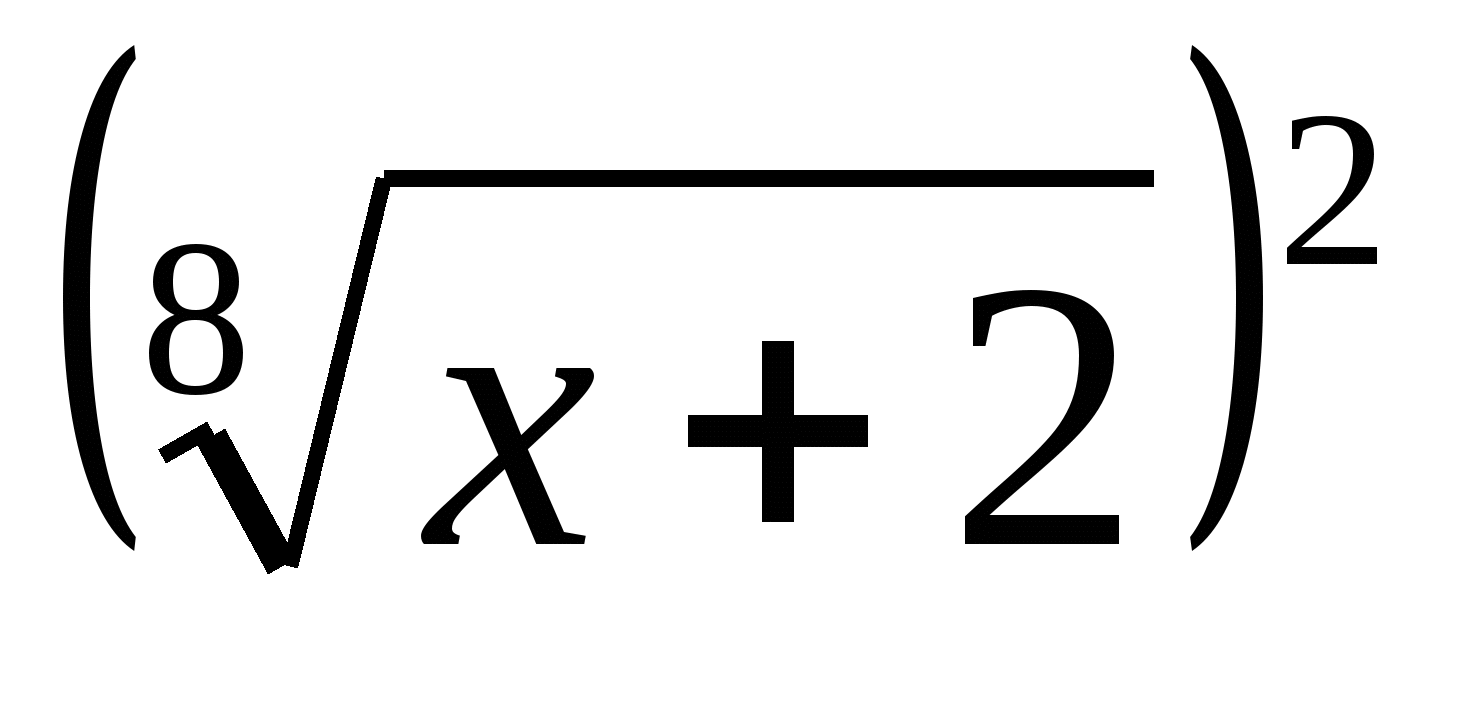
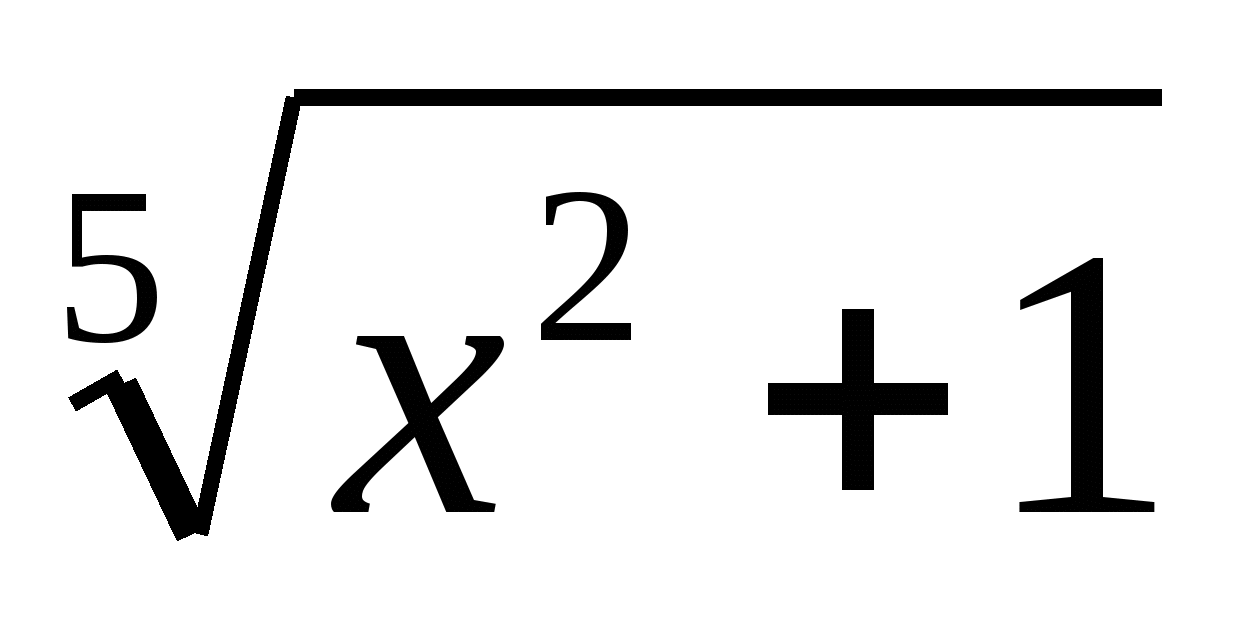
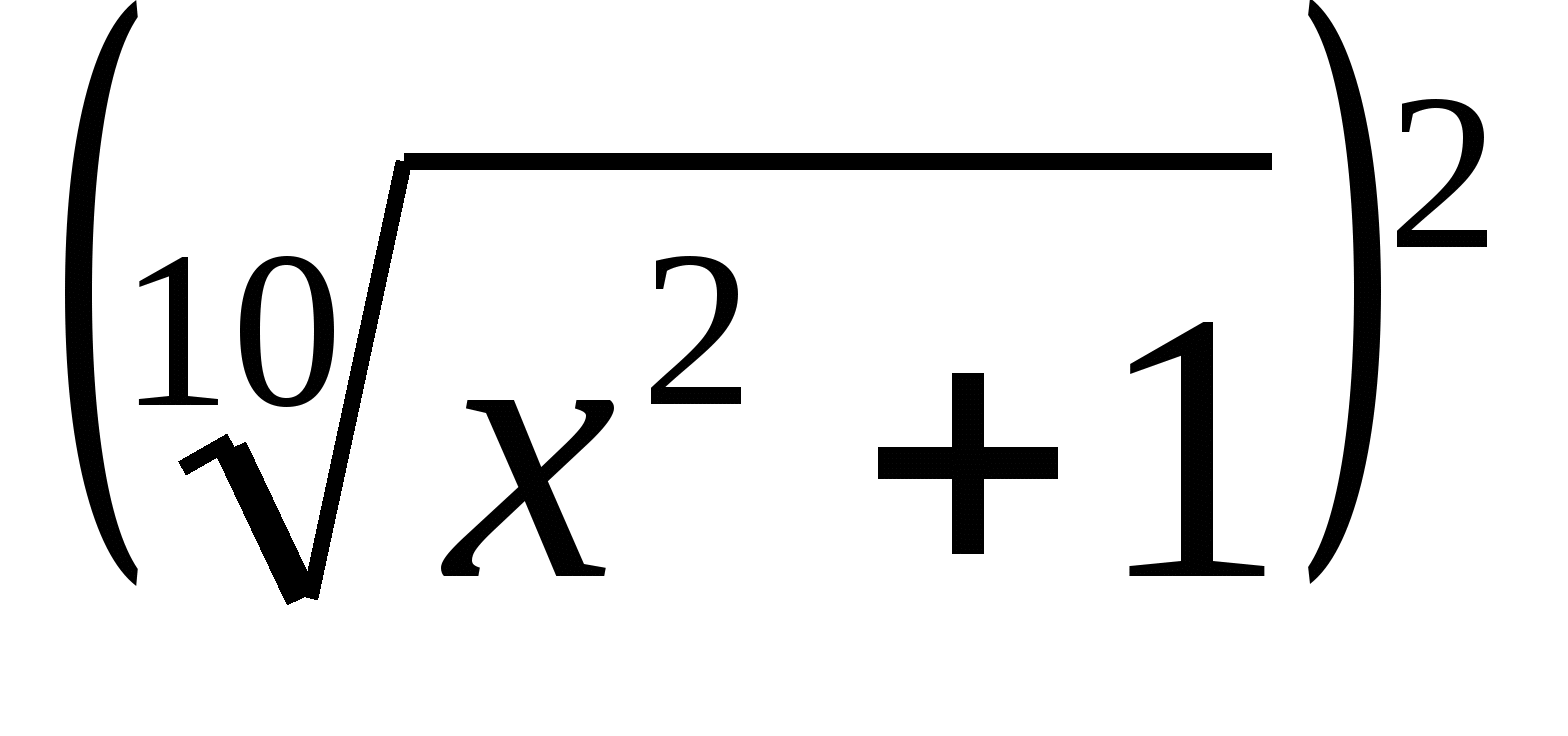
5. Запись числа, темы урока: «Решение иррациональных уравнений».
Решение уравнений:
У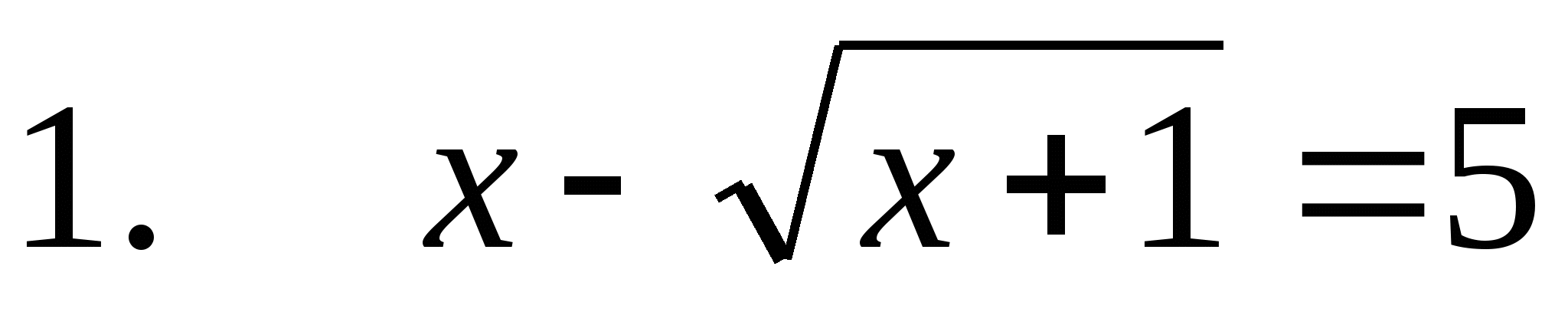 ченик №1
ченик №1
С чего обычно начинают решать иррациональные уравнения?
( с возведения в квадрат) Удобно ли это здесь? (нет)
Почему? (останется корень)
Упростим:
Решение с пояснениями О.О.У х>-1 Д.У. х>5
х-5=Öх+1
х 2-10х+25=х+1
х 2 -11х+24=0
х1=8 х 2=3 — вне Д.У.
Ответ: 8
У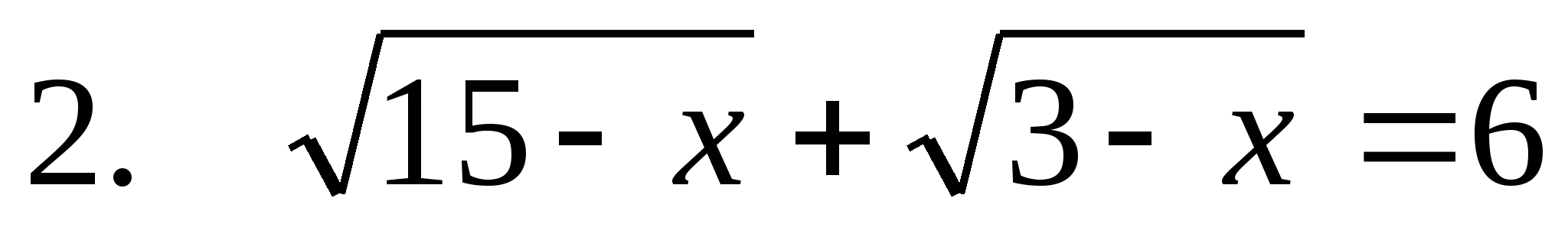 ченик №2
ченик №2
Сразу от корней не избавиться.
15-х+2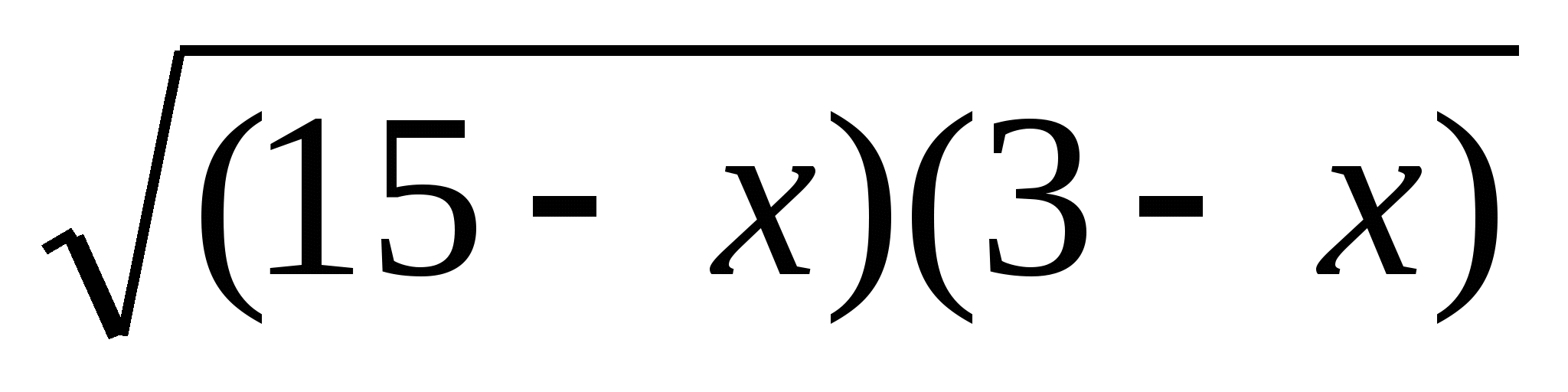 +3-х=36 Возведём в квадрат дважды.
+3-х=36 Возведём в квадрат дважды.
2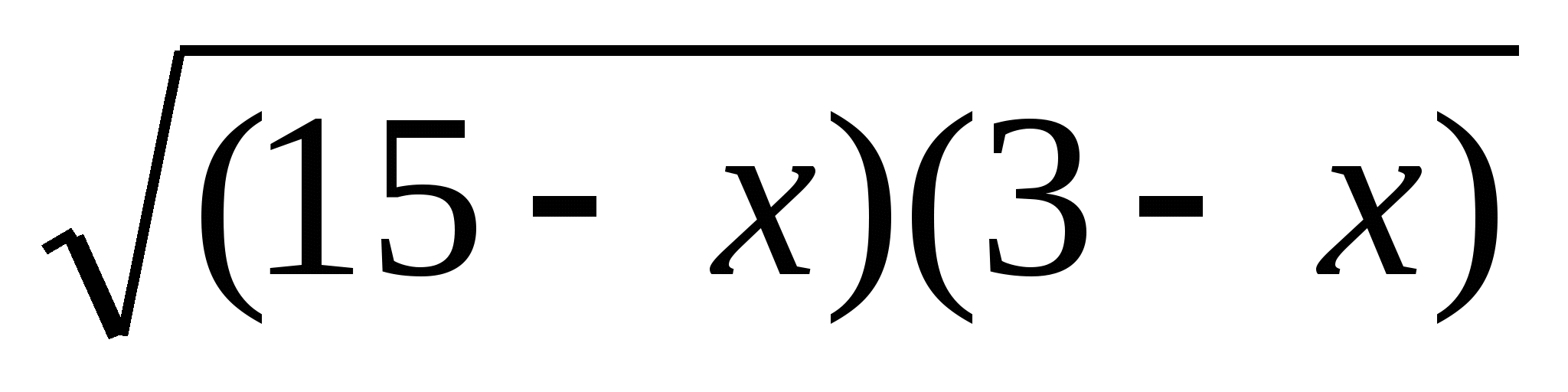 =18+2х
=18+2х
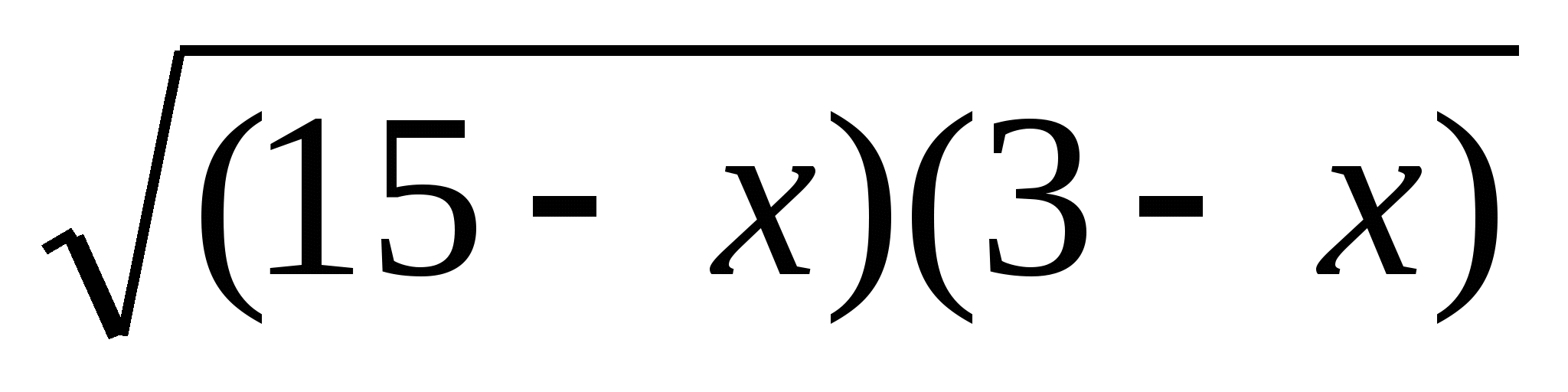 =х+9
=х+9
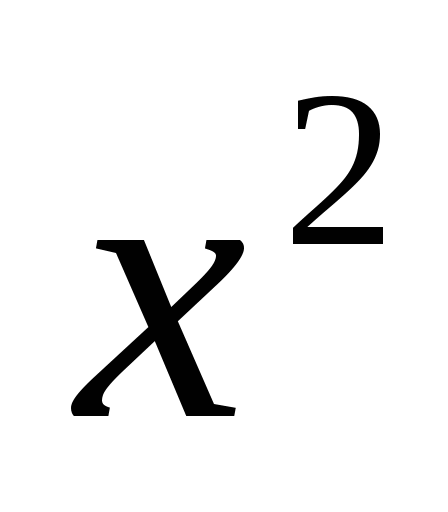 -18х+45=
-18х+45=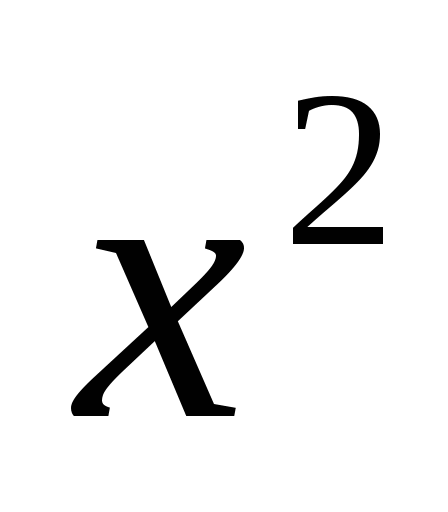 +18х+81
+18х+81
-36х=36
х=-1
Проверка: Л.ч. Ö15+1+Ö3+1=4+2=6
Пр. ч. 6 ; Л.ч.=Пр.ч.
Ответ: -1
Данный способ можно использовать не только с квадратными корнями, но и с корнями других степеней.
У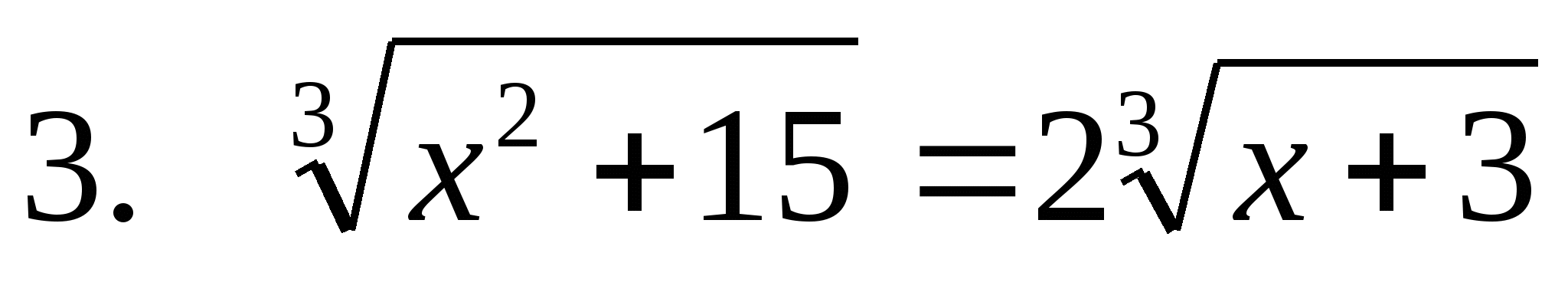 ченик №3
ченик №3
О.Д.З.
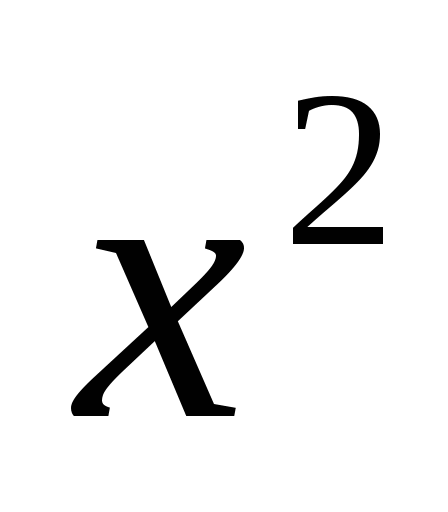 +15=8(х+3) (-∞; +∞)
+15=8(х+3) (-∞; +∞)
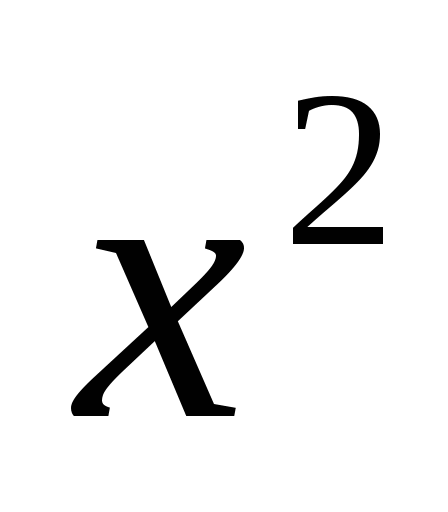 +15=8х+24
+15=8х+24
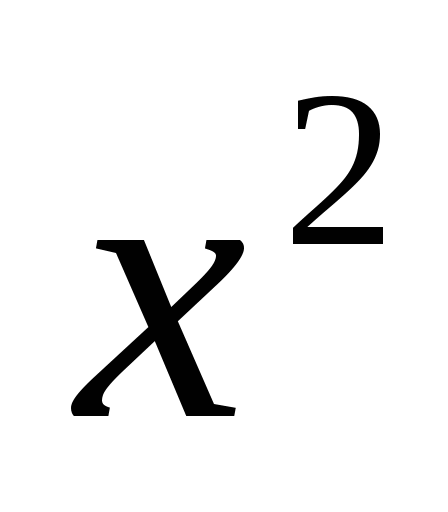 +8х-9=0
+8х-9=0
х1=9 х2=-1
Ответ: 9 ; -1
У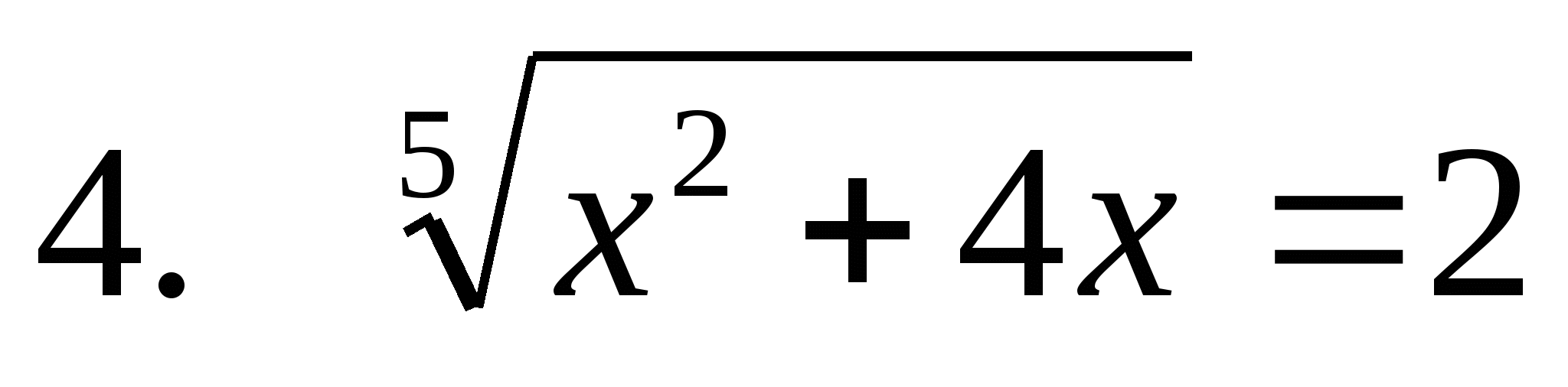 ченик№4
ченик№4
О.Д.З.
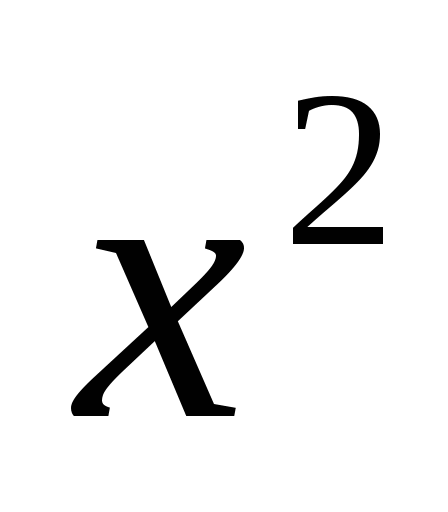 +4х=32 (-∞; +∞)
+4х=32 (-∞; +∞)
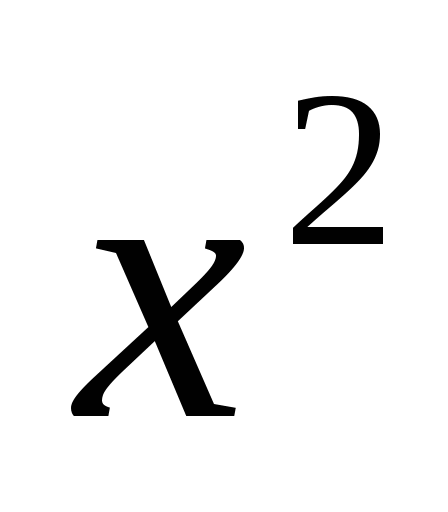 +4х-32=0
+4х-32=0
х1=-8 х2=4
Ответ: 4 ; -8
Ученик №5
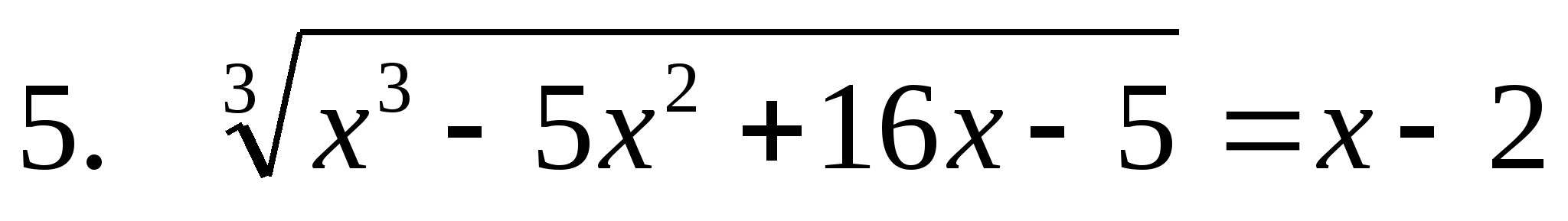 О.Д.З.
О.Д.З.
 -5
-5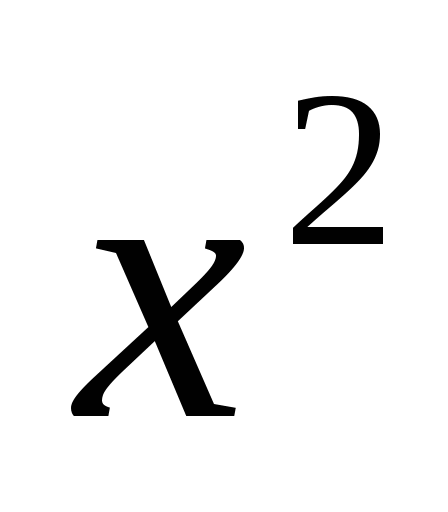 +16х-5=
+16х-5= -6
-6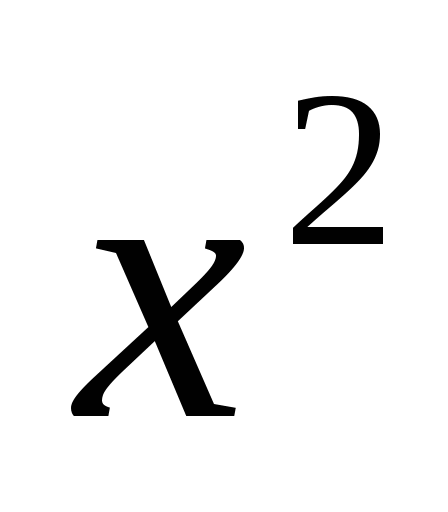 +12х-8 (-∞; +∞)
+12х-8 (-∞; +∞)
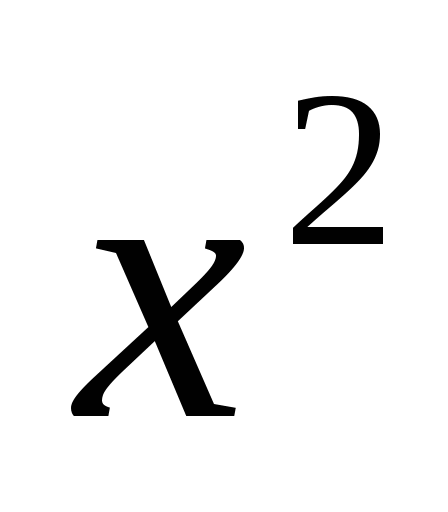 +4х+3=0
+4х+3=0
х1=-3 х2=-1
Ответ: -3 ; -1
У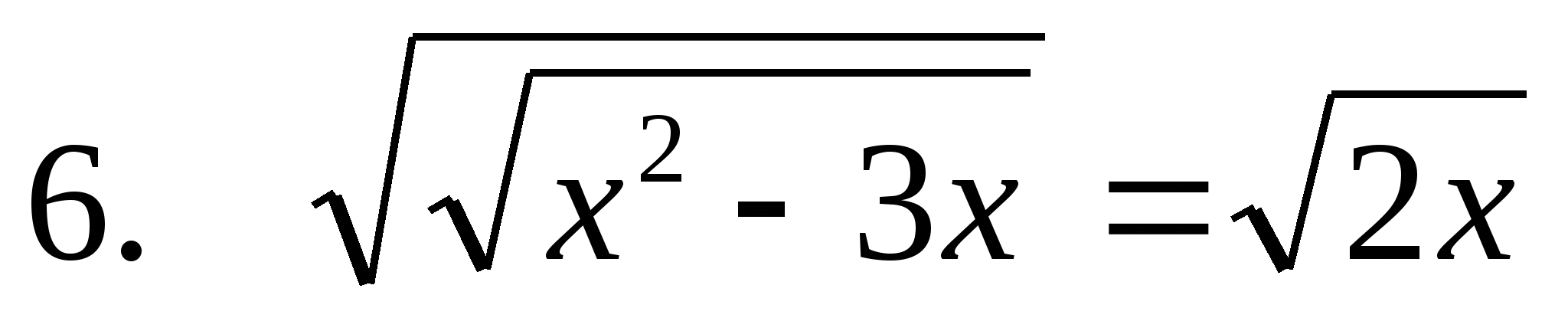 ченик№6
ченик№6
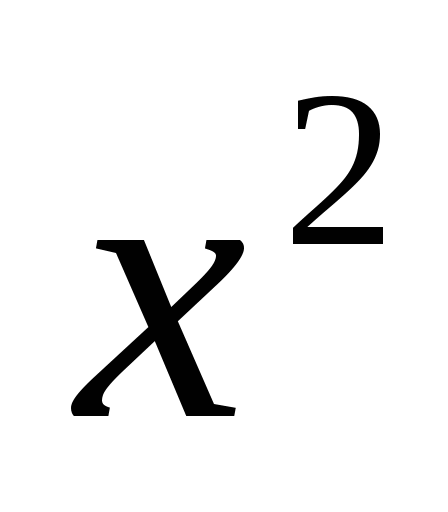 -3х=0
-3х=0
3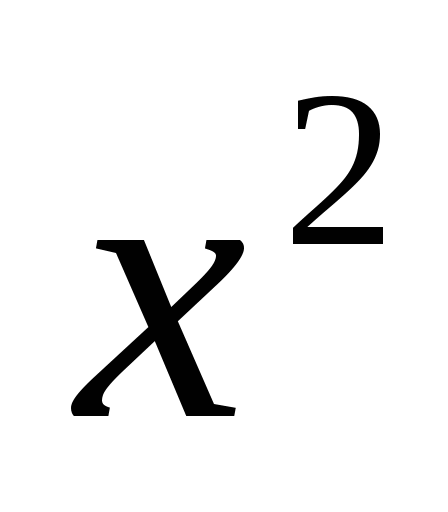 +3х=0
+3х=0
3х(х+1)=0
х1=0 х2=-1
Проверка: х=0
Л.ч. 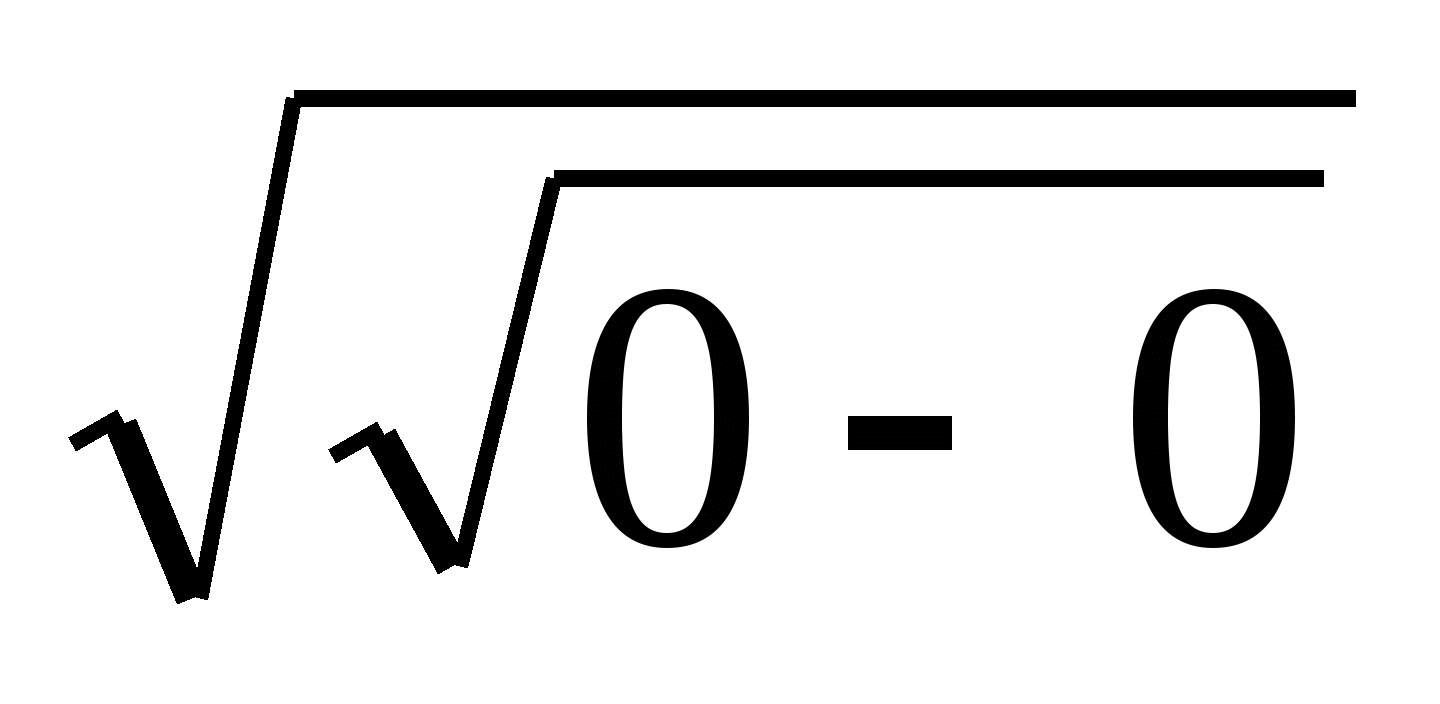 =0 Пр. 0
=0 Пр. 0
Л.ч. =Пр. ч.
Л.ч. 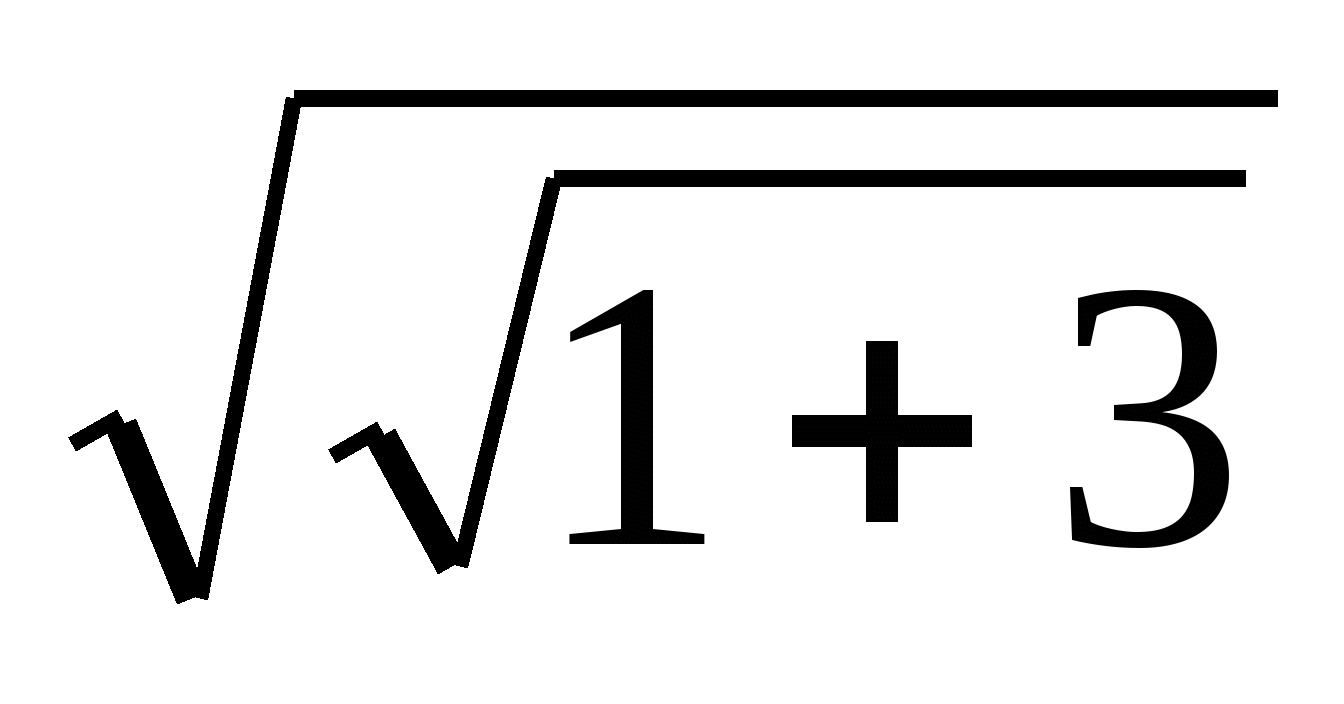 =
=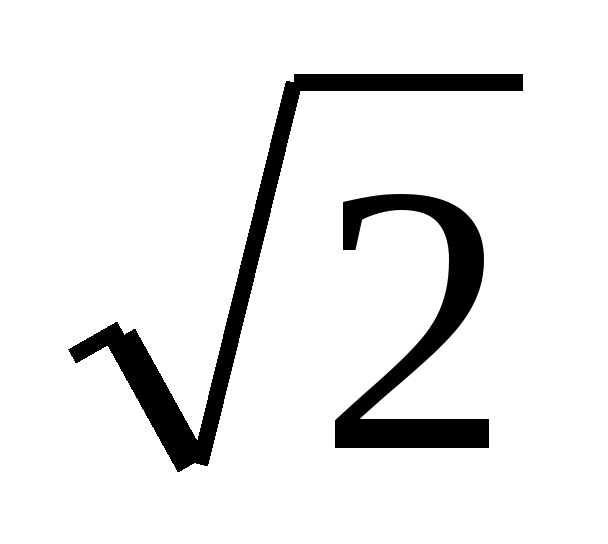 Пр.ч.
Пр.ч. 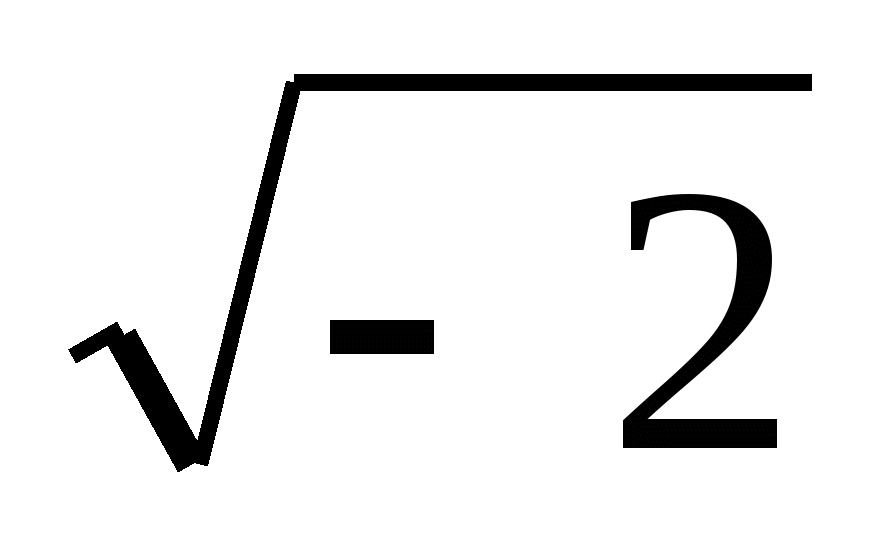 — не существует.
— не существует.
Ответ: 0
7.)Возьмем уравнения посложнее
Ребята такие уравнения подготовили дома:
У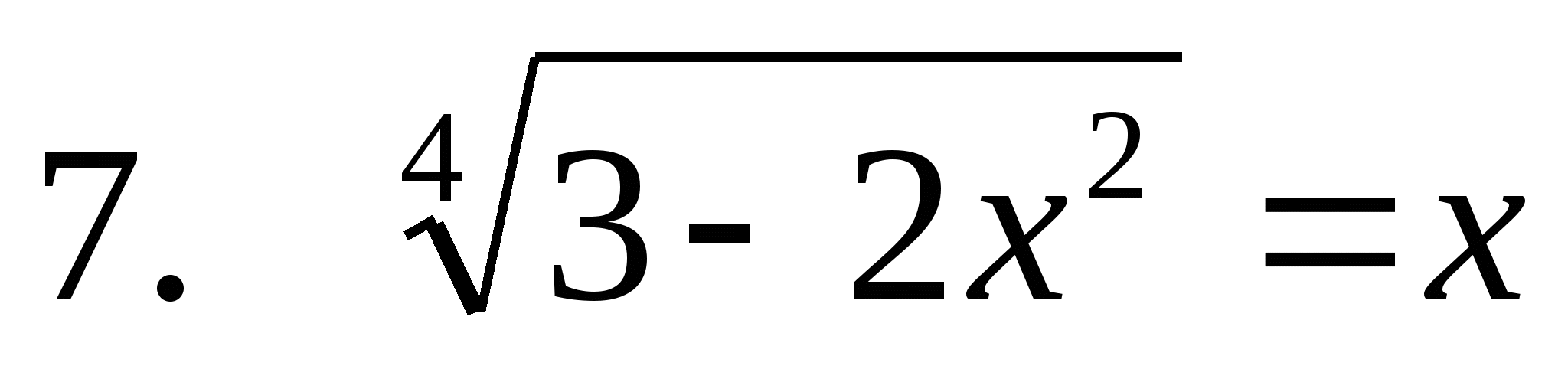 ченик№7
ченик№7
а) Д.У. х >0
3-2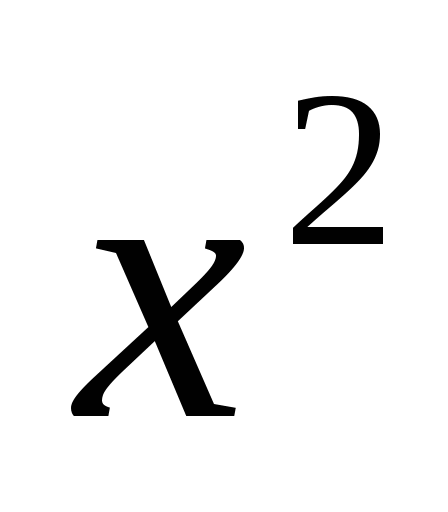 =
=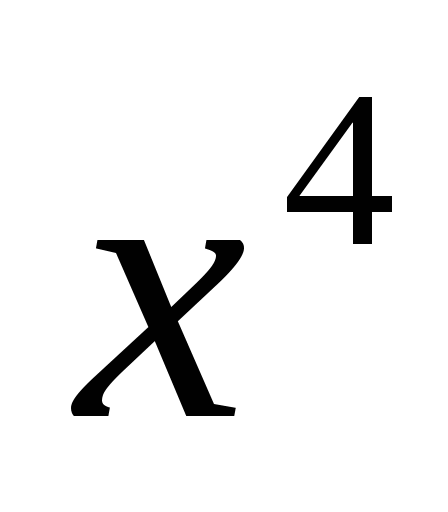
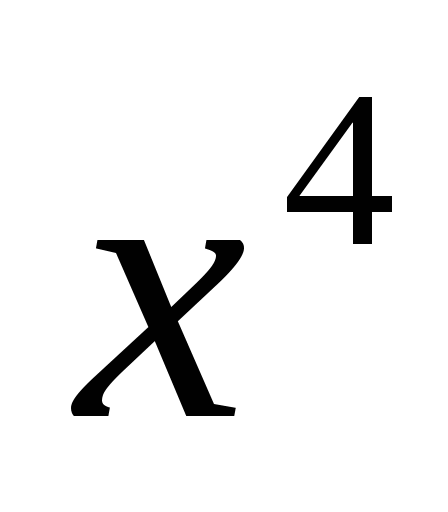 +2
+2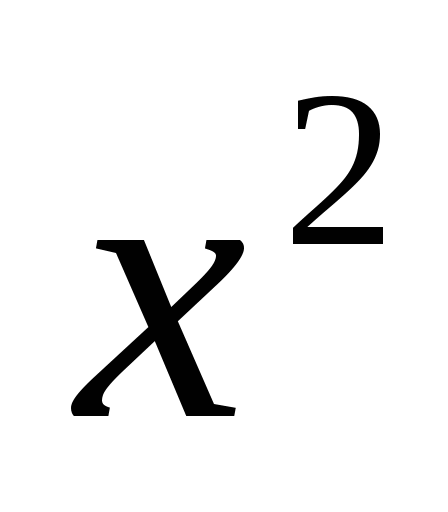 -3=0
-3=0
Пусть 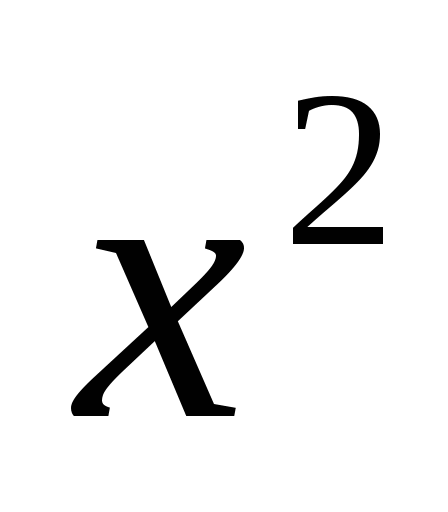 =t, t>0 , тогда t2+2t-3=0
=t, t>0 , тогда t2+2t-3=0
t1=-3, но t>0 , t2=1
Т.к. t2=1, то х2=1
х1=1 х1=-1 — вне Д.У.
Ответ: 1
У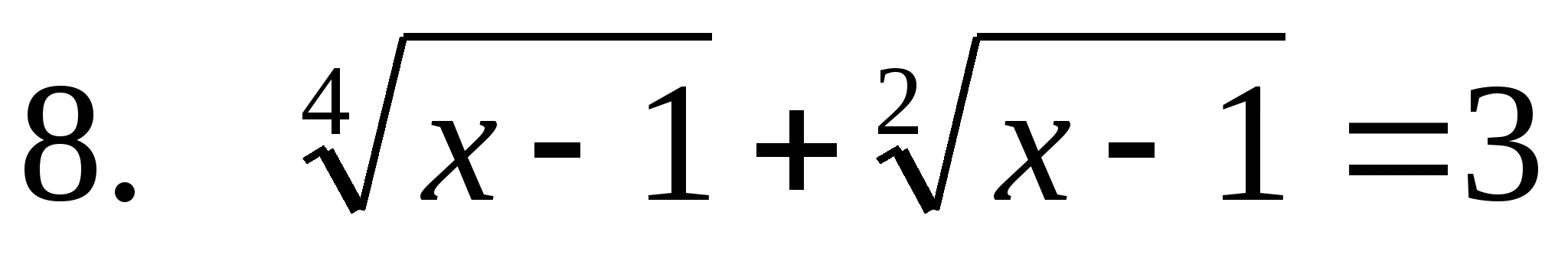 ченик№8
ченик№8
б) О.Д.З. х >1
Пусть 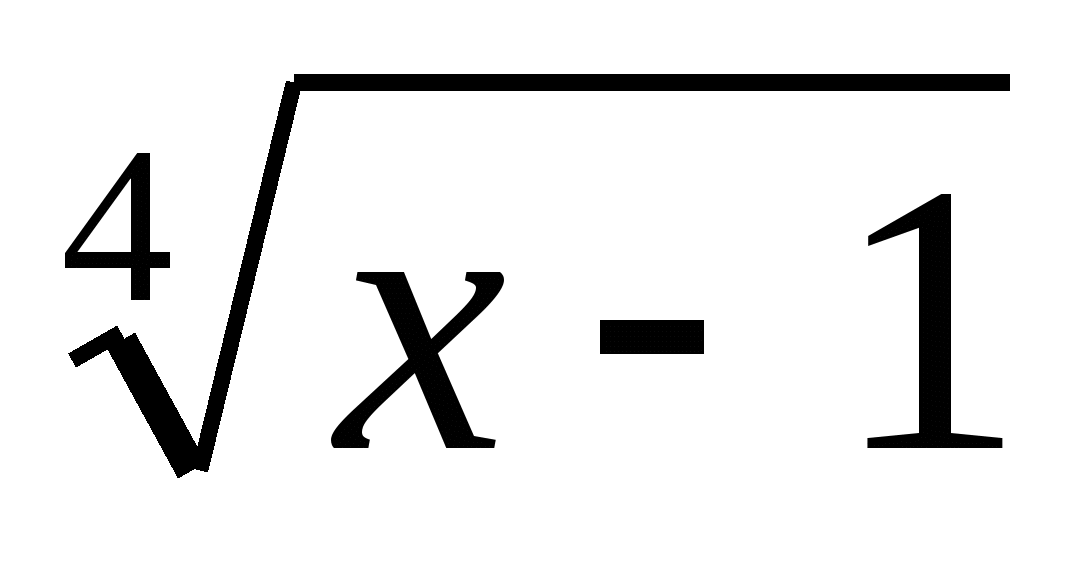 =t, t>0 то
=t, t>0 то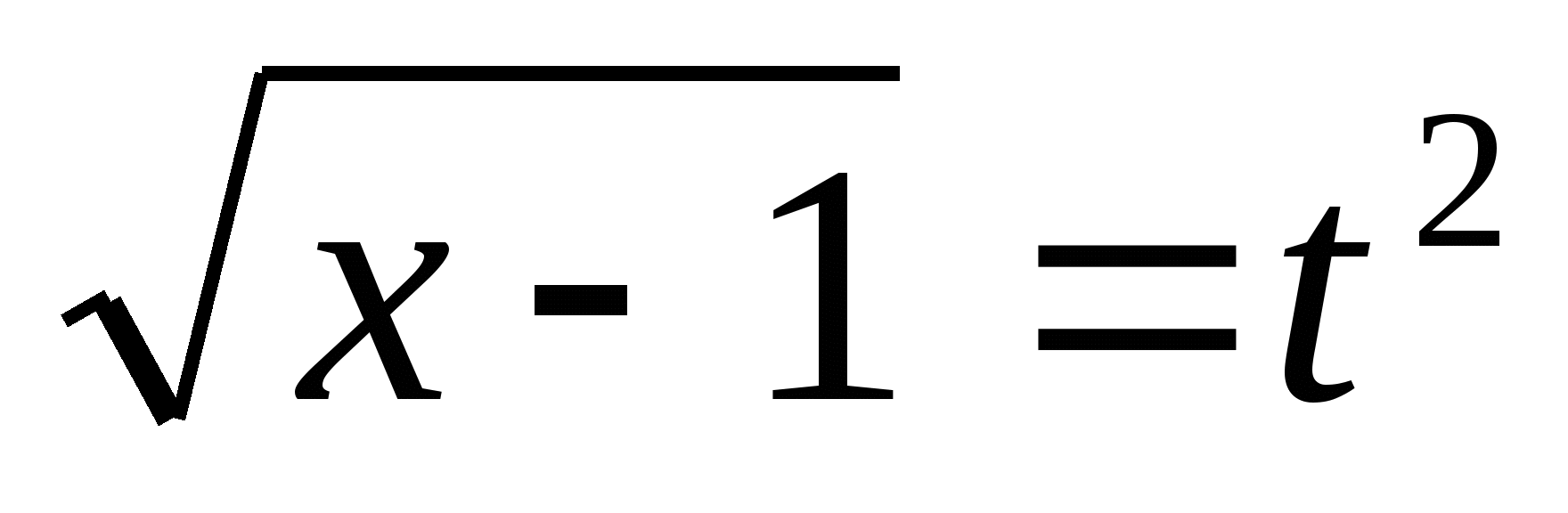 тогда
тогда
2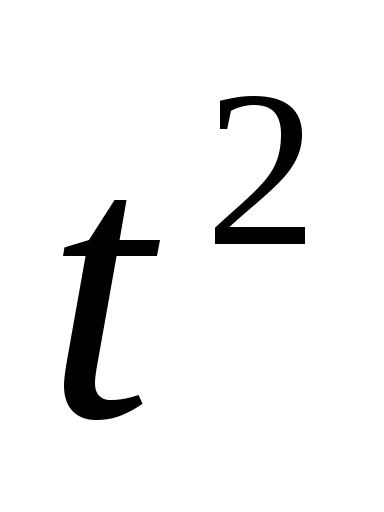 +t-3=0
+t-3=0
t1=1,5 ,но t>0 t2=1
Т.к. t=1 , то 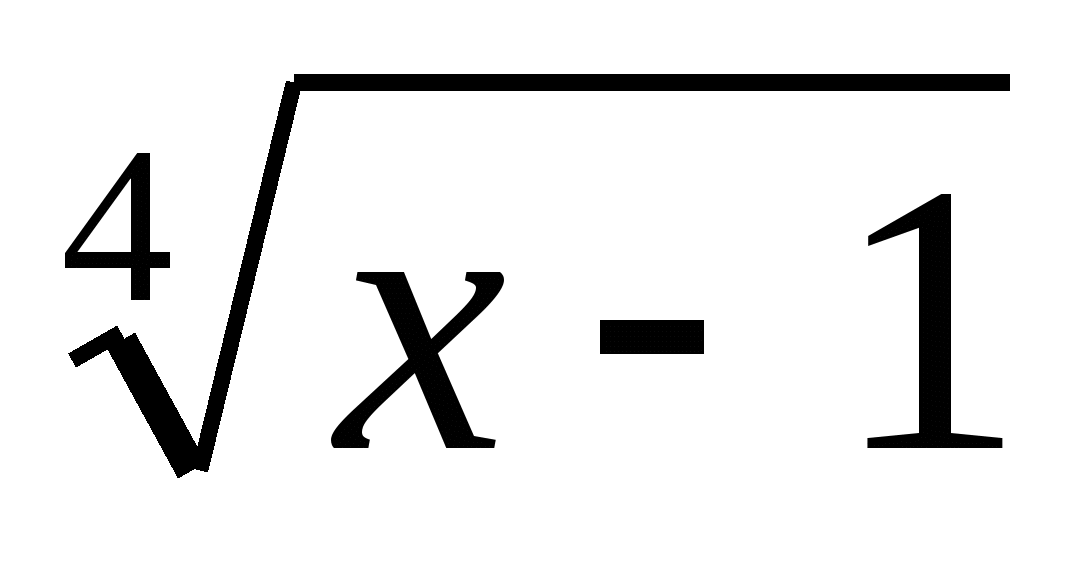 =1
=1
х-1=1
х=2
Ответ: 2
У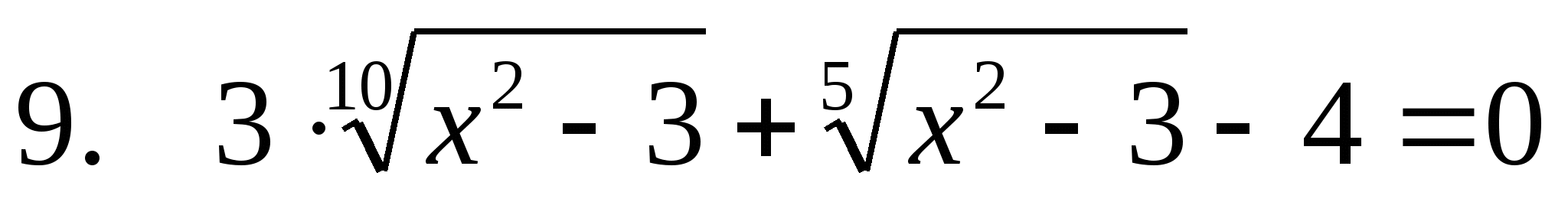 ченик№9
ченик№9
в)
Пусть 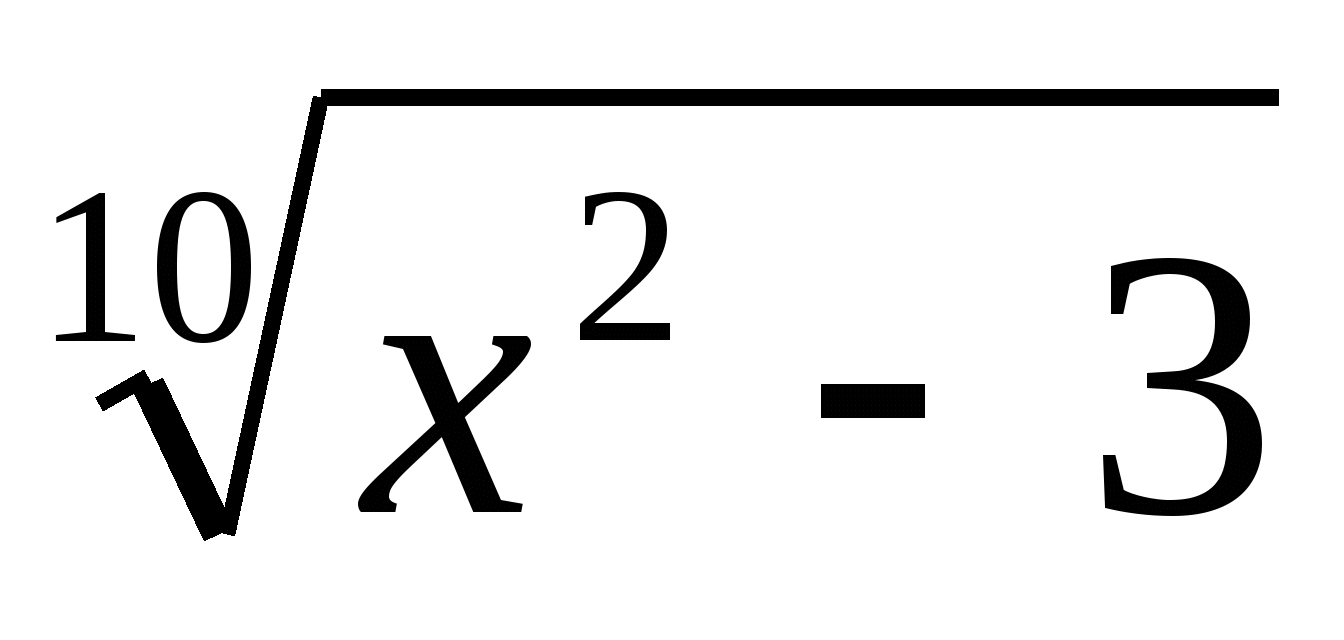 =t, t>0
=t, t>0
то 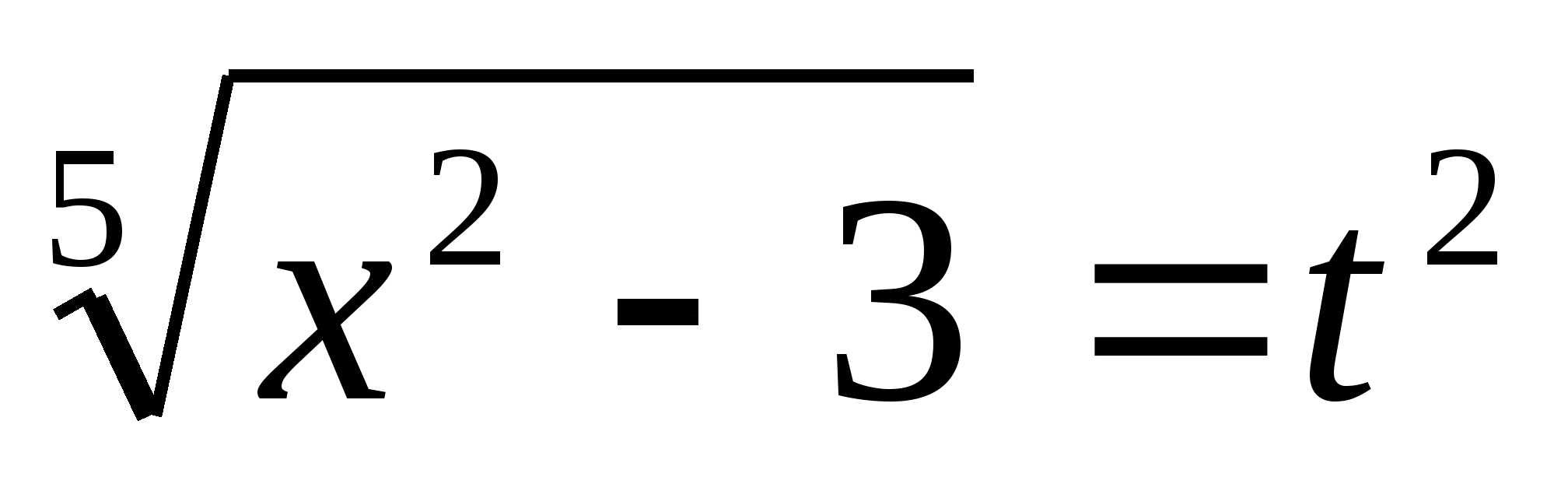 тогда
тогда
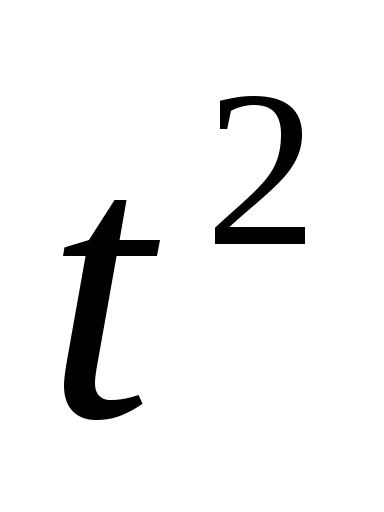 +3t-4=0
+3t-4=0
t1=-4 , но t>0, t2=1
Значит, 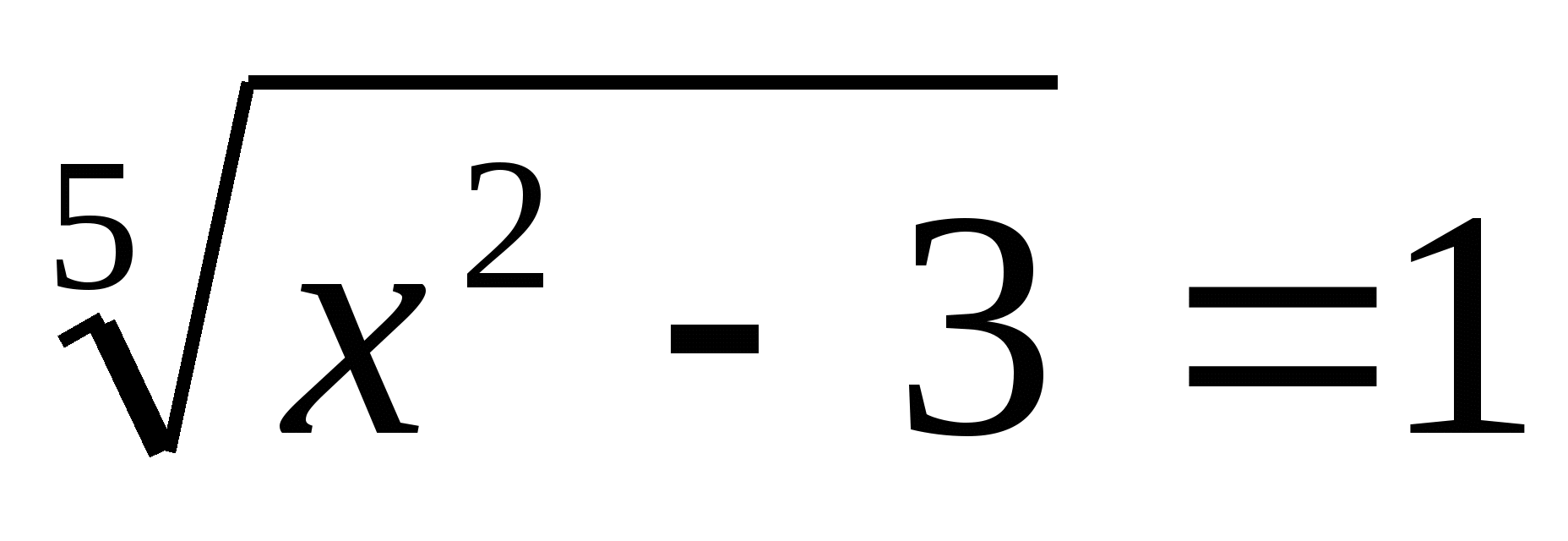
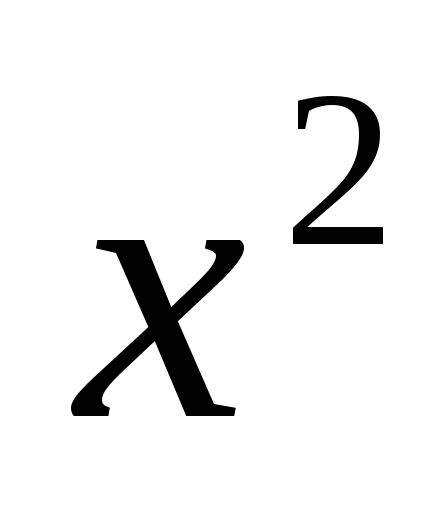 -3=1
-3=1
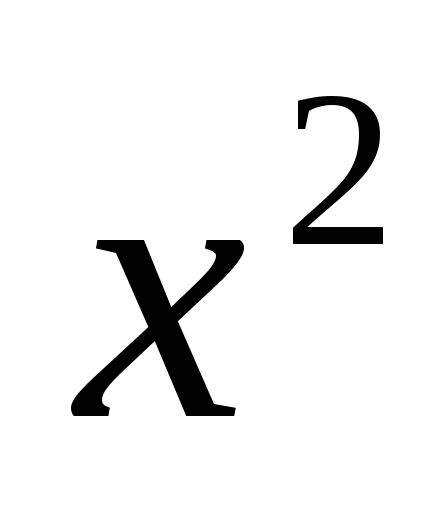 =4
=4
х1=2 х2=-2
П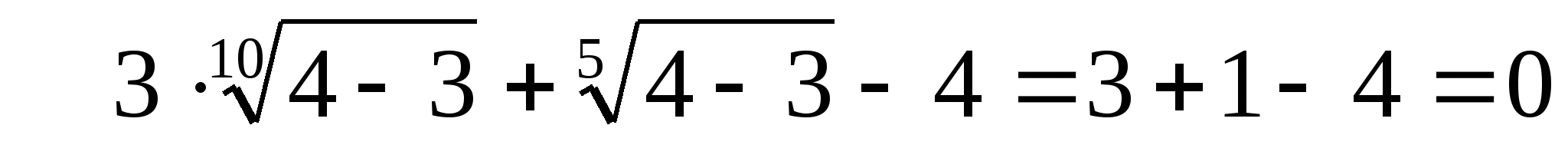 роверка: х1,2=±2
роверка: х1,2=±2
Л.ч.
П.ч. 0 Л.ч.=Пр.ч.
Ответ: 2 ;-2
6. Запишем домашнее задание:
№168(5), №169(3), №644(2,4), №645(1).
Индивидуально раздать карточки с заданиями на следующий урок, который продолжает эту тему.
Карточка №1
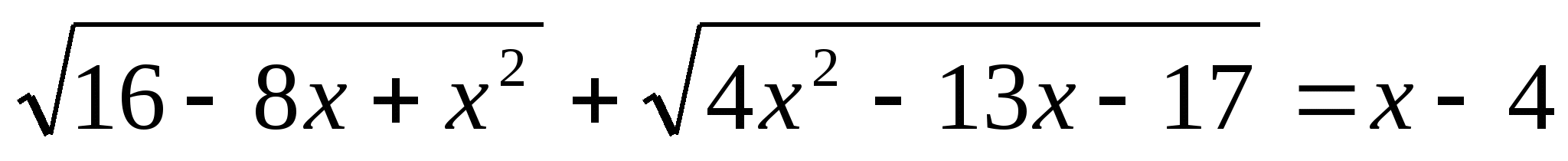
Карточка №2
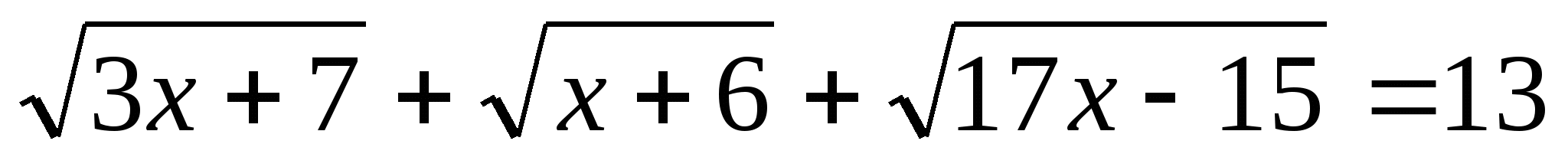
Карточка№3
Ö11х+3-Ö2-х-Ö9х+7+Öх-2=0
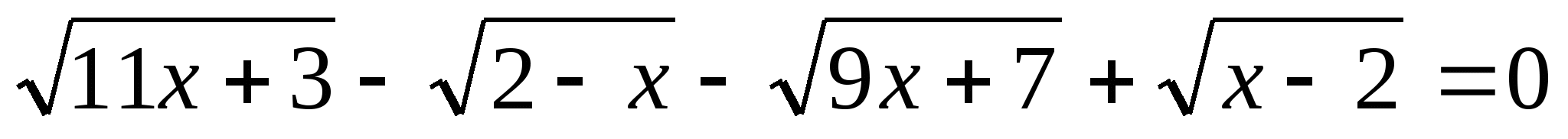
7. Подведение итогов:
1)Как же решаются иррациональные уравнения?
Какие способы мы повторили?
(возведение в квадрат, замена переменной)
При решении этих уравнений всегда ли мы делаем равносильные преобразования?
Как уберечься от ошибки?
(следить за равносильностью преобразований или делать проверку)
2)Выставить оценки учащимся.
infourok.ru
Учебно-методическое пособие по алгебре (10 класс) по теме: Иррациональные уравнения и неравенства
По теме: методические разработки, презентации и конспекты
 Изучение темы «Иррациональные уравнения и неравенства» в 10 классе
Изучение темы «Иррациональные уравнения и неравенства» в 10 классеМатериал содержит подробную технологическую карту уроков, которые проводятся при изучении темы «Иррациональные уравнения и неравенства» в 10 классе, где преподавание ведётся по учебнику Ш.А.Алимова. Д…
Мастер-класс по математике «Методика решений иррациональных уравнений и неравенств»Содержание:1.Пояснительная записка.2. Актуальность и перспективность мастер-класса.3.Теоретическая база.4. Новизна.5. Методы работы.6. Итоги и анализ проведения мастер-класса.7. Предполагаемые р…
 Материал к теме: «Решение иррациональных уравнений и неравенств».
Материал к теме: «Решение иррациональных уравнений и неравенств».В помощь учителю — материал к теме «Решение иррациональных уравнений и неравенств» (10 класс)….
Решение иррациональных уравнений и неравенств 11 классРешение иррациональных уравнений и неравенств. данная работа содержит рекомендации выпускникам школ и абитуриентам технических вузов Особенностью моей работы является то, что в школьном кур…
решение иррациональных уравнений и неравенств методом замены переменнойспособ решения иррациональных уравнений и неравенств методом замены переменной…
решение иррациональных уравнений и неравенств методом замены переменнойспособ решения иррациональных уравнений и неравенств методом замены переменной…
 Элективный курс «Иррациональные уравнения и неравенства»
Элективный курс «Иррациональные уравнения и неравенства»Элективный курс «Иррациональные уравнения и неравенства» предназначен для предпрофильной подготовки в 9 классе, своим содержанием сможет привлечь внимание учащихся, которым интересна…
nsportal.ru
Иррациональные уравнения
Тема урока: «Иррациональные уравнения»Тип урока: урок ознакомления с новым материалом и первичное его закрепление.
Цель урока: ввести понятие иррациональных уравнений и показать способы их решения.
Задачи: создать условия:
для формирования у обучающихся умений решать иррациональные уравнения;
для развития алгоритмического мышления, памяти, внимательности, умения излагать мысли, делать выводы, обобщать;
для усиления познавательной мотивации осознанием ученика своей значимости в образовательном процессе;
для воспитания у обучающихся самостоятельности.
Время проведения: 45 минут.
План урока.
I. Актуализация
1. Проверка домашнего задания.
2. Повторение пройденного материала.
II. Рассмотрение нового материала
1. Сообщение темы урока.
2. Постановка целей и задач.
3. Рассмотреть некоторые способы решения иррациональных уравнений.
III. Закрепление изученного материала
Устная работа.
Гимнастика для глаз.
Выполнение практических задании.
IV. Подведение итогов. Рефлексия.
V. Домашнее задание
Ход урока.
Эпиграф

I. Актуализация.
Проверка домашнего задания с помощью фронтального опроса при устной работе.


II. Рассмотрение нового материала.
На экране вы видите уравнения
Посмотрите внимательно и определите, какие уравнения вы уже умеете решать, а какие у вас вызывают затруднения?






– Кто может назвать тип уравнения, которые вам знакомы?
Вывод: Остались уравнения, которые вы еще не умеете решать.
– Чем отличается запись этих уравнений от тех, которые мы убрали?
Ответ: Неизвестное находится под знаком корня.
– Верно! Такие уравнения, в которых под знаком корня содержится переменная, называются иррациональными уравнениями.
Иррациональное (от лат. irrationalis неразумный, бессознательный) находящееся за пределами разума, противоречащее логике. Обычно противопоставляется рациональному как разумному, целесообразному, обоснованному.
Итак, тема нашего урока: “Иррациональные уравнения”.
Цель урока: Рассмотреть и отработать некоторые способы решения простейших иррациональных уравнений.
Определение: |
|
 Существует множество методов решения иррациональных уравнений, одни из них вы видите на экране. Сейчас мы рассмотрим в некоторые из них и на примерах. Вернемся к нашему эпиграфу, перефразировав слова Декарта, можно сказать, что чем труднее задача, тем больше удовольствия получит тот, кто ее решит. Что вам сейчас и предстоит испытать
Существует множество методов решения иррациональных уравнений, одни из них вы видите на экране. Сейчас мы рассмотрим в некоторые из них и на примерах. Вернемся к нашему эпиграфу, перефразировав слова Декарта, можно сказать, что чем труднее задача, тем больше удовольствия получит тот, кто ее решит. Что вам сейчас и предстоит испытать

 Метод возведения в квадрат обеих частей уравнения
Метод возведения в квадрат обеих частей уравнения





ПРОВЕРКА:

3 = 3 (верно)
Ответ: 4





Запомни!
Возвести обе части уравнения в квадрат.
Обязательно сделать проверку!!!
ТРЕНИРУЕМСЯ РЕШАТЬ


Корней нет
Метод замены переменной




Динамическая пауза (лёгкие упражнения для глаз, шеи, плеч, рук, спины)
III. Выполнение практических заданий
Выполнение практических заданий

IV. Подведение итогов
Рефлексия
Притча: Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго спросил мудрец: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
— Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.
— Кто работал так, как первый человек?
— Кто работал добросовестно?
— Кто принимал участие в строительстве храма науки?

V. Домашнее задание №152(1,3), 153(1,3), 154(1,3)
videouroki.net
Методическая разработка по алгебре (10 класс) на тему: Открытый урок по алгебре — тема » Решение иррациональных уравнений» для 10 класса
Урок по алгебре и началам анализа в 10 классе
Тема урока: «Иррациональные уравнения
Учитель: Цейтлина Марина Иосифовна
Цель урока: Знакомство с иррациональными уравнениями, приемы их решения.
Задачи урока:
— образовательные – познакомить учащихся с иррациональными уравнениями и приемами их решения;
— развивающие: развитие умений учебно-познавательной деятельности (умение организации учебного труда, работа с учебником и другими источниками информации). Развитие культуры устной и письменной речи.
Тип урока: комбинированный урок (ознакомление учащихся с новым материалом и проведение первичного закрепления материала)
Педагогические технологии: педагогика сотрудничества (учитель – ученик)
Метод обучения: обучение в сотрудничестве «Учимся вместе». Во время обсуждения учителю можно задавать любые вопросы.
Учебник: «Алгебра и начала анализа», Ш.А. Алимов, Ю. М. Калягин и др., Москва, «Просвещение», 2010г.
План урока
Так как тема «Иррациональные уравнения» рассчитана на 2часа, то данный урок охватывает не все приемы решения иррациональных уравнений. Данный урок позволяет рассмотреть только некоторые из них.
1. Организационные моменты. Сообщение темы урока.
2. Проверка домашнего задания.
3. Устная работа.
4. Изучение нового материала.
5. Выполнение упражнений по теме урока.
6. Подведение итогов урока.
7. Домашнее задание.
1.Организационные моменты.
Проверка готовности класса к уроку. Сообщение темы урока с последующей записью названия темы в тетрадь.
2. Проверка домашнего задания.
3. Устная работа.
Выполняются следующие устные упражнения:
а) Найдите значение выражения: ; .
б) Вычислите: .
в) Для каких значений переменных равенство верно:
; ; .
4. Изучение нового материала.
1) Определение. Уравнение, содержащее неизвестное под знаком корня, называется иррациональным уравнением.
Примеры: = х + 1; и т.д.
2) Основная задача — решить уравнение. А что это значит? (Найти корни уравнения или установить, что их нет). А что такое корень уравнения? (Ответ).
Давайте рассмотрим несколько иррациональных уравнений.
1.
5.
Задания 4; 5 разобрать на доске.
В уравнении «4.» интервалы неотрицательности левой и правой части не имеют области пересечения. Следовательно, не решая уравнения можно сказать, что уравнение не имеет решения.
В уравнении «5.» областью допустимых значений является число, равное 1, и только оно может являться корнем данного уравнения. При подстановке этого значения в левую часть уравнения получаем 0, а это означает, что уравнение не имеет решения. Нахождение О.Д.З. намного упростило решение данного уравнения.
Вывод. Прежде чем решать уравнение, желательно, если это возможно, проверить надо ли решать это уравнение.
3) Решение иррациональных уравнений. Простейшие иррациональные уравнения.
Решение иррациональных уравнений основано на следующем свойстве: при возведении обеих частей уравнения в натуральную степень получается уравнение – следствие данного.
а) Решение уравнения вида:
, где а — некоторое число.
Если а
Если а ≥ 0, уравнение равносильно уравнению f(x) = . Мы говорили о желательности записи О.Д.З. Почему в данном случае ее можно не писать?
(≥ 0).
Рассмотрим уравнение: ; х – 2 = 4;
; х =6.
Решаем №151 (1, 3, 5) устно.
б) Уравнение, в правой части которого стоит функция.
.
В этом случае при условии g(x) ≥ 0 имеем право обе части уравнения возвести в квадрат.
Получаем систему: .
Замечание. Если не пишем условия неотрицательности правой части, решение уравнения заканчиваем проверкой.
Пример:
Ответ: х = 2.
в) Уравнение, содержащее в левой и правой частях функции под знаком корня.
Это уравнения вида:
Решение этого уравнения равносильно решению системы:
.
Пример: .
Ответ: 10
Замечание. Можно решать уравнения возведением обеих частей в квадрат, с обязательной проверкой полученных решений.
г) Уравнение вида: + = a
Если a
Если а ≥ 0, то уравнение сводится к решению системы: .
Замечание. а) Иногда удобнее для вычислений уединить один из корней.
б) Возвести обе части уравнения в квадрат и сделать проверку
Пример:
Полученное уравнение сужает О.Д.З.
Ответ: 5
5. Выполнение упражнений по теме урока.
1.
2.
3.
4.
6. Подведение итогов урока.
На сегодняшнем уроке мы познакомились с иррациональным уравнением и некоторыми методами решения иррационального уравнения.
Рефлексия: Занятие подходит к концу. Пожалуйста, поделитесь своими мыслями о сегодняшнем занятии (хотя бы одним предложением).
Вам для этого помогут слова:
— Я узнал…
— Я почувствовал…
— Я увидел…
— Я заметил, что…, и т.д.
7. Домашнее задание.
№ 151(1), 154(2,4), 155(4), 156(3)
Второй урок позволит рассмотреть оставшиеся нерассмотренные методы решения иррациональных уравнений. Такие уравнения приведены ниже.
д) Уравнение вида: = 0
Это возможно тогда и только тогда, когда хотя бы один из множителей равен нулю.
а) Приравнивая каждый из множителей к нулю, получаем значения неизвестного и делаем проверку.
б) Используем О.Д.З.: g(x) ≥ 0. Делаем проверку по О.Д.З.
е) Использование свойств монотонности функции при решении иррациональных уравнений.
Рассмотрим это на примере решения уравнения
Пусть и у = 2, т.е. рассмотрим правую и левую части уравнений как функции переменной х f(x) и g(x) соответственно. Тогда f(x) является монотонно возрастающей для всех х ≥ 1, а g(x) = const. Используем утверждение, что, если одна из функций возрастающая (убывающая), другая – убывающая (возрастающая) или является постоянной, то уравнение имеет не более одного корня. В нашем случае х = 1.
ж) Решение иррациональных уравнений с помощью введения вспомогательной переменной.
Рассматриваем на примере:
Делаем следующую замену:
Тогда уравнение принимает вид: , а далее решение этого уравнения см.в разделе б).
З) Решение иррациональных уравнений с помощью разложения на множители.
Рассматриваем на примере:
Каждое подкоренное выражение содержит общий множитель х-1, тогда, перенеся все члены уравнения в одну сторону, можно общий множитель вынести за скобку и решать уравнение одним из рассмотренных ранее способов.
nsportal.ru
Методическая разработка по алгебре (10 класс) по теме: «Решение иррациональных уравнений»
Методическая разработка урока по алгебре в
10 классе (учитель Лифанова В.А.)
Тема урока: Решение иррациональных уравнений
Цель: дать представление о различных способах решения иррациональных уравнений
Задачи:
- повторить основные методы решения иррациональных уравнений;
- рассмотреть другие методы решения иррациональных уравнений
- развивать умение выделять главное в изучаемом материале, обобщать факты и понятия.
- развитие познавательных интересов, самоконтроля.
- воспитание эстетических качеств и умения общаться
Оборудование:
доска, интерактивная доска, компьютер, компьютерная презентация.
ПЛАН УРОКА. ( слайд 2)
- Организационный момент( сообщение темы урока и цели и задач урока)
- Проверка домашнего задания
- Анализ самостоятельной работы
- Устная работа с классом
- Изучение нового материала . Выполнение упражнений.
- Задание на дом
- Итог урока
ХОД УРОКА.
1. Организационный момент( сообщение темы урока и цели и задач урока) Слайд 2
Здравствуйте, ребята. Сегодня на уроке мы продолжим с вами заниматься решением иррациональных уравнений. Наша с вами задача: повторить и обобщить известные способы решения иррациональных уравнений и познакомиться с новыми.
Девизом нашего сегодняшнего урока предлагаю взять такте слова: Слайд 3
“Нельзя изучать математику глядя на то, как это делает сосед”.
Продолжим урок. Проверим домашнее задание.
2. (презентация учащегося)
№234(2,4,6)
2)х+√х=2(х-1)
√х=2х-2-х
√х=х-2
ó х=х²-4х+4
х-2≥0
ó х²-5х+4=0
х≥2
ó х=1, х=4
х≥2
Ответ: х=4.
4)√х-1=х-3
ó х-1=х²-6х+9
х-3≥0
ó х²-7х+10=0
х≥3
ó х=5, х=2
х≥3
Ответ: х=5.
6)√6+х-х²=1-х
1-х≥0
х≤1
х≤1
Ответ: х=-1.
№235(2,4,6)
2)√х²-36,75=х-3,5
х²-36,75=х²-7х+12,25
7х=49
х=7
Проверка:
√49-36,75=7-3,5
4)√5х+√14-х=8
√14-х=8-√5х
14-х=64-16√5х+5х
16√5х=50+6х
8√5х=25+3х
320х=625+150х+9х²
9х²-170х+625=0
D=6400
х1=125/9
х2=5
Пр-ка:
Х=125/9 – п.к.
√625/81+√14-125/9≠8
х= 5
√25+√14-5=8
8=8
Ответ: х=5.
6)√3-2х-√1-х=1
√3-2х=1+√1-х
3-2х=1+2√1-х+1-х
2√1-х=1-х
4-4х=1-2х+х²
х²+2х-3=0
х1=1
х2=-3
Пр-ка:
х=1
√3-2-√1-1=1
1-0=1
1=1
х=-3
√3+6-√1+3=1
3-2=1
1=1
Ответ: х=1, х=-3.
3,5=3,5
Ответ: х=7.
3) Анализ самостоятельной работы (слайд 4)
Основные ошибки: вычислительные, некорректная запись ответа.
Учитель: Уравнения с давних времен волновали умы человечества. Иррациональные уравнения тоже не исключение. Они очень важны и для математики, и для наук.
Чтобы лучше усвоить новый материал , давайте вспомним пройденный
4.Устная работа (слайд 5-7)
Дайте определение иррационального уравнения.
Каким способом можно решить данное уравнение?
Найти область определения функции
Какие из функций возрастают (убывают) на всей области определения?
5. Новый материал . (слайд8) Как можно решить данное уравнение? (графически)
Повторим графический способ решения уравнений. Учащийся у доски.
Самостоятельно решить графически уравнение:
(класс в тетрадях, учащийся на отвороте доски)
Рассмотрим ещё один метод решения иррациональных уравнений
-метод введения новой переменной (слайд 9-10)
Решить уравнение: (слайд 11) (учащийся у доски с комментированием)
Учитель: Иногда иррациональные уравнения можно решить гораздо быстрее и проще. Для этого нужно знать некоторые теоремы и свойства функций.
1.ИСПОЛЬЗОВАНИЕ СВОЙСТВ ФУНКЦИИ (слайд 12)
Теорема 1. Если в уравнении левая часть возрастающая (или убывающая) функция, а правая константа, то уравнение имеет не более одного корня.
Теорема 2 Если в уравнении левая часть возрастающая (или убывающая) функция, а правая часть убывающая (возрастающая) функция, то данное уравнение имеет не более одного корня.
Устно решим уравнения.(слайд 13)
2.ИСПОЛЬЗОВАНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИИ (слайд 14)
Решить уравнение:
Решение: (разбор вместе с учителем)
Первый радикал определен при
Второй радикал определен при любых значениях х. Выражение под третьим корнем неотрицательно при
Итак, единственной точкой, в которой определены эти радикалы, является x = 1. Легко проверить, что это число – корень уравнения.
Ответ: 1.
Решить уравнение: (слайд 15) (учащиеся комментируют решение данного уравнения и записывают его в тетрадь)
Учитель: Рассмотрим решение следующего уравнения (слайд 16)
В этом примере, как и в предыдущем, попытки найти корни, возводя обе части уравнения в квадрат, обречены на неудачу. Выпишем, как в предыдущем примере, условие существования функции, стоящей в левой части:
Решение этого неравенства также представляется проблематичным. Проверим неотрицательность правой части:
Последнее неравенство решений не имеет. Но тогда и исходное уравнение не имеет решений, так как левая часть его – неотрицательная функция! Ответ: Æ
Устно: Доказать, что уравнение не имеет решений: (слайд 17)
Арифметический корень не может быть отрицательным числом, поэтому уравнение решений не имеет.
Левая часть исходного уравнения определена при , при каждом таком значении х
Следовательно, их сумма всегда больше нуля.
Находим ОДЗ уравнения: Не существует такого значения х, при котором оба выражения имеют смысл. Поэтому уравнение решений не имеет.
ОДЗ уравнения их сумма не меньше 3.
Заметим,
6.Домашняя работа (Слайд 18)
- §12
- №241(3,4)
- №237(2,4,6)
7.Итог урока (слайд 19)
- Сегодня на уроке я повторил…
- Сегодня на уроке я узнал…
- Сегодня на уроке я научился…
И закончить урок мне хочется словами великого Эйнштейна «Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по – моему, гораздо важнее. Политика существует для данного момента, а уравнения будут существовать вечно». (слайд 20)
nsportal.ru
Этап урока | Деятельность учителя | Деятельность ученика | Организационный момент, постановка цели урока | Сегодня мы продолжим решать иррациональные уравнения, рассмотрим нестандартные методы их решения, решим несколько иррациональных уравнений из открытого банка заданий ЕГЭ 2012. | Дети записывают в тетрадь число | Актуализация знаний учащихся | Какие уравнения называются иррациональными? Какие приёмы решения иррациональных уравнений вы знаете? Назовите основные причины появления посторонних корней? Как избежать ошибки? Работаем по карточкам. Вам даётся 2 минуты, чтобы решить иррациональное уравнение. Учитель раздаёт карточки (приложение 1) с индивидуальными заданиями, когда все закончат, называет правильные ответы | Уравнение, содержащее переменную под знаком корня, называется иррациональным. При решении иррациональных уравнений используют тождественные преобразования, применяют метод возведения обеих частей уравнения в одну и ту же степень. Основными причинами появления посторонних корней является возведение обеих частей уравнения в одну и ту же натуральную степень, т.к. получается уравнение – следствие данного. Нужно обязательно сделать проверку, либо использовать область определения заданного уравнения. Учащиеся выполняют задание, после сверки ответов ставт себе на карточках либо «+», либо «-» (приложение 2) | Работа по теме урока | Решим несколько уравнений из «Открытого банка математических заданий ЕГЭ 2012» 1)Задание B5 (№ 26656) Найдите корень уравнения 2)Задание B5 (№ 26660) Найдите корень уравнения 3)Задание B5 (№ 26661) Найдите корень уравнения 4)Задание B5 (№ 26668) Найдите корень уравнения Если уравнение имеет более одного корня, укажите меньший из них. 5)Задание B5 (№ 28831) Найдите корень уравнения | Учащиеся решают у доски предложенные уравнения. 1) 15 – 2x = 9 2x = 6 x = 3 Проверка. 3=3 (верно) Ответ: x=3 2) = x=87 Проверка. = (верно) Ответ: x=87 3) 2x + 5 = 75 x = 35 Проверка. 5 = 5 (верно) Ответ: x = 35 4) -72 — 17x = Проверка. x= -9 меньший корень 9 = 9 x= -8 Ответ: x= -9 5) x + 2 = 64 x =62 Ответ: x = 62 | Новый материал | Рассмотрим несколько уравнений и найдем наиболее рациональные способы их решения. = — 1 При любом допустимом значении x левая часть неотрицательна, а его правая часть отрицательна. Следовательно, уравнение не имеет решения. Сумма двух неотрицательных выражений равна нулю, если они одновременно равны нулю. Следовательно, уравнение равносильно системе , которая противоречива. Следовательно, исходное уравнение не имеет решений. Решите самостоятельно №61(3) Подставляя корни первого уравнения во второе, узнаем, имеет ли система решение. Подкоренные выражения – противоположные числа =1; Проверка показала, что x=1 + 6t = 0
= 0; = — 5; — 5 | Учащиеся записывают решение в тетрадь Учащиеся выполняют задание №61(3) 3)=0 Система не имеет решений. Значит, уравнение не имеет решений. Ученик решает у доски: Т.к. ≥0 и ≥ 0, то левая часть уравнения равна нулю, если +3x-4=0 =1 Учащиеся выполняют задание и приходят к выводу: Учащиеся записывают решение в тетрадь. | Домашнее задание | №60(1), зад. В5 (№2999, 3285, 27471, 12561), дополнительно задание по карточкам. | Учащиеся записывают задание в дневник. |
nsportal.ru
 Иррациональными называются уравнения, в которых переменная содержится под знаком корня ( радикала)
Иррациональными называются уравнения, в которых переменная содержится под знаком корня ( радикала)