Что такое функция?. Видеоурок. Алгебра 7 Класс
В жизни мы часто исследуем не только сами объекты, но и отношения между ними (Петя дружит с Васей; платок лежит на столе, платок лежит под столом и т.д.). Эти отношения можно изучать. Об одном из таких отношений – соответствии между множествами – мы и поговорим на этом уроке.
Такие соответствия, если они удовлетворяют определенным условиям, называются функциями. В математике основное внимание уделяется числовым функциям, то есть соответствиям между числовыми множествами. Мы поговорим об области определения и области значений функции, какие существуют способы задания функций, рассмотрим примеры различных функций.
Любой объект (стул, стол, собака, человек) может быть предметом исследования. Но исследовать можно не только сами объекты, но и отношения между ними. Мы часто рассуждаем об отношениях между людьми – дружбе, ненависти, любви. На них непосредственно нельзя указать, они неосязаемы, но вместе с тем мы говорим о них, описываем, прекрасно друг друга понимаем, когда слышим: «Петя
В жизни мы вводим отношения не только между людьми. Например, на карте есть два города A и Б – это два объекта. А расстояние между A и Б – это отношение между ними. На него уже нельзя указать пальцем. Или фраза: «Плед лежит на стуле». Плед и стул – это объекты, а вот «лежит на» – это уже отношение между пледом и стулом. Оказывается, мы можем изучать не только сами объекты, но и отношения между ними. Этим мы сейчас и займёмся.
У каждого человека есть размер обуви. Людей очень много, а размеров обуви мало. Если с одной стороны отметить всех людей (например, в виде точек), а с другой – существующие размеры обуви, то можно от каждой точки провести стрелку к одному из размеров обуви (Рис. 1) (в математике используют такую терминологию: можно отобразить множество людей на множество размеров обуви). Или, говоря по-другому, между этими множествами можно установить соответствие.
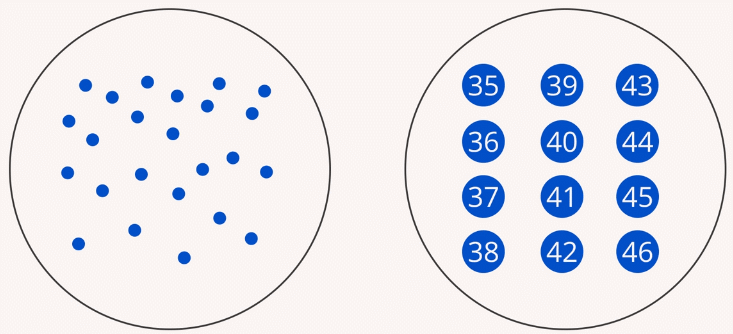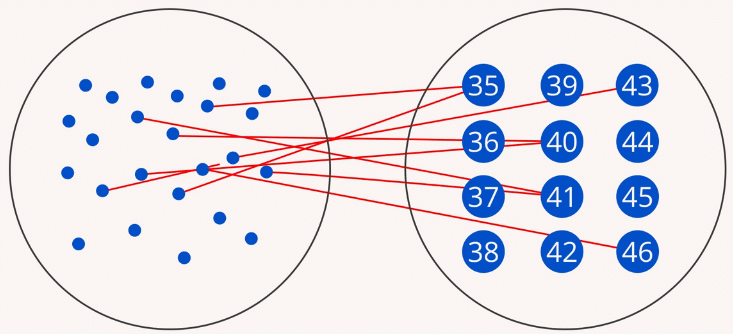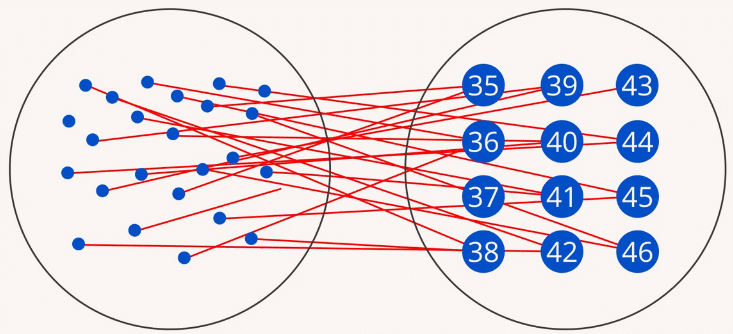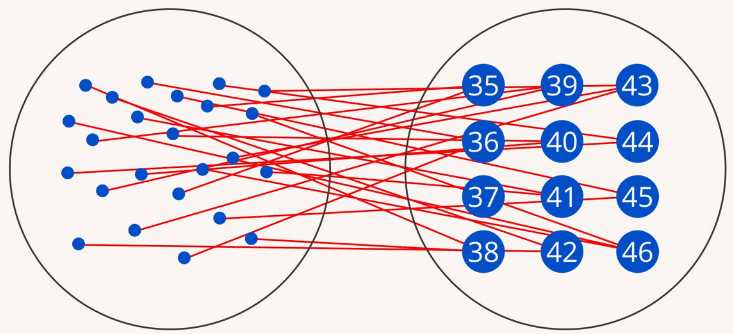
Рис. 1. Отображение множества людей на множество размеров обуви
Можно установить и обратное соответствие: каждый размер обуви есть у некоторого подмножества людей (Рис. 2). 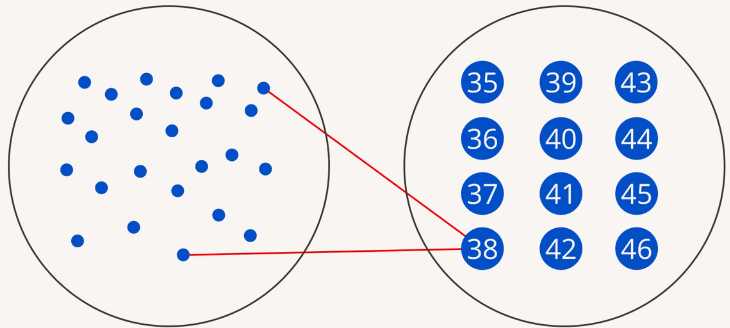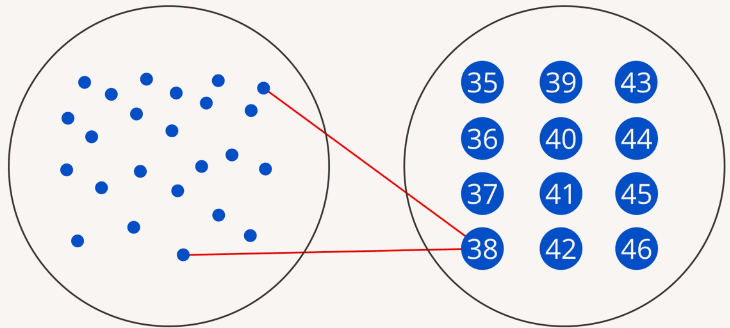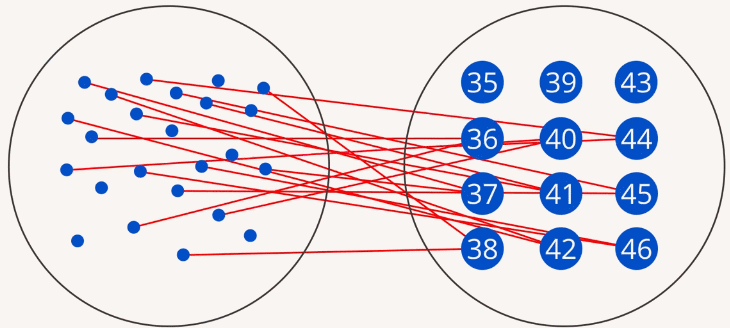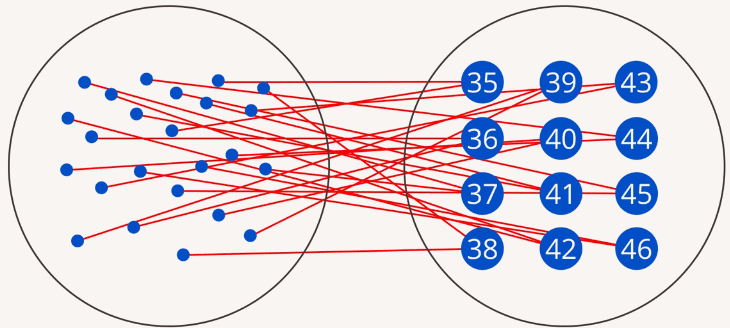
Рис. 2. Отображение множества размеров обуви на множество людей
Другой пример: обычные часы. Каждому времени суток соответствует какое-то определённое положение стрелок на этих часах. И, наоборот, каждое положение стрелок соответствует какому-то времени суток. Обратите внимание: во всех примерах мы рассматриваем не сами объекты (люди и обувь, время суток и стрелки часов), а новое понятие – отношение между объектами.
Итак, как видим, примеров разных отношений очень много. А как говорить о них точно? Все ли нужно изучать? И как это делать? Все отношения задают между множествами какое-то соответствие. Некоторые из соответствий особенные, они каждому элементу из одного множества ставят в соответствие ровно один элемент из другого множества. Такие соответствия, которые называются
В наших примерах: у человека может быть только один размер обуви, каждому времени суток соответствует только одно положение стрелок на часах. А вот, например, 36 размер обуви может быть у большого количества людей. Поэтому такие соответствия функциями не будут.
Дадим строгое определение функции. Функция – это соответствие между двумя множествами такое, что каждому элементу одного множества 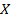 ставится в соответствие единственный элемент другого множества
ставится в соответствие единственный элемент другого множества 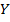
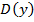 и
и 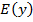 соответственно.
соответственно.Пример 1: задана функция, которая ставит в соответствие каждому человеку размер его обуви. Область определения функции 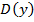 – множество людей, область значений функции
– множество людей, область значений функции 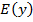
Пример 2: задана функция, которая ставит в соответствие каждому дню месяца среднюю температуру воздуха. Область определения функции 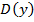 – множество дней месяца, область значений функции
– множество дней месяца, область значений функции 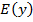 – множество температур (Рис. 3).
– множество температур (Рис. 3).

Рис. 3. Соответствие между днями месяца и средней температурой воздуха
В математике мы чаще будем работать с одним из видов функций – числовыми функциями. Числовая функция – это функция, областью определения 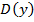
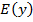 которой являются числовые множества. Например, функция пройденного пути в зависимости от времени (при равномерном движении):
которой являются числовые множества. Например, функция пройденного пути в зависимости от времени (при равномерном движении): 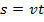 . Такая функция является числовой.
. Такая функция является числовой.Числовые функции можно задавать разными способами.
- Словесный.
- Аналитический.
- Графический.
- Табличный.
В рассмотренном выше примере мы задали функцию с помощью формулы, такое способ задания называется аналитическим. Рассмотрим другой пример. Каждому числу поставим в соответствие его квадрат. Это функция. На самом деле это будет функция площади квадрата в зависимости от длины его стороны: 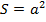
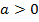 ).
).Мы будем изучать различные числовые функции. Что вообще можно в них изучать? У функций могут быть наибольшие и наименьшие значения – максимумы и минимумы, функции могут возрастать и убывать и т.д. Все эти свойства функций помогают решать конкретные прикладные задачи (например, нахождение оптимальных параметров, при которых та или иная величина достигает своего максимума – доход, эффективность и т.д., или минимума – расход, количество ошибок и т.д.). Но для того чтобы решать задачи, нужно выделить общие свойства функций и изучить их.
Повторим рассуждение, которое уже озвучивали в наших уроках. Есть заводы, которые создают различные инструменты. А дальше каждый сам использует созданные инструменты в своих целях: с помощью отвёртки можно закручивать и откручивать винты и шурупы, но можно ею же пытаться открыть дверь или забить гвозди. Так и математика – завод инструментальный, создаёт различные инструменты, которые потом могут использоваться в физике, экономике и других сферах для решения конкретных прикладных задач.
Естественные области определения и значений
В примере с площадью квадрата мы сказали, что 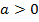 . Т.е. наложили некоторое ограничение на область определения функции:
. Т.е. наложили некоторое ограничение на область определения функции: 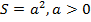 . Получается, что
. Получается, что 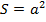 и
и 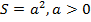
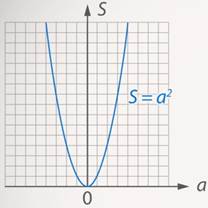
Рис. 1. График функции 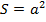
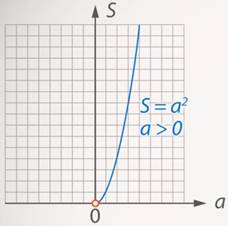
Рис. 2. График функции 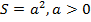
То есть для задания функции, вообще говоря, недостаточно просто задать формулу соответствия. Необходимо ещё указать области определения и значений функции. Но чаще всего этого не делают, предполагая, что они естественные. Естественная область определения при аналитическом задании – это область допустимых значений выражения, которое записано в формуле.
Пример 1.
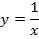
Область определения:
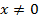
Записывают так:
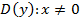
Пример 2.
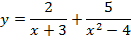
Область определения:
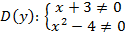
Отсюда:
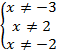
Естественная область значений – это множество значений, которые может принимать функция. Например, естественная область значений функции 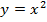 – это все числа больше либо равные
– это все числа больше либо равные 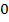 . Записывают так:
. Записывают так: 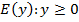
Анализировать функцию иногда легче, если построен её график. По нему часто легко определить, на каких промежутках функция убывает или возрастает, где у неё максимум и минимум и т.д. Таким образом, у графического способа задания функции (задание функции с помощью графика) и аналитического разные цели. Если сказать грубо, то аналитический способ более точный, он позволяет вычислить значение функции в любой точке и выполнять с функцией различные преобразования. Графический способ более наглядный – по графику можно сделать вывод о тех или иных свойствах функции.
Рассмотрим графический способ подробнее. График функции представляет собой совокупность точек 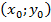 , где
, где 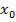
interneturok.ru
Что такое функция? Часть 1. Определение функции. Числовая функция
В жизни мы часто исследуем не только сами объекты, но и отношения между ними (Петя дружит с Васей; платок лежит на столе, платок лежит под столом и т.д.). Эти отношения можно изучать. Об одном из таких отношений – соответствии между множествами – мы и поговорим на этом уроке.
Такие соответствия, если они удовлетворяют определенным условиям, называются функциями. В математике основное внимание уделяется числовым функциям, то есть соответствиям между числовыми множествами. Мы поговорим об области определения и области значений функции, какие существуют способы задания функций, рассмотрим примеры различных функций.
Любой объект (стул, стол, собака, человек) может быть предметом исследования. Но исследовать можно не только сами объекты, но и отношения между ними. Мы часто рассуждаем об отношениях между людьми – дружбе, ненависти, любви. На них непосредственно нельзя указать, они неосязаемы, но вместе с тем мы говорим о них, описываем, прекрасно друг друга понимаем, когда слышим: «Петя дружит с Васей».
В жизни мы вводим отношения не только между людьми. Например, на карте есть два города A и Б – это два объекта. А расстояние между A и Б – это отношение между ними. На него уже нельзя указать пальцем. Или фраза: «Плед лежит на стуле». Плед и стул – это объекты, а вот «лежит на» – это уже отношение между пледом и стулом. Оказывается, мы можем изучать не только сами объекты, но и отношения между ними. Этим мы сейчас и займёмся.
У каждого человека есть размер обуви. Людей очень много, а размеров обуви мало. Если с одной стороны отметить всех людей (например, в виде точек), а с другой – существующие размеры обуви, то можно от каждой точки провести стрелку к одному из размеров обуви (Рис. 1) (в математике используют такую терминологию: можно отобразить множество людей на множество размеров обуви). Или, говоря по-другому, между этими множествами можно установить соответствие.

Рис. 1. Отображение множества людей на множество размеров обуви
Можно установить и обратное соответствие: каждый размер обуви есть у некоторого подмножества людей (Рис. 2). 
Рис. 2. Отображение множества размеров обуви на множество людей
Другой пример: обычные часы. Каждому времени суток соответствует какое-то определённое положение стрелок на этих часах. И, наоборот, каждое положение стрелок соответствует какому-то времени суток. Обратите внимание: во всех примерах мы рассматриваем не сами объекты (люди и обувь, время суток и стрелки часов), а новое понятие – отношение между объектами.
Итак, как видим, примеров разных отношений очень много. А как говорить о них точно? Все ли нужно изучать? И как это делать? Все отношения задают между множествами какое-то соответствие. Некоторые из соответствий особенные, они каждому элементу из одного множества ставят в соответствие ровно один элемент из другого множества. Такие соответствия, которые называются функциями, мы и будем изучать.
В наших примерах: у человека может быть только один размер обуви, каждому времени суток соответствует только одно положение стрелок на часах. А вот, например, 36 размер обуви может быть у большого количества людей. Поэтому такие соответствия функциями не будут.
Дадим строгое определение функции. Функция – это соответствие между двумя множествами такое, что каждому элементу одного множества 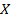 ставится в соответствие единственный элемент другого множества
ставится в соответствие единственный элемент другого множества 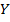 . Первое множество называют областью определения функции, а второе – областью значений функции. Обозначают:
. Первое множество называют областью определения функции, а второе – областью значений функции. Обозначают: 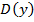 и
и 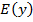 соответственно.
соответственно.
Пример 1: задана функция, которая ставит в соответствие каждому человеку размер его обуви. Область определения функции 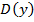 – множество людей, область значений функции
– множество людей, область значений функции 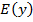 – множество размеров обуви.
– множество размеров обуви.
Пример 2: задана функция, которая ставит в соответствие каждому дню месяца среднюю температуру воздуха. Область определения функции 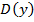 – множество дней месяца, область значений функции
– множество дней месяца, область значений функции 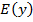 – множество температур (Рис. 3).
– множество температур (Рис. 3).

Рис. 3. Соответствие между днями месяца и средней температурой воздуха
В математике мы чаще будем работать с одним из видов функций – числовыми функциями. Числовая функция – это функция, областью определения 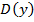 и областью значений
и областью значений 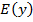 которой являются числовые множества. Например, функция пройденного пути в зависимости от времени (при равномерном движении):
которой являются числовые множества. Например, функция пройденного пути в зависимости от времени (при равномерном движении): 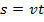 . Такая функция является числовой.
. Такая функция является числовой.
Числовые функции можно задавать разными способами.
- Словесный.
- Аналитический.
- Графический.
- Табличный.
В рассмотренном выше примере мы задали функцию с помощью формулы, такое способ задания называется аналитическим. Рассмотрим другой пример. Каждому числу поставим в соответствие его квадрат. Это функция. На самом деле это будет функция площади квадрата в зависимости от длины его стороны: 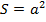 (если мы оговорим, что
(если мы оговорим, что 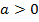 ).
).
Мы будем изучать различные числовые функции. Что вообще можно в них изучать? У функций могут быть наибольшие и наименьшие значения – максимумы и минимумы, функции могут возрастать и убывать и т.д. Все эти свойства функций помогают решать конкретные прикладные задачи (например, нахождение оптимальных параметров, при которых та или иная величина достигает своего максимума – доход, эффективность и т.д., или минимума – расход, количество ошибок и т.д.). Но для того чтобы решать задачи, нужно выделить общие свойства функций и изучить их.
Повторим рассуждение, которое уже озвучивали в наших уроках. Есть заводы, которые создают различные инструменты. А дальше каждый сам использует созданные инструменты в своих целях: с помощью отвёртки можно закручивать и откручивать винты и шурупы, но можно ею же пытаться открыть дверь или забить гвозди. Так и математика – завод инструментальный, создаёт различные инструменты, которые потом могут использоваться в физике, экономике и других сферах для решения конкретных прикладных задач.
Естественные области определения и значений
В примере с площадью квадрата мы сказали, что 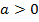 . Т.е. наложили некоторое ограничение на область определения функции:
. Т.е. наложили некоторое ограничение на область определения функции: 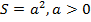 . Получается, что
. Получается, что 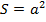 и
и 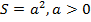 – это две различные функции? Да, именно так, потому что первая функция определена при неположительных значениях переменной (Рис. 1), а вторая – нет (Рис. 2).
– это две различные функции? Да, именно так, потому что первая функция определена при неположительных значениях переменной (Рис. 1), а вторая – нет (Рис. 2).

Рис. 1. График функции 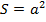

Рис. 2. График функции 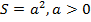
То есть для задания функции, вообще говоря, недостаточно просто задать формулу соответствия. Необходимо ещё указать области определения и значений функции. Но чаще всего этого не делают, предполагая, что они естественные. Естественная область определения при аналитическом задании – это область допустимых значений выражения, которое записано в формуле.
Пример 1.
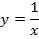
Область определения:
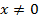
Записывают так:
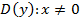
Пример 2.
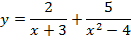
Область определения:
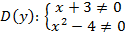
Отсюда:
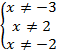
Естественная область значений – это множество значений, которые может принимать функция. Например, естественная область значений функции 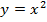 – это все числа больше либо равные
– это все числа больше либо равные 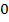 . Записывают так:
. Записывают так: 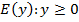
interneturok.ru
Понятие функции | Алгебра
Понятие функции в математике — одно из основных. Выражает зависимость одних переменных величин от других.
Определение.
Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества.
Пусть каждому числу x из множества значений D поставлено в соответствие число y из множества значений E.
«Поставлено в соответствие» — значит, указан определённый способ (правило), по которому для каждого x∈D находят y∈E. (∈ — знак принадлежности. Запись x∈D читают «икс принадлежит дэ»).
Чаще всего этот способ обозначают как y=f(x). Для обозначения функции применяют и другие буквы: y=g(x), s=f(t) и т.д.
Если функция задана соответствием y=f(x), переменная x называется независимой переменной или аргументом, y — зависимой переменной или функцией.
Множество значений D, которые может принимать x, называется областью определения функции.
Множество значений E, которые может принимать y, называется областью значений функции.
Функцию можно задать несколькими способами:
— аналитическим (с помощью формулы),
— графическим,
— табличным,
— описанием с помощью словесной формулировки).
Функции, в которых значения аргумента и значения функции — числа, называются числовыми функциями. В курсе алгебры изучаются, в основном, числовые функции.
Примеры функций.
1) При движении автомобиля с постоянной скоростью пройденный путь является функцией от времени .
Например, если автомобиль движется с постоянной скоростью 60 км/ч, зависимость пути от времени можно задать формулой s=60t, где s — пройденный путь (в километрах), t — время (в часах).
2) Периметр квадрата является функцией от его стороны.
Зависимость периметра от стороны квадрата можно задать формулой P=4a, где P — периметр, a — длина стороны.
www.algebraclass.ru
Функции: понятие функция и аргумент, функциональная зависимость
Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.
Функция – это зависимая переменная величина. Аргумент – это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.
Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:
y = f(x),
где f (начальная буква слова function – функция) заменяет слово функция
, y – это функция, а x – аргумент.
Иногда, чтобы показать, что y зависит от x, пишут просто:
y(x)
Обратите внимание, что вместо y и x могут использоваться любые другие буквы.
Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:
D(f) – область определения функции
(множество значений аргумента).
E(f) – множество значений функции.
f(x0) – значение функции в точке x0.
Пример. Возьмём формулу нахождения расстояния по скорости и времени:
S = vt
Где S – это расстояние, v – скорость, а t – время. Если взять скорость, равную 50 км/ч, то каждому неотрицательному значению t будет соответствовать строго определённое значение S:
| t (ч) | 1 | 1,5 | 2 | 2,5 | 3 |
|---|---|---|---|---|---|
| S (км) | 50 | 75 | 100 | 125 | 150 |
Следовательно, S является функцией от t – S(t)
, область определения функции – D(S) ⩾ 0, так как время не может быть отрицательным, но при этом можно не затратить времени вообще, если не двигаться, в этом случае t = 0. Значение этой функции в точке t0 можно обозначить в виде S(t0), то есть записать таблицу со значениями в таком виде:
S(1) = 50, S(1,5) = 75, S(2) = 100, S(2,5) = 125, S(3) = 150
naobumium.info
АЛГЕБРА ФУНКЦИИ — это… Что такое АЛГЕБРА ФУНКЦИИ?
— полупростая коммутативная банахова алгебра А , реализованная в виде алгебры непрерывных функций на пространстве максимальных идеалов. Если 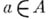 и f — нек-рая функция, определенная на спектре элемента а(т. е. на множестве значений функции
и f — нек-рая функция, определенная на спектре элемента а(т. е. на множестве значений функции 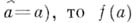 есть нек-рая функция на
есть нек-рая функция на 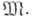 Условие
Условие 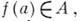 конечно, не обязано выполняться. Если, однако, f — целая функция, то
конечно, не обязано выполняться. Если, однако, f — целая функция, то 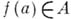 для любого
для любого 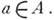 Использование интегральной формулы Коши позволяет существенно усилить этот результат: если функция f регулярна в нек-рой окрестности спектра элемента а, то
Использование интегральной формулы Коши позволяет существенно усилить этот результат: если функция f регулярна в нек-рой окрестности спектра элемента а, то 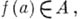 и отображение
и отображение 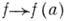 является гомоморфизмом А. ф., аналитических в нек-рой окрестности спектра элемента
является гомоморфизмом А. ф., аналитических в нек-рой окрестности спектра элемента 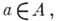 в алгебру
в алгебру 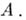 Это утверждение остается справедливым и для неполупростых коммутативных банаховых алгебр.
Кроме того, класс функций, аналитических в окрестности спектра данного элемента, может оказаться не расширяемым: напр., если
Это утверждение остается справедливым и для неполупростых коммутативных банаховых алгебр.
Кроме того, класс функций, аналитических в окрестности спектра данного элемента, может оказаться не расширяемым: напр., если 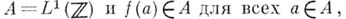 спектр к-рых принадлежит отрезку
спектр к-рых принадлежит отрезку 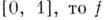 аналитична в нек-рой окрестности этого отрезка.
аналитична в нек-рой окрестности этого отрезка.
В отдельных случаях элемент 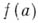 можно определить и для многозначных аналитпч. функций f, но это определение встречает естественные затруднения. Напр., пусть А — алгебра непрерывных функций в круге
можно определить и для многозначных аналитпч. функций f, но это определение встречает естественные затруднения. Напр., пусть А — алгебра непрерывных функций в круге 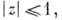 аналитических в круге
аналитических в круге 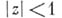 н удовлетворяющих условию
н удовлетворяющих условию 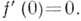 Единичный круг естественно отождествляется с пространством максимальных идеалов А. Непрерывная на пространстве максимальных идеалов функция
Единичный круг естественно отождествляется с пространством максимальных идеалов А. Непрерывная на пространстве максимальных идеалов функция 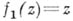 не принадлежит алгебре А, но является решением квадратного уравнения
не принадлежит алгебре А, но является решением квадратного уравнения
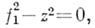
где 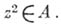
Если А — полупростая алгебра с пространством максимальных идеалов 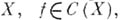

 (простой корень), то
(простой корень), то 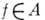 . Аналогично, если
. Аналогично, если 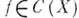 и
и 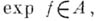 то
то 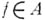 .
.
А. ф. наз. алгеброй с равномерной сходимостью, если норма в этой алгебре определяет сходимость, эквивалентную равномерной сходимости функций 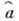 на пространстве максимальных идеалов. Если
на пространстве максимальных идеалов. Если 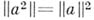 для всех
для всех 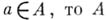 — алгебра с равномерной сходимостью. Общим примером алгебры с равномерной сходимостью является замкнутая подалгебра в алгебре ограниченных непрерывных функций на некотором топологич. пространстве, наделенной естественной sup-нормой.
— алгебра с равномерной сходимостью. Общим примером алгебры с равномерной сходимостью является замкнутая подалгебра в алгебре ограниченных непрерывных функций на некотором топологич. пространстве, наделенной естественной sup-нормой.
Если А — алгебра с равномерной сходимостью, и ее пространство максимальных идеалов метризуемо, то среди всех кольцевых границ (не только замкнутых) существует минимальная граница Г 0, замыканием к-рой служит граница Шилова. Множество Г 0 состоит из «точек пика»: 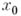 наз. точкой пика, если существует такая функция
наз. точкой пика, если существует такая функция 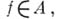 что
что  для всех
для всех 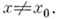 В рассматриваемом случае для любой точки из пространства максимальных идеалов существует представляющая мера, сосредоточенная на
В рассматриваемом случае для любой точки из пространства максимальных идеалов существует представляющая мера, сосредоточенная на 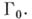
А. ф. наз. аналитической, если всякая функция из этой алгебры, равная нулю на непустом открытом подмножестве пространства максимальных идеалов, равна нулю тождественно. Аналогично определяются алгебры, аналитические относительно границы. Всякая аналитич. алгебра является аналитической относительно границы Шилова; обратное, вообще говоря, неверно.
А. ф. Аназ. регулярной, если для любого замкнутого множества Fв пространстве Xмаксимальных идеалов алгебры Аи любой не содержащейся в Fточки х 0 найдется такая функция 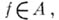 что
что 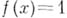 для всех
для всех 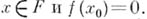 Всякая регулярная алгебра нормальна, т. е. для любой пары непересекающихся замкнутых множеств
Всякая регулярная алгебра нормальна, т. е. для любой пары непересекающихся замкнутых множеств 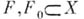 существует элемент
существует элемент 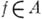 такой, что
такой, что  для всех
для всех  для всех
для всех 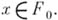 Более того, в регулярной алгебре для любого конечного открытого покрытия
Более того, в регулярной алгебре для любого конечного открытого покрытия 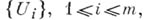 пространства Xимеется разбиение единицы, принадлежащее А, т. е. система функций
пространства Xимеется разбиение единицы, принадлежащее А, т. е. система функций 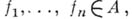 для к-рых
для к-рых
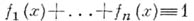
и
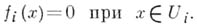
Функция gназ. локально принадлежащей А. ф. А, если для любой точки 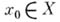 существует такая окрестность, в к-рой эта функция совпадает с нек-рой функцией из алгебры. Всякая функция, локально принадлежащая регулярной алгебре, сама является элементом этой алгебры.
существует такая окрестность, в к-рой эта функция совпадает с нек-рой функцией из алгебры. Всякая функция, локально принадлежащая регулярной алгебре, сама является элементом этой алгебры.
Элемент 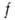 А. ф. наз. вещественным, если
А. ф. наз. вещественным, если 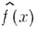 вещественно при всех
вещественно при всех 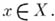 Если А — алгебра с вещественными образующими
Если А — алгебра с вещественными образующими 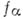 и
и
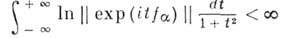
для всех 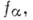 то Арегулярна.
то Арегулярна.
Идеал в банаховой алгебре наз. примарным, если он содержится только в одном максимальном идеале. Если А — регулярная А. ф., то в каждом максимальном идеале х 0 имеется наименьший замкнутый примерный идеал 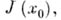 к-рый содержится в любом замкнутом примерном идеале, содержащемся в х 0 ; идеал
к-рый содержится в любом замкнутом примерном идеале, содержащемся в х 0 ; идеал  есть замыкание идеала, образованного функциями
есть замыкание идеала, образованного функциями  , равными нулю в нек-рой (зависящей от f) окрестности точки
, равными нулю в нек-рой (зависящей от f) окрестности точки 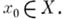
В алгебре абсолютно сходящихся интегралов Фурье с присоединенной единицей всякий максимальный идеал совпадает с соответствующим примарным идеалом.
Пусть А — замкнутая подалгебра алгебры 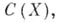 где X- нек-рый компакт (не обязательно совпадающий с пространством максимальных идеалов алгебры А). Пусть Аразделяет точки компакта X,
где X- нек-рый компакт (не обязательно совпадающий с пространством максимальных идеалов алгебры А). Пусть Аразделяет точки компакта X,
т. е. для любых двух различных точек 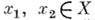 существует такая функция f из алгебры А, для к-рой
существует такая функция f из алгебры А, для к-рой 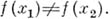 АлгебраЛ наз. симметричной, если вместе с функцией f алгебре принадлежит и функция
АлгебраЛ наз. симметричной, если вместе с функцией f алгебре принадлежит и функция 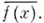 Согласно теореме Стоуна-Вейерштрасса, если Асимметрична, то
Согласно теореме Стоуна-Вейерштрасса, если Асимметрична, то 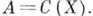 Алгебра A наз. антисимметричной, если из условий
Алгебра A наз. антисимметричной, если из условий 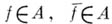 следует, что
следует, что 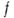 — постоянная функция. Антисимметричными являются, в частности, алгебры аналитич. функций. Подмножество
— постоянная функция. Антисимметричными являются, в частности, алгебры аналитич. функций. Подмножество  наз. множеством антисимметрии (относительно алгебры А), если любая функция
наз. множеством антисимметрии (относительно алгебры А), если любая функция 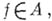 вещественная на S, постоянна на этом множестве. Согласно этому определению алгебра Аантисимметрична, если все Xявляются множеством антисимметрии. В общем случае пространство Xможно представить в виде объединения непересекающихся замкнутых максимальных множеств антисимметрии. Каждое максимальное множество антисимметрии является пересечением множеств пика (множество Рназ. множеством пика, если существует такая функция
вещественная на S, постоянна на этом множестве. Согласно этому определению алгебра Аантисимметрична, если все Xявляются множеством антисимметрии. В общем случае пространство Xможно представить в виде объединения непересекающихся замкнутых максимальных множеств антисимметрии. Каждое максимальное множество антисимметрии является пересечением множеств пика (множество Рназ. множеством пика, если существует такая функция 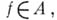 что
что 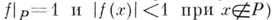 . Отсюда следует, что сужение А |Y алгебры Ана максимальное множество антисимметрии есть замкнутая (антисимметричная) подалгебра алгебры
. Отсюда следует, что сужение А |Y алгебры Ана максимальное множество антисимметрии есть замкнутая (антисимметричная) подалгебра алгебры 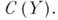 Если Xесть пространство максимальных идеалов алгебры А, то максимальные множества антисимметрии связны. Если непрерывная функция такова, что на каждом максимальном множестве антисимметрии она совпадает с нек-рой функцией из алгебры А, то и сама эта функция принадлежит А. Это обобщение теоремы Стоуна- Вейерштрасса позволяет в принципе свести изучение произвольных алгебр с равномерной сходимостью к изучению антисимметричных алгебр А. Вместе с тем изучение произвольных алгебр Ане может быть сведено к аналитическим алгебрам: существует пример алгебры тина
Если Xесть пространство максимальных идеалов алгебры А, то максимальные множества антисимметрии связны. Если непрерывная функция такова, что на каждом максимальном множестве антисимметрии она совпадает с нек-рой функцией из алгебры А, то и сама эта функция принадлежит А. Это обобщение теоремы Стоуна- Вейерштрасса позволяет в принципе свести изучение произвольных алгебр с равномерной сходимостью к изучению антисимметричных алгебр А. Вместе с тем изучение произвольных алгебр Ане может быть сведено к аналитическим алгебрам: существует пример алгебры тина 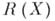 (замкнутой подалгебры алгебры
(замкнутой подалгебры алгебры 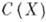 ), не совпадающей с
), не совпадающей с 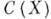 , антисимметричной и регулярной.
, антисимметричной и регулярной.
Пусть 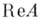 — вещественное пространство функций вида
— вещественное пространство функций вида 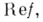 где
где 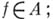 если Re A -алгебра, или если Re A замкнуто в
если Re A -алгебра, или если Re A замкнуто в 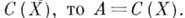 Пространство Xможно рассматривать как часть пространства максимальных идеалов алгебры А; поэтому на X можно рассматривать не только обычную топологию пространства максимальных идеалов, но и метрику, индуцированную вложением Xв пространство, сопряженное А. Расстояние в смысле этой метрики обозначим
Пространство Xможно рассматривать как часть пространства максимальных идеалов алгебры А; поэтому на X можно рассматривать не только обычную топологию пространства максимальных идеалов, но и метрику, индуцированную вложением Xв пространство, сопряженное А. Расстояние в смысле этой метрики обозначим 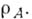 Для любых точек
Для любых точек 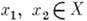 имеет место неравенство
имеет место неравенство 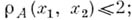 отношение
отношение 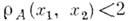 является отношением эквивалентности, и классы эквивалентности наз. долями Глисона. Если X — круг
является отношением эквивалентности, и классы эквивалентности наз. долями Глисона. Если X — круг 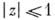 и A- замкнутая подалгебра в С (X), состоящая из аналитических при
и A- замкнутая подалгебра в С (X), состоящая из аналитических при 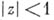 функций, то метрика
функций, то метрика 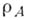 неевклидова, а долями Глисона служат одноточечные множества на границе и внутренность круга. Доли Глисона не всегда обладают аналитич. структурой: любое s-компактное вполне регулярное пространство гомеоморфно доле Глисона пространства максимальных идеалов нек-рой алгебры, такой, что сужение алгебры на эту долю содержит всякую ограниченную непрерывную функцию. Принадлежность двух точек к одной и той же доле Глисона может быть охарактеризована в терминах представляющих мер на границе Шилова: такие две точки обладают взаимно абсолютно непрерывными представляющими мерами с ограниченными производными. Алгебра, для к-рой
неевклидова, а долями Глисона служат одноточечные множества на границе и внутренность круга. Доли Глисона не всегда обладают аналитич. структурой: любое s-компактное вполне регулярное пространство гомеоморфно доле Глисона пространства максимальных идеалов нек-рой алгебры, такой, что сужение алгебры на эту долю содержит всякую ограниченную непрерывную функцию. Принадлежность двух точек к одной и той же доле Глисона может быть охарактеризована в терминах представляющих мер на границе Шилова: такие две точки обладают взаимно абсолютно непрерывными представляющими мерами с ограниченными производными. Алгебра, для к-рой 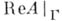 плотно в
плотно в 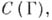 наз. алгеброй Дирихле; если Р- доля Глисона в пространстве максимальных идеалов алгебры Дирихле, состоящая более, чем из одной точки, то существует такое непрерывное взаимно однозначное отображение
наз. алгеброй Дирихле; если Р- доля Глисона в пространстве максимальных идеалов алгебры Дирихле, состоящая более, чем из одной точки, то существует такое непрерывное взаимно однозначное отображение 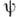 круга
круга 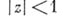 на Р, что для любой функции
на Р, что для любой функции 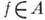 функция
функция 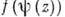 аналитична при
аналитична при  Таким образом, Робладает структурой, относительно к-рой функции
Таким образом, Робладает структурой, относительно к-рой функции 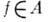 аналитичны; отображение
аналитичны; отображение 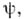 вообще говоря, не является гомеоморфизмом, если Рснабжено обычной топологией пространства максимальных идеалов, но
вообще говоря, не является гомеоморфизмом, если Рснабжено обычной топологией пространства максимальных идеалов, но 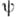 является гомеоморфизмом, если снабдить Рметрикой
является гомеоморфизмом, если снабдить Рметрикой 
Лит. см. при статье Банахова алгебра. Е. А. Горин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru