Методы изучения комбинаторных объектов и чисел — МегаЛекции
1. Теоретико-множественный подход.
Примером использования такого подхода является принцип включений и исключений. Согласно нему, число  объектов, не удовлетворяющих ни одному из свойств набора
объектов, не удовлетворяющих ни одному из свойств набора  , определяется равенством
, определяется равенством
N0 = N –  +
+  + … +
+ … +
+ (– 1)k 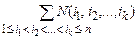 + … + (–1)n N(1, 2, … , n). (1)
+ … + (–1)n N(1, 2, … , n). (1)
Число  объектов, удовлетворяющих точно
объектов, удовлетворяющих точно
 , равно
, равноNk =  + …+(– 1)s–k
+ …+(– 1)s–k +
+
+…+ (–1)n–k ×N(1, 2, … , n). (2)
×N(1, 2, … , n). (2)
Задача 1. В отделе НИИ каждый сотрудник владеет хотя бы одним иностранным языком. Известно, что английским языком владеют 6 человек, немецким – 6, французским – 7, английским и немецким – 4, немецким и французским – 3, английским и французским – 2, все три языка знает 1 человек. Определить, сколько всего человек в отделе, сколько человек владеют только английским, только немецким, только французским, и сколько человек знает только 1 иностранный язык.
Решение. Согласно условиям задачи N0 = 0, т.к. в отделе нет сотрудников, не владеющих иностранными языками. Следовательно, по формуле (1) получаем:
N =  –
– 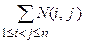 + N(1, 2, 3) (3)
+ N(1, 2, 3) (3)
N = (6 + 6 + 7) – (4 + 3 + 2) + 1 = 11 человек всего в отделе.
Для вычисления остальных показателей также воспользуемся формулой (1). Найдем, например N(только А) – число человек, не владеющих никаким другим языком, кроме английского. Для этого формулу (1) надо применить только к множеству людей, владеющих английским языком. В этом случае n = 2. Тогда N = N(A), N(1) и N(2) – число людей, владеющих, помимо английского, еще немецким и французским, соответственно,
N(только A) = 6 – (4 + 2) + 1 = 1.
Аналогично
N(только Н) = 6 – (4 + 3) + 1 = 0.
N(только Ф) = 7 – (2 + 3) + 1 = 3.
Вычислим теперь N1 – число людей, владеющих только 1 языком. Воспользуемся формулой (2) при k = 1.
N1 = N(1) + N(2) + N(3) + (–1)2–1× 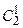 × [N(1,2) + N(2,3) + N(1,3)] +
× [N(1,2) + N(2,3) + N(1,3)] +
+ (–1)3–1×  × N(1,2,3) = 6 + 6 + 7 – 2×(4 + 3 + 2) + 3×1 = 4.
× N(1,2,3) = 6 + 6 + 7 – 2×(4 + 3 + 2) + 3×1 = 4.
Такой же результат получим, если сложим N(только A) + N(только Н) + N(только Ф).
2. Алгебраические методы.
Приведем основные свойства числа сочетаний.
1)  =
= 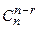
2)  =
=  +
+ 
3) 
4) 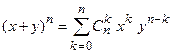 – бином Ньютона.
– бином Ньютона.
5) 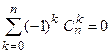
6) 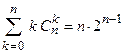
3. Метод производящих функций.
Последовательности {un}, фигурирующей в какой-либо задаче, например, комбинаторной, удобно поставить в соответствие формальный степенной ряд
 ,
,
который называется производящей функцией данной последовательности.
Задача 2.Найти производящую функцию, формулу общего члена последовательности и  , зная рекуррентное соотношение
, зная рекуррентное соотношение  и начальные члены
и начальные члены  ,
, 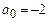 .
.
Решение.Найдем производящую функцию последовательности 
 .
.
Коэффициенты  определим как коэффициенты произведения производящих функций из соотношений:
определим как коэффициенты произведения производящих функций из соотношений:
 ,
,  .
.
Следовательно,  .
.
Формулу общего члена последовательности можно получить, разложив производящую функцию на простые дроби и приведя подобные при одинаковых степенях. Однако проще воспользоваться теоремой об общем виде решения линейного рекуррентного соотношения. Выпишем характеристический многочлен соотношения 
Уравнение  , согласно теореме Виета имеет два простых корня
, согласно теореме Виета имеет два простых корня  , т.е.
, т.е. 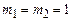 . Тогда общее решение линейного рекуррентного соотношения имеет вид
. Тогда общее решение линейного рекуррентного соотношения имеет вид
 .
.
Коэффициенты  определяются из начальных условий, т.е. из системы линейных уравнений
определяются из начальных условий, т.е. из системы линейных уравнений  . Решив данную систему, получим
. Решив данную систему, получим 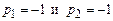
 , а
, а  .
.Контрольные вопросы и задания
1. Определить наибольший коэффициент разложения 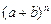 , если сумма всех его коэффициентов равна 4096.
, если сумма всех его коэффициентов равна 4096.
2. Найти наибольший член разложения  .
.
3. Найти коэффициент при  в разложении
в разложении

4. Определить число членов разложения 
5. Найти коэффициент при  в разложении
в разложении  .
.
6. Найти коэффициент при  в разложении
в разложении  .
.
7. Найти коэффициент при  в разложении
в разложении
 .
.
8. Найти коэффициент при 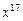 и
и 
 .
.9. В каком из выражений 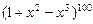 или
или  будет наибольший коэффициент при
будет наибольший коэффициент при 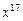 .
.
10. Доказать, что: 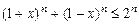 .
.
11. Вычислить суммы:
a)  ;
;
b)  ;
;
c) 
d)  ;
;
e)  ;
;
f) 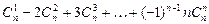 ;
;
g) 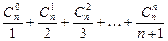 ;
;
h) 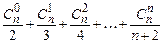 ;
;
i) 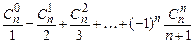 ;
;
j) 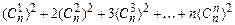 ;
;
k) 
l) 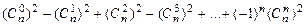 .
.
12. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38, с ветчиной – 42, и с сыром и с колбасой – 28, и с колбасой и с ветчиной – 31, и с сыром и с ветчиной – 26. Все 3 вида бутербродов взяли 25 человек, а несколько человек захватили с собой пирожки. Сколько человек взяли с собой пирожки? Только бутерброды с ветчиной? Только два вида бутербродов?
13. Сколькими способами можно посадить за круглый стол 7 мужчин и 7 женщин так, чтобы никакие две женщины не сидели рядом?
14. Девушка написала 5 писем и подписала 5 конвертов. Спеша на свидание, она разложила письма по конвертам, не сверив имя адресата с адресом. Сколько имеется вариантов, когда ни одно письмо не дойдёт до своего адресата?
15. Найти общее решение рекуррентного соотношения:
a)  ;
;
b)  ;
;
c)  ;
;
d)  ;
;
e)  ;
;
f)  ;
;
g)  ;
;
h)  .
.
16. Найти производящую функции, формулу общего члена последовательности и 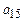 , зная рекуррентное соотношение и начальные члены:
, зная рекуррентное соотношение и начальные члены:
a)  ,
,  ,
,  ;
;
b) 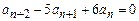 ,
,  ,
,  ;
;
c) 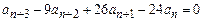 ,
,  ,
,  ,
,  ;
;
d) 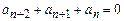 ,
,  ,
,  .
.
17. Найти производящую функцию и общее решение рекуррентного соотношения:  ,
, 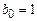 ,
,  , найти
, найти 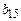 .
.
18. Доказать, что члены последовательности Фибоначчи  удовлетворяют следующим соотношениям:
удовлетворяют следующим соотношениям:
a)  ;
;
b) 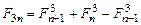 ;
;
c)  ;
;
d) 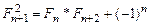 ;
;
e) 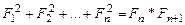 .
.
Библиографический список
Основной
1. Новиков, Ф.А. Дискретная математика для программистов [Текст] : учебное пособие для студ. вузов (гриф МО) / Ф. А. Новиков. — 2-е изд. — СПб. : ПИТЕР, 2006. — 364 с.
2. Забуга, А.А. Теоретические основы информатики : учеб. пособие / А.А. Забуга – Новосибирск: Изд-во НГТУ, 2013. – 168 с. (http://www.iprbookshop.ru)
3. Губарев, В.В. Введение в теоретическую информатику: учеб. пособие / В.В. Губарев – Новосибирск: Изд-во НГТУ, 2015. – Ч. 2. – 472 с. (http://www.knigafund.ru)
Дополнительный
4. Комбинаторный анализ. Задачи и упражнения [Текст] : учебное пособие / Под ред. Рыбникова Н.А. — М.: Наука,1985. — 210 с.
5. Липский, В. Комбинаторика для программистов [Текст] / В. Липский — М.: Мир, 1988. — 213 с.
Электронное издание
МНОЖЕСТВА. ЭЛЕМЕНТЫ
КОМБИНАТОРНОГО АНАЛИЗА
Методические указания
к практическим занятиям
Для студентов, обучающихся по направлениям
09.03.02 – “Информационные системы и технологии”
09.03.03 – “Прикладная информатика”
очной формы обучения
Составители БУГАЕВ Юрий Владимирович,
ШУРУПОВА Ирина Юрьевна,
ЛИТВИНОВ Дмитрий Анатольевич
Подписано в печать . .201. Формат 60х84 1/16
Усл. печ. л. . Тираж 50 экз. Заказ С-
ФГБОУ ВПО “Воронежский государственный университет инженерных технологий”
(ФГБОУ ВПО “ВГУИТ”)
Отдел полиграфии ФГБОУ ВПО “ВГУИТ”
Адрес академии и отдела полиграфии:
394036, Воронеж, пр. Революции, 19
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
2. Свойства комбинаторных объектов и чисел
1. 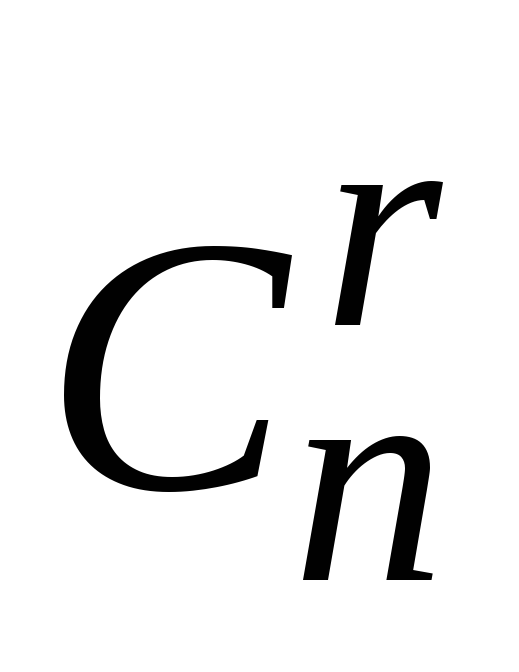 =
= .
Это свойство вытекает из формулы числа
сочетаний.
.
Это свойство вытекает из формулы числа
сочетаний.
2.  =
= +
+ .
.
3. 
4. 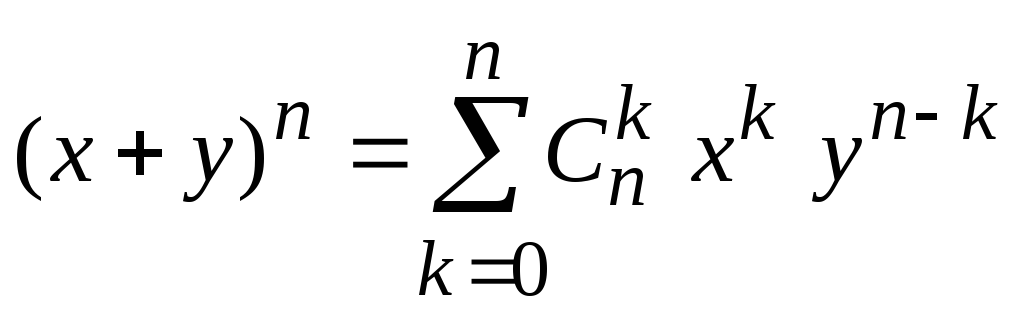 –
бином Ньютона. В частности, (х + у)2 = х2 + 2ху + у2;
(х + у)3 = х3 + 3х2у
+ 3ху2 + у3 и т.д.
–
бином Ньютона. В частности, (х + у)2 = х2 + 2ху + у2;
(х + у)3 = х3 + 3х2у
+ 3ху2 + у3 и т.д.
5.  .
Доказать легко с использованием бинома
Ньютона на основе тождества (1 – 1)n = 0.
.
Доказать легко с использованием бинома
Ньютона на основе тождества (1 – 1)n = 0.
6.  .
.
Контрольные вопросы и задания
Определить наибольший коэффициент разложения
 ,
если сумма всех его коэффициентов равна
4096.
,
если сумма всех его коэффициентов равна
4096.Найти наибольший член разложения
 .
.Найти коэффициент при
 в разложении
в разложении

Определить число членов разложения
 .
.Найти коэффициент при
 в разложении
в разложении .
.Найти коэффициент при
 в разложении
в разложении .
.Найти коэффициент при
 в разложении
в разложении
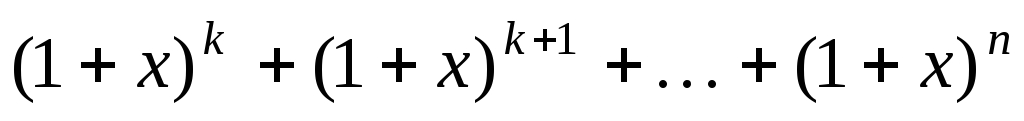 .
.
Найти коэффициент при
 и
и в разложении
в разложении .
.В каком из выражений
 или
или будет наибольший коэффициент при
будет наибольший коэффициент при .
.Доказать, что:
 .
.Вычислить суммы:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 .
.
3. Методы изучения комбинаторных объектов и чисел
N0 = N –  +
+ 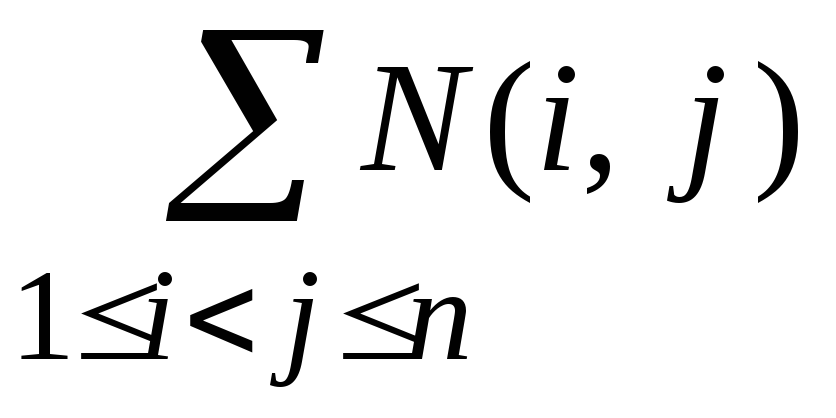 + … +
+ … +
+
(– 1)k + … + (–1)nN(1,
2, … , n).
(1)
+ … + (–1)nN(1,
2, … , n).
(1)
Nk = 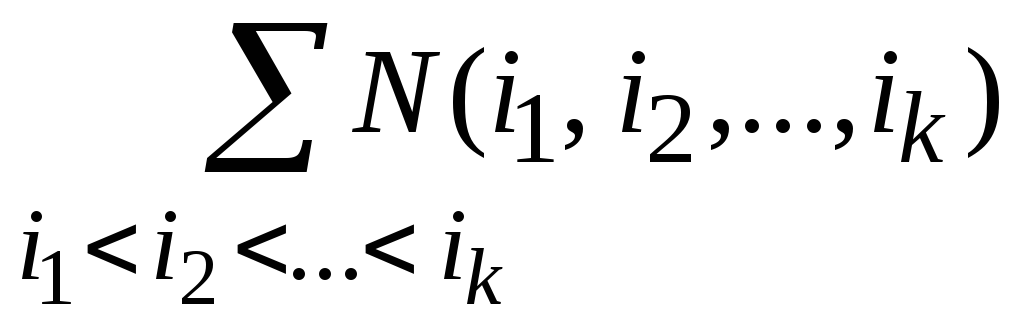 + …+(– 1)s–k
+ …+(– 1)s–k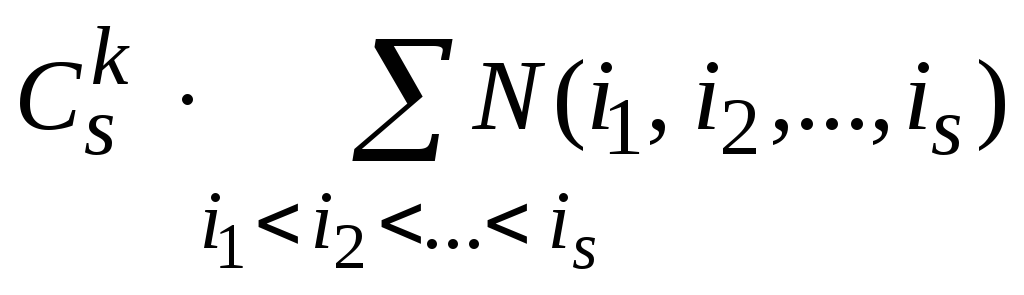 +
+
+…+
(–1)n–k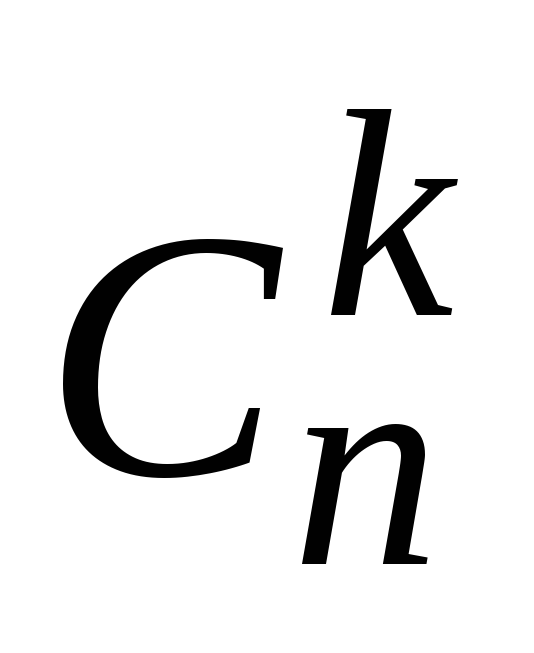 N(1,
2, … , n).
(2)
N(1,
2, … , n).
(2)
Задача 1. В отделе НИИ каждый сотрудник владеет хотя бы одним иностранным языком. Известно, что английским языком владеют 6 человек, немецким – 6, французским – 7, английским и немецким – 4, немецким и французским – 3, английским и французским – 2, все три языка знает 1 человек. Определить, сколько всего человек в отделе, сколько человек владеют только английским, только немецким, только французским, и сколько человек знает только 1 иностранный язык.
Решение. Согласно условиям задачи N0 = 0, т.к. в отделе нет сотрудников, не владеющих иностранными языками. Следовательно, по формуле (1) получаем:
N =  –
–  + N(1,
2, 3) (3)
+ N(1,
2, 3) (3)
N = (6 + 6 + 7) – (4 + 3 + 2) + 1 = 11 человек всего в отделе.
Для вычисления остальных показателей также воспользуемся формулой (1). Найдем, например N(только А) – число человек, не владеющих никаким другим языком, кроме английского. Для этого формулу (1) надо применить только к множеству людей, владеющих английским языком. В этом случае n = 2. Тогда N = N(A), N(1) и N(2) – число людей, владеющих, помимо английского, еще немецким и французским, соответственно, N(1, 2) – число людей, владеющих помимо английского еще одновременно немецким и французским. Отсюда
N(только A) = 6 – (4 + 2) + 1 = 1.
Аналогично
N(только Н) = 6 – (4 + 3) + 1= 0.
N(только Ф) = 7 – (2 + 3) + 1 = 3.
Вычислим теперь N1 – число людей, владеющих только 1 языком. Воспользуемся формулой (2) при k = 1.
N1 = N(1)
+ N(2)
+ N(3)
+ (–1)2–1
[N(1,2)
+ N(2,3)
+ N(1,3)]
+
[N(1,2)
+ N(2,3)
+ N(1,3)]
+
+
(–1)3–1 N(1,2,3)
= 6 + 6 + 7 – 2(4
+ 3 + 2) + 31
= 4.
N(1,2,3)
= 6 + 6 + 7 – 2(4
+ 3 + 2) + 31
= 4.
Такой же результат получим, если сложим N(только A) + N(только Н) + N(только Ф).
Задача
2. Найти
производящую функции, формулу общего
члена последовательности и  ,
зная рекуррентное соотношение
,
зная рекуррентное соотношение и начальные члены
и начальные члены ,
, .
.
Решение. Найдем
производящую функцию последовательности 
 .
.
Коэффициенты 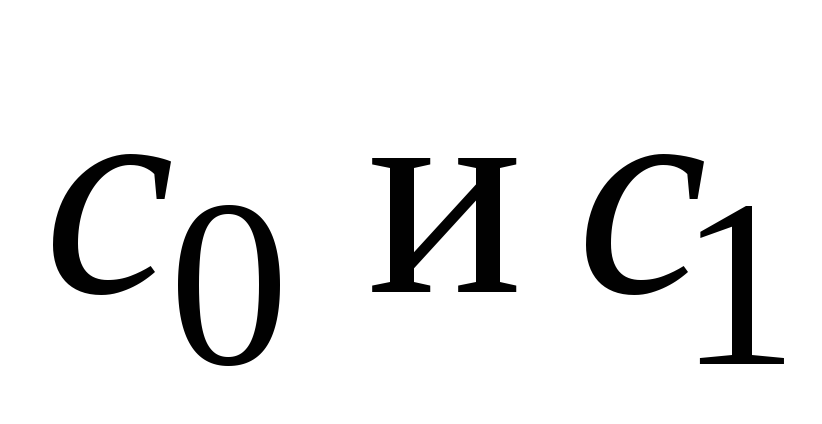 определим как коэффициенты произведения
производящих функций из соотношений:
определим как коэффициенты произведения
производящих функций из соотношений:
 ,
.
,
.
Следовательно,  .
.
Формулу
общего члена последовательности можно
получить, разложив производящую функцию
на простые дроби и приведя подобные при
одинаковых степенях. Однако проще
воспользоваться теоремой об общем виде
решения линейного рекуррентного
соотношения. Выпишем характеристический
многочлен соотношения  и найдём его корни.
и найдём его корни.
Уравнение  ,
согласно теореме Виета имеет два простых
корня
,
согласно теореме Виета имеет два простых
корня ,
т.е.
,
т.е. .
Тогда общее решение линейного рекуррентного
соотношения имеет вид
.
Тогда общее решение линейного рекуррентного
соотношения имеет вид
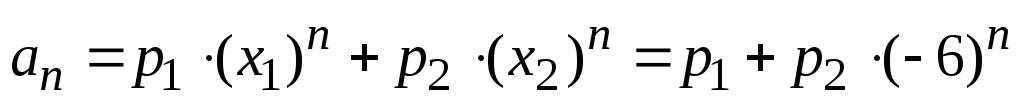 .
.
Коэффициенты  определяются из начальных условий, т.е.
из системы линейных уравнений
определяются из начальных условий, т.е.
из системы линейных уравнений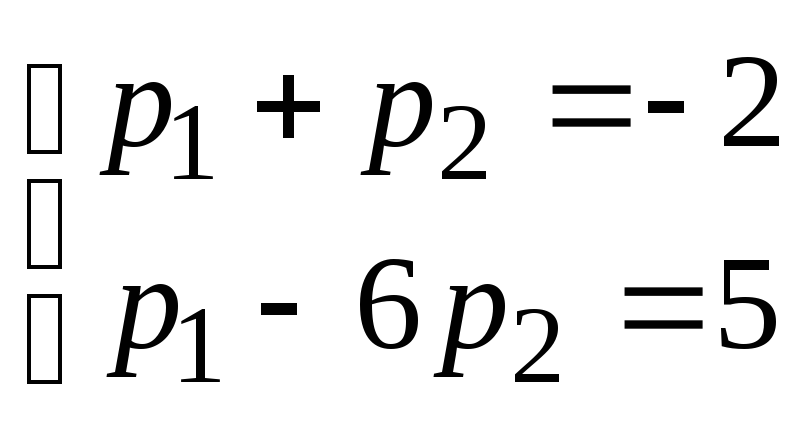 .
Решив данную систему, получим
.
Решив данную систему, получим .
Следовательно,
.
Следовательно,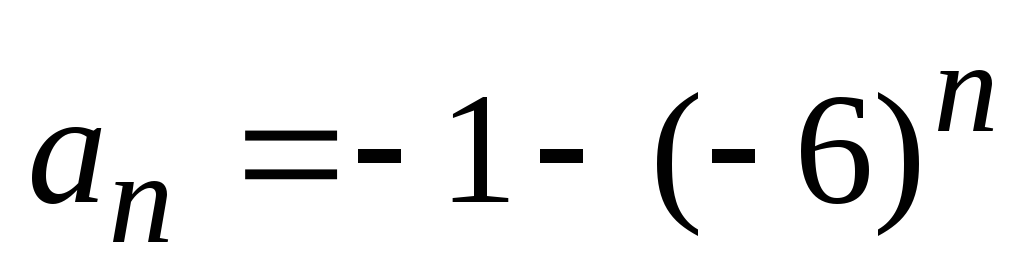 ,
а
,
а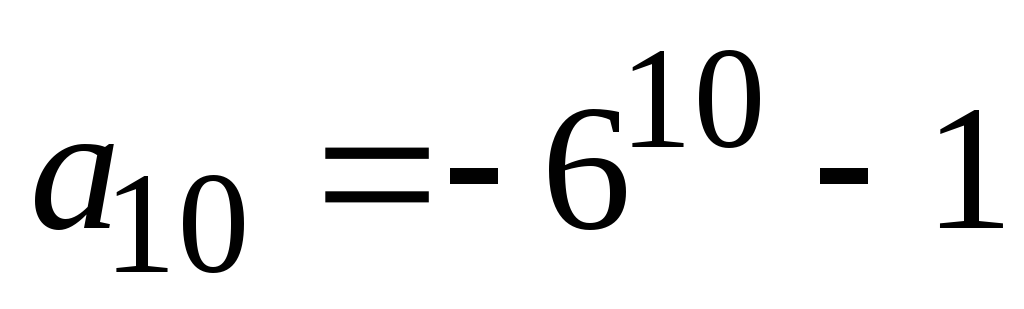 .
.
Подходы к изучению комбинаторных объектов и чисел Понятие продуктивной функции
Пусть задана некоторая последовательность
чисел 
Определение.Если степенной ряд
 (5.21)
(5.21)
совпадает при некоторых  с функцией
с функцией ,
то
,
то называетсяпродуктивной функцией для последовательности
называетсяпродуктивной функцией для последовательности .
.
С последовательностью  можно связать еще один степенной ряд:
можно связать еще один степенной ряд:
 (5.22)
(5.22)
Определение.Если этот ряд совпадает
с функцией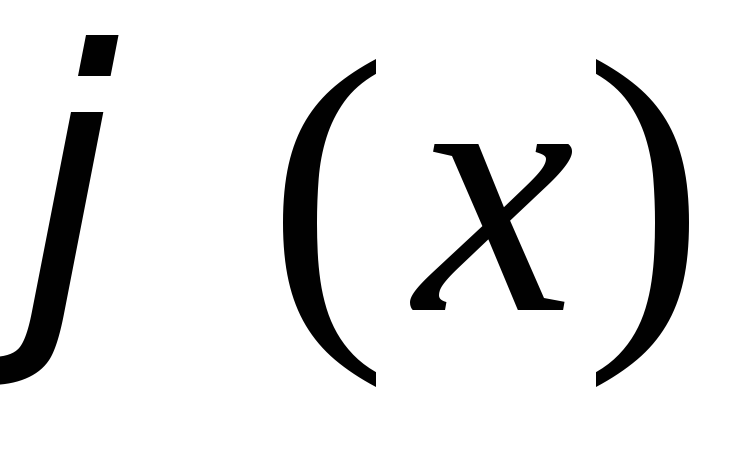 ,
то
,
то называетсяэкспоненциальной
продуктивной функциейдля
последовательности
называетсяэкспоненциальной
продуктивной функциейдля
последовательности Это название объясняется тем, что для
последовательности
Это название объясняется тем, что для
последовательности экспоненциальной продуктивной функцией
(5.22) есть экспонента
экспоненциальной продуктивной функцией
(5.22) есть экспонента :
:
 (5.23)
(5.23)
Для той же последовательности обычная
функция есть 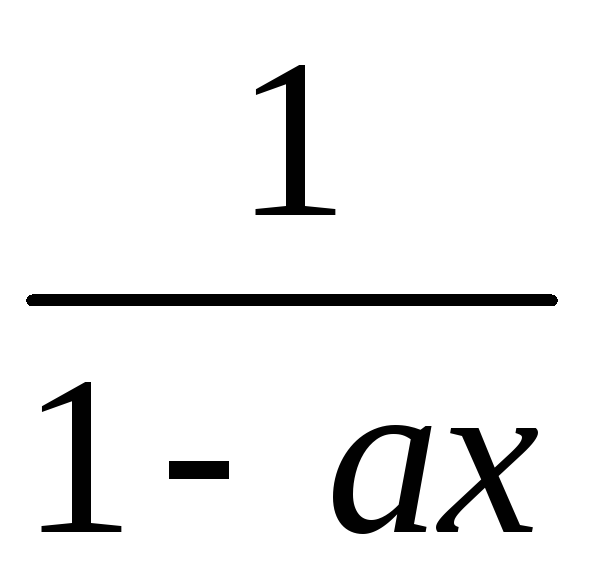 :
:
 (5.24)
(5.24)
Действительно, если  ,
то есть
,
то есть ,
тогда по формуле суммы бесконечно
спадающей геометрической прогрессии
(5.24) получаем:
,
тогда по формуле суммы бесконечно
спадающей геометрической прогрессии
(5.24) получаем:

В частности, если  ,
то
,
то
 (5.25)
(5.25)
Дифференцирование (5.25) приводит к равенству
 (5.26)
(5.26)
А умножение (5.26) на дает
 (5.27)
(5.27)
Таким образом,  есть продуктивная функция для
последовательности чисел натурального
ряда
есть продуктивная функция для
последовательности чисел натурального
ряда (5.26),
(5.26),
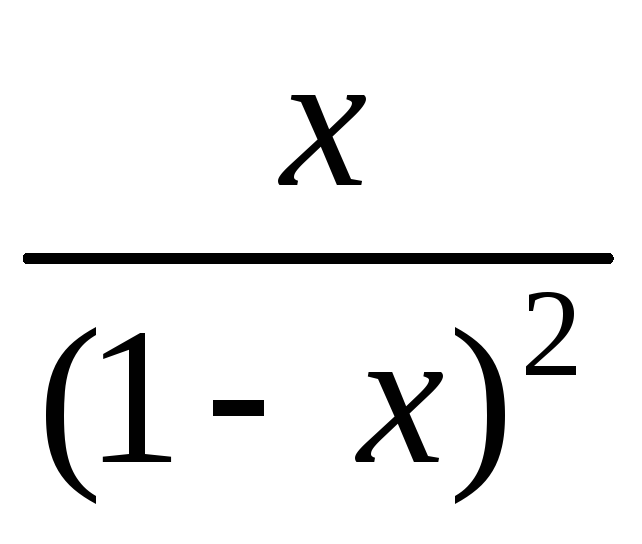 – продуктивная функция для последовательности
– продуктивная функция для последовательности (5.27).
(5.27).
Функцию  ,
у которой есть производные произвольно
высокого порядка при
,
у которой есть производные произвольно
высокого порядка при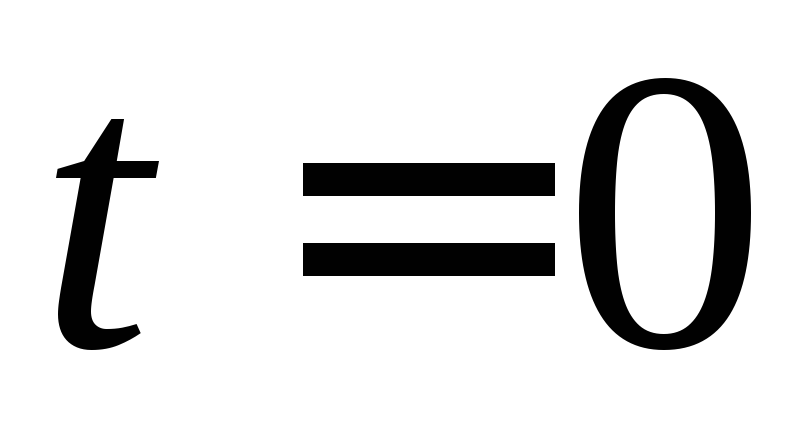 ,
можно считать экспоненциальной
продуктивной функцией для последовательности
своих производных
,
можно считать экспоненциальной
продуктивной функцией для последовательности
своих производных
Действительно получается разложение в рад Тейлора:
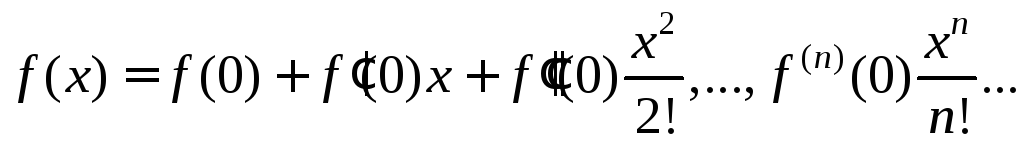
Рекуррентные соотношения в комбинаторике
1. Задача о наклейке марок.
Имеются марки достоинством в 4, 6, 10 копеек. На конверт нужно наклеить марки так, чтобы сумма составляла 18 копеек. Будем считать, что порядок наклеиваемых марок важен, т. е. способы наклейки марок достоинством в 4, 10, 4 копейки и 10, 4, 4 разные способы. Тогда можно написать следующее рекуррентное соотношение:
 ,
,
где под  понимается количество вариантов наклейки
марок общей стоимостью
понимается количество вариантов наклейки
марок общей стоимостью .
Подсчитаем значения
.
Подсчитаем значения для некоторых начальных
для некоторых начальных .
.
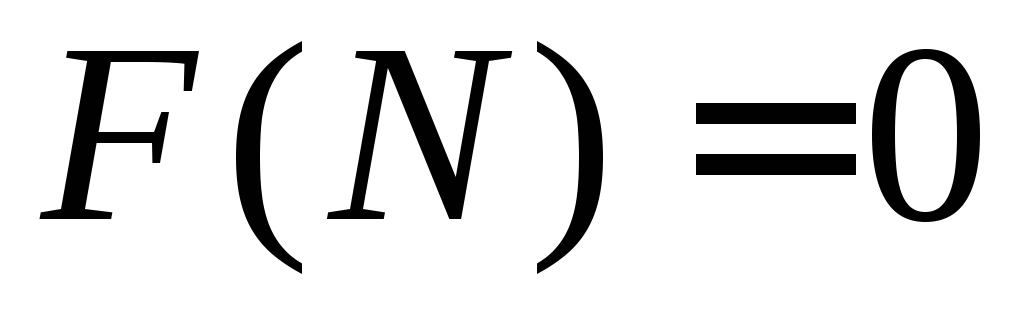 при
при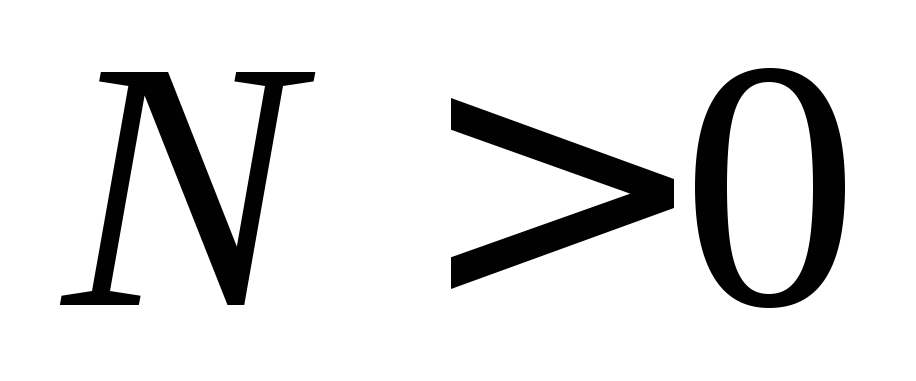 .
.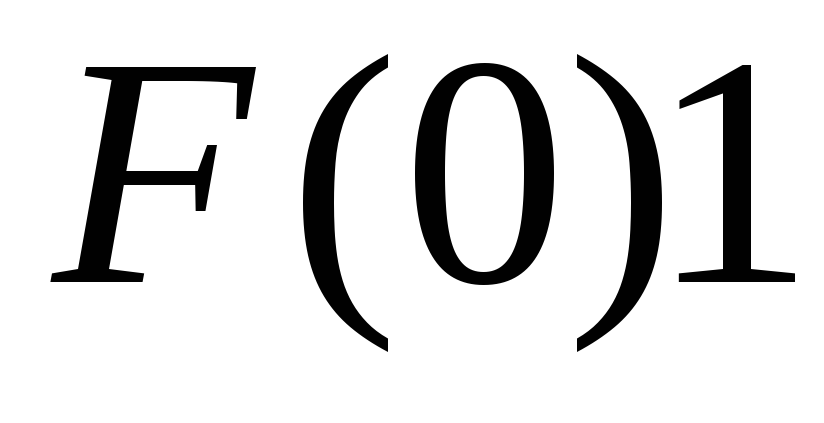 .
. .
. .
. .
.
 .
. .
. .
. .
. .
.
Тогда для  получаем:
получаем:

2. Задача об уплате долга.В кошельке имеются монеты достоинством в 1, 2, 3, 5, 10, 15, 20, 50 копеек (по одной штуке). Требуется уплатить долг в 73 копейки.
Запишем рекуррентное соотношение в
общем случае, когда монеты имеют
достоинства в копеек и требуется набрать сумму в
копеек и требуется набрать сумму в копеек:
копеек:
 .
.
Первый член правой части учитывает количество комбинаций, в которых монета старшего достоинства использована, второй член – в которых монета старшего достоинства не использована. Для рассматриваемого примера
 (1,
2, 3, 5, 10, 15, 20, 50;
73)=
(1,
2, 3, 5, 10, 15, 20, 50;
73)=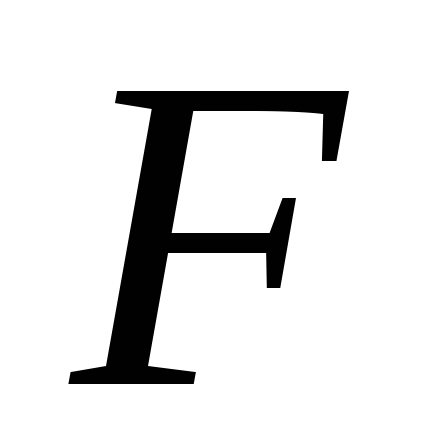 (1,2,3,5,10,15,20;73)+
(1,2,3,5,10,15,20;73)+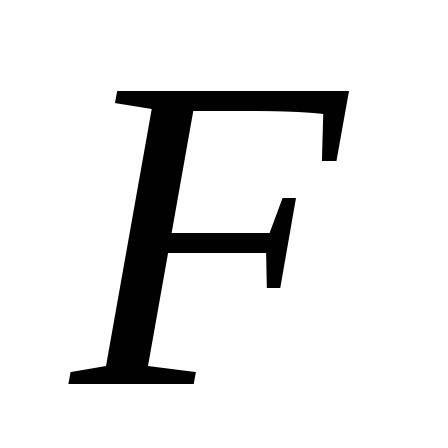 (1,2,3,5,10,15,20;
23).
(1,2,3,5,10,15,20;
23).
Первый член равен 0, так как сумма оставшихся монет меньше набираемой суммы. Применим ту же рекуррентную формулу к оставшемуся члену. В результате получим:
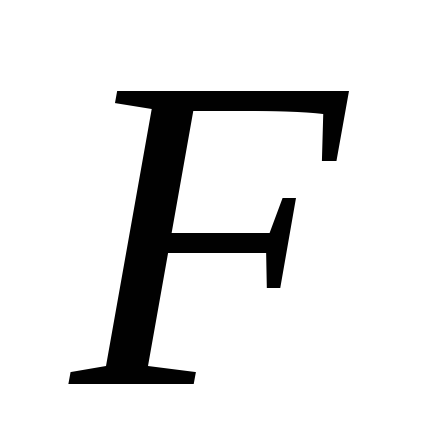 (1,
2, 3, 5, 10, 15, 20; 23) =
(1,
2, 3, 5, 10, 15, 20; 23) =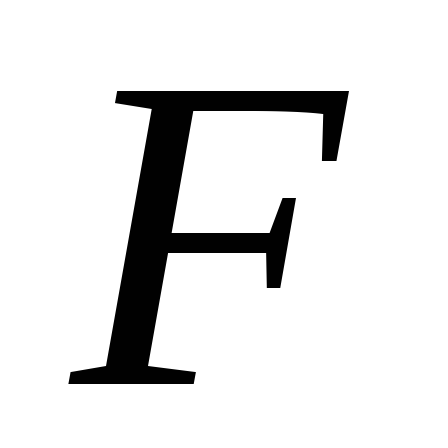 (1, 2, 3, 5, 10, 15; 3) +
(1, 2, 3, 5, 10, 15; 3) + (1, 2, 3, 5, 10, 15; 23)
(1, 2, 3, 5, 10, 15; 23)
В первом члене правой части монеты достоинством в 5, 10 и 15 копеек можно не учитывать, так как достоинство каждой из этих монет больше набираемой суммы, т. е. можно правую часть переписать так:
 (1, 2, 3; 3) +
(1, 2, 3; 3) + (1,
2, 3, 5, 10, 15; 23) =
(1,
2, 3, 5, 10, 15; 23) =
= (1, 2; 0) +
(1, 2; 0) + (1,
2;3 ) +
(1,
2;3 ) +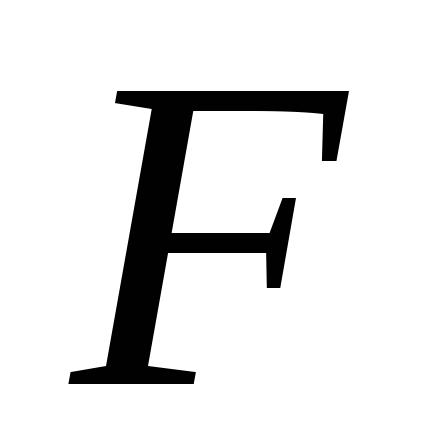 (1,
2, 3, 5, 10; 8) +
(1,
2, 3, 5, 10; 8) +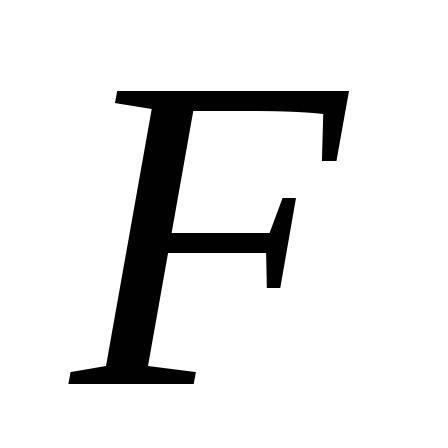 (1,
2, 3, 5, 10; 23) =
(1,
2, 3, 5, 10; 23) =
= 1+  (1; 1) +
(1; 1) +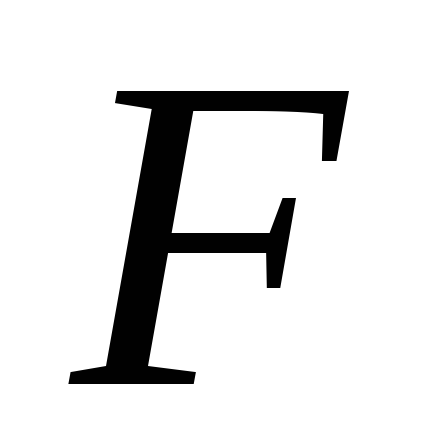 (1;
3) +
(1;
3) + (1,
2, 3, 5; 8) +
(1,
2, 3, 5; 8) + (1,
2, 3, 5, 10; 23).
(1,
2, 3, 5, 10; 23).
Очевидно, что  (1,
2; 0) = 1;
(1,
2; 0) = 1;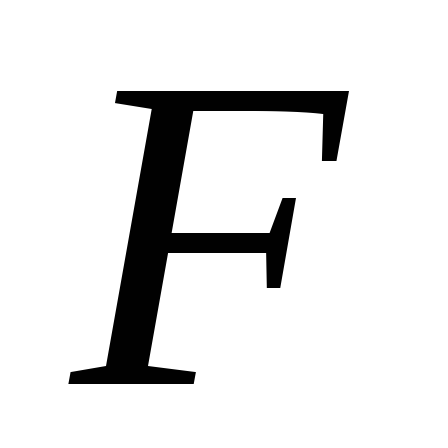 (1,
2; 3) =
(1,
2; 3) = (1;1)
= 1;
(1;1)
= 1;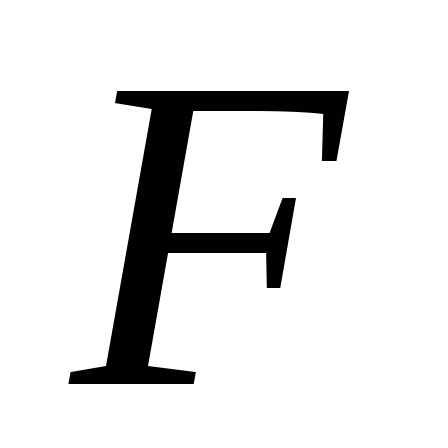 (1;
3) = 0;
(1;
3) = 0;
 (1,
2, 3, 5, 10; 23) = 0. Поэтому правая часть
перепишется в виде:
(1,
2, 3, 5, 10; 23) = 0. Поэтому правая часть
перепишется в виде:
1 + 1 + 0 +  (1,
2, 3, 5; 8) + 0 = 2 +
(1,
2, 3, 5; 8) + 0 = 2 + (1,
2, 3; 3) +
(1,
2, 3; 3) +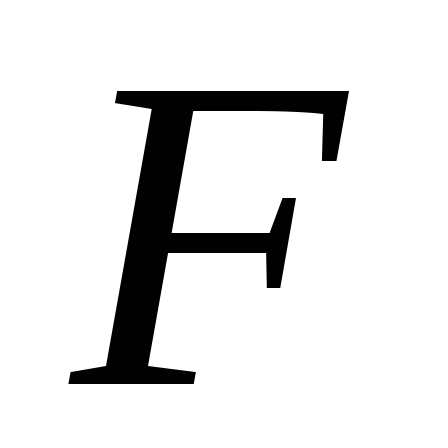 (1,
2, 3; 8) = 2 + 2 + 0 = 4. Таким образом, задача
имеет 4 различных решения.
(1,
2, 3; 8) = 2 + 2 + 0 = 4. Таким образом, задача
имеет 4 различных решения.
Подчеркнем еще раз, что в этой задаче порядок монет не важен.
3. Задача о размене гривенника (10 копеек). Рассмотрим задачу, в которой сняты ограничения, как на порядок предметов, так и на их количество: размен гривенника монетами достоинством в 1, 2, 3, 5 копеек.
Для этого случая рекуррентное соотношение имеет вид
 (1,
2, 3, 5; 10) =
(1,
2, 3, 5; 10) = (1,
2, 3; 10) +
(1,
2, 3; 10) + (1,
2, 3; 5) +
(1,
2, 3; 5) +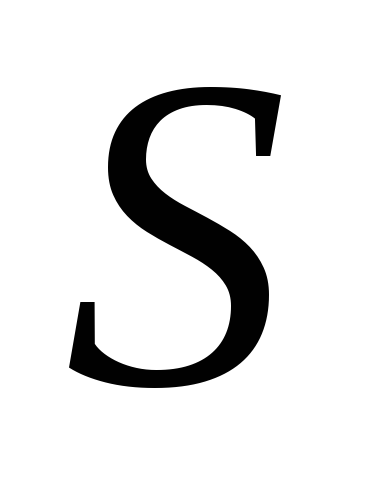 (1,
2, 3; 0).
(1,
2, 3; 0).
Таким образом, все множество решений разбивается на подмножества в зависимости от числа монет старшего достоинства, использованных для размена. Находим все 20 способов размена:
5*2; 5+1*5; 3+2*3+1; 2*4+1*2;
5+3+2; 3*3+1; 3+2*2+1*3; 2*3+1*4;
5+3+1*2; 3*2+2*2; 3+2+1*5; 2*2+1*6;
5+2*2+1; 3*2+2+1*2; 3+1*7; 2+1*8;
5+2+1*3; 3*2+1*4; 2*5; 1*10.
1.2. Комбинаторные объекты и комбинаторные числа
В комбинаторном анализе изучаются
различные объекты, порождаемые элементами
из конечного множества  ,
а также числовые характеристики этих
объектов.
,
а также числовые характеристики этих
объектов.
При подсчете числа объектов с наперед заданными свойствами используются следующие два правила.
Правило суммы.
Если объект может быть выбран
может быть выбран способами, а объект
способами, а объект
 способами, то выбор «либо
способами, то выбор «либо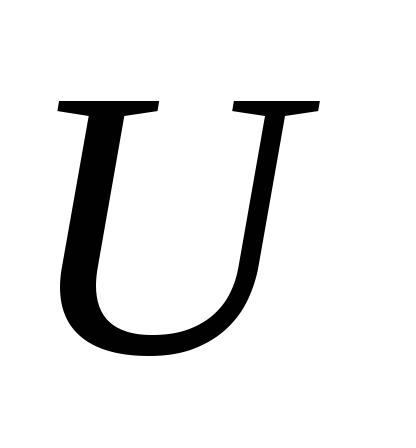 ,
либо
,
либо »
может быть осуществлен
»
может быть осуществлен способами.
способами.
Правило произведения.
Если объект может быть выбран
может быть выбран способами и после каждого из таких
выборов объект
способами и после каждого из таких
выборов объект в свою очередь может быть выбран
в свою очередь может быть выбран способами, то выбор «
способами, то выбор «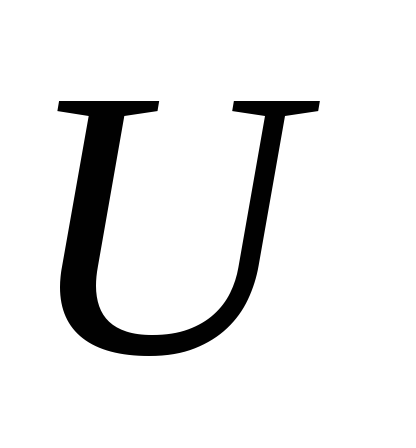 и
и »
в указанном порядке может быть осуществлен
»
в указанном порядке может быть осуществлен способами.
способами.
Набор элементов 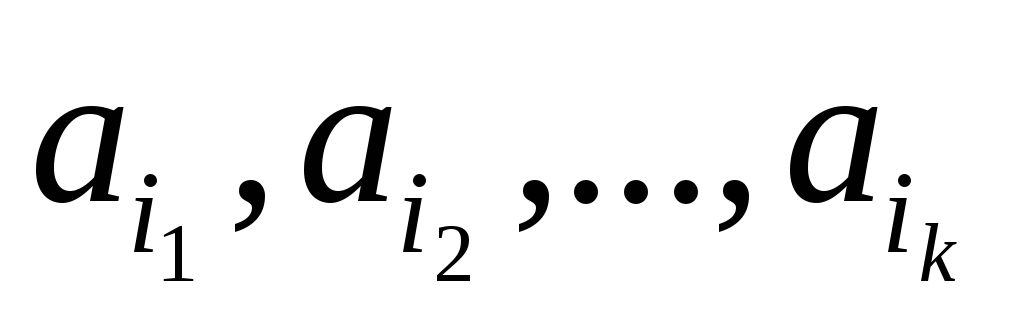 из множества
из множества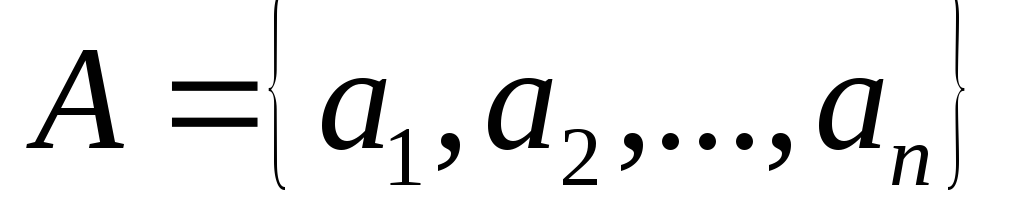 называетсявыборкойобъема
называетсявыборкойобъема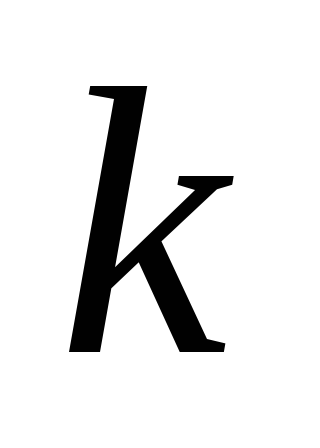 из
из элементов или
элементов или -выборкой.
-выборкой.
Выборка называется упорядоченной, если порядок следования элементов в ней задан. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными. Если порядок следования элементов не является существенным, то выборка называетсянеупорядоченной.
В выборках могут допускаться или не допускаться повторения элементов.
Рассмотрим некоторые комбинаторные объекты и их комбинаторные числа.
1.Размещения.Размещениемэлементов из по
по (илиразмещениемизnэлементов поk)
называется упорядоченная
(илиразмещениемизnэлементов поk)
называется упорядоченная -выборка,
в которой элементы попарно различны.
-выборка,
в которой элементы попарно различны.
Пример 1.
Пусть и
и .
Выпишем все размещения из этого множества
по два:
.
Выпишем все размещения из этого множества
по два:
 ,
, ,
, ,
,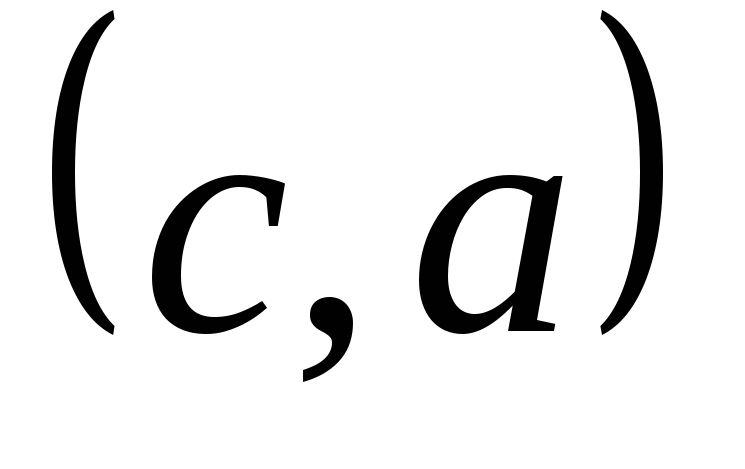 ,
, ,
, .
.
Обозначим число размещений из nпоkчерез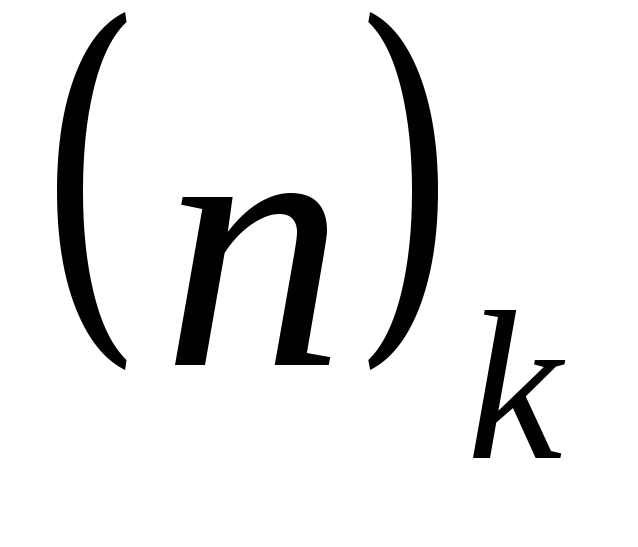 .
Для подсчета числа
.
Для подсчета числа используем правило произведения. При
построении конкретного размещения
первым элементом в нем можно взять любой
из
используем правило произведения. При
построении конкретного размещения
первым элементом в нем можно взять любой
из элементов множества
элементов множества ,
вторым элементом – любой из
,
вторым элементом – любой из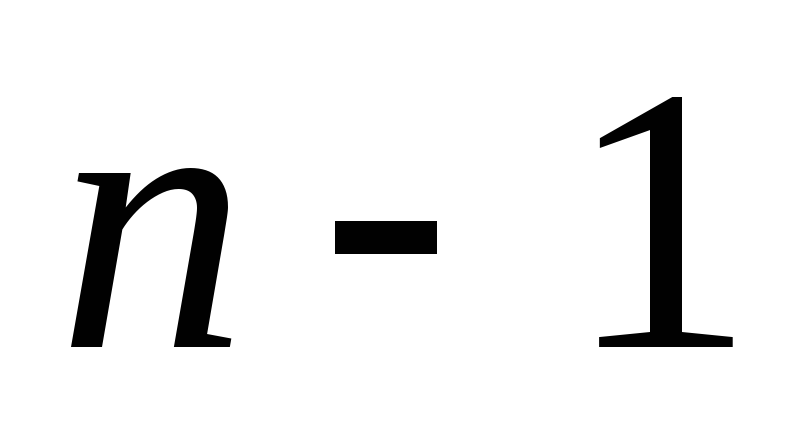 оставшихся в
оставшихся в элементов и т.д. Поэтому
элементов и т.д. Поэтому
 при
при .
.
При 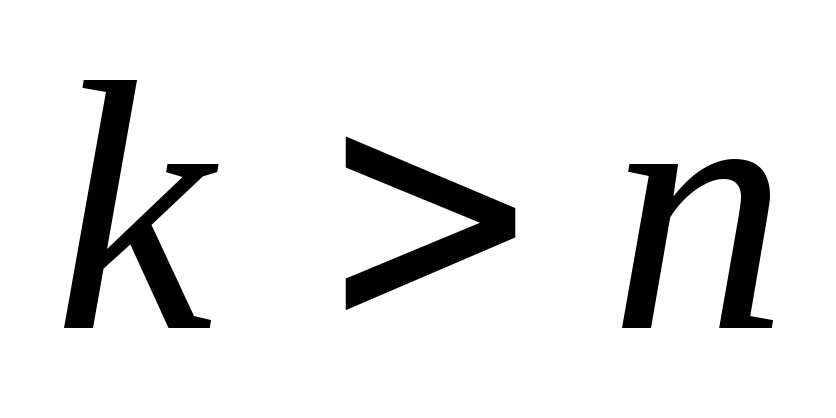 не существует размещений из
не существует размещений из по
по ,
следовательно,
,
следовательно,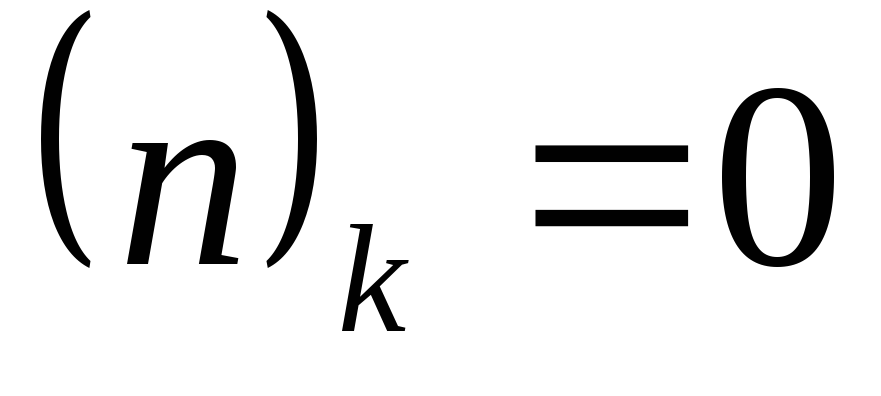 при
при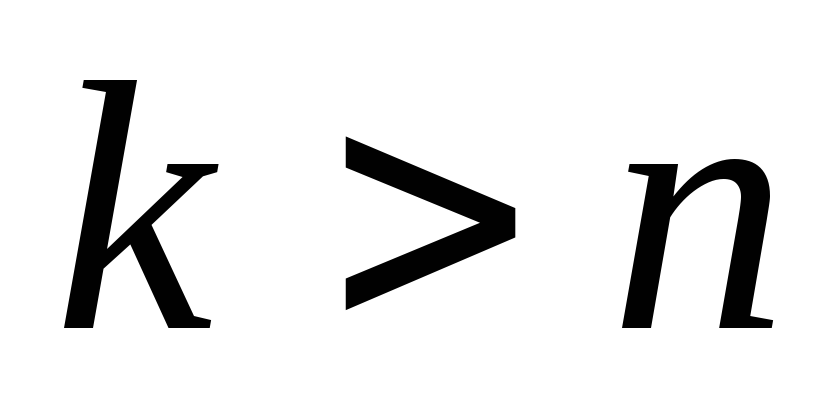 ;
при
;
при полагаем
полагаем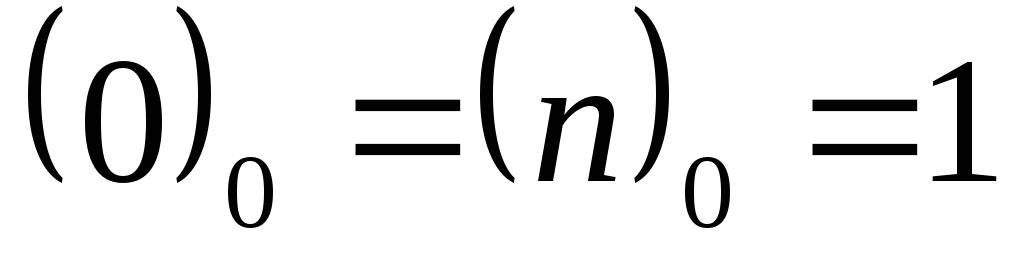 .
.
Упражнение 1.Показать, что для чисел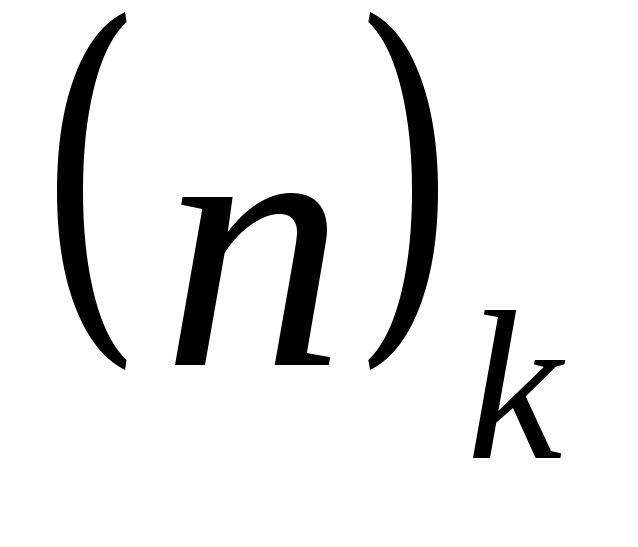 выполняются тождества
выполняются тождества
 ,
,
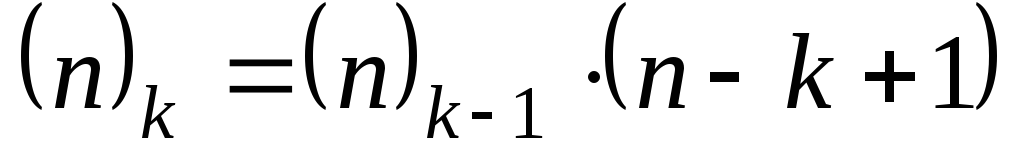 .
.
2.Перестановки.Перестановками элементов множества  (илиперестановками из nэлементов) называются упорядоченная
(илиперестановками из nэлементов) называются упорядоченная -выборка,
в которой элементы попарно различны
-выборка,
в которой элементы попарно различны .
.
Пример 2.
Пусть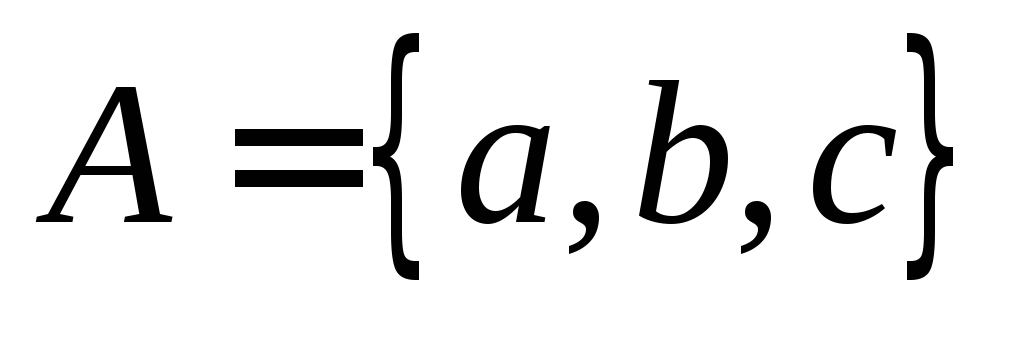 .
Выпишем все перестановки этого множества:
.
Выпишем все перестановки этого множества:
 ,
, ,
,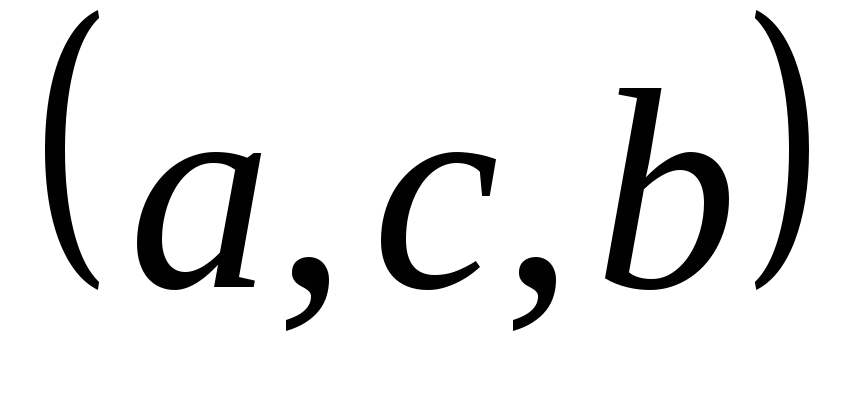 ,
,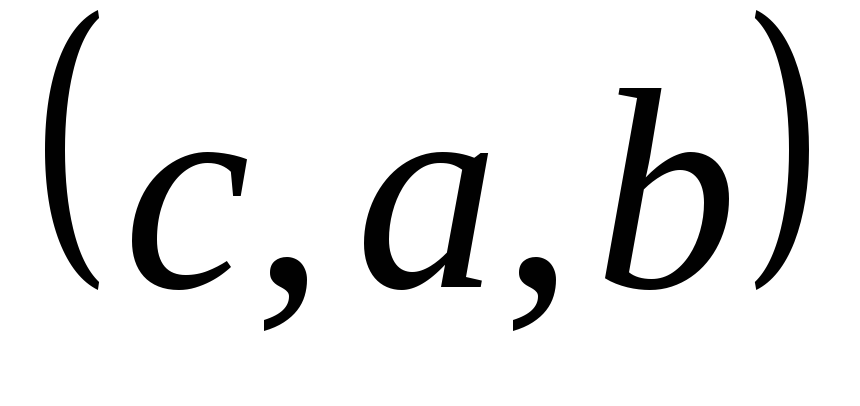 ,
,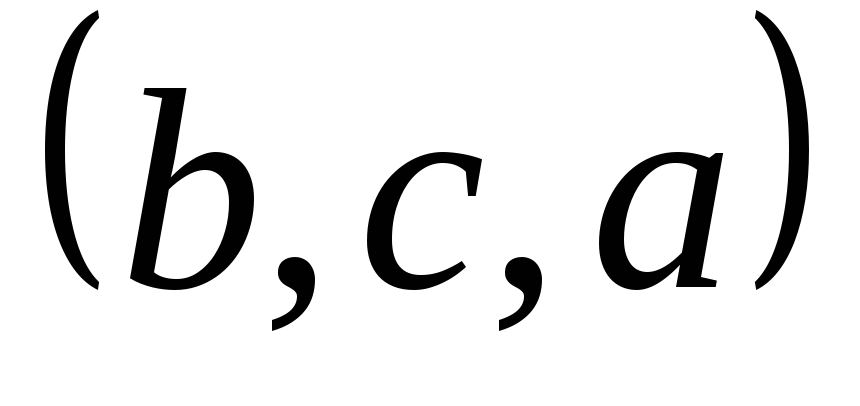 ,
, .
.
Очевидно, что перестановки из  элементов – частный случай размещений
из
элементов – частный случай размещений
из элементов по
элементов по ,
когда
,
когда .
Поэтому их число равно
.
Поэтому их число равно
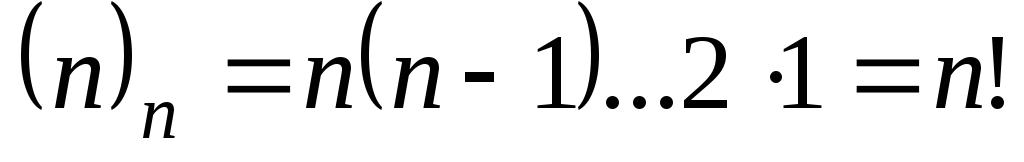
3.Сочетания.Сочетаниемэлементов из по
по (илисочетаниемизnэлементов поk)
неупорядоченная
(илисочетаниемизnэлементов поk)
неупорядоченная -выборка,
в которой элементы попарно различны.
-выборка,
в которой элементы попарно различны.
Пример 3.
Пусть и
и .
Выпишем все сочетания из этого множества
по два:
.
Выпишем все сочетания из этого множества
по два:
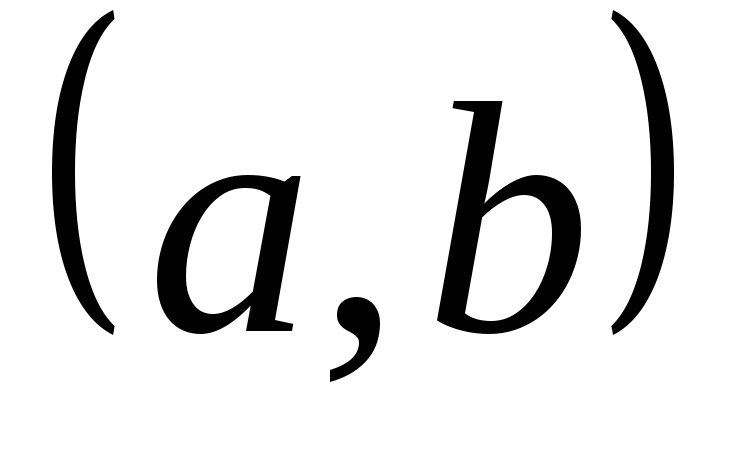 ,
, ,
, .
.
В сочетании, в отличие от размещения,
порядок следования элементов не
учитывается. Поэтому из одного сочетания
из nэлементов поkполучается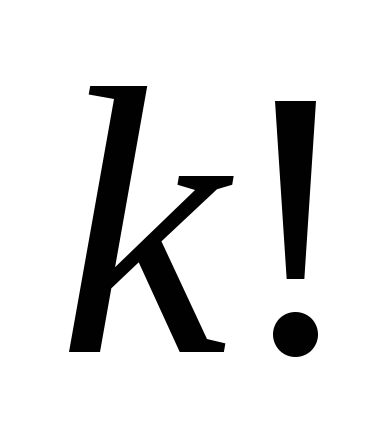 размещений. Отсюда для числа
размещений. Отсюда для числа сочетаний изnэлементов
поkполучается формула
сочетаний изnэлементов
поkполучается формула
 ,
,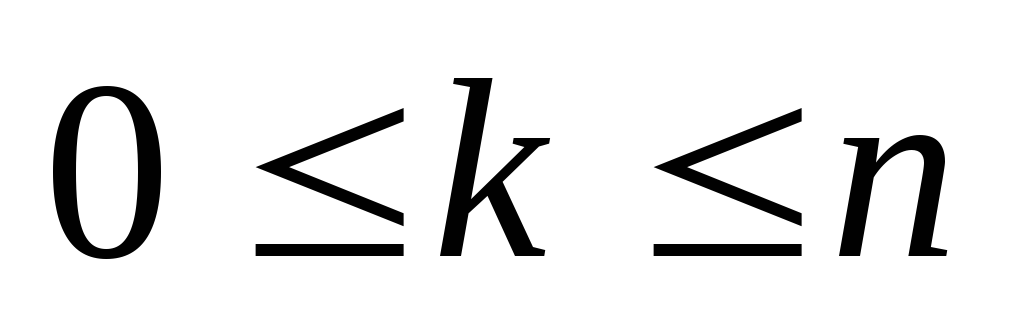 .
.
Из последней формулы следует
 и
и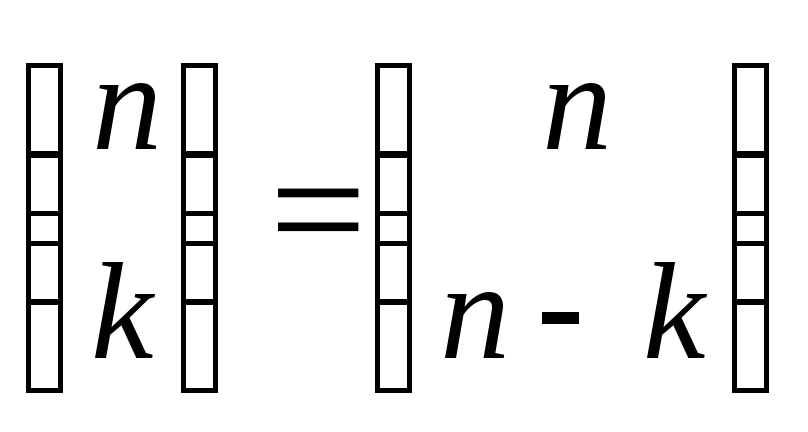 .
.
При  полагают
полагают .
При
.
При полагают
полагают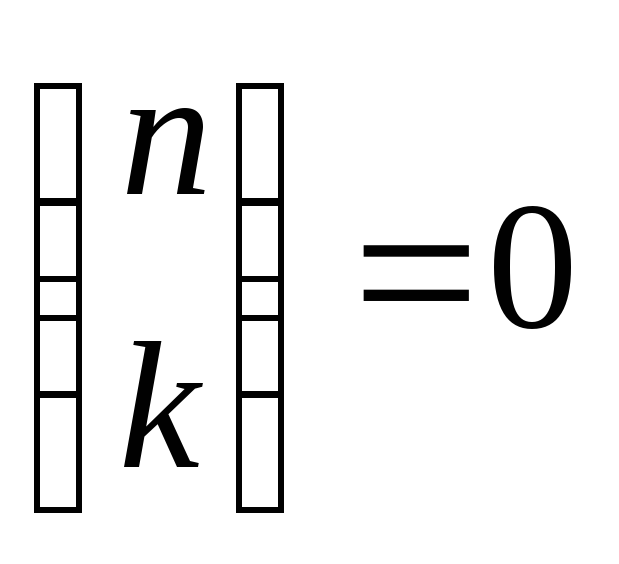 ,
поскольку при
,
поскольку при не
существует сочетаний из
не
существует сочетаний из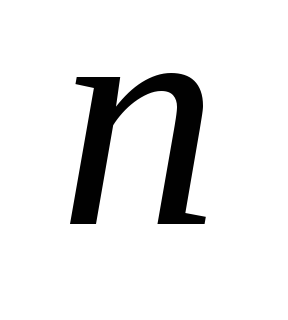 элементов по
элементов по .
.
Наряду с обозначением  часто используется обозначение
часто используется обозначение .
.
Числа 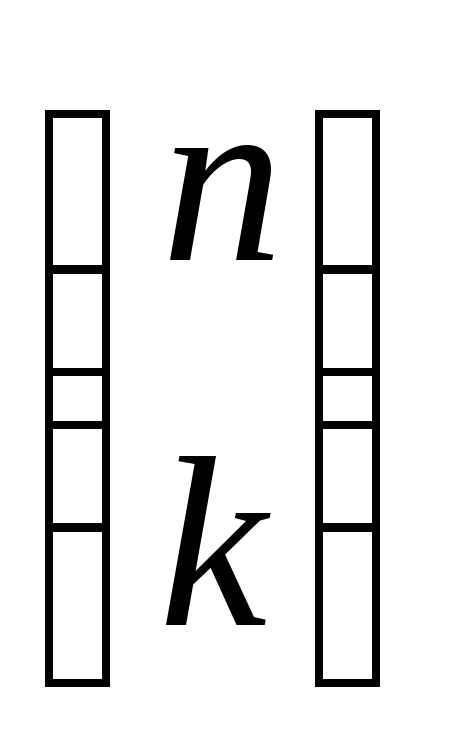 называются такжебиномиальными
коэффициентами, поскольку они
фигурируют в функциональном тождестве,
называемом формулой бинома Ньютона:
называются такжебиномиальными
коэффициентами, поскольку они
фигурируют в функциональном тождестве,
называемом формулой бинома Ньютона:
 .
(1)
.
(1)
Формулу (1) несложно доказать, используя метод математической индукции. Советуем провести доказательства в качестве упражнения.
Полагая в (1)  ,
получим тождество
,
получим тождество
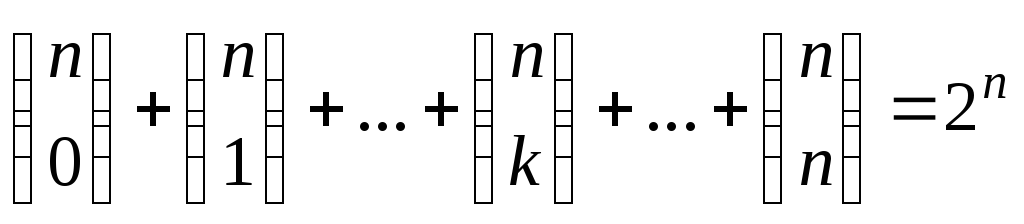 ;
(2)
;
(2)
При  получим
получим
 .
(3)
.
(3)
При четном nиз соотношений (2) и (3) следуют тождества
 ,
, .
.
При нечетном nиз соотношений (2) и (3) следуют тождества
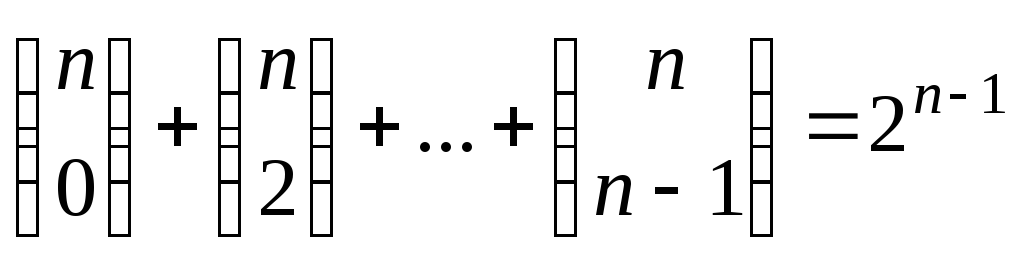 ,
, .
.
Упражнение 2.Показать, что для чисел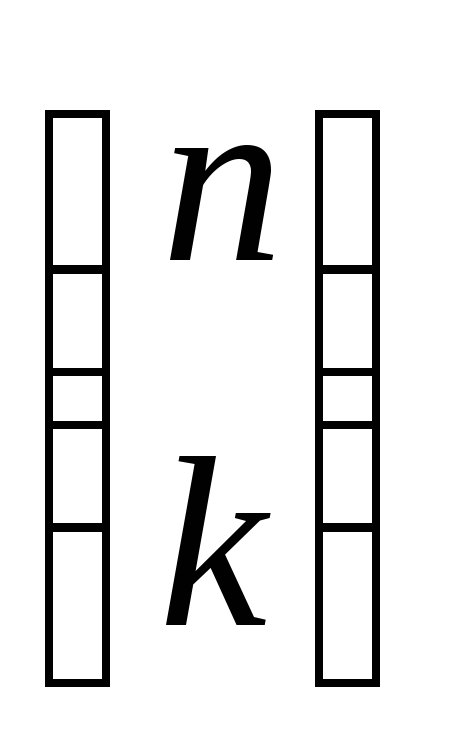 выполняется тождество
выполняется тождество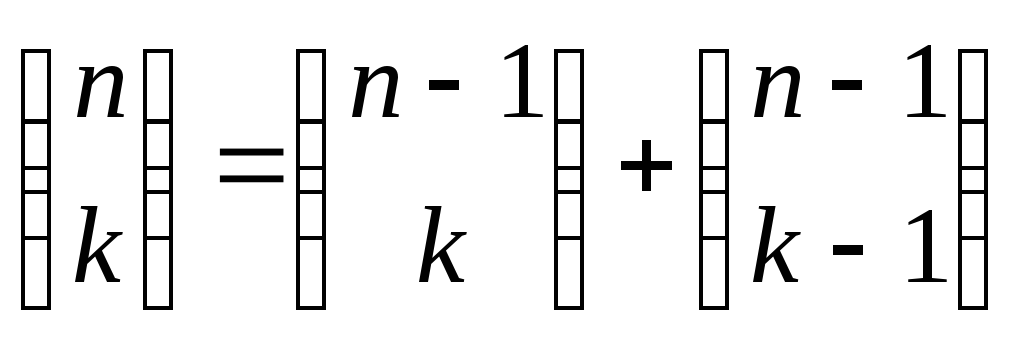 .
.
Из последнего тождества вытекает
эффективный способ реккурентного
вычисления биномиальных коэффициентов  ,
который можно представить в графической
форме, известной кактреугольник
Паскаля.
,
который можно представить в графической
форме, известной кактреугольник
Паскаля.
1 | ||||||||||
1 | 1 | |||||||||
1 | 2 | 1 | ||||||||
1 | 3 | 3 | 1 | |||||||
1 | 4 | 6 | 4 | 1 | ||||||
. | . | . | . | . | . |
В этом равнобедренном треугольнике
каждое число (кроме единиц на боковых
сторонах) является суммой двух чисел,
стоящих над ним. Число  находится в (
находится в (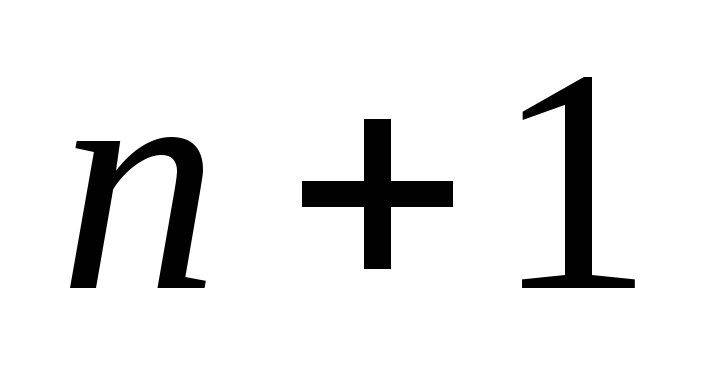 )
ряду на (
)
ряду на ( )
месте.
)
месте.
Упражнение 3.Показать, что последовательность ,
где
,
где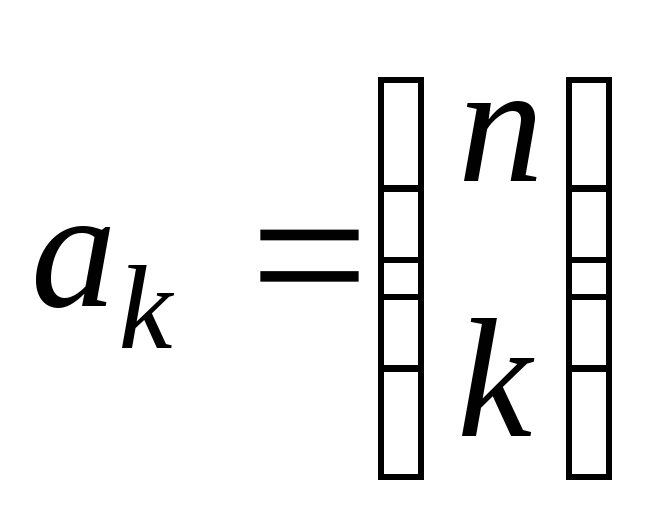 обладает свойством:
обладает свойством:
 ,
еслиnчетно
,
еслиnчетно
и
 еслиnнечетно.
еслиnнечетно.
4.Размещения с повторениями.Размещением с повторениями элементов
из по
по (илиразмещением с повторением изnэлементов поk)
упорядоченная
(илиразмещением с повторением изnэлементов поk)
упорядоченная -выборка,
в которой элементы могут повторяться.
-выборка,
в которой элементы могут повторяться.
Пример 4.
Пусть и
и .
Выпишем все размещения с повторениями
из этого множества по два:
.
Выпишем все размещения с повторениями
из этого множества по два:
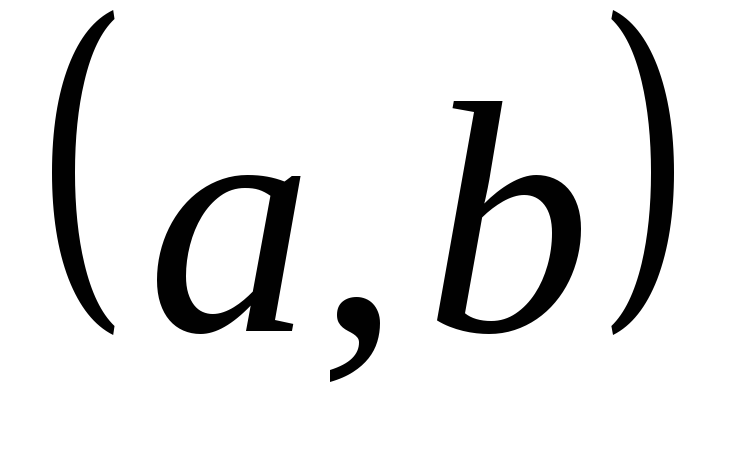 ,
,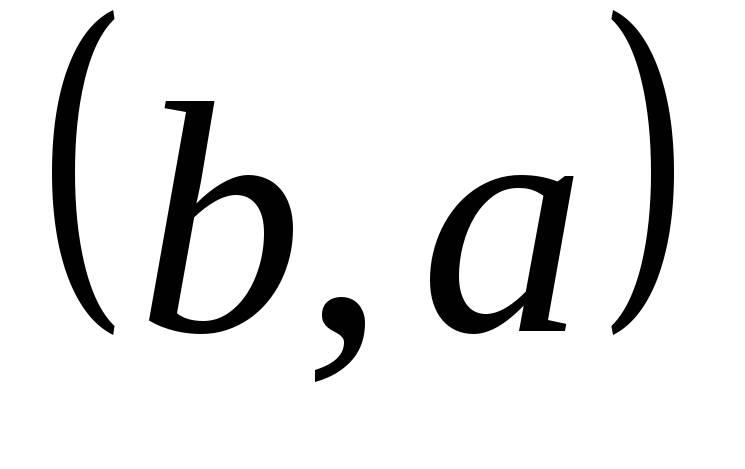 ,
, ,,
,, ,
, ,,
,, ,
, .
.
Для подсчета числа размещений с
повторениями из nэлементов поkиспользуем
правило произведения. При построении
конкретного размещения первым элементом
в нем можно взять любой из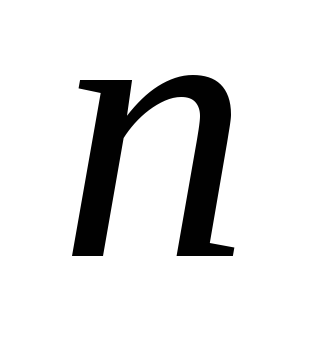 элементов множества
элементов множества ,
вторым элементом – также любой из
,
вторым элементом – также любой из элементов множества
элементов множества т.д. Таким образом, число размещений изnэлементов поk равно
т.д. Таким образом, число размещений изnэлементов поk равно
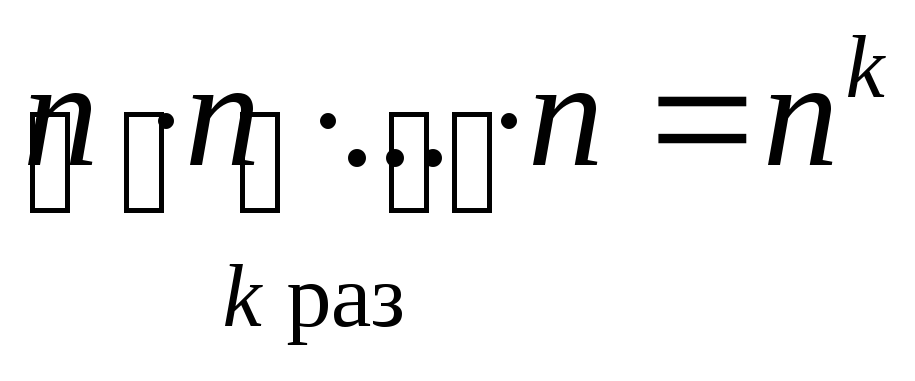 .
.
В частности, если в качестве множества  взято множество
взято множество ,
то совокупность всех размещений с
повторениями из
,
то совокупность всех размещений с
повторениями из по
по называетсяединичным
называетсяединичным  -мерным
кубоми обозначают
-мерным
кубоми обозначают .
. .
.
Пример 5. 3-х мерный куб размера 2 состоит из следующих элементов: (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1).
5.Сочетания с повторениями.Сочетанием с повторениями элементов
из по
по (илисочетанием с повторением изnэлементов поk)
неупорядоченная
(илисочетанием с повторением изnэлементов поk)
неупорядоченная -выборка,
в которой элементы могут повторяться.
-выборка,
в которой элементы могут повторяться.
Пример 5.
Пусть и
и .
Выпишем все сочетания с повторениями
из этого множества по два:
.
Выпишем все сочетания с повторениями
из этого множества по два:
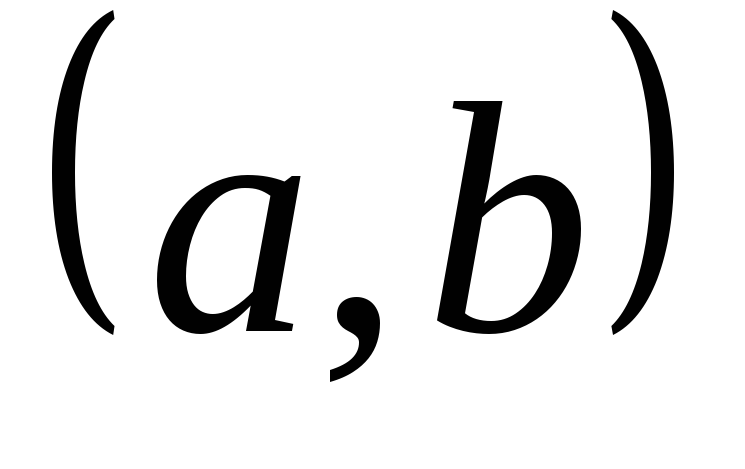 ,
, ,
, ,
, ,
, ,
,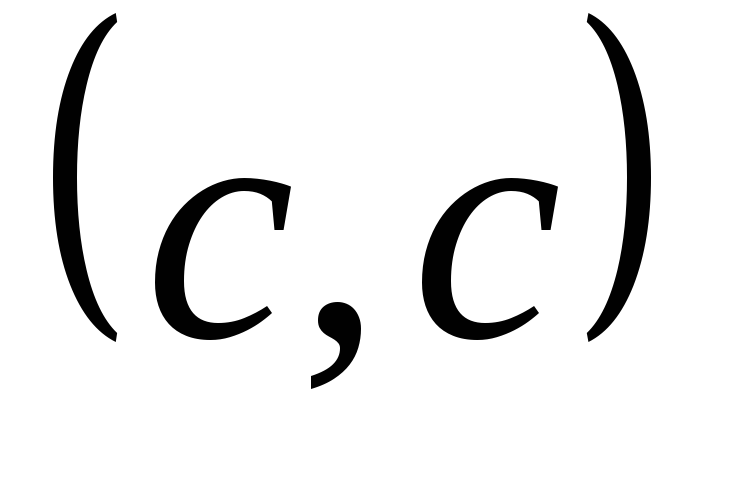 .
.
Можно показать, что число сочетаний с
повторениями изnэлементов поkравно .
.
6.Булеан множества  .Множество всех подмножеств называетсябулеаноммножества
.Множество всех подмножеств называетсябулеаноммножества  и
обозначается как
и
обозначается как  .
.
Пример 6.
Пусть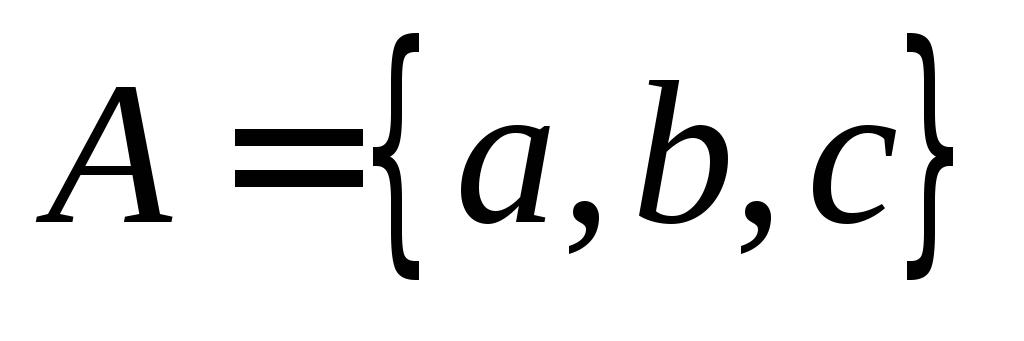 .
Тогда множество
.
Тогда множество есть булеан множества
есть булеан множества .
.
Мощность булеана множества  равна
равна  .Докажем это. Пусть
.Докажем это. Пусть .
Возьмем произвольное множество
.
Возьмем произвольное множество и сопоставим ему взаимнооднозначным
образом двоичный набор
и сопоставим ему взаимнооднозначным
образом двоичный набор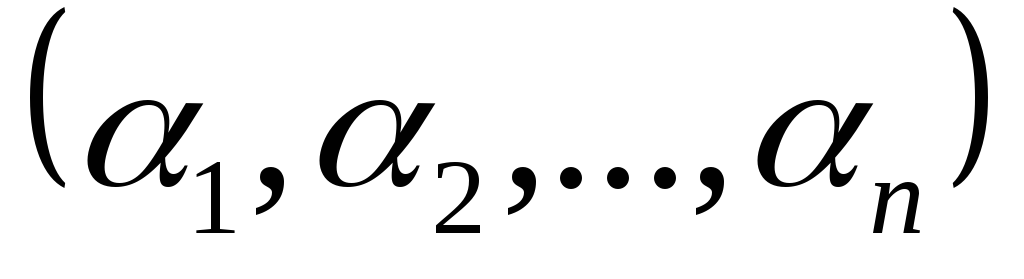 :
:

Отсюда получаем, что мощность булеана
совпадает с мощностью множества,
образованного всеми двоичными наборами,
т.е. с мощностью единичного 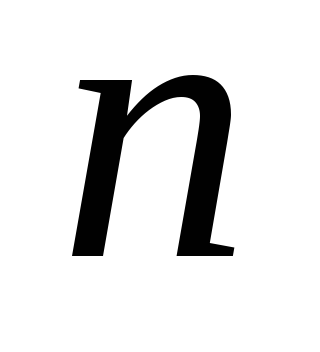 -мерного
куба. Таким образом,
-мерного
куба. Таким образом, .
.
7. Покрытие множества  .Семейство подмножеств
.Семейство подмножеств множества
множества называютпокрытием
называютпокрытием ,
если
,
если .
.
8. Разбиение множества  .Покрытие, образованное семейством
.Покрытие, образованное семейством непустых, попарно непересекающихся
подмножеств множества
непустых, попарно непересекающихся
подмножеств множества ,
называютразбиением
,
называютразбиением .
Множества
.
Множества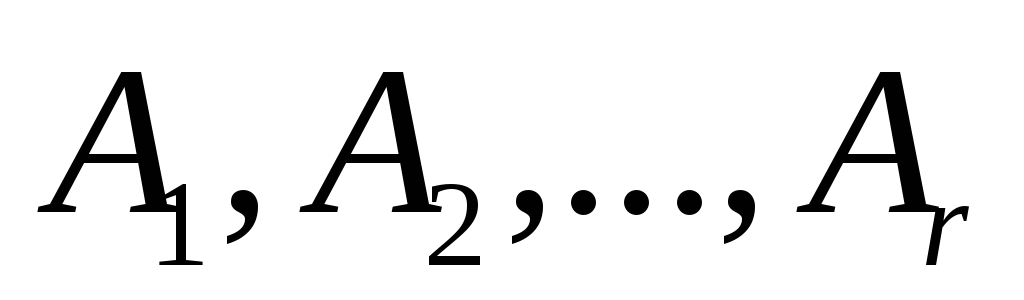 называют
блоками разбиения.
называют
блоками разбиения.
Пример 7.
Пусть .
Тогда семейство подмножеств
.
Тогда семейство подмножеств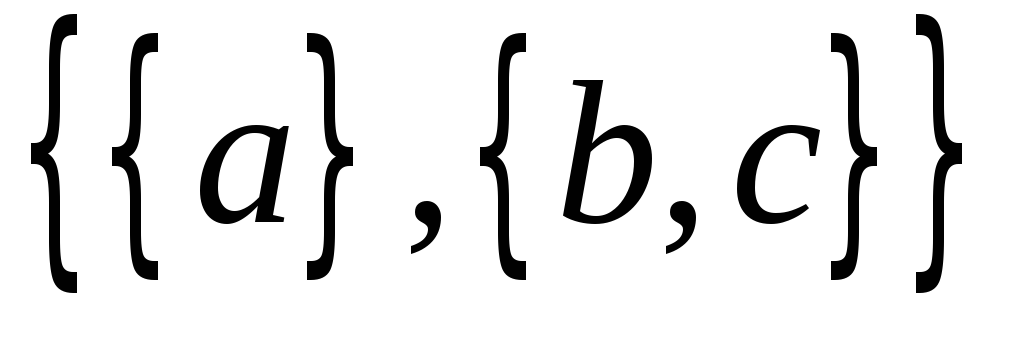 является как разбиением, так и покрытием.
В то время как семейство
является как разбиением, так и покрытием.
В то время как семейство является покрытием, но не является
разбиением.
является покрытием, но не является
разбиением.
Явные формулы для числа покрытий и разбиений множества получаются довольно трудоемко. За неимением времени в нашем курсе эти задачи не рассматриваются.
Исследования по алгебраической теории комбинаторных объектов : Тр. семинара
Поиск по определенным полям
Чтобы сузить результаты поисковой выдачи, можно уточнить запрос, указав поля, по которым производить поиск. Список полей представлен выше. Например:
author:иванов
Можно искать по нескольким полям одновременно:author:иванов title:исследование
Логически операторы
По умолчанию используется оператор AND.
Оператор AND означает, что документ должен соответствовать всем элементам в группе:
исследование разработка
author:иванов title:разработка
оператор OR означает, что документ должен соответствовать одному из значений в группе:исследование OR разработка
author:иванов OR title:разработка
оператор NOT исключает документы, содержащие данный элемент:исследование NOT разработка
author:иванов NOT title:разработка
Тип поиска
При написании запроса можно указывать способ, по которому фраза будет искаться. Поддерживается четыре метода: поиск с учетом морфологии, без морфологии, поиск префикса, поиск фразы.
По-умолчанию, поиск производится с учетом морфологии.
Для поиска без морфологии, перед словами в фразе достаточно поставить знак «доллар»:
$исследование $развития
Для поиска префикса нужно поставить звездочку после запроса:исследование*
Для поиска фразы нужно заключить запрос в двойные кавычки:«исследование и разработка«
Поиск по синонимам
Для включения в результаты поиска синонимов слова нужно поставить решётку «#» перед словом или перед выражением в скобках.
В применении к одному слову для него будет найдено до трёх синонимов.
В применении к выражению в скобках к каждому слову будет добавлен синоним, если он был найден.
Не сочетается с поиском без морфологии, поиском по префиксу или поиском по фразе.
#исследование
Группировка
Для того, чтобы сгруппировать поисковые фразы нужно использовать скобки. Это позволяет управлять булевой логикой запроса.
Например, нужно составить запрос: найти документы у которых автор Иванов или Петров, и заглавие содержит слова исследование или разработка:
author:(иванов OR петров) title:(исследование OR разработка)
Приблизительный поиск слова
Для приблизительного поиска нужно поставить тильду «~» в конце слова из фразы. Например:
бром~
При поиске будут найдены такие слова, как «бром», «ром», «пром» и т.д.Можно дополнительно указать максимальное количество возможных правок: 0, 1 или 2. Например:
бром~1
По умолчанию допускается 2 правки.Критерий близости
Для поиска по критерию близости, нужно поставить тильду «~» в конце фразы. Например, для того, чтобы найти документы со словами исследование и разработка в пределах 2 слов, используйте следующий запрос:
«исследование разработка«~2
Релевантность выражений
Для изменения релевантности отдельных выражений в поиске используйте знак «^» в конце выражения, после чего укажите уровень релевантности этого выражения по отношению к остальным.
Чем выше уровень, тем более релевантно данное выражение.
Например, в данном выражении слово «исследование» в четыре раза релевантнее слова «разработка»:
исследование^4 разработка
По умолчанию, уровень равен 1. Допустимые значения — положительное вещественное число.Поиск в интервале
Для указания интервала, в котором должно находиться значение какого-то поля, следует указать в скобках граничные значения, разделенные оператором TO.
Будет произведена лексикографическая сортировка.
author:[Иванов TO Петров]
Будут возвращены результаты с автором, начиная от Иванова и заканчивая Петровым, Иванов и Петров будут включены в результат.author:{Иванов TO Петров}
Такой запрос вернёт результаты с автором, начиная от Иванова и заканчивая Петровым, но Иванов и Петров не будут включены в результат.Для того, чтобы включить значение в интервал, используйте квадратные скобки. Для исключения значения используйте фигурные скобки.
Алгебраическая комбинаторика — Algebraic combinatorics
 Фано матроидом , полученный из плоскости Фано . Матроиды являются одним из многих областей , изучаемых в алгебраической комбинаторике .
Фано матроидом , полученный из плоскости Фано . Матроиды являются одним из многих областей , изучаемых в алгебраической комбинаторике .Алгебраическая комбинаторика является областью математики , которая использует методы абстрактной алгебры , в частности теории групп и теорию представлений , в различных комбинаторных контекстах и, наоборот, относится комбинаторные методы к проблемам в алгебре .
история
Через начале или середине 1990-х годов, типичные комбинаторные объекты , представляющие интерес в алгебраической комбинаторике либо допускали много симметрий ( ассоциативных схем , сильно регулярных графов , ч.у.м. с действием группы ) или обладал богатой алгебраической структурой, часто из представления теоретического происхождения ( симметричный функции , Юнга ). Этот период находит свое отражение в области 05E, алгебраические комбинаторики , в AMS Subject Classification математики , введенный в 1991 году.
Объем
Алгебраическая комбинаторика пришла увидеть более расширительно как область математики , где взаимодействие комбинаторных и алгебраических методов является особенно сильным и значительным. Таким образом, комбинаторные темы могут быть исчислительными в природе или включают матроиды , многогранники , частично упорядоченные множества , или конечные геометрии . Об алгебраической стороны, помимо группы и теории представлений, теория решеток и коммутативной алгебры являются общими.
Важные темы
Симметричные функции
Кольцо симметрических функций является специфическим пределом колец симметричных многочленов в п неизвестного, а п стремится к бесконечности. Это кольцо служит в качестве универсальной структуры , в которой отношения между симметрическими многочленами могут быть выражены таким образом , не зависит от числа п от неизвестных (но его элементов не являются ни полиномы , ни функция). Среди прочего, это кольцо играет важную роль в теории представлений симметрических групп .
схемы ассоциации
Схема объединения представляет собой совокупность бинарных отношений , удовлетворяющие определенные условия совместимости. Схемы ассоциаций обеспечивают единый подход ко многим темам, например , комбинаторные конструкции и теория кодирования . В алгебре, схемы объединения обобщать группы и теория ассоциативных схем обобщает теорию символов из линейных представлений групп.
Сильно регулярные графы
Сильно регулярный граф определяется следующим образом . Пусть G = ( V , E ) является регулярным графом с V вершинами и степени к . G называется сильно регулярным , если существуют и целые числа λ и ц такие , что:
- Каждые две соседние вершины имеют λ общих соседей.
- Каждые две несмежные вершины имеют х общих соседей.
График такого рода иногда говорят, является SRG ( v , к , λ, μ).
Некоторые авторы исключают графики , которые удовлетворяют определению тривиально, а именно те графы , которые являются объединением непересекающихся одного или более одинакового размера полных графов и их комплементы , то графики Туран .
Юнга
Юнга (пл .: Tableaux ) является комбинаторным объектом полезным в теории представлений и Шуберт исчислении . Это обеспечивает удобный способ для описания представлений групп из симметричных и общих линейных групп и изучить их свойство. Юнга был введен Альфредом Янг , в математике в Кембриджском университете , в 1900 г. Они были затем применены к изучению симметрической группы по Георгу Фробениусу в 1903. Их теории получили дальнейшее развитие многих математиков, включая Percy MacMahon , Ходжа , Г. де Б. Робинсон , Джан-Карло Рота , Ален Ласко , Марсель-Пол Шутзенбергер и Ричард П. Стенли .
Матроиды
Матроидом является структурой , которая захватывает и обобщает понятие линейной независимости в векторных пространствах . Есть много эквивалентных способов определения матроидом, наиболее существенными из которых с точки зрения независимых множеств, баз, схем, замкнутых множеств или квартиры, операторы замыкания и функции ранга.
Матроида теория заимствована из терминологии линейной алгебры и теорий графов , в основном потому , что это абстракция различных понятий центрального значения в этих областях. Матроиды нашли применение в геометрии, топологии , комбинаторной оптимизации , теории сетей и теории кодирования .
Конечные геометрии
Конечная геометрия является любой геометрической системой , которая имеет только конечное число точек . Знакомый евклидова геометрия не является конечной, так как евклидова линия содержит бесконечно много точек. Геометрия на основе графики , отображаемую на экране компьютера, в котором пиксели рассматриваются как точки, была бы конечная геометрия. Хотя существует много систем , которые можно было бы назвать конечных геометрий, внимание в основном уделяется конечных проективных и аффинных пространств в силу их регулярности и простоты. Другие важные виды конечной геометрии являются конечным Мебиусом или инверсных самолетами и Лагерра самолеты , которые являются примерами общего типа под названием Benz самолеты , и их многомерных аналогов , такие как высшая конечная инверсная геометрия .
Конечные геометрии могут быть построены с помощью линейной алгебры , начиная с векторных пространств над конечным полем ; аффинная и проективные плоскости сконструированы таким образом , называются геометрии Галуа . Конечные геометрии могут быть определены чисто аксиоматически. Наиболее распространенные конечные геометрии являются геометриями Галуа, так как любое конечного проективного пространства размерности три или больше , это изоморфен проективным пространства над конечным полем (то есть, проективизация векторного пространства над конечным полем). Тем не менее, измерение имеет два аффинные и проективные плоскости, которые не изоморфна геометрия Галуа, а именно недезарговые плоскости . Аналогичные результаты справедливы и для других видов конечных геометрий.
Смотрите также
Рекомендации
дальнейшее чтение
- Баннаи, Eiichi; Ито, Tatsuro (1984). Алгебраическая комбинаторика I: схемы ассоциации . Менло — Парк, Калифорния: The Benjamin / Cummings Publishing Co., Inc. С. XXIV + 425.. ISBN 0-8053-0490-8 . MR 0882540 .
- Billera, Луис Дж ; Бьорнер, Андерс ; Greene, Curtis ; Симион, Родик ; Стэнли, Ричард П. , ред. (1999). Новые перспективы в алгебраической комбинаторике . MSRI публикации. 38 . Cambridge University Press .
- Godsil, Крис Д. (1993). Алгебраическая комбинаторика . Нью — Йорк: Чепмен и Холл. ISBN 0-412-04131-6 . MR 1220704 .
- Такаюки Hibi, Алгебраическая комбинаторика на выпуклых многогранниках , Carslaw Публикация, Глеб, Австралия, 1992
- Мелвин Хохстера , Коэна-Маколея кольца, комбинаторика и симплициальные комплексы . Теории колец, II , (Proc. Второй конф., Ун — та. Оклахома, Норман, штат Оклахома., 1975), стр. 171-223. Lecture Notes в Pure Appl. И Математика., Т. 26, Dekker, New York, 1977.
- Эзра Миллер, Бернд Штурмфельс , комбинаторная коммутативная алгебра , Graduate тексты по математике , т. 227, Springer-Verlag, New York, NY, 2005. ISBN 0-387-22356-8
- Ричард Стэнли , Комбинаторика и коммутативной алгебры . Второе издание, Прогресс в области математики, т. 41. Birkhäuser, Boston, MA, 1996. ISBN 0-8176-3836-9
- Штурмфельса, Бернд (1996). Грёбнер основа и выпуклые многогранники . Университет Серия лекций. 8 . Providence, RI: Американское математическое общество . ISBN 0-8218-0487-1 .
- Дорон Цейльбергер , исчисляющей и алгебраическая комбинаторика , в Принстона Компаньоне математики , 2008.
внешняя ссылка
Алгебраическая комбинаторика — Gpedia, Your Encyclopedia
 Матроид Фано, полученный из плоскости Фано. Матроиды — одна из многих областей, изучаемых в алгебраической комбинаторике.
Матроид Фано, полученный из плоскости Фано. Матроиды — одна из многих областей, изучаемых в алгебраической комбинаторике.Алгебраическая комбинаторика — это область математики, использующая методы общей алгебры, в особенности теории групп и теории представлений, в различных комбинаторных контекстах и, наоборот, применяющая комбинаторные техники к задачам в алгебре.
История
В начале или середине 1990-х типичные комбинаторные объекты, которые рассматривались в алгебраической комбинаторике, либо имели большое число общепризнанных симметрий (схема отношений[en], сильно регулярные графы, частично упорядоченные множества с действием группы), либо обладали богатой алгебраической структурой, как правило, имеющей теоретические источники (симметрические функции, диаграммы Юнга). Этот период отражён в разделе 05E, «Алгебраическая комбинаторика», математической предметной классификации AMS, предложенной в 1991 году.
Сфера применения
Алгебраическую комбинаторику можно рассматривать как область математики, где взаимодействие комбинаторных и алгебраических методов особенно сильно и существенно. Такими комбинаторными темами могут быть перечисления по свойствам или области, вовлекающие матроиды, многогранники, частично упорядоченные множества или конечные геометрии. Со стороны алгебры, кроме теории групп и теории представлений, часто используются решётки и коммутативная алгебра. Журнал «Journal of Algebraic Combinatorics[en]», выпускаемый издательством Springer-Verlag, является интернациональным журналом для статей из этой области.
Важные разделы
Симметрические функции
Кольцо симметрических функций[en] является своеобразным пределом колец симметрических многочленов от n переменных при n, стремящемся к бесконечности. Это кольцо служит универсальной структурой, в которой связи между симметрическими многочленами могут быть выражены без привязки к числу переменных (но элементы кольца не являются ни многочленами, ни функциями). Кроме всего прочего, это кольцо играет важную роль в теории представлений симметрических групп[en].
Схемы отношений
Схема отношений[en] — это набор бинарных отношений, удовлетворяющих определённым условиям совместимости. Схемы отношений дают единообразный подход ко многим разделам, например, комбинаторным схемам и теории кодирования[1][2]. В алгебре схемы отношений обобщают группы, а теория схем отношений обобщает теорию характеров линейных представлений групп[3][4][5].
Сильно регулярные графы
Сильно регулярный граф определяется следующим образом. Пусть G = (V,E) — регулярный граф с v вершинами и степенью k. Говорят, что G сильно регулярен, если существуют целые числа λ и μ, такие, что:
- Любые две смежные вершины имеют λ общих соседей.
- Любые две несмежные вершины имеют μ общих соседей.
Графы такого вида иногда обозначаются srg(v, k, λ, μ).
Некоторые авторы исключают графы, которые удовлетворяют определению тривиально, а именно те графы, которые являются объединением непересекающихся (одного и более) одинаковых полных графов[6][7], и их дополнения, графы Турана.
Диаграммы Юнга
Диаграммы Юнга — комбинаторные объекты, полезные в теории представлений и исчислении Шуберта[en]. Они дают удобный способ описания представлений симметрических групп и полных линейных групп и позволяют изучать свойства этих объектов. Диаграммы были предложены Альфредом Юнгом[en], математиком Кембриджского университета, в 1900 году. В 1903 году они были применены для изучения симметрических групп Фердинандом Георгом Фробениусом. Позднее их теория была развита многими математиками, включая Перси Макмагона[en], В. В. Д. Ходжа, Г. де Б. Робинсона[en], Д.-К. Рота[en], Алена Ласку[en], М.-П. Шютценберже[en] и Ричарда Стэнли.
Матроиды
Матроид — это структура, которая вбирает и обобщает понятие линейной независимости в векторных пространствах. Имеется много эквивалентных путей определения матроида, и наиболее важные из них — в терминах независимых множеств, баз, замкнутых множеств или плоскостей, операторов замыкания и функций ранга.
Теория матроидов в значительной степени заимствует терминологию из линейной алгебры и теории графов, в основном потому, что в ней используются абстракции различных центральных понятий из этих областей, из топологии, комбинаторной оптимизации, теории сетей[en] и теории кодирования[8][9].
Конечные геометрии
Конечная геометрия — это любая геометрическая система, имеющая лишь конечное число точек. Привычная Евклидова геометрия не конечна, поскольку евклидова прямая содержит бесконечно много точек. Геометрию, основанную на графике компьютерного экрана, где пиксели считаются точками, можно считать конечной геометрией. Хотя существует много систем, которые можно было бы считать конечными геометриями, в основном внимание уделяется конечным проективным и аффинным пространствам ввиду их регулярности и простоты. Другие существенные типы конечных геометрий — конечные плоскости Мёбиуса или инверсные плоскости и плоскости Лагерра[en], которые являются примерами более общих объектов, называемых плоскостями Бенца[en], и их аналогами в более высоких размерностях, таких как конечные инверсионные геометрии[en].
Конечные геометрии могут быть построены с помощью линейной алгебры, начиная с векторных пространств над конечными полями. Аффинные и проективные плоскости, построенные таким образом, называются геометриями Галуа. Конечные геометрии могут также быть определены чисто аксиоматически. Самые распространенные конечные геометрии — геометрии Галуа, поскольку любое конечное проективное пространство размерности три и более изоморфно проективному пространству над конечным полем. Однако в размерности два имеются аффинные и проективные плоскости, которые не изоморфны геометриям Галуа, а именно, недезарговы плоскости. Похожие результаты имеют место для других видов конечных геометрий.
См. также
Примечания
- ↑ Bannai, Ito, 1984.
- ↑ Godsil, 1993.
- ↑ Bailey, 2004, с. 387.
- ↑ Zieschang, 2005b.
- ↑ Zieschang, 2005a.
- ↑ Brouwer, Haemers, 2010, с. 116.
- ↑ Godsil, Royle, 2001, с. 218.
- ↑ Neel, Neudauer, 2009, с. 26–41.
- ↑ Kashyap, Soljanin, Vontobel, 2009.
Литература
- Bailey, Rosemary A. (2004), Association Schemes: Designed Experiments, Algebra and Combinatorics, Cambridge University Press, ISBN 978-0-521-82446-0, <http://www.maths.qmul.ac.uk/~rab/Asbook> .
- Andries E Brouwer, Willem H Haemers. Spectra of Graphs. — New York, Dordrecht, Heidelberg, London: Springer-Verlag, 2010. — (Universitext). — ISBN 9781461419389. — doi:10.1007/9781461419396. Архивная копия от 16 марта 2012 на Wayback Machine
- David L. Neel, Nancy Ann Neudauer. Matroids you have known // Mathematics Magazine. — 2009. — Т. 82, вып. 1. — С. 26—41. — doi:10.4169/193009809×469020.
- Navin Kashyap, Emina Soljanin, Pascal Vontobel. Applications of Matroid Theory and Combinatorial Optimization to Information and Coding Theory. — 2009.
- Eiichi Bannai, Tatsuro Ito. Algebraic combinatorics I: Association schemes. — Menlo Park, CA: The Benjamin/Cummings Publishing Co., Inc., 1984. — С. xxiv+425. — ISBN 0-8053-0490-8.
- New Perspectives in Algebraic Combinatorics / L. J. Billera, A. Björner, C. Greene, R. Simion, R. P. Stanley. — MSRI Publications. — Cambridge University Press, 1999. — Т. 38.
- Chris Godsil, Gordon Royle. Algebraic Graph Theory. — New York: Springer-Verlag, 2001. — Т. 207. — (Graduate Texts in Mathematics). — ISBN 0-387-95220-9. — ISBN 0-387-95241-1.
- C. D. Godsil. Algebraic Combinatorics. — New York: Chapman and Hall, 1993. — ISBN 0-412-04131-6.
- Takayuki Hibi. Algebraic combinatorics on convex polytopes. — Glebe, Australia: Carslaw Publications, 1992.
- Melvin Hochster. Ring theory, II (Proc. Second Conf., Univ. Oklahoma, Norman, Okla., 1975). — New York: Dekker, 1977. — Т. 26. — С. 171—223. — (Lecture Notes in Pure and Appl. Math.).
- Ezra Miller, Bernd Sturmfels. Combinatorial commutative algebra. — New York, NY: Springer-Verlag, 2005. — Т. 227. — (Graduate Texts in Mathematics). — ISBN 0-387-22356-8.
- Richard Stanley. Combinatorics and commutative algebra. — 2nd. — Boston, MA: Birkhäuser, 1996. — Т. 41. — (Progress in Mathematics). — ISBN 0-8176-3836-9.
- Bernd Sturmfels. Gröbner bases and convex polytopes. — Providence, RI: American Mathematical Society, 1996. — Т. 8. — (University Lecture Series). — ISBN 0-8218-0487-1.
- Doron Zeilberger. The Princeton Companion to Mathematics[en]. — Princeton University Press, 2008. — ISBN 978-0-691-11880-2.
- Zieschang, Paul-Hermann (2005a), Association Schemes: Designed Experiments, Algebra and Combinatorics by Rosemary A. Bailey, Review, Bulletin of the American Mathematical Society Т. 43 (02): 249–253, doi:10.1090/S0273-0979-05-01077-3, <http://www.ams.org/bull/2006-43-02/S0273-0979-05-01077-3/S0273-0979-05-01077-3.pdf>
- Zieschang, Paul-Hermann (2005b), Theory of association schemes, Springer, с. xii+283, ISBN 3-540-26136-2
- Zieschang, Paul-Hermann (2006), The exchange condition for association schemes, Israel Journal of Mathematics Т. 151 (3): 357–380, ISSN 0021-2172, DOI 10.1007/BF02777367
 ,
если сумма всех его коэффициентов равна
4096.
,
если сумма всех его коэффициентов равна
4096.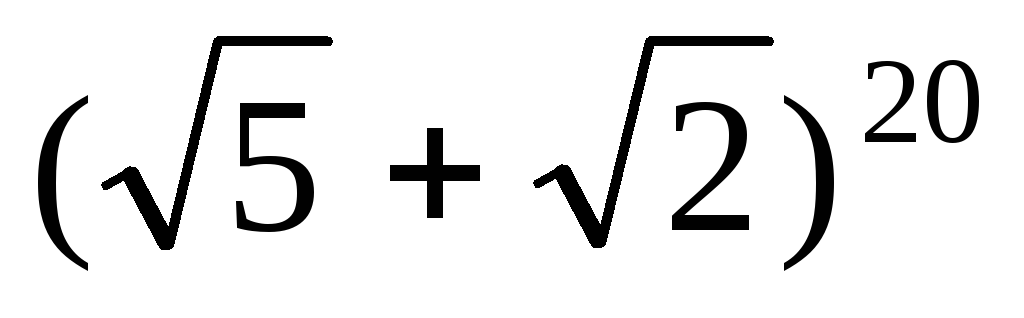 .
. в разложении
в разложении .
.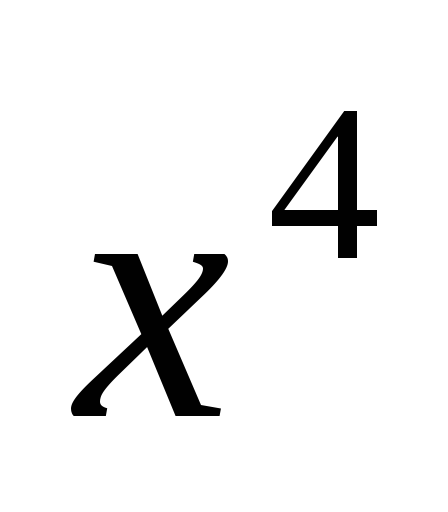 в разложении
в разложении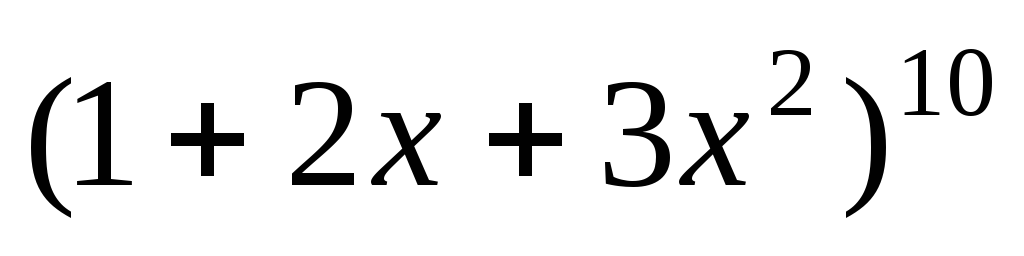 .
.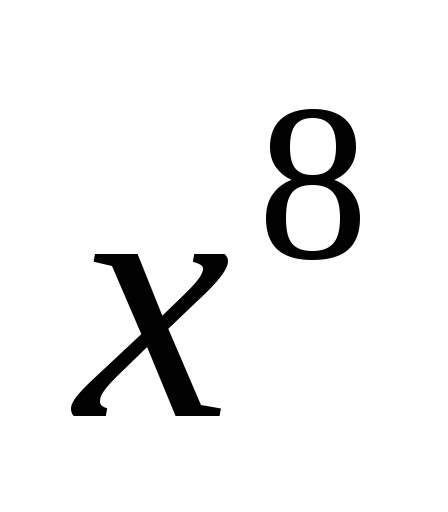 в разложении
в разложении .
.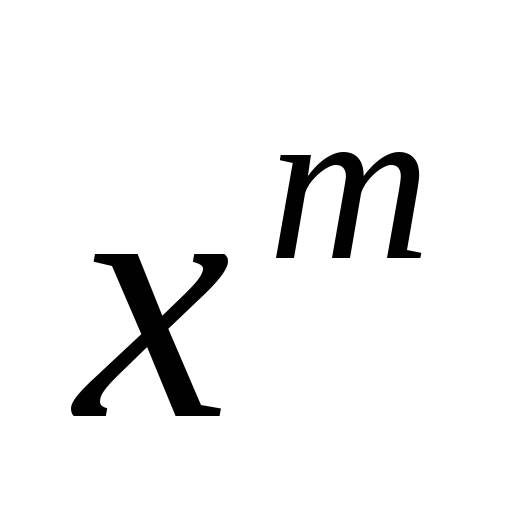 в разложении
в разложении и
и в разложении
в разложении .
. или
или будет наибольший коэффициент при
будет наибольший коэффициент при .
. .
.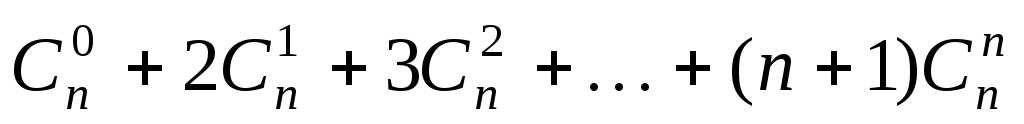 ;
; ;
; ;
;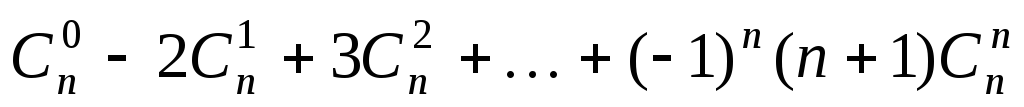 ;
; ;
; ;
; ;
;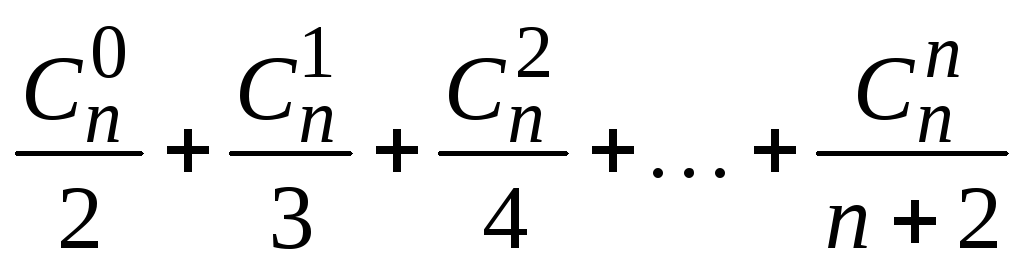 ;
; ;
; ;
;
 .
.