Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Арксинусом числа а называется число , такое, что Или, можно сказать, что это такой угол , принадлежащий отрезку , синус которого равен числу а.
Арккосинусом числа а называется число , такое, что
Арктангенсом числа а называется число , такое, что
Арккотангенсом числа а называется число , такое, что
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Помните, мы уже встречались с обратными функциями.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
При этом
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
Угол, принадлежащий отрезку , синус которого равен — это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?
Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке .
Взгляните на тригонометрический круг. Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка отвечает одно-единственное значение угла на отрезке . Это значит, что на отрезке можно задать функцию принимающую значения от до
Повторим определение еще раз:
Арксинусом числа a называется число , такое, что
Обозначение: Область определения арксинуса — отрезок Область значений — отрезок .
Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Поскольку , следовательно, х лежит в пределах от -1 до 1.
Значит, областью определения функции y = arcsin x является отрезок
Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок .
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.
Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это
Продолжаем: — это такое число из отрезка , синус которого равен . Да, это
Строим график функции
Свойства функции
1. Область определения
2. Область значений
3. , то есть эта функция является нечетной.
Ее график симметричен относительно начала координат.
4. Функция монотонно возрастает. Ее наименьшее значение, равное — , достигается при , а наибольшее значение, равное , при
5. Что общего у графиков функций и ? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции и график функции , или как графики показательной и логарифмической функций?
Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до , а затем развернули его вертикально — и мы получим график арксинуса.
То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это при и , а также показательная и логарифмическая функции.
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.
Выберем отрезок . На этом отрезке функция монотонно убывает, то есть соответствие между множествами и взаимно однозначно.
Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.
Заполним таблицу, пользуясь определением арккосинуса.
Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку , что
Значит, , поскольку ;
, так как ;
, так как ,
, так как ,
Вот график арккосинуса:
Свойства функции
1. Область определения
2. Область значений
3.
4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при , а наименьшее значение, равное нулю, принимает при
5. Функции и являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Обозначение: . Область определения арктангенса — промежуток Область значений — интервал .
Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.
Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что
Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:
— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция принимает значения от до
Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от до а областью значений — интервал
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
, значит,
, значит,
, значит,
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
Свойства функции
1.
Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
График функции :
Свойства функции
1. Область определения
2. Область значений
3. Функция — общего вида, то есть ни четная, ни нечетная.
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
Урок 6. обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №6. Обратные тригонометрические функции.
Перечень вопросов, рассматриваемых в теме
- Рассмотреть свойства арксинуса и арккосинуса;
- Рассмотреть свойства арктангенса и арккотангенса;
- Объяснять расположение промежутков монотонности;
- Определять наибольшее и наименьшее значение функции;
- Применять знания при решении задач.
Глоссарий по теме
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения и множество значений .
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения и множество значений
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Объяснение нового материала
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
Свойства | Функции y=arcsin х |
E(f) | |
D(f) | |
Чётность | Нечётная, т. |
Промежутки монотонности | Возрастающая |
к. arcsin(-x)= — arcsin xРис.1 График функции y=arcsin х
Рассмотрим свойства функции y=arcos x и построим ее график.
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ).
Свойства | Функции y=arccos х |
E(f) | |
D(f) |
|
Чётность | Ни чётная, ни нечётная |
Промежутки монотонности | Убывающая |
Рис.2 График функции y=arccos х
Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики.
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ).
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ).
Свойства | y=arctg х | y=arcctg х |
E(f) | R | R |
D(f) | ||
Чётность | Нечётная | Нечётная |
Промежутки монотонности | Возрастающая | Убывающая |
Рис.3 График функции y=arctgx
Рис.4 График функции y=arcсtgx
Примеры и разборы решения заданий тренировочного модуля:
Пример 1.
Найдите значение выражения
Обозначим , по определения арктангенса получаем х=60°, т.е. нам нужно найти
Ответ:
Пример 2.
Решите неравенство
;
;
;
;
Накладываем ограничения по свойствам арксинуса:
;
Ответ:
Что такое метод Arccos в C#?
Что такое метод arccos в c#?
Я нашел один acos, но не уверен, что он правильный.
http://msdn.microsoft.com/en-us/ библиотека / system.math.acos.aspx
Поделиться Источник redfrogsbinary 09 августа 2011 в 21:37
2 ответа
- Математика — как рассчитать формулу arccos?
может ли кто-нибудь помочь мне вычислить Arccos(X) ? с какой-то формулой ? Я пытаюсь сделать это в какой-то среде (SAP WEBI) с ограниченными математическими формулами. ( есть только cos , sin , tan.. ).
- как вычислить arccos() в bash?
Мне нужно вычислить arccos() в скрипте bash. поглазеть можно рассчитать cos(theta) и sin(theta) как вычислить arccos() в linux ?
12
Math.Acos()-это функция cos -1 в .NET, так что вы все правильно поняли.
Поделиться KeithS 09 августа 2011 в 21:41
1
Да, это тот самый.
Арккосинус :
Арккосинус-это обратная функция Косинуса. Он также записывается как arccos или cos-1. Если y = cos x, то x = arccos y.
Определение на странице, на которую вы ссылаетесь:
Возвращает угол, Косинус которого равен указанному числу.
Поделиться Guffa 09 августа 2011 в 21:43
Похожие вопросы:
Как задать системе Mathematica для преобразования ArcCosh к ArcCos
В ситуляции вроде I ArcCosh[x] что является либо ArcCos[x] или -ArcCos[x] . Как заставить ММА сделать это?
что такое виртуальный метод в c++?
что такое виртуальный метод в c++?
Что такое глобальный метод?
Что такое глобальный метод в .
net? Я говорю о тех, которые созданы методом ModuleBuilder.DefineGlobalMethod . Могут ли эти методы быть вызваны из C# или других .net языков?
Математика — как рассчитать формулу arccos?
может ли кто-нибудь помочь мне вычислить Arccos(X) ? с какой-то формулой ? Я пытаюсь сделать это в какой-то среде (SAP WEBI) с ограниченными математическими формулами. ( есть только cos , sin ,…
как вычислить arccos() в bash?
Мне нужно вычислить arccos() в скрипте bash. поглазеть можно рассчитать cos(theta) и sin(theta) как вычислить arccos() в linux ?
Что такое прозрачный класс или прозрачный метод в C#?`
У меня есть код C#, и когда я запускаю против него FXCop, он выдает странную ошибку, которую я пытался понять, но не смог. Ошибка говорит Прозрачные Методы Не Должны Удовлетворять Требованиям…
RuntimeWarning: недопустимое значение, обнаруженное в arccos
Я новичок в использовании Python, но довольно хорошо с ним справляюсь. Я продолжаю получать ошибку, которую вы видите ниже, и не уверен, в чем именно заключается проблема, поскольку я считаю, что…
dask/ python недопустимое значение, встречающееся в arccos
Я совсем новичок в python и пытался использовать dask, но я продолжаю получать RuntimeWarning и на самом деле не понимаю, почему. Некоторое понимание было бы неплохо. код: x2 =…
Как использовать maple для упрощения тригонометрических выражений, включающих arccos и cos?
Мне трудно убедить Мэйпл упростить сложное тригонометрическое выражение. Похоже, узкое место заключается в том, что я не знаю, как сказать maple, что это OK для упрощения таких выражений, как:…
arccos в c (без использования acos)
У меня есть вопросы, которые требуют, чтобы я использовал Косинус и fabs для написания кодов, которые вычисляют arccos значения. Дело в том, что я уже некоторое время смотрю в интернете, и все.
..
Arc это в математике
Задача, обратная нахождению значения синуса, косинуса, тангенса и котангенса данного угла (числа), подразумевает нахождение угла (числа) по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.
В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение упомянем про аркфункции и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.
Навигация по странице.
Определения, обозначения, примеры
Арксинус, арккосинус, арктангенс и арккотангенс можно определить как угол и как число. Это связано с тем, что мы определили синус, косинус, тангенс и котангенс как угла, так и числа (смотрите синус, косинус, тангенс и котангенс в тригонометрии). Остановимся на обоих подходах к определению арксинуса, арккосинуса, арктангенса и арккотангенса.
Арксинус, арккосинус, арктангенс и арккотангенс как угол
Пусть про угол альфа α известно лишь то, что его синус равен числу 1/2 , то есть, sinα=1/2 . Последнее равенство определяет угол α неоднозначно, так как ему удовлетворяет бесконечное множество углов α=(−1) k ·30°+180°·k ( α=(−1) k ·π/6+π·k ), где k∈Z . Однако, если потребовать, чтобы величина угла α в градусах принадлежала отрезку [−90, 90] (в радианах – отрезку [−π/2, π/2] ), то равенство sinα=1/2 будет определять угол альфа однозначно. При этом условии равенству удовлетворяет единственный угол в 30 градусов ( π/6 радианов).
Вообще, равенство sinα=a (не путайте a и альфа: a и α ) при любом числе a∈[−1, 1] и условии −90°≤α≤90° ( −π/2≤α≤π/2 ) определяет единственный угол α . Этот угол называют арксинусом числа a .
Арксинус числа a∈[−1, 1] – это угол −90°≤α≤90° ( −π/2≤α≤π/2 ), синус которого равен a .
Аналогично определяются арккосинус, арктангенс и арккотангенс.
Арккосинус числа a∈[−1, 1] – это угол 0°≤α≤180° ( 0≤α≤π ), косинус которого равен a .
Арктангенс числа a∈(−∞, +∞) – это угол −90° ( −π/2 ), тангенс которого равен a .
Арккотангенс числа a∈(−∞, +∞) – это угол 0° ( 0 ), котангенс которого равен a .
Для записи арксинуса, арккосинуса, арктангенса и арккотангенса приняты следующие обозначения: arcsin , arccos , arctg и arcctg . То есть, арксинус числа a можно записать как arcsin a , арккосинус, арктангенс и арккотангенс числа a запишутся соответственно как arccos a , arctg a и arcctg a .
Также можно встретить обозначения arctan и arccot , они являются другой формой обозначения арктангенса и арккотангенса, которая принята в англоязычной литературе. Мы же арктангенс и арккотангенс будем обозначать как arctg и arcctg .
В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа можно записать более формально:
arcsin a , a∈[−1, 1] , есть такой угол α , что −90°≤α≤90° ( −π/2≤α≤π/2 ) и sinα=a ;
arccos a , a∈[−1, 1] , есть такой угол α , что 0°≤α≤180° ( 0≤α≤π ) и cosα=a ;
arctg a , a∈(−∞, +∞) , есть такой угол α , что −90° ( −π/2 ) и tgα=a ;
arcctg a , a∈(−∞, +∞) , есть такой угол α , что 0° ( 0 ) и ctgα=a .
Подчеркнем, что арксинус и арккосинус числа определен для чисел, принадлежащих отрезку [−1, 1] , для остальных чисел арксинус и арккосинус не определен. Например, не имеет смысла запись arcsin2 . Аналогично не определен арксинус пяти, арксинус минус корня из трех, арккосинус семи целых двух третьих и арккосинус минус пи, так как числа 2 , 5 , , −π выходят за пределы числового отрезка от −1 до 1 . В свою очередь записи arctg a и arcctg a имеют смысл для любого действительного числа a , например, имеют смысл записи arctg0 , arctg(−500,2) , arcctg(6·π+1) и т.п.
Теперь можно привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Начнем с примеров арксинуса. Определение арксинуса позволяет утверждать, что угол π/3 является арксинусом числа , то есть, (здесь и α=π/3 ). Действительно, число принадлежит отрезку [−1, 1] , угол π/3 лежит в пределах от −π/2 до π/2 и . Приведем еще несколько примеров арксинуса числа: arcsin(−1)=−90° , arcsin(0,5)=π/6 , .
А вот π/10 не является арксинусом 1/2 , так как sin(π/10)≠1/2 . Еще пример: несмотря на то, что синус 270 градусов равен −1 , угол 270 градусов не является арксинусом минус единицы, так как 270 градусов не является углом в пределах от −90 до 90 градусов. Более того, угол 270 градусов вообще не может быть арксинусом какого-либо числа, так как арксинус числа должен лежать в пределах от −90 до 90 градусов.
Для полноты картины приведем примеры арккосинуса, арктангенса и арккотангенса числа. Например, угол 0 радианов является арккосинусом единицы, то есть, arccos1=0 (так как выполняются все условия из определения арккосинуса: число 1 принадлежит отрезку от −1 до 1 , угол нуль радианов лежит в пределах от нуля до пи включительно и cos0=1 ). Аналогично, угол π/2 есть арккосинус нуля: arccos0=π/2 . По определению арктангенса числа arctg(−1)=−π/4 или arctg(−1)=−45° . Арктангенс корня из трех равен 60 градусам ( π/3 рад). А из определения арккотангенса можно заключить, что arcctg0=π/2 , так как угол π/2 лежит в рамках от 0 до пи и ctg(π/2)=0 .
Подобный подход к определению арксинуса, арккосинуса, арктангенса и арккотангенса описан в учебнике Кочеткова [1, с. 260-278] .
Арксинус, арккосинус, арктангенс и арккотангенс как число
Когда мы имеем дело с синусом, косинусом, тангенсом и котангенсом угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять как угол. Если же мы начинаем говорить про синус, косинус, тангенс и котангенс числа, а не угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять уже как число.
Арксинусом числа a∈[−1, 1] называется такое число t∈[−π/2, π/2] , синус которого равен a .
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов. Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс.
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.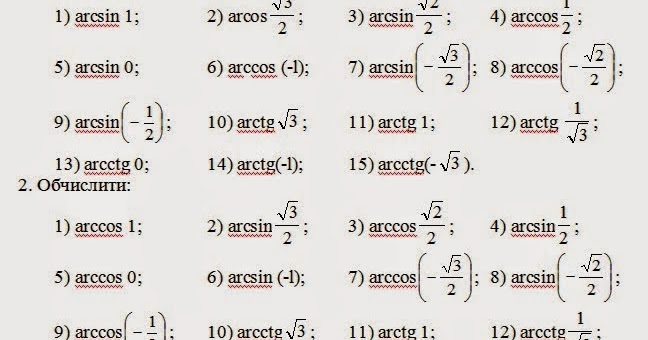
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8. Скока-скока!? 1,8!? Косинус не бывает больше единицы.
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов. Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус. Что такое арктангенс, арккотангенс. То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да. ) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого. Ну и так далее. Если сведущий человек знает ещё и таблицу синусов. Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё. Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8). Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Те, кто освоил темы «Тригонометрический круг», и «Отсчёт углов на тригонометрическом круге» — люди грамотные. И, возможно, уже приготовили мне убойный вопрос.) По определению, скажем, arcsin 0,5 — это угол, синус которого равен 0,5.
Т.е 30°. Но.
Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:
И так до бесконечности. Неоднозначно получается! Получается, что arcsin0,5 это и 30°, и 150°, и 390°, и 510°, и .
Да. Именно так. Арксинус 0,5 — это действительно бесконечный набор углов. Но обозначается такой арксинус вот как: Arcsin0,5. С заглавной буквы. В школе такие арксинусы не изучают. В школе изучают арки с маленькой буквы: arcsin, arccos, arctg, arcctg. Такие арки называются главными значениями арксинуса, арккосинуса и т.д. и имеют жёсткие ограничения по величине. Для однозначности.
С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:
arсsin (любой) — это угол, который располагается в интервале:
arсcos (любой) — это угол, который располагается в интервале:
arсtg (любой) — это угол, который располагается в интервале:
arсctg (любой) — это угол, который располагается в интервале:
Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:
Зелёным нарисованы углы, которые пробегают значения от — Пи/2 до + Пи/2. Это и есть разрешённая зона для арксинусов. И никаких дополнительных оборотов! Строго от -90° до +90°! Никакой arcsin не может быть равным, например 120°, 180° или 330°. А вот 50°, -65°, 90° или 25° — пожалуйста!
Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только 30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус, равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого диапазона.
А теперь наведите курсор мышки на рисунок, или коснитесь картинки на планшете. Вы увидите диапазон арктангенсов. Найдите 2 отличия.) Да! Конечные точки на оси ОУ стали белыми! Это означает, что они не включаются в диапазон арктангенсов. Арктангенс не может быть равным ±90°.
По той простой причине, что тангенс 90° (и -90°) не существует.
Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):
Надеюсь, зрительная память вас спасёт, если что. )
А зачем все эти арки? — слышу ещё один осторожный вопрос.)
Вопрос резонный. В математике просто так, чисто для красоты, ничего не бывает. Только по острой необходимости!) А вы попробуйте ответить на такой вопрос:
У какого угла синус равен 0,4?
Для ответа в градусах или радианах вам придётся открывать таблицы Брадиса, или включать солидный калькулятор. Искать там значение синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу. )
А через арксинус мгновенно даётся абсолютно точный ответ: угол, у которого синус равен 0,4 — это arcsin 0,4 ! Просто по смыслу арксинуса: arcsin 0,4 — это и есть угол, синус которого равен 0,4. Разумеется, это не единственный угол, синус которого равен 0,4, но через арки и все остальные записываются в три секунды. Этим мы в тригонометрических уравнениях займёмся.
Если вы осознали этот забавный факт, то легко ответите на все подобные вопросы:
У какого угла синус равен -0,7 ?
У угла arcsin (-0,7).
У какого угла косинус равен 0,03 ?
У угла arccos 0,03.
У какого угла тангенс равен 3 ?
У угла arctg 3.
У какого угла котангенс равен 0,123 ?
У угла arcctg 0,123.
Вам кажутся странными эти вопросы? Привыкайте.) Это главные вопросы любого тригонометрического уравнения. Для решения таких уравнений арки подходят — лучше некуда.
Здесь важно понимать, что arcsin (-0,7), arctg 3 и т.
п. — это просто какие-то числа, величины углов. И отличаются от привычных градусов или радианов только компактной формой записи. Например, можно записать (точно!) величину угла в виде:
А можно записать (приблизительно) тот же самый угол через градусы. Это будет:
≈ 23,57817847820183110402. °
Осознали простой и важный смысл арков? Тогда порешаем самостоятельно. Примерчики от устных до хитрых.)
Арксинус, арккосинус, арктангенс и арккотангенс — обратные тригонометрические функции. Они обладают рядом свойств, которые мы рассмотрим в этой статье. Помимо словесных и математических формулировок основных свойств арксинуса, арккосинуса, арктангенса и арккотангенса, будут приведены доказательства этих свойств.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса
Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа
- sin a r c sin a = a , a ∈ 1 ; — 1 ;
- cos a r c cos a = a , a ∈ 1 ; — 1 ;
- t g ( a r c t g a ) = a , a ∈ — ∞ ; + ∞ ;
- c t g ( a r c c t g a ) = a , a ∈ — ∞ ; + ∞ .
Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.
Рассмотрим доказательство на примере арксинуса. Согласно определению, арксинус числа — это такой угол или число, синус которого равен числу a . При этом число a лежит в пределах от — 1 до + 1 включительно. В виде формулы определение запишется так:
sin ( a r c sin a ) = a
Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.
Пример 1. Свойства обратных тригонометрических функций
sin ( a r c sin ( 0 , 3 ) = 0 , 3 cos a r c cos — 3 2 = — 3 2 t g ( a r c t g ( 8 ) ) = 8 c t g ( a r c c t g ( 15 8 9 ) ) = 15 8 9
Важно отметить, что для обратных функций синуса и косинуса имеет место ограничение для значений числа a .
Так, при a , лежащем вне пределов отрезка — 1 , 1 , арксинус и арккосинус не определены и записи a r c sin a и a r c cos a попросту не имеют смысла. Это связано с тем, что область значений синуса и косинуса — от минус единицы до плюс единицы. Например, нельзя записать cos ( a r c cos ( 9 ) ) , так как 9 больше 1 и данное выражение не имеет смысла. Делать подобные записи — ошибочно!
Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел
Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.
arcsin, arccos, arctg и arcctg противоположных чисел
- a r c sin — a = — a r c sin a , a ∈ — 1 , 1 ;
- a r c cos — a = π — a r c cos a , a ∈ — 1 , 1 ;
- a r c t g — a = — a r c t g a , a ∈ — ∞ , + ∞ ;
- a r c c t g — a = π — a r c c t g a , a ∈ — ∞ , + ∞ .
Докажем записанное. Начнем, как всегда, с доказательства для арксинусов. При — 1 ≤ a ≤ 1 имеет место равенство a r c sin — a = — a r c sin a . Согласно дефиниции, a r c sin ( — a ) — это угол (число) в пределах от — π 2 до π 2 , синус которого равен — a . Для доказательства справедливости первого равенства необходимо доказать, что — a r c sin a лежит в тех же пределах от — π 2 до π 2 , что и a r c sin ( — a ) . Также необходимо обосновать, что sin ( — a r c sin a ) = — a .
Для арксинуса, по определению, справедливо двойное неравенство — π 2 ≤ a r c sin a ≤ π 2 . Умножим каждую часть неравенства на — 1 и получим эквивалентное неравенство π 2 ≥ — a r c sin a ≥ — π 2 . Переписав его, получим — π 2 ≤ — a r c sin a ≤ π 2 .
Переходим ко второй части доказательства. Теперь осталось показать, что sin ( — a r c sin a ) = — a . Для этого воспользуемся свойством синусов противоположных углов и запишем: sin — a r c sin a = — sin a r c sin a . С учетом свойства арксинуса, рассмотренного в предыдущем пункте, закончим доказательство.
sin — a r c sin a = — sin a r c sin a = — a
Доказательство свойства арксинусов противоположных чисел завершено.
Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.
Для того, чтобы доказать, что a r c cos — a = π — a r c cos a при a ∈ — 1 , 1 необходимо во-первых показать, что число undefined.
Для арккосинуса, по определению, справедливо двойное неравенство 0 ≤ a r c cos a ≤ π . Умножив каждую часть неравенства на — 1 и поменяв знаки, получим эквивалентное неравенство 0 ≥ — a r c cos a ≥ — π . Перепишем его в другом виде. По свойствам неравенств, можно добавить к каждой части слагаемое, не меняя знаков. Добавим в каждую часть неравенства слагаемое π . Получим π ≥ π — a r c cos a ≥ 0 , или 0 ≤ π — a r c cos a ≤ π .
Теперь покажем, что cos π — arccos a = — a . Для этого воспользуемся формулами приведения, согласно которым можно записать cos π — arccos a = — cos ( a r c cos a ) . Обратившись к свойству арккосинуса, разобранному ранее (см. 1 пункт), заканчиваем доказательство.
cos π — arccos a = — cos ( a r c cos a ) = — a .
Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.
Основная польза данного свойства — возможность избавиться от операций с отрицательными числами при работе с арксинусами, арккосинусами, арктангенсами и арккотангенсами. Например, справедливы записи:
a r c sin — 1 2 = — a r c sin 1 2 a r c cos — 5 5 7 = π — arccos 5 5 7 arctg — 1 = — arctg 1 arcctg ( — 3 ) = π — arcctg 3
Сумма арксинуса и арккосинуса, арктангенса и арккотангенса
Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.
Сумма arcsin и arccos
a r c sin a + a r c cos a = π 2 , a ∈ — 1 , 1
Соответственно, для арктангенса и арккотангенса
Сумма arctg и arcctg
a r c t g a + a r c c t g a = π 2 , a ∈ — ∞ , + ∞
Приведем доказательство для арксинуса и арккосинуса. Формулу для суммы arcsin и arccos можно переписать в виде a r c sin a = π 2 — a r c cos a .
Теперь обратимся к определению, согласно которому арксинус — это число (угол), лежащее в пределах от — π 2 до π 2 , синус которого равен a .
Запишем неравенство, вытекающее из определения арккосинуса: 0 ≤ a r c cos a ≤ π . Умножим все его части на — 1 , а затем прибавим к каждой части π 2 . Получим:
0 ≤ a r c cos a ≤ π 0 ≥ — arccos a ≥ — π π 2 ≥ π 2 — arccos a ≥ — π 2 — π 2 ≤ π 2 — arccos a ≤ π 2
Завершая доказательство, покажем, что sin π 2 — a r c cos a = a . Для этого используем формулу приведения и свойство косинуса от арккосинуса.
sin π 2 — a r c cos a = cos a r c cos a = a
Таким образом, доказано, что сумма арксинуса и арккосинуса равна π 2 . По такому же принципу проводится доказательство для суммы арктангенса и арккотангенса.
Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.
Пример 2. Сумма арксинуса и арккосинуса
Известно, что a r c sin 6 — 2 2 = π 12 . Найдем арккосинус этого числа.
a r c sin 6 — 2 2 + a r c cos 6 — 2 2 = π 2 a r c cos 6 — 2 2 = π 2 — a r c sin 6 — 2 2 a r c cos 6 — 2 2 = π 2 — π 12 = 5 π 12
Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса
Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса
- a r c sin ( sin α ) = α , — π 2 ≤ α ≤ π 2 ;
- a r c cos ( cos α ) = α , 0 ≤ α ≤ π ;
- a r c t g ( t g α ) = α , — π 2 ≤ α ≤ π 2 ;
- a r c c t g ( c t g α ) = α , 0 ≤ α ≤ π .
Данные равенства и неравенства являются прямым следствием определений арксинуса, арккосинуса, арктангенса и арккотангенса. Покажем это, доказав, что a r c sin ( sin α ) = α при — π 2 ≤ α ≤ π 2 .
Обозначим sin α через a . a — число, лежащее в интервале от — 1 до + 1 .
Тогда равенство a r c sin ( sin α ) = α можно переписать в виде a r c sin a = α . Данное равенство, при заданных условиях, аналогично определению синуса. Таким образом, мы доказали, что a r c sin ( sin α ) = α при — π 2 ≤ α ≤ π 2 .
Выражение a r c sin ( sin α ) имеет смысл не только при α , лежащем в пределах от — π 2 до π 2 . Однако, равенство a r c sin ( sin α ) = α выполняется только при соблюдении условия — π 2 ≤ α ≤ π 2 .
Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.
Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.
ACOS (функция ACOS) — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции ACOS в Microsoft Excel.
Описание
Возвращает арккосинус числа. Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».
Синтаксис
ACOS(число)
Аргументы функции ACOS описаны ниже.
Замечания
Если нужно преобразовать результат из радиан в градусы, умножьте его на 180/ПИ() или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=ACOS(-0,5) |
Арккосинус числа -0,5 в радианах, 2*ПИ/3 (2,094395) |
2,094395102 |
|
=ACOS(-0,5)*180/ПИ() |
Арккосинус -0,5 в градусах |
120 |
|
=ГРАДУСЫ(ACOS(-0,5)) |
Арккосинус -0,5 в градусах |
120 |
Урок алгебры в 11-м классе «Обратные тригонометрические функции»
Тип урока: комбинированный, состоит из 7 учебно-воспитательных моментов: организационный момент, повторение изученного, подготовка к изучению материала, изучение и закрепление нового материала, тестовая работа, итог урока.
Цели урока:
- сформировать умение применять определения аркфункций для нахождения тригонометрических функций от аркфункций;
- развивать познавательный интерес учащихся к предмету через систему нестандартных задач;
- воспитывать нестандартно, логически мыслящую
личность.
Оборудование: доска, таблицы, компьютер, мультимедийная установка, экран, учебник.
Ход урока
I. Организационный момент.
Ребята, сегодня мы проводим урок — обобщение по теме: «Обратные тригонометрические функции». Материал этого параграфа в учебнике вынесен для самостоятельного изучения, но поскольку задания с аркфункциями стали включать в ЕГЭ, я решила не только изучить новый материал на уроке, но обобщить ваши знания по данной теме.
II. Актуализация опорных знаний:
1. Значения аркфункций:
Вспомните, для чего в 10 классе были введены понятия арксинуса, арккосинуса, арктангенса? (Для решения тригонометрических уравнений).
Давайте вспомним формулы, по которым решаются простейшие тригонометрические уравнения.
Слайд1:
вопросы к классу: -формула нахождения корней уравнения соs х=а;
-дать определение арккосинуса числа а ;
Слайд 2 :(вопросы аналогичные предыдущим)
Слайд 3
Слайд 4
Заполним таблицу значений аркфункций: Слайд 5
Пользуясь ей решим следующие упражнения:
№655(из учебника)
2) arcsin(1/v2)-4 arcsin1=
4) arccos(-1)- arcsin(-1)=
6)4 arctg(-1)+3 arctg(v3)=
Из ЕГЭ:
1) arcsin(sin /3)+ arcsin (-v3/2)=
3)10cos(arctg(v3))=
Проверим получившиеся ответы: Слайд 6
2.Вспомним формулы, связывающие аркфункции с тригонометрическими функциями:
Слайд 7
С помощью них вычислим устно:
sin(arcsin(-1/5))=
sin(+ arcsin 3/4)=
(из ЕГЭ) 5 sin(+ arcsin (-3/5)=
cos(arccos(-2/3))=
sin(/2+ arccos 1/3)=
tg(arctg(-3))=
сtg(/2+ arctg 6)=
3.
Нахождение значения тригонометрической
функции от аркфункции.
1. Сильный ученик:
sin(arccos v3/4)=
2.(Из ЕГЭ) — сильный ученик
5v2 sin(/2- arctg(-1/7))=
б) Ребята, существует другой способ решения подобных заданий. Я буду рада, если кто-нибудь из вас его запомнит и будет его применять.
Посмотрите, во всех ранее решённых примерах — угол, лежащий в первой четверти, а это значит, что — угол острый. Вспомните, что называется синусом(косинусом, тангенсом и котангенсом) острого угла прямоугольного треугольника?
Решим следующий пример так:2v13 cos (arctg 2/3)=
tg 2/3-это значит, что отношение противолежащего катета к прилежащему равно 2:3
-А как найти гипотенузу?
-Гипотенуза по теореме Пифагора равна:
v4+9=v13
-Тогда cos =3/v13, а 2v13 cos (arctg 2/3)=
2v133/v13=6
в) Решим вторым способом следующие примеры:
1) tg(arccos (-1/3))=
2) 3v5 tg(arcsin(2/7)=
3) по вариантам:
а) сtg(arccos (2/5))=
б) v15 tg(arcsin(1/4))
4) Средний ученик:
sin(2 arctg 5)=
III. Изучение нового материала:
В материалах для подготовки к ЕГЭ есть задания, в которых необходимо знать свойства обратных тригонометрических функций. Обратные тригонометрические функции это математические функции, являющиеся обратными к тригонометрическим функциям. Название обратных тригонометрических функций образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (в переводе с латинского — дуга).
Пусть дана функция у=sin х. На всей области определения она являются кусочно-монотонной, и, значит, обратное соответствие у=arcsin х функцией не является.
Поэтому мы рассмотрим отрезок, на котором она
возрастает и принимает все свои значения на [-|2;|2].
Так как для функции у=sin х на интервале
[-|2;|2] каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция у=arcsin х, график которой симметричен графику у=sin х на отрезке [-1;1] относительно прямой у=х.
Пусть дана функция у=cos х. На всей области определения она являются кусочно-монотонной, и, значит, обратное соответствие у=arccos х функцией не является.
Поэтому мы рассмотрим отрезок, на котором она убывает и принимает все значения на [0;?]. Так как для функции у=cos х на интервале [0;?] каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция у=arccos х, график которой симметричен графику у=cos х на отрезке [-1;1] относительно прямой у=х.
2.Выполняем задания:
1. Найти число целых значений функции у= 12arccos х. (Объясняю сама)
0<arccos х<, тогда 0<12arccos х<12
12=123,14=37,8, значит, целых значений будет 38.
Ответ:38
2. Найти число целых значений функции у=5 arctg х. — (сильный ученик).
3. Самостоятельно:
у=1,7 arсctg х.
4. Найти наибольшее целое число, входящее в область значений функции у= 6 arcсtg(|sin х|).
5. Найти разность между наибольшим и наименьшим значениями функции:
у=24/ arcsin(sin хcos х)
IV. Дом.задание:
Вычислите:
- sin(2 arcsin 3/5)
- sin(arccos 1/3+arccos 2/3)
- sin( arccos 5/13)
2*.Постройте графики функций:
а) у=arccos|х|;
б) у=arccos х +arcsin х;
в) |у|=arctg х.
3.* Найдите разность между наибольшим и наименьшим значениями функции:
у=arccos (sin х cos х)
4*. Найдите наименьшее целое число, входящее в область значений функции:
у=40arcctg(cos х).
V. Рефлексия. Оценки учащихся за урок.
Приложение 1.
arccos что это
Вы искали arccos что это? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и arccos это что, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «arccos что это».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как arccos что это,arccos это что,арккосинус четная или нечетная функция,арксинус график функции,арксинус область определения,арксинус область определения функции,график cos arccos x,график функции арксинус,область определения арксинус,область определения арксинуса,функция арккосинус четная или нечетная,функция арксинус ее свойства и график. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и arccos что это. Просто введите задачу в окошко и нажмите
«решить» здесь (например, арккосинус четная или нечетная функция).
Где можно решить любую задачу по математике, а так же arccos что это Онлайн?
Решить задачу arccos что это вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Тригонометрическая функция arccos () — обратный косинус — определение математического слова
Тригонометрическая функция arccos () — обратный косинус — определение математического слова — Math Open Reference Функция arccos является обратной функцией косинуса.
Возвращает угол, косинус которого является заданным числом.
Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке.Эти обратные функции имеют то же имя, но с дугой впереди. (На некоторых калькуляторах кнопка arccos может быть обозначена как acos, а иногда и cos -1 .) Итак, косинус, обратный cos, равен arccos и т. Д. Когда мы видим «arccos x», мы понимаем его как «угол, косинус которого равен x».
| cos30 = 0,866 | Означает: косинус 30 градусов равен 0,866 |
| arccos 0,866 = 30 | означает: угол, косинус которого равен 0,866, равен 30 градусам. |
См. Также Обратные функции — тригонометрия
Пример — использование arccos для нахождения угла
На рисунке выше нажмите «Сброс».
Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что поэтому нам нужно знать угол, косинус которого равен 0,866, или формально:
С помощью калькулятора находим arccos 0.866 равным 30 °.
Большие и отрицательные углы
Напомним, что мы можем применить триггерные функции на любой угол, включая большие и отрицательные углы.Но когда мы Рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, которые имеют один и тот же косинус. Например, 45 ° и 360 + 45 ° будут иметь одинаковый косинус. Подробнее об этом см. Обратные тригонометрические функции.
Чтобы решить эту проблему, диапазон обратных триггерных функций ограничены таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Диапазон и область действия arccos
Напомним, что область определения функции — это набор допустимых входных данных для нее.Диапазон — это набор возможных выходов.
Для y = arccos x:
По соглашению диапазон arccos ограничен от 0 до + 180 °. Итак, если вы используете калькулятор для решения, скажем, arccos 0,55, из бесконечного числа возможностей он вернет 56,63 °, тот, который находится в диапазоне функции.
Что попробовать
- На рисунке выше нажмите «Сброс» и «Скрыть детали».
- Отрегулируйте треугольник до нового размера
- Используя функцию arccos, вычислите значение угла C из длин сторон
- Нажмите «Показать подробности», чтобы проверить ответ.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Arccos. Поиск обратного косинуса
Добро пожаловать в калькулятор arccos, также известный как калькулятор обратного косинуса.
Благодаря нашему инструменту вы можете быстро найти arccos — что, как ни удивительно, является основным применением этого калькулятора.Однако для тех из вас, кто хочет узнать больше, мы подготовили короткую статью, объясняющую , что такое обратный косинус , сопровождаемую таблицей и графиком обратного косинуса . Кроме того, если вы немного неохотно или запутались, перейдите к разделу о приложениях arccos , чтобы узнать, что общего у обратного косинуса с физикой, химией или даже с эргономикой строительства и работы!
Что является обратным косинусу (arccos)?
Arccos — это функция, обратная тригонометрической функции, а именно обратная функция косинуса.Однако, поскольку тригонометрические функции являются периодическими, в строгом смысле, они не могут быть инвертированы . Мы можем решить эту проблему, выбрав интервал, в котором основная функция является монотонной. Вы можете выбрать много разных диапазонов, но для косинуса обычно выбирается [0, π] . Этот диапазон называется набором основных значений .
| Аббревиатура | Определение | Домен arccos x для реального результата | Диапазон обычных основных значений |
|---|---|---|---|
| arccos (x) cos -1 x, acos | х = соз (у) | -1 ≤ х ≤ 1 | 0 ≤ y ≤ π 0 ° ≤ y ≤ 180 ° |
Arccos (x) — наиболее часто используемое обозначение, поскольку cos -1 x может вводить в заблуждение — помните, что обратный косинус — это не то же самое, что обратная величина функции (другими словами, возведение в степень — 1):
cos -1 x ≠ 1 / cos (x)
График обратного косинуса
Функция f имеет обратную функцию тогда и только тогда, когда f является взаимно однозначной функцией.
Вся функция косинуса не является взаимно однозначной, поскольку
cos (x) = cos (x + 2πn) , для каждого целого числа n
Что же тогда делать?
Как указано в предыдущем абзаце, нам нужно ограничить область определения базовой периодической косинусной функции. Таким образом, поскольку косинус всегда находится в диапазоне [-1,1], и мы выбираем область, [0, π], свойства функции обратного косинуса будут обратными:
Область обратного косинуса x для реального результата: [-1,1]
Диапазон обратного косинуса обычного главного значения: [0, π]
В таблице ниже вы найдете график обратного косинуса, а также некоторые часто используемые значения arccos:
| х | arccos (x) | График | |
|---|---|---|---|
| ° | рад | ||
| -1 | 180 ° | π | |
| -√3 / 2 | 150 ° | 5π / 6 | |
| -√2 / 2 | 135 ° | 3π / 4 | |
| -1/2 | 120 ° | 2π / 3 | |
| 0 | 90 ° | π / 2 | |
| 1/2 | 60 ° | π / 3 | |
| √2 / 2 | 45 ° | π / 4 | |
| √3 / 2 | 30 ° | π / 6 | |
| 1 | 0 ° | 0 | |
Хотите знать, откуда взялся этот график обратного косинуса? Он просто создается путем отражения графика cos x через линию y = x (не забывайте о наших доменных ограничениях!):
Обратный косинус — какое мне дело? Некоторые малоизвестные приложения arccos
Вы можете подумать, что arccos — еще один бесполезный термин из тригонометрии, но мы хотим убедить вас, что это не так! Функция обратного косинуса действительно полезна для решения многих научных и реальных задач (круто, не правда ли?):
I Наука
Математика:
- 📐 Решаем треугольник по закону косинусов. Если вы знаете три стороны треугольника и хотите найти любой из углов треугольника, вам нужно использовать arccos.
Если вы знаете три стороны треугольника и хотите найти любой из углов треугольника, вам нужно использовать arccos.Физика:
Химия:
- 🧪 Arccos полезен для оценки оптимальных валентных углов многоатомных молекул, таких как, например, H 2 O или CH 4
II Примеры из реальной жизни
- 🏠 Расчет угла наклона крыши или угла наклона лестницы (хотя, в зависимости от того, какие размеры указаны, могут также пригодиться калькуляторы обратного синуса или тангенса)
- ♿ Проектирование пандуса для инвалидов или колясок.Обратный косинус будет чрезвычайно полезен, если вы знаете длину пандуса и доступное расстояние по горизонтали.
- 🖥️ Даже выбор эргономичного положения на работе ! Если вы хотите правильно настроить рабочее место, вам необходимо знать оптимальную высоту стола или высоту стоячего стола, но, что касается расположения монитора, с помощью этого калькулятора arccos гораздо проще определить угол наклона или угол обзора.
Теперь вы уверены? Не ждите больше, воспользуйтесь нашим калькулятором обратного косинуса, чтобы решить (почти все) ваши проблемы!
Arccos
Arccosine, записанный как arccos или cos-1 (не путать с), является функцией обратного косинуса.Косинус имеет обратное значение только в ограниченной области 0≤x≤π. На рисунке ниже часть графика, выделенная красным, показывает часть графика cos (x), которая имеет инверсию.
Область должна быть ограничена, потому что для того, чтобы функция имела инверсию, функция должна быть взаимно однозначной, что означает, что ни одна горизонтальная линия не может пересекать график функции более одного раза. Поскольку косинус является периодической функцией, без ограничения области определения, горизонтальная линия будет периодически пересекать функцию бесконечно много раз.
Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, точка (b, a) находится на графике ее обратной функции.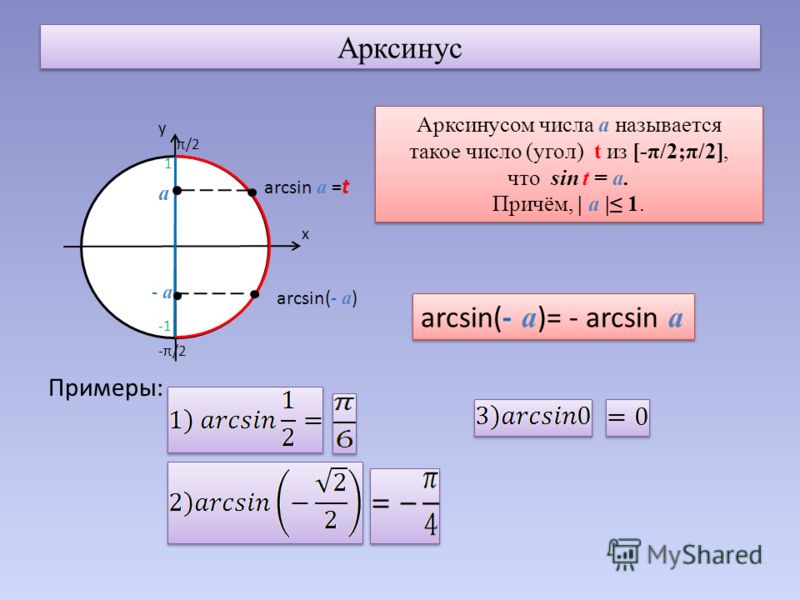
Это фактически означает, что график обратной функции является отражением графика функции через линию y = x.
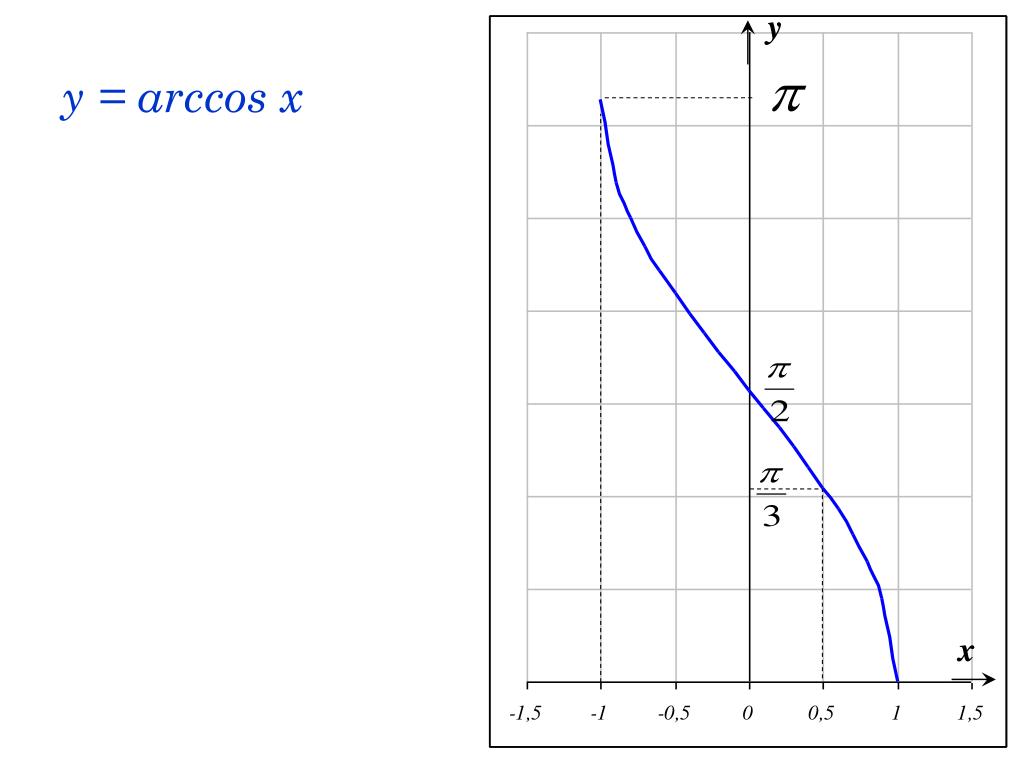
График y = arccos (x) показан ниже.
Как видно из рисунка, y = arccos (x) является отражением cos (x) в ограниченной области 0≤x≤π через линию y = x.Область arccos (x), -1≤x≤1, является диапазоном cos (x), а ее диапазон, 0≤x≤π, является областью cos (x).
Калькулятор Arccos
Ниже приведен калькулятор, позволяющий определить значение arccos числа от -1 до 1 или значение косинуса угла.
Использование специальных углов для поиска arccos
Хотя мы можем найти значение арккозинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 ° и их кратные и радианные эквиваленты), значения косинуса и арккосинуса которых, возможно, стоит запомнить.Ниже приведена таблица, показывающая эти углы (θ) в градусах и их соответствующие значения косинуса, cos (θ).
Один из методов, который может помочь запомнить эти значения, — это выразить все значения cos (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° и до 90 °, cos (0 °) = 1 =. Последующие значения cos (30 °), cos (45 °), cos (60 °) и cos (90 °) следуют шаблону, так что при использовании значения cos (0 °) в качестве эталона для нахождения значений косинуса для последующих углов, мы просто уменьшаем число под знаком корня в числителе на 1, как показано ниже:
| θ | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
| cos (θ) | 0 |
С 90 ° до 180 ° вместо этого мы увеличиваем число под корнем на 1, но также должны учитывать квадрант, в котором находится угол.Косинус отрицателен во втором и третьем квадрантах, поэтому значения будут равными, но отрицательными.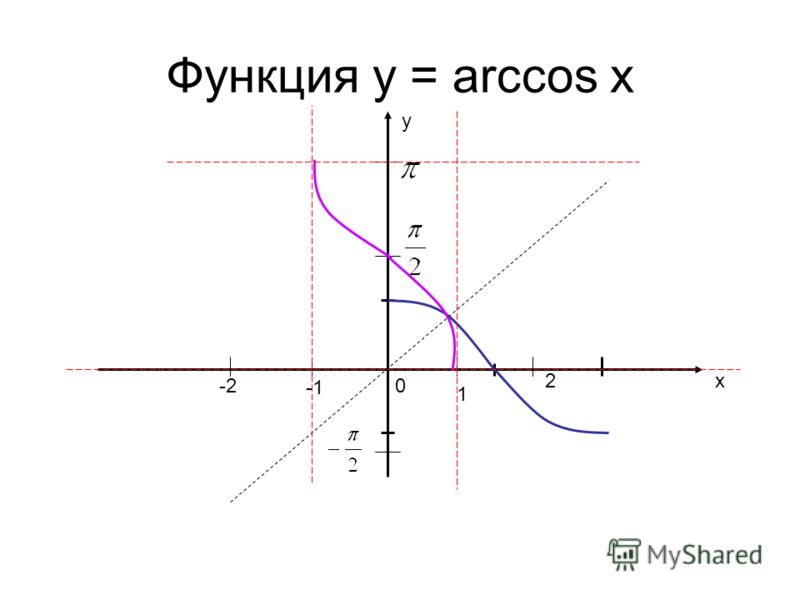
В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений.
После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознать и определить значения косинуса или арккосинуса для специальных углов.
Обратные свойства
Как правило, функции и обратные им функции демонстрируют взаимосвязь
f (f -1 (x)) = x и f -1 (f (x)) = x
при условии, что x находится в области определения функции.То же самое верно для cos (x) и arccos (x) в их соответствующих ограниченных областях:
cos (arccos (x)) = x для всех x в [-1, 1]
и
arccos (cos (x)) = x для всех x в [0, π]
Эти свойства позволяют нам оценивать состав тригонометрических функций.
Состав арккосинуса и косинуса
Если x находится в пределах домена, вычислить композицию арккозинуса и косинуса относительно просто.
Примеры:
1.
2.
Если x не находится в пределах домена, нам нужно определить опорный угол, а также соответствующий квадрант. Учитывая arccos (cos ()), мы не можем оценить это, как мы делали выше, потому что x не находится в пределах [0, π], поэтому решение не может быть. Чтобы оценить это, нам нужно сначала определить cos (), прежде чем использовать arccos:
3.
В приведенном выше примере опорный угол равен, и cos () равен, но поскольку он лежит в квадранте III, его косинус отрицателен, и единственный угол, косинус которого равен, который находится в пределах области arccos (x), равен.
Состав других тригонометрических функций
Мы также можем составлять композиции, используя все другие тригонометрические функции: синус, тангенс, косеканс, секанс и котангенс.
Пример:
Найдите грех (arccos ()).
Так как это не одно из соотношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции.
Учитывая arccos () = θ, мы можем найти, что cos (θ) =. Правый треугольник ниже показывает θ и отношение его смежной стороны к гипотенузе треугольника.
Чтобы найти синус, нам нужно найти противоположную сторону, так как sin (θ) =. Пусть a будет длиной противоположной стороны. Используя теорему Пифагора,
а 2 + 12 2 = 13 2
а 2 + 144 = 169
а 2 = 25
а = 5
и
грех (arccos ()) = грех (θ) =
Тот же процесс можно использовать с выражением переменной.
Пример:
Найдите загар (arccos (4x)).
Учитывая arccos (4x) = θ, мы можем найти, что cos (θ) = и построить следующий прямоугольный треугольник:
Чтобы найти касательную, нам нужно найти противоположную сторону, так как tan (θ) =. Пусть b — длина противоположной стороны. Используя теорему Пифагора,
(4x) 2 + b 2 = 1 2
16x 2 + b 2 = 1
b 2 = 1 — 16x 2
б =
и
tan (arccos (4x)) = tan (θ) =, где — Arccosine также можно использовать для решения тригонометрических уравнений, включающих функцию косинуса. Пример: Решите следующие тригонометрические уравнения относительно x, где 0≤x <2π. 1. 2cos (x) = 2cos (x) = cos (x) = x = arccos () Косинус отрицателен в квадрантах II и III, поэтому есть два решения: x = и x =. Это единственные два угла в пределах 0≤x <2π, значение косинуса которых равно. 2. 6cos 2 (x) + 9cos (x) — 36 = 0 6cos 2 (x) + 9sin (x) — 6 = 0 (6cos (x) — 3) (cos (x) + 2) = 0 6cos (x) — 3 = 0 или cos (x) + 2 = 0 cos (x) = или cos (x) = -2 x = arccos () или x = arccos (-2) Решение относительно x = arccos (), x = или Мы не можем найти x = arccos (-2), потому что оно не определено, поэтому x = или являются единственными решениями. обратный
Косинус функция, обратная косинусу. Основная идея : Найти cos -1 (½),
мы спрашиваем «что
угол имеет косинус, равный ½? »
ответ 60 °. В результате мы говорим cos -1 (½)
= 60 °.
В радианах это cos -1 (½).
= π / 3. Подробнее : На самом деле существует много углов, у которых косинус равен ½.
Мы действительно спрашиваем, «какой самый простой, самый основной угол, который
косинус равен ½? «Как и прежде,
ответ 60 °. Таким образом, cos -1 (½)
= 60 ° или cos -1 (½) = π / 3. Подробности : Что такое cos -1 (–½)?
Выбираем ли мы 120 °, –120 °, 240 °,
или под другим углом?
Ответ — 120 °.Обратным косинусом выбираем угол в верхней половине блока.
круг. Таким образом, cos -1 (–½)
= 120 ° или
cos -1 (–½) = 2π / 3. В
другими словами, диапазон cos -1 равен
ограничивается [0, 180 °] или [0, π]. Примечание: arccos означает «арккосинус»,
или радианная мера дуги на окружности, соответствующая
заданное значение косинуса. Техническое примечание : Поскольку ни одна из шести триггерных функций не синусоида,
косинус, тангенс, косеканс, секанс и котангенс взаимно однозначны,
их инверсии не являются функциями.Каждая триггерная функция может иметь свой
домен ограничен, однако, чтобы сделать его инверсию функцией.
Некоторые математики пишут эти ограниченные триггерные функции и их
переворачивается с заглавной буквы (например, Cos или Cos -1 ). См.
также обратный
тригонометрия, обратная
триггерные функции, интервальное обозначение Это проблема нотации и, вероятно, отсутствия определений.Мы определяем $ \ sec x $ как мультипликативную обратную к $ \ cos x $, другими словами, фиксированное $ a \ in \ mathbb {R} $, $ \ sec a $ — это такое число, что $ \ sec a \ cos а = 1 $. Теперь $ \ arccos x $ — это немного другое: это функция, обратная к $ \ cos x $. Не знаю, усвоили ли вы это, но формальное определение функции — это набор упорядоченных пар. Другими словами, поскольку функция из набора $ A $ в набор $ B $ должна быть правилом, назначающим для каждого $ a \ in A $ некоторый $ b \ in B $, мы можем просто определить функцию как набор всех упорядоченных пар элементов в $ a $ вместе со связанными элементами в $ b $.Однако нам требуется дополнительное свойство: если $ (a, b) \ in f $ и если $ (a, c) \ in f $, то $ b = c $, и это всего лишь формальный способ обозначить «вертикальную линию правило ». Поскольку второй элемент в каждой паре уникален, мы даем ему имя: если $ (a, b) \ in f $, то $ b = f (a) $. Также, чтобы указать начальный и конечный наборы, мы пишем функции от $ A $ до $ B $ как $ f: A \ to B $. Теперь, если у вас есть функция, у вас есть набор упорядоченных пар, верно? Итак, вы можете создать новый набор упорядоченных пар, поменяв местами пары.{-1} (f (x)) = x $. Итак, $ \ arccos $ определяется именно так: фиксируя один интервал, где $ \ cos $ является однозначным, вы определяете $ \ arccos $ в этом интервале с помощью того свойства, что $ \ arccos x $ — это число $ y $ такое, что $ \ cos y = x, $ другими словами, он возвращает значение угла, косинус которого равен $ x $. Они совсем разные. $ \ сек x = \ frac 1 {\ cos x} = 1 \ div \ cos x $. Это мультипликативная обратная величина, которую иногда называют мультипликативной обратной величиной . $ \ arccos x $ — это функция, так что если $ x = \ cos y $, то $ \ arccos x $ «движется назад», чтобы получить $ y $, для которого $ x $ — это $ \ cos y $.поэтому $ \ arccos x $ определяется как: Если есть какие-либо $ w $, так что $ \ cos w = x $, то один из этих $ w $ будет находиться между $ 0 $ и $ \ pi $; мы определяем $ \ arccos x $ как $ w $. Это называется инверсией с функционалом . Вот и все. КОНЕЦ. ……………………… Все еще читаете? Ну … наверное поэтому и запутались: Мультипликативный , обратный значению $ K $, — это значение $ m $, так что $ m \ times K = 1 $.{-1} (x) $ отменяет функцию . Они оба отменяют и возвращают вас туда, откуда вы начали, но один отменяет умножение. Они другие отменяют функцию.) (Не знаю. Может, мне не стоило упоминать об этом, и, может быть, это еще больше сбивает с толку. Забудьте, что я сказал что-нибудь.) Функция arccos позволяет вычислять арккосинус числа.
Функция арккосинуса — это функция, обратная функции косинуса. Функция arccosine является обратной функцией
функция косинуса,
Он вычисляет арккосинус числа онлайн . Число, к которому вы хотите применить функцию arccosine fonction, должно принадлежать диапазону [-1,1]. Использование арккосинуса для решения тригонометрических уравнений
математических слов: обратный косинус
cos -1
Cos -1
arccos
Arccos 
Однако большинство математиков не следуют этой практике. Этот
веб-сайт не делает различий между заглавными и не заглавными буквами
триггерные функции. функций — В чем разница между arccos (x) и sec (x)
{- 1} $, и это обычно происходит со всеми тригонометрическими функциями. .Поэтому, чтобы избежать путаницы, я рекомендую писать $ \ arccos $, $ \ arcsin $ и так далее для обратных функций. тригонометрия — В чем разница между arccos (x) и sec (x)?
— arccos (1) — Solumaths
Описание:
Описание:
