Уравнение и его корни: определения, примеры
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Определение 1Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t, r, m др., но чаще всего используются x, y, z. Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x=5, y=6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x+7=38, z−4=2, 8·t=4, 6:x=3.
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7·(x−1) =19, x+6·(x+6·(x−8))=3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x+2+4·x−2−x=10. Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x·(8+1)−7=8, 3−3=z+3 или 8·x−9=2·(x+17).
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Определение 2Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x+3=6·x+7 – это уравнение с переменной x, а 3·y−1+y=0 – уравнение с переменной y.
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно ур
zaochnik.com
Примеры решения показательных уравнений
Решение показательных уравнений различными способами
методы решения
образцы решения
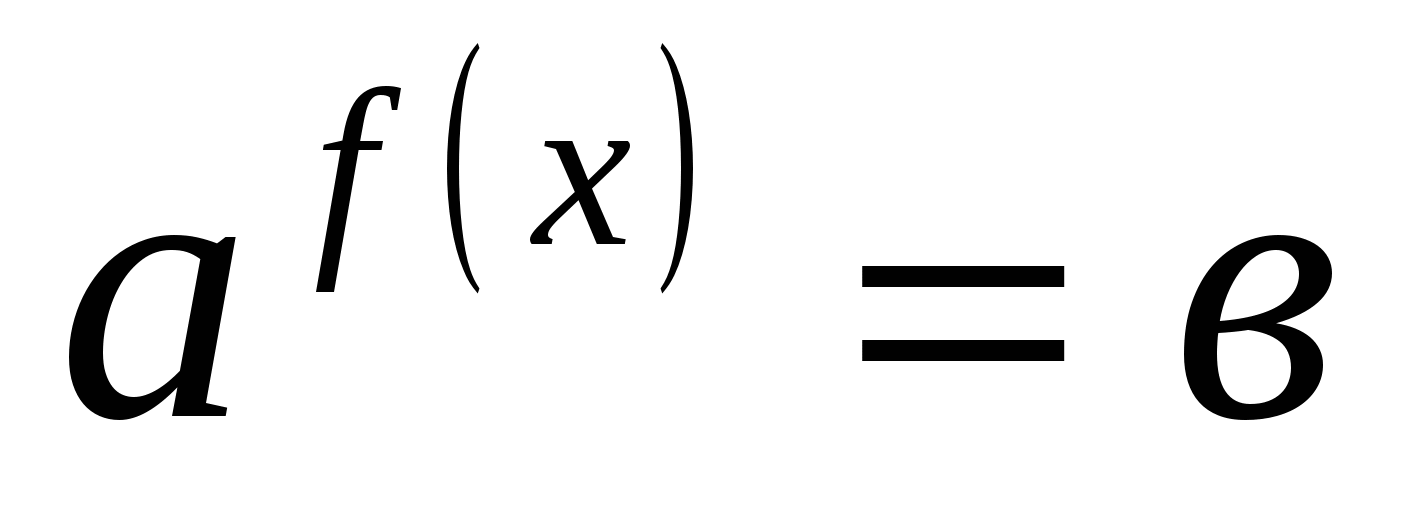
1) в обеих частях уравнения привести степени к одному основанию
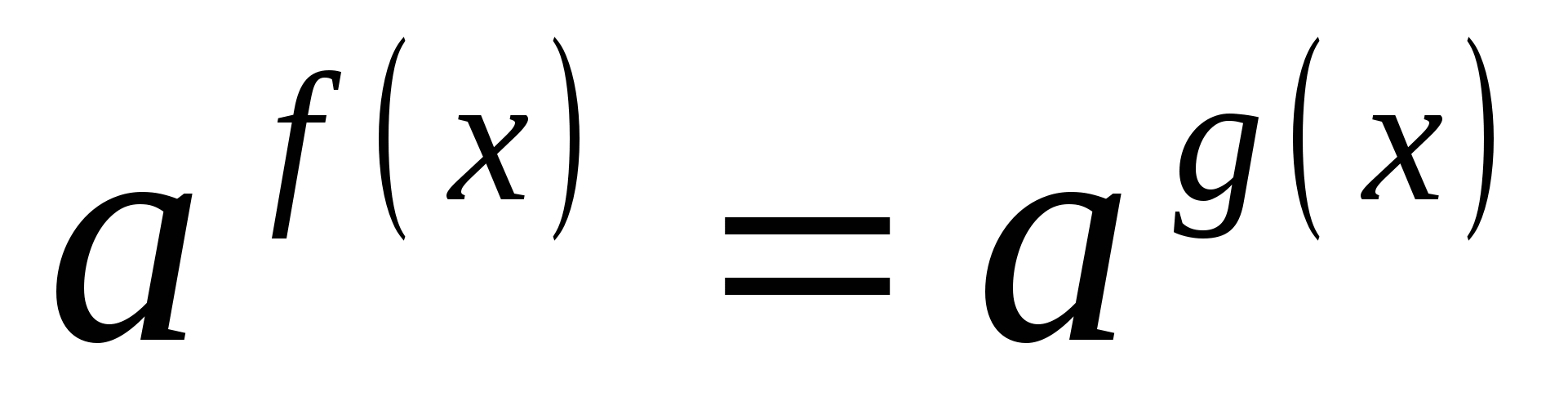
2) приравнять показатели степеней 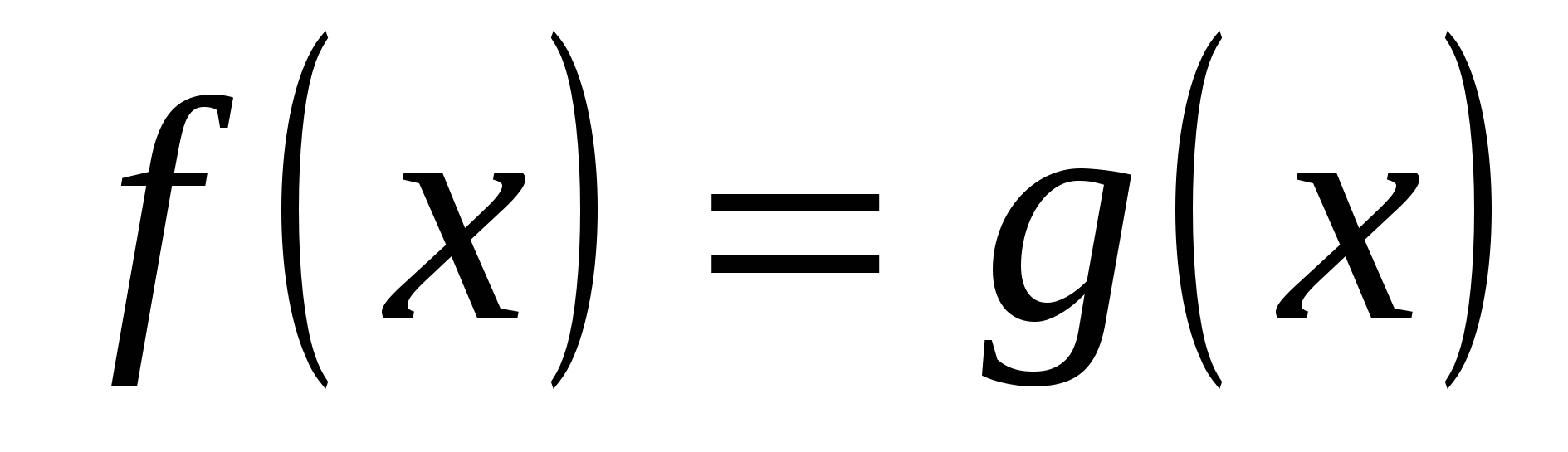
а) 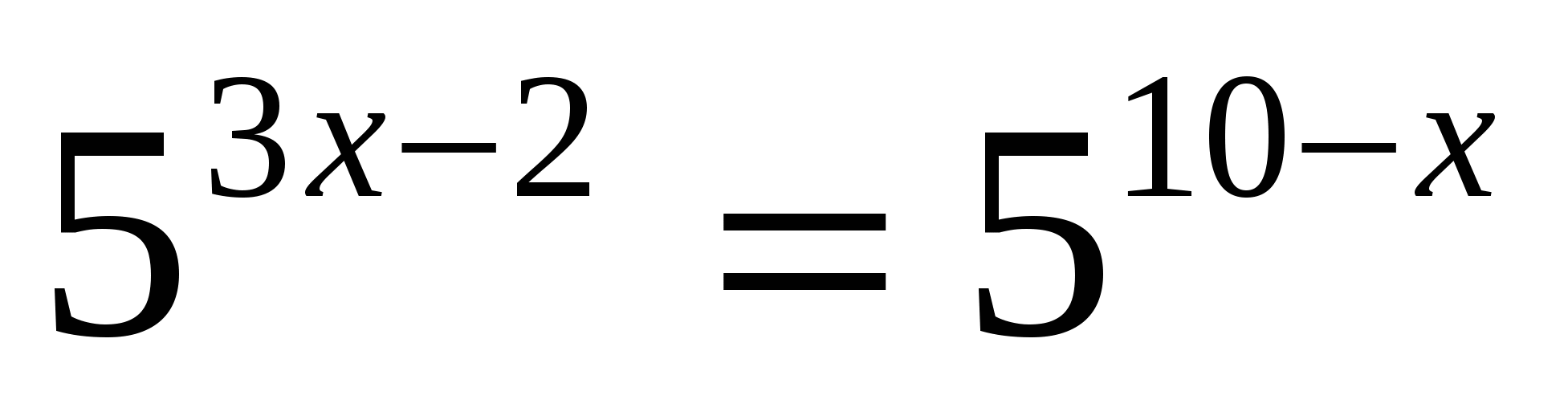

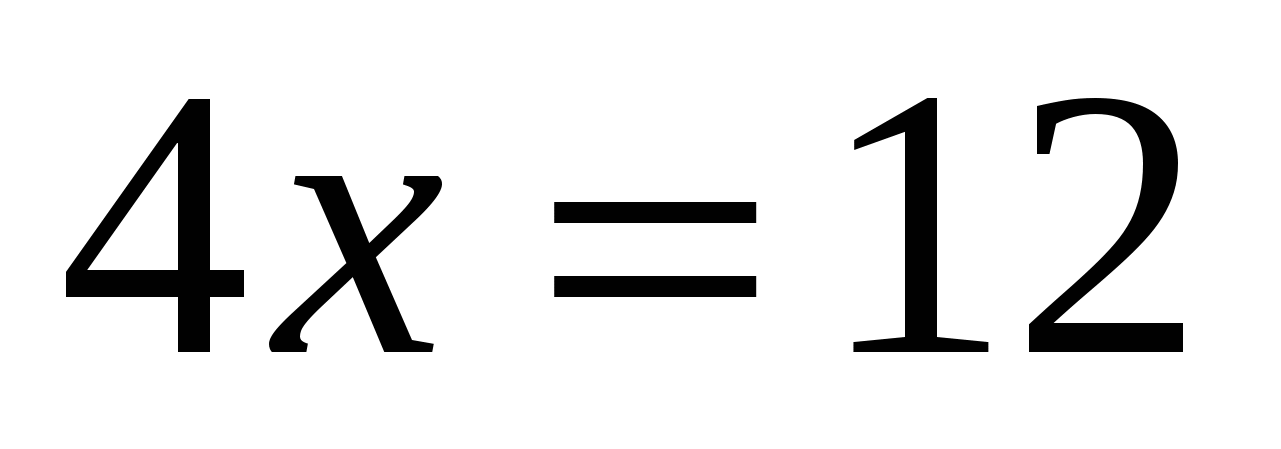
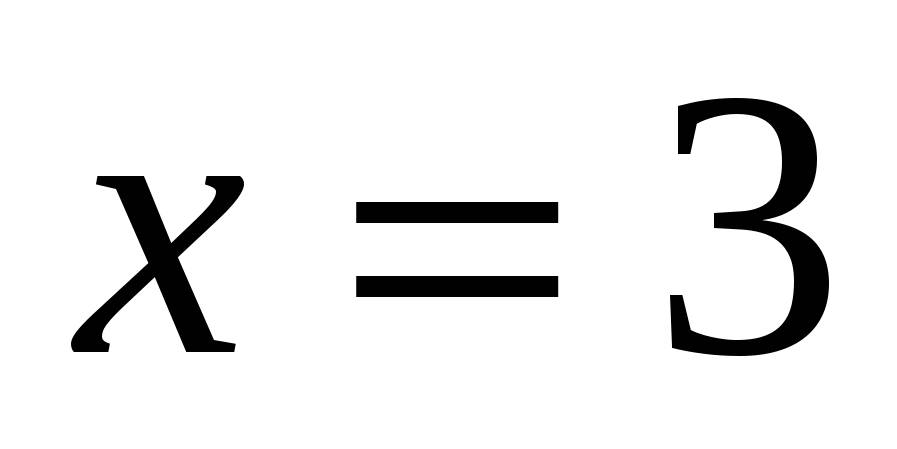
Ответ: 3.
б) 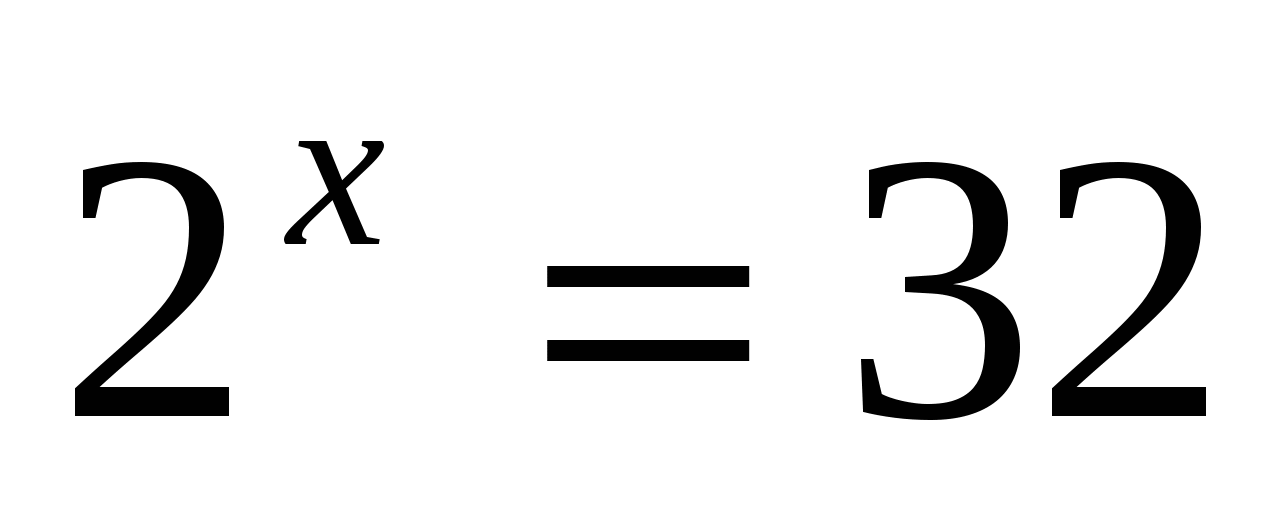
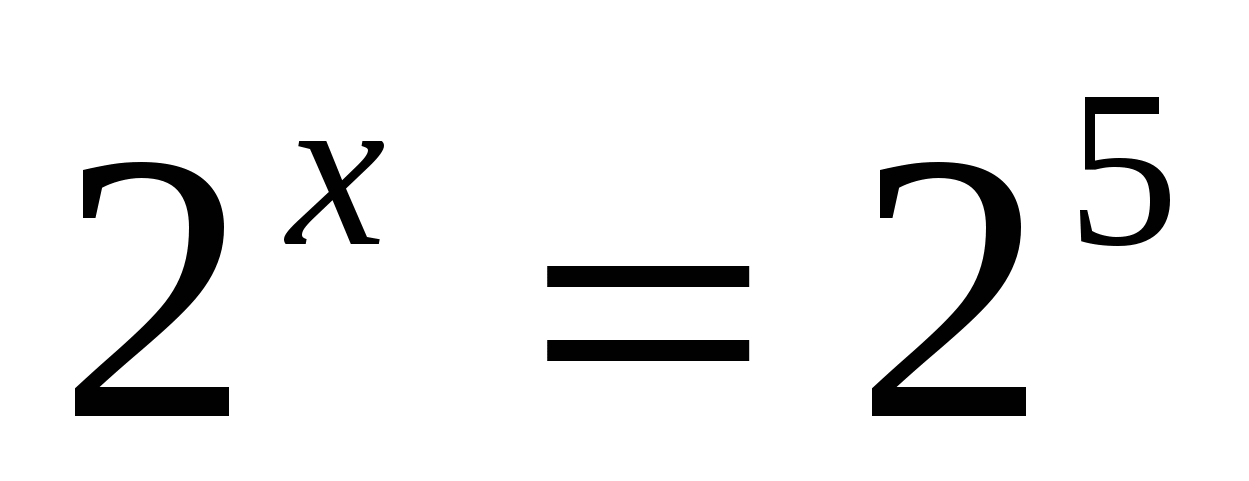
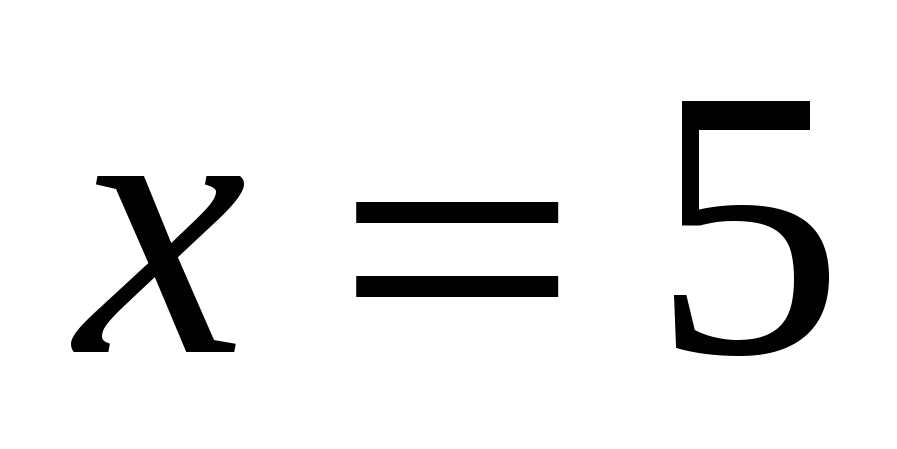 Ответ: 5
Ответ: 5
в) 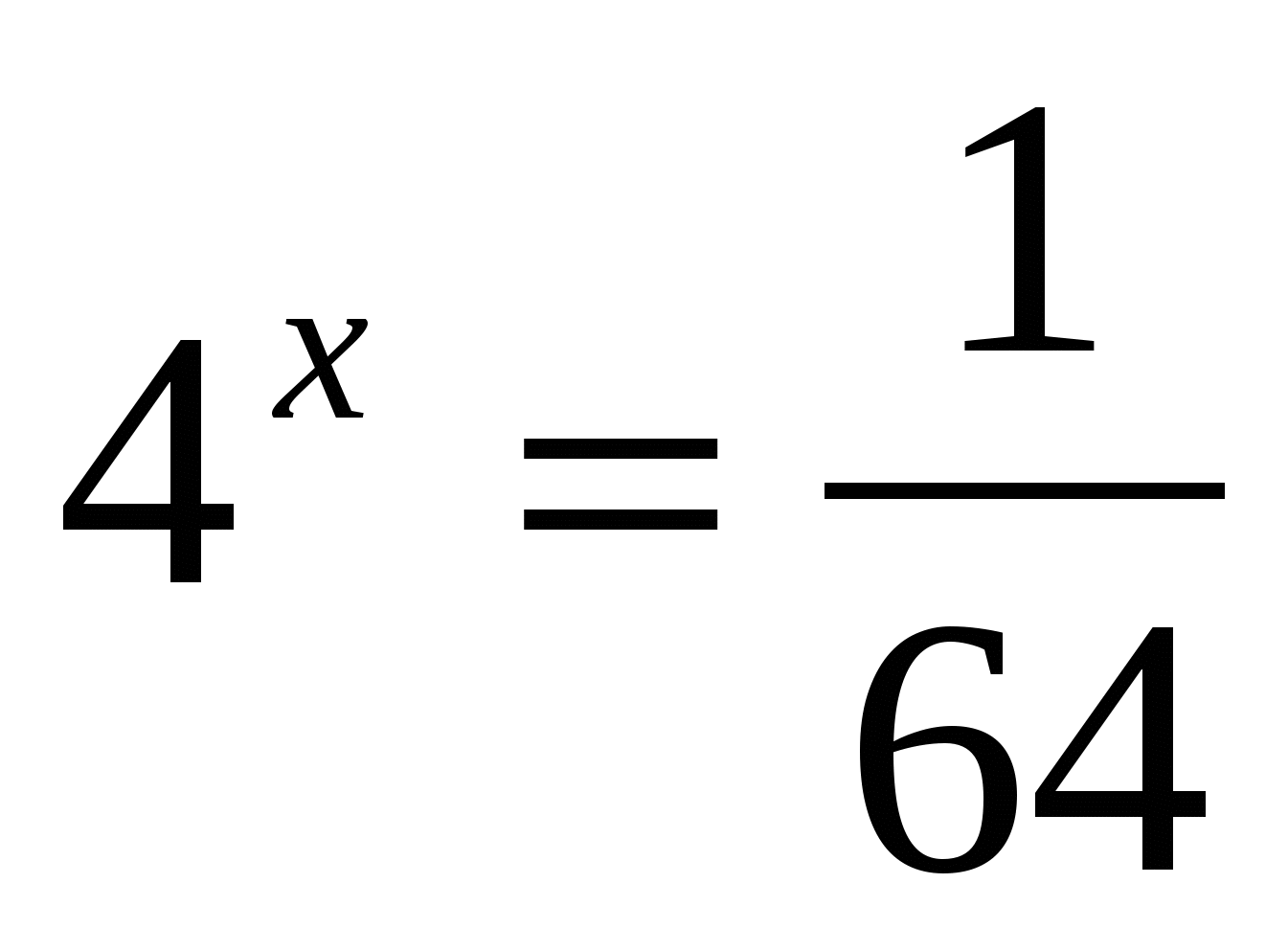

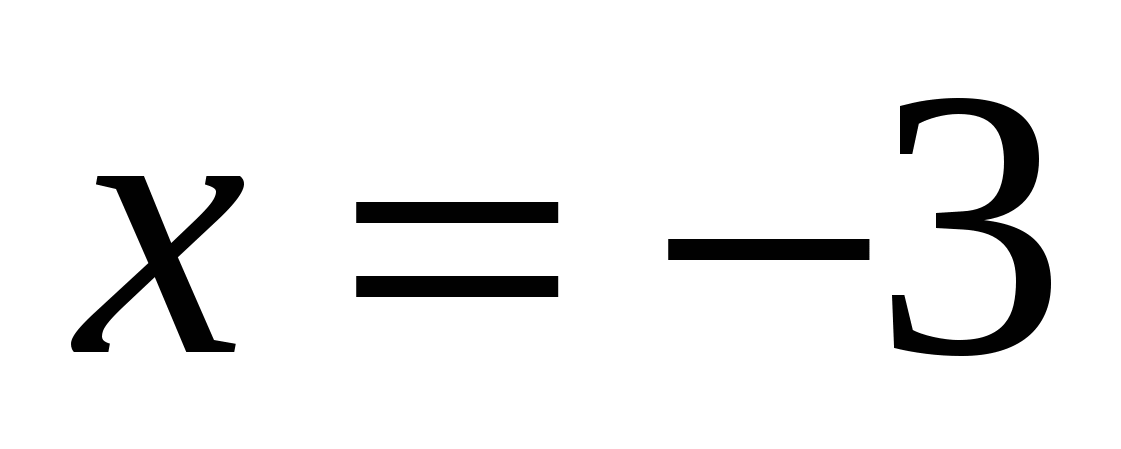
Ответ: — 3.
г) 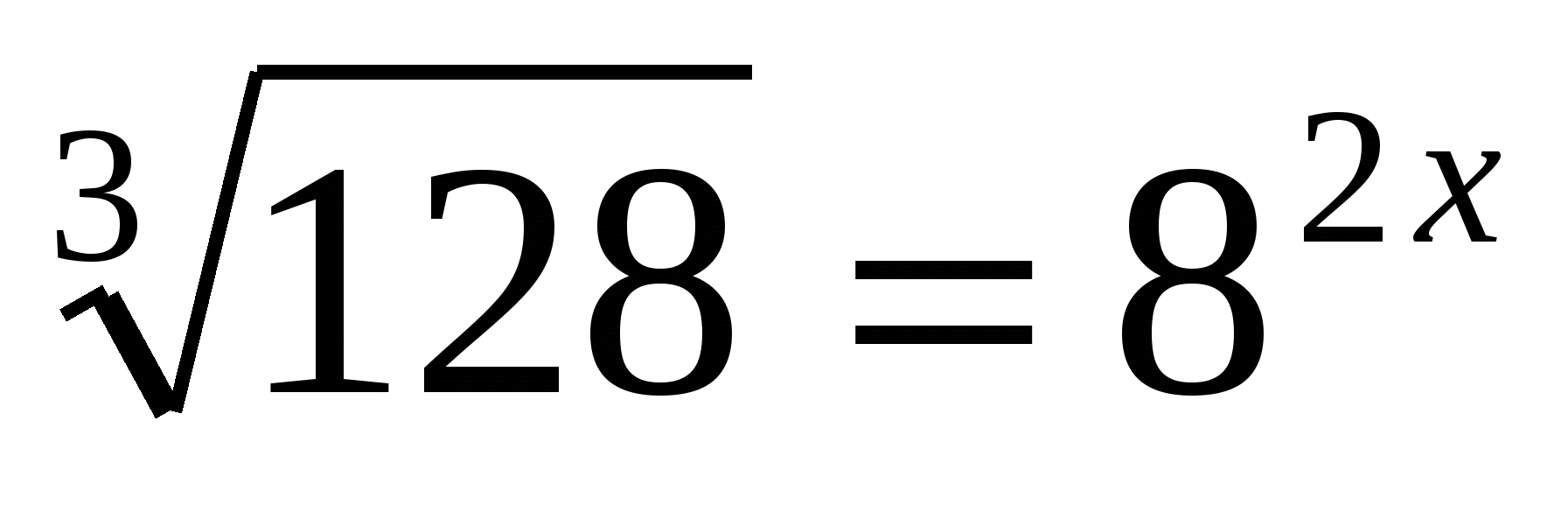
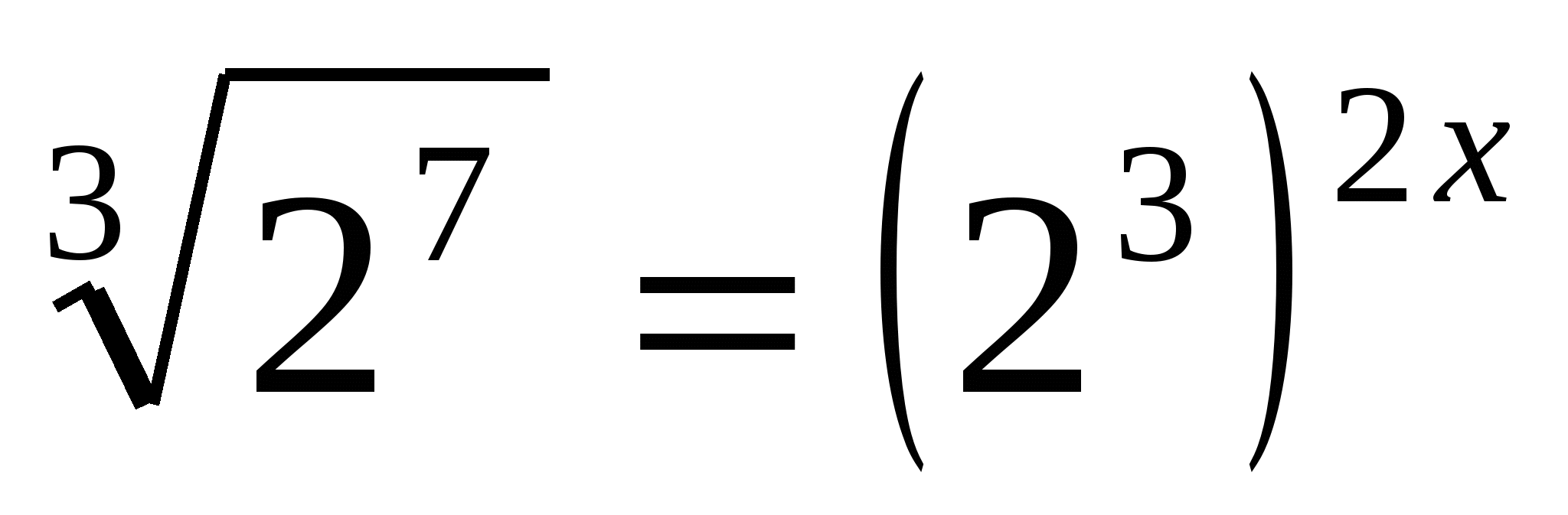
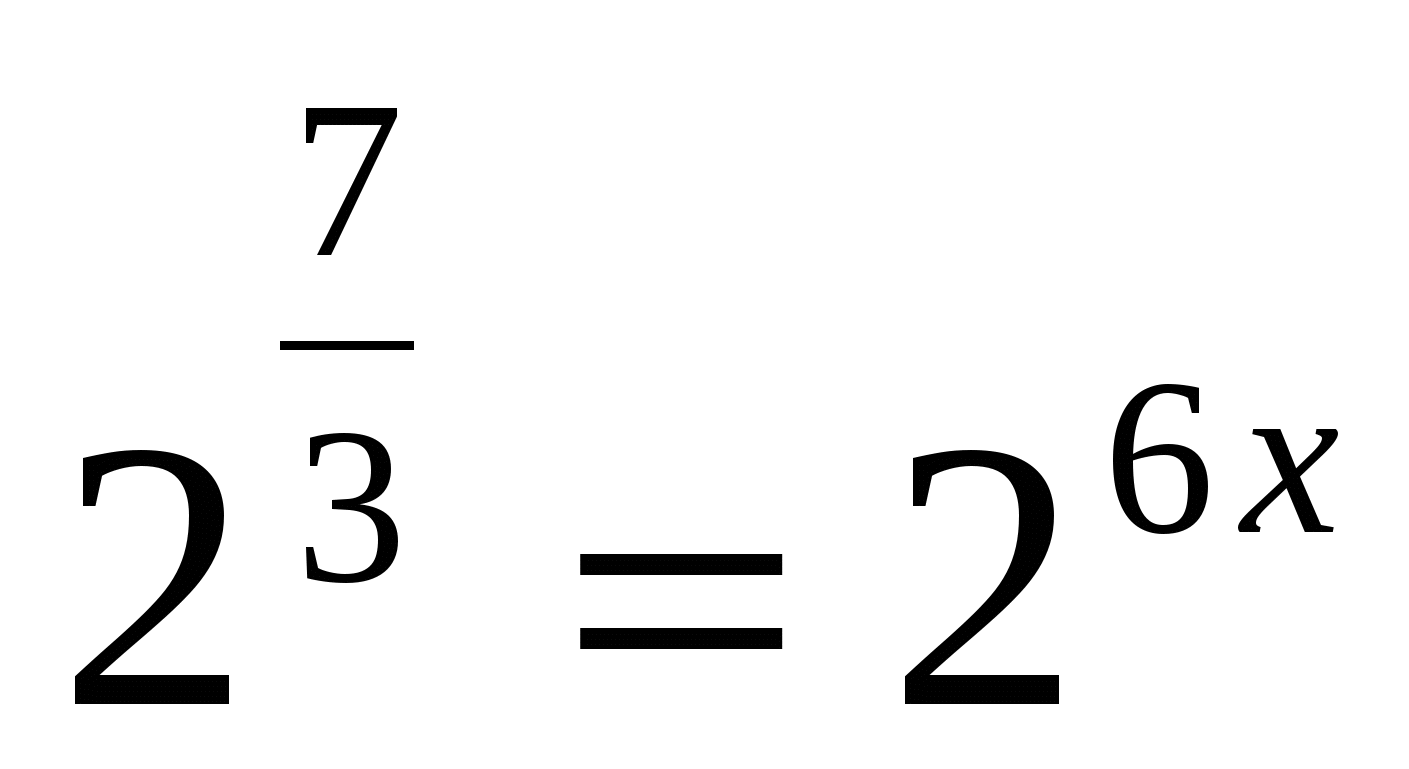
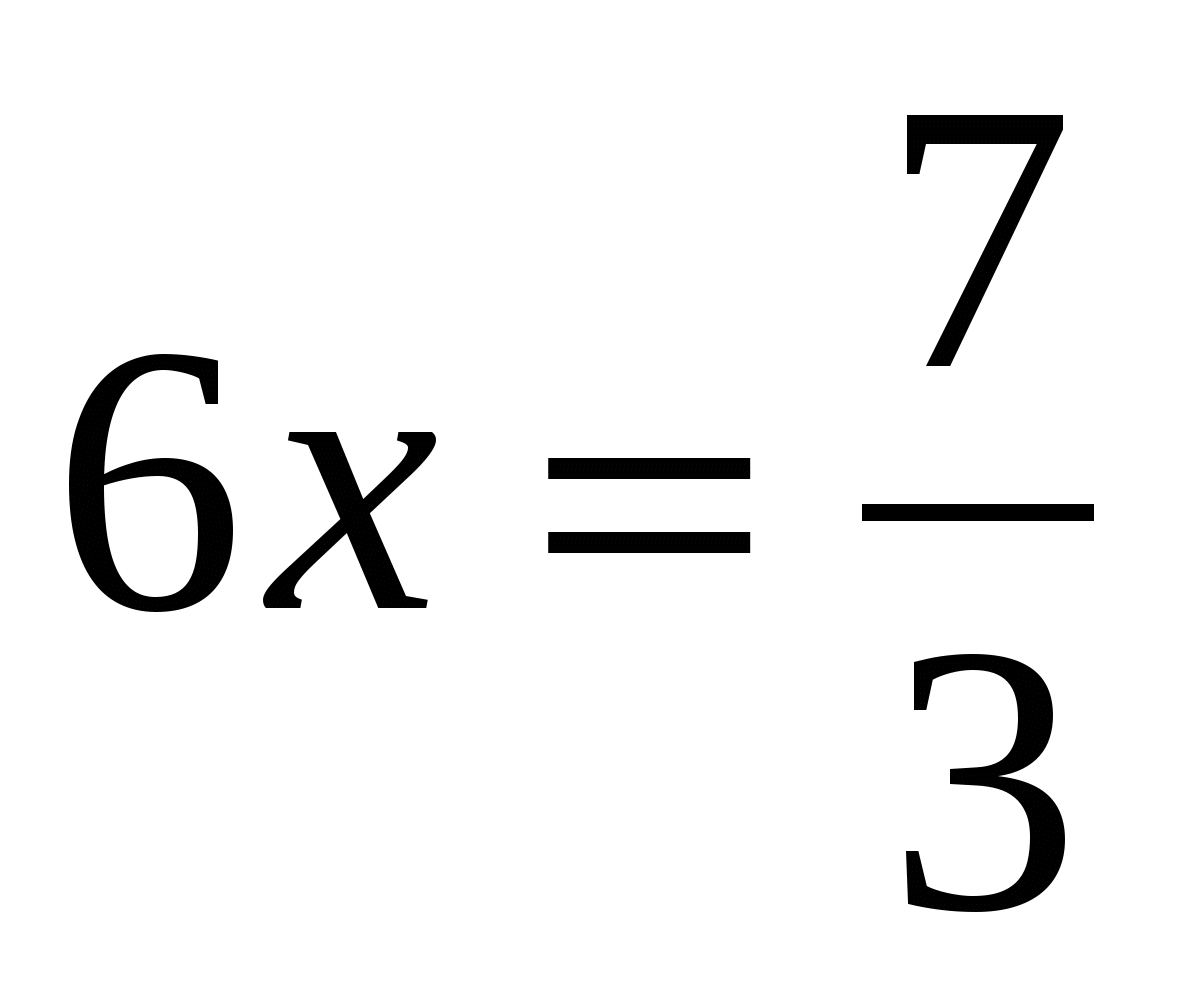
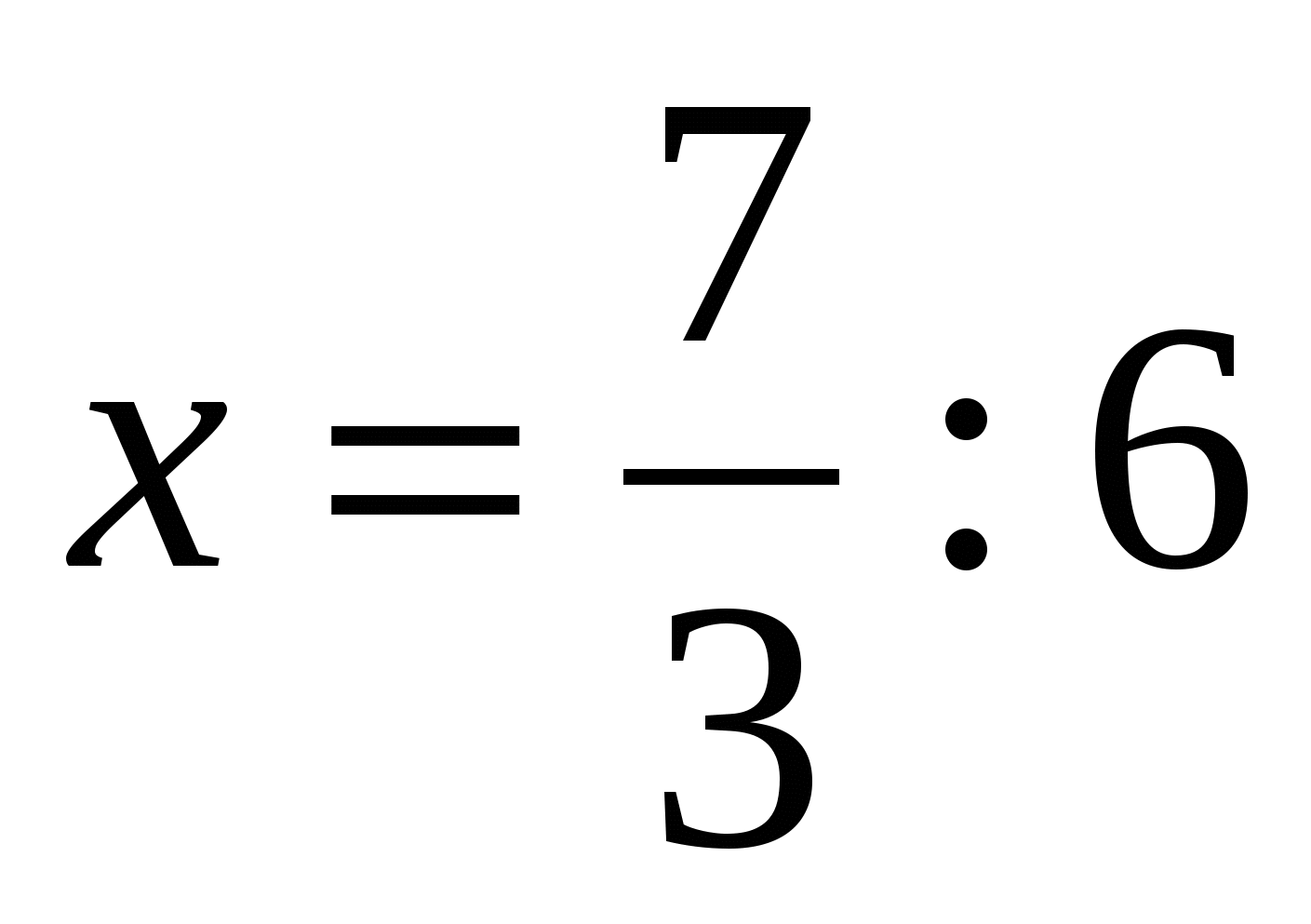
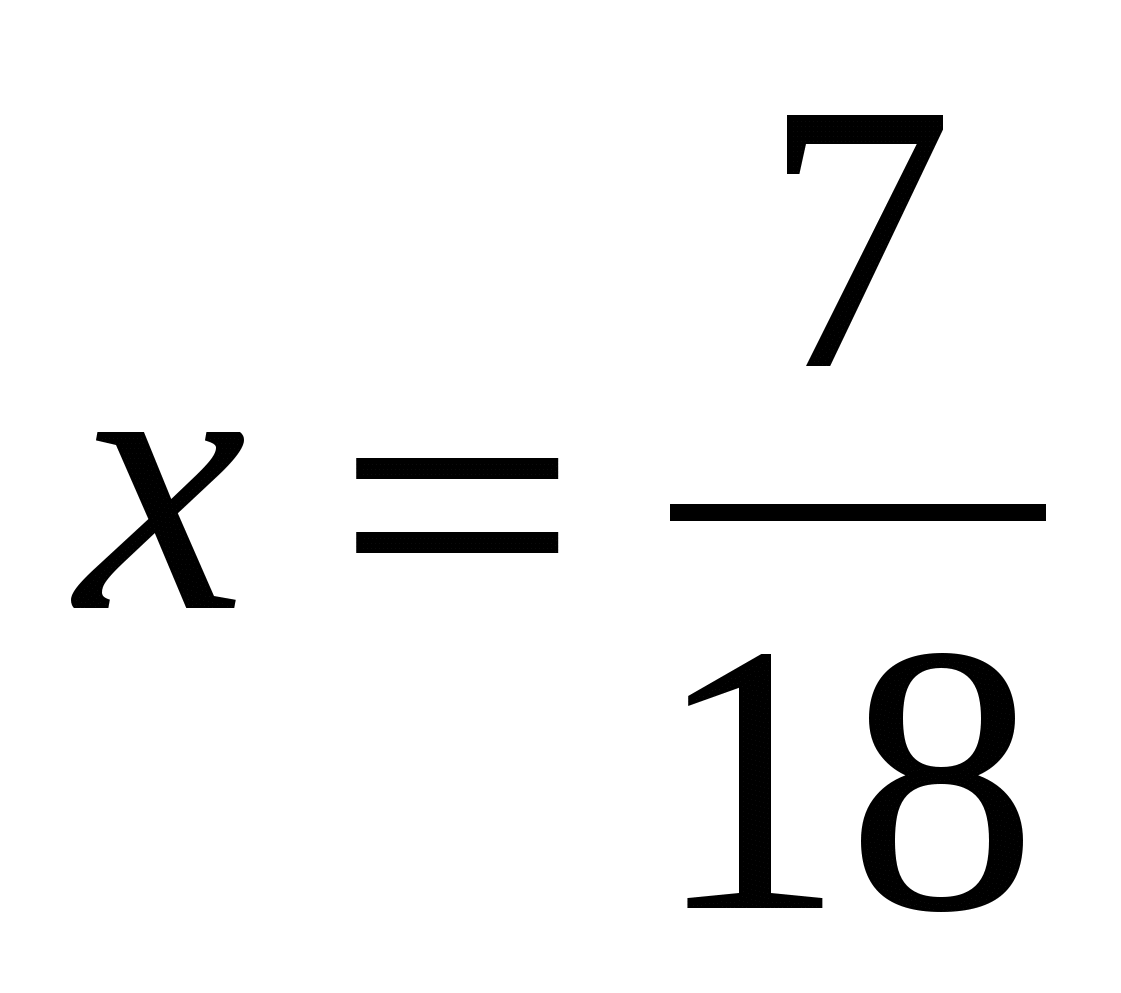
Ответ: 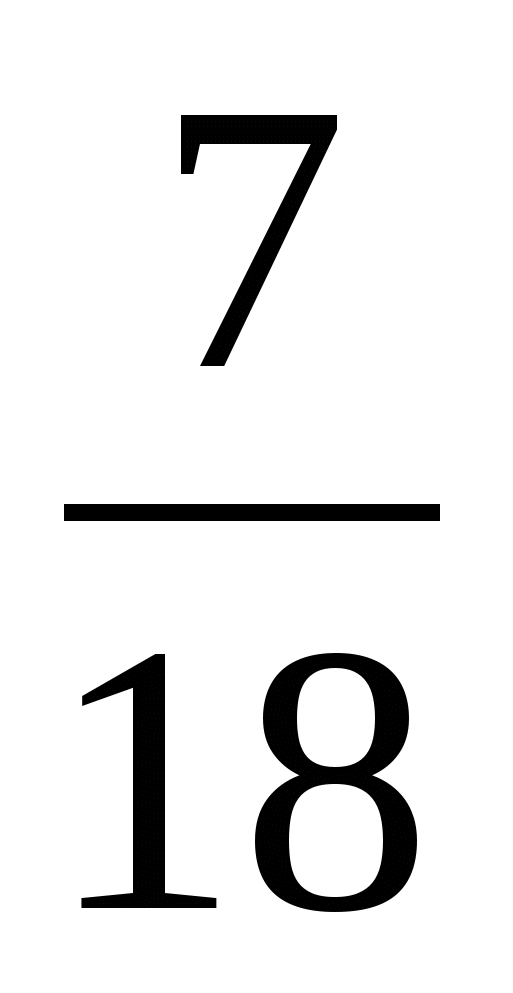 .
.
д) 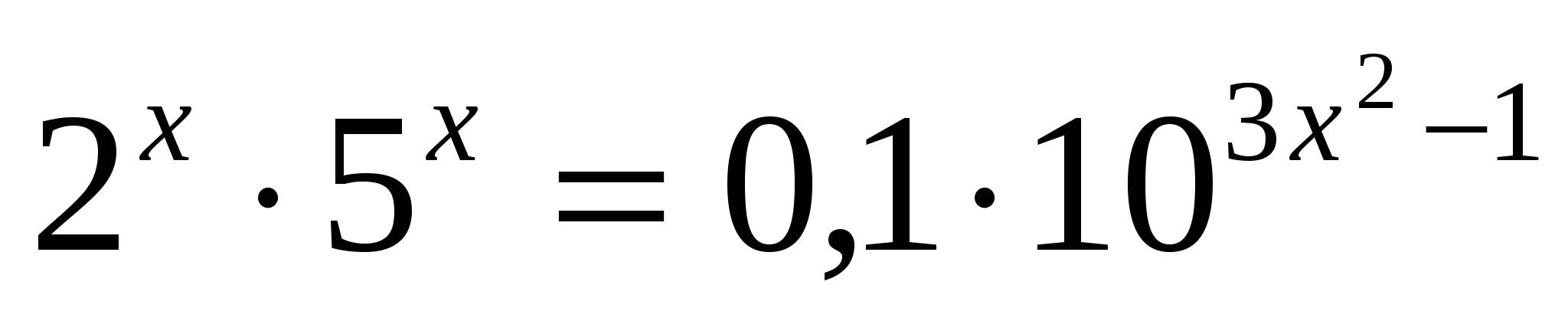
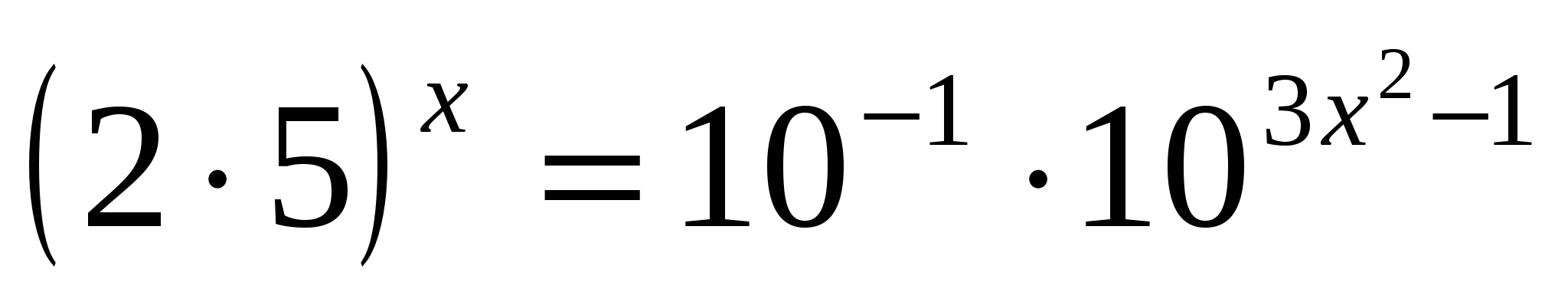
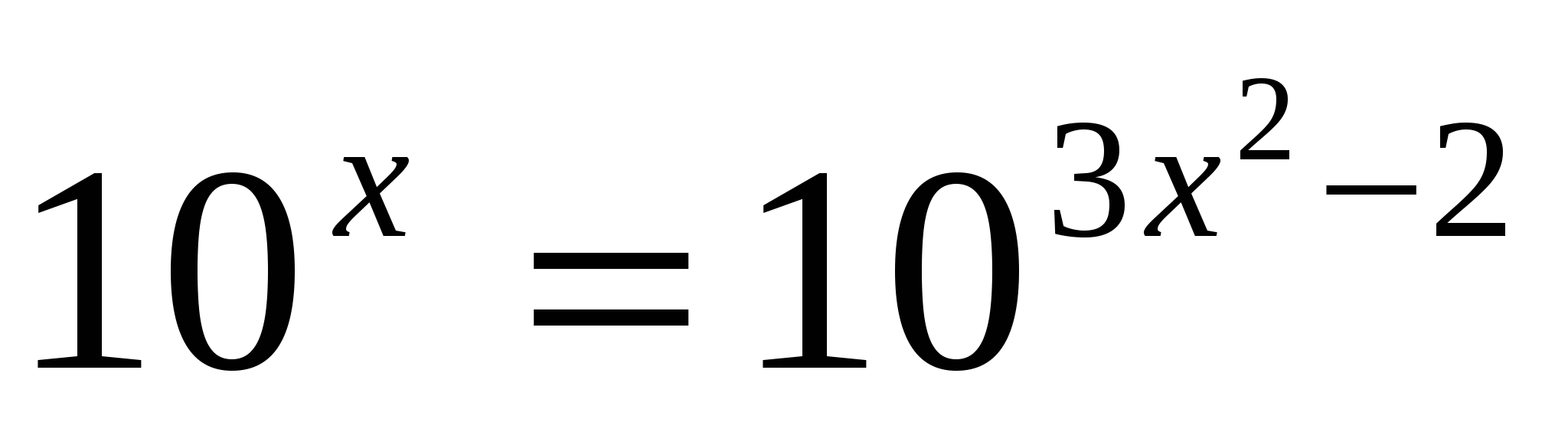
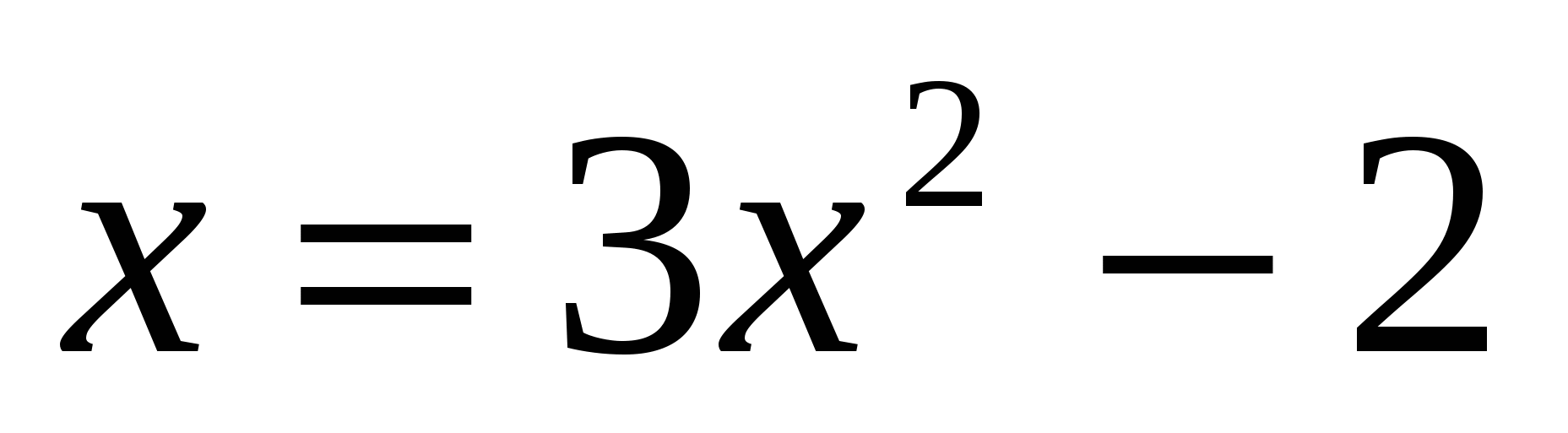
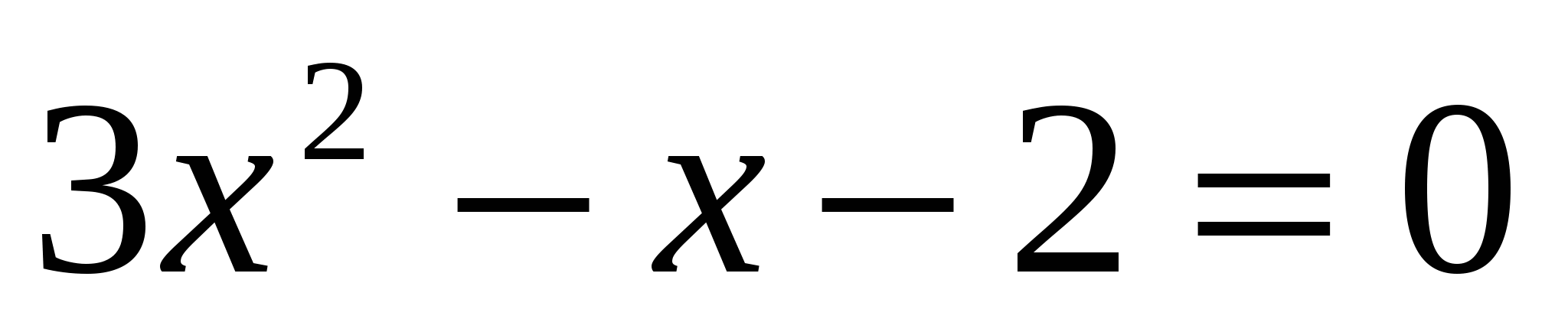
D=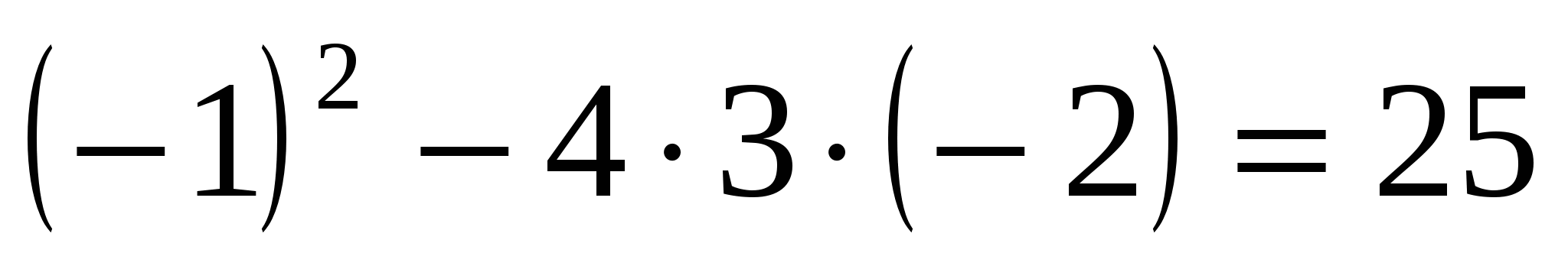
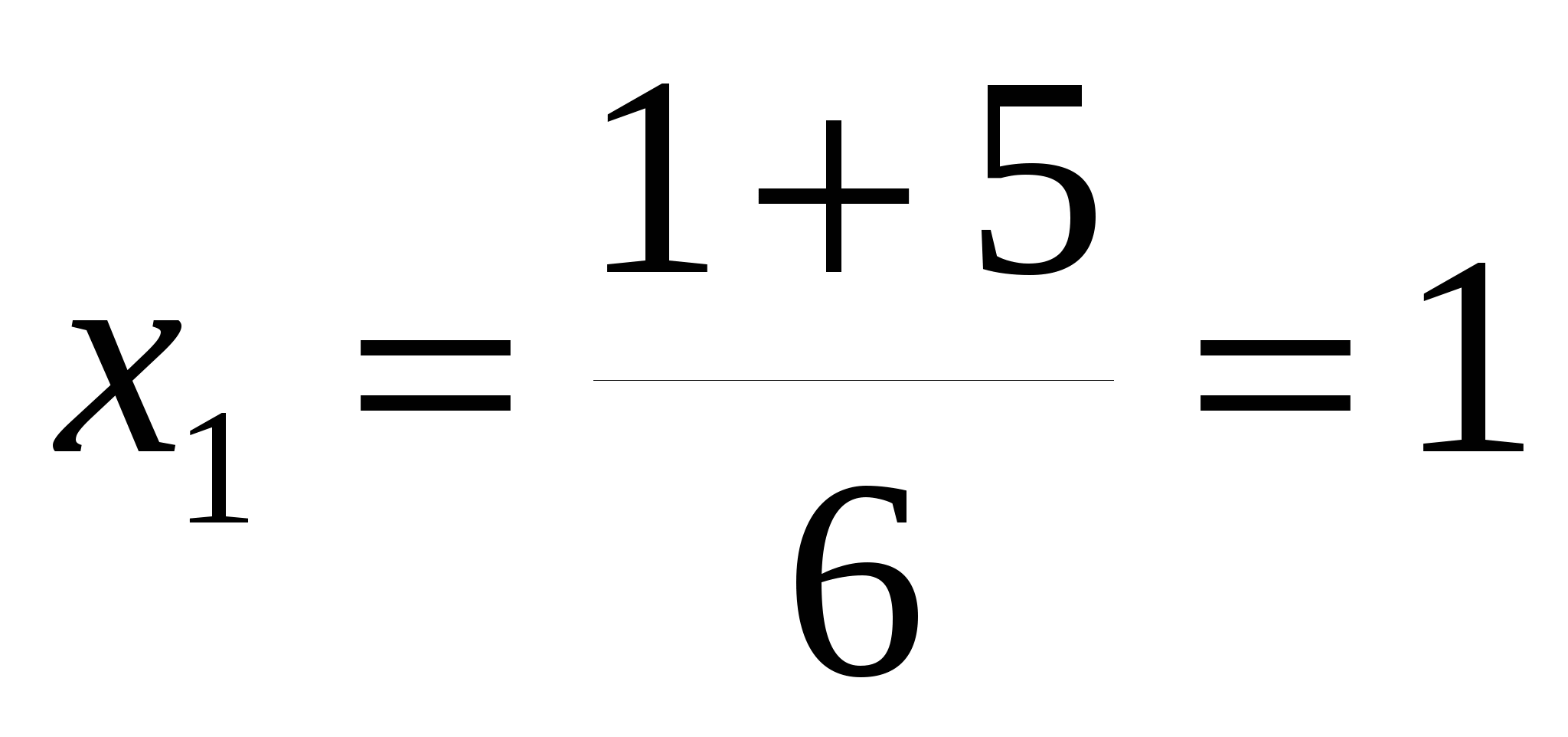
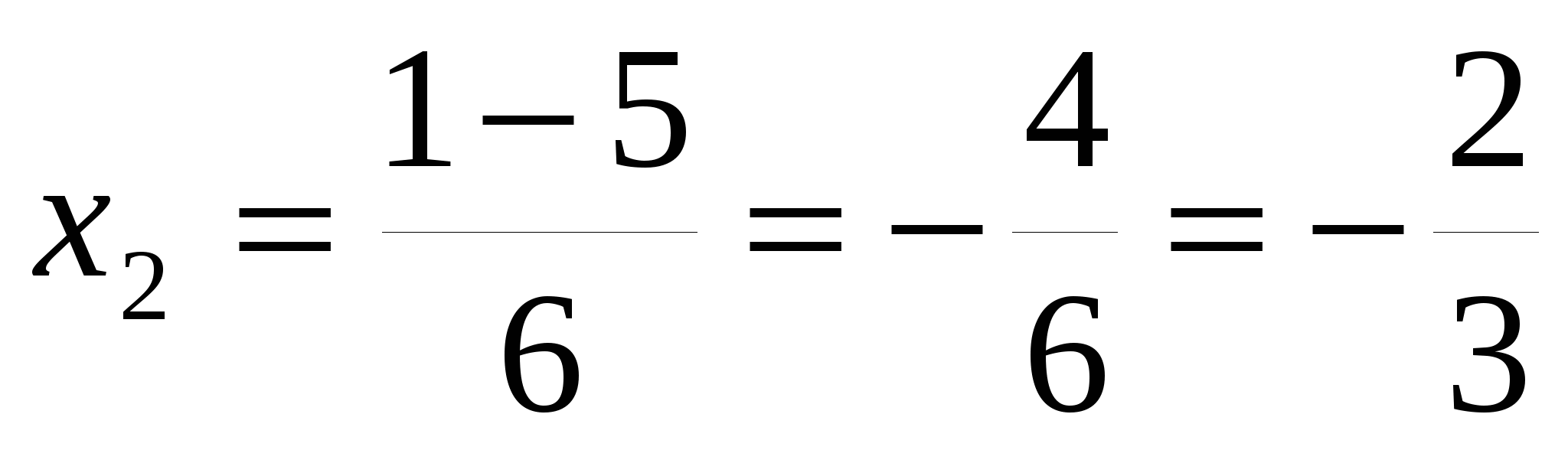
Ответ: 1; 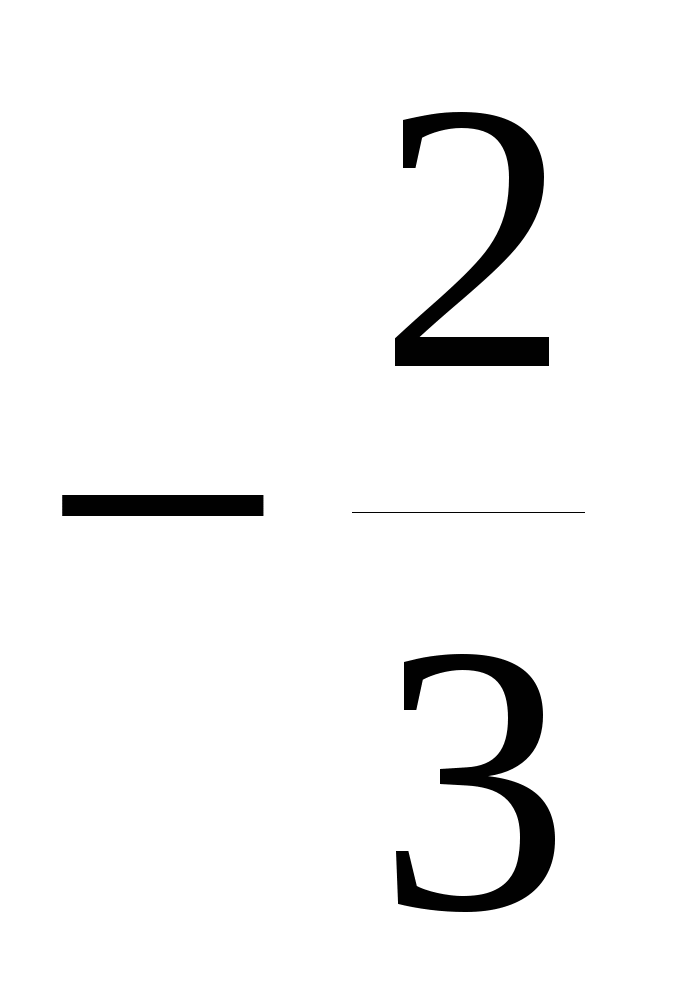 .
.
е) 
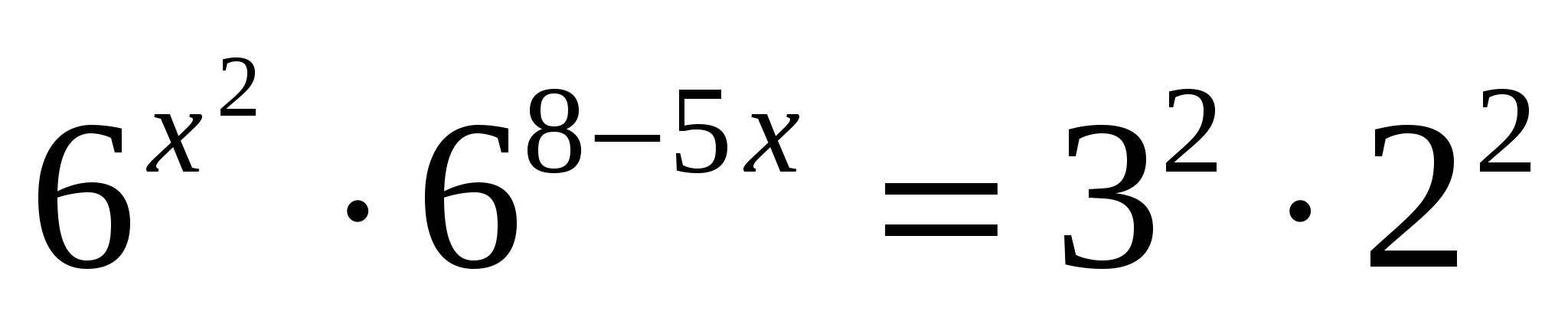
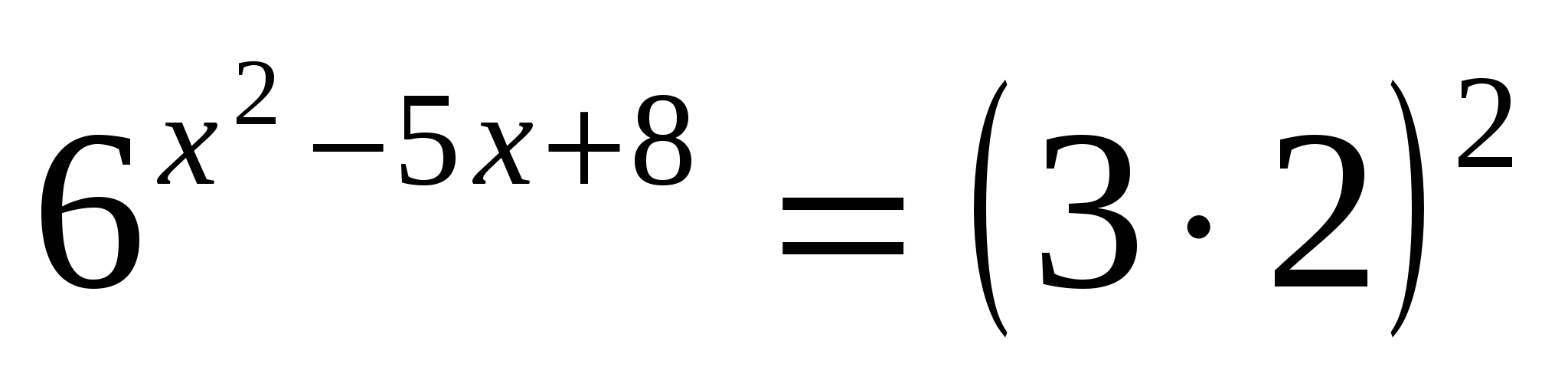
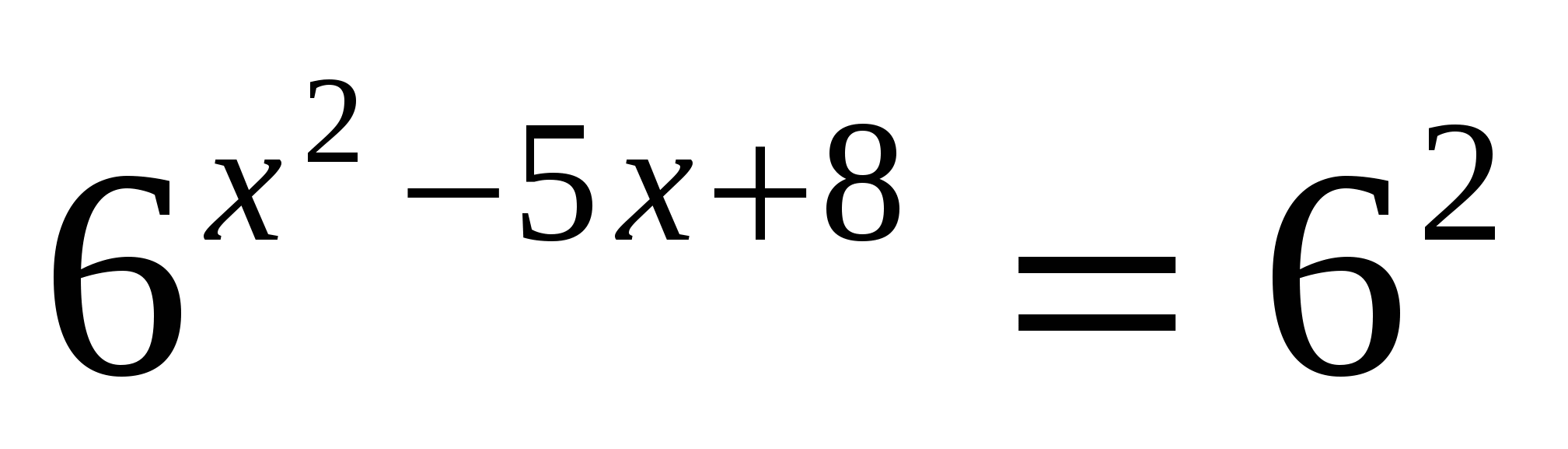
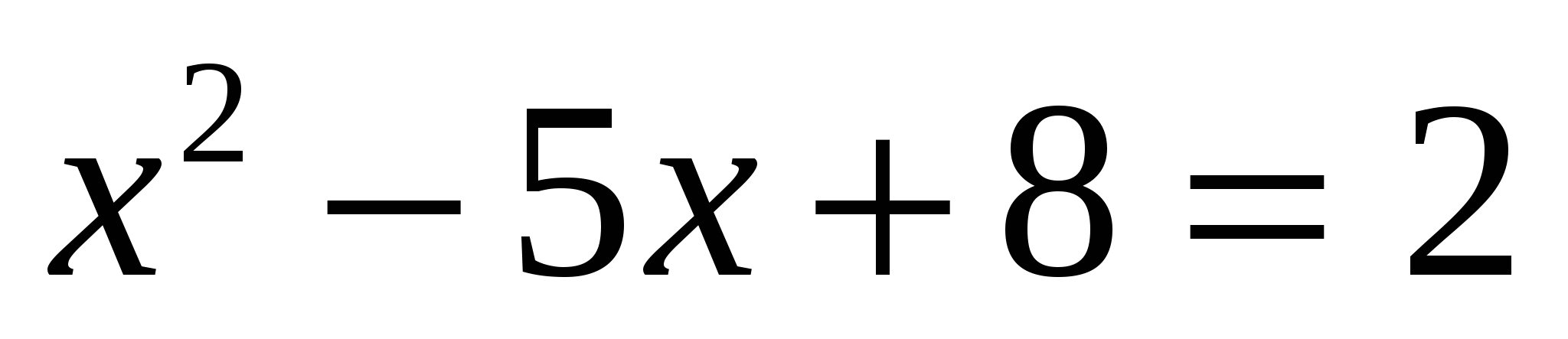
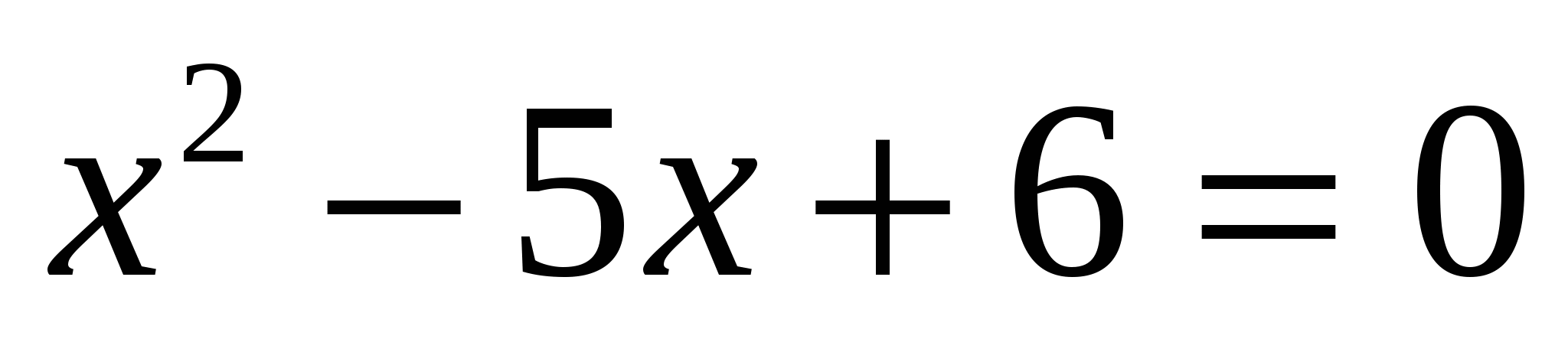
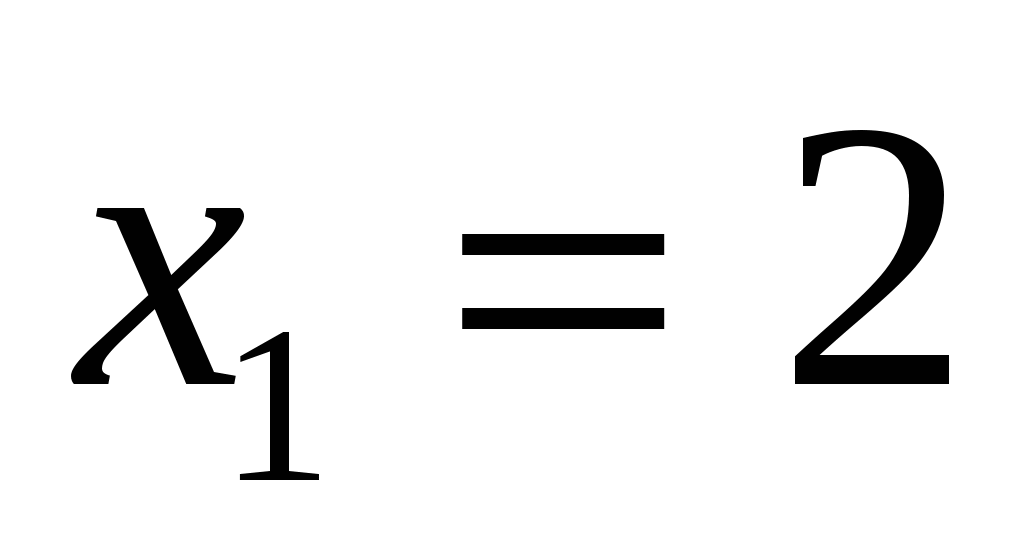
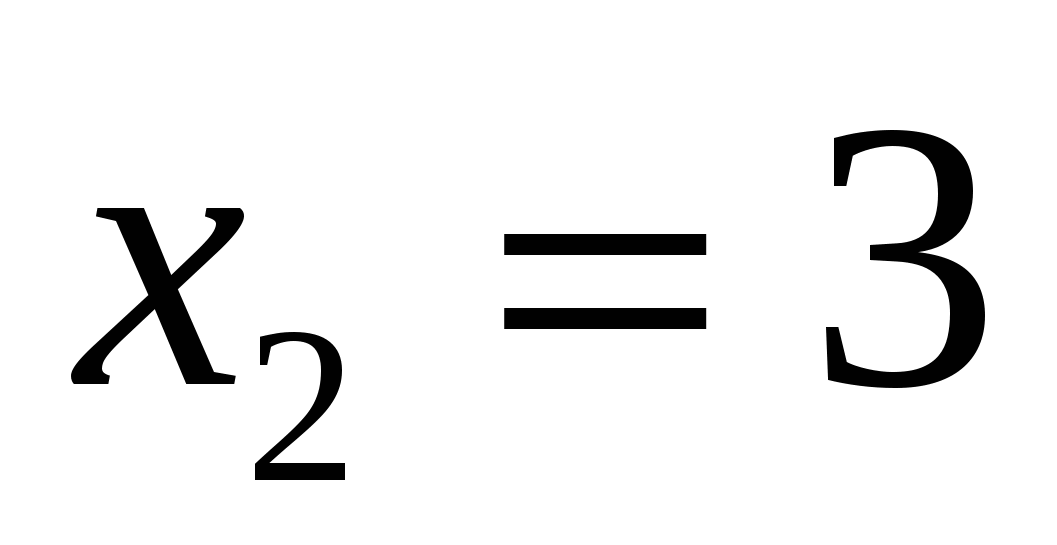
Ответ: 2; 3.
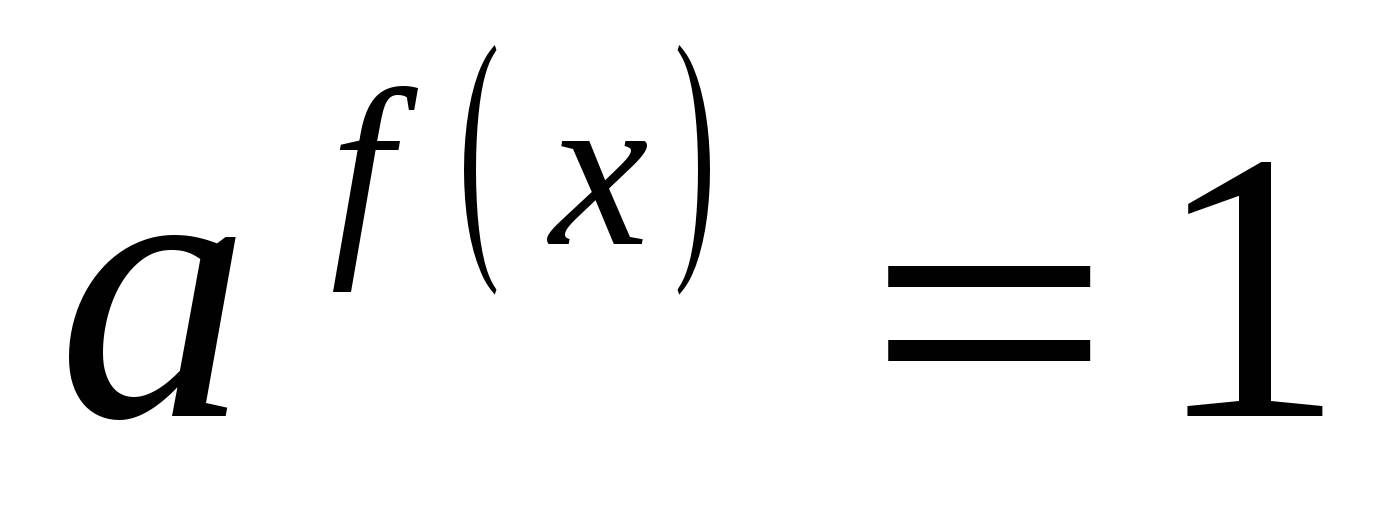
представить 1 в виде степени числа а с нулевым показателем
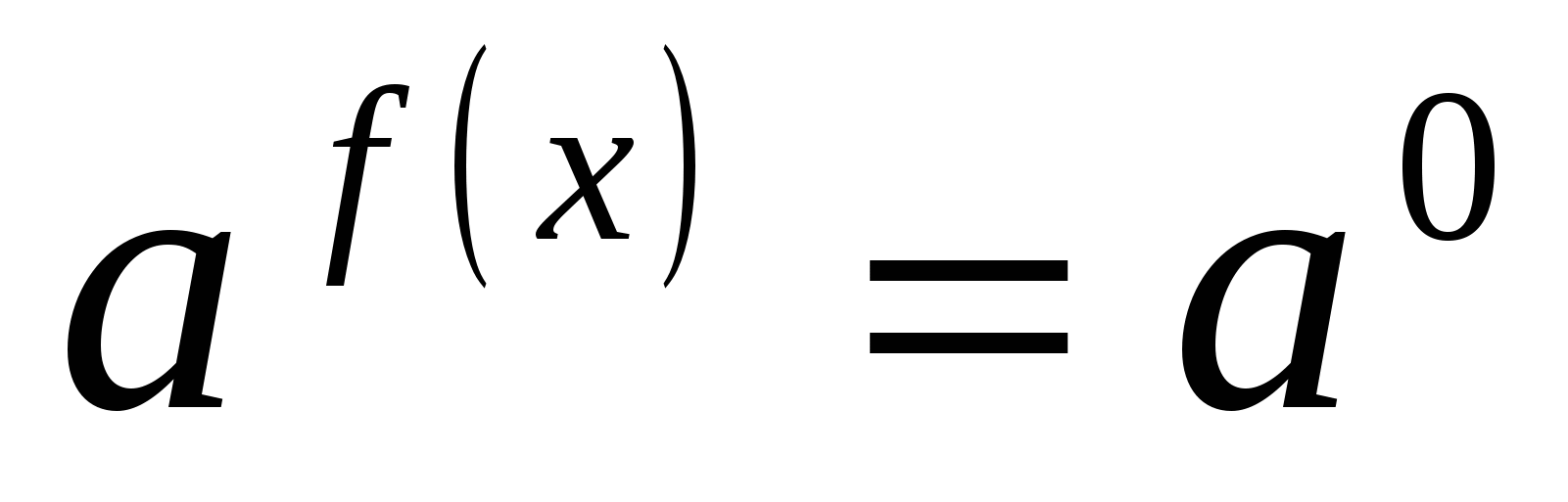
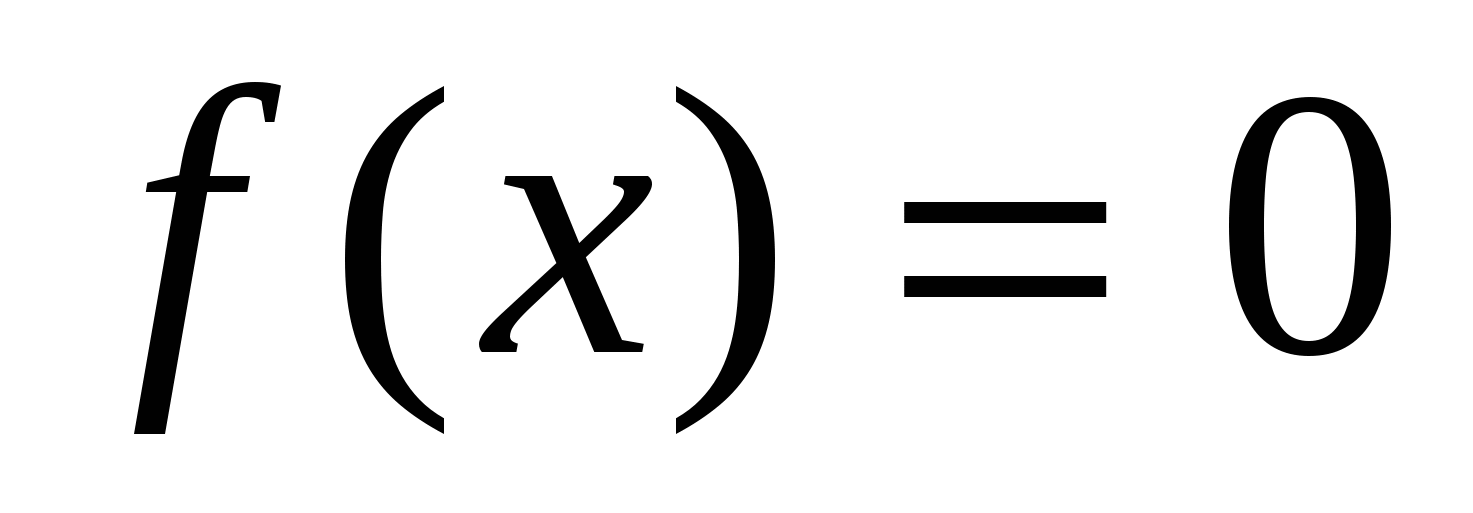
а) 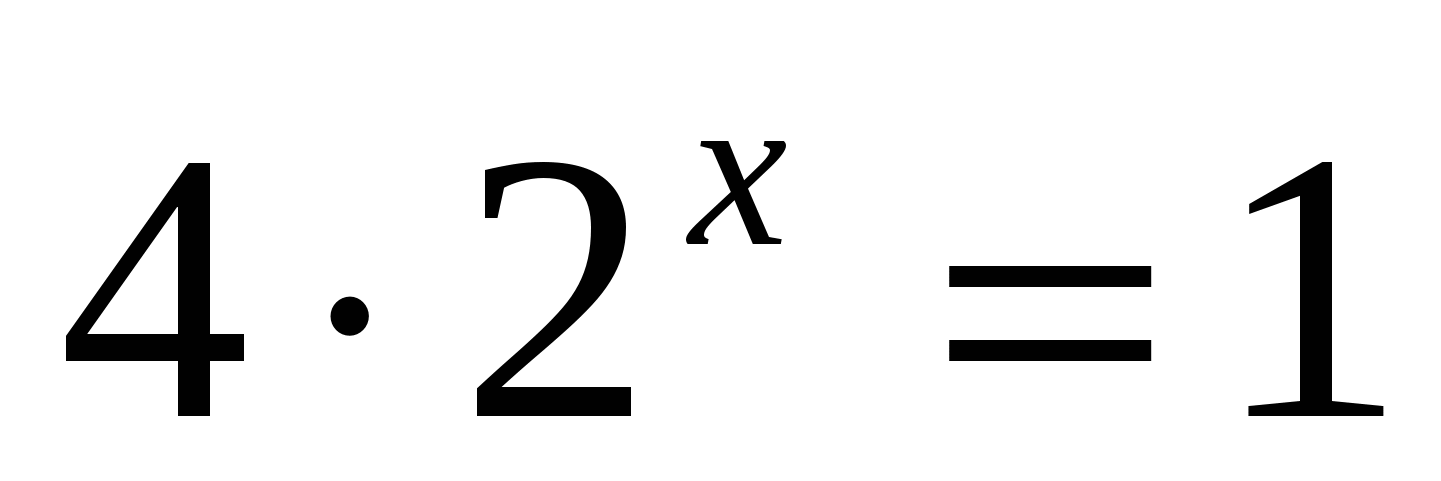
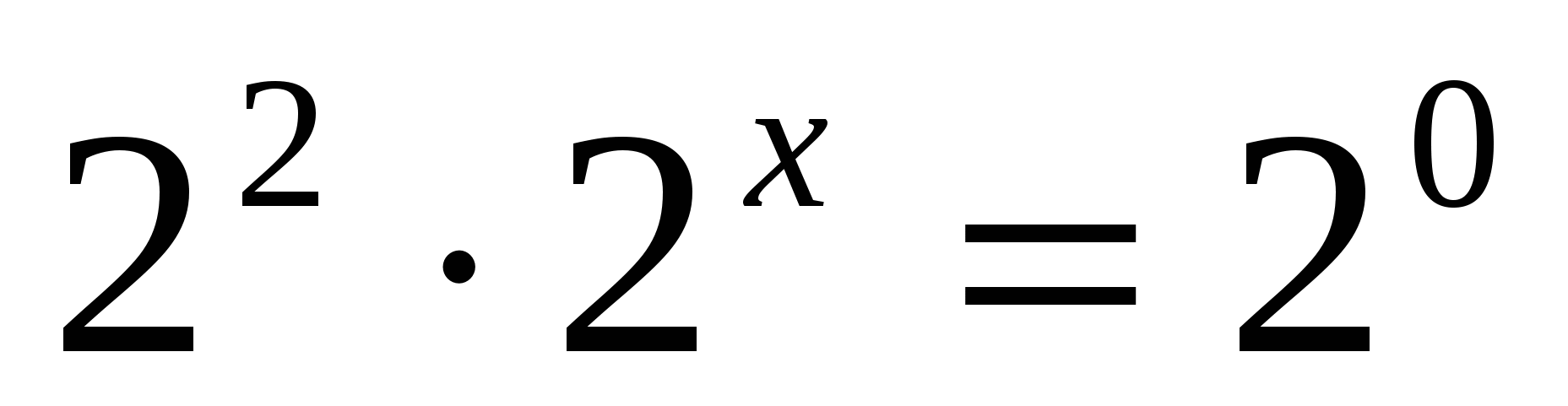
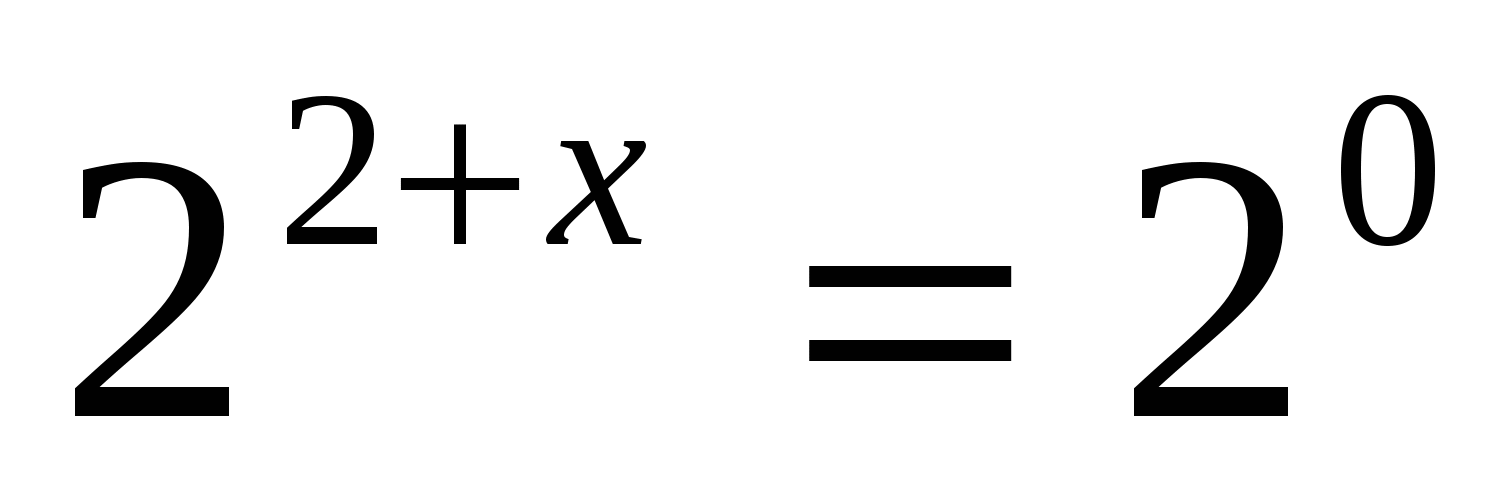
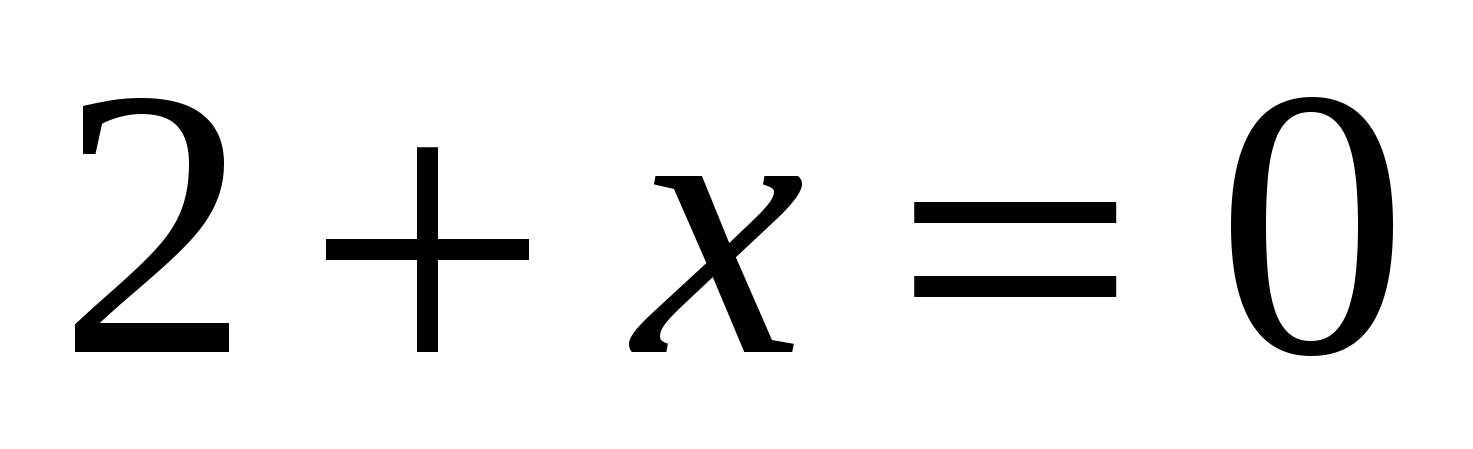
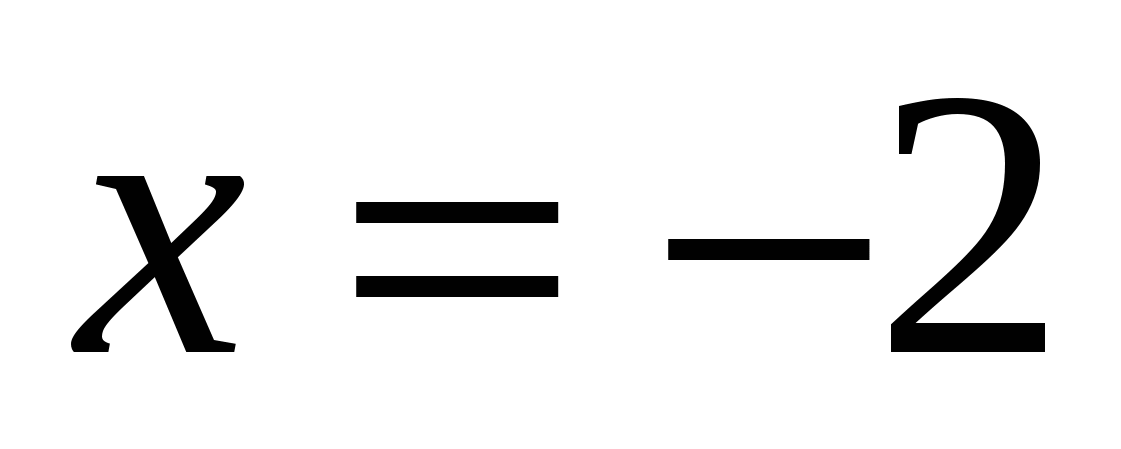
Ответ: — 2.
б) 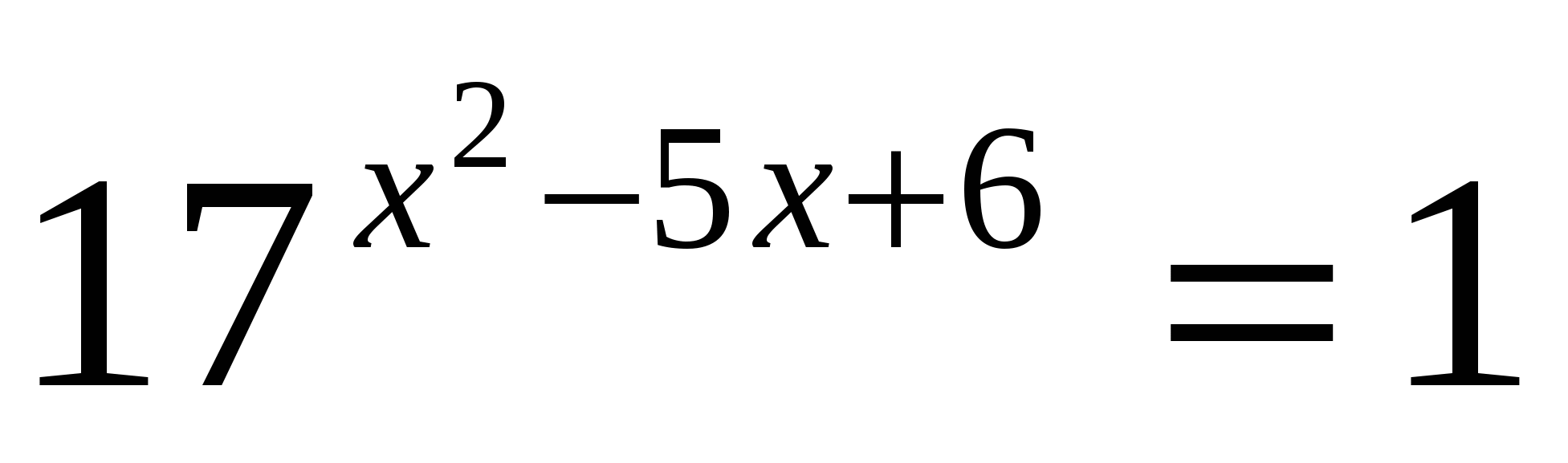
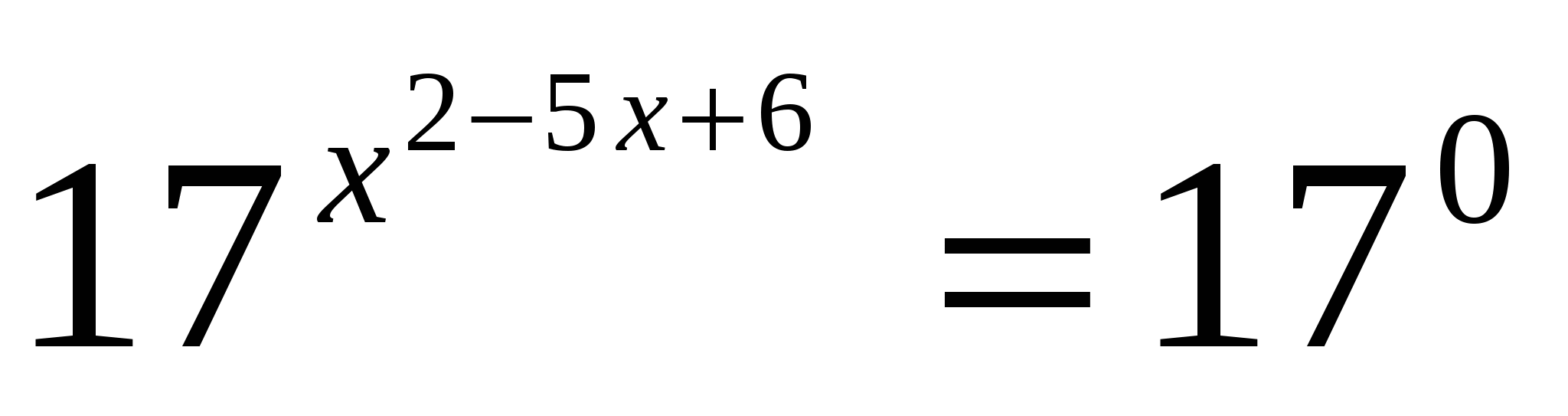
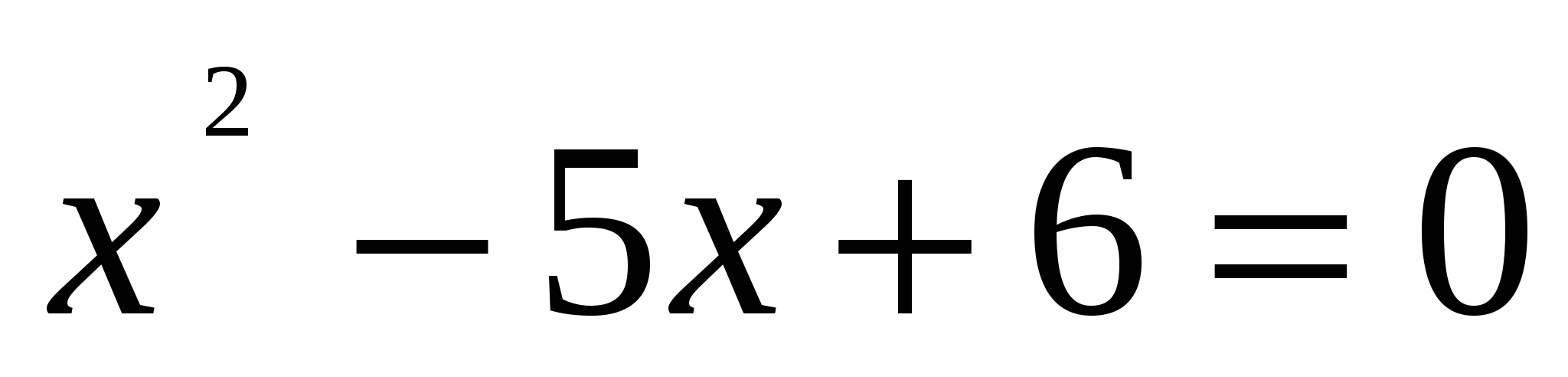
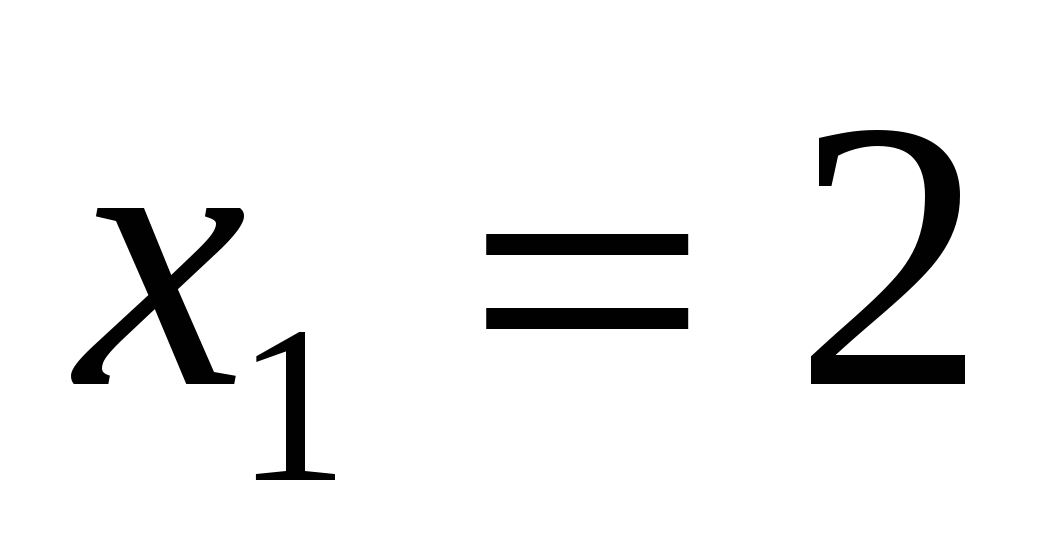 или
или 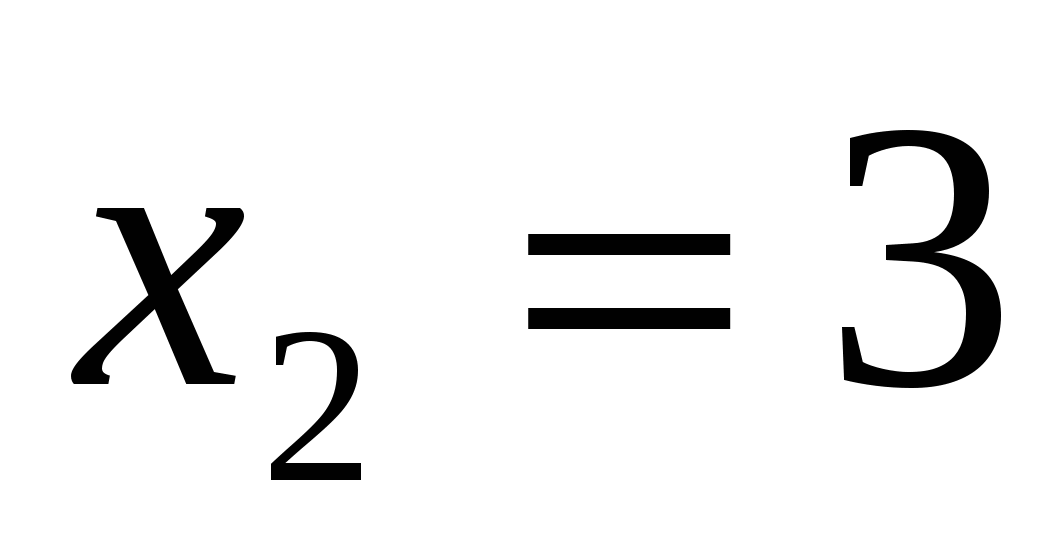
Ответ: 2; 3.
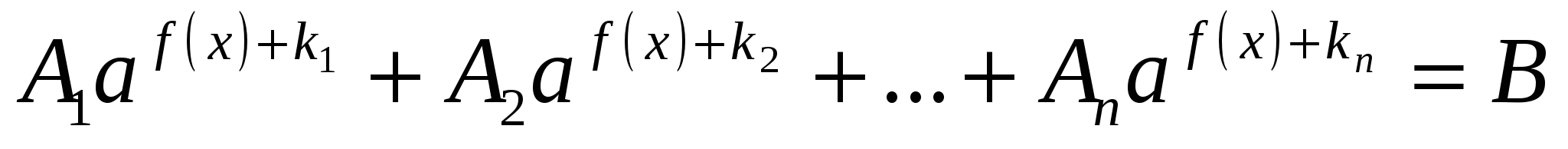
1 )вынести общий множитель за скобки
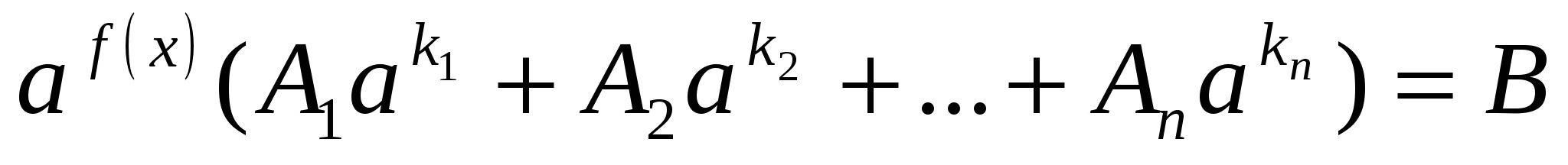
2) выполнить преобразования и привести уравнение к виду
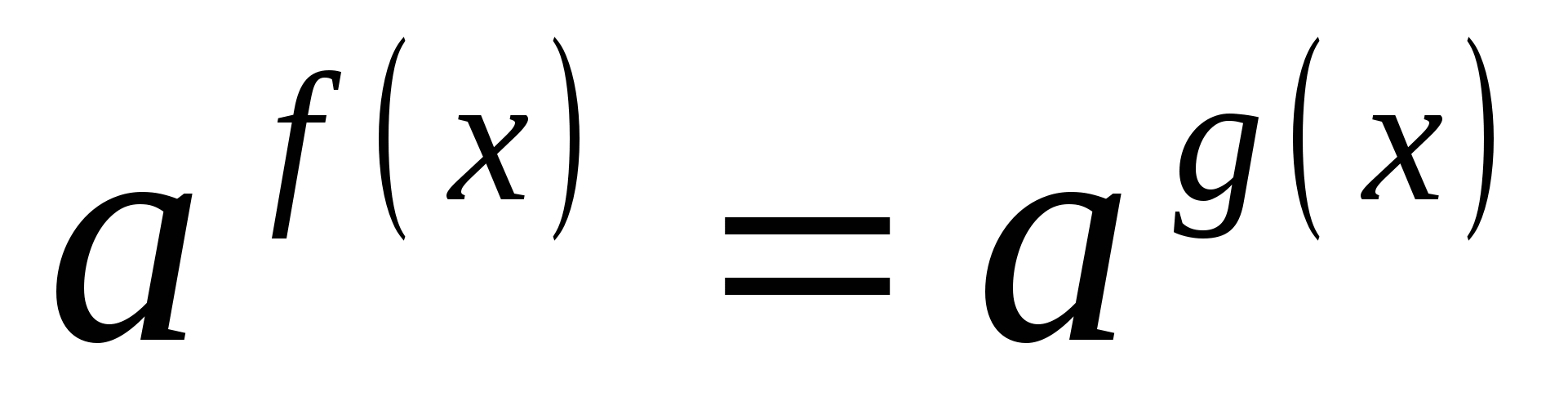
а) 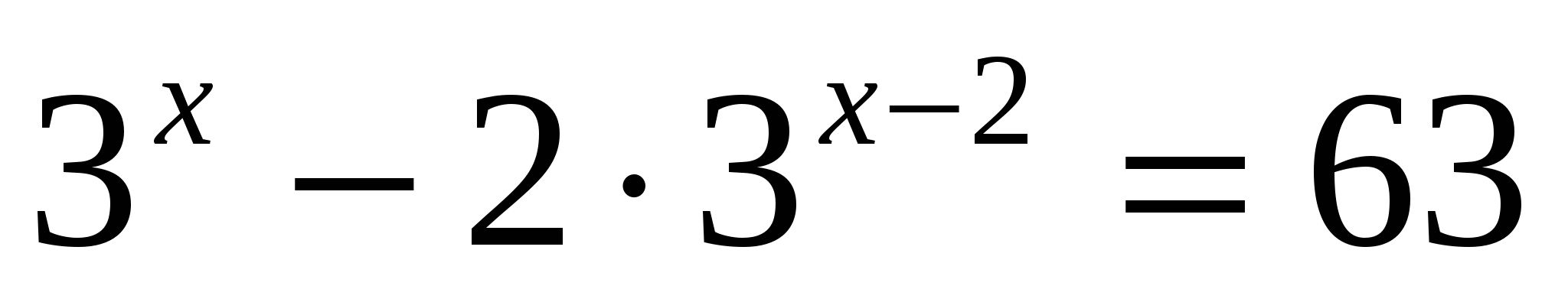
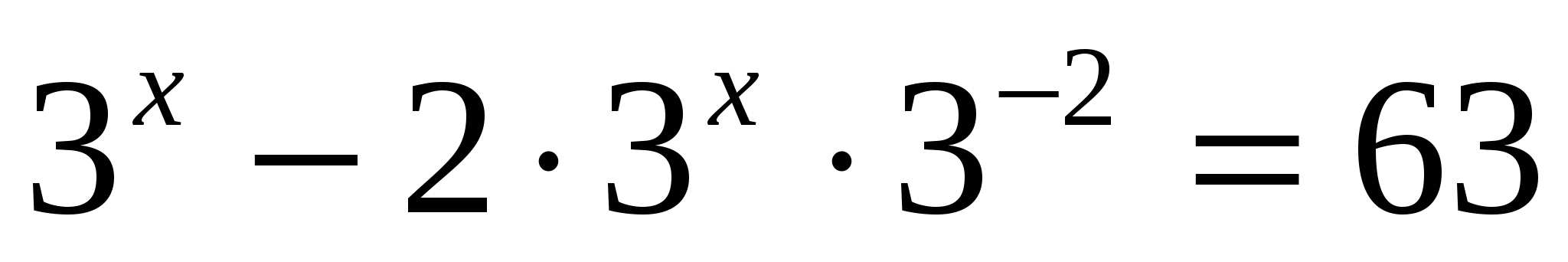
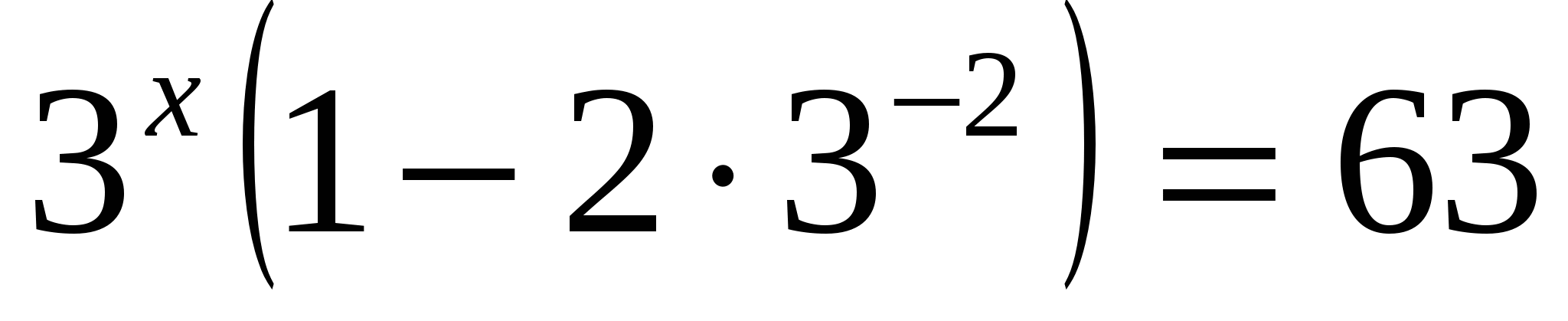
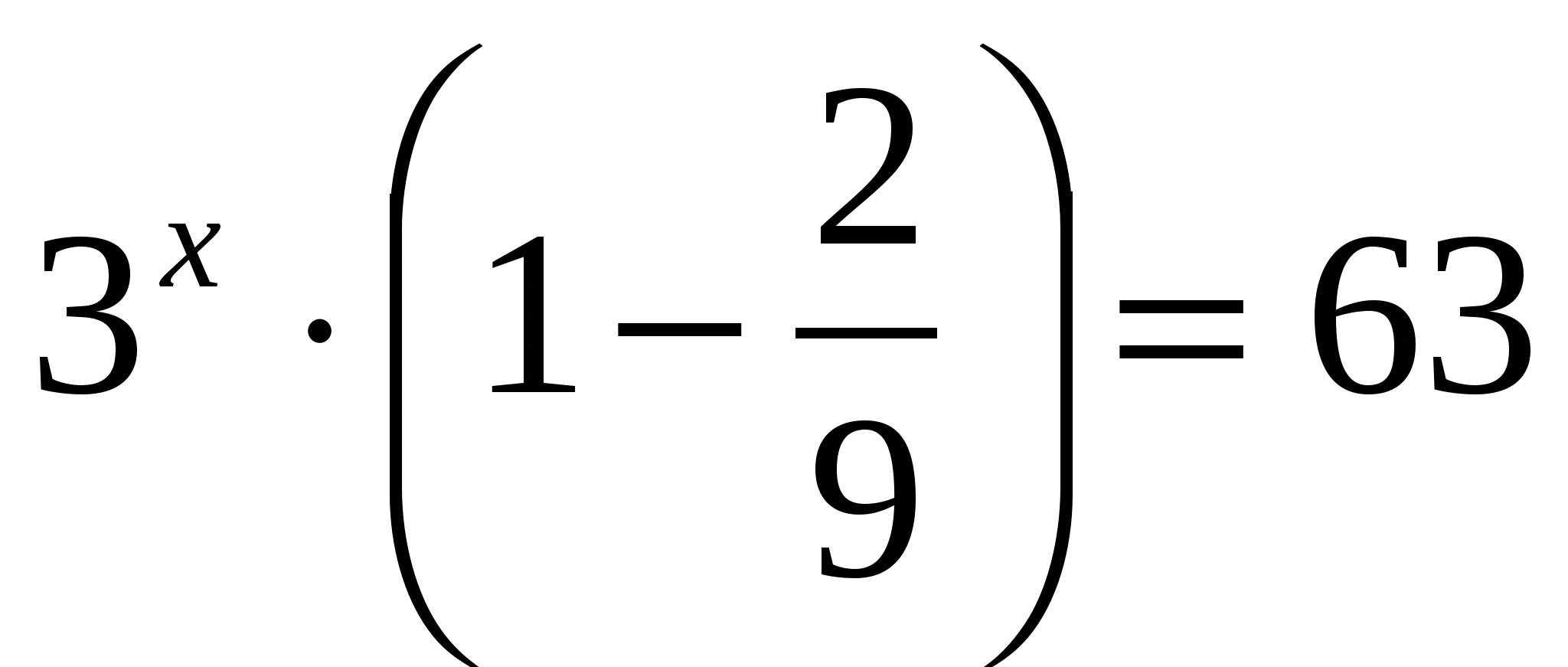
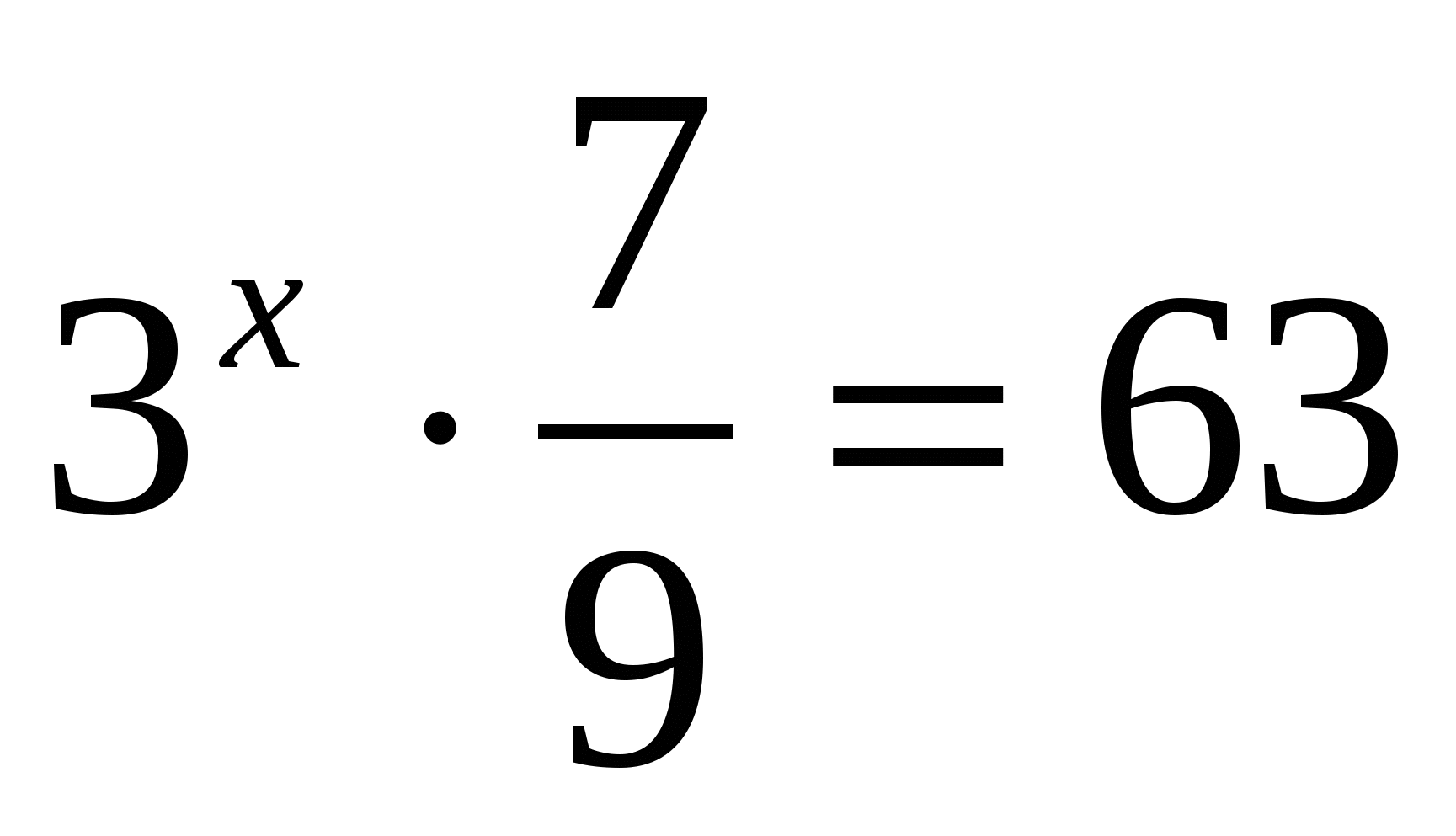
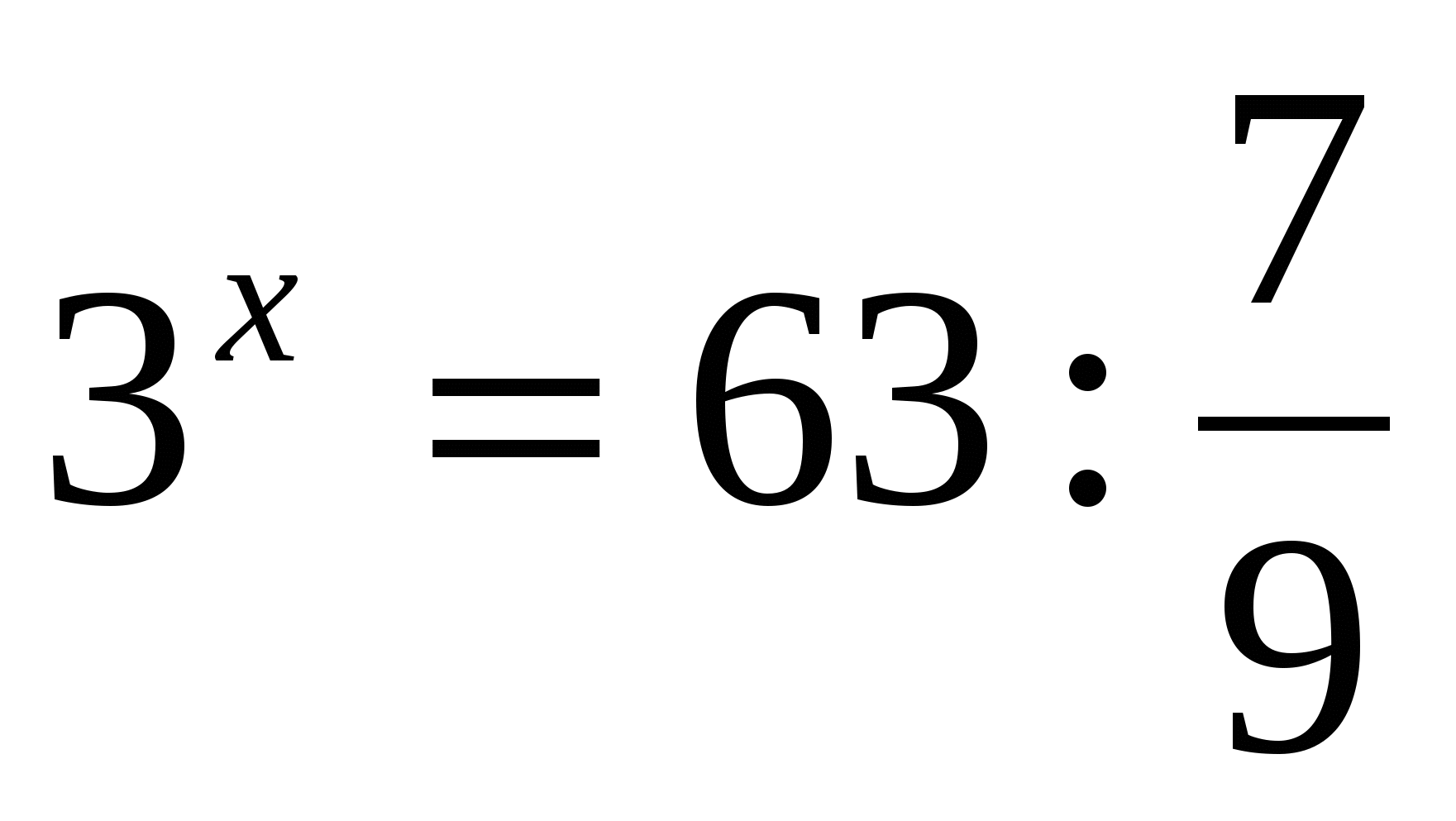

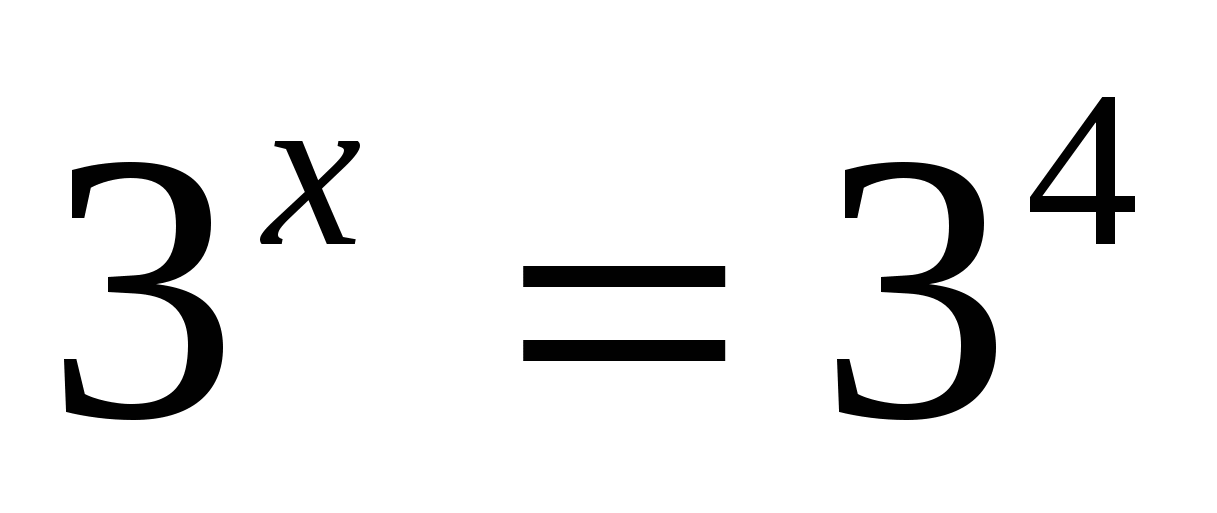
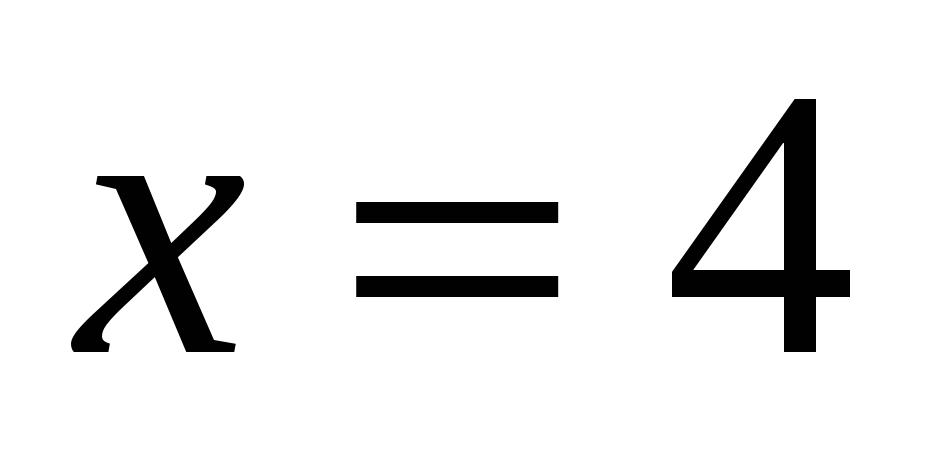
Ответ: 4.
б) 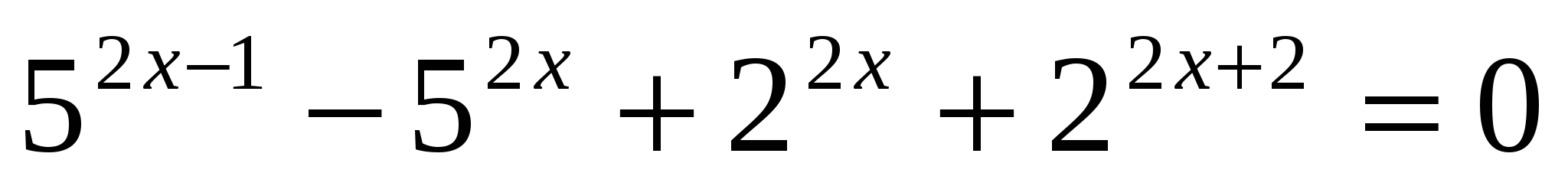
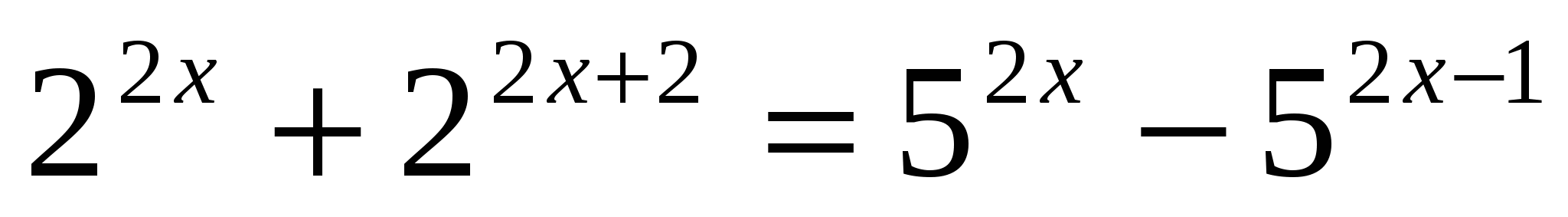
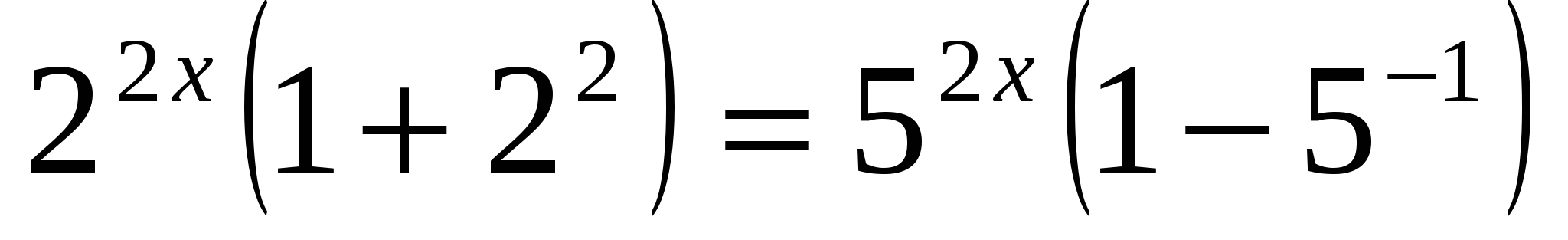
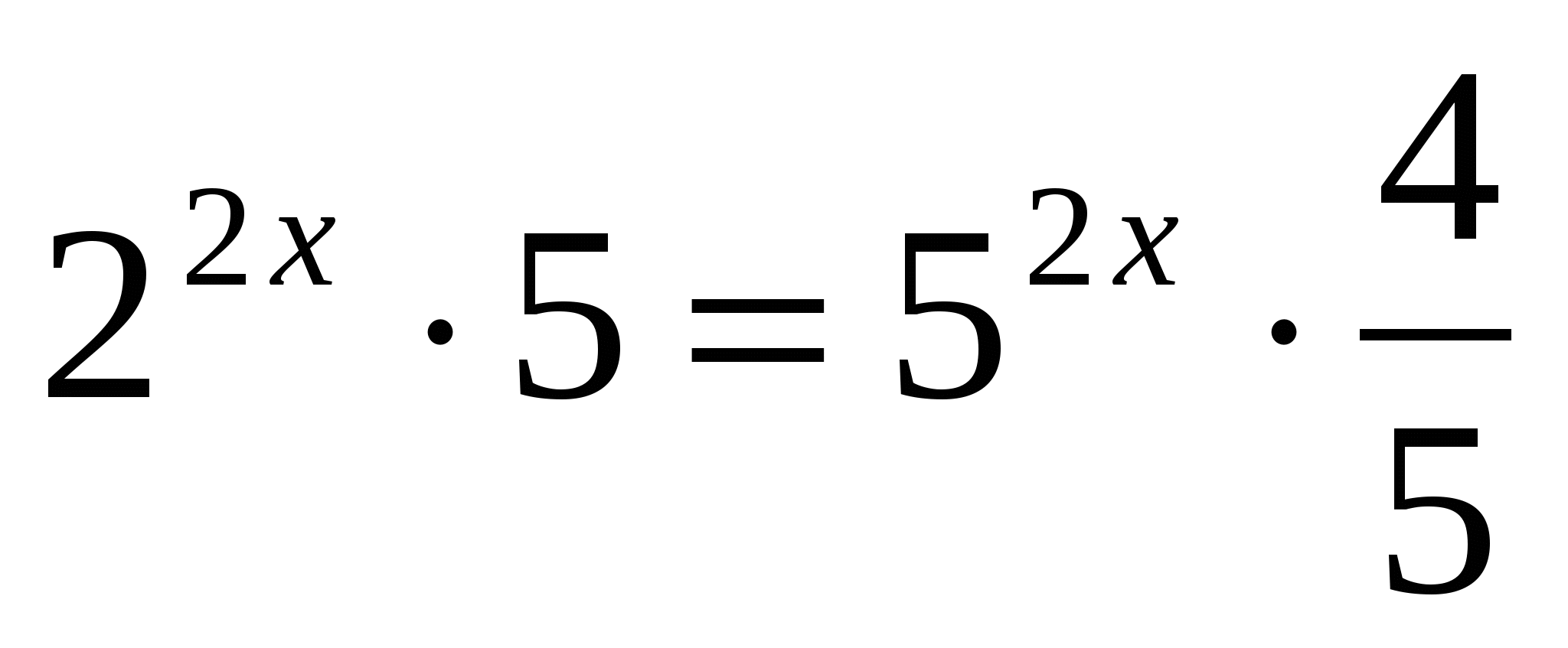
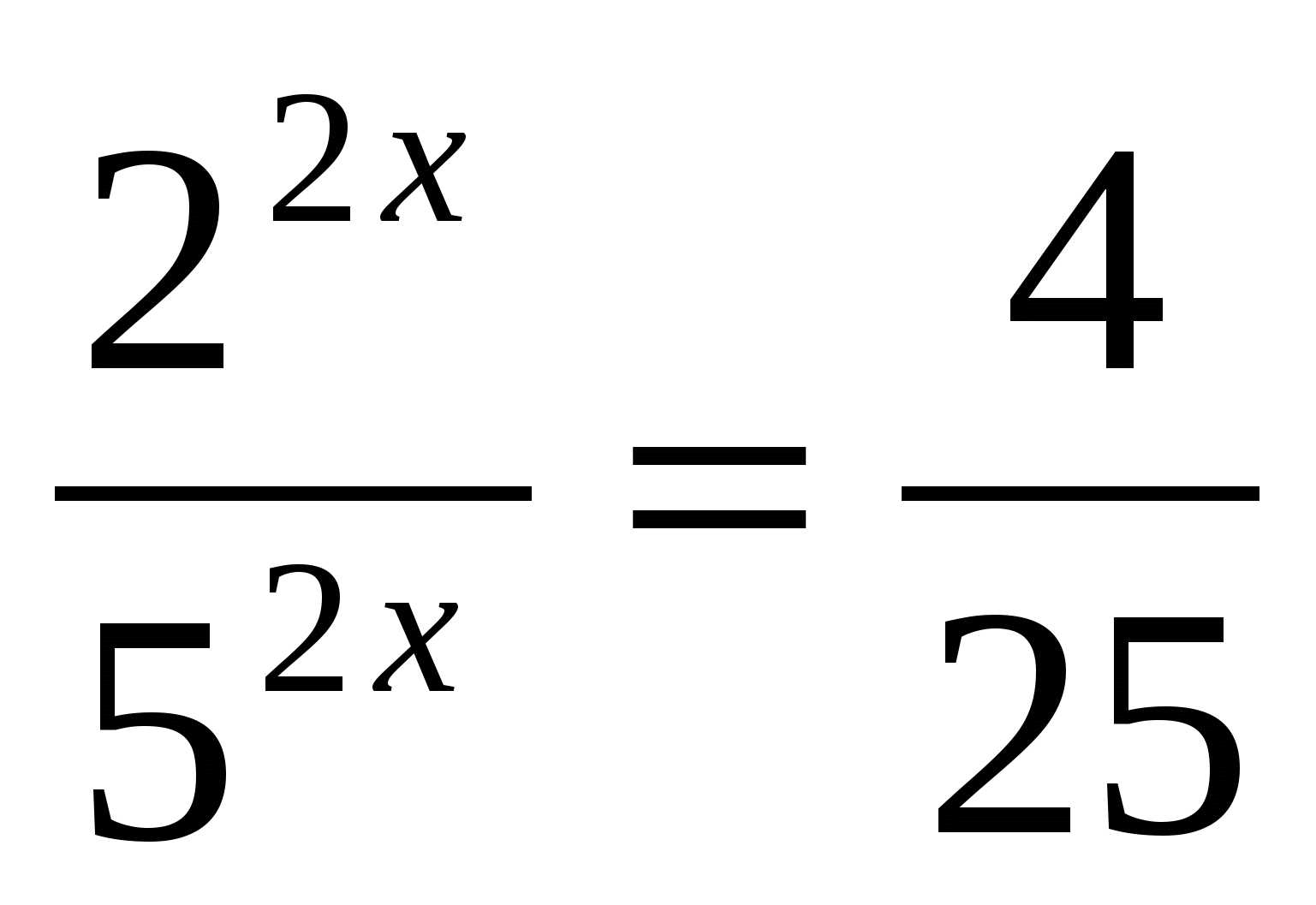
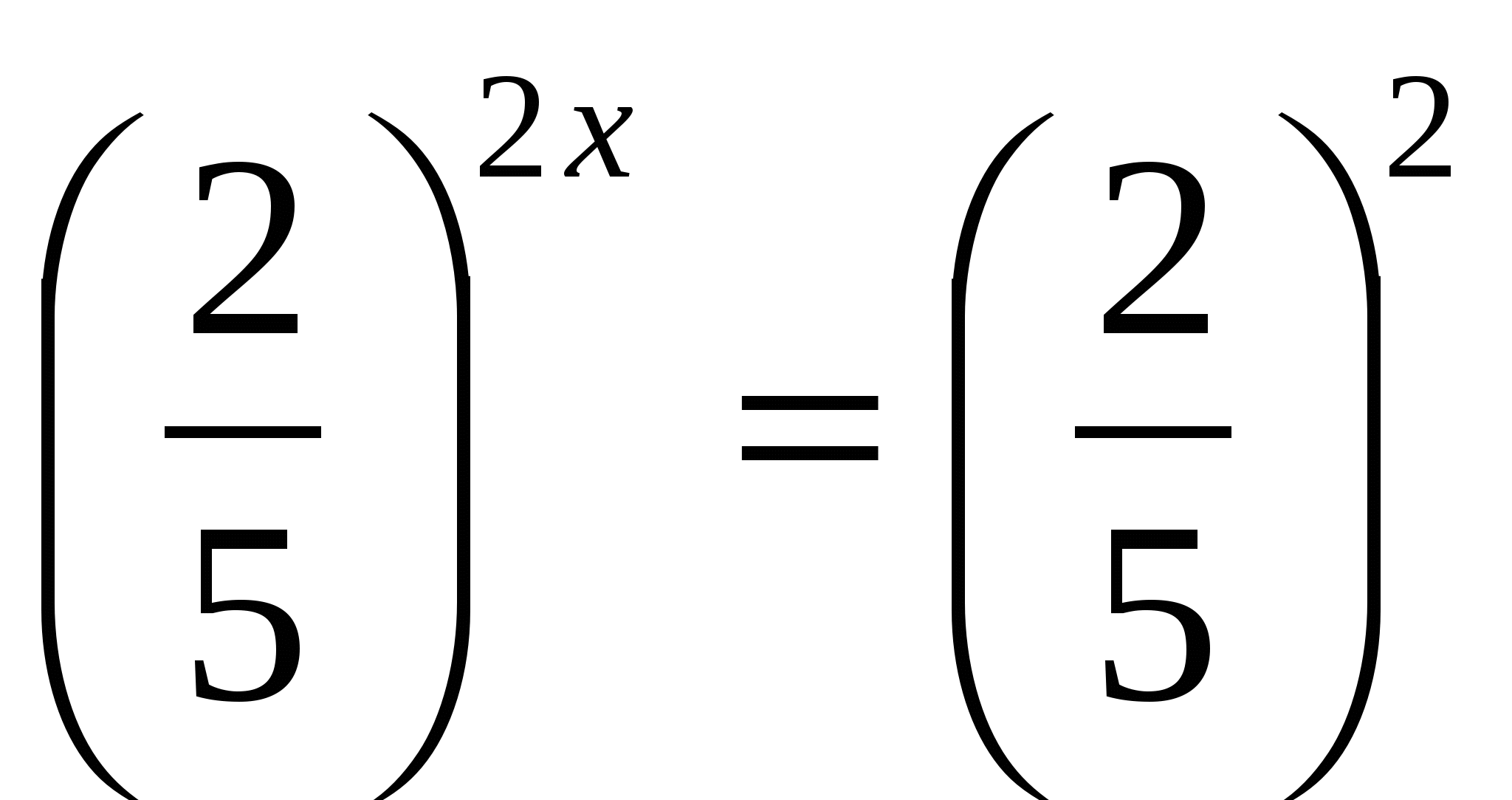
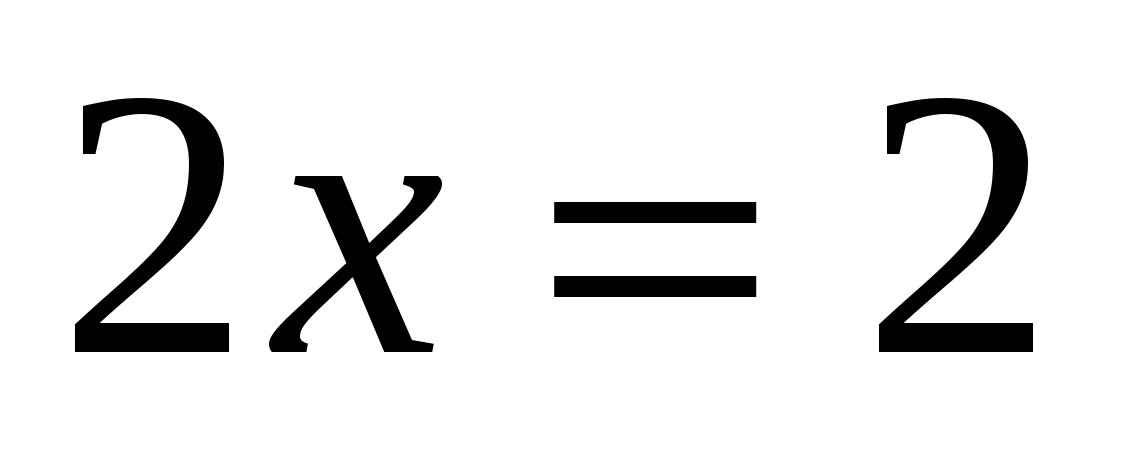
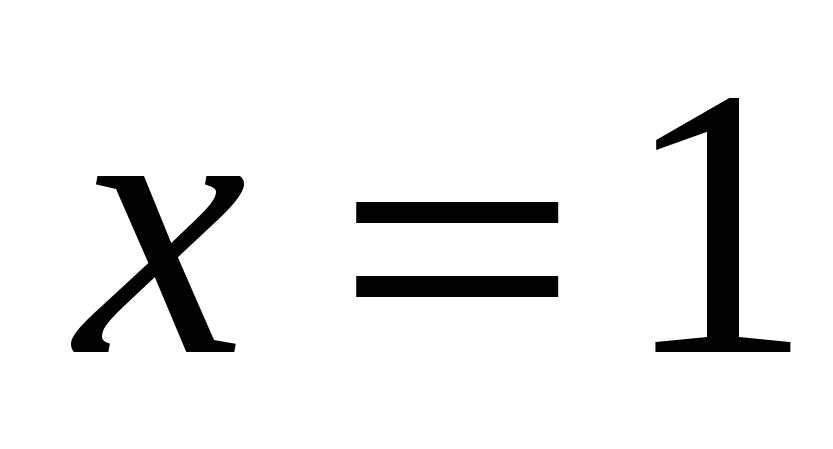
Ответ: 1.
в) 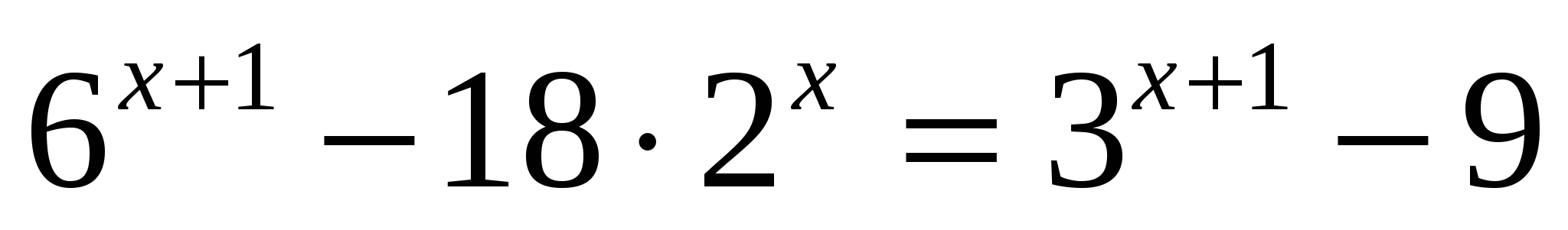
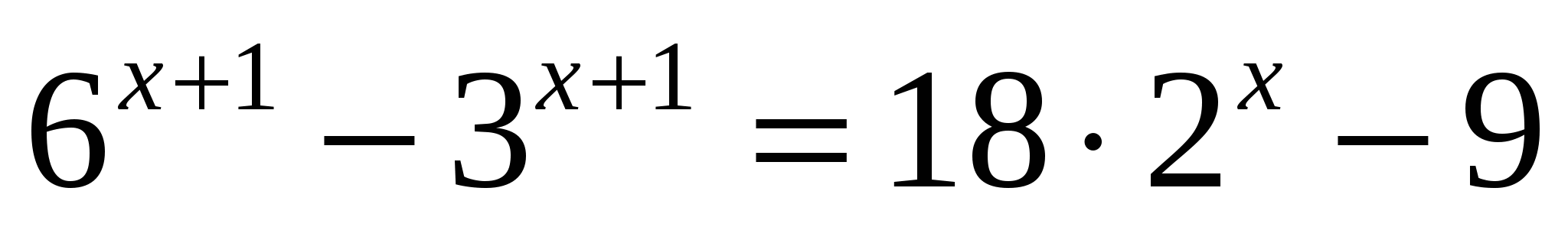
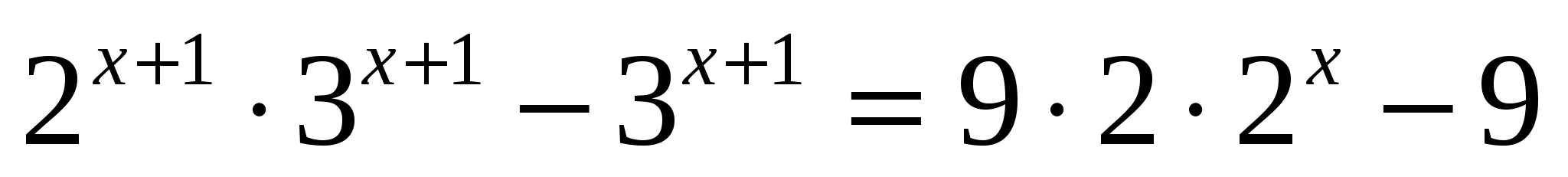
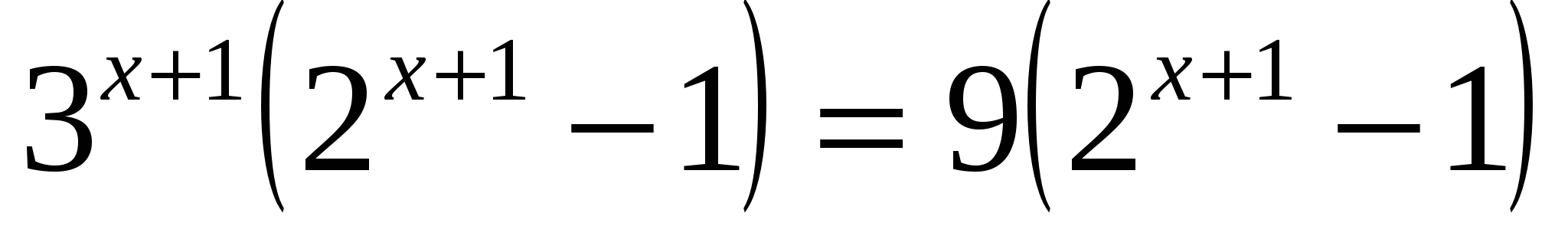
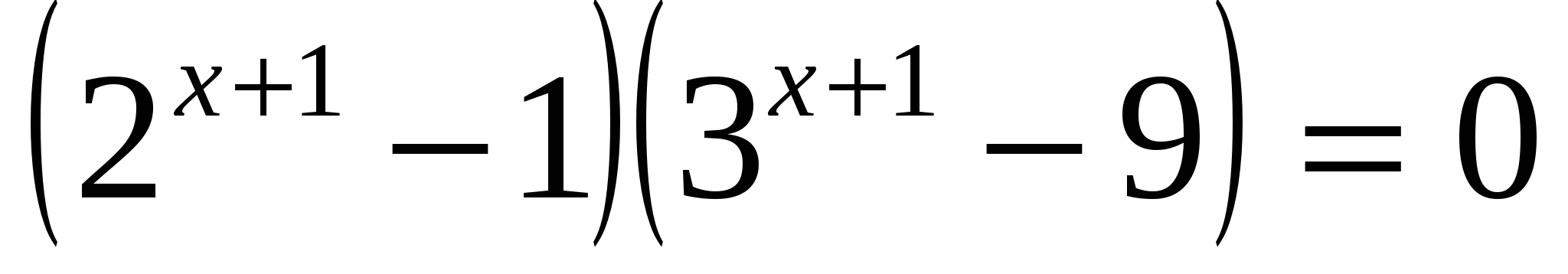
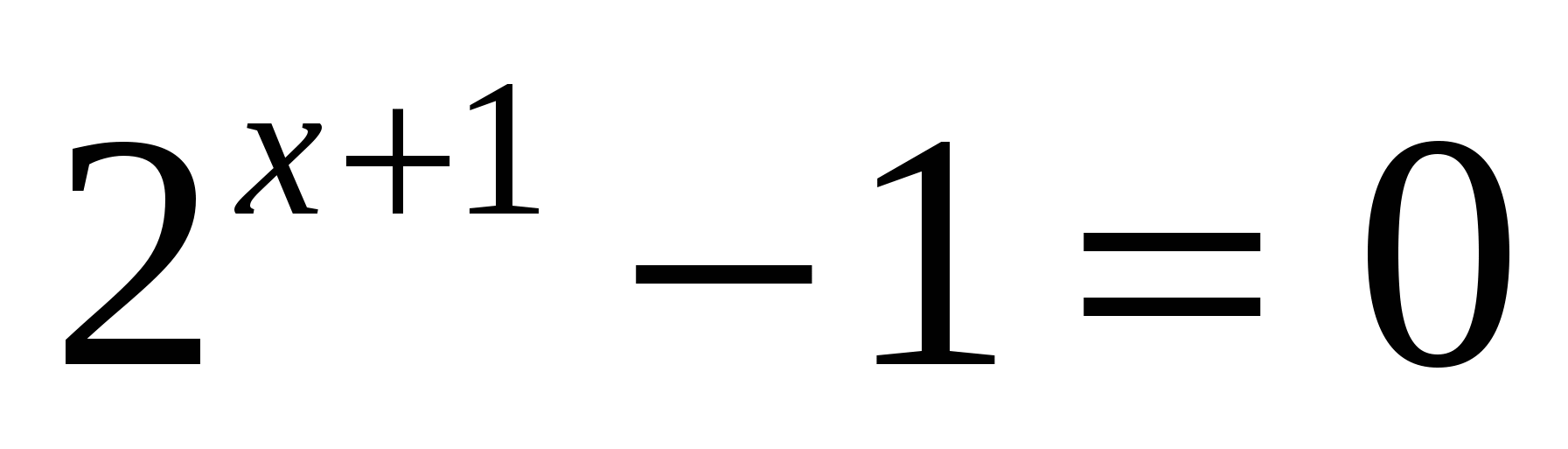 или
или 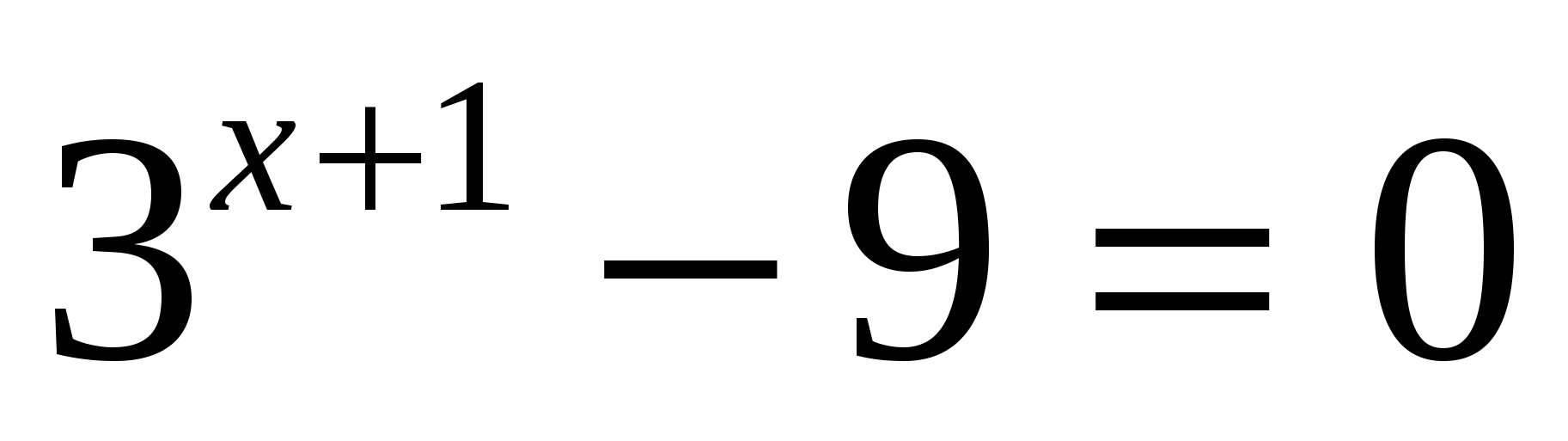
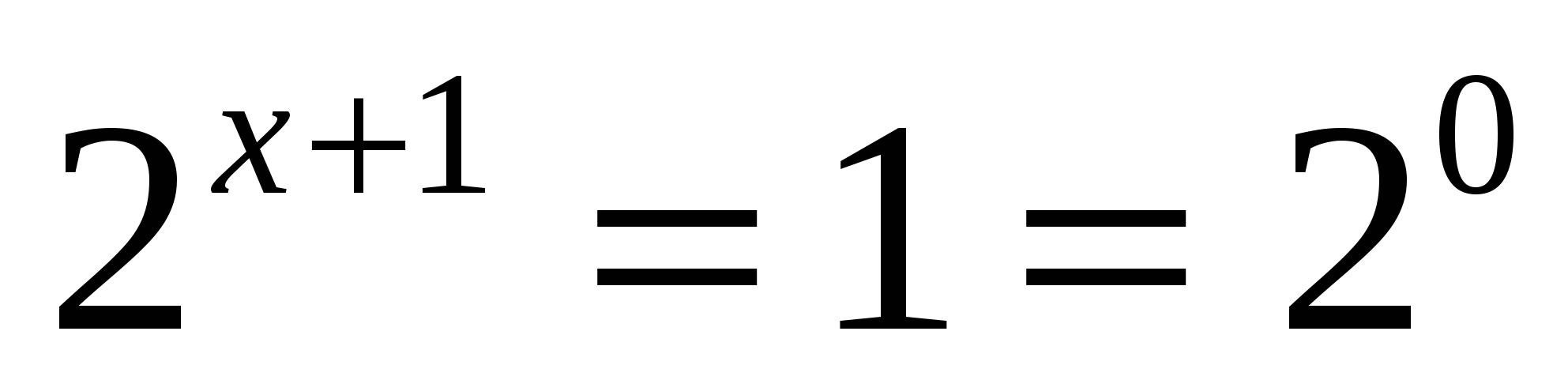

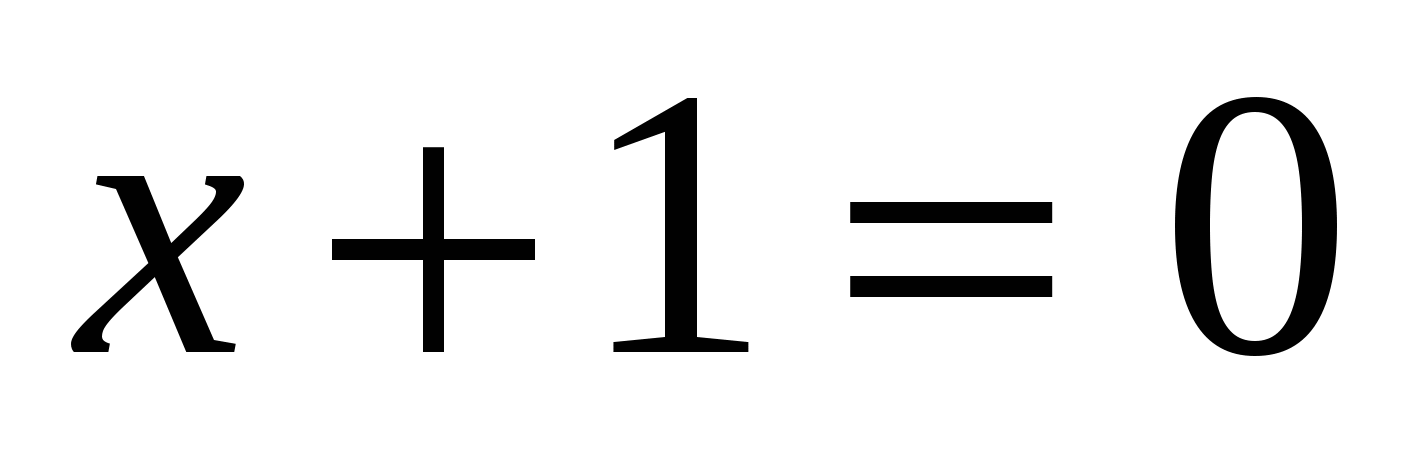
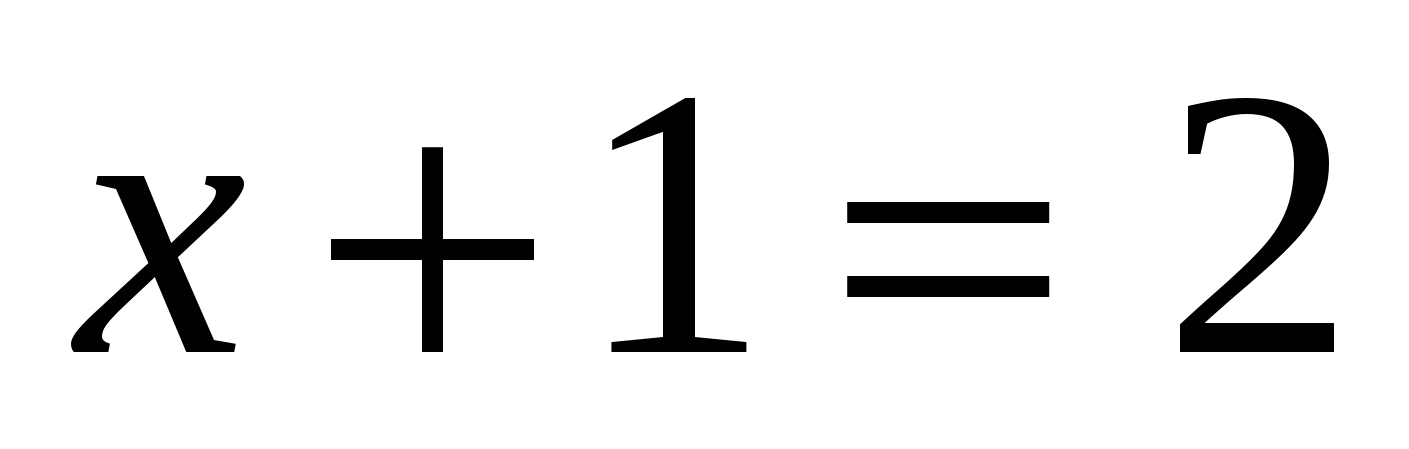
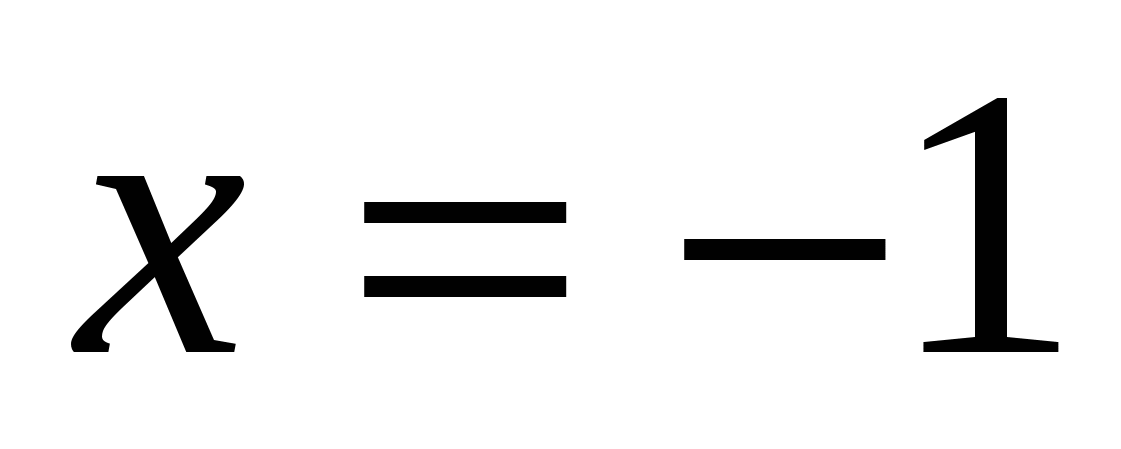
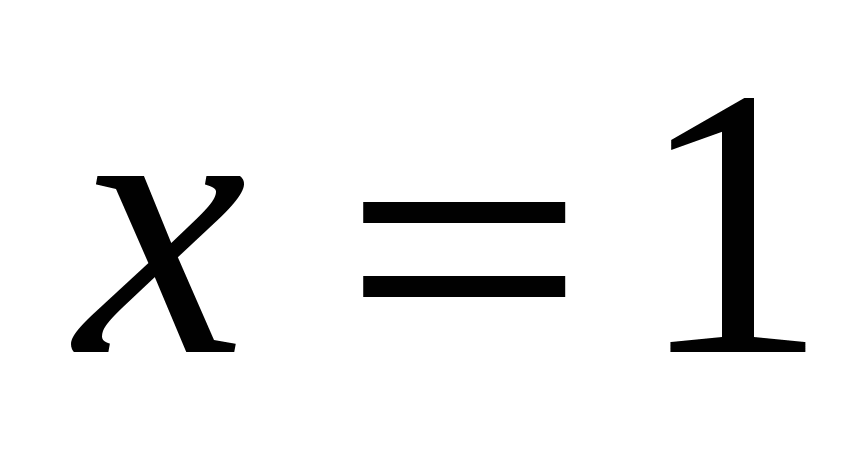
Ответ: -1; 1.
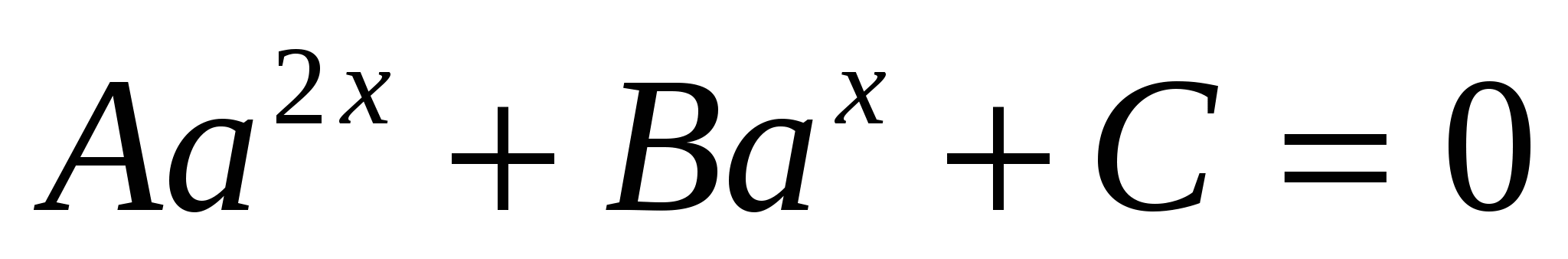
1) обозначить 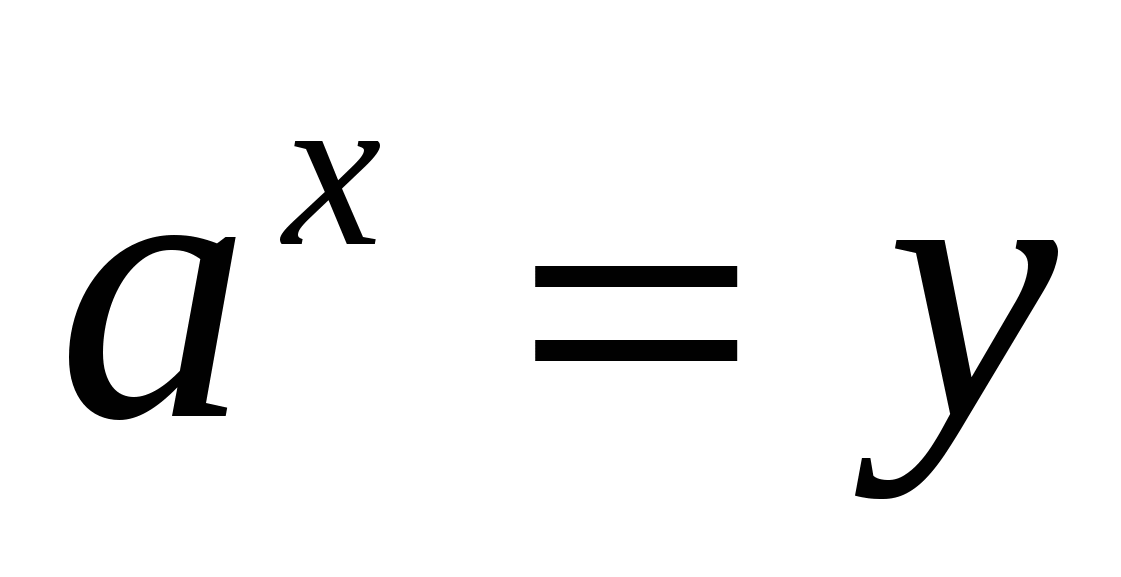
2) решить полученное квадратное уравнение 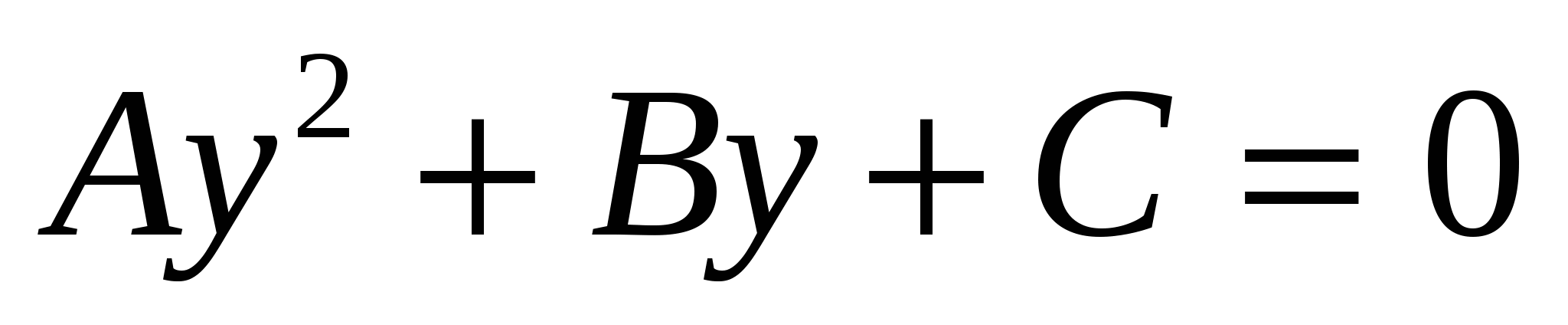 относительно у
относительно у
3) выполнить обратную замену и решить уравнения 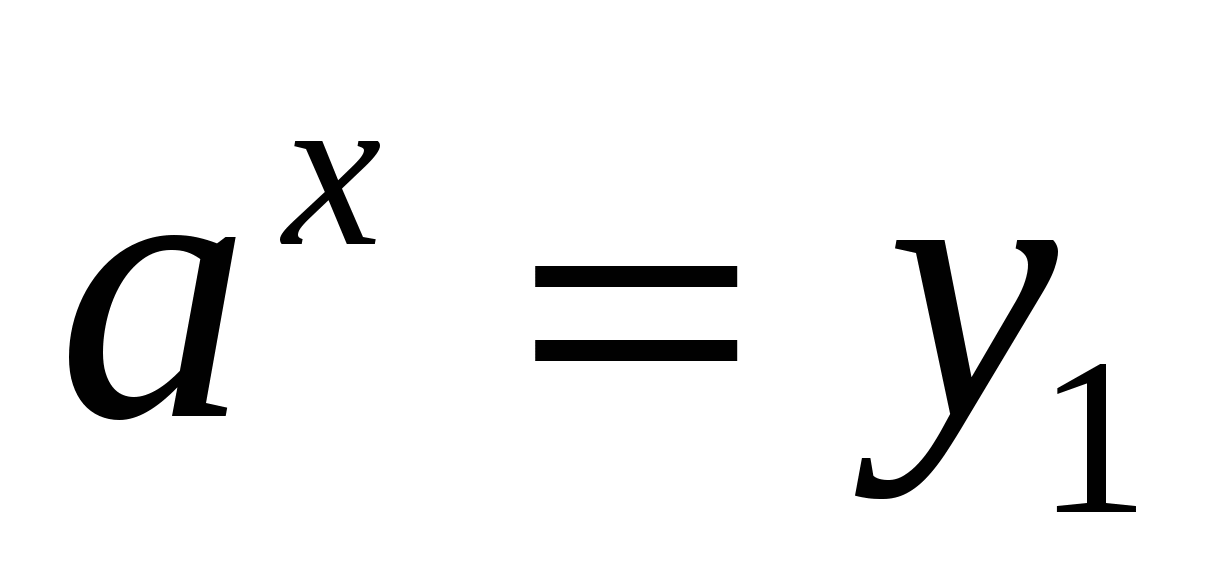 ,
, 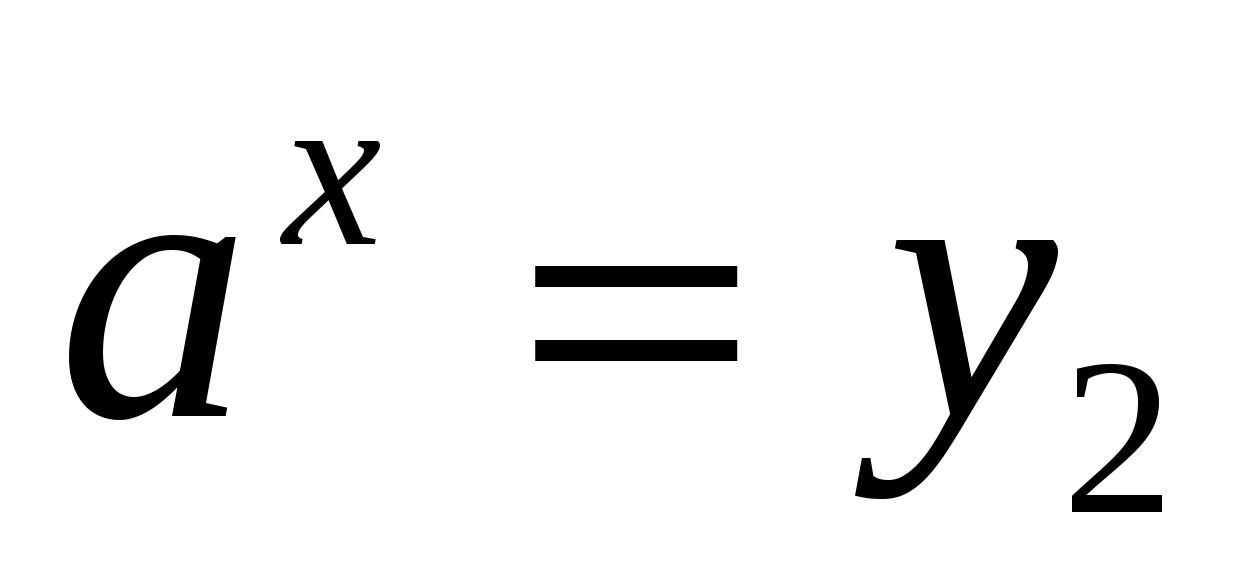 относительно х
относительно х
а) 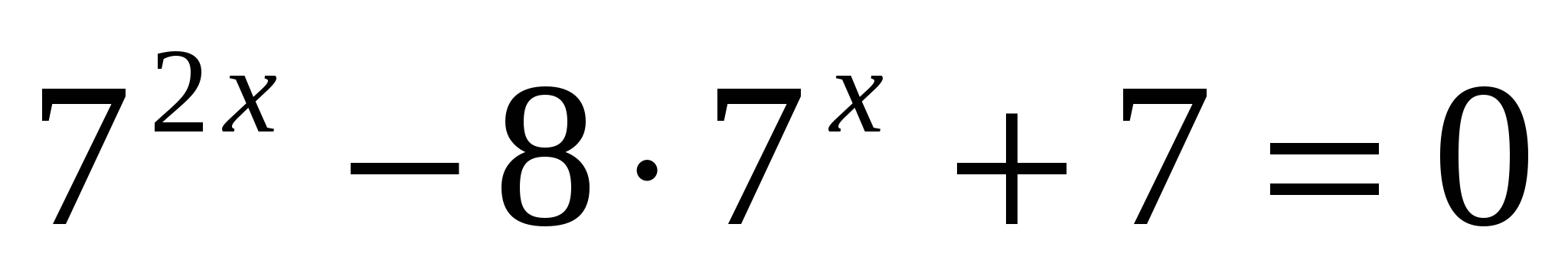
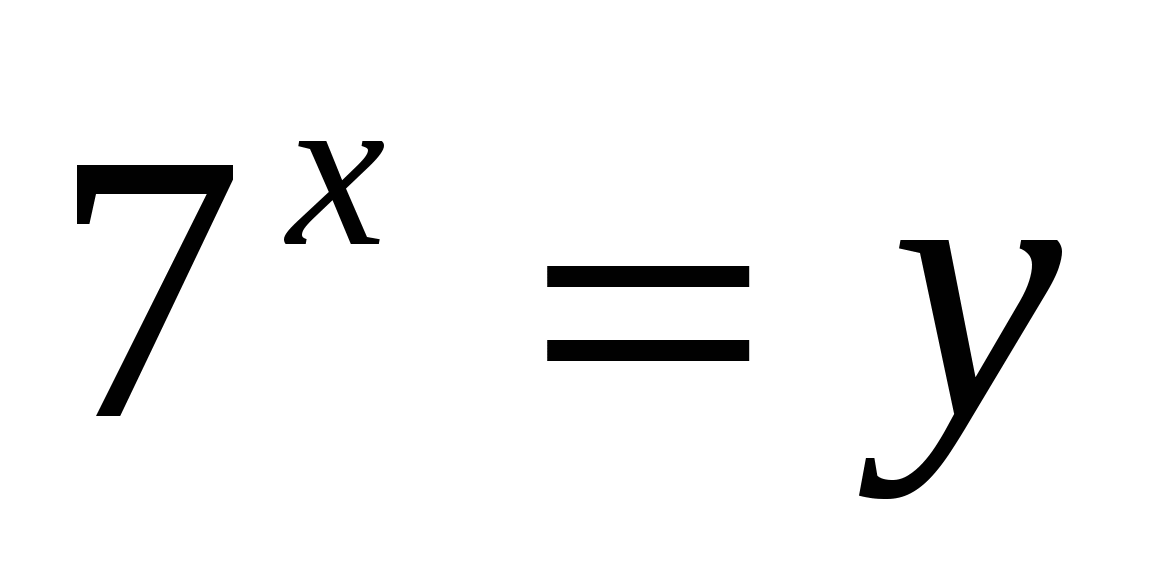
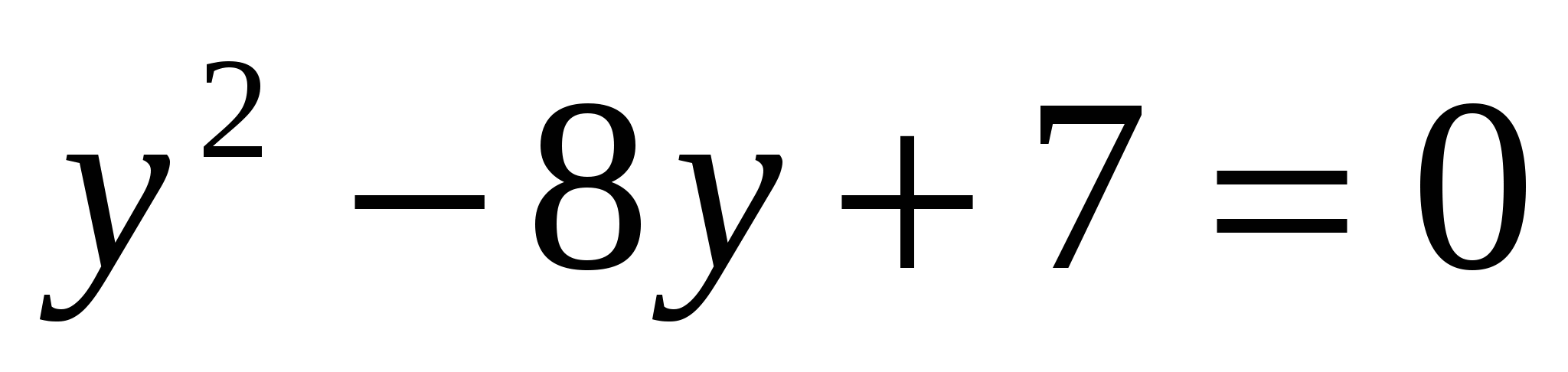
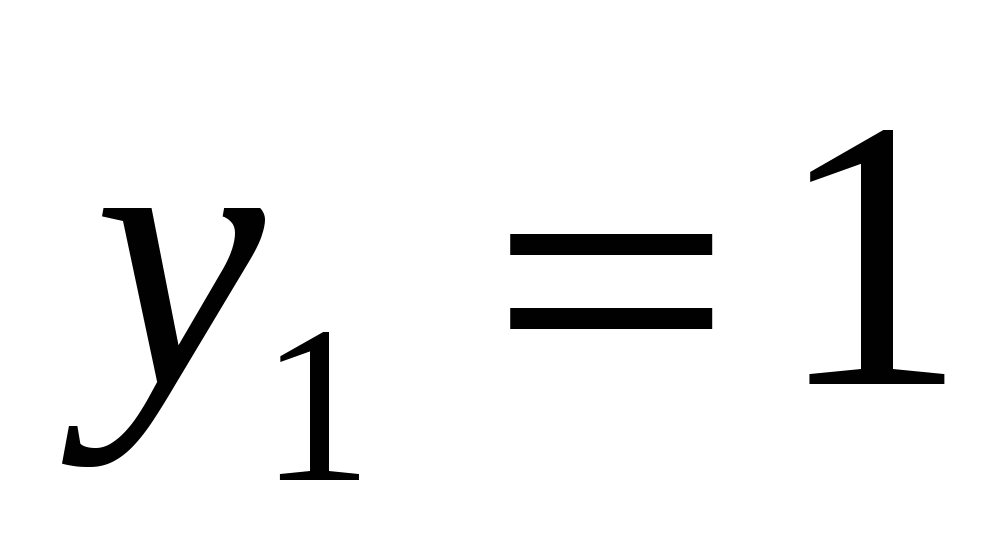 или
или 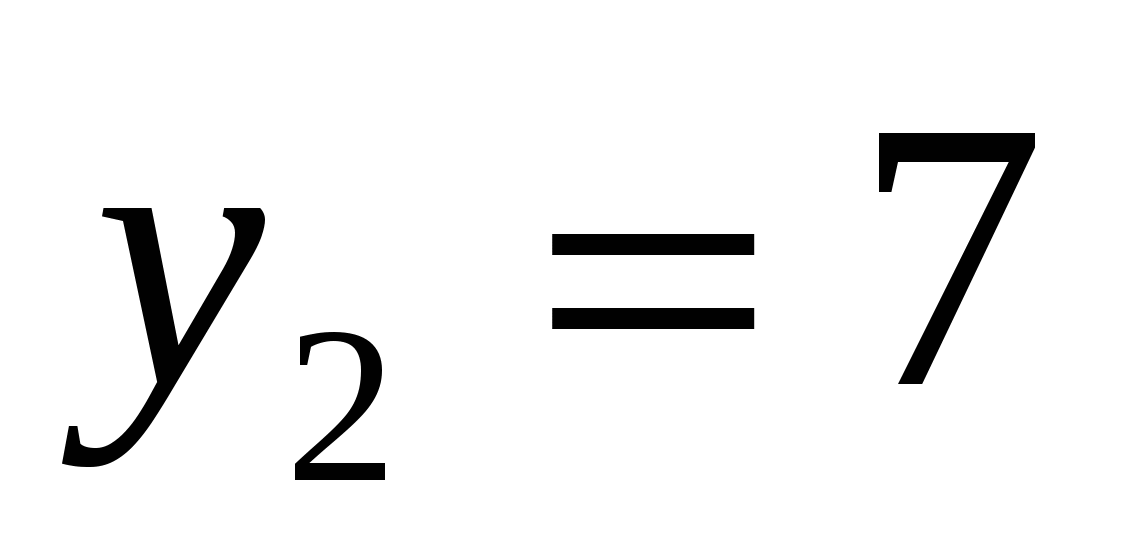
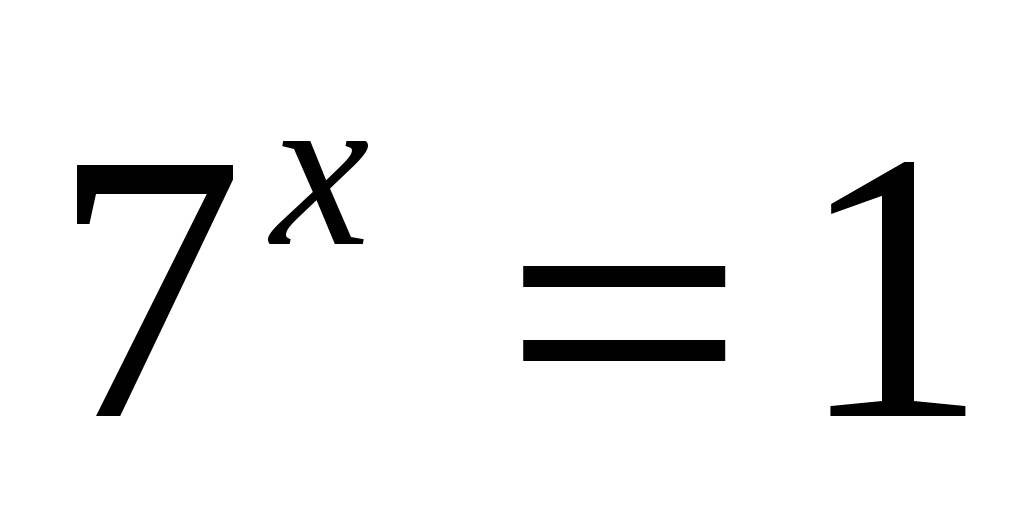
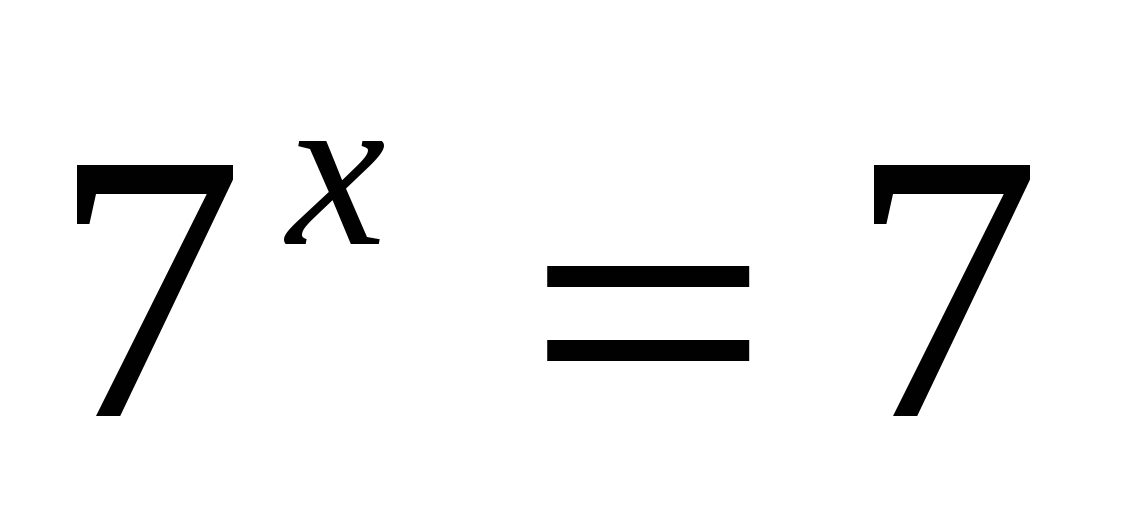
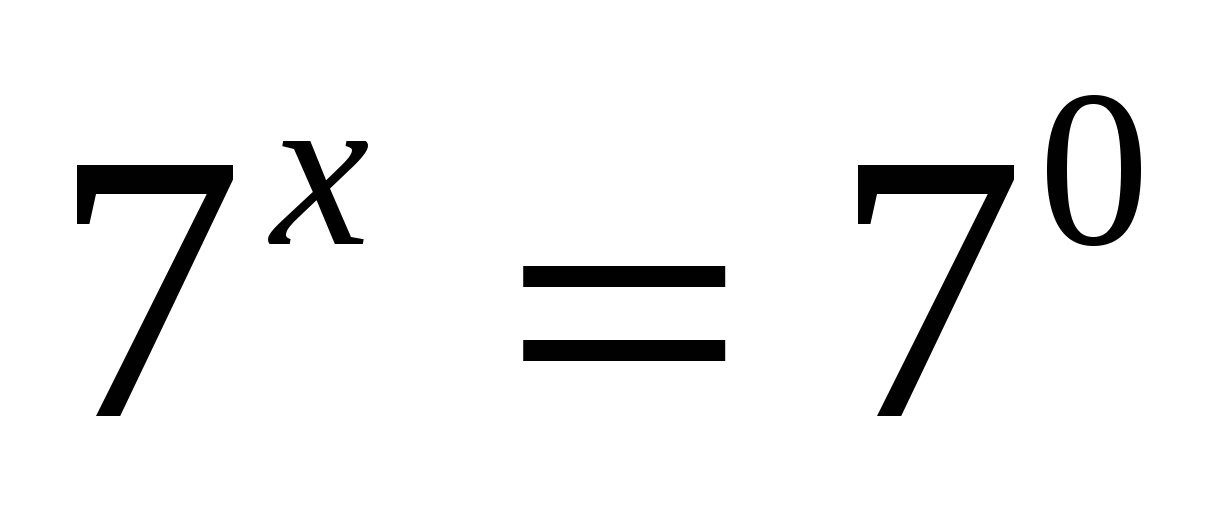
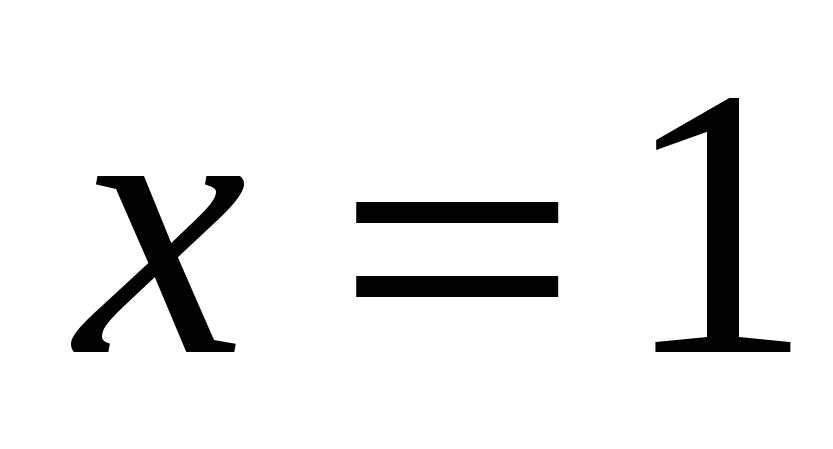
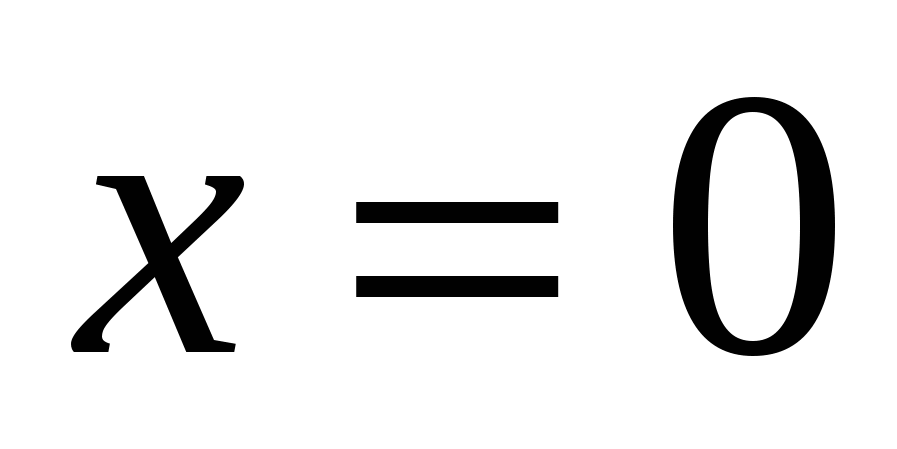
Ответ: 0; 1.
б) 
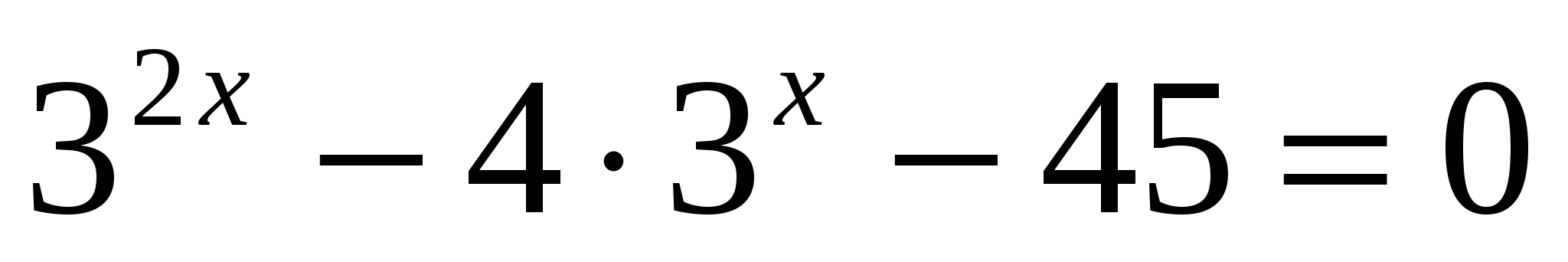
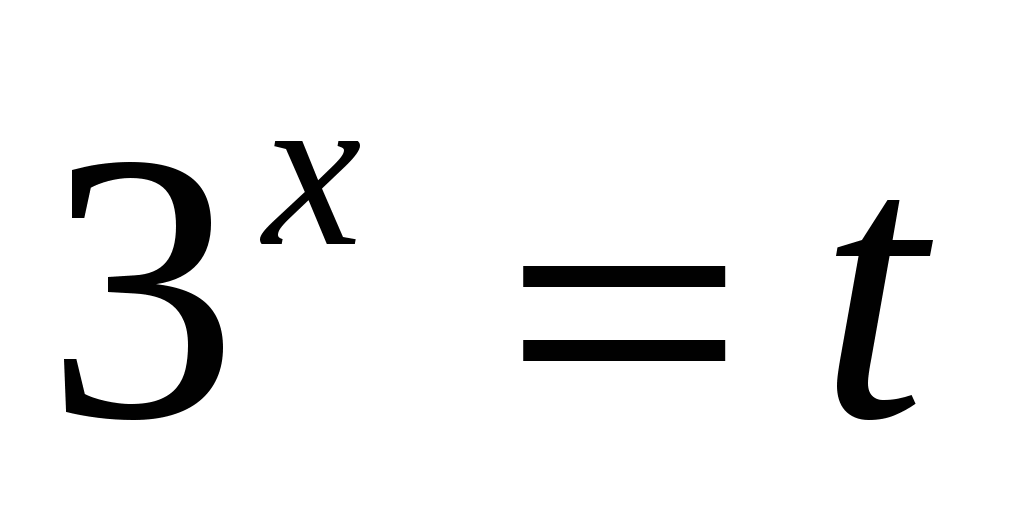
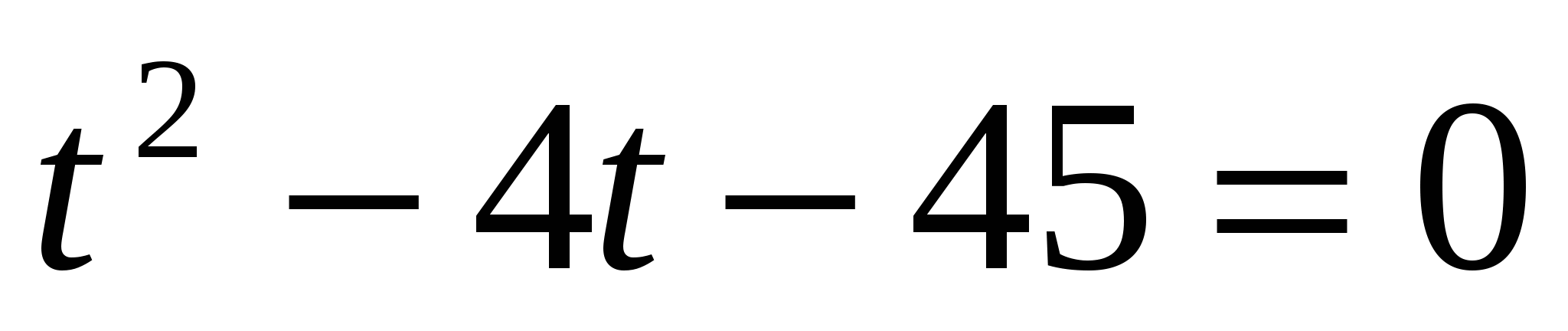
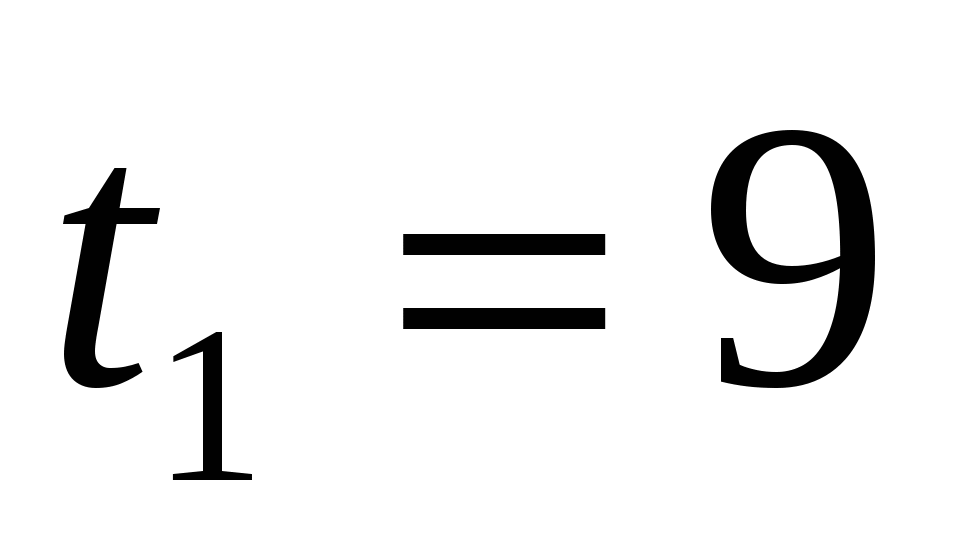 или
или 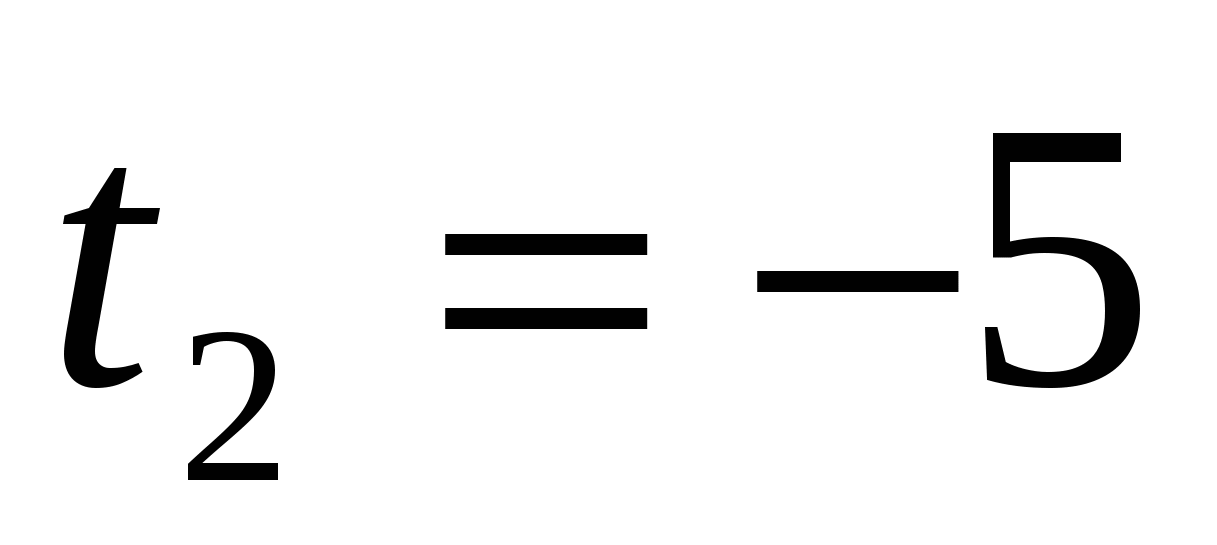
1) 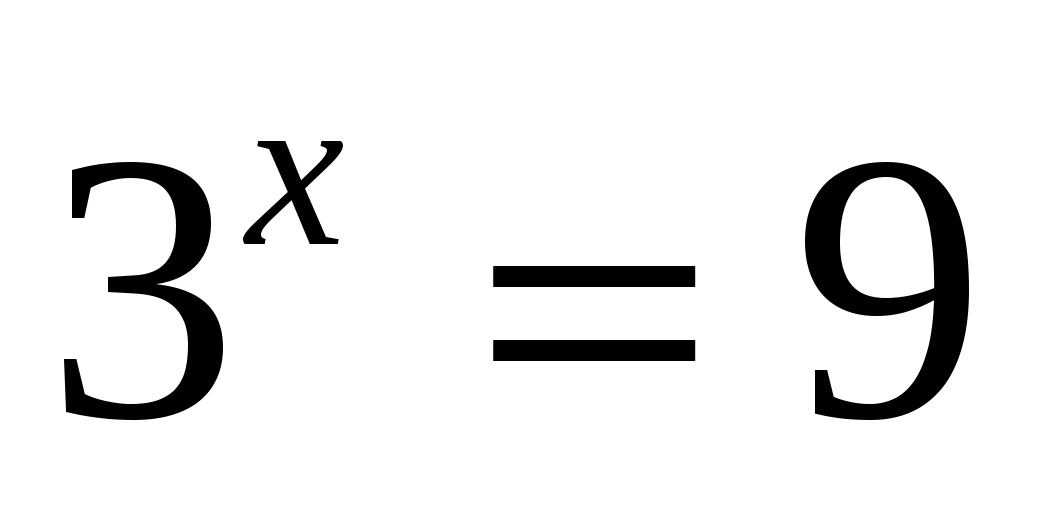
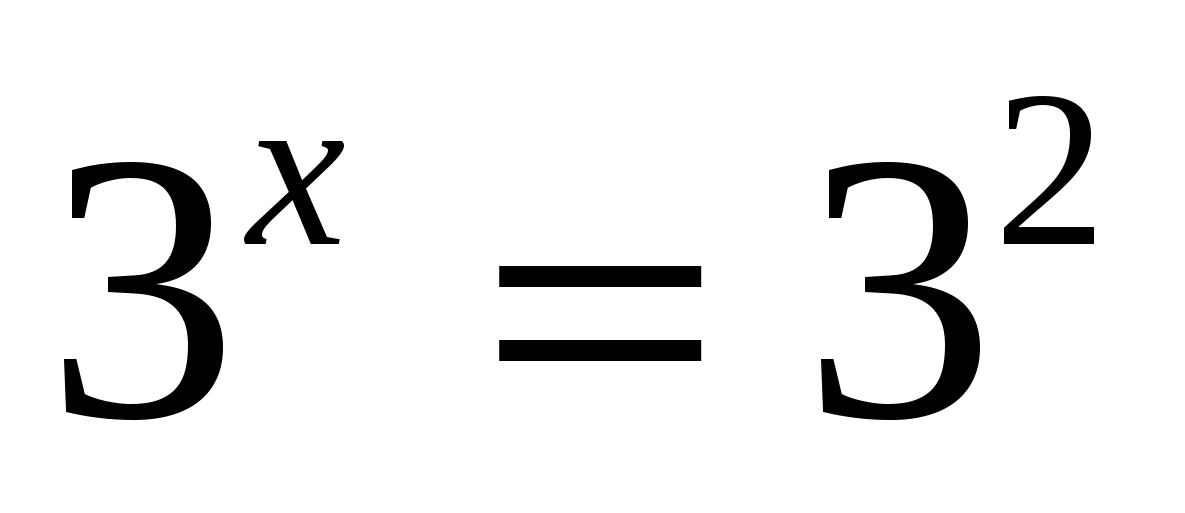
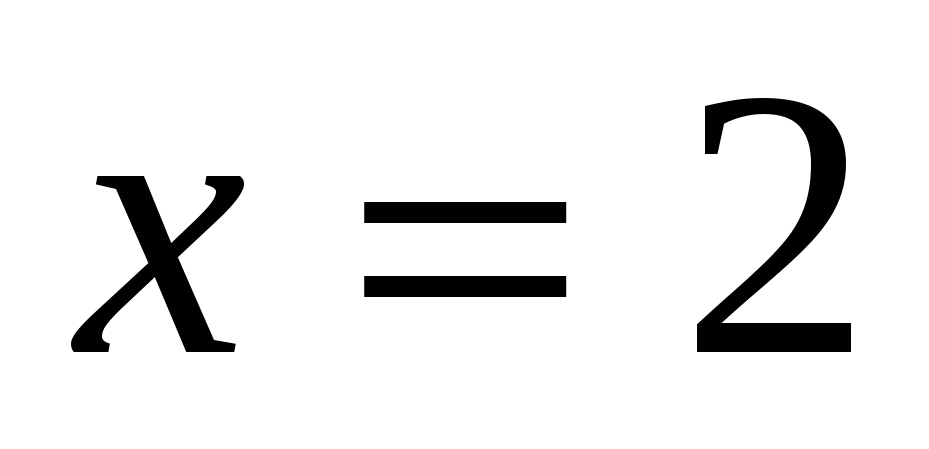
2) 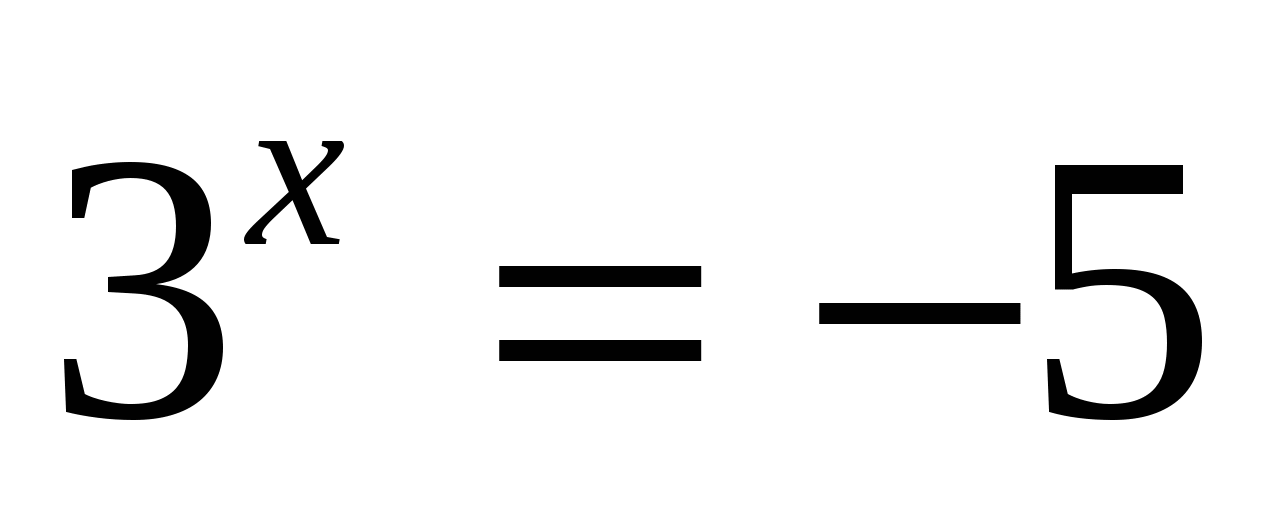
корней нет,
т.к. 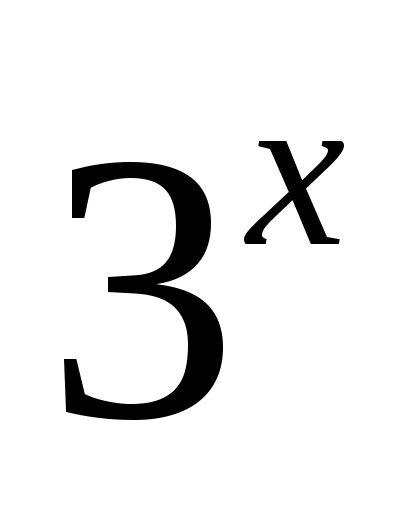 > 0 при любом
> 0 при любом 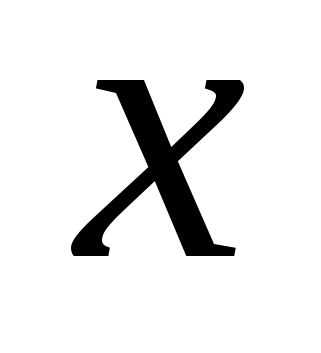
Ответ: 2.
в) 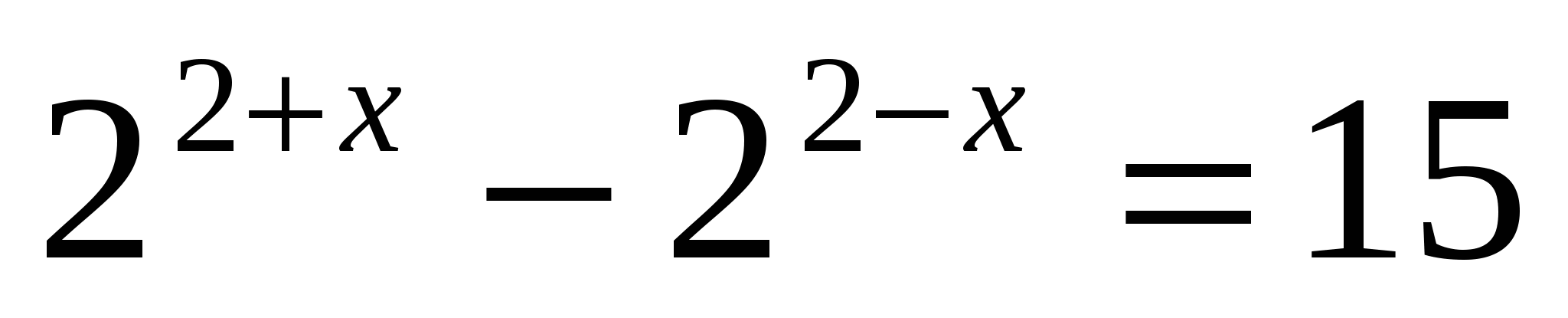
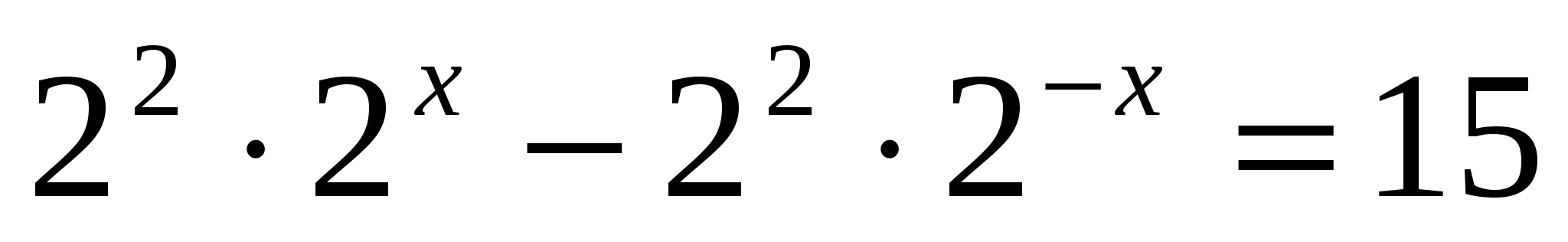
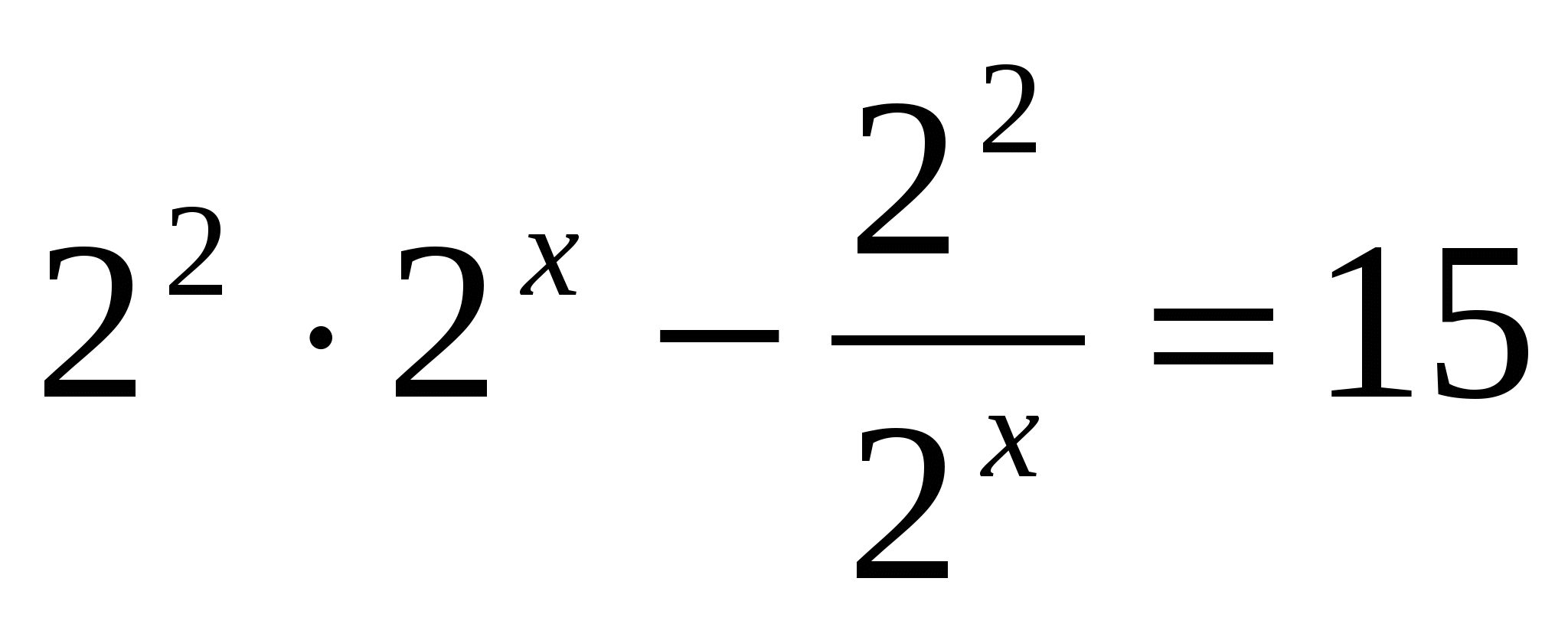
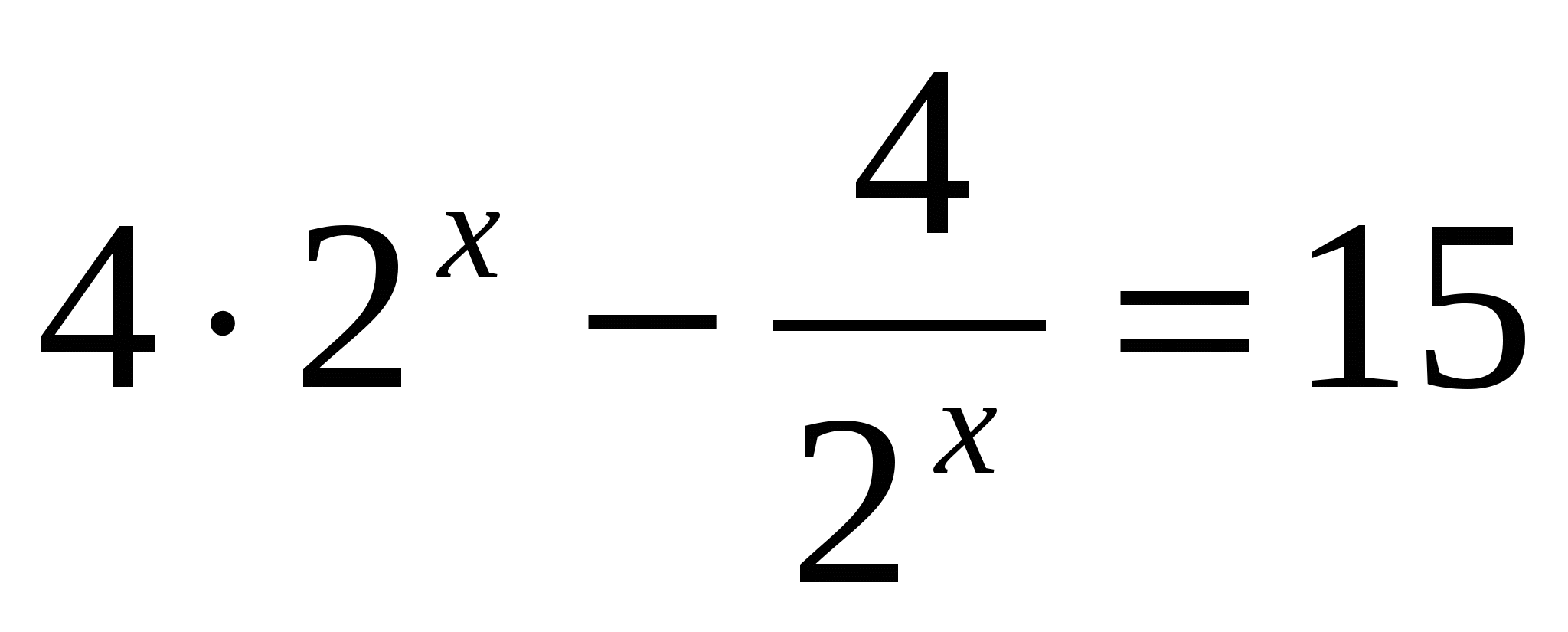
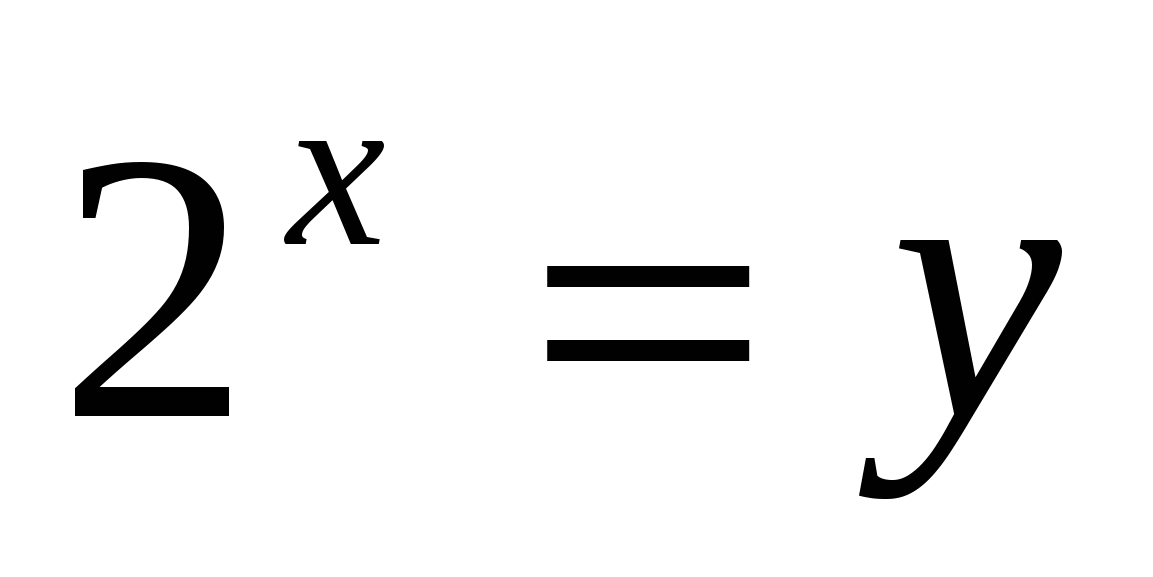
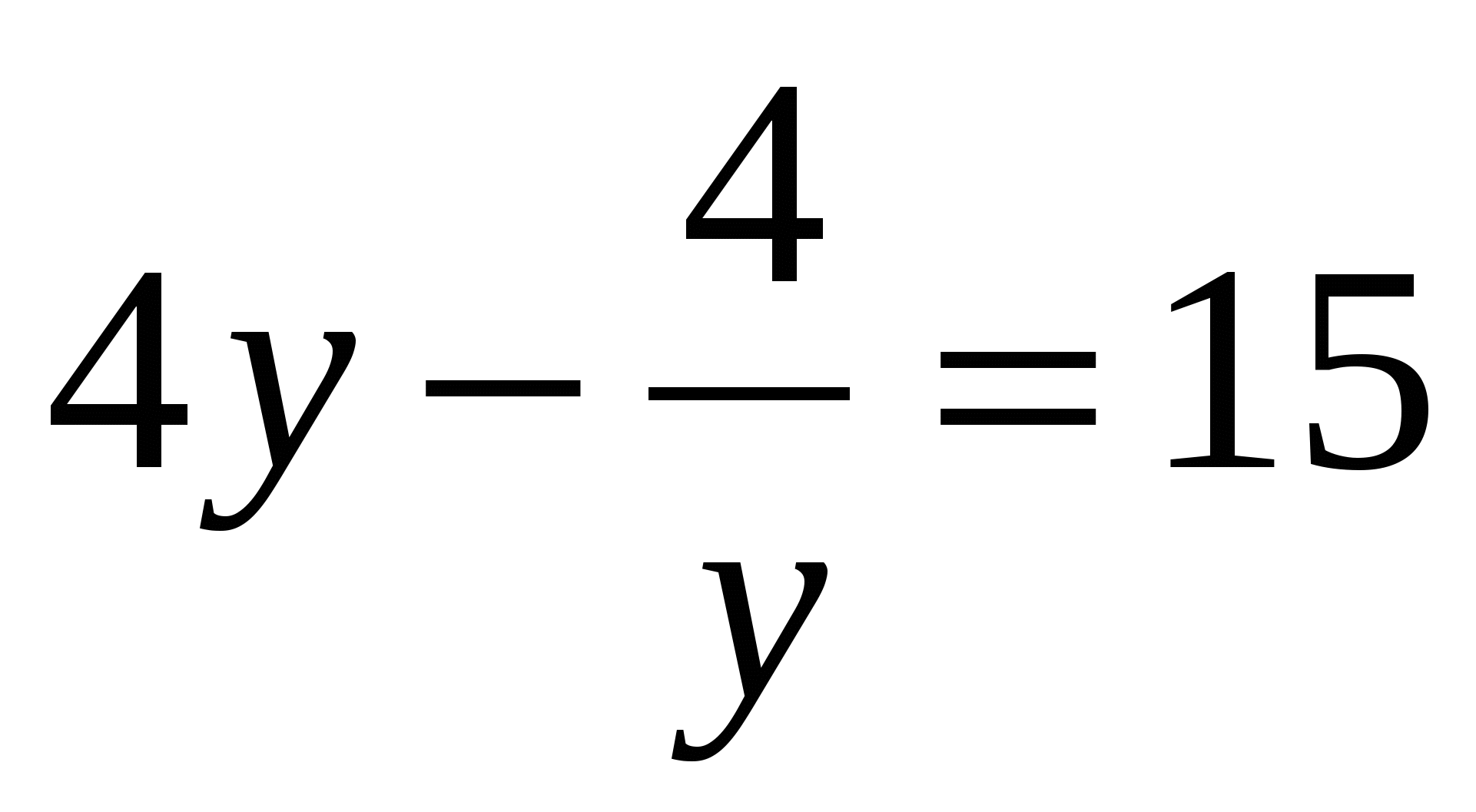
т.к 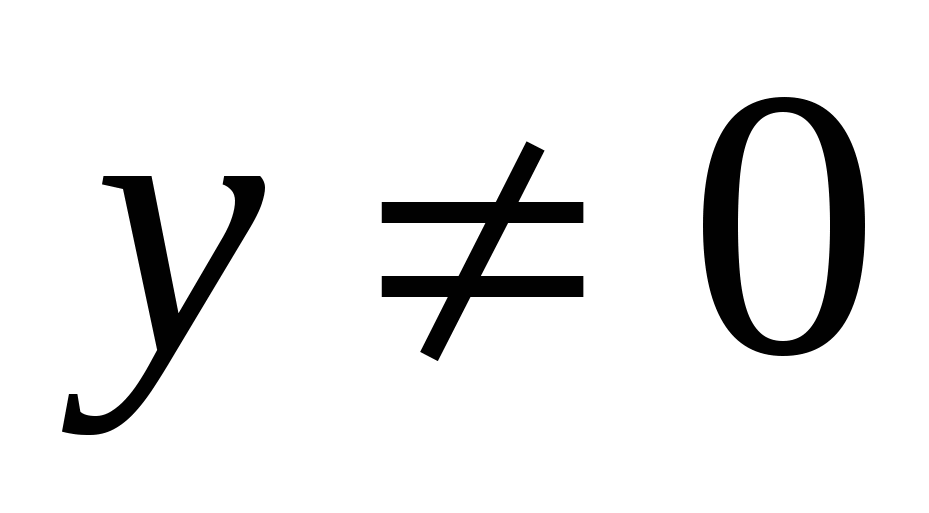 , умножим всё уравнение на
, умножим всё уравнение на 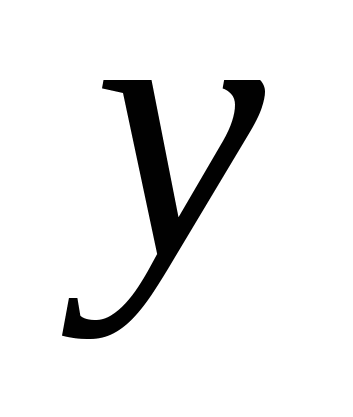
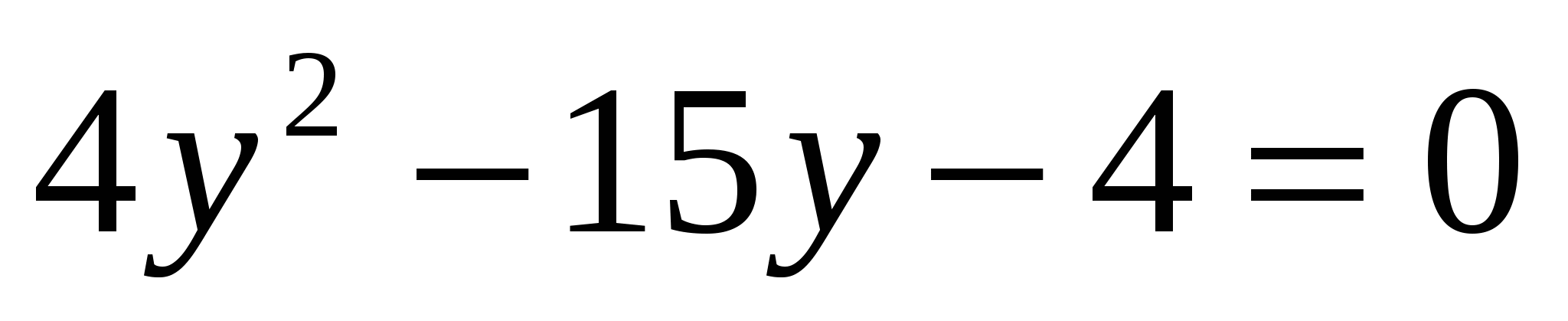
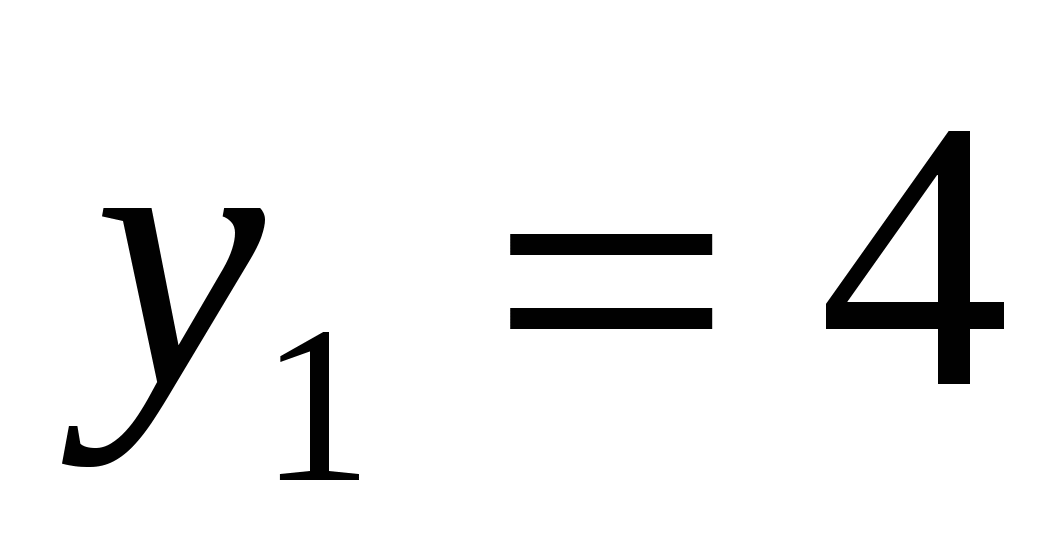 или
или 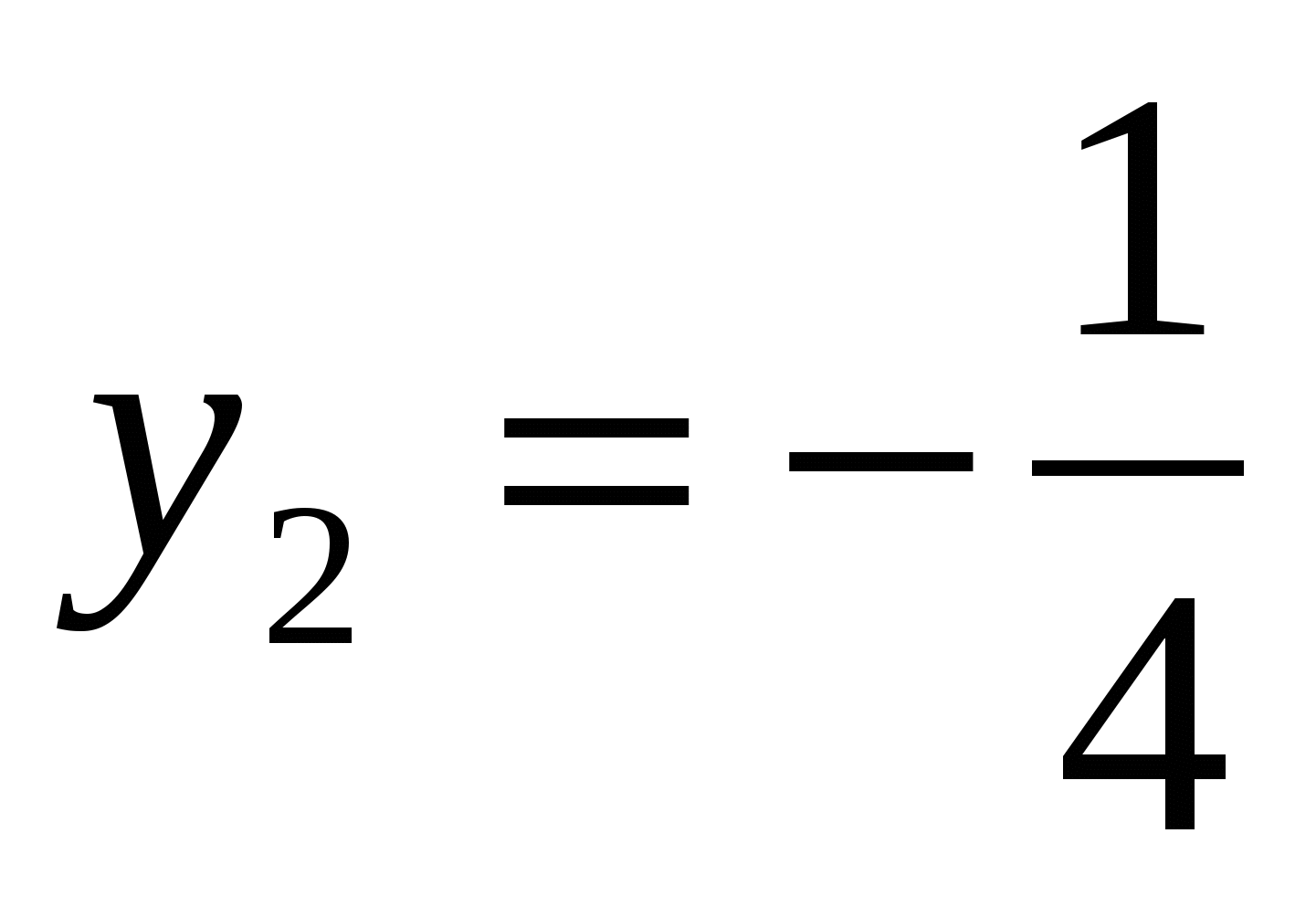
1) 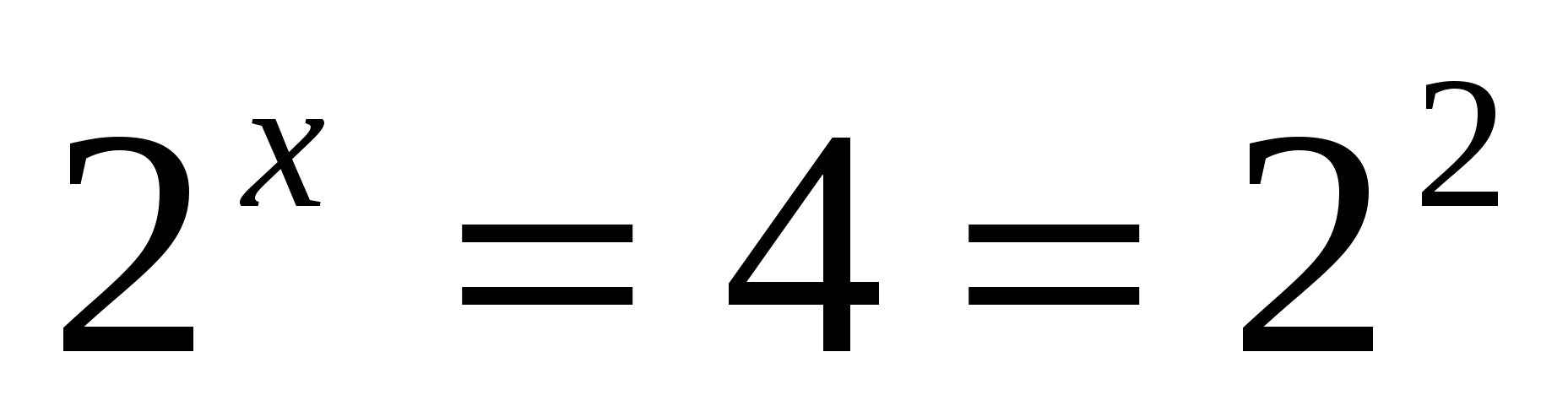
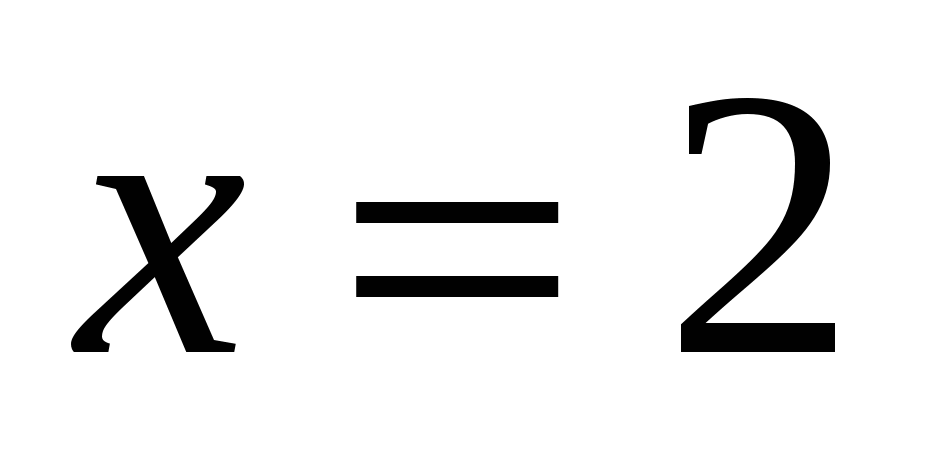
2) 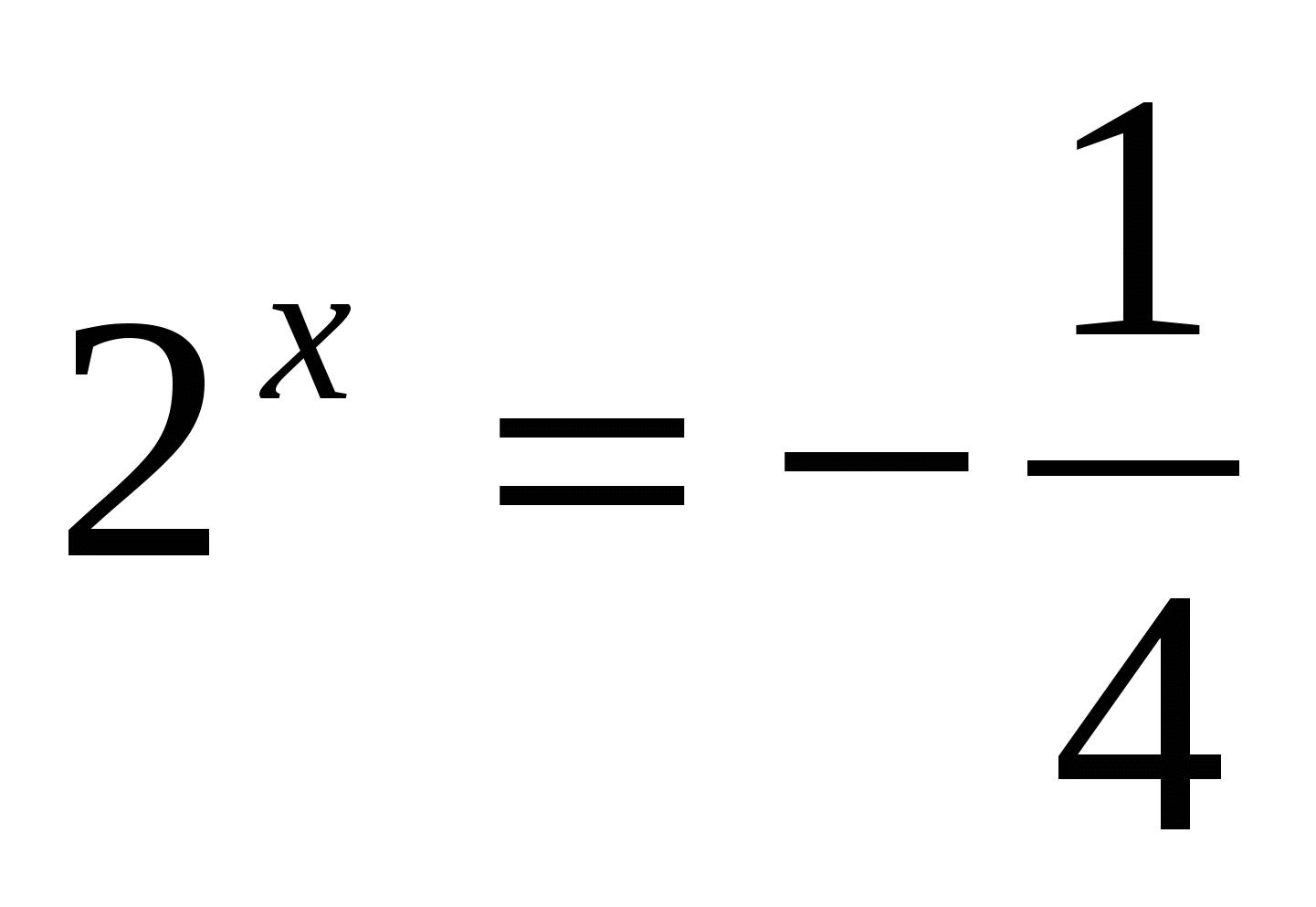
нет решений,
т. к.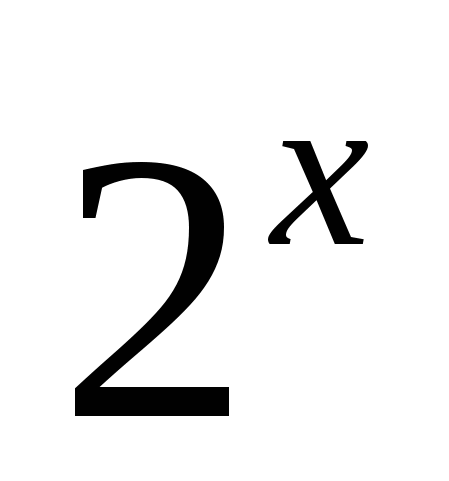 > 0 при любом
> 0 при любом 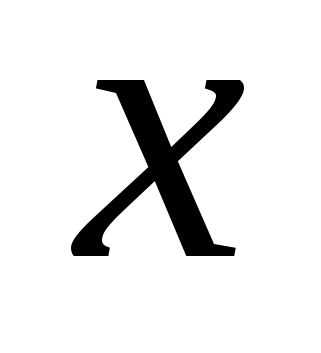
Ответ: 2.
г) 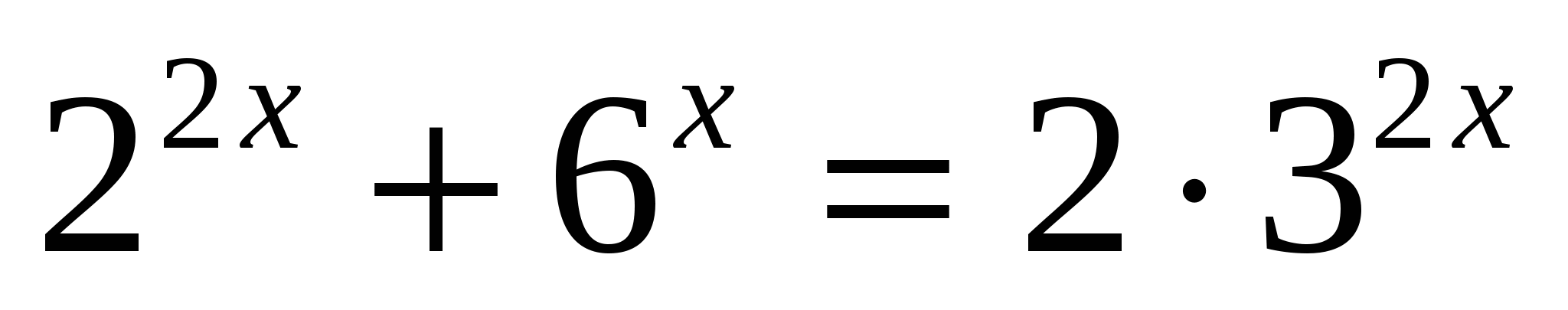
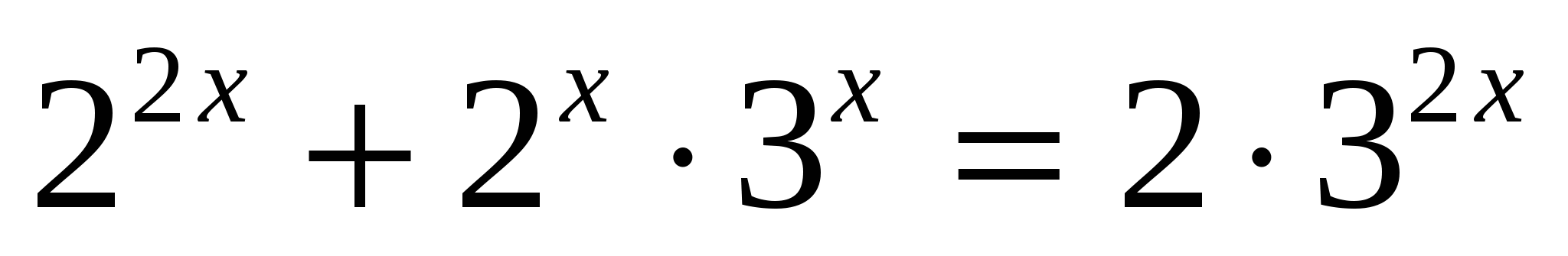
всё уравнение можно поделить на 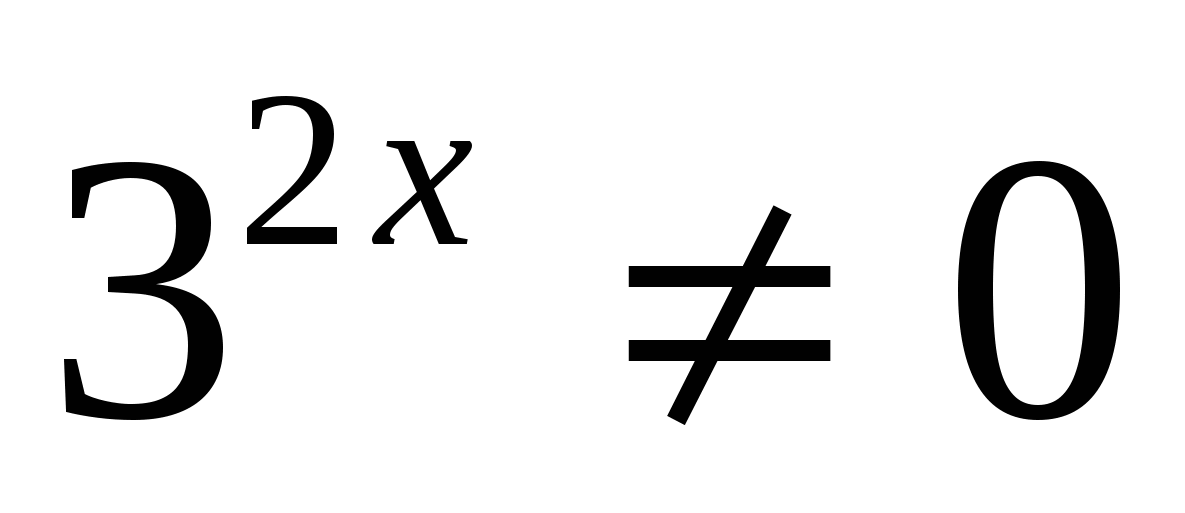
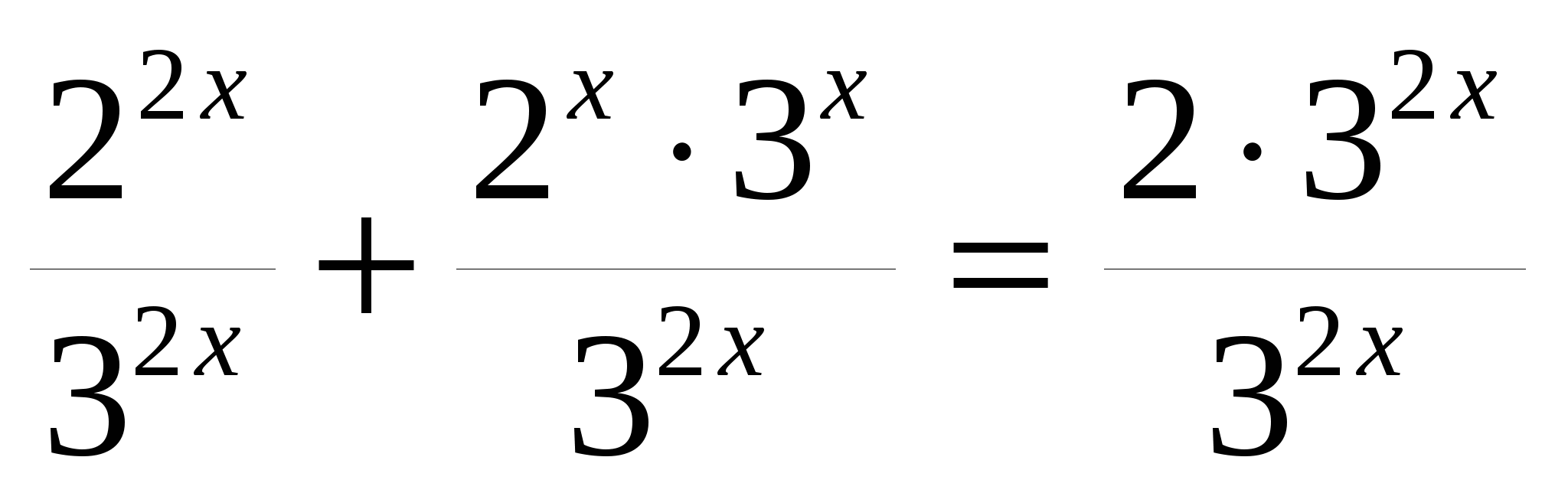
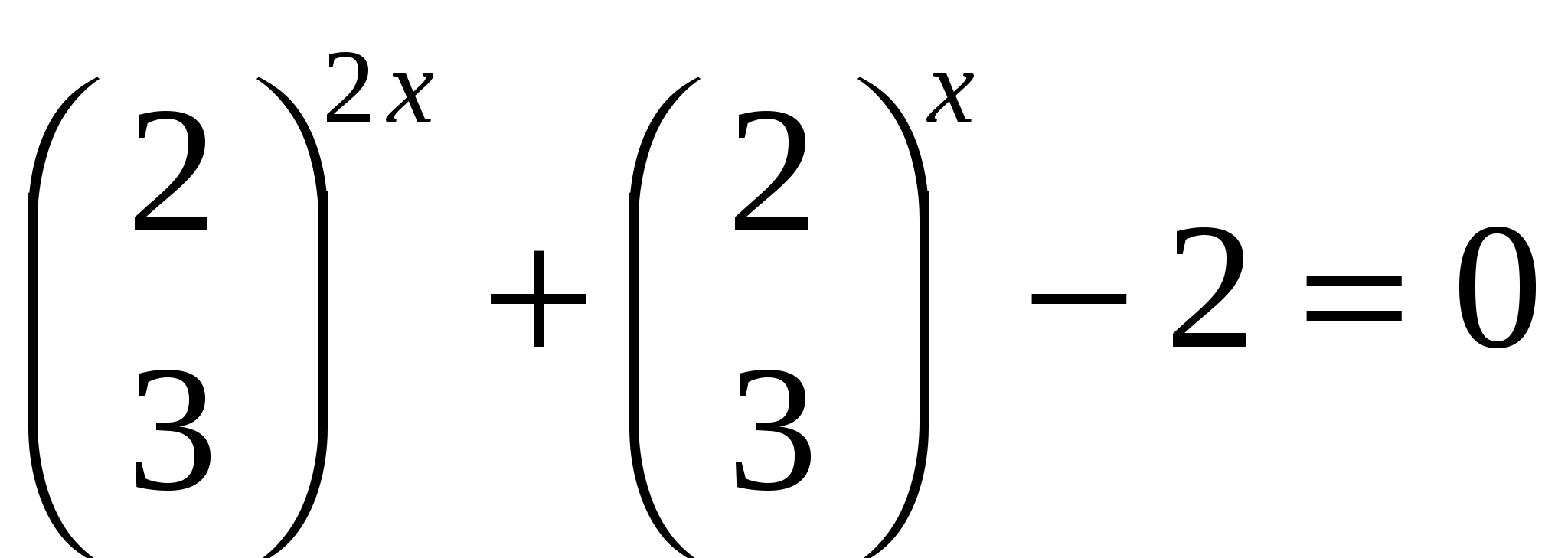
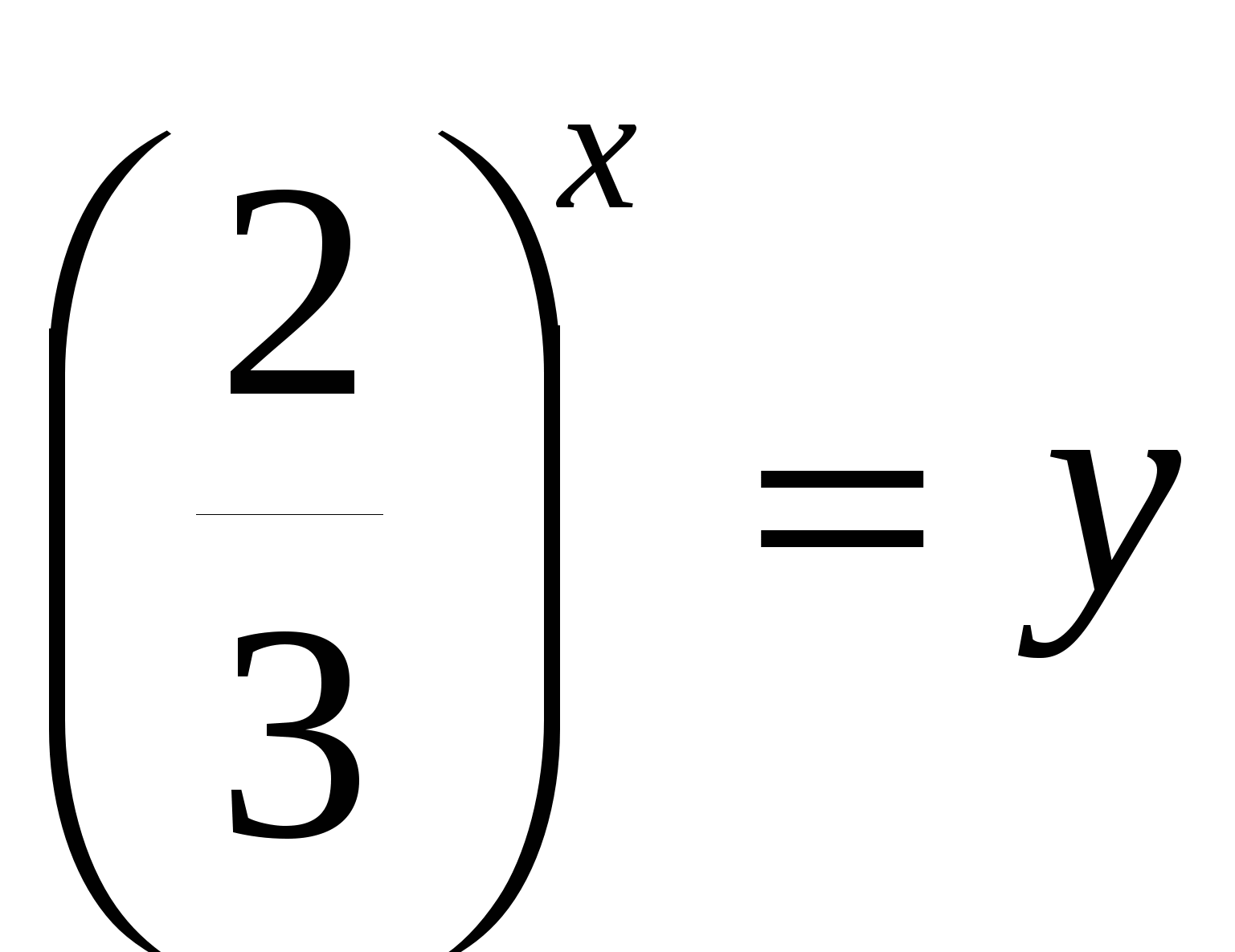
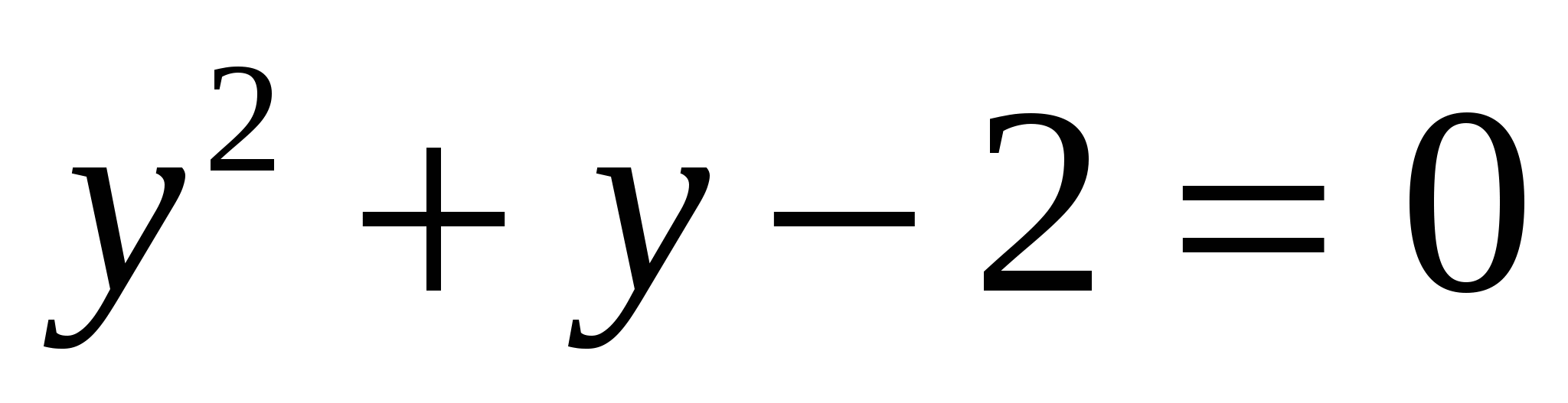
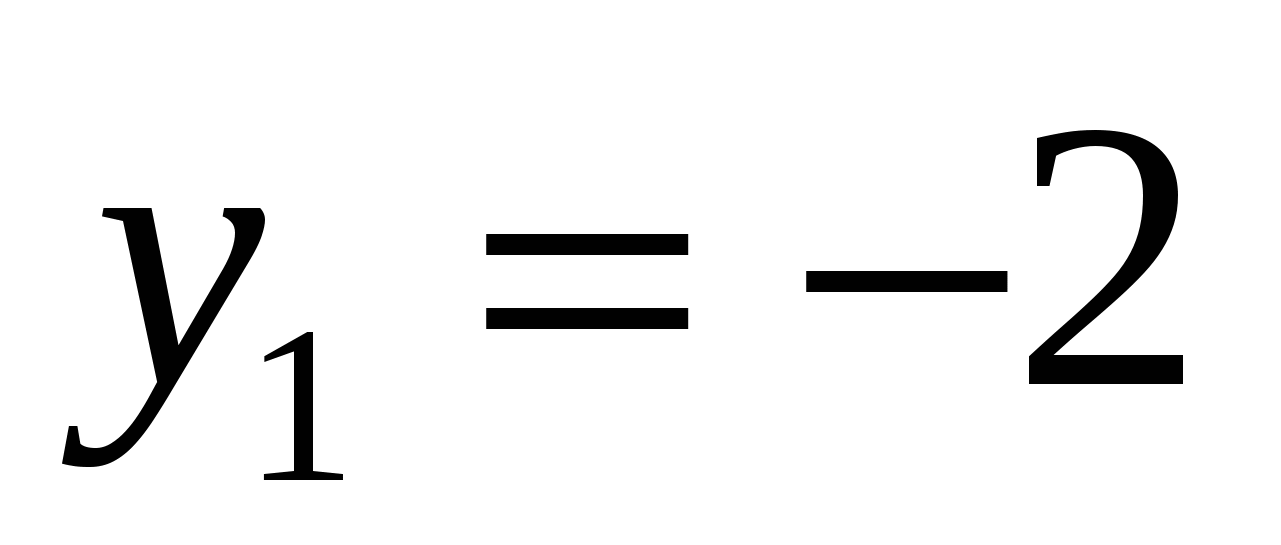 или
или 
1) 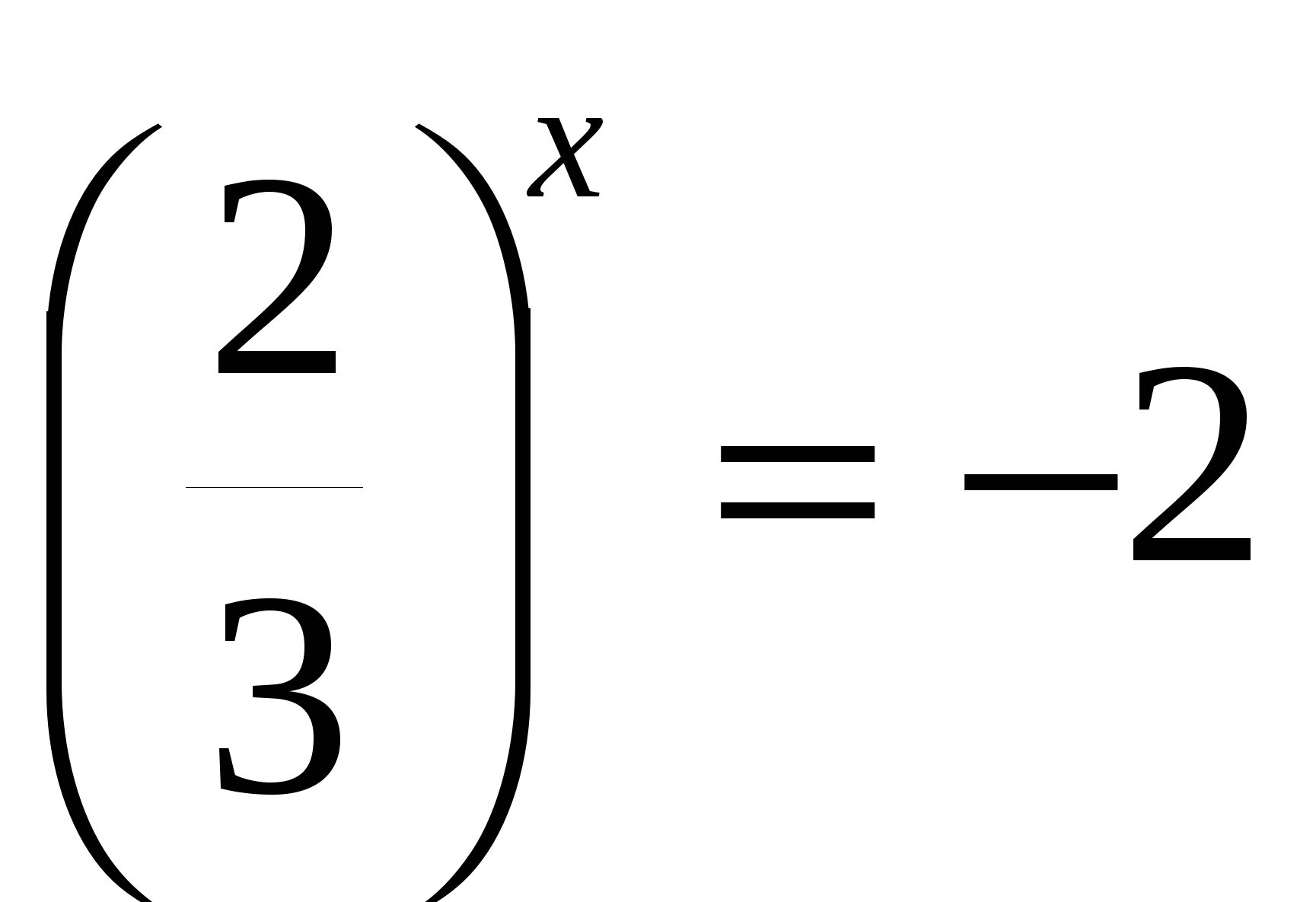
корней нет
2) 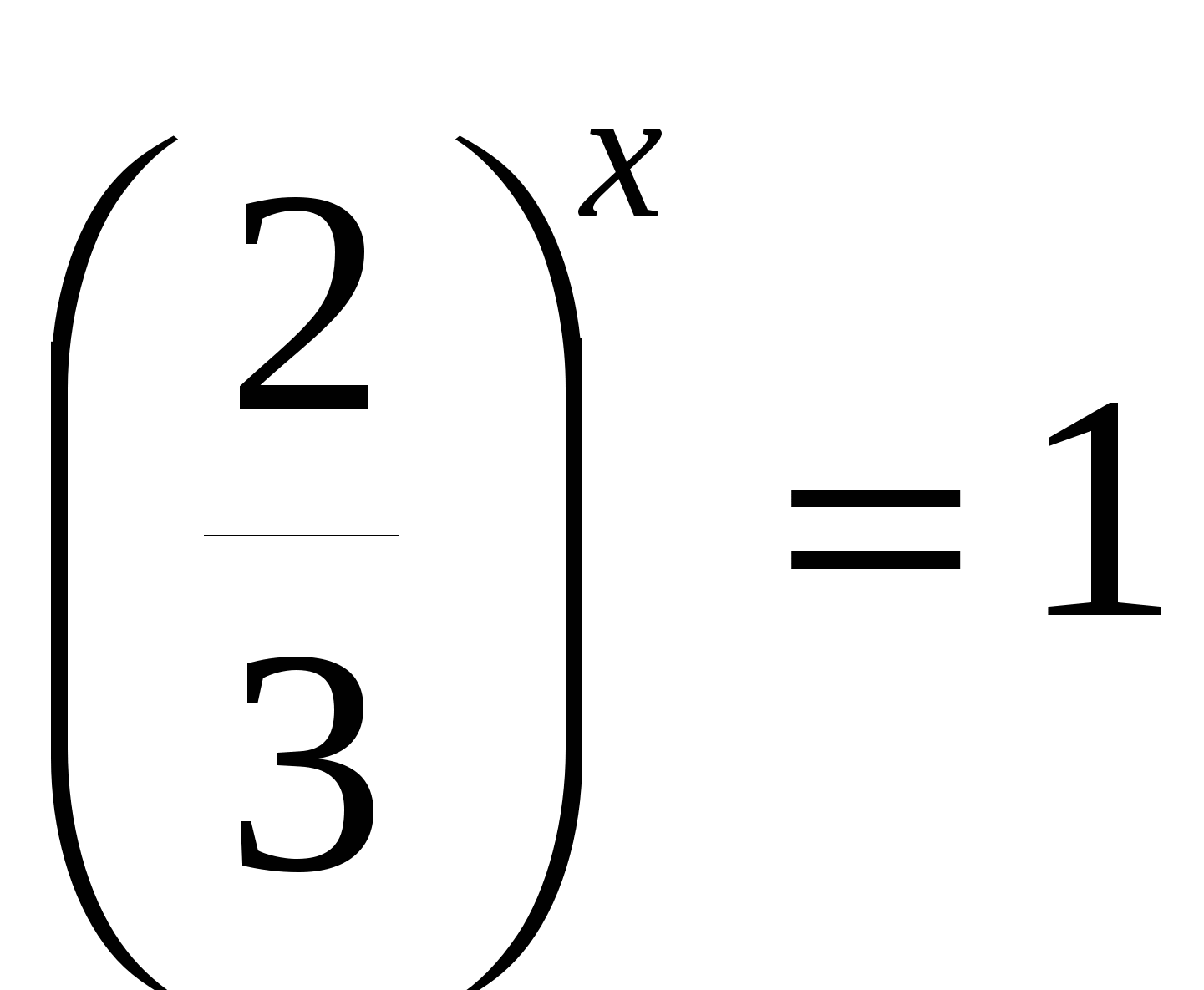
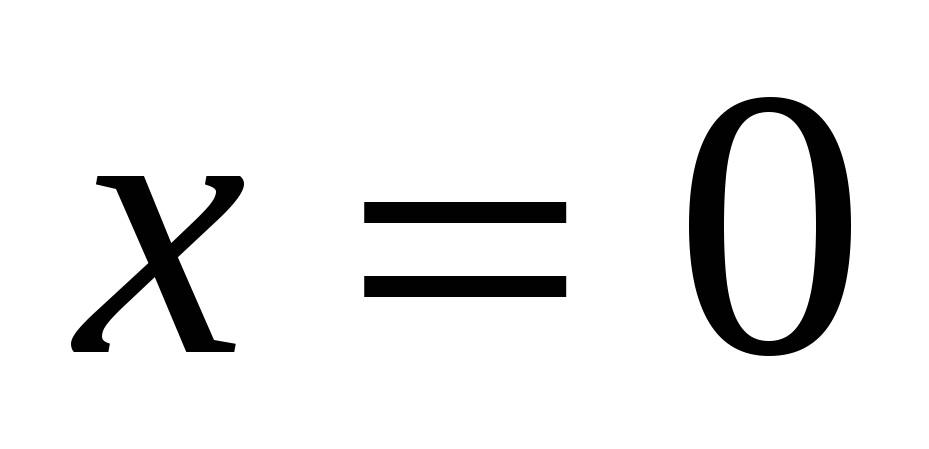
Ответ: 0.
infourok.ru
Методы решения уравнений
 Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Основные методы решения уравнений
Решить уравнение значит найти все его корни или доказать, что их не существует. Стандартных методов решения уравнений много, нестандартных — еще больше. Последние подходят для решения небольшого количества (часто вообще одного) типа уравнений. При решении уравнений почти всегда приходится прибегать к тождественным преобразованиях алгебраических выражений. Поэтому целесообразно разобраться сперва с этим материалом, прежде чем переходить к решению уравнений. В данной статье разобраны в основном стандартные методы решения уравнений. Некоторые нестандартные методы кратко охарактеризованы в завершающей части статьи. Также на сайте есть отдельные статьи о решении тригонометрических, логарифмических и показательных уравнений, с которыми я также рекомендую читателю ознакомиться.
Метод разложения на множители
Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.
Пример 1. Решите уравнение методом разложения на множители: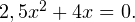
Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную 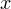 за скобки:
за скобки: 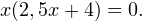
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, 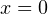 или
или 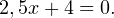 Из последнего уравнения получаем:
Из последнего уравнения получаем:  или
или 
Ответ: 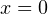 и
и 
Задача для самостоятельного решения №1. Решите уравнение методом разложения на множители: 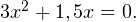
Показать ответ
Ответ: 0 или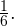 Пример 2. Решите уравнение методом разложения на множители:
Пример 2. Решите уравнение методом разложения на множители: 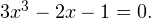
Решение. Для разложения на множители используем прием деления многочленов столбиком (или, как еще иногда говорят, уголком). Несложно догадаться, что 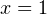 — корень многочлена
— корень многочлена 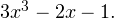 Следовательно, по теореме Безу он без остатка делится на
Следовательно, по теореме Безу он без остатка делится на 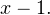 Осуществим это деление (см. подробнее в видеоуроке):
Осуществим это деление (см. подробнее в видеоуроке):

Деление многочленов уголком (столбиком)
Таким образом 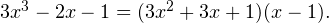 То есть исходное уравнение принимает вид:
То есть исходное уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ (3x^2+3x+1)(x-1) = 0\Leftrightarrow\left[\begin{array}{l}3x^2+3x+1 = 0, \\ x-1=0.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ada9685868ad0a3ed95611b86e34af30_l3.png)
Дискриминант первого квадратичного уравнения 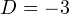 — отрицателен, поэтому корней у него нет. Из второго уравнения получается уже известный нам результат, что корень
— отрицателен, поэтому корней у него нет. Из второго уравнения получается уже известный нам результат, что корень  Это единственный корень уравнения.
Это единственный корень уравнения.
Ответ: 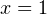 .
.
Задача для самостоятельного решения №2. Решите уравнение методом разложения на множители: 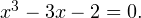
Показать ответ
Ответ: 2 и -1.
Метод замены переменной
Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной. Все эти идеи проще осознать на конкретном примере.
Пример 3. Решите уравнение методом замены переменной: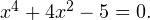
Решение. Такие уравнения называются биквадратными. Перепишем его в виде: 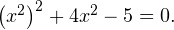 Введем новую переменную
Введем новую переменную 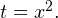 Тогда исходное уравнение примет следующий простой вид:
Тогда исходное уравнение примет следующий простой вид: 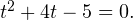 Решая полученное квадратичное уравнение, получаем, что
Решая полученное квадратичное уравнение, получаем, что  или
или 
Возвращаемся теперь к старой переменной (обратная замена): 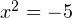 или
или  Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня
Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня 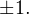
Ответ: 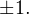
Задача для самостоятельного решения №3. Решите уравнение методом замены переменной: 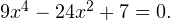
Показать ответ
Ответ: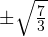 или
или 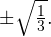 Пример 4. Решите уравнение методом замены переменной:
Пример 4. Решите уравнение методом замены переменной: ![Rendered by QuickLaTeX.com \[ \frac{4x}{4x^2-8x+7}+\frac{3x}{4x^2-10x+7}=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-cb2d94cd76971a1677a251ddb57ae7a7_l3.png)
Решение. Обращаем внимание на то, что 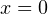 не является корнем данного уравнения. Следовательно, без потери или приобретения лишних корней можно разделить числитель и знаменатель обеих дробей на
не является корнем данного уравнения. Следовательно, без потери или приобретения лишних корней можно разделить числитель и знаменатель обеих дробей на 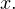 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ \frac{4}{4x-8+\frac{7}{x}}+\frac{3}{4x-10+\frac{7}{x}}=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bf2c84275e98fd7ada1591368bf50d68_l3.png)
Введем новую переменную:  Тогда уравнение примет вид:
Тогда уравнение примет вид:
![Rendered by QuickLaTeX.com \[ \frac{4}{t-8}+\frac{3}{t-10} = 1\Leftrightarrow \frac{t^2-25t+144}{(y-8)(y-10)} = 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5f93daae7b3c8a5fa32b7591a6b3aca6_l3.png)
Дробь равна нулю, если нулю равен ее числитель, а знаменатель при этом не равен нулю. То есть уравнение равносильно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}t^2-25+144 = 0, \\ t\ne 8,\\ t\ne 10\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l} t = 16, \\ t =9, \end{array}\right. \\ t\ne 8,\\ t\ne 10\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ed0cea315f9850dd60c6b3d1bf6d373c_l3.png)
Итак, 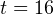 или
или 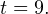 Переходя к обратной подстановке, получаем:
Переходя к обратной подстановке, получаем:
 что при
что при  равносильно уравнению
равносильно уравнению  Откуда
Откуда  или
или 
 что при
что при  равносильно уравнению
равносильно уравнению  у которого решений нет, поскольку его дискриминант отрицателен.
у которого решений нет, поскольку его дискриминант отрицателен.
Ответ: 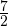 и
и 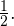
Задача для самостоятельного решения №4. Решите уравнение методом разложения на множители: 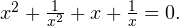
Показать ответ
Ответ: -1.
Метод оценки области значений
Суть данного метода в сравнении областей значений выражений, входящих в уравнение. Часто такой анализ позволяет легко решать сложные уравнения, содержащие различные выражения (рациональные, тригонометрические, логарифмические, показательные и др.). Разберем это на конкретном примере.
Пример 5. Решите уравнение, используя метода оценки области значений: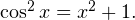
Решение. Рассмотрим функцию 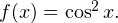 Известно, что
Известно, что 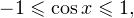 поэтому
поэтому 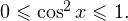 Итак, функция
Итак, функция 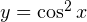 может принимать значения только из промежутка
может принимать значения только из промежутка ![Rendered by QuickLaTeX.com [0;1].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f38f9c6cd6a33efe8e18680325511e5b_l3.png)
Рассмотрим теперь функцию 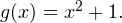 Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке
Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке 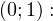

График соответствующей квадратичной функции
То есть область значений данной функции (те значения, которые может принимать переменная 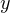 ) представляет собой промежуток
) представляет собой промежуток 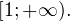
Таким образом выражения, стоящее справа и слева от знака равенства в исходном уравнении, могут оказаться равными, только если их значения окажутся равными 1, причем при одном и том же значении 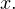 Непосредственной подстановкой убеждаемся, что это условие выполняется при
Непосредственной подстановкой убеждаемся, что это условие выполняется при  Действительно,
Действительно, 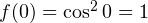 и
и 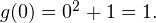 При всех остальных значениях
При всех остальных значениях 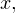 функция
функция 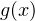 больше 1 (см. график). Значит
больше 1 (см. график). Значит 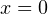 — единственный корень уравнения.
— единственный корень уравнения.
Ответ: 0.
Задача для самостоятельного решения №5. Решите уравнение с использованием метода оценки области значений: 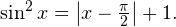
Показать ответ
Ответ: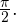
Нестандартные методы решения уравнений
Пример 6. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{2x-x^2+8}+\sqrt{x^2-4x}=\sqrt{-x-2}+1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-51821c880f5c7f760afa7eba43e35408_l3.png)
Решение. Определим область допустимых значений (те значения, которые может принимать переменная 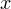 в данном уравнении). Исходим из того, что подкоренное выражение не может быть отрицательным:
в данном уравнении). Исходим из того, что подкоренное выражение не может быть отрицательным:
![Rendered by QuickLaTeX.com \[ \begin{cases}2x-x^2+8\geqslant 0, \\ x^2-4x\geqslant 0, \\ -x-2\geqslant 0\end{cases}\Leftrightarrow\begin{cases}2x-x^2+8\geqslant 0, \\ x^2-4x\geqslant 0, \\ x\leqslant -2.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1be607765444b4eb8936cc9d90924a82_l3.png)

Изображение решений каждого из неравенств системы на числовой прямой
Получается, что область допустимых значений содержит одно единственное значение 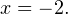 Является ли это значение корнем уравнения, проще всего проверить прямой подстановкой:
Является ли это значение корнем уравнения, проще всего проверить прямой подстановкой:
![Rendered by QuickLaTeX.com \[ \sqrt{2\cdot (-2)-(-2)^2+8}+\sqrt{(-2)^2-4\cdot (-2)}\ne \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4c3df8b5a732d7682acef485b61d5e0c_l3.png)
![Rendered by QuickLaTeX.com \[ \ne\sqrt{-(-2)-2}+1,\, \sqrt{12}\ne 1,\, 2\sqrt{3}\ne 1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-119f9a007f6f7d605ffe7131671868a0_l3.png)
Нет, не является.
Ответ: корней нет.
Задача для самостоятельного решения №6. Решите уравнение: 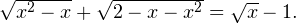
Показать ответ
Ответ: 1.
Пример 7. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{x^2+3x-2}-\sqrt{x^2+2x}=2-x. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4419f76b43ae7d9a7a7fa35c0779a6f9_l3.png)
Решение. Домножим уравнение на 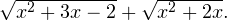 Вообще говоря, это преобразование не является равносильным, даже в области допустимых значений. Ведь могут найтись такие значения
Вообще говоря, это преобразование не является равносильным, даже в области допустимых значений. Ведь могут найтись такие значения 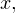 при которых это выражение обратится в ноль. При таком преобразовании могут появиться лишние корни, поэтому полученные ответы нужно будет проверить непосредственной подстановкой. Но главное, что в результате такого преобразования не произойдет потери корней. Итак, преобразуем:
при которых это выражение обратится в ноль. При таком преобразовании могут появиться лишние корни, поэтому полученные ответы нужно будет проверить непосредственной подстановкой. Но главное, что в результате такого преобразования не произойдет потери корней. Итак, преобразуем:
![Rendered by QuickLaTeX.com \[ x^2+3x-2-x^2-2x = (2-x)\times \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-db201b6447e9a0a18316fea99d1d4c10_l3.png)
![Rendered by QuickLaTeX.com \[ \times (\sqrt{x^2+3x-2}+\sqrt{x^2+2x}) \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f738727c9dbf476e2f7c336ae3b16018_l3.png)
![Rendered by QuickLaTeX.com \[ (x-2) + (x-2)(\sqrt{x^2+3x-2}+\sqrt{x^2+2x}) = 0 \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-70028e02810e409a9ad826c48e404001_l3.png)
![Rendered by QuickLaTeX.com \[ (x-2)(1+\sqrt{x^2+3x-2}+\sqrt{x^2+2x}) = 0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bbf14b0a9d5126a4b9c7babb4a0378af_l3.png)
Выражение во вторых скобках не может быть равно нулю. Действительно, оба корня по крайней мере неотрицательны, поэтому если к их сумме прибавить 1, получится положительное выражение. То есть остается, что 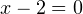 или
или 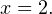 Непосредственной подстановкой убеждаемся, что это корень данного уравнения:
Непосредственной подстановкой убеждаемся, что это корень данного уравнения:
![Rendered by QuickLaTeX.com \[ \sqrt{2^2+3\cdot 2-2}-\sqrt{2^2+2\cdot 2}=2-2,\, \sqrt{8}=\sqrt{8}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-eab84f3ab8be034b5f72a70bff7e7c38_l3.png)
Ответ: 2.
Задача для самостоятельного решения №7. Решите уравнение: 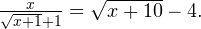
Показать ответ
Ответ: -1.
Пример 8. Решите уравнение: ![Rendered by QuickLaTeX.com \[ x^2+\frac{81x^2}{(9+x)^2} = 40. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e44c878d3c712e1f7b129cd34908d8d_l3.png)
Решение. В область допустимых значений уравнения не входит число -9. Введем новую переменную 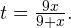 Тогда в области допустимых значений последнее выражение преобразуется к виду
Тогда в области допустимых значений последнее выражение преобразуется к виду  или
или 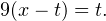 Тогда имеет место система уравнений:
Тогда имеет место система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases}x^2+t^2=40, \\ 9(x-t)-xt=0\end{cases}\Leftrightarrow\begin{cases}(x-t)^2=40-2xt, \\ 9(x-t)-xt=0\end{cases}\Lefrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-3eedda8026f5ad0f30731944d9510608_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\begin{cases}x-t=-20, \\ xt=-180\end{cases} \\ \begin{cases}x-t=2, \\ xt=18\end{cases}\end{array}\right.\Leftrightarrow x = 1\pm\sqrt{19}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-484ef31cadc4f91559bf9903965d4a5e_l3.png)
Ответ: 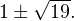
Задача для самостоятельного решения №8. Решите уравнение ![Rendered by QuickLaTeX.com \sqrt[4]{x+8}-\sqrt[4]{x-8}=2.](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e36f56e2e85e2221188303f9d031e825_l3.png)
Показать ответ
Ответ: 8.
Вопрос методов решения уравнений изложенным в статье материалом, конечно, не исчерпывается. Существуют десятки других методов. Существуют также совершенно уникальные уравнения, для которых имеются свои собственное методы решения. Так что научиться здесь можно еще очень и очень многому. Самым хорошим помощником в этот деле для вас станет профессиональный репетитор по математике. Учите математику, сдавайте на отлично выпускные экзамены, поступайте в престижные вузы. Удачи вам!
Сергей Валерьевич
Частный преподаватель по математике
У любой сложной задачи есть простое, легкое для понимания неправильное решение. © Артур Блох
yourtutor.info
Квадратные уравнения, примеры решений
Теория по квадратным уравнениям
ОПРЕДЕЛЕНИЕ Квадратным уравнением называется уравнение вида , где .Возможны такие случаи:
, тогда имеем квадратное уравнение вида и .
, тогда имеем квадратное уравнение вида , если ; если – корней нет.
, тогда имеем квадратное уравнение вида .
, тогда имеем полное квадратное уравнение , которое решается или с помощью дискриминанта:
Или по теореме Виета:
Примеры
ПРИМЕР 1| Задание | Решить следующие неполные квадратные уравнения
|
| Решение | 1) В уравнении вынесем за скобки . Произведение равно нулю, если один из сомножителей равен нулю, следовательно:
или
2) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :
3) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :
У данного квадратного уравнения нет корней. 4) уравнение равносильно уравнению , которое имеет два совпадающих корня . |
| Ответ |
Корней нет |
| Задание | Решить квадратное уравнение |
| Решение | Подсчитаем для заданного уравнения, чему равен дискриминант:
Так как , то уравнение имеет два совпадающих корня:
|
| Ответ |
| Задание | Решить уравнение |
| Решение | Вычислим дискриминант для исходного уравнения, получим:
Так как , данное уравнение решений не имеет. |
| Ответ | Корней нет. |
| Задание | Решить квадратное уравнение |
| Решение | Дискриминант заданного уравнения, равен
Следовательно, уравнение имеет два различных корня
|
| Ответ |
| Задание | Решить уравнение, используя теорему Виета: |
| Решение | Пусть и – корни квадратного уравнения, по следствию из теоремы Виета
Проанализируем полученные равенства. Произведение корней отрицательно, следовательно, корни имеют разные знаки. Разложим –12 на множители, учитывая, что они должны быть числами разного знака. Возможны такие варианты: –12 и 1; 12 и –1; –6 и 2; 6 и –2; –4 и 3; 4 и –3. Так как сумма корней равна 1, то корнями будут числа и . |
| Ответ |
ru.solverbook.com
Показательные уравнения, формулы и примеры
Простейшие показательные уравнения
В зависимости от знака такое уравнение имеет различное количество корней:
- если , то уравнение (1) решений не имеет, то есть
- если , то
- Если .
- Если .
Уравнения такого типа равносильны уравнению
Уравнения вида
- Если , то обе части такого уравнения равны для любых .
- Если , то уравнение эквивалентно уравнению .
- В случае, если , то уравнение эквивалентно системе
Решение показательных уравнений сведением к общему основанию
Если левая и правая части заданного показательного уравнения содержат только произведения, частные, корни или степени, то рациональнее при помощи основных формул для степеней привести обе части равенства к одному основанию, то есть к уравнению вида (2).
Решение показательных уравнений вынесением общего множителя
Если показательное уравнение содержит выражение вида , причем показатели степени отличаются только свободным коэффициентом, то для решения необходимо вынести за скобки наименьшую степень .
Приведение показательных уравнений к квадратным
К показательным уравнениям, которые можно привести к квадратным, относятся следующие уравнения.
где — некоторые числа, .
В этом случае выполняется замена
где — некоторые ненулевые числа, причем , — произвольное действительное число. Для сведения к квадратному обе части уравнения необходимо умножить на :
Далее заменой получаем квадратное уравнение
Однородные показательные уравнения
Делением обеих его частей на (или ), сводим уравнение к показательному вида :
Схема решения таких уравнений следующая:
1) Делим обе части уравнения или на , или на , в результате получаем:
или
;2) заменой последнее уравнение сводится к квадратному:
ru.solverbook.com
Решение уравнений, формулы и примеры
Определение и степень уравнения
Например. .
Например. Уравнение является уравнением седьмой степени, поскольку максимальную — седьмую — степень имеет одночлен .
Решение уравнения и его корни
Два уравнения называются равносильными, если они имеют одно и то же множество решений.
Основные свойства уравнений
- Если хотя бы в одной части уравнения выполнить тождественные преобразования, то в результате получим уравнение, равносильное заданному.
Например. .
- Если из одной части уравнения перенести слагаемые в другую его часть, при этом изменив их знак на противоположный, то получим уравнение, равносильное заданному.
Например. .
- Если обе части уравнения умножить или поделить на одно и тоже ненулевое число, то получим уравнение, равносильное данному.
Например. .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
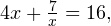 что при
что при 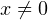 равносильно уравнению
равносильно уравнению 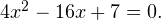 Откуда
Откуда 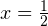 или
или 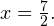
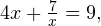 что при
что при 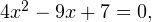 у которого решений нет, поскольку его дискриминант отрицателен.
у которого решений нет, поскольку его дискриминант отрицателен.