Площадь боковой поверхности пирамиды — формула, пример расчета

Пирамида – это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.

Если в основании лежит квадрат, то пирамиду называется четырехугольной, если треугольник – то треугольной. Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:

Рассмотрим пример расчета площади боковой поверхности пирамиды.

Пусть дана пирамида с основанием ABCDE и вершиной F. AB=BC=CD=DE=EA=3 см. Апофема a = 5 см. Найти площадь боковой поверхности пирамиды.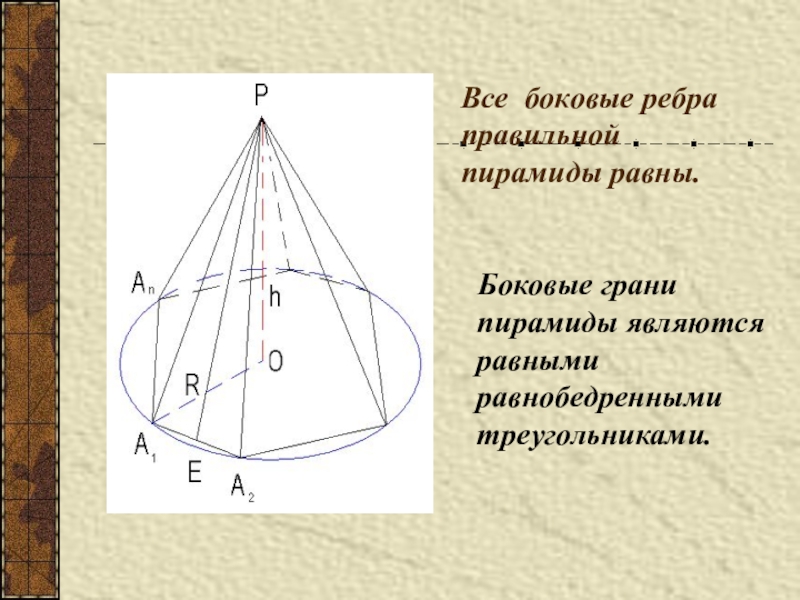
Найдем периметр. Так как все грани основания равны, то периметр пятиугольника будет равен:
Теперь можно найти боковую площадь пирамиды:

Площадь правильной треугольной пирамиды

Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.

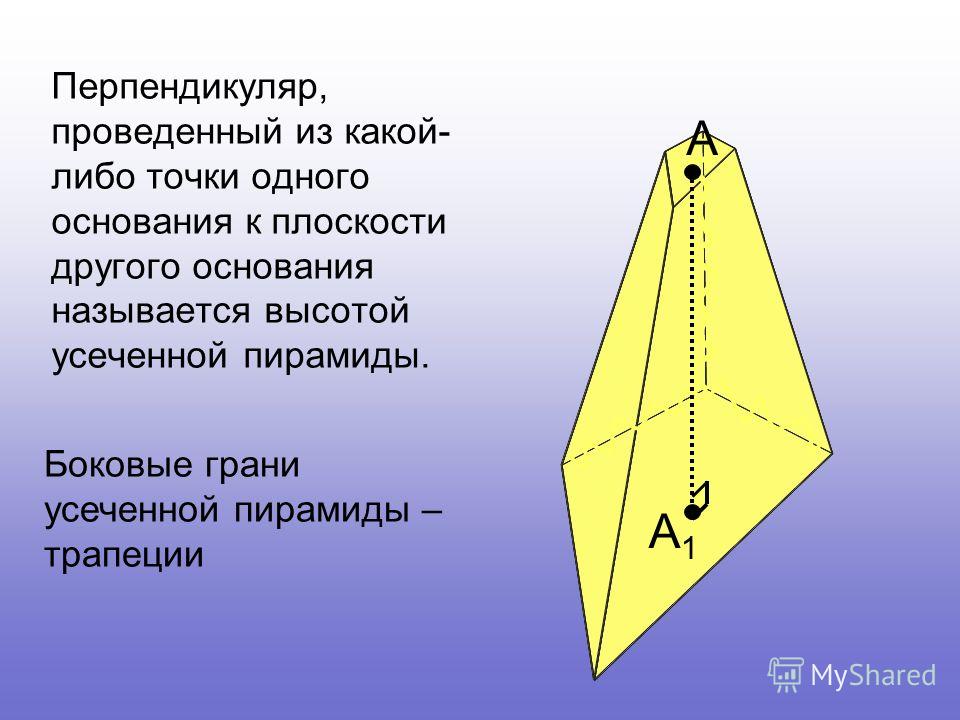
Площадь усеченной пирамиды

Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.
Формула площади боковой поверхности усеченной пирамиды очень проста.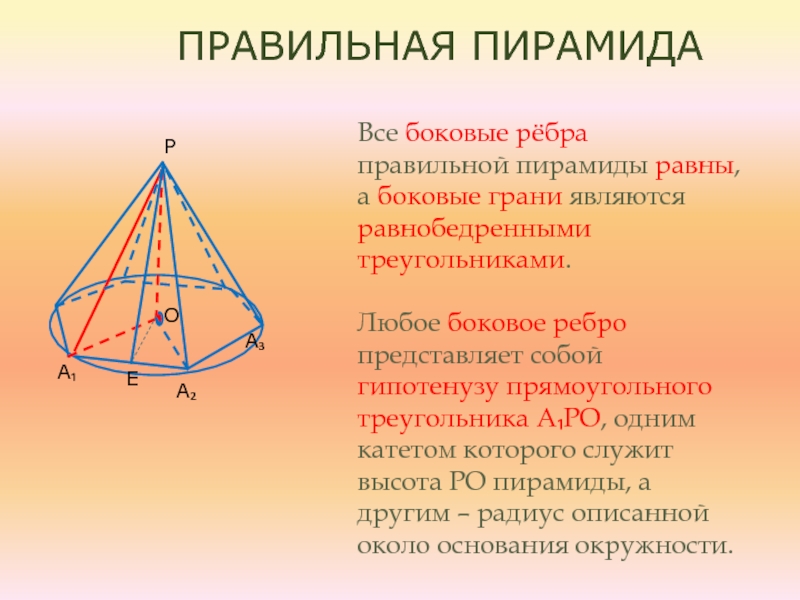

Площадь равняется произведению половины суммы периметров оснований на апофему:

Рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.

Дана правильная четырехугольная пирамида. Длины основания равны b = 5 см, c = 3 см. Апофема a = 4 см. Найдите площадь боковой поверхности фигуры.
Для начала найдем периметр оснований. В большем основании он будет равен:
В меньшем основании:
Посчитаем площадь:

Таким образом, применив несложные формулы, мы нашли площадь усеченной пирамиды.

Пирамида, её основание, вершина, боковые рёбра, высота, боковая поверхность

Пирамида, её основание,
вершина, боковые рёбра, высота,
боковая поверхность.
Правильная пирамида, апофема,
площадь боковой поверхности
правильной пирамиды.
Повторение
1.
2.
3.
4.
5.
6.
Что такое призма?
Что может являться в основании призмы?
Что является боковой стороной призмы?
Призма имеет n граней. Какой многоугольник лежит в её основании?
Какая призма называется прямой?
Является ли призма прямой, если две её смежные боковые грани
перпендикулярны к плоскости основания?
7. В какой призме боковые рёбра параллельны и равны её высоте?
8. Какая призма называется правильной?
9. Является ли призма правильной, если все её рёбра равны друг другу?
10.Может ли высота одной из боковых граней наклонной призмы являться
и высотой призмы?
11.Чему равна диагональ параллелепипеда?
12.Как найти площадь боковой поверхности призмы?
13.Как найти площадь полной поверхности призмы?
Задача № 1.
Основание прямой призмы – треугольник со сторонами 5 см и 3
см и углом в 120° между ними. Наибольшая из площадей
боковых граней равна 35 см². Найдите площади боковой и
полной поверхности призмы.
Изучение нового материала
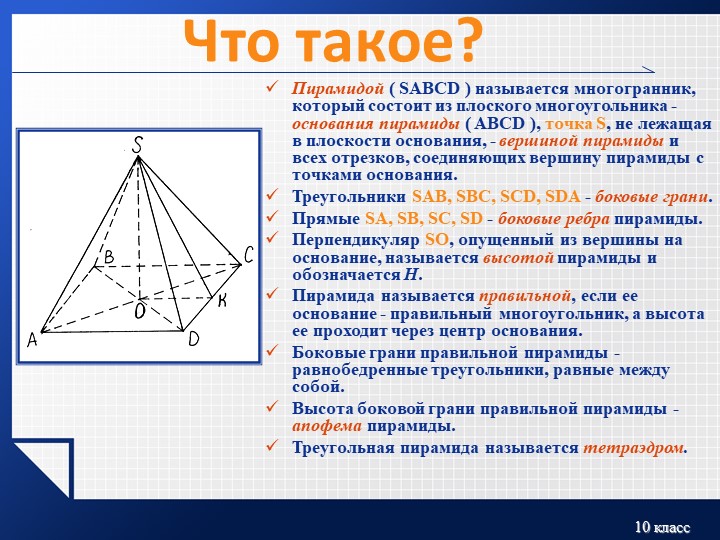
Рассмотрим многоугольник А1А2А3…Аn
и точку Р, не лежащую в плоскости
этого многоугольника.
Соединим точку Р с вершинами
многоугольника.
Получим n треугольников:
РА1А2, РА2А3, … , РАnА1.
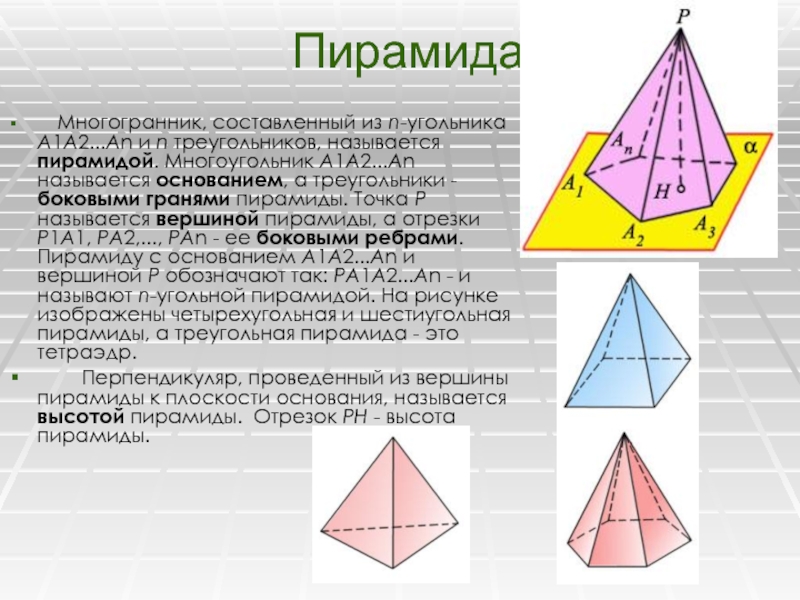
Многогранник, составленный из nугольника А1А2А3…Аn и n
треугольников РА1А2, РА2А3, … , РАnА1
называется пирамидой.
Точка Р – называется вершиной
пирамиды.
Отрезки РА1, РА2, … , Раn называются
боковыми рёбрами пирамиды.
Многоугольник А1А2А3…Аn называется
основанием пирамиды.
Треугольники РА1А2, РА2А3, … , РАnА1
называются боковыми гранями
пирамиды.
Виды пирамид
Четырёхугольная
Шестиугольная
Треугольная
Высота пирамиды.
Высотой пирамиды называется перпендикуляр,
опущенный из вершины пирамиды на
плоскость основания.
Площадь полной поверхности
пирамиды
Площадью полной поверхности пирамиды называется
сумма всех её граней, то есть основания и боковых граней.
S полн S осн S бок
Площадью боковой поверхности
пирамиды называется сумма
площадей её боковых граней.
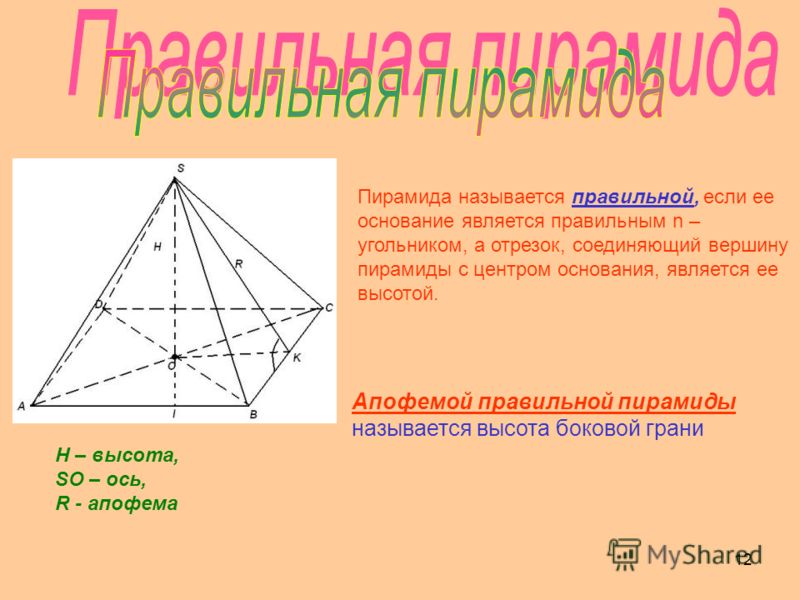
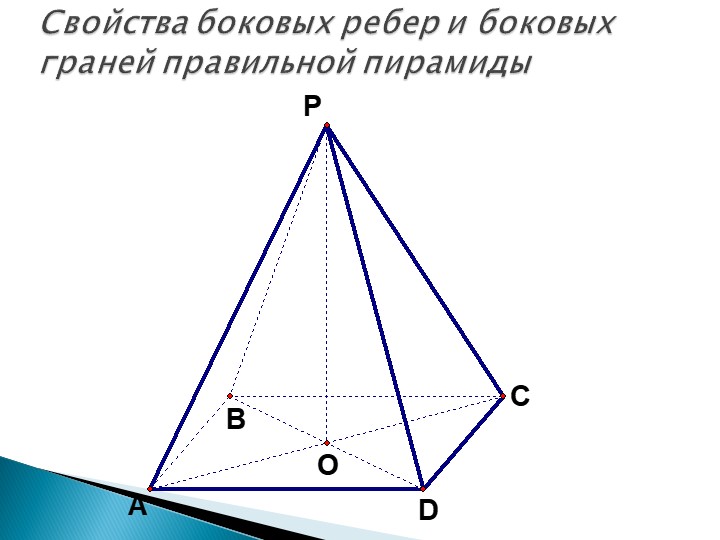
Правильная пирамида
Пирамида называется правильной, если её основание –
правильный многоугольник, а отрезок, соединяющий вершину
пирамиды с центром основания, является её высотой.
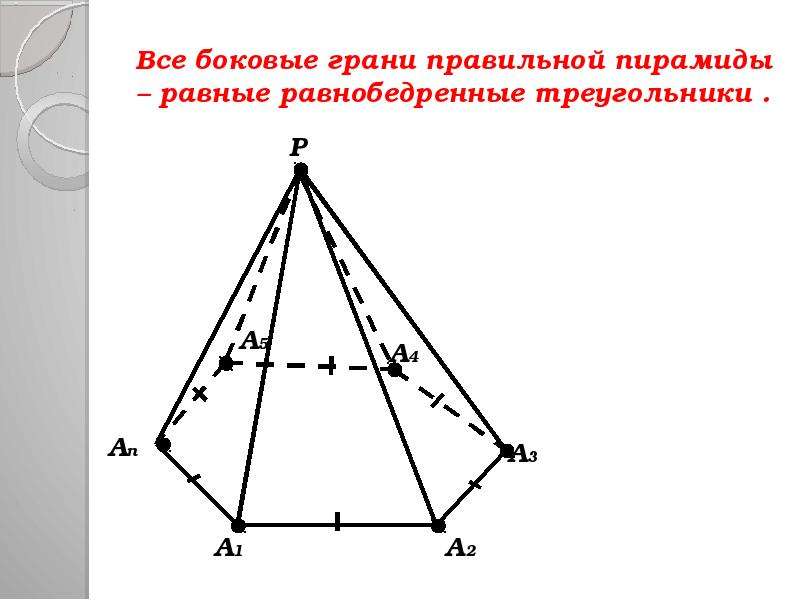
Все боковые рёбра правильной пирамиды равны, а боковые
грани являются равными равнобедренными треугольниками.
Теорема
Все боковые рёбра правильной пирамиды равны, а боковые
грани являются равными равнобедренными треугольниками.
Доказательство.
Докажем на примере правильной треугольной
пирамиды SABCD.
1) Рассмотрим треугольники SMA, SMC и SMB.
АМ=ВМ=СМ (как радиусы описанной окружности),
SМ – общая высота, значит, треугольники равны по
двум катетам.
Следовательно, AS=BS=CS.
2) Рассмотрим треугольники SCA, SCB и SAB.
По доказанному выше AS=BS=CS (значит, они
являются равнобедренными), с другой стороны
АС=ВС=АВ (так как в основании правильный
треугольник), следовательно, треугольники SCA,
SCB и SAB равны по трём сторонам.
ЧТД.
Аналогично доказывается для любой правильной пирамиды.
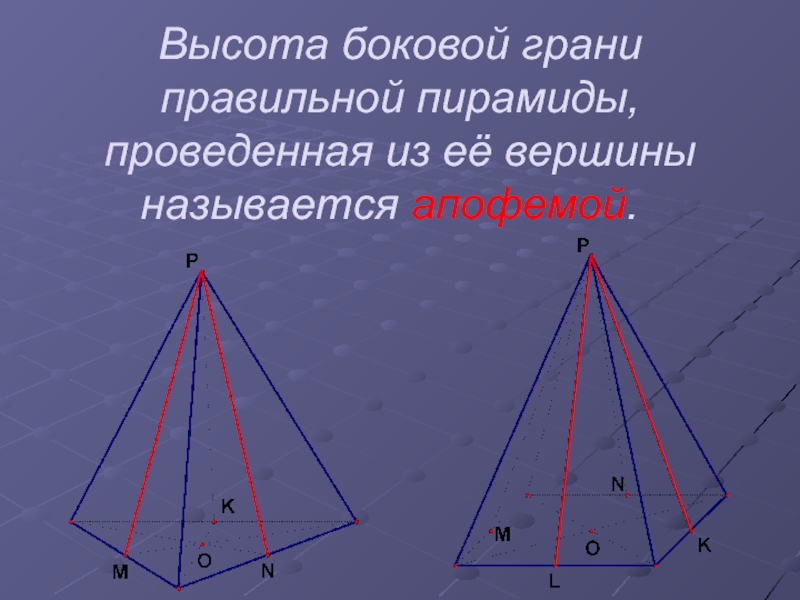
Апофема правильной пирамиды.
Высота боковой грани правильной пирамиды,
проведённая из её вершины, называется апофемой.
Апофема правильной пирамиды.
Площадь боковой поверхности
правильной пирамиды
Теорема. Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на апофему.
1
S Росн l Росн – периметр основания, l – апофема.

2
Доказательство.
Докажем на примере произвольной пирамиды
РА1А2…Аn.
1) Рассмотрим боковую грань РА1А2. Это
равнобедренный треугольник с основанием А1А2.
Площадь этого треугольника равна:
S
1
РК А1 А2 , где РК – апофема,
2
А1А2 – сторона основания.
Аналогично площади других граней будут
вычисляться по формуле
S
1
апофема Ат Ап
2
Площадь боковой поверхности
правильной пирамиды
Теорема. Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на апофему.
1
S Росн l Росн – периметр основания, l – апофема.
2
Доказательство (продолжение).
Sбок S РА1 А2 S РА2 А3 . .. S РАп 1 Ат
1
1
1
l А1 А2 l А2 А3 … l Ап 1 Ап
2
2
2
1
1
l А1 А2 A2 A3 … An 1 An l P
2
2
ЧТД
Закрепление
1.
2.
3.
4.
5.
6.
7.
8.
Что такое пирамида?
Что такое основание пирамиды?
Что может лежать в основании пирамиды?
Из какой фигуры всегда состоит боковая грань пирамиды?
Что такое высота пирамиды?
Чему равна площадь полной поверхности пирамиды?
Какая пирамида называется правильной?
Каким свойством обладают боковые рёбра и грани
правильной пирамиды?
9. Как называется отрезок, соединяющий вершину пирамиды с
серединой стороны основания правильной пирамиды?
10. Как найти площадь боковой поверхности правильной
пирамиды?
11. Решить задачу № 240.
Задача № 240.
Основанием пирамиды является параллелограмм,
стороны которого равны 20 см и 36 см, а площадь равна
360 см². Высота пирамиды проходит через точку
пересечения диагоналей основания и равна 12 см.
Найдите площадь боковой поверхности пирамиды.
Дано: SABCD – пирамида,
АВСD – параллелограмм,
АВ=36 см, АD =20 см, SABCD=360 см²,
SO – высота, SO =12 см.
Найти: Sбок.
Задача № 240.
Найдите угол А и угол D.
Найдите ВD.
Найдите SD и SB.
Найдите АС.
Найдите SA и SC.
по формуле Герона
найдите площади
боковых граней
(подумайте, какие из них
одинаковые).
7. Найдите площадь полной
поверхности.
1.
2.
3.
4.
5.
6.
Домашнее задание
1) Прочитать пункты 32 – 33, выучить все определения и
две теоремы с доказательствами.
2) Решить задачи № 239, 241.

Тема №5123 Задачи по геометрии элементы правильных пирамид

Тема №5123

Ответы в самом низу встроенного документа

 

4001.    Докажите, что в любой правильной пирамиде все боковые ребра равны.
4002.    Докажите, что в любой правильной пирамиде все боковые грани образуют равные углы с плоскостью основания.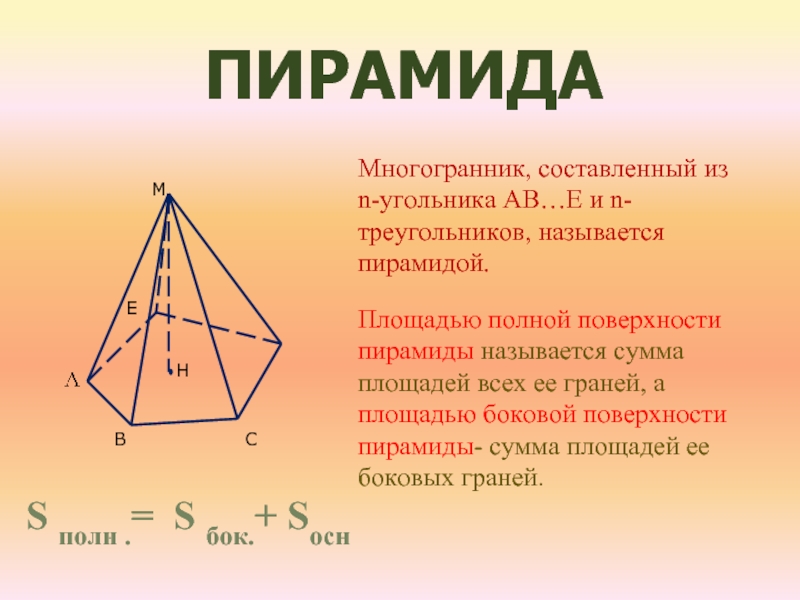

4003.    Докажите, что в любой правильной пирамиде углы между соседними боковыми гранями равны.
4004°. Сторона основания правильной треугольной пирамиды равна а. Боковое ребро образует с плоскостью основания угол, равный 60° (рис. 165). Найдите высоту пирамиды.
 

4005°. Сторона основания правильной треугольной пирамиды равна а. Боковое ребро образует с плоскостью основания угол, равный 60°. Найдите объем пирамиды.
4006.    Сторона основания правильной четырехугольной пирамиды равна а. Боковая грань образует с плоскостью основания угол, равный 45°. Найдите высоту пирамиды.
4007.    Сторона основания правильной четырехугольной пирамиды равна а. Боковая грань образует с плоскостью основания угол, равный 45°. Найдите объем пирамиды.
4008.    Высота правильной шестиугольной пирамиды равна стороне ос 
нования. Найдите угол бокового ребра с плоскостью основания.

4009.    Сторона основания правильной треугольной пирамиды равна а, боковая грань образует с плоскостью основания угол 60°. Найдите высоту пирамиды.
4010.    Сторона основания правильной треугольной пирамиды равна а, боковая грань образует с плоскостью основания угол 60°. Найдите объем пирамиды.
4011°. Найдите высоту правильного тетраэдра с ребром, равным а.
4012.    Найдите объем правильного тетраэдра с ребром, равным а.
4013.    Найдите площадь полной поверхности правильного тетраэдра с ребром, равным а.
4014°. Все ребра правильной четырехугольной пирамиды равны а. Найдите высоту пирамиды.
4015.    Все ребра правильной четырехугольной пирамиды равны а. Найдите объем пирамиды.
4016.    Все ребра правильной четырехугольной пирамиды равны. Найдите угол между противоположными боковыми ребрами.
4017.    Боковая грань образует с плоскостью основания правильной шестиугольной пирамиды угол, равный 60°. Найдите угол бокового ребра с плоскостью основания.
4018.    Боковое ребро правильной треугольной пирамиды образует с плоскостью основания угол, равный 60°. Найдите угол боковой грани с плоскостью основания.
4019.    Сторона основания правильной треугольной пирамиды равна а. Боковое ребро образует с плоскостью основания угол, равный 60°. Найдите площадь боковой поверхности пирамиды.
4020°. Сторона основания правильной четырехугольной пирамиды равна а. Боковая грань образует с плоскостью основания угол, равный 45°.
Найдите площадь боковой поверхности пирамиды.
4021°. Боковая грань правильной четырехугольной пирамиды образует с плоскостью основания угол, равный 45°. Найдите угол бокового ребра с плоскостью основания.
4022.    Сторона основания и высота правильной шестиугольной пирамиды равны а. Найдите объем пирамиды.
4023.    Высота правильной шестиугольной пирамиды равна стороне основания. Найдите угол между боковой гранью и плоскостью основания.
4024°. Сторона основания правильной треугольной пирамиды равна а. Боковая грань образует с плоскостью основания угол, равный 60°. Найдите площадь боковой поверхности пирамиды.
4025.    Боковая грань образует с плоскостью основания правильной треугольной пирамиды угол, равный 60°. Найдите угол бокового ребра с плоскостью основания.
4026.    В правильном тетраэдре найдите угол между ребром и плоскостью грани, не содержащей это ребро.
4027.    Найдите угол между гранями правильного тетраэдра.
4028.    Все ребра правильной четырехугольной пирамиды равны. Найдите угол между соседними боковыми гранями.
4029.    Сторона основания правильной шестиугольной пирамиды равна
Л , а угол боковой грани с плоскостью основания равен 60°. Найдите высоту пирамиды.
4030.    Высота правильной четырехугольной пирамиды равна 8, апофема пирамиды равна 10. Найдите площадь сечения пирамиды плоскостью, проведенной через середину высоты параллельно плоскости основания.
4031.    Угол боковой грани с плоскостью основания правильной треугольной пирамиды равен (3. Найдите угол бокового ребра с плоскостью основания.
4032.    Сторона основания правильной шестиугольной пирамиды равна
V3 , а угол боковой грани с плоскостью основания равен 60° (рис. 166). Найдите объем пирамиды.
 

4033.    Угол бокового ребра с плоскостью основания правильной треугольной пирамиды равен а. Найдите угол боковой грани с плоскостью основания.
4034.    Угол бокового ребра с плоскостью основания правильной четырехугольной пирамиды равен а. Найдите угол боковой грани с плоскостью основания.
4035.    Угол боковой грани с плоскостью основания правильной четырехугольной пирамиды равен (3. Найдите угол бокового ребра с плоскостью основания.
4036.    Угол бокового ребра с плоскостью основания правильной шестиугольной пирамиды равен а. Найдите угол боковой грани с плоскостью основания.
4037.    Угол боковой грани с плоскостью основания правильной шестиугольной пирамиды равен (3. Найдите угол бокового ребра с плоскостью основания.
4038.    Сторона основания и высота правильной шестиугольной пирамиды равны а. Найдите площадь боковой поверхности пирамиды.
4039.    Найдите площадь сечения, проведенного через высоту и одно из ребер правильного тетраэдра, если ребро тетраэдра равно а.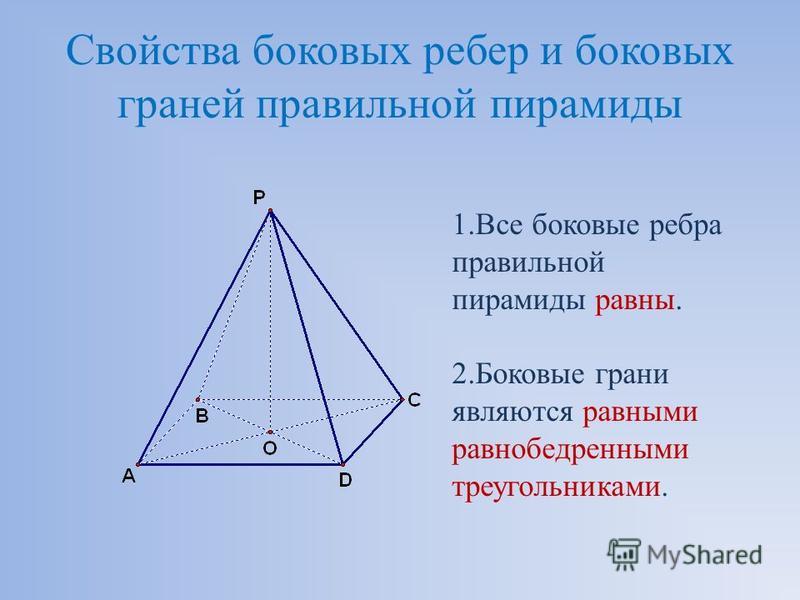
4040.    Сторона основания правильной шестиугольной пирамиды равна
J3 , а угол боковой грани с плоскостью основания равен 60°. Найдите площадь полной поверхности пирамиды.
4041.    Сторона основания правильной шестиугольной пирамиды равна
J3 , а угол боковой грани с плоскостью основания равен 60°. Найдите площадь сечения, проведенного через вершину пирамиды, и меньшую диагональ основания.
4042.    Сторона основания правильной четырехугольной пирамиды равна а. Найдите боковую поверхность и объем пирамиды, если ее диагональное сечение равновелико основанию.
4043.    Все ребра правильной четырехугольной пирамиды равны о. Найдите расстояние между стороной основания и противоположной боксовой гранью.
4044.    Все ребра правильной четырехугольной пирамиды равны а. Найдите радиус описанной сферы.
4045.    Вычислите объем правильного тетраэдра, если радиус окружности, описанной около его грани, равен R.
4046.    Боковое ребро правильной треугольной призмы равно высоте основания, а площадь сечения, проведенного через это боковое ребро и высоту основания, равна Q.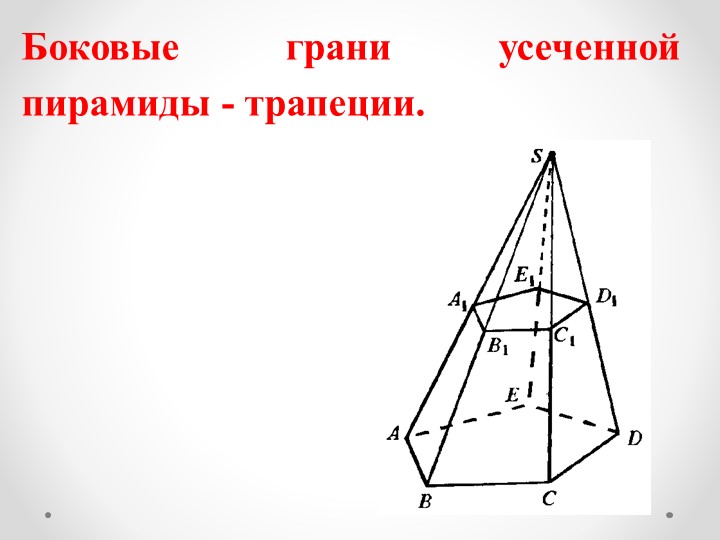 Найдите объем призмы.
4047.    Боковая грань правильной четырехугольной пирамиды образует с плоскостью основания угол, равный 45°. Найдите угол между противоположными боковыми гранями.
4048.    Все ребра правильной четырехугольной пирамиды равны. Найдите угол между противоположными боковыми гранями.
4049.    Все ребра правильной четырехугольной пирамиды равны. Найдите угол между боковой гранью и плоскостью основания.
4050.    В правильной усеченной четырехугольной пирамиде высота равна 2, а стороны оснований равны 3 и 5. Найдите диагональ усеченной пирамиды.
4051.    Высота правильной треугольной пирамиды вдвое больше стороны основания. Найдите: а) угол между боковым ребром и плоскостью основания; б) угол между боковой гранью и плоскостью основания.
4052.    Высота правильной четырехугольной пирамиды вдвое больше стороны основания. Найдите: а) угол между боковым ребром и плоскостью основания; б) угол между боковой гранью и плоскостью основания.
4053.    Высота правильной треугольной пирамиды образует с боковой гранью угол, косинус которого равен
|. Найдите: а) угол боковой грани с 5
плоскостью основания; б) угол бокового ребра с плоскостью основания.
4054.    Апофема правильной четырехугольной пирамиды вдвое больше стороны основания. Найдите: а) угол бокового ребра с плоскостью основания; б) угол боковой грани с плоскостью основания.
4055.    Апофема правильной треугольной пирамиды вдвое больше стороны основания. Найдите: а) угол боковой грани с плоскостью основания; б) угол бокового ребра с плоскостью основания.
4056.    Противоположные боковые грани правильной четырехугольной пирамиды взаимно перпендикулярны. Найдите: а) угол бокового ребра с плоскостью основания; б) угол боковой грани с плоскостью основания.
4057.    Докажите, что в правильной треугольной пирамиде противоположные ребра попарно перпендикулярны.
4058.    Сторона основания правильной треугольной пирамиды равна а. Боковое ребро образует с плоскостью основания угол, равный 60°. Найдите расстояние между противоположными ребрами пирамиды.
4059.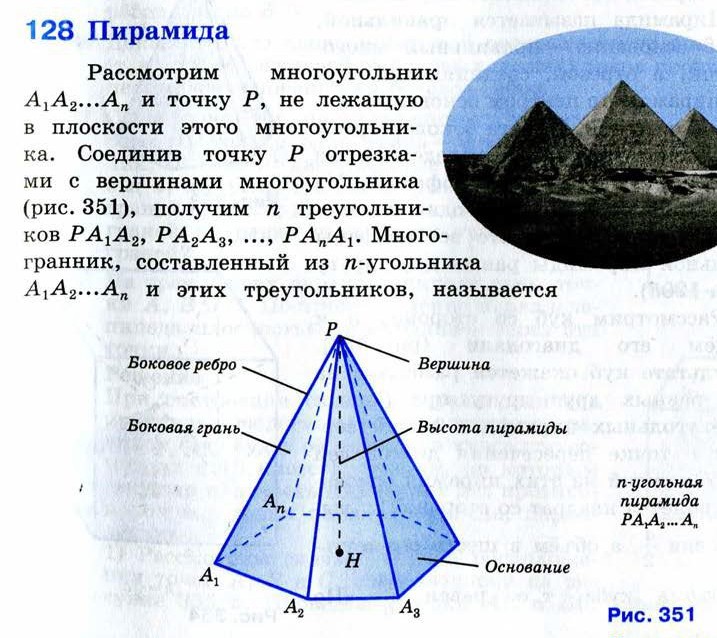     Боковое ребро правильной треугольной пирамиды образует с плоскостью основания угол, равный 60° (рис. 167). Найдите угол между боковыми гранями пирамиды.
 

4060.    Боковая грань правильной четырехугольной пирамиды образует с плоскостью основания угол, равный 45°. Найдите угол между соседними боковыми гранями.
4061.    Сторона основания и высота правильной шестиугольной пирамиды равны а. Найдите радиус сферы, описанной около пирамиды.
4062.    Сторона основания правильной треугольной пирамиды равна а, боковая грань образует с плоскостью основания угол 60°. Найдите расстояние между противоположными ребрами.
4063.    Боковая грань образует с плоскостью основания правильной треугольной пирамиды угол, равный 60°. Найдите угол между боковыми гранями.
4064.    Все ребра правильной четырехугольной пирамиды равны а. Найдите расстояние между диагональю основания и скрещивающимся с ней боковым ребром. 

4065.    Сторона основания правильной шестиугольной пирамиды равна
Уз , а угол боковой грани с плоскостью основания равен 60°. Найдите радиус сферы, описанной около пирамиды.
4066.    Боковое ребро правильной шестиугольной пирамиды вдвое больше стороны основания. Найдите угол боковой грани с плоскостью основания.
4067.    Боковые грани правильной треугольной пирамиды взаимно перпендикулярны. Найдите угол бокового ребра с плоскостью основания.
4068.    Сторона основания правильной треугольной пирамиды равна а, боковое ребро образует с плоскостью основания угол 45°. Найдите радиус описанной сферы.
4069.    Сторона основания правильной четырехугольной пирамиды равна 8, а высота равна 3. Найдите площадь сечения пирамиды плоскостью, проходящей через одну из сторон основания и середину противоположного бокового ребра.
4070.    Все ребра правильной треугольной призмы равны а. Найдите площадь сечения этой призмы плоскостью, проходящей через ребро основания и середину не параллельного ему ребра другого основания.
4071.    Через вершину правильной четырехугольной пирамиды и середины двух соседних сторон основания проведена плоскость. Найдите площадь полученного сечения, если сторона основания пирамиды равна а, а боковое ребро равно 2а.
4072.    Угол бокового ребра с плоскостью основания правильной треугольной пирамиды равен а. Найдите плоский угол при вершине пирамиды.
4073.    Плоский угол при вершине правильной треугольной пирамиды равен ф. Найдите угол бокового ребра с плоскостью основания пирамиды.
4074.    Угол боковой грани с плоскостью основания правильной треугольной пирамиды равен (3. Найдите плоский угол при вершине пирамиды.
4075.    Плоский угол при вершине правильной треугольной пирамиды равен ф. Найдите угол боковой грани с плоскостью основания пирамиды.
4076.    Угол бокового ребра с плоскостью основания правильной четырехугольной пирамиды равен а. Найдите плоский угол при вершине пирамиды.
4077.    Плоский угол при вершине правильной четырехугольной пирамиды равен ф. Найдите угол бокового ребра с плоскостью основания пирамиды.
4078.    Угол боковой грани с плоскостью основания правильной четырехугольной пирамиды равен (3. Найдите плоский угол при вершине пирамиды.
4079.    Плоский угол при вершине правильной четырехугольной пирамиды равен ф. Найдите угол боковой грани с плоскостью основания пирамиды.
4080.    Угол бокового ребра с плоскостью основания правильной шестиугольной пирамиды равен а. Найдите плоский угол при вершине пирамиды.
4081.    Плоский угол при вершине правильной шестиугольной пирамиды равен ф. Найдите угол бокового ребра с плоскостью основания пирамиды.
4082.    Угол боковой грани с плоскостью основания правильной шестиугольной пирамиды равен [3. Найдите плоский угол при вершине пирамиды.
4083.    Плоский угол при вершине правильной шестиугольной пирамиды равен ф. Найдите угол боковой грани с плоскостью основания пирамиды.
4084.    Найдите боковую поверхность правильной шестиугольной пирамиды, если сторона основания равна 1, а боковая грань равновелика диагональному сечению, проведенному через большую диагональ основания.
4085.    Плоские углы при вершине правильной тгугольной пирамиды равны сс.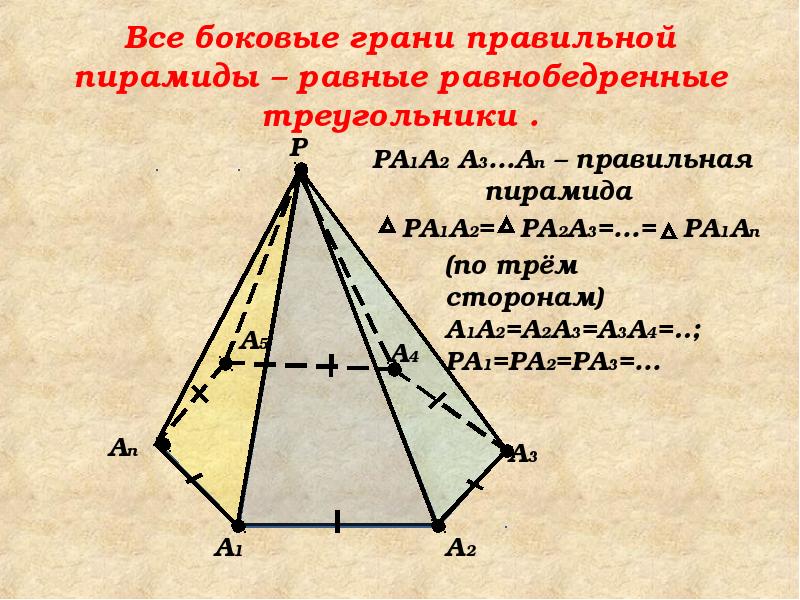 Найдите двугранные углы при основании пирамиды. 
4086.    Имеются две правильные треугольные пирамиды с общим основанием (рис. 168). Все плоские углы при вершине одной из пирамид равны 60°, а у другой они равны 90°. Найдите отношение высот этих пирамид.
 

4087.    Сторона основания правильной треугольной пирамиды равна а. Боковое ребро образует с плоскостью основания угол, равный 60°. Найдите радиус сферы, описанной около пирамиды.
4088.    Сторона основания правильной четырехугольной пирамиды равна а. Боковая грань образует с плоскостью основания угол, равный 45°. Найдите расстояние между боковым ребром и скрещивающейся с ним диагональю основания.
4089.    Сторона основания правильной четырехугольной пирамиды равна а. Боковая грань образует с плоскостью основания угол, равный 45°. Найдите радиус сферы, описанной около пирамиды.
4090.    Сторона основания правильной треугольной пирамиды равна а, боковая грань образует с плоскостью основания угол 60°. Найдите радиус сферы, описанной около пирамиды.
4091.    Найдите расстояние между противоположными ребрами правильного тетраэдра с ребром, равным а.
4092.    Сторона основания ABCD правильной четырехугольной пирамиды SABCD равна а, боковое ребро равно Ъ. Найдите площадь сечения пирамиды плоскостью, проходящей через прямую BD параллельно прямой AS.
4093.    Сторона основания правильной треугольной пирамиды равна а, высота пирамиды равна 2а. Найдите расстояние между противоположными ребрами.
4094.    Сторона основания правильной четырехугольной пирамиды равна а, высота пирамиды равна 2а. Найдите расстояние между диагональю основания и скрещивающимся с ней боковым ребром.
4095.    Высота правильной треугольной пирамиды равна а и образует с боковой гранью угол, косинус которого
О
равен £. Найдите расстояние между 5
противоположными ребрами.
4096.    Сторона основания правильной четырехугольной пирамиды равна а, апофема пирамиды равна 2а. Найдите расстояние между диагональю основания и скрещивающимся с ней боковым ребром.
4097.    Сторона основания правильной треугольной пирамиды равна а, апофема пирамиды равна 2а. Найдите расстояние между противоположными ребрами.
4098.    Апофема правильной четырехугольной пирамиды равна а, а противоположные боковые грани пирамиды взаимно перпендикулярны. Найдите расстояние между диагональю основания и скрещивающимся с ней боковым ребром.
4099.    Сторона основания правильной треугольной пирамиды равна а. Боковое ребро образует с плоскостью основания угол, равный 60°. Найдите радиус сферы, вписанной в пирамиду.
4100.    Сторона основания правильной четырехугольной пирамиды равна а. Боковая грань образует с плоскостью основания угол, равный 45°. Найдите радиус сферы, вписанной в пирамиду. 
4101.    Высота правильной шестиугольной пирамиды равна стороне основания (рис. 169). Найдите угол между соседними боковыми гранями.
 

4102.    Сторона основания правильной треугольной пирамиды равна о, боковая грань образует с плоскостью основания угол 60°. Найдите радиус сферы, вписанной в пирамиду.
4103.    Найдите радиус сферы, описанной около правильного тетраэдра с ребром, равным о.
4104.    Найдите радиус сферы, вписанной в правильный тетраэдр с ребром, равным о.
4105.    Боковая грань образует с плоскостью основания правильной шестиугольной пирамиды угол, равный 60°. Найдите угол между соседними боковыми гранями.
4106.    Высота правильной треугольной пирамиды равна 6*j6 , боковое ребро образует с плоскостью основания угол 45°. Найдите расстояние от центра основания пирамиды до боковой грани.
4107.    Сторона основания правильной четырехугольной пирамиды равна а, боковая грань образует с плоскостью основания угол 60°. Найдите радиус вписанной сферы.
4108.    Высота правильной четырехугольной пирамиды равна 8, апофема пирамиды равна 10. Найдите расстояние между диагональю основания и скрещивающимся с ней боковым ребром.
4109.    Основание пирамиды совпадает с одной из граней куба, а вершина — с центром противоположной грани. Найдите угол между соседними боковыми гранями пирамиды.
4110.    Через середину ребра правильного тетраэдра проведена плоскость, перпендикулярная соседнему ребру. Найдите площадь полученного сечения, если ребро тетраэдра равно о.
4111.    Через вершину D правильного тетраэдра АВСН с ребром, равным о, и середины ребер АВ и АС проведена плоскость. Найдите площадь полученного сечения.
4112.    Сторона основания правильной треугольной пирамиды равна о, боковое ребро равно Ь. Найдите площадь сечения пирамиды плоскостью, проходящей через середины двух ребер основания и середину одного из боковых ребер.
4113.    Все ребра правильной четырехугольной пирамиды равны о. Через сторону основания и середину одного из противоположных боковых ребер проведена плоскость. Найдите площадь полученного сечения.
4114.    Через диагональ BlD1 грани ■AjBiCjH, и середину ребра DC правильной четырехугольной призмы ABCDA1B1C1D1 проведена плоскость. Найдите площадь сечения призмы этой плоскостью, если АВ = о, CCj = 2а.
4115.    Угол бокового ребра с плоскостью основания правильной треугольной пирамиды равен а. Найдите угол между боковыми гранями.
4116.    Угол между боковыми гранями правильной треугольной пирамиды равен у. Найдите угол бокового ребра с плоскостью основания.
4117.    Угол боковой грани с плоскостью основания правильной треугольной пирамиды равен |3. Найдите угол между боковыми гранями.
4118.    Угол между боковыми гранями правильной треугольной пирами 
ды равен у. Найдите угол боковой грани с плоскостью основания.

4119.    Угол между боковыми гранями правильной треугольной пирамиды равен у Найдите плоский угол при вершине пирамиды.
4120.    Плоский угол при вершине правильной треугольной пирамиды равен <р. Найдите угол между боковыми гранями пирамиды.
4121.    Угол бокового ребра с плоскостью основания правильной четырехугольной пирамиды равен а. Найдите угол между соседними боковыми гранями.
4122.    Угол между соседними боковыми гранями правильной четырехугольной пирамиды равен у. Найдите угол бокового ребра с плоскостью основания.
4123.    Угол боковой грани с плоскостью основания правильной четырехугольной пирамиды равен |3. Найдите угол между соседними боковыми гранями.
4124.    Угол между соседними боковыми гранями правильной четырехугольной пирамиды равен у. Найдите угол боковой грани с плоскостью основания.
4125.    Угол между соседними боковыми гранями правильной четырехугольной пирамиды равен у. Найдите плоский угол при вершине пирамиды.
4126.    Плоский угол при вершине правильной четырехугольной пирамиды равен ф. Найдите угол между соседними боковыми гранями пирамиды.
4127.    Угол бокового ребра с плоскостью основания правильной шестиугольной пирамиды равен а. Найдите угол между соседними боковыми гранями.
4128.    Угол между соседними боковыми гранями правильной шестиугольной пирамиды равен у. Найдите угол бокового ребра с плоскостью основания.
4129.    Угол боковой грани с плоскостью основания правильной шестиугольной пирамиды равен |3. Найдите угол между соседними боковыми гранями.
4130.    Угол между соседними боковыми гранями правильной шестиугольной пирамиды равен у. Найдите угол боковой грани с плоскостью основания.
4131.    Угол между соседними боковыми гранями правильной шестиугольной пирамиды равен у. Найдите плоский угол при вершине пирамиды.
4132.    Плоский угол при вершине правильной шестиугольной пирамиды равен ф. Найдите угол между соседними боковыми гранями пирамиды.
4133.    В правильной четырехугольной пирамиде SABCD через середины сторон АВ и АО основания проведена плоскость, параллельная боковому ребру SA (рис. 170). Найдите площадь сечения, зная сторону основания а и боковое ребро Ъ.
S
 

4134.    В правильную четырехугольную пирамиду SABCD вписан куб. Все четыре вершины одной из граней куба лежат на основании ABCD пирамиды. Все четыре вершины противоположной грани куба лежат на апофемах пирамиды. Известно, что SA — АВ = о, т. е. боковое ребро пирамиды равно о и равно стороне ее основания. Чему равен объем куба?
4135.    Найдите объем правильной четырехугольной пирамиды со стороной основания, равной о, и плоскими углами при вершине, равными углам боковых ребер с плоскостью основания.
4136.    В правильную четырехугольную пирамиду вписана сфера, которая касается основания и всех боковых граней. Сфера делит высоту пирамиды в отношении 9 : 7, считая от вершины пирамиды. Найдите объем пирамиды, если сторона основания пирамиды равна о.
4137.    Высота правильной треугольной пирамиды вдвое больше стороны основания. Найдите угол между боковыми гранями.
4138.    Высота правильной четырехугольной пирамиды вдвое больше стороны основания. Найдите угол между соседними боковыми гранями.
4139.    Высота правильной треугольной пирамиды образует с боковой гранью угол, косинус которого равен
О
. Найдите угол между боковыми гра
5    ы    «
нями.
4140.    Апофема правильной четырехугольной пирамиды вдвое больше стороны основания. Найдите угол между соседними боковыми гранями.
4141.    Апофема правильной треугольной пирамиды вдвое больше стороны основания. Найдите угол между боковыми гранями.
4142.    Противоположные боковые грани правильной четырехугольной пирамиды взаимно перпендикулярны. Найдите угол между соседними боковыми гранями.
4143.    Через середину ребра правильной треугольной пирамиды проведено сечение, параллельное двум ее скрещивающимся ребрам. Найдите площадь этого сечения, если сторона основания пирамиды равна а, а боковое ребро равно Ь.
4144.    Покажите, что в кубе можно выбрать четыре вершины, являющиеся вершинами правильного тетраэдра, причем сделать это можно двумя способами.
4145.    Сторона основания правильной треугольной пирамиды равна а, боковое ребро равно Ь. Найдите радиус описанного шара.
4146.    Сторона основания правильной четырехугольной пирамиды равна а, боковое ребро равно Ь. Найдите радиус описанного шара.
4147.    Сторона основания правильной шестиугольной пирамиды равна а, боковое ребро равно Ь. Найдите радиус описанного шара.
4148.    Найдите объем правильной четырехугольной пирамиды со стороной основания, равной а, и углом между соседними боковыми гранями, равным у.
4149.    Найдите объем правильной четырехугольной пирамиды с высотой, равной Л, и углом между соседними боковыми гранями, равным у.
4150.    Сторона основания и высота правильной шестиугольной пирамиды равны о. Найдите радиус сферы, вписанной в пирамиду.
4151.    Все ребра правильной четырехугольной пирамиды равны о. Найдите радиус вписанной сферы.
4152.    Сторона основания правильной шестиугольной пирамиды равна
7з , а угол боковой грани с плоскостью основания равен 60°. Найдите радиус сферы, вписанной в пирамиду.
4153.    Сторона основания правильной треугольной пирамиды равна а, боковое ребро образует с плоскостью основания угол 45°. Найдите радиус вписанной сферы.
4154.    Сторона основания правильной четырехугольной пирамиды равна о, боковая грань образует с плоскостью основания угол 60°. . Найдите радиус
О
описанной сферы.
4156.    Сторона основания правильной четырехугольной пирамиды равна а, а расстояние между диагональю основания и скрещивающимся с ней боковым ребром равно ~ . Найдите радиус описанной сферы.
4157.    В правильной треугольной пирамиде РАВС с вершиной Р сторона основания равна 2 (рис. 171). Через сторону основания ВС проведено сечение, которое пересекает ребро РА в точке М, причем PM : МА = 1 : 3, а площадь сечения равна 3. Найдите высоту пирамиды.
Р
 

4158.    Найдите объем параллелепипеда, все грани которого — равные ромбы со стороной, равной о, и острым углом 60°.
4159.    В шар вписана правильная четырехугольная пирамида. Радиус шара равен 1. Плоский угол при вершине пирамиды равен 45°. Найдите площадь боковой поверхности пирамиды.
4160.    Сторона основания правильной четырехугольной пирамиды равна о, высота пирамиды равна 2а. Найдите радиусы описанной и вписанной сфер.
4161.    Высота правильной треугольной пирамиды равна а и образует с бо
ковой гранью угол, косинус которого
О
равен .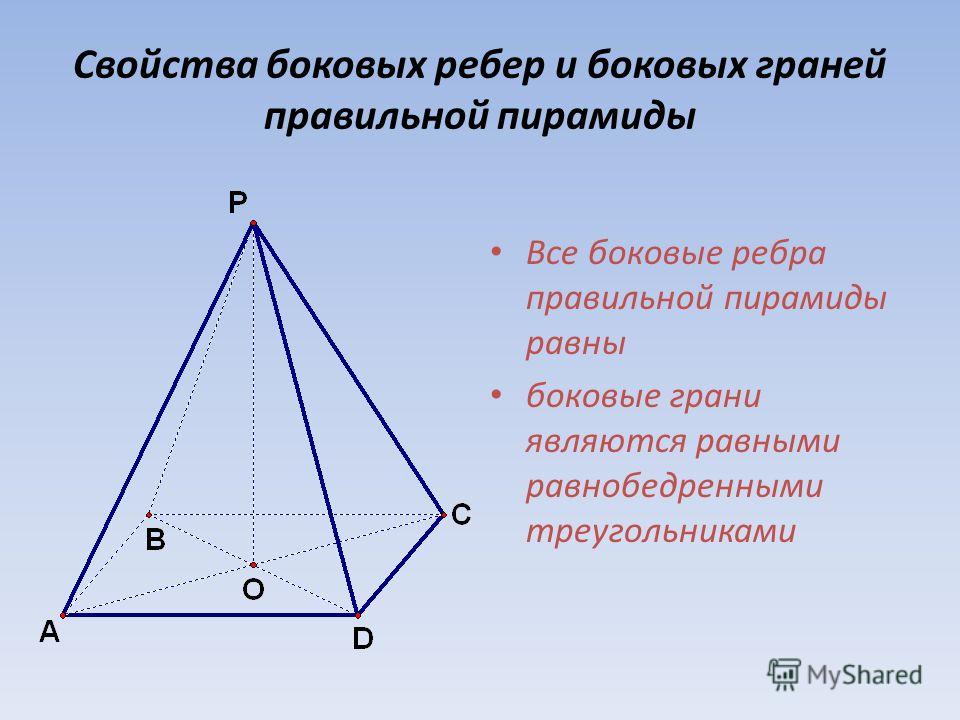 Найдите радиусы описанной 5
и вписанной сфер.
4162.    Сторона основания правильной четырехугольной пирамиды равна а, апофема пирамиды равна 2а. Найдите радиусы описанной и вписанной сфер.
4163.    Сторона основания правильной треугольной пирамиды равна а, апофема пирамиды равна 2а. Найдите радиусы описанной и вписанной сфер.
4164.    Апофема правильной четырехугольной пирамиды равна а, а противоположные боковые грани пирамиды взаимно перпендикулярны. Найдите радиусы описанной и вписанной сфер.
4165.    Докажите, что пирамида с равными боковыми ребрами и с равными двугранными углами при основании является правильной.
4166.    Сторона основания правильной треугольной пирамиды равна а, боковое ребро равно Ь. Найдите радиус вписанного шара.
4167.    Сторона основания правильной четырехугольной пирамиды равна а, боковое ребро равно Ъ. Найдите радиус вписанного шара.
4168.    Сторона основания правильной шестиугольной пирамиды равна а, боковое ребро равно Ъ. Найдите радиус вписанного шара.
4169.    Сторона основания правильной треугольной пирамиды равна а, боковое ребро равно Ь. Найдите радиус шара, касающегося всех ребер пирамиды.
4170.    Сторона основания правильной четырехугольной пирамиды равна а, боковое ребро равно Ъ. Найдите радиус шара, касающегося всех ребер пирамиды.
4171.    Сторона основания правильной шестиугольной пирамиды равна а, боковое ребро равно Ъ. Найдите радиус шара, касающегося всех ребер пирамиды. ‘
4172.    Сторона основания правильной треугольной пирамиды равна о, боковое ребро равно Ъ. Найдите радиус шара, касающегося сторон основания и продолжений боковых ребер пирамиды.
4173.    Сторона основания правильной четырехугольной пирамиды равна о, боковое ребро равно Ъ. Найдите радиус шара, касающегося сторон основания и боковых ребер пирамиды.
4174.    Сторона основания правильной шестиугольной пирамиды равна о, боковое ребро равно Ъ. Найдите радиус шара, касающегося сторон основания и продолжений боковых ребер пирамиды.
4175.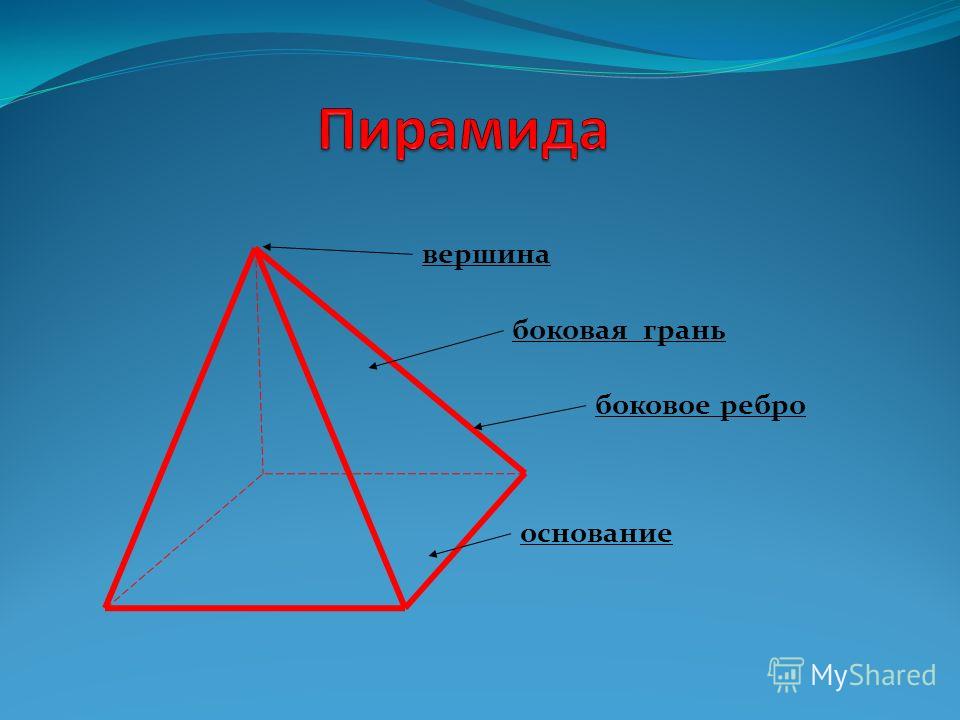     Сторона основания правильной треугольной пирамиды равна о, боковое ребро равно Ъ. Найдите радиус шара, касающегося плоскости основания и боковых ребер пирамиды.
4176.    Сторона основания правильной четырехугольной пирамиды равна а, боковое ребро равно Ь. Найдите радиус шара, касающегося плоскости основания и боковых ребер пирамиды.
4177.    Сторона основания правильной шестиугольной пирамиды равна о, боковое ребро равно Ъ. Найдите радиус шара, касающегося плоскости основания и боковых ребер пирамиды.
4178.    Боковое ребро правильной четырехугольной пирамиды равно Ъ, а плоский угол при вершине равен а (рис. 172). Найдите радиус сферы, описанной около пирамиды.
 

4179.    Найдите объем правильной шестиугольной пирамиды с радиусом вписанной сферы, равным г, и плоским углом при вершине, равным <р.
4180.    Сторона основания правильной четырехугольной пирамиды равна о, а расстояние между диагональю основания и скрещивающимся с ней боковым ребром равно . Найдите ради
4
ус вписанной сферы.
4181.    Сторона основания правильной четырехугольной пирамиды
ABCDP (Р — вершина) равна 4 J2 , а угол между соседними боковыми гранями равен 

120°. Найдите площадь сечения пирамиды плоскостью, проходящей через диагональ BD основания параллельно боковому ребру СР.
4182.    Правильную четырехугольную пирамиду пересекает плоскость, проходящая через вершину основания перпендикулярно противоположному боковому ребру. Площадь получившегося сечения в два раза меньше площади основания пирамиды. Найдите отношение высоты пирамиды к боковому ребру.
4183.    Правильную четырехугольную пирамиду SABCD с вершиной S пересекает плоскость, проходящая через середины ребер SB и SC и перпендикулярная грани SAD. Площадь основания пирамиды восемь раз больше площади получившегося сечения. Найдите угол между боковой гранью и плоскостью основания пирамиды.
4184.    На гранях правильного тетраэдра с ребром, равным о, как на основаниях построены правильные тетраэдры. Докажите, что новые вершины построенных тетраэдров являются вершинами правильного тетраэдра.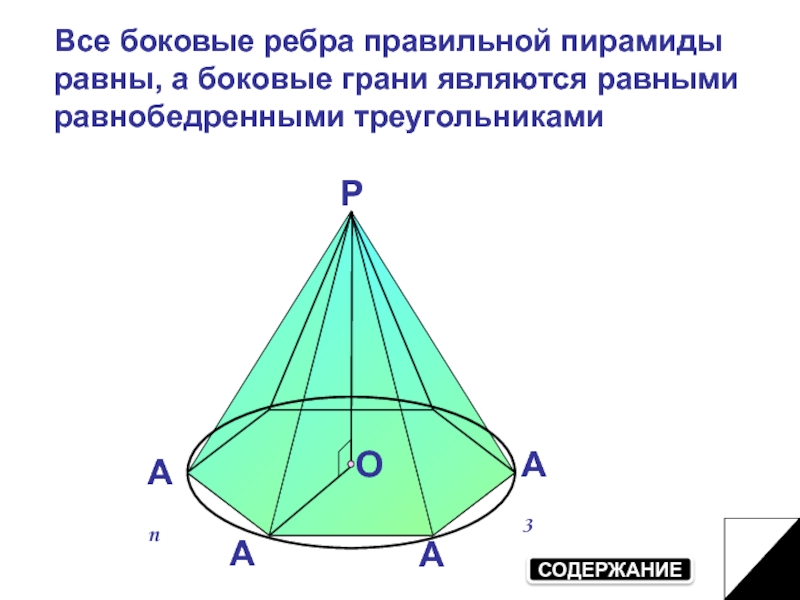 Найдите его ребро.
4185.    Площадь основания правильной /гугольной пирамиды равна S, а площадь боковой грани равна Q. Найдите двугранные углы при основании этой пирамиды.
4186.    Найдите ребро куба, одна грань которого лежит в плоскости основания правильной треугольной пирамиды, а четыре оставшиеся вершины — на ее боковой поверхности, если стороны основания пирамиды равны о, а высота пирамиды равна h.
4187.    Через сторону основания правильной четырехугольной пирамиды проведена плоскость, отсекающая от противоположной грани треугольник с площадью о2. Найдите боковую поверхность пирамиды, которая отсечена проведенной плоскостью от данной пирамиды, если боковая поверхность данной пирамиды равна Ъ2.
4188.    Сторона основания правильной треугольной пирамиды равна о, боковое ребро образует с плоскостью основания угол а. Найдите радиус описанного шара.
4189.    Сторона основания и высота правильной четырехугольной пирамиды равны о. Найдите радиус вписанного шара.
4190. . Найдите радиус
О
вписанной сферы.
4191.    Вершины пирамиды KLMN расположены в точках пересечения медиан граней некоторой правильной треугольной пирамиды со стороной основания о и боковым ребром Ъ. Найдите полную поверхность пирамиды KLMN.
4192.    Найдите радиус сферы, касающейся всех ребер правильного тетраэдра с ребром, равным о.
4193.    Все грани параллелепипеда — равные ромбы со стороной, равной а, и острым углом 60°. Найдите высоту параллелепипеда.
4194.    Двугранный угол при основании правильной nугольной пирамиды равен р. Найдите двугранный угол между соседними боковыми гранями.
4195.    На продолжении ребра SK правильной четырехугольной пирамиды SKLMN с вершиной S взята точка А так, что расстояние от точки А до плоскости SMN равно 24. Найдите
КА, если SL = 2    , a MN = 16.
4196.    На продолжении ребра SD правильной четырехугольной пирамиды SABCD с вершиной S взята точка N так, что DN =11. Найдите расстояние от точки N до плоскости SAB, если АВ = 6, a SB = 5.
4197.    Высота правильной треугольной пирамиды вдвое больше стороны основания. Найдите угол между апофемой и соседней боковой гранью.
4198.    Высота правильной четырехугольной пирамиды вдвое больше стороны основания. Найдите угол между апофемой и соседней боковой гранью.
4199.    Высота правильной треугольной пирамиды образует с боковой гранью угол, косинус которого равен
я «    ~
. Найдите угол между апофемой и со
5
седней боковой гранью.
4200.    Апофема правильной четырехугольной пирамиды вдвое больше стороны основания. Найдите угол между апофемой и соседней боковой гранью.
4201.    Апофема правильной треугольной пирамиды вдвое больше стороны основания. Найдите угол между апофемой и соседней боковой гранью.
4202.    Противоположные боковые грани правильной четырехугольной пирамиды взаимно перпендикулярны. Найдите угол между апофемой и соседней боковой гранью.
4203.    На гранях правильного тетраэдра с ребром, равным о, как на основаниях построены равные правильные пирамиды.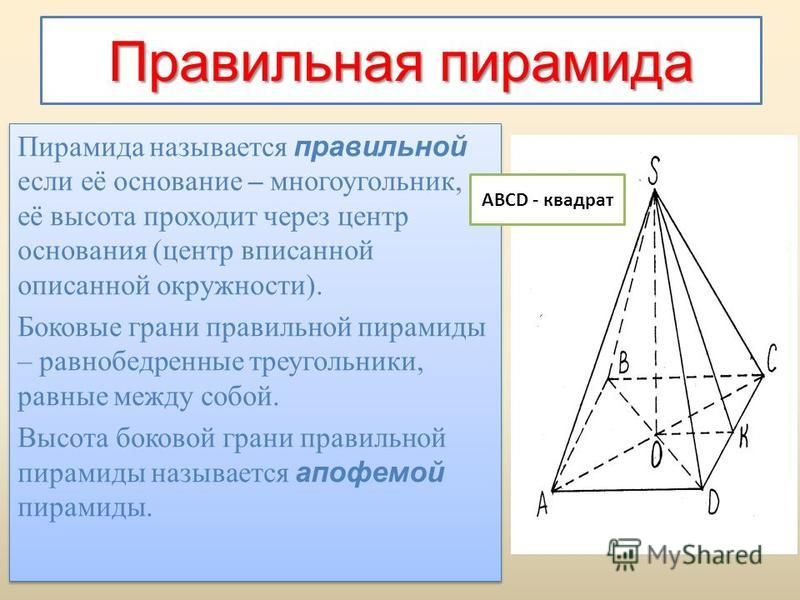 Плоские углы в этих пирамидах при вершинах, противолежащих граням тетраэдра, прямые. Рассмотрите многогранник, образованный тетраэдром и построенными пирамидами (рис. 173). Сколько граней у этого многогранника? Как он называется?
 
Рис. 173

4204.    В правильной четырехугольной пирамиде SABCD боковое ребро SA и диагональ BD основания образуют равные углы плоскостью боковой грани SBC. Найдите угол между ребром SA и плоскостью грани SBC.
4205.    Боковое ребро правильной треугольной пирамиды образует с плоскостью основания угол, равный 60°. Найдите угол апофемы с плоскостью соседней грани.
4206.    Боковая грань правильной четырехугольной пирамиды образует с плоскостью основания угол, равный 45°. Найдите угол между апофемой пирамиды и плоскостью соседней грани.
4207.    Высота правильной шестиугольной пирамиды равна стороне основания. Найдите угол между апофемой и плоскостью соседней боковой грани.
4208.    Боковая грань образует с плоскостью основания правильной треугольной пирамиды угол, равный 60°. Найдите угол между апофемой и плоскостью соседней боковой грани.
4209.    Все ребра правильной четырехугольной пирамиды равны. Найдите угол между апофемой и плоскостью соседней боковой грани.
4210.    Боковое ребро правильной треугольной пирамиды образует с плоскостью основания угол, равный 45°. Найдите угол между апофемой пирамиды и соседней боковой гранью.
4211.    Боковая грань правильной четырехугольной пирамиды образует с плоскостью основания угол 60°. Найдите угол апофемы с соседней боковой гранью.
4212.    Расстояние между противоположными ребрами правильной тре
О
угольной пирамиды равно £ ее боково
О
го ребра. Найдите угол апофемы с соседней боковой гранью.
4213.    Расстояние между диагональю основания и скрещивающимся с ней боковым ребром правильной четырехугольной пирамиды равно четверти стороны основания. Найдите угол апофемы с соседней боковой гранью.
4214.    Сторона основания правильной треугольной пирамиды равна о, угол апофемы с соседней боковой гранью равен 45°. Найдите радиусы вписанной и описанной сфер.
4215.    Дан правильный тетраэдр с ребром, равным а. Найдите объем многогранника, полученного в пересечении этого тетраэдра со своим образом при симметрии относительно середины высоты.
4216.    Два правильных тетраэдра ABCD и MNPQ расположены так, что плоскости BCD и NPQ совпадают, вершина М лежит на высоте АО первого тетраэдра, а плоскость MNP проходит через центр грани АВС и середину ребра BD. Найдите отношение ребер тетраэдров.

 

Пирамида

Пирамидой называется многогранник, у которого одна из граней — основание — какой — нибудь многоугольник, а все остальные — боковые — треугольники, имеющие общую вершину.
Общая вершина S боковых граней называется вершиной пирамиды, а перпендикуляр SO, опущенный из вершины на плоскость основания, — высотой ее (фиг.286,а).

Пирамиды бывают: треугольные, четырехугольные и т. д., смотря по тому, что является основанием — треугольник, четырехугольник и т. д.
Пирамида называется правильной (фиг.286,б), если, во — первых, ее основанием является правильный многоугольник, и, во — вторых, высота проходит через центр этого многоугольника.
В противном случае пирамида называется неправильной (фиг.286,в). В правильной пирамиде все боковые ребра равны между собой (как наклонные с равными проекциями). Поэтому все боковые грани правильной пирамиды есть равные равнобедренные треугольники.
Анализ элементов правильной шестиугольной пирамиды и их изображение на комплексном чертеже (фиг.287).

а) Комплексный чертеж правильной шестиугольной пирамиды. Основание пирамиды расположено на плоскости П₁; две стороны основания пирамиды параллельны плоскости проекций П₂.
б) Основание ABCDEF — шестиугольник, расположенный в плоскости проекций П₁.
в) Боковая грань ASF — треугольник, расположенный в плоскости общего положения.
г) Боковая грань FSE — треугольник, расположенный в профильно — проектирующей плоскости .
д) Ребро SE — отрезок общего положения.
е) Ребро SA — фронтальный отрезок.
ж) Вершина S пирамиды — точка в пространстве.
На (фиг.288 и фиг.289) приведены примеры последовательных графических операций при выполнении комплексного чертежа и наглядных изображений (аксонометрии) пирамид.
Изображение правильной пятиугольной пирамиды.

Дано:
1. Основание расположено на плоскости П₁.
2. Одна из сторон основания параллельна оси х₁₂.
I. Комплексный чертеж.
I, а. Проектируем основание пирамиды — многоугольник, по данному условию лежащий в плоскости П₁.
Проектируем вершину — точку, расположенную в пространстве. Высота точки S равна высоте пирамиды. Горизонтальная проекция S₁ точки S будет в центре проекции основания пирамиды (по условию).
I, б. Проектируем ребра пирамиды — отрезки; для этого соединяем прямыми проекции вершин основания ABCDE с соответствующими проекциями вершины пирамиды S. Фронтальные проекции S₂ С₂и S₂ D₂ ребер пирамиды изображаем штриховыми линиями, как невидимые, закрытые гранями пирамиды (SBА и SAE).
I, в. Дана горизонтальная проекция К₁ точки К на боковой грани SBА, требуется найти ее фронтальную проекцию. Для этого проводим через точки S₁и K₁ вспомогательную прямую S₁F₁, находим ее фронтальную проекцию и на ней при помощи вертикальной линии связи определяем место искомой фронтальной проекции K₂ точки К.
II. Развертка поверхности пирамиды — плоская фигура, состоящая из боковых граней — одинаковых равнобедренных треугольников одна сторона которых равна стороне основания, а две другие — боковым ребрам, и из правильного многоугольника — основания.
Натуральные размеры сторон основания выявлены на его горизонтальной проекции. Натуральные размеры ребер на проекциях не выявлены.
Гипотенуза S₂¯A₂ (фиг.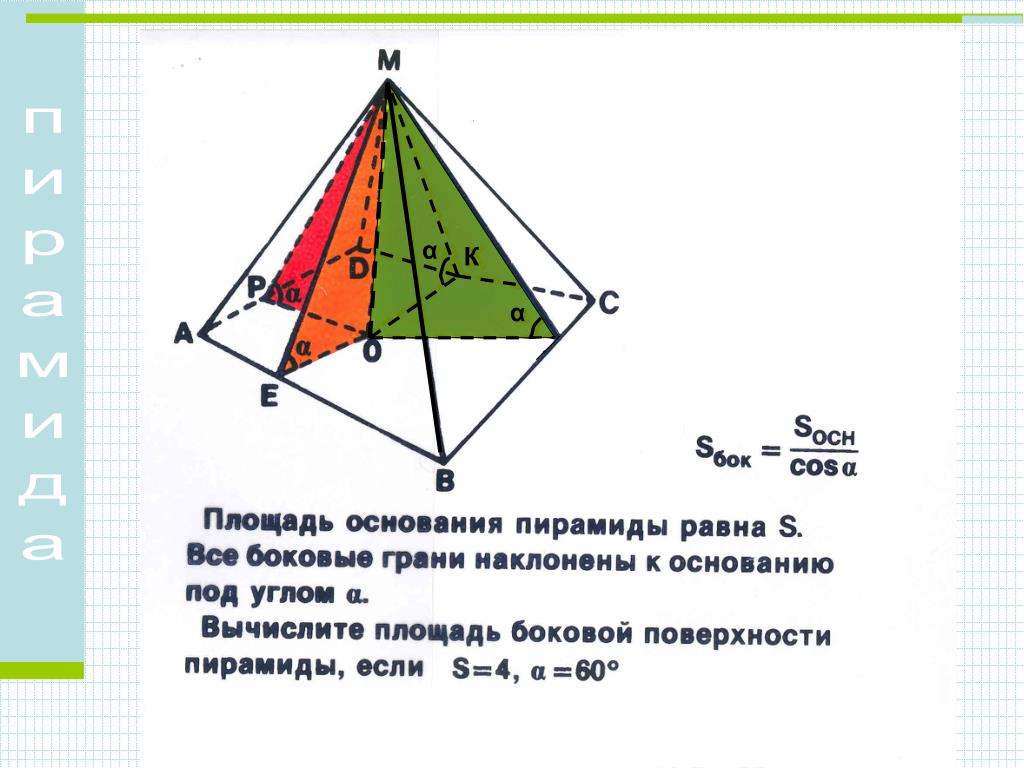 288, 1, б) прямоугольного треугольника S₂O₂¯A₂, у которого большой катет равен высоте S₂O₂ пирамиды, а малый — горизонтальной проекции ребра S₁A₁является натуральной величиной ребра пирамиды. Построение развертки следует выполнять в следующем порядке:
а) из произвольной точки S (вершины) проводим дугу радиусом R, равным ребру пирамиды;
б) на проведенной дуге отложим пять хорд размером R₁ равным стороне основания;
в) соединим прямыми точки D, С, В, А, Е, D последовательно между собой и с точкой S, получим пять равнобедренных равных треугольников, составляющих развертку боковой поверхности данной пирамиды, разрезанной по ребру SD;
г) пристраиваем к любой грани основание пирамиды — пятиугольник, пользуясь способом триангуляции, например к грани DSE.
Перенос на развертку точки К осуществляется вспомогательной прямой с помощью размера В₁F₁, взятого на горизонтальной проекции, и размера А₂К₂, взятого на натуральной величине ребра.
III. Наглядное изображение пирамиды в изометрии.
III, а. Изображаем основание пирамиды, пользуясь координатами согласно (фиг.288, 1, а).
Изображаем вершину пирамиды, пользуясь координатами по (фиг.288, 1, а).
III, б. Изображаем боковые ребра пирамиды, соединяя вершину с вершинами основания. Ребро S’D’ и стороны основания C’D’ и D’E’ изображаем штриховыми линиями, как невидимые, закрытые гранями пирамиды C’S’B’, B’S’A’ и A’S’E’.
III, e. Определяем на поверхности пирамиды точку К, пользуясь размерами у_F и х_K. Для ди-метрического изображения пирамиды следует придерживаться той же последовательности.
Изображение неправильной треугольной пирамиды.

Дано:
1. Основание расположено на плоскости П₁.
2. Сторона ВС основания перпендикулярна оси X.
I. Комплексный чертеж
I, а. Проектируем основание пирамиды — равнобедренный треугольник, лежащий в плоскости П₁, и вершину S — точку, расположенную в пространстве, высота которой равна высоте пирамиды.
I, б. Проектируем ребра пирамиды — отрезки, для чего соединяем прямыми одноименные проекции вершин основания с одноименными проекциями вершины пирамиды. Горизонтальную проекцию стороны основания ВС изображаем штриховой линией, как невидимую, закрытую двумя гранями пирамиды ABS, ACS.
I, в. На фронтальной проекции A₂С₂S₂ боковой грани дана проекция D₂ точки D. Требуется найти ее горизонтальную проекцию. Для этого через точку D₂ проводим вспомогательную прямую параллельно оси х₁₂ — фронтальную проекцию горизонтали, затем находим ее горизонтальную проекцию и на ней, при помощи вертикальной линии связи, определяем место искомой горизонтальной проекции D₁ точки D.
II. Построение развертки пирамиды.
Натуральные размеры сторон основания выявлены на горизонтальной проекции. Натуральная величина ребра AS выявлена на фронтальной проекции; натуральной величины ребер BS и CS в проекциях нет, величину этих ребер выявляем путем вращения их вокруг оси i, перпендикулярной к плоскости П₁ проходящей через вершину пирамиды S.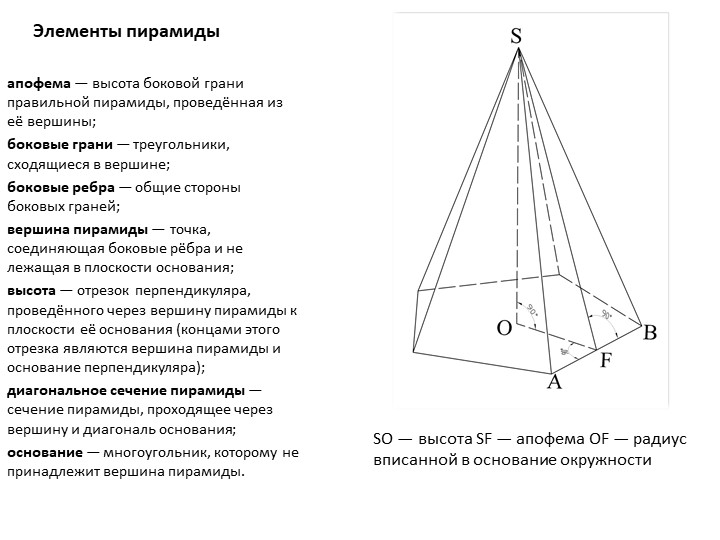 Новая фронтальная проекция ¯C₂S₂ является натуральной величиной ребра CS.
Последовательность построения развертки поверхности пирамиды:
а) вычерчиваем равнобедренный треугольник — грань CSB, основание которого равно стороне основания пирамиды СВ, а боковые стороны — натуральной величине ребра SC;
б) к сторонам SC и SB построенного треугольника пристраиваем два треугольника — грани пирамиды CSA и BSA, а к основанию СВ построенного треугольника — основание СВА пирамиды, в результате получаем полную развертку поверхности данной пирамиды.
Перенос на развертку точки D выполняется в следующем порядке: сначала на развертке боковой грани ASC проводим линию горизонтали при помощи размера R₁ а затем определяем на линии горизонтали место точки D при помощи размера R₂.
III. Наглядное изображение пирамиды е фронтальной диметрической проекции
III, а. Изображаем основание А’В’С и вершину S’ пирамиды, пользуясь координатами согласно (фиг. 289, 1, а).

III, б. Изображаем ребра S’A, S’C’ и S’B’ пирамиды, соединяя вершину S’ с вершинами основания А’В’С’. Ребро S’B’ и стороны основания A’В’ и В’С’ изображаем штриховыми линиями, как невидимые, закрытые гранью A’S’C’. Для определения на поверхности пирамиды места точки D пользуемся координатами точки x_D, y_D, z_D (фиг.289, 1, в), причем координата y_D сокращается вдвое.

Вращения и развертки поверхностей…..



 

Пирамиды

Когда мы думаем о пирамидах, мы думаем о Великих пирамидах Египта .

На самом деле это Квадратные Пирамиды , потому что их основание — Квадрат.

Части пирамиды

Пирамида получается путем соединения основания с вершиной

Основание — многоугольник (плоский с прямыми краями), а все остальные грани — треугольники.Никаких кривых!

Типы пирамид

Существует много типов пирамид, и они названы в честь формы их основания.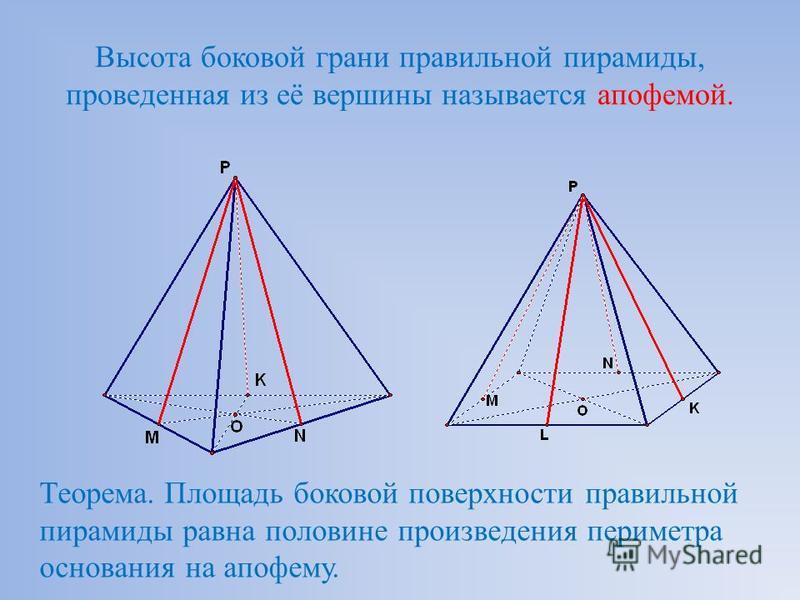

 

Пролетите здесь через несколько пирамид.

Правая и наклонная пирамида

Это говорит нам, где вершина (вершина) пирамиды. Когда вершина находится прямо над центром основания, это правильная пирамида , в противном случае это наклонная пирамида .

Правая пирамида	Наклонная пирамида

Правильная и неправильная пирамида

Это говорит нам о форме основания .Когда основание представляет собой правильный многоугольник, это правильная пирамида , иначе это неправильная пирамида .

Обычная пирамида	Неправильная пирамида
Основание стандартное	Основание неправильной формы

Площадь и объем

Объем пирамиды

• ¹ / ₃ × [Площадь основания] × Высота

Площадь поверхности пирамиды

Когда все боковые грани одинаковые:

• [База] + ¹ / ₂ × периметр × [наклонная длина]

Если боковые грани разные:

• [Основная область] + [Боковая область]

 

Примечания по площади поверхности

Площадь поверхности состоит из двух частей: площадь основания ( Базовая зона ) и площадь боковых граней ( Боковая зона ).

Для Базовая зона :

Это зависит от формы, существуют разные формулы для треугольника, квадрата и т. д. Формулы см. в разделе «Площадь» или в нашем инструменте расчета площади

Для Боковая область :

Когда все боковые грани одинаковые:

• Умножьте периметр на «наклонную длину» и разделите на 2. Это потому, что боковые грани всегда являются треугольниками, а формула треугольника равна «основание, умноженное на высоту, деленное на 2»

Но когда боковые грани разные (например, в «неправильной» пирамиде), мы должны сложить площади каждого треугольника, чтобы найти общую боковую площадь.

 

Боковая площадь квадратной пирамиды

Площадь боковой стороны квадратной пирамиды определяется как площадь, покрытая наклоном ее боковых граней. Пирамида — это трехмерный объект, основание которого может быть любым многоугольником, а все его боковые грани — конгруэнтными треугольниками.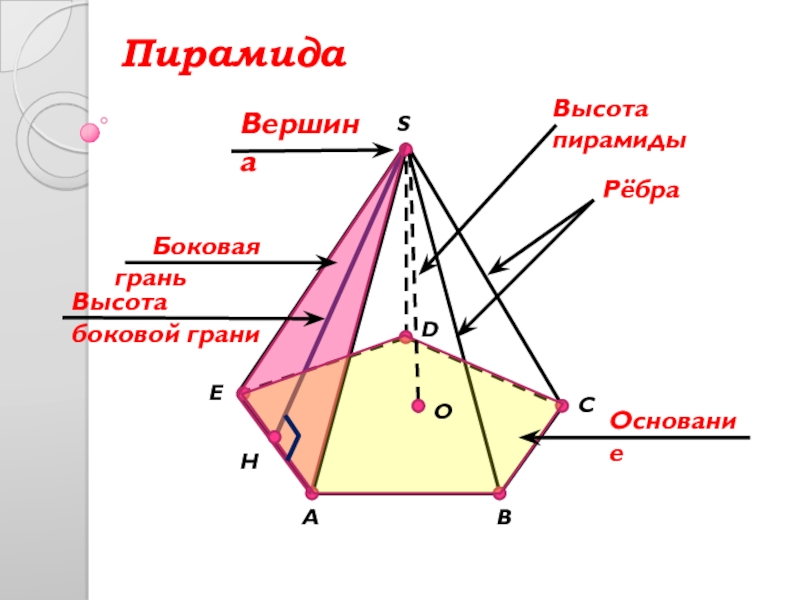 Одна сторона каждого из этих треугольников совпадает с одной стороной базового многоугольника. Пирамиды названы в соответствии с формой их оснований. Квадратная пирамида — это пирамида, основание которой — квадрат.Как и другие трехмерные фигуры, квадратная пирамида также имеет два типа областей.

• Площадь боковой поверхности (LSA)
• Общая площадь поверхности (TSA)

Давайте узнаем о боковой площади квадратной пирамиды вместе с формулой и несколькими решенными примерами здесь. В конце вы также найдете несколько практических вопросов для практики.

Какова боковая площадь квадратной пирамиды?

Слово «латеральный» означает «принадлежащий стороне».Таким образом, площадь боковой стороны квадратной пирамиды равна сумме площадей ее боковых граней. Это также известно как площадь боковой поверхности (LSA) квадратной пирамиды. Мы знаем, что квадратная пирамида имеет:

• основание, представляющее собой квадрат.
• 4 боковые грани, каждая из которых представляет собой треугольник.

Все эти треугольники конгруэнтны и равнобедренны, каждый из которых имеет сторону, совпадающую со стороной основания (квадрата).

Итак, площадь боковой поверхности квадратной пирамиды равна сумме площадей четырех ее треугольных боковых граней.

Формула площади боковой поверхности квадратной пирамиды

Рассмотрим квадратную пирамиду, у которой длина основания (длина стороны квадрата) равна «a», а высота каждой боковой грани (треугольника) равна «l» (это также известно как наклонная высота). т. е. основание и высота каждой из четырех треугольных граней равны «a» и «l» соответственно. Таким образом, площадь каждой такой треугольной грани равна 1/2 × a × l. Таким образом, сумма площадей всех 4 треугольных граней равна 4 (½ al) = 2 al. Таким образом, площадь стороны квадратной пирамиды, равная = 2al

Что, если нам дана высота пирамиды, а не высота наклона? Предположим, что высота пирамиды (высота) равна «h».Затем, применяя теорему Пифагора (вы можете обратиться к рисунку ниже),

л=√[(а ² /4) + ч ² ]

Подставив это в приведенную выше формулу,

Площадь боковой стороны квадратной пирамиды = 2al = 2a√[(a ² /4) + h ² ]

Примечание: √[(a ² /4) + h ² ] можно упростить как (1/2)√(a ²  + 4h ² ).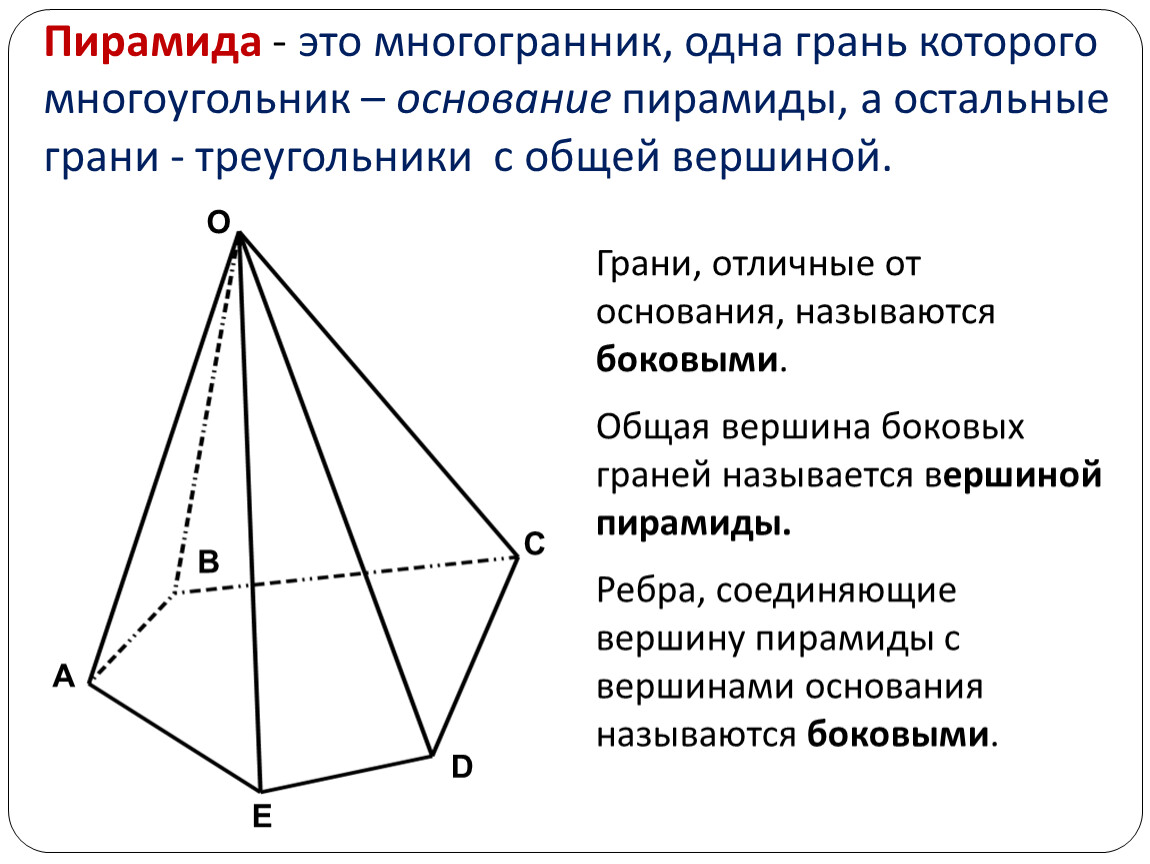 Таким образом, формула площади поперечной стороны квадратной пирамиды может быть записана как 2a[(1/2)√(a ² + 4h ² )] = a√(a ² + 4h ² ).

Как рассчитать боковую площадь квадратной пирамиды?

Площадь поверхности боковой пирамиды можно рассчитать, следуя приведенным шагам,

• Обратите внимание на заданные размеры квадратной пирамиды и убедитесь, что они должны иметь одинаковые единицы измерения.
• Применить формулу для расчета площади боковой поверхности квадратной пирамиды,
  Боковая площадь квадратной пирамиды = 2al = 2a√[(a ² /4) + h ² ], где «a» — длина основания, «h» — высота, а «l» — наклонная высота пирамиды. квадратная пирамида.
• Выразите ответ в квадратных единицах.

Теперь, когда мы поняли площадь боковой поверхности квадратной пирамиды, давайте посмотрим на несколько решенных примеров, чтобы лучше понять.

Часто задаваемые вопросы о боковой площади квадратной пирамиды

Какова боковая площадь квадратной пирамиды?

Площадь боковой поверхности квадратной пирамиды равна сумме площадей всех ее четырех треугольных боковых граней. Если a, h и l — длина основания, высота пирамиды и наклонная высота соответственно, то площадь боковой поверхности квадратной пирамиды = 2al (или) 2a√[(a ² /4) + h ² ].

Как найти площадь боковой поверхности квадратной пирамиды?

Чтобы найти площадь боковой стороны квадратной пирамиды, найдите площадь одной боковой грани (треугольника) и умножьте ее на 4. Если a и l — длина основания и наклонная высота квадратной пирамиды, то площадь боковой стороны квадрата пирамида = 4 (½ × a × l) = 2al. Если h — высота пирамиды, то ее площадь = 2a√[(a ² /4) + h ² ].

Какова площадь одной из треугольных граней квадратной пирамиды?

Если a и l — длина основания и наклонная высота квадратной пирамиды, то площадь одной из 4 треугольных боковых граней составляет ½ × a × l.

Как найти площадь боковой поверхности и общую площадь поверхности квадратной пирамиды?

Площадь боковой поверхности квадратной пирамиды равна сумме площадей только боковых граней, тогда как площадь поверхности равна площади боковой поверхности + площади основания. Площадь боковой поверхности квадратной пирамиды = 2al (или) 2a√[(a ² /4) + h ² ].

Чтобы получить площадь поверхности, нам нужно добавить площадь основания (которая равна ² ) к каждой из этих формул. Площадь поверхности квадратной пирамиды = a ²  + 2al (или) a ²  + 2a√[(a ² /4) + h ² ].
где,

• а = Длина основания (квадрат)
• л = наклонная высота
• h = высота пирамиды

Как найти боковую площадь квадратной пирамиды с наклонной высотой?

Боковая площадь квадратной пирамиды с использованием наклонной высоты может быть рассчитана следующим образом: Боковая площадь квадратной пирамиды = 2al, где «a» — длина основания, а «l» — наклонная высота квадратной пирамиды.

Пирамида

Пирамида — это многогранник с многоугольным основанием и треугольными гранями, которые сходятся в точке, называемой вершиной, которая не лежит в плоскости многоугольного основания.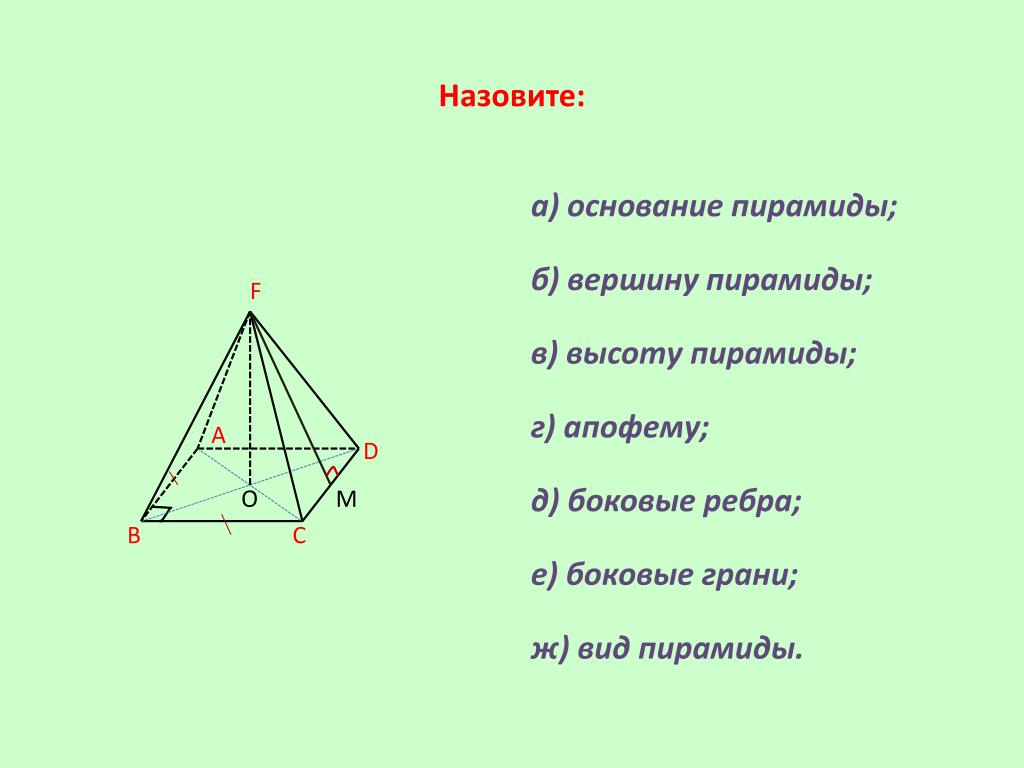

Большинство пирамид, изучаемых в средней школе, правильные пирамиды . Эти пирамиды имеют следующие характеристики:

• 1 ) Основание – правильный многоугольник.
• 2 ) Все боковые ребра равны.
• 3 ) Все боковые грани — равные равнобедренные треугольники.
• 4 ) Высота встречается с основанием в его центре.

Высота боковой грани правильной пирамиды равна наклонная высота. В неправильной пирамиде высота наклона не определена.

Площадь боковой поверхности

То боковой площадь поверхности правильной пирамиды есть сумма площадей его боковых граней.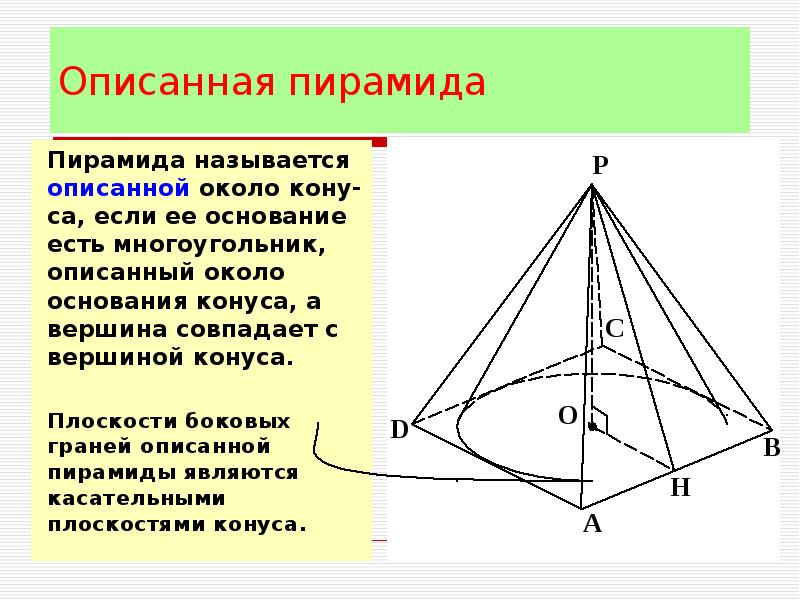

Общая формула для площадь боковой поверхности правильной пирамиды л . С . А . знак равно 1 2 п л где п представляет собой периметр основания и л наклонная высота.

Пример 1:

Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждое ребро основания равно 8 дюймов, а наклонная высота 5 дюймы.

Периметр основания равен сумме сторон.

п знак равно 3 ( 8 ) знак равно 24 дюймы

л . С . А . знак равно 1 2 ( 24 ) ( 5 ) знак равно 60 дюймы 2

Общая площадь поверхности

То общая площадь правильной пирамиды есть сумма площадей его боковых граней и основания.Общая формула для общая площадь поверхности правильной пирамиды Т . С . А . знак равно 1 2 п л + Б где п представляет собой периметр основания, л наклонная высота и Б площадь базы.

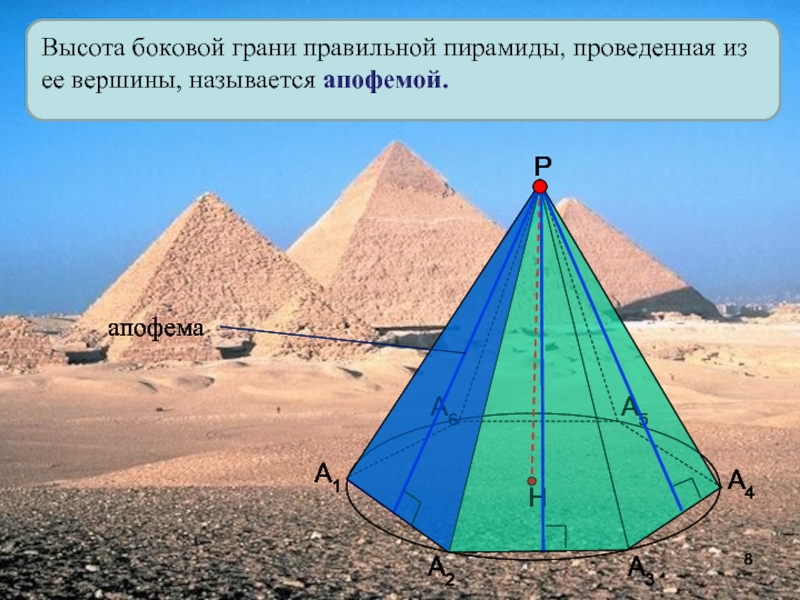
Пример 2:

Найдите площадь полной поверхности правильной пирамиды с квадратным основанием, если каждое ребро основания равно 16 дюймов, наклонная высота стороны равна 17 дюймов, а высота 15 дюймы.

Периметр основания равен 4 с так как это квадрат.

п знак равно 4 ( 16 ) знак равно 64 дюймы

Площадь базы составляет с 2 .

Б знак равно 16 2 знак равно 256 дюймы 2

Т . С . А . знак равно 1 2 ( 64 ) ( 17 ) + 256 знак равно 544 + 256 знак равно 800 дюймы 2

Формулы площади поверхности неправильных пирамид не существует, так как наклонная высота не определена.Чтобы найти площадь, найдите площадь каждой грани и площадь основания и сложите их.

Объем

То объем пирамиды равна одной трети произведения площади основания на высоту (высоту) пирамиды. ( В знак равно 1 3 Б час ) .

Пример 3:

Найдите объем правильной квадратной пирамиды с основаниями 10 см и высота 12 см.

В знак равно 1 3 Б час В знак равно 1 3 ( 10 ) 2 ( 12 ) знак равно 400 см 2

Площадь поверхности пирамиды

То боковой площадь поверхности регулярного пирамида есть сумма площадей его боковых граней.

То общая площадь правильной пирамиды есть сумма площадей его боковых граней и основания.

Общая формула для площадь боковой поверхности правильной пирамиды л . С . А . знак равно 1 2 п л где п представляет собой периметр основания и л наклонная высота.

Пример 1:

Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждое ребро основания равно 8 дюймов, а наклонная высота 5 дюймы.

Периметр основания равен сумме сторон.

п знак равно 3 ( 8 ) знак равно 24 дюймы

л .С . А . знак равно 1 2 ( 24 ) ( 5 ) знак равно 60 дюймы 2

Общая формула для общая площадь поверхности правильной пирамиды Т . С . А . знак равно 1 2 п л + Б где п представляет собой периметр основания, л наклонная высота и Б площадь базы.

Пример 2:

Найдите площадь полной поверхности правильной пирамиды с квадратным основанием, если каждое ребро основания равно 16 дюймов, наклонная высота стороны равна 17 дюймов, а высота 15 дюймы.

Периметр основания равен 4 с так как это квадрат.

п знак равно 4 ( 16 ) знак равно 64 дюймы

Площадь базы составляет с 2 .

Б знак равно 16 2 знак равно 256 дюймы 2

Т . С . А .знак равно 1 2 ( 64 ) ( 17 ) + 256 знак равно 544 + 256 знак равно 800 дюймы 2

Формулы площади поверхности неправильных пирамид не существует, так как наклонная высота не определена. Чтобы найти площадь, найдите площадь каждой грани и площадь основания и сложите их.

Пирамида

Пирамида в геометрии — это пространственная фигура, в основе которой лежит многоугольник, а все остальные грани — треугольники. Все грани пирамиды, кроме основания, пересекаются в одной точке. Ниже приведены некоторые примеры.

Вне геометрии термин «пирамида» часто используется в отношении египетских пирамид, которые служили гробницами для древнеегипетских царей.Пирамиды иногда используются в современном строительстве, например, в Лувре, известном парижском музее.

Свойства пирамиды

Грани пирамиды, не являющиеся ее основанием, называются боковыми гранями. Количество боковых граней в пирамиде равно количеству сторон в ее многоугольном основании. Отрезки линий, образованные двумя пересекающимися гранями, называются ребрами. Вершины — это точки, в которых встречаются три или более ребер. Вершина, противоположная основанию, называется его вершиной. Вершину часто считают «вершиной» пирамиды.Это также общая точка всех боковых граней пирамиды.

Квадратная пирамида имеет пять граней. У него 4 боковые грани — треугольники, а основание — квадрат. Квадратная пирамида имеет 8 ребер и 5 вершин.

Любое поперечное сечение, параллельное основанию пирамиды, образует многоугольник, аналогичный основанию.

Три треугольника, заштрихованные зеленым цветом, образованные поперечными сечениями, параллельными основанию треугольной пирамиды выше, подобны (такой же формы, но разного размера) основанию пирамиды.

Классификация пирамид

Обычно мы называем пирамиду по форме ее многоугольного основания. Ниже приведены некоторые примеры.

Правая пирамида и косая пирамида

Если вершина пирамиды находится прямо над центром основания, это правильная пирамида. В противном случае это наклонная пирамида.

Правая пирамида	Косая пирамида
Перпендикулярная линия из вершины пересекает основание в его центре.	Перпендикулярная линия из вершины не пересекает основание в его центре.

Правильная пирамида

Если в основании пирамиды правильный многоугольник, то это правильная пирамида. В противном случае это неправильная пирамида. Часто под правильной пирамидой понимают правильную пирамиду.

Правильная пирамида	Неправильная пирамида
Основание квадратной пирамиды выше представляет собой квадрат, который представляет собой правильный многоугольник.	Основанием трапециевидной пирамиды выше является трапеция, представляющая собой неправильный многоугольник.

Тетраэдр

Тетраэдр — это особая пирамида, все грани которой — треугольники. Это единственный тип пирамиды, в которой любая из ее граней может быть основанием, а любая из ее вершин может быть вершиной.

Объем пирамиды

Объем пирамиды:

B — площадь основания, h — высота пирамиды, то есть расстояние от ее вершины до основания.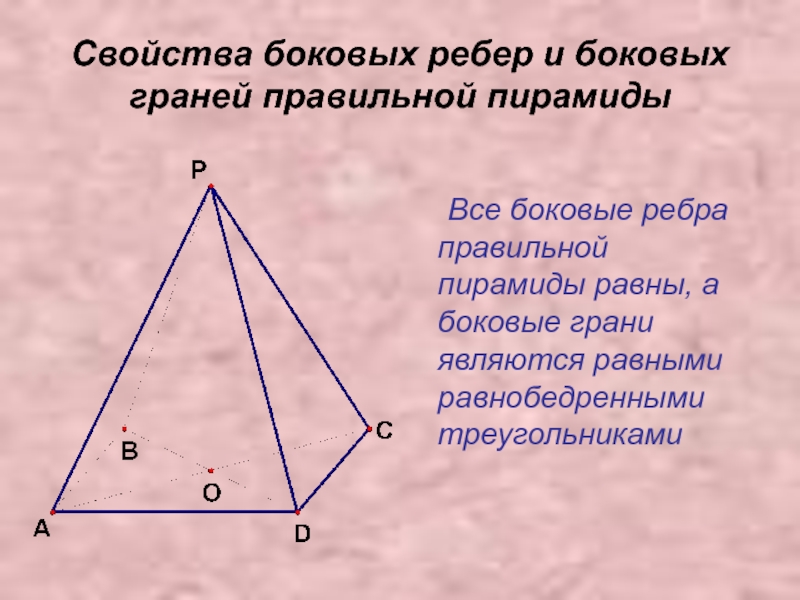

Сколько боковых граней у пирамиды

Сколько боковых граней у пирамиды

Сколько граней у пирамиды?

| Пирамида — это многогранник с основанием, которым может быть любой многоугольник, и тремя или более треугольными гранями, которые сходятся в точке, называемой вершиной. Эти треугольные стороны иногда называют боковыми гранями, чтобы отделить их от основания.

Точно так же вы можете спросить, сколько граней у квадратной пирамиды?

Имеет 5 сторон.4 боковые ступеньки представляют собой треугольники. Основание – квадрат.

Имеет 5 углов (вершин) Какая пирамида также имеет 4 грани?

Треугольная пирамида. Сколько граней у пирамиды?

Четыре граниМожет ли квадратная пирамида иметь все грани треугольной формы?

Все квадратные пирамиды имеют: квадратное основание, четыре треугольные стороны, пять углов, восемь ребер. Квадратную пирамиду можно назвать пятигранником, потому что у нее пять граней: четыре треугольные и одна квадратная.

Какие 2 фигуры образуют квадратную пирамиду?

Квадратная пирамида имеет 5 граней, 4 равных треугольника и квадрат. Ребро — это прямая линия, на которой встречаются две твердые поверхности. Эта сеть состоит из 4 треугольников и квадрата.

Чему равна боковая грань пирамиды?

Итак, в квадратной пирамиде сторонами являются четыре треугольника, которые образуют вершину и сторону фигуры. Общая формула площади боковой стороны правильной пирамиды: Площадь стороны = (длина окружности основания х высота наклона пирамиды) ÷ 2.

Какова площадь квадрата?

Ребро — это сегмент, соединяющий два угла. Лицо – это индивидуальная поверхность. У квадрата 4 угла и 1 грань, потому что это двумерная фигура, а у куба 6 граней и 12 углов, потому что это трехмерная фигура

Сколько ребер у квадратной пирамиды?

8 Что такое пирамида?

Пирамида — это многогранник с основанием, которым может быть любой многоугольник, и тремя или более треугольными гранями, которые сходятся в точке, называемой вершиной.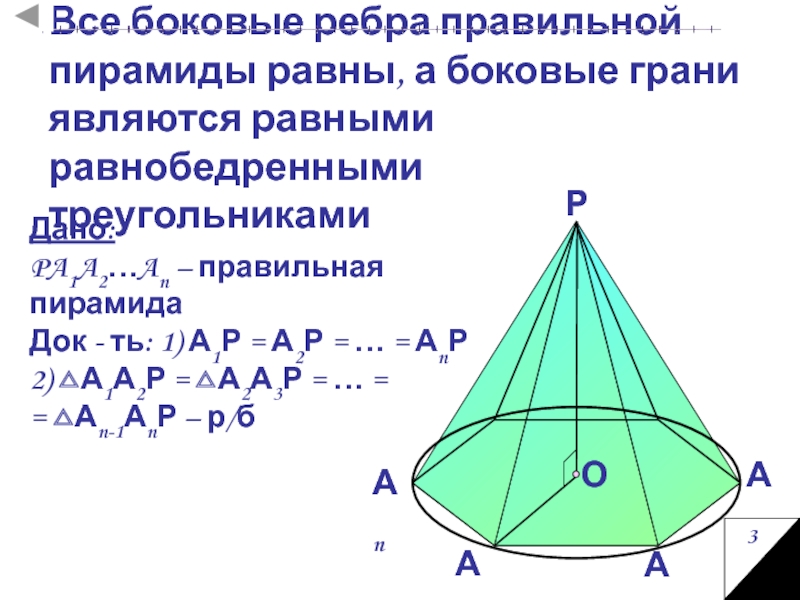 Эти треугольные стороны иногда называют боковыми гранями, чтобы отделить их от основания.

Какова общая площадь квадратной пирамиды?

Общая формула общей площади обычной пирамиды – Т.С.А. = 12pl + B, где p — периметр основания, l — наклон, а B — основание.

Какова формула боковой площади?

Площадь стороны объекта равна площади минус площадь основания объекта. Формула площади поверхности цилиндра: 2πrh, где r = радиус, а h = высота.

Сколько ребер у сферы?

У куба 6 граней, 8 углов и 12 ребер. Цилиндр имеет 0 углов, 0 ребер и 2 грани. Сфера не имеет граней, ребер и углов. У параллелепипеда 6 граней, 8 углов и 12 ребер.

Конус — это пирамида?

Конус с многоугольным основанием называется пирамидой. В зависимости от контекста конус может также относиться конкретно к сферическому конусу или проективному конусу. Конусы также могут быть обобщены до больших размеров.

Что вы называете трехгранной пирамидой?

Трехгранная пирамида называется тетраэдром. Имеет четыре поверхности (трехгранная пирамида + основание)

Какова форма пирамиды?

Бумажные весы представляют собой декоративные изделия из стекла, керамики и твердого пластика. Они часто имеют форму пирамиды и кладутся на стопки бумаги, чтобы отдельные листы не двигались или не летали в ветреную погоду.

Почему у пирамид 4 стороны?

Таким образом, простейшей обычной пирамидой является четырехгранная пирамида (основание + 3 стороны). Правильное название — тетраэдр. Тетраэдры обладают еще одним интересным свойством: у них четыре равные стороны треугольника.Египетская пирамида имеет квадратное основание и четыре треугольные стороны.

Каков угол пирамиды?

Вершина — это вершина трехмерной фигуры. Угол квадрата — это вершина, вершина пирамиды — это вершина и так далее. Основные моменты находятся в основном наверху. А у пирамиды с квадратным основанием 5 углов.

Сколько граней в прямоугольнике?

6 сторон

Как сделать пирамиду?

Вырежьте четыре треугольные картонные коробки шириной 20 см и высотой 30 см каждая. Склейте стороны четырех треугольников вместе, чтобы сформировать форму пирамиды. Вырежьте 14-дюймовый квадратный кусок картона. Приклейте дно пирамиды к центру этого куска картона.

Как проявляет себя тетраэдр?

Если координаты даны, как доказать, что это тетраэдр?

Квора. Возьмите координаты трех точек и определите плоскость, проходящую через эти три точки. Если четвертая точка не находится на этой планете, объект, углом которого являются эти 4 координаты, является тетраэдром.

Что такое настоящая треугольная пирамида?

Треугольная пирамида представляет собой трехмерную фигуру с прямоугольным треугольником в основании, вытянутым в одну точку.

Сколько боковых граней у пирамиды

Площадь поверхности пирамиды

Площадь поверхности пирамиды состоит из боковой поверхности, которая представляет собой площадь множества треугольников, образующих стороны (или грани) фигуры, а также площадь основания, которое может быть любым многоугольником.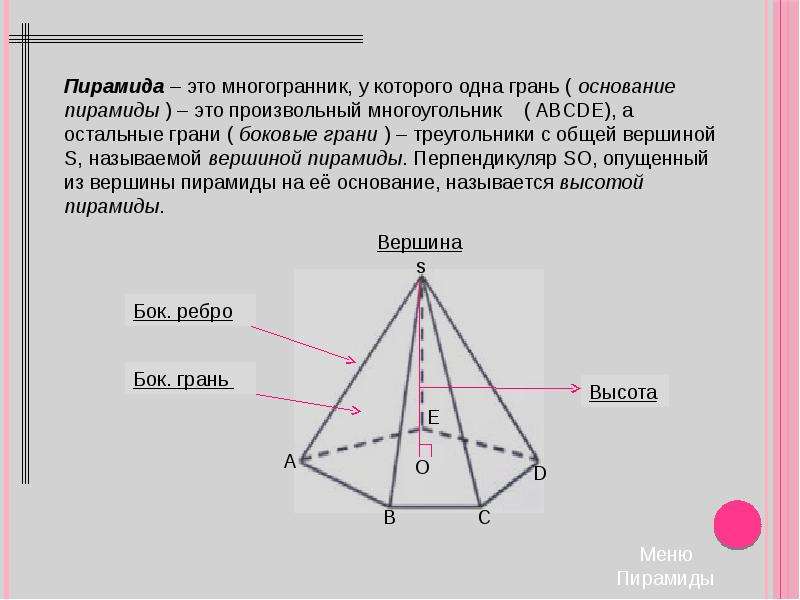

Площадь боковой стороны прямоугольной пирамиды равна сумме площадей треугольников, образующих грани пирамиды. В правильной пирамиде по определению это конгруэнтные треугольники. Также по определению основание правильной пирамиды является правильным многоугольником. Следовательно, основания треугольных граней равны, и их высоты также равны, и они равны наклонной высоте пирамиды.

 

Правила:

1. Площадь боковой стороны правильной пирамиды равна периметру основания, умноженному на половину наклонной высоты.2}} $$

 

Пример :

Пирамида на квадратном основании имеет четыре равносторонних треугольника. Для остальных его граней каждое ребро равно $9$$ см. Найдите всю поверхность.

 

Решение :

Пусть $$OABCD$$ — пирамида с квадратным основанием $$ABCD$$.