Конспект «Центральный угол. Вписанный угол»
«Центральный угол. Вписанный угол»

Центральный угол в окружности — плоский угол с вершиной в его центре.
Градусная мера дуги окружности — градусная мера соответствующего центрального угла.
Вписанный угол в окружность — угол, вершина которого лежит на окружности^ стороны пересекают эту окружность.
Доказательство теоремы о вписанном угле приводится в «Началах» Эвклида. То, что вписанный угол, опирающийся на диаметр, — прямой, знали вавилоняне еще 4000 лет назад.
Свойства вписанного угла. Радианная мера углов

Свойства вписанного угла:
1. Вписанный угoл равен половине дуги, на которую он опирается.
2. Вписанный угoл, опирающийся на диаметр, является прямым.
3. Вписaнные углы, опирающиеся на одну и ту же дугу, равны.
4. Вписaнные углы, опирающиеся на одну и ту же хорду, либо равны, либо их сумма равна 180°.
Радианная мера углов
1 радиан — центральный угол, опирающийся на дугу, равную радиусу окружности. 1 радиан = примерно 57°.
• Угол с вершиной за окружностью (стороны которого пересекают окружность) равен половине разности дуг, лежащих внутри угла.
• Угол между двумя касательными к окружности, проведенными через одну точку, равен половине разности дуг, ограниченных его сторонами.
Это конспект по теме «Центральный угол. Вписанный угол». Выберите дальнейшие действия:
Вписанные и центральные углы. | Подготовка к ЕГЭ по математике
Вписанный угол – угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.

Свойства вписанных углов

Рассмотрим примеры, после чего для вас – тест по теме “Вписанные, центральные углы”.
Задача 1.
Найдите вписанный угол, опирающийся на дугу, которая составляет  окружности.
окружности.
Решение: + показать
Задача 2.
Найти величину угла А0С (см. рис.), если угол АВС равен 

Решение: + показать
 Заметим, тот угол АОС, что помечен на картинке, хоть и является центральным углом, но не является соответствующим для вписанного угла АВС, так как они опираются на разные дуги (угол АВС опирается на дугу АС, а угол АОС – на дугу АВС).
Заметим, тот угол АОС, что помечен на картинке, хоть и является центральным углом, но не является соответствующим для вписанного угла АВС, так как они опираются на разные дуги (угол АВС опирается на дугу АС, а угол АОС – на дугу АВС).
Так как вписанный угол АВС, равный  , опирается на дугу АС, то она равна
, опирается на дугу АС, то она равна  . Значит дуга АВС равна
. Значит дуга АВС равна  . А значит центральный угол АОС, который измеряется градусной мерой дуги, на которую опирается, равен
. А значит центральный угол АОС, который измеряется градусной мерой дуги, на которую опирается, равен  .
.
Ответ: 
Задача 3.
Найти величину угла ВАD, изображенного на картинке:

Решение: + показать
 Так как углы ВСА и ВDA опираются на одну дугу (АВ), то они равны, то есть
Так как углы ВСА и ВDA опираются на одну дугу (АВ), то они равны, то есть  .
.
Теперь обратимся к треугольнику АВD. Он прямоугольный, так как угол АВD, опирающийся на диаметр, – прямой. Значит,  .
.
Ответ: 
Задача 4.
Найти величину угла D, изображенного на картинке:

Решение: + показать
1)  как вертикальные.
как вертикальные.
2) Из треугольника АВS: 
3)  , так как углы опираются на одну дугу.
, так как углы опираются на одну дугу.
Ответ: 
Задача 5.
Центральный угол на  больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.
больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.
Решение: + показать
Задача 6.
Найти градусную меру угла ВАD:

Решение: + показать
Задача 7.
Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно  и
и  .
.

Решение: + показать
Задача 8.
Найдите величину угла АВС.

Решение: + показать
Задача 9.
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности?

Решение: + показать
Задача 10.
Найти градусную меру угла, изображенного на рисунке:

Решение: + показать
Задача 11.
Найдите величину угла АВС, изображенного на рисунке. Видео New*

Решение: + показать
Задача 12.
Четырёхугольник  вписан в окружность. Угол
вписан в окружность. Угол  равен 106°, угол
равен 106°, угол  равен 64°. Найдите угол
равен 64°. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение:

Вписанный угол  равен половине дуги
равен половине дуги  , на которую опирается.
, на которую опирается.
Заметим при этом  , аналогично
, аналогично 

Тогда 
Ответ: 42.
 Вы можете пройти тест “Вписанные, центральные углы”. Тест хорош как для подготовки к ГИА, так и к ЕГЭ.
Вы можете пройти тест “Вписанные, центральные углы”. Тест хорош как для подготовки к ГИА, так и к ЕГЭ.
Углы в окружности, центральный и вписанный. Свойства и способы нахождения
Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?
Что такое центральный угол?
Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).
Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.
Рассмотрим пример №1.
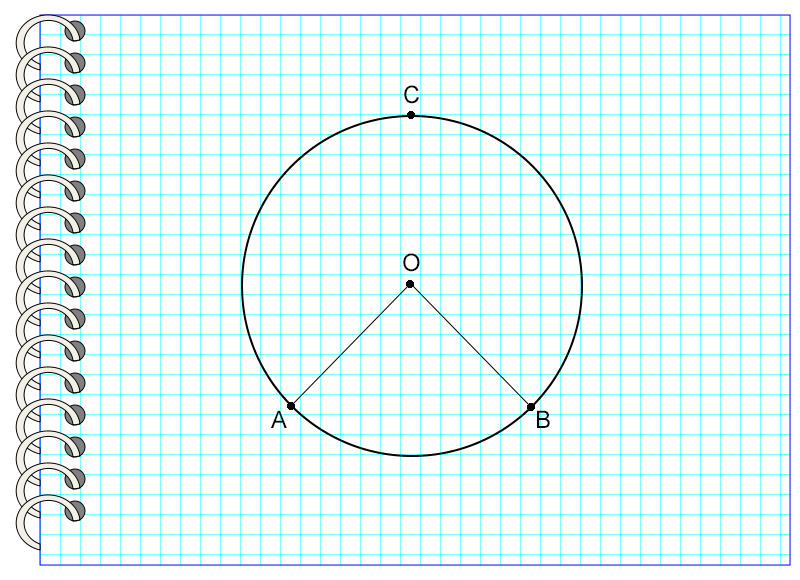
На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.
Чем вписанный угол отличается от центрального?
Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.
Приведем следующий пример.
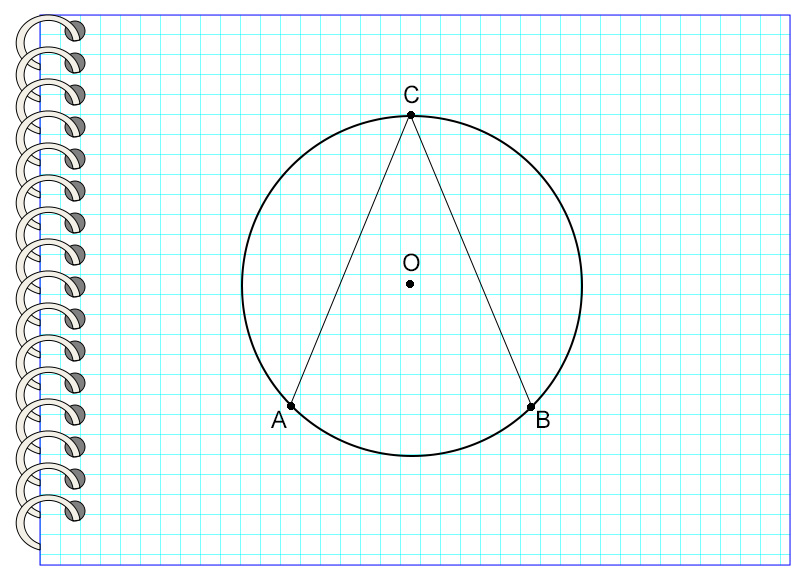
Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.
Чему равен центральный угол
Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.
Итак, центральный угол равен градусной мере дуги, на которую он опирается.
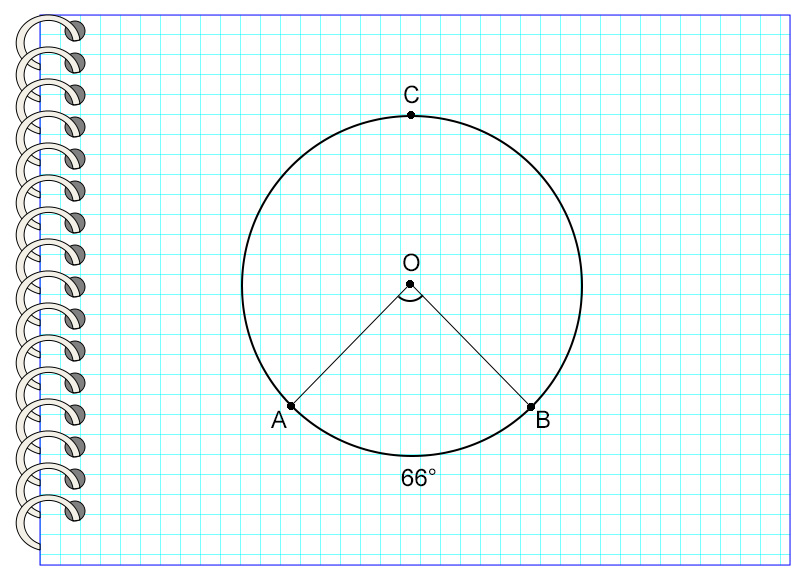
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.
Таким образом, центральные углы, опирающиеся на равные дуги, равны.
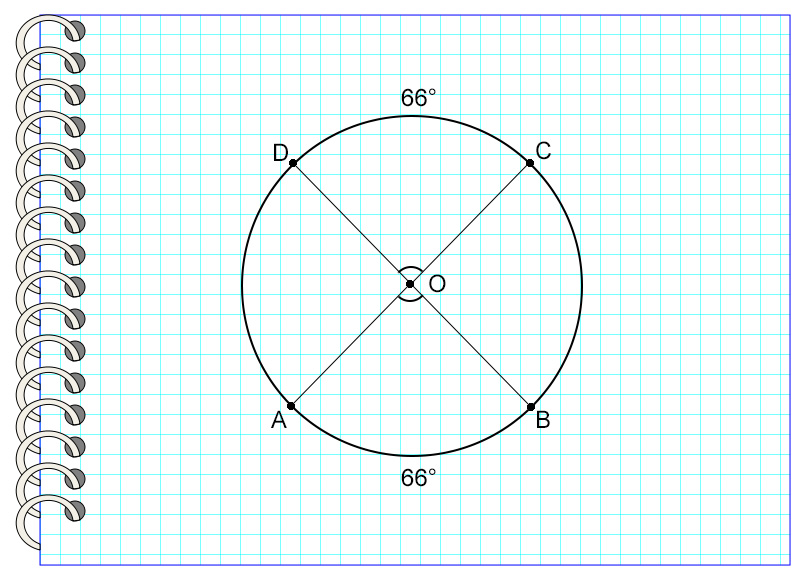
На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.
Как найти вписанный угол
Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?
Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.
Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.
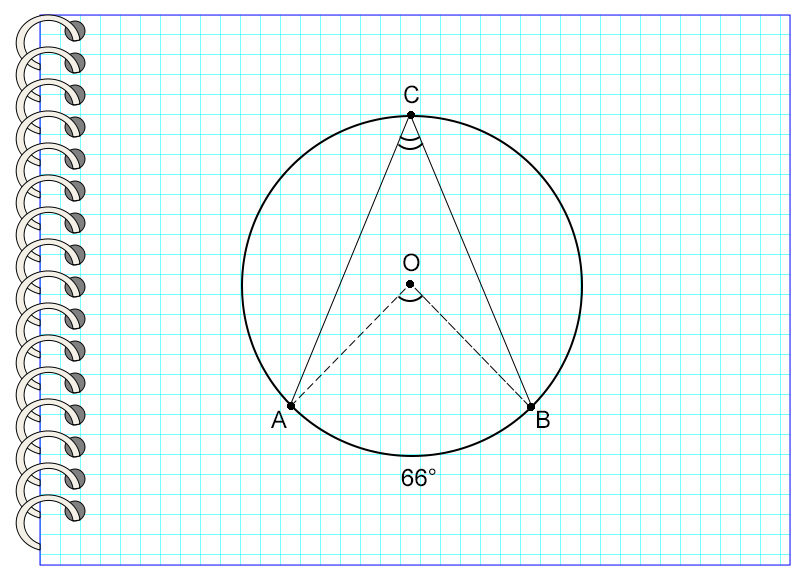
Значит, угол АСВ = 66° : 2 = 33°
Рассмотрим некоторые следствия из этой теоремы.
- Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
- Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
- Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
- Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.
Где могут встретиться задачи на эту тему? Их виды и способы решения
Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.
Углы, опирающиеся на одну дугу
Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.
Задача №1
Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.
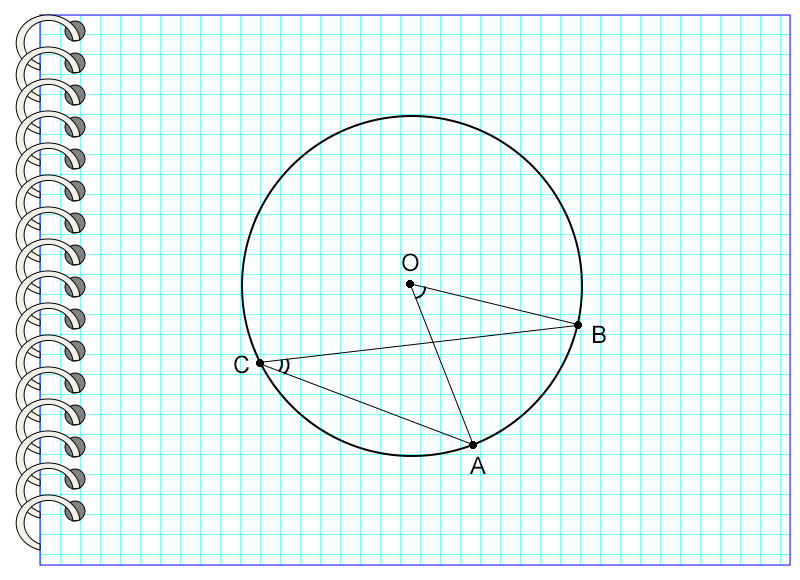
Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла — общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,
1) АОВ = 54° : 2 = 27°.
Ответ: 54°.
Углы, опирающиеся на разные дуги одной окружности
Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.
Задача 2
В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.
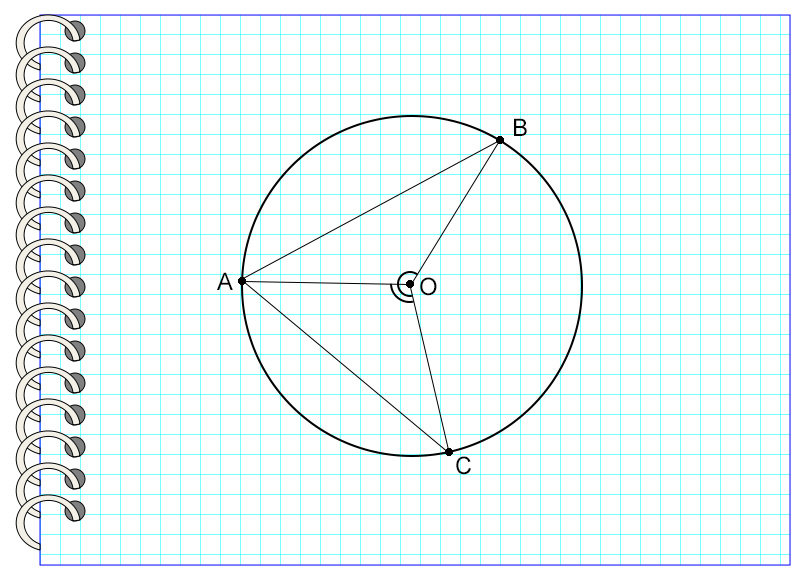
Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.
Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.
АС = 120°
Точно так же угол АОВ опирается на дугу АВ.
АВ = 30°.
Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.
ВС = 360° — АС — АВ
ВС = 360° — 120° — 30° = 210°
Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.
Угол САВ = 210° : 2 = 110°
Ответ: 110°
Задачи, основанные на соотношении дуг
Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.
Задача 1
Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.
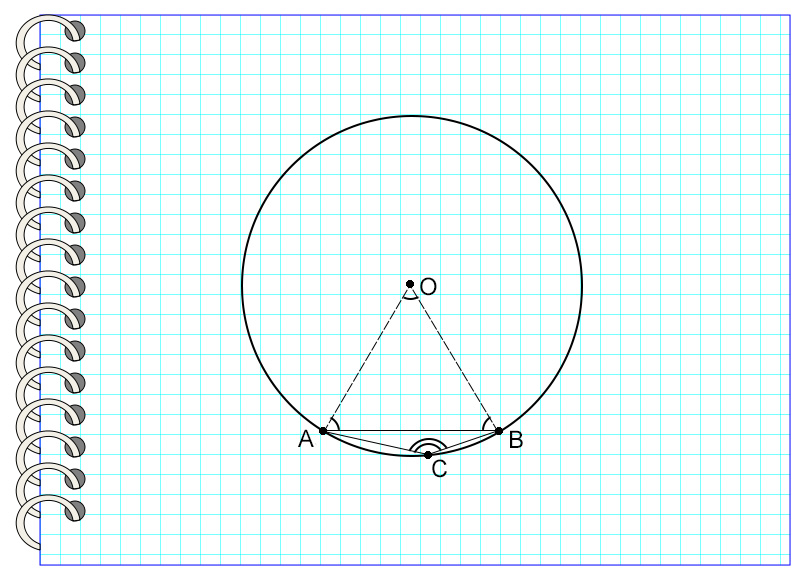
Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.
АВ = 360° — 60° = 300°
Угол АВС = 300° : 2 = 150°
Ответ: 150°
Задача 2
В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.
Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.
3Х + 7Х = 360°
10Х = 360°
Х = 36°
По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.
Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°
Ответ: 54°
Задача 3
В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги — 50. Вычислите длину большей дуги.
Для того чтобы вычислить длину большей дуги, нужно составить пропорцию — как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.
Большая дуга равна 360° — 60° = 300°.
Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.
Большая дуга = 50 * 5 = 250
Ответ: 250
Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.
Центральные и вписанные углы ℹ️ определение, основные свойства и признаки, формулы и обозначения, теоремы о вписанных углах окружности, правила построения

Общие сведения
Перед обучением необходимо ознакомиться с основными понятиями об углах, а также подробно разобрать их классификацию. Углом называется геометрическая фигура, состоящая из общей точки и двух исходящих лучей, которые не лежат на одной прямой. Он обозначается символом «∠». Луч — часть прямой линии, ограниченной с одной стороны и неограниченной с другой.
Точкой называется базовая единица геометрии, при помощи которой строятся другие фигуры. Прямая — линия, которая не имеет начала и конца. Следует отметить, что угол может состоять не только из двух лучей, но и из отрезков. Отрезком называется часть прямой или луча, имеющая ограничения с обеих сторон. Однако базовых элементов недостаточно для построения более сложных фигур. В этом случае применяются аксиомы геометрии Евклида.
Аксиомы плоскостной геометрии
Аксиома — утверждение, не требующее доказательств. Оно воспринимается как неоспоримый факт. Плоскостная геометрия называется Евклидовой. Она основана на базовых элементах, аксиомах и теоремах. Теоремой называется гипотеза, которую следует доказать при помощи аксиом или их комбинаций.
В геометрии существует всего 5 базовых утверждений: принадлежности, порядка, равенства (конгруэнтности), параллельности прямых линий и непрерывности. Знать формулировки этих базисов очень важно. Они характеризуются такими определениями:

- Первая: на любой геометрической плоскости существует множество точек, и через две из них можно провести одну прямую.
- Вторая: на произвольной прямой существует точка, лежащая между двумя другими точками.
- Третья: если на плоскости даны три отрезка (угла), причем первый равен третьему, а второй — первому, то они конгруэнтны между собой.
- Четвертая: в случае когда на плоскости существует произвольная прямая и некоторая точка, не лежащая на ней, тогда через последнюю можно провести другую прямую параллельную заданной.
- Пятая (Архимедова): если на некоторой прямой на плоскости лежат два отрезка, расстояния между точками одного отрезка равны таким же параметрам другого, то они равны по косвенному признаку.
Для понимания первой аксиомы необходимо представить лист бумаги. Это некоторая плоскость, состоящая из множества точек. Однако для удобства и читабельности их не отмечают, а берут только нужные. Известно, что достаточно всего двух точек, чтобы провести прямую. На листе бумаги можно их отметить и провести ее. Необходимо отметить, что лист бумаги является ограниченной плоскостью.
Что касается второго утверждения, то любая прямая включает в себя простейшие элементы (точки), которые могут лежать между другими. Это свойство позволяет отмечать на искомой фигуре любое количества элементов для выполнения чертежей.
Архимедова аксиома считается сложной для понимания на первоначальных этапах обучения. Однако все очень просто. Следует начертить прямую, и отметить на ней два равных отрезка. Каждый из них поделить на две части, чтобы первая часть одного отрезка была эквивалентна части другого. Пусть первый отрезок АВ = 10 см, а второй — DЕ = 10 см. На первом нужно отметить точку С (АС = 3 и СВ = 7). На втором — отметить точку F, лежащую между D и E (DF = 3 и FE = 7). Следовательно, АС = DF = 3 и СВ = FE = 7.
Классификация треугольников
Углы отличаются между собой по градусной мере. Последняя является главной характеристикой и исчислением его размерности. На основании этого свойства их можно классифицировать таким образом по интервалам:

- (0;90) или 0 < x < 90: острый.
- 90: прямой.
- (90;180): тупой.
- 180: развернутый.
- (180;360): выпуклый.
- 360: полный.
Запись (90;180) расшифровывается следующим образом: значение принадлежит интервалу от 90 градусов не включительно до 180 не включительно. Смежным является угол, который лежит на одной прямой с основным. Например, на прямой нужно отметить произвольную точку. Затем через нее следует провести луч под углом 60 градусов. Чтобы найти смежный ∠, нужно выполнить такие действия: 180 — 60 = 120. Прямая — развернутый ∠, т. е. его размерность составляет 180.
- Градусная мера (размерность) существует у всех ∠. Она может быть отрицательной и положительной (по или против часовой стрелки соответственно).
- У равных ∠ одинаковые размерности.
- Часть угла всегда меньше основного.
Для доказательства теорем следует разобрать классификацию треугольников. Она более сложная включает в себя некоторые критерии:
- Углы.
- Стороны.
- Подобие.
Сумма углов фигуры эквивалентна 180 градусам. Следовательно, у него бывают только острые, тупой и прямой углы. Если один из них является прямым или тупым, то значит два других — острые. Исходя из этого можно выделить три вида фигур, которые классифицируются по данному параметру (∠): остроугольные, прямоугольные и тупоугольные.

Следующий критерий — стороны. Если у треугольника три стороны не равны между собой, то его принято называть разносторонним. Когда равны две стороны, тогда он является равнобедренным (третья — основание). В случае равенства всех сторон он считается правильным или равносторонним. У него каждый из углов равен 60.
Подобными называются треугольники, у которых прослеживается равенство ∠, а стороны пропорциональны между собой. Соотношение последних зависит от некоторой величины. Ее в геометрии называют коэффициентом подобия. Всего три признака подобия: по всем ∠, по двум ∠ и стороне, а также по двум сторонам и ∠ между ними.
Информация об окружности

Окружностью называет геометрическое место точек, соединенных между собой и удаленных от центра на равные расстояния. Отрезок, проходящий через ее центр и соединяющий две соседние точки, является диаметром (d). Радиус некоторый отрезок, соединяющий центральную точку с любой из точек на окружности. Его принятое обозначение литерой «R». Если из центра провести два луча (радиуса), то часть окружности, образованная ими, называется дугой.
Следует отметить, что любой отрезок, проходящий только через две точки окружности, является хордой. Если последняя проходит через центр, то она является диаметром. Площадью окружности называется произведение квадрата радиуса на число ПИ, которое примерно соответствует значению 3,1416. Формула имеет такой вид: S = ПИ * R 2. Соотношение можно править таким образом: S = (ПИ * d 2 ) / 4. Из соотношения можно сделать вывод, что d = R / 2. Длиной окружности является произведение ПИ на диаметр заданной окружности.
Вписанные углы
Вокруг любого угла можно описать окружность. Он бывает центральным или вписанным. Термины нужно различать между собой, чтобы правильно применять следствия из утверждения. Центральным называется произвольный угол, у которого вершина совпадает с центральной точкой окружности, а его стороны эквивалентны радиусам. Вписанным является любой угол с вершиной, расположенной на окружности и сторонами, пересекающими ее.

Затем следует рассмотреть теоремы о вписанных углах. Кроме того, центральный также является вписанным, но отличие состоит в том, что его вершина совпадает с центром круга. На основании утверждений можно сформулировать некоторые свойства вписанного угла. Последние могут также оказаться полезными при вычислении параметров некоторых фигур.
Основные теоремы
Теоремы применяются для оптимизации вычислений некоторых величин и параметров фигур, образованных углами и описанной окружностью вокруг них. Необходимо отметить, что специалисты классифицируют их на два вида: для вписанных и углов, образованных хордами и касательными . В первом случае утверждения, которые следует доказать, являются следующими:

- Градусная мера вписанного угла в некоторую окружность равна половине центрального, опирающегося с ним на одну дугу.
- Если два угла опираются на одну дугу, то они конгруэнтны.
- Когда углы опираются на одну хорду и лежат по одну сторону от нее, тогда их градусные меры равны между собой.
- Сумма углов эквивалентна 180 градусам, когда их вершины лежат по разные стороны от общей хорды.
- Если некоторый угол опирается на диаметр, то он соответствует 90 градусам, т. е. является прямым.
- Средняя точка гипотенузы прямоугольного треугольника совпадает с центром окружности, описанной вокруг него.
- Угол, который опирается на дугу, равен ½ от ее градусной меры.
Необходимо отметить, что вышеописанные теоремы являются также и свойствами. Следует ввести обозначение вписанного ∠ АВС. В первом случае свойство доказывается для двух вариантов. Первый — ∠ АВС лежит на диаметре АВ. Необходимо обозначит центральный ∠ АОС. Следовательно, АО = ВО = R. Треугольник АОВ является равнобедренным, а его ∠ при основании равны (∠ АВО = ∠В АО). Для внешнего ∠ АОС справедливо такое равенство: ∠ АОС = 2 * ∠В АО. Если центральная точка круга лежит внутри ∠ABC. Следует провести биссектрису вписанного ∠, пересекающую окружность в точке D. Тогда ∠ABC = ∠AОC / 2.
Другие случаи
Однако бывают и другие случаи, в результате которых образовываются углы внутри окружности. Специалисты выделяют следующие теоремы о них, образованных касательными и хордами:

- Размерность угла, который образован при пересечении хорд, эквивалентна ½ от суммы размеров его дуг. Углы между собой равны, поскольку являются вертикальными.
- Если существуют две секущие, которые пересекаются за пределами окружности, то угол равен ½ от разности соответствующих дуг.
- Когда проведена касательная и хорда к общей точке окружности, тогда градусная мера эквивалентна половине дуги, образованной данными элементами.
- Угол, образованный секущей и касательной, эквивалентен ½ разности образованных при этом дуг.
- Если угол образуют две касательные к заданной окружности, то его размерность соответствует ½ от разности дуг между сторонами первого.
Как правило, теорем бывает достаточно для доказательства геометрических тождеств. Однако для закрепления материала нужно разобрать пример решения задания.
Пример решения
Для практического применения знаний следует разобрать задачу на данную тематику. Задания состоят из двух частей: исходных данных и неизвестной величины. Например, дана хорда АВ. Она делит окружность на две дуги, градусные меры которых относятся между собой как 5:7. Дана также еще точка, расположенная на дуге меньшей части. Необходимо вычислить вписанный ∠АСВ. Для решения следует воспользоваться следующим алгоритмом:

- Сумма градусных мер двух дуг составляет 360.
- Необходимо составить уравнение: 5у + 7у = 360.
- Корень уравнения: у = 360 / 12 = 30.
- Меньшая дуга вычисляется таким образом: 5 * 30 = 150.
- Для расчета большей дуги следует произвести такой расчет: 7 * 30 = 210.
- Проверка правильности вычислений: 150 + 210 = 360 (уравнение решено верно).
- ∠АСВ опирается на большую дугу. Следовательно, его размерность эквивалентна ½ от размерности этой дуги: 210 / 2 = 105 (градусов).
В седьмом пункте алгоритма было использовано свойство под номером 7. Если его не применять, то решение займет больше времени, поскольку потребует строить треугольник и искать его стороны. После этих операций можно будет найти его ∠ по теореме косинусов или синусов.
Таким образом, для проведения расчетов размерностей углов, которые являются центральными или вписанными, необходимы знания основных теорем и формул.
Теорема о вписанном угле / Окружность / Справочник по геометрии 7-9 класс
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
На рисунке 1 угол ВАС вписанный, дуга ВLС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу ВLC.
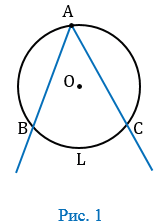
Теорема
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Доказательство
Дано: окружность (О),  АВС — вписанный,
АВС — вписанный,  АС — внутри
АС — внутри  АВС.
АВС.
Доказать:  АВС =
АВС =  АС.
АС.
Доказательство:
1 случай
Луч ВО совпадает с одной из сторон угла АВС.
Пусть ВО совпадает с ВС (Рис. 2).
В данном случае дуга АС меньше полуокружности, следовательно,  АОС =
АОС = АС (т.к.
АС (т.к.  АОС — центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
АОС — центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
 АВО — равнобедренный с основанием АВ (т.к. ОА = ОВ — радиусы),
АВО — равнобедренный с основанием АВ (т.к. ОА = ОВ — радиусы), 
 1 =
1 =  2 (углы при основании).
2 (углы при основании).  АОС — внешний угол
АОС — внешний угол  АВО,
АВО, 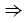
 АОС =
АОС =  1 +
1 +  2 = 2
2 = 2 1. Следовательно, учитывая то, что
1. Следовательно, учитывая то, что  АОС =
АОС = АС, получим:
АС, получим:  АС = 2
АС = 2  1, откуда
1, откуда  1 =
1 =  АС, т.е.
АС, т.е.  АВС =
АВС =  АС.
АС.
2 случай
Луч ВО делит угол АВС на два угла.
В данном случае луч ВО пересекает дугу АС в некоторой точке D (Рис. 3).
Точка D разделят дугу АС на две дуги:  АD и
АD и  DС, поэтому
DС, поэтому  АС =
АС =  АD +
АD +  DС.
DС.
Луч ВD разделяет угол АВС на два угла, поэтому  АВС =
АВС =  АВD +
АВD +  DВС.
DВС.
По доказанному в 1 случае  АВD =
АВD =  АD и
АD и  DВС =
DВС =  DС. Складывая эти равенства, получаем:
DС. Складывая эти равенства, получаем:  АВD +
АВD +  DВС =
DВС =  АD +
АD +  DС или
DС или  АВD +
АВD +  DВС = (
DВС = ( АD +
АD +  DС). Следовательно,
DС). Следовательно,  АВС =
АВС =  АС.
АС.
3 случай
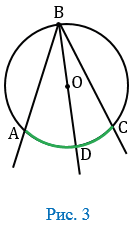
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
В данном случае луч ВС пересекает дугу АD в точке С (Рис. 4).
Точка С разделят дугу АD на две дуги:  АC и
АC и  CD, поэтому
CD, поэтому  АD =
АD =  АC +
АC +  CD, откуда
CD, откуда  АC =
АC =  АD —
АD —  CD.
CD.
Луч ВС разделяет угол АВD на два угла, поэтому  АВD =
АВD =  АВC +
АВC +  CВD, откуда
CВD, откуда  АВC =
АВC =  АВD —
АВD —  CВD.
CВD.
По доказанному в 1 случае  АВD =
АВD =  АD и
АD и  СВD =
СВD =  СD. Вычитая из первого равенства второе, получаем:
СD. Вычитая из первого равенства второе, получаем:  АВD —
АВD —  СВD =
СВD =  АD —
АD —  CD или
CD или  АВD —
АВD —  СВD = (
СВD = ( АD —
АD —  CD). Следовательно,
CD). Следовательно,  АВС =
АВС =  АС.
АС.
Теорема доказана.
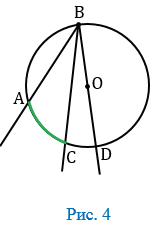
Следствия из теоремы о вписанном угле
| 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис. 5). |
| 2. Вписанный угол, опирающийся на полуокружность, — прямой (рис. 6). |
Теорема
Доказательство
Дано: окружность, АВ и СD — хорды, АВСD = Е (Рис. 7).
Доказать: АЕ ВЕ = СЕ
ВЕ = СЕ DЕ.
DЕ.
Доказательство:
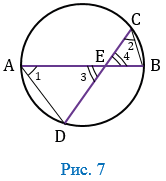
В  АDЕ и
АDЕ и 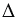 СВЕ:
СВЕ:  1 =
1 =  2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле),
2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле),  3 =
3 =  4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому
4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому 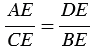 , откуда АЕ
, откуда АЕ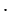 ВЕ = СЕ
ВЕ = СЕ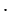 DЕ. Теорема доказана.
DЕ. Теорема доказана.
Теорема
| Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. |
Доказательство
Дано: окр.(О, 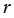 ), АВ — хорда, АС — касательная, А — точка касания.
), АВ — хорда, АС — касательная, А — точка касания.
Доказать:  ВАС =
ВАС =  АВ.
АВ.
Доказательство:
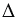 АОВ — равнобедренный с основанием АВ, т.к. ОА = ОВ =
АОВ — равнобедренный с основанием АВ, т.к. ОА = ОВ = 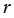 , значит,
, значит,  ОАВ =
ОАВ =  ОВА (как углы при основании), при этом ОА
ОВА (как углы при основании), при этом ОА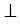 АС (свойство касательной), поэтому
АС (свойство касательной), поэтому  ОАВ =
ОАВ =  ОВА = 900 —
ОВА = 900 —  ВАС. Следовательно, по теореме о сумме углов треугольника:
ВАС. Следовательно, по теореме о сумме углов треугольника:  АОВ = 1800 — 2·(900 —
АОВ = 1800 — 2·(900 —  ВАС) = 1800 — 1800 + 2
ВАС) = 1800 — 1800 + 2 ВАС = 2
ВАС = 2 ВАС, откуда
ВАС, откуда  ВАС =
ВАС =  АОВ.
АОВ.  АОВ — центральный, поэтому
АОВ — центральный, поэтому  ВАС =
ВАС =  АВ. Теорема доказана.
АВ. Теорема доказана.
| 1. | Вписанный угол, дана градусная мера дуги | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление вписанного угла, если известна градусная мера дуги, на которую он опирается. |
| 2. | Центральный угол | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление центрального угла, если известен соответствующий вписанный угол. |
| 3. | Градусная мера дуги окружности | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление градусной меры дуги окружности, если известна величина вписанного угла, опирающегося на данную дугу. |
| 4. | Вписанный угол | 2 вид — интерпретация | лёгкое | 1 Б. | Вычисление вписанного угла. |
| 5. | Вписанный и центральный угол | 2 вид — интерпретация | лёгкое | 2 Б. | Вычисление вписанного и центрального углов, если известны дуги. |
| 6. | Хорда окружности | 1 вид — рецептивный | среднее | 3 Б. | Вычисление длины хорды с использованием свойства хорд. |
| 7. | Центральный угол, углы треугольника | 2 вид — интерпретация | среднее | 3 Б. | Вычисление углов треугольника, если один из них является центральным углом, дана дуга окружности. |
| 8. | Дуги окружности | 2 вид — интерпретация | среднее | 2 Б. | Вычисление градусных мер дуг с общими концами. |
| 9. | Угол между хордами | 2 вид — интерпретация | среднее | 2 Б. | Вычисление угла между хордами. |
| 10. | Центральный и вписанный в окружность угол | 2 вид — интерпретация | среднее | 2 Б. | Вычисление вписанного (центрального) угла, если дана дуга. |
| 11. | Отрезки хорды | 2 вид — интерпретация | сложное | 2 Б. | Вычисление длин отрезков, на которые делится хорда. |
| 12. | Вычисление хорды окружности | 3 вид — анализ | сложное | 3 Б. | Вычисление хорды окружности, если дана информация о диаметре. |
| 13. | Отрезки хорды и диаметра | 3 вид — анализ | сложное | 3 Б. | Вычисление отрезков касательной и секущей, если известно их соотношение. |
| 14. | Радиус окружности, пропорциональные линии в окружности | 3 вид — анализ | сложное | 6 Б. | Вычисление радиуса окружности с использованием пропорциональных линий в окружности. |
Центральные и вписанные углы
Понятие вписанного и центрально угла
Введем сначала понятие центрального угла.
Определение 1
Угол, вершина которого лежит в центре окружности называется центральным углом (рис. 1).
Рисунок 1. Центральный угол
Замечание 1
Отметим, что градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Введем теперь понятие вписанного угла.
Определение 2
Угол, вершина которого лежит на окружности и стороны которого пересекают эту же окружность, называется вписанным углом (рис. 2).
Рисунок 2. Вписанный угол
Теорема о вписанном угле
Теорема 1
Градусная мера вписанного угла равняется половине градусной меры дуги, на которую он опирается.
Доказательство.
Пусть нам дана окружность с центром в точке $O$. Обозначим вписанный угол $ACB$ (рис. 2). Возможны три следующих случая:
- Луч $CO$ совпадает с какой либо стороной угла. Пусть это будет сторона $CB$ (рис. 3).
Рисунок 3.
В этом случае дуга $AB$ меньше ${180}^{{}^\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:
- Луч $CO$ делит внутренний угол на два угла. Пусть он пересекает окружность в точке $D$ (рис. 4).
Рисунок 4.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
- Луч $CO$ не делит внутренний угол на два угла и не совпадает ни с одной его стороной (Рис. 5).
Рисунок 5.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
Теорема доказана.
Приведем следствия из данной теоремы.
Следствие 1: Вписанные углы, которые опираются на одну и туже дугу равны между собой.
Следствие 2: Вписанный угол, который опирается на диаметр — прямой.
Пример задачи на использование понятий центрально и вписанного углов
Пример 1
Найти градусные меры вписанных углов, изображенных на рисунке (рис.6).
Рисунок 6.
Решение.
По теореме 1, имеем:
\[\angle ABC=\frac{{120}^0}{2}={60}^0\]По теореме 1, имеем:
\[\angle ABC=\frac{{90}^0}{2}={45}^0\]Из следствия 2 сразу получаем, что искомый угол — прямой.