Аксиома — Википедия

Аксио́ма (др.-греч. ἀξίωμα «утверждение, положение») или постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами^[1].

Необходимость в принятии аксиом без доказательств следует из индуктивного соображения: любое доказательство вынуждено опираться на какие-либо утверждения, и если для каждого из них требовать своих доказательств, цепочка получится бесконечной. Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами^[2].

В современной науке вопрос об истинности аксиом, лежащих в основе какой-либо теории, решается либо в рамках других научных теорий, либо посредством интерпретации данной теории

[3].

Аксиоматиза́ция теории — явное указание конечного или счётного, рекурсивно перечислимого (как, например, в аксиоматике Пеано) набора аксиом и правил вывода. После того как даны названия изучаемым объектам и их основным отношениям, а также аксиомы, которым эти отношения должны подчиняться, всё дальнейшее изложение должно основываться исключительно на этих аксиомах и не опираться на обычное конкретное значение этих объектов и их отношений.

Выбор аксиом, которые составляют основу конкретной теории, не является единственным. Примеры различных, но равносильных наборов аксиом можно встретить в математической логике и евклидовой геометрии.

Набор аксиом называется непротиворечивым, если исходя из аксиом набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание.

Австрийский математик Курт Гёдель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система), в которой можно определить натуральные числа, сложение и умножение, неполна. Это значит, что найдётся бесконечное количество математических утверждений (функций, выражений), ни истинность, ни ложность которых не сможет быть доказана на основании данной системы аксиом. Также, по теореме о неполноте, среди этих невыводимых утверждений будет утверждение о непротиворечивости этой системы.

Впервые термин «аксиома» встречается у Аристотеля (384—322 до н. э.) и переходит в математику от философов Древней Греции. Евклид различает понятия «постулат» и «аксиома», не объясняя их различия. Со времён Боэция постулаты переводят как требования (petitio), аксиомы — как общие понятия. Первоначально слово «аксиома» имело значение «истина, очевидная сама по себе». В разных манускриптах «Начал» Евклида разбиение утверждений на аксиомы и постулаты различно, не совпадает их порядок. Вероятно, переписчики придерживались разных воззрений на различие этих понятий.

Отношение к аксиомам как к неким неизменным самоочевидным истинам сохранялось долгое время. Например, в словаре Даля аксиома — это «очевидность, ясная по себе и бесспорная истина, не требующая доказательств».

Толчком к изменению восприятия аксиом послужили работы российского математика Николая Лобачевского о неевклидовой геометрией, впервые опубликованные в конце 1820-х годов. Ещё будучи студентом, он пытался доказать пятый постулат Евклида, но позднее отказался от этого. Лобачевский сделал вывод о том, что пятый постулат является лишь произвольным ограничением, которое можно заменить другим ограничением. Если бы пятый постулат Евклида был доказуем, то Лобачевский столкнулся бы с противоречиями. Однако, хотя новая версия пятого постулата и не была наглядно-очевидной, она полностью выполняла роль аксиомы, позволяя построить новую непротиворечивую систему геометрии.

Сперва идеи Лобачевского не были признаны (например, о них отрицательно отзывался академик Остроградский). Позднее, когда Лобачевский опубликовал работы на других языках, он был замечен Гауссом, который тоже имел некоторые наработки в области неевклидовой геометрии. Он косвенно высказал восхищение этой работой. Настоящее признание геометрия Лобачевского получила лишь через 10-12 лет после смерти автора, когда была доказана её непротиворечивость в случае непротиворечивости геометрии Евклида. Это привело к революции в математическом мире. Гильберт развернул масштабный проект по аксиоматизации всей математики для доказательства её непротиворечивости. Его планам не суждено было сбыться из-за последовавших теорем Гёделя о неполноте. Однако это послужило толчком к формализации математики. Например, появились аксиомы натуральных чисел и их арифметики, работы Кантора по созданию теории множеств. Это позволило математикам создавать строго истинные доказательства для теорем.

Сейчас аксиомы обосновываются не сами по себе, а в качестве необходимых базовых элементов теории — аксиомы могут быть достаточно произвольными, они не обязаны быть очевидными. Единственным неизменным требованием к аксиоматическим системам является их внутренняя непротиворечивость. Критерии формирования набора аксиом в рамках конкретной теории часто являются прагматическими: краткость формулировки, удобство манипулирования, минимизация числа исходных понятий и т. п. Такой подход не гарантирует истинность принятых аксиом

[1]. В соответствии с критерием Поппера, единственный отрицательный пример опровергает теорию и, как следствие, доказывает ложность системы аксиом, при этом множество подтверждающих примеров лишь увеличивает вероятность истинности системы аксиом.

Примеры аксиом[править | править код]

1. Аксиома выбора
2. Аксиома параллельности Евклида
3. Аксиома Архимеда
4. Аксиома объёмности
5. Аксиома регулярности
6. Аксиома полной индукции
7. Аксиома Колмогорова
8. Аксиома булеана.

Примеры систем аксиом[править | править код]

1. Аксиоматика теории множеств
2. Аксиоматика вещественных чисел
3. Аксиоматика Евклида
4. Аксиоматика Гильберта.

• Начала Евклида. Книги I—VI. М.-Л., 1950
• Гильберт Д. Основания геометрии. М.-Л., 1948

Теорема — Википедия

Теорема Пифагора имеет не менее 370 известных доказательств^[1]

В математике теорема — это утверждение, которое было доказано на основе ранее установленных утверждений: других теорем и общепринятых утверждений, аксиом. Теорема является логическим следствием аксиом. Доказательство математической теоремы является логическим аргументом для утверждения теоремы, приведенного в соответствии с правилами формальной системы. Доказательство теоремы часто интерпретируется как обоснование истинности утверждения теоремы. В свете требования, чтобы теоремы были доказаны, концепция теоремы является принципиально дедуктивной, в отличие от понятия научного закона, который является экспериментальным^[2].

Многие математические теоремы являются условными утверждениями. В этом случае доказательство выводит заключение из условий, называемых

гипотезами или предпосылками. В свете интерпретации доказательства как оправдания истины, заключение часто рассматривается как необходимое следствие гипотез, а именно, что заключение верно в случае, если гипотезы верны, без каких-либо дополнительных предположений. Тем не менее, условия могут интерпретироваться по-разному в некоторых дедуктивных системах, в зависимости от значений, присвоенных правилам вывода и символа условия.

Хотя теоремы могут быть написаны в полностью символической форме, например, с помощью исчисления высказываний, они часто выражаются на естественном языке (английском, русском, французском и др.). То же верно и для доказательств, которые часто выражаются в виде логически организованной и четко сформулированной цепи неформальных аргументов, предназначенных для того, чтобы убедить читателей в истинности формулировки теоремы, из каковой цепи в принципе можно построить формальное символическое доказательство. Такие аргументы, как правило, легче проверить, чем чисто символические, и, на самом деле, многие математики отдают предпочтение доказательству, которое не только демонстрирует справедливость теоремы, но и каким-то образом объясняет,

почему она, очевидно, верна. В некоторых случаях одной картины достаточно для доказательства теоремы.

Поскольку теоремы лежат в основе математики, они также играют центральную роль в ее эстетике. Теоремы часто описываются как «тривиальные», «сложные», «глубокие» или даже «красивые». Эти субъективные суждения варьируются не только от человека к человеку, но и со временем: например, когда доказательство упрощено или лучше понято, теорема, которая когда-то была трудной, может стать тривиальной. С другой стороны, глубокая теорема может быть сформулирована просто, но ее доказательство может включать в себя удивительные и тонкие связи между различными областями математики. Особенно известным примером такой теоремы является Великая теорема Ферма.

С точки зрения логики, многие теоремы имеют форму условного условного обозначения : если A, то B. Такая теорема утверждает не истинность B, а только то, что B является необходимым следствием A. В этом случае A называется логической гипотезой теоремы, а B — выводом (формально A и B называются предшествующим и последующим утверждениями). Следует подчеркнуть, что логическая гипотеза и математическая гипотеза — суть разные понятия. Так, утверждение «Если n — четное натуральное число, то n / 2 — натуральное число» — пример теоремы, в которой гипотезой является утверждение «n — чётное натуральное число», а утверждение «n / 2 — также натуральное число» является выводом.

Для доказательства теорема должна быть выражена в виде точного формального утверждения. Тем не менее, для удобства читателя теоремы обычно выражаются не в полностью символической форме, а на естественном языке. Читатель же самостоятельно преобразует неформальное утверждение в формальное.

В математике часто выбирают несколько гипотез и создают теорию, которая состоит из всех утверждений, логически вытекающих из этих гипотез. Гипотезы, которые составляют основу теории, называются аксиомами или постулатами. Область математики, изучающая формальные языки, аксиомы и структуру доказательств, называется теорией доказательств.

Планарная карта с пятью цветами, так что нет двух областей с одинаковым цветом. Это может быть окрашено таким образом только с четырьмя цветами. Теорема о четырех цветах утверждает, что такие раскраски возможны для любой плоской карты, но каждое известное доказательство включает в себя вычислительный поиск, который слишком длинный, чтобы проверить его вручную.

Некоторые теоремы являются «тривиальными» в том смысле, что они очевидным образом следуют из определений, аксиом и других теорем и не содержат никаких удивительных идей. С другой стороны, некоторые теоремы могут быть названы «глубокими», потому что их доказательства могут быть длинными и трудными, включать области математики, внешне отличные от формулировки самой теоремы, или демонстрировать удивительные связи между различными областями математики. Теорема может быть простой в изложении и в то же время глубокой. Прекрасным примером глубокой теоремы является Великая теорема Ферма. В теории чисел и в комбинаторике, а также в других областях математики имеется множество примеров простых в изложении, но глубоких теорем.

С другой стороны, есть теоремы, имеющие доказательство, которое невозможно записать в простом виде. Наиболее яркими примерами таких теорем являются теорема о четырех цветах и гипотеза Кеплера. Обе эти теоремы известны тем, что они сводятся к определённому алгоритму, который затем проверяется компьютерной программой. Первоначально многие математики не принимали эту форму доказательства, но сейчас она стала разрешённой. Математик Дорон Цейлбергер даже утверждает, что это, пожалуй, единственные нетривиальные результаты, которые когда-либо были доказаны математиками^[3]. Многие математические теоремы могут быть сведены к более простым вычислениям, включая полиномиальные тождества, тригонометрические тождества и гипергеометрические тождества^[4].

Чтобы установить математическое утверждение в качестве теоремы, требуется доказательство, то есть должна быть продемонстрирована линия рассуждений от аксиом в системе (и других уже установленных теорем) к данному утверждению. Однако доказательство обычно рассматривается отдельно от утверждения теоремы. Хотя для одной теоремы может быть известно более одного доказательства, для установления статуса утверждения как теоремы требуется только одно доказательство. Теорема Пифагора и закон квадратичной взаимности являются претендентами на название теоремы с наибольшим количеством различных доказательств.

Теоремы в математике и теории в науке принципиально отличаются по своей эпистемологии . Научная теория не может быть доказана; его ключевой атрибут заключается в том, что он фальсифицируется, то есть он делает предсказания о мире природы, которые можно проверить экспериментально . Любое несоответствие между предсказанием и экспериментом демонстрирует неверность научной теории или, по крайней мере, ограничивает ее точность или область действия. Математические теоремы, с другой стороны, являются чисто абстрактными формальными утверждениями: доказательство теоремы не может включать эксперименты или другие эмпирические доказательства так же, как эти доказательства используются для поддержки научных теорий.

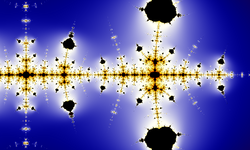Гипотеза Коллатца : один из способов проиллюстрировать ее сложность — расширить итерацию от натуральных чисел до комплексных чисел. Результатом является фрактал, который (в соответствии с универсальностью) напоминает множество Мандельброта .

Тем не менее, существует определенная степень эмпиризма и сбора данных, связанных с открытием математических теорем. Устанавливая модель, иногда с использованием мощного компьютера, математики могут иметь представление о том, что доказывать, а в некоторых случаях даже о том, как приступить к выполнению доказательства. Например, гипотеза Коллатца была проверена для начальных значений примерно до 2,88 × 10 ¹⁸ . Гипотеза Римана была проверена для первых 10 триллионов нулей дзета-функции . Ни одно из этих утверждений не считается доказанным.

Такие доказательства не являются доказательством. Например, гипотеза Мертенса представляет собой утверждение о натуральных числах, которые теперь известны как ложные, но нет явного контрпримера (то есть натурального числа n, для которого функция Мертенса M (n) равна или превышает квадратный корень из n), известно: все числа меньше 10 ¹⁴ имеют свойство Мертенса, а наименьшее число, не обладающее этим свойством, известно только как показательная функция 1,69 × 10 ⁴⁰, что примерно равно 10 в степени 4,3 × 10 ^{39[уточнить]}. Поскольку число частиц во вселенной обычно считается меньше 10 от степени 100 (гугол), нет надежды найти явный контрпример с помощью полного перебора .

Слово «теория» также существует в математике для обозначения совокупности математических аксиом, определений и теорем, как, например, теория групп. Есть также «теоремы» в науке, особенно в физике, и в технике, но они часто имеют утверждения и доказательства, в которых физические предположения и интуиция играют важную роль; физические аксиомы, на которых основаны такие «теоремы», сами по себе фальсифицируемы.

Существует ряд различных терминов для математических утверждений; эти термины указывают на роль, которую заявления играют в конкретной теме. Различие между различными терминами иногда довольно произвольно, и со временем некоторые термины использовались чаще других.

• Аксиома или постулат — это утверждение, которое принимается без доказательств и считается фундаментальным для субъекта. Исторически аксиомы считались «само собой разумеющимися», но в последнее время они считаются предположениями, которые характеризуют предмет исследования. В классической геометрии аксиомы являются общими утверждениями, а постулаты — утверждениями о свойствах геометрических объектов^[5]. Определение также принимается без доказательств, поскольку оно просто дает значение слова или фразы в терминах известных понятий.

• Непроверенное утверждение, которое считается верным, называется гипотезой. Чтобы считаться гипотезой, заявление обычно должно предлагаться публично, и в этот момент к предположению может быть присоединено имя инициатора, как и в случае с гипотезой Гольдбаха . Другие известные примеры гипотез: гипотеза Коллатца и гипотеза Римана . С другой стороны, великая теорема Ферма всегда была известна под этим именем, даже до того, как она была доказана; её никогда не называли «гипотезой Ферма».
• Предложение — теорема меньшей важности. Этот термин иногда означает утверждение с простым доказательством, в то время как термин теорема обычно зарезервирован для наиболее важных результатов или результатов с длинными или трудными доказательствами. Некоторые авторы никогда не используют термин «предложение», а другие используют термин «теорема» только для фундаментальных результатов. В классической геометрии этот термин использовался по-разному: в «Началах» Евклида (ок. 300 г. до н. э.) все теоремы и геометрические конструкции назывались «суждениями» независимо от их важности.
• Лемма — это «вспомогательная теорема», предложение с малой применимостью, которое однако является частью доказательства большей теоремы. В некоторых случаях, когда относительная важность различных теорем становится более ясной, то, что когда-то считалось леммой, начинает считаться теоремой, хотя слово «лемма» остается в её названии. В качестве примеров можно привести лемму Гаусса, лемму Цорна и фундаментальную лемму (англ.).
• Следствием является утверждение, которое следует с небольшим доказательством из другой теоремы или определения^[6]. Также следствием может быть теорема, переформулированная для более ограниченного частного случая. Например, теорема о том, что все углы в прямоугольнике являются прямыми углами, имеет следствие того, что все углы в квадрате (частный случай прямоугольника) являются прямыми углами .
• Обратное утверждение теоремы — это утверждение, образованное переменой того, что в теореме дано и того, что должно быть доказано. Например, теорема о равнобедренном треугольнике гласит, что если две стороны треугольника равны, то два угла равны. Поменяв местами то, что дано (две стороны равны) и то, что должно быть доказано (два угла равны), получаем обратное утверждение: если два угла треугольника равны, то и две стороны равны. В этом примере обратное утверждение может быть доказано как еще одна теорема, но зачастую это не так. Например, обратным утверждением к теореме о том, что два прямых угла равны, является утверждением, что два равных угла должны быть прямыми, но это явно не всегда так^[7].
• Обобщением называется теорема, которая включает ранее доказанную теорему как частный случай, а значит, как следствие.

Существуют и другие, реже используемые термины, которые обычно присоединяются к доказанным утверждениям, поэтому некоторые теоремы упоминаются под историческими или общепринятыми названиями. Например:

• Тождество — это теорема о равенстве между двумя математическими выражениями, которое верно всегда независимо от того, какие значения используются для любых переменных или параметров, фигурирующих в выражениях. Примерами являются формула Эйлера и тождество Вандермонда .
• Правило — это теорема, которая устанавливает полезную формулу. Например, правило Байеса и правило Крамера,
• Закон или принцип — это теорема, которая применяется в широком диапазоне обстоятельств. Примерами можно считать закон больших чисел, теорему косинусов, закон Колмогорова «ноль — один», принцип Гарнака, свойство наименьшей верхней границы (англ.) и принцип Дирихле^[8].

Несколько известных теорем имеют еще более своеобразные названия. Алгоритм деления (см. Деление с остатком) — это теорема, выражающая результат деления на натуральные числа и более общие кольца. Соотношение Безу — это теорема, утверждающая, что наибольший общий делитель двух чисел может быть записан как линейная комбинация этих чисел. Парадокс Банаха — Тарского — это теорема в теории меры, которая парадоксальна в том смысле, что она противоречит распространенным представлениям о объеме в трехмерном пространстве.

Теорема и ее доказательство обычно выкладываются следующим образом:

Теорема (имя человека, который доказал это и год открытия, доказательства или публикации).

Утверждение теоремы (иногда называемое суждением ).

Доказательство

Описание доказательства.

Конец

Конец доказательства может быть обозначен буквами QED (quod erat manifrand) или одним из надгробных знаков «□» или «∎», означающим «Конец доказательства», введенным Полом Халмосом после их использования в журнальных статьях.

Точный стиль зависит от автора или публикации. Многие публикации предоставляют инструкции или макрокоманды для набора текста в стилистическом справочнике .

Обычно теореме предшествуют определения, описывающие точное значение терминов, используемых в теореме. Обычно теореме предшествует ряд предложений или лемм, которые затем используются в доказательстве. Однако леммы иногда включаются в доказательство теоремы либо с вложенными доказательствами, либо с их доказательствами, представленными после доказательства теоремы.

Следствия из теоремы представлены либо между теоремой и доказательством, либо непосредственно после доказательства. Иногда следствия имеют свои собственные доказательства, которые объясняют, почему они следуют из теоремы.

Подсчитано, что ежегодно доказывается более четверти миллиона теорем^[9].

Хорошо известный афоризм «математик — это устройство для превращения кофе в теоремы» часто приписывают выдающемуся математику Палу Эрдёшу, который был знаменит доказательством большого количества теорем, числом Эрдёша, характеризующем количество его возможных соавторов и огромным количеством выпиваемого им кофе^[10]. Однако это высказывание принадлежит коллеге Эрдёша, Альфреду Реньи (хотя Реньи, произнося эту фразу, скорее всего имел в виду Эрдёша).

Классификация простых конечных групп рассматривается некоторыми математиками как самое длинное доказательство теоремы. Ее произвели около 100 авторов в 500 журнальных статьях, занимающих в общей сложности десяток тысяч страниц. Считается, что эти публикации вместе дают полное доказательство, и многие математики надеются сократить и упростить это доказательство^[11]. Другая теорема этого типа — проблема четырех красок, чье компьютерное доказательство слишком длинное, чтобы человек мог его прочитать. Это, безусловно, самое длинное из известных доказательств теоремы, утверждение которых легко понять непрофессионалу.

• Вывод
• Список теорем
• Игрушечная теорема
• Metamath — язык для разработки строго формализованных математических определений и доказательств, сопровождаемый средством проверки для этого языка и растущей базой данных тысяч доказанных теорем

• Heath, Sir Thomas Little. The works of Archimedes (неопр.). — Dover, 1897.
• Hoffman, P. The Man Who Loved Only Numbers (англ.)русск.: The Story of Paul Erdős and the Search for Mathematical Truth (англ.). — Hyperion, New York, 1998.
• Hofstadter, Douglas. Gödel, Escher, Bach: An Eternal Golden Braid (нем.). — Basic Books, 1979.
• Hunter, Geoffrey. Metalogic: An Introduction to the Metatheory of Standard First Order Logic (англ.). — University of California Press (англ.)русск., 1996.
• Mates, Benson. Elementary Logic (англ.). — Oxford University Press, 1972.
• Petkovsek, Marko; Wilf, Herbert. A = B (неопр.). — A.K. Peters, Wellesley, Massachusetts, 1996.

1. ↑ Elisha Scott Loomis. The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs (неопр.). Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Дата обращения 26 сентября 2010.
2. ↑ However, both theorems and scientific law are the result of investigations. See Heath, 1897 Introduction, The terminology of Archimedes, p. clxxxii: «theorem (θεὼρνμα) from θεωρεἳν to investigate»
3. ↑ Doron Zeilberger. Opinion 51 (неопр.).
4. ↑ Петковсек и соавт. 1996.
5. ↑ Wentworth, G.; Smith, D.E. Art. 46, 47 // Plane Geometry (неопр.). — Ginn & Co., 1913.
6. ↑ Wentworth & Smith Art. 51
7. ↑ Следует Wentworth & Smith Art. 79
8. ↑ Слово закон также может относиться к аксиоме, правилу вывода или, в теории вероятности, распределению вероятности .
9. ↑ Hoffman 1998, p. 204.
10. ↑ Hoffman 1998, p. 7.
11. ↑ Огромная теорема: классификация конечных простых групп, Richard Elwes, Plus Magazine, Issue 41 December 2006.

Аксиома выбора — Википедия

Где (S_i) семейство непустых множеств, проиндексированных множеством действительных чисел R. То есть для каждого действительного числа i существует множество S_i. На рисунке приведен пример выбора элементов множеств. Каждое такое множество S_i непусто, а возможно и бесконечно. Аксиома выбора позволяет нам произвольно выбирать один элемент из каждого множества, формируя соответствующее семейство элементов (x_i), также проиндексированных множеством действительных чисел R, где x_i выбраны из S_i.

Аксиомой выбора, англ. аббр. AC (от axiom of choice) называется следующее высказывание теории множеств:

Для всякого семейства[1]X{\displaystyle X} непустых множеств существует функция f{\displaystyle f}, которая каждому множеству семейства сопоставляет один из элементов этого множества[2]. Функция f{\displaystyle f} называется функцией выбора для заданного семейства.

На формальном языке:

∀X[∅∉X⇒∃f:X→⋃X∀A∈X(f(A)∈A)].{\displaystyle \forall X\left[\emptyset \notin X\Rightarrow \exists f\colon X\rightarrow \bigcup X\quad \forall A\in X\,(f(A)\in A)\right]\,.}

Если мы ограничимся рассмотрением только конечных семейств множеств, то утверждение аксиомы выбора может быть доказано исходя из других аксиом теории множеств^[2] и не требует постулирования в качестве отдельной аксиомы. Оно также может быть доказано для некоторых бесконечных семейств, однако в общем случае для бесконечных семейств аксиома выбора не следует из других аксиом и является независимым утверждением.

Аксиома выбора была сформулирована и опубликована Эрнстом Цермело в 1904 году (хотя впервые её отметил Беппо Леви на 2 года раньше). Новая аксиома вызвала бурную полемику и до сих пор не все математики принимают её безоговорочно. Бытует мнение, что доказательства, полученные с её привлечением, имеют «иную познавательную ценность», чем доказательства, не зависящие от неё. Появление аксиомы выбора вызвало также дискуссию о том, что означает в математике понятие «существование» — в частности, о том, можно ли считать существующим множество, ни один элемент которого не известен.

Неприятие аксиомы выбора некоторыми математиками обосновано, прежде всего, тем, что в ней лишь утверждается существование множества d{\displaystyle d}, но не дается никакого способа его определения. Это мнение, например, Бореля и Лебега. Противоположного мнения придерживались, например, Гильберт, Хаусдорф и Френкель, которые принимали аксиому выбора без всяких оговорок, признавая за ней ту же степень «очевидности», что и за другими аксиомами теории множеств: аксиома объёмности, аксиома существования пустого множества, аксиома пары, аксиома суммы, аксиома степени, аксиома бесконечности.

Более того, среди следствий аксиомы выбора есть много довольно парадоксальных, вызывающих интуитивный протест части математиков. Например, появляется возможность доказать парадокс удвоения шара, который вряд ли могут счесть «очевидным» все исследователи (см. также Квадратура круга Тарского). Подробный анализ многочисленных доказательств, использующих аксиому выбора, провел Вацлав Серпинский. Однако, без сомнения, многие важные математические открытия нельзя было бы сделать без аксиомы выбора^[3].

Бертран Рассел так отозвался об аксиоме выбора: «Сначала она кажется очевидной; но чем больше вдумываешься, тем более странными кажутся выводы из этой аксиомы; под конец же вообще перестаешь понимать, что же она означает».

Независимость аксиомы выбора от остальных аксиом Цермело — Френкеля доказал Пол Коэн.^[4][5]

Существует множество других, эквивалентных формулировок аксиомы выбора.

Функция выбора — функция на множестве множеств X{\displaystyle X} такая, что для каждого множества s{\displaystyle s} в X{\displaystyle X}, f(s){\displaystyle f(s)} является элементом из s{\displaystyle s}. С использованием понятия функции выбора аксиома утверждает:

• Для любого семейства непустых множеств X{\displaystyle X} существует функция выбора f{\displaystyle f}, определённая на X{\displaystyle X}.

Или наиболее сжато:

Каждое множество непустых множеств имеет функцию выбора.

Вторая версия аксиомы выбора утверждает:

Для данного произвольного множества попарно непересекающихся непустых множеств существует по крайней мере одно множество, которое содержит точно один элемент, общий с каждым из непустых множеств.

Некоторые авторы используют другую версию, которая эффективно утверждает:

Для любого множества A{\displaystyle A}, его булеан за вычетом пустого подмножества P(A)∖{∅}{\displaystyle {\mathcal {P}}(A)\setminus \{\varnothing \}} имеет функцию выбора.

Авторы, которые используют эту формулировку, часто также говорят о «функции выбора на A{\displaystyle A}», но оговаривают, что имеют в виду немного другое понятие функции выбора. Её область определения — булеан (минус пустое подмножество), тогда как в других местах этой статьи, область определения функции выбора — «множество множеств». С этим дополнительным понятием функции выбора, аксиома выбора может быть сжато сформулирована так:

Каждое множество имеет функцию выбора.

До конца XIX века аксиома выбора использовалась безоговорочно. Например, после определения множества X{\displaystyle X}, содержащего непустое множество, математик мог сказать: «Пусть F(s){\displaystyle F(s)} будет определено для каждого s{\displaystyle s} из X{\displaystyle X}». Без аксиомы выбора в общем случае невозможно доказать, что F{\displaystyle F} существует, но это, кажется, оставалось без внимания до Цермело.

Не во всех случаях требуется аксиома выбора. Для конечного набора X{\displaystyle X} аксиома выбора следует из других аксиом теории множеств. В этом случае это то же самое, что говорить, если мы имеем несколько (конечное число) коробок, каждая из которых содержит в себе по одной одинаковой вещи, тогда мы можем выбрать ровно одну вещь из каждой коробки. Ясно, что мы можем сделать это: мы начнём с первой коробки, выберем вещь; отправимся ко второй коробке, выберем вещь; и т. д. Так как есть конечное число коробок, то действуя нашей процедурой выбора, мы придём к концу. Результатом будет функция явного выбора: функция, которая первой коробке сопоставляет первый элемент, который мы выбрали, второй коробке — второй элемент и т. д. (Для получения формального доказательства для всех конечных множеств следует воспользоваться принципом математической индукции.)

В случае с бесконечным множеством X{\displaystyle X} иногда также можно обойти аксиому выбора. Например, если элементы X{\displaystyle X} — множества натуральных чисел. Каждый непустой набор натуральных чисел имеет наименьший элемент, таким образом, определяя нашу функцию выбора, мы можем просто сказать, что каждому множеству сопоставляется наименьший элемент набора. Это позволяет нам сделать выбор элемента из каждого множества, поэтому мы можем записать явное выражение, которое говорит нам, какое значение наша функция выбора принимает. Если возможно таким образом определить функцию выбора, в аксиоме выбора нет необходимости.

Сложности появляются в случае, если невозможно осуществить естественный выбор элементов из каждого множества. Если мы не можем сделать явный выбор, то почему уверены, что такой выбор можно совершить в принципе? Например, пусть X{\displaystyle X} — это множество непустых подмножеств действительных чисел. Во-первых, мы могли бы попробовать поступить как в случае, если бы X{\displaystyle X} было конечным. Если мы попробуем выбрать элемент из каждого множества, тогда, так как X{\displaystyle X} бесконечно, наша процедура выбора никогда не придёт к концу, и вследствие этого мы никогда не получим функции выбора для всего X{\displaystyle X}. Так что это не срабатывает. Далее, мы можем попробовать определить наименьший элемент из каждого множества. Но некоторые подмножества действительных чисел не содержат наименьший элемент. Например, таким подмножеством является открытый интервал (0,1){\displaystyle (0,\;1)}. Если x{\displaystyle x} принадлежит (0,1){\displaystyle (0,\;1)}, то x/2{\displaystyle x/2} также принадлежит ему, причем меньше, чем x{\displaystyle x}. Итак, выбор наименьшего элемента тоже не работает.

Причина, которая позволяет выбрать нам наименьший элемент из подмножества натуральных чисел — это факт, что натуральные числа обладают свойством вполнеупорядоченности. Каждое подмножество натуральных чисел имеет единственный наименьший элемент в силу естественной упорядоченности. Может быть, если бы мы были умнее, то могли бы сказать: «Возможно, если обычный порядок для действительных чисел не позволяет найти особое (наименьшее) число в каждом подмножестве, мы могли бы ввести другой порядок, который давал бы свойство вполнеупорядоченности. Тогда наша функция сможет выбрать наименьший элемент из каждого множества в силу нашего необычного упорядочивания». Проблема тогда возникает в этом построении вполнеупорядоченности, которая для своего решения требует наличия аксиомы выбора. Иными словами, каждое множество может быть вполне упорядочено тогда и только тогда, когда аксиома выбора справедлива.

Доказательства, требующие аксиомы выбора, всегда неконструктивны: даже если доказательство создаёт объект, невозможно сказать, что же именно это за объект. Следовательно, хоть аксиома выбора позволяет вполне упорядочить множество действительных чисел, это не даёт нам никакой наглядности и конструктивизма в целом. Сама причина, по которой наш вышеуказанный выбор вполне упорядочения действительных чисел был таким для каждого множества X{\displaystyle X}, мы могли явно выбрать элемент из такого множества. Если мы не можем указать, что мы используем вполне упорядоченность, тогда наш выбор не вполне явный. Это одна из причин, почему некоторые математики не любят аксиому выбора (см. также Кризис оснований математики). Например, конструктивистская установка что все существующие доказательства должны быть полностью явными; должно быть возможным построение чего бы то ни было что существует. Они отвергают аксиому выбора потому, что она заявляет существование объекта без описания. С другой стороны, факт — что для доказательства существования используется аксиома выбора — не означает, что мы не сможем совершить построение другим способом.

Принцип вполне упорядочивания (теорема Цермело)[править | править код]

Очень распространённая и удобная формулировка использует понятие вполне упорядоченного множества. Нам потребуется несколько определений, и мы начнём со строгого определения линейного порядка, выражающего знакомую нам идею на языке теории множеств. Напомним, что упорядоченная пара элементов обозначается (x,y){\displaystyle (x,\;y)}, и что декартово произведение множеств X×Y{\displaystyle X\times Y} состоит из всех возможных упорядоченных пар (x,y){\displaystyle (x,\;y)}, где x∈X,y∈Y{\displaystyle x\in X,\;y\in Y}.

Линейным порядком на множестве A{\displaystyle A} называется подмножество декартова произведения R⊆A×A{\displaystyle R\subseteq A\times A}, обладающее следующим свойствами:

1. Полное: ∀x,y∈A((x,y)∈R∨(y,x)∈R){\displaystyle \forall x,\;y\in A\;((x,\;y)\in R\lor (y,\;x)\in R)}.
2. Антисимметричное: ∀x,y∈A((x,y)∈R∧(y,x)∈R→y=x){\displaystyle \forall x,\;y\in A\;((x,\;y)\in R\wedge (y,\;x)\in R\to y=x)}.
3. Транзитивное: ∀x,y,z∈A((x,y)∈R∧(y,z)∈R→(x,z)∈R){\displaystyle \forall x,\;y,\;z\in A\;((x,\;y)\in R\wedge (y,\;z)\in R\to (x,\;z)\in R)}.

Полным порядком на множестве A{\displaystyle A} называется такой линейный порядок, что каждое непустое подмножество X⊆A{\displaystyle X\subseteq A} имеет наименьший элемент.

Принцип полного порядка заключается в том, что любое множество может быть вполне упорядочено.

Например, множество натуральных чисел может быть вполне упорядоченно обычным отношением «меньше или равно чем». С тем же отношением множество целых чисел не имеет наименьшего элемента. В этом случае мы можем собрать целые числа в последовательность (0,−1,1,−2,2,…,−n,n,…){\displaystyle (0,\;-1,\;1,\;-2,\;2,\;\ldots ,\;-n,\;n,\;\ldots )} и сказать, что младшие члены меньше, чем старшие. Очевидно, такое отношение будет полным порядком на целых числах.

Гораздо менее очевидно, что действительные числа, формирующие несчётное множество, могут быть вполне упорядочены.

Лемма Цорна[править | править код]

Если в частично упорядоченном множестве любая цепь (то есть линейно упорядоченное подмножество) имеет верхнюю грань, то всё множество имеет хотя бы один максимальный элемент.

Более формально:

Пусть (P,⩽){\displaystyle (P,\;\leqslant )} — частично упорядоченное множество, то есть, отношение ⩽{\displaystyle \leqslant } — рефлексивно, антисимметрично и транзитивно:

• ∀x∈Px⩽x;{\displaystyle \forall x\in P\quad x\leqslant x;}
• ∀x,y∈Px⩽y∧y⩽x→x=y;{\displaystyle \forall x,\;y\in P\;x\leqslant y\land y\leqslant x\to x=y;}
• ∀x,y,z∈Px⩽y∧y⩽z→x⩽z.{\displaystyle \forall x,\;y,\;z\in P\;x\leqslant y\land y\leqslant z\to x\leqslant z.}

Подмножество S⊂P{\displaystyle S\subset P} называется линейно упорядоченным, если ∀x,y∈Sx⩽y∨y⩽x{\displaystyle \forall x,\;y\in S\;x\leqslant y\lor y\leqslant x}. Элемент u∈P{\displaystyle u\in P} называется верхней гранью, если ∀x∈Sx⩽u{\displaystyle \forall x\in S\;x\leqslant u}.

Допустим, что любое линейно упорядоченное подмножество множества P{\displaystyle P} имеет верхнюю грань. Тогда ∃m∈P∄x∈Px>m{\displaystyle \exists m\in P\;\nexists x\in P\;x>m}, то есть m{\displaystyle m} — максимальный элемент.

Принцип максимума Хаусдорфа[править | править код]

Если ограничить применение аксиомы выбора только конечными и счётными семействами множеств, получается «аксиома счётного выбора». Она вполне достаточна для обоснования большинства теорем анализа и не создаёт указанных выше парадоксов. Однако её недостаточно для обоснования многих положений теории множеств. Ещё один, несколько более сильный вариант — Аксиома зависимого выбора^[en], но и она не подходит для нужд теории множеств.

В 1962 году польские математики Ян Мычельский и Гуго Штейнгауз предложили взамен аксиомы выбора так называемую «аксиому детерминированности»^[7]. В отличие от аксиомы выбора, которая имеет интуитивно понятную формулировку и противоречащие интуиции следствия, аксиома детерминированности, наоборот, имеет неочевидную формулировку, однако её следствия куда лучше согласуются с интуицией. Из аксиомы детерминированности вытекает аксиома счётного выбора, но не полная аксиома выбора^[5].

Следствия аксиомы детерминированности в ряде ситуаций противоречат следствиям аксиомы выбора — например, из аксиомы детерминированности следует, что все множества вещественных чисел измеримы по Лебегу, в то время как из аксиомы выбора следует существование неизмеримого по Лебегу множества вещественных чисел. Используя аксиому детерминированности, можно строго доказать, что между счётной мощностью и мощностью континуума нет промежуточных мощностей, в то время как это утверждение независимо от аксиомы выбора^[8].

1. ↑ семейство в математике — множество множеств.
2. ↑ ^{1 2} Выбора аксиома // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1.
3. ↑ Элементы: Пределы доказуемости
4. ↑ П. ДЖ. Коэн. Теория множеств и континуум-гипотеза. — Москва: Мир, 1969.
5. ↑ ^{1 2} Казимиров Н. И. Введение в аксиоматическую теорию множеств. Учебное пособие. — Петрозаводск, 2000. — 104 с. — § 2.4.
6. ↑ Евгений Вечтомов. Математика: основные математические структуры 2-е изд. Учебное пособие для академического бакалавриата. — Litres, 2018. — С. 26. — 297 с.
7. ↑ Mycielski, Jan; Steinhaus, H. (1962). A mathematical axiom contradicting the axiom of choice. Bulletin de l’Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques 10: 1–3. ISSN 0001-4117. MR 0140430.
8. ↑ Кановей В. Г., 1984, с. 4, 37.

Знаете отличие теории от теоремы?

Теоремы в математике, а теории нет

Знаю. Пипец. . На Ответах задаёт вопрос и сам же на этот вопрос отвечает.

вы задали вопрос, на который сами ответили. а нам что делать?)))

Теорема имеет доказательства. А теория, она и есть теория — не имеет твердых доказательств.

Теория (θεωρία, «рассмотрение, исследование» ) — совокупность умозаключений, отражающая объективно существующие отношения и связи между явлениями объективной реальности. Таким образом, теория — это интеллектуальное отражение реальности ученые сомневаются, строят различные теории, с оговорками, а господин Лесин знает все, палеонтолог блин великий

Курица и яйцо, и что ЕСТЬ что, для особо одарённых

теория — это МЫСЛЬ, теорема — это ДОКАЗАТЕЛЬСТВО правильности или неправильности этой мысли…. главное отличие :МЫСЛить могут — ВСЕ, а доказать — ЕДИНИЦЫ….

доказывая теоремы, сформированные в рамках теории, подтверждаем теорию

Аксиома объёмности — Википедия

Аксиомой объёмности называется следующее высказывание теории множеств:

∀a1∀a2 (∀b (b∈a1↔b∈a2)→a1=a2){\displaystyle \forall a_{1}\forall a_{2}\ (\forall b\ (b\in a_{1}\leftrightarrow b\in a_{2})\to a_{1}=a_{2})}

Если переписать аксиому объёмности в виде

∀a1∀a2 (∀b (b∈a1→b∈a2) ∧ ∀b (b∈a2→b∈a1)→a1=a2){\displaystyle \forall a_{1}\forall a_{2}\ (\forall b\ (b\in a_{1}\to b\in a_{2})\ \land \ \forall b\ (b\in a_{2}\to b\in a_{1})\to a_{1}=a_{2})},

тогда названную аксиому можно сформулировать следующим образом:

«Каковы бы ни были два множества, если каждый элемент 1-го множества принадлежит 2-му множеству, а каждый элемент 2-го множества принадлежит 1-му множеству, тогда первое множество идентично второму множеству.»

Другая формулировка^[1]:

«Два множества равны в том и только в том случае, когда они состоят из одних и тех же элементов.»

Другие формулировки аксиомы объёмности[править | править код]

∀a1∀a2 (a1⊆a2 ∧ a2⊆a1→a1=a2){\displaystyle \forall a_{1}\forall a_{2}\ (a_{1}\subseteq a_{2}\ \land \ a_{2}\subseteq a_{1}\to a_{1}=a_{2})}

∀a1∀a2 (a1≠a2→∃b (b∈a1 ⊻ b∈a2) ){\displaystyle \forall a_{1}\forall a_{2}\ (a_{1}\neq a_{2}\to \exists b\ (b\in a_{1}\ \veebar \ b\in a_{2})\ )}

Аксиома объёмности выражает необходимое условие равенства двух множеств. Достаточное условие равенства множеств выводится из аксиом предиката ={\displaystyle =}, а именно:

∀a (a=a){\displaystyle \forall a\ (a=a)},

∀a1∀a2 (a1=a2→(φ[a1]→φ[a2])){\displaystyle \forall a_{1}\forall a_{2}\ (a_{1}=a_{2}\to (\varphi [a_{1}]\to \varphi [a_{2}]))}, где φ[a1]{\displaystyle \varphi [a_{1}]} — любое математически корректное суждение об a1{\displaystyle a_{1}}, а φ[a2]{\displaystyle \varphi [a_{2}]} — то же самое суждение, но об a2{\displaystyle a_{2}}.

Соединяя указанное достаточное условие равенства множеств с аксиомой объёмности, получаем следующий критерий равенства множеств:

∀a1∀a2 (a1=a2↔∀b (b∈a1↔b∈a2) ){\displaystyle \forall a_{1}\forall a_{2}\ (a_{1}=a_{2}\leftrightarrow \forall b\ (b\in a_{1}\leftrightarrow b\in a_{2})\ )}

Указанный критерий равенства множеств не хуже и не лучше других аналогичных критериев, включая:

1) критерий равенства комплексных чисел

∀x∀y∀u∀v (x,y,u,v∈R→(x+iy=u+iv↔x=u ∧ y=v)){\displaystyle \forall x\forall y\forall u\forall v\ (x,y,u,v\in \mathbb {R} \to (x+iy=u+iv\leftrightarrow x=u\ \land \ y=v))},

2) критерий равенства упорядоченных пар

∀x∀y∀u∀v ( (x,y)=(u,v)↔x=u ∧ y=v) ){\displaystyle \forall x\forall y\forall u\forall v\ (\ (x,y)=(u,v)\leftrightarrow x=u\ \land \ y=v)\ )},

3) критерий равенства неупорядоченных пар

∀x∀y∀u∀v ({x,y}={u,v}↔x=u ∧ y=v∨x=v ∧ y=u) ){\displaystyle \forall x\forall y\forall u\forall v\ (\{x,y\}=\{u,v\}\leftrightarrow x=u\ \land \ y=v\quad \lor \quad x=v\ \land \ y=u)\ )},

4) критерий равенства двух последовательностей

{xn}={yn}↔∀i (i∈N→xi=yi){\displaystyle \{x_{n}\}=\{y_{n}\}\leftrightarrow \forall i\ (i\in \mathbb {N} \to x_{i}=y_{i})}.

Из изложенного ясно, что аксиома объёмности является органичной частью аксиоматики теории множеств.

Аксиому объёмности применяют при доказательстве единственности множества, существование которого уже декларировано [аксиомой] либо установлено [доказательством теоремы].

Примеры

1. Доказательство единственности пустого множества

Существование [по меньшей мере одного] пустого множества декларировано аксиомой

∃a∀b (b∉a){\displaystyle \exists a\forall b\ (b\notin a)}.

Требуется доказать существование не более, чем одного множества a{\displaystyle a}, для которого верно высказывание

∀b (b∉a){\displaystyle \forall b\ (b\notin a)}.

Иначе говоря, требуется доказать

∃{0,1}a (∀b (b∉a)){\displaystyle \exists \{0,1\}a\ (\forall b\ (b\notin a))}

Или, что то же самое, требуется доказать

∀a1∀a2 (∀b(b∉a1) ∧ ∀b(b∉a2)→a1=a2){\displaystyle \forall a_{1}\forall a_{2}\ (\forall b(b\notin a_{1})\ \land \ \forall b(b\notin a_{2})\to a_{1}=a_{2})}

Доказательство

∀b(b∉a1) ∧ ∀b(b∉a2)⇔∀b(b∉a1 ∧ b∉a2)⇒∀b(b∉a1↔b∉a2) ⇔∀b(b∈a1↔b∈a2)⇒a1=a2{\displaystyle {\begin{aligned}\forall b(b\notin a_{1})\ \land \ \forall b(b\notin a_{2})\Leftrightarrow \forall b(b\notin a_{1}\ \land \ b\notin a_{2})\Rightarrow \forall b(b\notin a_{1}\leftrightarrow b\notin a_{2})\\\ \Leftrightarrow \forall b(b\in a_{1}\leftrightarrow b\in a_{2})\Rightarrow a_{1}=a_{2}\end{aligned}}}

Поскольку ∃a∀b (b∉a) ∧ ∃{0,1}a∀b (b∉a)⇔∃{1}a∀b (b∉a){\displaystyle \exists a\forall b\ (b\notin a)\ \land \ \exists \{0,1\}a\forall b\ (b\notin a)\Leftrightarrow \exists \{1\}a\forall b\ (b\notin a)}, постольку доказательство единственности пустого множества завершено.

2. Доказательство единственности множества подмножеств

Существование [по меньшей мере одного] множества подмножеств декларировано аксиомой

∀a∃d∀b (b∈d↔b⊆a){\displaystyle \forall a\exists d\forall b\ (b\in d\leftrightarrow b\subseteq a)}

Требуется доказать существование не более, чем одного множества d{\displaystyle d}, для которого верно высказывание

∀b (b∈d↔b⊆a){\displaystyle \forall b\ (b\in d\leftrightarrow b\subseteq a)}

Иначе говоря, требуется доказать

∃{0,1}d (∀b (b∈d↔b⊆a)){\displaystyle \exists \{0,1\}d\ (\forall b\ (b\in d\leftrightarrow b\subseteq a))}

Или, что то же самое, требуется доказать

∀d1∀d2 (∀b (b∈d1↔b⊆a) ∧ ∀b (b∈d2↔b⊆a)→d1=d2){\displaystyle \forall d_{1}\forall d_{2}\ (\forall b\ (b\in d_{1}\leftrightarrow b\subseteq a)\ \land \ \forall b\ (b\in d_{2}\leftrightarrow b\subseteq a)\to d_{1}=d_{2})}

Доказательство

∀b(b∈d1↔b⊆a) ∧ ∀b(b∈d2↔b⊆a)⇔∀b((b∈d1↔b⊆a) ∧ (b∈d2↔b⊆a)) ⇒∀b(b∈d1↔b∈d2)⇒d1=d2{\displaystyle {\begin{aligned}\forall b(b\in d_{1}\leftrightarrow b\subseteq a)\ \land \ \forall b(b\in d_{2}\leftrightarrow b\subseteq a)\Leftrightarrow \forall b((b\in d_{1}\leftrightarrow b\subseteq a)\ \land \ (b\in d_{2}\leftrightarrow b\subseteq a))\\\ \Rightarrow \forall b(b\in d_{1}\leftrightarrow b\in d_{2})\Rightarrow d_{1}=d_{2}\end{aligned}}}

Поскольку ∃d∀b (b∈d↔b⊆a) ∧ ∃{0,1}d∀b (b∈d↔b⊆a)⇔∃{1}d∀b (b∈d↔b⊆a){\displaystyle \exists d\forall b\ (b\in d\leftrightarrow b\subseteq a)\ \land \ \exists \{0,1\}d\forall b\ (b\in d\leftrightarrow b\subseteq a)\Leftrightarrow \exists \{1\}d\forall b\ (b\in d\leftrightarrow b\subseteq a)}, постольку доказательство единственности множества подмножеств завершено.

1. ↑ Столл Р. Множества. Логика. Аксиоматические теории. — М., Просвещение, 1968. — Тираж 70 000 экз. — С. 13