Модуль числа
Мóдуль числá a — это расстояние от начала координат до точки А(a).
Чтобы понять это определение, подставим вместо переменной a любое число, например 3, и снова прочитаем его:
Мóдуль числá 3 — это расстояние от начала координат до точки А(3).
То есть модуль это ни что иное как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3)
Расстояние от начала координат до точки А(3) составляет 3 (три единицы или три шага).
Модуль числа обозначает двумя вертикальными линиями, например:
Модуль числа 3 обозначается так: |3|
Модуль числа 4 обозначается так: |4|
Модуль числа 5 обозначается так: |5|
Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:
|3| = 3
Читается как «Модуль числа три равен три»
Теперь попробуем найти модуль числа −3.
Модулем числа −3 называют расстояние от начала координат до точки B(−3).
Расстояние от одного пункта до другого не может быть отрицательным. Модуль это тоже расстояние, поэтому тоже не может быть отрицательным.
Модуль числа −3 равен 3. Расстояние от начала координат до точки B(−3) равно трём единицам:
|−3| = 3
Читается как «Модуль числа минус три равен три»
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом координат. То есть расстояние от начала координат до точки O(0) равно нулю:
|0| = 0
«Модуль нуля равен нулю»
Сделаем выводы:
- Модуль числа не может быть отрицательным;
- Для положительного числа и нуля модуль равен самомý числу, а для отрицательного – противоположному числу;
- Противоположные числа имеют равные модули.

Противоположные числа
Числа, отличающиеся только знаками называют противоположными.
Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числá −2 знак минуса, а у числá 2 знак плюса, но мы его не видим, поскольку плюс как говорилось ранее, не записывают.
Еще примеры противоположных чисел:
−1 и 1
−3 и 3
−5 и 5
−9 и 9
Противоположные числа имеют равные модули. Например, найдём модули чисел −3 и 3
|−3| и |3|
3 = 3
На рисунке видно, что расстояние от начала координат до точек A(−3) и B(3) одинаково равно трём шагам.
Понравился урок?
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
что это такое и как его найти?
Модуль — математическое понятие, которое проходят в шестом классе. Сам по себе числовой модуль не представляет собой ничего сложного, это одна из простейших тем в начальной математике. Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.
Сам по себе числовой модуль не представляет собой ничего сложного, это одна из простейших тем в начальной математике. Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.
Модуль с точки зрения геометрии
Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.
Как найти модуль числа?
Теперь, когда мы визуально представляем, что же такое модуль, будет проще понять формулировку из учебника. Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.
Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.
Это можно сформулировать и иначе — модулем любого числа будет само это число в абсолютном выражении, то есть без учета знака. Записывается модуль так — по обе стороны от нужного числа ставятся вертикальные линии, например, модуль для числа «5» будет равен «5», а записываться он будет, как |5|.
Из всего, что мы рассказали выше, можно вывести несколько строгих правил для модулей.
- Может ли модуль быть отрицательным? Нет! Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, -7, то его модуль будет равен |7| — числу, противоположному исходному.
- Для нуля модуль всегда будет равен нулю. Верно и другое — нуль может быть модулем исключительно в том случае, если вычисляется он для числа нуль, и ни в каком другом.
- Если нужно найти модуль для выражения типа a*b, то есть модуль произведения, то можно сначала найти модуль а, затем модуль b, и перемножить их друг на друга.

- То же самое касается и деления — если нам нужно разделить y на z и найти модуль получившегося числа, то можно взять модуль y и разделить его на модуль z. Результат будет одним и тем же.
Похожие статьи
Чему равен модуль 7. Что такое модуль числа в математике
Модуль — математическое понятие, которое проходят в шестом классе. Сам по себе числовой модуль не представляет собой ничего сложного, это одна из простейших тем в начальной математике. Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.
Модуль с точки зрения геометрии
Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.
Как найти модуль числа?
Теперь, когда мы визуально представляем, что же такое модуль, будет проще понять формулировку из учебника. Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.
Это можно сформулировать и иначе — модулем любого числа будет само это число в абсолютном выражении, то есть без учета знака. Записывается модуль так — по обе стороны от нужного числа ставятся вертикальные линии, например, модуль для числа «5» будет равен «5», а записываться он будет, как |5|.
Из всего, что мы рассказали выше, можно вывести несколько строгих правил для модулей.
- Может ли модуль быть отрицательным? Нет! Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, -7, то его модуль будет равен |7| — числу, противоположному исходному.
- Для нуля модуль всегда будет равен нулю. Верно и другое — нуль может быть модулем исключительно в том случае, если вычисляется он для числа нуль, и ни в каком другом.
- Если нужно найти модуль для выражения типа a*b, то есть модуль произведения, то можно сначала найти модуль а, затем модуль b, и перемножить их друг на друга.
- То же самое касается и деления — если нам нужно разделить y на z и найти модуль получившегося числа, то можно взять модуль y и разделить его на модуль z. Результат будет одним и тем же.
Модуль числа — это расстояние от этого числа до нуля на координатной прямой.
Модуль обозначается с помощью символа: | |.
- Запись |6| читается как «модуль числа 6», или «модуль шести».
- Запись |8| читается как «модуль 8-ми».
Для лучшего понимания темы: «модуль числа» предлагаем воспользоваться методом ассоциаций.
Представим, что модуль числа — это баня , а знак «минус» — грязь .
Оказываясь под знаком модуля (то есть в «бане») отрицательное число «моется» , и выходит без знака «минус» — чистым .
В бане могут «мыться» (то есть стоять под знаком модуля) и отрицательные , и положительные числа , и число ноль . Однако будучи «чистым» положительные числа , и ноль свой знак при выходе из «бани» (то есть из под знака модуля) не меняют !
История модуля числа или 6 интересных фактов о модуле числа
1. Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
2. Ввел в обращение этот термин ученик Исаака Ньютона — английский математик и философ Роджер Котс (1682 – 1716).
3. Великий немецкий физик, изобретатель, математик и философ Готфрид Лейбниц в своих работах и трудах использовал функцию модуля, которую он обозначил mod x .
4. Обозначение модуля было введено в 1841 году немецким математиком
Карлом Вейерштрассом (1815 — 1897).
5. При написании модуль обозначается с помощью символа: | |.
6. Еще одной версии термин «модуль» был введен в 1806 году французским
математиком по имени Жан Робер Аргáн (1768 — 1822). Но это не совсем так.
В начале девятнадцатого века математики Жан Робер Аргáн (1768 — 1822)
и Огюстен Луи Коши (1789 — 1857) ввели понятие «модуль комплексного числа»,
Решение задач на тему «Модуль числа»
Задача №1. Расположи выражения: -|12|, 0, 54, |-(-2)|, -17 в порядке возрастания.
— | 12 | = — 12
| — (— 2) | = 2
17 -17
Ответ: -17
Задача№2. Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) |
Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) |
в порядке убывания.
Для начала раскроем скобки и модули:
— | — 14| = — 14
— |30| = -30
|-16| = 16
| -(-9) | = 9
16 > 9 > -14 > — 21 > — 30 что будет равносильно:
|-16| > | -(-9) | > — | — 14| > — 21 > — |30|.
Ответ: |-16| > | -(-9) | > — | — 14| > — 21 > — |30|
Цели урока
Познакомить школьников с таким математическим понятием, как модуль числа;
Научить школьников навыкам нахождения модулей чисел;
Закрепить изученный материал с помощью выполнения различных заданий;
Задачи
Закрепить знания детей о модуле числа;
С помощью решения тестовых заданий проверить, как усвоили ученики изученный материал;
Продолжать прививать интерес к урокам математики;
Воспитывать у школьников логическое мышление, любознательность и усидчивость.
План урока
1. Общие понятия и определение модуля числа.
2. Геометрический смысл модуля.
3. Модуль числа его свойства.
4. Решение уравнений и неравенств, которые содержат модуль числа.
5. Историческая справка о термине «модуль числа».
6. Задание на закрепление знаний пройденной темы.
7. Домашнее задание.
Общие понятия о модуле числа
Модулем числа принято называть само число, если оно не имеет отрицательного значения, или это же число отрицательное, но с противоположным знаком.
То есть, модулем неотрицательного действительного числа a является само это число:
А, модулем отрицательного действительного числа х будет противоположное число:
В записи это будет выглядеть так:
Для более доступного понимания приведем пример. Так, например, модулем числа 3 будет 3, и также модулем числа -3, является 3.
Из этого следует, что под модулем числа подразумевается абсолютная величина, то есть, ее абсолютное значение, но без учета его знака. Если говорить еще более просто, то необходимо от числа отбросить знак.
Обозначаться и выглядеть модуль числа может так: |3|, |х|, |а| и т.д.
Так, например, модуль числа 3 обозначается |3|.
Также, следует помнить, что модуль числа никогда не бывает отрицательным: |a|≥ 0.
|5| = 5, |-6| = 6, |-12,45| = 12,45 и т.д.
Геометрический смысл модуля
Модулем числа называют расстояние, которое измеряется в единичных отрезках от начала координат до точки. В этом определении раскрывается модуль с геометрической точки зрения.
Возьмем координатную прямую и обозначим на ней две точки. Пускай этим точкам будут соответствовать такие числа, как −4 и 2.
Теперь давайте обратим внимание на данный рисунок. Мы видим, что обозначенная на координатной прямой точка А соответствует числу -4 и если вы внимательно посмотрите, то увидите, что эта точка находится от точки отсчета 0 на расстоянии 4 единичных отрезков. Отсюда следует, что длина отрезка OA равняется четырем единицам. В этом случае, длина отрезка ОА, то есть число 4 будет модулем числа -4.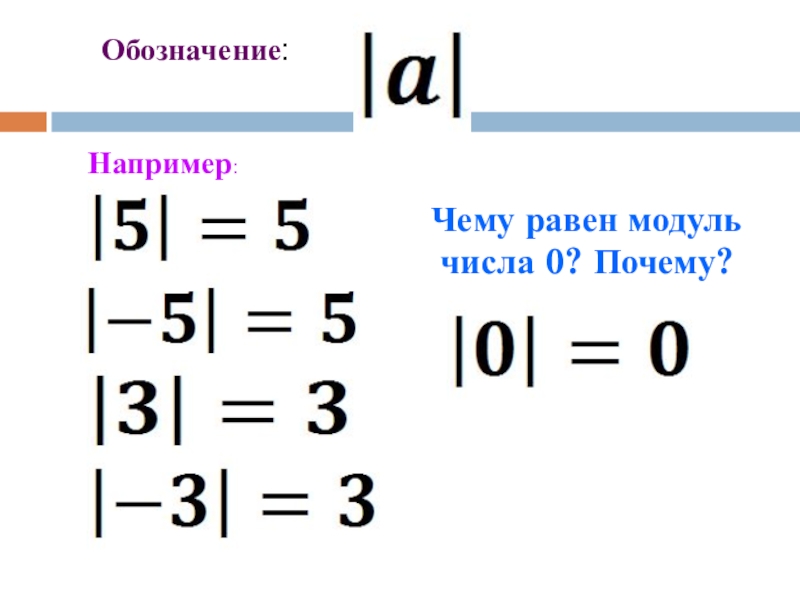
Обозначается и записывается в данном случае модуль числа таким образом: |−4| = 4.
Теперь возьмем, и на координатной прямой обозначим точку В.
Эта точка В будет соответствовать числу +2, и находится она, как мы видим, от начала отсчета на расстоянии двух единичных отрезков. Из этого следует, что длина отрезка OB равняется двум единицам. В этом случае число 2 будет модулем числа +2.
В записи это будет выглядеть так: |+2| = 2 или |2| = 2.
А теперь подведем итог. Если мы с вами возьмем какое-то неизвестное число а и обозначим его на координатной прямой точкой А, то в этом случае расстояние от точки A до начала отсчёта, то есть длинна отрезка ОА, как раз и является модулем числа «a».
В записи это будет выглядеть так: |a| = OA.
Модуль числа его свойства
А теперь давайте попробуем выделить свойства модуля, рассмотреть всевозможные случаи и записать их с помощью буквенных выражений:
Во-первых, модулем числа является число неотрицательное, а значит модуль положительного числа, равен самому числу: |a| = a, если a > 0;
Во-вторых, модули, которые состоят из противоположных чисел, равны: |а| = |–а|. То есть это свойство говорит нам о том, что противоположные числа всегда имеют равные модули, та как на координатной прямой, хотя они и имеют противоположные числа, но они находятся на одинаковом расстоянии от точки отсчета. Из этого следует, что и модули этих противоположных чисел равны.
То есть это свойство говорит нам о том, что противоположные числа всегда имеют равные модули, та как на координатной прямой, хотя они и имеют противоположные числа, но они находятся на одинаковом расстоянии от точки отсчета. Из этого следует, что и модули этих противоположных чисел равны.
В-третьих, модуль нуля равняется нулю в том случае, если это число является нулем: |0| = 0, если a = 0. Здесь можно с уверенностью сказать, что модулем нуля является ноль по определению, так как ему соответствует начало отсчета координатной прямой.
Четвертым свойством модуля является то, что модуль произведения двух чисел равен произведению модулей этих чисел. Теперь подробнее рассмотрим, что это значит. Если следовать определению, то мы с вами знаем, что модуль произведения чисел a и b будет равен a b, или −(a b), если, а в ≥ 0, или же – (а в), если, а в больше 0. В записи это будет выглядеть так: |а b| = |а| |b|.
Пятым свойством является то, что модуль частного от деления чисел равен отношению модулей этих чисел: |а: b| = |а| : |b|.
И следующие свойства модуля числа:
Решение уравнений и неравенств, которые содержат модуль числа
Приступив к решению задач, которые имеют модуль числа, следует помнить, что чтобы решить такое задание, необходимо раскрыть знак модуля, используя знания свойств, которым эта задача соответствует.
Задание 1
Так, к примеру, если под знаком модуля стоит выражение, которое зависит от переменной, то раскрывать модуль следует в соответствии с определением:
Конечно же, при решении задач бывают случаи, когда модуль раскрывается однозначно. Если, например, взять
, здесь мы видим, что такое выражение под знаком модуля неотрицательно при любых значениях х и у.
Или, же для примера берем
, мы видим, что это выражение под модулем не положительно при любых значениях z.
Задание 2
Перед вами изображена координатная прямая. На этой прямой необходимо отметить числа, модуль которых будет равен 2.
Решение
В первую очередь, мы должны начертить координатную прямую. Вам уже известно, что для этого, вначале на прямой необходимо выбрать начало отсчета, направление и единичный отрезок. Далее, нам нужно от начала отсчета поставить точки, которые равны расстоянию двух единичных отрезков.
Как видим, таких точек на координатной прямой две, одна из которых соответствует числу -2, а другая числу 2.
Историческая справка о модуле числа
Термин «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера». Ввел в обращение этот термин английский математик Роджер Котес. А вот знак модуля был введен благодаря немецкому математику Карлу Вейерштрассу. При написании модуль обозначается с помощью такого символа: | |.
Вопросы на закрепление знаний материала
На сегодняшнем уроке мы с вами познакомились с таким понятием, как модуль числа, а теперь давайте проверим, как вы усвоили эту тему, ответив на поставленные вопросы:
1. Как называется число, которое противоположно положительному числу?
Как называется число, которое противоположно положительному числу?
2. Какое название носит число, которое противоположно отрицательному числу?
3. Назовите число, которое является противоположным нулю. Существует ли такое число?
4. Назовите то число, которое не может являться модулем числа.
5. Дайте определение модулю числа.
Домашнее задание
1. Перед вами изображены числа, которые вам нужно расположить в порядке убывания модулей. Если вы правильно выполните задание, то узнаете фамилию человека, который впервые ввел в математику термин «модуль».
2. Начертите координатную прямую и найдите расстояние от М(-5) и К (8) до начала отсчета.
Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а обозначается как |a| .
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.
Графически это можно выразить следующим образом: |a| = OA.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
Особенности решения уравнений с модулем
Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5 , если, А больше или равняется нулю.
5-А , если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
Модуль числа a — это расстояние от начала координат до точки А (a ).
Чтобы понять это определение, подставим вместо переменной a любое число, например 3 и попробуем снова прочитать его:
Модуль числа 3 — это расстояние от начала координат до точки А (3 ).
Становится ясно, что модуль это ни что иное, как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3 )
Расстояние от начала координат до точки А(3 ) равно 3 (трём единицам или трём шагам).
Модуль числа обозначает двумя вертикальными линиями, например:
Модуль числа 3 обозначается так: |3|
Модуль числа 4 обозначается так: |4|
Модуль числа 5 обозначается так: |5|
Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:
Так и записываем:
Читается как: «Модуль числа три равен три»
Теперь попробуем найти модуль числа -3. Опять же возвращаемся к определению и подставляем в него число -3. Только вместо точки A используем новую точку B . Точку A мы уже использовали в первом примере.
Модулем числа —3 называют расстояние от начала координат до точки B (—3 ).
Расстояние от одного пункта до другого не может быть отрицательным. Поэтому и модуль любого отрицательного числа, будучи являясь расстоянием тоже не будет отрицательным. Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:
Читается как: «Модуль числа минус три равен три»
Модуль числа 0 равен 0, та как точка с координатой 0 совпадает с началом координат, т.е. расстояние от начала координат до точки O(0) равно нулю:
«Модуль нуля равен нулю»
Делаем выводы:
- Модуль числа не может быть отрицательным;
- Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу;
- Противоположные числа имеют равные модули.

Противоположные числа
Числа, отличающиеся только знаками называют противоположными . Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числа −2 знак минуса, а у 2 знак плюса, но мы его не видим, потому что плюс, как мы говорили ранее, по традиции не пишут.
Еще примеры противоположных чисел:
Противоположные числа имеют равные модули. Например, найдём модули для −2 и 2
На рисунке видно, что расстояние от начала координат до точек A(−2) и B(2) одинаково равно двум шагам.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Чему равен модуль х 2. Как решать уравнения с модулем: основные правила
Инструкция
Если модуль представлен в виде непрерывной функции, то значение ее аргумента может быть как положительным, так и отрицательным: |х| = х, х ≥ 0; |х| = — х, х
Модуль нулю, а модуль любого положительного числа – ему . Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных равны: |-х| = |х| = х.
Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Возведенный в степень аргумент одновременно находится под знаком корня того же порядка – он решается при помощи : √a² = |a| = ±a.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| >
Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| >
Модуль нуля равен нулю, а модуль любого положительного числа – ему самому. Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных чисел равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя целое положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Отрицательным модуль быть не может, поэтому любое отрицательное число преобразуется в положительное: |-x| = x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается изменение порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| > 0, то в итоге получится 2 * |4-b| = 2 *(4 — b). В качестве неизвестного элемента также может быть задано конкретное число, которое следует принимать во внимание, т.к. оно будет влиять на знак выражения.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
А вычисляется в соответствии с такими правилами:
Для краткости записи применяют |а| . Так, |10| = 10; — 1 / 3 = | 1 / 3 |; | -100| =100 и т. д.
Всякой величине х соответствует достаточно точная величина |х |. И значит тождество у = |х | устанавливает у как некоторую функцию аргумента х .
График этой функции представлен ниже.
Для x > 0 |x | = x , а для x x
|= —x ; в связи с этим линия у = |x | при x > 0 совмещена с прямой у =х (биссектриса первого координатного угла), а при х у = -х
(биссектриса второго координатного угла).
Отдельные уравнения включают в себя неизвестные под знаком модуля .
Произвольные примеры таких уравнений — |х — 1| = 2, |6 — 2х | =3х + 1 и т. д.
Решение уравнений содержащих неизвестную под знаком модуля базируется на том, что если абсолютная величина неизвестного числа х равняется положительному числу а, то само это число х равняется или а, или -а.
Например :, если |х | = 10, то или х =10, или х = -10.
Рассмотрим решение отдельных уравнений .
Проанализируем решение уравнения |х — 1| = 2.
Раскроем модуль тогда разность х — 1 может равняться или + 2, или — 2. Если х — 1 = 2, то х = 3; если же х — 1 = — 2, то х = — 1. Делаем подставновку и получаем, что оба эти значения удовлетворяют уравнению.
Ответ. Указанное уравнение имеет два корня: x 1 = 3, x 2 = — 1.
Проанализируем решение уравнения | 6 — 2х | = 3х + 1.
После раскрытия модуля получаем: или 6 — 2х = 3х + 1, или 6 — 2х = — (3х + 1).
В первом случае х = 1, а во втором х = — 7.
Проверка. При х = 1 |6 — 2х | = |4| = 4, 3x + 1 = 4; от суда следует, х = 1 — корен ь данного уравнения .
При x = — 7 |6 — 2x | = |20| = 20, 3x + 1= — 20; так как 20 ≠ -20, то х = — 7 не является корнем данного уравнения.
Ответ. У уравнения единственный корень: х = 1.
Уравнения такого типа можно решать и графически .
Так решим, например , графически уравнение |х- 1| = 2.
Первоначально выполним построение графика функции у = |x — 1|. Первым начертим график функции у =х- 1:
Ту часть этого графика , которая расположена выше оси х менять не будем. Для нее х — 1 > 0 и потому |х -1|=х -1.
Часть графика, которая расположена под осью х , изобразим симметрично относительно этой оси. Поскольку для этой части х — 1 х — 1|= — (х — 1). Образовавшаяся в результате линия (сплошная линия) и будет графиком функции у = |х —1|.
Эта линия пересечется с прямой у = 2 в двух точках: M 1 с абсциссой -1 и М 2 с абсциссой 3. И, соответственно, у уравнения |х — 1| =2 будет два корня: х 1 = — 1, х 2 = 3.
Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?
На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
Но для начала вспомним определение модуля . Итак, модулем числа a называется само это число, если a неотрицательно и -a , если число a меньше нуля. Записать это можно так:
|a| = a, если a ≥ 0 и |a| = -a, если a
Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.
Теперь перейдем непосредственно к решению уравнений.
1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.
Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:
{±c, если с > 0
Если |x| = c, то x = {0, если с = 0
{нет корней, если с
1) |x| = 5, т.к. 5 > 0, то x = ±5;
2) |x| = -5, т.к. -5
3) |x| = 0, то x = 0.
2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b
1) |x + 2| = 4, т.к. 4 > 0, то
x + 2 = 4 или x + 2 = -4
2) |x 2 – 5| = 11, т.к. 11 > 0, то
x 2 – 5 = 11 или x 2 – 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 нет корней
3) |x 2 – 5x| = -8 , т. к. -8
к. -8
3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:
f(x) = g(x) или f(x) = -g(x) .
1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.
1. О.Д.З. 5x – 10 ≥ 0
2. Решение:
2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)
3. Объединяем О.Д.З. и решение, получаем:
Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.
Ответ: x = 3
2) |x – 1| = 1 – x 2 .
1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:
(1 – x)(1 + x) ≥ 0
2. Решение:
x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)
x 2 + x – 2 = 0 x 2 – x = 0
x = -2 или x = 1 x = 0 или x = 1
3. Объединяем решение и О.Д.З.:
Подходят только корни x = 1 и x = 0.
Ответ: x = 0, x = 1.
4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).
1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:
x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5
x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0
x = 3 или x = 4 x = 2 или x = 1
Ответ: x = 1, x = 2, x = 3, x = 4.
5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:
|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:
t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:
|x| = 1 или |x| = 5
x = ±1 x = ± 5
Ответ: x = -5, x = -1, x = 1, x = 5.
Рассмотрим еще один пример:
x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому
По свойству модуля x 2 = |x| 2 , поэтому
|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:
t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:
|x| = -2 или |x| = 1
Нет корней x = ± 1
Ответ: x = -1, x = 1.
6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.
1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:
3 – |x| = 4 или 3 – |x| = -4.
Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.
Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1
Ответ x = -7, x = 7.
2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:
3 + |x + 1| = 5 или 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 или x + 1 = -2.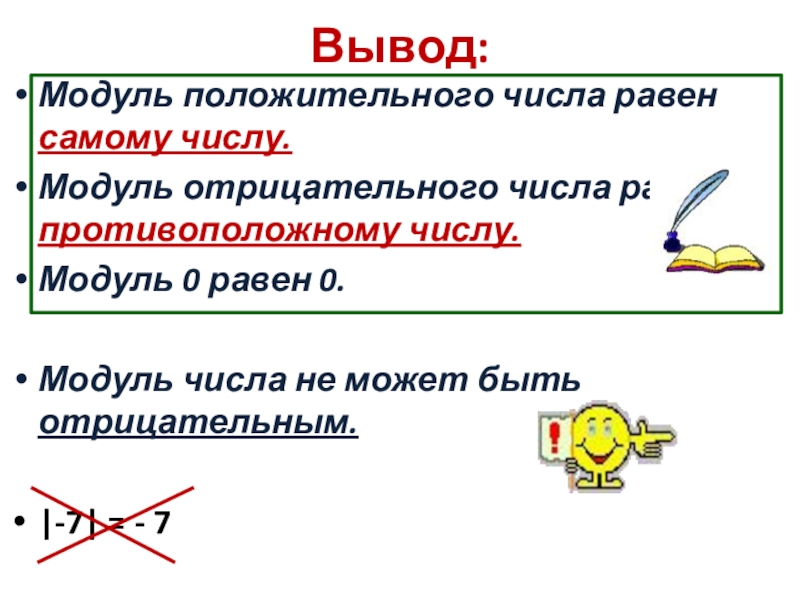 Нет корней.
Нет корней.
Ответ: x = -3, x = 1.
Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам. Заработай деньги с помощью своих знаний на https://teachs.ru !
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.
Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
Модуль комплексного числа
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi , поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi .
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a , потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x|
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2 .
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2 .
Ответ: 2 и −2 .
Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0 . Получено: x = –2 .
Это означает, что –2 – поворотная точка.
Разделим интервал на 2 части:
- для x + 2 ≥ 0
[−1; + ∞).
- для х + 2
Общим ответом для этих двух неравенств является интервал (−∞; –3].
Окончательное решение – объединение ответов отдельных частей:
x ∈ (–∞; –3] ∪ [–1; + ∞).
Ответ: x ∈ (–∞; –3] ∪ [–1; + ∞) .
Уравнения вида |x| = |y|
Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
Ответ: x 1 = 3; x 2 = − 1.
Пример 2 (алгебра 8 класс). Решить неравенство:
Решение:
Уравнения вида |x| = y
Пример 1 (алгебра 10 класс). Найти x:
Решение:
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке.
Ответ: x = 0 .
Модуль суммы
Модуль разности
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.
Пример 1.
Пример 2.
Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
То есть,
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Известно свойство:
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение : из рисунка видно, что график симметричен относительно оси Y.
Пример 2 . Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное.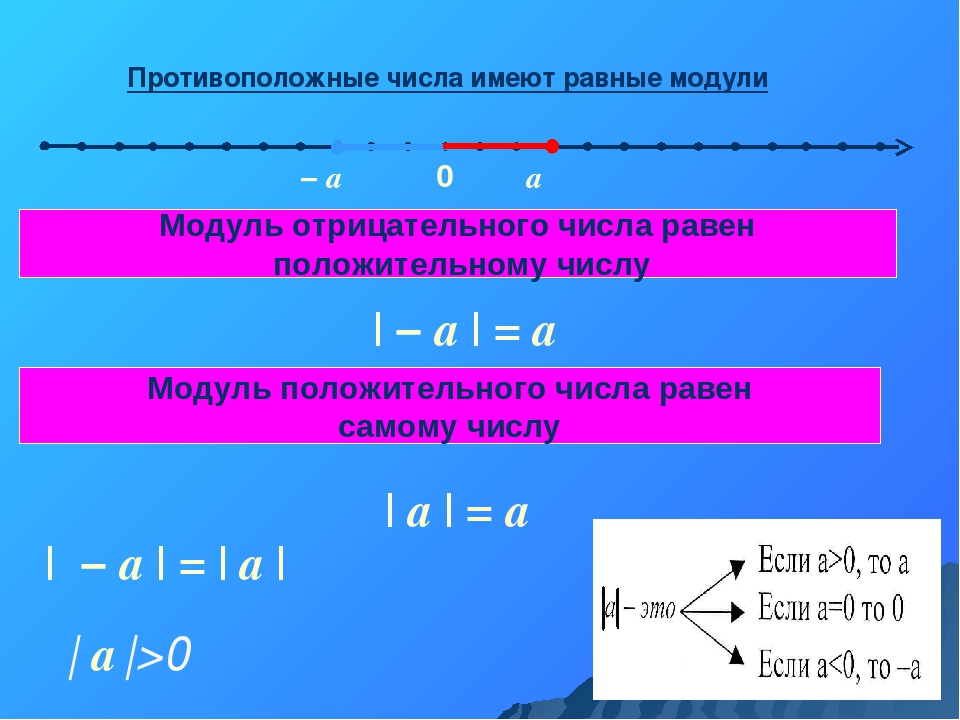 Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)) .
Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)) .
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
- Приравнять каждое выражение к нулю.
- Найти значения переменных.
- Нанести на числовую прямую точки, полученные в пункте 2.
- Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно.
 Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка). - Решить неравенства с полученными знаками.
Пример 1 . Решить методом интервалов.
Решение:
В Омской области открыли вторую крупную солнечную электростанцию
https://ria.ru/20211210/elektrostantsiya-1763102692.html
В Омской области открыли вторую крупную солнечную электростанцию
В Омской области открыли вторую крупную солнечную электростанцию — РИА Новости, 10.12.2021
В Омской области открыли вторую крупную солнечную электростанцию
Пуск второго крупного объекта солнечной генерации в Омской области – солнечной электростанции группы компаний «Хевел» состоялся в пятницу в Русско-Полянском… РИА Новости, 10.12.2021
2021-12-10T12:51
2021-12-10T12:51
2021-12-10T12:51
омская область
экономика
нововаршавский район
омская область
александр бурков
газпром нефть
министерство энергетики рф (минэнерго россии)
хевел
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21. img.ria.ru/images/106938/53/1069385386_0:146:2000:1271_1920x0_80_0_0_c5d7dd7f945d23b09542db47f0cb7501.jpg
img.ria.ru/images/106938/53/1069385386_0:146:2000:1271_1920x0_80_0_0_c5d7dd7f945d23b09542db47f0cb7501.jpg
ОМСК, 10 дек – РИА Новости. Пуск второго крупного объекта солнечной генерации в Омской области – солнечной электростанции группы компаний «Хевел» состоялся в пятницу в Русско-Полянском районе, сообщает областное правительство.В церемонии открытия Русско-Полянской солнечной электростанции мощностью 30 МВт приняли участие министр энергетики РФ Николай Шульгинов и губернатор Омской области Александр Бурков. Станция состоит из 84 тысяч солнечных модулей и занимает площадь чуть более 80 гектаров. Строительные работы на площадке начались в июне 2021 года, а с 1 декабря СЭС вышла на оптовый рынок электроэнергии и мощности. Проект реализован при поддержке правительства Омской области.»Электростанция уже начала выполнять свои обязательства по поставке мощности электроэнергии на оптовый рынок. Ожидаемая выработка электростанции составляет 35,5 миллиона киловатт-часов в год, что дает снижение выбросов CO2 — эквивалента около 12 тысяч тонн. На станции применены современные технические решения: оборудование электростанции интегрировано в единую энергосистему, выполняет обязательства по участию в первичном регулировании частоты, в урегулировании активной реактивной мощности», — сказал глава Минэнерго РФ.В свою очередь, Бурков отметил, что Омская область входит в десятку российских регионов с самым большим количеством солнечных дней (более 300 в году), чем нужно пользоваться.»Сегодня наша область включилась в процесс развития зелёной энергетики, как и многие цивилизованные страны, которые давно уже ушли далеко в этом направлении. Два года назад с компанией «Хевел» была запущена экспериментальная станция небольшой мощности на территории нефтезавода вместе с компанией «Газпром нефть». В прошлом году была открыта солнечная станция в Нововаршавском районе мощностью в 30 МВт. И вот сегодня мы запускаем уже третий объект солнечной электростанции в Русско-Полянском районе тоже мощностью 30 МВт», — сказал глава региона.Бурков отметил, что среднегодовой объем произведенной на электростанции электроэнергии будет равен ее годовому потреблению таких крупных предприятий области, как производственное объединение «Полет» и «Омсктехуглерод», поэтому новая станция будет иметь большое значение.
На станции применены современные технические решения: оборудование электростанции интегрировано в единую энергосистему, выполняет обязательства по участию в первичном регулировании частоты, в урегулировании активной реактивной мощности», — сказал глава Минэнерго РФ.В свою очередь, Бурков отметил, что Омская область входит в десятку российских регионов с самым большим количеством солнечных дней (более 300 в году), чем нужно пользоваться.»Сегодня наша область включилась в процесс развития зелёной энергетики, как и многие цивилизованные страны, которые давно уже ушли далеко в этом направлении. Два года назад с компанией «Хевел» была запущена экспериментальная станция небольшой мощности на территории нефтезавода вместе с компанией «Газпром нефть». В прошлом году была открыта солнечная станция в Нововаршавском районе мощностью в 30 МВт. И вот сегодня мы запускаем уже третий объект солнечной электростанции в Русско-Полянском районе тоже мощностью 30 МВт», — сказал глава региона.Бурков отметил, что среднегодовой объем произведенной на электростанции электроэнергии будет равен ее годовому потреблению таких крупных предприятий области, как производственное объединение «Полет» и «Омсктехуглерод», поэтому новая станция будет иметь большое значение. Также, по его словам, очень важны вопросы экологии, дополнительных налоговых отчислений и создания новых рабочих мест для омичей.
Также, по его словам, очень важны вопросы экологии, дополнительных налоговых отчислений и создания новых рабочих мест для омичей.
https://ria.ru/20211209/zhivotnovody-1762870154.html
https://ria.ru/20211209/omsk-1762866318.html
нововаршавский район
омская область
россия
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2021
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/106938/53/1069385386_7:0:1786:1334_1920x0_80_0_0_68de116c43ac96d1fd6ebbbf3c7ba011. jpg
jpgРИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
экономика, нововаршавский район, омская область, александр бурков, газпром нефть, министерство энергетики рф (минэнерго россии), хевел, николай шульгинов, россия
В Омской области открыли вторую крупную солнечную электростанцию
Оператор по модулю — Что такое натуральные числа
В модульной арифметике мы работаем только с целыми числами, а используемые операции — это сложение, вычитание, умножение и деление. Разница между евклидовой (регулярной) и гауссовой (по модулю) арифметикой, евклидова работает с бесконечным набором целых чисел, тогда как гауссовский работает только с конечный набор целых чисел.
В модульной арифметике вместо того, чтобы продолжать длинную прямую линию, числа идут по кругу и оборачиваются вокруг определенного значения. Это значение называется модулем . Модуль также можно определить как длину круговой числовой линии в модульной арифметике.
Лучший способ описать модульную математику — использовать часы.
12-часовые часы работают с бесконечным набором целых чисел, то есть от 1 до 12. Эти числа идут по кругу и оборачиваются вокруг 12. Это 12 модуль. После 12 часов он снова начинается с 1, поэтому, когда сейчас 13 часов, на самом деле это 1 час.
Математически мы представляем это как:
- 13≅1 мод 12
13≅1 мод 12
(Когда вы делите 13 на 12, остаток равен 1)
Это читается как,
13 соответствует 1 модулю (или модулю) 12
- 40≅2 мод 12
(Когда вы делите 40 на 12, остаток равен 2)
Это читается как,
40 сравнимо с 2 по модулю (или по модулю) 12
Оператор по модулю
«Операция по модулю» находит остаток от деления одного числа на другое (иногда называемый модулем).
Оператор по модулю (сокращенно мод) — это остаток от деления положительного числа на другое положительное число. Когда мы делим два положительных числа, уравнение будет выглядеть так:
`A / B = X` текст (остаток)` Y`
Где,
A — дивиденд
B — делитель
X — частное
Y — остаток
Пример 1:
`9/2 = 4« текст (остаток) `1`
` 9` mod `2` =` 1`, потому что `9` деленное на` 2` оставляет частное `4` и остаток от `1`
Пример 2:
`6/3 = 2` текст (остаток)` 0`
`6` mod` 3 = 0 `потому что` 6` деленное на `3` оставляет частное` 2` и остаток `0`
Задача 1:
`2`Пояснение:
Когда `8` делится на` 3`, остается остаток `2`
`8/3 = 2` текст (остаток)` 2`, где,
Первый «2» — это частное
Вторая «2» — это остаток или мод.
Задача 2:
`0`Пояснение:
Когда `9` делится на` 3`, остается остаток `0`
`9/3 = 3« текст (остаток) `0`, где,
`3` — это частное
`0` — это остаток или мод
Оператор по модулю Python — что означает символ% в Python? (Решено)
Когда вы видите символ%, вы можете подумать «процент». Но в Python, как и в большинстве других языков программирования, это означает нечто иное.
Но в Python, как и в большинстве других языков программирования, это означает нечто иное.
Символ % в Python называется оператором по модулю. Он возвращает остаток от деления левого операнда на правый операнд. Он используется для получения остатка от задачи деления.
Оператор по модулю считается арифметической операцией вместе с + , - , /, * , ** , // .
Основной синтаксис:
a% b В предыдущем примере a делится на b , и возвращается остаток.Давайте посмотрим на пример с числами.
7% 2 Результатом предыдущего примера является единица . Два переходит в семь трижды, и остается , один .
На диаграмме ниже показано визуальное представление 7/2 и 7% 2 («R» означает «остаток»). Единственный логотип справа (с указывающей на него зеленой стрелкой) — это остаток от проблемы разделения. Это также ответ на
Это также ответ на 7% 2 .
Вот еще один пример:
3% 4 Это даст три . Четыре не входит в тройку никаких раз, поэтому исходный три все еще остается. На схеме ниже показано, что происходит. Помните, что оператор по модулю возвращает остаток после выполнения деления. Остальное — три.
Пример использования оператора по модулю
Одним из распространенных способов использования оператора по модулю является поиск четных или нечетных чисел.В приведенном ниже коде оператор по модулю используется для печати всех нечетных чисел от 0 до 10.
для числа в диапазоне (1, 10):
если (число% 2! = 0):
print (число) Результат:
1
3
5
7
9 Калькулятор по модулюФорматы
Вы можете видеть операции по модулю над числами, выраженными одним из следующих
- a по модулю n
- a mod n (сокращенная версия)
Примеры математических задач
17 по модулю 3
- 17 — 3 = 14
- 14–3 = 11
- 11–3 = 8
- 8–3 = 5
- 5–3 = 2
20 мод 5
- 20-5 = 15
- 15 — 5 = 10
- 10-5 = 5
- 5–5 = 0
Modulo: определение, как это работает и использование в реальной жизни
— Руководство Автор: Корин Б. Арены , опубликовано 24 октября 2019 г.
Арены , опубликовано 24 октября 2019 г.
Большинство людей не слышали о модульной арифметике или модификациях вне математических классов.
Однако, если вы когда-либо оценивали обед на 10 человек и обнаруживали, что осталось много еды, вы на самом деле имеете дело с проблемой модификации. Люди постоянно используют модульную арифметику, особенно когда дело касается остатков, времени и календарных графиков.
В этом разделе вы узнаете о модуле, его основных операциях и использовании в реальной жизни.
Что такое Modulo?
Модульная арифметика, иногда называемая арифметикой часов, является расчет, который включает число, которое сбрасывается до нуля каждый раз, когда целое число больше 1, которое является модом, достигнуто. Примером этого является 24-часовые цифровые часы, которые сбрасываются на 0 в полночь.
В математике, модуль — это остаток или число, оставшееся после деления числа на другое значение. Modulo также называют «мод. ’
’
Стандартный формат для мода:
a mod n
Где a — значение, которое делится на n .
Например, вы вычисляете 15 по модулю 4. Когда вы делите 15 на 4, получается остаток.
15/4 = 3,75
Вместо десятичной формы (0,75), когда вы используете функцию mod в калькуляторе, остаток представляет собой целое число. В этом примере 15/4 = , остаток 3 , что также равно 15 = (4 * 3) + 3. Вот как рассчитать это вручную:
15 мод 4
15-4 = 11
11-4 = 7
7-4 = 3
Расчетный мод с отрицательным числом
Можно предположить, что функция mod генерирует те же значения, что и положительные числа, когда одно число отрицательное. На самом деле это не так.
Например, если у вас 340 mod 60 , остаток равен 40 .
Но если у вас -340 mod 60 , остаток составит 20 .
Почему это происходит? Mathforum.org объясняет, что с положительным числом, например 340, вычитаемое кратное на меньше абсолютного значения , что дает 40.
340 мод 60
340 — 60 = 280
280 — 60 = 220
220 — 60 = 160
160 — 60 = 100
100 — 60 = 40
Но с -340 мы вычитаем число с большим абсолютным значением , поэтому функция mod генерирует положительное значение. Результирующий остаток также меньше по сравнению с положительными значениями обоих чисел.
Вот как решить mod с отрицательным числом:
a mod n is a / n = r (остаток)
Следовательно, a mod n = a — r * n
Обратите внимание: Когда мы вводим a / b в калькулятор, мы берем десятичную часть сгенерированного значения и округляем ее до следующего целого числа . Давайте сделаем это на примере ниже:
-340 mod 60
-340/60 = 5. 6, когда мы берем десятичную часть, она становится целым числом -6
6, когда мы берем десятичную часть, она становится целым числом -6
= -340 — (- 6) * 60
= -340 — (- 360)
= 20
Для облегчения визуализации числовая линия ниже показывает разницу в стоимости.
Кто создал модульную арифметику?
Согласно Британнике, концепция модульной арифметики использовалась древними цивилизациями, такими как индийцы и китайцы. Примером может служить китайская книга «Математическое руководство Мастера Саня» , которая датируется 300 годом нашей эры.
Кроме того, модульная арифметика использовалась для решения астрономических и сезонных расчетов, которые были проблемами, связанными с естественными и искусственными циклами.
Карл Фридрих Гаусс и теория чисел
В западной математике немецкий математик и физик Карл Фридрих Гаусс
сделал первое систематическое изучение модульной арифметики.Гаусс рассматривается как один
из самых влиятельных фигур в современной математике.
В 1801 году, когда ему было чуть за 20, он опубликовал Disquisitiones Arithmeticae , которые заложили основу современной теории чисел и представили первое доказательство закона квадратичной взаимности.
В теории чисел ученые анализируют свойства естественных числа, которые являются целыми числами, например -1, -2, 0, 1, 2 и т. д. Их цель — обнаружить неожиданные математические закономерности и взаимодействия между натуральными числами.
Britannica отмечает, что в модульной арифметике, где mod N , все числа (0, 1, 2,…, N — 1,) известны как остатки по модулю N . В остатки складываются путем нахождения арифметической суммы чисел, а мод вычитается из суммы как можно больше раз. Это уменьшает сумму до число M, , которое находится между 0 и N — 1.
В свою книгу Гаусс включил обозначение с символом ≡,
который читается как «соответствует.”Вместо обычного символа = три
сегменты горизонтальной линии означают равенство и определение.
Например, если мы сложим сумму 2, 4, 3 и 7, сумма будет равна 6 (mod 10). Это 16 центов (модификация 10). Это означает, что разделение 16 на 10 дает остаток 6. Аналогично, 16-10 = 6.
Другой пример, 13 ≡ 1 (мод. 12). Это означает, что 13, разделенное на 12, дает остаток 1. Точно так же 13 — 12 = 1.
Каково реальное использование мода?
Для практических применений мод особенно полезен для работы с со временем.
Поскольку в сутках 24 часа, имеет смысл обратиться к время в 24-часовом формате. Это принцип, лежащий в основе системы военного времени, начиная с в полночь с 00:00 и окончание часа с 23:00 до 23:00.
Вместо 9 часов вечера они говорят 21:00. В военные используют это для координации с базами и другим персоналом, находящимся в разные часовые пояса. Более того, все пилоты (коммерческие или иные) используют 24-часовой часы, чтобы избежать путаницы при перемещении между часовыми поясами.
Чтобы установить стандарт, пилоты и военные используют среднее время по Гринвичу (GMT), которое они также называют зулусским временем (Z). Например, когда пилоты сообщают, что самолет достигнет базы в 21:00 по Гринвичу, это означает, что он прибудет в 21:00 по Гринвичу.
Например, когда пилоты сообщают, что самолет достигнет базы в 21:00 по Гринвичу, это означает, что он прибудет в 21:00 по Гринвичу.
Как это связано с модулем? Для проживающих в одном часовом поясе важнее определять время, отделяя ночь от дня. Вот почему 12-часовое стандартное время используется по модулю.
Вместо 1600 часов мы просто говорим 4 часа.В 12-часовое стандартное время использует mod 12 , так что 1600 часов становится 4 часа.
Когда мы назначаем встречи, это обычно понимают люди значит 4 часа дня. Если не указано иное, встреча в 4 часа утра абсурдна, если вы не работаете по ночам и не проводите онлайн-встречи с клиентами из других часовых поясов.
Организация книг, банковская информация и ставки жилищного кредита
Мод пригодится для организации большой информации. Книги
отслеживается с использованием модульной арифметики для расчета контрольных сумм по международному стандарту
номера книг (ISBN). В 2007 году была введена 13-значная система счисления ISBN.
(который ранее был 10) был введен, чтобы помочь производителям идентифицировать большие
объем книг.
В 2007 году была введена 13-значная система счисления ISBN.
(который ранее был 10) был введен, чтобы помочь производителям идентифицировать большие
объем книг.
Тот же принцип также используется банками для выявления ошибок в международных номерах банковских счетов (IBAN) при отслеживании транзакций из других стран.
Когда дело касается жилищного кредита, используется мод для сброса расчетов на новый период. Например, ипотека с регулируемой ставкой 5/6 (ARM) периодически сбрасывает процентные ставки каждые 6 месяцев.Мод используется для соответствующей корректировки ставок.
Криптография и компьютерное искусство
Модульная арифметика имеет и другие приложения в области криптографии, искусства и графического дизайна.
На протяжении многих лет художники использовали математические формы на основе формул для создания рисунков. Сегодня та же концепция применяется к компьютерной графике, а также к скульптуре и современной живописи.
В криптографии, коды написаны для защиты секретных данных.Криптографы используют мод в Диффи-Хеллмана Обмен ключами при настройке SSL-соединений для шифрования веб-трафика.
Шифрование важно, потому что оно позволяет пользователям защитить информацию. Вот почему ваши личные электронные письма, номер кредитной карты и другие личные данные должны быть зашифрованы всякий раз, когда вы отправляете информацию через Интернет.
Итог
Mod — математическая функция, которая позволяет нам измерить остаток в сумме. Мы используем эту фундаментальную концепцию всякий раз, когда определяем время.
Концепция модульной арифметики использовалась древними Китайцы и индийцы веками. Но это было введено в западные математики немецким ученым Карлом Фридрихом Гауссом, который также разработал основы теории чисел.
Реальное использование мода включает в себя организацию ISBN и банковской информации, сброс ставок ARM, дизайн компьютерной графики и криптографию, которая помогает защитить личные данные.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающий экономические тенденции, их влияние на население, а также то, как помочь потребителям принимать более мудрые финансовые решения.Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма в Филиппинском университете, одном из ведущих учебных заведений в мире, и степень бакалавра коммуникационных искусств в колледже Мириам.
Функция MOD— формула, примеры, как использовать MOD
Что такое функция MOD?
Функция MOD относится к математическим функциям Excel и функциям тригонометрии ФункцииСписок наиболее важных функций Excel для финансовых аналитиков.Эта шпаргалка охватывает 100 функций, которые критически важно знать аналитику Excel. Функция помогает найти остаток от деления числа (делимого) на другое число (делитель).
Как финансовый аналитик Описание работы финансового аналитика Описание работы финансового аналитика, приведенное ниже, дает типичный пример всех навыков, образования и опыта, необходимых для работы аналитиком в банке, учреждении или корпорации. Выполняйте финансовое прогнозирование, отчетность и отслеживание операционных показателей, анализируйте финансовые данные, создавайте финансовые модели, функция полезна, когда нам нужно обработать каждое n-е значение.Например, если наши данные состоят из нескольких столбцов чисел, мы можем использовать MOD для суммирования каждого столбца n.
Выполняйте финансовое прогнозирование, отчетность и отслеживание операционных показателей, анализируйте финансовые данные, создавайте финансовые модели, функция полезна, когда нам нужно обработать каждое n-е значение.Например, если наши данные состоят из нескольких столбцов чисел, мы можем использовать MOD для суммирования каждого столбца n.
Формула
= MOD (число, делитель)
Эта функция использует следующие аргументы:
- Число (обязательный аргумент) — это число, для которого мы хотим найти остаток .
- Делитель (обязательный аргумент) — это число, на которое мы хотим разделить число.
Как использовать функцию MOD в Excel?
Чтобы понять использование функции MOD, давайте рассмотрим несколько примеров:
Пример 1
Предположим, нам даны следующие данные :
В приведенных выше данных мы использовали следующая формула:
Результаты, которые мы получаем в Excel, показаны ниже:
Пример 2
Предположим, нам даны следующие данные:
Если мы хотим получить максимальное значение каждого n-го столбца, мы можем использовать формулу массива, основанную на функциях MAX, MOD и COLUMN.
Используемая формула:
Поскольку это формула массива, нам нужно ввести ее, используя Ctrl + Shift + Enter. В приведенной выше формуле мы использовали функции MOD и COLUMN, чтобы отфильтровать значения не в n-м столбцах, а затем запустить MAX для результата.
Мы получаем результат ниже:
Предположим, нам нужно найти функцию MIN, формула будет {= MIN (IF (MOD (COLUMN (B5: H5) -COLUMN (B5) +1) , I5) = 0, B5: H5))}.
Далее, если мы хотим получить СУММПРОИЗВ четных строк, мы можем использовать следующую формулу:
Мы получаем результат ниже:
Для нечетных строк формула будет иметь вид:
Результат будет ниже:
Несколько вещей, которые нужно запомнить
- # DIV / 0! ошибка — возникает, когда значение делителя равно нулю.
- Функция MOD вернет результат с тем же знаком, что и делитель.

Щелкните здесь, чтобы загрузить образец файла Excel
Дополнительные ресурсы
Спасибо за то, что прочитали руководство CFI по важным функциям Excel! Потратив время на изучение и освоение этих функций Excel, вы значительно ускорите свой финансовый анализ. Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:
- Функции Excel для FinanceExcel for Finance Это руководство по Excel для финансов научит 10 основных формул и функций, которые вы должны знать, чтобы стать отличным финансовым аналитиком в Excel.
- Расширенный курс по формулам Excel
- Расширенные формулы Excel, которые вы должны знать Расширенные формулы Excel, которые необходимо знатьЭти расширенные формулы Excel очень важно знать и выведут ваши навыки финансового анализа на новый уровень. Загрузите нашу бесплатную электронную книгу Excel!
- Ярлыки Excel для ПК и MacExcel Ярлыки ПК MacExcel Ярлыки — Список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета.
 Сочетания клавиш ускоряют ваши навыки моделирования и экономят время.Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.
Сочетания клавиш ускоряют ваши навыки моделирования и экономят время.Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.
Что такое 10 mod 10? (10 модуль 10)
Вам нужно знать, что означает 10 mod 10? Может нужно его посчитать? В этом небольшом руководстве мы покажем вам, как точно вычислить модификацию числа. Вы также можете увидеть, что это называется модулем или модулем.
Хотите быстро выучить или показать студентам, как вычислить 10 по модулю 10? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Итак, что такое модуль или модуль? Проще говоря, по модулю это математическая операция нахождения остатка при делении двух чисел вместе.Если вы спрашиваете «что такое 10 по модулю 10?» тогда вам действительно нужно знать, «каков остаток, когда я делю 10 на 10?».
Существует множество причин, по которым вы хотели бы использовать модуло, включая проверку того, является ли число четным или нечетным, подсчет чего-либо в течение определенного количества раз, и даже обычные часы в вашем доме будут использовать модуло для определения времени.
Давайте рассмотрим два метода вычисления 10 по модулю 10. Мы назовем их методом по модулю и методом модуля.
Примечание: первое число (10) называется Дивидендом, а второе число (10) — Делителем. Когда вы делите дивиденд на делитель, у вас остается ответ на коэффициент. Это Частное состоит из целой числовой части (называемой Целым) и части десятичных знаков, которая называется Дробной.
Метод по модулю
Сначала необходимо разделить дивиденд на делитель:
10 / 10 = 1,00
Затем мы берем целую часть частного (1) и умножаем ее на делитель (10):
1 х 10 = 10
И, наконец, мы берем ответ на втором этапе и вычитаем его из Дивиденда, чтобы получить ответ на 10 mod 10:
10–10 = 0
Как видите, ответ на 10 mod 10: 0 .
Метод модуля упругости
Метод модуля требует, чтобы мы сначала выяснили, какое наибольшее общее кратное делителя (10) равно или меньше дивиденда (10).
Мы видим, что кратные 10 равны 0, 10, 20, 30 и т. Д. Наивысшее кратное, которое меньше или равно 10, равно 10.
Д. Наивысшее кратное, которое меньше или равно 10, равно 10.
Итак, последний шаг в методе модуля здесь — вычесть наибольшее кратное делителя из дивиденда и ответить на вопрос «что такое 10 модуль 10?»:
10–10 = 0
Как мы видим, это тот же ответ, что и метод по модулю, и ответ равен 0 .
Надеюсь, вы поняли это краткое, но увлекательное путешествие по расчетам по модулю и модулю. Если вам хочется, возьмите ручку и бумагу и сделайте пару из них самостоятельно, чтобы проверить, действительно ли вы чему-нибудь научились.
Цитируйте, ссылайтесь или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 10 мод 10?».
 VisualFractions.com . По состоянию на 4 января 2022 г. http://visualfractions.com/calculator/modulo/what-is-10-mod-10/.
VisualFractions.com . По состоянию на 4 января 2022 г. http://visualfractions.com/calculator/modulo/what-is-10-mod-10/.«Что такое 10 мод 10?». VisualFractions.com , http://visualfractions.com/calculator/modulo/what-is-10-mod-10/. По состоянию на 4 января 2022 г.
Что такое 10 мод 10 ?. VisualFractions.com. Получено с http: // visualfractions.ru / калькулятор / по модулю / what-is-10-mod-10 /.
Калькулятор по модулю
Хотите решить больше задач по модулю? Введите свои числа ниже и нажмите рассчитать.
Следующее вычисление по модулю
Определениев кембриджском словаре английского языка
Кроме того, любые пароли, хешированные с использованием более слабого 256-битного модуля , будут взломаны примерно в 64 раза быстрее.Затем уравнения упругости контакта используются вместе с данными о разгрузке для определения модуля упругости и твердости материалов образца. Окончательное значение твердости и модуля упругости было получено путем усреднения 10 измерений.Один с меньшим модулем упругости , как ожидается, будет более прочным.
Были представлены частотные распределения модуля и аргумент этих состояний для конкретных значений параметра β.Чтобы выразить это точно, нам понадобится понятие модуля усилия.
Наконец, уникальное установившееся состояние является локально асимптотически устойчивым в заштрихованной области, где все модули собственных значений меньше 1.
Окончательное значение твердости и модуля упругости было получено путем усреднения 10 измерений.Один с меньшим модулем упругости , как ожидается, будет более прочным.
Были представлены частотные распределения модуля и аргумент этих состояний для конкретных значений параметра β.Чтобы выразить это точно, нам понадобится понятие модуля усилия.
Наконец, уникальное установившееся состояние является локально асимптотически устойчивым в заштрихованной области, где все модули собственных значений меньше 1. Настоящие данные подтверждают их вывод, за исключением того, что упругий модуль давления легочного ствола увеличивался с возрастом.
Упругое давление , модуль и% изменение радиуса легочного ствола составили 447 г / см и 4% соответственно.Максимум модулей обозначим ‖ ·.
Размеры и вес в зависимости от модуля сдвига находятся в уравнениях (10) и (11).В (а) модуль сдвига влияет на массовую плотность и предел текучести.
Парадигма, которой мы следуем при построении пространств модулей, вполне стандартна.
Настоящие данные подтверждают их вывод, за исключением того, что упругий модуль давления легочного ствола увеличивался с возрастом.
Упругое давление , модуль и% изменение радиуса легочного ствола составили 447 г / см и 4% соответственно.Максимум модулей обозначим ‖ ·.
Размеры и вес в зависимости от модуля сдвига находятся в уравнениях (10) и (11).В (а) модуль сдвига влияет на массовую плотность и предел текучести.
Парадигма, которой мы следуем при построении пространств модулей, вполне стандартна. Если система эргодична, то каждое собственное значение имеет модуль 1 и каждая собственная функция имеет постоянный модуль модуля µ — почти наверняка.
Первый состоит из аффинных преобразований, в которых ни одно из собственных значений линейной части не имеет модуля и единиц.
Если система эргодична, то каждое собственное значение имеет модуль 1 и каждая собственная функция имеет постоянный модуль модуля µ — почти наверняка.
Первый состоит из аффинных преобразований, в которых ни одно из собственных значений линейной части не имеет модуля и единиц.Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
Что такое модуль Юнга?
Каждый раз, когда вы едете по дороге и видите подвешенные электрические кабели, вы наблюдаете модуль Юнга в действии.Поднятые электрические провода имеют высокий модуль упругости и сохраняют свою форму даже при высоком давлении воздушной подвески и погодных условий.
Объяснение модуля Юнга
Модуль Юнга / Начальный модуль упругости — это начальная часть кривой напряжения / деформации и описывает способность проволоки, кабеля, пряжи или нити противостоять упругой деформации под нагрузкой. Он описывает склонность материала сохранять свою форму, даже когда он растягивается, растягивается, скручивается или сжимается.
Когда материал имеет высокий модуль упругости, даже при экстремальной деформации материал сопротивляется первоначальной силе и хорошо восстанавливается.Для материала с более низким модулем упругости деформация вызывает напряжение и создает риск разрушения, что показано на приведенной ниже кривой зависимости напряжения от деформации.
Отношение напряжения к деформации — это модуль упругости — жесткость, только напряжение, определяет прочность материала. Жесткость измеряет сопротивление упругой деформации, тогда как прочность измеряет, какое напряжение может выдержать материал до того, как произойдет остаточная деформация или разрушение.
Сила и деформация
Существует также проблема необратимой деформации.Пряжа с высоким модулем упругости может выдерживать большую начальную силу даже при многократных действиях давления и разрыва, не проявляя при этом необратимой деформации своей формы.
Пряжа с низким модулем упругости не такая упругая. Даже когда сила спадает, материал с низким модулем упругости с трудом восстанавливается и снова принимает форму.
Вернемся к нашему примеру с подвесными силовыми кабелями. Легко понять, почему пряжа с высоким модулем упругости предпочтительнее в проволочной и кабельной промышленности, где безопасность коммунальных служб и населения всегда вызывает беспокойство.
Высокомодульное армирование предотвращает провисание антенных кабелей из-за проскальзывания от длительной нагрузки, а также помогает противостоять ветреным условиям. При армировании с низким модулем упругости кабели не будут столь устойчивы к сильным ветрам и могут растянуться достаточно далеко, чтобы ударить автомобиль или человека поблизости или даже сломаться, что приведет к простою электросети, провисание в такой степени наверняка повлияет на характеристики передачи кабеля в вопрос как стекло треснуло бы.
Высокомодульные материалы
Высокий модуль упругости является предпочтительным для широкого спектра промышленных и коммерческих материалов с целью обеспечения упругости, безопасности и надежности.Из-за более желательных характеристик растяжения для конкретных применений варианты высокомодульного материала часто бывают более дорогими, чем стандартные материалы модуля упругости, и могут быть не столь легкодоступными.
Например, DuPont ™ Kevlar® Para-Aramid — это волокно, которое бывает как стандартного, так и высокомодульного. Хотя обе разновидности имеют схожий основной химический состав, точку плавления, температуру разложения, удельный вес и прочность на разрыв, тем не менее, более высокий модуль упругости наряду с более низким удлинением при разрыве являются желательными свойствами, основанными на конечном использовании.
Высокомодульная пряжа часто является лучшим выбором для любого приложения, несущего нагрузку или силового элемента, где будет постоянная нагрузка на конечный продукт.
Следующие преимущества делают желательным высокомодульный арамид :
- Устойчивость к погодным и экологическим воздействиям
- Сохранение прочности при статических и постоянных нагрузках
- Долговечность установок, особенно проводов и кабелей
- Прочность, в пять раз превышающая фунт стали на фунт
- Прочный, но не громоздкий
- Стабильно без разложения в широком диапазоне температур
- Низкая воспламеняемость и отсутствие температуры плавления
Термины, относящиеся к модулю Юнга
Вот краткое руководство по некоторым терминам, которые часто используются при обсуждении модуля Юнга.
Напряжение : Напряжение, создаваемое приложением продольной нагрузки.
Деформация : изменение длины из-за напряжения, действующего параллельно продольной оси материала.
Ползучесть : Неустранимое повреждение, связанное со временем, из-за длительного напряжения.
Усталость : Усталость — это ослабление материала из-за повторяющихся нагрузок.
Жесткость : Жесткий материал имеет высокий модуль Юнга.
Деформация : Это деформация, также известная как пластическая деформация, происходит под напряжением.
Предел упругости : это предел, за которым материал деформируется.
Податливость : Сразу за пределом упругости наблюдается остаточная деформация, известная как податливость.
Деформационное упрочнение : Помимо текучести, это максимальное или предельное напряжение.
Трещина : За пределами предельного напряжения находится точка разрушения или разрушения.
Модуль определенного текстильного волокна всегда можно измерить и обычно выражается в граммах-силе / денье (гс / ден).
Если вам нужна дополнительная информация и совет по выбору промышленной пряжи с правильным модулем упругости, Service Thread обрабатывает широкий спектр волокон и предлагает продукты с различными физическими свойствами.




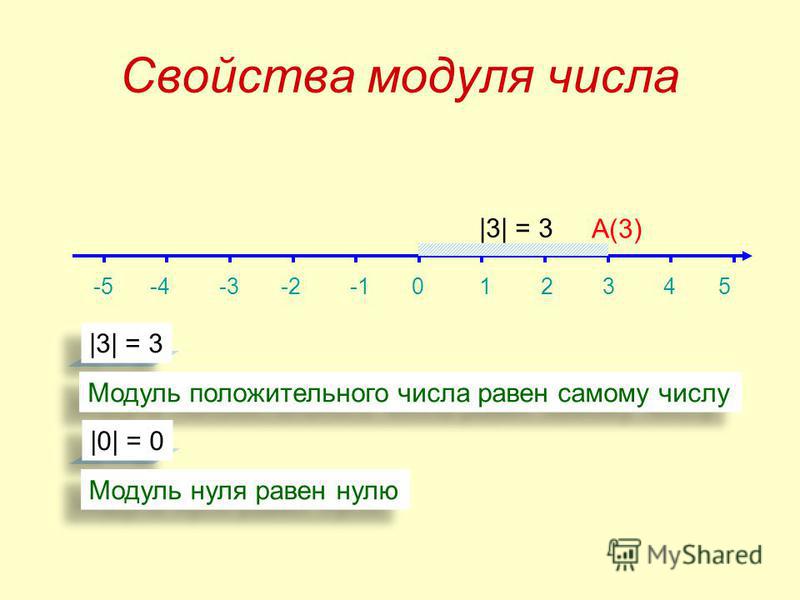 Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).

 Сочетания клавиш ускоряют ваши навыки моделирования и экономят время.Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.
Сочетания клавиш ускоряют ваши навыки моделирования и экономят время.Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения. VisualFractions.com . По состоянию на 4 января 2022 г. http://visualfractions.com/calculator/modulo/what-is-10-mod-10/.
VisualFractions.com . По состоянию на 4 января 2022 г. http://visualfractions.com/calculator/modulo/what-is-10-mod-10/.