Числа которые не на что не делятся – Как называется число которое делится без остатка только н себя и на единицу? — Детская игровая комната «Волшебный лес»

Posted on 19.05.202020.01.2020 by alexxlab

Содержание

Признаки делимости, или Что не поделили числа

Признак делимости – это своеобразный алгоритм, который позволяет быстро определить, делится ли заданное число на другое заданное число. Знание признаков делимости значительно сокращает время при счете, а также позволяет развивать память и логическое мышление при выполнении вычислений в уме.

Кроме того, существует ряд заданий, где нужно определить, делится ли какое-либо число без остатка на иное число. И при его решении вовсе не нужно производить деление (а числа в таких заданиях немаленькие), нужно всего лишь воспользоваться признаком делимости.

Самым простым признаком делимости является признак делимости на 2. Число делится на 2 только тогда, когда его последняя цифра делится на 2, иными словами, она должна быть четной.

Число 123456 делится на 2, т.к. 6 – последняя цифра – четная. Число 12345 на 2 не делится, т.к. на 2 не делится 5.

Признак делимости на 3: число делится на 3 тогда, когда суммы всех его цифр кратна 3.

Число 123456 делится на 3, т.к. 1 + 2 + 3 + 4 + 5 + 6 = 21, где 21 : 3 = 7.

Число 1234 не делится на 3, т.к 1 + 2 + 3 + 4 = 10, где 10 : 3 ≠.

Признак делимости на 4: число делится на 4 тогда, когда его две последние цифры делятся на 4.

Число 123456 делится на 4, т.к. 56 : 4 = 14.

Число 1234 не делится на 4, т.к 34 : 4 ≠.

А как быть с признаком делимости на 4, если число двузначное? Для двузначных чисел работает такое правило: если сумма половины единиц числа и десятков делится на 2, то само число делится на 4; в противном случает – число на 4 не делится.

Число 92 делится на 4, т.к. (2 : 2) + 9 = 1 + 9 = 10, где 10 : 2 = 5.

Одним из наиболее простых признаков является признак делимости на 5: число делится на 5, если его последняя цифра делится на пять.

Число 12345 делится на 5, т.к. 5 – последняя цифра и она делится на 5.

Число 1234 на 5 не делится, т.к. 4 : 5 ≠.

Признак делимости на 6: на 6 делится число, которое делится на делители 6, т.е. на 2 и на 3. Значит, нам нужно вспомнить признаки делимости на 2 и 3: последняя цифра числа должна быть четной, а сумма всех цифр должна делиться на 3.

Число 123456 делится на 6, т.к. его последняя цифра четная (6), а сумма цифр 1 + 2 + 3 + 4 + 5 + 6 = 21 делится на 3.

Число 12345 не делится на 6, т.к. не подходит по одному признаку: 5 – нечетное число (хотя сумма цифр делится на 3).

Признак делимости на 7: на 7 делится число, в котором результат вычитания удвоенной последней цифры этого числа без последней цифры делится на 7.

Число 364 мы сможем разделить на 7 без остатка, т.к. удвоенная последняя цифра – это 4 ∙ 2, т.е. 8; результат вычитания равен 36 – 8 = 28, где 28 : 7 = 4.

Признак делимости на 8: если три последних цифры числа делятся на 8, то тамо число делится на 8. Процесс определения делимости трехзначного числа на 8 более сложный: нужно к десяткам прибавить половину единиц и повторить то же самое с получившимся числом; если результат делится на 2, то он делится и на 8.

952 делится на 8, потому что:

1. 95 + 1 = 96

2. 9 + 3 = 12

3. 12 : 2 = 6.

Признак делимости на 9: на 9 делится число, сумма цифр которого без остатка делится на 9.

Число 12348 делится на 9, т.к. 1 + 2 + 3 + 4 + 8 = 18, где 18 : 9 = 2.

Признак делимости на 10 очень прост: число делится на 10 в том случае, если оно оканчивается на 0. Например: 100, 3458903456890 и др.

Простой множитель — Википедия

Материал из Википедии — свободной энциклопедии

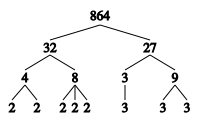Это изображение демонстрирует нахождение простых множителей числа 864. Сокращённый способ написания — 2⁵ × 3³

В теории чисел, простые множители (простые делители) положительного целого числа — это простые числа, которые делят это число нацело (без остатка)^[1]. Выделить простые множители положительного целого числа означает перечислить эти простые множители вместе с их кратностями. Процесс определения простых множителей называется факторизацией целых чисел. Основная теорема арифметики утверждает, что любое натуральное число можно представить в виде единственного (с точностью до порядка следования) произведения простых множителей^[2].

Чтобы сократить выражение, простые множители часто представляются в виде степеней простых чисел (кратностей). Например,

360=2×2×2×3×3×5=23×32×5{\displaystyle 360=2\times 2\times 2\times 3\times 3\times 5=2^{3}\times 3^{2}\times 5}

в котором множители 2, 3 и 5 имеют кратности 3, 2 и 1, соответственно.

Для простого множителя р числа n кратность числа p — это наибольший из показателей степени а, для которых ра делит n нацело.

Для положительного целого числа n, количество простых множителей n и сумма простых множителей n (без учёта кратности) — это примеры арифметических функций из n (аддитивных арифметических функций)^[3].

Квадрат числа имеет то свойство, что все его простые множители имеют чётные кратности. Например, число 144 (квадрат 12) имеет простые множители

144=2×2×2×2×3×3=24×32.{\displaystyle 144=2\times 2\times 2\times 2\times 3\times 3=2^{4}\times 3^{2}.}

В более понятной форме:

144=2×2×2×2×3×3=(2×2×3)×(2×2×3)=(2×2×3)2=(12)2.{\displaystyle 144=2\times 2\times 2\times 2\times 3\times 3=(2\times 2\times 3)\times (2\times 2\times 3)=(2\times 2\times 3)^{2}=(12)^{2}.}

Поскольку каждый простой множитель присутствует здесь чётное число раз, исходное число можно представить в виде квадрата некоторого числа. Таким же образом, куб числа — это число, у которого кратности простых множителей делятся на три, и так далее.

Положительные целые числа, не имеющие общих простых множителей, называются взаимно простыми. Два целых числа a и b можно назвать взаимно простыми, если их наибольший общий делитель НОД(a, b) = 1. Если для двух целых чисел неизвестны их простые множители, то для определения того, являются ли они взаимно простыми, используется алгоритм Евклида; алгоритм выполняется за полиномиальное время по количеству цифр.

Целое число 1 является взаимно простым для любого положительного целого числа, включая само себя. Иными словами, число 1 не имеет простых множителей, оно — empty product. Это означает, что НОД(1, b) = 1 для любого b ≥ 1.

Определение простых множителей числа — это пример задачи, которая часто используется для обеспечения криптографической защиты в системах шифрования^[4]. Предполагается, что эта задача требует супер-полиномиального времени по количеству цифр. Это значит, что относительно легко сконструировать задачу, решение которой заняло бы больше времени, чем известный возраст Вселенной при текущем развитии компьютеров и с помощью современных алгоритмов.

Функция ω(n) (омега) представляет собой число различных простых множителей n, в то время как функция Ω(n) (большая Омега) представляет собой число простых множителей n, пересчитанное с учётом кратности^[2]. Если

n=∏i=1ω(n)piαi,{\displaystyle n=\prod _{i=1}^{\omega (n)}p_{i}^{\alpha _{i}},}

тогда

Ω(n)=∑i=1ω(n)αi.{\displaystyle \Omega (n)=\sum _{i=1}^{\omega (n)}\alpha _{i}.}

Например, 24 = 2³ × 3¹, Так что ω(24) = 2 и Ω(24) = 3 + 1 = 4.

ω(n) для n = 1, 2, 3, … соответственно 0, 1, 1, 1, 1, 2, 1, 1, 1, … — последовательность A001221 в OEIS.
Ω(n) для n = 1, 2, 3, … соответственно 0, 1, 1, 2, 1, 2, 1, 3, 2, … — последовательность A001222 в OEIS.

↑ Jensen, Gary R. Arithmetic for Teachers: With Applications and Topics from Geometry (англ.). — American Mathematical Society, 2004.
↑ ¹ ² Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9
↑ Melvyn B. Nathanson. Additive Number Theory: the Classical Bases (англ.). — Springer-Verlag, 1996. — Vol. 234. — (Graduate Texts in Mathematics). — ISBN 0-387-94656-X.
↑ Menezes, Alfred; van Oorschot, Paul C.; Vanstone, Scott A. Handbook of Applied Cryptography (неопр.). — CRC Press, 1996. — ISBN 0-8493-8523-7.

Как найти простые числа? :: SYL.ru

Числа бывают разными: натуральными, естественными, рациональными, целыми и дробными, положительными и отрицательными, комплексными и простыми, нечетными и четными, действительными и др. Из данной статьи можно узнать, что такое простые числа.

Какие числа называют английским словом “симпл”?
Очень часто школьники на один из самых несложных на первый взгляд вопросов математики, о том что такое простое число, не знают, как ответить. Они часто путают простые числа с натуральными (то есть числа, которые используются людьми при счете предметов, при этом в некоторых источниках они начинаются с нуля, а в других — с единицы). Но это совершенно два разных понятия. Простые числа — это, натуральные, то есть целые и положительные числа, которые большее единицы и которые имеют всего лишь 2 натуральных делителя. При этом один из этих делителей — это данное число, а второй – единица. Например, три — это простое число, поскольку он не делится без остатка ни на какое другое число, кроме себя самого и единицы.
Составные числа
Противоположностью простых чисел являются составные. Они также являются натуральным, также больше единицы, но имеют не два, а большее количество делителей. Так, например, числа 4, 6, 8, 9 и т. д. являются натуральными, составными, но не простыми числами. Как видите – это в основном четные числа, но не все. А вот “двойка” – четное число и “первый номер” в ряду простых чисел.
Последовательность
Чтобы построить ряд простых чисел, необходимо совершить отбор из всех натуральных чисел с учетом их определения, то есть нужно действовать методом от противного. Необходимо рассмотреть каждое из натуральных положительных чисел на предмет того, имеет ли оно более двух делителей. Давайте постараемся построить ряд (последовательность), который составляют простые числа. Список начинается с двух, следующим идет три, поскольку оно делится только на себя и на единицу. Рассмотрим число четыре. Имеет ли оно делители, кроме четырех и единицы? Да, это число 2. Значит, четыре не является простым числом. Пять также является простым (оно, кроме 1 и 5, ни на какое другое число не делится), а вот шесть – делится. И вообще, если проследить за всеми четными числами, то можно заметить, что кроме “двух”, ни одно из них не является простым. Отсюда сделаем вывод, что четные числа, кроме двух, не являются простыми. Еще одно открытие: все числа, делящиеся на три, кроме самой тройки, будь то четные или нечетные, также не являются простыми (6, 9, 12, 15, 18, 21, 24, 27 и т.д.). То же самое касается и чисел, которые делятся на пять и на семь. Все их множество также не является простым. Давайте подведем итоги. Итак, к простым однозначным числам относятся все нечетные числа, кроме единицы и девятки, а из четных – только “два”. Сами десятки (10, 20,… 40 и др.) не являются простыми. Двузначные, трехзначные и т. д. простые числа можно определить, исходя из вышеизложенных принципов: если они не имеют других делителей, кроме их самих и единицы.
Теории о свойствах простых чисел
Существует наука, которая изучает свойства целых чисел, в том числе и простых. Это раздел математики, которая называется высшей. Помимо свойств целых чисел, она также занимается алгебраическими, трансцендентными числами, а также функциями различного происхождения, связанными с арифметикой этих чисел. В этих исследованиях, помимо элементарных и алгебраических методов, также используются аналитические и геометрические. Конкретно изучением простых чисел занимается “Теория чисел”.
Простые числа — “строительные блоки” натуральных чисел
В арифметике есть теорема, которая называется основной. Согласно ей, любое натуральное число, кроме единицы, можно представить в виде произведения, множителями которого являются простые числа, причем порядок следования множителей единственен, этот означает, что и способ представления единственен. Он называется разложением натурального числа на простые множители. Есть и другое название этого процесса – факторизация чисел. Исходя из этого, простые числа можно назвать “строительным материалом”, «блоками» для построения натуральных чисел.
Поиск простых чисел. Тесты простоты
Множество ученых разных времен пытались найти какие-то принципы (системы) для нахождения списка простых чисел. Науке известны системы, которые называются решето Аткина, решето Сундартама, решето Эратосфена. Однако они не дают каких-то существенных результатов, и для нахождения простых чисел используется простая проверка. Также математиками были созданы алгоритмы. Их принято называть тестами простоты. Например, существует тест, разработанный Рабином и Миллером. Его используют криптографы. Также существует тест Каяла-Агравала- Саскены. Однако он, несмотря на достаточную точность, очень сложен в вычислении, что принижает его прикладное значение.
Имеет ли множество простых чисел предел?
О том, что множество простых является бесконечностью, писал в книге “Начала” древнегреческий ученый Евклид. Он говорил так: “Давайте на минуту представим, что простые числа имеют предел. Тогда давайте перемножим их друг с другом, а к произведению прибавим единицу. Число, полученное в результате этих простых действий, не может делиться ни на одно из ряда простых чисел, потому что в остатке всегда будет единица. А это значит, что существует какое-то другое число, которое еще не включено в список простых чисел. Следовательно, наше допущение не верно, и это множество не может иметь предела. Помимо доказательства Евклида, существует более современная формула, данная швейцарским математиком восемнадцатого века Леонардом Эйлером. Согласно ему, сумма, обратная сумме первых n чисел растет неограниченно с ростом числа n. А вот формула теоремы относительно распределения простых чисел: (n) растёт, как n/ln (n).
Какое наибольшее простое число?
Все тот же Леонард Эйлер смог найти самое большое для своего времени простое число. Это 2³¹– 1 = 2147483647. Однако к 2013 году было вычислено другое наиболее точное самое большое в списке простых чисел – 2^57885161– 1. Его называют числом Мерсенна. Оно содержит около 17 миллионов десятичных цифр. Как видите, число, найденное ученым из восемнадцатого века, в несколько раз меньше этого. Так и должно было быть, ведь Эйлер вел данный подсчет вручную, нашему же современнику наверняка помогала вычислительная машина. Более того, это число было получено на факультете математики в одном из американских факультетов. Числа, названные в честь этого ученого, проходят через тест простоты Люка-Лемера. Однако наука не желает останавливаться на достигнутом. Фонд Электронных рубежей, который был основан в 1990 году в Соединенных Штатах Америки (EFF), назначил за нахождение больших простых чисел денежную награду. И если до 2013 года приз полагался тем ученным, которые найдут их из числа 1 и 10 миллионов десятичных чисел, то сегодня это цифра достигла от 100 миллионов до 1 миллиарда. Размер призов составляет от 150 до 250 тысяч долларов США.
Названия специальных простых чисел
Те числа, которые были найдены благодаря алгоритмам, созданным теми или иными учеными, и прошли тест простоты, называются специальными. Вот некоторые из них:
1. Мерссена.
2. Вудаа.
3. Ферма.
4. Каллена.
5. Прота.
6. Миллса и др.
Простота этих чисел, названных в честь вышеперечисленных ученых, устанавливается с использованием следующих тестов:
1. Люка-Лемера.
2. Пепина.
3. Ризеля.
4. Биллхарта – Лемера – Селфриджа и др.
Современная наука не останавливается на достигнутом, и, вероятно, в ближайшем будущем мир узнает имена тех, кто смог получить приз в 250.000 долларов, найдя наибольшее простое число.
Последовательность, почти всегда возвращающая простые числа
Тимофей Приходько (Технологический институт ВТУ, старший преподаватель)
Возможно, самым интересным в теории чисел является раздел, посвященный простым числам. При этом он один из самых малоизученных. Из простейшего определения понятия простого числа — это число, которое делится на себя и единицу, — вытекает множество загадок, многие из которых удалось разгадать сравнительно недавно, а некоторые еще ждут своего разрешения. Разгадав некоторые из них, человечество продвинется далеко вперед, а возможно, спровоцирует мировой кризис.
О важности простых чисел в математике говорит основная теорема арифметики: любое число можно представить в виде произведения простых множителей. Вся математика опирается на простые числа, но закономерности появления их в натуральном ряду так никто еще и не объяснил.
Математики всего мира не раз пытались найти ту формулу, при вычислениях по которой всегда получались бы простые числа. Если в этой фразе отбросить слово «всегда», то таких формул удастся привести довольно много, например: f(n)=n2 + n + 17; f(n) = n2 – n + 41; f(n) = 2n2 + 29.
Последовательно подставляя, например, в первую формулу вместо n натуральные числа, получим числа 19, 23, 29, 37. Все они являются простыми, но торжествовать рано — уже f(16) = 289 = 172, то есть получилось составное число.
Эти формулы порождают много простых чисел, но это «много» еще не означает «всегда»! Более того, можно доказать, что никакой многочлен с целыми коэффициентами не может для всякого натурального значения n равняться простому числу.
На самом деле для простых чисел не существует никакой формулы, никакой комбинации алгебраических операций над n, выполняя которые можно было бы получить очередное nное простое число. Многие люди впадали в заблуждение на этот счет, достигнув некоторых первоначальных успехов.
Полотно Улама
Так чем же объясняются закономерности в распределении простых чисел? Пока ответа на этот вопрос нет, но все же есть множество визуальных наблюдений. Одну из таких закономерностей случайно открыл Станислав Улам, американский математик, поляк по происхождению. Сидя както на скучной лекции, он, ни о чем не думая, начал рисовать решетку из горизонтальных и вертикальных линий. В одной из полученных таким образом клеток он поставил 1 и стал нумеровать остальные клетки по спирали, расходящейся от первой клетки:
5 4 3
6 1 2
7 8 9
Когда спираль совершила несколько оборотов, Улам начал обводить кружками простые числа, не преследуя никакой определенной цели. Однако вскоре заметил, как на его глазах возникает довольно любопытная закономерность. Откуда ни возьмись, стали появляться прямые линии. Улам, конечно, сразу понял, что такие линии говорят о закономерности, которую можно облечь в формулу для простых чисел.
Составление формулы простого числа
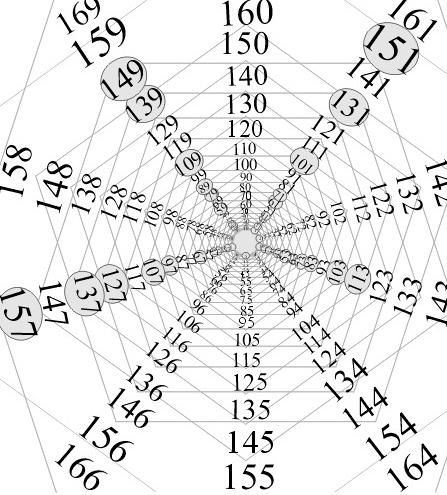
Чтобы увидеть всё своими глазами, а не полагаться только на слова, составим простую компьютерную программу, которая бы рисовала точку в центре, а вокруг нее по спирали располагала бы все числа натурального ряда. Программа будет отмечать черным цветом точки, соответствующие простым числам, а серыми — составные. Вот что мы получим:
У самого центра диаграммы одна такая закономерность пролегает сверху вниз и слева направо. Она состоит из последовательности чисел: 7, 23, 47, 79… Оказывается, эту последовательность можно описать квадратичной функцией р = 4х2 + 4х – 1.
С помощью этого графика можно задать формулой любую последовательность простых чисел. Рассмотрим, например, последовательность, берущую свое начало из точки 5 и идущую справа налево сверху вниз. Следующее число в этой последовательности 19, затем идут 41, 71… Попробуем описать ее рекуррентной формулой. Для этого сначала рассмотрим каждый квадрат, состоящий из точек. У любого такого квадрата на восемь точек больше, чем у вложенного в него, — это очень легко доказать. Значит, разность между любыми двумя точками, лежащими в соседних квадратах по одному правилу, будет увеличиваться на восемь по сравнению с предыдущими. Для определенности за отношение «лежать по одному правилу» примем точки, лежащие в соседних квадратах, причем из точки, лежащей в меньшем квадрате, можно перейти к точке из большего квадрата, если перейти в другой квадрат по кратчайшему расстоянию и затем сместиться на число t, где t целое, причем t — постоянное число для данного правила. В нашем случае t = 1.
Если разность между точками, лежащими в 1м и 2м квадратах от центра, равна 14, то разность между точками 2го и 3го квадратов возрастет на 8 и будет равна 22. Теперь можно составить формулу: следующий член последовательности будет отличаться от предыдущего на
14 + 8·n, где n — номер члена последовательности, то есть номер квадрата от центра. Если считать 5 нулевым членом и каждый член больше предыдущего на 8·(n – 1), где n — номер квадрата, то получим:
x_n = x_{n – 1} + 14 + 8(n – 1)
x_n = x_{n – 1} + 8n + 6
Это и есть формула данной последовательности.
И таким образом можно составить сколько угодно формул последовательностей простых чисел, но всегда на какомто номере окажется, что число вовсе не простое. Примечательно, что если в качестве начальной точки взять число не 1, а 41, то мы увидим последовательность, состоящую из 41 простого числа!
Никакая целая рациональная функция от х с целыми коэффициентами не может для любого натурального значения

х равняться простому числу (теорема Гольбаха).
САПР и графика 1`2010
Признаки делимости | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Числа от 2 до 10 имеют признаки делимости, позволяющие определить, если число делится на них без остатка.
Как определить делится ли число на 2: последняя цифра числа должна быть четной. Пример: 1864 делится на 2, так как 4 – четная цифра; 2593 не делится на 2, так как 3 – нечетная цифра.
Как определить делится ли число на 3: сумма всех цифр в числе должна делиться на 3. Пример: 243 делится на 3, так как 2+4+3=9 и 9 делится на 3 без остатка; 760 не делится на 3, так как 7+6+0=13 и 13 не делится на три полностью.
Как определить делится ли число на 4: две последние цифры в числе должны делиться на 4 (00 принимается за 100). Пример: 87524 делится на 4, так как последние цифры 24 делятся 4; 6500 делится на 4, так как последние цифры – 00, а 100 делится на 4; 59431 не делится на 4, так как 31 не делится на 4 без остатка.
Как определить делится ли число на 5: последняя цифра числа должна быть 0 или 5. Пример: 58 не делится на 5, так как последняя цифра 8; 1580 делится на 5, так как последняя цифра числа – 0.

Как определить делится ли число на 6: число должно делится одновременно на 2 и на 3, согласно вышеописанным признакам. Пример: 81 не делится на 6, так как оно делится на 3, но не делится на 2; 100 не делится на 6, так как оно делится на 2, но не делится на 3; 72 делится на 6, так как оно делится и на 2, и на 3.
Как определить делится ли число на 7: число десятков, умноженное на 3, в сумме с числом единиц должно делиться на 7. Пример: 511 делится на 7, так как 51*3+1=154 и 154 делится на 7; 635 не делится на 7, так как 63*3+5=194 и 194 не делится на 7.
Как определить делится ли число на 8: последние три цифры числа должны делится на 8 (000 берутся за 1000, которая делится на 8). Пример: 86240 делится на 8, так как 240 делится на 8; 56343 не делится на 8, так как 343 не делится на 8.
Как определить делится ли число на 9: сумма всех цифр в числе должна быть кратна 9. Пример: 243 делится на 9 без остатка, так как 2+4+3=9 и 9 делится на 9; 5081 не делится на 9, так как 5+0+8+1=14 и 14 не делится на 9

Как определить, что число делится на 10: последняя цифра числа должна быть 0. Пример: 1530 делится на 10, так как последняя цифра 0; 6572 не делится на 10, так как последняя цифра 2.
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 10, на 5 и на 2
Вопрос: что такое признаки делимости чисел ?
Ответ: признаки делимости чисел — это особенности чисел, которые помогают быстро определить, делится ли данное число на другое.
Знать эти признаки необходимо при решении многих арифметических задач.

Признак делимости на 10
Рассмотрим несколько чисел, запись которых оканчивается цифрой 0, например,
60, 130, 2340
Каждое из этих чисел делится без остатка на
10
Чтобы получить частное, достаточно отбросить цифру 0.
60 : 10 = 6
130 : 10 = 13
2340 : 10 = 234
Вывод: любое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10

Если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10
Проверим это утверждение, например, на числе 234
234 : 10 = 23 целых в остатке 4
(неполное частное 23 и остаток 4 — последняя цифра в записи числа 234)
Вывод: если последняя цифра в записи натурального числа отлична от нуля
, то это число не делится без остатка на 10.

Определение
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10.
Остаток в этом случае равен последней цифре в записи числа.

Обратим внимание на то, что число 10 = 2 · 5 (число 10 делится без остатка и на 2, и на 5).
Вывод: число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.
Например, 70 = 7 · 10 = 7 · (2 · 5) = (7 · 2) · 5 = 14 · 5, значит, 70 : 5 = 14.
А из того что 70 = 7 · (5 · 2) = (7 · 5) · 2 = 35 · 2, получаем, что 70 : 2 = 35.

Полные десятки
Существует такое понятие, как «круглое» число — это целое число, запись которого оканчивается одним или несколькими нулями.
Такие числа принято называть «круглыми» («полными«) десятками.
Например, числа 40, 530, 3270, 3200 являются полными десятками.
40 — четыре десятка
530 — пятьдесят три десятка
3270 — триста двадцать семь десятков
3200 — триста двадцать десятков
Полные десятки делятся и на 10, и на 5, и на 2.

Признак делимости на 5
Каждое число можно представить в виде суммы полных десятков и единиц, например,
46 = 40 + 6, 539 = 530 + 9, 3278 = 3270 + 8.
Так как полные десятки делятся на 5, то и всё число делится на 5 лишь в том случае, когда на 5 делится число единиц.
Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.

Определение
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Например, числа 270 и 275 делятся без остатка на 5

Если же запись числа оканчивается другой цифрой, то число без остатка на 5 не делится.
Например, числа 272 и 273 на 5 без остатка не делятся.

Четные и нечетные числа
Определение
Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными.

Из однозначных чисел числа 0, 2, 4, 6 и 8 чётные, а числа 1, 3, 5, 7 и 9 нечётные
Цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными.

Все полные десятки делятся на 2 без остатка (т. е. они чётны).
Вывод: любое натуральное число чётно, когда в разряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра.

Определение
Если запись натурального числа оканчивается чётной цифрой, то это число чётно (делится без остатка на 2), а если запись числа оканчивается нечётной цифрой, то это число нечётно.
Например, числа 2, 30, 74, 56, 108 чётные, а числа 3, 31, 75, 57, 109 нечётные.

Это интересно
Древнегреческий философ (профессиональный мыслитель), математик и мистик (верил в существование сверхъестественных сил) Пифагор Самосский, чётные числа считал женскими, а нечётные — мужскими
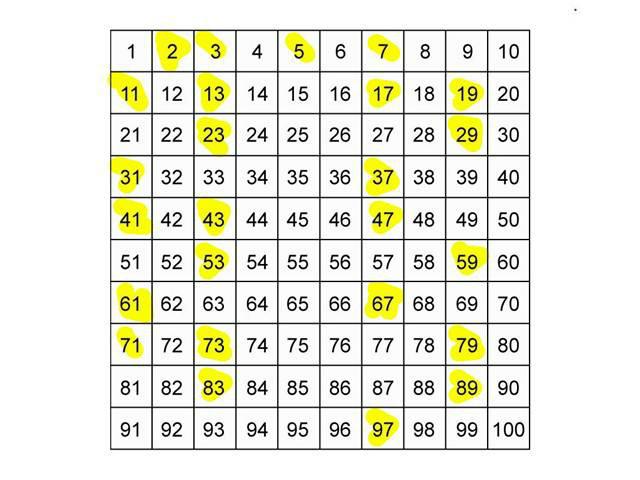
На рисунке числа от 1 до 100 (чётные и нечётные числа разного цвета)
В старину люди верили в магию чисел, где всё хорошее ассоциировалось с нечётными цифрами, а плохое – с чётными. Поэтому, например, в Рождество на стол всегда ставили нечётное количество блюд. Люди верили, что нечётные числа символизируют постоянное продолжение жизни, незавершенность. А чётные, наоборот, означают конечность всего живого, остановку движения.
Таблица признаков делимости чисел