Числовая окружность. Видеоурок. Алгебра 10 Класс

Тема: Тригонометрические функции

Урок: Числовая окружность

Для  любой функции независимый аргумент откладывается либо на числовой прямой, либо на окружности. Охарактеризуем и числовую прямую, и числовую окружность.

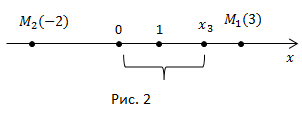
Прямая становится числовой (координатной) прямой, если отмечено начало координат, выбраны направление и масштаб (рис. 1).

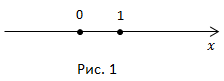
Числовая прямая устанавливает взаимно-однозначное соответствие между всеми точками прямой и всеми действительными числами.

Например, берем число 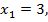 откладываем на координатной оси, получаем точку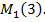

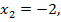 Возьмем число  откладываем на оси, получаем точку  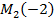(рис. 2).

И наоборот, если мы взяли любую точку 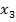 на координатной прямой, то найдется единственное соответствующее ей действительное число (рис. 2).

К такому соответствию люди пришли не сразу. Чтобы понять это, вспомним основные числовые множества.

Сначала ввели множество натуральных чисел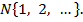

Затем множество целых чисел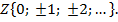

Множество рациональных чисел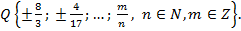

Предполагалось, что этих множеств будет достаточно, и существует взаимно-однозначное соответствие между всеми рациональными числами и точками прямой. Но оказалось, что на числовой прямой есть бесчисленное множество точек, которые нельзя описать числами вида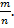

Пример – гипотенуза прямоугольного треугольника с катетами 1 и 1. Она равна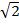

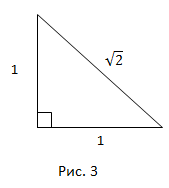
 (рис. 3).

Найдется ли среди множества рациональных чисел число, в точности равное 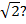 Нет, не найдется. Докажем этот факт.

Докажем методом от противного. Предположим, что существует дробь, равная т.е.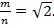

Тогда 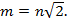 Возведем обе части в квадрат,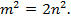 

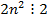 Очевидно, что правая часть равенства делится на 2, . Значит и  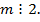Тогда  Но тогда и 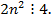 А значит,  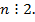Тогда получается, что дробь  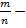сократимая. Это противоречит условию, значит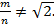

Число 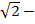 иррациональное. Множество рациональных и иррациональных чисел образуют множество действительных чисел  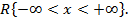Если мы возьмем любую точку на прямой, ей будет соответствовать какое-либо действительное число. И если мы возьмем любое действительное число, ему будет соответствовать единственная точка на координатной прямой.

Уточним, что такое числовая окружность и каковы взаимоотношения между множеством точек окружности и множеством действительных чисел.

Начало отсчета – точка A. Направление отсчета – против часовой стрелки – положительное, по часовой стрелке – отрицательное.  Масштаб – длина окружности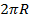

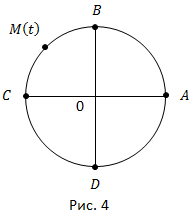
 (рис. 4).

Вводя эти три положения, мы имеем числовую окружность. Укажем, каким образом каждому числу 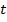 поставить в соответствие точку на окружности и наоборот.

Задав число 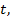 получаем точку на окружности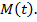  

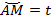
 (рис. 4).

Каждому действительному числу соответствует точка на окружности. А наоборот?

Точка  соответствует числу 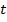. А если взять числа  Все эти числа своим образом на окружности имеют только одну точку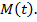

Например, 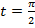 соответствует точке

B (рис. 4).

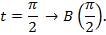
Возьмем все числа 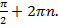 Все они соответствуют точке B. Нет взаимно-однозначного соответствия между всеми действительными числами и точками окружности.

Если есть фиксированное число 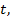 то ему соответствует только одна точка окружности

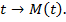
Если есть точка окружности, то ей соответствует множество чисел

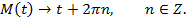
В отличии от прямой, координатная окружность не обладает взаимно-однозначным соответствием между точками и числами. Каждому числу соответствует только одна точка, но каждой точке соответствует бесчисленное множество чисел, и мы можем их записать.

Рассмотрим основные точки на окружности.

Задано число 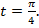 Найти, какой точке на окружности оно соответствует.

Разделив дугу 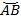 пополам, получаем точку  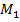(рис. 5).

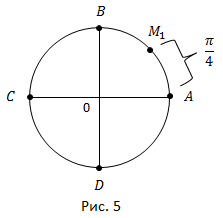
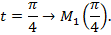
Обратная задача – дана точка 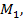 середина дуги  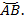Найти все действительные числа, которые ей соответствуют.

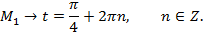
Отметим на числовой окружности все дуги, кратные 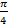 (рис. 6).

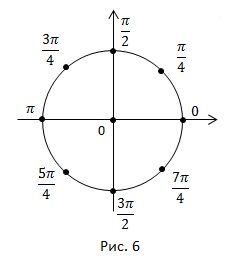
Важны также дуги, кратные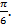

Дано число 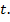 Нужно найти соответствующую точку.

Обратная задача – дана точка, нужно найти каким числам она соответствует.

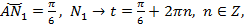 (рис. 7). 

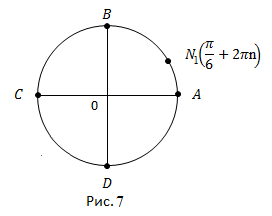
Мы рассмотрели две стандартные задачи на двух важнейших точках.

Пример 1.

a) Найти на числовой окружности точку с координатой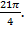

Решение:

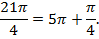
Откладываем от точки A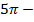это два целых оборота и еще половина, и  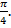Получаем точку M – это середина третьей четверти (рис. 8).

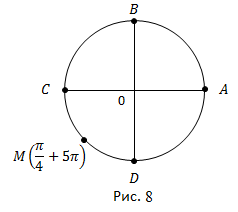
Ответ. Точка M – середина третьей четверти.

b) Найти на числовой окружности точку с координатой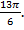

Решение:

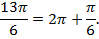
Откладываем от точки A полный оборот и еще 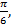 получаем точку N (рис. 9).

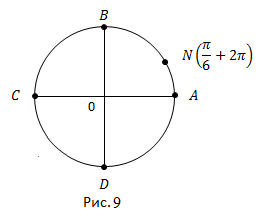
Ответ: Точка N находится в первой четверти.

Мы рассмотрели числовую прямую и числовую окружность, вспомнили их особенности. Особенностью числовой прямой является взаи

interneturok.ru

Тригонометрический круг. Основные значения тригонометрических функций

 

Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы,  или вы совсем нетерпеливы,  – то вот он, тригонометрический круг:

Мы же здесь будем все подробно разбирать шаг за шагом.

Тригонометрический круг – не роскошь, а необходимость

 

Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций,  столько формул…  А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…

Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.

Если вы постоянно смотрите в таблицу со значениями тригонометрических формул,  давайте избавляться от этой привычки!

Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!

К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, 300 градусов, или -45.

Никак?.. можно, конечно, подключить формулы приведения…  А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!

А при решении тригонометрических уравнений и неравенств   без тригонометрического круга  – вообще никуда.

Знакомство с тригонометрическим кругом

 

Давайте по порядку.

Сначала выпишем вот такой ряд чисел:

А теперь такой:

И, наконец, такой:

Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .

Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».

И зачем оно нам?

Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.

Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).

От луча  «0-Старт» откладываем в направлении стрелки (см. рис.) углы .

Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.

Это почему же, спросите вы?

Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.

Треугольник АОВ – прямоугольный, в нем  . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).

Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора

Надеюсь, уже что-то становится понятно?

Наконец, что такое синус, косинус в прямоугольном треугольнике?

 

Так вот точка  В и будет соответствовать  значению , а точка М – значению

Аналогично с остальными значениями первой четверти.

Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось  (oy) – осью синусов.   Про тангенс и котангенс позже.

Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.

Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.

 

egemaximum.ru

Тригонометрический круг со всеми значениями

Тригонометрический круг — один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.

Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.

Тригонометрическая окружность

Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.

Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.

Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике

Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты — две стороны треугольника, которые прилегают к углу 90°, а третья — гипотенуза, она всегда длиннее катетов.

Синусом называется отношение одного из катетов к гипотенузе, косинусом — отношение другого катета к ней, а тангенсом — отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.

Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).

Построение единичной окружности

Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.

Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х — косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.

Сделать перевод этих показателей просто — полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.

Углы на тригонометрическом круге

Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.

Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три — 360°. Как пользоваться этой информацией?

Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.

Измеряются углы в радианах:

• от 0 до 90° — значения углов от 0 до ∏/2;
• от 90 до 180° — значения углов от ∏/2 до ∏;
• от 180 до 270° — от ∏ до 3*∏/2;
• последняя четверть от 270⁰ до 360⁰ — значения от 3*∏/2 до 2*∏.

Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.

Перевод углов из градусов в радианы

Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.

Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:

1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956

В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:

1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

Косинус, синус, тангенс, котангенс на тригонометрической окружности

Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности — функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.

Заключение

В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.

1001student.ru

Тригонометрический круг. Значения тангенса и котангенса на круге

 

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом? Об этом и поговорим сегодня.

 

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов  (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается  вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному  рассуждать. Можете, например, использовать тот факт, что и

 

Изучаем картинку:

Собственно, картинка за себя сама говорит.

Если  не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Решение:

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Решение:

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Решение:

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как .  Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит, 

Ответ:

Пример 4.

Вычислить

Решение:

Поэтому от точки  (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что 

Ответ:

Пример 5.

Вычислить

Решение:

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что 

Ответ:  

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройти тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

egemaximum.ru

Тетрадка в клеточку — Числовая окружность

Назовём этот урок «Концепция числовой окружности». В этом случае по моему мнению, слово «концепция» замечательно укладывается в название того, что нам с вами предстоит разобрать. Одно из пояснений слова «концепция» в Википедии это ведущий замысел. Не смотря на кажущуюся сложность концепция нашей окружности проста и логична, и что важно, её понимание открывает двери к легкому восприятию последующих материалов по тригонометрии. Концепцию числовой окружности я решил передать так, как я это делаю на своих индивидуальных занятиях. Однажды на занятии, когда я преподавал эту тему, моя ученица воскликнула: «Это так просто! Почему нам это не рассказывают в школе?!» Надеюсь в большинстве случаев всё таки рассказывают, но для тех кто пропустил или не успел за текущим учебным процессом, предоставляю возможность прочитать об этом.

Вы заметили, что сайт на котором мы занимаемся называется «Тетрадка в клеточку»? Это не просто так 🙂 Вооружимся тетрадкой в клеточку, циркулем, линейкой, ластиком, простым карандашом и ручкой. Это необходимый и достаточный набор для участия в нашем мастер классе. Мозг человека не сохраняет информацию, которую не считает важной, иначе переполнение памяти было бы неминуемым. Надо передать мозгу сигнал, что эта информация важна. С этой целью обязательно проделайте самостоятельные упражнения.

Начнём! Числовая окружность это… Как вы думаете, что это? Правильно, это прежде всего окружность 🙂 Но это ведь не просто окружность, она ещё и числовая 🙂 По аналогии с числовой прямой, она должна иметь начальную точку отсчёта, то есть ноль. И действительно за начало отсчёта на числовой окружности принята её крайняя правая точка. На рисунке 1 эта точка обозначена буквой A0. Но опять же по аналогии с числовой прямой, наша окружность должна иметь положительное и отрицательное направление. И действительно для числовой окружности принято, что направление против часовой стрелки будет положительным, а по часовой соответственно — отрицательным. Подытожим: на числовой окружности ноль соответствует крайней правой точке, положительным направлением принято направление против часовой стрелки и отрицательным — по часовой.

Рисунок 1. Числовая окружность

B можно добраться по различным траекториям. Как отмечалось ранее, если двигаться против часовой стрелки, то значение будет положительным, а если по часовой, то — отрицательным. Каждая траектория представляет собой дугу, которой ставится в соответствие угол поворота. Величина угла поворота измеряется в градусной или радианной мере.

Рисунок 2. Числовая окружность

Например: 360° — полный оборот, 180° — половина оборота, 90° — четверть оборота, 270° — три четверти оборота, и т.д. На рисунке 3 показаны некоторые значения в градусах, которые соответствуют точке B. Обратите внимание, как отличаются значения углов соответствующие точке B. Различия в значениях углов кратны 360. Что вполне логично, все траектории от начала отсчета A0 к точке B отличаются на целое количество оборотов, а значит на целое количество углов в 360°.

Рисунок 3. Числовая окружность

Если радиус изогнуть вдоль окружности, получим дугу размером 1 радиан. Это проиллюстрировано на рисунке 4. Проблема состоит в том, что количество радиан в половине окружности является не целым числом, более того это число нельзя записать в виде десятичной дроби с конечным количеством дробных разрядов. Количество радиан в половине окружности примерно равно 3,141592653… Это число, как вы уже наверное догадались, обозначают буквой π. Называют это число константой пи или просто числом π. Таким образом, величина угла равная 180°, в радианной мере равна π радиан. Все значения в радианах удобно привязывать к числу пи. Как выразить в радианы величину угла, градусная мера которого известна? Изучите примеры, поупражняйтесь с заданиями и проверьте свои знания выполнив тест. Пример 1Пример 2Пример 3ЗаданияТестирование

Рисунок 4. Радиан на числовой окружности

Длина одного оборота окружности, очевидно равна 2π радиан, а значит значения соответствующие точке на окружности будут отличаться на целое количество длин равных 2π радиан, смотрим рисунок 5. Ниже приведены ссылки на примеры нахождения точки на числовой окружности по значению угла в радианах. Поупражняйтесь в решении заданий и протестируйте себя. Пример 3Пример 4ЗаданияТестирование Что касается числовой окружности, то её концепция нами разобрана, но это ещё не всё. Для тригонометрии нужна не просто числовая окружность, нужна единичная числовая окружность. Добавив прилагательное «единичная» мы добавляем к нашей числовой окружности ещё одно условие — её радиус должен быть равен единице. Это свойство единичной числовой окружности пригодится в дальнейшем.

Рисунок 5. Числовая окружность

Для превращения единичной числовой окружности в тригонометрическую добавим координатную плоскость с началом координат в её центре, как показано на рисунке 6. Обратите внимание, что единичные отрезки осей координатной плоскости, являются радиусами окружности, поскольку ее радиус так же равен единице. Ещё один важный момент: начало отсчёта числовой окружности, в котором находится А0 попадает на пересечение с осью x. В тригонометрической окружности ось y принято называть осью синусов, а ось x — осью косинусов.

Рисунок 6. Тригонометрическая окружность

Отметим на числовой окружности точку B и найдём её координаты, построив проекции на ось косинусов и ось синусов. Пусть точке B соответствует одно из значений углов равное α, тогда координата x точки B будет равна cosα (косинусу альфа), а координата y — sinα (синусу альфа). Построения проиллюстрированы на рисунке 7. В этом случае значение α называется аргументом тригонометрической функции а координаты точки Bα(x, y), которой соответствует угол α, значением тригонометрической функции: значение косинуса альфа cosα = x , значение синуса альфа sinα = y.

Рисунок 7. Нахождение синуса и косинуса на тригонометрической окружности

К числовой окружности через её крайнюю правую точку проведем касательную, задав ей направление аналогичное направлению оси синусов. Отметим на полученной новой оси начало отсчета в точке пересечения с осью косинусов и единичный отрезок размером в один радиус окружности. Такую ось принято называть осью тангенсов. Построим ещё одну ось. Эта ось будет касаться верхней точки окружности и будет со направлена с осью косинусов. Начало её отсчета отметим в точке пересечения с осью синусов, а единичный отрезок традиционно будет равен радиусу окружности. Такую ось принято называть осью котангенсов. Через начало координат и точку Bα, которой соответствует значение угла α, проведем прямую. Построенная прямая пересекает ось тангенсов и ось котангенсов в определенных точках. Так как оси тангенса и котангенса являются числовыми, то точкам пересечений можно поставить в соответствие числовые значения. Они и есть значения тангенса и котангенса исходного угла альфа. Построения проиллюстрированы на рисунке 8. Координатную плоскость условно можно разделить на четыре части. Все точки координатной плоскости, находящиеся выше оси x и правее оси y называют первой четвертью. Дальше против часовой стрелки: выше оси x и левее оси y — второй четвертью, ниже оси x и левее оси y — третей четвертью, ниже оси x и правее оси y — четвертой четвертью.

Рисунок 8. Нахождение тангенса и котангенса на тригонометрической окружности

Рассмотрим знаки тригонометрических функций значений углов для точек окружности находящихся в I четверти. Из рисунка 9 видно, что для точки Bα, находящейся в I четверти: cosα > 0, sinα > 0, tgα > 0, ctgα > 0. Из чего делаем вывод, что синус, косинус, тангенс и котангенс аргументов соответствующих точкам I четверти положительны.

Рисунок 9. Определение знаков тригонометрических функций в I четверти

Для II четверти. Из рисунка 10 видно, что для точки Bα, находящейся во II четверти: cosα < 0, sinα > 0, tgα < 0, ctgα < 0. Из чего делаем вывод, что синус аргументов соответствующих точкам II четверти положителен, а вот косинус, тангенс и котангенс — отрицательны.

Рисунок 10. Определение знаков тригонометрических функций во II четверти

Для III четверти. Из рисунка 11 видно, что для точки Bα, находящейся в III четверти: cosα < 0, sinα < 0, tgα > 0, ctgα > 0. Из чего делаем вывод, что синус и косинус аргументов соответствующих точкам III четверти отрицательны, а тангенс и котангенс — положительны.

Рисунок 11. Определение знаков тригонометрических функций в III четверти

Для IV четверти. Из рисунка 12 видно, что для точки Bα, находящейся в IV четверти: cosα > 0, sinα < 0, tgα < 0, ctgα < 0. Из чего делаем вывод, что косинус аргументов соответствующих точкам IV четверти положителен, а синус, тангенс и котангенс — отрицательны.

Рисунок 12. Определение знаков тригонометрических функций в IV четверти

На рисунке 13 показаны знаки синуса в четвертях координатной плоскости.

Рисунок 13. Знаки синуса в различных четвертях тригонометрической окружности

На рисунке 14 показаны знаки косинуса в четвертях координатной плоскости.

Рисунок 14. Знаки косинуса в различных четвертях тригонометрической окружности

На рисунке 15 показаны знаки тангенса и контангенса в четвертях координатной плоскости.

Рисунок 15. Знаки тангенса и контангенса в различных четвертях тригонометрической окружности

tetradkavkletochku.ru

Тригонометрический круг синус и косинус

Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.

Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.

Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)

Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали.

В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат — там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).

Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.

Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.

Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.

Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).

Найти решение:

Синусы и косинусы круг — здесь картинка во всей своей тригонометрической красе.

Угол 120 градусов в радианах — равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.

Значения синусов косинусов углов в радианах — на картинке есть такие, надеюсь, именно те углы, которые вы ищете.

Значение косинуса угла в 45 градусов — равно корню из двух деленному на два, можете проверить по рисунку.

Тригонометрическая окружность — я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности — вылитая тригонометрия.

Тригонометрический круг рисунок — есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию — почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» — картина гениального художника эпохи Раннего Математического Возрождения …» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!

Круг синусов и косинусов — именно такой круг совершенно случайно оказался здесь на картинке.

Угол 9 градусов сколько это в пи — в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20

Ответ: 9 градусов = 1/20 пи.

Синус это вверх или в сторону — синус — это вверх, в сторону — это косинус.

Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.

www.webstaratel.ru

Основные значения тригонометрических функций. Часть 2

Продолжение (начало здесь)

Перевод радиан в градусы и градусы в радианы

 

На тригонометрическом круге  помимо углов  в градусы мы наблюдаем радианы.

Подробнее про радианы:+ показать

 Радиан определяется как угловая величина дуги, длина которой равна её радиусу. Соответственно, так как длина окружности равна , то очевидно, что в окружности укладывается радиан, то есть радиан.

1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″.

Все знают, что радиан –  это

Так вот, например, , а . Так, мы научились переводить радианы в углы.

Теперь наоборот, давайте переводить градусы в радианы.

Допустим, нам надо перевести в радианы. Нам поможет пропорция. Поступаем следующим образом:

Так как, радиан, то заполним таблицу:

Откуда

 

Тренируемся находить  значения  синуса и косинуса по кругу

 

Давайте еще уточним следующее.

Ну хорошо, если нас просят вычислить, скажем, , – здесь обычно путаницы не возникает – все начинают первым делом искать на круге.

А если просят вычислить, например, … Многие, вдруг, начинают не понимают где искать этот ноль… Частенько ищут его  в начале координат. Почему?

1) Давайте договоримся раз и навсегда! То, что стоит после или  – это аргумент=угол, а  углы у нас располагаются на круге, не ищите их на осяx! (Просто отдельные точки попадают и на круг, и на ось…) А сами значения синусов и косинусов – ищем на осях!

2) И еще! Если мы от точки «старт» отправляемся против часовой стрелки (основное направление обхода тригонометрического круга), то мы откладываем положительные значения углов, значения углов растут при движении в этом направлении.

Если же мы от точки «старт» отправляемся по часовой стрелке, то мы откладываем отрицательные значения углов. 

 

Пример 1. 

Найти значение .

Решение:

Находим на круге . Проецируем точку на ось синусов (то есть проводим перпендикуляр из точки  к оси синусов (оу)).

Приходим в 0. Значит, .

Пример 2. 

Найти значение .

Решение:

Находим на круге (проходим против часовой стрелки  и еще  ). Проецируем точку на ось синусов (а она уже лежит на оси синусов).

Попадаем в -1 по оси синусов.

Значит, .

Заметим, за точкой «скрываются» такие точки, как  (мы могли бы пойти в точку, помеченную как  ,  по часовой стрелке, а значит появляется знак минус), и бесконечно много других.

Можно привести такую аналогию:

Представим тригонометрический круг как беговую дорожку стадиона.

Вы ведь можете оказаться в точке «Флажок», отправляюсь со старта против часовой стрелки, пробежав, допустим, 300 м.   Или пробежав, скажем, 100м  по часовой стрелке (считаем длину дорожки 400 м).

А также вы можете оказаться в точке «Флажок» (после «старт»), пробежав, скажем, 700 м, 1100 м, 1500 м и т. д. против часовой стрелки. Вы можете оказаться в точке «Флажок», пробежав 500 м или 900 м и т. д.  по часовой стрелке от «старт».

Разверните мысленно беговую дорожку стадиона в числовую прямую. Представьте, где на этой прямой будут, например,  значения 300, 700, 1100, 1500 и т.д. Мы  увидим точки на числовой прямой, равноотстоящие друг от друга. Свернем обратно в круг. Точки «cлепятся» в одну.

Так и с тригонометрическим кругом. За каждой точкой скрыто бесконечно много других.

Скажем,  углы , , ,  и т.д. изображаются одной точкой. И  значения синуса, косинуса в них, конечно же, совпадают. (Вы заметили, что мы прибавляли/вычитали или ? Это период для функции синус и косинус.)

Пример 3. 

Найти значение .

Решение:

Переведем для простоты в градусы

(позже, когда вы привыкнете к тригонометрическому кругу, вам не потребуется переводить радианы в градусы):

Двигаться будем по часовой стрелки от точки  Пройдем полкруга () и еще 

Понимаем, что значение синуса совпадает со значением  синуса     и равняется

.

 

Заметим, если б мы взяли, например, или и т.д., то мы получили бы все тоже значение синуса.

Пример 4. 

Найти значение .

Решение:

Все же, не будем переводить радианы в градусы, как в предыдущем примере.

.

То есть нам надо пройти против часовой стрелки полкруга и еще четверть полкруга и спроецировать полученную точку на ось косинусов (горизонтальная ось).

Пример 5. 

Найти значение .

Решение:

Как отложить на тригонометрическом круге ?

Если мы пройдем или , да хоть , мы все равно окажемся   в точке, которую мы обозначили как  «старт».   Поэтому, можно сразу пройти в точку на круге

Пример 6. 

Найти значение .

Решение:

Мы окажемся в точке ( приведет нас все равно в точку ноль). Проецируем  точку круга   на ось косинусов (смотри тригонометрический круг), попадаем в . То есть .

Тригонометрический круг – у вас в руках

 

Вы же уже поняли, что главное – запомнить значения тригонометрических функций первой четверти. В остальных четвертях все аналогично, нужно лишь следить за знаками.  А «цепочку-лесенку»  значений тригонометрических функций, вы, надеюсь уже не забудете. 

Как находить значения тангенса и котангенса основных углов смотрите здесь.

После чего, познакомившись с основными значениями тангенса и котангенса, вы можете пройти   тест по теме «Нахождение значений косинусов, синусов, тангенсов и котангенсов различных углов»

 

Ссылочка на пустой шаблон круга. Тренируйтесь!

egemaximum.ru