Неподвижная точка — Википедия

Материал из Википедии — свободной энциклопедии

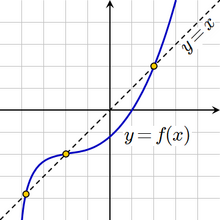Отображение с тремя неподвижными точками

Неподвижная точка в математике — точка, которую заданное отображение переводит в неё же, иными словами, решение уравнения f(x)=x{\displaystyle f(x)=x}.

К примеру, отображение f(x)=x2−3x+3{\displaystyle f(x)=x^{2}-3x+3} имеет неподвижные точки x=1{\displaystyle x=1} и x=3{\displaystyle x=3}, поскольку f(1)=1{\displaystyle f(1)=1} и f(3)=3{\displaystyle f(3)=3}.

Неподвижные точки есть не у всякого отображения — скажем, отображение f(x)=x+1{\displaystyle f(x)=x+1} вещественной прямой в себя неподвижных точек не имеет.

Точки, возвращающиеся в себя после определённого числа итераций, то есть, решения уравнения

f(f(…f(x)…))=x{\displaystyle f(f(\dots f(x)\dots ))=x},

называются периодическими (в частности, неподвижные точки — это периодические точки периода 1).

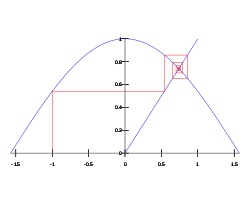
Неподвижная точка x=f(x) отображения f — притягивающая, если итерации любой начальной точки y, достаточно близкой к x, будут стремиться к x:

f(f(…f(y)…⏟ntimes))→x,n→∞{\displaystyle f(f(\underbrace {\dots f(y)\dots } _{n\,{\text{times}}}))\rightarrow x,\quad n\rightarrow \infty }.

(При этом, обычно, требуют, чтобы итерации y не покидали некоторой большей окрестности точки x — то есть, чтобы точка x была асимптотически устойчива.)

В частности, достаточным условием, чтобы точка была притягивающей, является условие на производную: |f′(x)|<1{\displaystyle |f'(x)|<1}.

Метод Ньютона[править | править код]

Одним из применений идеи притягивающей неподвижной точки является метод Ньютона: искомое решение оказывается притягивающей неподвижной точкой построенного отображения, и потому может быть найдено как предел (очень быстро сходящейся) последовательности итераций.

Наиболее известное применение этого метода нахождение квадратного корня из числа a>0 как последовательности итераций отображения

f(x)=x+ax2{\displaystyle f(x)={\cfrac {x+{\frac {a}{x}}}{2}}}.

• Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука, 1976. — Гл. 2, п. 4.
• Красносельский М. А., Забрейко П. П. Геометрические методы нелинейного анализа. — М.: Наука, 1975. — Гл. 5.
• Agarwal R. P., Meehan M., O’Regan D. Fixed Point Theory and Applications. — Cambridge University Press, 2001. — ISBN 0-521-80250-4.
• Borisovich Yu. G., Gel’man B. D., Myshkis A. D., Obukhovskii V. V. Multivalued mappings // Journal of Soviet Mathematics, 1984. — Vol. 24, Issue 6, pp 719-791.
• Fitzpatrick P. M., Petryshyn W. V. Fixed point theorems for multivalued noncompact acyclic mappings // Pacific Journal of Mathematics, 54:2, 1974.

математическая точка — это… Что такое математическая точка?



математическая точка

математи́чна то́чка

Русско-украинский политехнический словарь. 2013.

• математическая статистика
• математическая физика

Смотреть что такое «математическая точка» в других словарях:

• точка — сущ., ж., употр. очень часто Морфология: (нет) чего? точки, чему? точке, (вижу) что? точку, чем? точкой, о чём? о точке; мн. что? точки, (нет) чего? точек, чему? точкам, (вижу) что? точки, чем? точками, о чём? о точках 1. Точка это маленькое… …   Толковый словарь Дмитриева

• МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА — математическая дисциплина, предметом к рой являются модели экономич. объектов и процессов и методы их исследования. Однако понятия, результаты, методы М. э. удобно и принято излагать в тесной связи с их экономич. происхождением, интерпретацией и… …   Математическая энциклопедия

• Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… …   Большая советская энциклопедия

• МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — полная математическая индукция (наз. в математике часто просто полной индукцией; в этом случае это понятие следует отличать от рассматриваемого в нематематич. формальной логике понятия полной индукции), – прием доказательства общих предложений в… …   Философская энциклопедия

• МАТЕМАТИЧЕСКАЯ ЛОГИКА — один из ведущих разделов современной логики и математики. Сформировался в 19 20 ст. как реализация идеи о возможности записать все исходные допущения на языке знаков, аналогичных математическим и тем самым заменить рассуждения вычислениями.… …   Новейший философский словарь

• Точка — I Точка (математическая)         одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых… …   Большая советская энциклопедия

• Точка электронейтральности —     Графен …   Википедия

• Математическая сингулярность — Особая точка указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например,… …   Википедия

• Математическая морфология — Форма (синяя) и её морфологическое расширение (зеленое) и сужение (желтое) ромбическим структурным элементом. Математическая морфология (ММ)  (Морфология от греч …   Википедия

• Математическая константа — У этого термина существуют и другие значения, см. Константа. Математическая константа  величина, значение которой не меняется; в этом она противоположна переменной. В отличие от физических констант, математические константы определены… …   Википедия

• Точка Курнакова — Многие твёрдые растворы замещения при относительно невысоких температурах способны находиться в упорядоченном состоянии, то есть вместо статистического распределения разносортных атомов в узлах пространственной решетки атомы одного и другого… …   Википедия

точка — это… Что такое точка?

Морфология: (нет) чего? то́чки, чему? то́чке, (вижу) что? то́чку, чем? то́чкой, о чём? о то́чке; мн. что? то́чки, (нет) чего? то́чек, чему? то́чкам, (вижу) что? то́чки, чем? то́чками, о чём? о то́чках

1. Точка — это маленькое круглое пятнышко, след от прикосновения чем-либо острым или пишущим.

Узор из точек. | Точка от укола. | Город на карте указан маленькой точкой и о наличии объездной дороги остаётся только догадываться.

2. Точка — это что-то очень маленькое, плохо видимое из-за удалённости или по другим причинам.

Точка на горизонте. | Когда шар приблизился к горизонту в западной части неба, он стал медленно уменьшаться в размерах, пока не превратился в точку.

3. Точка — знак препинания, который ставится в конце предложения или при сокращении слов.

Поставить точку. | Не забудьте поставить точку в конце предложения

4. В математике, геометрии и физике точка — это единица, имеющая положение в пространстве, граница отрезка линии.

Математическая точка.

5. Точкой называют определённое место в пространстве, на местности или на поверхности чего-либо.

Точка размещения. | Болевая точка.

6. Точкой называют место, где расположено или осуществляется что-либо, определённый узел в системе или сети каких-либо пунктов.

Каждая торговая точка должна иметь свою вывеску.

7. Точкой называют предел развития чего-либо, определённый уровень или момент в развитии.

Наивысшая точка. | Точка в развитии. | Состояние дел достигло критической точки. | Это высшая точка проявления духовной силы человека.

8. Точкой называют температурный предел при котором наступает превращение вещества из одного агрегатного состояния в другое.

Точка кипения. | Точка замерзания. | Точка плавления. | Чем больше высота, тем ниже точка кипения воды.

9. Точкой с запятой (;) называют знак препинания, употребляемый для разделения распространенных, более самостоятельных частей сложносочиненного предложения.

В английском языке используются практически те же самые знаки препинания, что и в русском: точка, запятая, точка с запятой, тире, апостроф, скобки, многоточие, вопросительный и восклицательный знаки, дефис.

10. Когда говорят о точке зрения, имеют в виду чьё-либо мнение об определённой проблеме, взгляд на вещи.

Менее популярна теперь другая точка зрения, ранее почти общепризнанная. | Эту точку зрения в наше время не разделяет никто.

11. Если о людях говорят, что у них есть точки соприкосновения, значит, у них есть общие интересы.

Возможно, нам удастся найти точки соприкосновения.

12. Если о чём-то говорится точка в точку, имеется в виду абсолютно точное соответствие.

Точка в точку в том месте, где было указано, стояла кофейного цвета машина.

13. Если о каком-то человеке говорят, что он дошёл до точки, значит, он достиг крайнего предела в проявлении каких-то отрицательных качеств.

Мы дошли до точки! Так больше жить нельзя! | Не скажешь ведь ему, что спецслужбы дошли до точки под его мудрым руководством.

14. Если кто-то ставит точку в каком-то деле, значит, он прекращает его.

Тогда он вернулся из эмиграции на родину, в Рос сию, в Советский Союз, и этим поставил точку под всеми своими исканиями и раздумьями.

15. Если кто-то ставит точки над «и» (или над i), значит, он доводит дело до логического конца, не оставляет ничего недосказанного.

Давайте расставим все точки над i. Я ничего не знал о вашей самодеятельности.

16. Если кто-то бьёт в одну точку, значит, он сосредоточил все силы на достижении одной цели.

Оттого-то его изображения так отчётливы; он всегда бьёт в одну точку, никогда не увлекаясь второстепенными подробностями.

| Он очень хорошо понимает, какова задача его бизнеса, и целенаправленно бьёт в одну точку.

17. Если кто-то попал в точку, значит, он сказал или сделал именно то, что нужно, угадал.

Первое же письмо, которое пришло на очередной тур конкурса, приятно удивило редакцию — в одном из перечисленных вариантов наш читатель сразу же попал в точку!

• то́чечный

Точечный массаж.

Ответы@Mail.Ru: что такое точка — дайте определение

А невозможно дать определение. Потому как «дать определение» — значит свести данное понятие к чему-то ещё более простому. Что может быть проще точки? Во всякой науке есть аксиоматика. Это набор неких исходных, фундаментальных вещей, которые принимаются как есть, без доказательств, объяснений и определений. Потому что иначе не построить саму логическую систему науки. Ведь если считать науку системой ДОКАЗЫВАЕМЫХ положений, то должны же быть какие-то вещи, НА ОСНОВАНИИ которых всё остальное и доказывается. Вот одно из таких необсуждаемых понятий — точка.

Это такая маааленькая штучка!!!

Начало и конец одновременно

Определение — самая малая единица измерения пространства. Моё мнение, ещё один мир)

Точка? ЭТО КОНЕЦ! ТОЛИ ПРЕДЛОДЕНИЯ, ТОЛИ ДРУЖБЫ, ТОЛИ ОТНОШЕНИЙ!

Точка — Любое тело, размерами и массой которого можно пренебречь при рассчете данных

Строго говоря, точка — понятие НЕОПРЕДЕЛЯЕМОЕ, то есть базисное. Для её определения придется привлечь кучу других понятий, каждое из еоторых, в свою очередь, придется определять. Мне же больше всего нравится формулировка Евклида : точка есть нечто неделимое

Точка (знак препинания) . Точка (диакритический знак) — диакритический знак, который может ставиться над или под буквой или в середине буквы. Точка (геометрия) — абстрактный объект в пространстве. Точки (игра) — игра на бумаге. Точка (единица длины) — единица измерения расстояния в русской и английской системах мер. Точка — один из символов азбуки Морзе. Точка (журнал) — Красноярский молодежно-субкультурный журнал Точка (альбом) — альбом группы «Ленинград» Точка (ДРК) — дивизионный ракетный комплекс Точка зрения — физическая или личностная перспектива, с которой субъект наблюдает происходящие вокруг него события. Материальная точка. Точки Лагранжа, также известные как то&#769;чки либра&#769;ции или ‘L-точки — это такие точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил со стороны этих двух массивных тел, может оставаться неподвижным относительно этих тел. Тройная точка в термодинамике — точка на фазовой диаграмме. Точка росы — температура, до которой должен охладиться воздух, чтобы содержащийся в нем водяной пар достиг состояния насыщения и начал конденсироваться в росу. Квантовая точка — фрагмент проводника или полупроводника ограниченный по всем трём пространственным измерениям и содержащий электроны проводимости. Точка присутствия. Сеть точка-точка — простейший вид компьютерной сети. Огневая точка. Точка с запятой (;) — знак препинания. Микроточка — разновидность стеганографии (тайнописи) . Радиоточка — в проводной радиотрансляционной сети. Думаю подходящее сами выберете. Удачи

Между прочим, если раскрыть школьный учебник по геометрии, Погорелова, то там на первых страницах сказано, что в геометрии (вы, я так понял, имели в виду точку в геометрическом смысле? ) понятия точки, линии, плоскости и т. д. не определяются. Вообще. Кстати, в математике точно так же не определяется понятие числа. Вот так…

Область общая для трех и более пересекающихся плоскостей

Вот доступно, по-моему

Внутренняя точка множества — Википедия

Материал из Википедии — свободной энциклопедии

Вну́тренняя то́чка мно́жества в топологии есть точка, входящая в данное множество вместе с некоторой своей окрестностью.

Пусть X{\displaystyle X} — топологическое пространство, с топологией T{\displaystyle T}, и M⊆X{\displaystyle M\subseteq X}. Точка x∈M{\displaystyle x\in M} является внутренней для M{\displaystyle M} тогда и только тогда, когда существует открытое множество S∈T{\displaystyle S\in T}, такое что x∈S{\displaystyle x\in S} и S⊆M{\displaystyle S\subseteq M}.

• Из определения сразу следует, что в открытом множестве все точки внутренние.
• Также верно и обратное: множество, все точки которого внутренние, является открытым.

В метрическом пространстве определение внутренней точки принимает следующий вид. Пусть X{\displaystyle X} — метрическое пространство с метрикой d{\displaystyle d}, и M{\displaystyle M} — его подмножество. Точка x∈M{\displaystyle x\in M} является внутренней для M{\displaystyle M} тогда и только тогда, когда существует ε>0{\displaystyle \varepsilon >0}, такое что ∀y∈X,d(x,y)<ε⇒y∈M{\displaystyle \forall y\in X,\,d(x,y)<\varepsilon \Rightarrow y\in M}. Иначе говоря, x{\displaystyle x} входит в M{\displaystyle M} вместе с шаром радиуса ε{\displaystyle \varepsilon } с центром в x{\displaystyle x}.

• Кудрявцев Л.Д. — Математический анализ. Том 1.

кто может дать определение точки ?

Точка знак припинания….

Точка — объект в пространстве, обладающий координатами, но не имеющий размеров. Точка — знак препинания для обозначения законченной мысли (предложения) , для обозначения сокращения слов и выражений.

точка — конечный пункт в межличностных отношениях во времени и пространстве.

точка — фигура в пространстве, образованная пересечением двух непараллельных прямых

tochka — matematicheski — ob’ekt kotoryi mozhet byt’ opisan N-nnym kol-vom koordinat v N-nom kol-ve prostrantsv i ne imeet razmera. tochka — znak pripinania tochka zrenia — mnenie

определений точки так много, но я скажу, что это знак препинания

Точка — место пересечения двух прямых линий

Энциклопедия «Кругосвет» МАТЕРИАЛЬНАЯ ТОЧКА — модельное понятие (абстракция) классической механики, обозначающее тело исчезающе малых размеров, но обладающее некоторой массой. С одной стороны, материальная точка — простейший объект механики, так как его положение в пространстве определяется всего тремя числами. Например, тремя декартовыми координатами той точки пространства, в которой находится наша материальная точка. С другой стороны, материальная точка — основной опорный объект механики, так как именно для нее сформулированы основные законы механики. Все другие объекты механики — материальные тела и среды — могут быть представлены в виде той или иной совокупности материальных точек. Например, любое тело можно «разрезать» на малые части и каждую из них принять в качестве материальной точки с соответствующей массой. Когда можно «заменить» реальное тело материальной точкой при постановке задачи о движении тела, зависит от тех вопросов, на которые должно ответить решение формулируемой задачи. Возможны различные подходы к вопросу об использовании модели материальной точки. Один из них носит эмпирический характер. Считают, что модель материальной точки применима тогда, когда размеры движущихся тел пренебрежимо малы по сравнению с величиной относительных перемещений этих тел. В качестве иллюстрации можно привести Солнечную систему. Если считать, что Солнце — неподвижная материальная точка и считать оно действует на другую материальную точку-планету по закону всемирного тяготения, то задача о движении точки-планеты имеет известное решение. Среди возможных траекторий движения точки есть и такие, на которых выполняются законы Кеплера, эмпирически установленные для планет солнечной системы. Таким образом, при описании орбитальных движений планет модель материальной точки вполне удовлетворительна. (Однако, построение математической модели таких явлений как солнечные и лунные затмения требует учета реальных размеров Солнца, Земли и Луны, хотя эти явления, очевидно, связаны с орбитальными движениями. ) Отношение диаметра Солнца к диаметру орбиты ближайшей планеты — Меркурию — составляет величину ~ 1Ї10-2, а отношения диаметров ближних к Солнцу планет к диаметрам их орбит — величины ~ 1 ч 2Ї10-4. Могут ли эти числа служить формальным критерием для пренебрежения размерами тела в других задачах и, следовательно, для приемлемости модели материальной точки? Практика показывает, что нет. Например, маленькая пуля размером l = 1 ч 2 см пролетает расстояние L = 1 ч 2 км, т. е. отношение, однако траектория полета (да и дальность) существенно зависит не только от массы пули, но и от ее формы, и от того, вращается ли она. Поэтому даже маленькую пулю, строго говоря, нельзя считать материальной точкой. Если в задачах внешней баллистики метаемое тело часто считают материальной точкой, то это сопровождается оговорками ряда дополнительных условий, как правило, эмпирически учитывающих реальные характеристики тела. Если обратиться к космонавтике, то когда космический аппарат (КА) выведен на рабочую орбиту, при дальнейших расчетах траектории его полета он считается материальной точкой, так как никакие изменения формы КА не оказывают сколько-нибудь заметного влияния на траекторию. Лишь иногда, при коррекциях траектории возникает необходимость обеспечения точной ориентации реактивных двигателей в пространстве. Когда же спускаемый отсек приблизится к поверхности Земли на расстояние ~100 км, он сразу «превращается» в тело, поскольку от того, каким «боком» он входит в плотные слои атмосферы, зависит, доставит ли отсек в нужную точку Земли космонавтов и возвращаемые материалы. Модель материальной точки оказалась практически неприемлемой для описания движений таких физических объектов микромира, как элементарные частицы, атомные ядра, электрон и т. п. Другой подход к вопросу об использовании модели материальной точки носит рациональный характер. По закону изменения количества дви

так как будеш делить 10 то

Точка- простейшая из геометрических фигур. изображение точки можно получить, прикасаясь к листу бумаги строго отточеным карандашом.

Точка — результат мгновенного касания.

Точка- простейшая геометрическая фигура

Система координат — Википедия

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.

В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Точка P и её координаты в трёхмерной системе координат (с осью Х, направленной к читателю)

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты[править | править код]

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел (x,y):{\displaystyle (x,y):}

• x{\displaystyle x} — расстояние от точки P до оси y с учетом знака
• y{\displaystyle y} — расстояние от точки P до оси x с учетом знака

В пространстве необходимы уже три координаты (x,y,z):{\displaystyle (x,y,z):}

• x{\displaystyle x} — расстояние от точки P до плоскости yz
• y{\displaystyle y} — расстояние от точки P до плоскости xz
• z{\displaystyle z} — расстояние от точки P до плоскости xy

Полярные координаты[править | править код]

Полярные координаты.

В полярной системе координат, применяемой на плоскости, положение точки P определяется её расстоянием до начала координат r = |OP| и углом φ её радиус-вектора к оси Ox.

В пространстве применяются обобщения полярных координат — цилиндрические и сферические системы координат.

Цилиндрические координаты[править | править код]

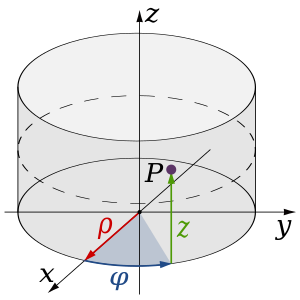Цилиндрические координаты.

Цилиндрические координаты — трёхмерный аналог полярных, в котором точка P представляется упорядоченной тройкой (r,φ,z).{\displaystyle (r,\varphi ,z).} В терминах декартовой системы координат,

• 0⩽r{\displaystyle 0\leqslant {r}} (радиус) — расстояние от оси z до точки P,
• 0⩽φ<360∘{\displaystyle 0\leqslant \varphi <360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») частью оси x и отрезком, проведённым от полюса до точки P и спроектированной на плоскость xy.
• z{\displaystyle z} (высота) равна декартовой z-координате точки P.

Примечание: в литературе для первой (радиальной) координаты иногда используется обозначение ρ, для второй (угловой, или азимутальной) — обозначение θ, для третьей координаты — обозначение h.

Полярные координаты имеют один недостаток: значение φ не определено при r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных относительно некоторой оси. Например, длинный цилиндр с радиусом R в декартовых координатах (с осью z, совпадающей с осью цилиндра) имеет уравнение x2+y2=R2,{\displaystyle x^{2}+y^{2}=R^{2},} тогда как в цилиндрических координатах оно выглядит гораздо проще, как r = R.

Сферические координаты[править | править код]

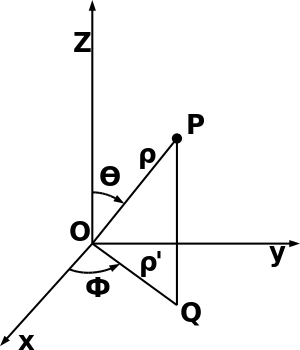Сферические координаты.

Сферические координаты — трёхмерный аналог полярных.

В сферической системе координат расположение точки P определяется тремя компонентами: (ρ,φ,θ).{\displaystyle (\rho ,\varphi ,\theta ).} В терминах декартовой системы координат,

• 0⩽ρ{\displaystyle 0\leqslant \rho } (радиус) — расстояние от точки P до полюса,
• 0⩽φ⩽360∘{\displaystyle 0\leqslant \varphi \leqslant 360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») полуосью x и проекцией отрезка, проведённого из полюса до точки P, на плоскость xy.
• 0⩽θ⩽180∘{\displaystyle 0\leqslant \theta \leqslant 180^{\circ }} (широта или полярный угол) — угол между положительной («плюсовой») полуосью z и отрезком, проведённым из полюса до точки P.

Примечание: в литературе иногда азимут обозначается θ, а полярный угол — φ. Иногда для радиальной координаты используется r вместо ρ. Кроме того, диапазон углов для азимута может выбираться как (−180°, +180°] вместо диапазона [0°, +360°). Наконец, полярный угол может отсчитываться не от положительного направления оси z, а от плоскости xy; в этом случае он лежит в диапазоне [−90°, +90°], а не в диапазоне [0°, 180°]. Иногда порядок координат в тройке выбирается отличным от описанного; например, полярный и азимутальный углы могут быть переставлены.

Сферическая система координат также имеет недостаток: φ и θ не определены, если ρ = 0; угол φ не определён также и для граничных значений θ = 0 и θ = 180° (или для θ = ±90°, в случае принятия соответствующего диапазона для этого угла).

Для построения точки P по её сферическим координатам нужно от полюса вдоль положительной полуоси z отложить отрезок, равный ρ, повернуть его на угол θ вокруг оси y в направлении положительной полуоси x, и затем повернуть на угол θ вокруг оси z в направлении положительной полуоси y.

Сферические координаты полезны при изучении систем, симметричных относительно точки. Так, уравнение сферы с радиусом R в декартовых координатах с началом отсчёта в центре сферы выглядит как x2+y2+z2=R2,{\displaystyle x^{2}+y^{2}+z^{2}=R^{2},} тогда как в сферических координатах оно становится намного проще: ρ=R.{\displaystyle \rho =R.}

Другие распространённые системы координат[править | править код]

• Аффинная (косоугольная) система координат — прямолинейная система координат в аффинном пространстве. На плоскости задается точкой начала координат О и двумя упорядоченными неколлинеарными векторами, которые представляют собой аффинный базис. Осями координат в данном случае называются прямые, проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве, соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса^[1].
• Барицентрические координаты были впервые введены в 1827 году А. Мебиусом, решавшим вопрос о центре тяжести масс, расположенных на вершинах треугольника. Они аффинно инвариантны, представляют собой частный случай общих однородных координат. Точка с барицентрическими координатами расположена в n-мерном векторном пространстве Eⁿ, а собственно координаты при этом относятся к фиксированной системе точек, которые не лежат в (n−1)-мерном подпространстве. Барицентрические координаты используются также и в алгебраической топологии применительно к точкам симплекса^[2].
• Биангулярные координаты — частный случай бицентрических координат, система координат на плоскости, задаваемая двумя фиксированными точками С₁ и С₂, через которые проводится прямая, выступающая в качестве оси абсцисс. Позиция некоторой точки P, которая не лежит на этой прямой, определяется углами PC₁C₂ и PC₂C₁.
• Биполярные координаты ^[3] характеризуются тем, что в качестве координатных линий на плоскости в этом случае выступают два семейства окружностей с полюсами A и B, а также семейство окружностей, ортогональных к ним. Преобразование биполярных координат в декартовы прямоугольные осуществляется посредством специальных формул. Биполярные координаты в пространстве называются бисферическими; в этом случае координатными поверхностями являются сферы, поверхности, образуемые вращением дуг окружностей, а также полуплоскости, проходящие через ось O_z^[4].
• Бицентрические координаты — всякая система координат, которая основана на двух фиксированных точках и в рамках которой положение некоторой другой точки определяется, как правило, степенью её удаления или вообще позицией относительно этих двух основных точек. Системы подобного рода могут быть довольно полезны в определённых сферах научных исследований^[5][6].
• Бицилиндрические координаты — система координат, которая образуется в том случае, если система биполярных координат на плоскости O_xy параллельно переносится вдоль оси O_z. В качестве координатных поверхностей в этом случае выступают семейство пар круговых цилиндров, оси которых параллельны, семейство ортогональных к ним круговых цилиндров, а также плоскость. Для перевода бицилиндрических координат в декартовы прямоугольные для трехмерного пространства также применяются специальные формулы^[7].
• Конические координаты — трехмерная ортогональная система координат, состоящая из концентрических сфер, которые описываются посредством их радиуса, и двух семейств перпендикулярных конусов, расположенных вдоль осей x и z^[8].
• Координаты Риндлера используются преимущественно в рамках теории относительности и описывают ту часть плоского пространства-времени, которая обыкновенно называется пространством Минковского. В специальной теории относительности равномерно ускоряющаяся частица находится в гиперболическом движении, и для каждой такой частицы в координатах Риндлера может быть выбрана такая точка отсчёта, относительно которой она покоится.
• Параболические координаты — это двумерная ортогональная система координат, в которой координатными линиями является совокупность конфокальных парабол. Трехмерная модификация параболических координат строится путём вращения двумерной системы вокруг оси симметрии этих парабол. У параболических координат также имеется определенный спектр потенциальных практических приложений: в частности, они могут использоваться применительно к эффекту Штарка. Параболические координаты связаны определенным отношением с прямоугольными декартовыми^[9].
• Проективные координаты существуют, согласно наименованию, в проективном пространстве П_n (К) и представляют собой взаимно однозначное соответствие между его элементами и классами конечных подмножеств элементов тела К, характеризующихся свойствами эквивалентности и упорядоченности. Для определения проективных координат проективных подпространств достаточно определить соответствующие координаты точек проективного пространства. В общем случае относительно некоторого базиса проективные координаты вводятся чисто проективными средствами^[10].
• Тороидальная система координат — трехмерная ортогональная система координат, получаемая в результате вращения двумерной биполярной системы координат вокруг оси, разделяющей два её фокуса. Фокусы биполярной системы, соответственно, превращаются в кольцо с радиусом а, лежащее на плоскости xy тороидальной системы координат, в то время как ось z становится осью вращения системы. Фокальное кольцо также называют иногда базовой окружностью^[11].
• Трилинейные координаты являются одним из образцов однородных координат и имеют своей основой заданный треугольник, так что положение некоторой точки определяется относительно сторон этого треугольника — главным образом степенью удаленности от них, хотя возможны и другие вариации. Трилинейные координаты могут быть относительно просто преобразованы в барицентрические; кроме того, они также конвертируемы в двумерные прямоугольные координаты, для чего используются соответствующие формулы^[12].
• Цилиндрические параболические координаты — трехмерная ортогональная система координат, получаемая в результате пространственного преобразования двумерной параболической системы координат. Координатными поверхностями, соответственно, служат конфокальные параболические цилиндры. Цилиндрические параболические координаты связаны определенным отношением с прямоугольными, могут быть применены в ряде сфер научных исследований^[13].
• Эллипсоидальные координаты — эллиптические координаты в пространстве. Координатными поверхностями в данном случае являются эллипсоиды, однополостные гиперболоиды, а также двуполостные гиперболоиды, центры которых расположены в начале координат. Система ортогональна. Каждой тройке чисел, являющихся эллипсоидальными координатами, соответствуют восемь точек, которые относительно плоскостей системы O_xyz симметричны друг другу^[14].

Переход из одной системы координат в другую[править | править код]

Декартовы и полярные[править | править код]

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

где u₀ — функция Хевисайда с u0(0)=0,{\displaystyle u_{0}(0)=0,} а sgn — функция signum. Здесь функции u₀ и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая возвращает правильный φ в необходимом квадранте, определённом координатами x и y.

Декартовы и цилиндрические[править | править код]

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

z=z.{\displaystyle z=z.\quad }

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

z=z.{\displaystyle z=z.\quad }

(dxdydz)=(rcos⁡θ−rsin⁡φ0rsin⁡θrcos⁡φ0001)⋅(drdφdz),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}r\cos \theta &-r\sin \varphi &0\\r\sin \theta &r\cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}},}

(drdφdz)=(xx2+y2yx2+y20−yx2+y2xx2+y20001)⋅(dxdydz).{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{\sqrt {x^{2}+y^{2}}}}&{\frac {x}{\sqrt {x^{2}+y^{2}}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}

Декартовы и сферические[править | править код]

x=ρsin⁡θcos⁡φ,{\displaystyle {x}=\rho \,\sin \theta \,\cos \varphi ,\quad }

y=ρsin⁡θsin⁡φ,{\displaystyle {y}=\rho \,\sin \theta \,\sin \varphi ,\quad }

z=ρcos⁡θ;{\displaystyle {z}=\rho \,\cos \theta ;\quad }

ρ=x2+y2+z2,{\displaystyle {\rho }={\sqrt {x^{2}+y^{2}+z^{2}}},}

θ=arccos⁡zρ=arctg⁡x2+y2z,{\displaystyle {\theta }=\arccos {\frac {z}{\rho }}=\operatorname {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y.{\displaystyle {\varphi }=\operatorname {arctg} {\frac {y}{x}}+\pi \,u_{0}(-x)\,\operatorname {sgn} y.}

(dxdydz)=(sin⁡θcos⁡φρcos⁡θcos⁡φ−ρsin⁡θsin⁡φsin⁡θsin⁡φρcos⁡θsin⁡φρsin⁡θcos⁡φcos⁡θ−ρsin⁡θ0)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}\sin \theta \cos \varphi &\rho \cos \theta \cos \varphi &-\rho \sin \theta \sin \varphi \\\sin \theta \sin \varphi &\rho \cos \theta \sin \varphi &\rho \sin \theta \cos \varphi \\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}

(dρdθdφ)=(x/ρy/ρz/ρxzρ2×2+y2yzρ2×2+y2−(x2+y2)ρ2×2+y2−yx2+y2xx2+y20)⋅(dxdydz).{\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}x/\rho &y/\rho &z/\rho \\{\frac {xz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}

Цилиндрические и сферические[править | править код]

r=ρsin⁡θ,{\displaystyle {r}=\rho \,\sin \theta ,}

φ=φ,{\displaystyle {\varphi }=\varphi ,\quad }

z=ρcos⁡θ;{\displaystyle {z}=\rho \,\cos \theta ;}

ρ=r2+z2,{\displaystyle {\rho }={\sqrt {r^{2}+z^{2}}},}

θ=arctg⁡zr+πu0(−r)sgn⁡z,{\displaystyle {\theta }=\operatorname {arctg} {\frac {z}{r}}+\pi \,u_{0}(-r)\,\operatorname {sgn} z,}

φ=φ.{\displaystyle {\varphi }=\varphi .\quad }

(drdφdh)=(sin⁡θρcos⁡θ0001cos⁡θ−ρsin⁡θ0)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dh\end{pmatrix}}={\begin{pmatrix}\sin \theta &\rho \cos \theta &0\\0&0&1\\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}

(dρdθdφ)=(rr2+z20zr2+z2−zr2+z20rr2+z2010)⋅(drdφdz).{\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}{\frac {r}{\sqrt {r^{2}+z^{2}}}}&0&{\frac {z}{\sqrt {r^{2}+z^{2}}}}\\{\frac {-z}{r^{2}+z^{2}}}&0&{\frac {r}{r^{2}+z^{2}}}\\0&1&0\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}.}

Географическая система координат обеспечивает возможность идентификации любой точки на поверхности земного шара совокупностью цифробуквенных обозначений. Как правило, координаты назначаются таким образом, что один из указателей обозначает позицию по вертикали, а другой или совокупность других — по горизонтали. Традиционный набор географических координат — широта, долгота и высота^[15]. Географическая система координат с использованием трёх перечисленных указателей является ортогональной.

Широта точки на поверхности Земли определяется как угол между плоскостью экватора и прямой, проходящей через эту точку в виде нормали к поверхности базового эллипсоида, примерно совпадающего по форме с Землей. Эта прямая обычно проходит в нескольких километрах от центра Земли, за исключением двух случаев: полюсов и экватора (в этих случаях она проходит непосредственно через центр). Линии, соединяющие точки одной широты, именуются параллелями. 0° широты соответствуют плоскости экватора, Северный полюс Земли соответствует 90° северной широты, Южный — соответственно, 90° южной широты. В свою очередь, долгота точки на поверхности Земли определяется как угол в восточном или западном направлении от основного меридиана к другому меридиану, проходящему через эту точку. Меридианы, соединяющие точки одной долготы, представляют собой полуэллипсы, сходящиеся на полюсах. Нулевым считается меридиан, проходящий через королевскую обсерваторию в Гринвиче, близ Лондона. Что касается высоты, то она отсчитывается от условной поверхности геоида, являющегося абстрактным пространственным представлением земного шара.