Что нужно указать для задания функции. Функции и способы задания функций

Что означают слова «задать функцию»? Они означают: объяснить всем желающим, о какой конкретной функции идёт речь. Причём, объяснить чётко и однозначно!

Как это можно сделать? Как задать функцию?

Можно написать формулу. Можно нарисовать график. Можно составить табличку. Любой способ — это какое-то правило, по которому можно узнать значение игрека для выбранного нами значения икса. Т.е. «задать функцию» , это значит — показать закон, правило, по которому икс превращается в игрек.

Обычно, в самых различных заданиях присутствуют уже готовые функции. Они нам уже заданы. Решай себе, да решай.) Но… Чаще всего школьники (да и студенты) работают с формулами. Привыкают, понимаешь… Так привыкают, что любой элементарный вопрос, относящийся к другому способу задания функции, тотчас огорчает человека…)

Во избежание подобных случаев, имеет смысл разобраться с разными способами задания функций. Ну и, конечно, применить эти знания к «хитрым» вопросам. Это достаточно просто. Если знаете, что такое функция…)

Поехали?)

Аналитический способ задания функции.

Самый универсальный и могучий способ. Функция, заданная аналитически, это функция, которая задана формулами. Собственно, это и есть всё объяснение.) Знакомые всем (хочется верить!)) функции, например: y = 2x, или y = x 2 и т.д. и т.п. заданы именно аналитически.

К слову сказать, не всякая формула может задавать функцию. Не в каждой формуле соблюдается жёсткое условие из определения функции. А именно — на каждый икс может быть только один игрек. Например, в формуле у = ±х , для одного значения х=2, получается два значения у: +2 и -2. Нельзя этой формулой задать однозначную функцию. А с многозначными функциями в этом разделе математики, в матанализе, не работают, как правило.

Чем хорош аналитический способ задания функции? Тем, что если у вас есть формула — вы знаете про функцию

всё! Вы можете составить табличку. Построить график. Исследовать эту функцию по полной программе. Точно предсказать, где и как будет вести себя эта функция. Весь матанализ стоит именно на таком способе задания функций. Скажем, взять производную от таблицы крайне затруднительно…)

Аналитический способ достаточно привычен и проблем не создаёт. Разве что некоторые разновидности этого способа, с которыми сталкиваются студенты. Я про параметрическое и неявное задание функций.) Но такие функции — в специальном уроке.

Переходим к менее привычным способам задания функции.

Табличный способ задания функции.

Как следует из названия, этот способ представляет собой простую табличку. В этой таблице каждому иксу соответствует (ставится в соответствие ) какое-то значение игрека. В первой строчке — значения аргумента. Во второй строчке — соответствующие им значения функции, например:

Таблица 1.

x	— 3	— 1	0	2	3	4
y	5	2	— 4	— 1	6	5

Прошу обратить внимание! В данном примере игрек зависит от икса как попало. Я специально так придумал.) Нет никакой закономерности. Ничего страшного, так бывает. Значит, именно так я задал эту конкретную функцию. Именно так я установил правило, по которому икс превращается в игрек.

Можно составить другую табличку, в которой будет закономерность. Этой табличкой будет задана другая функция, например:

Таблица 2.

x	— 3	— 1	0	2	3	4
y	— 6	— 2	0	4	6	8

Уловили закономерность? Здесь все значения игрека получаются умножением икса на двойку. Вот и первый «хитрый» вопрос: можно ли функцию, заданную с помощью Таблицы 2, считать функцией у = 2х ? Подумайте пока, ответ будет ниже, в графическом способе. Там это всё очень наглядно.)

Чем хорош табличный способ задания функции? Да тем, что считать ничего не надо. Всё уже посчитано и написано в таблице.) А более ничего хорошего нет. Мы не знаем значения функции для иксов, которых нет в таблице. В этом способе такие значения икса просто не существуют. Кстати, это подсказка к хитрому вопросу.) Мы не можем узнать, как ведёт себя функция за пределами таблицы. Ничего не можем. Да и наглядность в этом способе оставляет желать лучшего… Для наглядности хорош графический способ.

Графический способ задания функции.

В данном способе функция представлена графиком. По оси абсцисс откладывается аргумент (х), а по оси ординат — значение функции (у). По графику тоже можно выбрать любой х и найти соответствующее ему значение у . График может быть любой, но… не какой попало.) Мы работаем только с однозначными функциями. В определении такой функции чётко сказано: каждому х ставится в соответствие единственный у . Один игрек, а не два, или три… Для примера, посмотрим на график окружности:

Окружность, как окружность… Почему бы ей не быть графиком функции? А давайте найдем, какой игрек будет соответствовать значению икса, например, 6? Наводим курсор на график (или касаемся рисунка на планшете), и… видим, что этому иксу соответствует

два значения игрека: у=2 и у=6.

Два и шесть! Стало быть, такой график не будет графическим заданием функции. На один икс приходится два игрека. Не соответствует этот график определению функции.

Но если условие однозначности выполнено, график может быть совершенно любым. Например:

Эта самая кривулина — и есть закон, по которому можно перевести икс в игрек. Однозначный. Захотелось нам узнать значение функции для х = 4, например. Надо найти четвёрку на оси иксов и посмотреть, какой игрек соответствует этому иксу. Наводим мышку на рисунок и видим, что значение функции у для х=4 равно пяти. Какой формулой задано такое превращение икса в игрек — мы не знаем. И не надо. Графиком всё задано.

Теперь можно вернуться к «хитрому» вопросу про у=2х. Построим график этой функции. Вот он:

Разумеется, при рисовании этого графика мы не брали бесконечное множество значений х.

Взяли несколько значений, посчитали у, составили табличку — и всё готово! Самые грамотные вообще всего два значения икса взяли! И правильно. Для прямой больше и не надо. Зачем лишняя работа?

Но мы совершенно точно знали, что икс может быть любым. Целым, дробным, отрицательным… Любым. Это по формуле у=2х видно. Поэтому смело соединили точки на графике сплошной линией.

Если же функция будет нам задана Таблицей 2, то значения икса нам придётся брать только из таблицы. Ибо другие иксы (и игреки) нам не даны, и взять их негде. Нет их, этих значений, в данной функции. График получится из точек. Наводим мышку на рисунок и видим график функции, заданной Таблицей 2. Значения икс-игрек на осях я не писал, разберётесь, поди, по клеточкам?)

Вот и ответ на «хитрый» вопрос. Функция, заданная Таблицей 2 и функция у=2х — разные.

Графический способ хорош своей наглядностью. Сразу видно, как ведёт себя функция, где возрастает. где убывает. По графику сразу можно узнать некоторые важные характеристики функции. А уж в теме с производной, задания с графиками — сплошь и рядом!

Вообще, аналитический и графический способы задания функции идут рука об руку. Работа с формулой помогает построить график. А график частенько подсказывает решения, которые в формуле и не заметишь… Мы с графиками дружить будем.)

Почти любой ученик знает три способа задания функции, которые мы только что рассмотрели. Но на вопрос: «А четвёртый!?» — зависает основательно.)

Такой способ есть.

Словесное описание функции.

Да-да! Функцию можно вполне однозначно задать словами. Великий и могучий русский язык на многое способен!) Скажем, функцию у=2х можно задать следующим словесным описанием: каждому действительному значению аргумента х ставится в соответствие его удвоенное значение. Вот так! Правило установлено, функция задана.

Более того, словесно можно задать функцию, которую формулой задать крайне затруднительно, а то и невозможно. Например:

каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично. А вот табличку легко составить. И график построить. Кстати, график забавный получается…) Попробуйте.

Способ словесного описания — способ достаточно экзотичный. Но иногда встречается. Здесь же я его привёл, чтобы придать вам уверенности в неожиданных и нестандартных ситуациях. Нужно просто понимать смысл слов «функция задана…» Вот он, этот смысл:

Если есть закон однозначного соответствия между х и у — значит, есть функция. Какой закон, в какой форме он выражен — формулой, табличкой, графиком, словами, песнями, плясками — сути дела не меняет. Этот закон позволяет по значению икса определить соответствующее значение игрека. Всё.

Сейчас мы применим эти глубокие знания к некоторым нестандартным заданиям.) Как и обещано в начале урока.

Задание 1:

Функция у = f(x) задана Таблицей 1:

Таблица 1.

Найти значение функции p(4), если p(х)= f(x) — g(x)

Если вы вообще не можете понять, что к чему — прочитайте предыдущий урок «Что такое функция?» Там про такие буковки и скобочки очень

Способы задания функций

Способы задания функций

Способы задания функций

Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами — наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

Функция может быть определена разными формулами на разных участках области своего задания.

Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Пример 1: функция E(x) — целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, где r — целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [x] = r. Функция E(x) = [x] постоянна на промежутке [r; r+1) и на нем [x] = r.

Пример 2: функция y = {x} — дробная часть числа. Точнее y ={x} = x — [x], где [x] — целая часть числа x. Эта функция определена для всех x. Если x — произвольное число, то представив его в виде x = r + q ( r = [x]), где r — целое число и q лежит в интервале [0; 1), получим {x} = r + q — r=q

Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.

Какое правило задает функцию. Алгоритмический и словесный способы задания функций

Одними из классических определений понятия «функция» считаются определения на базе соответствий. Приведем ряд таких определений.

Определение 1

Зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется функцией .

Определение 2

Пусть даны два непустых множества $X$ и $Y$. Соответствие $f$, которое каждому $x\in X$ сопоставляет один и только один $y\in Y$ Называется функцией ($f:X → Y$).

Определение 3

Пусть $M$ и $N$ — два произвольных числовых множества. Говорят, что на $M$ определена функция $f$, принимающая значения из $N$, если каждому элементу $x\in X$ поставлен в соответствие один и только один элемент из $N$.

Следующее определение дается через понятие переменной величины. Переменной величиной называется величина, которая в данном исследовании принимает различные числовые значения.

Определение 4

Пусть $M$ — множество значений переменной величины $x$. Тогда, сели каждому значению $x\in M$ соответствует одно определенное значение другой переменной величины $y$ есть функция величины $x$, определенной на множестве $M$.

Определение 5

Пусть $X$ и $Y$ — некоторые числовые множества. Функцией называется множество $f$ упорядоченных пар чисел $(x,\ y)$ таких, что $x\in X$, $y\in Y$ и каждое $x$ входит в одну и только одну пару этого множества, а каждое $y$ входит, по крайней мере, в одну пару .

Определение 6

Всякое множество $f=\{\left(x,\ y\right)\}$ упорядоченных пар $\left(x,\ y\right)$ таких, что для любых пар $\left(x»,\ y»\right)\in f$ и $\left(x»»,\ y»»\right)\in f$ из условия $y»≠ y»»$ следует, что $x»≠x»»$ называется функцией или отображением .

Определение 7

Функция $f:X → Y$ — это множество $f$ упорядоченных пар $\left(x,\ y\right)\in X\times Y$, таких, что для любого элемента $x\in X$ существует единственный элемент $y\in Y$ такой, что $\left(x,\ y\right)\in f$, то есть функция — кортеж объектов $\left(f,\ X,\ Y\right)$.

В этих определениях

$x$ — независимая переменная.

$y$ — зависимая переменная.

Все возможные значения переменной $x$ называется областью определения функции , а все возможные значения переменной $y$ называется областью значения функции.

Аналитический способ задания функции

Для этого способа нам понадобится понятие аналитического выражения.

Определение 8

Аналитическим выражением называется произведение всех возможных математических операций над какими-либо числами и переменными.

Аналитическим способом задания функции и является её задание с помощью аналитического выражения.

Пример 1

$y=x^2+7x-3$, $y=\frac{x+5}{x+2}$, $y=cos5x$.

Плюсы:

1. С помощью формул мы можем определить значение функции для любого определенного значения переменной $x$;
2. Функции, заданные таким способом можно изучать с помощью аппарата математического анализа.

Минусы:

1. Малая наглядность.
2. Иногда приходится производить очень громоздкие вычисления.

Табличный способ задания функции

Данный способ задания состоит в том, что для нескольких значений независимой переменной выписываются значения зависимой переменной. Все это вносится в таблицу.

Пример 2

Рисунок 1.

Плюс: Для любого значения независимой переменной $x$, которая внесена в таблицу, сразу узнается соответствующее значение функции $y$.

Минусы:

1. Чаще всего, нет полного задания функции;
2. Малая наглядность.

Задать функцию означает установить правило (закон) с помощью которого по данным значениям независимой переменной находим соответствующие им значения функции. Рассмотрим различные способы задания функции.

Эта запись определяет температуру Т как функцию от времени t:T=f(t). Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения функции сразу, без дополнительных изменений или вычислений. Недостатки: определяет функцию не полностью, а лишь для некоторых значений аргумента; не дает наглядного изображения характера изменения функции с изменением аргумента.

2. Графический способ. Графиком функцииy=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Это может быть некоторая кривая, в частности прямая, множество точек на плоскости.

Преимущество – наглядность, недостаток – нет возможности точно определить значения аргумента. В технике и физике часто он является единственно доступным способом задания функции, например, при пользовании самопишущими приборами, которые автоматически записывают изменение одной величины относительно другой (барограф, термограф и др.).

3. Аналитический способ. По этому способу функция задается аналитически, с помощью формулы. Такой способ дает возможность по каждому численному значению аргумента х найти соответствующее ему численное значение функции у точно или с некоторой точностью.

При аналитическом способе функция может быть задана и несколькими разными формулами. Например, функция

задана в области определения [-, 15] с помощью трех формул.

Если зависимость между х и у задана формулой, разрешенной относительно у, т.е. имеет вид у = f(x) , то говорят, что функция от х задана в явном виде, например,. Если же значения х и у связаны некоторым уравнением видаF(x,y) = 0, т.е. формула не разрешена относительно у, то говорят, что функция задана неявно. Например,. Заметим, что не всякую неявную функцию можно представить в виде у =f(x), наоборот, любую явную функцию всегда можно представить в виде неявной:
. Еще одна разновидность аналитического задания функции – параметрическое, когда аргумент х и функция у являются функциями третьей величины – параметраt: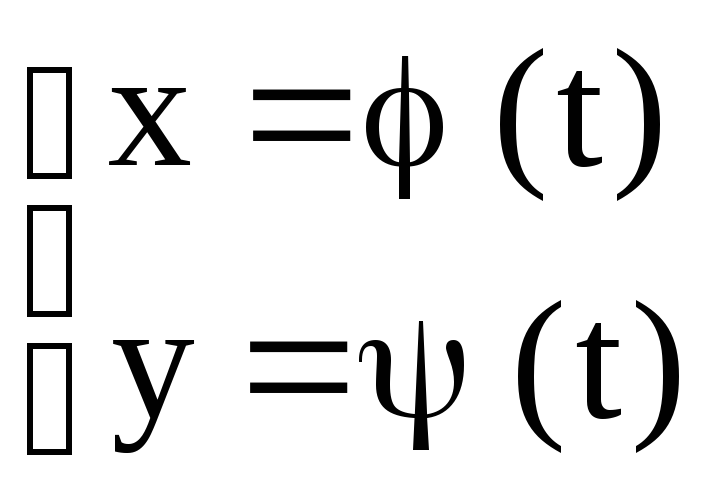
, где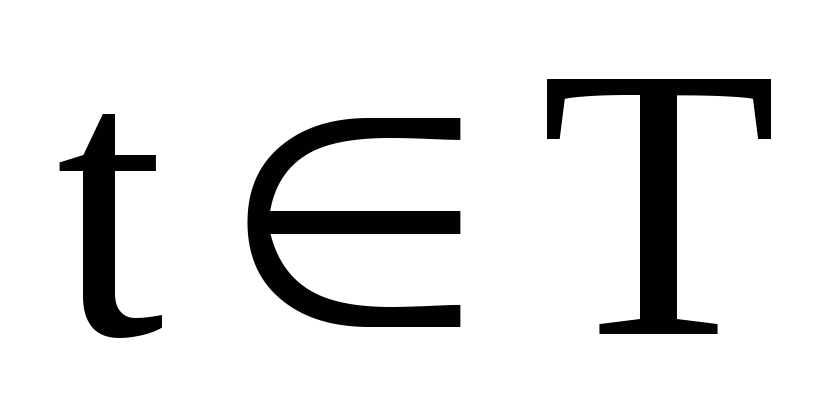
, Т – некоторый промежуток. Такой способ широко применяется в механике, в геометрии.

Аналитический способ является самым распространенным способом задания функции. Компактность, возможность применения к данной функции аппарата математического анализа, возможность вычисления значений функции при любых значениях аргумента – его основные преимущества.

4. Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами. Например, функция Е(х) – целая часть числа х, функция Дирихле, функция Римана,n!,r(n) – число делителей натурального числаn.

5. Полуграфический способ. Здесь значения функции представляются в виде отрезков, а значения аргумента – в виде чисел, проставленных на концах отрезков, указывающих значения функции. Так, например, в термометре есть шкала с равными делениями, у которых проставлены числа. Эти числа являются значениями аргумента (температуры). Они стоят на том месте, которое определяет графическое удлинение столбца ртути (значения функции) в связи с ее объемным расширением в результате температурных изменений.

>>Математика: Способы задания функции

Способы задания функции

Приводя в предыдущем параграфе различные примеры функций, мы несколько обеднили само понятие функции .

Ведь задать функцию — это значит указать правило, которое позволяет по произвольно выбранному значению х из Б(0 вычислить соответствующее значение у. Чаще всего это правило связано с формулой или с несколькими формулами — такой способ задания функции обычно называют аналитическим. Все функции, рассмотренные в § 7, были заданы аналитически. Между тем есть другие способы задания функции, о них и пойдет речь в настоящем параграфе.

Если функция была задана аналитически и нам удалось по

Способы задания функции

Из предыдущего параграфа следует, что основным признаком функциональной зависимости между двумя переменными величинами является наличие соответствия между значениями этих величин: каждому (допустимому) значению одной из них соответствует вполне определенное значение другой.

Как только такое соответствие установлено, то говорят, что задана функция.

Это соответствие может быть установлено различными способами. Рассмотрим некоторые из них.

1. Табличный способ. Всего проще установить соответствие между значениями двух переменных так: указать значения аргумента и для каждого из них указать соответствующее значение функции. Такой способ задания функции называется табличным.

Вообще, всякие таблицы, как например таблицы квадратов чисел, квадратных корней, таблицы синусов и др., являются не чем иным, как табличным заданием функции. Так, в таблице синусов аргументом является угол, а функцией — его синус. Каждому данному в таблице значению угла соответствует в той же таблице определенное значение его синуса.

2. Графический способ. Табличное значение функции неудобно тем, что дает значения функции только для тех значений аргумента, которые приведены в таблице.

Если надо иметь значения функции для любых значений аргумента (в тех или иных границах) и если при этом не требуется для значений функции большой точности, то в этих случаях часто применяется графический способ. Он основан на следующем: для каждого значения аргумента на плоскости строится точка, абсцисса которой равна данному значению аргумента, а ордината — соответствующему значению функции.

При всевозможных изменениях абсциссы (то есть аргумента) соответствующие точки на плоскости образуют некоторую линию, которая называется графиком данной функции. Дав аргументу определенное значение, восставляем в соответствующей точке оси абсцисс перпендикуляр к ней. Ордината точки пересечения с графиком и дает соответствующее значение функции.

Пример. В § 89 был дан график зависимости y = x². Здесь любое данное число является значением аргумента, а соответствующая ордината является значением функции этого аргумента, именно его квадратом.

Из сказанного видно, что если задана некоторая функция, то можно построить ее график; графиком можно пользоваться для нахождения приближенных значений функции. В практике нередко функция задается готовым, начерченным графиком. Так, например, в современном производстве широко применяются самопишущие приборы, которые автоматически вычерчивают графики изменения тех или иных величин (температуры, давления и т. п.).

3. Аналитический способ. Функция может быть задана формулой, показывающей, как по данному значению аргумента вычислить соответствующее значение функции. Такой способ задания функции называется аналитическим.

Пример. Функция y = x² задана формулой, показывающей, как для каждого значения аргумента x вычислить соответствующее значение функции.

Возможны и другие способы задания функции.

Выше было сказано, что переменные величины принято обозначать последними буквами латинского алфавита — x, y, z, … При этом обычно аргумент обозначают буквой x, а функцию — буквой y. Такое обозначение связано с тем, что при графическом изображении функциональной зависимости значения аргумента отсчитываются по оси абсцисс (оси «иксов»), а соответствующие значения функции — по оси ординат (оси «игреков»). Выше это показано на примере графика функции y = x².

Способы задания функций.

В математике для решения разных задач очень часто используют разные функции. А знаете ли вы как их можно задавать и в каких случаях надо использовать тот или иной вид? Для начала рассмотрим определение:

Функция считается заданной (известной), если для каждого значения аргумента (из числа возможных) можно узнать соответствующее её значение.

Наиболее употребительны три методы:

• табличный,
• графический,
• аналитический.

Далее остановимся более подробно на каждом из них.

Табличный способ — общеизвестен (таблицы логарифмов, квадратных корней и т. д.). Он сразу дает числовое значение функции. В этом его преимущество перед другими способами. Недостатки: таблица трудно обозрима в целом; она часто не содержит всех нужных значений аргумента.

Графический способ состоит в построении линии (графика) в разных системах координат, например в Декартовой – абсциссы (по горизонтали) изображают значения аргумента, а ординаты (по вертикали) — соответствующие значения функции. Часто бывает, что функция быстро стремится вверх или вниз, поэтом тогда удобнее масштабы на осях брать разными.

Преимущества графического способа — легкость обозрения в целом и непрерывность изменения аргумента; недостатки: ограниченная степень точности и утомительность прочитывания значений функции с максимально возможной точностью.

Аналитический способ состоит в задании функции одной или несколькими формулами, например, $y=f(x)$. Если зависимость между х и у выражена уравнением, разрешенным относительно у, то величина у называется явной функцией аргумента х, в противном случае — неявной. Преимущество здесь в том, что всегда можно вычислить точно значение для любого аргумента. Недостатки, что по самой формуле сложно понять общее поведение функции.

Теперь вы знаете основные методы, и можете использовать любой тот, какой будет удобнее для вас при решении конкретной задачи. Вот, например, вы хотите зарабатывать на форекс, и вам надо проанализировать состояние рынка, спрогнозировать будущее тенденции. То для начала вы таблично выводите уже имеющие данные, потом по ним ищите аналитический вид и график, по которому и делаете необходимые выводы.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

Числовые функции. Определение и способы задания

Вопросы занятия:

·     повторить определение числовых функций;

·     повторить способы задания функций;

·     повторить основные преобразования графиков числовых функций;

·     повторить вид графиков основных функций.

Материал урока

Определение.

Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.

Область определения обозначается D(f).

x – независимая переменная или аргумент.

y – зависимая переменная.

Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).

Определение.

Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости  отмечены все точки вида (x, y), где x принадлежит множеству X, а y=f(x), то множество этих точек называют графиком функции y=f(x), где x принадлежит множеству X.

Перед вами графики некоторых функций и их названия.

Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a<0, и влево, если a>0 на │b│ вверх, если b>0, и вниз, если b<0.

Пример.

Определение.

Задать функцию – указать правило, которое позволяет по произвольно выбранному значению x из области определения функции вычислить соответствующее значение y.

Способы задания функции.

Чаще всего это правило связано с формулой (например, y=3x+5). Такой способ задания функции называется аналитическим.

Пример.

Тем самым на отрезке [a; b] задана функция y=f(x). Такой способ задания функции называют графическим.

Заметим, что если функция была задана аналитически и нам удалось построить ее график, то тем самым мы фактически осуществили переход от аналитического способа задания функции к графическому.

Табличный способ задания функции – с помощью таблицы, в которой указаны значения функции для конечного множества значений аргумента.

Например:

Словесный способ задания функции – способ, при котором правило задания функции описывается словами.

Пример.

Материал по математике на тему «Задание функции несколькими способами»

Понятие «функция» часто используется при изучении реальных процессов в природе, науке и технике. Само понятие «функция» возникло в XVII веке и прошло сложный и трудный путь развития. Среди ученых, внесших большой вклад в развитие представлений о функции, были Г.В. Лейбниц (немецкий философ и математик), И. Ньютон (английский физик и математик), Л. Эйлер (швейцарец по происхождению, многие годы живший и работавший в России по приглашению Екатерины II), Н.И. Лобачевский (русский математик), Л. Дирихле (немецкий математик), А.Н. Колмогоров (советский математик) и др. На практике изменение одной величины обычно связано с изменением одной или нескольких других величин.

Функция является заданной,  иначе говоря,  известной,  если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции.  Наиболее распространенные три способа задания функции: табличный,  графический,  аналитический,  существуют еще словесный и рекурсивный способы.

1. Табличный способ наиболее широко распространен (таблицы логарифмов,  квадратных корней) ,  основное его достоинство – возможность получения числового значения функции,  недостатки заключаются в том,  что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.

 Аргумент х принимает заданные в таблице значения,  а у определяется соответственно этому аргументу х.

2. Графический способ заключается в проведении линии (графика) ,  у которой абсциссы изображают значения аргумента,  а ординаты – соответствующие значения функции.  Часто для наглядности масштабы на осях принимают разными.

Достоинства этого способа задания функций заключаются в легкости и целостности восприятия,  в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

3. Аналитический способ состоит в задании функции одной или несколькими формулами.  Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента,  а недостатком является затрата времени на проведение дополнительных математических операций.

Например:

Функцию можно задать с помощью математической формулы y=x²,  тогда если х равно 2,  то у равно 4,  возводим х в квадрат.

4. Словесный способ состоит в задании функции обычным языком,  т. е.  словами.  При этом необходимо дать входные,  выходные значения и соответствие между ними.

Например:

Словесно можно задать функцию (задачу) ,  принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр,  из которых состоит значение у.  Поясняем: если х равно 4,  то у равно 4,  а если х равно 358,  то у равен сумме 3 + 5 + 8,  т.  е 16.  Далее аналогично.

5. Рекурсивный способ состоит в задании функции через саму себя,  при этом значения функции определяются через другие ее же значения.  Такой способ задания функции используется в задании множеств и рядов.

Весь материал — смотрите документ.