Обнаружены скелеты древних египтян с загадочными конусами на головах
На рисунках, дошедших до наших дней, ученые замечали, что головы некоторых древних египтян венчают небольшие конусы. Особенно часто они появлялись на изображениях, выполненных 3-4 тысячи лет назад.
Изображения древних египтян с конусами на головах.
До сих пор ни одного «головного конуса» найдено не было. И ученые считали их своего рода мифами — художественными дополнениями, которые каким-то образом выделяли тех или иных изображенных людей, указывая на их особенный статус.
Но вот недавно нашлись сразу два конуса, — сообщает портал ScienceAlert со ссылкой на журнал Antiquity. Нашлись не отдельно, а вместе с владельцами. Один был надет на голову 20-летней женщины, другой — на голову молодого человека, чей пол определить не удалось. И те и другие останки извлекли из могил, которые располагались на месте древнеегипетского города Амарна (Amarna), который был основан фараоном Эхнатоном (Akhetaten) в 1346 году до нашей эры.
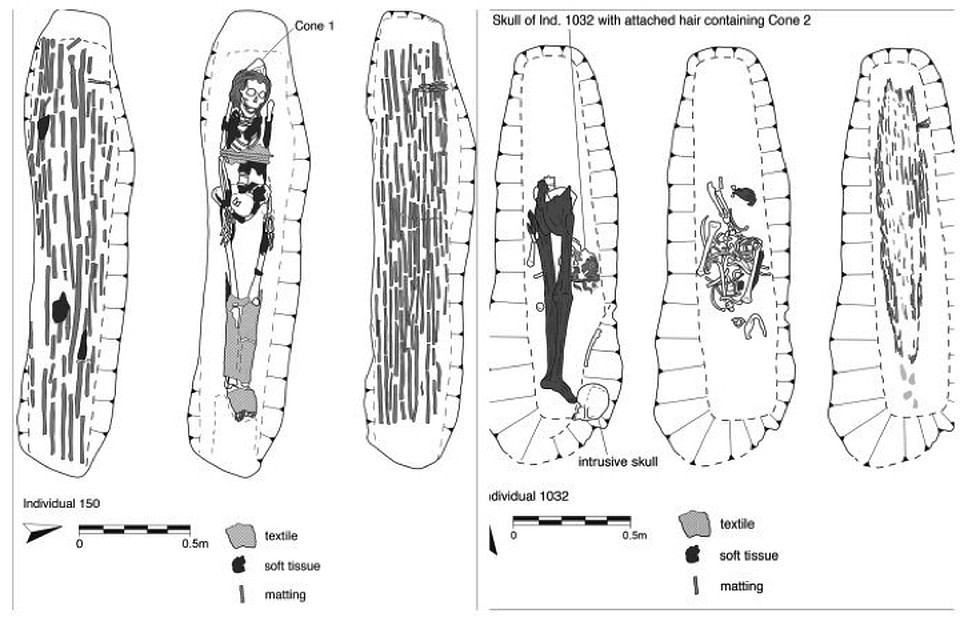
Захоронения со скелетами с конусами на головах.
Конусы оказались полыми, изготовленными из пчелиного воска и армированными льняными волокнами. Что сильно озадачило археологов. И никак не проясняло функцию этих, с позволения сказать, головных уборов. Так же пока не ясно: предназначались ли они для загробной жизни или конусы зачем-то носили еще при жизни. Никаких письменных свидетельств, проясняющих ситуацию, пока не найдено. Известно лишь одно, что древние египтяне не снабжали покойников вещами, совсем уж бесполезными на том свете. Стало быть, конусы были предметами весьма необходимыми.
КСТАТИ
А что за цилиндры держат в руках представители верховной власти Древнего Египта
Странные предметы цилиндрической формы присутствуют и на изваяниях и на рисунках, изображающих фараонов и жрецов. Ни одного пока не найдено. Как когда-то было с конусами. Поэтому ответить на вопрос о предназначении этих цилиндров, будет еще сложнее.
Цилиндры не могли быть печатями — печати носили на шее. Это и не атрибуты власти — ими служили длинные жезлы с загнутым концом. Тубусы для хранения папирусов? Вряд ли. Хватило бы и одного тубуса. А цилиндров всегда пара — по одному в каждой руке. Они похожи на гантели, но вряд ли фараоны, держащие их, занимались физкультурой.
Цилиндры в руках древних египтян.
Цилиндры не выдавали покойникам — в могилах и погребальных камерах похожие предметы не попадались. Значит они были нужны исключительно живым. Но зачем? Загадка. Похлеще, чем шапочки конусами.
Изваяний с цилиндрами полно. Есть весьма монументальные.
СЛУШАЙТЕ ТАКЖЕ
Что будет с нами, когда исчезнет Солнце
Что утонет, если растает Гренландия? Как наш мозг поддаётся чужому внушению? Как древние майя достигли невероятных высот развития без ничего? Об этом и еще очень-очень многом другом в научном и очень популярном подкасте «Передача данных» Радио «Комсомольская правда» рассказывает Мария Баченина. Подписывайтесь на новые выпуски в Apple Podcasts и Google Podcasts и слушайте, когда удобно! Пожалуйста, не забудьте поставить оценку и написать комментарий к новым выпускам, нам важно ваше мнение!
www.kp.ru
Цилиндр. Виды, объём цилиндра, площадь поверхности :: SYL.ru
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия – раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье – цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже – коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец – знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
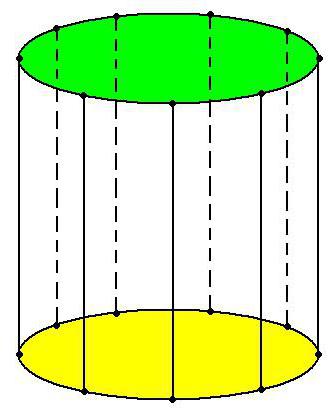
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами – усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра – один из элементов данной геометрической фигуры. Другая её важная составляющая – рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра – круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
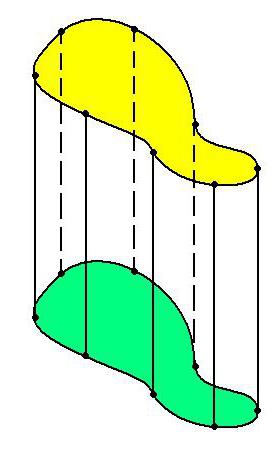
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр – наклонный.
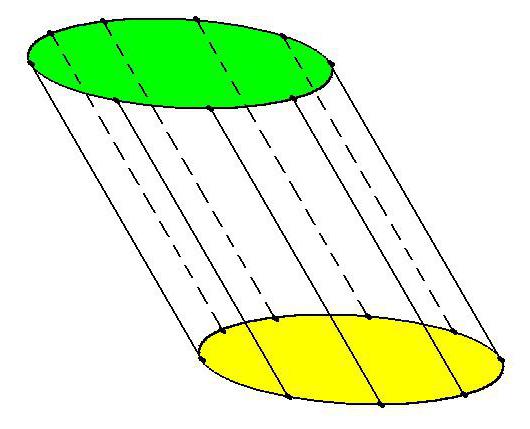
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения – самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a, расположенная вертикально. ABCD – прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения – прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
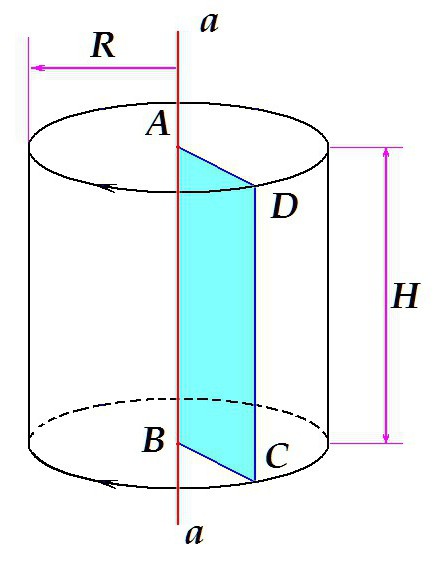
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг – шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
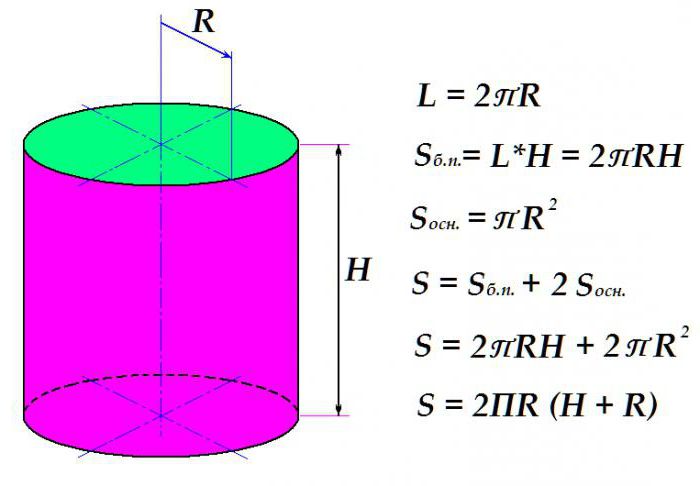
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
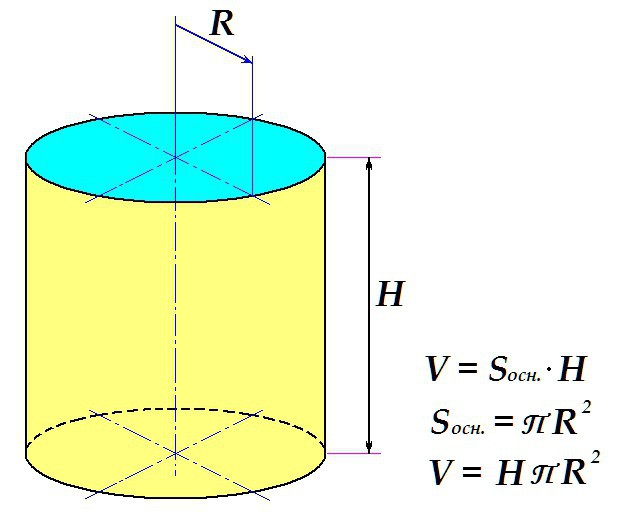
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
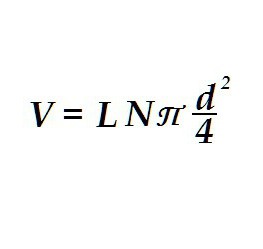
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.
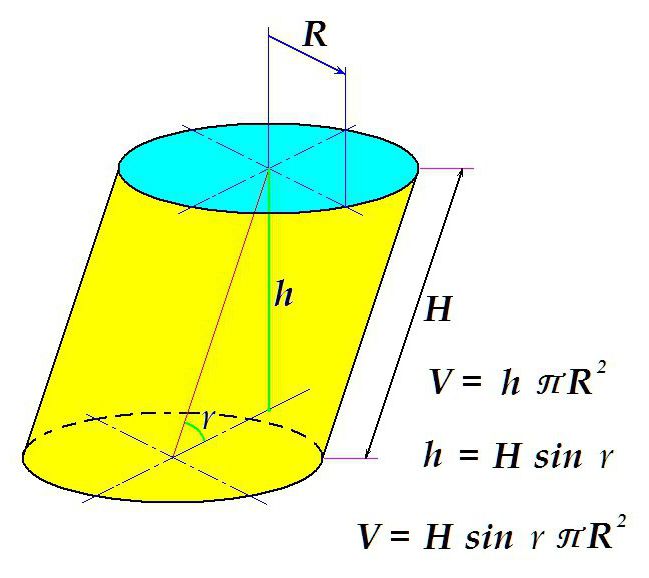
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
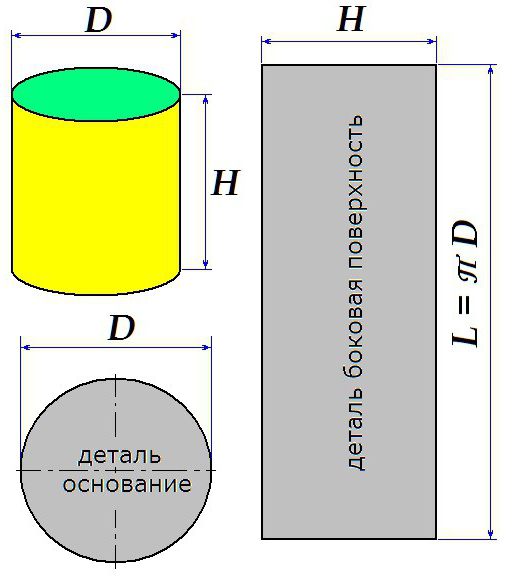
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
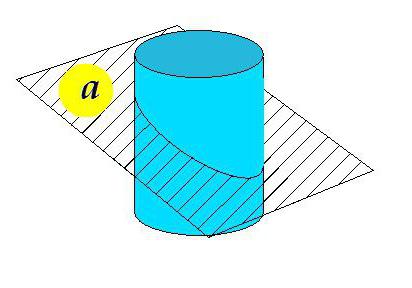
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
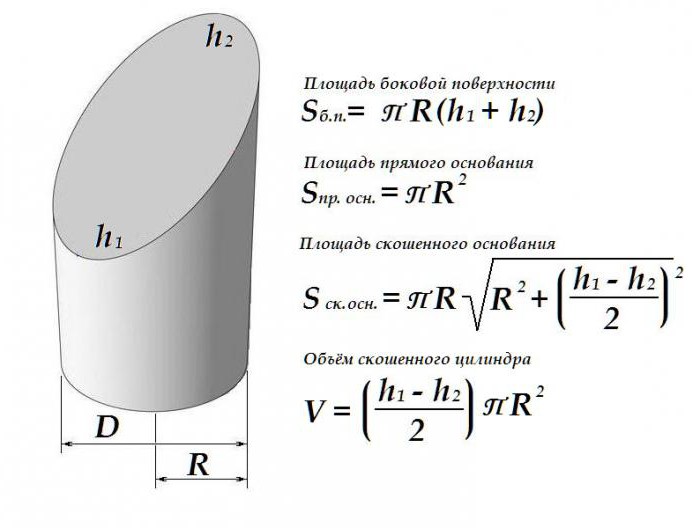
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
www.syl.ru
Цилиндр как геометрическая фигура
Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.
Основания цилиндра равны и лежат в параллельных плоскостях, а образующие цилиндра параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковую поверхность составляют образующие.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из сторон как оси. Существуют и другие виды цилиндра – эллиптический, гиперболический, параболический. Призму так же рассматривают, как разновидность цилиндра.
На рисунке 2 изображён наклонный цилиндр. Круги с центрами О и О1 являются его основаниями.
Радиус цилиндра – радиус его основания. Высота цилиндра – расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра.
Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Призмой, вписанной в цилиндр, называется такая призма, основания которой – равные многоугольники, вписанные в основания цилиндра. Её боковые рёбра являются образующими цилиндра. Призма называется описанной около цилиндра, если её основания — равные многоугольники, описанные около оснований цилиндра. Плоскости её граней касаются боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра можно найти по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, которая равна периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:
Sb = Ph.
В частности, для прямого кругового цилиндра:
P = 2πR, и Sb = 2πRh.
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:
Sp = 2πRh + 2πR2 = 2πR(h + R)
Для нахождения объёма наклонного цилиндра существуют две формулы.
Можно найти объём, умножив длину образующей на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
Объём наклонного цилиндра равен произведению площади основания на высоту (расстояние между плоскостями, в которых лежат основания):
V = Sh = S l sin α,
где l – длина образующей, а α – угол между образующей и плоскостью основания. Для прямого цилиндра h = l.
Формула для нахождения объёма кругового цилиндра выглядит следующим образом:
V = π R2 h = π (d2 / 4)h,
где d – диаметр основания.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Предметы похожие на цилиндр — БэбиБлог
Компания «Умница» 5 апреля 2015, 01:52 ТН с «Умницей». «Геометрия для малышей». День 5. День 5. Книги, логические задания, загадки 1.При помощи цветных карточек из набора «Творчество с пеленок» постройте паровоз из прямоугольных разноцветных вагонов. 2. Задание на развитие логики для деток постарше (см. прикрепленные).
Рассмотрите и назовите геометрические фигуры, помещенные на странице слева. Сначала называй меньшую по величине фигуру, затем — большую. Например, круг в квадрате, круг в овале, овал в круге.
Вам нужно перенести каждую меньшую по величине фигуру на новое место — на соответствующие фигуры большего размера…
www.babyblog.ru
Рисуем цилиндрические и конусообразные предметы — Копилка знаний
Цилиндр.
Еще одна простая геометрическая форма -это цилиндр, который встречается повсюду в природе. Основная форма ствола дерева — цилиндр; с этой же формой можно сравнить вашу шею и бедра. Потренируйтесь рисовать очертания цилиндров заостренным кончиком карандаша. Не переживайте но поводу того, что рисунок получается не очень точным. I (пошлите линия несколько раз, пока они не станут правильными.
Размещение светотени на цилиндре.
Подберите непрозрачный предмет цилиндрической формы, например, рулон бумажных полотенец, и изучите расположение на нем светотени. На цилиндре, изображенном на этом рисунке, вы видите плавные переходы от света к полутени, от полутени к тени, от тени к рефлексу. Падающая от цилиндра тень находится справа. На цилиндре, в отличие от куба, тона плавно переходят один в другой.
Банка.
Среди большого количества предметов домашнего обихода цилиндрическую форму имеет байка. Нарисуйте различные цилиндрические предметы, какие только сможете найти. Если ваши предметы не стеклянные, представьте, что они прозрачны и вы видите их дно, имеющее форму эллипса. У этой банки, как и у цилиндра слева, верхний эллипс более узкий, чем нижний.
Размещение светотени на банке.
Банка демонстрирует те же постепенные переходы от света к полутени, от полутени к тени, от тени к рефлексу. Та же последовательность тонов отражена на крышке, от которой падает тень на горлышко банки. Нанесите градации светотени уверенными и быстрыми штрихами, как это сделал в данном случае художник. Аккуратность рисунка менее важна, чем внимание и наблюдательность.
По этой теме читайте на сайте :
kopilca.ru
Цилиндр — урок. Геометрия, 11 класс.
Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
Прямоугольник AOO1A1 вращается вокруг стороны OO1.
OO1 — ось симметрии цилиндра и высота цилиндра.
AA1 — образующая цилиндра, длина которой равна длине высоты цилиндра.
\(AO\) — радиус цилиндра.
Полученная цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги — основаниями цилиндра.
Осевое сечение цилиндра — это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является прямоугольником.
При сечении цилиндра плоскостью, параллельной оси цилиндра (т. е. перпендикулярной основанию), также получается прямоугольник.
На рисунке изображён цилиндр, пересечённый плоскостью, которая параллельна оси цилиндра OO1.
ABB1A1 — прямоугольник.
\(OA = OB = R\) — радиусы.
\(OC\) — расстояние от оси цилиндра до плоскости сечения.
Дуга \(AB\) равна центральному углу \(AOB\).
При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем круг, равный основаниям цилиндра.
Если представить, что боковая цилиндрическая поверхность разрезана по образующей AA1 и развёрнута, получаем прямоугольник.
Сторона AA1 равна высоте \(H\), а другую сторону образует развёрнутая окружность основания длиной 2πR.
Так как развёртка — прямоугольник, то боковая поверхность определяется по формуле:
Sбок.=2πR⋅H.
Основания цилиндра — два круга с общей площадью 2⋅πR2.
Полная поверхность цилиндра определяется по формуле:
Sполн.=2πRH+2πR2=2πR⋅H+R.
www.yaklass.ru
Чем похожи человек и спиннер?
Для топологии нет разницы между шаром или мячом, блином или цилиндром. Это один из самых высоких уровней математической абстракции, который рассматривает свойства поверхности как таковой, без привязки к ее размерам или конкретной форме. Так, шар можно увеличить или уменьшить, раскатать в цилиндр, а цилиндр — расплющить в блинчик. Но вот чтобы сделать бублик, придется либо склеивать цилиндр, либо прорвать отверстие в блинчике.
С точки зрения топологии именно дырки — одно из ключевых свойств поверхности. Если выложить на поверхности шара или цилиндра петлю из нитки, ее можно стянуть без узелка, и такое пространство называется односвязным. С бубликом такое не получится: помешает отверстие. Нельзя превратить фигуры разной линейной связности одну в другую без разрывов или склеек. Топологические фигуры, для которых такое возможно, связываются гомеоморфными — как при игре с куском пластилина — преобразованиями. Чашка и бублик гомеоморфны, бублик и цилиндр — нет. Но чему гомеоморфен человек?
Традиционная китайская медицина учит, что у человека имеется семь отверстий: вход и выход желудочно-кишечного тракта, уши, ноздри и выходы наружных половых органов. Современная анатомия считает иначе — например, наружные половые органы у мужчин заканчиваются яичками, поэтому с точки зрения топологии отверстия они не образуют. Это тупик, «впадина», которую гомеоморфными преобразованиями можно устранить без всяких склеек и разрывов. Просветы женских половых органов завершаются фаллопиевыми трубами, которые открываются в полость тела. Она также не сообщается с внешней средой, делая это «отверстие» всего лишь «впадиной».
Это касается и ушей, отверстия которых закрываются герметичной (в норме) барабанной перепонкой. Но вот с оставшимися отверстиями дело обстоит сложнее: помимо «входа» и «выхода» желудочно-кишечного тракта, к нему в области носоглотки подходят просветы, начинающиеся ноздрями. У нас остается четыре соединенных друг с другом отверстия — непростой случай. Редакции «ПМ» пришлось привлечь математика-тополога, чтобы выяснить: человек гомеоморфен спиннеру. Говоря точнее, тройному тору.
Андрей Коняев, кандидат физико-математических наук, доцент кафедры дифференциальной геометрии и приложений мехмата МГУ
«В топологии не всегда легко сказать, к какой простейшей фигуре можно свести поверхность: к сфере, тору и т. п. Общего правила на этот счет нет, все зависит от конкретной поверхности и от того, как она задана. Если мы описываем ее формулой (как сферу: x2 + y2 + z2 = 1), то эта задача обычно бывает очень сложна. Если же поверхность задается атласом, то есть набором отдельных составляющих ее фигур (картами) и правилами их склейки, то найти исходную фигуру можно достаточно быстро».
Статья «Гомеоморфные человечки» опубликована в журнале «Популярная механика» (№3, Март 2018).www.popmech.ru