Касательная к графику функции и производная с примерами решения
Вы уже знаете, какую прямую называют касательной к окружности. А что понимают, например, под касательной к синусоиде? Прямая
Пусть даны график функции и на ней точка которая не является концом графика (рис. 60). Обозначим на данном графике по разные стороны от произвольные точки Прямые — секущие. Если же точки двигаясь по графику, приближать достаточно близко к как угодно близко будут приближаться к некоторой прямой Такую прямую (если она существует) называют касательной к графику функции в точке
Если график функции такой, как показано на рисунке 61, то при неограниченном приближении точек к точке предельные положения секущих — прямые — не совпадут. Говорят, что в точке касательной к графику функции не существует.
И если — крайняя точка графика, то касательной к нему в точке не существует.
Понятие касательной к графику часто используют для исследования функций.
Касательная — это прямая. Её уравнение имеет вид где — угловой коэффициент — тангенс угла между лучом касательной, расположенным выше оси и положительным направлением этой оси. Обратите внимание на угловой коэффициент касательной, проведённой к графику какой-либо функции в его точке с абсциссой Если число принадлежит промежутку возрастания функции, то соответствующее значение положительное (рис. 62). Если принадлежит промежутку убывания функции, то — отрицательное (рис. 63). И наоборот: если каждому значению из некоторого промежутка соответствует положительное значение то на данная функция возрастает; если каждому значению из некоторого промежутка соответствует отрицательное значение то на функция убывает. Заслуживают внимания и те точки графика функции, в которых касательная не существует, и в которых она параллельна оси
Итак, зная угловые коэффициенты касательных к графику функции в тех или иных точках, можно сделать вывод, возрастает данная функция в этих точках, или убывает.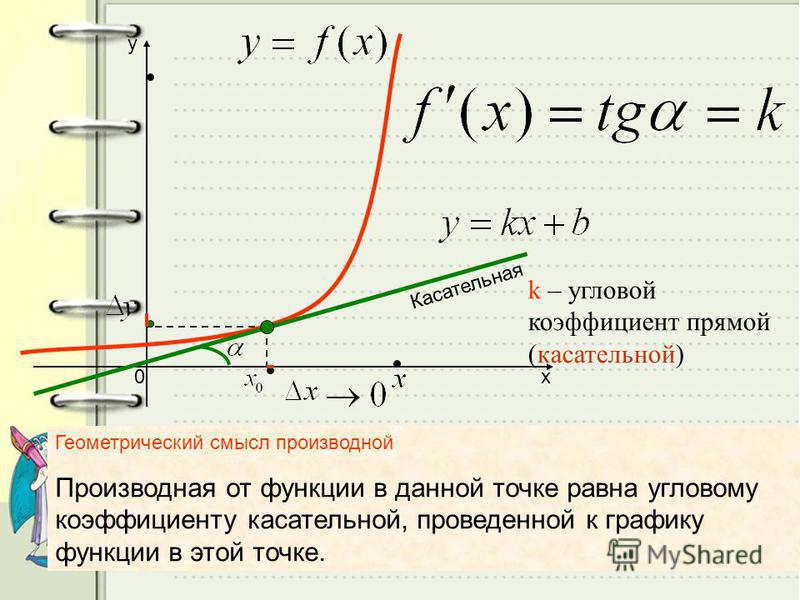
Поскольку для исследования функций важно уметь определять угловой коэффициент касательной к её графику, то рассмотрим подробнее связь этого коэффициента с исследуемой функцией.
Пусть даны график функции и на ней точку в которой существует касательная к графику (рис. 64). Если абсцисса точки равна то её ордината — Дадим значению аргумента приращение Тогда значению аргумента на графике функции соответствует точка с абсциссой и ординатой
Через точки проведём прямые параллельные осям абсцисс и ординат. Они пересекутся в некоторой точке Тогда — приращение аргумента, а — приращение функции на
Угловой коэффициент секущей равен тангенсу угла т. е. отношению
Если то секущая поворачиваясь вокруг точки приближается к касательной, проведённой в точке к графику данной функции. Итак, если — угловой коэффициент этой касательной и то
Так определяется угловой коэффициент касательной к графику функции в некоторой точке если касательная в ней не параллельна оси Если касательная к графику функции в некоторой точке параллельна оси то угловой коэффициент этой касательной равен нулю.
К вычислению значения выражения или приводит решение многих задач по механике, электричеству, биологии, экономике, статистике и т. д. Именно поэтому это выражение получило специальное название — производная.
Производной функции в точке называют предел отношения приращения функции в точке к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует.
Производную функции в точке обозначают Её определение записывают также в виде равенства:
Пример:Найдите производную функции в точке
Решение:
Дадим аргументу приращение Соответствующее приращение функции
Тогда Если
Следовательно,
Ответ.
Так решают задачу, пользуясь определением производной функции в точке.
До сих пор речь шла о производной функции в точке. А можно рассматривать производную функции и как функцию. Пусть, например, дана функция Найдём её производную в произвольной точке Для этого дадим значению приращение Соответствующее ему приращение функции
Поэтому Если
Имеем
Следовательно, производная функции в каждой её точке равна Пишут: или, если
Обратите внимание! Производная функции в точке — это число. Когда же говорят о производной, не указывая «в точке», подразумевают производную как функцию: производной функции есть функция производной функции есть функция и т. д.
Когда же говорят о производной, не указывая «в точке», подразумевают производную как функцию: производной функции есть функция производной функции есть функция и т. д.
Зная это, производную функции в точке можно вычислять проще, чем по определению производной функции в точке. Пример 2. Дана функция Найдите Решение. Производной функции является функция Поэтому
Нахождение производной называется дифференцированием. Функция, которая имеет производную в точке называется дифференцируемой в точке Функция, дифференцируемая в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.
Докажем, например, что линейная функция дифференцируема в каждой точке Действительно, приращению её аргумента соответствует приращение функции Поэтому и если А это и значит, что в каждой точке функция имеет производную
Пишут
В частности:
Производная постоянной равна нулю.
Из курса планиметрии известно, что уравнение прямой, проходящей через заданную точку имеет вид где — угловой коэффициент прямой.
Поскольку для касательной к графику функции угловой коэффициент равен значению производной в точке касания то можем записать общий вид уравнения касательной, проведённой к графику функции в точке касания
До сих пор речь шла о касательных к криволинейным графикам. Но графиком функции может быть и прямая или часть прямой. Поэтому для обобщения договариваются касательной к прямой в любой её точке считать эту самую прямую. Касательной к отрезку или лучу в любой его внутренней точке считают прямую, которой принадлежит этот отрезок или луч.
Выше было установлено, что производная линейной функции равна коэффициенту при переменной, т.е
Полученный результат имеет очевидный геометрический смысл: касательная к прямой — графику функции — есть эта самая прямая, её угловой коэффициент равен
Пример:
Найдите угол, который образуете положительным направлением оси касательная к графику функции в точке
Решение:
Определим сначала угловой коэффициент этой касательной по формуле — приращения функции и приращения аргумента соответственно.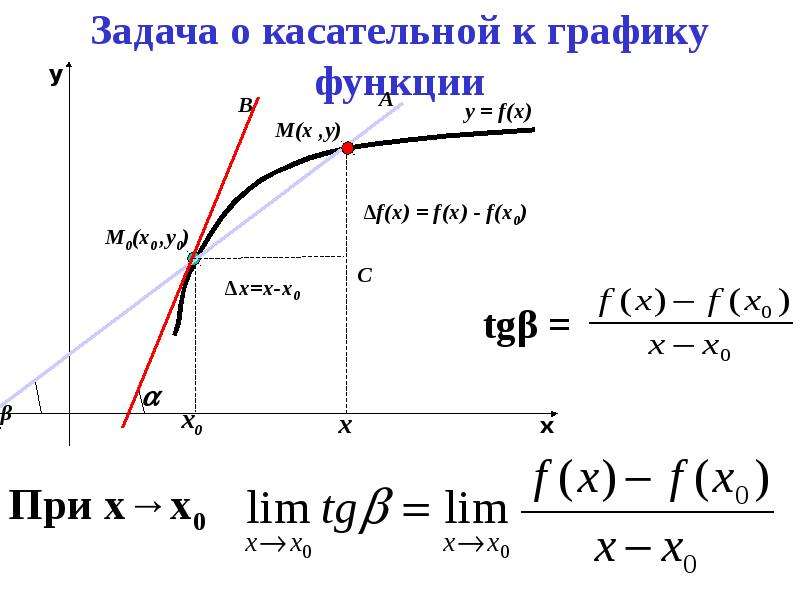
Найдем приращение функции в точке
Найдём угловой коэффициент касательной:
Поскольку
Известно также, что поэтому отсюда
Пример:
Докажите, что для функции производной есть функция
Решение:
Если А это и означает, что производной функции является функция
Пример:
Напишите уравнение касательной к графику функции в его точке с абсциссой
Решение:
Способ 1. Уравнение касательной имеет вид Угловой коэффициент равен значению производной функции в точке Значит, уравнение касательной Координаты точки касания Точка с такими координатами принадлежит касательной, поэтому отсюда Следовательно, уравнение касательной имеет вид:
Способ 2. Запишем общий вид уравнения касательной:
Найдём
Подставим найденные значения в уравнение касательной:
Касательная параллельна прямой
Задания из №7 ЕГЭ, в которых известно, что касательная к графику функции параллельна данной прямой, могут быть связаны как с графиком функции, так и с графиком производной. Поэтому очень важно внимательно читать условие.
Поэтому очень важно внимательно читать условие.
1) На рисунке изображен график функции y=f(x), определённой на интервале(-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
Решение:
Касательная к графику функции параллельна оси абсцисс, а значит, и любой прямой вида y=b, где b — число, в точках экстремума, в которых производная существует, и в точках перегиба. То есть это задание аналогично заданию на определение точек графика функции, в которых производная равна нулю.
На графике данной функции y=f(x) таких точке две (с абсциссами x=-1 и x=2). Значит, касательная к графику функции параллельна прямой y=12 в двух точках.
Ответ: 2.
Теперь рассмотрим аналогичное задание, в котором дан график производной функции.
2)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
Решение:
Прямые y=k1x+b1 y=k2x+b2 параллельны, если их угловые коэффициенты равны: k 1=k2.
y=12=0x+12, ⇒k1=0.
Угловой коэффициент касательной равен значению производной в точке касания: k2=f'(xo).
Значит, ищем точки, в которых значение производной равно нулю.
Таких точек три (с абсциссами x=-3, x=1 и x=3).
Ответ: 3.
3)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=3x-11 или совпадает с ней.
Решение:
y=3x-12, ⇒k1=3.
Прямые параллельны, если k1=k2.
k2=f'(xo).
Поэтому ищем точки, в которых значение производной равно 3.
Таких точек в данном примере четыре.
Ответ: 4.
4)На рисунке изображён график производной функции f(x).
Решение:
y=4-x,⇒k1=-1.
Прямые параллельны, если k1=k2.
Прямые параллельны, если k1=k2.
k2=f'(xo).
Ищем точку, в которой значение производной равно -1. Абсцисса этой точки xo=7.
Ответ: 7.
Касательная к графику функции. Задача с параметром.
Задание 7 (№ 119973) из Открытого банка заданий для подготовки к ЕГЭ по математике.
Прямая является касательной к графику функции . Найдите b, учитывая, что абсцисса точки касания больше 0.
Решение.
Для начала, как обычно, вспомним теорию, и «вытащим» из условия задачи все факты, которые помогут ее решению.
1. Так как прямая является касательной к графику функции , следовательно:
а) Производная функции в точке касания равна коэффициенту наклона прямой .
То есть y’=-5
Найдем производную функции :
y’=56x+b
Получаем: ,
Так как на значение абсциссы точки касания накладывается дополнительное условие (абсцисса точки касания больше 0), выразим переменную х через параметр
.
б) Прямая является касательной к параболе, если имеет с ней одну общую точку.
Чтобы найти точку пересечения прямой и параболы , нужно составить систему уравнений
В конечном итоге, нам нужно определить, при каком значении параметра эта система имеет единственное решение.
Приравняем правые части уравнений системы:
Перенесем все слагаемые влево и сгруппируем:
Мы получили квадратное уравнение, которое имеет единственный корень, если дискриминант равен нулю. Приравняем дискриминант к нулю:
Решим квадратное уравнение:
Отсюда , .
По условию задачи абсцисса точки касания больше 0.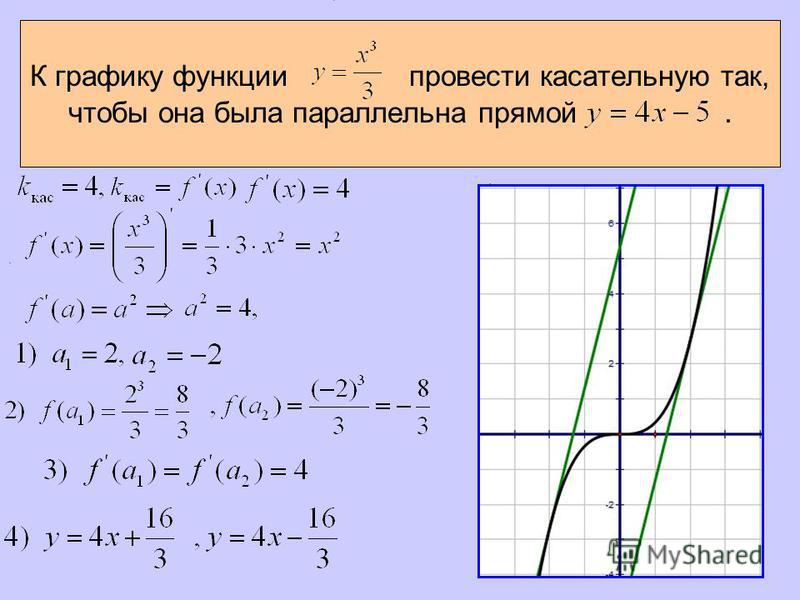
Вспомним, как мы выразили абсциссу точки касания через параметр :
Подставим значения параметра в это равенство.
а) ,
б) ,
Нас устраивает случай б)
Ответ:
Вероятно, Ваш браузер не поддерживается. Попробуйте скачатьFirefox
И.В. Фельдман, репетитор по математике.
Касательная к графику функции — презентация онлайн
1. Касательная к графику функции
10 класс2. Повторение:
График — прямаяЛинейная функция: y= k x + b
k — угловой коэффициент прямой
Уравнение прямой с угловым
коэффициентом
3. Повторение:
k = tg αПрямая, проходящая через точку (хо; f(хо)), с
угловым коэффициентом f `(xo))
4. Повторение:
Если в точке xo существуетпроизводная, то существует и
касательная (невертикальная) к
графику функции в точке xo.
5. Если же f’ (x0) не существует, то касательная либо
не существует (как уфункции у = |х|)
вертикальна (как у
графика функции у=3√х
6.
 Повторение: Варианты взаимного расположения
Повторение: Варианты взаимного расположениякасательной и оси абсцисс
k>0
k=0
у
k
у
у
β
β
х
х
угол
угол = 00
х
угол > 900 (тупой)
7. Повторение:
Геометрический смысл производной:Угловой коэффициент касательной равен
значению производной функции в точке
проведения касательной
k = f `(xo)
8. Выполните задание:
Дана функция у = х3Напишите
уравнение касательной
к графику этой функции
в точке х0 = 1.
9. Тема урока:
Уравнение касательной.Цели урока:
1. Вывести уравнение касательной к
графику функции в точке х0.
2. Научиться составлять уравнение
касательной для заданной функции.
10. Дана функция у = х3
Дана функция у =3
х
• Необходимо:
написать уравнение
касательной к графику этой
функции в точке х0 = 1.
Уравнение касательной
у = 3х — 2
11. Дана функция у = f (x)
Необходимо:написать
уравнение
касательной к
графику этой
функции в
точке х0.

12. Вывод:
Уравнение касательнойимеет вид:
y = f(xo) + f `(xo)( x – xo)
13. Алгоритм
• Найти значение функции в точке хо• Вычислить производную функции
• Найти значение производной функции в
точке хо
• Подставить полученные числа в формулу
y = f(xo) + f `(xo)( x – xo)
• Привести уравнение к стандартному
виду
15. Минута отдыха
16. Алгоритм
• Найти значение функции в точке хо• Вычислить производную функции
• Найти значение производной функции в
точке хо
• Подставить полученные числа в формулу
y = f(xo) + f `(xo)( x – xo)
• Привести уравнение к стандартному
виду
17. Задание*:
На параболе у = 3х2 — 4х + 6• найти точку, в которой
касательная к ней // прямой
у =2х+4,
• написать уравнение
касательной в этой точке.
18. Домашнее задание:
• Формула, алгоритм• №43.3(в,г),№43.7(в,г), №43.26(в,г)
• задание*:
На параболе у = х2 + 5х – 16 найти
точку, в которой касательная к ней //
прямой 5х+у+4 =0 и написать
уравнение касательной в этой точке.

Уравнение касательной по двум точкам. Касательная к графику функции в точке
Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис.1).
Другое определение : это предельное положение секущей при Δx →0.
Пояснение : Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.
Строгое определение касательной:
Касательная к графику функции f , дифференцируемой в точке x о , — это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).
Угловой коэффициент имеет прямая вида y = kx + b . Коэффициент k и является угловым коэффициентом этой прямой.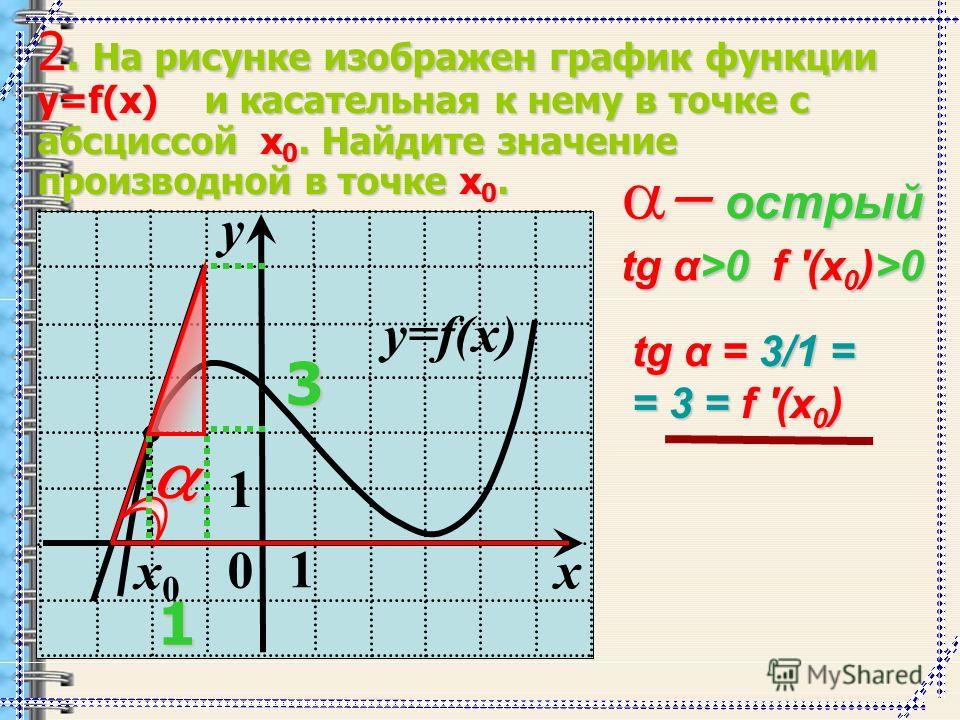
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c , где c – некоторое действительное число (рис. 4).
4).
Уравнение касательной к графику функции y = f (x ) в точке x о :
Пример
: Найдем уравнение касательной к графику функции f (x ) = x 3 – 2x 2 + 1 в точке с абсциссой 2.
Решение .
Следуем алгоритму.
1) Точка касания x о равна 2. Вычислим f (x о ):
f (x о ) = f (2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x ). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х 2 = 2х , а х 3 = 3х 2 . Значит:
f ′(x ) = 3х 2 – 2 ∙ 2х = 3х 2 – 4х .
Теперь, используя полученное значение f ′(x ), вычислим f ′(x о ):
f ′(x о ) = f ′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: x о = 2, f (x о ) = 1, f ′(x о ) = 4.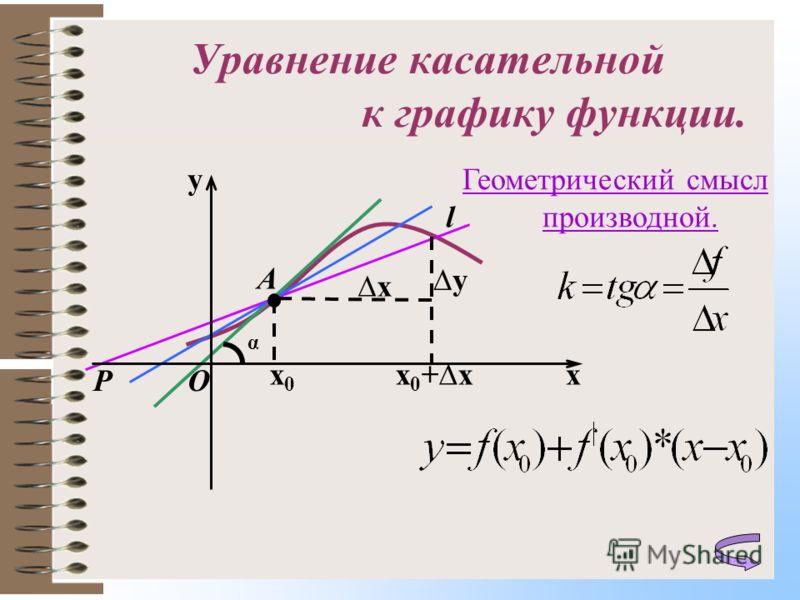 Подставляем эти числа в уравнение касательной и находим окончательное решение:
Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f (x о ) + f ′(x о ) (x – x о ) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ : у = 4х – 7.
Инструкция
Определяем угловой коэффициент касательной к кривой в точке М.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).
Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
Найдите значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет ее х-координате.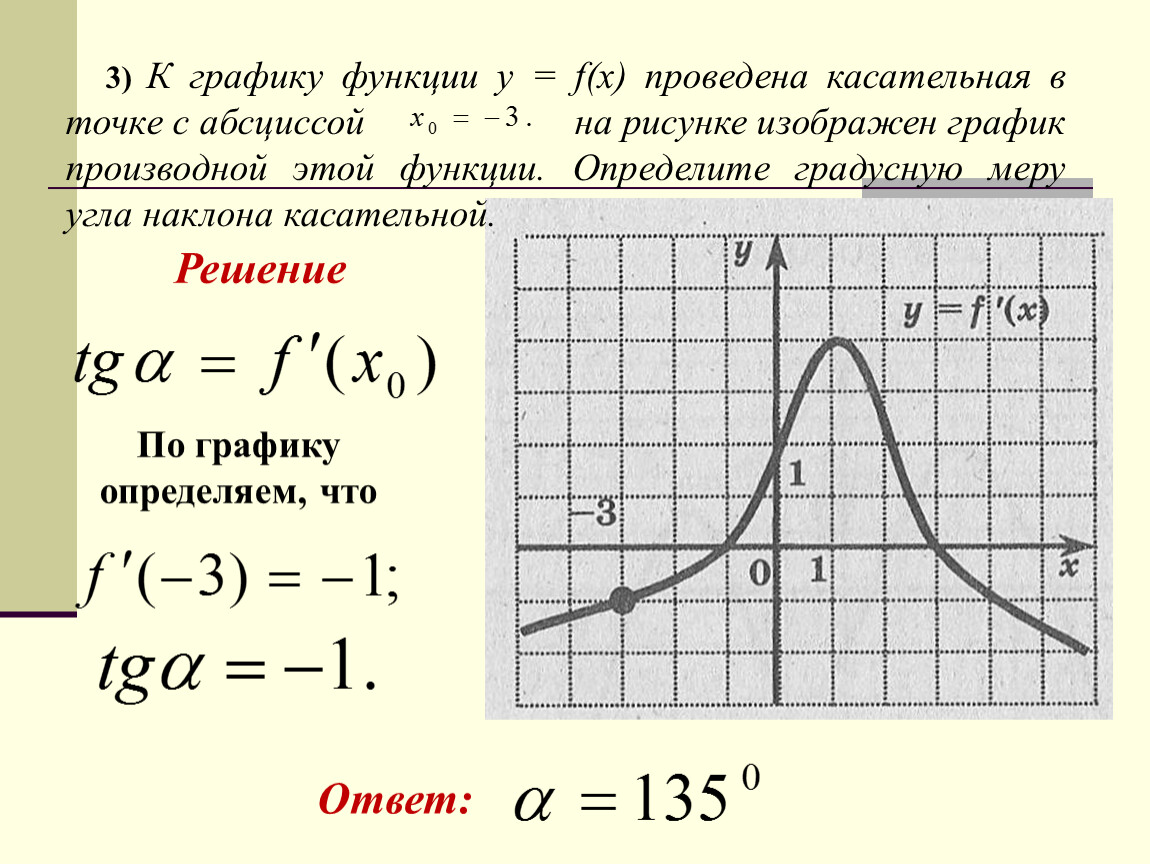 Определите значение функции f(a), подставив в уравнение функции величину абсциссы.
Определите значение функции f(a), подставив в уравнение функции величину абсциссы.
Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».
Возьмите общее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него найденные значения a, f(a), f «(a). В результате будет найдено решение графика и касательной.
Решите задачу иным способом, если заданная точка касательной не совпала с точкой касания. В этом случае необходимо в уравнение касательной вместо цифр подставить «а». После этого вместо букв «х» и «у» подставьте значение координат заданной точки. Решите получившееся уравнение, в котором «а» является неизвестной. Поставьте полученное значение в уравнение касательной.
Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии относительно искомой касательной. После этого необходимо производную функции , чтобы координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.
Подставьте соответствующее значение в уравнение касательной и решите функцию.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Касательная — это прямая , которая касается графика функции в одной точке и все точки
которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно
графика функции под определённым углом и не могут проходить через точку касания несколько касательных
под разными углами. Уравнения касательной и уравнения
нормали к графику функции составляются с помощью производной.
Поэтому касательная проходит касательно
графика функции под определённым углом и не могут проходить через точку касания несколько касательных
под разными углами. Уравнения касательной и уравнения
нормали к графику функции составляются с помощью производной.
Уравнение касательной выводится из уравнения прямой .
Выведем уравнение касательной, а затем — уравнение нормали к графику функции.
y = kx + b .
В нём k — угловой коэффициент.
Отсюда получаем следующую запись:
y — y 0 = k (x — x 0 ) .
Значение производной f «(x 0
) функции y = f (x ) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции,
проведённой через точку M 0
(x 0
, y 0
) ,
где y 0
= f (x 0
) .
В этом состоит геометрический смысл производной .
Таким образом, можем заменить k на f «(x 0 ) и получить следующее уравнение касательной к графику функции :
y — y 0 = f «(x 0 )(x — x 0 ) .
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде . Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали :
(x — x 0 ) + f «(x 0 )(y — y 0 ) = 0
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть
решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».
Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Найдём производную функции:
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.
Пример 2.
Решение. Найдём ординату точки касания:
Найдём ординату точки касания:
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 4. Составить уравнение касательной и уравнение нормали к
графику функции , если абсцисса точки
касания .
Составить уравнение касательной и уравнение нормали к
графику функции , если абсцисса точки
касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).
Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
Внимание! Данная функция — сложная, так как аргумент тангенса (2x )
сам является функцией.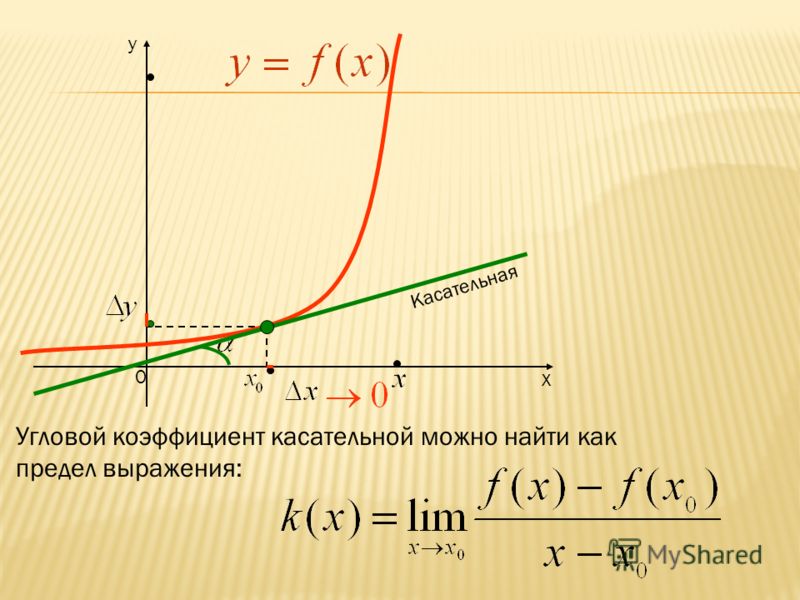 Поэтому найдём производную функции как производную сложной функции.
Поэтому найдём производную функции как производную сложной функции.
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Yandex.RTB R-A-339285-1 Определение 1
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Определение 2
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 .
 Значит, вид уравнения будет y = b .
Значит, вид уравнения будет y = b . - Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х. Равенство задается при помощи равенства x = c со значением с, являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2
Секущей называют прямую, которая проходит через 2 точки функции f (x) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что А В является секущей, а f (x) – черная кривая, α — красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Определение 4
Получаем формулу для нахождения секущей вида:
k = t g α = B C A C = f (x B) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f (x A) , f (x B) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f (x B) — f (x A) x B — x A или k = f (x A) — f (x B) x A — x B , причем уравнение необходимо записать как y = f (x B) — f (x A) x B — x A · x — x A + f (x A) или
y = f (x A) — f (x B) x A — x B · x — x B + f (x B) .
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Определение 5
Касательная к графику функции f (x) в точке x 0 ; f (x 0) называется прямая, проходящая через заданную точку x 0 ; f (x 0) , с наличием отрезка, который имеет множество значений х, близких к x 0 .
Пример 1
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами (1 ; 2) . Для наглядности, необходимо рассмотреть графики с приближенными к (1 ; 2) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y = 2 x сливается с прямой у = х + 1 .
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая А В, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Определение 6
Касательной к графику функции y = f (x) в точке А считается предельное положение секущей А В при В стремящейся к А, то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.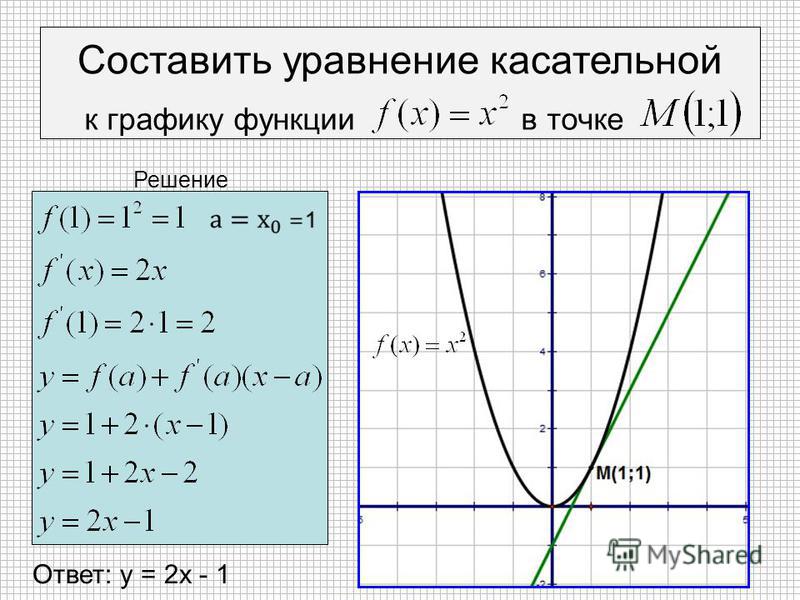
Перейдем к рассмотрению секущей А В для функции f (x) , где А и В с координатами x 0 , f (x 0) и x 0 + ∆ x , f (x 0 + ∆ x) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f (x) = f (x 0 + ∆ x) — f (∆ x) . Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник А В С. Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f (x) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Отсюда следует, что f » (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ (x) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 (x 0) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f » (x 0) .
Тогда получаем, что k x = f » (x 0) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f (x) в точке x 0 , f 0 (x 0) принимает вид y = f » (x 0) · x — x 0 + f (x 0) .
Имеется в виду, что конечным значением производной f » (x 0) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f » (x) = ∞ и lim x → x 0 — 0 f » (x) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f » (x) ≠ lim x → x 0 — 0 f » (x) .
Расположение касательной зависит от значения ее углового коэффициента k x = f » (x 0) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x
Пример 2
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами (1 ; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1 ; 3) является точкой касания, тогда x 0 = — 1 , f (x 0) = — 3 .
Необходимо найти производную в точке со значением — 1 . Получаем, что
y » = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 » = = e x + 1 » + x 3 3 » — 6 — 3 3 x » — 17 — 3 3 » = e x + 1 + x 2 — 6 — 3 3 y » (x 0) = y » (- 1) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3
Значение f ’ (x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y » (x 0) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
y = f » (x 0) · x — x 0 + f (x 0) y = 3 3 (x + 1) — 3 y = 3 3 x — 9 — 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Рисунок, располагаемый справа, показывает в увеличенном виде.
Пример 3
Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами (1 ; 1) . Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y » = 3 · x — 1 5 + 1 » = 3 · 1 5 · (x — 1) 1 5 — 1 = 3 5 · 1 (x — 1) 4 5
Если x 0 = 1 , тогда f ’ (x) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 (x — 1) 4 5 = 3 5 · 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 (x — 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке (1 ; 1) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Для наглядности изобразим графически.
Пример 4
Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где
- Касательная не существует;
- Касательная располагается параллельно о х;
- Касательная параллельна прямой y = 8 5 x + 4 .

Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞) . Получаем, что
y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞)
Необходимо продифференцировать функцию. Имеем, что
y » = — 1 15 x 3 + 18 x 2 + 105 x + 176 » , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 » , x ∈ [ — 2 ; + ∞) ⇔ y » = — 1 5 (x 2 + 12 x + 35) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞)
Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → — 2 — 0 y » (x) = lim x → — 2 — 0 — 1 5 (x 2 + 12 x + 35 = — 1 5 (- 2) 2 + 12 (- 2) + 35 = — 3 lim x → — 2 + 0 y » (x) = lim x → — 2 + 0 1 5 (x 2 — 4 x + 3) = 1 5 — 2 2 — 4 — 2 + 3 = 3
Вычисляем значение функции в точке х = — 2 , где получаем, что
- y (- 2) = 1 15 — 2 + 2 3 — 4 5 (- 2) 2 — 16 5 (- 2) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке (- 2 ; — 2) не будет существовать.

- Касательная параллельна о х, когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f » (x 0) . То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f ’ (x) и будут являться точками касания, где касательная является параллельной о х.
Когда x ∈ — ∞ ; — 2 , тогда — 1 5 (x 2 + 12 x + 35) = 0 , а при x ∈ (- 2 ; + ∞) получаем 1 5 (x 2 — 4 x + 3) = 0 .
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 (x 2 — 4 x + 3) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞
Вычисляем соответствующие значения функции
y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 — 7 + 2 3 — 4 5 (- 7) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3
Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y » (x) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 (x 2 + 12 x + 35) = 8 5 , а если x ∈ (- 2 ; + ∞) , тогда 1 5 (x 2 — 4 x + 3) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28
Другое уравнение имеет два действительных корня, тогда
1 5 (x 2 — 4 x + 3) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · (- 5) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y (- 1) = 1 15 — 1 + 2 3 — 4 5 (- 1) 2 — 16 5 (- 1) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3
Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .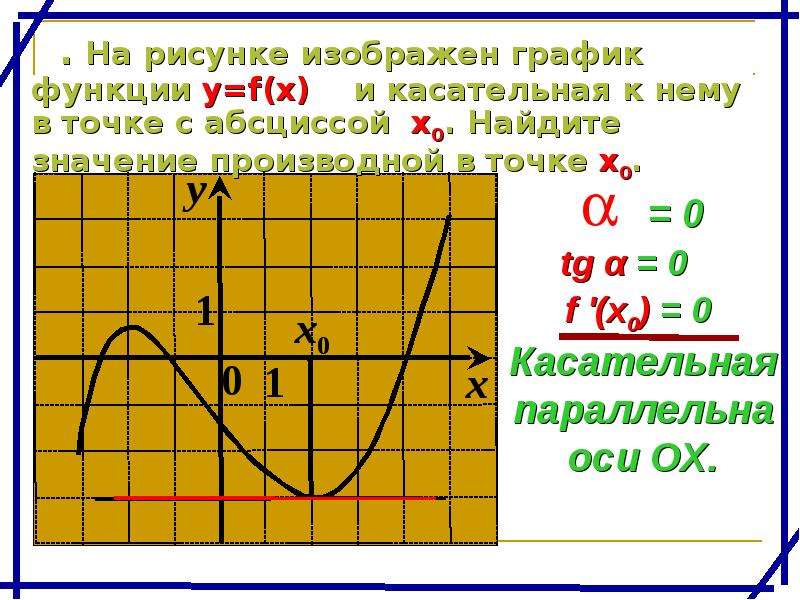
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .
Возможно существование бесконечного количества касательных для заданных функций.
Пример 5
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции.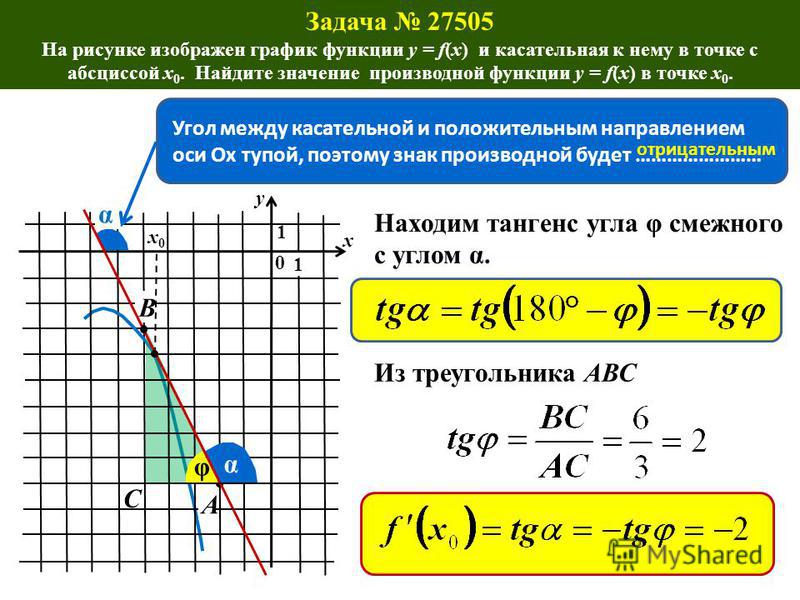 Отметим, что из геометрического смысла производной в точке
Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y » (x 0) . Из данного равенства найдем значения х для точек касания.
Получаем, что
y » (x 0) = 3 cos 3 2 x 0 — π 4 — 1 3 » = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 » = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y » (x 0) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk
3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z — множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y 0 = 3 cos 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3
y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3
Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .
Данное равенство может быть записано как объединение двух функций:
y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.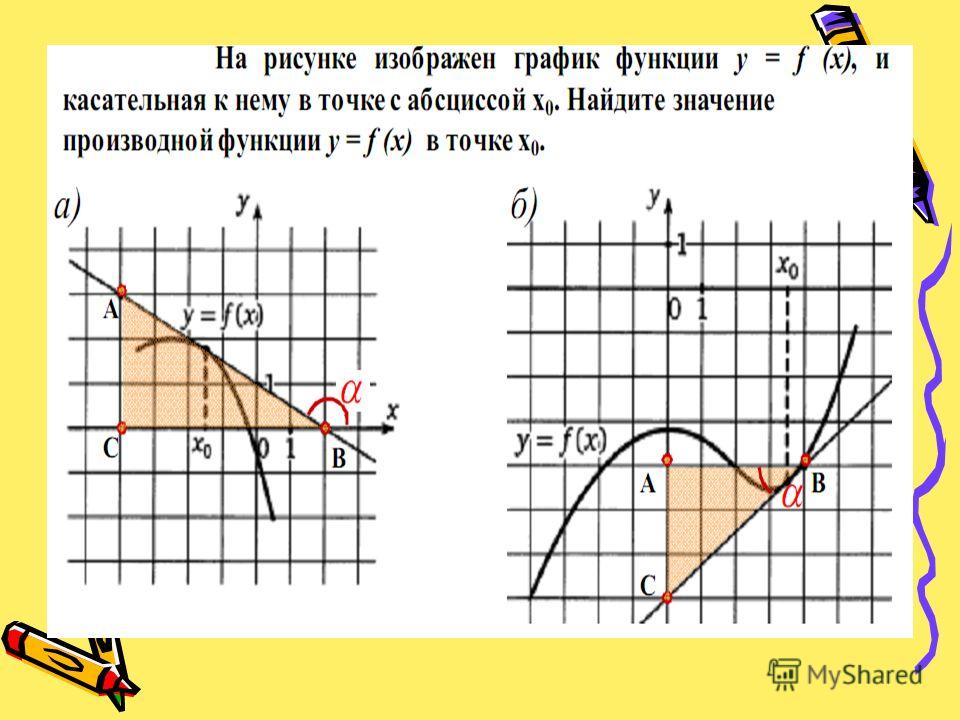
Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у, тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .
Касательная к эллипсу
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
Тогда получаем, что
y = b a · a 2 — (x — x c e n t e r) 2 + y c e n t e r y = — b a · a 2 — (x — x c e n t e r) 2 + y c e n t e r
Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у. Ниже для наглядности рассмотрим рисунок.
Пример 6
Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .
Решение
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 (y — 5) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y » = 5 + 5 2 4 — x — 3 2 » = 5 2 · 1 2 4 — (x — 3) 2 · 4 — (x — 3) 2 » = = — 5 2 · x — 3 4 — (x — 3) 2 ⇒ y » (x 0) = y » (2) = — 5 2 · 2 — 3 4 — (2 — 3) 2 = 5 2 3 ⇒ y = y » (x 0) · x — x 0 + y 0 ⇔ y = 5 2 3 (x — 2) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид
y » = 5 — 5 2 4 — (x — 3) 2 » = — 5 2 · 1 2 4 — (x — 3) 2 · 4 — (x — 3) 2 » = = 5 2 · x — 3 4 — (x — 3) 2 ⇒ y » (x 0) = y » (2) = 5 2 · 2 — 3 4 — (2 — 3) 2 = — 5 2 3 ⇒ y = y » (x 0) · x — x 0 + y 0 ⇔ y = — 5 2 3 (x — 2) — 5 3 2 + 5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .
Гипербола может быть представлена в виде двух объединенных функций вида
y = b a · (x — x c e n t e r) 2 — a 2 + y c e n t e r y = — b a · (x — x c e n t e r) 2 — a 2 + y c e n t e r или y = b a · (x — x c e n t e r) 2 + a 2 + y c e n t e r y = — b a · (x — x c e n t e r) 2 + a 2 + y c e n t e r
В первом случае имеем, что касательные параллельны о у, а во втором параллельны о х.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Пример 7
Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .
Очевидно, что для проверки первой функции необходимо y (7) = 3 2 · (7 — 3) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y (7) = — 3 2 · (7 — 3) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y » = — 3 2 · (x — 3) 2 — 4 — 3 » = — 3 2 · x — 3 (x — 3) 2 — 4 ⇒ k x = y » (x 0) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3
Ответ: уравнение касательной можно представить как
y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y (x 0) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y » (x 0) · x — x 0 + y (x 0) . Такая касательная в вершине параллельна о х.
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a (c — x) y = — b + b 2 — 4 a (c — x) 2 a y = — b — b 2 — 4 a (c — x) 2 a
Графически изобразим как:
Для выяснения принадлежности точки x 0 , y (x 0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Пример 8
Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
2 y 2 — 5 y + 3 — x = 0 D = (- 5) 2 — 4 · (- 2) · (3 — x) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
Получаем:
k x = y » (x 0) = t g α x = t g 150 ° = — 1 3
Отсюда определим значение х для точек касания.
Первая функция запишется как
y » = 5 + 49 — 8 x — 4 » = 1 49 — 8 x ⇒ y » (x 0) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
y » = 5 — 49 — 8 x — 4 » = — 1 49 — 8 x ⇒ y » (x 0) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y (x 0) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4
Имеем, что точки касания — 23 4 ; — 5 + 3 4 .
Ответ: уравнение касательной принимает вид
y = — 1 3 · x — 23 4 + — 5 + 3 4
Графически изобразим это таким образом:
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Конспект урока по алгебре «Касательная к графику функции»
Тема урока: «Касательная к графику функции».
Тип урока: изучение нового материала Класс: 11 Дата: 12.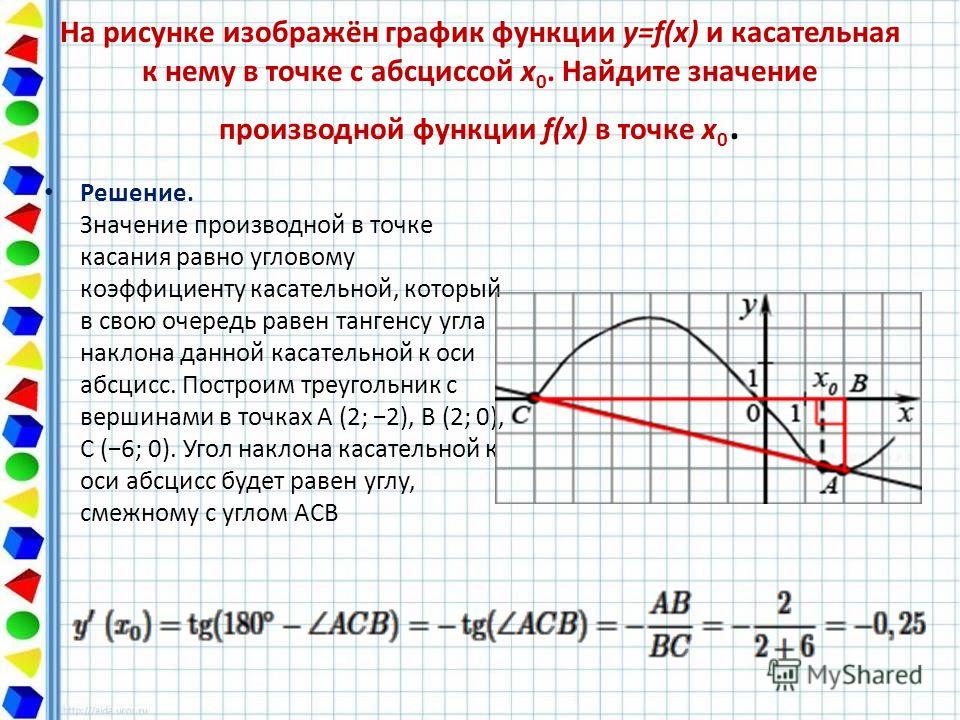 10.18
10.18
Цели: ввести понятие касательной к графику функции в точке; понятие углового коэффициента касательной
Задачи: формировать умения определять угловой коэффициент касательной к графику в точке; развивать логическое мышление, математическую речь; воспитывать волю и упорство для достижения конечных результатов.
Ход урока:
Орг.момент.
Приветствует обучающихся, создает эмоциональный настрой на урок.
— Сегодня мы начинаем изучать новую тему, название которой мы определим в процессе нашей совместной работы.
Актуализация знаний. Постановка темы и целей урока.
— Назовите знак тангенса острого (тупого) угла.
— Что изображено на рисунке? Какая прямая называется касательной?
— Какие понятия нам встретились на этапе повторения?
— Как вы считаете, взаимосвязаны ли эти понятия? (Ответы учащихся)
— Тема нашего урока «Касательная к графику функции». Сегодня мы узнаем, что такое касательная к графику функции в точке, изучим угловой коэффициент и научимся его определять.
Сегодня мы узнаем, что такое касательная к графику функции в точке, изучим угловой коэффициент и научимся его определять.
Изучение нового материала.
Работа с учебником стр.28 -30. Учащиеся знакомятся с понятием. Оформляют конспект в тетради.
ОПР: Касательная к кривой в её точке М0 – это предельное положение секущей М0М, когда М стремится к М0.
! Касательная к кривой не существует в точках разрыва.
! Если касательная к графику функции существует в точке, то функция непрерывна в этой точке.
Обратное утверждение неверно. Если график функции и непрерывен в данной точке, то он может не иметь касательную в этой точке.
Исследование. (Работа в парах)
Перед вами графики функции f(x). Через данную точку на графике проведите касательную. Определите значение углового коэффициента касательной в сравнении с нулем. Определите вид угла α.
Сравнение с эталоном:
k>0 k=0 k<0
α- острый α=0 α- тупой
Формирование умений и навыков.
№1 (устно по готовым чертежам) В каких точках графика функции касательная к нему:
а) горизонтальна;
б) образует с осью абсцисс острый угол?
в) образует с осью абсцисс тупой угол?
№2. Найдите угловые коэффициенты касательных к графикам функций в точке.
№3. На рисунке изображен график функции у=f(x) и восемь точек на оси абцисс: х1, х2, х3, х4, х5, х6, х7, х8. В скольких из этих точек угловой коэффициент касательно отрицателен?
№4.На рисунке изображен график функции На оси абсцисс отмечены точки -2, 1, 3, 4. В какой из этих точек угловой коэффициент касательной наибольший?
Работа с учебником
№34(у), №35(у), №36(в)
Творческое задание.
Составьте задачу, используя рисунок:
Самостоятельная работа.
№1. Найдите угловой коэффициент касательной к графику функции в точке:
№2. На рисунке изображен график функции у=f(x) и восемь точек на оси абцисс: х1, х2, х3, х4, х5, х6, х7, х8, х9, х10 . В скольких из этих точек угловой коэффициент касательной положителен?
На рисунке изображен график функции у=f(x) и восемь точек на оси абцисс: х1, х2, х3, х4, х5, х6, х7, х8, х9, х10 . В скольких из этих точек угловой коэффициент касательной положителен?
Ответ:_____________________
Итог урока.
Вопросы:
— Дайте определение касательной к графику функции в точке.
— Верно ли, что в любой точке, где функция непрерывна, к ее графику можно провести касательную?
— Как располагается касательная к графику функции в точке, если угловой коэффициент больше нуля, равен нулю, меньше нуля?
— Что получилось (не получилось) выполнить сегодня на уроке? Что необходимо для выполнения заданий по данной теме?
Домашнее задание: №33(1,2), №36(а,б), доп.задание:
Уравнение касательной к графику функции для чайников. Уравнение касательной к графику функции
Тип задания: 7
Условие
Прямая y=3x+2
является касательной к графику функции y=-12x^2+bx-10. 2+5x-7
в произвольной точке x_0
равен y»(x_0).
Но y»=-2x+5,
значит, y»(x_0)=-2x_0+5.
Угловой коэффициент прямой y=-3x+4,
указанной в условии, равен -3.
Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0,
что =-2x_0 +5=-3.
2+5x-7
в произвольной точке x_0
равен y»(x_0).
Но y»=-2x+5,
значит, y»(x_0)=-2x_0+5.
Угловой коэффициент прямой y=-3x+4,
указанной в условии, равен -3.
Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0,
что =-2x_0 +5=-3.
Получаем: x_0 = 4.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
Показать решениеРешение
По рисунку определяем, что касательная проходит через точки A(-6; 2) и B(-1; 1). Обозначим через C(-6; 1) точку пересечения прямых x=-6 и y=1, а через \alpha угол ABC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \pi -\alpha, который является тупым.
Как известно, tg(\pi -\alpha)
и будет значением производной функции f(x)
в точке x_0. 2=1,
значит либо x_0=-1,
либо x_0=1.
Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1,
тогда b=-2-32x_0=-34.
2=1,
значит либо x_0=-1,
либо x_0=1.
Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1,
тогда b=-2-32x_0=-34.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
На рисунке изображён график функции y=f(x), определённой на интервале (-2; 8). Определите количество точек, в которых касательная к графику функции параллельна прямой y=6.
Показать решениеРешение
Прямая y=6 параллельна оси Ox . Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 4 .
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 7
Тема:
Геометрический смысл производной.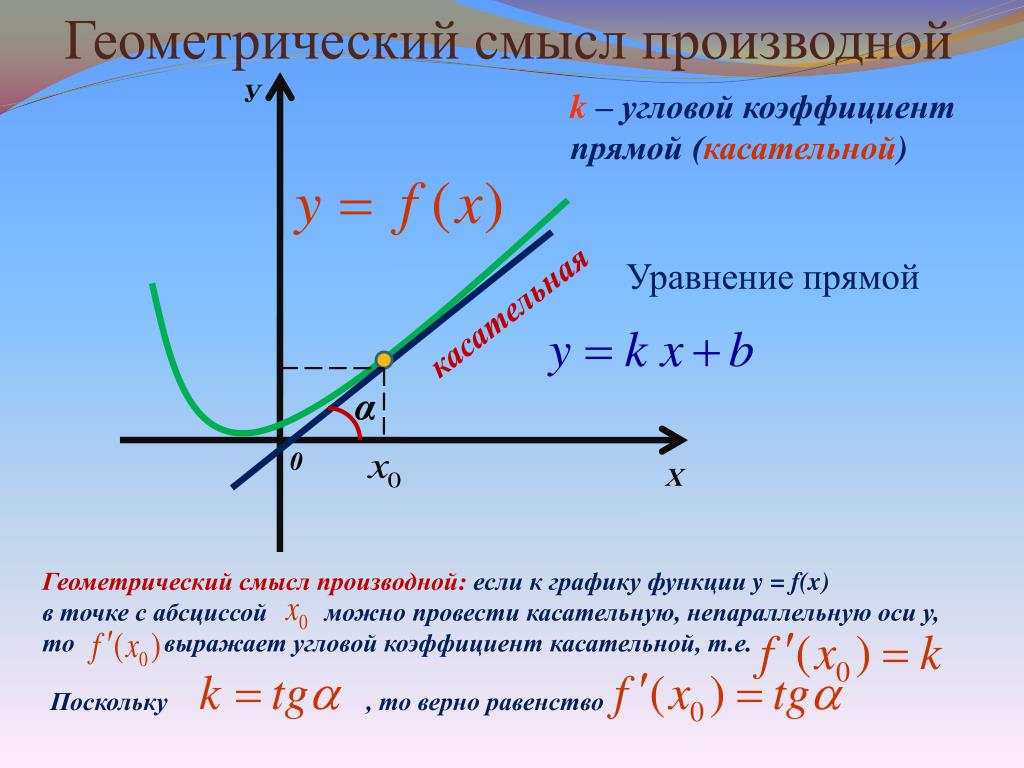 2-4x+9
в произвольной точке x_0
равен y»(x_0).
Но y»=2x-4,
значит, y»(x_0)=2x_0-4.
Угловой коэффициент касательной y=4x-7,
указанной в условии, равен 4
. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0,
что 2x_0-4=4.
Получаем: x_0=4.
2-4x+9
в произвольной точке x_0
равен y»(x_0).
Но y»=2x-4,
значит, y»(x_0)=2x_0-4.
Угловой коэффициент касательной y=4x-7,
указанной в условии, равен 4
. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0,
что 2x_0-4=4.
Получаем: x_0=4.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Показать решениеРешение
По рисунку определяем, что касательная проходит через точки A(1; 1)
и B(5; 4).
Обозначим через C(5; 1)
точку пересечения прямых x=5
и y=1,
а через \alpha
угол BAC
(на рисунке видно, что он острый). Тогда прямая AB
образует с положительным направлением оси Ox
угол \alpha.
Рассмотрим следующий рисунок:
На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.
Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.
Касательная к графику функции
Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.
При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной. Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Уравнение касательной
Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:
Так как у нас угловой коэффициент равен производной f’(x0) , то уравнение примет следующий вид: y = f’(x0) *x + b.
Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.
f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) — f’(x0)*x0.
Подставляем полученное значение в уравнение касательной:
y = f’(x0)*x + b = f’(x0)*x + f(x0) — f’(x0)*x0 = f(x0) + f’(x0)*(x — x0).
y = f(x0) + f’(x0)*(x — x0).
Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x 3 — 2*x 2 + 1 в точке х = 2.
2. f(x0) = f(2) = 2 2 — 2*2 2 + 1 = 1.
3. f’(x) = 3*x 2 — 4*x.
4. f’(x0) = f’(2) = 3*2 2 — 4*2 = 4.
5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x — 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x — 7.
Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x — 7.
Ответ: y = 4*x — 7.
Общая схема составления уравнения касательной к графику функции y = f(x):
1. Определить х0.
2. Вычислить f(x0).
3. Вычислить f’(x)
У = f(х) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f»(а). Мы этим уже несколько раз пользовались. Например, в § 33 было установлено, что график функции у = sin х(синусоида) в начале координат образует с осью абсцисс угол 45° (точнее, касательная к графику в начале координат составляет с положительным направлением оси х угол 45°), а в примере 5 § 33 были найдены точки на графике заданной функции , в которых касательная параллельна оси абсцисс. В примере 2 § 33 было составлено уравнение касательной к графику функции у = х 2 в точке х = 1 (точнее, в точке (1; 1), но чаще указывают только значение абсциссы, полагая, что если значение абсциссы известно, то значение ординаты можно найти из уравнения у = f(х)). В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции.
В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции.
Пусть даны функция у = f(х) и точка М (а; f(а)), а также известно, что существует f»(а). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид у = кх+m, поэтому задача состоит в отыскании значений коэффициентов к и m.
С угловым коэффициентом к проблем нет: мы знаем, что к = f»(а). Для вычисления значения т воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(а) = ка+m, откуда находим, что m = f(а) — ка.
Осталось подставить найденные значения коэффициентов кит в уравнение прямой:
Нами получено уравнение касательной к графику функции у = f(х) в точке х=а.
Если, скажем,
Подставив в уравнение (1) найденные значения а = 1, f(а) = 1 f»(а) = 2, получим: у = 1+2(х-f), т. е. у = 2х-1.
е. у = 2х-1.
Сравните этот результат с тем, что был получен в примере 2 из § 33. Естественно, получилось то же самое.
Составим уравнение касательной к графику функции у = tg х в начале координат. Имеем: значит, соs х f»(0) = 1. Подставив в уравнение (1) найденные значения а= 0, f(а)= 0, f»(а) = 1, получим: у=х.
Именно поэтому мы и провели тангенсоиду в § 15 (см. рис. 62) через начало координат под углом 45° к оси абсцисс.
Решая эти достаточно простые примеры, мы фактически пользовались определенным алгоритмом, который заложен в формуле (1). Сделаем этот алгоритм явным.
АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x)
1) Обозначить абсциссу точки касания буквой а.
2) Вычислить 1 (а).
3) Найти f»(х) и вычислить f»(а).
4) Подставить найденные числа а, f(а), (а) в формулу (1).
Пример 1. Составить уравнение касательной к графику функции в точке х = 1.
Воспользуемся алгоритмом, учитывая, что в данном примере
На рис. 126 изображена гипербола , построена прямая у= 2-х.
126 изображена гипербола , построена прямая у= 2-х.
Чертеж подтверждает приведенные выкладки: действительно, прямая у = 2-х касается гиперболы в точке(1; 1).
Ответ: у =2- х.
Пример 2. К графику функции провести касательную так, чтобы она была параллельна прямой у =4х — 5.
Уточним формулировку задачи. Требование «провести касательную» обычно означает «составить уравнение касательной». Это логично, ибо если человек смог составить уравнение касательной, то вряд ли он будет испытывать затруднения с построением на координатной плоскости прямой по ее уравнению.
Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Но в отличие от предыдущего примера здесь имеется неясность: не указана явно абсцисса точки касания.
Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = 4х-5. Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: Таким образом, значение а мы можем найти из уравнения f»(а)= 4.
Имеем:
Из уравнения Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
Теперь можно действовать по алгоритму.
Пример 3. Из точки (0; 1) провести касательную к графику функции
Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее действуем по алгоритму.
По условию касательная проходит через точку (0; 1). Подставив в уравнение (2) значения х = 0, у = 1, получим:
Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение а =4 в уравнение (2), получим:
На рис. 127 представлена геометрическая иллюстрация рассмотренного примера: построен график функции
В § 32 мы отметили, что для функции у = f(х), имеющей производную в фиксированной точке х, справедливо приближенное равенство:
Для удобства дальнейших рассуждений изменим обозначения: вместо х будем писать а, вместо будем писать х и соответственно вместо будем писать х-а. Тогда написанное выше приближенное равенство примет вид:
Тогда написанное выше приближенное равенство примет вид:
А теперь взгляните на рис. 128. К графику функции у = f(х) проведена касательная в точке М (а; f (а)). Отмечена точка х на оси абсцисс близко от а. Ясно, что f(х) — ордината графика функции в указанной точке х. А что такое f(а) + f»(а) (х-а)? Это ордината касательной, соответствующая той же точке х — см. формулу (1). В чем же смысл приближенного равенства (3)? В том, что для вычисления приближенного значения функции берут значение ординаты касательной.
Пример 4. Найти приближенное значение числового выражения 1,02 7 .
Речь идет об отыскании значения функции у = х 7 в точке х = 1,02. Воспользуемся формулой (3), учтя, что в данном примере
В итоге получаем:
Если мы воспользуемся калькулятором, то получим: 1,02 7 = 1,148685667…
Как видите, точность приближения вполне приемлема.
Ответ: 1,02 7 =1,14.
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн , Математика в школе скачать
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиСтатья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями.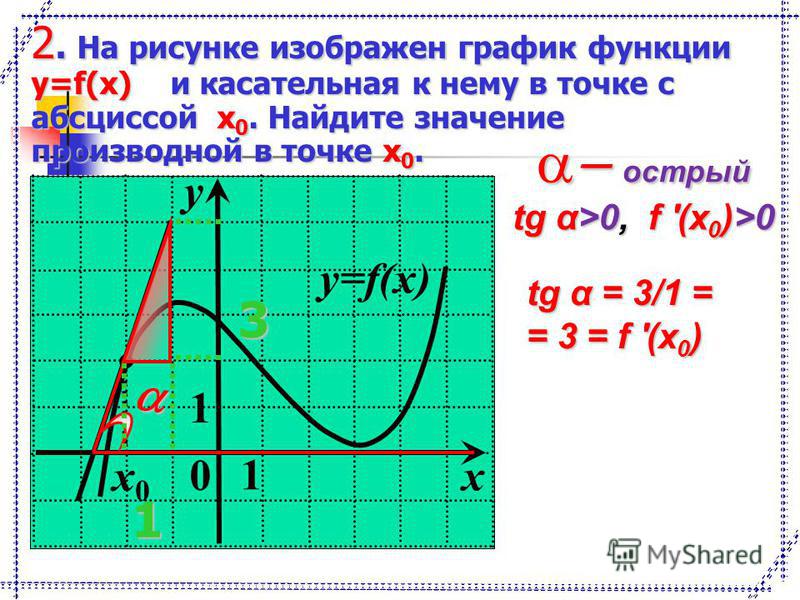 Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Yandex.RTB R-A-339285-1 Определение 1
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Определение 2
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х.
 Равенство задается при помощи равенства x = c со значением с, являющимся действительным числом.
Равенство задается при помощи равенства x = c со значением с, являющимся действительным числом. - Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2
Секущей называют прямую, которая проходит через 2 точки функции f (x) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что А В является секущей, а f (x) – черная кривая, α — красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Определение 4
Получаем формулу для нахождения секущей вида:
k = t g α = B C A C = f (x B) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f (x A) , f (x B) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f (x B) — f (x A) x B — x A или k = f (x A) — f (x B) x A — x B , причем уравнение необходимо записать как y = f (x B) — f (x A) x B — x A · x — x A + f (x A) или
y = f (x A) — f (x B) x A — x B · x — x B + f (x B) .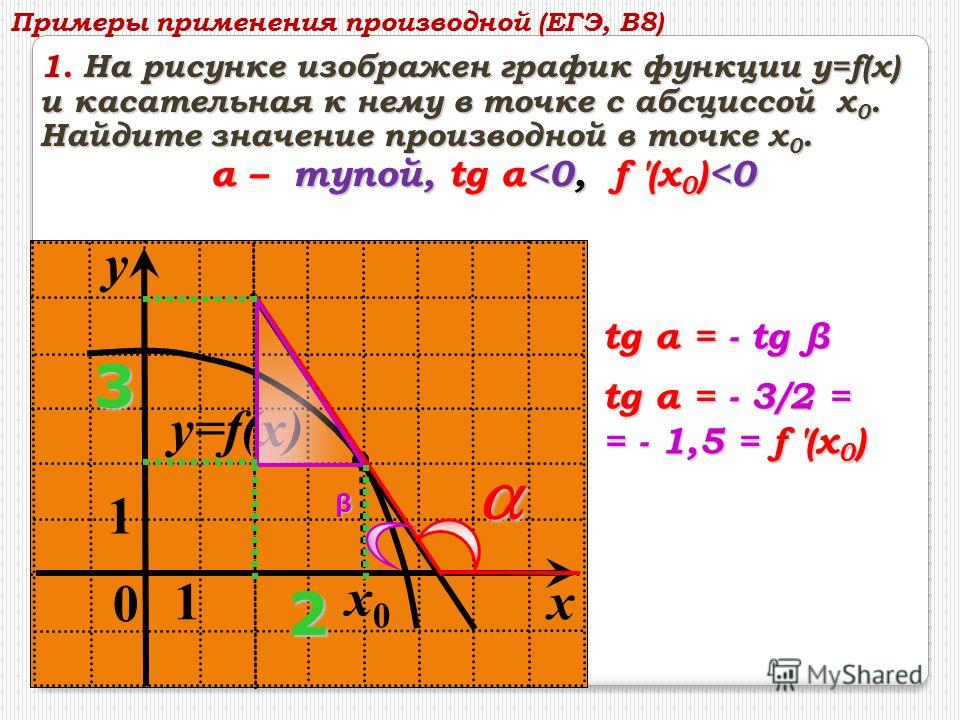
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Определение 5
Касательная к графику функции f (x) в точке x 0 ; f (x 0) называется прямая, проходящая через заданную точку x 0 ; f (x 0) , с наличием отрезка, который имеет множество значений х, близких к x 0 .
Пример 1
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами (1 ; 2) . Для наглядности, необходимо рассмотреть графики с приближенными к (1 ; 2) значениями.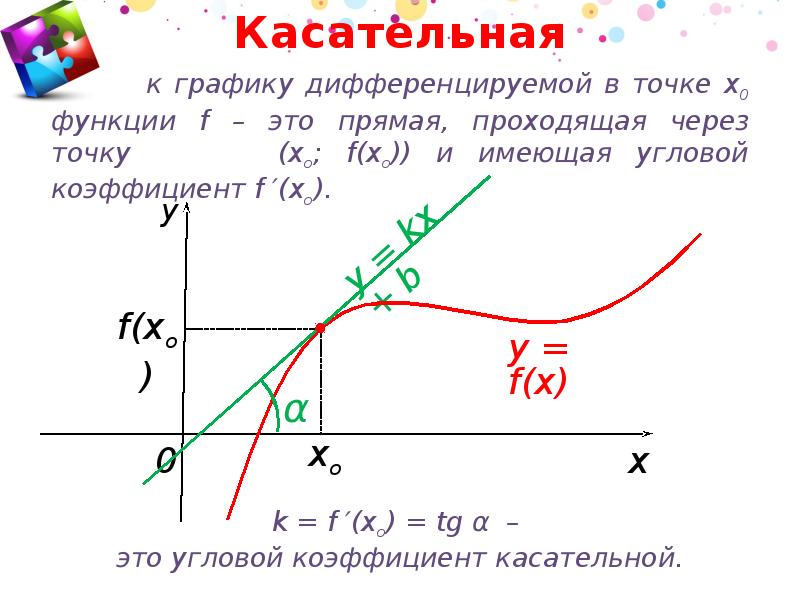 Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y = 2 x сливается с прямой у = х + 1 .
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая А В, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Определение 6
Касательной к графику функции y = f (x) в точке А считается предельное положение секущей А В при В стремящейся к А, то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Перейдем к рассмотрению секущей А В для функции f (x) , где А и В с координатами x 0 , f (x 0) и x 0 + ∆ x , f (x 0 + ∆ x) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f (x) = f (x 0 + ∆ x) — f (∆ x) . Для наглядности приведем в пример рисунок.
Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник А В С. Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f (x) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Отсюда следует, что f » (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ (x) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 (x 0) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f » (x 0) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f (x) в точке x 0 , f 0 (x 0) принимает вид y = f » (x 0) · x — x 0 + f (x 0) .
Имеется в виду, что конечным значением производной f » (x 0) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f » (x) = ∞ и lim x → x 0 — 0 f » (x) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f » (x) ≠ lim x → x 0 — 0 f » (x) .
Расположение касательной зависит от значения ее углового коэффициента k x = f » (x 0) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x
Пример 2
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами (1 ; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1 ; 3) является точкой касания, тогда x 0 = — 1 , f (x 0) = — 3 .
Необходимо найти производную в точке со значением — 1 . Получаем, что
y » = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 » = = e x + 1 » + x 3 3 » — 6 — 3 3 x » — 17 — 3 3 » = e x + 1 + x 2 — 6 — 3 3 y » (x 0) = y » (- 1) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3
Значение f ’ (x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y » (x 0) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
y = f » (x 0) · x — x 0 + f (x 0) y = 3 3 (x + 1) — 3 y = 3 3 x — 9 — 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания.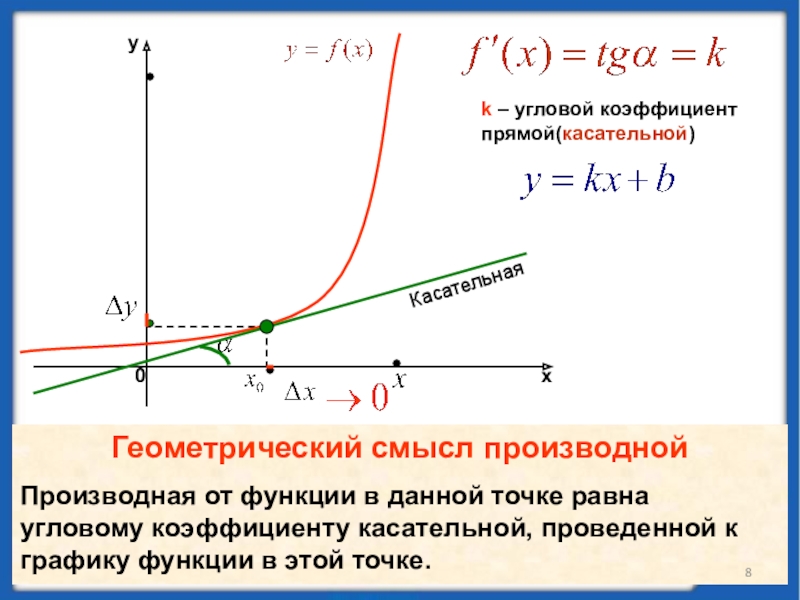 Рисунок, располагаемый справа, показывает в увеличенном виде.
Рисунок, располагаемый справа, показывает в увеличенном виде.
Пример 3
Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами (1 ; 1) . Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y » = 3 · x — 1 5 + 1 » = 3 · 1 5 · (x — 1) 1 5 — 1 = 3 5 · 1 (x — 1) 4 5
Если x 0 = 1 , тогда f ’ (x) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 (x — 1) 4 5 = 3 5 · 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 (x — 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке (1 ; 1) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Для наглядности изобразим графически.
Пример 4
Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где
- Касательная не существует;
- Касательная располагается параллельно о х;
- Касательная параллельна прямой y = 8 5 x + 4 .

Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞) . Получаем, что
y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞)
Необходимо продифференцировать функцию. Имеем, что
y » = — 1 15 x 3 + 18 x 2 + 105 x + 176 » , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 » , x ∈ [ — 2 ; + ∞) ⇔ y » = — 1 5 (x 2 + 12 x + 35) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞)
Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → — 2 — 0 y » (x) = lim x → — 2 — 0 — 1 5 (x 2 + 12 x + 35 = — 1 5 (- 2) 2 + 12 (- 2) + 35 = — 3 lim x → — 2 + 0 y » (x) = lim x → — 2 + 0 1 5 (x 2 — 4 x + 3) = 1 5 — 2 2 — 4 — 2 + 3 = 3
Вычисляем значение функции в точке х = — 2 , где получаем, что
- y (- 2) = 1 15 — 2 + 2 3 — 4 5 (- 2) 2 — 16 5 (- 2) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке (- 2 ; — 2) не будет существовать.

- Касательная параллельна о х, когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f » (x 0) . То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f ’ (x) и будут являться точками касания, где касательная является параллельной о х.
Когда x ∈ — ∞ ; — 2 , тогда — 1 5 (x 2 + 12 x + 35) = 0 , а при x ∈ (- 2 ; + ∞) получаем 1 5 (x 2 — 4 x + 3) = 0 .
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 (x 2 — 4 x + 3) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞
Вычисляем соответствующие значения функции
y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 — 7 + 2 3 — 4 5 (- 7) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3
Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.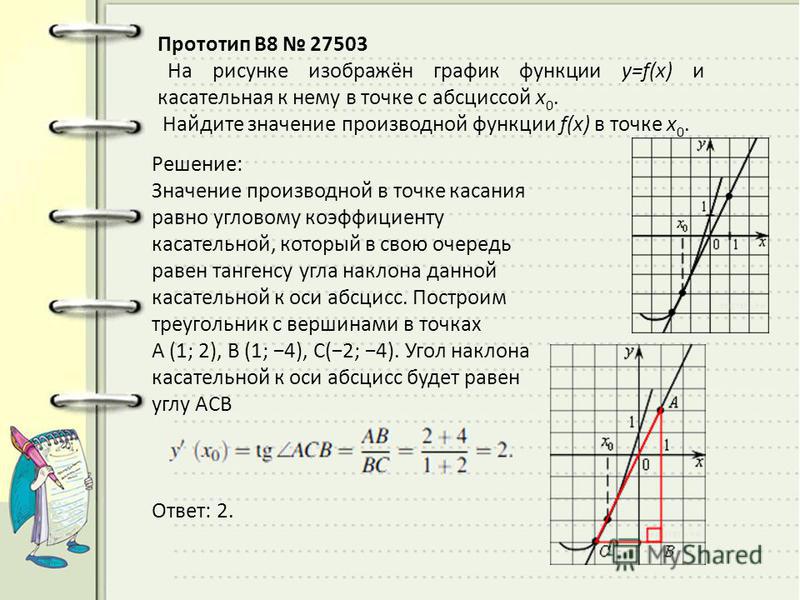
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y » (x) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 (x 2 + 12 x + 35) = 8 5 , а если x ∈ (- 2 ; + ∞) , тогда 1 5 (x 2 — 4 x + 3) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28
Другое уравнение имеет два действительных корня, тогда
1 5 (x 2 — 4 x + 3) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · (- 5) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y (- 1) = 1 15 — 1 + 2 3 — 4 5 (- 1) 2 — 16 5 (- 1) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3
Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .
Возможно существование бесконечного количества касательных для заданных функций.
Пример 5
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y » (x 0) . Из данного равенства найдем значения х для точек касания.
Получаем, что
y » (x 0) = 3 cos 3 2 x 0 — π 4 — 1 3 » = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 » = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y » (x 0) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk
3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z — множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y 0 = 3 cos 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3
y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3
Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .
Данное равенство может быть записано как объединение двух функций:
y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у, тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .
Касательная к эллипсу
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса.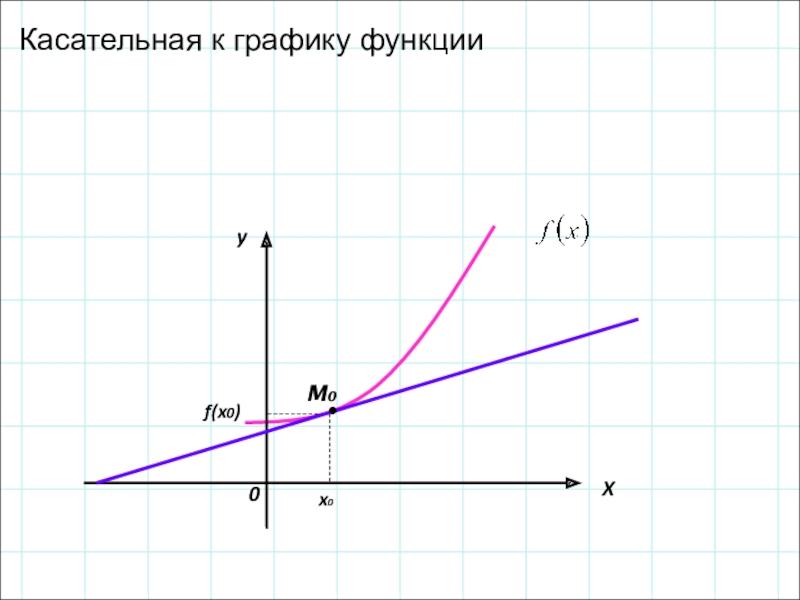 Тогда получаем, что
Тогда получаем, что
y = b a · a 2 — (x — x c e n t e r) 2 + y c e n t e r y = — b a · a 2 — (x — x c e n t e r) 2 + y c e n t e r
Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у. Ниже для наглядности рассмотрим рисунок.
Пример 6
Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .
Решение
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 (y — 5) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .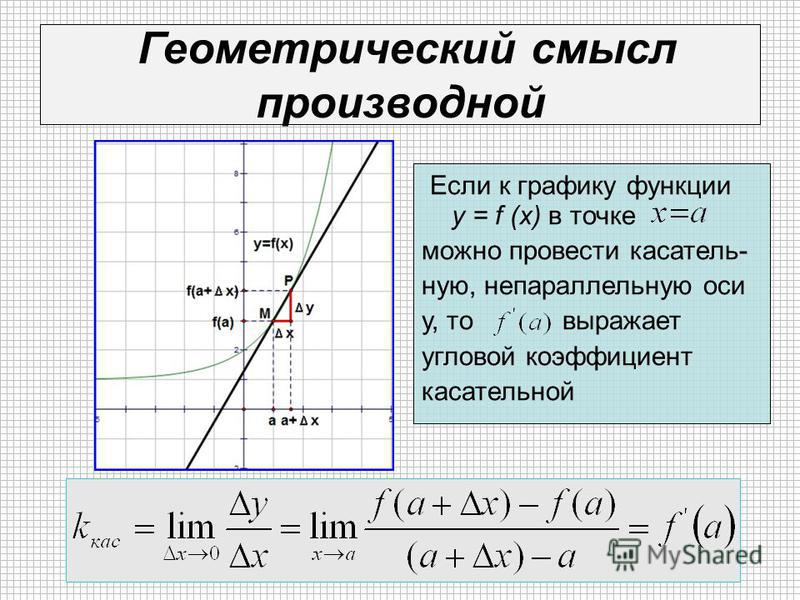
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y » = 5 + 5 2 4 — x — 3 2 » = 5 2 · 1 2 4 — (x — 3) 2 · 4 — (x — 3) 2 » = = — 5 2 · x — 3 4 — (x — 3) 2 ⇒ y » (x 0) = y » (2) = — 5 2 · 2 — 3 4 — (2 — 3) 2 = 5 2 3 ⇒ y = y » (x 0) · x — x 0 + y 0 ⇔ y = 5 2 3 (x — 2) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид
y » = 5 — 5 2 4 — (x — 3) 2 » = — 5 2 · 1 2 4 — (x — 3) 2 · 4 — (x — 3) 2 » = = 5 2 · x — 3 4 — (x — 3) 2 ⇒ y » (x 0) = y » (2) = 5 2 · 2 — 3 4 — (2 — 3) 2 = — 5 2 3 ⇒ y = y » (x 0) · x — x 0 + y 0 ⇔ y = — 5 2 3 (x — 2) — 5 3 2 + 5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .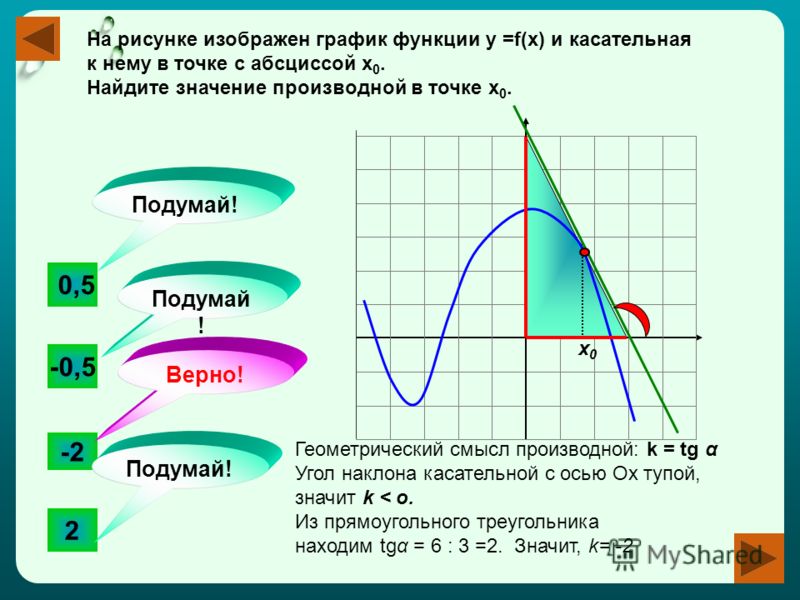
Гипербола может быть представлена в виде двух объединенных функций вида
y = b a · (x — x c e n t e r) 2 — a 2 + y c e n t e r y = — b a · (x — x c e n t e r) 2 — a 2 + y c e n t e r или y = b a · (x — x c e n t e r) 2 + a 2 + y c e n t e r y = — b a · (x — x c e n t e r) 2 + a 2 + y c e n t e r
В первом случае имеем, что касательные параллельны о у, а во втором параллельны о х.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Пример 7
Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .
Очевидно, что для проверки первой функции необходимо y (7) = 3 2 · (7 — 3) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y (7) = — 3 2 · (7 — 3) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y » = — 3 2 · (x — 3) 2 — 4 — 3 » = — 3 2 · x — 3 (x — 3) 2 — 4 ⇒ k x = y » (x 0) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3
Ответ: уравнение касательной можно представить как
y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y (x 0) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y » (x 0) · x — x 0 + y (x 0) . Такая касательная в вершине параллельна о х.
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a (c — x) y = — b + b 2 — 4 a (c — x) 2 a y = — b — b 2 — 4 a (c — x) 2 a
Графически изобразим как:
Для выяснения принадлежности точки x 0 , y (x 0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Пример 8
Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
2 y 2 — 5 y + 3 — x = 0 D = (- 5) 2 — 4 · (- 2) · (3 — x) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
Получаем:
k x = y » (x 0) = t g α x = t g 150 ° = — 1 3
Отсюда определим значение х для точек касания.
Первая функция запишется как
y » = 5 + 49 — 8 x — 4 » = 1 49 — 8 x ⇒ y » (x 0) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
y » = 5 — 49 — 8 x — 4 » = — 1 49 — 8 x ⇒ y » (x 0) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y (x 0) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4
Имеем, что точки касания — 23 4 ; — 5 + 3 4 .
Ответ: уравнение касательной принимает вид
y = — 1 3 · x — 23 4 + — 5 + 3 4
Графически изобразим это таким образом:
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Пример 1. Дана функция f (x ) = 3x 2 + 4x – 5. Напишем уравнение касательной к графику функции f (x ) в точке графика с абсциссой x 0 = 1.
Решение.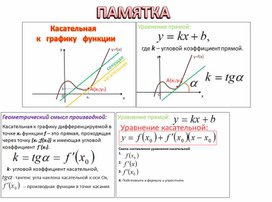 Производная функции f (x ) существует для любого x R . Найдем ее:
Производная функции f (x ) существует для любого x R . Найдем ее:
= (3x 2 + 4x – 5)′ = 6x + 4.
Тогда f (x 0) = f (1) = 2; (x 0) = = 10. Уравнение касательной имеет вид:
y = (x 0) (x – x 0) + f (x 0),
y = 10(x – 1) + 2,
y = 10x – 8.
Ответ. y = 10x – 8.
Пример 2. Дана функция f (x ) = x 3 – 3x 2 + 2x + 5. Напишем уравнение касательной к графику функции f (x ), параллельной прямой y = 2x – 11.
Решение. Производная функции f (x ) существует для любого x R . Найдем ее:
= (x 3 – 3x 2 + 2x + 5)′ = 3x 2 – 6x + 2.
Так как касательная к графику функции f (x ) в точке с абсциссой x 0 параллельна прямой y = 2x – 11, то ее угловой коэффициент равен 2, т. е. (x 0) = 2. Найдем эту абсциссу из условия, что 3x – 6x 0 + 2 = 2. Это равенство справедливо лишь при x 0 = 0 и при x 0 = 2. Так как в том и в другом случае f (x 0) = 5, то прямая y = 2x + b касается графика функции или в точке (0; 5), или в точке (2; 5).
е. (x 0) = 2. Найдем эту абсциссу из условия, что 3x – 6x 0 + 2 = 2. Это равенство справедливо лишь при x 0 = 0 и при x 0 = 2. Так как в том и в другом случае f (x 0) = 5, то прямая y = 2x + b касается графика функции или в точке (0; 5), или в точке (2; 5).
В первом случае верно числовое равенство 5 = 2×0 + b , откуда b = 5, а во втором случае верно числовое равенство 5 = 2×2 + b , откуда b = 1.
Итак, существует две касательные y = 2x + 5 и y = 2x + 1 к графику функции f (x ), параллельные прямой y = 2x – 11.
Ответ. y = 2x + 5, y = 2x + 1.
Пример 3. Дана функция f (x ) = x 2 – 6x + 7. Напишем уравнение касательной к графику функции f (x ), проходящей через точку A (2; –5).
Решение.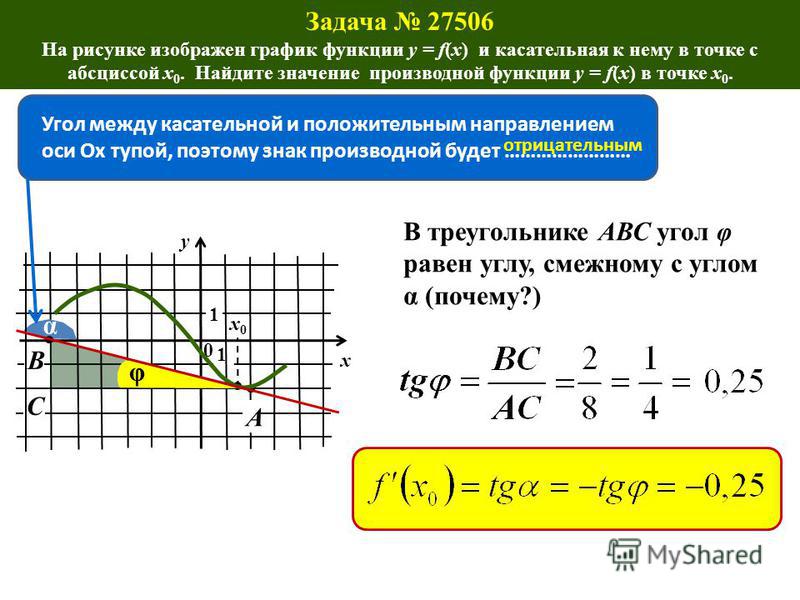 Так как f (2) –5, то точка A не принадлежит графику функции f (x ). Пусть x 0 — абсцисса точки касания.
Так как f (2) –5, то точка A не принадлежит графику функции f (x ). Пусть x 0 — абсцисса точки касания.
Производная функции f (x ) существует для любого x R . Найдем ее:
= (x 2 – 6x + 1)′ = 2x – 6.
Тогда f (x 0) = x – 6x 0 + 7; (x 0) = 2x 0 – 6. Уравнение касательной имеет вид:
y = (2x 0 – 6)(x – x 0) + x – 6x + 7,
y = (2x 0 – 6)x – x + 7.
Так как точка A принадлежит касательной, то справедливо числовое равенство
–5 = (2x 0 – 6)×2– x + 7,
откуда x 0 = 0 или x 0 = 4. Это означает, что через точку A можно провести две касательные к графику функции f (x ).
Если x 0 = 0, то уравнение касательной имеет вид y = –6x + 7. Если x 0 = 4, то уравнение касательной имеет вид y = 2x – 9.
Ответ. y = –6x + 7, y = 2x – 9.
Пример 4. Даны функции f (x ) = x 2 – 2x + 2 и g (x ) = –x 2 – 3. Напишем уравнение общей касательной к графикам этих функции.
Решение. Пусть x 1 — абсцисса точки касания искомой прямой с графиком функции f (x ), а x 2 — абсцисса точки касания той же прямой с графиком функции g (x ).
Производная функции f (x ) существует для любого x R . Найдем ее:
= (x 2 – 2x + 2)′ = 2x – 2.
Тогда f (x 1) = x – 2x 1 + 2; (x 1) = 2 x 1 – 2. Уравнение касательной имеет вид:
y = (2x 1 – 2)(x – x 1) + x – 2x 1 + 2,
y = (2x 1 – 2)x – x + 2. (1)
Найдем производную функции g (x ):
= (–x 2 – 3)′ = –2x .
Графическая функция касательной
То тригонометрические отношения также можно рассматривать как функции переменной, являющейся мерой угла. Эта угловая мера может быть либо задана в градусов или радианы . Здесь мы будем использовать радианы.
С, загар ( Икс ) знак равно грех ( Икс ) потому что ( Икс ) касательная функция не определена, когда потому что ( Икс ) знак равно 0 .Следовательно, тангенс-функция имеет вертикальная асимптота в любое время потому что ( Икс ) знак равно 0 .
Точно так же функции тангенса и синуса имеют нули при целых числах, кратных
π
так как
загар
(
Икс
)
знак равно
0
когда
грех
(
Икс
)
знак равно
0
.
График касательная функция у знак равно загар ( Икс ) выглядит так:
Свойства касательной функции, у знак равно загар ( Икс ) .Домен : Икс е ℝ , Икс ≠ π 2 + н π , где н является целым числом.
Диапазон : ( − ∞ , ∞ )
у -перехват : ( 0 , 0 )
Икс -перехват : н π , где н является целым числом.
Период: π
Симметрия: происхождение (нечетная функция)
Амплитуда и период касательной функции Касательная функция не имеет амплитуды, потому что у нее нет максимального или минимального значения.
Период касательной функции, у знак равно а загар ( б Икс ) , — расстояние между любыми двумя последовательными вертикальными асимптотами.
Период = π | б |
Также см Тригонометрические функции .
Тригонометрические функции и их графики: Тангенс
Пурпурная математика
На предыдущей странице мы рассмотрели, как отношения синусов и косинусов для прямоугольных треугольников могут быть расширены с помощью единичного круга до полноценных графических функций.Следующее тригонометрическое соотношение, которое мы рассмотрим, — это отношение тангенса. Но значения касательной трудно отобразить на единичной окружности. Это связано с тем, что тангенс формируется путем деления значения единичного круга для синуса на его значение для косинуса, каждое из которых иногда равно нулю, а мы не можем делить на ноль.
Это связано с тем, что тангенс формируется путем деления значения единичного круга для синуса на его значение для косинуса, каждое из которых иногда равно нулю, а мы не можем делить на ноль.
Итак, вместо этого давайте подробнее рассмотрим графики синусов и косинусов, помня о том, что tan(θ) равен этому делению: sin(θ) ÷ cos(θ).
MathHelp.com
Тангенс, будучи дробью, будет равен нулю, если его числитель (то есть значение синуса для этой меры угла) равен нулю.Синус равен нулю в точках 0, π, 2π, 3π и т. д., а также в точках −π, −2π, −3π и т. д.; то есть тангенс будет иметь нулевое значение при каждом кратном π. Давайте пока рассмотрим только область от −π до 2π. Таким образом, касательная будет равна нулю (то есть пересечет ось x ) в точках −π, 0, π и 2π.
Давайте пока рассмотрим только область от −π до 2π. Таким образом, касательная будет равна нулю (то есть пересечет ось x ) в точках −π, 0, π и 2π.
Тангенс, будучи дробью, будет равен undefined везде, где его знаменатель (то есть значение косинуса для этой меры угла) равен нулю.И, возвращаясь к тому времени, когда вы узнали о построении графиков рациональных функций, вы знаете, что ноль в знаменателе функции означает, что у вас будет вертикальная асимптота. Таким образом, тангенс будет иметь вертикальные асимптоты везде, где косинус равен нулю. Придерживаясь того же интервала от -π до 2π, вертикальные асимптоты будут при -π/2, π/2 и 3π/2. Другими словами, между каждым числом, кратным π, будет вертикальная асимптота.
Точно так же, как отношения синуса и косинуса были преобразованы в функции, мы также можем преобразовать отношение тангенса в функцию.Тангенс неявно будет чем-то вроде рациональной функции, за исключением того, что его отношение образуется путем деления двух тригонометрических функций (а не двух многочленов).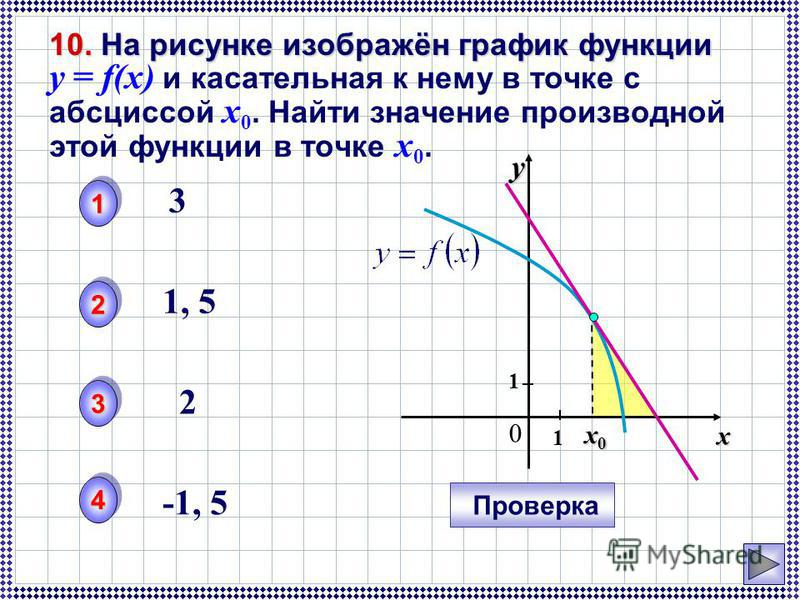 Эта функция обозначается как tan() или просто [TAN] на вашем калькуляторе. Эта функция периодична, как и синус и косинус, образующие тангенс. Но график не может быть хорошей простой волной, не в последнюю очередь из-за вертикальных асимптот.
Эта функция обозначается как tan() или просто [TAN] на вашем калькуляторе. Эта функция периодична, как и синус и косинус, образующие тангенс. Но график не может быть хорошей простой волной, не в последнюю очередь из-за вертикальных асимптот.
График функции касательной
Чтобы построить тангенс, начнем с «интересных» точек, то есть с нулей и асимптот.Поставьте точки вместо нулей и пунктирные вертикальные линии для асимптот:
← смахните , сколько нужно, чтобы просмотреть полное изображение →
А куда идет функция от этих нулей? Здесь мы используем то, что знаем о синусе, косинусе и асимптотах, чтобы заполнить остальную часть графика касательной. Рассмотрим интервал между нулем в точке 0π и асимптотой в точке ½π.
- Мы знаем, что график никогда не коснется и не пересечет вертикальные асимптоты
- Мы знаем, что между нулем и асимптотой график будет либо ниже оси (и скользить вниз по асимптоте до отрицательной бесконечности), либо выше оси (и тоньше вверх по асимптоте до положительной бесконечности).

- Между нулем и π/2 и синус, и косинус положительны.
- Тогда тангенс, будучи их частным, также должен быть положительным, поэтому график скользит вверх по асимптоте.
С этой информацией мы можем начать наш график:
← смахните , сколько нужно, чтобы просмотреть полное изображение →
Теперь рассмотрим следующий интервал.Между π/2 и π синус положительный, а косинус отрицательный. Эти противоположные знаки означают, что тангенсное частное будет отрицательным, поэтому оно будет скользить вверх по правой стороне асимптоты снизу, изгибаться и встречаться с осью x в точке x = π. Давайте нарисуем этот бит:
← смахните , сколько нужно, чтобы просмотреть полное изображение →
Так как синус и косинус периодические, то и тангенс тоже должен быть периодическим.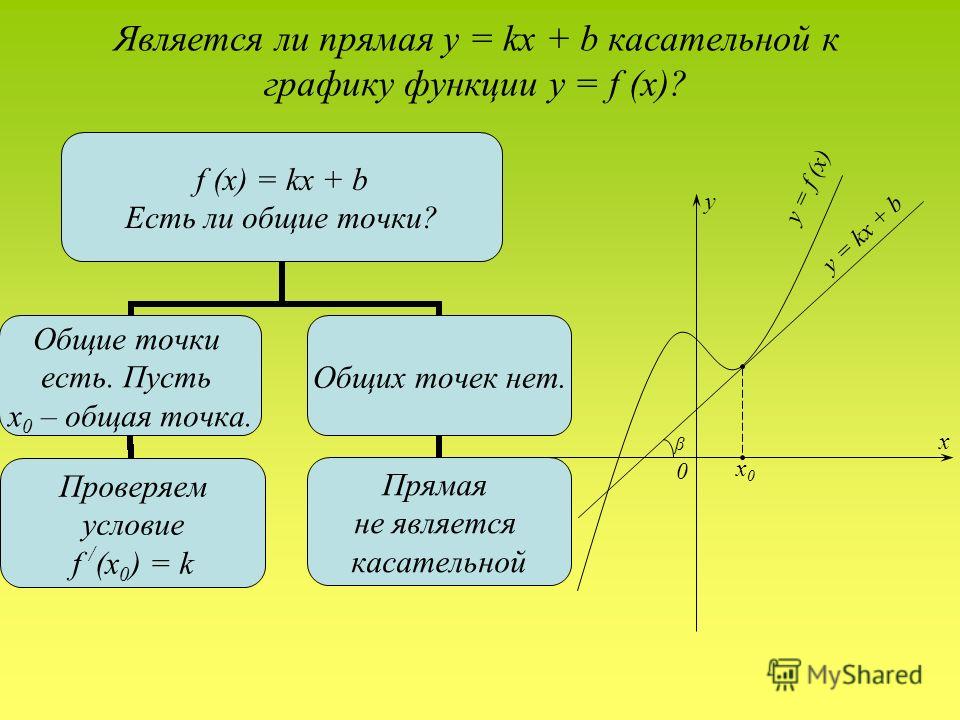 Быстрая проверка знаков подсказывает нам, как заполнить остальную часть графика:
Быстрая проверка знаков подсказывает нам, как заполнить остальную часть графика:
- От −π до −π/2: синус отрицательный, а косинус отрицательный, поэтому тангенс положительный; эта часть графика должна дублировать график между 0 и ½π
- от −π/2 до 0: синус отрицательный, но косинус положительный, поэтому тангенс отрицательный; эта часть графика должна дублировать график между ½π и π От
- π до 3π/2: синус отрицателен, а косинус отрицателен, поэтому тангенс положителен; часть графика должна дублировать график между 0 и ½π
- От 3π/2 до 2π: синус отрицательный, но косинус положительный, поэтому тангенс отрицательный; эта часть графика должна дублировать график между ½π и π
Используя эту периодичность (повторяющуюся для каждого числа, кратного π), мы можем завершить наш график:
← смахните , сколько нужно, чтобы просмотреть полное изображение →
Как видите, тангенс имеет период π, причем каждый период разделен вертикальной асимптотой. Понятие «амплитуда» действительно не применяется. Благодаря асимптотам значения тангенса не ограничены; то есть значения изменяются от -∞ до +∞; диапазон вывода y -значения «все».
Понятие «амплитуда» действительно не применяется. Благодаря асимптотам значения тангенса не ограничены; то есть значения изменяются от -∞ до +∞; диапазон вывода y -значения «все».
Филиал
Для построения графика придерживайтесь «интересных» точек. Нарисуйте нули на x = 0, π, 2π и т. д. (они совпадают с нулями синуса), а затем прочеркните вертикальные асимптоты посередине между каждым нулем.Затем нарисуйте кривую. Вы можете нанести еще несколько точек, если хотите, но обычно от этого мало что выигрывают.
Если вы предпочитаете запоминать графики, запомните интервал по вашему выбору из графика выше. Вы можете предпочесть интервал 0 и π или, возможно, −½π и асимптоту при ½π. Что бы вы ни нашли полезным, это «правильная» вещь для запоминания. Что касается меня лично, у меня всегда были проблемы с поддержанием прямолинейности чего-либо, выходящего далеко за пределы синуса и косинуса, поэтому я использовал рассуждения, продемонстрированные выше, чтобы выяснить графики тангенса (и кофункции).
Пока вы знаете свои синусы и косинусы, и хорошо их знаете , вы сможете понять все остальное.
URL: https://www.purplemath.com/modules/triggrph3.htm
Является ли производная функции касательной? — Magoosh Blog
В исчислении мы узнаем, что касательная для функции может быть найдена путем вычисления производной.Таким образом, существует тесная связь между производными и касательными. Однако это не одно и то же. Для начала, производная f ‘( x ) — это функция, а касательная — это, в общем-то, прямая.
Вместо этого правильное утверждение будет таким: «Производная измеряет наклон касательных».
Подумайте об этом: часы — это не то же самое, что время . Но если вы хотите узнать время суток, вы можете посмотреть на часы, чтобы узнать. Часы измеряют время в любой момент дня .
Часы измеряют время в любой момент дня .
Давайте подробнее рассмотрим касательные.
Что такое касательная?
касательная для функции f ( x ) в заданной точке x = это линия (линейная функция), которая соответствует графику функции в x =
6 =
6 и имеет тот же наклон , что и кривая в этой точке. Иногда мы можем сказать, что касательная « только что касается » кривой или « пересекает кривую только один раз », но эти идеи иногда могут ввести нас в заблуждение.
На приведенном ниже графике показаны касательные линии (выделены красным, фиолетовым и пурпурным цветом) в трех разных точках кривой y = f ( x ) (черным цветом) .
Наклон и производные
Так как же узнать, каким должен быть наклон касательной? Узнав о производных , вы можете использовать простую формулу:
m = f ( a ).
В этой формуле заданы функции f и x — значения a . Ваша задача — найти м , что представляет собой наклон касательной. Если у вас есть наклон, написать уравнение касательной линии довольно просто.
Нахождение касательной
Предположим, вас попросили найти касательную для функции f ( x ) в заданной точке x = a . Вот пошаговый подход:
- Найдите производную, f ‘( x ).
- Подставьте x = к , чтобы получить уклон. То есть вычислите м = f ( a ).
- Если еще не задано в задаче, найти y -координату точки. Как всегда, вы подставляете значение x в функцию, чтобы получить значение y . Пусть b = f ( a ).
- Используйте форму точка-наклон и найдите y , чтобы найти уравнение касательной.Другими словами, подставьте ваши значения m , a и b в уравнение:
Наклон производных
Давайте еще раз взглянем на первый шаг: « Найдите производную ». Помните, что производная — это функция (входной переменной x ). Подставляя различные входные значения, x = a , выходные значения f ‘( x ) дают вам наклоны касательных линий в каждой точке x = a .
Помните, что производная — это функция (входной переменной x ). Подставляя различные входные значения, x = a , выходные значения f ‘( x ) дают вам наклоны касательных линий в каждой точке x = a .
Вот что мы имеем в виду, когда говорим, что «производная измеряет наклон касательных».
Если я хочу узнать наклон f при x = 1, то я вычисляю f ‘(1). И если я хочу узнать наклон при x = -352/13, то я вычисляю f ‘(-352/13). Просто как тот!
Пример: полином
Теперь давайте рассмотрим пример функции, f ( x ) = x 3 + 3 x + 2 9.0346Мы найдем касательные линии в нескольких разных точках.
Прежде всего, найдите производную: f ‘( x ) = 3 x 2 + 6 x . (чтобы попрактиковаться в поиске деривативов, ознакомьтесь с этой статьей Magoosh о деривативах).
Функциональное значение и производное значение в нескольких точках отображаются в таблице ниже:
x -3 -3 2 -1 -1 -1 0 1 5 5 3 1 5 5 F ‘( x ) = 3 x 2 + 6 x 9 0 -3 0 9
Для перечисленных точек мы можем легко найти уравнение касательной.Обратите внимание, что на экзамене AP по математическому анализу ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам как форму точки-наклона, так и упрощенную, или наклон-пересечение , форму касательной.
x y = 9 x + 28 -2 y = 0 ( y = 0 ( x + 2) + 5 y = 5 -1 y = -3 ( x + 1) + 3 y = -3 y = -3 x 0 y = 0 ( x — 0) + 1 y = 1 1 y = 9 ( y = 9 ( x — 1) + 5 y = 9 x — 4
Теперь давайте посмотрим график y = F ( x ) вместе с касательными, которые мы только что нашли.
Резюме
Итак, теперь вы знаете. Производная — это не то же самое, что касательная. Вместо этого производная является инструментом для измерения наклона касательной в любой конкретной точке, точно так же, как часы измеряют время в течение дня. Имея это в виду, у вас не возникнет проблем с решением задач касательной линии на экзамене AP Calculus!
Имея это в виду, у вас не возникнет проблем с решением задач касательной линии на экзамене AP Calculus!
Чтобы узнать больше о наклоне, касательных и производных, ознакомьтесь со следующими статьями Magoosh: Является ли производная функции наклоном? и Как найти наклон линии, касательной к кривой.
Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!
Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (вперёд!). В 2002 году он получил степень бакалавра математики со специализацией в области компьютерных наук в Оберлинском колледже. Кроме того, Шон получил степень бакалавра музыки. в том же году окончил Оберлинскую консерваторию по специальности «музыкальная композиция».Шон по-прежнему любит музыку — почти так же сильно, как математику! — и он (думает, что он) умеет играть на фортепиано, гитаре и басу. Шон преподавал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!
Шон преподавал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!
Посмотреть все сообщения
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
Касательные: определение и свойства | Study.com
Свойства
Касательные имеют несколько интересных свойств.Мы только что коснулись их в разделе определений.
1. Касательные аппроксимируют кривую в точке. Они дают наилучшее приближение в этой точке, показывая наклон кривой в этой точке.
2. Тангенс едва касается кривой в одной точке.
3. Чтобы точка на кривой имела касательную, она должна быть дифференцируемой в этой точке. Если он не дифференцируем в этой точке, он не имеет определенного наклона и, следовательно, не имеет определенной касательной, поскольку касательная определяется наклоном в этой точке.
Формула
Поскольку касательная представляет собой линию наклона кривой в любой заданной точке, формула касательной включает производную кривой . Производная кривой дает вам изменение кривой в любой заданной точке, которая является наклоном. Таким образом, оценка производной в данной точке даст вам наклон, который вы можете использовать для нахождения касательной.
Производная кривой дает вам изменение кривой в любой заданной точке, которая является наклоном. Таким образом, оценка производной в данной точке даст вам наклон, который вы можете использовать для нахождения касательной.
Формула нахождения касательной.
Касательная линия находится с использованием формы точки-наклона линии и подстановки заданной точки вместе с производной, вычисленной в этой точке.Затем уравнение решается для y , чтобы найти уравнение.
Вычисление тангенса
Давайте теперь посмотрим, как работает формула для функции. Мы будем работать над следующей функцией, чтобы увидеть, как мы можем найти нашу касательную.
Наша проблемная функция кривой.
Мы хотим оценить его в точке, где x=1. Чтобы узнать точную точку, мы можем подставить наши x , чтобы найти наши y . Наше выражение f(x) совпадает с y . Мы можем поменять их местами по желанию.
Наше выражение f(x) совпадает с y . Мы можем поменять их местами по желанию.
Нахождение точных координат точки.
Наши и равны 1, поэтому наша точка равна (1, 1).
Согласно нашей формуле, есть точка и теперь нам нужна наша производная. Теперь мы возьмем производную нашей функции и будем следовать любым известным нам свойствам производной.
Берем производную.
Мы использовали правило степени производных, чтобы найти нашу производную. Теперь нам нужно оценить нашу производную в точке, где x=1. Мы можем сделать это, подставив наше x в производную, чтобы найти наклон.
Оценка производной.
Наш наклон равен 3. Теперь мы можем подставить все наши значения в форму точки-наклона уравнения прямой и найти y , чтобы получить уравнение касательной линии.3 в точке, где x=1 равно y=3x-2 .
Теперь мы можем подставить все наши значения в форму точки-наклона уравнения прямой и найти y , чтобы получить уравнение касательной линии.3 в точке, где x=1 равно y=3x-2 .
Резюме
Подводя итог, можно сказать, что касательная кривой представляет собой уравнение прямой с наклоном кривой в этой точке. Формула для нахождения касательной к кривой в заданной точке представляет собой точечно-наклонную форму уравнения прямой с производной, оцениваемой в точке как наклон.
Касательные Темы и пояснения
Темы Пояснения Тангенс линия наклона кривой в конкретной точке; линия, которая касается кривой в любой конкретной точке и идет в том же направлении, что и кривая в этой точке Свойства касательных аппроксимируют кривую в точке и едва касаются кривой в точке; чтобы точка на кривой имела касательную, она должна быть дифференцируемой в этой точке Формула касательная линия находится с использованием формы точки-наклона линии и подстановки заданной точки вместе с производной, вычисленной в этой точке
Результаты обучения
Когда вы закончите здесь, вы сможете выполнить следующее:
- Определить касательную
- Определить свойства касательной
- Объясните формулу для решения касательной
- Приведите примеры вычисления тангенсов
Как вычислить тангенс функции — x-engineer.
 org
org
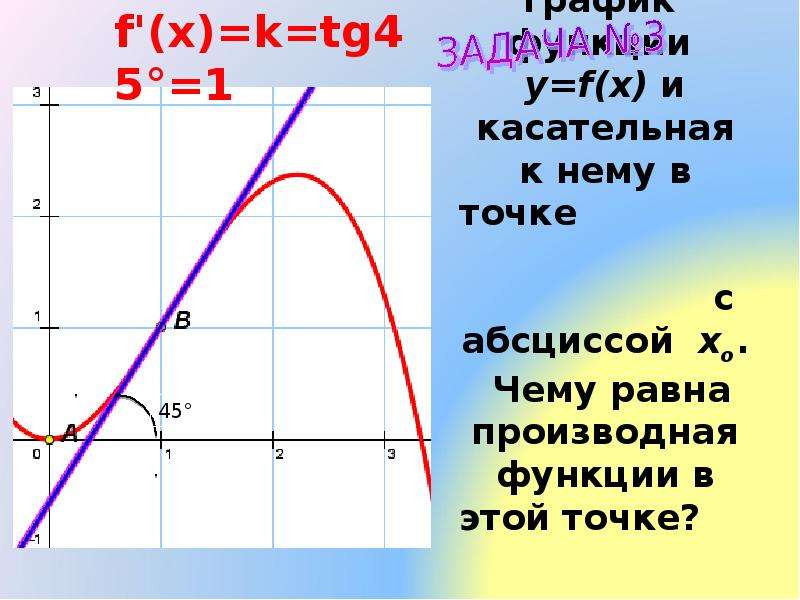
 Помните, что производная — это функция (входной переменной x ). Подставляя различные входные значения, x = a , выходные значения f ‘( x ) дают вам наклоны касательных линий в каждой точке x = a .
Помните, что производная — это функция (входной переменной x ). Подставляя различные входные значения, x = a , выходные значения f ‘( x ) дают вам наклоны касательных линий в каждой точке x = a .

 Имея это в виду, у вас не возникнет проблем с решением задач касательной линии на экзамене AP Calculus!
Имея это в виду, у вас не возникнет проблем с решением задач касательной линии на экзамене AP Calculus! Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (вперёд!). В 2002 году он получил степень бакалавра математики со специализацией в области компьютерных наук в Оберлинском колледже. Кроме того, Шон получил степень бакалавра музыки. в том же году окончил Оберлинскую консерваторию по специальности «музыкальная композиция».Шон по-прежнему любит музыку — почти так же сильно, как математику! — и он (думает, что он) умеет играть на фортепиано, гитаре и басу. Шон преподавал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!
Шон преподавал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!
Посмотреть все сообщения
 Производная кривой дает вам изменение кривой в любой заданной точке, которая является наклоном. Таким образом, оценка производной в данной точке даст вам наклон, который вы можете использовать для нахождения касательной.
Производная кривой дает вам изменение кривой в любой заданной точке, которая является наклоном. Таким образом, оценка производной в данной точке даст вам наклон, который вы можете использовать для нахождения касательной. Наше выражение f(x) совпадает с y . Мы можем поменять их местами по желанию.
Наше выражение f(x) совпадает с y . Мы можем поменять их местами по желанию. Теперь мы можем подставить все наши значения в форму точки-наклона уравнения прямой и найти y , чтобы получить уравнение касательной линии.3 в точке, где x=1 равно y=3x-2 .
Теперь мы можем подставить все наши значения в форму точки-наклона уравнения прямой и найти y , чтобы получить уравнение касательной линии.3 в точке, где x=1 равно y=3x-2 .Касательная к функции в точке — это линия, которая соприкасается с графическим представлением функции только в этой конкретной точке.
Касательная касается функции (графика) только в указанной точке. Другими словами, касательная едва касается функции (графика).
Линия, которая пересекает (пересекает) график функции, называется секущей .
Изображение: Тангенс и секанс графика функции
В приведенном выше примере красная линия — это тангенс.Она касается функции f(x) в точке P(x 1 , y 1 ) . Синяя линия — это секущая, и, как вы видите, она пересекает функцию f(x) в двух точках.
Учитывая функцию f(x) и точку P 1 (x 1 , y 1 ) , как вычислить тангенс? Нахождение касательной означает нахождение уравнения прямой, касательной к функции f(x) в точке P 1 (x 1 , y 1 ) . {3}=1\]
{3}=1\]
Мы знаем, что:
\[y_{1}=f(x_{1})\]Это означает, что результатом вычисления функции в точке x 1 является y 1 координата. Теперь мы определили точку P 1 (1, 1) . Построим график функции f(x) для x = 0 … 2 и точки P 1 с x 1 и y 1
Изображение: График кубической функции с точкой касания
.
Мы выберем точку P 0 x 0 = 0,6 и P 2 at x 2 2 Эти точки должны быть равномерно распределены слева и справа от точки касания P 1 .
Шаг 3 . Вычислите координаты y точек P 0 и P 2 точек
Сначала давайте вычислим координату y точки P 05 Теперь мы определили точку P 2 (1,4,-0,744) . Теперь давайте обновим наш график функции точками P 0 и P 2 и их координатами. Изображение: График кубической функции с точкой касания и двумя точками смещения Шаг 4 . Вычислите наклоны линий, определенных между точками P 0 -P 1 и P 1 -P 2 Имея две определенные точки, мы можем легко провести прямую линию между ними.Также с помощью координат двух точек мы можем рассчитать наклон линии. В нашем случае у нас будет две линии: одна между точками P 0 и P 1 , а вторая между P 1 и P 2. Для обеих линий мы можем вычислить их наклон. Обычным обозначением уклона линии является буква м . Для первой линии уклон м 0 рассчитывается как: Для второй линии уклон м 2 равен рассчитывается как: Ниже приведено графическое представление двух линий и функция f(x) . Обе линии являются секущей нашей функции f(x) . Изображение: График кубической функции с точкой касания и двумя секущими Шаг 5 . Вычислить наклон касательной в точке P 1 (1, 1) Наклон касательной в точке P 1 будет средним арифметическим наклонов двух секущие линии . Этот метод расчета возможен, потому что мы выбрали x 0 и x 2 точек на равном расстоянии от x 1 . Изображение: квадратичная функция график с точкой касания и линией касания Изображение: график функции квадратного корня с точкой касания и линией касания Примените тот же метод к своей функции и дайте нам результат! Если у вас есть какие-либо вопросы или замечания относительно этого урока, пожалуйста, используйте форму комментариев ниже. Не забудьте поставить лайк, поделиться и подписаться! В начале сегодняшнего обсуждения мы рассмотрим две достаточно общие проблемы. По мере того, как мы будем работать над решением этих проблем, мы начнем замечать некоторое сходство между ними. Линия, которая касается кривой в некоторой точке, просто касается кривой, не пересекая ее.До изобретения исчисления геометры знали, что большинство кривых имеют уникальные касательные в каждой точке кривой. Во многих случаях они даже разработали умные геометрические методы построения для построения касательных линий для многих различных типов кривых. Ни один из этих методов построения не имел ничего общего с понятием предела. В каждом случае строительство было выполнено с использованием простых инструментов, таких как линейка и циркуль. Вот пример, чтобы дать вам представление об этих методах. Геометрический метод построения параболы заключается в проведении линии, называемой директрисой, и точки, не лежащей на этой линии, называемой фокусом. Множество всех точек в пространстве, лежащих на одинаковом расстоянии от фокуса и директрисы, очерчивает кривую, называемую параболой. Рассмотрим зеленую линию, соединяющую фокус (0,4) с точкой, где вертикальная синяя линия касается направляющей в точке (r,-4) .Если вы нарисуете линию, проходящую через середину зеленой линии и точку, где встречаются две синие линии, вы построили касательную к параболе. Проблема с этими методами построения касательных линий заключается в том, что для их создания требовалась немалая смекалка, а также они были очень специфичны для кривых. Техника, которую использовали для построения касательной к параболе, сильно отличалась от техники, используемой для построения касательной к эллипсу, и вообще не годилась для чего-то вроде графика функции y = x 3 / 16 . Предположим, мы хотим вычислить уравнение прямой, касательной к графику y = x 3 /16 в точке (2,1/2) . Что делает это сложным, так это то, что для вычисления наклона нам нужны две точки на рассматриваемой линии. Здесь у нас есть только один для работы. Один из способов оценить наклон — заметить, что если вы немного наклоните касательную, она коснется кривой в двух точках, а не только в одной — если мы сможем выяснить, где находятся эти две точки, мы сможем вычислить наклон этого секанса. линию и используйте ее для оценки наклона касательной. Чем ближе точка (a , a 3 /16 ) к точке ( 2 , 1/2 ) , тем больше секущая становится похожей на касательную. В пределе наклон секущей становится равным Линия, проходящая через (2,1/2) с наклоном 3/4, имеет уравнение или Исчисление — это изучение величин, которые непрерывно изменяются.Центральный вопрос исчисления — как определить мгновенную скорость изменения некоторой величины. у = f(x) скорость изменения х по отношению к х за некоторый интервал в х определяется как Математики используют более компактную запись, называемую дельта-записью, для описания изменений. В дельта-обозначении скорость изменения равна Более конкретно, мы определяем эту скорость изменения, выбирая два соседних значения x , x 1 и x 2 , и вычисляя x и y две дельты от этих значений. Чтобы вычислить мгновенную скорость изменения, мы вычисляем скорость изменения для очень малого и берем предел, когда он приближается к 0. Несколько более удобный способ сделать это — зафиксировать одно из двух значений x и взять предел, когда первое x перемещается произвольно близко ко второму x . В качестве альтернативы, вы можете выразить x 1 как x 2 + h для небольшого числа h и взять предел, поскольку h обращается в 0. Наконец, поскольку у нас остался только один x, мы опускаем нижний индекс и рассматриваем мы называем эту величину мгновенной скоростью изменения f(x) при x или, альтернативно, производной от f(x) при x . Математическая модель размера популяции бактерий, растущих в культуре, говорит, что через x часов размер популяции составляет Какова мгновенная скорость роста населения в х = 3 часов? Предел здесь не может быть решен алгебраическими приемами, поэтому мы должны оценить его численно. Скорость изменения при x = 3 приблизительно равна Предел называется производной от f(x) при x . Мы видели, что этот предел (или очень похожие на него пределы) проявляется, когда мы пытаемся вычислить наклоны касательных линий или оценить мгновенные скорости изменения. Следующие несколько лекций мы посвятим изучению этого предела и разработке методов его более быстрого и простого вычисления. Раздел 2.7: 1, 2, 5, 7, 8, 15, 16, 22, 27, 28 Для графика функции касательной создайте таблицу значений и нанесите их на координатную плоскость. Поскольку tan(theta)=y/x, всякий раз, когда x=0, функция тангенса не определена (деление на ноль не определено). Я хочу построить график функции тангенса. У меня есть таблица значений, написанная здесь, и определение функции касательной к единичному кругу здесь. Теперь вот единичный круг. Я хочу напомнить вам, что еще один способ увидеть функцию тангенса как наклон стороны терминала op. Это почему? Ну, это потому, что вы нарисовали вот этот маленький треугольник, вертикальный катет треугольника равен y, а горизонтальный катет — x, где x и y — эти координаты.И наклон этой линии будет y над x подъемом над пробегом. Итак, y над x — это наклон op, и это помогает нам увидеть, как ведет себя тангенс. Но касательная дает мне наклон этой линии. 2{3}=-0,744\\
y_{2}&=-0,744
\end{split} \end{equation*} \]
м_{0}&=\frac{y_{1}-y_{ 0}}{x_{1}-x_{0}}=\frac{1-1.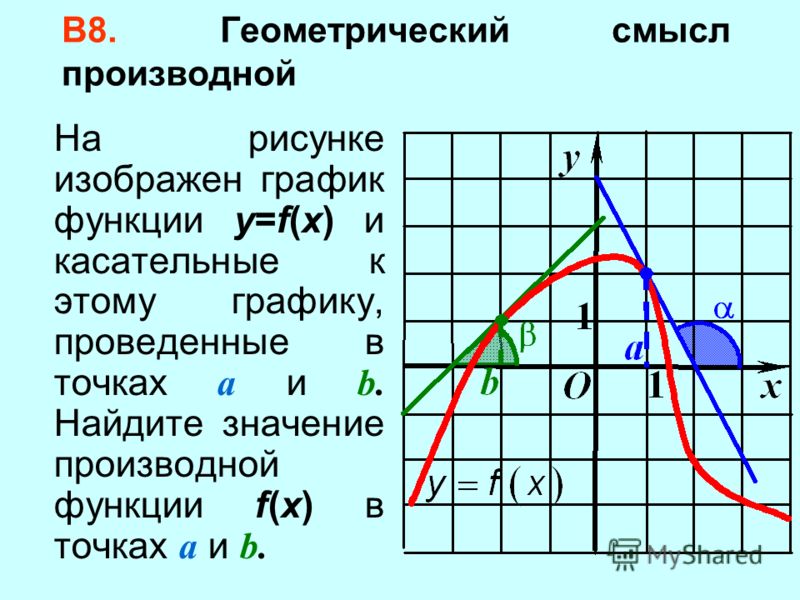 784}{1-0.6}=-1.96\\
784}{1-0.6}=-1.96\\
м_{0}&=-1.96
\end{split} \end{equation*} \]
m_{2}&=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\ frac{-0.744-1}{1.4-1}=-4.36\\
m_{2}&=-4.36
\end{split} \end{equation*} \]
m_{1}&=\frac{m_{0}+m_{2}}{2}=\frac{-1. 2 + 2 \cdot x + 1\]
2 + 2 \cdot x + 1\] 031Tangents.lbz
031Tangents.lbz Две проблемы
 Можем ли мы вычислить для такой величины мгновенную скорость изменения , которая измеряет, насколько быстро величина изменяется в данный момент времени?
Можем ли мы вычислить для такой величины мгновенную скорость изменения , которая измеряет, насколько быстро величина изменяется в данный момент времени? Касательная задача
 Например, парабола с фокусом (0,4) и директрисой, равной прямой y = -4 , имеет уравнение y = x 2 /16.
Например, парабола с фокусом (0,4) и директрисой, равной прямой y = -4 , имеет уравнение y = x 2 /16. Использование предела для построения касательной
 Чтобы вычислить это уравнение, нам нужно знать наклон касательной в этой точке.
Чтобы вычислить это уравнение, нам нужно знать наклон касательной в этой точке. Мгновенная скорость изменения
 Если эта величина описывается соотношением
Если эта величина описывается соотношением
Пример
ч 0,5 3,656854249492380 0,1 2,311444133449163 0,05 2,191389441356901 0,01 21276 2101212570719335 0,0001 2,079657760523101 903 0. 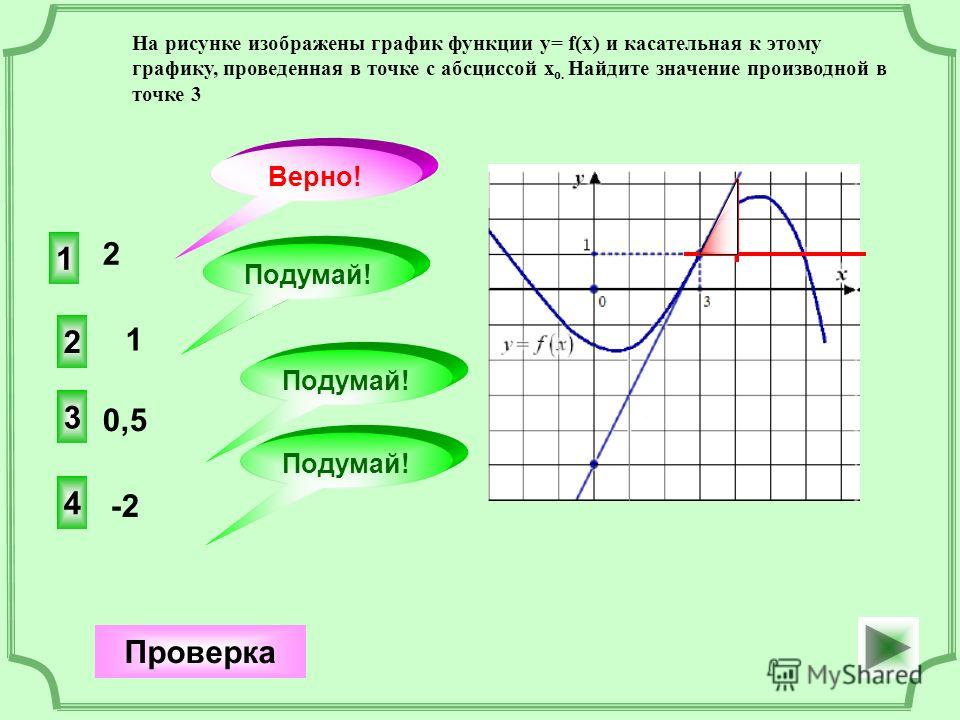 000001
000001 2,079443703673078 Производная
Домашнее задание
График касательной функции — Концепция
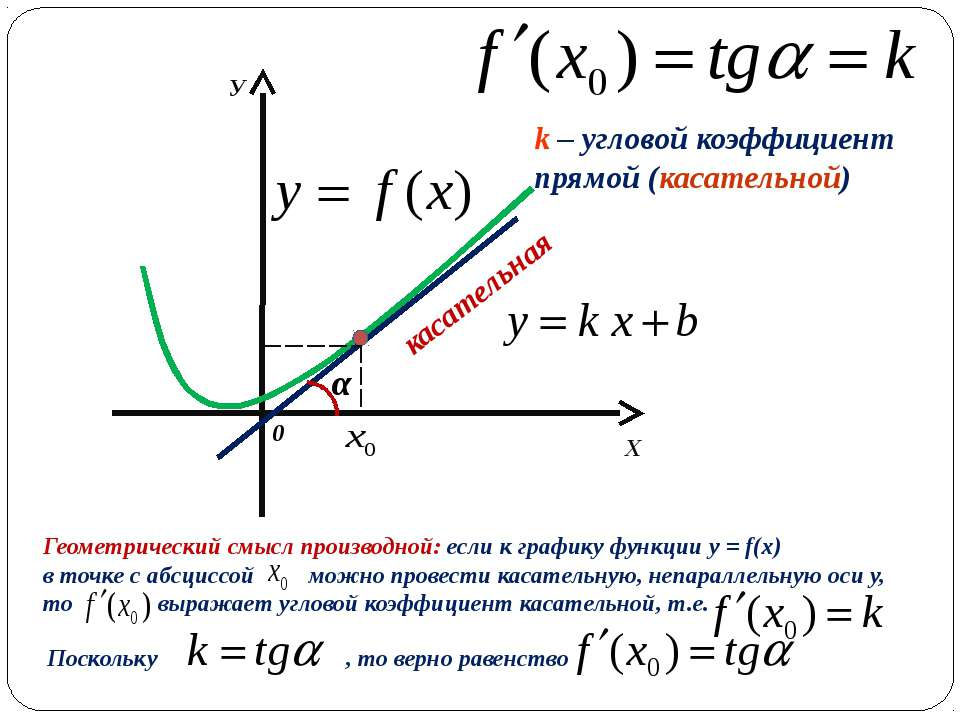 Эти точки с тета=пи/2, 3пи/2 и их целыми кратными представлены на графике вертикальными асимптотами или значениями, которым функция не может равняться.Из-за симметрии единичного круга относительно оси y период равен пи/2.
Эти точки с тета=пи/2, 3пи/2 и их целыми кратными представлены на графике вертикальными асимптотами или значениями, которым функция не может равняться.Из-за симметрии единичного круга относительно оси y период равен пи/2.
Хорошо. Давайте начнем с построения нескольких точек, я вернусь к вопросу наклона через секунду.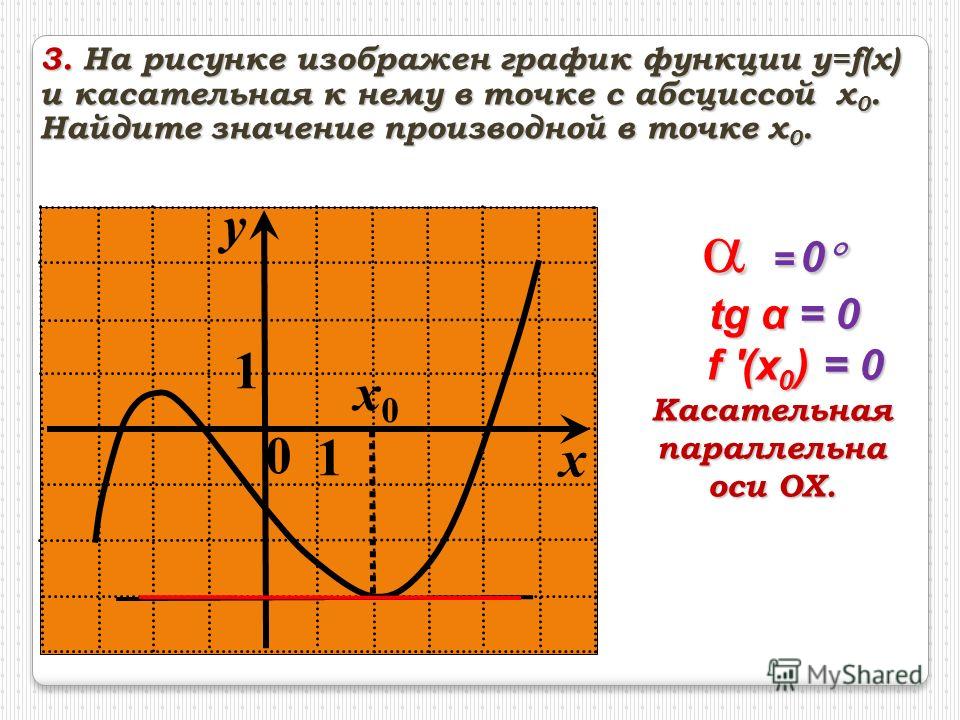 Первая точка — 0 0, она идет прямо туда. И я просто собираюсь использовать эти 2 пункта. Пи больше 4, 1. Пи больше 4 находится на полпути между 0 и пи больше 2, так что прямо здесь. И я собираюсь сделать это 1. Итак, здесь число пи больше 4, 1.И затем пи больше 3, корень 3. Корень 3 примерно равен 1,7, поэтому я собираюсь изобразить это как 1,7, а число пи больше 3 составляет две трети пути от 0 до числа пи больше 2. Итак, это число пи больше 3. . Хорошо. Если это 1,5, а это 2, то здесь примерно 1,7. Итак, вот моя точка зрения, и я рисую свою кривую. Таким образом, он очень быстро возрастает и имеет вертикальную асимптоту. Он просто возрастает более круто и круто по мере приближения x или по мере того, как тета приближается к pi больше 2. И причина этого снова в том, что он снова возвращается к наклону.По мере того, как этот угол становится все ближе и ближе к числу пи больше 2, наклон этой линии становится все круче и круче. Он приближается к бесконечности, и поэтому касательная стремится к бесконечности.
Первая точка — 0 0, она идет прямо туда. И я просто собираюсь использовать эти 2 пункта. Пи больше 4, 1. Пи больше 4 находится на полпути между 0 и пи больше 2, так что прямо здесь. И я собираюсь сделать это 1. Итак, здесь число пи больше 4, 1.И затем пи больше 3, корень 3. Корень 3 примерно равен 1,7, поэтому я собираюсь изобразить это как 1,7, а число пи больше 3 составляет две трети пути от 0 до числа пи больше 2. Итак, это число пи больше 3. . Хорошо. Если это 1,5, а это 2, то здесь примерно 1,7. Итак, вот моя точка зрения, и я рисую свою кривую. Таким образом, он очень быстро возрастает и имеет вертикальную асимптоту. Он просто возрастает более круто и круто по мере приближения x или по мере того, как тета приближается к pi больше 2. И причина этого снова в том, что он снова возвращается к наклону.По мере того, как этот угол становится все ближе и ближе к числу пи больше 2, наклон этой линии становится все круче и круче. Он приближается к бесконечности, и поэтому касательная стремится к бесконечности.
 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Значит, вид уравнения будет y = b .
Значит, вид уравнения будет y = b .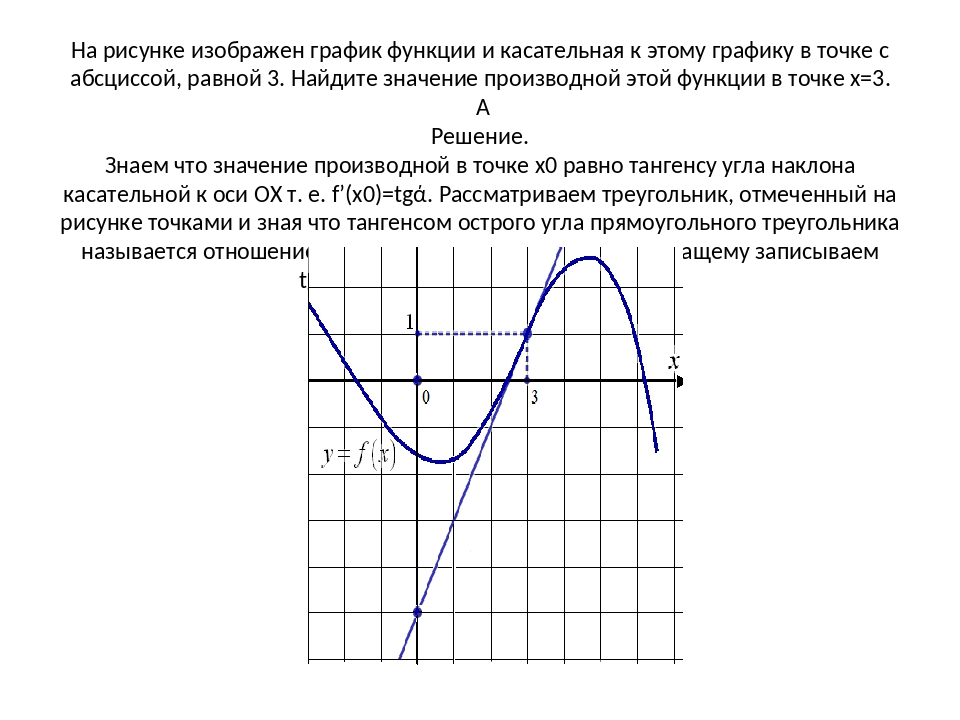

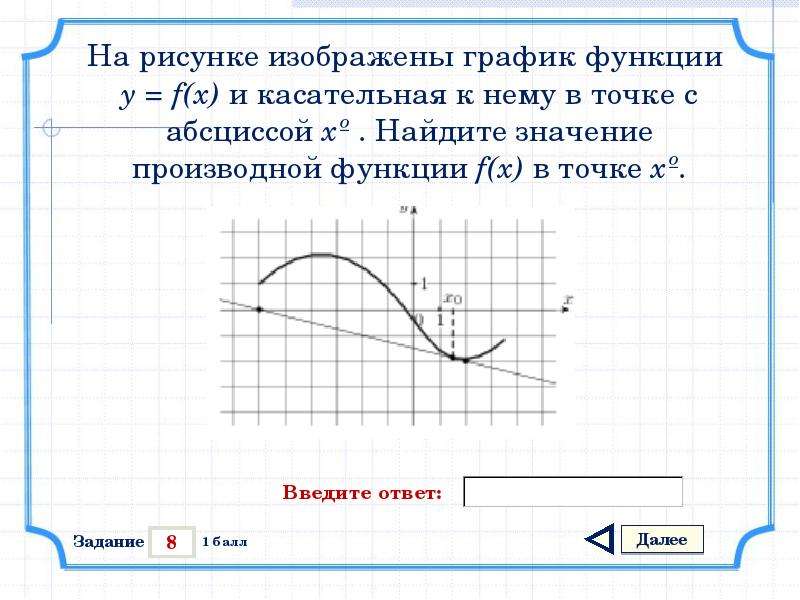 Равенство задается при помощи равенства x = c со значением с, являющимся действительным числом.
Равенство задается при помощи равенства x = c со значением с, являющимся действительным числом.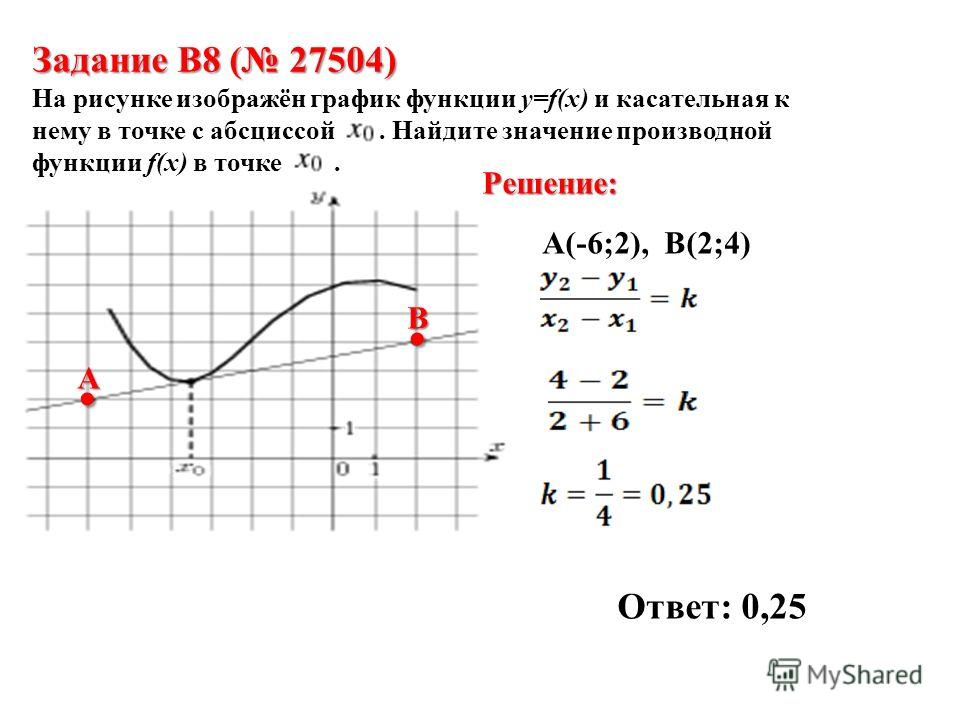


 org
org