Комбинаторные задачи — это… Что такое Комбинаторные задачи?
Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения, например в информатике и статистической физике.
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.
Примеры комбинаторных конфигураций и задач
Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:
- Размещением из n элементов по k называется упорядоченный набор из k
- Перестановкой из n элементов (обычно чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
- Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
- Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
- Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.
Примерами комбинаторных задач являются:
- Сколькими способами можно разместить n предметов по m ящикам так, что бы выполнялись заданные ограничения?
- Сколько существует функций F из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?
- Сколько существует различных перестановок из 52 игральных карт?
- Ответ: 52! (52 факториал) то есть 80658175170943878571660636856403766975289505440883277824000000000000 или примерно 8.0658 × 1067.
- При игре в кости бросаются две кости и выпавшие очки складываются, сколько существует комбинаций, таких, что сумма очков на верхних гранях равна двенадцати?
- Решение: Каждый возможный исход соответствует функции
 (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 дает нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.
(аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 дает нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.
- Решение: Каждый возможный исход соответствует функции
Разделы комбинаторики
Перечислительная комбинаторика
Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определенные ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.
Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.
Типичным примером задач данного раздела является подсчете количества перестановок (см. выше). Число перестановок n-элементного множества равно факториалу числа n, то есть n!. Другой пример — известная Задача о письмах.
Структурная комбинаторика
К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.
Экстремальная комбинаторика
Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определенным свойствам.
Теория Рамсея
Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:
- в группе из 6 человек всегда можно найти три человека, которые либо попарно знакомы друг с другом, либо попарно незнакомы.
В терминах структурной комбинаторики это же утверждение формулируется так:
- в любом графе с 6 вершинами найдется либо клика, либо независимое множество размера 3.
Вероятностная комбинаторика
Этот раздел отвечает на вопросы вида: какова вероятность присутствия определенного свойства у заданного множества.
Топологическая комбинаторика
Аналоги комбинаторных концепций и методов используются и в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.
См. также
Литература
- Андерсон Джеймс Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — С. 960. — ISBN 0-13-086998-8
- Р. Стенли Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 440. — ISBN 5-03-001348-2
- Липский В. Комбинаторика для программистов: Пер. с польск. — М.: Мир, 1988. — 213 с, ил.
- Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 c.
- Риордан Дж. Введение в комбинаторный анализ, пер. с англ., М., 1963; Раизер Г. Дж. Комбинаторная математика, пер. с англ., М., 1966.
Wikimedia Foundation. 2010.
dic.academic.ru
Комбинаторная задача. Простейшие комбинаторные задачи. Комбинаторные задачи: примеры
Преподаватели математики знакомят своих учеников с понятием «комбинаторная задача» еще в пятом классе. Это необходимо для того, чтобы они сумели в дальнейшем работать с более сложными заданиями. Под комбинаторностью задачи можно понимать возможность решить ее с помощью перебора элементов конечного множества.
Главным признаком задач такого порядка является вопрос к ним, который звучит как «Сколько вариантов?» или «Сколькими способами?» Решение комбинаторных задач напрямую зависит от того, понял ли решающий их смысл, сумел ли он правильно представить действие или процесс, которые были описаны в задании.
Как решить комбинаторную задачу?

Важно корректно определить тип всех имеющихся в рассматриваемой задаче соединений, но при этом необходимо произвести проверку относительно того, имеются ли в ней повторы элементов, изменяются ли сами элементы, играет ли большую роль их порядок, а также относительно некоторых других факторов.
Комбинаторная задача может иметь целый ряд ограничений, которые могут быть наложены на соединения. В этом случае понадобится просчитать полностью ее решение и проверить, оказывают ли эти ограничения какое-либо влияние на соединение всех элементов. Если влияние действительно имеется, необходимо проверить, какое именно.
С чего начать?
Для начала необходимо научиться решать простейшие комбинаторные задачи. Овладение простым материалом позволит научиться разбираться в более сложных заданиях. Рекомендуется сначала начать решать задачи с ограничениями, которые не учитываются при рассмотрении более простого варианта.
Также рекомендуется попытаться решать сначала те задачи, в которых нужно рассматривать меньшее количество общих элементов. Таким образом вы сможете понять принцип создания выборок и научиться в дальнейшем самостоятельно создавать их. Если задача, для которой необходимо использовать комбинаторику, состоит из комбинации нескольких более простых, рекомендуется решать ее по частям.
Решение комбинаторных задач
Такие задачи могут показаться простыми в решении, однако комбинаторика достаточно сложна для освоения, некоторые из них не имеют решения уже на протяжении последних сотен лет. Одной из самых известных задач является определение количества магических квадратов специального порядка, когда число n больше 4.

Комбинаторная задача тесно связана с теорией вероятности, которая появилась еще в средневековые времена. Вероятность происхождения того или иного события можно вычислить только с использованием комбинаторики, в данном случае понадобится чередовать все факторы местами, чтобы получить оптимальное решение.
Решение задач
Комбинаторные задачи с решением используются для обучения учеников и студентов работе с данным материалом. Если же говорить в целом, они должны вызвать у человека интерес и желание найти общее решение. Помимо математических расчетов, необходимо применять умственное напряжение и использовать догадку.
В процессе решения поставленных задач ребенок сможет развить у себя математическое воображение и комбинаторные способности, это может серьезно пригодиться ему в дальнейшем. Постепенно уровень сложности решаемых заданий необходимо повышать, чтобы не забывать имеющиеся знания и добавлять к ним новые.
Способ 1. Перебор
Методы решения комбинаторных задач очень сильно отличаются друг от друга, но все они могут быть использованы учеником для получения ответа. Одним из самых простых, но в то же время и самых долгих способов является перебор. При нем необходимо просто перебрать все возможные варианты решения, не составляя каких-либо схем и таблиц.
Как правило, вопрос в такой задаче связан с возможными вариантами происхождения того или иного события, например: какие числа можно составить с помощью цифр 2, 4, 8, 9? Путем перебора всех вариантов составляется ответ, состоящий из возможных комбинаций. Такой способ прекрасно подходит, если количество возможных вариантов сравнительно невелико.
Способ 2. Дерево из вариантов
Некоторые комбинаторные задачи можно решить, только составляя схемы, в которых будет подробно указана информация о каждом элементе. Составление дерева возможных вариантов – еще один способ нахождения ответа. Он подходит для решения не слишком-то сложных задач, в которых имеется дополнительное условие.
Пример такой задачи:
- Какие пятизначные числа можно составить из цифр 0, 1, 7, 8? Для решения понадобится построить дерево из всех возможных комбинаций, при этом имеется дополнительное условие – число не может начинаться с нуля. Таким образом, ответ будет состоять из всех чисел, которые будут начинаться с 1, 7 или 8.
Способ 3. Формирование таблиц
Решение комбинаторных задач можно выполнить и с помощью таблиц. Они схожи с деревом возможных вариантов, поскольку предлагают наглядное решение ситуации. Для нахождения правильного ответа нужно сформировать таблицу, причем она будет зеркальной: горизонтальные и вертикальные условия будут одинаковыми.
Возможные варианты ответов будут получаться на пересечении столбцов и строчек. При этом ответы на пересечении столбца и строки с одинаковыми данными получаться не будут, эти пересечения необходимо особо пометить, чтобы не запутаться при составлении итогового ответа. Этот способ не слишком-то часто выбирается учениками, многие отдают предпочтение дереву с вариантами.
Способ 4. Умножение
Есть еще один способ, с помощью которого можно решить комбинаторные задачи, – правило умножения. Он прекрасно подходит в том случае, когда по условию не нужно перечислять все возможные варианты решения, необходимо просто найти их максимальное количество. Этот метод единственный в своем роде, им пользуются очень часто, когда только начинают решать комбинаторные задачи.
Пример такой задачи может выглядеть следующим образом:
- 6 человек ожидают экзамена в коридоре. Сколько способов можно использовать, чтобы расположить их в общем списке? Для получения ответа необходимо уточнить, сколько их них может быть на первом месте, сколько на втором, на третьем и т. д. Ответом будет число 720.
Комбинаторика и ее виды

Комбинаторная задача не является только лишь школьным материалом, студенты вузов также изучают ее. В науке существует несколько видов комбинаторики, и у каждого из них имеется собственная миссия. Перечислительная комбинаторика должна рассматривать задачи на перечисление и подсчет возможных конфигураций с дополнительными условиями.
Структурная комбинаторика является компонентом вузовской программы, в ней изучаются теории матроидов и графов. Экстремальная комбинаторика также имеет отношение к вузовскому материалу, и здесь имеются свои индивидуальные ограничения. Еще один раздел – теория Рамсея, занимающаяся изучением структур в случайных вариациях элементов. Существует и лингвистическая комбинаторика, которая занимается рассмотрением вопроса о сочетаемости тех или иных элементов между собой.
Методика преподавания комбинаторных задач
Согласно учебным планам, возраст учеников, который рассчитан на первичное знакомство с данным материалом и на решение комбинаторных задач, – 5 класс. Именно там впервые данная тема предлагается на рассмотрение ученикам, они знакомятся с явлением комбинаторности и пытаются решать поставленные перед ними задачи. При этом очень важно, чтобы при постановке комбинаторной задачи использовался метод, когда дети сами занимаются поиском ответов на вопросы.
Кроме всего прочего, после изучения указанной темы будет намного легче вводить понятие факториала и использовать его при решении уравнений, задач и пр. Таким образом, комбинаторность играет важную роль при получении дальнейшего образования.
Комбинаторные задачи: зачем они нужны?
Если вы знаете, что такое комбинаторные задачи, то никаких сложностей с их решением вы испытывать не будете. Методика их решения может пригодиться при необходимости составления расписаний, графиков работы, а также сложных математических вычислений, для выполнения которых не подойдут электронные устройства.
В школах с углубленным изучением математики и информатики комбинаторные задачи изучаются дополнительно, для этого составляются спецкурсы, методические пособия и задачи. Как правило, несколько задач подобного типа могут входить в состав Единого Государственного Экзамена по математике, обычно их «прячут» в части С.
Как решить комбинаторную задачу быстро?
Очень важно суметь разглядеть комбинаторную задачу быстро, поскольку она может иметь завуалированную формулировку, это особенно важно при сдаче ЕГЭ, где каждая минута на счету. Выпишите отдельно информацию, которую вы видите в тексте задачи, на листок, а затем попытайтесь проанализировать ее с точки зрения четырех известных вам способов.
Если вы можете уложить информацию в таблицу или другое образование, пробуйте ее решать. Если классифицировать ее вы не можете, в этом случае лучше всего оставить ее ненадолго и перейти к решению другой задачи, чтобы не терять драгоценное время. Данной ситуации можно избежать, если заранее порешать некоторое количество задач этого типа.
Где найти примеры?
Единственное, что поможет вам научиться решать комбинаторные задачи, – примеры. Их вы можете найти в специальных математических сборниках, которые продаются в магазинах образовательной литературы. Однако там можно найти информацию лишь для студентов вуза, школьникам придется искать задачи дополнительно, как правило, для них задания придумываются остальными учителями.
Преподаватели вузов считают, что студентам необходимо тренироваться и постоянно предлагают им дополнительную учебную литературу. Одним из лучших сборников считается «Методы дискретного анализа в решении комбинаторных задач», написанный в 1977 году и выпускаемый неоднократно ведущими издательствами страны. Именно там можно найти задачи, которые были актуальны на тот момент и остаются актуальными сегодня.
Что делать, если нужно составить комбинаторную задачу?
Чаще всего комбинаторные задачи необходимо составлять преподавателям, которые обязаны научить студентов мыслить нешаблонно. Здесь все будет зависеть от творческого потенциала составителя. Рекомендуется обратить внимание на уже существующие сборники и попробовать составить задачу так, чтобы она сочетала в себе сразу несколько способов ее решения и имела отличные от книжных данные.
Преподаватели вузов в этом плане намного свободнее школьных, они зачастую дают своим студентам задание самим придумать комбинаторные задачи с подробными методами решения и объяснениями. Если вы не относитесь ни к тем, ни к другим, можно попросить помощи у тех, кто действительно разбирается в вопросе, а также нанять частного репетитора. Одного академического часа достаточно для того, чтобы составить несколько подобных задач.
Комбинаторика – наука будущего?
Многие специалисты в области математики и физики считают, что именно комбинаторная задача может стать толчком в развитии всех технических наук. Достаточно лишь нестандартно подойти к решению тех или иных проблем, и тогда можно будет ответить на вопросы, которые уже несколько веков не дают покоя ученым. Некоторые из них всерьез утверждают, что комбинаторика является подспорьем для всех современных наук, особенно космонавтики. Намного проще будет высчитывать траектории полета кораблей с помощью комбинаторных задач, также они позволят определить точное нахождение тех или иных небесных светил.

Реализация нестандартного подхода уже давно началась в азиатских странах, там ученики даже элементарные задачи по умножению, вычитанию, сложению и делению решают, используя комбинаторные методы. На удивление многих европейских ученых, методика действительно работает. Школы Европы пока что только начали перенимать опыт своих коллег. Когда именно комбинаторика станет одним из основных разделов математики, предположить сложно. Сейчас наука изучается ведущими учеными планеты, которые стремятся популяризировать ее.
fb.ru
Содержание
Понятие комбинаторной задачи……………………….…………13История возникновения и развития комбинаторики…………13
Конечные множества…………………………………………..…..24
Операции над множествами………………………………………25
Декартово произведение множеств А и В………………………33
Задачи для самостоятельного решения…………………………34
Нахождение числа всех подмножеств данного множества……36
Понятие факториала………………………………….…………….38
Задания для самостоятельного решения…………….…………..39
Правила суммы и произведения……………………….…………40
Задачи для самостоятельного решения………………….……….45
Вопросы для самопроверки……………………………….……….48
Виды соединений без повторений……………………………49
Перестановки без повторений…………………………….……….49
Задачи для самостоятельного решения…….……………..…….52
Размещения без повторений……………………………………….52
Задачи для самостоятельного решения…………………………..54
Сочетания без повторений………………………………………….56
Свойства чисел  …………………………………………………58
…………………………………………………58
Задачи для самостоятельного решения…………………………..61
Почему 0!=1?…………………………………………………………………………..62
Вопросы для самопроверки………………………………….……62
Виды соединений с повторениями……………………….…..65
Сочетания и размещения с повторениями…………..…………65
Перестановки с повторениями……………………….……………69
Задачи для самостоятельного решения…..………………………70
Бином Ньютона…………………….……………………….………71
Задачи для самостоятельного решения…………………………77
Вопросы для самопроверки………………………………………77
Контрольные вопросы………………………………………………78
Примеры решения некоторых комбинаторных задач…….…..79
Задачи для самостоятельного решения…………………………88
Примеры решения некоторых комбинаторных задач…….…. 90
Задачи для самостоятельного решения…………………………93
Примеры решения некоторых комбинаторных задач…….…..94
Задачи для самостоятельного решения…………………………96
Примеры решения некоторых комбинаторных задач…….…..97
Задачи для самостоятельного решения…………………………99
Формула включений и исключений……………………………100
Задачи для самостоятельного решения по курсу «Комбинаторика»……………………………………………………..……………112
Задачи для самостоятельного решения………………..….……143
Понятие комбинаторной задачи
Комбинаторика – один из разделов дискретной математики, который приобрел важное значение, в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике. Комбинаторные соображения лежат в основе решения многих задач теории вероятностей – важного раздела современной математики, посвященного изучению случайных явлений.
Решая разнообразные жизненные задачи, мы нередко сталкиваемся с теми, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения, называются комбинаторными. Область математики, в которой изучают комбинаторные задачи, называюткомбинаторикой.
«Комбинаторика – раздел математики, посвящённый решению задач выбора и расположения элементов, обычно конечного, множества в соответствии с заданными условиями»1.
Комбинаторика (теория соединений) – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, удовлетворяющих тем или иным условиям, можно составить из заданных объектов.
Комбинаторика изучает количество комбинаций, удовлетворяющих определенным условиям, которые можно составить из элементов заданного конечного множества. «Особая примета» комбинаторных задач вопрос, который можно сформулировать так, чтобы он начинался словами: «Сколькими способами…»2. В данном разделе математики решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств.
studfile.net
Комбинаторные задачи Википедия
Комбинато́рика (комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана с другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.
Примеры комбинаторных конфигураций и задач
Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:
- Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
- Перестановкой из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
- Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
- Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
- Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.
Примеры комбинаторных задач:
- Сколькими способами можно разместить n предметов по m ящикам, чтобы выполнялись заданные ограничения?
- Сколько существует функций F{\displaystyle F} из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?
- Сколько существует различных перестановок из 52 игральных карт?
- Ответ: 52! (52 факториал), то есть, 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 824 000 000 000 000 или примерно 8,0658 ⋅ 1067.
- При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, в которых сумма очков на верхних гранях равна двенадцати?
- Решение: Каждый возможный исход соответствует функции F:{1,2}→{1,2,3,4,5,6}{\displaystyle F:\{1,2\}\to \{1,2,3,4,5,6\}} (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6 + 6 даёт нам нужный результат 12. Таким образом, существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, при которой сумма очков на верхних гранях равна двенадцати.
Разделы комбинаторики
Перечислительная комбинаторика
Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.
Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.
Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.
Структурная комбинаторика
К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.
Экстремальная комбинаторика
Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.
Теория Рамсея
Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:
- в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.
В терминах структурной комбинаторики это же утверждение формулируется так:
- в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.
Вероятностная комбинаторика
Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.
Топологическая комбинаторика
Топологическая комбинаторика применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.
Инфинитарная комбинаторика
Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам.
Открытые проблемы
Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно).[1]
Исторический очерк
Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока Шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.
Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику[2]. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.
В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).
После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.[3]
Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:
Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.
Комбинаторика в языкознании
Комбинаторика (языкознание) — это свойство единиц языка и соответствующих им единиц речи вступать в синтагматические отношения, то есть в отношения сочетаемости.
См. также
Примечания
Литература
- Андерсон, Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — 960 с. — ISBN 0-13-086998-8.
- Виленкин Н. Я. . Популярная комбинаторика. — М.: Наука, 1975.
- Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.
- Липский В. . Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.
- Райгородский А. М. . Линейно-алгебраические и вероятностные методы в комбинаторике. — Летняя школа «Современная математика». — Дубна, 2006.
- Райзер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.
- Рейнгольд Э., Нивергельт Ю., Део Н. . Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.
- Риордан Дж . Введение в комбинаторный анализ. — пер. с англ. — М., 1963.
- Стенли Р . Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — 440 с. — ISBN 5-03-001348-2.
- Стенли Р . Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — 767 с. — ISBN 978-5-03-003476-8.
Ссылки
wikiredia.ru
Простые комбинаторные задачи
Представляем вашему вниманию три задачи, которые можно решить, имея всего лишь знания на уровне 7 класса.Не секрет, что один из важнейших навыков современного программиста – математическое мышление. Именно строгое и формальное мышление позволяет быстро и четко реализовать алгоритм. При этом важен именно аналитический тип мышления, который совершенно не требует глубоких познаний в математике. В действительности вам совсем не обязательно знать и помнить страшные формулы и теоремы, достаточно баловать себя несложными задачами. Вроде таких:
Маша, ее младший брат и еще пятеро друзей должны выстроиться в очередь за шоколадом. Вопрос: сколько вариантов различных очередей возможно?
Всего детей в очереди 7. Количество свободных мест для первого ребенка 7, так что первый ребенок может стоять, где угодно. Второму ребенку доступно уже 6 мест, т. к. одно место занято. Третьему ребенку доступно 5 мест и так далее. В итоге получаем 7 * 6 * 5 * 4 * 3 * 2 * 1 = 7! = 5040.
Сколькими способами из 12 молодых программистов можно выбрать сеньора и мидла.
На позицию сеньора можно выбрать любого человека из 12, и выберем одного из 11 оставшихся в мидлы. Получится 12 * 11 = 132.
Сколько различных слов можно составить из букв proglib? А из proglibio?
Первый вопрос очень похож на первую задачу, только вместо детей буквы. Заметим что в слове proglib 7 букв, так что количество перестановок будет 7! = 5040. В слове proglibio 9 букв, так что ответ очевидно 9!, не так ли? Не совсем. в слове proglibio буквы i и o повторяются дважды. То есть мы берем в расчет еще и случаи, когда одинаковые буквы меняются местами, но слово то от этого не меняется. Каждая перестановка двух одинаковых букв увеличивает количество комбинации в два раза. Поэтому за каждый такой случай нам нужно поделить итоговый ответ на два. В итоге получится 9!/2 * 2 = 9! / 4 = 90720.
Напишите в комментариях, какие задачи вы бы хотели увидеть на сайте. Из какой области математики и какой сложности.
proglib.io
Комбинаторика и ее применение
Тип урока: урок-проект.
Эпиграф урока: «Учимся не для школы, а для жизни» (Сенека).
Проблемный вопрос: Может ли нам помочь
комбинаторика в реальной жизни?
Из этой проблемы вытекает такая цель.
Цель урока: показать учащимся на примерах практическое применение комбинаторики в повседневной жизни.
Задачи:
- научить находить возможные комбинации, составленные из чисел, слов, предметов, отвечающие условию задачи;
- развитие математического мышления и логической речи учащихся;
- развитие познавательного интереса учащихся;
- воспитание интереса к предмету.
Гипотеза: решение комбинаторных задач развивает творческие способности, помогает при решении олимпиадных задач, задач из ЕГЭ, вырабатывает уверенность в собственных силах.
Результат (продукт): понимание всеми учащимися значимости данной темы в практической деятельности человека.
Использование компьютерных технологий: создание слайдовой презентации, выпуск учащимися буклета «Комбинаторика в жизни»
Необходимые принадлежности у учащихся: учебник «Математика», авторы: Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков и др., тетрадь, линейка, карандаш, ручка.
Урок предназначен для учащихся 5-ых классов в рамках изучения темы «Комбинаторика».
ХОД УРОКА
I этап. Погружение в проблемную ситуацию (проходит в виде беседы с учащимися)
Приветствие учащихся.
– Всем здравствуйте (добрый день!). Давайте
здороваться, т.е. все пожмем друг другу руки.
Рядом сидящим пожмем руку, а с остальными будем
здороваться мысленным рукопожатием.
– В классе нас сколько?
Вопрос: Сколько было всего рукопожатий?
– Итак, какие будут ответы? Ответы записать на доске.
Основной педагогический акцент на уроке делается на проговаривание и обязательное устное пояснение решения задачи.
Допустим нас 25.
Способ 1.
Каждый из 25-и человек пожал руки 24-м. Однако произведение 25 * 24 = 600 дает удвоенное число рукопожатий (так как в этом расчете учтено, что первый пожал руку второму, а затем второй первому, на самом же деле было одно рукопожатие). Итак, число рукопожатий равно: (25 * 24) : 2 = 300.
Способ 2.
Первый ученик пожал руки 24-м, второй – 23-м (плюс
рукопожатие с первым, которое уже учтено), третий
– 22-мя и т.д.
двадцать четвертый ограничился одним
рукопожатием, а на долю двадцать пятого
выпала пассивная роль – принимать приветствия.
Таким образом, общее число рукопожатий
выражается суммой:
N = 24 + 23 + 22 + … + 3 + 2 + 1 или
N = 1 + 2 + 3 + … + 22 + 23 + 24.
Сложив почленно обе суммы получаем:
2N = (24 + 1) + (23 + 2) + (22 + 3) +… + (3 + 22) + (2 + 23) + (1 + 24) = 25 * 24;
N = (25 * 24) : 2 = 300.
II этап. Выдвижение предположений и обоснования гипотезы
– Мы с вами столкнулись с комбинаторной
задачей.
Поиском ответов на вопросы: сколько всего есть
комбинаций в том или другом случае, занят целый
раздел математики, называемый комбинаторикой.
Особая примета комбинаторных задач – это
вопрос, который можно сформулировать
таким образом, что он начинался бы словами:
- Сколькими способами…?
- Сколько вариантов…?
У нас сегодня урок-проект «Комбинаторика и
ее применение». (Приложение 1.
Слайд 1)
Перед нами была жизненная ситуация, которую мы
решили при помощи науки комбинаторика.
Комбинаторика – это раздел математики, в
котором изучается, сколько различных комбинаций
можно составить из заданных объектов.
Каждый из Вас сегодня постарается ответить на … проблемный
вопрос: Может ли нам комбинаторика помочь в
реальной жизни? «Нужна ли нам наука
комбинаторика?» (Приложение 1.
Слайд 2)
Из этой проблемы вытекает следующая цель:
продолжить знакомство с наукой комбинаторика.
Чтобы достичь поставленной цели я ставлю такую задачу:
научиться находить возможные комбинации
для решения комбинаторных задач (Приложение
1. Слайд 3)
А чтобы у вас была путеводная звезда, к которой бы
вы шли, я выдвинула следующую гипотезу:
решение комбинаторных задач развивает
творческие способности, помогает при решении
олимпиадных задач, задач из ЕГЭ. (Приложение
1. Слайд 4)
В конце урока вам предстоит подтвердить или
опровергнуть ее.
III этап. Доказательство гипотезы
– Сегодня с вами рассмотрим некоторые задачи комбинаторики.
Устный счет (готовит учащихся к работе на уроке)
1. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7 (цифры в числе не повторяются)? (Шесть: 14, 17, 41, 47, 71, 74). (Приложение 1. Слайд 5)
Ответ на вопрос, конечно, можно получить,
выписывая сами числа, т.е. методом перебора
вариантов. Но это не очень удобно. Будем
рассуждать так. Первую цифру можно выбрать тремя
способами, а вторую цифру можно выбрать (из
оставшихся двух) двумя способами. Следовательно,
общее число искомых двузначных чисел равно
произведению 3 * 2 = 6.
Мы нашли ответ на поставленный вопрос, используя
так называемое комбинаторное правило умножения.
Такую схему называют деревом возможных
вариантов.
Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. (Приложение 1. Слайд 6)
2. Сколько различных 3-значных чисел можно составить из цифр 3, 7 и 8 (цифры не повторяются)? (Приложение 1. Слайд 7)
(Тоже шесть: 378, 387, 738, 783, 873, 837). (Приложение 1. Слайд 8)
3. Сколько 4-значных чисел можно составить из 4 цифр? (Приложение 1. Слайд 9)
Разбор решения. «На 1-е место в 4-значном числе – 4 варианта, на 2-е – 3 варианта, на 3-е – 2 варианта, на 4-е – 1 вариант». 4 * 3 * 2 * 1 = 24. 4! = 1 * 2 * 3 * 4. 3! = 1 * 2 *3. (Приложение 1. Слайд 10)
– Давайте откроем тетради, запишем дату и тему: Комбинаторика и ее применение
IV этап. Проверка правильности решения проблемы. Обобщение и систематизация знаний
Решение задач по теме:
– С утра вы очень часто отправляетесь к
расписанию или открываете дневники, посмотреть
порядок уроков. А представьте на миг, чтобы стало
в школе, если бы не было расписания. Трудно
пришлось бы всем: и детям, и учителям. Даже в одном
классе и то вряд ли легко решили бы проблему.
В помощь тому, кто составляет расписание, решим
задачу.
Задача 1. В 6 классе во вторник 5 уроков: физкультура, русский язык, литература, обществознание и математика. Сколько можно составить вариантов расписания на день, зная точно, что математика – последний урок? (Приложение 1. Слайд 11)
Ответ: 4 * 3 * 2 * 1 = 24 способа (Приложение 1. Слайд 12)
Без переменки заглянем в столовую.
Задача 2. В школьной столовой имеются 2 первых, 5 вторых и 4 третьих блюд. Сколькими способами ученик может выбрать обед, состоящий из первых, вторых и третьих блюд? (Приложение 1. Слайд 13)
Решение: Первое блюдо можно выбрать 2
способами. Для каждого выбора первого блюда
существует 5 вторых блюд. Первые два блюда можно
выбрать 2 * 5 = 10 способами. И, наконец, для каждой 10
этих выборов имеются четыре возможности выбора
третьего блюда, т. е. Существует 2 * 5 * 4 способов
составления обеда из трех блюд. Итак, обед может
быть составлен 40 способами. (Приложение
1. Слайд 14)
Заглянем в гардероб наших девочек.
Задача 3. У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светланы? (Приложение 1. Слайд 15)
Решение: Получается 15 различных комбинаций одежды. (Приложение 1. Слайд 16)
Задача 4. На полке лежат 3 книги. В каком порядке можно расставить эти книги? (Приложение 1. Слайд 17)
Решение: Обозначим их буквами а, в, с. Эти книги можно расставить на полке по – разному: авс, асв, вас, вса, сав, сва.
Ответ: 6 способов расстановки книг (Приложение 1. Слайд 18)
Физкультминутка
Сильно зажмурить глаза на 3-5 секунд, а затем открыть их на такое же время. Повторять 5-6 раз. Быстро моргать в течение 10-12 секунд, открыть глаза, отдыхать 10-12 секунд. Повторять 3 раза.
Задача 5. Опыт с листом бумаги (Приложение 1. Слайд 19)
Дима сложил квадратный листок бумаги пополам, потом еще раз и еще раз. В центре того, что получилось, он проделал дырку, а потом снова развернул лист. Сколько дырок он увидел?
(A)2; (B) 3; (C) 4; (D) 6; (E) 8;
Решение: Каждое складывание
увеличивает толщину (в слоях) бумаги в два раза.
Дима складывал бумагу три раза и получил толщину
2 * 2 * 2 = 8.
Дырки получатся на каждом листе. Итого 8 дырок.
Верен ответ (Е). (Приложение 1. Слайд 20)
V этап. Самостоятельная работа
Задания для самостоятельной работы сформулированы по принципу ЕГЭ.
1-й вариант
В розыгрыше первенства страны по футболу
принимает участие 16 команд. Сколькими способами
могут быть распределены золотая и серебряная
медали?
Выберите букву правильного ответа. А)
256 Б) 31 В) 240 Г)
16
Решение: Золотую медаль может получить одна из 16 команд. После того как определен владелец золотой медали, серебряную медаль может иметь одна из 15 команд. Следовательно, общее число способов, которыми могут быть распределены золотая и серебряная медали, равно 16 * 15 = 240.
Ответ: В
2-й вариант
В классе 25 учащихся, сколькими способами можно выбрать старосту класса и его заместителя? Выберите букву правильного ответа.
А) 25 Б) 600 В) 49 Г) 625
Решение:Староста класса может быть выбран 1 из 25 человек, значит существует 25 способов выбора старосты и 24 способа выбора его заместителя. Существует 25 * 24 = 600 способов выбора старосты класса и его заместителя.
Ответ: Б
VI этап. Обсуждение результатов и подведение итогов
На примере решенных задач мы увидели практическое применение «Комбинаторики» в различных сферах деятельности человека, т. е. выяснили, где в реальной жизни мы встречаемся с комбинаторикой.
Области применения комбинаторики: (Приложение 1. Слайды 21, 22)
- учебные заведения ( составление расписаний)
- сфера общественного питания (составление меню)
- лингвистика (рассмотрение вариантов комбинаций букв)
- география (раскраска карт)
- спортивные соревнования (расчёт количества игр между участниками)
- производство (распределение нескольких видов работ между рабочими)
- агротехника (размещение посевов на нескольких полях)
- азартные игры (подсчёт частоты выигрышей)
- химия (анализ возможных связей между химическими элементами)
- экономика (анализ вариантов купли-продажи акций)
- криптография (разработка методов шифрования)
- доставка почты (рассмотрение вариантов пересылки)
- биология (расшифровка кода ДНК)
- военное дело (расположение подразделений)
- астрология (анализ расположения планет и созвездий
В ближайшем будущем мы научимся решать более сложные задачи комбинаторики, а ваши знания по теме будут востребованы при решении задач олимпиадного типа, задач из ЕГЭ. Комбинаторика играет большую роль в практической деятельности человека.
Вывод:
Комбинаторика повсюду.
Комбинаторика везде.
Комбинаторика вокруг нас. (Приложение
1. Слайд 23)
Но как говорят «Без знания прошлого
нет настоящего, нет будущего» (Приложение 1. Слайд 24)
Презентация проекта «Истоки комбинаторики» (Приложение 2)
VII этап.Домашнее задание:
– Придумать свою комбинаторную задачу и решить
её.
– Применение комбинаторики в практической
деятельности людей (рассказ или эссе) (Слайд
25)
VIII этап. Рефлексия
Учащиеся осмысливают свою деятельность на уроке, проводят самооценку своей деятельности (на листочках).
– А какие навыки, кроме решения задач, Вы
приобрели сегодня для себя? (Выслушать и
обобщить ответы учащихся)
– Спасибо всем за работу. Надеюсь,
присутствующие получили много интересной и
актуальной информации. Мне было очень приятно
работать с вами на уроке.
Список литературы:
1. Н.Я. Виленкин, А.Н. Виленкин, П.А. Виленкин.
Комбинаторика. М., 2006.
2. В.Е.Гмурман. Руководство к решению задач по
теории вероятностей и математической
статистике. – М.: Высшая школа, 1975.
3. И.И.Ежов, А.В.Скороход, М.И.Ядренко. Элементы
комбинаторики. М., 1977.
4. Д.Ж.Риордан. Введение в комбинаторный
анализ. М., 1963.
urok.1sept.ru
Творческая работа учащихся по алгебре (6 класс) на тему: Комбинаторика и комбинаторные задачи
Муниципальное образовательное учреждение «Средняя общеобразовательная школа №1 имени М.А. Бухтуева»
г. Кызыла РТ
XII научно-практическая конференция учащихся
Комбинаторика и комбинаторные задачи
Автор: Табаева Светлана 6 «а» класс
Руководитель: Цырмаева Анна Сергеевна,
предмет — математика
Кызыл, 2011 г.
СОДЕРЖАНИЕ:
Введение……………………………………………………………………3
Глава I. История науки «Комбинаторика»………..……………………4
Глава II. Решение комбинаторных задач
- основные понятия и правила комбинаторики..………………………8
- примеры решения задач.………………………………………………9
Заключение…………..…………………………………………………..11
Литература…………………………………………………………….…12
Введение
В математике есть задачи, в которых требуется из элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, составленных по определённому правилу.
Многие жизненные проблемы требуют для своего решения комбинаторного подхода, умения просчитать все возможные варианты и с учетом дополнительных условий выбрать наилучший. Поэтому весьма актуальным является формирование и развитие таких качеств мышления, как системность, гибкость, многовариантность, избирательность. Все эти качества характеризуют комбинаторный стиль мышления.
Целый раздел математики, именуемый комбинаторикой, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.
Проблемный вопрос: Может ли комбинаторика помочь в реальной жизни?
Из этой проблемы вытекает цель работы: самостоятельное приобретение знаний по комбинаторике, применение полученных знаний к решению новых познавательных задач и практическое применение комбинаторики в повседневной жизни.
Исходя из целей поставлены следующие задачи:
- познакомить с историей возникновения науки «Комбинаторика»;
- дать определение комбинаторики;
- изучить основные методы решения комбинаторных задач;
- научиться находить возможные комбинации для решения комбинаторных задач;
- рассмотреть практическое применение комбинаторики в повседневной жизни.
Методы исследования:
- работа с дополнительной литературой;
- метод наблюдения и сравнения.
Люди, которые умело владеют техникой решения комбинаторных задач, а, следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций. Примером мог бы послужить сказочный герой Барон Мюнхгаузен, который находил выход из любой сложной и трудной ситуации. В жизни эти умения очень часто помогают человеку. Ведь в повседневной жизни нередко перед нами возникают проблемы, которые имеют не одно, а несколько различных вариантов решения. Чтобы сделать правильный выбор, очень важно не упустить ни один из них. Для этого надо осуществить перебор всех возможных вариантов или хотя бы подсчитать их число.
Глава I
История науки «Комбинаторика»
Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов.
Уже несколько тысячелетий назад в Древнем Китае увлеклись составлением магических квадратов, в которых заданные числа располагались так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата и т.д.
Комбинаторика возникла в 17 веке. Долгое время она лежала вне основного русла развития математики.
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов — во время работы.
Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника.
Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н.Тарталье (1499-1557), Г.Галилею (1564-1642) и французским ученым Б.Паскалю (1623-1662) и П.Ферма.
Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г.Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер. В современном обществе с развитием вычислительной техники комбинаторика «добилась» новых успехов. Были изданы журналы, книги по комбинаторике. Элементы комбинаторики были включены в школьный курс математики. Затем изъяты из программы. По желанию учителей и учащихся в 80–90 г.г. прошлого столетия основы комбинаторики изучались на факультативных занятиях старших классов общеобразовательной школы. В настоящее время в образовательный стандарт по математике включены основы комбинаторики, решение комбинаторных задач методом перебора, составлением дерева вариантов (еще его называют “дерево возможностей”) с применением правила умножения.
Глава II
Решение комбинаторных задач
1. Основные понятия и правила комбинаторики
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Комбинаторика — раздел математики, изучающий вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Комбинаторные методы лежат в основе решения многих задач теории вероятностей и ее приложений.
Задачу можно назвать комбинаторной, если ее решением является перебор элементов некоторого конечного множества.
Особая примета комбинаторных задач – вопрос, который можно сформулировать таким образом, что он начинался бы словами:
• Сколькими способами…?
• Сколько вариантов…?
Для того, чтобы решить задачу по комбинаторике, необходимо сначала понять её смысл, то есть, представить мысленно процесс или действие, описанное в задаче.
Нужно чётко определить тип соединений в задаче, а для этого надо, составив несколько различных комбинаций, проверить повторяются ли элементы, меняется ли их состав, важен ли порядок элементов.
Если же комбинаторная задача содержит ряд ограничений, налагающихся на соединения, то нужно понять, как влияют или не влияют эти ограничения на соединения.
В том случае, если трудно сразу определить какие-либо важные моменты задачи, то не плохо было бы попытаться разобраться в более лёгкой задаче, например в той, в которой не учитываются ограничения, если они есть в исходной задаче, или же в задаче, в которой рассматривается меньшее количество элементов, тогда проще будет понять принцип образования выборок.
Когда комбинаторная задача состоит из различных комбинаций элементарных задач, то нужно просто разбить задачу на подзадачи.
Комбинаторные задачи бывают самых разных видов. Однако, большинство задач решается с помощью двух основных правил — правила суммы и правила произведения.
Правило суммы.
Если некоторый объект A можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить (m+n) способами.
Например: Имеется 8 шаров: в первый ящик положили 5 шаров, а во второй 3 шара. Сколькими способами можно вытащить 1 шар?
Решение: из первого ящика шар можно вытащить 5-ю способами, а из второго 3-мя. Значит, всего 5+3=8 способов.
При использовании правила суммы надо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-либо способом выбора объекта В. Если такие совпадения есть, правило суммы утрачивает силу, и мы получаем лишь (m + n — k) способов выбора, где k—число совпадений.
Правило произведения.
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А,В) в указанном порядке можно осуществить mn способами.
При этом число способов выбора второго элемента не зависит от того, как именно выбран первый элемент.
Например: В первом ящике 5 зелёных шаров, а во втором 3 красных шара. Сколькими способами можно вытащить 1 зелёный и 1 красный шар?
Решение: зелёный шар можно выбрать 5-ю способами, а красный – 3-мя. Значит, 1 зелёный и 1 красный шар можно выбрать 3х5 = 15 способами.
Так же комбинаторные задачи можно решить методом перебора.
Например: Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?
Решение. Для того чтобы не пропустить и не повторить ни одно из чисел, надо выписывать их в порядке возрастания. Сначала вписываем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.
Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.
Существует единый подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. Решение комбинаторных задач методом составления дерева вариантов с применением правила умножения. Так, например, “дерево возможностей” помогает решать разнообразные задачи, касающиеся перебора вариантов происходящих событий. Каждый путь по этому “дереву” соответствует одному из способов выбора, число способов выбора равно числу точек в нижнем ряду “дерева”. Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Например: Сколько двузначных чисел можно составить, используя цифры 1, 5 и 8?
*
Первая цифра 1 5 8
Вторая цифра 1 5 8 1 5 8 1 5 8
Число 11 15 18 51 55 58 81 85 88
Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Знак «*» изображает корень дерева, ветви дерева – различные варианты решения. Чтобы получить двузначное число, надо сначала выбрать первую его цифру, а для нее есть три варианта: 1, 5 или 8. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 5 и 8.
Теперь надо выбрать вторую цифру, а для этого также есть три варианта: 1, 5 или 8. Поэтому от каждой первой цифры проведено по три отрезка, на концах которых снова записано 1, 5 или 8. Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.
В задачах по комбинаторике часто применяется такое понятие как факториал (в переводе с английского “factor” — “множитель”).
Факториал числа — это произведение всех натуральных чисел до этого числа включительно.
Обозначается с восклицательным знаком в конце. n! = 1 · 2 · 3 · 4 · … · (n-2) · (n-1) · n
Случай 0! определен и имеет значение 0!=1, соответствующее комбинаторной интерпретации комбинации нуля объектов, другими словами, есть единственная комбинация нуля элементов, а именно: пустое множество.
Ниже приведены значения факториалов от 0 до 10.
0! = 1
1! = 1
2! = 1 · 2 = 2
3! = 1 · 2 · 3 = 6
4! = 1 · 2 · 3 · 4 = 24
5! = 1 · 2 · 3 · 4 · 5 = 120
6! = 1 · 2 · 3 · 4 · 5 · 6 = 720
7! = 1 · 2 · 3 · 4 · 5 · 6 · 7 = 5040
8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320
9! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 = 362880
10! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 = 3628800
Свойство факториала: (n + 1)! = (n + 1) · n!
Например: (5 + 1)! = (5 + 1) · 5!
Действительно 6! = (1 · 2 · 3 · 4 · 5) · 6 = 720
А значение (1 · 2 · 3 · 4 · 5) = 5! = 120
В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
2. Примеры решения задач
1. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе — мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье — чай и компот. Сколько различных обедов можно составить из указанных блюд?
1 способ. Перечислим возможные варианты
Чай(Ч) | Мясо с макаронами(М) | Рыба с картошкой(Р) | Курица с рисом(Кр) |
Борщ (Б) | БМЧ/ БМК | БРЧ/БРК | БКрЧ/БКрК |
Солянка(С) | СМЧ/ СМК | СРЧ/СРК | СКрЧ/СКрК |
Грибной суп(Г) | ГМЧ/ГМК | ГРЧ/ГРК | ГКрЧ/ГКрК |
18 вариантов.
2 способ. Дерево возможностей.
3 способ. Используя правило умножения, получаем: 3х3х2=18
2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу?
1 способ. Обозначим мячи — М1, М2, игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5. Перечислим возможные варианты:
М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5,
М1-И2-К1, М1-И2-К2, М1-И2-К3, М1-И2-К4, М1-И2-К5,
М1-И3-К1, М1-И3-К2, М1-И3-К3, М1-И3-К4, М1-И3-К5,
М1-И4-К1, М1-И4-К2, М1-И4-К3, М1-И4-К4, М1-И4-К5
М2-И1-К1, М2-И1-К2, М2-И1-К3, М2-И1-К4, М2-И1-К5,
М2-И2-К1, М2-И2-К2, М2-И2-К3, М2-И2-К4, М2-И2-К5,
М2-И3-К1, М2-И3-К2, М2-И3-К3, М2-И3-К4, М2-И3-К5,
М2-И4-К1, М2-И4-К2, М2-И4-К3, М2-И4-К4, М2-И4-К5
Ответ: 40 вариантов.
2 способ. Используя правило умножения, получаем: 2х4х5= 40
3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?
1 способ. Перечислим возможные варианты.
| 0 | 2 | 6 |
2 | 20 | 22 | 26 |
3 | 30 | 32 | 36 |
6 | 60 | 62 | 66 |
7 | 70 | 72 | 76 |
9 | 90 | 92 | 96 |
2 способ. Дерево возможностей.
3 способ. Используя правило умножения, получаем: 5х3=15 .
4. Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?
1 способ. Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:
№1 — Саша — есть возможность выбрать из 5 вариантов (стульев)
№2 — Петя — 4 варианта
№3- Денис — 3 варианта
№4- Оля — 2 варианта
№5 — Настя- 1 вариант
Используя правило умножения, получаем: 5х4х3х2х1=120
2 способ. Решаем, используя понятие факториала: 5!=120
6. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)?
1 способ. Перечислим возможные варианты состава пары:
11А-11Б, 11А-11В, 11А-11Г, 11А-11Д,
11Б-11В, 11Б-11Г, 11Б-11Д, 11В-11Г, 11В-11Д, 11Г-11Д
Ответ: 10 пар.
2 способ. Из пяти классов нужно выбрать 2 дежурных.
Число элементарных событий = = 10
7. В 8 “а” классе лучше всех математику знают 5 учеников: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами учительница может эту пару выбрать?
1 способ. Обозначим имена детей первыми заглавными буквами.
Получаем следующие пары:
В-К, В-А, Д-К, Д-А, О-К, О-А.
Ответ: 6 пар.
2 способ. Мальчиков 3, из них 1 можно выбрать , девочек 2, из них можно 1 выбрать , используя правило умножения, получаем:
х = 6
8. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы.
Сколькими способами могут распределится места по окончании соревнований?
Обозначим участников по первой заглавной букве страны и пронумеруем: Р1, И2, У3, Н4,К5, Ф6
Р1 — имеют возможность занять с1-6 места, т.е. 6 вариантов
И2 — 5 вариантов
У3- 4 варианта
Н4- 3 варианта
К5- 2 варианта
Ф6- 1 вариант
Используя правило умножения, получаем: 6х5х4х3х2х1= 720
2 способ. Используя понятие факториала, получаем: 6!=720
9. В 9 “б” классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Департамент образования премировал лучших учащихся путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора учеников на отдых?
Обозначим первыми заглавными буквами имен учащихся.
Возможны следующие тройки:
Г-С-К-О, Г-С-К-М, Г-С-К-В,
Г-С-О-М, Г-С-О-В, Г-С-М-В
С-К-О-М, С-К-О-В, С-К-М-В,
К-О-М-В, С-О-М-В, Г-К-О-В,
Г-К-О-В, Г-О-М-В, Г-К-М-В
2 способ. Из 6 человек нужно выбрать 4, число элементарных событий равно = 15
10. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого?
Вычислим, сколько четверок из 7 дисков можно составить у Пети:
=35, число четверок у Вали из 9 дисков -= 126
По правилу умножения находим число обменов 35х126=4410
11. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых?
Из 5 офицеров выбрать 2 можно с помощью числа сочетаний =10 способами, из 8 сержантов 4 — =70, из 70 рядовых 15 -. По правилу умножения находим число выбора отряда:
10х70х= 700х
12. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет?
Из 6 изумрудов 3 он может выбрать =20 способами, из 9 алмазов 5 -=126, из 7 сапфиров 2 — =21. По правилу умножения находим число вариантов 20х126х21=52920
13. На выборах победили 9 человек — Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать?
Здесь речь идет о размещениях
Можно было решать по-другому. На должность председателя выбираем из 9 человек, на заместителя — из 8, на профорга — из 7
По правилу умножения получаем 9х8х7=504
14. В районе построили новую школу. Из пришедших 25 человек нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими способами это можно сделать?
На должность директора выбираем из 25 человек, на завуча начальной — из 24, завуча среднего звена — из 23, завуча по воспитательной работе — 22. По правилу умножения получаем:
25х24х23х22 = 303600
Или, зная формулу размещения, получаем
15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)?
Для Пети набор можно набрать 6х8х10=480 способами, для Васи — 5х7х9=315, для Коли — 4х6х8=192. По правилу умножения получаем
480х315х192=29030400 способами.
16. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся?
В русском языке 9 гласных букв — а, е, е, и, о, у, э, ю, я. Выбрать из них 2 можно =36 способами. Из 10 цифр выбрать 3 можно=120 способами. Применяя правило умножения, получаем:
36х120=4320
17. Сколькими способами можно составить трехцветный флаг из полос разной ширины, если имеются материи из 8 тканей?
Эта задача на размещение
Другой способ решения.
1цвет выбирается из 8 тканей 8 способами
2цвет выбирается 7 способами
3 цвет — 6способами
Используя правило умножения, получаем 8х7х6=336 способов.
18. В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различные?
Из 15 предметов 5 любых можно выбрать
19. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета?
1 способ. Обозначим белые — Б1, Б2, Б3, алые — А1,А2, чайные — Ч1, Ч2, Ч3,Ч4
Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3, Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3, Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3, Б3-А2-Ч4
Ответ: 24 варианта.
2способ. Дерево возможностей
3 способ. Используя правило умножения, получаем: 2х3х4=24
20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка-Быковка- Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М- пешком или на автобусе, из М в В — по реке, пешком или автобусе. Сколько вариантов похода есть у щкольников?
1 способ. Обозначим СБ — путь из Сосновки в Бытовку, ВГ — путь из Быковки в Масловку, МВ — путь из Масловки в Видово.
По реке -Р, пешком — П, на автобусе — А
Перечислим возможные варианты:
СБР- БМП-МВР, СБР- БМП-МВП, СБР- БМП-МВА
СБР-БМА-МВР, СБР-БМА-МВП, СБР-БМА-МВА
СБА- БМП-МВР, СБА- БМП-МВП, СБА- БМП-МВА
СБА-БМА-МВР, СБА-БМА-МВП, СБА-БМА-МВА
Ответ: 12 вариантов.
2 способ. Дерево возможностей
Заключение
На примере решенных задач видно практическое применение «Комбинаторики» в различных сферах деятельности человека, т. е. где в реальной жизни можно встретиться с комбинаторикой.
Комбинаторика играет большую роль в практической деятельности человека. Области применения комбинаторики:
- учебные заведения (составление расписаний)
- сфера общественного питания (составление меню)
- лингвистика (рассмотрение вариантов комбинаций букв)
- география (раскраска карт)
- спортивные соревнования (расчёт количества игр между участниками)
- производство (распределение нескольких видов работ между рабочими)
- агротехника (размещение посевов на нескольких полях)
- азартные игры (подсчёт частоты выигрышей)
- биология (расшифровка кода ДНК)
Математика это оружие, с помощью которого человек познаёт и покоряет себе окружающий мир. Чтобы сделать в математике что-то действительно ценное, надо любить её так, как многие великие математики. Нужно сделать хотя бы малую часть того, что сделали они, и мир навсегда останется благодарным вам. А сегодня мы сделали маленький шаг к познанию математической мысли.
В ближайшем будущем я научусь решать более сложные задачи комбинаторики, а эти знания по теме будут востребованы при решении задач олимпиадного типа.
Литература
1) Еженедельное учебно-методическое приложение “Математика” Изд. Пресса. Москва.1999 г
3) Л.Г. Петерсон. Математика 4 класс. Изд. Баласс. Москва.1999 г.
1. Н.Я. Виленкин, А.Н. Виленкин, П.А. Виленкин. Комбинаторика. М., 2006.
2. В.Е.Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1975.
3. И.И.Ежов, А.В.Скороход, М.И.Ядренко. Элементы комбинаторики. М., 1977.
4. Д.Ж.Риордан. Введение в комбинаторный анализ. М., 1963.
Савина Л.Н., Попырев А.В. «КОМБИНАТОРИКА» издательство Елабужский государственный педагогический институт 1999 г
Халамайзер А. Я. «Математика? – Забавно!» издание автора 1989 г
- Дмитриев И. Г., Попов М. В., Федоров М. П.
Решение олимпиадных задач по математике. – Якутск: ДНСПО МО РС(Я), 2000.
- Когаловский С.Р.
Роль комбинаторных задач в обучении математики. // Математика в школе. – 2004. — №4.
- Макарычев Ю. Н., Миндюк Н. Г.
Алгебра: элементы статистики и теории вероятностей. – М.: Просвещение, 2003.
- Семеновых А.
Комбинаторика. // Математика. – 2004, №15, № 16.
- Гитман М.Б., Цылова Е.Г. Введение в комбинаторику и теорию вероятностей. Учеб. пособие.: Пермь, 1999
- Грэхем Р., Кнут Д., Паташник О. Конкретная математика. М.: Мир, 1998.
- История математики с древнейших времён до начала XIX столетия / Под ред. А.Н. Колмогорова, А.П. Юшкевича. М: Наука, 1970-1972. T.1-3.
- Клейн Ф. Лекции о развитии математики в XIX столетии. М.: Наука, 1989.
- Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных. М.: Мнемозина, 2005
- http://portfolio.1september.ru
- http://ru.wikipedia.org
nsportal.ru
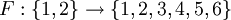 (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 дает нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.
(аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 дает нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.