ЛИНИЯ (в геометрии) — это… Что такое ЛИНИЯ (в геометрии)?



ЛИНИЯ (в геометрии)

ЛИНИЯ (в геометрии)

ЛИ́НИЯ (от лат. linea), общая часть двух смежных областей поверхности. Движущаяся точка описывает при своем движении некоторую линию. В аналитической геометрии на плоскости линии выражаются уравнениями между координатами их точек. В прямоугольной системе координат линии разделяются в зависимости от вида уравнений. Если уравнение линии имеет вид F(x, y)=0, где F(x,y) — многочлен n-й степени относительно x, y, то линия называется алгебраической кривой n-го порядка. Линия 1-го порядка есть прямая. Конического сечения относятся к линиям 2-го порядка. Примеры неалгебраических линий — графики тригонометрических функций, логарифмические функции, показательные функции.

Энциклопедический словарь. 2009.

• ЛИНИЯ (в генетике)
• ЛИНИЯ (единицы длины)

Смотреть что такое «ЛИНИЯ (в геометрии)» в других словарях:

• Линия (геометрич. понятие) — Линия (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной геометрии рассматриваются… …   Большая советская энциклопедия

• Линия (значения) — Линия: Линия  объект в геометрии. Линия  музыкальный коллектив. Линия  старая русская мера длины. Линия  сеть гипермаркетов и супемаркетов России. Линия фильм 2008 года Джеймса Коттена …   Википедия

• ЛИНИЯ — (от лат. linea) общая часть двух смежных областей поверхности. Движущаяся точка описывает при своем движении некоторую линию. В аналитической геометрии на плоскости линии выражаются уравнениями между координатами их точек. В прямоугольной системе …   Большой Энциклопедический словарь

• ЛИНИЯ — ЛИНИЯ, непрерывный ряд точек. Термин может обозначать кривую или прямую линию кратчайшее расстояние между двумя точками в ЕВКЛИДОВОЙ ГЕОМЕТРИИ. В прямоугольной ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ прямая линия выражается равенством: у=тх+с, где т… …   Научно-технический энциклопедический словарь

• Линия — I Линия (от лат. linea)         геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно.          1) В элементарной… …   Большая советская энциклопедия

• Линия (кривая) — Кривая или линия  геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана …   Википедия

• ЛИНИЯ

  — кривая, геометрическое понятие, точное и в то же время достаточно общее определение к рого представляет значитю трудности и осуществляется в разных разделах геометрии различно. В рамках элементарной геометрии понятие Л. не получает отчетливой… …   Математическая энциклопедия

• ГЕОМЕТРИИ ОБЗОР — Геометрия раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми… …   Энциклопедия Кольера

• ЛИНИЯ ВТОРОГО ПОРЯДКА — плоская линия, декартовы прямоугольные координаты к рой удовлетворяют алгебраич. уравнению 2 й степени Уравнение (*) может и не определять действительного геометрич. образа, но для сохранения общности в таких случаях говорят, что оно определяет… …   Математическая энциклопедия

• линия — и; ж. 1. Узкая полоса, черта, проведённая на какой л. поверхности от одной точки к другой. Провести линию. Волнообразная л. Обозначить точки на линии. Пересекающиеся линии. // Матем. Граница поверхности, имеющая только одно измерение длину. //… …   Энциклопедический словарь

Книги

• Вторая линия. Рассказы и истории разных лет, Фрай Макс. Автор сам толком не знает, что за линии такие, о чем вообще речь? Сюжетные? Поведения? Защиты? Линии жизни на двух руках, левой и правой? Или же в честь питерских улиц, что на Васильевском… Подробнее  Купить за 425 руб
• Вторая линия, Фрай Макс. Автор сам толком не знает, что за линии такие, о чем вообще речь? Сюжетные? Поведения? Защиты? Линии жизни на двух руках, левой и правой? Или же в честь питерских улиц, что на Васильевском… Подробнее  Купить за 345 руб
• Вторая линия, Макс Фрай. Автор сам толком не знает, что за линии такие, о чем вообще речь? Сюжетные? Поведения? Защиты? Линии жизни на двух руках, левой и правой? Или же в честь питерских улиц, что на Васильевском… Подробнее  Купить за 285 руб

Другие книги по запросу «ЛИНИЯ (в геометрии)» >>

Кривая — Википедия

Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».

По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.

Отображение отрезка[править | править код]

Чаще всего кривая определяется как непрерывное

отображение из отрезка в топологическое пространство:

γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}

При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [a,b]=[0,1]{\displaystyle [a,b]=[0,1]}, путями.

Отношение эквивалентности[править | править код]

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

γ1:[a1,b1]→X{\displaystyle \gamma _{1}\colon [a_{1},b_{1}]\to X} и γ2:[a2,b2]→X{\displaystyle \gamma _{2}\colon [a_{2},b_{2}]\to X}

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h{\displaystyle h} из отрезка [a1,b1]{\displaystyle [a_{1},b_{1}]} на отрезок [a2,b2]{\displaystyle [a_{2},b_{2}]}, такая что

γ1≡γ2∘h.{\displaystyle \gamma _{1}\equiv \gamma _{2}\circ h.}

Определяемые этим отношением классы эквивалентности называются

непараметризованными кривыми или просто кривыми.

Комментарий[править | править код]

Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.

Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.

Кривая Жордана[править | править код]

Кривая Жордана на плоскости с положительной мерой Лебега.

Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.

Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.

Кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, этот пример аналогичен кривой Пеано был построен Осгудом^[1]. .

В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в R2{\displaystyle \mathbb {R} ^{2}}). Пусть x(t){\displaystyle x(t)} и y(t){\displaystyle y(t)} — функции на отрезке [a,b]{\displaystyle [a,b]}, непрерывно дифференцируемые на этом отрезке, и такие, что (x′(t))2+(y′(t))2{\displaystyle (x'(t))^{2}+(y'(t))^{2}} ни для какого t не равно нулю. Тогда отображение γ:[a,b]→R2,t↦(x(t),y(t)){\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2},t\mapsto (x(t),y(t))} задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую параметризацию. Длину гладкой кривой можно вычислить по формуле

L(γ)=∫ab(x′(t))2+(y′(t))2dt.{\displaystyle {\text{L}}(\gamma )=\int _{a}^{b}{\sqrt {(x'(t))^{2}+(y'(t))^{2}}}\,dt.}

Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.

Определение в дифференциальной геометрии[править | править код]

Если X{\displaystyle X} — гладкое многообразие, можно определить гладкую кривую на X{\displaystyle X} как гладкое отображение γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}, дифференциал которого нигде не обращается в нуль. Если класс гладкости многообразия X{\displaystyle X} равен k{\displaystyle k}, то Ck{\displaystyle C_{k}}-кривая вводится как кривая, для которой γ{\displaystyle \gamma } — k{\displaystyle k} раз непрерывно дифференцируемое отображение. Если X{\displaystyle X} — аналитическое многообразие (например, евклидово пространство) и γ{\displaystyle \gamma } — аналитическое отображение, кривую называют аналитической.

Гладкие кривые γ1:I→X{\displaystyle \gamma _{1}\colon I\to X} и γ2:J→X{\displaystyle \gamma _{2}\colon J\to X} называются эквивалентными, если существует диффеоморфизм p:I→J{\displaystyle p\colon I\to J} (замена параметра), такой что γ1=γ2∘p{\displaystyle \gamma _{1}=\gamma _{2}\circ p}. Классы эквивалентности по этому отношению называют непараметризованными гладкими кривыми.

Алгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она называется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x² + y² + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.

Алгебраические кривые можно определить и в пространствах большей размерности; они определяются как множество решений системы полиномиальных уравнений.

Любая плоская кривая может быть дополнена до кривой на проективной плоскости. Если плоская кривая определяется многочленом f(x, y) полной степени d, то многочлен

zd⋅f(x/z,y/z){\displaystyle z^{d}\cdot f(x/z,y/z)}

после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма xⁿ + yⁿ = zⁿ в аффинной форме принимает вид xⁿ + yⁿ = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.

Часто встречающиеся примеры плоских кривых — коники (кривые второго порядка) и эллиптические кривые, имеющие важные приложения в криптографии. В качестве примеров алгебраических кривых, задаваемых уравнениями более высоких степеней, можно указать следующие:

Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций). Примеры трансцендентных кривых:

Типы точек на кривой[править | править код]

Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:

Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.

Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L{\displaystyle L}, она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L′{\displaystyle L’}, гомеоморфное L{\displaystyle L}. Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.

Впоследствии это определение было обобщено Урысоном:

Кривой Урысона называется связное компактное топологическое пространство C{\displaystyle C} топологической размерности 1.

Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.

1. ↑ W. F. Osgood. A Jordan curve of positive area (англ.) // Trans. Am. Math. Soc.. — 1903. — Vol. 4. — P. 107–112.

ЛИНИЯ — это… Что такое ЛИНИЯ?

кривая,- геометрическое понятие, точное и в то же время достаточно общее определение к-рого представляет значитю трудности и осуществляется в разных разделах геометрии различно.

В рамках элементарной геометрии понятие Л. не получает отчетливой формулировки и иногда определяется как «длина без ширины» или как «граница поверхности». По существу в элементарной геометрии изучение Л. сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных Л. (конич. сечения, нек-рые алгебраич. Л. высших порядков и трансцендентные Л.), применяя в каждом случае специальные приемы.

В аналитич. еометрии Л. на плоскости определяется как множество точек, координаты к-рых удовлетворяют уравнению F(x, у)=0. При этом на функцию Fдолжны быть наложены ограничения так, чтобы, с одной стороны, уравнение это имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло «куска плоскости».

Важный класс Л. составляют те, для к-рых функция F(x, у).есть многочлен от двух переменных; в этом случае Л., определяемая уравнением F(x, y) = 0, наз. алгебраической. Алгебраич. Л., задаваемые уравнением 1-й степени, суть прямые. Уравнение 2-й степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или Л., распадающуюся на две прямые. Алгебраич. Л., определяемые уравнениями высших степеней, рассматриваются в алгебраич. геометрии. При этом большую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебранч. Л. определяется уравнением вида

где F — однородный многочлен трех переменных, являющихся проективными координатами точек.

Для тех разделов математики, в к-рых господствуют методы теории функций (анализ, дифференциальная геометрия и др.), естественное определение Л.- задание ее пара метрически мп уравнениями. Так, в случае плоскости, Л., заданная параметрич. уравнениями

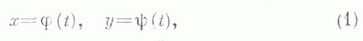
где 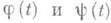— непрерывные функции, определенные на отрезке 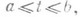есть множество точек ( х, у), соответствующих всевозможным значениям параметра tпри условии, что эти точки рассматриваются в определенном порядке: если точка M₁ соответствует значению параметра t₁ а точка М ₂ — значению t₂, то М ₁ считается предшествующей М ₂ при t₁<t₂;точки, отвечающие различным значениям параметра, считаются различными. Уравнения 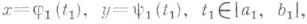задают ту же Л., что и уравнения (1), если существует такой гомеоморфизм 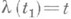отрезка [a₁, b₁] на отрезок 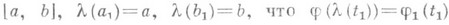и 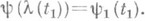Аналогично Л. в произвольном топологич. пространстве Xопределяется параметрич. уравнением вида 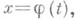где 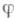— функция действительного переменного t, непрерывная на отрезке [ а, Ь], значения к-рой суть точки хпространства X.

Кроме такого подхода существует п другая точка зрения (К. Жордан, С. Jordan, 1882) на определение Л. параметрич. уравнениями: Л. наз. множество точек плоскости, координаты к-рыХ суть непрерывные функции 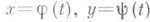параметра t, заданные на отрезке [a, b]; теперь точки, соответствующие различным значениям параметра, но имеющие одни и те же координаты, уже не считаются различными, и множество, составляющее Л., уже не рассматривается как упорядоченное значениями t. Это определение обобщается на любое топологич. пространство: множество точек топологич. пространства, являющееся непрерывным образом отрезка, наз. жордановой кривой.

Однако построены такие непрерывные функци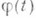и и 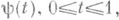что множество точек, координаты к-рых определяются. этими функциями, заполняют квадрат 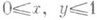(см. Пеано кривая). Более общо, всякий локально связный континуум (т. е. континуум, каждая точка к-рого обладает сколь угодно малой связной окрестностью) является непрерывным образом отрезка (теорема М а з у р к е в и ч а). Таким образом, не только квадрат, но и куб любого числа измерений и даже бесконечномерный гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что Л. не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений. Так, в дифференциальной геометрии эти ограничения выражаются в том, что на функции, фигурирующие в параметрическом задании Л., налагаются условия существования производных различных порядков. С другой стороны, существуют континуумы, которые естественно рассматривать как Л., но к-рые, не будучи локально связными, не являются непрерывными образами отрезка. Таков, напр., континуум, определяемый

условиями:

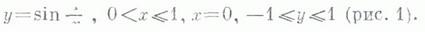
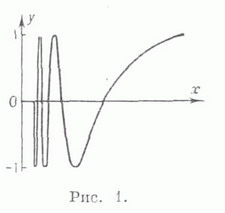
Общее определение Л. для случая плоскости было дано (Г. Кантор, G. Cantor, 1870-е гг.) в связи с созданием теории точечных множеств. Плоский континуум, в любой окрестности каждой точки к-рого имеются точки плоскости, не принадлежащие континууму, наз. канторовой кривой. Важный пример канторовой кривой доставляет ковер Серпиньского, строящийся следующим образом. Квадрат Qсо стороной 1 делят на девять равных квадратов прямыми, параллельными его сторонам, и удаляют все

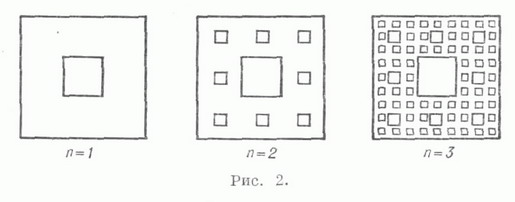
внутренние точки центрального квадрата (рис. 2,. n=1). Так же поступают и с каждым из оставшихся восьми квадратов первого ранга, получается 64 квадрата второго ранга (рис. 2, n = 2). Продолжая процесс для всех натуральных n, на n-м шаге получают 8ⁿ квадратов n- горанга со стороною Пересечение полученных таким образом множеств и есть ковер Серпинь-ского (рис. 2).

Какова бы ни была канторова кривая L, она может быть топологически вложена в ковер Серпиньского 5, т. е. в Sсодержится континуум L’, гомеоморфный Л. L. Ковер Серпиньского является локально связным континуумом и потому может быть получен как непрерывный образ отрезка.

В топологии пользуются понятием Л., введенным в 1921 П. С. Урысоном и являющимся наиболее общим (но не чрезмерно). Определение Л. формулируется следующим образом: линией наз. одномерный континуум, т. с. связное компактное метрич. пространство

С, каждая точка к-рого обладает сколь угодно малой окрестностью с границей размерности нуль. Другими словами, при любом e>0 пространство Сможет быть представлено в виде суммы конечного числа замкнутых множеств диаметра, меньшего е, обладающих тем свойством, что никакие три из этих множеств не имеют общей точки. Ковер Серпиньского удовлетворяет этому определению Л., так что всякая канторова кривая является также и Л. в смысле П. С. Урысона. Обратно, если плоский континуум является Л. в смысле П. С. Урысона, то он будет канторовой кривой. Определение Л., данное П. С. Урысоном, является внутренним: оно характеризуется лишь свойствами самого пространства С и не зависит от того, рассматривается ли это пространство само по себе или как подмножество другого топологич. пространства.

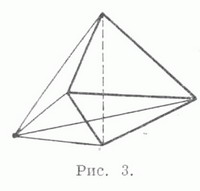
Существуют Л., к-рые не гомеоморфны никакому подмножеству плоскости. Такова, напр., Л., лежащая в трехмерном пространстве и состоящая из шести ребер тетраэдра и четырех отрезков, соединяющих какую-либо точку пространства, не лежащую ни на одной из его граней, с его вершинами (рис. 3). Но всякая Л. (в смысле П. С. Урысона) гомеоморфна нек-рому подмножеству трехмерного евклидова пространства (теорема М е н г е р а). Континуум

М, обладающий тем свойством, что какова бы ни была Л.. С, в М найдется подконтинуум С’, гомео-морфный континууму С, строится следующим образом. Куб К с ребром 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из куба Кудаляются центральный куб и все прилежащие к нему по двумерным граням кубы этого подразделения. Получается множество K₁, состоящее из 20 оставшихся замкнутых кубов первого ранга. Поступая точно так же с каждым из кубов первого ранга, получим множество K₂, состоящее из 400 кубов второго ранга (рис. 4). Продолжая этот процесс бесконечно, получим последовательность континуумов пересечение к-рых есть одномерный континуум М, паз. универсальной кривой М е н г е р а.

В исследовании Л. важную роль играет понятие индекса ветвления. Л. Св точке химеет индекс ветвления т, если каково бы ни было число e>0, существует открытое множество Uдиаметра, меньшего, чем е, содержащее точку х. граница к-рого есть множество мощности, не превосходящей т, но для достаточно малого e’>0 граница всякого открытого множества, содержащего точку х, диаметр к-рого меньше e’, имеет мощность, не меньшую, чем т. Точки Л. относительно их индекса ветвления классифицируются следующим образом.

1) Точки с индексом ветвления п, п — натуральное.

2) Точки неограниченного индекса ветвления w. (Точка х Л. С имеет индекс ветвления со, если каково бы ни было число e>0, существует открытое множество, содержащее точку х, с диаметром, меньшим, чем е, граница к-рого состоит’из конечного множества точек; но каково бы ни было натуральное п, найдется такое e_n>0, что граница всякого открытого множества,

содержащего хи имеющего диаметр меньший, чем e_n состоит не менее, чем из га точек.)

3) Точки счетного индекса ветвления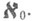

4) Точки континуального индекса ветвления с.

Точка Л. С, индекс ветвления к-рой больше двух, наз. точкой ветвления; точка, индекс ветвления к-рой равен единице, наз. концевой точкой.

Примеры, а) Отрезок во всех своих внутренних точках имеет индекс ветвления, равный двум; индекс ветвления концов отрезка равен единице, б) Окружность в каждой своей точке имеет индекс ветвления два. в) Л., состоящая из га прямолинейных отрезков,.

исходящих из одной точки О, имеет в точке Оиндекс ветвления п. г) Л., состоящая из отрезков 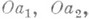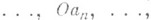выходящих из начала координат О, имеющих длины и образующих с осью Ох углы, соответственно равные имеет в точке Онеограниченно возрастающий: индекс ветвления со (рис. 5). д) Л., состоящая из отрезка Оа ₀ длины 1 и отрезков длины 1, выходящих из точки Ои образующих с отрезком Оа ₀ углы, соответственно равные имеет в каждой точке отрезка Оа ₀ счетный индекс ветвления 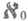(рис. 6). е) Л., состоящая из отрезков, соединяющих точку Осо всеми точками канторова множества, лежащего на отрезке

y=0, имеет во всех своих точках континуальный индекс ветвления с (рис. 7). ж) Ковер Серпиньского также имеет во всех своих точках континуальный индекс ветвления.

Если у Л. совсем нет точек ветвления, т. е. если в каждой точке Л. индекс ветвления равен 1 или 2, то эта Л. есть либо простая дуга — топологич. образ отрезка, либо простая замкнутая линия — топологич. образ окружности. При этом, если индекс ветвления Л. во всех точках равен 2, то это — простая замкнутая Л., если же у Л., не имеющей точек ветвления, есть концевые точки (при этом оказывается, что их непременно две), то она будет простой дугой. Если Л. имеет лишь конечное число точек ветвления, причем индекс ветвления каждой из них также конечен, то такая Л. может быть разбита на конечное число простых дуг, не имеющих попарно никаких других общих точек, кроме своих концов.

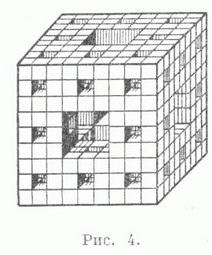
Окружность является единственной Л., все точки к-рой имеют один и тот же конечный индекс ветвления 2; других Л., имеющих во всех точках один и тот же конечный индекс ветвления, нет, более того, если все точки Л. Lимеют индекс ветвления больший или равный п, то на Л. Lнайдется точка, индекс ветвления к-рой больше или равен 2п-2, и при всяком натуральном псуществует Л., состоящая только из точек, имеющих индекс ветвления пи 2п-2 (теорема У р ы с о н а). Пример Л., состоящий только из точек с индексом ветвления 3 и 4, строится следующим образом. В равностороннем треугольнике со стороною 1 проводятся три средние линии, и из него выбрасываются внутренние точки треугольника, ограниченного средними Л. С каждым из оставшихся трех треугольников первого ранга проделывается аналогичная операция, в результате к-рой получается девять треугольников второго ранга. Поступая с ними так же, получим 27 треугольников третьего ранга и так далее для всякого натурального п. Пересечение полученных в результате выполнения этих операций множеств есть линия С(рис. 8). Л., состоящая из точек с индексом ветвления 3 и 4,- это два континуума С ₁ и С ₂, каждый из к-рых гомеоморфен Л. С и к-рые не имеют никаких других общих точек, кроме точек, соответствующих вершинам основного треугольника континуума С.

Существуют также Л., имеющие во всех своих точках неограниченный индекс ветвления, счетный индекс ветвления и континуальный индекс ветвления. Лит.:[1] Александров П. С., Введение в общую теорию множеств и функций, М.- Л., 1948; [2] К у р а т о в с к и й К., Топология, пер. с англ., т. 2, М., 1969; [3] М е n g е r К., Kurventheorie, Lpz.- В., 1932; [4] Пархоменко А. С., Что такое линия, М., 1954; [5] У р ы с о н П. С., Труды по топологии и другим областям математики, т. 2, М.- Л., 1951; [6] Хаусдорф Ф., Теория множеств, пер. с нем., М.- Д., 1937. А. С. Пархоменко.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

Основы геометрии. Определения основных элементов, пятый элемент

Ну а для определения формы предмета нужно знать еще несколько понятий. Их Евклид сформулировал настолько просто, что даже сейчас понимание некоторых из них вызывает определенные сложности. Сколь полезной для гимнастики ума была новая трактовка евклидовых определений, я уже писал выше. А здесь я просто изложу свое понимание геометрии, далеко не всегда совпадающее с трактовкой Евклида и других геометров, однако с использованием аналогий к системе координат Декарта (также одного из комментаторов Евклида). Вообще-то прообразом системы координат является крест, использовавшийся людьми за тысячи лет до появления христианства, и смысл у него был приблизительно такой же как и у нынешней системы координат, но к кресту мы еще вернемся. В отличие от описательных определений Евклида я постараюсь дать большей частью генетические определения: Первый и простейший элемент геометрии — точка, точнее геометрическая точка Применять к точке понятия размеров или формы бессмысленно, если точка только одна. Точка изначальна, как слово в библии, но без точки невозможна геометрия, все остальные геометрические фигуры состоят как бы из точек. Впрочем, это утверждение справедливо только для моего абстрактного геометрического мира. Не все точки одинаково важны при решении задач геометрии, но обсуждать этот вопрос более подробно, пока мы ничего кроме точек не знаем, не имеет смысла. Второй важнейший элемент геометрии — это линии линии бывают разными. На мой взгляд наиболее важными из них являются: 2.1. Элементарный отрезок Элементарный отрезок образован двумя точками, а значит появляется расстояние между точками, условно говоря — длина, а так как рассматривается элементарный отрезок, то это некое элементарное расстояние, в данном случае длина. Примечание 1: В классической геометрии не используются понятия элементарного отрезка, элементарных размеров, элементарной поверхности и др. С одной стороны это значительно упрощает решение многих практических задач, а с другой стороны плохо соотносится с наблюдаемым нами реальным миром. Например, любое наблюдаемое нами твердое тело реального мира, имеющее некоторую массу, состоит из атомов, во всяком случае атомистическая модель строения мира пока не опровергнута. В однородном (изотропном) пространстве расстояние между атомами определяется взаимодействием атомов тела и если на тело не действуют никакие силы кроме указанной силы взаимодействия, то расстояние между атомами будет приблизительно одинаковым и для тела из данного материала элементарным. Т.е. определять какие-либо геометрические характеристики для некоего условно однородного материала с межатомным расстоянием 0.3 нм на расстоянии 0.15 нм от одного из атомов бессмысленно, тем не менее классическая геометрия это допускает. Впрочем геометрия используется не только для определения размеров материальных тел. Уникальность геометрии в том, что она как пустой горшок Винни Пуха, может вместить в себя что угодно. Например, если речь идет о траектории движения некоей материальной точки, то такая траектория также может рассматриваться как геометрическая фигура и тогда понятие элементарного отрезка становится весьма условным, так как в этом случае расстояния между точками траектории действительно можно рассматривать стремящимися к нулю. Это иногда приводит к другим парадоксам, не разрешимым с точки зрения классической геометрии, но о них речь ниже. Элементарный отрезок — одномерен. Пользуясь аналогией с системой координат можно сказать, что отрезок измеряется только по одной оси, например оси х. Например, для ребенка, который нашел палку, важна только длина, на остальные характеристики он пока не обращает внимания и мы не будем. Из отрезков может слагаться линия сколь угодно большой длины. Таким образом можно сказать, что любая линия — это множество точек, однако такое определение будет не совсем полным. Более точным будет следующее определение: 2.2. Линия — это множество расстояний между точками однако с точки зрения геометрии нет необходимости рассматривать каждое расстояние между точками отдельно, если свойства линии не меняются. Достаточно знать расстояние между начальной и конечной точкой, что и является главной характеристикой для элементарного отрезка. Это значительно упрощает решение задач. Таким образом для определения свойства линии достаточно знать характеристики главных точек. Я бы назвал эти точки характерными точками. 2.3. Самая простая линия — это прямая линия Прямая линия, как и просто линия — это множество расстояний между точками, свойства же прямой линии меняются только в двух точках, в начале и в конце. Можно сказать, что прямая линия характеризуется расстоянием между начальной и конечной точкой или что сумма расстояний между соседними точками равна расстоянию между крайними точками. Однако самым лучшим на мой взгляд будет следующее определение: Для полного описания прямой линии достаточно указать расстояние между начальной и конечной точками. Прямая линия одномерна. Это означает, что прямую линию всегда можно расположить так, что наблюдатель будет видеть только одну начальную точку. Например, когда школьник, плюющий через трубочку жеванной бумагой в понравившуюся девочку, приставляет к глазу трубочку, чтобы посмотреть на мишень, он как раз и совмещает центр окружности начала трубочки с центром окружности конца трубочки, а по ходу и все центры поперечных сечений трубочки, если трубочка ровная. Прямая линия подобна элементарному отрезку. Единственное отличие — в длине. Прямая линия — частный случай всех возможных линий, тем не менее важность прямой линии для геометрии очень велика. В реальном мире к прямой линии приближаются, например, траектория падения камня под действием силы тяжести, или форма нити отвеса, который также притягивается к земле силой тяжести. Приближаются, а не соответствуют потому, что на камень, падающий в земной атмосфере, также действует сила сопротивления воздуха, порывы ветра, возможно другие факторы, влияющие на траекторию полета и тем самым нарушающие прямолинейность траектории. Для нити кроме указанных факторов также немаловажными будут свойства материала нити и особенности ее изготовления. Однако геометрия, оперируя понятием прямой линии в случаях, когда вышеуказанными факторами можно пренебречь, значительно упрощает решение задач. Линия — это грань, граница между чем-либо, которую мы вполне отчетливо себе представляем, хотя в реальном мире никакой реальной границы может и не быть, а есть просто оптический эффект. Например, черный квадрат Малевича был бы невозможен на полностью черном фоне, т.е. без границ, условно говоря, линий, отделяющих черное от белого. Вот только сама по себе линия одномерного мира мало что значит, ей нужно что-то разделять или ограничивать. Пока все вроде бы просто и достаточно понятно, но Есть в геометрии такая линия, которая и очень простая и очень сложная одновременно — это окружность Дать определение окружности не смог даже Евклид. Оно ведь как получается, с одной стороны окружность — это множество точек, расположенных на одинаковом расстоянии от центра окружности (современное определение), да только Евклид не рассматривал линии, как множество точек, а мыслил их как некий элемент геометрии, не имеющий прямого отношения к точкам. А с другой стороны, если рассматривать окружность, как линию, образованную элементарными отрезками, то получается, что окружность — можно составить из коротких прямолинейных отрезков. А значит окружность — это просто ломаная замкнутая линия. Например, из трех элементарных отрезков можно составить равносторонний треугольник, но треугольник — явно не окружность, из четырех — квадрат, но и это никак не окружность по виду, равносторонние пятиугольник и шестиугольник и т.д. выглядят уже лучше, но все равно от окружности далеки. И тут вспоминается древнейший софистический парадокс, звучавший примерно так: «Одно зерно — не куча, два — зерна — не куча, три зерна — не куча и если прибавлять по одному зерну, то куча никогда не получится». А между тем, что такое куча зерна мы очень хорошо себе представляем. Куча — это когда много зерна. Примерно то же самое можно сказать и о окружности: Окружность — это когда прямолинейных отрезков, образующих окружность, настолько много, что они представляются одной сплошной линией Между тем современная геометрия рассматривает окружность, как некую плавную замкнутую линию, которую сколько ни разбивай на отрезки, они все равно будут не прямолинейными. Это приводит к тому, что даже сейчас невозможно совершенно точно определить длину окружности, да и площадь круга даже теоретически. Т.е. многие из вас слышали про число П, но не многие знают, что это постоянное число, выражающее отношение длины окружности к радиусу, точно рассчитать не возможно, так как П является иррациональным и трансцендентальным числом. Использовать точное значение числа П для абсолютного большинства расчетов нет никакой практической необходимости, поэтому люди обычно пользуются приближенным значением П, допускающим некоторый, хотя и очень малый, но процент погрешности. Вот и выходит, что как окружность ни крути, а она все еще остается загадкой. Ну а чтобы закруглить этот парадокс, отмечу, что в современной геометрии прямая линия может рассматриваться, как часть окружности с бесконечно большим радиусом, т.е. является как бы элементарным отрезком. Такие дела. Третий важный элемент геометрии — это поверхности Поверхности, как и линии бывают разными, причем разнообразие поверхностей еще больше, чем линий. 3.1. Элементарная поверхность Основная характеристика элементарной поверхности — площадь и вообще можно назвать элементарную поверхность элементарной частью площади. Для определения площади элементарной поверхности недостаточно знать только длину, необходимо оперировать еще и шириной. Таким образом элементарная поверхность — это уже элемент двухмерного мира. Как и линия, поверхность образована точками, минимум тремя, или линиями, как минимум тремя. Но с точки зрения классической геометрии это не совсем так. В геометрии Эвклида поверхность качественно новый элемент геометрии, связанный с предыдущими тем, что поверхность ограничивается линиями, поэтому определение поверхности как некоего элемента главная характеристика которого — площадь, вполне допустима. 3.2. Из элементарных поверхностей может слагаться поверхность сколь угодно большой площади При этом как и в случае с линиями рассматривать все расстояния между точками вовсе не обязательно и даже расстояния между всеми линиями, которые могут быть образованы из этих точек — тоже не обязательно. Достаточно знать характеристики главных линий, я бы назвал эти линии характерными линиями. Характерные линии ограничивают поверхность, например черный квадрат Малевича ограничен 4 линиями. 3.3. Самая простая поверхность — плоская поверхность или как сейчас говорят — плоскость Плоскость двухмерна, это означает, что плоскость всегда можно расположить так, что наблюдателю будет видна только одна линия. Например, плотники с древнейших времен проверяют точность обработки деревянного бруса, смотря на исследуемую поверхность так, чтобы линия, ограничивающая начало поверхности, совпала с линией, ограничивающей конец поверхности. Плоскость — это частный случай всех возможных плоскостей, но как и прямая линия, плоскость очень важна для решения задач геометрии. Более того, прямая линия и плоскость интуитивно понятны даже людям, никогда геометрию не изучавшим. Например, когда человеку нужно добраться из точки А в точку В, то он старается проложить маршрут, максимально близкий к прямой линии, а если путь будет проходить по равнине, а не по пересеченной местности, то совсем хорошо. А еще люди делают тоннели в горах и засыпают овраги, чтобы сделать дорогу из одного пункта в другой максимально приближающейся к прямой линии. И точка и линия и поверхность в геометрии могут рассматриваться и как отдельные элементы и как формообразующие элементы, например, точка формообразующий элемент для линии, а линия формообразующий элемент для поверхности. Также точка, линия и поверхность могут быть общими элементами геометрических фигур. Для основной части школьного курса геометрии этих элементов вполне достаточно, да и у Евклида трехмерные геометрические фигуры рассматриваются в книгах XI-XIII. Тем не менее хочется закончить этот ряд. Четвертый важный элемент геометрии — это тело Тело — это трехмерная геометрическая фигура. Большинство предметов окружающего нас мира представляют собой трехмерные тела. Основная характеристика тела — объем. Для определения объема тела недостаточно знать только длину и ширину, нужно знать еще и высоту. Ограничивается тело поверхностями. 4.1. Элементарное тело — это тело, имеющее элементарный объем Например, при определении свойств материалов с кристаллической решеткой используется понятие — элементарная ячейка кристаллической решетки, характеризуемое расстояниями между атомами решетки. Суть этого понятия в том, что для определения геометрических свойств решетки нет необходимости рассматривать все элементарные ячейки, достаточно описать свойства только элементарной ячейки. Очень условно элементарное тело можно рассматривать, как подобие элементарной ячейки кристаллической решетки. 4.2. Из элементарных тел может быть образовано тело сколь угодно большого объема 4.3. Самое простое тело — это куб, так как оно ограничено плоскостями, при этом плоскости ограничены прямыми линиями А теперь закончим этот ряд: Линия, состоящая из нескольких элементарных отрезков, может быть одномерной, двухмерной и трехмерной. Поверхность, состоящая из нескольких элементарных поверхностей, может быть двухмерной и трехмерной. Тело любое — только трехмерным. С точки зрения геометрии (если условия задачи позволяют) любое из окружающих нас материальных тел, имеющих вполне определенный объем, может рассматриваться, как геометрическая точка. Например, если нужно определить расстояние от одной звезды до другой, то учитывать при этом объемы звезд и уточнять, что определяется расстояние между центрами звезд, вовсе не обязательно, так как расстояние между звездами значительно больше чем диаметры звезд. Другими словами, если подобное уточнение даст изменение результата в пределах нескольких тысячных процента и даже менее, то нет большого смысла тратить время на подробные вычисления. Примечание 2: Считается, что первым теорию относительности сформулировал Эйнштейн, однако основы теории относительности сформулировали далекие предки Эйнштейна — шумеры, даже задолго до Евклида. Ведь они первые ввели понятие процента. А процент — это и есть основа теории относительности. Ведь что такое, например расстояние между двумя звездами в 100000 световых лет или состояние человека в 100000 денежных единиц? Это некие абсолютные величины, по большому счету человеку ни о чем не говорящие. А вот рассмотрение этих величин по отношению к чему-либо сильно влияет на человеческое восприятие. Например, если на эти самые 100000 денежных единиц можно купить 5 булочек, то это в общем-то хорошо, но на прожить не хватит. А вот если на эти же самые 100000 денежных единиц можно купить 5 хлебобулочных заводов — это совсем другое дело. Недаром процент с древнейших времен использовался как один из важнейших критериев оценки окружающего нас мира. Конечно, современное понятие процента намного шире, но подробное рассмотрение этого понятия в цели данной статьи не входит. Таким образом в геометрии есть 4 формообразующих элемента из которых может быть образована любая геометрическая фигура. Эти перечисленные выше элементы характеризуются абсолютными характеристиками длиной, шириной и высотой Рисунок 1. а) Условное изображение физического тела, состоящего из атомов б) геометрическая модель физического тела или просто геометрическое тело На рисунке 1.б) точка показана фиолетовым цветом, линия — малиновым цветом, плоскость — розовым цветом. А еще любое тело можно рассматривать, как образованное некоторым количеством параллельных плоскостей, а если эти плоскости имеют постоянную высоту и ширину, то как и в случае с прямой линией рассматривать все эти плоскости совершенно не обязательно, достаточно определить основные характеристики только для одной плоскости. Так современный школьный курс геометрии на 90% посвящен рассмотрению свойств плоских фигур. Теперь, после ознакомления с формообразующими элементами можно бы и начать более полное изучение геометрии, но В геометрии есть еще один очень важный элемент, который по праву можно назвать пятым элементом — это угол Угол — это часть целого и вместе с тем относительная характеристика геометрических фигур По большому счету длина, ширина и высота также не являются абсолютными характеристиками, например длина линии — это расстояние между двумя точками, а значит характеристика одной точки относительно другой. Тем не менее размеры можно считать абсолютными понятиями по отношению к такой характеристике как угол. Особенность угла в том, что размеры линий, поверхностей или тел, образовавших данный угол, не имеют принципиального значения. Для определения угла важно только взаимное расположение геометрических фигур, угол образовавших. Как и другие элементы геометрии, углы бывают разными, но как правило для решения большинства задач геометрии люди используют малую часть возможных углов. Так из всех возможных углов чаще всего рассматривается плоский угол. Такой угол может быть образован двумя линиями, находящимися в одной плоскости. Из плоских углов наибольшее значение имеет прямолинейный угол. Такой угол образован не просто линиями, а прямыми линиями, что позволяет определить характеристики угла максимально просто. Из прямолинейных углов выделяются еще два частных случая: прямой угол и развернутый угол. Если при пересечении двух прямых образуются 4 одинаковых угла, то такие углы называются прямыми, а линии называются перпендикулярными друг другу А в целом такие прямые образуют упоминавшийся нами крест — древнейший человеческий оберег, используемый людьми задолго до появления христианства и символизирующий защиту от темных сил со всех четырех сторон света. Мне кажется вполне вероятным, что если бы наши предки использовали понятие трех сторон света или трех времен года, то современная геометрия была бы совсем другой, так как в процессе человеческого познания нет ничего не нужного и не важного. Кстати и сейчас некоторое целое может быть разбито углами на 360 частей, называемых градусами, когда-то эти 360 частей означали количество дней в календарном году и были получены разбиением зодиакального круга. Изображение зодиакального круга можно увидеть во вступительной статье. Если прямая образована из отрезков, то угол между всеми отрезками является развернутым Это означает, что никаких изменений параметров в общих точках не происходит, что позволяет рассматривать не каждый отрезок прямой линии в отдельности, а всю прямую линию в целом. Таким образом развернутый угол — это как бы показатель стабильности. Например, если четыре нижних точки на рисунке 1.а) соединить отрезками, то в итоге мы получим прямую линию состоящую из трех отрезков. Также тут стоит упомянуть и о нулевом угле. Например, если рассматривать две прямые, расположенные в одной плоскости (например, прямые ограничивающие плоскость на рисунке 1.б) сверху и снизу), то угол между ними условно можно считать нулевым или развернутым в зависимости от того, какие точки будут приниматься за начало линий. Условно — потому что не существует точки пересечения параллельных прямых (в евклидовой геометрии), а значит и угла никакого нет, ни нулевого ни развернутого. Главными характеристиками угла в свою очередь являются синус и косинус Значения синуса и косинуса можно условно сравнить с коэффициентом полезного действия. Коэффициент полезного действия — очень важный показатель для человека, чем ближе этот показатель к 100% или к единице, тем человеку приятнее, проще говоря, никто не любит делать дурную работу. Так синус прямого угла равен единице или 100%, а синус развернутого угла и нулевого угла = 0. Попробуем проиллюстрировать это на примере определения площади плоской геометрической фигуры. Например плоскость, показанная на рисунке 1.б) может рассматриваться как план комнаты. Комната образована 4 линиями — стенами. При этом даже если длина стен будет постоянной и одинаковой, то площадь комнаты может сильно изменяться в зависимости от значения углов между стенами: Рисунок 2. На рисунке 2 показаны плоские геометрические фигуры образованные прямыми линиями одинаковой длины. При этом даже без подробных расчетов понятно, что максимальная площадь будет у квадрата — рисунок 2.а). Квадрат — это частный случай прямоугольника. А прямоугольник — это такая плоская фигура, ограниченная параллельными линиями, у которой длина боковых линий равна высоте фигуры, а кроме того углы между всеми сторонами — прямые. А вот если строители плохо учились в школе и не выдержали прямые углы между стенами, при этом длина стен не изменилась, то вполне может получиться ромб, показанный на рисунках 2.б) или 2.в). Это может показаться шуткой, но я в своей жизни такие комнаты наблюдал неоднократно, хотя и не в таком явном виде, как показано на рисунках. Ромб — плоская геометрическая фигура, у которой все стороны равны и соответственно противоположные границы параллельны, однако углы между смежными линиями не равны прямому. Как видно из этих рисунков, чем больше угол между смежными линиями отличается от прямого, тем меньше площадь фигуры. Если повернуть левую боковую сторону на все 90о, то в итоге получится линия, равная сумме длин нижней и боковой сторон и вообще никакой площади не имеющая, так как у линии никакой высоты нет. Площадь показанных на рисунке 2 фигур равна произведению длины на высоту. Длина у всех фигур условно одинаковая — это нижняя стена, а вот высота (показана на рисунке 2 синим цветом) — разная. А высота во всех случаях равна произведению длины боковой стороны на синус угла между смежными стенами. Вот и получается, что синус как бы показывает коэффициент полезного действия, т.е. при прямом угле между смежными сторонами квадрата площадь квадрата максимальна, а при нулевом угле (развернутом угле) площадь равна нулю. А если рассматривать геометрическую фигуру, образованную боковой стеной, высотой и красной линией, то это будет прямоугольный треугольник, вписанный в окружность. Если длина боковой стены — радиуса окружности = 1, то синяя линия — это синус угла, а еще противолежащий катет, а красная линия — это косинус угла, а еще прилежащий катет, а боковая наклонившаяся стена — гипотенуза. Таким образом косинус прямого угла равен нулю, а косинус развернутого угла = -1, косинус нулевого угла = 1. Получить такие геометрические фигуры можно с помощью обычного детского магнитного конструктора. Достаточно взять 4 палочки и 4 шарика и соединить их между собой так, чтобы получился квадрат, а затем надавить соответствующим образом на один из шариков. При этом квадрат будет постепенно превращаться в ромб, показанный на рисунке 2.б), а если давить и дальше, то и в ромб, показанный на рисунке 2.в. При этом общая точка для нижней и левой боковой линии станет центром вращения для левой боковой стороны, а сама левая боковая сторона станет радиусом окружности. Конечно же человеку, решая различные возникающие перед ним задачи, приходится иметь дело не только с прямым и развернутым углом, но также и со всеми остальными. А чтобы каждый раз не вычислять значения синуса, косинуса и других тригонометрических функций, люди пользуются соответствующими таблицами или калькулятором, который сам все посчитает, для того он и придуман. Это далеко не все, что можно рассказать о формообразующих элементах, но для начала хватит.

Линейное пространство (геометрия) — Википедия

Материал из Википедии — свободной энциклопедии

Линейное пространство — это базовая структура геометрии инцидентности. Линейное пространство состоит из множества элементов, называемых точками, и множества элементов, называемых прямыми. Каждая прямая является различным подмножеством точек. Говорят, что точки прямой инцидентны прямой. Любые две прямые могут иметь не более одной общей точки. Интуитивно, это правило можно продемонстрировать как две прямые на евклидовой плоскости, которые никогда не пересекаются более чем в одной точке.

(Конечные) линейные пространства можно рассматривать как обобщения проективной и аффинной плоскостей^[en], и в более широком смысле, как 2-(v,k,1){\displaystyle (v,k,1)} блок-схемы, для которых требуется, чтобы каждый блок содержал одинаковое число точек и существенной структурной характеристикой является то, что две точки инцидентны в точности одной прямой.

Термин линейное пространство ввёл Либоис в 1964, хотя многие результаты относительно линейных пространств существенно старше.

Пусть L = (P, G, I) — структура инцидентности, для которой элементы P называются точками, а элементы G называются прямыми. L является линейным пространством, если выполняются следующие три аксиомы:

• (L1) две точки инцидентны в точности одной прямой.
• (L2) любая прямая инцидентна по меньшей мере двум точкам.
• (L3) L содержит по меньшей мере две прямые.

Некоторые авторы опускают (L3) при определении линейных пространств. В этом случае линейные пространства, соблюдающие (L3), считаются нетривиальными, а не соблюдающие — тривиальными.

Регулярная евклидова плоскость с её точками и прямыми образует линейное пространства, более того, все аффинные и проективные пространства являются линейными пространствами.

Таблица ниже показывает все возможные нетривиальные пространства из пяти точек. Поскольку любые две точки всегда инцидентны одной прямой, прямые, инцидентные только двум точкам, не показаны. Тривиальный случай — прямая через пять точек.

В первом примере десять прямых, соединяющих десять пар точек, не нарисованы. На второй иллюстрации не нарисованы семь прямых, соединяющих семь пар точек.

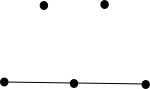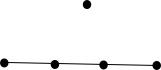10 прямых	8 прямых	6 прямых	5 прямых

Линейное пространство из n точек, содержащее прямую, инцидентную n − 1 точкам, называется почти пучком. (См. «Пучок»)

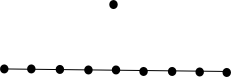Почти пучок с 10 точками

• Albrecht Beutelspacher. Einführung in die endliche Geometrie II (нем.). — Bibliographisches Institut, 1983. — S. 159. — ISBN 3-411-01648-5.
• J. H. van Lint, R. M. Wilson. A Course in Combinatorics. — Cambridge University Press, 1992. — С. 188. — ISBN 0-521-42260-4.
• L. M. Batten, Albrecht Beutelspacher. The Theory of Finite Linear Spaces. — Cambridge: Cambridge University Press, 1992..

ЛИНИЯ ВТОРОГО ПОРЯДКА — это… Что такое ЛИНИЯ ВТОРОГО ПОРЯДКА?

плоская линия, декартовы прямоугольные координаты к-рой удовлетворяют алгебраич. уравнению 2-й степени

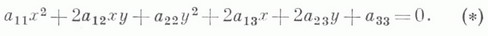
Уравнение (*) может и не определять действительного геометрич. образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат на нек-рый угол к одному из 9 приведенных ниже канонич. видов, каждому из к-рых соответствует определенный класс линий. Именно, нераспадающиеся линии:

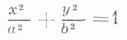
эллипсы,

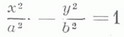
гиперболы,

у ²=2рх параболы,

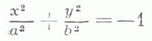
мнимые эллипсы;

распадающиеся линии:

пары мнимых пересекающихся прямых,

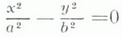
пары действительных пересекающихся

прямых,

х ²-a²=0 пары действительных параллельных прямых,

x²+а ²=0 пары мнимых параллельных прямых,

x²=0 пары совпадающих действительных прямых.

Л. в. п., имеющие единственный центр симметрии (центр Л. в. п.), наз. центральной линией. Координаты центра Л. в. п. определяются решением системы:

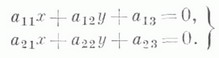
Л. в. п. без центра симметрии или снеопределенным центром наз. нецентральной линией.

Исследование вида Л. в. п. может быть проведено без приведения общего уравнения к канонич. виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов Л. в. п. — выражений, составленных из коэффициентов уравнения (*), значения к-рых не меняются при параллельном переносе и повороте системы координат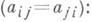

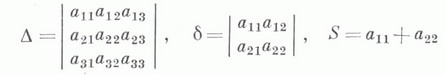
и семиинварианта (полуинварианта):

к-рый является инвариантом относительно поворота системы координат (см. табл.).

Многие важные свойства Л. в. п. могут быть изучены при помощи характеристической квадратичной формы

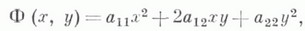
соответствующей уравнению (*). В частности, нераспадающаяся Л. в. п. оказывается эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости От того, будет ли Ф ( х, у).положительно определенной, отрицательно определенной, неопределенной или полуопределенной квадратичной формой, что устанавливается по корням ее характеристического уравнения:

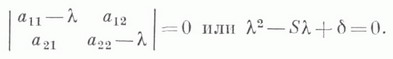
Три основных инварианта 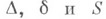определяют Л. в. п. (кроме случая параллельных прямых) с точностью до движения евклидовой плоскости: если соответствующие инварианты 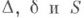двух линий равны, то такие линии могут быть совмещены движением. Иными словами, эти линии эквивалентны по отношению к группе движений плоскости (метрически эквивалентны).

Существует классификация Л. в. п. с точки зрения других групп преобразований. Так, относительно более общей (чем группа движений) группы аффинных преобразований эквивалентными являются любые две линии, определяемые уравнениями одного канонич. вида. Напр., две подобные Л. в. п. считаются эквивалентными. Связи между различными аффинными классами Л. в. п. позволяет установить классификация с точки зрения проективной геометрии, в к-рой бесконечно удаленные элементы не играют особой роли. Действительные нераспадающиеся Л. в. п.: эллипсы, гиперболы и параболы образуют один проективный класс — класс действительных овальных линий (овалов). Действительная овальная линия является эллипсом, гиперболой или параболой в зависимости от того, как она расположена относительно бесконечно удаленной прямой: эллипс пересекает несобственную прямую в двух мнимых точках, гипербола — в двух различных действительных точках, парабола касается несобственной прямой; существуют проективные преобразования, переводящие эти линии одна в другую. Существует 5 классов проективной эквивалентности Л. в. п. Именно, невырождающиеся линии (x₁ х ₂, х ₃ — однородные координаты):

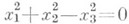действительный овал, 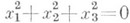мнимый овал; вырождающиеся линии:

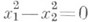пара действительных прямых, 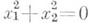пара мнимых прямых, пара совпадающих прямых. Кроме аналитич. способа определения Л. в. п. (заданием уравнения) существуют и другие способы. Напр., эллипс, гипербола и парабола могут быть получены как сечения конич. поверхности плоскостью (см. Конические сечения).

Исследование вида линий второго порядка с помощью инвариантов

Лит.:[1] Александров П. С., Лекции по аналитической геометрии, М., 1968; [2J Ефимов Н. В., Краткий курс аналитической геометрии, 11 изд., М., 1972. А. Б. Иванов.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

кривая линия — это… Что такое кривая линия?

кривая линия — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN curved line …   Справочник технического переводчика

Кривая Линия — В китайском символизме кривая линия используется для обозначения неискреннего человека, искусственных стандартов, показного и броского великолепия. Прямая линия символ праведности и совершенного человека …   Словарь символов

Подошвенная кривая линия — (Podaire) данной плоской кривой есть геометрическое место оснований перпендикуляров, опущенных из какой либо точки плоскости на касательные, проведенные к точкам данной кривой. Например, П. кривая эллипса по отношению к его центру есть кривая… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Линия — В Викисловаре есть статья «линия» Линия (от лат. linea «льняная нить, шнур; линия») протяжённый и тонкий п …   Википедия

линия — сущ., ж., употр. часто Морфология: (нет) чего? линии, чему? линии, (вижу) что? линию, чем? линией, о чём? о линии; мн. что? линии, (нет) чего? линий, чему? линиям, (вижу) что? линии, чем? линиями, о чём? о линиях 1. Линия это узкая полоса, черта …   Толковый словарь Дмитриева

линия — ▲ последовательность ↑ непрерывный, геометрический линия непрерывная геометрическая последовательность; отображение функции одной переменной; след движущейся точки; фигура, изображающая функцию одной переменной; одномерная фигура, т. е. положение …   Идеографический словарь русского языка

Линия (кривая) — Кривая или линия  геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана …   Википедия

Линия (геометрич. понятие) — Линия (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной геометрии рассматриваются… …   Большая советская энциклопедия

Кривая Жордана — Кривая или линия  геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана …   Википедия

Линия Коха — Кривая Коха Кривая Коха фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом. Кривая Коха примечательна тем, что нигде не имеет касательной, т. е. нигде не дифференцируема, хотя всюду непрерывна. Три копии кривой Коха,… …   Википедия