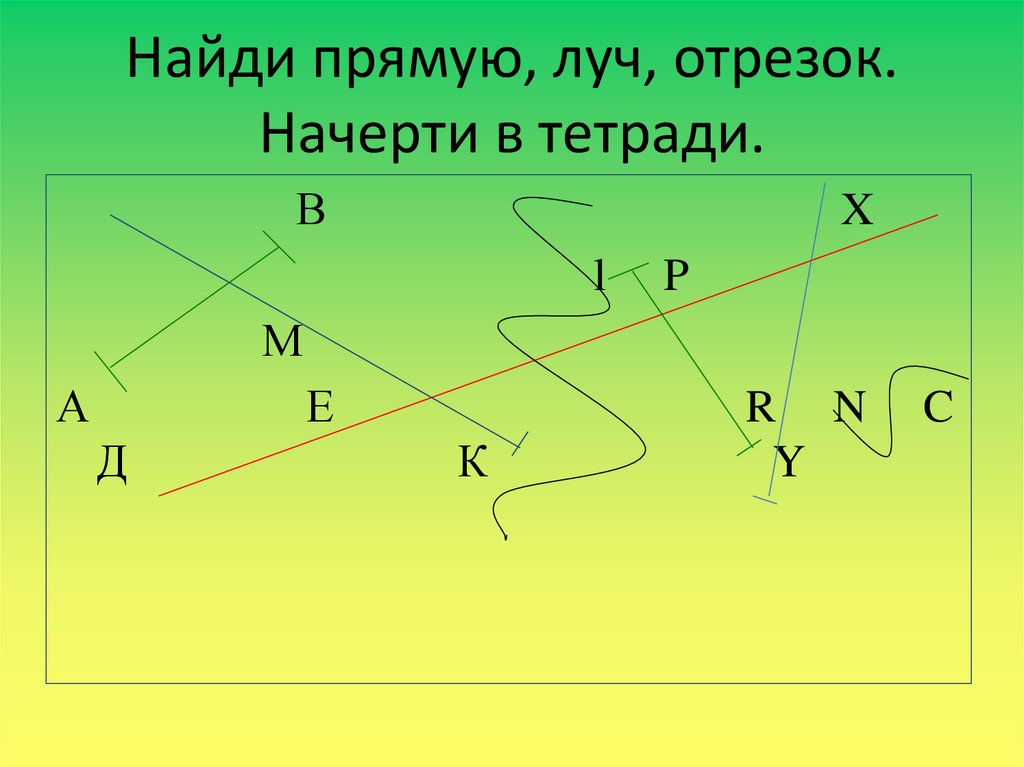
Точка прямая луч отрезок способы обозначения. Прямая линия
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Посещая дополнительные занятия мы поняли, что не умеем оперировать понятиями точка, линия, угол, луч, отрезок, прямая, кривая, замкнутая линии и рисовать их, точнее рисовать можем, но идентифицировать не получается.
Дети должны различать линии, кривые, окружности. Это развивает у них графику и чувство правильности при занятиях рисованием, аппликацией. Важно знать, какие основные геометрические фигуры существую, что из себя представляют. Разложите карточки перед ребенком, попросите нарисовать точно так же как на картинке. Повторите несколько раз.
На занятиях нам выдали следующие материалы:
Небольшая сказка.
В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.)
Посмотрите, какие это были линии. (Прямые и кривые.)
Прямые линии похожи на натянутые веревочки, а веревочки, которые не натянули, — это кривые линии.
Сколько прямых линий? (2.)
Сколько кривых? (3.)
Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
Вот так маленькая точка смогла изменить жизнь больших линий.
Так кто догадался кто вместе с котиком пришел к нам в гости?(прямая линия, луч, отрезок и точка)
Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.
Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)
О каких линиях вы узнали? (О прямой, луче, отрезке.)
Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)
Она бесконечная.)
(Берем две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)
Что узнали о луче? (У него есть начало, но нет конца.) (Педагог берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)
Что узнали об отрезке? (Унего есть и начало, и конец.) (Педагог отрезает другой конец нитки и показывает, что нитка не тянется. У нее есть и начало, и конец.)
Как начертить прямую линию? (Провести по линейке линию.)
Как начертить отрезок? (Поставить две точки и соединить их.)
И конечно прописи:
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Прямая линия — одно из фундаментальных понятий геометрии.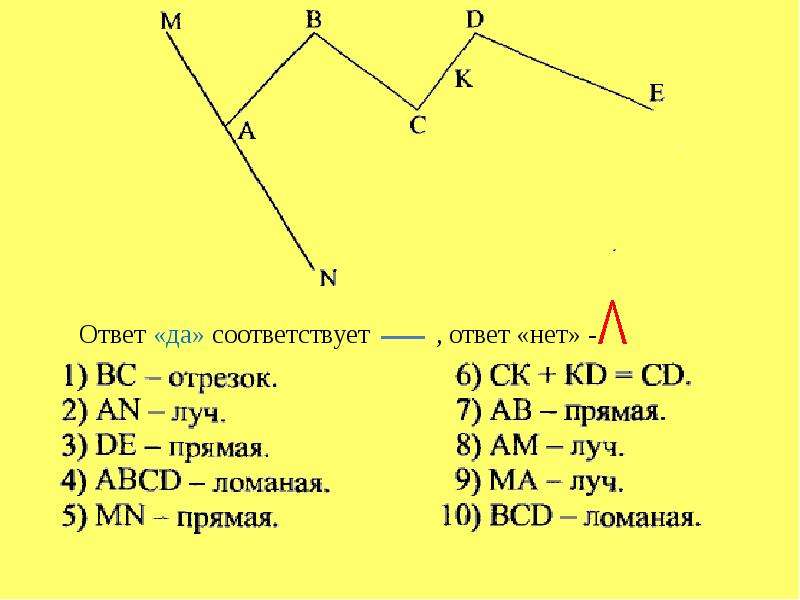
Наглядно прямую линию может продемонстрировать туго натянутый шнур, кромка стола, край листа бумаги, место, соединения двух стен комнаты, луч света. При начертании прямых линий на практике применяют линейку.
Прямой линии присущи такие характерные особенности :
1.У прямой линии нет ни начала ни конца, то есть она бесконечна. Существует возможность начертить только ее часть.
2.Через две произвольные точки можно провести прямую линию , и притом только одну.
3. Через произвольную точку можно провести не ограниченное количество прямых на плоскости .
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны .
Для обозначения прямой линии используют или одну малую букву латинского алфавита, или две большие буквы, написанные в двух различных местах этой прямой.
Если на прямой линии указать точку , то в результате получим два луча :
Лучом называют часть прямой линии , ограниченную с одной стороны.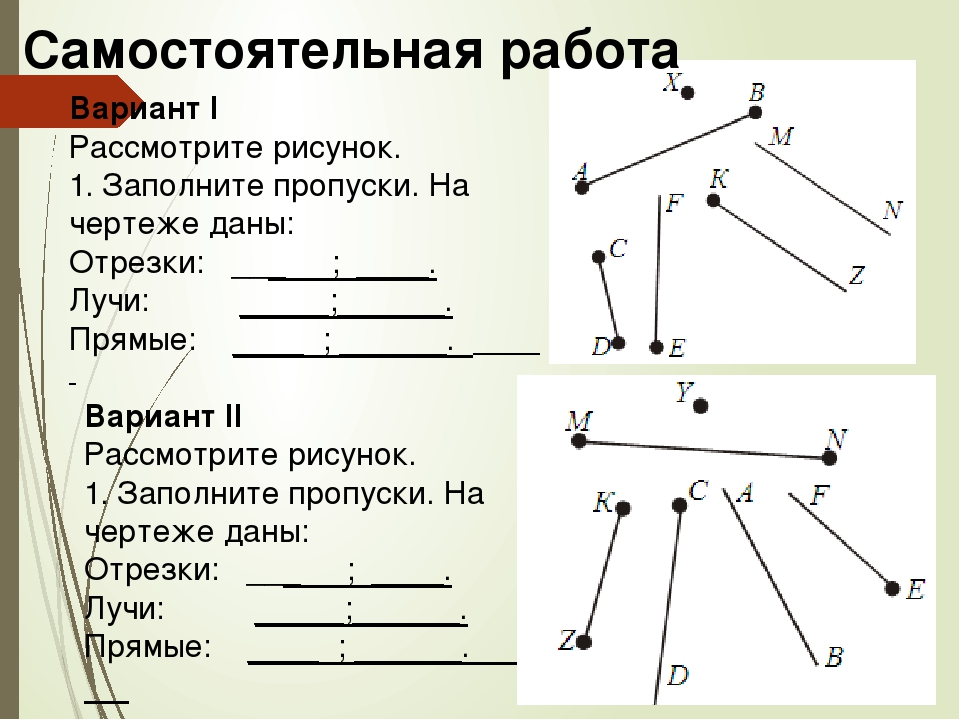
Часть прямой, ограниченная с обеих сторон, именуют ее отрезком . Отрезок, как и прямая линия , обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Линию, сформированную несколькими отрезками, не лежащими на одной прямой, принято называть ломаной . Когда концы ломаной совпадают, то такая ломаная именуется замкнутой .
Рекомендуем также
Как объяснить, что такое луч в геометрии. Точка, линия, прямая, луч, отрезок, ломанная
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике.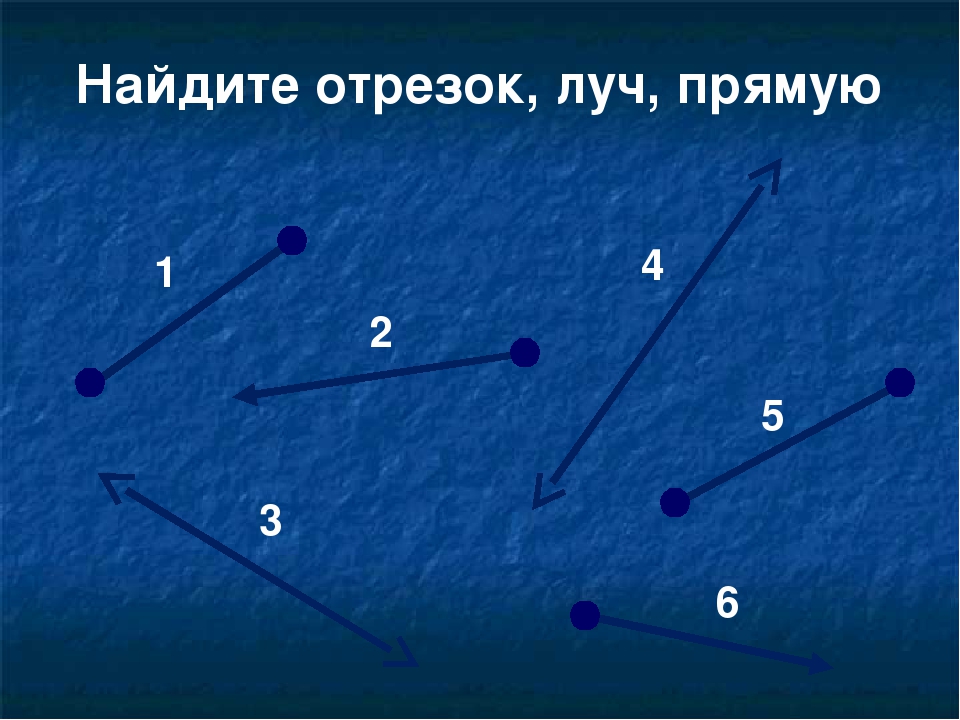
Определение понятий
Для начала давайте вспомним, что называется геометрией. Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. К ним относятся треугольник, квадрат, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два .
Он состоит из точек, расположенных по одну сторону. Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
В основе геометрической фигуры, имеющей углы, лежат полупрямые. Они начинаются в точке, где пересекаются, но второй стороной направлены в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
Нужно знать: Что такое и горизонтальное положение?
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света . Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Конспект урока по математике
в 1 классе.
Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч.
Составила и провела
Бувайлова Елена Ивановна
Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч
Цель: в ходе выполнения практических заданий и наблюдений научить различать разные виды линий.
Планируемые результаты: учащиеся научатся различать и называть прямую линию, кривую, отрезок, луч, ломаную; пользоваться линейкой для черчения; соотносить реальные предметы и их элементы с изученными геометрическими линиями и фигурами; выполнять мыслительные операции анализа и синтеза и делать умозаключения; применять полученные ранее знания в измененных условиях; слушать собеседника и вести диалог; слушать учителя и выполнять его требования; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.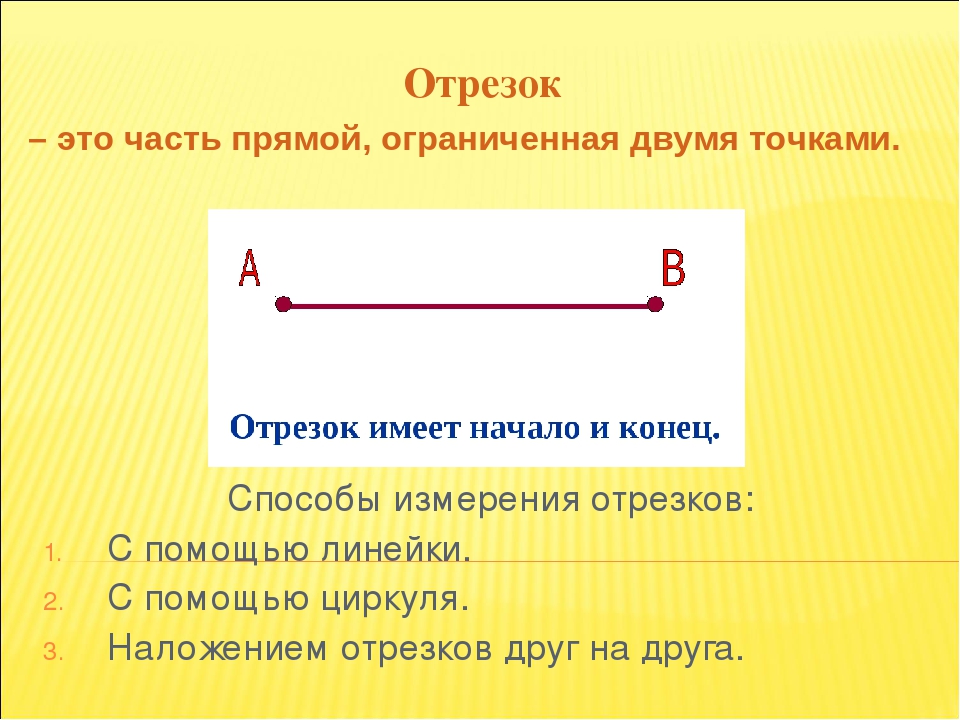
Ход урока
1.Организационный момент
Математика зовёт
Первоклашек на урок,
Числа нас ведут вперёд
Будем знать всё «на зубок»
2.Актуализация знаний
К нам сегодня на урок пришел в гости кот Тишка с незнакомыми друзьями, а какие это друзья вы назовете их чуть позже
а) Прямой и обратный счёт в пределах 10.
Индивидуальный опрос.
б) Задачи в стихах:
Тишка – кот такой глупышка,
Очень рыбу любит Тишка.
На рыбалке побывал,
Два пескарика поймал,
Щуки две и два ерша.
Жизнь у Тишки хороша!
Кто быстрее сосчитал,
Сколько рыбок кот поймал? (6)
На забор взлетел петух,
Повстречал ещё там двух.
Сколько стало петухов? (3)
По тропинке в лесок
Покатился колобок.
Встретил серого зайчишку,
Встретил волка, встретил мишку,
Да плутовку лису
Повстречал он в лесу
Отвечай поскорей
Сколько встретил колобок зверей. (4)
(4)
Игра «Молчанка»
(Учитель показывает пропуск, учащиеся соответствующую цифру на веере цыфр.)
4 — □ = 2 5 — □= 2
4 — □ = 3 5 — 1 = □
1 + 3 = □ □ — 3=1
□ -4=1 1 + □ = 2
3. Физкультминутка
4. Самоопределение к деятельности
В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.) (Математический планшет)
Посмотрите, какие это были линии. (Прямые и кривые.)
Прямые линии похожи на натянутые веревочки, а веревочки,
которые не натянули, — это кривые линии.
Сколько прямых линий? (2.)
Сколько кривых? (3.)
Прямая линия начала хвастаться: « Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
Вот так маленькая точка смогла изменить жизнь больших линий.
Так кто догадался кто вместе с котиком пришел к нам в гости?( прямая линия, луч, отрезок и точка )
Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.
Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)
5. Работа по теме урока
Практическая работа
О каких линиях вы узнали? (О прямой, луче, отрезке. )
)
Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)
(Учитель берет две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)
Что узнали о луче? (У него есть начало, но нет конца.) (Учитель берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)
Что узнали об отрезке? (Унего есть и начало, и конец.) (Учитель отрезает другой конец нитки и показывает, что нитка
не тянется. У нее есть и начало, и конец.)
6.Работа по учебнику
— Посмотрите на рисунок на с. 40 . Расскажите, чем прямая линия отличается от кривой. (Прямая линия натянута, кривая — нет.)
Что вы запомнили о прямой линии, луче, отрезке? (Ответы детей.)
Как начертить прямую линию? (Провести по линейке линию .)
Как начертить отрезок? (Поставить две точки и соединить их. )
)
7.Физкультминутка
В понедельник я купался,
(Движения руками, выполняемые при плавании.)
А во вторник рисовал,
(Изобразить рисование.)
В среду долго умывался,
(Изобразить умывание.)
А в четверг в футбол играл.
(Бег на месте.)
В пятницу я бегал, прыгал,
(Прыжки на месте.)
Очень долго танцевал.
(Покружиться.)
А в субботу, воскресенье
(Хлопки в ладоши.)
Целый день я отдыхал.
(Сесть на корточки, руки под щеку.)
8.Закрепление изученного материала
Работа в тетради с печатной основой
Откройте тетрадь на с. 15. Рассмотрите линии. На какие группы их можно разделить? (Прямые — 2,3, 5 и кривые -1,4.)
Выполните следующее задание.
Сколько прямых можно провести через две точки? (Одну. )
)
Сколько кривых можно провести через две точки? (Много.)
Прочитайте следующее задание.
Раскрасьте рисунки самостоятельно.
9. Пальчиковая гимнастика
Работа в тетради
Тишка хочет научиться изображать прямую, отрезок, луч.
А теперь начертите в тетради прямую, отрезок, луч и кривую линию, по которым побежит кот Тишка.
Обсудить в парах начерченные линии.
10.Работа по учебнику
Прочитайте задание на полях на с. 40. Как узнать, какой отрезок самый длинный? (Посчитать, сколько клеточек составляет длина каждого отрезка.)
Посчитайте и скажите, какой отрезок самый длинный. (Синий.)
Какой отрезок самый короткий? (Красный.)
Рассмотрите рисунок на с. 41. Расскажите соседу по парте, какие линии вы видете.
(Работа в парах.)
Посмотрите на рисунки и записи, приведенные ниже.
Какие записи подходят к рисункам?
Объясните их смысл.
(4 + 1 = 5- к 4 цыплятам прибежал еще один.
Стало 5 цыплят. 5-2 = 3- плавали 5 утят, 2 утенка ушли.
Осталось 3утенка.
Записи 4- 1 = 3и 5- 1 = 4не подходят.)
урок понравился
Было трудно, но интересно
урок не понравился
Подведение итогов урока
Что нового вы узнали о линиях?
Где в жизни встречаются прямые линии? кривые линии?
А, что могут означать для кота: точка, прямая, кривая линия?
(Точка похожа на клубок –он может поиграть, покатать;
Луч – попускать «зайчиков»
Прямая линия на дорогу –где нужно соблюдать правила ПДД;
Кривая линия – на извилистую тропинку, где он может поиграть в догонялки со своими друзьями)
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.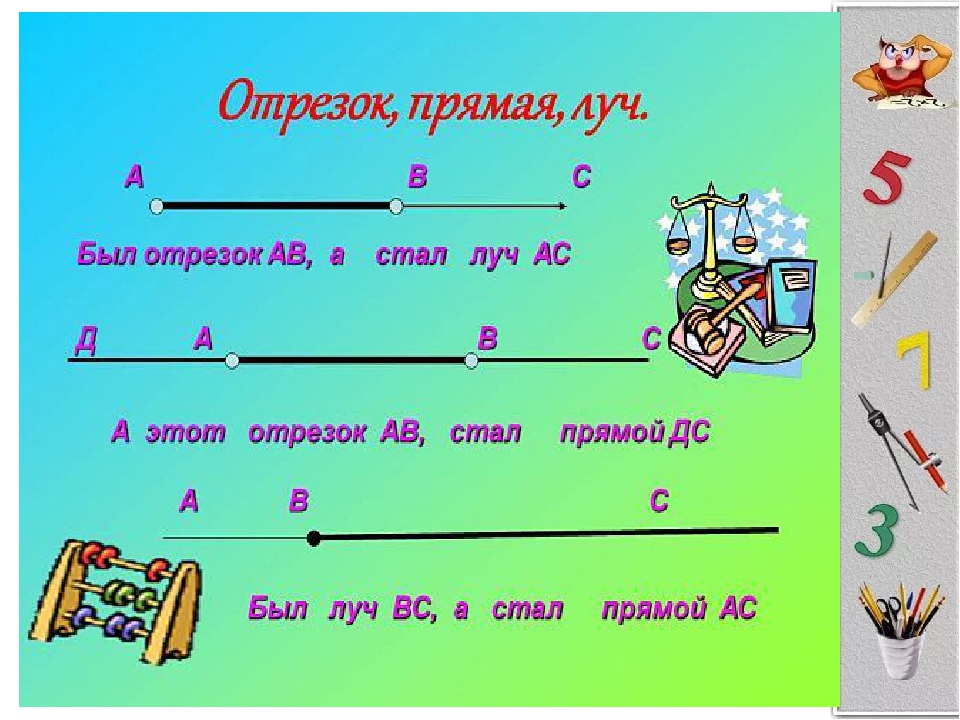 д.
д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.
К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия.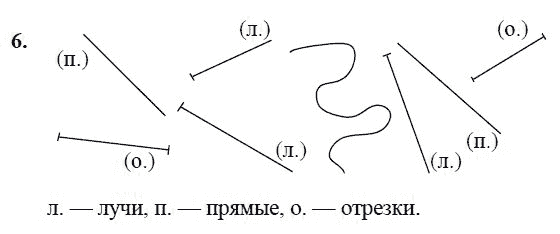 Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.
Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.
Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная. Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.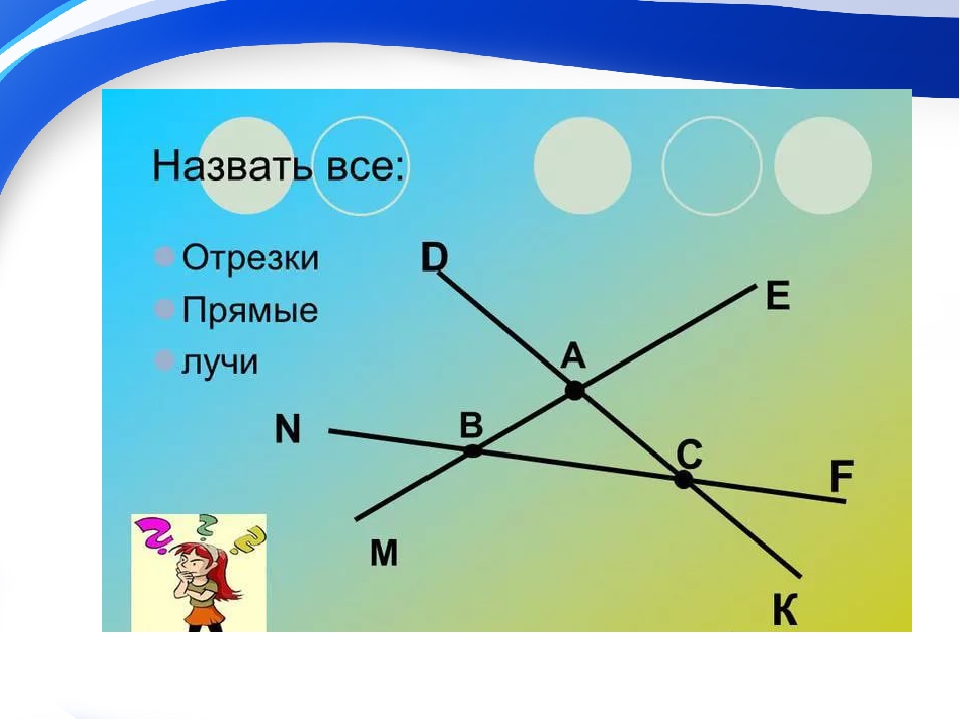
В дальнейшем будут определения для разных фигур кроме двух — точка и прямая. Значит иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая\(AB\), так как никакая другая прямая через эти две точки не может быть проведена. Символически записываем отрезок \(AB\).
Что такое точка в математике?
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.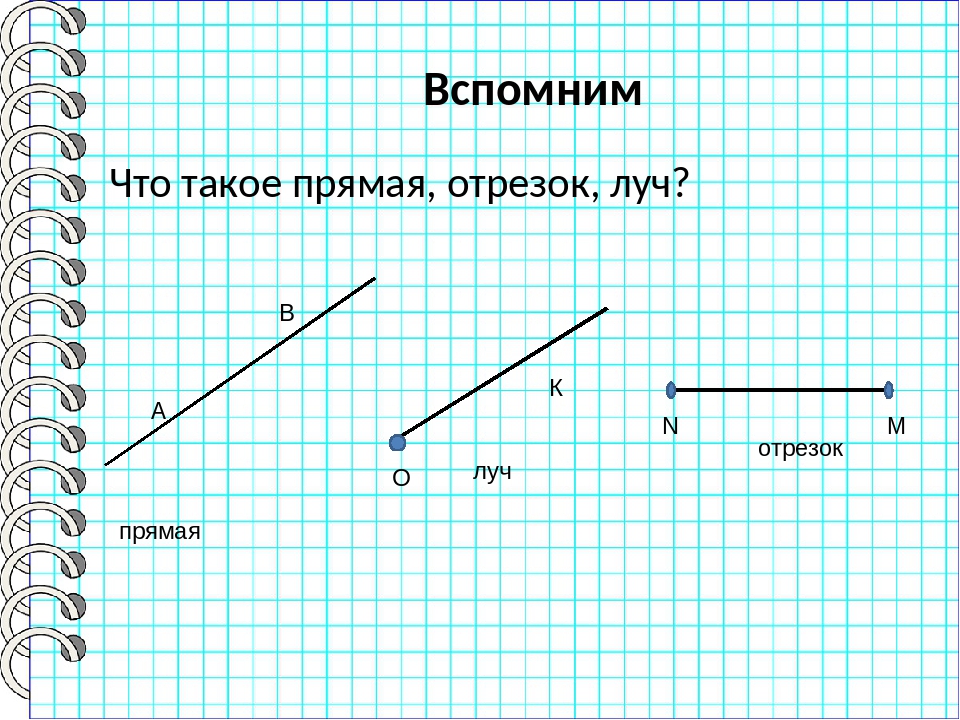
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Прямая линия — одно из фундаментальных понятий геометрии.
Наглядно прямую линию может продемонстрировать туго натянутый шнур, кромка стола, край листа бумаги, место, соединения двух стен комнаты, луч света. При начертании прямых линий на практике применяют линейку.
Прямой линии присущи такие характерные особенности :
1.У прямой линии нет ни начала ни конца, то есть она бесконечна. Существует возможность начертить только ее часть.
2.Через две произвольные точки можно провести прямую линию , и притом только одну.
3. Через произвольную точку можно провести не ограниченное количество прямых на плоскости .
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны .
Для обозначения прямой линии используют или одну малую букву латинского алфавита, или две большие буквы, написанные в двух различных местах этой прямой.
Если на прямой линии указать точку , то в результате получим два луча :
Лучом называют часть прямой линии , ограниченную с одной стороны. Для обозначения луча применяют или одну малую букву латинского алфавита, или две большие буквы, из которых одна обозначается в начале луча.
Часть прямой, ограниченная с обеих сторон, именуют ее отрезком . Отрезок, как и прямая линия , обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Линию, сформированную несколькими отрезками, не лежащими на одной прямой, принято называть ломаной . Когда концы ломаной совпадают, то такая ломаная именуется замкнутой .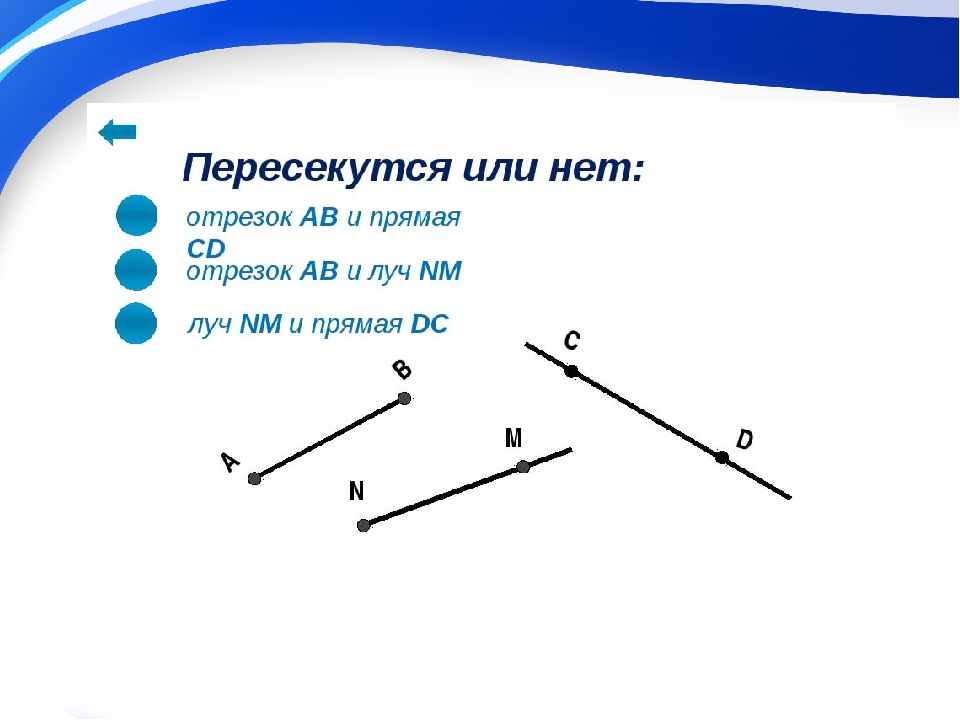
Конспект + презентация к уроку математики во 2 классе по теме: «Луч.Прямая, Отрезок» — Математика — Начальные классы
Тема: Прямая. Луч. 2 класс
Цель: сформировать представление о понятии луч, развивать умения различать прямую и луч, сравнивать прямую и луч, отрезок и луч, точка и луч.
Оборудование: компьютер, проектор.
Ход урока
1.Орг – момент
2.Сообщение темы
— Сегодня мы совершим увлекательное путешествие в страну Геометрию. Узнаем ещё об одной геометрической фигуре. А в течении всего урока нам будет светить тёплое солнышко. И оно вам приготовило пожелания:
«Будьте смелыми, добрыми, активными. В добрый вам путь!»
3.Устный счет
(1слайд) Продолжите числовой ряд
3 9 12 . . . . . .
— Какая закономерность?
(2слайд) Решите примеры.
24 + . =30 40 + . =80
35 — . =30 . +5 = 20
60 — . =40 73 — . = 3
( 3слайд) По каким признакам можно разделить эти фигуры?
1)По форме (на доске запишите соответствующее выражение)
4 + 5 = 9
2)По цвету
3 + 6 = 9
3)По размеру
2 + 7 = 9
4)По настроению
8 + 1 = 9
—
Посмотрите на выражения. Состав какого
числа вспомнили? (9)
Состав какого
числа вспомнили? (9)
— Молодцы! С устным счётом справились. Солнышко светит нам ещё ярче и теплее.
4.Новый материал
— Начертите прямую (в тетради и на доске)
— Что такое прямая? О каком свойстве прямой вы знаете? (она бесконечна)
— К одной стороне беру и прикрепляю жёлтый кружок. Можно теперь эту прямую дополнить в обе стороны? (нет) На что это похоже? (на солнечный луч) Эта фигура так и называется – луч. Луч имеет начало, но не имеет конца. Сравните прямую и луч.
— Затем прикрепляю кружочек с другой стороны. Теперь можно продолжить прямую в обе стороны? Что за фигура получилась?
— Сравните луч и отрезок.
( 4слайд) 3
1 6
2 4 5
— Под каким номером прямая? Отрезок? Луч? (ответы комментируются)
Физминутка
( 5слайд) Что это? ( ) У нас у каждого есть имя, назовём точку А.
Сколько прямых проходит через точку А ? (3) А сколько ещё
можно п ровести? (множество)
Поставьте в тетради точку, назовите её О и проведите несколько прямых (проверяю)
5. Самостоятельная
работа
Самостоятельная
работа
— Каждому раздаю тест:
К расным цветом обведи пересекающиеся лучи, синим непересекающиеся.
1 2
3
( 6слайд) Реши задачу по краткой записи.
М. — 9 лучей ? лучей
С. — ? на 2 больше, чем
(1 ученик решает у доски)
6.Итог
— С какой новой геометрической фигурой мы познакомились?
С каким настроением вы подошли к концу урока?
(Солнышко раздаёт активным детям призы)
Из чего состоит прямая линия. Точка, линия, прямая, луч, отрезок, ломанная
В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.
Навигация по странице.
Прямая на плоскости — понятие.
Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости .
Теперь можно переходить и к понятию прямой линии на плоскости .
Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.
Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.
Взаимное расположение прямой и точки.
Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.
Точки принято обозначать большими латинскими буквами, например, точки А и F . В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a и d .
Возможны два варианта взаимного расположения прямой и точки на плоскости : либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).
Для обозначения принадлежности точки некоторой прямой используют символ «». К примеру, если точка А лежит на прямой а , то можно записать . Если точка А не принадлежит прямой а , то записывают .
Справедливо следующее утверждение: через любые две точки проходит единственная прямая.
Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А
и В
), можно обозначать двумя этими буквами (в нашем случае прямая АВ
или ВА
).
К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А
и В
), можно обозначать двумя этими буквами (в нашем случае прямая АВ
или ВА
).
Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком . Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А
и В
являются концами отрезка, тогда этот отрезок можно обозначить АВ
или ВА
. Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».
Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».
Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ принадлежит прямой а , можно кратко записать .
Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А , В и С лежат на одной прямой, причем точка В лежит между точками А и С . Тогда можно говорить, что точки А и С находятся по разные стороны от точки В . Также можно сказать, что точки В и С лежат по одну сторону то точки А , а точки А и В лежат по одну сторону от точки С .
Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – два луча . Для этого случая дается аксиома: произвольная точка О
, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О
, а две любые точки разных лучей – по разные стороны от точки О
.
Для этого случая дается аксиома: произвольная точка О
, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О
, а две любые точки разных лучей – по разные стороны от точки О
.
Взаимное расположение прямых на плоскости.
Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?
Во-первых, две прямые на плоскости могут совпадать .
Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.
Во-вторых, две прямые на плоскости могут пересекаться .
В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «», к примеру, запись означает, что прямые а
и b
пересекаются в точке М
. Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми . Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a
перпендикулярна прямой b
, то можно использовать краткую запись .
Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми . Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a
перпендикулярна прямой b
, то можно использовать краткую запись .
В-третьих, две прямые на плоскости могут быть параллельными.
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой . В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.
Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой . О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости .
О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости .
Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:
- если две прямые параллельны третьей прямой, то они параллельны между собой;
- если две прямые перпендикулярны третьей прямой, то они параллельны между собой;
- если на плоскости некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую.
Способы задания прямой на плоскости.
Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.
Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.
Во-первых, прямую можно задать, указав две точки на плоскости.
Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.
Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки .
Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.
Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение.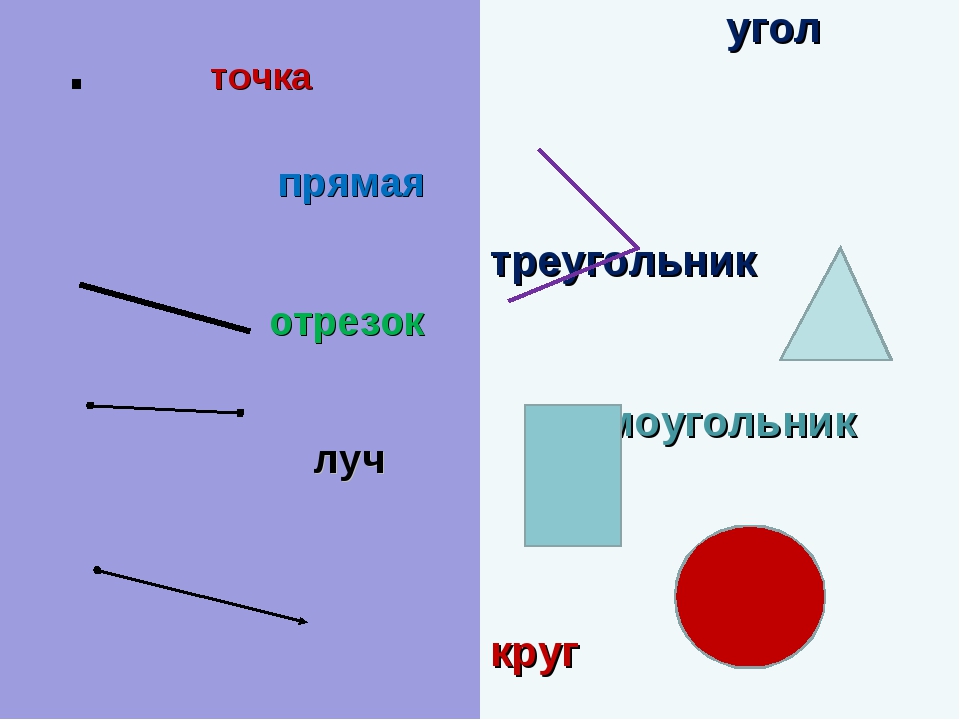 Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой .
Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой .
В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.
Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости .
Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.
Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.
Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой .
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т. д.
д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца.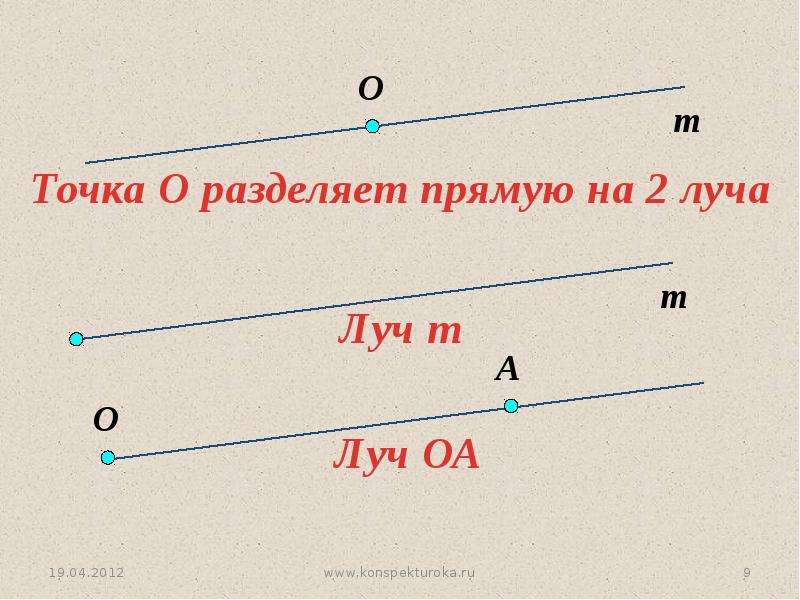 В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др. , а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
, а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.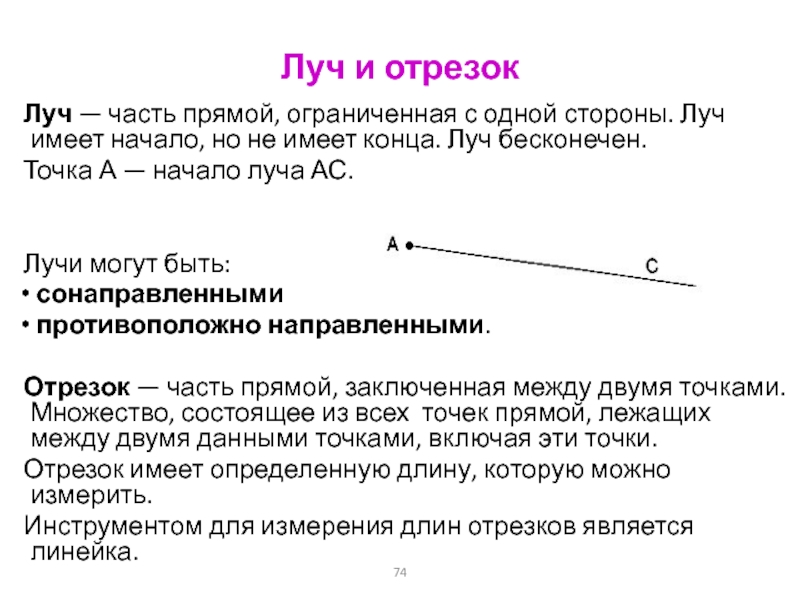
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие?
A
A
A
Но как понять через какие?
A
A
A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точкамиЧерез одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого.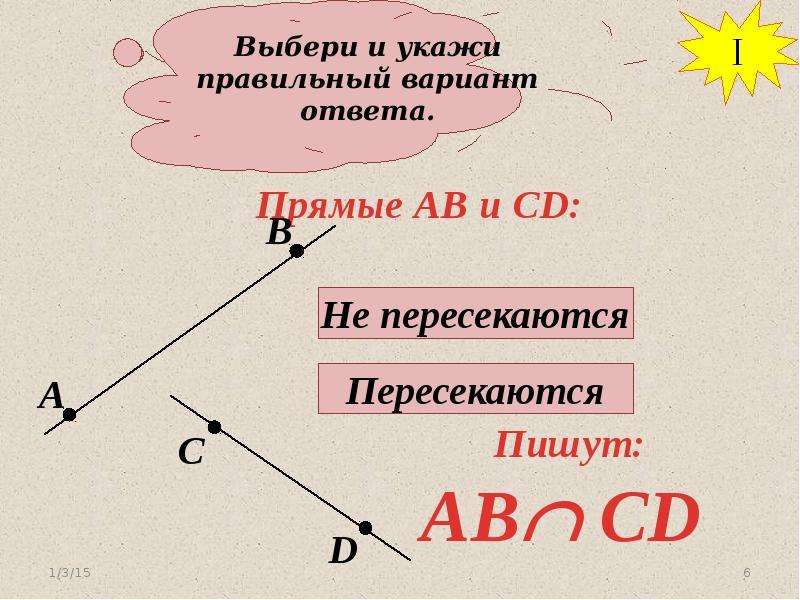 Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.
К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия. Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.
Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная. Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.
В дальнейшем будут определения для разных фигур кроме двух — точка и прямая. Значит иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая\(AB\), так как никакая другая прямая через эти две точки не может быть проведена. Символически записываем отрезок \(AB\).
Что такое точка в математике?
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Разница между линией и сегментом линии
Везде, где есть формы, мы можем видеть линии. Каждая фигура, заданная на двумерной плоскости, состоит из линий. Линия – это базовое понятие геометрии , бесконечно простирающееся в обоих направлениях. Линии прямые без изгибов. У них нет ни толщины, ни ширины, поэтому они одномерны. Для нас важно идентифицировать линии в геометрических фигурах, с которыми мы сталкиваемся, и различать линии, отрезки линий и лучи.
Для нас важно идентифицировать линии в геометрических фигурах, с которыми мы сталкиваемся, и различать линии, отрезки линий и лучи.
Определение линии и сегмента линии
Линия — это набор бесконечных точек, бесконечно простирающихся с обеих сторон на плоскости. Линии могут быть горизонтальными, вертикальными, диагональными, наклонными или кривыми. Две линии могут быть параллельными или перпендикулярными. Линии могут быть толстыми или тонкими. Изогнутые линии также меняют направление.
Отрезок представляет собой совокупность конечных точек определенной длины. У него есть начальная точка и конечная точка.Это кратчайшее расстояние между двумя точками, которое можно измерить. Мы можем измерить его длину с помощью линейки или дюймовой шкалы. Отрезок линии является частью линии. Ниже показан отрезок АВ.
Любая двумерная фигура состоит из отрезков. Вот несколько полигонов. Мы можем заметить, что треугольник состоит из 3 отрезков, пятиугольник – из 5 отрезков, а четырехугольник – из 4 отрезков. Многоугольники называются по количеству сторон, из которых они состоят.Стороны состоят из отрезков.
Многоугольники называются по количеству сторон, из которых они состоят.Стороны состоят из отрезков.
Различия между линией и линейным сегментом
Давайте четко сравним различия между прямой и отрезком прямой. Их знание поможет нам различать их и, таким образом, поможет нам идентифицировать их в плоских формах.
| Линия | Линейный сегмент |
|---|---|
| Это набор точек, который бесконечно простирается в обоих направлениях. | Это кратчайшее расстояние между двумя точками. |
| Линии не имеют начальной или конечной точки. | Линейные сегменты имеют начальную и конечную точки. |
| Линии длинные, непрерывные и безграничные. | Сегменты короткие и являются частью линии. |
Линия AB обозначается как \(\overleftrightarrow{\rm AB}\).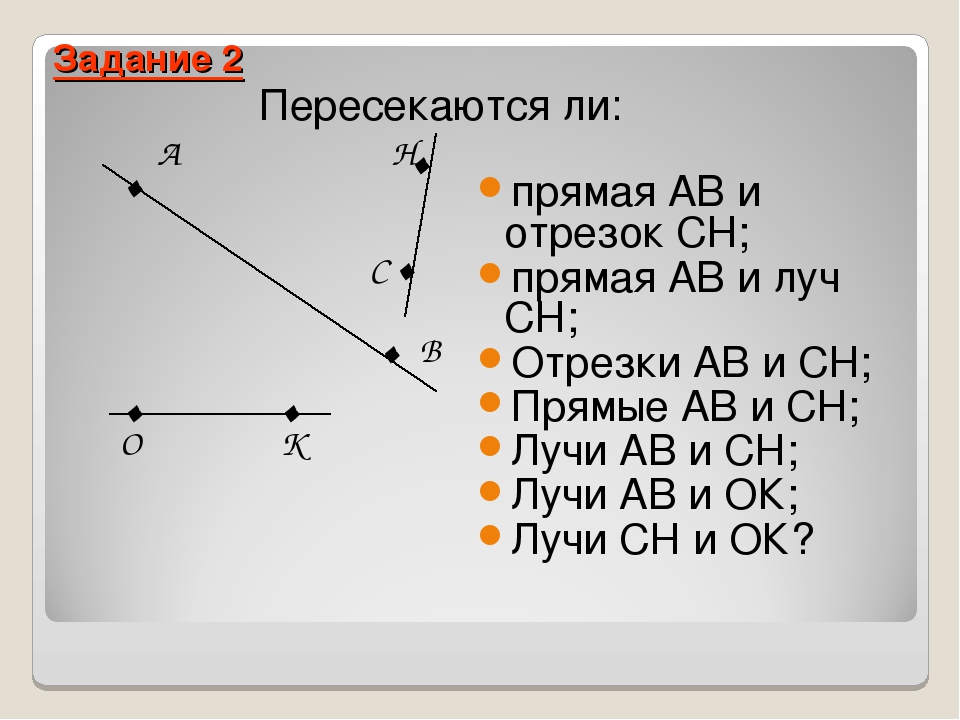 | Отрезок линии AB обозначается \(\overline{\rm AB}\) |
| Линия не может быть измерена или начерчена, так как она бесконечно тянется в обоих направлениях и имеет неограниченную длину. | Отрезок линии можно визуально нарисовать и измерить, поскольку он имеет определенную длину. |
Похожие темы
Важные примечания
- Линия — это одномерная фигура, бесконечно простирающаяся в обоих направлениях.
- Отрезок линии — это часть линии, представляющая собой кратчайшее расстояние между двумя точками, которое можно измерить.
Решенные примеры различий между линией и линейным сегментом
Пример 1. Определите сегменты линии и назовите их.
Решение: Мы знаем, что отрезок прямой имеет две конечные точки. Поскольку это кратчайшее расстояние между этими конечными точками, отрезки легко именовать по их конечным точкам. Таким образом,
Таким образом,
а) АВ и CD
б) PQ, PR, RQ и RS
. в) DE и EFПример 2: Классифицируйте каждое из следующего на линии и линейные сегменты.
Решение: Поскольку мы знаем, что линия тянется бесконечно, а отрезок имеет концы, мы можем легко их классифицировать.Таким образом,
Линия: АВ
Сегменты линии: ST, XY и XY, YZ, XZ (стороны треугольника XYZ)
Показать ответ >
перейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу с Cuemath.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о разнице между линией и линейным сегментом
Что такое луч, линия и отрезок линии?
Луч имеет начальную точку и бесконечно тянется.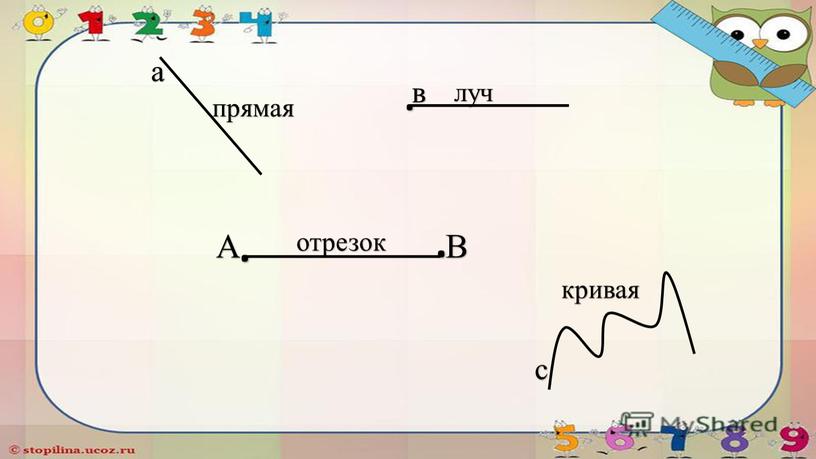 У линии нет конечных точек, и она бесконечно тянется в обоих направлениях. Отрезок линии — это кратчайшее расстояние между двумя точками.
У линии нет конечных точек, и она бесконечно тянется в обоих направлениях. Отрезок линии — это кратчайшее расстояние между двумя точками.
Каковы три реальных примера линейных сегментов?
Края книги или стола, карандаш, перила, жалюзи, стрелки часов и так далее.
Как измеряется отрезок линии?
Отрезок линии измеряется с помощью линейки в обычных единицах измерения, таких как сантиметры, метры, дюймы, футы или ярды.
Сколько сегментов линии составляют квадрат?
Четыре отрезка составляют квадрат.Место встречи отрезков прямой называется вершиной или углом. Таким образом, квадрат имеет 4 стороны и 4 угла, составленные из 4 отрезков.
Чем линия отличается от сегмента линии?
Линия не имеет конечных точек. Он бесконечно тянется в обоих направлениях, тогда как отрезок имеет начальную и конечную точки.
Что такое линейный сегмент? (Определение, формула расстояния, пример)
Что такое линии, сегменты линий и лучи?
Линии, отрезки и лучи встречаются в геометрии повсюду. Используя эти простые инструменты, вы можете создавать параллельные линии, перпендикулярные биссектрисы, многоугольники и многое другое. На этом уроке вы узнаете определения линий, сегментов линий и лучей, как их называть, а также несколько способов измерения сегментов линий.
Используя эти простые инструменты, вы можете создавать параллельные линии, перпендикулярные биссектрисы, многоугольники и многое другое. На этом уроке вы узнаете определения линий, сегментов линий и лучей, как их называть, а также несколько способов измерения сегментов линий.
Содержание
- Что такое линии, сегменты линий и лучи?
- Линейный сегмент
- Что такое линия?
- Лучи
- Измерение сегментов линии
- Как найти длину диагонального сегмента на координатной плоскости
- Формула расстояния
- Примеры сегментов линии в реальной жизни
Линейный сегмент
Сегмент линии — это часть или часть линии, которая позволяет строить многоугольники, определять наклоны и выполнять вычисления.Его длина конечна и определяется двумя его концами.
Сегмент линии является фрагментом линии. Независимо от длины отрезка, он конечен.
Символ сегмента линии
Вы называете отрезок по двум его конечным точкам. Сокращением для отрезка прямой является запись отрезков прямой с двумя конечными точками и рисование тире над ними, например, CX¯:
Сокращением для отрезка прямой является запись отрезков прямой с двумя конечными точками и рисование тире над ними, например, CX¯:
Вы изображаете отрезок линии на бумаге для рисования, используя линейку, чтобы провести линию и поставить две точки на ее концах, обозначенные заглавными буквами; это конечные точки сегмента линии:
Что такое линия?
Определение линии — это набор точек между двумя точками и за ними.Линия имеет бесконечную длину. Все точки на прямой коллинеарны.
Символ прямой линии
В геометрии символ прямой линии представляет собой отрезок с двумя стрелками на концах, например CX↔. Вы идентифицируете его с помощью двух именованных точек, обозначенных заглавными буквами. Выберите точку на линии и присвойте ей букву, затем выберите вторую; теперь у вас есть имя вашей линии:
Лучи
Луч — это часть линии, которая имеет одну конечную точку и бесконечно продолжается только в одном направлении. Вы не можете измерить длину луча.
Вы не можете измерить длину луча.
Луч именуется сначала по его конечной точке, а затем по любой другой точке луча. В этом примере у нас есть точка B и точка A (BA→).
Сегменты измерительной линии
Отрезок линии именуется по его конечным точкам, но другие точки вдоль его длины также могут быть названы. Каждая часть линейного сегмента может быть помечена по длине, поэтому вы можете сложить их, чтобы определить общую длину линейного сегмента.
Пример сегмента линии
Здесь у нас есть отрезок CX¯, но мы добавили по пути две точки, точку G и точку R:
Чтобы определить общую длину сегмента линии, вы добавляете каждый сегмент сегмента линии.Формула для отрезка линии CX будет следующей: CG + GR + RX = CX
.Линейный сегмент на 7 единиц CG
5 сегментов линии GR
3 линейных сегмента RX
7 + 5 + 3 = 15 единиц длины для CX¯
Координатная плоскость
Координатная плоскость , также называемая декартовой плоскостью (спасибо, Рене Декарт!), представляет собой сетку, построенную из осей x и y. Вы можете думать об этом как о двух перпендикулярных числовых линиях или как о карте территории, занятой отрезками прямых.
Вы можете думать об этом как о двух перпендикулярных числовых линиях или как о карте территории, занятой отрезками прямых.
Чтобы определить длину сегментов горизонтальной или вертикальной линии на плоскости, подсчитайте отдельные единицы от конечной точки до конечной точки:
Чтобы определить длину отрезка LM¯, мы начинаем с точки L и отсчитываем пять единиц вправо от нас, заканчивая точкой M. Вы также можете вычесть значения x: 8 — 3 = 5. Для вертикальных линий вы бы вычесть y-значения.
Работая в Квадрантах II, III и IV или между ними, помните, что вычитание отрицательного числа на самом деле означает добавление положительного числа.
Как найти длину отрезка диагональной линии на координатной плоскости
Используйте теорему Пифагора для вычисления длин диагоналей на координатных плоскостях. Напомним, что теорема Пифагора гласит: a2 + b2 = c2 для любого прямоугольного треугольника. Диагональ на координатной сетке образует гипотенузу прямоугольного треугольника, поэтому можно быстро подсчитать единицы двух сторон:
Подсчитайте единицы прямо вниз от точки J до значения x 2 (которое совпадает с точкой L):
8 — 2 = 6, поэтому отрезок JK¯ = 6
Подсчет единиц прямо от точки K до точки L:
6 — (-3) = 9, поэтому отрезок линии KL¯ = 9
Теперь у нас есть 62 + 92 = c2:
36 + 81 = c2
117 = c2
10. 816 = с
816 = с
Длина отрезка JL¯ составляет примерно 10,816 единиц.
Формула расстояния
Частным случаем теоремы Пифагора является формула расстояния , используемая исключительно в координатной геометрии. Вы можете подставить две конечные точки x- и y-значения диагональной линии и определить ее длину. Формула выглядит так:
D = (x2 — x1)2 + (y2 — y1)2
Чтобы использовать формулу расстояния, возьмите квадраты изменения значения x и изменения значения y и сложите их, затем извлеките из этой суммы квадратный корень.
Выражение (x2 — x1) читается как изменение x , а (y2 — y1) изменение y .
Представьте, что у нас есть диагональная линия, протянувшаяся от точки P(6, 9) до точки I(-2, 3), и вы хотите измерить расстояние между двумя точками.
Формула расстояния упрощает расчет:
Д = (-2 — 6)2 + (3 — 9)2
Д = (-8)2 + (-6)2
Д = 64 + 36
Д = 100
Д = 10
Используя формулу расстояния, мы находим, что отрезок прямой PI¯ = 10 единиц.
Примеры сегментов линии в реальной жизни
Реальными примерами отрезков являются карандаш, бейсбольная бита, шнур зарядного устройства для мобильного телефона, край стола и т. д. Подумайте о реальном четырехугольнике, например, о шахматной доске; он состоит из четырех отрезков линии. В отличие от отрезков прямых, примеры отрезков прямых в реальной жизни бесконечны.
Следующий урок:
Прямые линии
Разница между линией и сегментом линии
Что такое сегмент линии и линия?
В геометрии часто встречаются такие термины, как точка, линия, луч, отрезок, угол и т. д.Линия — это наиболее часто используемый термин, который вы найдете в своем учебнике по геометрии. Сегодня мы рассмотрим, что такое отрезок. Мы также рассмотрим разницу между линией и отрезком линии. Проще говоря, линия — это расстояние, соединяющее любые две заданные точки. Линия всегда прямая и простирается бесконечно в обоих направлениях. Напротив, отрезок линии имеет отмеченные границы, т. Е. Он имеет фиксированную начальную точку и фиксированную конечную точку.
Е. Он имеет фиксированную начальную точку и фиксированную конечную точку.
Определение линии
Линия — это кратчайшее расстояние между любыми двумя заданными точками на плоскости.Линия всегда прямая. Изогнутые, наклонные или неровные фигуры, которые не проходят прямолинейно, не являются линией. Лучший способ определить линию — это сказать, что залог — это соединение между двумя точками.
Что такое линейный сегмент?
Отрезок представляет собой часть прямой с определенными конечными точками с обеих сторон (начальной и конечной точками). Линии проходят на бесконечное расстояние в обоих направлениях, тогда как отрезок линии является частью линии. Отрезок линии — это расстояние, которое соединяет две точки на прямой.Это та часть линии, которая соединяет два конца одного и того же пути. Отрезок линии имеет конечные точки.
Существуют существенные различия между линией и отрезком линии. Важно понимать особенности, которые отличают линию от сегмента линии. Давайте изучим некоторые существенные различия между этими двумя терминами.
Давайте изучим некоторые существенные различия между этими двумя терминами.
Разница между линейной и линейной сегментом
| 4 | | 4 сегмент линии | 4 a Line не имеет определенных конечных точек. | Отрезок прямой имеет определенные конечные точки. Линия может проходить в обоих направлениях. Отрезок линии может продолжаться, но не в любом направлении.
Длина линии неограничена. Длина отрезка определена. Линия не имеет ни начала, ни конца. Линейный сегмент имеет начальную и конечную точки. Линия непрерывна, бесконечна и пряма. Отрезок — это небольшая часть линии. Длина линии не может быть измерена. Длину отрезка можно измерить. |
Различные типы линий
Вы знаете, что линия бесконечна, у нее нет концов и она всегда прямая. Однако важно понимать, что линия тоже имеет разные формы.Дайте нам знать о различных типах линий в геометрии. Четыре типа линий, о которых вы часто слышали:
Горизонтальная линия – проходит прямо слева направо.
Вертикальные линии – проходят прямо сверху вниз
Перпендикулярные линии – когда две прямые линии пересекаются под прямым углом, говорят, что две линии перпендикулярны друг другу.
Параллельные линии – когда две линии никогда не пересекаются и не встречаются, независимо от того, сколько удлинителей они могут получить, эти две линии параллельны друг другу.

Об сегментах линии
Когда вы пишете seg PQ, это означает, что часть более значимой линии соединяет точки P и Q на линии. P и Q — конечные точки отрезка. Само слово «сегмент» обозначает часть чего-либо. Здесь, в геометрии, это часть или малая часть большей линии. Линия простирается до бесконечности в обоих направлениях и не может быть измерена, но можно оценить отрезок.
Об именовании сегментов линии
Сегменты линии получают имена двумя распространенными способами:
Именование сегмента линии по конечным точкам
В этом методе сегмент линии является PQ, поскольку он связывает две точки , Р и Q.Важно помнить, что точки обычно обозначаются заглавными буквами. Итак, вы должны написать отрезок прямой как отрезок прямой PQ. Над двумя буквами есть полоса или маленькая черточка, которая указывает на то, что две буквы PQ представляют собой отрезок линии.
Присвоение имени сегменту одной буквой
В этом типе именования сегмент обозначается одной маленькой буквой, например p, q или x. в этом шрифте маленькие буквы используются для обозначения сторон треугольников и многоугольников.
Забавные факты
Отрезок — это композиция из двух слов: линии и сегмента. Линия берет свое начало в латинском, староанглийском и старофранцузском языках и означает веревку или ряд. Слово «сегмент» происходит от латинского segmentum — полоса или отрезанный кусок.
Линейный сегмент
Часть прямой линии называется отрезком.
Фактически, значение отрезка прямой происходит от двух слов «Линия» и «Отрезок».
- Линия означает прямой путь.
- Сегмент означает часть.
Отрезок линии графически представлен линией с двумя конечными точками. Она также известна как линия между двумя точками.
Представительство
- Графически отрезок изображается линией с двумя концами.
- Отрезок записывается в математике на основе графического представления. Итак, пишите названия точек одну за другой и выводите линию над обеими точками.
Формирование
Отрезок линии формируется геометрически двумя различными способами.
Часть прямой линии
Отрезок прямой представляет собой выделенную часть прямой линии.
$\overleftrightarrow{EF}$ — это прямая линия на плоскости, обозначающая любые две точки ($P$ и $Q$) на прямой. Затем отделите маленькую линию в точках $P$ и $Q$ от прямой.
Небольшая линия, заканчивающаяся точками $P$ и $Q$, является частью прямой линии $\overleftrightarrow{EF}$. Поэтому геометрически он называется отрезком.
На основе графического представления отрезка прямой отрезок в этом примере записывается как $\overline{PQ}$, а его длина записывается как $PQ$ в математике.
Линия между точками
Линия, соединяющая любые две точки на плоскости, считается отрезком. Есть две основные причины для такого рассмотрения.
Есть две основные причины для такого рассмотрения.
- Маленькая линия содержит две конечные точки.
- Расстояние между двумя конечными точками можно измерить, оно равно длине маленькой линии.
$M$ и $N$ — две точки на плоскости, соединяющие их линией. Расстояние между двумя точками равно длине линии. Более того, он кажется отрезком. Следовательно, прямую, соединяющую любые две точки плоскости, можно рассматривать как отрезок прямой.
Отрезок в математике записывается как $\overline{MN}$, а его длина обозначается как $MN$.
Что такое отрезок в геометрии? — Определение, формула и пример — видео и стенограмма урока
Формула для нахождения длины отрезка
Если вы хотите найти длину отрезка, вам нужно составить уравнение на основе информации, предоставленной вам в задаче.Можно использовать измерения для двух отрезков прямой, чтобы найти длину третьего отрезка прямой. Какова длина отрезка АС?
Какова длина отрезка АС?
Уравнение будет таким:
отрезок AB + отрезок BC = отрезок AC
5 + 3 = 8
Длина отрезка AC равна 8.
Отрезок на декартовой плоскости сегменты также видны на графиках
или декартовой плоскости .Длину отрезка можно найти, посчитав единицы, которые охватывает отрезок. Подсчет единиц на графике подобен подсчету количества блоков, пройденных между вашим домом и домом вашего друга.Подсчитайте количество единиц между двумя конечными точками. На этом конкретном графике отрезок имеет длину 5 единиц.
Формула для теоремы Пифагора
Вы можете найти длину диагональной линии, используя теорему Пифагора .
При нахождении длины отрезка в прямоугольном треугольнике можно воспользоваться теоремой Пифагора: А в квадрате плюс В в квадрате равно С в квадрате.
В этом примере при поиске длины отрезка ST можно использовать длину отрезков TU и SU.
Используя теорему Пифагора, мы можем видеть, что 5 в квадрате плюс 7 в квадрате равно 74. 5 в квадрате равно 25, а 7 в квадрате равно 49. 25 плюс 49 равно 74.Квадратный корень из 74 равен примерно 8,6. Таким образом, отрезок ST имеет длину примерно 8,6 единиц.
Формула расстояния
Вы также можете использовать формулу расстояния , чтобы найти длину сегмента прямой. Формулу расстояния можно использовать для нахождения длины отрезка ST. Найдите длину горизонтальной и вертикальной сторон, вычитая значения x и y. Затем выполните шаги по использованию теоремы Пифагора, чтобы найти длину неизвестной стороны.
Не забудьте использовать точки на каждом конце отрезка, чтобы найти длину горизонтальной и вертикальной сторон.
Резюме урока
Таким образом, отрезок является частью линии с двумя отдельными конечными точками.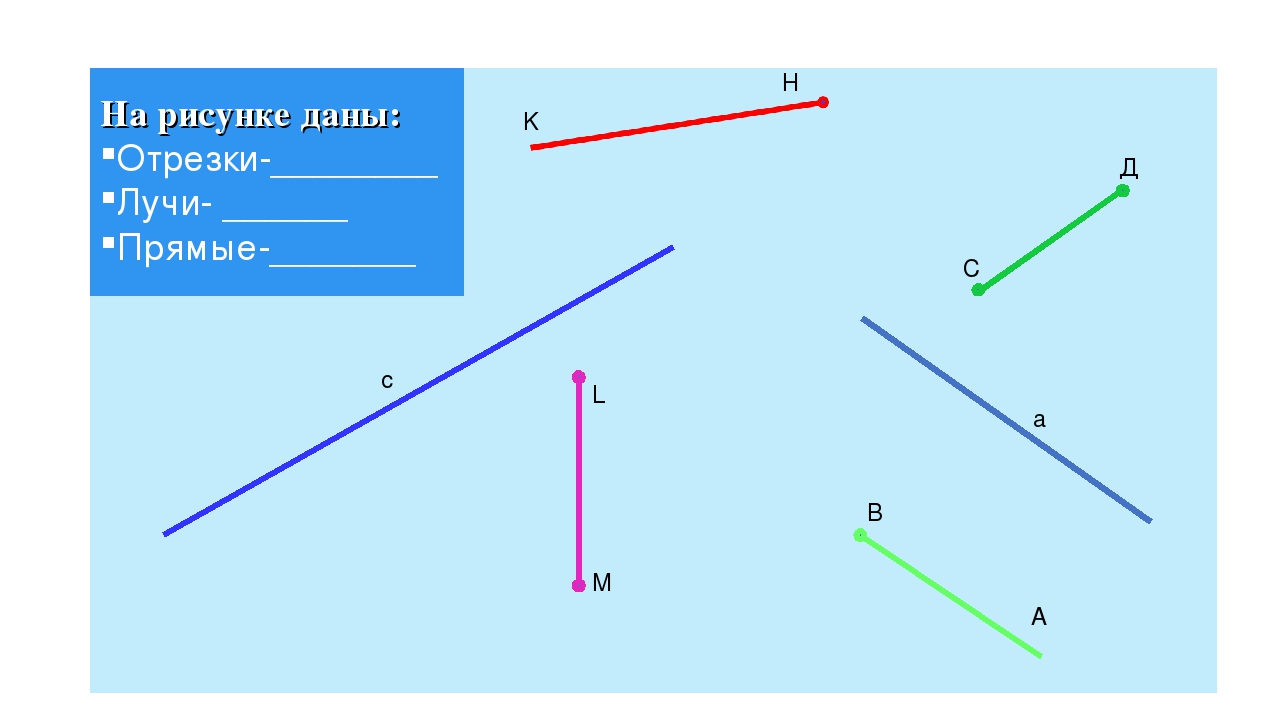 Длину отрезка можно найти, решив уравнение, если известна длина двух отрезков. Длину отрезков на декартовой плоскости можно найти, подсчитав единицы, которые покрывает отрезок.При работе с прямоугольным треугольником можно использовать теорему Пифагора и формулу расстояния для нахождения длины отрезка. Отрезок линии отличается от линии тем, что он не продолжается вечно.
Длину отрезка можно найти, решив уравнение, если известна длина двух отрезков. Длину отрезков на декартовой плоскости можно найти, подсчитав единицы, которые покрывает отрезок.При работе с прямоугольным треугольником можно использовать теорему Пифагора и формулу расстояния для нахождения длины отрезка. Отрезок линии отличается от линии тем, что он не продолжается вечно.
Ключевые термины
сегмент линии: часть линии с двумя различными концами что квадрат гипотенузы равен сумме квадратов двух других сторон.
формула расстояния: получено из теоремы Пифагора, уравнения, которое помогает найти расстояние между двумя точками.
Результаты обучения
После просмотра этого урока вы сможете сделать следующее:
- Определить отрезок
- Определить расстояние между двумя точками
Урок Видео: Прямые линии, сегменты линий и лучи
Стенограмма видео
В этом видео мы научимся
идентифицировать точки, линии, лучи, сегменты линий и конечные точки и связанные с ними
обозначения, которые мы используем для их описания. Самостоятельно этот навык может
кажутся несколько неважными. Но как только мы можем начать описывать
они используют математический язык и обозначения, это открывает нам целый мир в
геометрии, от простого описания многоугольников до тригонометрии и геометрических
доказательство. Начнем с рассмотрения некоторых
эти определения.
Самостоятельно этот навык может
кажутся несколько неважными. Но как только мы можем начать описывать
они используют математический язык и обозначения, это открывает нам целый мир в
геометрии, от простого описания многоугольников до тригонометрии и геометрических
доказательство. Начнем с рассмотрения некоторых
эти определения.
Определения, которые мы рассмотрим вообще вытекают из этого первого определения.Это определение точки. Точка — это просто положение или место расположения. Он не имеет размера, такого как ширина или длина или глубина, и мы представляем это с помощью точки. Здесь мы нарисовали точку представляющая точку 𝐴. И как только мы получим определение точку, давайте сформируем определение линии.
Линия представляет собой прямой набор точек
которые бесконечно простираются в двух направлениях. Он имеет только одно измерение и
это его длина.Представляем его как показано. Эти две стрелки показывают, что
простирается бесконечно в этих направлениях. Если мы представим эту линию как
проходя через точки 𝐴 и 𝐵, мы видим, что определяем линию, как показано, с
наконечник стрелы. Мы говорим, что точки 𝐴 и 𝐵 равны
колинеарный; они на одной линии.
Он имеет только одно измерение и
это его длина.Представляем его как показано. Эти две стрелки показывают, что
простирается бесконечно в этих направлениях. Если мы представим эту линию как
проходя через точки 𝐴 и 𝐵, мы видим, что определяем линию, как показано, с
наконечник стрелы. Мы говорим, что точки 𝐴 и 𝐵 равны
колинеарный; они на одной линии.
Итак, что мы подразумеваем под лучом? Луч — это часть линии. Он начинается в заданной точке, и мы
назовем это конечной точкой, а затем она пойдет в определенном направлении к
бесконечность.Луч, конечная точка которого равна 𝐴, а затем
проходит через 𝐵, представлен как показано с одной стрелкой, определяющей его
направление. Конечная точка, которую мы могли бы также
в качестве альтернативы рассмотрим начальную точку нашего луча 𝐴. Однако раньше мы говорили, что
endpoint — точка, в которой заканчивается луч.
Есть еще одно определение, которое мы нужно, и это определение сегмента линии. Отрезок является частью прямой это ограничено двумя различными конечными точками.И он содержит каждую точку на линию между этими точками. Это всегда кратчайшее расстояние между этими точками. В этом отрезке 𝐴 и 𝐵 равны конечные точки. И так мы определяем отрезок прямой 𝐴𝐵 с помощью полосы, как показано на рисунке. Теперь, когда у нас есть некоторые определения, мы рассмотрим некоторые вопросы.
Что нарисовано?
Теперь, если мы внимательно посмотрим, мы можем
неофициально говорят, что похоже, что у нас есть часть линии.Мы сможем определить его
официальное имя, глядя на то, что происходит в конце нарисованной линии. У нас есть две стрелки. Теперь эти стрелки говорят нам, что это
линия идет в обе стороны. На самом деле он простирается бесконечно в
оба направления. Итак, напомним, что формальное
математическое определение линии — это прямой набор точек, которые простираются бесконечно
в обоих направлениях. И поэтому мы можем сказать, что здесь мы
есть линия.
Итак, напомним, что формальное
математическое определение линии — это прямой набор точек, которые простираются бесконечно
в обоих направлениях. И поэтому мы можем сказать, что здесь мы
есть линия.
Что нарисовано?
Похоже, нам дали линия или, конечно, часть строки. Здесь важно учитывать то, что происходит на концах нашей линии. На концах нашей линии имеем эти две сплошные точки. Они показывают нам, что эта линия заканчивается на оба эти места. Теперь, по сути, линия — это прямая множество точек, бесконечно простирающихся в обоих направлениях. Мы видим, что наш прямой набор точки были ограничены с обоих концов.
И так вспоминаем секунду
определение. Мы говорим, что отрезок – это
часть прямой, ограниченной двумя концами. Мы видим, что наш прямой набор
точек действительно ограничен двумя конечными точками. Итак, у нас есть отрезок.
Итак, у нас есть отрезок.
В нашем следующем примере мы рассмотрим как эти определения могут помочь нам определить многоугольники.
Сколько сегментов линии это форма есть?
Начнем с того, что вспомним определение отрезка.Мы знаем, что отрезок – это часть линии, которая ограничена двумя различными конечными точками. И он содержит каждую точку линия между этими конечными точками. Поскольку линия представляет собой прямое множество точек, бесконечно простирающихся в двух направлениях, мы знаем, что по определению линия сегмент также должен быть прямым.
Итак, чтобы ответить на этот вопрос,
мы просто подсчитаем количество прямых участков линии.Мы будем выделять их по ходу дела. Здесь есть один. Тогда есть еще один здесь, так что
это два. У нас есть меньший здесь;
это три. А у нас тут еще один. Это дает нам в общей сложности четыре.
На самом деле не имеет значения, что отрезки линии имеют разную длину. У нас есть четыре различных сегмента линии в нашей форме. Фактически это позволяет определить наша форма. Это многоугольник с четырьмя сторонами.Помните, многоугольники имеют прямые ребра, и поэтому мы можем сказать, что эта фигура является четырехугольником.
В следующих двух примерах мы посмотрите, как определения, которые мы видели до сих пор, помогут нам ответить на вопросы про баллы.
По данному рисунку определить верно или ложно следующее. Отрезок линии, который проходит через точки 𝐵 и 𝐷 также проходит через точку 𝐶.
Чтобы ответить на этот вопрос,
нам нужно будет вспомнить, что мы на самом деле подразумеваем под отрезком линии.Отрезок – это часть прямой,
и эта часть ограничена двумя различными конечными точками. Нам говорят, что наш отрезок
проходит через точки 𝐵 и 𝐷. На самом деле, его две конечные точки, как мы
Как видно из схемы, это 𝐵 и 𝐷. Таким образом, мы представляем это, как показано. Это 𝐵𝐷 с линией над ним.
На самом деле, его две конечные точки, как мы
Как видно из схемы, это 𝐵 и 𝐷. Таким образом, мы представляем это, как показано. Это 𝐵𝐷 с линией над ним.
Итак, давайте сравним точки 𝐶 с точками 𝐵 и 𝐷. Он находится на линии, проходящей через этих точек и примерно на полпути между точками 𝐵 и 𝐷, на полпути между концы отрезка.По определению отрезок должен быть прямой и содержать каждую точку на прямой между ее концами. Так что можно сказать, что это правда. Отрезок 𝐵𝐷 проходит через точку 𝐶.
Давайте рассмотрим другой пример, например это.
Позволяет ли данная цифра
сделать вывод, что луч, начинающийся в 𝐶 и проходящий через 𝐷, проходит через точку
𝐵. Чтобы ответить на этот вопрос,
нам нужно вспомнить, что мы подразумеваем под лучом.Мы говорим, что луч является частью
линия. Однако, в отличие от линейного отрезка, он
простирается от одной конечной точки и уходит в определенном направлении к
бесконечность. Наш луч начинается с 𝐶, поэтому 𝐶 — это
конечная точка, и она проходит через 𝐷. Мы можем представить это с помощью
одиночная стрелка 𝐶𝐷, как показано на рисунке.
Наш луч начинается с 𝐶, поэтому 𝐶 — это
конечная точка, и она проходит через 𝐷. Мы можем представить это с помощью
одиночная стрелка 𝐶𝐷, как показано на рисунке.
Значит, этот луч проходит через точку 𝐵? Ну, нет, мы сказали, что точка 𝐶 конечная точка.Это точка, в которой линия отрезок или луч заканчивается. Он не простирается назад в прошлое этой конечной точки в направлении 𝐵. И поэтому мы можем сказать нет, данный рисунок не позволяет сделать вывод, что луч, начинающийся в 𝐶 и проходящий через 𝐷 проходит и через точку 𝐵.
Используя данный рисунок, ответьте на следующее: лежит ли точка 𝐶 на прямой?
Начнем с того, что вспомним
определение слова линия.Математически мы говорим, что линия
представляет собой прямой набор точек, бесконечно простирающихся в двух направлениях. Как показано на схеме, это
представлен двумя стрелками. Эти стрелки указывают нам, что
линия продолжается в обоих направлениях. И поэтому, если бы мы продолжили это
линию вниз на нашей диаграмме, мы могли бы сделать вывод, что эта линия, скорее всего, проходит
через точку 𝐸. Но может ли он пройти через точку
𝐶? Ну, нет, мы можем видеть совершенно ясно
что точки 𝐶 и 𝐷 не лежат на этой прямой.А так ответ нет.
Эти стрелки указывают нам, что
линия продолжается в обоих направлениях. И поэтому, если бы мы продолжили это
линию вниз на нашей диаграмме, мы могли бы сделать вывод, что эта линия, скорее всего, проходит
через точку 𝐸. Но может ли он пройти через точку
𝐶? Ну, нет, мы можем видеть совершенно ясно
что точки 𝐶 и 𝐷 не лежат на этой прямой.А так ответ нет.
В нашем последнем примере мы рассмотрим как применять математические обозначения.
На схеме показано несколько точки, 𝐴, 𝐵, 𝐶 и 𝐷. Используйте математическую запись, чтобы описать прямое множество точек от 𝐵 и через 𝐷, прямое множество точки от 𝐴 до 𝐶, прямой набор точек через 𝐴 и 𝐶, которые продолжают бесконечно в обе стороны.
Начнем с рассмотрения
прямой набор точек от 𝐵 и через 𝐷.Вот и все. Этот набор точек имеет конечную точку,
но он бесконечно простирается через 𝐷 и дальше. Поэтому мы можем сказать, что это множество
точек является лучом. Мы представляем луч с помощью
одностороннюю стрелку, как показано, и мы используем конечную точку в качестве первой буквы. И поэтому мы можем сказать, что прямо
показан набор точек от 𝐵 и до 𝐷. Это 𝐵𝐷 со стрелкой.
Поэтому мы можем сказать, что это множество
точек является лучом. Мы представляем луч с помощью
одностороннюю стрелку, как показано, и мы используем конечную точку в качестве первой буквы. И поэтому мы можем сказать, что прямо
показан набор точек от 𝐵 и до 𝐷. Это 𝐵𝐷 со стрелкой.
Далее нам предлагается описать прямой набор точек от 𝐴 до 𝐶.Вот эта линия показана. Мы знаем, что эта точка имеет очень конкретная начальная и конечная точка. Но на самом деле мы называем их обоих конечные точки. И так прямой набор точек между этими конечными точками должен быть отрезок линии. Мы используем полосу для представления линии сегмент. И так прямой набор точек от 𝐴 до 𝐶 обозначается 𝐴𝐶 с чертой.
Наконец, смотрим на прямую
множество точек через 𝐴 и 𝐶, бесконечно простирающихся в обоих направлениях.И так мы видим, что это все
эта строка здесь. Две стрелки говорят нам, что это
линия простирается бесконечно. Прямой набор точек, который
бесконечно простирается в двух направлениях — это линия. И мы используем двустороннюю стрелку, намного
как на картинке, чтобы представить это. Это 𝐴𝐶 с двусторонним
стрелка.
Две стрелки говорят нам, что это
линия простирается бесконечно. Прямой набор точек, который
бесконечно простирается в двух направлениях — это линия. И мы используем двустороннюю стрелку, намного
как на картинке, чтобы представить это. Это 𝐴𝐶 с двусторонним
стрелка.
В этом видео мы узнали сначала что точка — это место. У него нет ни размера, ни ширины, ни длина и обозначается точкой.Мы узнали, что линия – это множество прямых точек, бесконечно простирающихся в обоих направлениях. Мы использовали две конкретные точки, чтобы описать его и двустороннюю стрелку над этими точками, чтобы обозначить, что у нас есть линия. Когда точки лежат на одной прямой, они называются коллинеарными точками.
Мы видели, что луч — это специфический
часть строки. У него одна конечная точка — в нашем
диаграмма, это 𝐴 — и она простирается бесконечно в заданном направлении. Вот, это через точку 𝐵. Мы представляем это с помощью
односторонняя стрелка. Тогда отрезок также является частью
линия. Но на этот раз у него есть два разных
конечные точки, и он содержит каждую точку на линии между этими точками. Мы представляем это с помощью бара, как
показано.
Вот, это через точку 𝐵. Мы представляем это с помощью
односторонняя стрелка. Тогда отрезок также является частью
линия. Но на этот раз у него есть два разных
конечные точки, и он содержит каждую точку на линии между этими точками. Мы представляем это с помощью бара, как
показано.
Геометрические термины — Бесплатная помощь по математике
Точка:
Точка показывает местоположение и не имеет размера или измерения.Точка обозначается точкой и обычно обозначается буквой по выбору. На приведенном ниже рисунке точки обозначены расположенными рядом буквами.
Строка:
Линия представляет собой набор точек, простирающихся в двух противоположных направлениях без конца. Линия одномерна и не имеет ширины. Это определяется путем обозначения двух точек на линии или написания строчной буквы выбора после линии.
Обозначение, например, AB (написанное с символом линии <---> над буквами), читается как «линия AB» и относится к линии, имеющей точки A и B.
Самолет:
Плоскость — это плоская поверхность, не имеющая толщины и простирающаяся без конца во ВСЕХ направлениях. Это двумерный объект. Плоскость представлена параллелограммом и может быть названа путем написания заглавной буквы по выбору в одном из его углов. Я подробно расскажу о том, что такое параллелограмм, в следующих уроках. А пока представьте себе параллелограмм как «оконное стекло». Для простоты вы можете думать о плоскости как о бесконечно большом листе бумаги.
На приведенном ниже рисунке показаны три точки, линия и плоскость.
Линейный сегмент:
Отрезок линии является частью линии, имеющей две точки, называемые конечными точками. Он также имеет точки между конечными точками. Сегмент линии не имеет набора НЕПРЕРЫВНЫХ точек, как линия. Конечная точка означает, что линия имеет начало и конец. Обозначение сегмента линии в строке над любой выбранной буквой. Скажем, на AB есть черта, вы бы прочитали это как «отрезок AB».
Рэй:
Луч — это часть линии, имеющей одну конечную точку и набор всех точек по одну сторону от конечной точки. Луч всегда именуется двумя буквами по выбору. Первая буква должна быть конечной точкой. Рисуем стрелку с концом над буквами.
Луч всегда именуется двумя буквами по выбору. Первая буква должна быть конечной точкой. Рисуем стрелку с концом над буквами.
Угол:
Угол – это соединение двух лучей, имеющих один и тот же конец. Конечная точка угла называется вершиной; лучи называются сторонами угла.
В геометрии есть несколько дополнительных терминов, которые также необходимо понимать. Они определяют отношения между геометрическими объектами:
коллинеарных точек: точек, лежащих на одной прямой.
копланарных точек: точек, лежащих в одной плоскости.
Противоположные лучи: 2 луча, лежащих на одной прямой, с общим концом и без других общих точек. Противоположные лучи образуют прямую линию и/или прямой угол, равный 180º.
Параллельные линии: две копланарные линии, которые не пересекаются.
.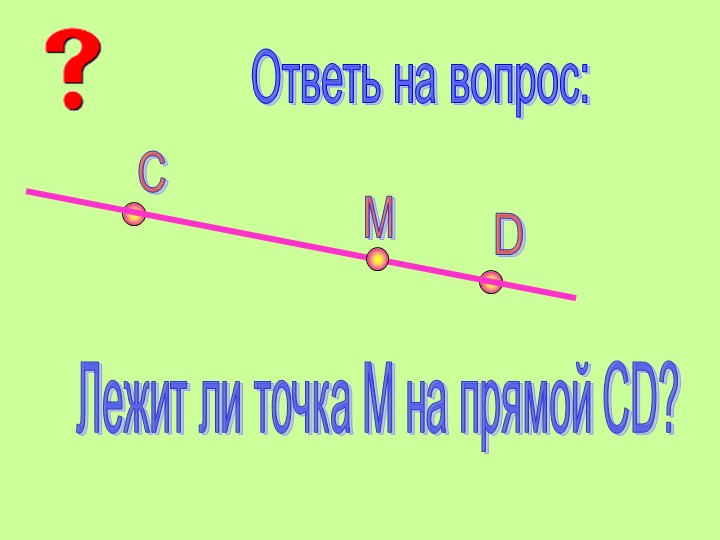
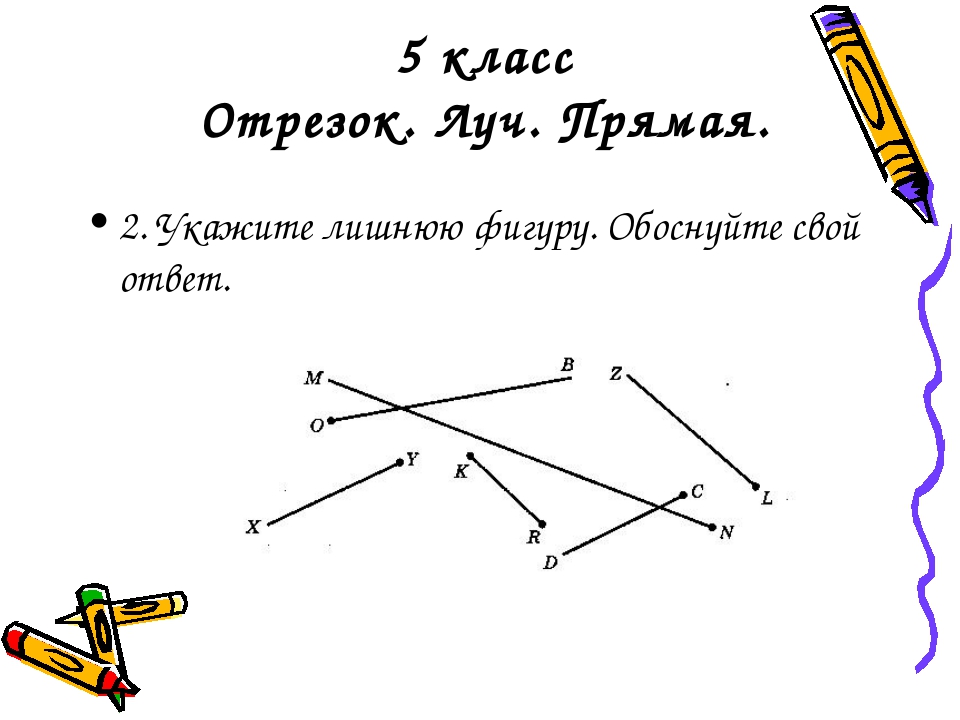 Таким образом,
Таким образом,