Периодические дроби
Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:
0,66666666666666…
0,33333333333333…
0,68181818181818…
Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.
Получаем периодическую дробь
Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.
Итак, делим 1 на 3
Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.
Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.
В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:
0, (3)
Читается как «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11
Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:
0, (45)
Читается как «ноль целых и сорок пять в периоде»
Пример 3. Разделить 15 на 13
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:
1, (153846)
Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».
Пример 4. Разделить 471 на 900
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:
0, 52 (3)
Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смéшанные.
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
0, (3)
0, (6)
0, (5)
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:
0,52 (3)
0,16 (5)
0,31 (6)
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Избавляемся от хвоста
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.
Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33
0, (3) ≈ 0,33
Округлим периодическую дробь 6,31 (6) до разряда тысячных.
Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317
6,31 (6) ≈ 6,317
Перевод чистой периодической дроби в обыкновенную дробь
Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.
Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.
Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.
Итак, записываем в числителе период дроби 0, (3) то есть тройку:
А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).
В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:
Полученную дробь можно сократить на 3, тогда получим следующее:
Получили обыкновенную дробь .
Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается
Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.
Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:
А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).
В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:
Полученную дробь можно сократить эту дробь на 9, тогда получим следующее:
Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается
Перевод смешанной периодической дроби в обыкновенную дробь
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)
В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)
В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Обыкновенная дробь
Обыкновенная дробь – это число, записанное в виде \(\frac{m}{n}\), где \(m\) и \(n\) – натуральные числа.
Например: \(\frac{1}{5}\); \(\frac{53}{2}\) или \(\frac{263}{5372}\).
При этом то, что стоит над дробной чертой (то есть \(m\)) называется числителем дроби, а то, что под чертой (то есть \(n\)) – знаменателем дроби.
Пример:
Изначально дроби были придуманы, чтобы обозначать некоторую часть от целого.
|
Например, если мы целую пиццу разрезали на \(8\) равных кусков и положили себе на тарелку один кусок, то какую часть пиццы мы взяли? |
Правильная дробь – дробь, в которой числитель меньше знаменателя.
Немного позже появились дроби неправильные:
Неправильные дроби – дроби, у которых числитель больше знаменателя.
Например, дробь \(\frac{3}{5}\) – правильная, а дробь \(\frac{17}{4}\) — неправильная. Но в любом случае — и очень важно это понять:
Любая обыкновенная дробь — это просто число.
Да, да, просто число, записанное вот в таком непривычном виде. Такое же число как пять, \(213,7\) или \(0,03\). Действительно, ведь ту же пятерку мы можем записать как \(\frac{5}{1}\). Значение при этом не поменяется. Значит, дробь \(\frac{5}{1}\) это тоже самое, что \(5\). А, например, \(213,7\) можно записать как \(\frac{2137}{10}\). В свою очередь, \(0,03\) – тоже самое, что \(\frac{3}{100}\) (потому и читается как «три сотых»), просто записанное в десятичном виде.
И так как дробь является числом, то с дробями можно делать все, что мы делаем с обычными числами: складывать и вычитать, умножать и делить, возводить в степень и т.д. (см. действия с дробями).
Смотрите также:
Смешанная дробь
Десятичные дроби
Мы уже говорили, что дроби бывают обыкновенные и десятичные. На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.
Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходится сочетать. То есть при решении задач приходиться работать с обоими видов дробей.
Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.
Выражение величин в дробном виде
Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:
Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:
Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде.
Итак, 6 целых сантиметров у нас уже есть:
Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см
Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.
В результате имеем шесть целых сантиметров и три десятых сантиметра:
Цифра 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра».
Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.
Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6
6
Целая часть записана. Сразу же после написания целой части ставим запятую:
6,
И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:
6,3
Любое число, которое представляется в таком виде, называется десятичной дробью.
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:
6,3 см
Выглядеть это будет следующим образом:
На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1000 или 10000.
Как и смешанное число, десятичная дробь имеет цéлую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .
В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.
Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:
0,5
Читается как «ноль целых, пять десятых».
Перевод смешанных чисел в десятичные дроби
Когда мы записываем смешанные числа без знаменателя, мы тем самым перевóдим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.
После того как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример: перевести смешанное число в десятичную дробь.
Сначала записываем целую часть и ставим запятую:
3,
И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать сколько нулей содержится в знаменателе дробной части.
Итак, посчитаем количество нулей в дробной части смешанного числа . Видим, что в знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2
3,2
Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2. Эта десятичная дробь читается так:
«Три целых, две десятых»
«Десятых» потому что в дробной части смешанного числа содержится число 10.
Пример 2. Перевести смешанное число в десятичную дробь.
Записываем цéлую часть и ставим запятую:
5,
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.
В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3
Теперь можно довести дело до конца. Записываем после запятой числитель дробной части:
5,03
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 5,03 читается так:
«Пять целых, три сотых»
«Сотых» потому что в знаменателе дробной части смешанного числа содержится число 100.
Пример 3. Перевести смешанное число в десятичную дробь.
Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.
Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.
В первую очередь смóтрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:
Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала цéлую часть и ставим запятую:
3,
и сразу записываем числитель дробной части
3,002
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 3,002 читается так:
«Три целых, две тысячных»
«Тысячных» потому что в знаменателе дробной части смешанного числа содержится число 1000.
Перевод обыкновенных дробей в десятичные дроби
Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.
Пример 1. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой цифру 5
0,5
В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,5 читается так:
«Ноль целых, пять десятых»
Пример 2. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует. Записываем сначала 0 и стáвим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
0,02
В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,02 читается так:
«Ноль целых, две сотых».
Пример 3. Перевести обыкновенную дробь в десятичную дробь.
Записываем 0 и стáвим запятую:
0,
Теперь посчитаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед цифрой 5 дописать четыре нуля:
Теперь можно продолжить десятичную дробь. Записываем после запятой числитель дроби
0,00005
В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,00005 читается так:
«Ноль целых, пять стотысячных».
Перевод неправильных дробей в десятичную дробь
Неправильная дробь это дробь, у которой числитель больше знаменателя.
Бывают неправильные дроби, у которых в знаменателе содержатся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять цéлую часть.
Пример 1. Перевести неправильную дробь в десятичную.
Дробь является неправильной. Чтобы перевести такую дробь в десятичную, нужно в первую очередь выделить у нее цéлую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к этой теме и хорошенько изучить её.
Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10. Деление нужно выполнить с остатком:
Посмóтрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части:
Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
11,
Теперь посчитаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать после запятой числитель дробной части:
11,2
Значит, неправильная дробь при переводе в десятичную обращается в 11,2
Десятичная дробь 11,2 читается так:
«Одиннадцать целых, две десятых».
Пример 2. Перевести неправильную дробь в десятичную дробь.
Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе содержится число 100.
В первую очередь выделим целую часть этой дроби. Для этого разделим уголком 450 на 100:
Соберём новое смешанное число — получим . Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую:
4,
Теперь посчитаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
4,50
Значит неправильная дробь при переводе в десятичную обращается в 4,50
При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5
Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны и между ними можно поставить знак равенства:
4,50 = 4,5
Возникает вопрос «а почему так происходит?» Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Перевод десятичной дроби в смешанное число
Любая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби.
Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:
6
и рядом три десятых:
Пример 2. Перевести десятичную дробь 3,002 в смешанное число
3,002 это три целых и две тысячных. Записываем сначала три целых
3
и рядом записываем две тысячных:
3
Пример 3. Перевести десятичную дробь 4,50 в смешанное число
4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых
4
и рядом пятьдесят сотых:
Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Докажем, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.
После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в
Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:
Теперь имеем две дроби и . Теперь вспоминаем основное свойство дроби, которое говорит о том, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не меняется.
Давайте разделим числитель и знаменатель первой дроби на число 10
Получили , а это есть вторая дробь. Значит и равны между собой и равны одному и тому же значению:
=
Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.
Перевод десятичной дроби в обыкновенную дробь
Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:
0
и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .
Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.
0,02 это ноль целых и две сотых. Ноль не записываем, поэтому сразу записываем две сотых
Пример 3. Перевести 0,00005 в обыкновенную дробь
0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных
Пример 4. Перевести 3,5 в обыкновенную дробь
Сначала переведём данную десятичную дробь в смешанное число:
Теперь смешанное число переведём в неправильную (обыкновенную) дробь:
Пример 5. Перевести 1,25 в обыкновенную дробь
Сначала переведём данную десятичную дробь в смешанное число:
Теперь смешанное число переведём в неправильную (обыкновенную) дробь:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Дроби, операции с дробями | umath.ru
Дробь — форма представления числа в математике. Дробная черта обозначает операцию деления. Числителем дроби называется делимое, а знаменателем — делитель. Например, в дроби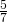 
числителем является число 5, а знаменателем — 7.
Правильной называется дробь, у которой модуль числителя больше модуля знаменателя. Если дробь является правильной, то модуль её значения всегда меньше 1. Все остальные дроби являются неправильными.
Дробь называют смешанной, если она записана как целое число и дробь. Это то же самое, что и сумма этого числа и дроби:
![\[5\frac{2}{3}=5+\frac{2}{3}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-b9e78d9af03db47501fc00cd6f4f63bf_l3.png)
Основное свойство дроби
Если числитель и знаменатель дроби умножить на одно и то же число, то значение дроби не изменится, то есть, например,
![\[\frac{3}{5}=\frac{4 \cdot 3}{4 \cdot 5}=\frac{12}{20}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-d0ab8cd23bda540d33799eb72eed7fd4_l3.png)
Приведение дробей к общему знаменателю
Чтобы привести две дроби к общему знаменателю, нужно:
- Числитель первой дроби умножить на знаменатель второй
- Числитель второй дроби умножить на знаменатель первой
- Знаменатели обеих дробей заменить на их произведение
Действия с дробями
Сложение. Чтобы сложить две дроби, нужно
- Привести дроби к общему знаменателю
- Сложить новые числители обеих дробей, а знаменатель оставить без изменений
Пример:
![\[\frac{3}{5}+\frac{1}{2}=\frac{6}{10}+\frac{5}{10}=\frac{11}{10}=1\frac{1}{10}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-a599416d158fb45c67a1d4ab86c19328_l3.png)
Вычитание. Чтобы вычесть одну дробь из другой, нужно
- Привести дроби к общему знаменателю
- Вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений
Пример:
![\[\frac{3}{5}-\frac{1}{2}=\frac{6}{10}-\frac{5}{10}=\frac{1}{10}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-6f6e23d72bddda9bdff759f6975216b2_l3.png)
Умножение. Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели:
![\[\frac{5}{3} \cdot \frac{1}{2} = \frac{5 \cdot 1}{3 \cdot 2} = \frac{5}{6}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-776ade7b370ed5feb95eaa373a5b08ca_l3.png)
Деление. Чтобы разделить одну дробь на другую, следует числитель первой дроби умножить на знаменатель второй, а знаменатель первой дроби умножить на числитель второй:
![\[\frac{5}{3} : \frac{1}{2} = \frac{5 \cdot 2}{3 \cdot 1} = \frac{10}{3} = 3 \frac{1}{3}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-badd4af108ecf9a5b43877db71b9c737_l3.png)
преобразовать смешанную дробь в не
Правильные и неправильные дроби Определение Обыкновенная дробь называется правильной, если ее числитель меньше знаменателя. Например. Дробь является правильной, так как ее числитель, равный 11, меньше, чем знаменатель, который равен 23: 11 < 23 .( 11/23) Определение Дробь называется неправильной, если ее числитель больше знаменателя или равен ему. Например. Дробь — неправильная, так как 23 > 11 . Дробь — неправильная, так как числитель дроби равен ее знаменателю. (23/11, 3/3) Смешанные дроби Определение Числа, в состав которых входит целое число и правильная дробь, называются смешанными числами. (3 11/23) Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа. Например. Для смешанной дроби число 3 — целая часть, 11/23- дробная. Неправильную дробь можно записать в виде смешанного числа, для этого нужно числитель поделить на знаменатель. Полученное неполное частное будет целой частью смешанной дроби, остаток — числителем дробной части, а знаменатель исходной неправильной дроби — знаменателем дробной части. 2 1/8 =17/8
спроси учителя она тебя не съест
Помощь школьникам Бесплатно! репетитор по математике. Уроки по математике занятия проходят онлайн. Поэтому можете смотреть тогда и где вам удобно совершенно бесплатно! Также в качестве большого подарка- приятный бонус! Готовые видео домашние задания ГДЗ все классы! Подготовка к огэ! присоединяйся нас уже более 100 тыс. Вот мои видео. Если нет вашей темы пишите тут же пришлю именно для вас то что вам нужно! Ваша
Рациональные числа
Тема рациональных чисел достаточно обширна. О ней можно говорить бесконечно и писать целые труды, каждый раз удивляясь новым фишкам.
Чтобы не допускать в будущем ошибок, в данном уроке мы немного углубимся в тему рациональных чисел, почерпнём из неё необходимые сведения и двинемся дальше.
Что такое рациональное число
Рациональное число — это число, которое может быть представлено в виде дроби , где a — это числитель дроби, b — знаменатель дроби. Причем b не должно быть нулём, поскольку деление на ноль не допускается.
К рациональным числам относятся следующие категории чисел:
- целые числа (например −2, −1, 0 1, 2 и т.д.)
- обыкновенные дроби (например , , и т.п.)
- смешанные числа (например , , и т.п.)
- десятичные дроби (например 0,2 и т.п.)
- бесконечные периодические дроби (например 0,(3) и т.п.)
Каждое число из этой категории может быть представлено в виде дроби .
Примеры:
Пример 1. Целое число 2 может быть представлено в виде дроби . Значит число 2 относится не только к целым числам, но и к рациональным.
Пример 2. Смешанное число может быть представлено в виде дроби . Данная дробь получается путём перевода смешанного числа в неправильную дробь
Значит смешанное число относится к рациональным числам.
Пример 3. Десятичная дробь 0,2 может быть представлена в виде дроби . Данная дробь получилась путём перевода десятичной дроби 0,2 в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему десятичных дробей.
Поскольку десятичная дробь 0,2 может быть представлена в виде дроби , значит она тоже относится к рациональным числам.
Пример 4. Бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби . Данная дробь получается путём перевода чистой периодической дроби в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему периодические дроби.
Поскольку бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби , значит она тоже относится к рациональным числам.
В дальнейшем, все числа которые можно представить в виде дроби, мы всё чаще будем называть одним словосочетанием — рациональные числа.
Рациональные числа на координатной прямой
Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:
На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.
Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.
Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.
Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей
Попробуем понять, почему дробь вдруг расположилась между нулём и единицей.
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину
Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.
Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5
Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь , а эта дробь также как и равна 0,5
А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь
Пример 2. Попробуем отметить на координатной рациональное число . Данное число располагается ровно между числами 1 и 2
Значение дроби равно 1,5
Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:
Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.
Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.
Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.
Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.
К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2
Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:
Пример 3. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться очень близко к нулю
Значение дроби равно 0,02
Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 0,02.
Пример 4. Отметим на координатной прямой рациональное число 0, (3)
Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная
0,33333….и так далее до бесконечности..
И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.
Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3
Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.
Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3
это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.
Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь
Значение дроби равно 2,5
Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 2,5
Минус перед рациональным числом
В предыдущем уроке, который назвался умножение и деление целых чисел мы научились делить целые числа. В роли делимого и делителя могли стоять как положительные, так и отрицательные числа.
Рассмотрим простейшее выражение
(−6) : 2 = −3
В данном выражении делимое (−6) является отрицательным числом.
Теперь рассмотрим второе выражение
6 : (−2) = −3
Здесь уже отрицательным числом является делитель (−2). Но в обоих случаях мы получаем один и тот же ответ −3.
Учитывая, что любое деление можно записать в виде дроби, мы можем рассмотренные выше примеры также записать в виде дроби:
А поскольку в обоих случаях значение дроби одинаково, минус стоящий либо в числителе либо в знаменателе можно сделать общим, поставив его перед дробью
Поэтому между выражениями и и можно поставить знак равенства, потому что они несут одно и то же значение
В дальнейшем работая с дробями, если минус будет нам встречаться в числителе или в знаменателе, мы будем делать этот минус общим, ставя его перед дробью.
Противоположные рациональные числа
Как и целое число, рациональное число имеет своё противоположное число.
Например, для рационального числа противоположным числом является . Располагается оно на координатной прямой симметрично расположению относительно начала координат. Другими словами, оба этих числа равноудалены от начала координат
Перевод смешанных чисел в неправильные дроби
Мы знаем что для того, чтобы перевести смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части и прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель остаётся прежним..
Например, переведём смешанное число в неправильную дробь
Умножим целую часть на знаменатель дробной части и прибавим числитель дробной части:
(2 × 2) + 1
Вычислим данное выражение:
(2 × 2) + 1 = 4 + 1 = 5
Полученное число 5 будет числителем новой дроби, а знаменатель останется прежним:
Полностью данная процедура записывается следующим образом:
Чтобы вернуть изначальное смешанное число, достаточно выделить целую часть в дроби
Но этот способ перевода смешанного числа в неправильную дробь применим только в том случае, если смешанное число является положительным. Для отрицательного числа данный способ не сработает.
Рассмотрим дробь . Выделим в этой дроби целую часть. Получим
Чтобы вернуть изначальную дробь нужно перевести смешанное число в неправильную дробь. Но если мы воспользуемся старым правилом, а именно умножим целую часть на знаменатель дробной части и к полученному числу прибавим числитель дробной части, то получим следующее противоречие:
Мы получили дробь , а должны были получить дробь .
Делаем вывод, что смешанное число в неправильную дробь переведено неправильно:
Чтобы правильно перевести отрицательное смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части, и из полученного числа вычесть числитель дробной части. В этом случае у нас всё встанет на свои места
Отрицательное смешанное число является противоположным для смешанного числа . Если положительное смешанное число располагается в правой части и выглядит так
то отрицательное смешанное число будет располагаться в левой части симметрично относительное начала координат
И если читается как «две целых и одна вторая», то читается как «минус две целых и минус одна вторая». Поскольку числа −2 и располагаются в левой части координатной прямой — они оба являются отрицательными.
Любое смешанное число можно записать в развёрнутом виде. Положительное смешанное число в развёрнутом виде записывается как .
А отрицательное смешанное число записывается как
Теперь мы можем понять, почему смешанное число расположилось в левой части координатной прямой. Минус перед двойкой указывает, что мы сдвинулись от нуля на два шага влево, в результате оказались в точке, где находится число −2
Затем, начиная от числа −2 сдвинулись ещё влево на шага. А поскольку значение равно −0,5 то наш шаг будет половиной от полного шага.
В итоге, мы окажемся посередине между числами −3 и −2
Пример 2. Выделить в неправильной дроби целую часть, затем полученное смешанное число обратно перевести в неправильную дробь
Выполним первую часть задания, а именно выделим в неправильной дроби целую часть
Выполним вторую часть задания, а именно переведём полученное смешанное число в неправильную дробь. Для этого умножим целую часть на знаменатель дробной части и из полученного числа вычтем числитель дробной части:
Если нет желания путаться и привыкать к новому правилу, то можно смешанное число заключить в скобки, а минус оставить за скобкой. Тогда можно будет применить старое доброе правило: умножить целую часть на знаменатель дробной части и к полученному числу прибавить числитель дробной части.
Выполним предыдущее задание этим способом, а именно переведём смешанное число в неправильную дробь
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже