Основные правила математики. Геометрия. Теоремы, определения. 7 класс
Основные правила математики. Геометрия. Теоремы, определения. 7 класс
Определения
1. Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
2.В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
3. Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
4. Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла.
5. Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
6. Две геометрические фигуры называются равными, если их можно совместить наложением.
8. Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
9.Угол называется прямым, если он равен 90°.
10. Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
11. Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
12. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
13. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
14. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
15 Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
16. Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
17. Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
18.Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
19.Треугольник называется равносторонним, если все его стороны равны.
20.Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений, на основе которых доказываются теоремы и строится вся геометрия.
22. Если все три угла треугольника острые, то треугольник называется остроугольным.
23. Если один из углов треугольника тупой, то треугольник называется тупоугольным.
24. Если один из углов треугольника прямой, то треугольник называется прямоугольным.
Теоремы
Теорема 1: Две прямые, перпендикулярные к третьей, не пересекаются.
Доказательство от противного. Есть две прямые АА1 и ВВ1 перпендикулярны к прямой PQ одновременно. Предположим, что, продолжая прямые, можно достичь некоторой точки M, в которой они пересекаются. Перегнем плоскость вдоль прямой PQ. В этом случае углы при данных прямых накладываются друг на друга, а наложенные лучи совпадают. При этом точка М, получит проекцию некоторой точки M1 (при пересечения АА1 и ВВ1 в нижней полуплоскости) . Это будет означать, что две прямые АА1 и ВВ1 пересекаются в двух точках М и М1. Но через любые две точки на плоскости можно провести только одну прямую! Таким образом, предположение о том, что данные прямые пересекаются неверно. Следовательно, две прямые, перпендикулярные к третьей, не пересекаются. Что и требовалось доказать.
Теорема 2
Первый признак равенства треугольников ( по двум сторонам и углу между ними)
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство:
Так как ∠A=∠A1, то можно треугольник A1B1C1 наложить на треугольник ABC так, чтобы
точка A1 совместилась с точкой A,
луч A1C1 наложился на луч AC,
луч A1B1 — на луч AB.
Аналогично, сторона A1C1 совместится со стороной AC, а точка C1 — с точкой C.
Следовательно, сторона B1C1 совместится со стороной BC.
Значит, при наложении треугольники полностью совместятся, поэтому ΔABC= ΔA1B1C1 (по определению).
Что и требовалось доказать.
Теорема 3
Теорема единственности перпендикуляра, проведенного из произвольной точки к заданной прямой
Из любой точки А, не лежащей на данной прямой, можно провести перпендикуляр к прямой. К тому же этот перпендикуляр единственный.
Дано: точка А не принадлежит прямой a.
Доказать: существует единственный отрезок АН, где АН- перпендикуляр к a из точки A.
Доказательство:
1. Построим 2 равных угла. ∠АВС =∠МВС или ∠1 = ∠2.
2. Равные углы можно совместить наложением. При этом точка А перейдет в точку A1. ВА = ВA1(перегибание по прямой ВС).
3. Соединим точки А и A1. Получим точку Н. Углы ∠ВНА = ∠3, ∠ВНA1 = ∠4.
4. Так как ∠1 = ∠2,ВА = ВA1, BC- общая,то треугольники ВНА = ВНA1 по первому признаку равенства треугольников, то есть по углу и двум прилежащим сторонам. Из равенства треугольников следует равенство всех элементов. А значит, ∠3 = ∠4. Эти углы лежат против равных сторон. Два смежных равны только в случае, если каждый из них равен по 90°. А значит, АН ⊥ ВС. Мы доказали, что из точки А можно провести перпендикуляр к прямой a.
Единственность перпендикуляра, проведенного из точки А к прямой, докажем методом «от противного».
5. Предположим, что из точки А можно провести к прямой a два разных перпендикуляра.
АН ⊥ a, Аh2 ⊥ a.
Это невозможно, поскольку из разных точек прямой a проведены 2 перпендикуляра, которые имеют общую точку А. Мы получили противоречие, значит, наше предположение неверно. Из точки А можно провести лишь один перпендикуляр к прямой a. Теорема доказана.
Определения и теоремы геометрия 7 класс
Геометрия 7 класс
Определения
Отрезок-часть прямой, ограниченная двумя точками.
Концы отрезка-точки, ограничивающие прямую.
Луч-прямая, имеющая начало в точке, но не имеющая конца.
Угол-геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки.
Стороны угла-лучи, составляющие угол.
Вершина угла-точка, из которой берут начало стороны угла.
Развернутый угол, если обе его стороны лежат на одной прямой.
Середина отрезка-точка, делящая отрезок пополам.
Прямой угол=900. Острый угол<900. 1800>Тупой угол>900.
Смежные-два угла, у которых одна сторона общая, а две другие-это продолжения друг друга.
Вертикальные-два угла, если стороны одного угла-это продолжение сторон другого.
Перпендикулярные-две пересекающиеся прямые, образующие четыре прямых угла.
Периметр-сумма длин всех сторон фигуры.
Перпендикуляр АН-отрезок, соединяющий точку А с точкой Н, лежащей на прямой. Этот отрезок с прямой образует прямой угол.
Биссектриса-луч, исходящий из вершины угла и делящий его на два равных угла.
Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Высота-перпендикуляр, проведенный из вершины угла к прямой, содержащей противолежащую сторону.
Равнобедренный треугольник, если две его стороны равны.
Окружность-геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от одной единственной точки-центр окружности.
Радиус r — отрезок, соединяющий центр окружности с любой точкой, лежащей на этой окружности.
Хорда-отрезок, соединяющий две точки, лежащие на окружности.
Диаметр-хорда, проходящая через центр окружности.
Дуга-часть окружности, полученная делением этой окружности двумя точками.
Параллельные прямые-две не пересекающиеся на плоскости прямые.
Параллельные отрезки, если они лежат на параллельных прямых.
Секущая к двум прямым-прямая, пересекающая данные прямые в двух точках.
Гипотенуза-сторона прямоугольного треугольника, лежащая напротив прямого угла. Две другие стороны прямоугольного треугольника-катеты.
Неравенства треугольника: АВ<АС+СВ, АС<АВ+ВС, ВС<ВА+АС.
Расстояние от точки до прямой-длина перпендикуляра, проведенного из точки к прямой.
Расстояние между прямыми-расстояние от любой точки одной из параллельных прямых до другой прямой.
Правила и теоремы
Через любые две точки можно провести только одну прямую.
Две прямые имеют либо одну общую точку, либо ни одной.
Две геометрические фигуры называются равными, если их можно совместить наложением.
Равные отрезки имеют равные длины.
Сумма смежных углов равна 1800.
Вертикальные углы равны.
Развернутый угол равен 1800. Неразвернутый меньше 1800.
Две прямые, перпендикулярные к третьей, не пересекаются.
Признаки равенства треугольников:
Теорема 1 (по двум сторонам и углу). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
Теорема 2 (по стороне и двум углам). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.
Теорема 3 (по трём сторонам). Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то эти треугольники равны.
2.2.Теорема (о перпендикуляре к прямой). Из точки, не лежащей на прямой, можно провести только один перпендикуляр к этой прямой.
2.3. Медиана делит сторону на два равных отрезка.
2.4. Свойства равнобедренного треугольника:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3.1. Признаки параллельности двух прямых (обратные теоремы тоже справедливы):
Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то данные прямые параллельны.
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
3.2. Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы:
10. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
20. Если две прямые параллельны третьей, то все три прямые параллельны.
4.1. Теорема (о сумме углов треугольника). Сумма углов треугольника равно 1800.
4.2. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
4.5. Теорема (о соотношении между сторонами и углами треугольника). В треугольнике против большей стороны лежит больший угол и против большего угла лежит большая сторона.
Следствия из теоремы:
10. В прямоугольном треугольнике гипотенуза больше катета.
20. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
4.6. Каждая сторона треугольника меньше суммы двух других сторон.
4.7. Свойства прямоугольного треугольника:
10. Сумма двух острых углов прямоугольного треугольника равна 900.
20. Катет прямоугольного треугольника, лежащий напротив угла в 300, равен половине гипотенузы.
30. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 300.
4.8. Признаки равенства прямоугольных треугольников:
1. Если катеты одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то эти треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого треугольника, то эти треугольники равны.
Теорема 1. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузы и острому углу другого прямоугольного треугольника, то эти треугольники равны.
Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
4.9. Угол падения равен углу отражения.
4.10. Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Справочный материал по геометрии за курс 7 класса «Основные определения и теоремы»
Середина отрезка – это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.
Прямой угол – угол, градусная мера которого равна 90 градусов.
Острый угол – угол, градусная мера которого меньше 90 градусов.
Тупой угол – угол, градусная мера которого больше 90 градусов, но меньше 180 градусов.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Свойство смежных углов. Сумма смежных углов равна 180 градусов.
Вертикальные углы. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов. Вертикальные углы равны.
Перпендикулярные прямые. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
Свойство перпендикулярных прямых. Две прямые, перпендикулярные к третьей, не пересекаются.
Периметр треугольника – это сумма длин трех сторон треугольника.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Треугольник называется равнобедренным, если его две стороны равны. Эти стороны называются боковыми, а третья – основанием.
Треугольник, все стороны которого равны, называется равносторонним.
В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.
Отрезок, соединяющий две точки окружности, называется её хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Часть окружности, ограниченная двумя точками, называется дугой окружности.
Часть плоскости, ограниченная окружностью, называется кругом.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Углы при параллельных прямых и секущей:
2) обратно, против большего угла лежит большая сторона.
Теория по геометрии 7-9 класс
Виды углов:
· острый угол – от 0 до 90 градусов;
· прямой угол – равен 90 градусам;
· тупой угол – от 90 до 180 градусов;
· развернутый угол (прямая) – равен 180 градусам.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжением друг друга.
Свойство смежных углов:
· сумма смежных углов равна 180 градусам.
Вертикальные углы – два угла, у которых стороны являются продолжением друг друга.
Свойство вертикальных углов:
· вертикальные углы равны.
Перпендикулярные прямые – прямые пересекающиеся под углом 90 градусов.
Перпендикуляр – отрезок, проведенный из точки к прямой под углом 90 градусов.
Теорема о перпендикуляре: из точки, не лежащей на прямой можно провести перпендикуляр к этой прямой и при том только один.
Периметр многоугольника – сумма длин всех его сторон.
Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов.
Виды треугольников:
· остроугольный треугольник – все три угла острые;
· прямоугольный треугольник – один угол прямой и два угла острые;
· тупоугольный треугольник – один угол тупой и два угла острые.
Равные треугольники – треугольники, которые можно совместить наложением.
Свойства равных треугольников:
· если два треугольника равны, то их элементы (углы и стороны) попарно равны;
· в равных треугольниках напротив равных сторон лежат равные углы и наоборот, напротив равных углов лежат равные стороны.
Признаки равенства треугольников:
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны;
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны;
3. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Биссектриса – отрезок, выходящий из вершины треугольника к противоположной стороне и делящий угол пополам.
Медиана – отрезок, выходящий из вершины треугольника к противоположной стороне и делящий эту сторону пополам.
Высота – отрезок, выходящий из вершины треугольника к прямой, содержащей противоположную сторону, под углом 90 градусов.
Равнобедренный треугольник – треугольник, у которого две стороны равны, а третья является основанием.
Свойства равнобедренного треугольника:
· углы при основании равны;
· биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Равносторонний треугольник – треугольник, у которого все стороны равны.
Свойства равностороннего треугольника:
· углы равны по 60 градусов;
· биссектриса равностороннего треугольника, проведенная к любой стороне, является медианой и высотой.
Параллельные прямые – прямые, которые не пересекаются.
Секущая – прямая, пересекающая параллельные прямые.
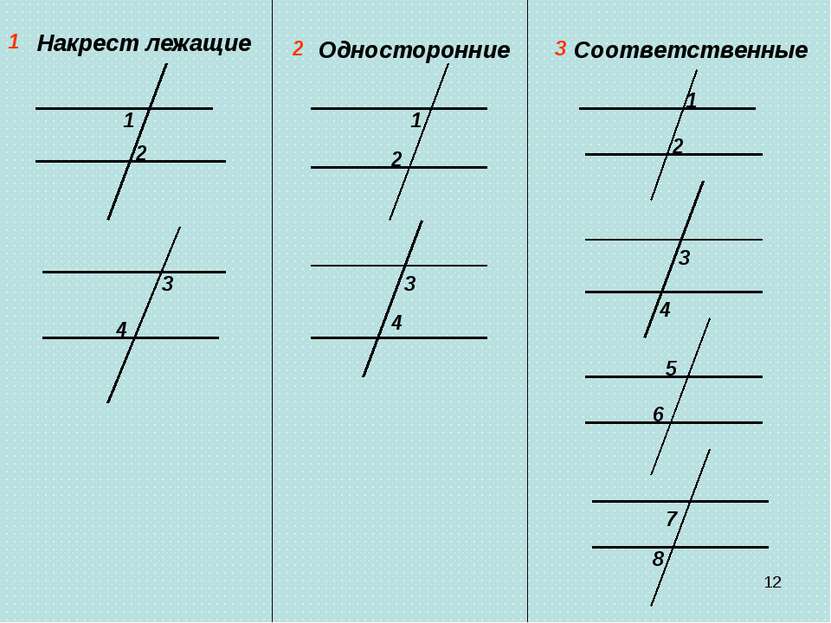
Виды углов, образованных при пересечении параллельных прямых секущей:
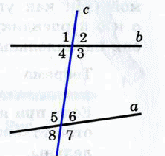
· накрест-лежащие;
· соответственные;
· односторонние.
Свойства параллельных прямых:
· при пересечении параллельных прямых секущей накрест-лежащие углы равны;
· при пересечении параллельных прямых секущей соответственные углы равны;
· при пересечении параллельных прямых секущей сумма односторонних углов равна 180 градусам.
Признаки параллельности прямых:
· если при пересечении двух прямых секущей накрест-лежащие углы равны, то прямые параллельны;
· если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
· если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусам, то прямые параллельны.
Аксиома о параллельных прямых: через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и при том только одну.
Следствия из аксиомы:
· если секущая пересекает одну из параллельных прямых, то она пересечет и вторую параллельную прямую;
· если каждая из двух прямых параллельна третьей, то они параллельны между собой.
Теорема о сумме углов треугольника: сумма углов треугольника равна 180 градусам.
Внешний угол треугольника – угол, смежный с одним из углов треугольника.
Свойство внешнего угла треугольника:
· внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.
Теорема о соотношении между сторонами и углами треугольника: в треугольнике напротив бОльшей стороны лежит бОльший угол и наоборот, напротив бОльшего угла лежит бОльшая сторона.
Теорема о сторонах треугольника: каждая сторона треугольника меньше суммы двух других сторон.
Прямоугольный треугольник – треугольник, у которого один угол равен 90 градусам.
Свойства прямоугольного треугольника:
· сумма острых углов треугольника равна 90 градусам;
· в прямоугольном треугольнике катет, лежащий на против угла 30 градусов, равен половине гипотенузы;
· если в прямоугольном треугольнике катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 градусов.
Признаки равенства прямоугольных треугольников:
1. если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны;
2. если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны;
3. если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны;
4. если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Расстояние от точки до прямой – перпендикуляр, проведенный от этой точки к данной прямой.
Расстояние между параллельными прямыми – перпендикуляр, проведенный от произвольной точки на одной прямой ко второй прямой.
Четырехугольник – геометрическая фигура, состоящая из 4 сторон и 4 углов.
Сумма углов выпуклого многоугольника равна (n-2)*180, где n – количество углов.
Сумма углов любого четырехугольника равна 360 градусов.
Параллелограмм – четырехугольник, у которого стороны попарно параллельны.
Свойства параллелограмма:
· противоположные углы и стороны равны;
· диагонали пересекаются и точкой пересечения делятся пополам.
Диагональ – отрезок, соединяющий две противоположные вершины четырехугольника.
Признаки параллелограмма:
· если в четырехугольнике стороны попарно равны, то данный четырехугольник – параллелограмм;
· если в четырехугольнике две стороны равны и параллельны, то данный четырехугольник параллелограмм;
· если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то данный четырехугольник параллелограмм.
Трапеция – четырехугольник, у которого две стороны параллельны (основания) а две другие – нет (боковые стороны).
Виды трапеций:
· произвольная;
· прямоугольная – трапеция, у которой два прямых угла;
· равнобедренная – трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции:
· углы при основаниях равны;
· диагонали равны.
Ромб – частный случай параллелограмма, у которого все стороны равны.
Свойство ромба:
· у ромба диагонали перпендикулярны и делят углы, из которых они исходят, пополам.
Прямоугольник – частный случай параллелограмма, у которого все углы по 90 градусов.
Свойство прямоугольника:
· у прямоугольника диагонали равны
Признак прямоугольника:
· если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник.
Квадрат – частный случай прямоугольника, у которого все стороны равны.
Теорема Фалеса – если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
Площадь многоугольника – часть плоскости, ограниченная сторонами многоугольника.
Свойство площадей:
· равные многоугольники имеют равные площади;
· если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей многоугольников, из которых он состоит.
Площадь квадрата равна квадрату его стороны: S =
Площадь прямоугольника равна произведению двух его смежных сторон: S =
Площадь трапеции равна половине произведения основания на высоту: S =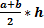 
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне: S =
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними: S =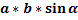 
Площадь ромба равна половине произведения его диагоналей: S =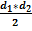 
Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне: S =
Площадь ромба равна произведению двух его смежных сторон на синус угла между ними:
S =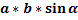
Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне: S =
Площадь треугольника равна половине произведения двух его смежных сторон на синус угла между ними: S =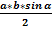 
Площадь треугольника равна произведению его сторон, деленное на 4 радиуса описанной окружности: S =
Формула Герона, где р – полупериметр: S =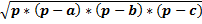 
Площадь прямоугольного треугольника равна половине произведения его катетов: S =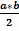 
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе из вершины прямого угла: S =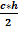 
Площадь равностороннего треугольника, где а – сторона треугольник: S =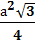 
Высота, медиана, биссектриса равностороннего треугольника, где а – сторона треугольника: h =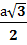 
Площадь круга, где r – радиус: S =
Длина окружности, где r – радиус: C = 2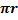 
Длина дуги окружности, где r – радиус, α – грудасная мера дуги: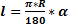 
Площадь кругового сектора, где r – радиус, α – грудасная мера дуги: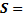 
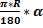
Площадь правильного шестиугольника, где а – сторона шестиугольника: S =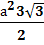 
Если в многоугольник можно вписать окружность, то его площадь можно найти как половина произведения периметра на радиус этой окружности: S =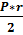 
Свойства площадей треугольников:
· если два треугольника имеют равные высоты, то их площади относятся как основания;
· если два треугольника имеют пару равных углов, то их площади относятся как произведение сторон, заключающих эти углы.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Обратная теорема Пифагора: если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то данный треугольник – прямоугольный.
Формула для нахождения гипотенузы равнобедренного прямоугольного треугольника: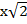 
, где х – катет равнобедренного прямоугольного треугольника.
Формула для нахождения диагонали квадрата: 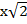, где х – сторона квадрата.
Отношение двух величин – деление одной величины на другую (дробь).
Пропорция – равенство нескольких дробей.
Основное свойство пропорции: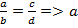 
*d = c*b
Подобные треугольники – треугольники, у которых углы равны, а стороны одного треугольника пропорциональны сходственным сторонам другого.
Сходственные стороны – стороны двух подобных треугольников, расположенные напротив равных углов.
Коэффициент подобия – отношение двух сходственных сторон подобных треугольников.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Коэффициент подобия равных треугольников равен единице.
Теорема о биссектрисе треугольника: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Признаки подобия треугольников:
1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны;
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами, равны, то такие треугольники подобны;
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Теорема о средней линии треугольника: средняя линия треугольника параллельна противоположной стороне и равна ее половине.
Среднее арифметическое для нескольких величин равно сумме этих величин, деленной на их количество.
Среднее геометрическое (пропорциональное) для нескольких величин равно квадратному корню из их произведения.
Свойства среднего геометрического в прямоугольных треугольниках:
· высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое для отрезков, на которые гипотенуза делится этой высотой;
· катет прямоугольного треугольника есть среднее геометрическое для гипотенузы и отрезка гипотенузы, заключенного между этим катетом и высотой, проведенной к гипотенузе.
Синус острого угла прямоугольного треугольника – отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника – отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника – отношение противолежащего катета к прилежащему.
Котангенс острого угла прямоугольного треугольника – отношение прилежащего катета к прилежащему.
Основное тригонометрическое тождество: sin2(a) + cos2(a) = 1
Тригонометрические формулы:
· 
· 
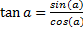
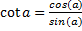
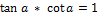
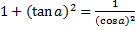
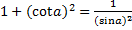
Табличные углы:
В прямоугольном треугольнике синус одного острого угла равен косинусу другого
В прямоугольном треугольнике косинус одного острого угла равен синусу другого
В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого
В прямоугольном треугольнике котангенс одного острого угла равен тангенсу другого
Синусы смежных углов равны
Косинусы смежных углов равны с противоположными знаками
Тангенсы смежных углов равны с противоположными знаками
Котангенсы смежных углов равны с противоположными знаками
Окружность – множество точек, равноудаленных от одной точки (центр окружности).
Радиус – отрезок, соединяющий центр окружности с любой точкой на окружности.
Хорда – отрезок, соединяющий любые две точки на окружности.
Диаметр – хорда, проходящая через центр окружности.
Соотношение диаметра и радиуса – диаметр равен двум радиусам.
Секущая – прямая, имеющая с окружностью две общих точки.
Касательная – прямая, имеющая с окружностью одну общую точку.
Теоремы о касательных:
1) Радиус, проведенный в точку касания, перпендикулярен касательной.
2) Отрезки касательных, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Теорема о хордах:
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Вписанный угол – угол, вершина которого лежит на окружности, а его стороны пересекают окружность.
Центральный угол – угол, вершина которого лежит в центре окружности, а его стороны пересекают окружность.
Дуга – часть окружности, ограниченная с двух сторон.
Вписанный угол равен половине дуги, на которую он опирается.
Центральный угол равен дуге, на которую он опирается.
Следствия из измерений центрального и вписанного углов:
1) вписанный угол равен половине центрального угла, опирающегося на ту же дугу;
2) если вписанные углы опираются на одну и ту же дугу, то они равны;
3) вписанный угол, опирающийся на диаметр равен 90 градусов.
Серединный перпендикуляр – прямая, проходящая через середину отрезка под углом 90 градусов.
Четыре замечательные точки треугольника:
· биссектрисы треугольника пересекаются в одной точке;
· медианы треугольника пересекаются в одной точке;
· высоты треугольника пересекаются в одной точке;
· серединные перпендикуляры треугольника пересекаются в одной точке.
Теорема о биссектрисе:
Любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.
Теорема о медианах:
Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины.
Теорема о серединном перпендикуляре:
Любая точка, лежащая на серединном перпендикуляре, проведенному к отрезку, равноудалена от концов этого отрезка.
Вписанная окружность – окружность, касающаяся всех сторон фигуры.
Описанная окружность – окружность, проходящая через каждую вершину фигуры.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Основные понятия и теоремы по курсу геометрии в 7 классе( мини-пособие)
Основные понятия и теоремы по геометрии за курс 7 класса по учебнику Л. Атанасяна
Аксиомы:
1. Через любые две точки можно провести прямую и притом только одну
2. Две прямые имеют одну общую точку, либо не имеют общих точек совсем
3
4. Угол называется развернутым, если обе его стороны лежат на одной прямой.
5.Две фигуры называются равными, если их можно совместить при наложении.
6. Биссектриса угла – это луч делящий угол пополам.
7. Развернутый угол равен 180 градусам.
Прямой угол равен 90 градусов, острый угол меньше 90 градусов, тупой – угол больше 90 градусов.
8. 
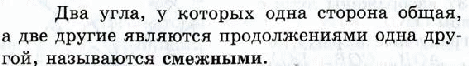
9. 
10. 
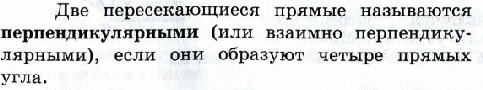
11. Две прямые перпендикулярные к третьей — не пересекаются
12. 
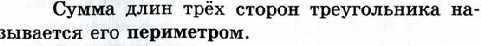
13. 
14. 
Первый признак равенства треугольников.
15. 
16. 
17. 
18. 
19. 
20. Треугольник называется равнобедренным ,если равны две его стороны, которые называются боковыми. Третья сторона называется основанием.
21. Треугольник называется равносторонним, если равны все его стороны.
22. 
23. 
24.
25.Второй признак равенства треугольников
26.Третий признак равенства треугольников
27. 
28. 
29. 
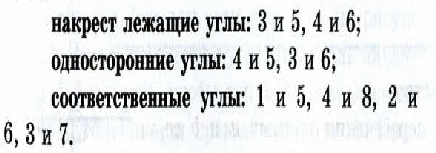
30. 
31. 
32. 
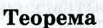
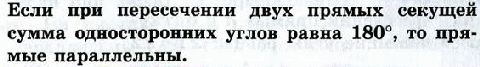
33. 
34. 
35. 
36. 
37. 
38.
39. 
40. 
41. 
42. 
43. 
44. 
45. 
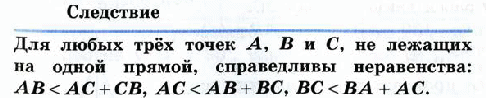
46. 
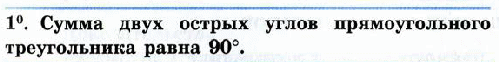
47. 
48. 
49. 
50. 
51. 
52. 
53. 
Учебник 7-9кл 
Теория по геометрии 7 класс
Теория по геометрии 7 класс
Основные понятия
Теорема — утверждение, которое доказывается путем рассуждений. Доказательство — сами рассуждения.
Определение — предложение, в котором разъясняется смысл того или иного выражения или названия.
Аксиома или постулат — исходное положение, принимаемое без доказательств и лежащее в основе доказательств истинности других положений (предложение, не требующее доказательств; самоочевидный факт).
Аксиомы геометрии можно разбить на пять групп.
1. Аксиомы принадлежности
1.1 Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.
1.2 Через любые две точки можно провести прямую и притом только одну.
1.3 Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости и точки, не принадлежащие ей.
2. Аксиомы расположения
2.1 Из трех точек на прямой одна и только одна лежит между двумя другими.
2.2 Прямая разбивает плоскость на две полуплоскости.
2.3 Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.
2.4 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
3. Аксиомы измерения
3.1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
3.2 Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
4. Аксиомы откладывания.
4.1 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и притом только один.
4.2 От любой полупрямой в заданную полуплоскость можно отложить угол, с заданной градусной мерой, меньшей и притом только один.
4.3 Каков бы ни был треугольник, существует треугольник, равный ему, в заданном расположении относительно данной полупрямой.
5. Аксиома параллельности.
5.1 Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной. (аксиома параллельных прямых).
Начальные геометрические сведения
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой. Сумма смежных углов равна 180º.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Вертикальные углы равны.
Перпендикулярные прямые — это прямые, при пересечении которых образуются четыре прямых угла.
Две прямые, перпендикулярные к третьей прямой, не пересекаются.
Треугольники
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Точки — вершины, отрезки — стороны. Элементы треугольника: углы и стороны.
Периметр треугольника— сумма длин всех сторон.
Если два треугольника равны, то соответственные элементы таких треугольников тоже равны.
Против соответственно равных сторон лежат соответственно равные углы и наоборот, против равных углов лежат соответственно равные стороны.
Признаки равенства треугольников
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Перпендикуляр к прямой — отрезок, проведенный из точки к прямой под углом 90 градусов.
Из точки, не лежащей на данной прямой, можно провести перпендикуляр к этой прямой, и при том только один.
Медиана треугольника — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.
Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.
В любом треугольнике:
медианты пересекаются в одной точке;
биссектрисы пересекаются в одной точке;
высоты пересекаются в одной точке.
Равнобедренный треугольник — треугольник, у которого две стороны равны.Равные стороны — боковые стороны, третья сторона — основание.
Свойства:
1.В равнобедренном треугольнике углы при основании равны.
2.В равнобедренном треугольнике высота, проведенная к основанию является биссектрисой и медианой (медиана является высотой и биссектрисой; биссектриса является высотой и медианой).
Признак равнобедренного треугольника: если в треугольнике два угла равны, то такой треугольник равнобедренный.
Равносторонний треугольник — треугольник, у которого все стороны равны.
Свойства:
1. В равностороннем треугольнике все углы равны по 60 градусов.
2. В равностороннем треугольнике все медианы — высоты и биссектрисы.
Признак: если в треугольнике все углы равны, то он равносторонний.
В треугольнике: 1) против большей стороны лежит больший угол; 2) против большего угла лежит большая сторона, и наоборот.
Неравенство треугольника: каждая сторона треугольника меньше суммы двух других сторон.
Сумма углов треугольника равна .
Внешний угол треугольника — угол, смежный с каким-нибудь внутренним углом треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Виды треугольников :
Остроугольный — треугольник, у которого все углы острые.
Тупоугольный — треугольник, у которого один угол тупой.
Прямоугольный — треугольник, у которого один угол прямой (сторона, лежащая напротив угла в 90 градусов, называется гипотенузой; стороны, образующие угол в 90 градусов, называются катетами). В прямоугольном треугольнике гипотенуза больше катета.
Свойства:
1. Катет, лежащий напротив угла в равен половине гипотенузы.
2. Сумма острых углов прямоугольного треугольника равна 90°.
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета, равен .
ОкружностьОкружность — геометрическая фигура, состоящая их всех точек плоскости, равноудаленных от заданной точки, называемой центром окружности.
Радиус — отрезок, соединяющий центр окружности и точку на окружности.
Хорда — отрезок, соединяющий две точки на окружности.
Диаметр — хорда, проходящая через центр окружности.
Дуга окружности — часть окружности, ограниченная двумя точками.
Круг — часть плоскости, ограниченная окружностью.
Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Параллельные прямые
Параллельные прямые — две прямые на плоскости, которые не пересекаются (не имеют общих точек).
Углы:
Образованы пересечением двух прямых и секущейНакрест лежащие
При пересечении двух параллельных прямых секущей накрест лежащие углы равны.
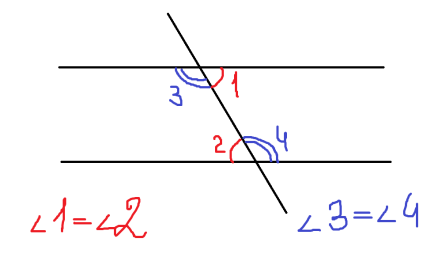
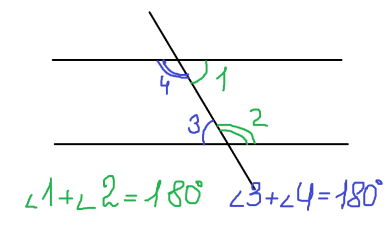
Односторонние
При пересечении двух параллельных прямых секущей сумма односторонних углов равна 180.
Соответственные
При пересечении двух параллельных прямых секущей соответственные углы равны.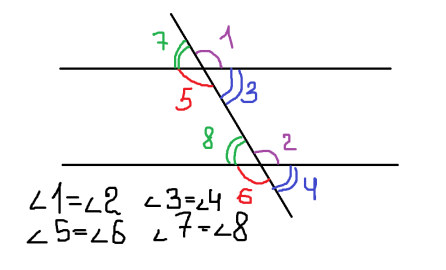
Признаки параллельности двух прямых:
1. Если при пересечении двух прямых третьей накрест лежащие(внутренние или внешние) углы равны, то такие прямые параллельны.
2. Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых третьей сумма односторонних (внутренних или внешних) углов равна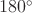 
, то прямые параллельны.
Аксиома параллельных прямых: Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной.
Следствия из аксиомы параллельных прямых:
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
2.Если две прямые параллельны третьей прямой, то они параллельны.
Теоремы об углах, образованных двумя параллельными прямыми и секущей
Если две параллельные прямые пересечены секущей, накрест лежащие углы равны.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Следствие: Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
Расстояние от точки до прямой — это перпендикуляр, проведенный из данной точки к данной прямой. Любая другая прямая, отличная от перпендикуляра, называется наклонной. Любая наклонная больше перпендикуляра. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Тест репетитора по математике для 7 класса. Определения и теоремы
Для успешного освоения геометрии в 7 классе репетитор по математике в той или иной форме отрабатывает с учеником определения, свойства и признаки изучаемых понятий. Предлагаю Вашему вниманию он-лайн вариант проверки уровня теоретических знаний школьника. Он рассчитан для работы с программой учебника Атанасяна. За исключением простейших вопросов на смежные / вертикальные углы и некоторых начальных сведений вводной части учебника тест позволяет репетитору по математике осуществить комплексную проверку всех основных фактов и понятий. Математика 7 класс он-лайн — Определения и теоремы.
Задание 1. Сопоставьте номера признаков равенства треугольников с их сокращенными формулировками.
Ответ:
| 1: …По двум сторонам и углу между нимиПо стороне и двум прилежащим к ней угламПо трем сторонам |
| 2: …По двум сторонам и углу между нимиПо стороне и двум прилежащим к ней угламПо трем сторонам |
| 3: …По двум сторонам и углу между нимиПо стороне и двум прилежащим к ней угламПо трем сторонам |
Задание 2. Как называется отрезок, проведенный из вершины треугольника к потиволежащей стороне и делящий эту сторону пополам?
Выберите ответ:
Задание 3. Как называется отрезок, проведенный из вершины треугольника к противолежащей стороне под прямым углом?
Выберите ответ:
Задание 4. Как называется отрезок, проведенный из вершины треугольника к противолежащей стороне и делящий угол пополам?
Выберите ответ:
Задание 5. Выберите неверное утверждение из списка.
Выберите ответ:
Задание 6. Выберите верное утверждение из списка.
Выберите ответ:
Задание 7. Выбирите неверное утверждение из списка.
Выберите ответ:
Задание 8. Треугольника называется равнобедренным, если у него …
Выберите ответ:
Задание 9. Укажите свойство медианы в равнобедренном треугольнике.
Выберите ответ:
Задание 10. Выберите верное продолжение фразы: в равнобедренном треугольнике…
Выберите ответ:
Задание 11. Дайте название слудующему утверждению: если в треугольнике все углы равны, то он равносторонний.
Выберите ответ:
Задание 12. Верно ли утверждение: в равнобедренном треугольнике медианы, проведенные с боковым стоонам равны?
Выберите ответ:
Задание 13. Как называются углы, изображенные на рисунке?
Выберите ответ:
Задание 14. Укажите верное утверждение.
Выберите ответ:
Задание 15. Укажите верное название для следующего утверждения: если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Выберите ответ:
Задание 16. Как называется сторона BC в прямоугольном треугольнике ABC с прямым углом А?
Выберите ответ:
Задание 17. Укажите верное свойство угла в 30 градусов в прямоугольном треугольнике.
Выберите ответ:
Задание 18. Выберите верное утверждение из списка.
Выберите ответ:
Задание 19. Укажите верно сформулированное неравенство треугольника.
Выберите ответ:
Задание 20. Укажите верно сформулированную теорему в внешнем угле треугольника.
Выберите ответ:
Задание 21. Чему равна сумма внутренних углов в треугольнике?
Выберите ответ:
Вопрос повышенной сложности: Чему равна сумма внешних углов в треугольнике?
Выберите ответ:
Я хочу отправить результаты на почту
Меня зовут
и я хочу отправить свои результаты
на e-mail
Практически все задания расположены в хронологическом порядке их изучения в школьной программе. С удовольствием бы выдержал эту последовательность полностью, но пока, к сожалению, я не могу менять порядок номеров. Это техническая проблема составления теста, которая в скором времени, я надеюсь, будет решена.
Пройдите тест за 7 класс до начала занятий с предполагаемым репетитором по математике. Его результаты помогут быстрее оценить уровень Вашей подготовки к изучению последующей математики (геометрии) в 8 классе.
Методическое указание репетитора:
Отличие программ 7 класса по учебникам Атанасяна и Погорелова не настолько велико, чтобы репетитору по математике полностью отказаться от использования теста в работе с Погореловым. Главным образом эта разница касается раздела «начальные понятия планиметрии» (которая в тесте не представлена) и некоторых мелких тем, не имеющих тесной связи с дальнейшим изложением: «свойство угла в 30 градусов», «соотношение между углами и сторонами в треугольнике», пересечение медиан, биссектрис и высот … Существенную разницу в учебниках составляет материалы 8 — 9 классов. В присутствии преподавателя ученик может работать с данным тестом в ограниченном режиме, отвечая только на выбранные репетитором по математике вопросы. Удачных размышлений над заданиями!
Информация для преподавателей: составляйте и присылайте Ваши собственные тесты по любым темам за 5 — 11 класс (с вариантами ответов) мне на почту. Если в ответах или формулировках заданий имеются формулы, их можно сфотографировать или сканировать. С удовольствие опубликую лучшие работы.
С уважением, Александр Николаевич, репетитор по математике в Москве.