чему равна, свойства, доказательство теоремы

Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.

Трапеция – это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD и BC), две другие – боковыми (на рисунке AB и CD).

Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL).

Свойства средней линии трапеции

1. Длина средней линии равна половине суммы длин ее оснований:

2. Средняя линия всегда параллельна ее основаниям.

Доказательство теоремы о средней линии трапеции

Доказать, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.

Дана трапеция ABCD со средней линией KL. Для доказательства рассматриваемых свойств требуется провести прямую через точки

B и L. На рисунке 2 это прямая BQ. А также продолжить основание AD до пересечения с прямой BQ.

Рассмотрим полученные треугольники LBC и LQD:

1. По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.
2. ∠ BLC = ∠ QLD, так как эти углы вертикальные.
3. ∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD.

Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD, BC=DQ и самое главное — BL=LQ => KL, являющаяся средней линией трапеции ABCD, также является и средней линией треугольника

ABQ. Согласно свойству средней линией треугольника ABQ получаем:

1. KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
2. KL || AD по свойству средней линии треугольника. А так как AD || BC по определению трапеции, то KL || BC.

Для закрепления материала рекомендуем Вам просмотреть видео урок по данной теме:

Понравилась статья, расскажите о ней друзьям:

Скорее всего, Вам будет интересно:

people-ask.ru

math-public:srednyaya_liniya_trapecii [Президентский ФМЛ №239]

Определение

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Свойства средней линии трапеции

Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

Доказательство

Рассмотрим трапецию $ABCD$, в которой проведена средняя линия $MN$.

Докажем, что $MN\parallel AD$ и $MN=\frac{AD+BC}{2}$.

Проведем через точку $M$ прямую $FE$ параллельно $CD$ ($F\in CB, E\in AD$).

Тогда $FCDE$ – параллелограмм ($FC\parallel ED, FE\parallel CD$).

Следовательно, $FE=CD$, $FC=ED$.

Кроме того $\triangle FBM=\triangle AME$, по второму признаку равенства ($\angle 1=\angle 2$, как накрест лежащие, $\angle 3=\angle 4$, как вертикальные, $AM=MB$, так как $M$ – середина).

Следовательно, $FM=ME$.

Тогда $FMNC$ и $MNDE$ — параллелограммы ($FM=ME=ND=NC$ и $FE\parallel CD$).

Следовательно, $MN\parallel BC$.

Кроме того, из равенства треугольников $\triangle FBM=\triangle AME$ следует,что $FB=AE$.

Пусть $FB=AE=x$ и $BC=x$.

Тогда $FC=ED=x+y$.

Следовательно, $MN=x+y$.

Кроме того, $BC+AD=BC+AE+ED=y+x+(x+y)=2x+2y$.

Таким образом, $MN=x+y=\dfrac{BC+AD}{2}$.

Признаки средней линии трапеции

1. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $M$ – середина боковой стороны, и $MN$ параллелен основаниям трапеции, то $MN$ – это средняя линия трапеции.

2. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $MN$ параллелен основанием трапеции и равен их полусумме, то $MN$ – средняя линия трапеции.

Доказательство

Первый пункт теоремы является прямым следствием теоремы Фалеса.

Докажем второй пункт теоремы.

Рассмотрим трапецию $ABCD$, в которой на боковых сторонах $AB$ и $CD$ выбраны точки $M$ и $N$ соответственно, и при этом $MN=\dfrac{AD+BC}{2}$.

Докажем, что тогда $MN$ – средняя линия трапеции $ABCD$.

Предположим противное, то есть $MN$ – не средняя линия данной трапеции.

Если ровно одна из точек $M$ или $N$ является серединой, то по первому пункту теоремы $MN$ – это средняя линия, так как $MN$ параллельна основаниям трапеции.

Пусть точки $M$ и $N$ – не середины боковых сторон.

Тогда пусть $M’N’$ – средняя линия трапеции.

Следовательно, $M’N’=\frac{BC+AD}{2}=MN$ и $MN\parallel BC\parallel MN$.

Но тогда $MNN’M’$ – параллелограмм, и, следовательно, $MM’\parallel NN’$, что противоречит тому, что $ABCD$ – это трапеция.

Следовательно, $MN$ – средняя линия.

Теорема (об отрезке, соединяющем середины диагоналей трапеции)

Отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее оснований.

Доказательство

Рассмотрим трапецию $ABCD$, в которой точки $E$ и $F$ – это середины диагоналей $AC$ и $BD$ соответственно.

Докажем, что $EF=\frac{AD-BC}{2}$.

По теореме Фалеса средняя линия трапеции $MN$ делит диагонали $AC$ и $BD$ пополам, то есть точки $E$ и $F$ лежат на средней линии.

Тогда $ME$ и $FN$ – это средние линии треугольников $\triangle ABC$ и $\triangle DBC$.

Следовательно, если обозначить $BC=2x$, то $ME=FN=x$.

Тогда $EF=\frac{2x+AD}{2}-x-x=\frac{AD-2x}{2}=\frac{AD-BC}{2}$.

math-public/srednyaya_liniya_trapecii.txt · Последние изменения: 2019/10/18 09:01 — labreslav

wiki.sch239.net

Средняя линия трапеции

Понятие средней линии трапеции

Для начала вспомним, какую фигуру называют трапецией.

Определение 1

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.

Определение 2

Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.

Теорема о средней линии трапеции

Теперь введем теорему о средней линии трапеции и докажем её векторным методом.

Теорема 1

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).

Рисунок 1. Средняя линия трапеции

Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.

Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что

С другой стороны

Сложим два последних равенства, получим

Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь

Получаем:

Следовательно

Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.

Теорема доказана.

Примеры задач на понятие средней линии трапеции

Пример 1

Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.

Решение.

Обозначим среднюю линию трапеции через $n$.

Сумма боковых сторон равна

\[15\ см+17\ см=32\ см\]

Следовательно, так как периметр равен $52\ см$, сумма оснований равна

\[52\ см-32\ см=20\ см\]

Значит, по теореме 1, получаем

\[n=\frac{20\ см}{2}=10\ см\]

Ответ: $10\ см$.

Пример 2

Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.

Решение.

Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).

Рисунок 2.

Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем

\[OH=\frac{AD+BC}{2}=\frac{9\ см+5\ см}{2}=7\ см.\]

Значит

\[d=2OH=2\cdot 7\ см=14\ см.\]

Ответ: $14$ см.

Пример 3

Доказать, что средняя линия трапеции проходит через середину произвольной диагонали данной трапеции.

Доказательство.

Пусть нам дана трапеция $ADCD$ со средней линией $MN$. Рассмотрим диагональ $AC$. Обозначим точкой $K$ — точку пересечения средней линии с этой диагональю (Рис. 3).

Рисунок 3.

Докажем, что $AK=KC$.

Так как $MN$ — средняя линия трапеции, то по теореме 1 $MN||BC$. Следовательно, $AM=NB$ и $MK||BC$. Тогда, по теореме о средней линии треугольника, получим что $MK$ — средняя линия треугольника $ABC$. Значит $AK=KC$.

ч. т. д.

spravochnick.ru

Свойство средней линии трапеции — доказательство

1. Главная
2. Геометрия
3. Средняя линия треугольника и трапеции. Свойства биссектрисы, высоты и медианы
4. Свойство средней линии трапеции — доказательство

Средняя линия трапециипараллельна основаниям трапеции и равна их полусумме. Доказательство. вот наша трапеция ABCD, вот её средняя линия — отрезок EF. И надо доказать, что отрезок EF параллелен основаниям трапеции CD и AB и равен половине суммы этих оснований, то есть (a + b) / 2. Чтобы доказать, вершину трапеции — точку B — соединим с концом средней линии — точкой E — и продолжим получившийся отрезок до пересечения с продолжением основания CD в точке G. Получились два треугольника GDE и BAE. В этих треугольниках углы с двумя дужками равны как вертикальные, стороны с галочкой равны по построению (как половинки стороны AD), и углы с кружком равны как накрест лежащие при пересечении параллельных оснований трапеции секущей боковой стороной AD. Значит, треугольники равны по второму признаку. Значит, равны и их соответственные стороны AB и GD — и они обе помечены буквой a. А средняя линия трапеции — отрезок EF — теперь одновременно является средней линией треугольника GBC, и следовательно отрезок EF параллелен основанию GC и равен половине основания GC. А основание GC содержит основание трапеции CD, то есть средняя линия трапеции параллельна основаниям трапеции. И также отрезок GC равен сумме оснований трапеции a+b, и значит средняя линия EF равна половине этого суммы оснований трапеции EF = (a + b) / 2. ЧТД.

blitztest.ru

Подготовка школьников к ЕГЭ и ОГЭ Справочник по математике — Планиметрия

Средние линии треугольника

      Определение. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

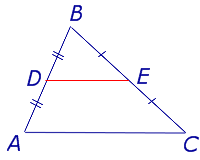
Рис.1

      На рисунке 1 средней линией является отрезок DE.

      Утверждение 1. Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

      Доказательство. Рассмотрим произвольный треугольник   ABC   и обозначим буквой   D   середину стороны   AB   (рис. 2). Проведем через точку   D   до пересечения с прямой   BC   прямую, параллельную прямой   AC .   Обозначим буквой   E   точку пересечения прямых   DE   и   BC .

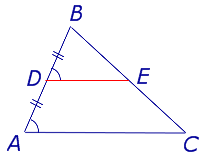
Рис.2

      Поскольку   AD = DB ,   а прямые   AC   и   DE   параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство:   CE = EB .   Отсюда вытекает, что точка   E   является серединой стороны   CB ,   а отрезок   DE   является средней линией треугольника.

      Первую часть утверждения 1 мы доказали.

      Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки   DE , EF   и   FD   (рис.3).

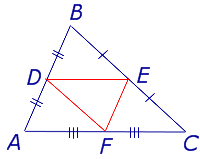
Рис.3

      Поскольку

DE | | FC ,       DF | | EC ,

то четырёхугольник DECF – параллелограммчетырёхугольник DECF – параллелограмм, следовательно,   DE = FC .

      Поскольку

DE | | AF ,       AD | | FE ,

то четырёхугольник   DEFA   – параллелограммчетырёхугольник   DEFA   – параллелограмм, следовательно,   DE = AF .

      Но поскольку   AF = FC ,   то отсюда вытекает равенство

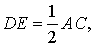
что и требуется доказать.

      Доказательство утверждения 1 закончено.

      Следствие.

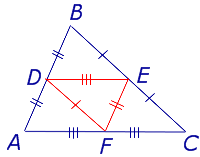
Рис.4

Средняя линия трапеции

      Напомним, что трапециейтрапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

      Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.

      Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

      Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

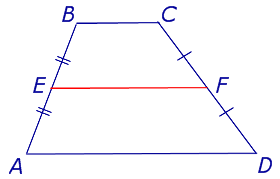
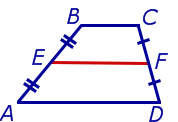
Рис.5

      На рисунке 5 средней линией трапеции является отрезок   EF .

      Утверждение 2. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

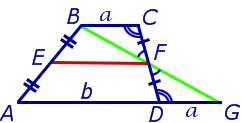
Рис.6

      Доказательство. Проведем через вершину   B   и середину боковой стороны   F   трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых   BF   и   AD   буквой   G .   Рассмотрим треугольники   BCF   и   FDG .   У этих треугольников стороны   CF   и   FD   равны, поскольку точка   F   – середина стороны   CD .   Углы   BCF   и   FDG   равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых   BC   и   AD   с секущей   CD .   Углы   BFC   и   DFG   равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники   BCF   и   FDG   равны. Из равенства треугольников   BCF   и   FDG   следует равенство отрезков   BF   и   FG ,   откуда вытекает, что отрезок   EF   является средней линией треугольника   ABG .   Поэтому

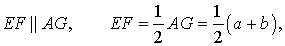
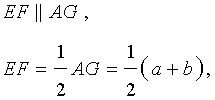
что и требовалось доказать.

      Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

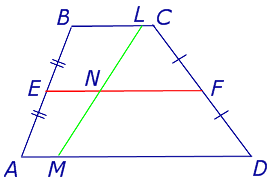
Рис.7

      Решение. Пусть   ABCD   – трапеция,   EF   –  её средняя линия,   LM   – указанный отрезок (рис.7). Поскольку   AE = EB ,   то, в силу теоремы Фалеса, выполнено равенство:   LN = NM ,   что и требовалось доказать.

      Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

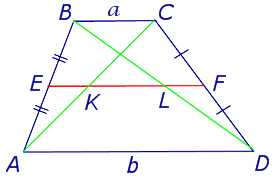
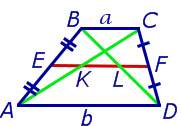
Рис.8

      Решение. Пусть   ABCD   – трапеция,   EF   – её средняя линия,   KL   – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка   K   – середина отрезка   AC ,   а точка   L   – середина отрезка   BD .   Поэтому отрезок   EK   – средняя линия треугольника   BAC ,   а отрезок   EL   – средняя линия треугольника   ABD .   В силу утверждения 1 выполнены равенства:

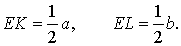
      Следовательно,

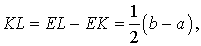
что и требовалось доказать.

      Утверждение 3. Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

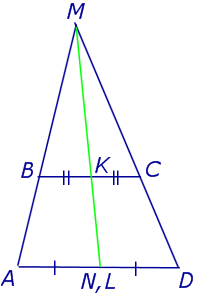
Рис.9

      Доказательство. Пусть   K   и   L   – середины оснований   BC   и   AD   трапеции   ABCD   соответственно (рис.9). Обозначим буквой   M   точку пересечения боковых сторон   AB   и   CD .   Проведем через точки   M   и   K   прямую и обозначим точку пересечения этой прямой с основанием   AD   символом   N .   Докажем, что точки   N   и   L   совпадают. Для этого заметим, что треугольник   BMK   подобен треугольнику   AMN .   Следовательно, выполнено равенство:

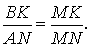
      Заметим также, что треугольник   KMC   подобен треугольнику   NMD .   Поэтому

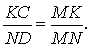
      Из этих соотношений получаем:

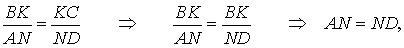
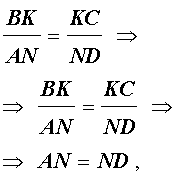
откуда вытекает, что точки   N   и   L   совпадают. Доказательство завершено.

      Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

      Утверждение 4. Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

      Следствие. Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника. Теорема Вариньона

      Определение. Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

      Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

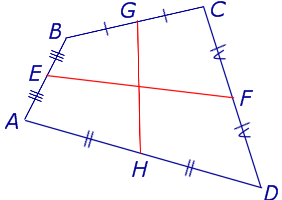
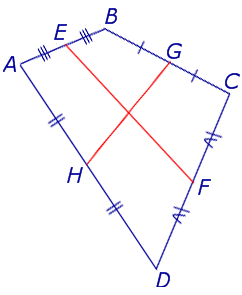
Рис.10

      На рисунке 10 средние линии – это отрезки   EF   и   GH .

      Замечание 1. Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

Рис.11

      На рисунке 11 изображен «пространственный четырёхугольник»   ABCD ,   средними линиями которого являются отрезки   EF   и   GH .

      Замечание 2. Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

      Замечание 3. В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

      Теорема Вариньона. Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограммапараллелограмма.

      Доказательство. Рассмотрим плоский четырёхугольник   ABCD ,   изображенный на рисунке 12. Точки   E, G, F, H   – середины сторон, отрезок   AC   – диагональ четырёхугольника.

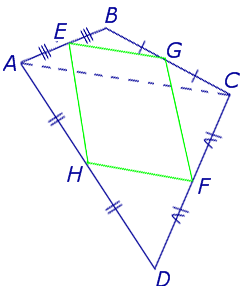
Рис.12

      Поскольку отрезок   EG   – средняя линия треугольника   ABC ,   то отрезок   EG   параллелен диагонали   AC   и равен её половине. Поскольку отрезок   FH   – средняя линия треугольника   CDA ,   то отрезок   FH   параллелен диагонали   AC   и равен её половине. Таким образом, в четырёхугольнике   EGFH   противоположные стороны   EG   и   FH   равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник   EGFH   – параллелограмм, что и требовалось доказать.

      Замечание 4 . В случае «пространственного четырёхугольника»   ABCD   доказательство остаётся тем же (рис. 13).

Рис.13

      Поскольку диагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополам, то справедливо следующее утверждение, непосредственно вытекающее из теоремы Вариньона.

      Утверждение 5. Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

Рис.14

      Утверждение 6. Рассмотрим произвольный плоский или «пространственный» четырёхугольник   ABCD ,   у которого отрезок   EF   является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

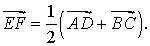
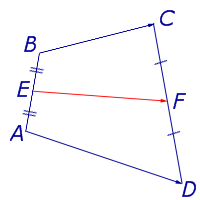
Рис.15

      Доказательство. Рассмотрим в пространстве или на плоскости произвольную декартову систему координат с началом в некоторой точке   O   (рис. 16).

Рис.16

      В соответствии со свойствами векторов справедливы следующие равенства:

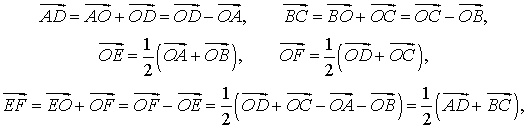
что и требовалось доказать.

      Следствие. Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

      Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапециейтрапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

      Тетраэдром называют произвольную треугольную пирамиду (рис.17).

Рис.17

      У каждого тетраэдра имеется   4   вершины,   4   грани и   6   рёбер, причем все рёбра делятся на   3   пары непересекающихся рёбер. На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых.

      Определение. Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

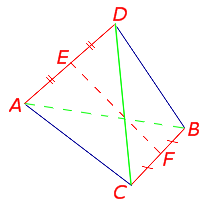
Рис.18

      У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок   EF   является одной из средних линий тетраэдра.

      Утверждение 7. Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

      Доказательство. Выберем какую-нибудь среднюю линию тетраэдра, например,   EF   и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка   EF .   Для этого рассмотрим, например, среднюю линию   GH ,   соединяющую середины рёбер   AC   и   BD ,   и соединим отрезками точки   E, H, F, G   (рис.19).

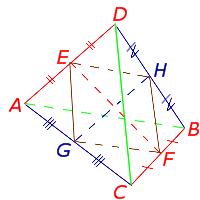
Рис.19

      Заметим, что отрезок   EH   является средней линией треугольника   ADB ,   поэтому

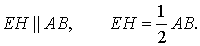
      Отрезок GF является средней линией треугольника   ACB ,   поэтому

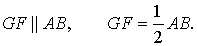
      Отсюда вытекает, что отрезки   EH   и   GF   равны и параллельны, следовательно, четырёхугольник   EHFG   – параллелограммследовательно, четырёхугольник   EHFG   – параллелограммследовательно, четырёхугольник   EHFG   – параллелограмм. Поскольку средние линии тетраэдра   EF   и   GH   являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.

      Определение. Точку пересечения средних линий тетраэдра называют центроидом тетраэдра.

      Утверждение 8. Рассмотрим в пространстве декартову систему координат с началом в точке   O   и произвольный тетраэдр   ABCD .   Если обозначить буквой   M   центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

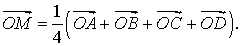
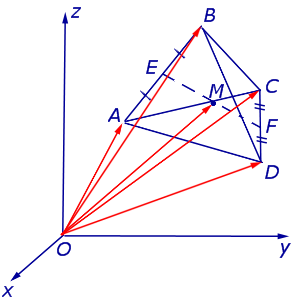
Рис.20

      Доказательство. По свойствам векторов

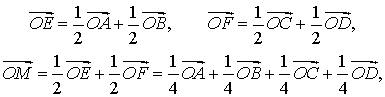
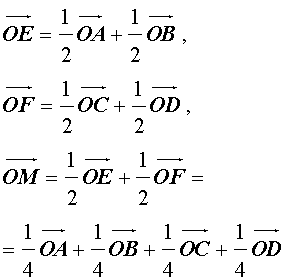
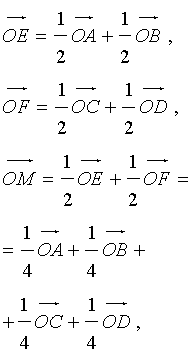
что и требовалось доказать.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Средняя линия трапеции | Треугольники

Что такое средняя линия трапеции? Какими свойствами она обладает?

Определение

Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.

ABCD — трапеция,

AD ∥ BC,

M — середина AB,

N — середина CD,

MN — средняя линия трапеции ABCD.

Свойства средней линии трапеции

1) Средняя линия трапеции параллельна основаниям.

2) Средняя линия трапеции равна полусумме оснований.

В трапеции ABCD (AD ∥ BC)

   

   

Задача 1.

Основания трапеции относятся как 4:7, а средняя линия равна 55 см. Найти основания трапеции.

Дано: ABCD — трапеция,

AD ∥ BC, MN- средняя линия трапеции,

MN=55 см, BC:AD=4:7.

Найти: AD, BC.

Решение:

Пусть k — коэффициент пропорциональности.

Тогда BC=4k см, AD=7k см.

По свойству средней линии трапеции,

   

Составляем уравнение:

   

   

   

Отсюда BC=4∙10=40 см, AD=7∙10=70 см.

Ответ: 40 см, 70 см.

Задача 2.

Средняя линия трапеции равна 15 см, а одно из оснований на 6 см больше другого. Найти основания трапеции.

Дано: ABCD — трапеция,

AD ∥ BC, MN- средняя линия трапеции,

MN=15 см, AD на 6 см больше BC.

Найти: AD, BC.

Решение:

Пусть BC=x см, тогда AD=(x+6) см.

Так как средняя линия трапеции равна полусумме оснований,

   

Составим уравнение и решим его:

   

   

   

Значит, BC=12 см, AD=12+6=18 см.

Ответ:12 см, 18 см.

 

www.treugolniki.ru

Средняя линия трапеции

Четырёхугольник, у которого две противоположные стороны параллельны, а другие две — не параллельны, называется трапецией.

На чертеже 252 у четырёхугольника АВDС АВ || СD, AC ||BD. АВDС — трапеция.

Параллельные стороны трапеции называются её основаниями; АВ и СD — основания трапеции. Остальные две стороны называются боковыми сторонами трапеции; АС и ВD — боковые стороны трапеции.

Если боковые стороны равны, то трапеция называется равнобедренной.

Трапеция АВОМ равнобедренная, так как АМ=ВО (рис. 253).

Трапеция, у которой одна из боковых сторон перпендикулярна к основанию, называется прямоугольной (рис. 254).

Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.

Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.

Дано: ОС — средняя линия трапеции АВDК, т. е. ОК = ОА и ВС = СD (рис. 255).

Надо доказать:

1) ОС || КD и ОС || АВ;

2) OC = \(\frac{KD + AB}{2}\)

Доказательство. Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.

В треугольниках АBС и DСЕ:

ВС = СD — по условию;

∠1 = ∠2, как вертикальные,

∠4 = ∠3, как внутренние накрест лежащие при параллельных АВ и KЕ и секущей ВD. Следовательно, \(\Delta\)АBС = \(\Delta\)DСЕ.

Отсюда АС = СЕ, т.е. ОС является средней линией треугольника КАЕ. Следовательно:

1) ОС || КЕ и, значит, ОС || КD и ОС || AВ;

2) OC = \(\frac{KE}{2} = \frac{KD + DE}{2}\), но DЕ = АВ (из равенства треугольников АBС и DСЕ), поэтому отрезок DЕ можно заменить равным ему отрезком АВ. Тогда получим:

OC = \(\frac{KD + AB}{2}\)

Теорема доказана.

Свойства трапеции, которые часто используются при решении задач:

1. Диагонали трапеции разбивают её начетыре треугольника с общей вершиной. Площади треугольников, прилежащие к боковым сторонам, равны.



2. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).



3. В равнобокой трапеции углы при основании равны.



4. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции



5. В равнобокой трапеции диагонали равны.



6. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой — их полусумме.



7. Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.


8. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.



9. Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.


10. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.


11. Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.

razdupli.ru